2. 中国石油勘探开发研究院廊坊分院,河北廊坊065007
3. 中国科学技术大学, 合肥230027
页岩气是从页岩中开采出来的天然气,以吸附态、游离态和溶解态等形式赋存在地层中,其主要成分是甲烷,另有少量的乙烷、二 氧化碳、丙烷和丁烷等[1, 2, 3]. 由于页岩气的成功开发,美国在2014年从能源进口国变为能源出口国. 我国高度重视页岩气开发,2010年完钻第一口页岩气井,至2013年7月已完钻70多口页岩气井[4, 5].
页岩气储层孔径一般为5~200 nm[2, 6],其渗透率在几十到几百纳达西间[7]. 这时壁面与气体分子的相互碰撞对流动的影响已不能忽略. 因而,在页岩气的流动规律中,除连续流外,还需考虑滑移流、过渡流、克努森扩散等. 其次,页岩的天然微裂缝发育不完善,还不能形成有效的流动通道,只有通过水平井多段压裂来提高接触面积,提高流动能力, 才能达到经济规模开采规模. 另外,页岩中气主要以自由态和吸附态的形式赋存,少量溶解在有机质中,以溶解态的形式赋存,极少部分溶解在油和水中[1].
这些给页岩的实验、数据解释、地层参数评价等都带来了全新的挑战. 首先是实验及其数据解释的挑战. 由于极低的渗透率使得 测量结果极易受到设备精度与各种噪音的干扰,同一岩心在不同实验室测量的结果会相差几个数量级[8]. 在进行吸附实验时,气体很难在短时间内进入页岩基岩内部,从而使测量的吸附量值偏小. 目前所报道的实验所测的页岩气吸附量在总储量中所占的比例偏低,基本处于下限,例如Ambrose等[9]所测的吸附气仅占总 储量的23%. 然而,学术界普遍认为,页岩气的吸附量可达总储量的80%. 例如,张金川等[3]认为吸附所占的气体含量在20~80%间. Nelson[2]认为吸附气体含量为20~85%.
由于气体在页岩流动时,多种流动机理并存,不同的流动机理都会对页岩的流动能力产生影响,因受到所考虑的流动机理的异 同、是否考虑吸附效应、应力敏感等影响,从而不同模型下的解释结果有很大的差异. Civian等[10]首先研究了视渗透率公式,然后将Langmuir吸附等引入到页岩气流动方程中[11],使用数值解对测试数据进行了解释. 2012年,Civan等[12]进行了模型改进,给出了更为严格的解析解,讨论了改进模型对解释结果的影响. 视渗透率模型是页岩气流动机理研究的热点之一,很多学者对此进行了研究. Javadpour[13]研究了滑脱效应及Knudsen扩散效应下的视渗透率公式. Darabi等[14]研究了克努森扩散效应对流动的影响. Niu等[15]研究了气体分子的固壁效应对流动的影响,并建立了新视渗透率公式. Zhang等[16]研究了表面扩散对流动的影响,并认为表面扩散在低压力情形下对流动贡献可达20%以上.
压力数据解释方法是传统的对地层与井筒参数进行解释与评价的方法. Brown等[17]研究了三线性流下的页岩压力响应 特征,Guo等[18]研究了双孔介质下的页岩气试井曲线特征. 然而,由于页岩气开发中的井底压力难以测量、现有解释方法的不适用性,更多的学者研究了生产数据分析方法. Hasan等[19]提出了两种基于解析模型的生产数据分析方法. Medeiros等[20]研究了半解析半数值和全数值的方法. Clarkson等[21]研究了考虑动态滑脱效应、Langmuir吸附、压敏性等情形下的生产数据分析方法. Moridis等[22]通过复杂数学模型,研究了温度等对页岩气流动的影响. 基于PEBI网格,Li 等[23]研究了吸附量对井底压力曲线转折角度的影响,渗透率对转折位置的影响. Freeman等[24]用能模拟传质运动的尘-气(Dusty-gas)模型研究了页岩气的组分变化规律. Cipolla等[25]则报道了双渗模型下的吸附、应力敏感等对页岩气产能的影响,但没有给出数学模型. Zhang 等[26]研究气体组分比例的变化规律. Li等[27]进一步研究了组分导数与吸附量间的关系.
本文在文献[26, 27]的基础上深入研究气体组分比例的变化规律,研究组分比例变化、组分比例导数在不同吸附量、不同渗 透率、不同孔隙度下的变化规律.
1 流动方程 1.1 组分模型对网格j,气体中第i个组分的质量守恒方程可表示为
| $\begin{array}{l} \sum\limits_l {} {(T{\lambda _{\rm{g}}}{\rho _{\rm{g}}}{y_i})_{lj}}({p_l} - {p_j}) = \\ \frac{\partial }{{\partial t}}{(V\phi {\rho _{\rm{g}}}{y_i} + V{\rho _{\rm{s}}}{V_{{\rm{ads}},i}}{\rho _{{\rm{g}},{\rm{std}}}})_j} + {\rho _{\rm{g}}}{y_i}{q_{\rm{g}}}{\mkern 1mu} ,\\ i = 1,2,\cdots ,m \end{array}$ | (1) |
视渗透率可写为如下形式[10]
$k_i = k_0 (1 + \alpha K_{n,i} ) \Big (1 + \dfrac{4K_{n,i} }{1 + K_{n,i} } \Big )$
其中$\alpha = \frac{{128}}{{15{\pi ^2}}}{\tan ^{ - 1}}\left( {4K_{n,i}^{0.4}} \right){\rm{,}}{K_{n,i}}$为组分i的克努森数.方程(1)的右边的气体吸附项中的Vads,i是组分i在当前压力下的吸附量,由多组分Langmuir等温吸附公式描述. 气体组分i的吸附体积可表示为
| ${V_{{\rm{ads}},i}} = {V_{{\rm{L}},i}}\frac{{{y_i}P}}{{{P_{{\rm{L}},i}}(1 + {\rm{ }}\sum\limits_{j = 1}^n {{y_j}} \frac{P}{{{P_{{\rm{L}},j}}}})}}{\mkern 1mu} ,\;\;i = 1,2, \cdots ,n{\rm{ }}$ | (2) |
| ${V_{{\rm{ads}}}} = {\rm{ }}\sum\limits_{i = 1}^n {{V_{{\rm{ads}},i}}} = {\rm{ }}\sum\limits_{i = 1}^n {{V_{{\rm{L}},j}}} \frac{{{y_i}P}}{{{P_{{\rm{L}},i}}(1 + {\rm{ }}\sum\limits_{j = 1}^n {{y_j}} \frac{P}{{{P_{{\rm{L}},j}}}})}}$ | (3) |
方程(1)右边的第2项为井项,表示气体生产或者注入的量
| ${q_{\rm{g}}} = \frac{{2\pi kh}}{{{\mu _{\rm{g}}}\left[ {\ln ({r_{\rm{e}}}/{r_{\rm{w}}}) + S} \right]}}({p_l} - {p_{{\rm{wf}}}})$ | (4) |
对定产量井,考虑井储时,还需附加方程
| $\frac{{2\pi kh}}{{{\mu _{\rm{g}}}\left[ {\ln ({r_{\rm{e}}}/{r_{\rm{w}}}) + S} \right]}}({p_l} - {p_{{\rm{wf}}}}) - \frac{C}{{\Delta t}}(p_{{\rm{wf}}}^{n + 1} - p_{{\rm{wf}}}^n) = Q$ | (5) |
非结构PEBI网格(perpendicular bisection) 是一种局部正交网格,其任意两个相邻网格的交界面垂直平分相应网格节点的连线. Heinemann 等首次将其应用到油藏模拟中[29]. 研究表明PEBI 网格具有易于描述油藏复杂边界、近井附近流动、描述水平井等优点. 由于PEBI 网格具有非结构网格的灵活性,最终的离散方程与笛卡尔网格有限差分格式相似,因而PEBI 网格兼有笛卡尔网格的规则性与有限元网格的灵活性,并在数值试井中得到了广泛的应用[28].
2.1 组分模型利用有限体积法对组分质量守恒方程进行离散,然后利用守恒格式对其进行线性化,最终得到线性方程组,即可采用牛顿迭代法进行求解.
这里以累积项$\dfrac{\partial }{\partial t}\left( {V\phi \rho _{\rm g} y_i } \right)$为例,给出离散与线性化过程. 累积项的离散格式为
| $\dfrac{\partial }{\partial t}\left( {V\phi \rho _{\rm g} y_i } \right) = V\dfrac{(\phi \rho _{\rm g} y_i )^{n + 1} - (\phi \rho _{\rm g} y_i )^n}{\Delta t}$ | (6) |
| $\rho _{\rm g} \phi )^n\delta y_i + y_i^{n + 1} \rho _{\rm g}^n\delta \phi + (y_i \phi )^{n + 1}\delta \rho _{\rm g}$ | (7) |
| $\delta \phi = \phi ^{n + 1} - \phi ^n = \left( {\dfrac{\partial \phi }{\partial p}} \right)^n\delta p$ | (8) |
| $\begin{array}{l} \delta \rho = {\left( {\frac{{\partial \rho }}{{\partial p}}} \right)^n}\delta p + \sum\limits_{i = 1}^m {{{\left( {\frac{{\partial \rho }}{{\partial {y_i}}}} \right)}^n}} \delta {y_i} = \\ \qquad {\left( {\frac{{\partial \rho }}{{\partial p}}} \right)^n}\delta p + \sum\limits_{i = 1}^m {{{\left( {\frac{{\partial \rho }}{{\partial {y_i}}} - \frac{{\partial \rho }}{{\partial {y_m}}}} \right)}^n}} \delta {y_i} \end{array}$ | (9) |
| $\frac{{\partial \rho }}{{\partial p}} = \frac{\rho }{p} - \frac{\rho }{Z}\frac{{\partial Z}}{{\partial p}},\frac{{\partial \rho }}{{\partial {y_i}}} = - \frac{\rho }{Z}\frac{{\partial Z}}{{\partial {y_i}}}$ | (10) |
| $\begin{array}{l} \frac{V}{{\Delta t}}\{ {(\phi \rho )^n}\delta {y_i} + [{({y_i}\phi )^v}{(\frac{{\partial \rho }}{{\partial p}})^n} + y_i^v{\rho ^n}{\left( {\frac{{\partial \phi }}{{\partial p}}} \right)^n}]\delta p + \\ \qquad {({y_i}\phi )^v}\sum\limits_{i = 1}^{m - 1} {{{\left( {\frac{{\partial \rho }}{{\partial {y_i}}} - \frac{{\partial \rho }}{{\partial {y_m}}}} \right)}^n}} \delta {y_i}\} \end{array}$ | (11) |
组分模型求解的更多内容可见文献[29]. 由于本文的组分模型不涉及相变,因而求解比一般的组分模型简单.
3 组分变化及组分导数为更好地描述组分比例变化规律,须定义组分比例变化与组分比例导数. 设气体组分随时间变化的序列为tj,cj, j= 0,1,2,... ,m. {t0,c0} 为初始时刻下的组分比例,即初始时间t0下的某气体的组分比例为c0,cj为时间tj下的组分比例. 组分比例变化dcj与组分比例导数dc'分别定义为
$\left\{ {_{{\rm{d}}c' = = \left| {\frac{{{\rm{d}}c}}{{{\rm{d}}t}}} \right|t}^{{\rm{d}}{c_j} = \left| {{c_j} - {c_0}} \right|}} \right.$
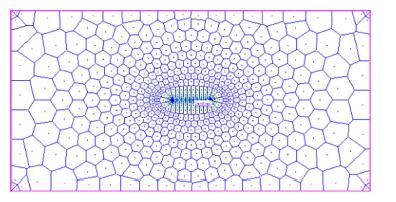
4 计算与分析气藏中央有一口垂直裂缝井,其位置分布及气藏网格划分如图 1所示,相关参数如表 1所示.
|
图 1 垂直裂缝井在页岩气藏中的位置及网格的分布 Fig. 1 Position of vertical fractured well and its gridding |
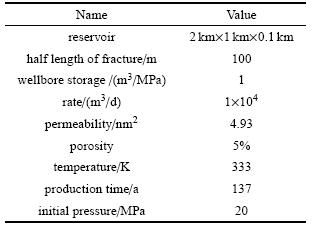
| 表 1 页岩气藏参数 Table 1 Shale-gas reservoir parameters |
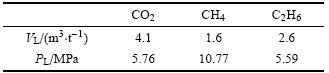
设气藏中初始气体组分为CO2,CH4和C2H6,其含量分别为2%, 80%和18%,吸附常数如表 2所示.
4.1 吸附能力对组分比例的影响根据其Langmuir吸附参数推算得知,吸附气的含量仅约占气体总储量的23%左右. 表 2中的吸附气占总气体储量约23%,属于低吸附能力气藏. 为研究不同吸附量下的气体组分比例变化规律,将表 2中的吸附体积扩大5倍和10倍,分别记为5VL和10VL. 将表 2中的吸附体积记为1VL. 下面将1VL,5VL和10VL分别称为低吸附、中吸附和高吸附.
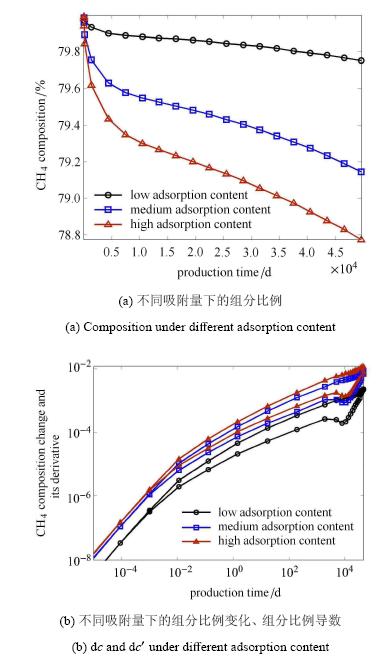
图 2给出了低吸附、中吸附、高吸附的组分变化规律. 图 2(a)表明,吸附量越大,生产井中的甲烷组分比例下降越快. 这表明组分比例的下降的速度反映地层吸附量的大小. 图 2(b)表明,不同吸附量下的组分曲线(组分比例变化曲线dcj 及其导数曲线dc'明显受吸附量的影响. 吸附量越大,dcj与dc'的曲线越高,而且吸附量影响曲线dcj与dc'的整体上下位置. 因而,dcj与dc'的曲线更能清晰反映吸附量的大小.
|
图 2 吸附量(低中高吸附量分别为1VL,5VL和10VL)对组分的影响 Fig. 2 Effect of adsorption content on composition (low,medium and high adsorption content are 1VL,5VL and 10V,respectively) |
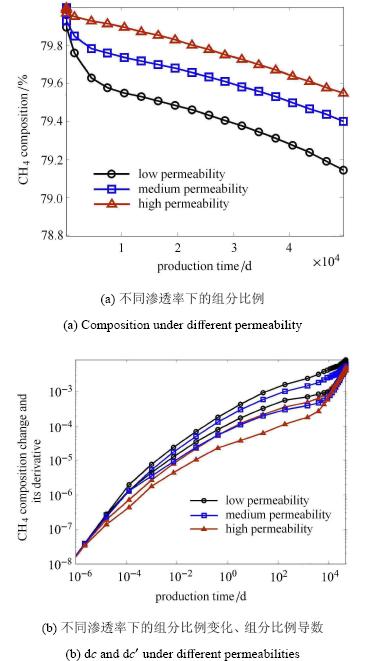
图 3给出了中吸附量(5VL)下的渗透率分别为5 × 10-18 m2,1 × 10-17 m2 和 5 × 10-17 m2时,甲烷组分比例随时间的变化规律. 图 3(a)表明, 在生产早期(100 d内)渗透率越小,甲烷组分比例下降越快,但在中后期不同渗透率下的组分比例下降速度相当. 这是因为当定产量生产时,渗透率越低,井周围压力下降就越快,导致解吸附的气体就越多. 由于解吸附气体的组分比例不同于自由气的组分比例,从而导致组分比例变化快. 随着生产时间的增大,在生产中后期(10 000 d后),吸附气对组分比例的影响趋于稳定,视渗透率对组分变化的影 响逐渐占主导地位. 不同组分的视渗透率差异导致组分比例的差异. 虽然压力对视渗透率的差异有影响,但不同压力下的视渗透率差异仍较为接近,从而导致生产中后期的组分比例趋势十 分接近,曲线基本平行.
|
图 3 渗透率(低中高渗分别为5 × 10-18 m2,1 × 10-17 m2和5 × 1017 m2)对组分比例影响 Fig. 3 Effect of permeability on composition (low,medium and high permeability are 5 × 10-18 m2,1 × 10-17 m2 and 5 × 1017 m2,respectively) |
图 3(b)给出的是不同渗透率下的组分比例变化及其导数曲线. 在生产初期,dcj及dc'的曲线重合. 随着时间的推移,不同渗透率下的dcj及dc'曲线开始分离. 渗透率越大,dcj及dc'的曲线位置越低. 这说明,渗透率越大,组分比例变化值越小.
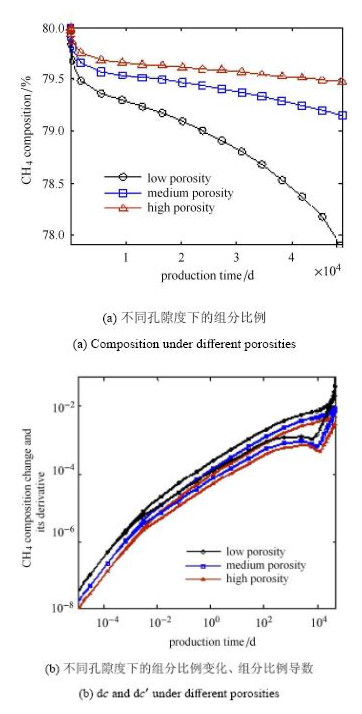
4.3 孔隙度对组分比例的影响图 4给出了中吸附量(5VL)下的孔隙度分别为0.3,0.5和0.7时甲烷组分比例随时间的变化规律. 图 4(a)表明,在整个生产期间,孔隙度越小,甲烷组分比例下降越快. 这是因为孔隙度越小,自由气所占比例就越小,吸附气的影响就越大. 在40 000 d以后,相对中高孔隙度,低孔隙度(\phi = 0.3)下的组分比例下降增速更快. 这是因为低孔隙度气藏的压力已很低,不同气体的视渗透率差异更大,视渗透率的差异导致甲烷气体的组分比例下降更快.
|
图 4 孔隙度(低中高孔隙度分别为3%,5%和7%)对组分比例影响 Fig. 4 Effect of porosity on composition (low,medium and high permeability are 3%,5% and 7%,respectively |
在开井初期,吸附气与孔隙度对甲烷组分比例的影响规律不相同. 在开井初期,吸附量对甲烷比例的影响更大,孔隙度对 甲烷比例的影响要小些. 这是因为,吸附量越大,压力降低所解吸附的气体就更多,从而有影响更大. 而孔隙度主要影响自由气占总储量的比例,由于自由气流动快,所以孔隙度的影响相对会弱些.
图 4(b)给出了不同孔隙度下的组分比例变化及其导数曲线. 由于孔隙度的变化会影响吸附气在总储量中的比例,因而,孔隙 度与吸附量对dcj及dc'的影响类似,即不同孔隙度下的dcj及dc'曲线开始分离. 孔隙度越大,dcj及dc'的曲线位置越低.
5 结 论本文首先给出了描述页岩气组分变化的组分模型,然后基于数值解进行了页岩气组分变化规律研究. 研究表明,吸附气与孔隙度对页岩气组分的影响较为类似,二者都可使组分比例变化及其导数曲线分离. 吸附量与孔隙度的大小决定组分比例的变化值及组分比例导数的曲线的上下位置,但二者在生产初期对组分比例影响有异. 渗透率影响组分比例初期变化规律,但在后期,不同渗透率对瞬态组分比例规律的影响较为类似. 吸附量、孔隙度、渗透率影响组分比例的变化规律,从组分比例中可解释出吸附量、孔隙度、渗透率. 因而,本文研究有望提供了一种进行页岩地层参数评价的新方法.
由于页岩气井的组分在线测量需要研发相关测试设备,我国页岩气开发刚处于起步阶段,现在还无法获得实际的页岩气井的组分比例随时间变化的数据,因而本文还未能基于实测数据进行地层参数的评价解释工作.
| [1] | Curtis JB. Fractured shale-gas systems. AAPG bulletin, 2002, 86(11): 1921-1938 |
| [2] | Nelson PH. Pore-throat sizes in sandstones, tight sandstones, and shales. AAPG bulletin, 2009, 93(3): 329-340 |
| [3] | 张金川,边瑞康,荆铁亚等. 页岩气理论研究的基础意义. 地质通报, 2011, 30(2): 318-323 (Zhang Jinchuan, Bian Ruikang, Jing Tieya, et al. Fundamental significance of gas shale theoretical research. Geological Bulletin of China, 2011, 30(2):318-323 (in Chinese)) |
| [4] | 王 南,裴 玲,雷丹凤等. 中国非常规天然气资源分布及开发现状. 油气地质与采收率, 2015, 22(1): 26-31 (Wang Nan,Pei Ling,Lei Danfeng,et al. Analysis of unconventional gas resources distribution and development status in China. Petroleum Geology and Recovery Efficiency, 2015, 22(1): 26-31 (in Chinese)) |
| [5] | 董大忠,邹才能,杨桦等. 中国页岩气勘探开发进展与发展前景. 石油学报,2012, 33(s1): 107-114 (Dong Dazhong, Zou Caineng, Yang Hua, et al. Progress and prospects of shale gas exploration and development in China. Acta Petrolei Sinica, 2012, 33(s1): 107-114 (in Chinese)) |
| [6] | 邹才能, 朱如凯,吴松涛等. 常规与非常规油气聚集类型, 特征, 机理及展望------以中国致密油和致密气为例. 石油学报, 2012. 33(2): 173-187 (Zou Caineng, Zhu Rukai, Wu Songtao, et al. Types, Characteristics, genesis and prospects of conventional and unconventional hydrocarbon accumulations: taking tight oil and tight gas in China as an instance. Acta Petrolei Sinica, 2012, 33(2): 173-187 (in Chinese)) |
| [7] | Luffel D, Hopkins C, Schettler Jr P. Matrix permeability measurement of gas productive shales. In: SPE Annual Technical Conference and Exhibition. 1993. Society of Petroleum Engineers. |
| [8] | Passey QR, Bohacs KM, Esch WL, et al. From oil-prone source rock to gas-producing shale reservoir--geologic and petrophysical characterization of unconventional shale-gas reservoirs. Beijing, China, June, 2010. 8 |
| [9] | Ambrose R, Hartman RC, Akkutlu IY. Multi-component sorbed phase considerations for Shale Gas-in-place Calculations, SPE Production and Operations Symposium, 2011 |
| [10] | Civan F. Effective correlation of apparent gas permeability in tight porous media. Transport in Porous Media, 2010, 82(2): 375-384 |
| [11] | Civan F, Rai CS, Sondergeld CH. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms. Transp Porous Med, 2011, 86: 925-944 |
| [12] | Civan F, Rai CS, Sondergeld CH. Determining shale permeability to gas by simultaneous analysis of various pressure tests. SPE Journal, 2012, 17(3): 717-726 |
| [13] | Javadpour F. Nanopores and apparent permeability of gas flow in mudrocks (shales and siltstone). Journal of Canadian Petroleum Technology, 2009, 48(8): 16-21 |
| [14] | Darabi H, Ettehad A, Javadpour F, et al. Gas flow in ultra-tight shale strata. J Fluid Mech, 2012, 710: 641-658 |
| [15] | Niu C, Hao YZ, Li DL, et al. 2nd-order gas permeability correlation of shale during slip-flow. SPEJ-168226-PA, 2014, 19(5): 786-792 |
| [16] | Zhang LJ, Li DL, Lu DT, et al. A new formulation of apparent permeability for gas transport in shale. Journal of Natural Gas Science and Engineering, 2015, 23: 221-226 |
| [17] | Brown M, Ozkan E, Raghavan R, et al. Practical solutions for pressure-transient responses of fractured horizontal wells in unconventional shale reservoirs. SPE Reservoir Evaluation & Engineering, 2011, 14(6): 663-676 |
| [18] | Guo JJ, Zhang LH, Wang HT, et al. Pressure transient analysis for multi-stage fractured horizontalwells in shale gas reservoirs. Transport Porous Med, 2012, 93: 635-653 |
| [19] | Hasan AA, Anas MA, Wattenbarger RA. Application of linear flow analysis to shale gas wells-field cases. Paper SPE 130370 presented at the SPE Unconventional Gas Conference, Pittsburgh, Pennsylvania, 23--25 February 2010 |
| [20] | Medeiros F, Ozkan E, Kazemi H. A semianalytical approach to model pressure-transients in heterogeneous reservoirs. SPE Reservoir Evaluation & Engineering, 2010, 13 (2): 341-358 |
| [21] | Clarkson C, Nobakht M, Kaviani D, et al. Production analysis of tight-gas and shale-gas reservoirs using the dynamic-slippage concept. SPE Journal, 2012, 17 (1): 230-242 |
| [22] | Moridis GJ, Blasingame TA, Freeman CM. Analysis of mechanisms of flow in fractured tight-gas and shale-gas reservoirs. SPE 139250-MS, 2010 |
| [23] | Li DL, Xu CY, Wang John YL, et al. Effect of Knudsen diffusion and Langmuir adsorption on pressure transient response in shale gas reservoir. J Petrol Science and Engineering, 2014, 124: 146-154 |
| [24] | Freeman C, Moridis G, Blasingame T. A numerical study of microscale flow behavior in tight gas and shale gas reservoir systems. Transport in Porous Media, 2011, 90(1): 253-268 |
| [25] | Cipolla CL, Lolon EP, Erdle JC, et al. Reservoir modeling in shale-gas reservoirs. SPE Res Eval & Eng, 2010, 13 (4): 638-653 |
| [26] | Zhang LJ, Li DL, Li L, et al. Development of a new compositional model with multi-component sorption isotherm and slip flow in tight gas reservoirs. Journal of Natural Gas Science and Engineering, 2014, 21: 1061-1072 |
| [27] | Li DL, Zhang LJ, Lu DT. Effect of distinguishing apparent permeability on flowing gas composition, composition change and composition derivative in tight- and shale-gas reservoir. J Petrol Science and Engineering, 2015, 128: 107-114 |
| [28] | 李道伦,查文舒. 数值试井理论与方法. 北京: 石油工业出版社,2013 (Li Daolun, Cha Wenshu. Numerical Well Test Theory and Method. Beijing: Petroleum Industry Press, 2013 (in Chinese)) |
| [29] | Heinemann ZE, Brand CW. Gridding techniques in reservoir simulation. In: Proceedings First and Second International Forum on Reservoir Simulation, Alpbach, Austria, September 12-16, 1988: 339-426 |
| [30] | Cao H. Development of Technique for General Purpose Simulators. [PhD Thesis]. Stanford: Stanford University, 2002 |
2. RIPED-LangFang, Hebei Langfang 065007, China
3. University of Science and Technology of China, Hefei 230027, China
 2015, Vol. 47
2015, Vol. 47