引 言
海姆(Geim)和诺沃消洛夫(Novoselov)
[1]根据石墨层间易于相对滑移的特性采用机械剥离的方法首次在实验室条件下制备了稳定存在的单层石墨烯.
基于二维纳米 结构的纳机电器件有着广阔的应用前景.
微纳尺度下结构的力学行为表现出的尺度效应变是不可忽视[2, 3, 4, 5, 6].
基于原子理论的离散模型计算规模过于庞大,能计算的空间尺寸与时间尺度都非常有限.
连续介质模型在研究规模较大的纳米结构时更有优势.
但是经典连续介质力学模型由于本构关系中缺少表征材料内部特征长度尺度参数,在描述微纳尺度范围内的力学行为时存在着明显的局限性.
二阶弹性应变梯度理论是一种考虑弱非局部效应的梯度型非局部理论[7],在本构关系中引入了高阶应变梯度项,即认为物
体一点的应力是该点应变以及该点应变梯度的函数. 连续介质力学薄板模型被广泛地应用于研究单层石墨烯的力学行为.
文献[8]基于应变梯度理论推导了基尔霍夫(Kirchhoff)板的方程,并解析地求解了四边简支基尔霍夫板静变形、稳定性和动力学问题.
应变梯度理论亦被应用于分析受压缩和横向载荷的基尔霍夫板的弯曲及非线性屈曲的尺度效应问题[9, 10].
我们发展了一种考虑应变梯度的4节点24自由度基尔霍夫板单元,并用于分析石墨烯振动的尺度效应问题[11].
但是,当板边长与其厚度的比值不大时,计算板横向弯曲变形时必须考虑一阶剪切变形的影响,因此需要采用考虑一阶剪切变形的
明德林(Mindlin)中厚板(明德林板)理论.
文献[12]分析了基于非局部弹性理论的基尔霍夫板和考虑一阶剪切变形明德林板在研究双层石墨烯自由振动特性方面的差异.
文献[13]建立了基于修改偶应力理论的明德林板模型,并推导了一般情况的边界条件.
文献[14]发展了适用于修改偶应力理论的高阶明德林板单元,并验证了该单元在计算静力、自由振动和屈曲问题时的收敛性.
非局部明德林板理论也被应用于研究双层石墨烯的波动特性[15].
但是相对于经典理论,非局部理论往往更为复杂,理论研究也只能处理简单边界、简单结构的力学问题.
有限元法作为一种有效的数值计算工具,为应用非局部弹性理论解决复杂结构问题提供了可行的方法[16, 17, 18].
本文采用基于二阶应变梯度理论的明德林板模型研究单层石墨烯的自由振动.
根据明德林板微元的平衡微分方程推导基于应变梯度理论
的四边简支明德林板自由振动理论解;利用虚功原理,建立考虑应变梯度的4节点36自由度的明德林板的有限元模型,用于研究
不同边界条件下石墨烯的振动问题.
1 单层石墨烯等效明德林板模型}
1.1 基于应变梯度理论的明德林板的动力学方程
梯度型非局部理论在经典连续介质力学本构关系中引入了高阶梯度项.
二阶应变梯度理论包括减法与加法两种形式,但加法形式 更适用于离散微观结构的等效均质化模型[19, 20].
二阶应变梯度理论加法形式可表示为
|
${\sigma _{ij}} = {C_{ijkl}}\left( {{\varepsilon _{kl}} + {g^2}{\nabla ^2}{{\tilde \varepsilon }_{kl}}} \right)$
|
(1)
|
式中,${C_{ijkl}}$是材料弹性系数张量,$g$是可以表征结构特征尺度的非局部参数,$\tilde {\varepsilon }_{kl}$为非局部应变张量. 对于应变梯度理论则有
|
${\varepsilon _{ij}} = \frac{1}{2}\left( {{u_{i,j}} + {u_{j,i}}} \right)$
|
(2a)
|
|
${\tilde \varepsilon _{kl}} = {\varepsilon _{kl}}$
|
(2b)
|
其中$u_i $为位移张量.
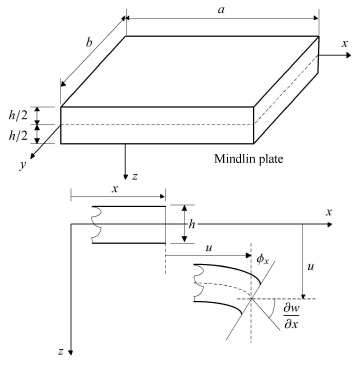
考察如图1所示厚度为$h$的矩形弹性中厚板模型,矩形板在$x$,$y$方向上的长度分别为$a$,$b$.
$xy$平面设为中厚板的几何中面,$\phi_x $,$\phi_y $分别为绕$y$轴和$x$轴 的转角.
考虑纯弯曲且忽略初始面内位移,则基于一阶剪切变形板理论的位移场可以表示为
|
$u = - z{\phi _x}\left( {x,y,t} \right),v = - z{\phi _y}\left( {x,y,t} \right),w = w\left( {x,y,t} \right)$
|
(3)
|
将位移函数(3)代入几何方程(2a),则由法向应变$\varepsilon _x $,$\varepsilon _y $以及剪切应变$\gamma _{xy}
$和$\gamma _{yz} $和$\gamma _{xz} $构成的应变矢量与广义位移$w$,$\phi _x $和$\phi _y $的关系可以表示成
|
$\left\{ {\begin{array}{*{20}{c}}
{{\varepsilon _x}}\\
{{\varepsilon _y}}\\
{{\gamma _{xy}}}\\
{{\gamma _{yz}}}\\
{{\gamma _{zx}}}
\end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}}
{ - z\partial {\phi _x}/\partial x}\\
{ - z\partial {\phi _y}/\partial y}\\
{ - z\left( {\partial {\phi _x}/\partial y + \partial {\phi _y}/\partial x} \right)}\\
{\partial w/\partial y - {\phi _y}}\\
{\partial w/\partial x - {\phi _x}}
\end{array}} \right.$
|
(4)
|
平面应力条件下,将式(4)代入应变梯度理论本构关系(1),则基于应变梯度理论的明德林板本构方程可以表示成
|
$\begin{array}{l}
{\sigma _x} = - \frac{{zE}}{{1 - {\nu ^2}}}\left( {\frac{{\partial {\phi _x}}}{{\partial x}} + \nu \frac{{\partial {\phi _y}}}{{\partial y}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\frac{{zE}}{{1 - {\nu ^2}}}\left( {\frac{{{\partial ^3}{\phi _x}}}{{\partial {x^3}}} + \frac{{{\partial ^3}{\phi _x}}}{{\partial x\partial {y^2}}} + \nu \frac{{{\partial ^3}{\phi _y}}}{{\partial {x^2}\partial y}} + \nu \frac{{{\partial ^3}{\phi _y}}}{{\partial {y^3}}}} \right)
\end{array}$
|
(5a)
|
|
$\begin{array}{l}
{\sigma _y} = - \frac{{zE}}{{1 - {\nu ^2}}}\left( {\nu \frac{{\partial {\phi _x}}}{{\partial x}} + \frac{{\partial {\phi _y}}}{{\partial y}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\frac{{zE}}{{1 - {\nu ^2}}}\left( {\nu \frac{{{\partial ^3}{\phi _x}}}{{\partial {x^3}}} + \nu \frac{{{\partial ^3}{\phi _x}}}{{\partial x\partial {y^2}}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial {y^3}}}} \right)
\end{array}$
|
(5b)
|
|
$\begin{array}{l}
{\tau _{xy}} = - \frac{{zE}}{{2\left( {1 + \nu } \right)}}\left( {\frac{{\partial {\phi _x}}}{{\partial y}} + \frac{{\partial {\phi _y}}}{{\partial x}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{zE}}{{2\left( {1 + \nu } \right)}}{g^2}\left( {\frac{{{\partial ^3}{\phi _x}}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}{\phi _x}}}{{\partial {y^3}}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial {x^3}}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial x\partial {y^2}}}} \right)
\end{array}$
|
(5c)
|
|
${\tau _{yz}} = G\left( {\frac{{\partial w}}{{\partial y}} - {\phi _y}} \right) + G{g^2}\left( {\frac{{{\partial ^3}w}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}w}}{{\partial {y^3}}} - \frac{{{\partial ^2}{\phi _y}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{\phi _y}}}{{\partial {y^2}}}} \right)$
|
(5d)
|
|
${\tau _{xz}} = G\left( {\frac{{\partial w}}{{\partial x}} - {\phi _x}} \right) + G{g^2}\left( {\frac{{{\partial ^3}w}}{{\partial {x^3}}} + \frac{{{\partial ^3}w}}{{\partial x\partial {y^2}}} - \frac{{{\partial ^2}{\phi _x}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{\phi _x}}}{{\partial {y^2}}}} \right)$
|
(5e)
|
其中$G = E/ {2\left( {1 + \nu } \right)}$为剪切模量,$E$为杨氏模量,$\nu $为泊松比,$\nabla ^2
= {\partial ^2}/ {\partial x^2} + {\partial ^2} / {\partial y^2}$
表示拉普拉斯算子,$g$即为应变梯度项的非局部参数,由下式决定[5, 19]
|
$g = \frac{d}{{\sqrt {12} }}$
|
(6)
|
$d$为离散化微观模型内部质点间的距离.
明德林板的平衡方程组为
|
$\frac{{\partial {Q_x}}}{{\partial x}} + \frac{{\partial {Q_y}}}{{\partial y}} + q = \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}}$
|
(7a)
|
|
$\frac{{\partial {M_x}}}{{\partial x}} + \frac{{\partial {M_{xy}}}}{{\partial y}} - {Q_x} = \rho J\frac{{{\partial ^2}{\phi _x}}}{{\partial {t^2}}}$
|
(7b)
|
|
$\frac{{\partial {M_{xy}}}}{{\partial x}} + \frac{{\partial {M_y}}}{{\partial y}} - {Q_y} = \rho J\frac{{{\partial ^2}{\phi _y}}}{{\partial {t^2}}}$
|
(7c)
|
其中,$J = {h^3} / {12}$为矩形板的转动惯性矩,$\rho $为密度,$q$为横向载荷.
由式(5)可以得到平衡方程组式(7)中的各内力表达式
|
$\begin{array}{l}
{M_x} = \int_{ - h/2}^{h/2} {{\sigma _x}z} = - D\left( {\frac{{\partial {\phi _x}}}{{\partial x}} + \nu \frac{{\partial {\phi _y}}}{{\partial y}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{g^2}\left( {\frac{{{\partial ^3}{\phi _x}}}{{\partial {x^3}}} + \frac{{{\partial ^3}{\phi _x}}}{{\partial x\partial {y^2}}} + \nu \frac{{{\partial ^3}{\phi _y}}}{{\partial {x^2}\partial y}} + \nu \frac{{{\partial ^3}{\phi _y}}}{{\partial {y^3}}}} \right)
\end{array}$
|
(8a)
|
|
$\begin{array}{l}
{M_y} = \int_{ - h/2}^{h/2} {{\sigma _y}z{\rm{d}}z} = - D\left( {\nu \frac{{\partial {\phi _x}}}{{\partial x}} + \frac{{\partial {\phi _y}}}{{\partial y}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{g^2}\left( {\nu \frac{{{\partial ^3}{\phi _x}}}{{\partial {x^3}}} + \nu \frac{{{\partial ^3}{\phi _x}}}{{\partial x\partial {y^2}}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial {y^3}}}} \right)
\end{array}$
|
(8b)
|
|
$\begin{array}{l}
{M_{xy}} = \int_{ - h/2}^{h/2} {{\tau _{xy}}zdz} = - D\frac{{1 - \nu }}{2}\left( {\frac{{\partial {\phi _x}}}{{\partial y}} + \frac{{\partial {\phi _y}}}{{\partial x}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D\frac{{1 - \nu }}{2}{g^2}\left( {\frac{{{\partial ^3}{\phi _x}}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}{\phi _x}}}{{\partial {y^3}}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial {x^3}}} + \frac{{{\partial ^3}{\phi _y}}}{{\partial x\partial {y^2}}}} \right)
\end{array}$
|
(8c)
|
|
$\begin{array}{l}
{Q_x} = \int_{ - h/2}^{h/2} {{\tau _{xz}}dz} = \kappa Gh\left( {\frac{{\partial w}}{{\partial x}} - {\phi _x}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\kappa Gh\left( {\frac{{{\partial ^3}w}}{{\partial {x^3}}} + \frac{{{\partial ^3}w}}{{\partial x\partial {y^2}}} - \frac{{{\partial ^2}{\phi _x}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{\phi _x}}}{{\partial {y^2}}}} \right)
\end{array}$
|
(8d)
|
|
$\begin{array}{l}
{Q_y} = \int_{ - h/2}^{h/2} {{\tau _{yz}}dz} = \kappa Gh\left( {\frac{{\partial w}}{{\partial y}} - {\phi _y}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\kappa Gh\left( {\frac{{{\partial ^3}w}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}w}}{{\partial {y^3}}} - \frac{{{\partial ^2}{\phi _y}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{\phi _y}}}{{\partial {y^2}}}} \right)
\end{array}$
|
(8e)
|
其中$D = {Eh^3} /{12\left( {1 - \nu ^2} \right)}$表示板的弯曲刚度,参数$\kappa
$为剪切修正因子,对于一阶剪切变形矩形板理论,$\kappa $一般取$5 /6$.
再将式(8)代入平衡方程组(7),则可得到基于应变梯度理论的明德林板自由振动控制方程组
|
$\begin{array}{l}
\kappa Gh\left( {{\nabla ^2}w - \frac{{\partial {\phi _x}}}{{\partial x}} - \frac{{\partial {\phi _y}}}{{\partial y}}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\kappa Gh\left[{{\nabla ^4}w - {\nabla ^2}\left( {\frac{{\partial {\phi _x}}}{{\partial x}} + \frac{{\partial {\phi _y}}}{{\partial y}}} \right)} \right] - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho h\frac{{{\partial ^2}w}}{{\partial {t^2}}} + q = 0
\end{array}$
|
(9a)
|
|
$\begin{array}{l}
D\left( {\frac{{{\partial ^2}{\phi _x}}}{{\partial {x^2}}} + \frac{{1 - \nu }}{2}\frac{{{\partial ^2}{\phi _x}}}{{\partial {y^2}}} + \frac{{1 + \nu }}{2}\frac{{{\partial ^2}{\phi _y}}}{{\partial x\partial y}}} \right) + \\
D{g^2}\left( {\frac{{{\partial ^4}{\phi _x}}}{{\partial {x^4}}} + \frac{{3 - \nu }}{2}\frac{{{\partial ^4}{\phi _x}}}{{\partial {x^2}\partial {y^2}}} + \frac{{1 - \nu }}{2}\frac{{{\partial ^4}{\phi _x}}}{{\partial {y^4}}} + } \right.\left. {\frac{{1 + \nu }}{2}\frac{{{\partial ^4}{\phi _y}}}{{\partial {x^3}\partial y}} + \frac{{1 + \nu }}{2}\frac{{{\partial ^4}{\phi _y}}}{{\partial x\partial {y^3}}}} \right) + \\
\kappa Gh\left( {\frac{{\partial w}}{{\partial x}} - {\phi _x}} \right) + {g^2}\kappa Gh\left( {\frac{{{\partial ^3}w}}{{\partial {x^3}}} + \frac{{{\partial ^3}w}}{{\partial x\partial {y^2}}} - \frac{{{\partial ^2}{\phi _x}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{\phi _x}}}{{\partial {y^2}}}} \right) + \\
\rho J\frac{{{\partial ^2}{\phi _x}}}{{\partial {t^2}}} = 0
\end{array}$
|
(9b)
|
|
$\begin{array}{l}
D\left( {\frac{{{\partial ^2}{\phi _y}}}{{\partial {y^2}}} + \frac{{1 - \nu }}{2}\frac{{{\partial ^2}{\phi _y}}}{{\partial {x^2}}} + \frac{{1 + \nu }}{2}\frac{{{\partial ^2}{\phi _x}}}{{\partial x\partial y}}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{\kern 1pt} {g^2}\left( {\frac{{{\partial ^4}{\phi _y}}}{{\partial {y^4}}} + \frac{{3 - \nu }}{2}\frac{{{\partial ^4}{\phi _y}}}{{\partial {x^2}\partial {y^2}}} + \frac{{1 - \nu }}{2}\frac{{{\partial ^4}{\phi _y}}}{{\partial {x^4}}} + } \right.\\
\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{1 + \nu }}{2}\frac{{{\partial ^4}{\phi _x}}}{{\partial x\partial {y^3}}} + \frac{{1 + \nu }}{2}\frac{{{\partial ^4}{\phi _x}}}{{\partial {x^3}\partial y}}} \right) + \kappa Gh\left( {\frac{{\partial w}}{{\partial y}} - {\phi _y}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\kappa Gh\left( {\frac{{{\partial ^3}w}}{{\partial {x^2}\partial y}} + \frac{{{\partial ^3}w}}{{\partial {y^3}}} - \frac{{{\partial ^2}{\phi _y}}}{{\partial {x^2}}} - \frac{{{\partial ^2}{\phi _y}}}{{\partial {y^2}}}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho J\frac{{{\partial ^2}{\phi _y}}}{{\partial {t^2}}} = 0
\end{array}$
|
(9c)
|
1.2 应变梯度四边简支明德林板自由振动解析解
矩形板的边界一般考虑3种简单的边界类型:简支(S);固支(C)以及自由(F). 对于矩形中厚板,上述边界类型可以表示为如下关系:
简支边界条件
|
$\begin{array}{*{20}{l}}
\begin{array}{l}
w\left( {0,y} \right) = 0{\mkern 1mu} ,\;\;{M_x}\left( {0,y} \right) = 0\\
w\left( {a,y} \right) = 0{\mkern 1mu} ,\;\;{M_x}\left( {a,y} \right) = 0\\
w\left( {x,0} \right) = 0{\mkern 1mu} ,\;\;{M_y}\left( {x,0} \right) = 0\\
w\left( {x,b} \right) = 0{\mkern 1mu} ,\;\;{M_y}\left( {x,b} \right) = 0
\end{array}
\end{array}$
|
固支边界条件
|
$\begin{array}{l}
w(0,y) = 0{\mkern 1mu} ,\;\;{\phi _x}(0,y) = 0\\
w(a,y) = 0{\mkern 1mu} ,\;\;{\phi _x}(a,y) = 0\\
w(x,0) = 0{\mkern 1mu} ,\;\;{\phi _y}(x,0) = 0\\
w(x,b) = 0{\mkern 1mu} ,\;\;{\phi _y}(x,b) = 0
\end{array}$
|
自由边界条件
|
$\begin{array}{*{20}{l}}
\begin{array}{l}
{Q_z}(0,y) = 0{\mkern 1mu} ,\;\;{M_x}(0,y) = 0{\mkern 1mu} ,\;\;{M_{xy}}(0,y) = 0\\
{Q_z}(a,y) = 0{\mkern 1mu} ,\;\;{M_x}(a,y) = 0{\mkern 1mu} ,\;\;{M_{xy}}(a,y) = 0\\
{Q_z}(x,0) = 0{\mkern 1mu} ,\;\;{M_y}(x,0) = 0{\mkern 1mu} ,\;\;{M_{yx}}(x,0) = 0\\
{Q_z}(x,b) = 0{\mkern 1mu} ,\;\;{M_y}(x,b) = 0{\mkern 1mu} ,\;\;{M_{yx}}(x,b) = 0
\end{array}
\end{array}$
|
其中$Q_z $为边界横向剪力.
对于四边简支的矩形明德林板,满足其边界假设的广义位移函数每阶模态试探解可以设为
|
$w\left( {x,y,t} \right) = {W_{mn}}\sin \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}{{\rm{e}}^{{\rm{i}}\omega t}}$
|
(10a)
|
|
${\phi _x}\left( {x,y,t} \right) = {\psi _{xmn}}\cos \frac{{m\pi x}}{a}\sin \frac{{n\pi y}}{b}{{\rm{e}}^{{\rm{i}}\omega t}}$
|
(10b)
|
|
${\phi _y}\left( {x,y,t} \right) = {\psi _{ymn}}\sin \frac{{m\pi x}}{a}\cos \frac{{n\pi y}}{b}{{\rm{e}}^{{\rm{i}}\omega t}}$
|
(10c)
|
其中$W_{mn} $,$\psi _{xmn} $和$\psi _{ymn} $分别为振型函数的未知系数,$
m$和$n$分别为$x$与$y$方向上的半波数,${\rm i} \equiv \sqrt { - 1} $,$\omega $为固有频率. 定义参数$A = m/a$,$B = n/b$,再将试探解(10)代入方程组(9),自由振动情况,$q = 0$,则有
|
$\begin{array}{l}
\kappa Gh\left[{ - {W_{mn}}\left( {{A^2} + {B^2}} \right) + {\psi _{xmn}}A + {\psi _{ymn}}B} \right] + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {g^2}\kappa Gh\left[{{W_{mn}}{{\left( {{A^2} + {B^2}} \right)}^2} - } \right.\\
\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{A^2} + {B^2}} \right)\left( {{\psi _{xmn}}A + {\psi _{ymn}}B} \right)} \right] + \rho h{\omega ^2}{W_{mn}} = 0
\end{array}$
|
(11a)
|
|
$\begin{array}{l}
D\left( {{A^2}{\psi _{xmn}} + \frac{{1 - \nu }}{2}{B^2}{\psi _{xmn}} + \frac{{1 + \nu }}{2}AB{\psi _{ymn}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{g^2}\left( {{A^4}{\psi _{xmn}} + \frac{{3 - \nu }}{2}{A^2}{B^2}{\psi _{xmn}} + } \right.\\
\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{1 - \nu }}{2}{B^4}{\psi _{xmn}} + \frac{{1 + \nu }}{2}{A^3}B{\psi _{ymn}} + \frac{{1 + \nu }}{2}A{B^3}{\psi _{ymn}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \kappa Gh\left( {{W_{mn}}A - {\psi _{xmn}}} \right) + {g^2}\kappa Gh\\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{A^3}{W_{mn}} + A{B^2}{W_{mn}}} \right. - \left. {{A^2}{\psi _{xmn}} - {B^2}{\psi _{xmn}}} \right)\\
+ \rho J{\omega ^2}{\psi _{xmn}} = 0
\end{array}$
|
(11b)
|
|
$\begin{array}{l}
D\left( {{B^2}{\psi _{ymn}} + \frac{{1 - \nu }}{2}{A^2}{\psi _{ymn}} + \frac{{1 + \nu }}{2}AB{\psi _{xmn}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{g^2}\left( {{B^4}{\psi _{ymn}} + \frac{{3 - \nu }}{2}{A^2}{B^2}{\psi _{ymn}} + } \right.\left. {\frac{{1 - \nu }}{2}{A^4}{\psi _{ymn}} + \frac{{1 + \nu }}{2}A{B^3}{\psi _{xmn}} + \frac{{1 + \nu }}{2}{A^3}B{\psi _{xmn}}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \kappa Gh\left( {{W_{mn}}B - {\psi _{ymn}}} \right) + {g^2}\kappa Gh\left( {{A^2}B{W_{mn}} + {B^3}{W_{mn}}} \right. - \left. {{A^2}{\psi _{ymn}} - {B^2}{\psi _{ymn}}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho J{\omega ^2}{\psi _{ymn}} = 0
\end{array}$
|
(11c)
|
为了便于求解四边简支矩形明德林板自由振动的固有频率$\omega
$解析表达式,可将方程组(11)化为如下矩阵形式求解
|
$\left( {{Q_{\rm{s}}} - {\omega ^2}{M_{\rm{s}}}} \right){F_{\rm{s}}} = {\bf{0}}$
|
(12)
|
其中${\pmb Q}_{\rm s} $为系数矩阵
|
${Q_{\rm{s}}} = \left[{\begin{array}{*{20}{c}}
{{e_1}}&{{e_2}}&{{e_3}}\\
{{e_2}}&{{e_4}}&{{e_5}}\\
{{e_3}}&{{e_5}}&{{e_6}}
\end{array}} \right]$
|
(13)
|
${\pmb Q}_{\rm s}$中系数$e_{1}\sim e_{6}$的具体表达式如下
|
${e_1} = \kappa Gh\left( {{A^2} + {B^2}} \right) - {g^2}\kappa Gh{\left( {{A^2} + {B^2}} \right)^2}$
|
(14a)
|
|
${e_2} = - \kappa GhA + {g^2}\kappa Gh\left( {{A^2} + {B^2}} \right)A$
|
(14b)
|
|
${e_3} = - \kappa GhB + {g^2}\kappa Gh\left( {{A^2} + {B^2}} \right)B$
|
(14c)
|
|
$\begin{array}{l}
{e_4} = - D\left( {{A^2} + \frac{{1 - \nu }}{2}{B^2}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{g^2}\left( {{A^4} + \frac{{3 - \nu }}{2}{A^2}{B^2} + \frac{{1 - \nu }}{2}{B^4}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \kappa Gh + {g^2}\kappa Gh\left( {{A^2} + {B^2}} \right)
\end{array}$
|
(14d)
|
|
${e_5} = - \frac{{1 + \nu }}{2}DAB + D{g^2}\left( {\frac{{1 + \nu }}{2}{A^3}B + \frac{{1 + \nu }}{2}A{B^3}} \right)$
|
(14e)
|
|
$\begin{array}{l}
{e_6} = - D\left( {{B^2} + \frac{{1 - \nu }}{2}{A^2}} \right) + \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} D{g^2}\left( {{B^4} + \frac{{3 - \nu }}{2}{A^2}{B^2} + \frac{{1 - \nu }}{2}{A^4}} \right) - \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \kappa Gh + {g^2}\kappa Gh\left( {{A^2} + {B^2}} \right)
\end{array}$
|
(14f)
|
${\pmb M}_{\rm s} $为广义质量矩阵
|
${M_{\rm{s}}}{\rm{ = }}\left[{\begin{array}{*{20}{c}}
{\rho h}&0&0\\
0&{\rho J}&0\\
0&0&{\rho J}
\end{array}} \right]$
|
(15)
|
${\pmb F}_{\rm s}$ 为振型函数的未知系数向量
|
${F_{\rm{s}}} = \left[{\begin{array}{*{20}{c}}
\begin{array}{l}
{W_{mn}}\\
{\psi _{xmn}}\\
{\psi _{ymn}}
\end{array}
\end{array}} \right]$
|
(16)
|
当${\pmb F}_{\rm s}
$为非零向量,求解方程(12)的广义特征值,即可得到基于应变梯度理论的四边简支矩形明德林板自由振动的固有频率理论解
|
$\begin{array}{l}
{\omega _1} = \sqrt {\left[{1 - {g^2}\left( {{A^2} + {B^2}} \right)} \right]} \cdot \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {\frac{{{\beta _t} - \sqrt {\beta _t^2 - 4\frac{\rho }{{\kappa G}}\frac{{\rho J}}{D}{{\left( {{A^2} + {B^2}} \right)}^2}} }}{{2\frac{\rho }{{\kappa G}}\frac{{\rho J}}{D}}}}
\end{array}$
|
(17a)
|
|
$\begin{array}{l}
{\omega _2} = \sqrt {\left[{1 - {g^2}\left( {{A^2} + {B^2}} \right)} \right]} \cdot \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {\frac{{{\beta _t} + \sqrt {\beta _t^2 - 4\frac{\rho }{{\kappa G}}\frac{{\rho J}}{D}{{\left( {{A^2} + {B^2}} \right)}^2}} }}{{2\frac{\rho }{{\kappa G}}\frac{{\rho J}}{D}}}}
\end{array}$
|
(17b)
|
|
$\begin{array}{l}
{\omega _3} = \sqrt {\left[{1 - {g^2}\left( {{A^2} + {B^2}} \right)} \right]} \cdot \\
{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sqrt {\frac{{\left( {1 - \nu } \right)D + 2\kappa Gh}}{{2\rho J}}}
\end{array}$
|
(17c)
|
其中
|
${\beta _t} = \left( {\frac{{\rho J}}{D} + \frac{\rho }{{\kappa G}}} \right)\left( {{A^2} + {B^2}} \right) + \frac{{\rho h}}{D}$
|
(18)
|
一般情况下,$\omega _1 \ll \omega _2 $以及$\omega _1 \ll \omega _3
$,即$\omega _1 $反映了自由振动的矩形明德林板低阶范围内的固有频率.
2 有限单元模型建立
参考经典理论的振动问题的解法,可以类似地设
|
$w\left( {x,y,t} \right) = W\left( {x,y} \right){{\rm{e}}^{{\rm{i}}\omega t}}$
|
(19a)
|
|
${\phi _x}\left( {x,y,t} \right) = {\psi _x}\left( {x,y} \right){{\rm{e}}^{{\rm{i}}\omega t}}$
|
(19b)
|
|
${\phi _y}\left( {x,y,t} \right) = {\psi _y}\left( {x,y} \right){{\rm{e}}^{{\rm{i}}\omega t}}$
|
(19c)
|
其中$W\left( {x,y} \right)$,$\psi _x \left( {x,y} \right)$和$\psi _y \left(
{x,y} \right)$为振动的振型函数.
基于应变梯度理论明德林板的虚功方程为
|
$\iiint_\Omega\left( {{\sigma _x}\delta {\varepsilon _x} + {\sigma _y}\delta {\varepsilon _y} + {\tau _{xy}}\delta {\gamma _{xy}} + {\tau _{yz}}\delta {\gamma _{yz}} + {\tau _{xz}}\delta {\gamma _{xz}}} \right){\rm{d}}V + $
$\iiint_\Omega\left( {\rho h\ddot w\delta w + \rho J{{\ddot \phi }_x}\delta {\phi _x} + \rho J{{\ddot \phi }_y}\delta {\phi _y}} \right){\rm{d}}V = 0$
|
(20)
|
其中$\varOmega $为弹性体整体积分域.
将式(4)和式(5)代入式(20)并分部积分,且采用类似经典弹性理论的简单边界条件,分部积分得到的边界项不再赘述,再引入式(19),则可以整理为
|
$\iint\left\{ {D\left[{2\frac{{\partial {\psi _x}}}{{\partial x}}\delta {\psi _{x,x}} + 2\nu \frac{{\partial {\psi _y}}}{{\partial y}}\delta {\psi _{x,x}}} \right.} \right. + 2\nu \frac{{\partial {\psi _x}}}{{\partial x}}\delta {\psi _{y,y}} + $
$2\frac{{\partial {\psi _y}}}{{\partial y}}\delta {\psi _{y,y}} + 4\left( {1 - \nu } \right)\left( {\frac{{\partial {\psi _x}}}{{\partial y}} + \frac{{\partial {\psi _y}}}{{\partial x}}} \right)\delta {\psi _{x,y}} + $
$\left. {4\left( {1 - \nu } \right)\left( {\frac{{\partial {\psi _x}}}{{\partial y}} + \frac{{\partial {\psi _y}}}{{\partial x}}} \right)\delta {\psi _{y,x}}} \right] - D{g^2}\left[{2\frac{{{\partial ^2}{\psi _x}}}{{\partial {x^2}}}\delta {\psi _{x,xx}}} \right. + $
$2\nu \frac{{{\partial ^2}{\psi _y}}}{{\partial x\partial y}}\delta {\psi _{x,xx}} + 4\left( {1 - \nu } \right)\left( {\frac{{{\partial ^2}{\psi _x}}}{{\partial x\partial y}} + \frac{{{\partial ^2}{\psi _y}}}{{\partial {x^2}}}} \right)\delta {\psi _{x,xy}} + $
$4\left( {1 - \nu } \right)\left( {\frac{{{\partial ^2}{\psi _x}}}{{\partial x\partial y}} + \frac{{{\partial ^2}{\psi _y}}}{{\partial {x^2}}}} \right)\delta {\psi _{y,xx}} + 2\nu \frac{{{\partial ^2}{\psi _x}}}{{\partial {x^2}}}\delta {\psi _{y,xy}} + $
$2\frac{{{\partial ^2}{\psi _y}}}{{\partial x\partial y}}\delta {\psi _{y,xy}} + 2\frac{{{\partial ^2}{\psi _x}}}{{\partial x\partial y}}\delta {\psi _{x,xy}} + 2\nu \frac{{{\partial ^2}{\psi _y}}}{{\partial {y^2}}}\delta {\psi _{x,xy}} + $
$2\nu \frac{{{\partial ^2}{\psi _y}}}{{\partial x\partial y}}\delta {\psi _{x,xx}} + 4\left( {1 - \nu } \right)\left( {\frac{{{\partial ^2}{\psi _x}}}{{\partial x\partial y}} + \frac{{{\partial ^2}{\psi _y}}}{{\partial {x^2}}}} \right)\delta {\psi _{x,xy}} + $
$4\left( {1 - \nu } \right)\left( {\frac{{{\partial ^2}{\psi _x}}}{{\partial {y^2}}} + \frac{{{\partial ^2}{\psi _y}}}{{\partial x\partial y}}} \right)\delta {\psi _{y,xy}} + \left. {\left. {2\frac{{{\partial ^2}{\psi _y}}}{{\partial {y^2}}}\delta {\psi _{y,yy}}} \right]} \right\}{\rm{d}}x{\rm{d}}y + $
$\iint\left\{ {Gh\kappa \left[{\frac{{\partial W}}{{\partial x}}\delta {W_{,x}} - \frac{{\partial W}}{{\partial x}}\delta {\psi _x} - {\psi _x}\delta {W_{,x}} + {\psi _x}\delta {\psi _x}} \right.} \right. + $
$\begin{array}{l}
\begin{array}{*{20}{l}}
{\left. {\frac{{\partial W}}{{\partial y}}\delta {W_{,y}} - \frac{{\partial W}}{{\partial y}}\delta {\psi _y} - {\psi _y}\delta {W_{,y}} + {\psi _y}\delta {\psi _y}} \right] - }\\
{Gh\kappa {g^2}\left( {2\frac{{{\partial ^2}W}}{{\partial {x^2}}}\delta {W_{,xx}} + } \right.2\frac{{\partial {\psi _x}}}{{\partial x}}\delta {W_{,xx}} + 2\frac{{{\partial ^2}W}}{{\partial {x^2}}}\delta {\psi _{x,x}} + }
\end{array}\\
\begin{array}{*{20}{l}}
{2\frac{{\partial {\psi _x}}}{{\partial x}}\delta {\psi _{x,x}} + 2\frac{{{\partial ^2}W}}{{\partial x\partial y}}\delta {W_{,xy}} + 2\frac{{\partial {\psi _y}}}{{\partial x}}\delta {W_{,xy}} + }\\
{2\frac{{{\partial ^2}W}}{{\partial x\partial y}}\delta {\psi _{y,x}} + 2\frac{{\partial {\psi _y}}}{{\partial x}}\delta {\psi _{y,x}} + 2\frac{{{\partial ^2}W}}{{\partial x\partial y}}\delta {W_{,xy}} + }\\
{2\frac{{\partial {\psi _x}}}{{\partial y}}\delta {W_{,xy}} + 2\frac{{{\partial ^2}W}}{{\partial x\partial y}}\delta {\psi _{x,y}} + 2\frac{{\partial {\psi _x}}}{{\partial y}}\delta {\psi _{x,y}} + }
\end{array}\\
\begin{array}{*{20}{l}}
{2\frac{{{\partial ^2}W}}{{\partial {y^2}}}\delta {W_{,yy}} + 2\frac{{\partial {\psi _y}}}{{\partial y}}\delta {W_{,yy}} + 2\frac{{{\partial ^2}W}}{{\partial {y^2}}}\delta {\psi _{y,y}} + }\\
\begin{array}{l}
2\frac{{\partial {\psi _y}}}{{\partial y}}\delta {\psi _{y,y}})\} dxdy - \\
{\omega ^2}{\rm{{\mathop \iint \limits}}}(\rho hW\delta W + \rho J{\psi _x}\delta {\psi _x} + \rho J{\psi _y}\delta {\psi _y}){\rm{d}}x{\rm{d}}y = 0
\end{array}
\end{array}
\end{array}$
|
(21)
|
传统的矩形明德林板弯曲单元内部的广义位移函数仅需在单元边界上要满足$C^{0}$连续性就能保证有限元法应用于经典连续介质
力学问题的收敛性.
考虑到应变梯度理论的本构关系中引入了广义位移的高阶梯度项,即相应的虚功方程的构造中包含了对位移的高阶导数.
而传统的矩形明德林板单元广义位移函数较低的次数使单元刚度矩阵变得奇异,而不再适用.
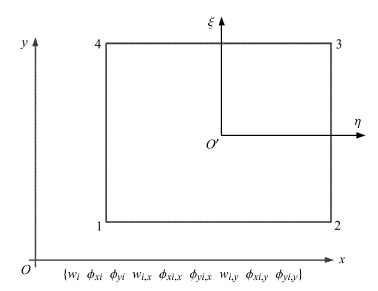
为了保证求解包含高阶梯度项的能量方程的收敛性,文献[14]在研究修改偶应力理论板问题时发展了一种广义位移函数满
足$C^{1}$连续性的4节点36自由度矩形明德林板单元(见图2). 分析表明,这种单元适用于分析纳尺度板振动的尺度效应.
引入一个如图2所示的自然坐标系${O}'\xi \eta $,取矩形中心$\left( {x_0 ,y_0 }
\right)$为原点${O}'$,$\xi $和$\eta $轴分别与$x$和$y$轴平行,正方向也一致,即
|
$\xi = \left( {x - {x_0}} \right)/{a_e}{\mkern 1mu} ,\;\eta = \left( {y - {y_0}} \right)/{b_e}$
|
(22)
|
设定4节点36自由度矩形明德林板单元的长度与宽度分别为$2a_e $和$2b_e
$,其广义位移场可以表示成
|
$\begin{array}{l}
W\left( {\xi ,\eta } \right) = {\alpha _1} + {\alpha _2}\xi + {\alpha _3}\eta + {\alpha _4}{\xi ^2} + {\alpha _5}\xi \eta + {\alpha _6}{\eta ^2} + \\
{\alpha _7}{\xi ^3} + {\alpha _8}{\xi ^2}\eta + {\alpha _9}\xi {\eta ^2} + {\alpha _{10}}{\eta ^3} + {\alpha _{11}}{\xi ^3}\eta + {\alpha _{12}}\xi {\eta ^3}
\end{array}$
|
(23a)
|
|
$\begin{array}{l}
{\psi _x}\left( {\xi ,\eta } \right) = {\beta _1} + {\beta _2}\xi + {\beta _3}\eta + {\beta _4}{\xi ^2} + {\beta _5}\xi \eta + {\beta _6}{\eta ^2} + \\
{\beta _7}{\xi ^3} + {\beta _8}{\xi ^2}\eta + {\beta _9}\xi {\eta ^2} + {\beta _{10}}{\eta ^3} + {\beta _{11}}{\xi ^3}\eta + {\beta _{12}}\xi {\eta ^3}
\end{array}$
|
(23b)
|
|
$\begin{array}{l}
{\psi _y}\left( {\xi ,\eta } \right) = {\gamma _1} + {\gamma _2}\xi + {\gamma _3}\eta + {\gamma _4}{\xi ^2} + {\gamma _5}\xi \eta + {\gamma _6}{\eta ^2} + \\
{\gamma _7}{\xi ^3} + {\gamma _8}{\xi ^2}\eta + {\gamma _9}\xi {\eta ^2} + {\gamma _{10}}{\eta ^3} + {\gamma _{11}}{\xi ^3}\eta + {\gamma _{12}}\xi {\eta ^3}
\end{array}$
|
(23c)
|
其中$\alpha _i $,$\beta _i $和$\gamma _i \ \left( {i = 1,2,\cdots ,12}
\right)$是位移场的未知常数,可以由单元4个节点的信息所确定.
对于4节点36自由度的矩形明德林板弯曲有限单元,每个节点有9个自由度,则节点自由度向量${\pmb d}_i $可以表示为如下形式
|
$\begin{array}{l}
d_i^e = {\left\{ {{w_i},{\phi _{xi}},{\phi _{yi}},{w_{i,x}},{\phi _{xi,x}},{\phi _{yi,x}},{w_{i,y}},{\phi _{xi,y}},{\phi _{yi,y}}} \right\}^{\rm{T}}} = \\
{\left\{ {w,{\phi _{xi}},{\phi _{yi}},\frac{{\partial {w_i}}}{{\partial x}},\frac{{\partial {\phi _{xi}}}}{{\partial x}},\frac{{\partial {\phi _{yi}}}}{{\partial x}},\frac{{\partial {w_i}}}{{\partial y}},\frac{{\partial {\phi _{xi}}}}{{\partial y}},\frac{{\partial {\phi _{yi}}}}{{\partial y}}} \right\}^{\rm{T}}} = \\
{\left\{ {w,{\phi _{xi}},{\phi _{yi}},\frac{{\partial {w_i}}}{{{a_e}\partial \xi }},\frac{{\partial {\phi _{xi}}}}{{{a_e}\partial \xi }},\frac{{\partial {\phi _{yi}}}}{{{a_e}\partial \xi }},\frac{{\partial {w_i}}}{{{b_e}\partial \eta }},\frac{{\partial {\phi _{xi}}}}{{{b_e}\partial \eta }},\frac{{\partial {\phi _{yi}}}}{{{b_e}\partial \eta }}} \right\}^{\rm{T}}}
\end{array}$
|
(24)
|
将矩形单元的4个节点坐标$\left( {\xi _i ,\eta _i } \right)$和对应的节点广义位移${\pmb d}_i^e$分别代入位移场 式 (24),考虑到式(23),得到36个关于未知常数$\alpha _i $,$\beta _i $和$\gamma_i \ \left( {i
= 1,2,\cdots ,12} \right)$的联立方程组. 求解$\alpha _i $,$\beta _i $和$\gamma _i
$,则单元内任意一点的广义位移可以分别用节点形函数${\pmb N}_{wi} \left( {\xi ,\eta } \right)$,${\pmb N}_{\phi
_{xi} } \left( {\xi ,\eta } \right)$和${\pmb N}_{\phi _{yi} } \left( {\xi ,\eta } \right)$表示为如下形式
|
$\left. \begin{array}{l}
w = \sum\limits_{i = 1}^4 {\left( {{N_i}{w_i} + {N_{ix}}{\phi _{xi}} + {N_{iy}}{\phi _{yi}}} \right)} = \\
\sum\limits_{i = 1}^4 {{N_{{\phi _{xi}}}}d_i^e = {N_{{\phi _x}}}{d^e}} \\
{N_{wi}} = \left[{{N_i}\;\;0\;\;0\;\;{N_{ix}}\;\;0\;\;0\;\;{N_{iy}}\;\;0\;\;0} \right]\\
{N_w} = \left[{{N_{w1}},{N_{w2}},{N_{w3}},{N_{w4}}} \right]
\end{array} \right\}$
|
(25a)
|
|
$\left. \begin{array}{l}
{\phi _x} = \sum\limits_{i = 1}^4 {\left( {{N_i}{\phi _{xi}} + {N_{ix}}{\phi _{xi,x}} + {N_{iy}}{\phi _{xi,y}}} \right)} = \\
\sum\limits_{i = 1}^4 {{N_{{\phi _{xi}}}}d_i^e} = {N_{{\phi _x}}}{d^e}\\
{N_{{\phi _{xi}}}} = \left[{0\;\;{N_i}\;\;0\;0\;\;{N_{ix}}\;\;0\;\;0\;\;{N_{iy}}\;\;0} \right]\\
{N_{{\phi _x}}} = \left[{{N_{{\phi _{x1}}}},{N_{{\phi _{x2}}}},{N_{{\phi _{x3}}}},{N_{{\phi _{x4}}}}} \right]
\end{array} \right\}$
|
(25b)
|
|
$\left. \begin{array}{l}
{\phi _y} = \sum\limits_{i = 1}^4 {\left( {{N_i}{\phi _{yi}} + {N_{ix}}{\phi _{yi,x}} + {N_{iy}}{\phi _{yi,y}}} \right)} = \\
\sum\limits_{i = 1}^4 {{N_{{\phi _{yi}}}}d_i^e} = {N_{{\phi _y}}}{d^e}\\
{N_{{\phi _{yi}}}} = \left[{0\;\;0\;\;{N_i}\;\;0\;0\;\;{N_{ix}}\;\;0\;\;0\;\;{N_{iy}}} \right]\\
{N_{{\phi _y}}} = \left[{{N_{{\phi _{y1}}}},{N_{{\phi _{y2}}}},{N_{{\phi _{y3}}}},{N_{{\phi _{y4}}}}} \right]
\end{array} \right\}$
|
(25c)
|
其中${\pmb d}^e = \left[{ {\pmb d}_1^e ,\;{\pmb d}_2^e ,\;{\pmb d}_3^e ,\;{\pmb d}_4^e }
\right]^{\rm T}$为单元位移向量.
局部坐标系下位移插值函数可以写成
|
${N_i} = \left( {1 + {\xi _i}\xi } \right)\left( {1 + {\eta _i}\eta } \right)\left( {2 + {\xi _i}\xi + {\eta _i}\eta - {\xi ^2} - {\eta ^2}} \right)/8$
|
(26a)
|
|
${N_{ix}} = - {a_e}{\xi _i}\left( {1 + {\xi _i}\xi } \right)\left( {1 + {\eta _i}\eta } \right)\left( {1 - {\xi ^2}} \right)/8$
|
(26b)
|
|
${N_{iy}} = - {b_e}{\eta _i}\left( {1 + {\xi _i}\xi } \right)\left( {1 + {\eta _i}\eta } \right)\left( {1 - {\eta ^2}} \right)/8$
|
(26c)
|
令${\varepsilon _b} = {\left\{ {{\varepsilon _x},{\varepsilon _y},{\gamma _{xy}}} \right\}^{\rm{T}}},{\varepsilon _s} = {\left\{ {{\gamma _{yz}},{\gamma _{zx}}} \right\}^{\rm{T}}}$,且代入式(25)和式(26),则式(4)可以整理为
|
$\varepsilon = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{\varepsilon _b}\\
{\varepsilon _s}
\end{array}
\end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
z{B_b}\\
{B_s}
\end{array}
\end{array}} \right\}{\delta ^e}$
|
(27)
|
其中${\pmb B}_b $和${\pmb B}_s $为几何矩阵,分别为
|
$\left. \begin{array}{l}
{B_b} = \left[{{B_{b1}}\;{B_{b2}}\;{B_{b3}}\;\;{B_{b4}}} \right]\\
{B_{bi}} = \left[{\begin{array}{*{20}{c}}
0&{{N_{i,\xi }}/{a_e}}&0&0&{{N_{i,\xi }}/{a_e}}&0&0&{{N_{i,\xi }}/{a_e}}&0\\
0&0&{{N_{i,\eta }}/{b_e}}&0&0&{{N_{i,\eta }}/{b_e}}&0&0&{{N_{i,\eta }}/{b_e}}\\
0&{{N_{i,\eta }}/{b_e}}&{{N_{i,\xi }}/{a_e}}&0&{{N_{ix,\xi }}/{b_e}}&{{N_{ix,\xi }}/{a_e}}&0&{{N_{iy,\eta }}/{b_e}}&{{N_{iy,\xi }}/{a_e}}
\end{array}} \right]
\end{array} \right\}$
|
(28a)
|
|
$\left. \begin{array}{l}
{B_s} = \left[{{B_{s1}}\;\;{B_{s2}}\;\;{B_{s3}}\;\;{B_{s4}}} \right]\\
{B_{si}} = \left[{\begin{array}{*{20}{c}}
{\partial {N_i}/{b_e}\partial \eta }&0&{{N_i}}&{\partial {N_{ix}}/{b_e}\partial \eta }&0&{{N_{ix}}}&{\partial {N_{iy}}/{b_e}\partial \eta }&0&{{N_{iy}}}\\
{\partial {N_i}/{a_e}\partial \xi }&{{N_i}}&0&{\partial {N_{ix}}/{a_e}\partial \xi }&{{N_{ix}}}&0&{\partial {N_{iy}}/{a_e}\partial \xi }&{{N_{iy}}}&0
\end{array}} \right]
\end{array} \right\}$
|
(28b)
|
应力向量可以表示为
|
$\sigma = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{\sigma _b}\\
{\sigma _s}
\end{array}
\end{array}} \right\} = \left\{ {\begin{array}{*{20}{c}}
\begin{array}{l}
{D_b}{\varepsilon _b}\\
{D_s}{\varepsilon _s}
\end{array}
\end{array}} \right\}$
|
(29)
|
其中${\pmb D}_b $和${\pmb D}_s $为弹性矩阵,分别为
|
${D_b} = D\left[{\begin{array}{*{20}{c}}
1&\nu &0\\
\nu &1&0\\
0&0&{\left( {1 - \nu } \right)/2}
\end{array}} \right]$
|
(30a)
|
|
${D_s} = \left[{\begin{array}{*{20}{c}}
{\kappa G}&0\\
0&{\kappa G}
\end{array}} \right]$
|
(30b)
|
将式(25),式(27)和式(29)代入式(21),则有
|
$\begin{array}{l}
{\mathop \iint \limits}\frac{{{h^3}}}{{12}}\left( {B_b^{\rm{T}}{D_b}{B_b} - {g^2}B_{bx}^{\rm{T}}{D_b}{B_{bx}} - {g^2}B_{by}^{\rm{T}}{D_b}{B_{by}}} \right)dx{\rm{d}}y + \\
{\mathop \iint \limits}\left( {B_s^{\rm{T}}{D_s}{B_s} - {g^2}B_{sx}^{\rm{T}}{D_s}{B_{sx}} - {g^2}B_{sy}^{\rm{T}}{D_s}{B_{sy}}} \right)dxdy - \\
{\omega ^2}{\mathop \iint \limits}\left( {\rho hN_w^{\rm{T}}{N_w} + \rho JN_{{\phi _x}}^{\rm{T}}{N_{{\phi _x}}} + \rho JN_{{\phi _y}}^{\rm{T}}{N_{{\phi _y}}}} \right)dxdy = 0
\end{array}$
|
(31)
|
其中,${B_{bx}} = \frac{\partial }{{\partial x}}{B_b}$,${B_{by}} = \frac{\partial }{{\partial y}}{B_b}$,${B_{sx}} = \frac{\partial }{{\partial x}}{B_s}$以及${B_{sy}} = \frac{\partial }{{\partial y}}{B_s}$.
由方程(31)可知,基于应变梯度理论的4节点36自由度矩形明德林板单元的刚度矩阵${\pmb K}^e$表示成
|
$\begin{array}{l}
{K^e} = \frac{{{h^3}}}{{12}}{\mathop \iint \limits}(B_b^{\rm{T}}{D_b}{B_b} - {g^2}B_{bx}^{\rm{T}}{D_b}{B_{bx}} - \\
{g^2}B_{by}^{\rm{T}}{D_b}{B_{by}})dxdy + \\
h{\mathop \iint \limits}(B_s^{\rm{T}}{D_s}{B_s} - {g^2}B_{sx}^{\rm{T}}{D_s}{B_{sx}} - \\
{g^2}B_{sy}^{\rm{T}}{D_s}{B_{sy}})dxdyn
\end{array}$
|
(32)
|
单元质量矩阵${\pmb M}^e$为
|
$\begin{array}{l}
{M^e} = \rho h{\mathop \iint \limits}N_w^{\rm{T}}{N_w}{\rm{d}}x{\rm{d}}y + \rho J{\mathop \iint \limits}N_{{\phi _x}}^{\rm{T}}{N_{{\phi _x}}}dx{\rm{d}}y\\
+ \rho J{\mathop \iint \limits}N_{{\phi _y}}^{\rm{T}}{N_{{\phi _y}}}dx{\rm{d}}y
\end{array}$
|
(33)
|
将各局部坐标下离散单元刚度矩阵(32)和质量矩阵(33)在全局坐标下进行组装,可得
|
$\left( {K - {\omega ^2}M} \right)d = 0$
|
其中${\pmb K}$,${\pmb M}$和${\pmb d }$分别是全局坐标系下的整体刚度矩阵,整体质量矩阵和整体位移向量.
3 结果与讨论
第2节推导了基于二阶应变梯度理论的明德林板振动的有限元模型.
本节将比较明德林板模型和基尔霍夫板模型在计算单层石墨烯自由振动特性的差异,并进一步探讨明德林板的边长、振动模态、非局部参数和边界条件类型对其自由振动尺度效应的影响.
考虑4种边界条件,分别为:SSSS(四边简支)、CCCC(四边固支)、SCSC(两对边简支,两对边固支)以及SFSF(两对边简支,其余边自由).
在下述讨论中,为了更直观地讨论石墨烯自由振动的尺度效应,将固有频率比定义为
|
${R_f} = \frac{\omega }{{\bar \omega }} = \frac{{\omega /2\pi }}{{\bar \omega /2\pi }} = \frac{f}{{\bar f\;{\mkern 1mu} }}$
|
(35)
|
其中,$\omega$ (rad/s)为基于应变梯度理论(SGT)得到的石墨烯自由振动的固有角频率,$f$ (Hz)
为基于应变梯度理论(SGT)得到的固有频率;$\bar {\omega }$和$\bar
{f}$分别为基于经典弹性理论(CET)的固有角频率和固有频率. 单层石墨烯等效成明德林板模型的力学参数为:杨氏模量${\rm{E = 2}}{\rm{.28TPa}}$,密度$\rho = 7.016 \times {10^3}kg/{m^3}$,等效板厚h = 0.11nm,泊松比v= 0.41[21].
对于石墨烯,由式(6)可设定${g}' = 0.035 5$nm.
为了验证第2节引入的基于应变梯度理论的4节点36自由度明德林板单元用于单层石墨烯自由振动固有频率值计算的收敛性,
文献[14]中给出了4节点36自由度的矩形明德林板单元各种边界类型所对应的节点自由度的取值. 表1给出了边长为$a
=4.261$nm,$b =2.706$nm的四边简支明德林板6种半波数$m$和$n$组合固有频率值的理论解和有限元结果.
表1中同时给出了当$g=0$时的结果,此时退化为经典弹性理论结果.
由表1的结果可以看出,随着网格数的增加,有限元数值计算的结果逐渐收敛于理论解,且基于应变梯度理论得到的固有频率值都小
于经典理论得到的结果. 表2给出了不同边界条件单层石墨烯等效明德林板自由振动的固有频率.
表2的结果验证了4节点36自由度板单元在计算SFSF,SCSC,CCCC 3种不同边界条件下边长$a =4.261$nm,$b
=2.706$nm 的明德林板的收敛性.
表 1(Table 1)
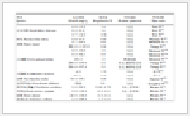
表 1 四边简支单层石墨烯等效明德林板自由振动固有频率理论解与有限元解比较 Table 1 Comparison between analytical solution and numerical solution of Mindlin plate of different sizes
with all edges simply-supported (THz)
|
表 1 四边简支单层石墨烯等效明德林板自由振动固有频率理论解与有限元解比较
Table 1 Comparison between analytical solution and numerical solution of Mindlin plate of different sizes
with all edges simply-supported (THz) |
表 2(Table 2)

表 2 不同边界条件单层石墨烯等效明德林板自由振动的固有频率 Table 2 The natural frequencies with varying mesh density for Mindlin plate with considering different
boundary conditions (BC) (THz)
|
表 2 不同边界条件单层石墨烯等效明德林板自由振动的固有频率
Table 2 The natural frequencies with varying mesh density for Mindlin plate with considering different
boundary conditions (BC) (THz) |
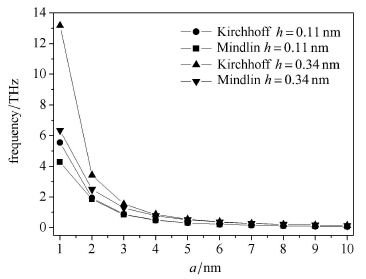
石墨烯的层间距一般为0.34nm,许多研究都将其设为石墨烯的等效厚度.
则由文献[21]的方法可以得到与此对应的力学参数 为$E = 0.74$TPa,$\rho = 7.016 \times {10^3}{\mkern 1mu} kg/{m^3}$以及$\nu
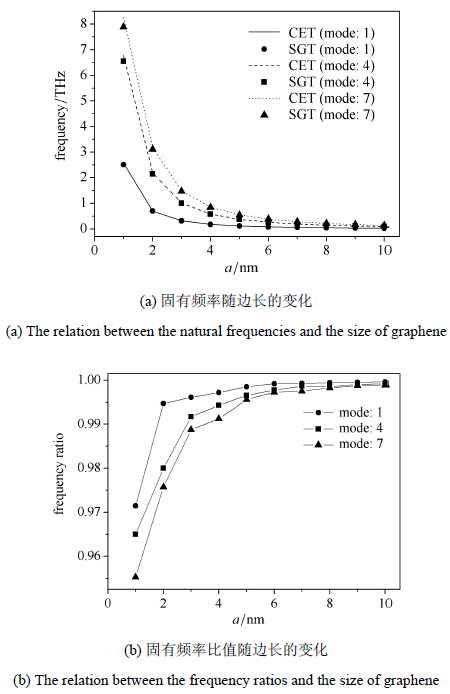
= 0.41$. 图3分别采用文献[11]
中基尔霍夫板有限元模型和本文发展的明德林板有限元模型计算的边长在1~10nm范围内两种等效厚度的四边简支石墨烯自由
振动第4阶固有频率随尺寸的变化.
显然明德林板得到的固有频率小于基尔霍夫板的结果,且h=0.34nm得到的固有频率值大于h=0.11nm.
随着尺寸的减少,这两种板模型在计算固有频率时的差异也随之增大,而等效厚度取h=0.34nm时的这种差异更明显.
图4为采用经典明德林板有限元模型与应变梯度明德林板有限元模型给出的四边固支的矩形石墨烯自由振动固有频率以及两者的比
值随边长$a$的变化. 图5 给出了两对边简支两对边固支的明德林板固有频率及其比值随边长$a$变化的结果. 图4和图5中明德林板长宽比$b/a$都为1.
由图4(a)可以看出基于应变梯度理论得到的固有频率值与基于经典弹性理论的结果之间的差异随着尺寸的增加而减小,随着模态阶
数的增加而变大. 图4(b)为基于上述两种理论计算的自由振动固有频率比值随明德林板边长$a$的变化.
显然,随着明德林板边长的减小,固有频率比值也相应的降低,且阶数越高,固有频率比值下降越急剧.
图4中,边长为1nm×1nm的四边固支石墨烯的第1阶、4阶和7阶固有频率比值相对于边长为10nm×10nm石墨烯分别减少了3.6%,16.0%,19.4%.
图4和图5均表明,石墨烯等效明德林板尺寸及模态阶数都对其自由振动的尺度效应存在显著的影响.
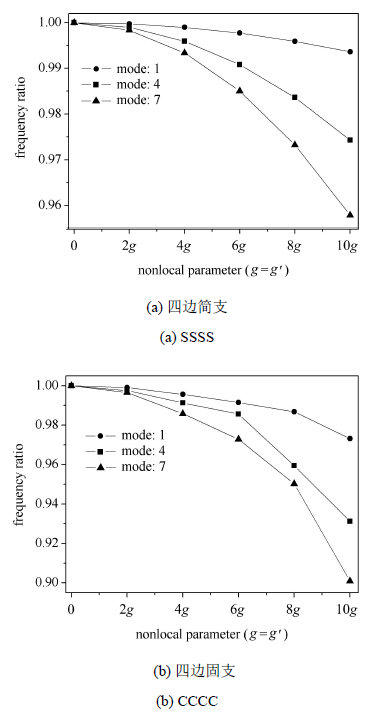
为了研究应变梯度理论中反映微观结构尺度特征的非局部参数$g$对石墨烯等效明德林板自由振动尺度效应的影响,图6计算了尺寸
为$4nm \times 14nm$,边界条件分别为SSSS和CCCC的明德林板的固有频率比值随非局部参数的变化.
图6中非局部参数g在0~10g'范围内变化.
显然,非局部参数值越高,自由振动尺度效应越明显,且阶数越高,固有频率比值对非局部参数的变化就越敏感.
4 结 论
本文建立基于应变梯度理论的明德林板自由振动方程.
发展了一种考虑应变梯度的4节点36自由度明德林板单元,利用虚功原理建立了
单层石墨烯的等效非局部弹性板的有限元模型.
研究结果表明,这种单元能够较好地适用于研究复杂边界条件下石墨烯自由振动的尺度效应.
明德林板得到的固有频率小于基尔霍夫板的结果,且这种板模型的差异也受到石墨烯等效厚度取值的影响.
基于应变梯度理论所获得的明德林板固有频率略小于基于经典明德林板理论得到的结果.
尺度效应对高阶模态以及较小尺寸石墨烯的振动特性影响较大.
应变梯度理论中的非局部参数$g$能够作为石墨烯内部反映出微观结构特性的尺度参数.
参考文献
| [1] |
Novoselov KS, Geim AK, Morozov SV, et al. Electric field effect in atomically thin carbon films. Science, 2004, 306(5696): 666-669
|
| [2] |
Stelmashenko NA, Walls MG, Brown LM, et al. Microindentations on W and Mo oriented single crystals: an STM study. Acta Metallurgica et Materials, 1993, 41(10): 2855-2865
|
| [3] |
Fleck NA, Muller GM, Ashby MF, et al. Strain gradient plasticity: theory and experiment. Acta Metallurgica et Materials, 1994, 42: 475-487
|
| [4] |
Stolken JS, Evans AG. A microbend test method for measuring the plasticity length scale. Acta Metallurgica et Materials, 1998, 46: 5109-5115
|
| [5] |
Wang LF, Hu HY. Flexural wave propagation in single-walled carbon nanotubes. Physical Review B, 2005, 71: 195412
|
| [6] |
冯秀艳, 郭香华, 方岱宁等. 微薄梁三点弯曲的尺度效应研究. 力学学报,2007,39(4): 479-485 (Feng Xiuyan, Guo Xianghua, Fang Daining, et al. Three-point microbend size effects for pure Ni foils. Chinese Journal of Theoretical and Applied Mechanics, 2007,39(4): 479-485 (in Chinese))
|
| [7] |
Bazant ZP, Jirasek M. Nonlocal integral formulations of plasticity and damage: survey of progress. Journal of Engineering Mechanics, 2002, 128(11): 1119-1149
|
| [8] |
Papargyri-Beskou S, Beskos DE. Static, stability and dynamic analysis of gradient elastic flexural Kirchhoff plates. Archive of Applied Mechanics, 2008, 78(8): 625-635
|
| [9] |
Lazopoulos KA. On the gradient strain elasticity theory of plates. European Journal of Mechanics, 2004, 23(5): 843-852
|
| [10] |
Lazopoulos KA. On bending of strain gradient elastic micro-plates. Mechanics Research Communications, 2009, 36(7): 777-783
|
| [11] |
徐巍, 王立峰, 蒋经农. 基于应变梯度有限元的单层石墨烯振动研究. 固体力学学报,2014,35(5): 441-450 (Xu Wei, Wang Lifeng, Jiang Jingnong. Finite element analysis of strain gradient on the vibration of single-layered graphene sheets. Chinese Journal of Solid Mechanics, 2014, 35(5): 441-450 (in Chinese))
|
| [12] |
Pradhan SC, Phadikar JK. Nonlocal elasticity theory for vibration of nanoplates. Journal of Sound and Vibration, 2009, 325: 206-223
|
| [13] |
Ma HM, Gao XL, Reddy JN. A non-classical mindlin plate model based on a modified couple stress theory. Acta Mechanica, 2011, 220: 217-235
|
| [14] |
Zhang B, He YM, Liu DB, et al. A non-classical mindlin plate finite element based on a modified couple stress theory. European Journal of Mechanics A/Solids, 2013, 42: 63-80
|
| [15] |
Shi JX, Ni QQ, Lei XW, et al. Study on wave propagation characteristics of double-layer graphene sheets via nonlocal Mindlin-Reissner plate theory. International Journal of Mechanical Sciences, 2014, 84: 25-30
|
| [16] |
Arash B, Wang Q, Liew KM. Wave propagation in graphene sheets with nonlocal elastic theory via finite element formulation. Computer Methods in Applied Mechanics and Engineering, 2012, 223: 1-9
|
| [17] |
Soh A, Chen WJ. Finite element formulations of strain gradient theory for microstructures and the C^0-1 patch test. International Journal for Numerical Methods in Engineering, 2004, 61(3): 433-454
|
| [18] |
Ansari R, Rajabiehfard R, Arash B. Nonlocal finite element model for vibrations of embedded multi-layered graphene sheets. Computational Materials Science, 2010, 49(4):831-838
|
| [19] |
Askes H, Suiker ASJ, Sluys LJ. A classification of higher-order strain-gradient models - linear analysis. Archive of Applied Mechanics, 2002, 72: 171-188
|
| [20] |
赵杰, 陈万吉, 冀宾. 关于两种二阶应变梯度理论. 力学学报,2010,42(1): 138-145 (Zhao Jie, Chen Wanji, Ji Bin. A study on the two second-order strain gradient theories. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(1): 138-145 (in Chinese))
|
| [21] |
Liu RM, Wang LF. Thermal vibrations of single-layered graphene sheets by molecular dynamics. Journal of Nanoscience and Nanotechnology, 2013, 13(2): 1059-1062
|
FINITE ELEMENT ANALYSIS OF STRAIN GRADIENT MIDDLE THICK PLATE MODEL ON THE VIBRATION OF GRAPHENE SHEETS
Xu Wei, Wang Lifeng, Jiang Jingnong

1. State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
2. China Aviation Powerplant Research Institute, Zhuzhou 412002, China
Fund: The project was supported by the Program for New Century Excellent Talents in University (NCET-11-0832), 333 Talents Program in Jiangsu
Province and Fundamental Research Funds for the Central Universities of China.
Abstract: The dynamics equation of the Mindlin middle thick plate model based on strain gradient theory is formulated to study the vibration of single-layered graphene sheets (SLGSs). Analytical solution of the natural frequency for free vibration of Mindlin plate with all edges simply-supported is derived. A 4-node 36-degree-of-freedom (DOF) Mindlin plate element is proposed to build the nonlocal finite element (FE) plate model with second order gradient of strain taken into consideration. This FE method is used to study the influences of the size, vibration mode and nonlocal parameters on the scale effect of vibration behaviors of SLGSs, which validates the reliability of the FE model for predicting the scale effect on the vibrational SLGSs with complex boundary conditions. The natural frequencies obtained by the strain gradient Mindlin plate are lower than that obtained by classical Mindlin plate model. The natural frequencies of SLGSs obtained by Mindlin plate model with first-order shear deformation taken into account are lower than that obtained by Kirchhoff plate model for both strain gradient model and classical case. The small scale effect increases with the increase of the mode order and the decrease of the size of SLGSs.
Key words:
strain gradient finite element method Mindlin plate vibration scale effect

 2015, Vol. 47
2015, Vol. 47


