2. 中国空气动力研究与发展中心, 计算空气动力研究所, 绵阳621000
当飞行器做一些复杂的机动运动时,其飞行高度、速度及姿态角都会发生非常剧烈的变化,并伴随着流动分离、漩涡脱落、漩涡破裂等 复杂的流动现象. 这些强非定常、非线性的流场会导致飞行器气动力变化的不连续,且非定常流动的迟滞效应、依赖于历史流场的特点也为飞行器的控制系 统设计带来严峻的挑战. 传统设计方法,如基于气动数据库的飞行力学仿真,或多或少都存在一些近似和简化,没有从整体上考虑各个学科之间的耦合特性,为了 保证飞行安全,往往在控制律设计时放大气动数据的不确定度,由此导致飞行性能的降低. 为了解决气动/运动/控制耦合问题,气动工作者发展了``虚拟飞行试验''技术.
20世纪90年代,美国阿诺德工程发展中心首先提出了``虚拟飞行试验''的概念[1],并对其进行了较全面的研究. 他们发展了可三自 由度运动的悬挂支撑系统,通过引入舵面控制/运动机构,实现了飞行器姿态角的实时变化,可以对流动/运动耦合问题开展更为细致的研 究,并且得到了和飞行试验较为接近的试验结果. 欧洲的德-荷风洞机构亦发展了类似的试验技术,并研制了六自由度运动的支撑机构. 国内以气动中心为代表的少数研究机构也相继发展了类似的虚拟飞行试验技术[2]. 然而由于支撑系统本身的复杂性及其对流场的干扰,做到完全的六自由度运动非常困难,且无法模拟真实飞行过程中常见的飞行速度、飞 行高度等变化的情况.
随着计算流体力学技术的不断进步,使得对``虚拟飞行''过程开展完全的数值研究成为可能[3, 4, 5, 6, 7, 8, 9, 10, 11, 12]. 美国和欧洲很多研 究机构已经开展了数值虚拟飞行技术的研究,如美国陆军实验室已经能够数值模拟超声速旋转弹箭飞行器的弹道靶无控飞行 过程[3];由美国国防部支持的``CREATE-AV(计算研究与工程应用平台)''项目于2007年开始研发气动/运动/控制一体化耦 合计算平台[4, 5, 6],并利用该软件平台对战斗机的机动过程进行了数值模拟[6]. 文献[7]针对飞行器简化的``开环控制''过程进行了数值模拟[7],德国宇航研究院模拟了无黏情况下X-31攻角保持和自由 滚转机动过程[10],而北约的合作研究组织也开展了代号为AVT-161的研究项目[8, 9]. 在国内,基于非定常流场计算和飞行力学耦合的研究已有较多的报道,但对耦合控制律的复杂飞行器机动过程的数值模拟仍较 少见[11, 12].
要进行复杂机动动作的数值模拟并尽可能考虑相关的真实物理效应,其挑战依然是非常严峻的,主要体现为:(1)真实飞行器普遍具有复杂的外形,且飞行器的运动、控制过程是一个典型的动边界问题,飞行器的大位移运动以及舵面偏转过程会带来很多网格生成方面的难题;(2)飞行器复杂的运动、变形会导致流场剧烈的非定常变化,包括流动分离、漩涡脱落、漩涡破裂等复杂的流动问题,因此对流体力学控制方程的数值模拟精度提出了更高要求;(3)流体力学/飞行力学之间是一个高度耦合的非线性系统,需要在考虑开环或闭环控制的情况下对流体力学控制方程、动力学方程进行统一的求解,才能得到和真实情况更为接近的计算结果,这就对耦合计算方法、数值模拟平台的集成度提出了更高要求.
本文以动态混合网格技术为基础,通过耦合求解刚体动力学方程、流体力学控制方程、飞行控制律,建立了适用于飞行器``虚拟飞行''过程研究的一体化数值模拟技术. 通过典型的外挂物投放算例对该算法进行了测试,并对某导弹的姿态角控制过程、过载控制过程以及变马赫数条件下的控制过程进行了数值模拟,得到了与实验非常一致的结果. 这些算例证明该一体化算法已经初步具备了针对复杂飞行器``数值虚拟飞行''的模拟能力.
1 数值虚拟飞行计算方法 1.1 动态混合网格生成技术飞行器的``虚拟飞行''过程中往往伴随着飞行姿态、位置的剧烈变化以及舵面偏转等动边界问题. 这些复合运动本身就非常复杂,且舵面的偏转往往会造成舵面、飞行器之间剧烈的相对运动,给动态网格技术带来了极大挑战.
针对运动边界问题而发展的网格变形技术有很多,如弹簧松弛法[13]、德罗内(Delaunay)背景网格映射方法[14]、基于径向基 函数的插值方法[15],以及基于结构网格的超限插值法等. 之前的工作中,作者所在的课题组发展了一种``网格变形+局部网格重构''的动态混合网格生成策略[16, 17, 18, 19],较好地解决了大变形、大位移情况下的动态混合网格生成难题.
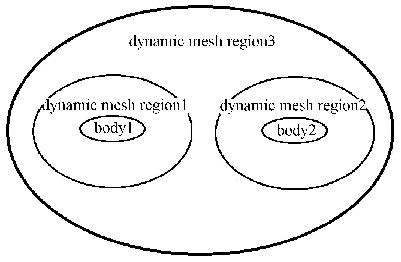
针对复杂的工程问题,为拓展动态混合网格技术的适用范围,本文进一步发展了基于``区域分解''的动态混合网格生成策略. 其基本原理是将计算区域按照实际计算需求分成若干个独立的子区域,每个子区域采用一种最合适的动态网格技术进行网格变形,以实现各种动态网格技术的最有效的利用. 一般情况下,网格的分区示意图如图1所示:对于每个物体,其周围的区域设置为``随体区域'',而随体区域内各设置了一个``主动变形区''和一个``被动变形区'',其中``主动变形区''通过解析的公式或者直接从数据库读取;而``被动变形区''的网格则通过网格变形技术得到;此外,每个物体和远场边界之间的区域设置为另外一个变形区域,可以通过各种网格变形技术进行网格变形.
|
图 1 动网格分区示意图 Fig.1 The sketch of zonal decomposition of dynamic mesh generation |
这种基于分区策略的动态混合网格生成技术有如下几个优点:
(1)针对每个区域的特点,可以采用最合适的网格变形方法,以实现网格变形能力的最大化;
(2)每个区域内网格的运动通过各自独立的参数进行控制. 如舵偏角、六自由度参数等(对于生物仿生流体力学问题其中的各种控制变形的参数更为复杂). 这种动态网格生成思路通过结合C++面向对象的程序设计方法,特别适合于大型计算流体力学软件的设计和开发,较易实现各种功能的耦合;
(3)可以适用于多种复杂的工程实际问题,例如带舵面偏转控制的多体分离问题、飞机机动运动过程中的气动弹性问题、生物外流仿生流体力学中的多自由度耦合运动问题等;
(4)这种动态混合网格生成策略为各种网格变形技术的集成、耦合提供了非常便利的条件. 例如针对舵面偏转的问题,可以在局部区域内采用重叠网格技术或滑移网格技术,则可大大降低动态网格生成的难度.
针对后文中导弹机动运动过程, 将计算域分解为如下几个区域:舵面附近的``变形区''、包围整个弹身的``随体运动区''以及弹体和远场边界之间的``扰动松弛区''.
``变形区''主要解决舵面偏转的动网格生成问题. 针对舵面偏转,如果偏转角度不大,超限插值技术往往是一个较好的选择;也可以事先将舵面偏转的网格生成好,并建立舵面偏转的``网格数据库'',在进行一体化计算时舵面偏转的网格直接从数据库中读取,可大幅提高一体化计算的计算效率;如果舵偏角度较大,以至于超出舵面平台,则需要采用前述的``变形+重构''的方法;此外,重叠网格技术、滑移网格技术也是不错的选择. 本文采用了基于``网格数据库''的方式,``变形区''的网格通过从网格数据库提取数据,然后根据舵偏角度插值得到.
``随体运动区''根据弹体的六自由度参数进行实时的刚性运动;扰动松弛区的变形可以采用各种成熟的网格变形技术如弹簧松弛法、径向基函数方法、德罗内背景网格映射方法等. 由于该问题不用考虑多体相对运动,本文采用了一种代数方法,直接给定一个扰动衰减规律,使网格的位移从物面附近到远场边界逐渐衰减到0.
1.2 动力学方程及纳维-斯托克斯方程的求解纳维-斯托克斯方程的求解采用二阶有限体积格式,时间离散采用双时间步策略和二阶隐式时间格式,采用一方程、剪切应力输运等湍流模型模拟湍流流动. 具体算法请参见文献[20].
飞行器一般通过舵面的偏转来进行飞行控制,由于舵面质量较小,舵面偏转过程中飞行器的质量特性变化非常微小,因此可以近似将飞行器当成刚体来考虑. 刚体六自由度动力学方程可以表述如下
| $ m\mathop v\limits^. = F $ | (1) |
| $ I\mathop \omega \limits^. {|_{xyz}} + \omega \times L = M $ | (2) |
其中$m$表示飞行器的质量,${\pmb I}$表示转动惯量,${\pmb \omega }$ 为角速度,${\pmb F}$和${\pmb M}$分别表示作用在飞行器上的力和力矩,${\pmb L}$为角动量
| $ L = I\omega = \left[\begin{array}{l} {I_{xx}}\;\;\;\;{I_{xy}}\;\;\;\;\; - {I_{xz}}\\ - {I_{xy}}\;\;\;{I_{yy}}\;\;\;\; - {I_{yz}}\\ - {I_{xz}}\;\;\; - {I_{yz}}\;\;\;\;{I_{zz}}\; \end{array} \right]\left[\begin{array}{l} {\omega _x}\\ {\omega _y}\\ {\omega _z} \end{array} \right] $ | (3) |
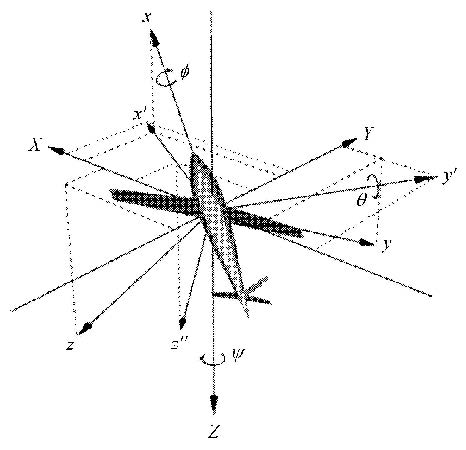
本文采用欧拉角描述飞行器的姿态(欧拉角定义方式如图2),因此刚体的运动学方程表述为
| $ \mathop r\limits^. = v $ | (4) |
| $ \left. \begin{array}{l} \dot \theta = {\omega _y}\cos \phi - {\omega _z}\sin \phi \\ \dot \psi = \left( {{\omega _y}\sin \phi - {\omega _z}\cos \phi } \right)/\sin \theta \\ \dot \phi = {\omega _x} + \left( {{\omega _y}\sin \gamma + {\omega _z}\cos \gamma } \right)\tan \theta {\rm{ }} \end{array} \right\} $ | (5) |
其中$\theta $,$\psi $和$\phi $ 分别表示俯仰角、偏航角和滚转角.
一体化数值模拟涉及到动力学方程、流体力学控制方程以及飞行控制律的耦合求解,因此建立一套有效的耦合求解策略是该方法能够成功的前提.
动力学方程、流体力学控制方程的耦合可以采用``紧耦合''或``松耦合''的方式,其区别在于动力学方程是采用显式还是隐式时 间离散. 松耦合过程中,物理时间每推进一步,动力学方程、流体力学控制方程之间仅进行一次信息交互,动网格进行一次调整;紧耦合的物 理时间推进过程中要进行若干次的内迭代,每一次内迭代里动力学方程、流体力学控制方程都需要进行信息交互,而计算网格也要进行 相应的调整. 松耦合、紧耦合有不同的适用范围,一般来讲,紧耦合计算的稳定性较好,对时间步长的限制也较小,但是动网格生成的计算量较大; 而在某些特定的条件下,如运动物体密度接近流体密度时,采用松耦合方法往往得不到收敛的计算结果,或者需要采用非常小的时间步 长,这样会严重影响计算效率,所以采用哪种耦合方式要根据实际问题来确定[22].
1.3 控制系统的耦合控制律作为飞行器控制过程的核心模块,是飞行器设计过程中非常重要的一个环节. 每一种飞行器会根据其自身的气动外形特点及机动飞 行要求设计专门的控制律函数. 控制过程可分为开环控制和闭环控制两类,开环控制没有引入反馈机制,舵偏角按照预先设计的规律进行偏转,因此会导致控制系统出现较 大的稳态误差;闭环控制则引入了反馈机制,使控制过程更为精准.
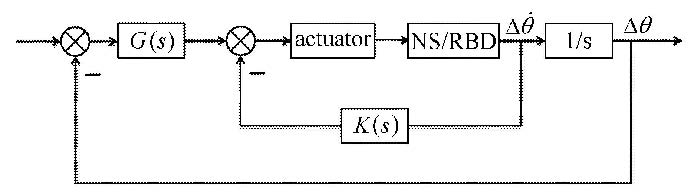
飞行器的控制系统是一个复杂的多学科多物理系统,对于姿态角控制过程,典型的控制回路如图3所示. 闭环控制引入了姿态角的反馈,因此可以达到更好的控制精度;而为了改善控制过程的动态性能,采用了测速反馈控制,通过引入姿态角速度的反馈,以减少调节时间,并可以避免``超调''现象的发生. 在传统的控制律设计过程中,舵偏角和姿态角之间的传递函数通过线化的模型方程和气动力数据库得到,本文的一体化算法则通过直接求 解流体力学控制方程、动力学方程以得到实时的姿态角和非定常气动力. 此外,为简化数值模拟过程,舵机模块的响应在本文中不予考虑.
|
图 3 姿态角控制过程的控制回路示意图 Fig.3 Sketch of the AOA controlling process |
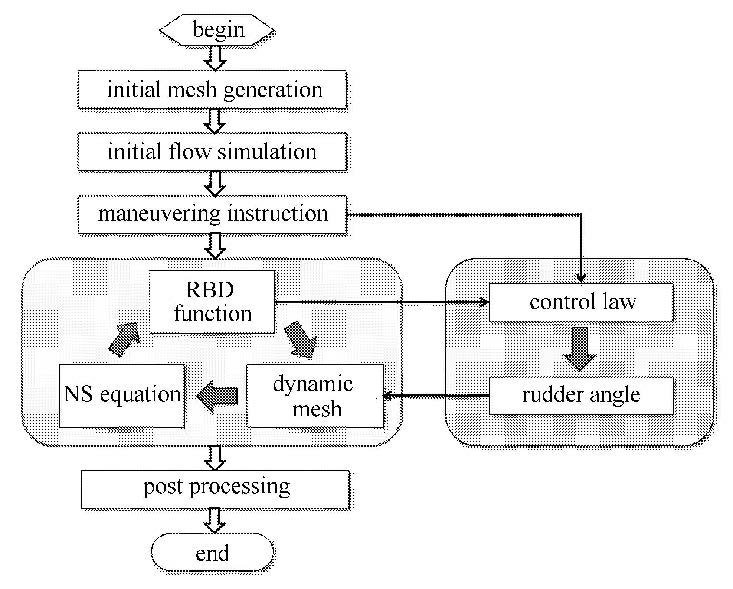
控制系统的执行是有一定的时间间隔的,对于本文的导弹模型,其控制系统的指令时间间隔为毫秒量级;此外,流体力学 控制方程、动力学方程的耦合求解仅作为整个控制回路的一个环节. 鉴于控制系统的这些特点,一体化数值模拟过程中控制律模块并不和流体力学控制方程、动力学方程进行实时耦合求解,而是当到达一定的物理时间之后,再进行控制律模块的求解. 考虑闭环控制的一体化算法的示意图如图4所示:流体力学控制方程、刚体动力学方程(rigid body dynamic function)、动态混合网格生成作为一个多学科耦合系统,可以采用松耦合或者紧耦合方式进行时间推进;控制系统作为一个相 对独立的模块,在达到调用条件时执行.
|
图 4 一体化计算策略 Fig.4 Procedure of coupling solver |
本文的一体化数值模拟技术基于``HyperFLOW (面向流体工程与研究的混合CFD平台)''软件平台开发[23]. 该软件平台采用C++面向对象的思想设计各 功能模块,并通过管理器对各个功能模块进行灵活的调度,以实现各种复杂的耦合过程. 对于后文的导弹姿态角控制过程,控制律和纳维-斯托克斯方程/动力学方程耦合求解系统之间的输入输出量主要有:导弹 的姿态角、姿态角速度、舵偏角、舵偏角增量等. 整个控制过程(以姿态角30$^\circ$阶跃响应过程为例)的具体执行过程如下:
(1)计算得到导弹在零度攻角下的定常流场,控制律模块输入姿态角30$^\circ$阶跃响应的输入条件;
(2)执行控制律模块,根据当前导弹的运动学参数得到舵偏角增量,同时根据控制系统的需要对该增量进行约束;
(3)不考虑舵机模型的影响,认为舵偏角的变化``瞬间''完成. 根据舵偏角增量,生成舵面附近``变形区''区域内的动态网格;
(4)流体力学控制方程、动力学方程以及``随体运动区''、``扰动松弛区''动态混合网格的耦合求解;
(5)重复(2)$\sim $(4),直到计算结束. 其中在执行(2)时要实时判断当前物理时间是否达到施加控制的条件(例如5ms的倍数).
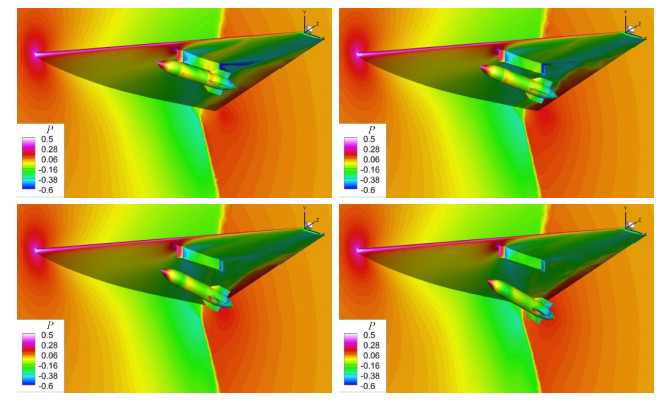
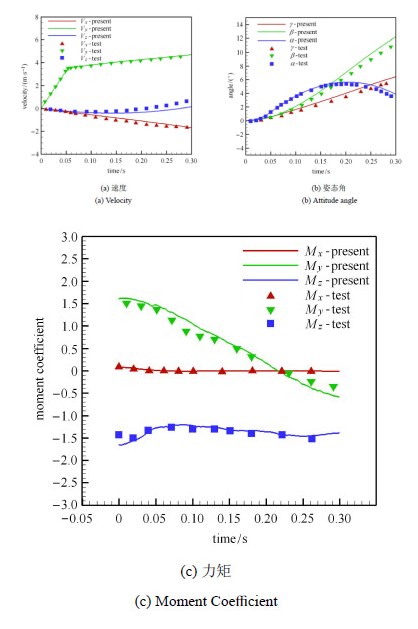
2 计算方法的验证本节通过典型的机翼外挂物投放算例对纳维-斯托克斯方程、动力学方程的耦合算法进行了考核与验证. 机翼、弹体外形与计算条件请参见文献[24]. 计算网格如图5所示,物体边界层内采用了半结构的三棱柱网格,并在前后缘附近采用各向异性的非结构单元进行加密,分离过程中在两体之间的区域进行了若干次局部重构. 图6所示为分离过程中物面及对称面的压力云图,图7所示为计算结果与实验结果对比. 本文的数值模拟对气动力矩的数值以及变化趋势进行了准确的预测,弹体运动速度、姿态角等运动学参数也与实验结果符合良好.

|
图 5 机翼外挂物分离过程的动态混合网格 Fig.5 Hybrid dynamic mesh during store separation process |
|
图 6 分离过程中典型时刻的压力云图 Fig.6 Pressure contours during store separation process |
|
图 7 计算结果与实验结果对比 Fig.7 Numerical results compared with test results |
采用上述数值模拟技术,分别对某战术导弹的姿态角及过载控制过程进行了数值模拟. 该战术导弹由轴对称的弹身和3组空气舵组成,通过4片尾舵的摆动对弹体的姿态进行控制.
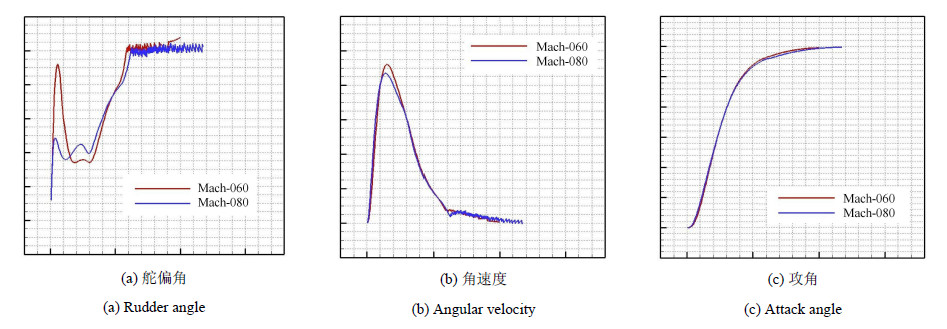
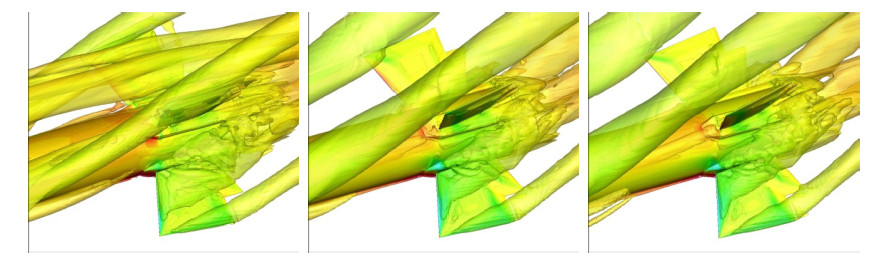
3.1 固定质心位置情况下的姿态角控制过程本节针对质心位置固定的情况,分别对马赫数0.6和0.8两种飞行条件下的姿态角控制过程进行了数值模拟. 飞行控制律的输入指令为 在给定时间内通过舵偏使导弹的攻角由0$^\circ$变为30$^\circ$攻角,并继续保持. 图8(a)所示为舵偏角随时间的变化曲线. 当指令下达后,舵偏角在很短的时间内迅速增加到最大值,并导致弹体俯仰角速度的迅速增加(图8(b)). 当俯仰角速度达到一定数值后,为避免俯仰运动的发散,在控制律的控制作用下,舵偏角开始减小至一个较小的数值. 之后随着俯仰角、角速度等运动参数的变化,舵偏角逐渐增大,并最终稳定在一个合适的数值,弹体的姿态角(图8(c))最终也 被控制至和输入指令相同的角度,说明完成了该机动过程. 图9所示为舵偏过程中尾舵附近的漩涡结构,由于前后有3组翼,因此在攻角较大时前后翼均诱导出较大范围的流动分离,并 与尾舵产生不同程度的干扰,本文的计算给出了较为清晰的分离流动结构.
|
图 8 姿态角控制过程中运动学参数的变化历程 Fig.8 Evolution history of kinetic parameter during maneuvering process of angle of attack |
|
图 9 尾舵附近的漩涡结构 Fig.9 The vortex structure near the rear rudders |
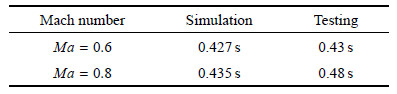
表1所示为本文数值模拟得到的响应时间和控制律仿真预设值的比较,可见结果符合较好,说明本文的一体化数值模拟技术 能够胜任此类虚拟飞行过程的数值模拟,数值模拟结果合理可信.
| 表 1 姿态角控制过程攻角响应时间 Table 1 Response time for the maneuvering process of angle of attack |
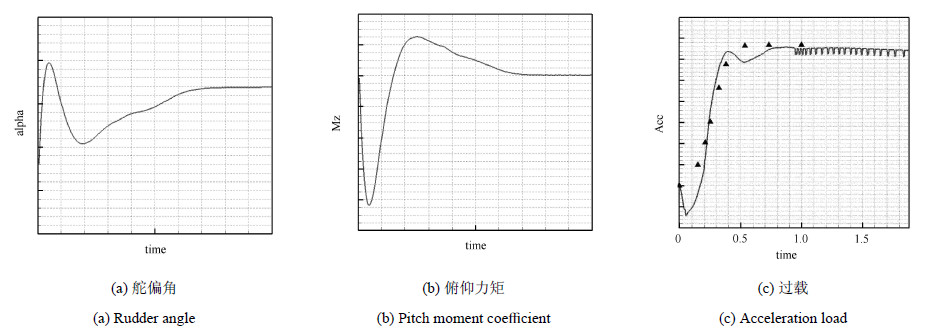
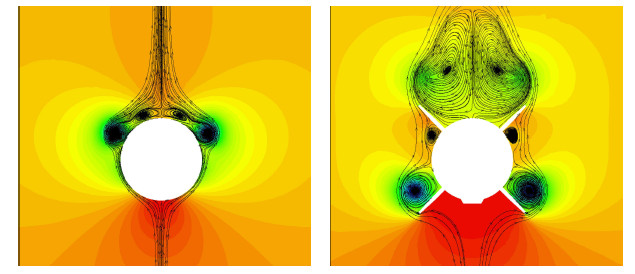
本节对质心位置固定情况下的过载控制过程进行了数值模拟. 过载控制是目前导弹控制律设计的主要方式. 输入参数为所需的过 载量,其指令仍然是在给定的时间内使导弹攻角由0$^\circ$变为30$^\circ$,并继续保持. 收到控制指令后,舵面迅速向下偏转至最大舵偏角(图10(a)),俯仰力矩很快达到峰值(图10(b)). 在俯仰力矩作用下,弹体攻角逐渐增大,并逐渐稳定在给定的攻角范围内. 舵面偏转角在达到最大之后逐渐减小,并出现负舵偏,之后舵偏逐渐增加并稳定在一定角度范围内. 在舵面这一系列运动的影响下,俯仰力矩出现了一次较大幅度的波动,之后逐渐稳定在0附近. 图10(c)为法向过载的变化情况,图中标注了飞控仿真的结果,二者符合良好. 图11所示为典型状态下的截面流线,受非定常流动迟滞效应的影响,在目前的舵面布局条件下并没有出现明显的流动非对称.
|
图 10 过载控制过程中运动学参数的变化历程 Fig.10 Evolution history of kinetic parameter during acceleration load controlling process |
|
图 11 过载控制过程中典型位置截面上的压力云图及流线 Fig.11 Pressure contour and streamlines at two cross section |
在实际的被动段飞行过载控制过程中,随着弹体姿态角的增大,受阻力影响其飞行速度会迅速降低,这样导致来流的动压减小. 控制系 统为了维持过载指令,必须根据弹体的运动信息进行适时调整,因此其整个控制过程必然和固定质心、固定来流条件下的情况不同.
针对``变马赫数''机动过程的数值模拟在惯性系下进行,即通过物体的运动来实现其相对马赫数的变化. 在惯性系下进行计算可以维持 来流条件,且流场的参考值如来流动压、来流速度等也可以维持不变,这样有助于数值模拟过程的简化. 但是在计算过程中需要考虑弹体的两自由度运动:俯仰运动以及沿来流方向的平动(为了简化运动方式,暂不考虑法向运动. 事实上,本文的方法能够进行六自由度运动的模拟). 对于较长的飞行时间,飞行器的位移会变得非常大,因此会造成动态网格生成上的问题. 为克服这一问题,本文给计算网格点引入了``虚拟速度'':物体发生位移后,计算网格并不进行运动,而是引入一个由该运动引入 的``虚拟速度'',在进行流场求解时,计算控制体边界运动速度时考虑该``虚拟速度''的影响即可.
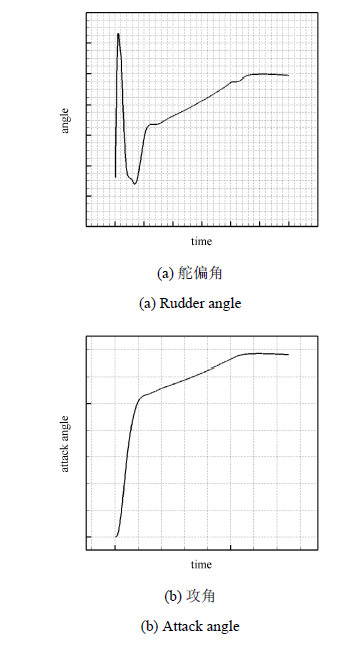
初始时刻马赫数为0.74,机动控制过程中导弹的飞行速度会发生较大变化,马赫数会逐渐减小至0.6左右. 输入指令为固定的法向过载. 图12所示为舵偏角随时间的变化曲线,在指令下达后最初的一 段时间内,舵偏角的变化规律和3.2节类似,之后由于来流马赫数的变化,来流动压逐渐减小,因此舵偏角会在较长的一段时间内持续增加,以维持其法向过载. 而攻角的变化也类似,会有较长一段时间的持续增加过程,以提高升力系数,从而匹配来流动压减小带来的过载损失. 从数值模拟结果来流,该控制律能够达到较好的过载控制效果.
|
图 12 过载控制过程中运动学参数的变化历程(变马赫数情况) Fig.12 Evolution history of kinetic parameters during acceleration load controlling process (with varying Mach number) |
本文基于动态混合网格技术,通过耦合求解动力学方程、流体力学控制方程和飞行控制律,建立了能够适用于``数值虚拟飞行''的一体 化计算方法. 采用该数值模拟技术,对某导弹的姿态角控制过程、过载控制过程以及变马赫数情况下的过载控制过程进行了初步的数值研究.
下一步将在如下几个方面开展进一步的研究工作:(1)更为高效的动态混合网格生成技术研究;(2)针对大攻角分离流动的脱体涡模 拟算法研究;(3)针对航空飞行器的复杂机动过程(如战斗机过失速机动飞行),开展有关飞行控制律的设计及应用研究.
| [1] | Lawrence FC and Mills BH. Status update of the AEDC wind tunnel virtual flight testing development program. AIAA Paper 2002-0168. |
| [2] | 李浩, 赵忠良, 范召林. 风洞虚拟飞行试验模拟方法研究. 实验流体力学, 2011, 25(6): 72-76 (Li Hao, Zhang Zhongliang, Fan Zhaolin. Simulation method for wing tunnel based virtual flight testing. Journal of Experiments in Fluid Mechanics, 2011, 25(6): 72-76 (in Chinese)) |
| [3] | Sahu J. Time-accurate numerical prediction of free-flight aerodynamics of a finned projectile. AIAA Paper 2005-5817 |
| [4] | Sahu J. Time-accurate calculations of free-flight aerodynamics of maneuvering projectiles. In: Proceedings of the HPCMP Users Group Conference 2007. High Performance Computing Modernization Program: A Bridge to Future Defense, Pittsburgh, Pennsylvania, 18-21 June 2007: 64-69 |
| [5] | Green BE. Analysis of the stability and control characteristics of the F/A-18E Super Hornet using the Kestrel CFD flow solver. AIAA Paper 2012-0715, 2012. |
| [6] | Dean JP, Clifton JD, Bodkin DJ, et al. High resolution CFD simulations of maneuvering aircraft using the CREATE/AV- Kestrel solver. AIAA Paper 2011-1109 |
| [7] | Allan MR, Badcock KJ, Richard BE. CFD based simulation of longitudinal flight mechanics with control. AIAA Paper 2005-0046 |
| [8] | Boelens OJ, Prananta BB, Soemarwoto BI, et al. Towards an aero-servo-elastic simulation capability for high-performance fighter aircraft. RTO-MP-AVT-123(30) |
| [9] | Schütte A, Boelens OJ, Loeser T, et al. Prediction of the flow around the X-31 aircraft using two different CFD methods. AIAA Paper 2010-4692 |
| [10] | Heinrich R, Kroll N, Neumann J, et al. Fluid-structure coupling for aerodynamic analysis and design - A DLR perspective. AIAA Paper 2008-561 |
| [11] | 达兴亚, 陶洋, 赵忠良. 基于预估校正和嵌套网格的虚拟飞行数值模拟. 航空学报, 2012, 33(6): 977-983 (Da Xingya, Tao Yang, Zhang Zhongliang. Numerical simulation of virtual flight based on prediction-correction coupling method and chimera grid. Acta Aeronautica et Astronautica Sinica, 2012, 33(6): 977-983(in Chinese)) |
| [12] | 陶洋, 范召林, 吴继飞. 基于CFD的方形截面导弹纵向虚拟飞行模拟. 力学学报, 2010, 42(2): 169-176 (Tao Yang, Fan Zhaolin, Wu Jifei. CFD based virtual flight simulation of square cross-section missile with control in longitudinal flight. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(2): 169-176(in Chinese)) |
| [13] | Frederic JB. Consideration on the spring analogy. International Journal for Numerical Methods in Fluids, 2000, 32: 647-668 |
| [14] | Liu XQ, Qin N, Xia H, Fast dynamic grid deformation based on Delaunay graph mapping. J Comput Phys, 2006, 211: 405-423 |
| [15] | Rendall TCS, Allen CB. Efficient mesh motion using radial basis functions with data reduction algorithms. J Comput Phys, 2009, 229(7): 6231-6249 |
| [16] | 张来平, 邓小刚, 张涵信. 动网格生成技术及非定常计算方法进展综述. 力学进展, 2010, 40(4): 424-447(Zhang Laiping, Deng Xiaogang, Zhang Hanxin. Reviews of moving grid generation techniques and numerical methods for unsteady flow. Advances in Mechanics, 2010, 40(4): 424-447(in Chinese)) |
| [17] | 张来平, 马戎, 常兴华等 . 虚拟飞行中气动、运动和控制耦合的数值模拟技术. 力学进展, 2014, 44 : 201410 (Zhang Laiping, Ma Rong, Chang Xinhua, et al. Review of aerodynamics/kinetics/flight-control coupling methods in virtual flight simulations. Advances in Mechanics, 2014, 44: 201410 (in Chinese)) |
| [18] | 张来平, 段旭鹏, 常兴华等. 基于Delaunay背景网格插值方法和局部网格重构的动态混合网格生成技术. 空气动力学学报, 2009, 27(1): 26-32(Zhang Laiping, Duan Xupeng, Chang Xinghua, et al. A hybrid dynamic grid generation technique for morphing bodies based on Delaunay graph and local remeshing. Acta Aerodynamica Sinica, 2009, 27(1): 26-32 (in Chinese)) |
| [19] | Zhang LP, Chang XH, Duan XP, et al. Applications of dynamic hybrid grid method for three-dimensional moving/deforming boundary problems. Computers & Fluids, 2012, 62: 45-63 |
| [20] | Zhang LP, Wang ZJ. A block LU-SGS implicit dual time-stepping algorithm for hybrid dynamic meshes. Computers & Fluids, 2004 , 33:891-916 |
| [21] | Prewitt NC, Belk DM, Shyy W. Parallel computing of overset grids for aerodynamic problems with moving objects. Progress in Aerospace Sciences, 2000, 36: 117-172 |
| [22] | Söding. How to integrate free motions of solids in fluids. Fourth Numerical Towing Tank Symposium, Hamburg, Germany, 2001 |
| [23] | He X, Zhang LP, Zhao Z. The research and development of structured-unstructured hybrid CFD software. The Ninth Asian CFD Conference, Nanjing, 2012, 08 |
| [24] | Hall LH, Parthasarathy V. Validation of an automated Chimera/6-DOF methodology for multiple moving body problems. The 6th AIAA Aerospace Sciences Meeting and Exhibit, January 12-15, 1998 |
2. China Aerodynamics Research and Development Center, Mianyang 621000, China
 2015, Vol. 47
2015, Vol. 47