引 言
当前,黏弹性材料在工程中获得了广泛应用,由弹性/黏弹性介质构成的组合结构日益增多,如固体火箭发动机的壳体/绝热层、芯片封装结构中的芯片/下填料以及高分子聚合物粘接结构等等.在这些组合结构中,界面往往是最薄弱的部位,由于使用环境变化、疲劳、蠕变等因素而萌生的界面裂纹,是导致界面剥离、结合部失效最为常见的原因. 因此,对黏弹性界面裂纹的分析和评价,对结合材料的强度和可靠性评估具有重要意义.自从Wlliams[1]首先分析双弹性材料界面裂纹奇异性以来,经过Rice 等[2, 3],Erdogan[4],Comninou[5]等学者的研究,双弹性材料界面的断裂分析,基本上已经建立了比较完整的理论体系和较为成熟的分析方法[6];均质线黏弹性材料断裂问题,应用黏弹性理论和有限元等数值方法,一般也能得到令人满意的解答[7].而对于弹性/黏弹性、黏弹性/黏弹性界面断裂,由于问题本身的复杂性,裂纹尖端奇异场几乎不可能得到精确地解析解,相关的研究文献较少.早期比较有代表性的工作是Atkinson等[8]和Chang[9]对黏弹性界面裂纹尖端应力奇异性的研究,研究对象大多为反平面问题,Han等[10, 11]运用解析法,通过对应原理和拉普拉斯逆变换研究了无限大平板黏弹性界面裂纹断裂参量的理论解.Kuo等[12]运用Stroh公式研究了黏弹性界面折点的应力奇异性,Wang等[13]采用复变函数法,推导了压电螺型位错和双黏弹性压电材料界面相互作用的解析解.刘玉岚等[14]根据经典梁的理论,计算了含有界面裂纹的黏弹性层合板应变能释放率.王振清等[15]建立了双材料界面扩展裂纹尖端的弹黏塑性控制方程,引入界面裂纹尖端的位移势函数和边界条件,对刚性-弹黏 塑性界面I型界面裂纹进行了数值分析.对结构和边界形状通常都比较复杂的工程界面断裂问题,一般只能用数值方法求解.Chen等[16]发展了一种可用于各向异性弹材料界面裂纹的边界元方法,沈辉等[17]构造了一种平面应力奇异薄层单元,用此单元研究了双材料界面层的刚度对界面裂纹尖端场的影响.李彪等[18]提出了一种由刚性元和零厚度的内聚力单元组合而成的新型界面单元,该界面单元嵌在板壳结构界面,用来模拟界面损伤的起始和演化. 王舒等[19]应用改进的虚拟裂纹闭合法对热、力载荷作用下多材料构件连接区界面进行断裂分析. 王亮等[20]在试验的基础上,采用基于损伤力学的黏聚区模型对压电复合材料界面的起裂和脱胶扩展进行了分析,并与虚拟裂纹闭合法进行了比较.汤丽华和许金泉[21]应用常规有限元方法研究了黏弹性界面裂纹奇异场,并和经典近似解做了对比.近年来,扩展有限元方法[22, 23]由于在断裂问题特别是裂纹扩展分析方面的突出优点,引起国内外学者广泛关注.Bouhala等[24]应用扩展有限元方法对裂尖位于双材料界面上的I型界面裂纹问题进行了研究,李录贤等[25],金峰等[26]对扩展有限元方法及其应用做了比较全面的综述,成斌斌等[27]对亚界面断裂问题的扩展有限元方法进行了研究,董文玉等[28]给出了一种可直接计算应力强度因子的扩展有限元方法,但该方法不适合于增量求解.目前,应用扩展有限元方法研究黏弹性界面断裂问题的文献还非常少见.
在界面断裂有限元分析中,常用具有$r^{\lambda -1}$奇异性的移动节点型奇异单元[29, 30],但由于黏弹性界面裂 纹问题奇异性指数$\lambda$是随时间变化的,此时,"加料"型奇异单元[31]能更好地反映这一特点,解决了移动节点型奇异单元只适用于某一特定奇异性指数的不足.与常规有限元方法相比,"加料"有限元方法可减小网格划分规模,降低计算成本,并且能通过求解有限元方程直接得到应力强度因子,避免了外插法等间接方法带来的精度损失.Bayram等[32, 33]分别应用"加料"有限元方法研究了双弹性材料二维、三维界面裂纹问题,段静波等[34, 35]提出了均质线黏弹性介质断裂分析的增量"加料"有限元方法,而用于黏弹性界面断裂分析的增量"加料"有限元方法还未见相关文献报道.
本文将"加料"有限元方法用于弹性/黏弹性界面裂纹的断裂分析,通过对应原理和拉普拉斯逆变换得到黏弹性界面裂纹位移场,将其加入常规单元位移模式中,推导增量"加料"有限元方程,由附加节点自由度得到黏弹性界面裂纹的应力强度因子和应变能释放率.通过和无限大黏弹性板中心界面裂纹断裂参量理论解对比,验证本文的方法的正确性和有效性,并对其在芯片封装结构弹性/黏弹性界面断裂分析中的应用进行了初步研究.
1 黏弹性界面裂纹尖端位移场
对图1所示两种线黏弹性介质构成的界面裂纹($E_1 (t),\nu _1 $,$E_2 (t),\nu _2$分别表示材料1和材料2的松弛模量和泊松比),将泊松比视为常量,根据双弹性材料界面裂纹尖端位移场解答[36],通过对应原理,可得到黏弹性界面裂纹尖端位移场在裂尖直角坐标系${o}'{x}'{y}'$中的表达式
|
\[\begin{array}{l}
{u_{x'}}\left( t \right) = {L^{ - 1}}\left[ {\tilde f_{11}^k\left( {r,\theta ,p} \right){{\tilde K}_1}\left( p \right)/\tilde E_k^*\left( p \right)} \right] + \\
{L^{ - 1}}\left[ {\tilde f_{12}^k\left( {r,\theta ,p} \right){{\tilde K}_2}\left( p \right)/\tilde E_k^*\left( p \right)} \right]
\end{array}\]
|
(1a) |
|
\[\begin{array}{l}
{u_{y'}}\left( t \right) = {L^{ - 1}}\left[ {\tilde f_{21}^k\left( {r,\theta ,p} \right){{\tilde K}_1}\left( p \right)/\tilde E_k^*\left( p \right)} \right] + \\
{L^{ - 1}}\left[ {\tilde f_{22}^k\left( {r,\theta ,p} \right){{\tilde K}_2}\left( p \right)/\tilde E_k^*\left( p \right)} \right]
\end{array}\]
|
(1b) |
其中,$u_{x'} $,$u_{y'} $为${x}'$和${y}'$方向的位移,$p$为拉普拉斯变换参数,${\cal L}^{ -1}$表示拉普拉斯逆变换,上标"$\sim $"表示拉普拉斯变换,$k$ 表示两种不同的材料($k= 1,2$),$\tilde {K}_1\left( p \right)$和 $\tilde {K}_2 \left( p\right)$表示界面裂纹张开和滑开型模态应力强度因子的拉普拉斯变换,$\tilde {E}_k^ * \left( p \right) = p\tilde{E}$,为拉普拉斯域中对应的弹性常数. $\tilde {K}_1 $和 $\tilde {K}_2 $定义如下
|
\[{\left. {{{\tilde \sigma }_{yy}} + {\rm{i}}{{\tilde \sigma }_{xy}}} \right|_{\theta = 0}} = \frac{{{{\tilde K}_1} + {\rm{i}}{{\tilde K}_2}}}{{\sqrt {2\pi r} }}{\left( r \right)^{i{{\tilde \zeta }^*}}}\]
|
(2a) |
式(1)裂尖位移场要求界面为完全结合界面,边界条件不包括时间相依的边界区域,且为准静态情况. 拉普拉斯平面中裂尖位移角函数$\tilde{f}_{ij}^k \left( {r,\theta ,p} \right)$可写为如下形式
|
\[\tilde f_{11}^k = \frac{{\sqrt {2\pi r} \left( {1 + {\nu _k}} \right)}}{{\cosh \left( {\pi {{\tilde \zeta }^*}} \right)}}\left[ {\left( {{D_k} + 2{\delta _k}\sin \theta \sin \Theta } \right)} \right]\]
|
(2b) |
|
\[\tilde f_{12}^k = \frac{{ - \sqrt {2\pi r} \left( {1 + {\nu _k}} \right)}}{{\cosh \left( {\pi {{\tilde \zeta }^*}} \right)}}\left[ {\left( {{H_k} - 2{\delta _k}\sin \theta \cos \Theta } \right)} \right]\]
|
(2c) |
|
\[\tilde f_{21}^k = \frac{{ - \sqrt {2\pi r} \left( {1 + {\nu _k}} \right)}}{{\cosh \left( {\pi {{\tilde \zeta }^*}} \right)}}\left[ {\left( {{H_k} + 2{\delta _k}\sin \theta \cos \Theta } \right)} \right]\]
|
(2d) |
|
\[\tilde f_{22}^k = \frac{{ - \sqrt {2\pi r} \left( {1 + {\nu _k}} \right)}}{{\cosh \left( {\pi {{\tilde \zeta }^*}} \right)}}\left[ {\left( {{D_k} - 2{\delta _k}\sin \theta \sin \Theta } \right)} \right]\]
|
(2e) |
|
\[{\delta _1} = {{\rm{e}}^{ - \left( {\pi - \theta } \right){{\tilde \zeta }^*}}}, {\delta _2} = {{\rm{e}}^{\left( {\pi + \theta } \right){{\tilde \zeta }^*}}}\]
|
(3a) |
|
\[\Theta = {\tilde \zeta ^*}\lg r + 0.5\theta \]
|
(3b) |
|
\[{D_k} = \alpha {\gamma _k}\cos \left( {0.5\theta } \right) + \alpha '{\gamma '_k}\sin \left( {0.5\theta } \right)\]
|
(3c) |
|
\[{H_k} = \alpha '{\gamma _k}\cos \left( {0.5\theta } \right) - \alpha {\gamma '_k}\sin \left( {0.5\theta } \right)\]
|
(3d) |
|
\[\alpha = \frac{{0.5\cos \left( {{{\tilde \zeta }^*}\lg r} \right) + {{\tilde \zeta }^*}\sin \left( {{{\tilde \zeta }^*}\lg r} \right)}}{{0.25 + {{\tilde \zeta }^{*2}}}}\]
|
(3e) |
|
\[\alpha ' = \frac{{0.5\sin \left( {{{\tilde \zeta }^*}\lg r} \right) - {{\tilde \zeta }^*}\cos \left( {{{\tilde \zeta }^*}\lg r} \right)}}{{0.25 + {{\tilde \zeta }^{*2}}}}\]
|
(3f) |
|
\[{\gamma _k} = {\kappa _k}{\delta _k} - 1/{\delta _k},{\gamma '_k} = {\kappa _k}{\delta _k} + 1/{\delta _k}\]
|
(3g) |
|
\[{\tilde \zeta ^*} = \ln \left[ {\left( {1 - {{\tilde \beta }^*}} \right)/\left( {1 + {{\tilde \beta }^*}} \right)} \right]/2\pi \]
|
(3h) |
|
\[{\tilde \beta ^*} = \frac{{p{{\tilde \mu }_1}({\kappa _2} - 1) - p{{\tilde \mu }_2}({\kappa _1} - 1)}}{{p{{\tilde \mu }_1}({\kappa _2} + 1) + p{{\tilde \mu }_2}({\kappa _1} + 1)}}\]
|
(3i) |
其中,$r$和$\theta $为裂尖局部极坐标下的径向和周向坐标,$\tilde {\mu}$为切变模量的拉普拉斯变换,$\tilde {\zeta }$为结合材料振荡指数$\zeta (t)$的拉普拉斯变换,$\kappa$为科洛索夫常数,对于平面应力$\kappa = {(3 - \nu )} \Big/ {(1 + \nu )}$,对于平面应变$\kappa = 3 - 4\nu $.由式(3)非常复杂,不可能通过拉普拉斯逆变换得到裂尖位移角函数的精确解析表达式,因此,采用基于直接逆变换和准静态法相结合的近似方 法[10],得到裂尖位移场近似表达式
|
\[{u_{x'}}\left( t \right) = f_{11}^k\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{1k}}\left( t \right) + f_{12}^k\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{2k}}\left( t \right)\]
|
(4a) |
|
\[{u_{y'}}\left( t \right) = f_{21}^k\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{1k}}\left( t \right) + f_{22}^k\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{2k}}\left( t \right)\]
|
(4b) |
|
\[{\psi _{1k}}\left( t \right) = {L^{ - 1}}\left[ {{{\tilde K}_1}\left( p \right)/\tilde E_k^*\left( p \right)} \right]\]
|
(5a) |
|
\[{\psi _{2k}}\left( t \right) = {L^{ - 1}}\left[ {{{\tilde K}_2}\left( p \right)/\tilde E_k^*\left( p \right)} \right]\]
|
(5b) |
变量$\psi _{ik} \left( t \right)$和节点位移$u_i \left( t \right)$是需要求解的基本量.将裂尖位移场加入到相应的常规单元位移场中,需要进行坐标变换,把裂尖直角坐标系${x}'{o}'{y}'$中的位移$u_{x'}$和$u_{y'} $变换为整体坐标系$xoy$中的位移$u_x $和$u_y $,变换关系式如下
|
\[{\left\{ {{u_x} - {x_{o'}}{u_y} - {y_{o'}}} \right\}^{\rm{T}}} = T{\left\{ {{u_{x'}}{u_{y'}}} \right\}^{\rm{T}}}\]
|
(6a) |
式中,$u_x $和$u_y $为整体坐标系$x$和$y$方向的位移,$\left( {x_{o'} ,y_{o'} }\right)$为裂尖在整体坐标系中的坐标. ${ T}$为变换矩阵
|
\[T = \left[ {\begin{array}{*{20}{l}}
{\cos \left( {x',x} \right)}&{\cos \left( {y',x} \right)}\\
{\cos \left( {x',y} \right)}&{\cos \left( {y',y} \right)}
\end{array}} \right]\]
|
(6b) |
2 黏弹性界面裂纹"加料"单元位移模式
2.1 "加料"裂尖单元
对于4节点四边形等参元,在常规单元位移模式中加入黏弹性界面裂纹尖端位移场后,可得
|
\[\begin{array}{l}
{u_i} = {\alpha _{i1}} + {\alpha _{i2}}\xi + {\alpha _{i3}}\eta + {\alpha _{i4}}\xi \eta + \\
{F_{i1}}\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{11}} + {F_{i2}}\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{21}} + \\
{F_{i3}}\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{12}} + {F_{i4}}\left( {r,\theta ,\zeta \left( t \right)} \right){\psi _{22}}
\end{array}\]
|
(7) |
式中,$u_i \left( {i = 1,2} \right)$分别表示总体坐标系下加料界面裂纹单元$x$和$y$方向的位移,$\xi $和 $\eta $分别为单元局部坐标系的坐标轴,对材料1有
|
\[\left. {\begin{array}{*{20}{l}}
{{F_{i1}}\left( {r,\theta ,\zeta \left( t \right)} \right) = F_{i1}^1\left( {r,\theta ,\zeta \left( t \right)} \right)}\\
{{F_{i2}}\left( {r,\theta ,\zeta \left( t \right)} \right) = F_{i2}^1\left( {r,\theta ,\zeta \left( t \right)} \right)}\\
{{F_{i3}}\left( {r,\theta ,\zeta \left( t \right)} \right) = 0}\\
{{F_{i4}}\left( {r,\theta ,\zeta \left( t \right)} \right) = 0}
\end{array}} \right\}\]
|
(8a) |
对材料2有
|
\[\left. {\begin{array}{*{20}{l}}
{{F_{i1}}\left( {r,\theta ,\zeta \left( t \right)} \right) = 0}\\
{{F_{i2}}\left( {r,\theta ,\zeta \left( t \right)} \right) = 0}\\
{{F_{i3}}\left( {r,\theta ,\zeta \left( t \right)} \right) = F_{i1}^2\left( {r,\theta ,\zeta \left( t \right)} \right)}\\
{{F_{i4}}\left( {r,\theta ,\zeta \left( t \right)} \right) = F_{i2}^2\left( {r,\theta ,\zeta \left( t \right)} \right)}
\end{array}} \right\}\]
|
(8b) |
|
\[\left\{ {\begin{array}{*{20}{l}}
{F_{i1}^k\left( {r,\theta ,\zeta \left( t \right)} \right)}\\
{F_{i2}^k\left( {r,\theta ,\zeta \left( t \right)} \right)}
\end{array}} \right\} = T\left\{ {\begin{array}{*{20}{l}}
{f_{i1}^k\left( {r,\theta ,\zeta \left( t \right)} \right)}\\
{f_{i2}^k\left( {r,\theta ,\zeta \left( t \right)} \right)}
\end{array}} \right\}\]
|
(8c) |
将等参元节点局部坐标$\left( {\xi _i ,\eta _i } \right)$代入式(7)中,可得到广义坐标$\alpha _{ij}$的表达式,再将得到的广义坐标$\alpha _{ij} $回代到式(7)中,并令$\psi _{11} = \psi _1 $,$\psi _{12} = \psi _2$,$\psi _{21} = \psi _3 $,$\psi _{22} = \psi _4 $,得到四节点加料界面裂尖单元的位移模式
|
\[\begin{array}{l}
{u_i} = \sum\limits_{m = 1}^4 {{N_m}} \left( {\xi ,\eta } \right){{\bar u}_{im}}\left( t \right) + \\
\sum\limits_{j = 1}^4 \{ {\psi _j}[{F_{ij}}\left( {r,\theta ,\zeta \left( t \right)} \right) - \\
\sum\limits_{m = 1}^4 {{N_m}} \left( {\xi ,\eta } \right){{\bar F}_{ijm}}\left( {r,\theta ,\zeta \left( t \right)} \right)]\}
\end{array}\]
|
(9) |
式中,$N_m \left( {\xi ,\eta } \right)$为常规等参元形函数,$\bar {u}_{im}$为加料裂纹单元第$m$个节点处的节点位移值,$\bar {F}_{ijm} \left( {r,\theta,\zeta \left( t \right)} \right)$为整体坐标系下角函数$F_{ij} \left({r,\theta ,\zeta \left( t \right)} \right)$在第$m$个节点处的函数值,$\psi _j$为附加节点自由度,它和时变应力强度因子相关,定义见式(5).
2.2 过渡单元
在"加料"裂尖单元和常规单元之间采用过渡单元,以消除两种单元因位移模式引起的位移不协调问题,从而保证有限元解得收敛,提高计算精度. 在"加料"裂尖单元位移模式的基础上,引入一个调整函数$Z(\xi ,\eta)$来构造过渡单元内位移函数,即
|
\[\begin{array}{l}
{u_i} = \sum\limits_{m = 1}^4 {{N_m}} \left( {\xi ,\eta } \right){{\bar u}_{im}} + \\
Z(\xi ,\eta )\sum\limits_{j = 1}^4 \{ {\psi _j}[{F_{ij}}\left( {r,\theta ,\zeta \left( t \right)} \right) - \\
\sum\limits_{m = 1}^4 {{N_m}} \left( {\xi ,\eta } \right){{\bar F}_{ijm}}\left( {r,\theta ,\zeta \left( t \right)} \right)]\}
\end{array}\]
|
(10) |
式中,调整函数$Z ( \xi ,\eta )$须满足:$Z ( \xi ,\eta)$在过渡单元与加料裂尖单元交界边上为1,在过渡单元与常规单元交界边上为0,实现从加料裂尖单元到常规单元的协调过渡.本文采用相对简单的线性调整函数
|
\[Z(\xi ,\eta ) = \left\{ {\begin{array}{*{20}{c}}
{0.25(1 \pm \xi )(1 \pm \eta )}&{\left( {\xi = \pm 1,\eta = \pm 1} \right)}\\
{0.5(1 \pm \xi )}&{\left( {\xi = \pm 1} \right)}\\
{0.5(1 \pm \eta )}&{\left( {\eta = \pm 1} \right)}
\end{array}} \right.\]
|
(11) |
在有限元分析过程中,需要根据过渡单元与加料裂尖单元的连接方式以及过渡单元的局部坐标系,选择适当的 表达式.例如,当过渡单元的边$\xi = 1$与加料裂尖单元连接时,满足条件的调整函数$Z(\xi ,\eta )$表达式为$Z(\xi ,\eta ) =0.5(1 + \xi )$.
3 增量型"加料"有限元法
3.1 位移和应变的增量形式
为了便于推导有限元方程,将"加料"单元、过渡单元位移模式统一写成如下向量形式
|
\[u\left( {{t_m}} \right) = \left[ {N{N_\psi }\left( {{t_m}} \right)} \right]\left\{ {\begin{array}{*{20}{c}}
{\bar u\left( {{t_m}} \right)}\\
{\bar \psi \left( {{t_m}} \right)}
\end{array}} \right\}\]
|
(12) |
式中,${ N}$是常规单元形函数,$ \bar { u} $是节点位移列向量;${ N }_\psi$为"加料"单元或过渡单元的附加形函数,$ \bar { \psi }$为附加自由度向量. ${ N }_\psi $的具体形式如下
|
\[{N_\psi }\left( {{t_m}} \right) = \left[ {\begin{array}{*{20}{c}}
{{N_{\psi 11}}}&{{N_{\psi 12}}}&{{N_{\psi 13}}}&{{N_{\psi 14}}}\\
{{N_{\psi 21}}}&{{N_{\psi 22}}}&{{N_{\psi 23}}}&{{N_{\psi 24}}}
\end{array}} \right]\]
|
(13a) |
|
\[\begin{array}{l}
{N_{\psi ij}} = Z(\xi ,\eta )\left[ {{F_{ij}}(r,\theta ,\zeta (t)) - } \right.\\
\left. {\sum\limits_{m = 1}^{{m_k}} {{N_m}(\xi ,\eta ){{\bar F}_{ijm}}(r,\theta ,\zeta (t))} } \right]
\end{array}\]
|
(13b) |
对于"加料"单元$Z(\xi ,\eta ) \equiv1$,过渡单元按式(11)取值,将位移向量式(12)代入位移应变关系${ \varepsilon } ={ L} { u} $中,得到
|
\[\varepsilon \left( {{t_m}} \right) = \left[ {B{B_\psi }\left( {{t_m}} \right)} \right]\left\{ {\begin{array}{*{20}{c}}
{\bar u\left( {{t_m}} \right)}\\
{\bar \psi \left( {{t_m}} \right)}
\end{array}} \right\}\]
|
(14) |
${ B}$表示单元常规应变矩阵,${ B}_\psi $则是由于 "加料"界面裂纹单元位移模式引入裂纹尖端位移项而产生的附加项,称之为附加应变矩阵.
由"加料"单元形函数矩阵和应变矩阵表达式可见,它们不仅是空间坐标的的函数,同时也是与时间相关的振荡 指数$\zeta(t)$的函数. 式(12)和式(14)对时间$t$微分,得到相应的增量形式
|
\[\begin{array}{l}
\Delta u\left( {{t_m}} \right) = \left[ {N{N_\psi }\left( {{t_m}} \right)} \right]{\left\{ {\Delta \bar u\left( {{t_m}} \right)\Delta \bar \psi \left( {{t_m}} \right)} \right\}^{\rm{T}}} + \\
\left[ {{\bf{0}}\Delta {N_\psi }\left( {{t_m}} \right)} \right]{\left\{ {\bar u\left( {{t_m}} \right)\bar \psi \left( {{t_m}} \right)} \right\}^{\rm{T}}}
\end{array}\]
|
(15) |
|
\[\begin{array}{l}
\Delta \varepsilon \left( {{t_m}} \right) = \left[ {B{B_\psi }\left( {{t_m}} \right)} \right]{\left\{ {\Delta \bar u\left( {{t_m}} \right)\Delta \bar \psi \left( {{t_m}} \right)} \right\}^{\rm{T}}} + \\
\left[ {{\bf{0}}\Delta {B_\psi }\left( {{t_m}} \right)} \right]{\left\{ {\bar u\left( {{t_m}} \right)\bar \psi \left( {{t_m}} \right)} \right\}^{\rm{T}}}
\end{array}\]
|
(16) |
式中$\Delta { N }_\psi \left( {t_m } \right)$和$\Delta {B }_\psi \left( {t_m } \right)$可写成如下形式
|
\[\Delta {N_\psi }\left( {{t_m}} \right) = \left[ {\partial {N_\psi }\left( {\zeta \left( {{t_m}} \right)} \right)/\partial \zeta \left( {{t_m}} \right)} \right]\Delta \zeta \left( {{t_m}} \right)\]
|
(17) |
|
\[\Delta {B_\psi }\left( {{t_m}} \right) = \left[ {\partial {B_\psi }\left( {\zeta \left( {{t_m}} \right)} \right)/\partial \zeta \left( {{t_m}} \right)} \right]\Delta \zeta \left( {{t_m}} \right)\]
|
(18) |
具有物理意义的$\zeta $绝对值不超过0.175[6],由式(2)和式(13)可知,${ N }_\psi \left( {\zeta \left(t \right)} \right)$和${ B }_\psi \left( {\zeta \left( t \right)} \right)$关于$\zeta \left( t\right)$连续可微且为有限值,$\Delta { N }_\psi \left( {t_m } \right)$和$\Delta { B }_\psi \left( {t_m} \right)$是$\Delta \zeta (t_m )$的一阶小量. 对于黏弹性界面裂纹,一定时间步长内$\zeta (t)$的变化量$\Delta\zeta (t_m )$是非常小的,因此忽略$\Delta \zeta (t)$的一阶小量,式(12)和式(14)的增量形式为
|
\[\Delta u\left( {{t_m}} \right) = \left[ {N{N_\psi }} \right]\left\{ {\begin{array}{*{20}{c}}
{\Delta \bar u\left( {{t_m}} \right)}\\
{\Delta \bar \psi \left( {{t_m}} \right)}
\end{array}} \right\}\]
|
(19) |
|
\[\Delta \varepsilon \left( {{t_m}} \right) = \left[ {B{B_\psi }} \right]\left\{ {\begin{array}{*{20}{c}}
{\Delta \bar u\left( {{t_m}} \right)}\\
{\Delta \bar \psi \left( {{t_m}} \right)}
\end{array}} \right\}\]
|
(20) |
3.2 增量型黏弹性本构方程
对各向同性线黏弹性材料,一般情况下泊松比可近似为常数,积分型本构关系可写为
|
\[\sigma (t) = DE(0)\varepsilon (t) + D\int_0^t \varepsilon (t - \tau ')\frac{{{\rm{d}}E(\tau ')}}{{{\rm{d}}\tau '}}{\rm{d}}\tau '\]
|
(21) |
${ \sigma }(t)$与${ \varepsilon }(t)$分别为$t$时刻的应力向量与应变向量,${ D}$为材料矩阵,$E(t)$为黏弹性材料的松弛模量,通常用普罗尼(Prony)级数表示
|
\[E(t) = {E_\infty } + \sum\limits_{n = 1}^N {{E_n}} \exp ( - t/{\tau _n})\]
|
(22) |
其中,$E_\infty $是持久模量,式(21)需要在全历程积分,不便于有限元分析,因此,通常假设在时间区间$\left[{t_{m - 1} ,t_m } \right]$内,应变是线性增加的,将积分型本构方程在时域中离散成增量格式
|
\[\left. {\begin{array}{*{20}{l}}
{\Delta \sigma ({t_m}) = D({E_\infty } + \sum\limits_{n = 1}^N {{\beta _n}(\Delta t){E_n}} )\Delta \varepsilon ({t_m}) - }\\
{\qquad \sum\limits_{n = 1}^N {{\alpha _n}(\Delta t){\sigma ^n}({t_{m - 1}})} }\\
{{\alpha _n}(\Delta t) = 1 - {{\rm{e}}^{ - {\textstyle{{\Delta t} \over {{\tau _n}}}}}}}\\
{{\beta _n}(\Delta t) = \frac{{{\tau _n}}}{{\Delta t}}\left( {1 - {{\rm{e}}^{ - {\textstyle{{\Delta t} \over {{\tau _n}}}}}}} \right)}
\end{array}} \right\}\]
|
(23) |
式中,$\Delta t$为时间增量步,$\Delta { \sigma }(t_m )$为$t_{m}$时刻的应力增量,$\Delta {\varepsilon }(t_m )$为$t_{m}$时刻的应变增量,${ \sigma }^n(t_m )$递推关系式如下
|
\[\left. {\begin{array}{*{20}{l}}
{{\sigma ^n}({t_m}) = {E_n}D{\beta _n}(\Delta t)\Delta \varepsilon ({t_m}) - }\\
{\qquad \left( {{\alpha _n}(\Delta t) - 1} \right){\sigma ^n}({t_{m - 1}})}\\
{{\sigma ^n}({t_0}) = {\bf{0}}}
\end{array}} \right\}\]
|
(24) |
3.3 黏弹性界面裂纹增量"加料"有限元方程
对于准静态黏弹性问题,可以忽略黏弹性体的内摩擦引起的能量消耗,根据虚功原理得其单元域内增量形式虚功方程
|
\[\begin{array}{l}
\int_{{\Omega ^e}} \delta {\varepsilon ^{\rm{T}}}\Delta \sigma {\rm{d}}\Omega = \int_{{\Omega ^e}} \delta {u^{\rm{T}}}\Delta f{\rm{d}}\Omega + \\
\int_{{\Gamma ^e}} \delta {u^{\rm{T}}}\Delta p{\rm{d}}\Gamma
\end{array}\]
|
(25) |
其中,$\delta { u }$和$\delta { \varepsilon }$分别为"加料"单元内任一点的虚位移和虚应变,$\Delta { f }(t_m)$为$t_m $时刻的体积力增量,$\Delta { p }(t_m )$为作用在边界上$t_m$时刻的面力增量或集中力增量.
将位移、应变增量关系式(19)和(20)和增量型本构方程式(23)代入虚功方程式(25)中,即可得到增量型"加料"界面裂纹单元平衡方程
|
\[\left[ {\begin{array}{*{20}{c}}
{{K_{uu}}}&{{K_{u\psi }}}\\
{{K_{\psi u}}}&{{K_{\psi \psi }}}
\end{array}} \right]\left\{ {\begin{array}{*{20}{l}}
{\Delta \bar u({t_m})}\\
{\Delta \bar \psi ({t_m})}
\end{array}} \right\} = \left\{ {\begin{array}{*{20}{l}}
{\Delta {F_u}({t_m})}\\
{\Delta {F_\psi }({t_m})}
\end{array}} \right\} - \left\{ {\begin{array}{*{20}{c}}
{F_u^0({t_m})}\\
{F_\psi ^0({t_m})}
\end{array}} \right\}\]
|
(26) |
|
\[\begin{array}{l}
{K_{uu}} = \int_{{\Omega ^e}} {{B^{\rm{T}}}} D({E_\infty } + \sum\limits_{n = 1}^N {{\beta _n}(\Delta t){E_n}} )B{\rm{d}}\Omega \\
{K_{u\psi }} = \int_{{\Omega ^e}} {{B^{\rm{T}}}} D({E_\infty } + \sum\limits_{n = 1}^N {{\beta _n}(\Delta t){E_n}} ){B_\psi }{\rm{d}}\Omega \\
{K_{\psi u}} = \int_{{\Omega ^e}} {B_\psi ^{\rm{T}}} D({E_\infty } + \sum\limits_{n = 1}^N {{\beta _n}(\Delta t){E_n}} )B{\rm{d}}\Omega \\
{K_{\psi \psi }} = \int_{{\Omega ^e}} {B_\psi ^{\rm{T}}} D({E_\infty } + \sum\limits_{n = 1}^N {{\beta _n}(\Delta t){E_n}} ){B_\psi }{\rm{d}}\Omega \\
\Delta {F_u}({t_m}) = \int_{{\Omega ^e}} {{N^{\rm{T}}}} \Delta f({t_m}){\rm{d}}\Omega + \int_{{\Gamma ^e}} {{N^{\rm{T}}}} \Delta p({t_m}){\rm{d}}\Gamma \\
\Delta {F_\psi }({t_m}) = \int_{{\Omega ^e}} {N_\psi ^{\rm{T}}} \Delta f({t_m}){\rm{d}}\Omega + \int_{{\Gamma ^e}} {N_\psi ^{\rm{T}}} \Delta p({t_m}){\rm{d}}\Gamma \\
F_u^0({t_m}) = - \int_{{\Omega ^e}} {{B^{\rm{T}}}} \sum\limits_{n = 1}^N {{\alpha _n}} (\Delta t){\sigma ^n}({t_{m - 1}}){\rm{d}}\Omega \\
F_\psi ^0({t_m}) = - \int_{{\Omega ^e}} {B_\psi ^{\rm{T}}} \sum\limits_{n = 1}^N {{\alpha _n}} (\Delta t){\sigma ^n}({t_{m - 1}}){\rm{d}}\Omega
\end{array}\]
|
从式(26)可以看出,黏弹性界面"加料"裂纹单元平衡方程与常规单元平衡方程相比,广义节点位移列阵中增加了附加自由度向量$\Delta \bar { \psi }(t)$,它包含4个未知分量.而这4个未知分量与裂纹两种模态的应力强度因子和变能释放率是相关的,因此,可以利用广义节点位移列阵中的附加自由度来求解裂纹断裂参量.
3.4 黏弹性界面裂纹应变能释放率
对于含裂纹黏弹性体而言,应力强度因子判据与应变能释放率判据不再等价[7]. 应力强度因子判据不再能反映黏弹性体的时间相依性,从而不能很好地预测黏弹性体可能发生的延迟断裂,而应变能释放率判据却能够反映这一断裂现象.Sun和Jih[37]给出了弹性界面裂纹应变能释放率表达式如下
|
\[G = \frac{{K_1^2 + K_2^2}}{{16{{\cosh }^2}\left( {\pi \zeta } \right)}}\left( {\frac{{{\kappa _1} + 1}}{{{\mu _1}}} + \frac{{{\kappa _2} + 1}}{{{\mu _2}}}} \right)\]
|
(27) |
由于本文应力强度因子定义与Sun和Jih的定义差一个系数$ \cosh^{-1} (\pi \zeta ) $,因此式(27)与其原始结果相差一个系数$ \cosh ^{-2}(\pi \zeta )$. 应用对应原理,得到黏弹性界面裂纹应变能释放率
|
\[G\left( t \right) = {L^{ - 1}}\left[ {\frac{{\tilde K_1^2 + \tilde K_2^2}}{{16{{\cosh }^2}\left( {\pi {{\tilde \zeta }^*}} \right)}}\left( {\frac{{\tilde \kappa _1^* + 1}}{{\tilde \mu _1^*}} + \frac{{\tilde \kappa _2^* + 1}}{{\tilde \mu _2^*}}} \right)} \right]\]
|
(28) |
泊松比为常数时有$\tilde {\kappa }_1^ * = \kappa _1 $,$\tilde {\kappa }_2^* = \kappa _2 $,
|
\[\tilde \mu _1^* = 1/[2p{\tilde C_1}(p)(1 + {\nu _1})], \tilde \mu _2^* = 1/[2p{\tilde C_2}(p)(1 + {\nu _2})]\]
|
式中$\tilde {C}_k \left( p \right) $ $ {\left( {k = 1,2} \right)} $ 为蠕变柔量$C_k \left( t\right)$的拉普拉斯变换,将上述表达式代入式(28)中,采用和位移场式(4)相同拉普拉斯逆变换法,得到应变能释放率表达式如下
|
\[\begin{array}{l}
G\left( t \right) = \left[ {\left( {{\kappa _1} + 1} \right)\left( {{\nu _1} + 1} \right){K_1}\left( t \right){\psi _{11}}\left( t \right) + } \right.\\
\left( {{\kappa _2} + 1} \right)\left( {{\nu _2} + 1} \right){K_1}\left( t \right){\psi _{12}}\left( t \right) + \\
\left( {{\kappa _1} + 1} \right)\left( {{\nu _1} + 1} \right){K_2}\left( t \right){\psi _{21}}\left( t \right) + \\
\left( {{\kappa _2} + 1} \right)\left( {{\nu _2} + 1} \right){K_2}\left( t \right){\psi _{22}}\left( t \right)]/\\
8{\cosh ^2}\left( {\pi \zeta (t)} \right)
\end{array}\]
|
(29) |
直接求解有限元方程,得到$\Delta { \psi } ( t )$后累加即可求得$\psi _{ij} (t)$,$K_i (t)$可通过$\Delta{ \psi }(t)$和$\psi _{ij} (t)$求出,其中$\psi _{ij} (t) = {\cal L}^{ - 1}\left[{\tilde {K}_i (p)p\tilde{C}_j (p)} \right]$,根据卷积定理
|
\[{\psi _{ij}}(t) = {K_i}(t)*{\rm{d}}{C_j}(t)\]
|
(30) |
式中"*"表示斯蒂尔杰斯(Stieltjes)卷积,$C(t)$表示蠕变柔量,根据均质线黏弹性材料裂纹的时变应力强度因子的递推公式[34],可得
|
\[\begin{array}{l}
{K_i}({t_m}) = {K_i}({t_{m - 1}}) + \Delta {K_i}({t_m}) \\
\Delta {K_i}({t_m}) = \frac{1}{{{B_j}(\Delta t)}}\left[ {\Delta {{\bar \psi }_{ij}}({t_m}) + \sum\limits_{n = 1}^N {A_j^n(\Delta t)\bar \psi _j^n({t_{m - 1}})} } \right] \\
A_j^n(\Delta t) = 1 - {{\rm{e}}^{ - \gamma _j^n\Delta t}} \\
{B_j}(\Delta t) = C_j^\infty + \sum\limits_{n = 1}^N {\frac{1}{{\gamma _j^n\Delta t}}(1 - {{\rm{e}}^{ - \gamma _j^n\Delta t}})C_j^n} \\
\bar \psi _j^n({t_{m - 1}}) = \frac{1}{{\gamma _j^n\Delta t}}A_j^n(\Delta t)C_j^n\Delta {K_i}({t_{m - 1}}) + {{\rm{e}}^{ - \gamma _j^nh}}\bar \psi _j^n({t_{m - 2}}) \\
{{\bar \psi }_j}(0) = 0,\bar \psi _j^n(0) = 0,{K_i}(0) = 0
\end{array}\]
|
(31) |
4 算例分析
4.1 算例1
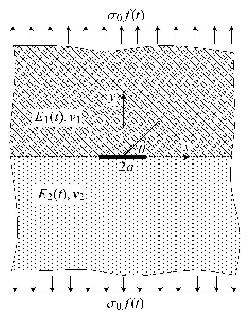
对含黏弹性中心界面裂纹的无限大板远端受拉问题(图2),按平面应变进行了计算. 有限元建模时,取 裂纹长度$2 a=2$,取平板边长$w= 20 a$,近似满足无限大条件. 根据对称性,取1/2模型建模,裂尖局部网格适当加密(网格尺度$l/a=1/40$),共划分为800个4节点四边形单元,850个节点,上半平面($y>0$,对应材料1)配置2个加料单元,4个过渡单元,下半平面(对应材料2)采用与上半平面同样的配置,有限元网格和加料单元配置如图3所示.计算单元刚度矩阵时,加料单元和过渡单元用10×10高斯积分,常规单元采用2×2高斯积分.
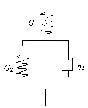
黏弹性材料采用图4所示的三参数标准线性固体模型,剪切松弛模量
|
\[\mu \left( t \right) = {G_1}\left[ {1 - \frac{{{G_1}}}{{{G_1} + {G_2}}}\left( {1 - {{\rm{e}}^{ - t/{\tau _G}}}} \right)} \right]\]
|
(32) |
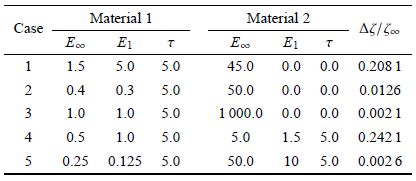
松弛时间$\tau _G = {\eta _2 } /{\left( {G_1 + G_2 } \right)}$,泊松比按常量计算,由此可求得松弛模量$E\left( t\right)$,并将其写成普罗尼级数的形式. 材料1和材料2的参数值列于表1中,工况1$\sim$3为弹性/黏弹性界面裂纹问题,工况4$\sim $5为黏弹性/黏弹性界面裂纹问题. ${\Delta \zeta } / {\zeta _\infty}$定义为${\left[{\zeta (\infty ) - \zeta (0)} \right]} /{\zeta (\infty )}$,表征$\zeta(t)$变化程度,其值越大表示$\zeta (t)$变化越大.
表1(Table 1)

表1 不同工况下材料参数Table 1 Material parameters at different case
|
表1 不同工况下材料参数
Table 1 Material parameters at different case |
远端拉力按单位阶跃加载($\sigma _0 =1.0$,$f(t)$为单位阶跃函数),作用时间为60,为了方便与解析解对比,暂不涉及物理单位. 无限大板黏弹性中心界面裂纹应变能释放率的理论解,可由相应弹性问题的应变能释放率式(27)和应力强度因子解答[6],通过对应原理得到.其拉普拉斯逆变换目前还不能获得精确解析表达式,应用基于直接逆变换和准静态的近似方法,得到近似解
|
\[\begin{array}{l}
G\left( t \right) = \frac{{\sigma _0^2\pi a\left[ {1 + 4{\zeta ^2}(t)} \right]}}{{8{{\cosh }^2}\left( {\pi \zeta (t)} \right)}}\left[ {\left( {{\kappa _1} + 1} \right)\left( {{\nu _1} + 1} \right){C_1}\left( t \right)} \right. + \\
\left. {\left( {{\kappa _2} + 1} \right)\left( {1 + {\nu _2}} \right){C_2}\left( t \right)} \right]
\end{array}\]
|
(33) |
表2给出了工况1、工况3和工况5在$t= 6$和$t= 60$时的应力强度因子计算结果,并与理论解进行了比较. 由结果可见,在恒定应力载荷作用下,张开模态应力强度因子$K_{1}$和复合应力强度因子$K$($K = \sqrt {K_1^2 + K_2^2 })$基本保持不变,本文解与理论解吻合的很好. 由于在位移和应变增量表达式中忽略$\Delta\zeta (t_m )$的影响,应力强度因子总体偏小,但$K_1$和$K$的相对误差均不超过$-5%$,表明本文计算方法的有效性和正确性,忽略$\Delta\zeta (t_m )$的影响不至于引起太大的误差,精度可满足工程要求.
表2(Table 2)

表2 应力强度因子计算结果Table 2 The Results of stress intensity factors
|
表2 应力强度因子计算结果
Table 2 The Results of stress intensity factors |
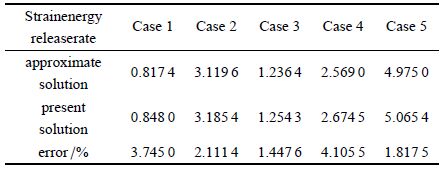
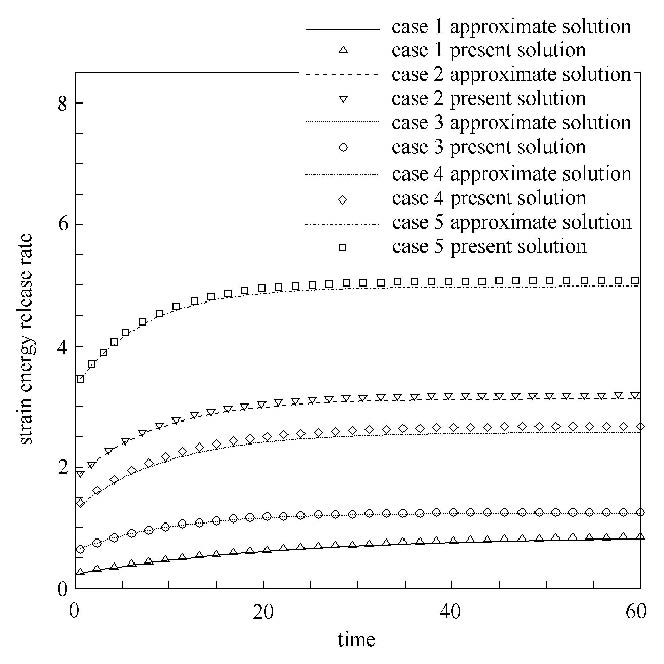
表3给出了以上几种工况下应变能释放率在时间$t=60$时的计算结果,计算时间步长统一取0.6.
由结果可见,各种工况下本文应变能释放率和近似解相对误差不超过5%,当${\Delta \zeta }/{\zeta _\infty
}$较大时,应变能释放率的误差也相对较大,这可能是由于忽略了$\Delta \zeta (t_m )$的影响所致.
应变能释放率随时间变化规律如图5所示,由图可见,本文解与近似解在整个加载历程内吻合.
表3(Table 3)

表3 $t =60$时应变能释放率计算结果Table 3 The results of strain energy release rate at $t= 60$
|
表3 $t =60$时应变能释放率计算结果
Table 3 The results of strain energy release rate at $t= 60$ |
由于黏弹性材料的蠕变,裂纹开口位移随时间增大而增大,因此,本例的应变能释放率随时间逐渐增大,并且趋向于定值.此时,应力强度因子判据已不再适用,而应变能释放率判据则可以较好地反映这一特性.
4.2 算例2
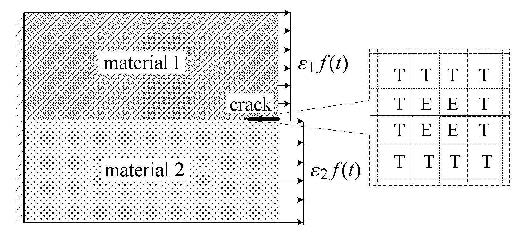
倒装芯片封装过程中可能出现的芯片和下填料之间以及下填料和基板之间的裂纹,是典型的黏弹性界面裂纹 问题.下填料是黏弹性材料,其线膨胀系数比芯片膨胀系数一般要高一个数量级左右,由温度载荷产生的应变导致裂纹尖端产生较强的剪应力,使下填料与芯片分层脱离,导致整个封装失效.本例针对芯片和下填料之间的黏弹性界面裂纹,考察不同应变加载历程下裂纹的应力强度因子和应变能释放率变化规律.
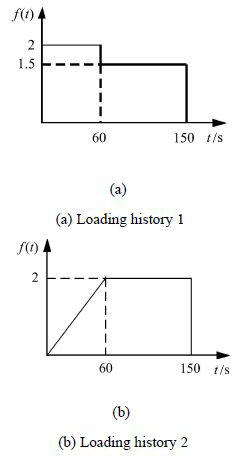
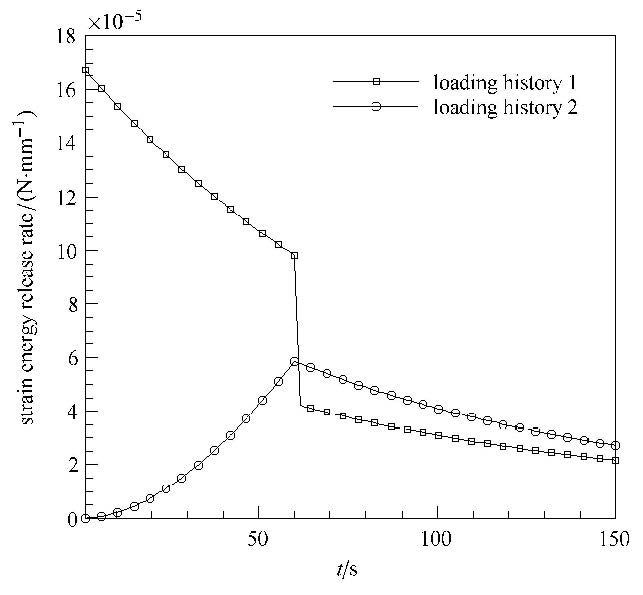
计算模型如图6所示,裂纹长度0.5 mm,材料1和材料2的长、宽分别为4 mm、1 mm,材料1属性与芯片相当,弹性模量131 GPa,泊松比0.35;材料2为黏弹性材料,采用标准线性固体模型,$E_\infty =0.9$ GPa,$E_1 =3.1$ GPa,$\tau_1 =80$ s,泊松比0.18.模型共划分为1 724个4节点4边形单元,1 817个节点,裂纹尖端附近设置4个界面裂纹裂尖加料单元,12个过渡单元(图6).应变加载历程如图7所示,其中$\varepsilon_1 =2.5\times 10^{-6}$,$\varepsilon _2 =2.5\times 10^{ -5}$,按平面应变问题进行计算.
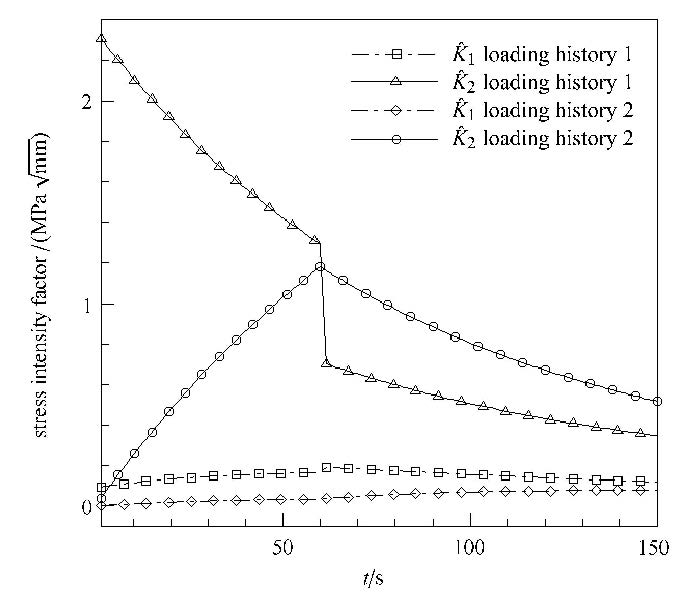
对于式(2a)定义的应力强度因子,计算结果通常乘以$L^{i\zeta }$ ($L$为参考长度,一般取裂纹长度),即$\hat {K}_1 +\hat {K}_2 = (K_1 + {\rm i}K_2 )L^{{\rm i}\zeta}$,使得界面裂纹应力强度因子量纲和普通意义上的应力强度因子量纲一致. 本文采用这种处理方式.
两种模态的应力强度因子计算结果如图8所示. 由计算结果可见,$\hat {K}_1 $与$\hat {K}_2 $相比较小,且在整个加载历程中变化不大;当施加恒定应变时,由于黏弹性材料的应力松弛特性,$\hat {K}_2$随着时间增大逐渐减小,并趋向于固定值;当施加的应变发生突变时,由于应力会瞬间响应,因此应力强度因子也会突变.
图9给出了应变能释放率变化曲线,按历程1加载时,应变能释放率由最大值16.7×10$^{-5}$ N/mm逐渐减小,并且位移发生突变时应变能释放率也会有相应的突变发生,由于应力松弛,应变能释放率最终趋向一固定值;按历程2加载时,应变能释放率随位移增大而逐渐增大,当应变达到最大值保持不变后,应变能释放率开始逐渐减小并趋向固定值.
5 结 论
本文在双材料弹性界面裂纹尖端位移场的基础上,应用对应原理和准静态拉普拉斯逆变换方法,得到了适用于黏弹性界面裂纹的尖端位移场表达式. 将该位移场加入常规等参元位移模式中,略去次要因素的影响,得到了黏弹性界面裂纹增量型加料单元有限元方程和应力强度因子、应变能释放率等断裂参量的表达式,有限元方程求解和断裂参量计算可在同一时间步中完成;
通过和无限大板黏弹性中心界面裂纹应力强度因子和应变能释放率理论解的对比分析,用本文方法得到的复合应力强度因子和应变能释放率相对误差不超过5%,证明了黏弹性界面裂纹增量"加料"有限元方法的正确性和有效性. 并且适用性较强,不仅可用于弹性/黏弹性界面断裂,也可用于黏弹性/黏弹性界面断裂的分析;
算例分析表明,在给定的应力和应变加载历程下,黏弹性界面裂纹增量"加料"有限元法能很好地反映黏弹性材料的蠕变和松弛特性,可推广应用于固体发动机壳体/绝热层脱粘、芯片封装结构分层脱离等黏弹性界面断裂问题的分析研究.
参考文献
| [1] |
Williams ML.The stresses around a fault or crack in dissimilar media. Bulletin of the Seismological Society of America, 1959, 49(2): 199-204 |
| [2] |
Rice JR, Sih GC. Plane problems of cracks in dissimilar media. Journal of Applied Mechanics, 1965, 32: 418-423 |
| [3] |
Rice JR. Elastic fracture me chanics concepts for interfacial cracks. Journal of Applied Mechanics, 1988, 55: 98-103 |
| [4] |
Erdogan F. Stress distribution in bonded dissimilar material with cracks. Journal of Applied Mechanics, 1965, 32: 403-410 |
| [5] |
Comninou M. The interface crack. Journal of Applied Mechanics, 1977, 44: 631-636 |
| [6] |
许金泉.界面力学.北京:科学出版社, 2006 (Xu Jinquan. The Mechanics of Interface. Beijing: Science Press, 2006 (in Chinese)) |
| [7] |
张淳源.粘弹性断裂力学.武汉:华中理工大学出版社, 1994 (Zhang Chunyuan. Viscoelastic Fracture Mechanics. Wuhan: Press of Huazhong University of Science and Technology, 1994 (in Chinese)) |
| [8] |
Atkinson C, Chen CY. The influence of layer thickness on the stress intensity factor of a crack lying in an elastic (viscoelastic) layer embedded in a different elastic (viscoelastic) medium (mode III analysis). International Journal of Engineering Science, 1996, 34: 639-658 |
| [9] |
Chang RC.Finite thickness cracked layer bonded to viscoelastic substrate subjected to antiplane shear. Int J Solids Structures, 1999, 36: 1781-1797 |
| [10] |
Han X, Ellyin F, Xia Z. Interface crack between two different viscoelastic media. Int J Solids Structures, 2001, 38: 7981-7997 |
| [11] |
Han X, Ellyin F, Xia Z. A crack near the interface of bonded elastic-viscoelastic planes. Int J Solids Structures, 2001, 38: 3453-3468 |
| [12] |
Kuo TL, Hwu C. Interface corners in linear anisotropic viscoelastic materials. Int J Solids Structures, 2013, 50(5): 710-724 |
| [13] |
Wang X, Pan E. Interaction between a screw dislocation and a viscoelastic piezoelectric bimaterial interface. Int J Solids Structures, 2008, 45: 245-257 |
| [14] |
刘玉岚, 王 彪,王殿富.含有界面裂纹的粘弹性层合板应变能释放率的计算. 应用数学和力学, 2003, 24(1): 12-18 (Liu Yulan, Wang Biao, Wang Dianfu. On the calculation of energy release rate for viscoelastic cracked laminates. Applied Mathematics and Mechanics, 2003, 24(1): 12-18 (in Chinese)) |
| [15] |
王振清, 梁文彦,吕红庆.双材料界面Ⅰ型扩展裂纹尖端的弹黏塑性场. 力学学报, 2011, 2: 417-422 (Wang Zhenqing, Liang Wenyan, Lu Hongqing. The elastic-viscoplastic field near mode I dynamic propagating crack-tip of interface in double dissimilar materials. Chinese Journal of Theoretical and Applied Mechanics, 2011, 2: 417-422 (in Chinese)) |
| [16] |
Chen YC, Hwu C. Boundary element method for vibration analysis of two-dimensional anisotropic elastic solids containing holes, cracks or interfaces. Engineering Analysis with Boundary Elements, 2014, 40: 22-35 |
| [17] |
沈辉,周储伟.奇异薄层单元及其在双材料界面断裂分析中的应用. 工程力学, 2012, 29(10): 69-74 (Shen Hui, Zhou Chuwei. Singular thin-layer element and its application in bimaterial interface fracture analysis. Engineering Mechanics , 2012, 29(10): 69-74 (in Chinese)) |
| [18] |
李彪, 李亚智, 刘向东 等.层合板层间断裂分析的组合界面单元及其特性. 复合材料学报, 2013, 30(5): 159-165 (Li Biao, Li Yazhi, Liu Xiangdong, et al. Characterization of a combined interfacial element for laminated composites. Acta Materiae Compositae Sinica, 2013, 30(5): 159-165 (in Chinese)) |
| [19] |
王舒, 任明法,陈浩然.热力载荷下多材料构件连接区的界面断裂分析. 复合材料学报, 2014, 31(1): 220-226 (Wang Shu, Ren Mingfa, Chen Haoran. Interface fracture analysis of jointed area in multi-material components under mechanical and thermal loadings. Acta Materiae Compositae Sinica, 2014, 31(1): 220-226 (in Chinese)) |
| [20] |
王亮, 白瑞祥, 雷振坤 等. 压电复合材料粘接界面断裂有限元模拟. 计算力学学报, 2012, 29(4): 517-521 (Wang Liang, Bai Ruixiang, Lei Zhenkun, et al. FEM simulation of adhesive interface fracture in piezoelectric composite. Chinese Journal of Computational Mechanics, 2012, 29(4): 517-521 (in Chinese)) |
| [21] |
汤丽华,许金泉.粘弹性界面裂纹奇异场. 力学季刊, 2007, 28(1): 116-123 (Tang Lihua, Xu Jinquan. Viscoelastic fields near interface crack tip. Chinese Quarterly of Mechanics , 2007, 28(1): 116-123 (in Chinese)) |
| [22] |
Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing. International journaI of Fracture Mechanics, 1999, 45: 601-620 |
| [23] |
Dolbow JE. An extended finite element method with discontinuous enrichment for applied mechanics. [PhD Thesis]. Evanston: Northwestern University,1999 |
| [24] |
Bouhala L, Shao Q, Koutsawa Y, et al. An XFEM crack-tip enrichment for a crack terminating at a bi-material interface. Engineering Fracture Mechanics, 2013, 102: 51-64 |
| [25] |
李录贤,王铁军.扩展有限元法(XFEM)及其应用. 力学进展, 2005, 35(1): 5-20 (Li Luxian, Wang Tiejun. The extended finite element method and its applications-A Review. Advances in Mechanics, 2005, 35(1): 5-20 (in Chinese)) |
| [26] |
金峰,方修君.扩展有限元法及与其它数值方法的联系. 工程力学, 2008, 25(Sup.I): 1-17 (Jin Feng, Fang Xiujun. The extended finite element method and its relations with other numerical methods. Engineering Mechanics , 2008, 25(Sup.I): 1-17 (in Chinese)) |
| [27] |
成斌斌.基于CB壳与亚界面断裂问题的扩展有限元算法研究[博士论文].北京:清华大学,2010 (Cheng Binbin. Research on the algorithm of the extended finite element method on CB shell and Sub-interfacial fracture problems. [PhD Thesis]. Beijing: Tsinghua University, 2010 (in Chinese)) |
| [28] |
董玉文, 余天堂,任文青.直接计算应力强度因子的扩展有限元法.计算力学学报, 2008, 25(1): 72-77 (Dong Yuwen, Yu Tiantang, Ren Qingwen. Extended finite element method for direct evaluation of strength intensity factors.Chines Journal of Computational Mechanics, 2008, 25(1): 72-77 (in Chinese)) |
| [29] |
许萌萌, 胡春波,何国强.固体火箭发动机界面脱粘裂纹分析. 固体火箭技术, 2008, 31(02): 121-124 (Xu Mengmeng, Hu Chunbo, He Guoqiang. Analysis on interfacial debond crack of SRM. Journal of Solid Rocket Technology, 2008, 31(02): 121-124 (in Chinese)) |
| [30] |
师俊平, 曹小杉, 胡义锋 等.两相材料界面裂纹的起裂方向及断裂参量研究. 应用力学学报, 2014, 3: 418-422 (Shi Junping, Cao Xiaoshan, Hu Yifeng, et al. Study on directions of crack orientation and failure characteristics of bi-material interface crack. Chinese Journal of Applied Mechanics, 2014, 3: 418-422 (in Chinese)) |
| [31] |
Benzley SE. Representation of singularities with isoparametric finite elements. International Journal for Numerical Methods in Engineering, 1974, 8(3): 537-545 |
| [32] |
Bayram YB, Nied HF. Enriched finite element-penalty function method for modeling interface cracks with contact. Engineering Fracture Mechanics, 2000, 65: 541-557 |
| [33] |
Ayhan AO, Kaya AC, Nied HF. Analysis of three-dimensional interface cracks using enriched finite elements. Int J Fract, 2006, 142: 255-276 |
| [34] |
段静波, 雷勇军,李道奎. 线粘弹性断裂分析的增量加料有限元法. 工程力学, 2012, 29(6): 22-31 (Duan Jingbo, Lei Yongjun, Li Daokui. The incremental enriched finite element method for fracture analysis in a linear viscoelastic body. Engineering Mechanics, 2012, 29(6): 22-31 (in Chinese)) |
| [35] |
Duan JB, Lei YJ, Li DK. Enriched finite element method for 2-D and 3-D blunt crack problems in a viscoelastic medium. Journal of Mechanical Science and Technology, 2012, 26(2): 869-882 |
| [36] |
Chen EP. Finite element analysis of a biomaterial interface crack. Theoretical and Applied Fracture Mechanics, 1985, 3: 257-262 |
| [37] |
Sun CT, Jih CJ. On strain energy release rates for interfacial cracks in biomaterial media. Engineering Fracture Mechanics, 1987, 28: 13-20 |
THE INCREMENTAL ENRICHED FINITE ELEMENT METHOD FOR FRACTURE ANALYSIS OF VISCOELASTIC INTERFACE
Yang Junhui, Meng Shangyang, Lei Yongjun

1. College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China;
2. Beijing Institute of Special Electromechanical Technology, Beijing 100012, China
Fund: The project was supported by the National Natural Science Foundation of China (11272348).
Abstract: The incremental enriched finite element method (FEM) is developed for viscoelastic interface crack problems. According to the basic displacements fields of elastic interface crack tip, the crack tip displacement fields of viscoelastic interface crack are derived through the correspondence principle and an approximate Laplace inverse transform method. By incorporating the displacement expressions to the common element, the displacement models of enriched and transition elements are obtained, and then the incremental formulations of the enriched FEM are deduced. The fracture parameters, stress intensity factors and strain energy release rate can be obtained through solving the finite element equation. The enriched finite element model of typical plane problems containing viscoelastic interface crack are constructed, and the fracture parameter solutions show that the presented method is quite accurate for both elastic/viscoelastic and viscoelastic/viscoelastic interface crack and can reflect the creep and relaxation characteristics. It can be applied to the fracture analysis of viscoelastic interface crack.
Key words:
viscoelastic interface crack enriched finite element stress intensity factor strain energy release rate


 2015, Vol. 47
2015, Vol. 47