随着陆地资源和空间日趋短缺,各国开始将经济发展的目光投向海洋中蕴藏着的丰富资源,21世纪人类将全面迈入海洋经济时代. 作为深远海资源开发的必备海洋工程重装备,超大型海洋浮式结构物的研究获得了普遍的重视. 超大型海洋浮式结构物尺度以公里计,远大于现有的船舶和海上钻井平台等海洋工程结构物尺度. 它以沿海岛屿或远海海岛泻湖为依托,带有永久或半永久性,具有综合性、多用途的功能. 在和平时期,超大型海洋浮式结构物可用作远海快速运输交通枢纽、深海空间站的水面平台、大型深远海 开发操作平台、远洋物资存储中继站以及科考勘探工作站;战时则可用作海上机动快速反应的综合军事平台等. 它的应用将对某一区域的经济活动乃至政治影响力和军事格局发挥巨大影响.
早在1924年美国人爱德华曾设想在大西洋上建造一个大型浮体中继站[1],以便给来往于美国和欧洲的飞机补充燃料. 然而这种设想直到20世纪80年代才开始受到人们的普遍关注,此后各国学者对超大型海洋浮式结构物开展了大量的理论和应用研究[2, 3, 4]. 最早日本研究了一种浮箱式的海上浮动机场[5, 6, 7]. 1995年,日本成立了海上浮动机场技术研究委员会,专门负责海上浮动机场的设计研制工作,并通过试验验证了海上浮动机场的可行性[8]. 相比于日本的海上浮动机场,美国提出一种半潜式的移动式海上基地[9, 10],并进行了相关研究[11, 12, 13]. 移动式海上基地是一种可快速布置在预定海域的多功能海上综合后勤补给基地,其由若干海上浮动模块拼接而成,可为固定翼飞机和直升机提供起降跑道. 除了日美以外,世界其他各国诸如挪威[14, 15]、英国[16]、荷兰[17]、韩国[18]、新加坡[19]等也对超大型海洋浮式结构物开展了研究. 中国具有狭长的海岸线和广阔的海上疆域,研制军民两用的超大型海洋浮动基地对我国具有深远的战略价值和意义,从20世纪90年代开始以吴有生、崔维成等为代表一批具有远见卓识的国内学者 也相继对超大型海洋浮式结构物开展了深入研究[20, 21, 22, 23].
海上浮动机场是一个超大型扁平结构物,最初的研究是将其简化为板梁模型[24, 25], 随着20世纪70年代末水弹性理论[26]的兴起,分析其水弹性响应特性[27, 28, 29, 30]. 由于它的巨大尺度,模块化结构设计是必然的选择[31],模块之间的连接问题变得至关重要. 有学者提出铰接弹性板梁模型[32, 33, 34],经过线性化处理的振动模态叠加获得结构响应的基本特性. 为了减小波浪对大型结构物的载荷作用,半潜式浮体模块被采用,为了简化计算通常将这类模块处理 为刚体[20]. 文献[35]采用片条理论方法研究了一维铰接$\!$-$\!$-$\!$刚体动力学模型的动力学特性. 在前期的工作基础上[36], 文献[37]采用有限元方法和片条理论方法完成了对大型半潜式浮体模块连接平台三维水弹性分析. 围绕着海上浮动机场和大型海上浮动结构物的动力响应预报有大量的研究报告,内容丰富,不详尽列举. 建模方法基本上是采用经典的板梁理论、有限元方法和考虑水弹性效应的水动力学理论. 在此基础上建立起来的动力学方程往往具有非线性特性,由于所涉及的结构维度庞大以及要确定水动力载荷的复杂性, 往往通过降阶线性化处理的方式来简化分析过程. 需要指出的是, 以传统经典的线性理论处理海上浮动机场的动力学预报问题可能导致过于乐观的设计结果. 在作者研究以橡胶钢索为连接件的超大型海上浮动机场的非线性动力学特性时[38, 39]揭示 了系统响应和载荷阶跃现象,集体性的振幅抑制状态,和复杂网络动力学的耦合协同效应. 对于海上浮动机场或更广泛意义上的大型海上浮动结构物动力响应预报而言,这些新现象和特性都值得深入研究.
由多模块浮体组成的海上浮动机场,在波浪作用下的每个浮体可视为一个独立振子,振子间通过连接件的弹性耦合,构成一个典型的网络动力学系统. 本文立足于非线性网络动力学这一新视角,采用一种新型连接件设计,研究了超大型海上浮动机场的动力学特性. 基于线性波浪理论、单浮体模块动力学模型、连接件力学模型以及锚泊约束条件,构建了具有链式拓扑结构特征的海上浮动机场的非线性网络动力学模型. 该建模方法能够适应于各类复杂拓扑网络结构的超大型海洋浮式结构物,灵活应对各类形式的系泊约束,重要的是该方法可以揭示传统分析方法无法企及的网络系统的协同效应等动力学特性. 通过数值仿真,分析了海上浮动机场非线性动力学响应以及柔性连接件载荷,揭示了经典的线性方法可能低估了系统结构的实际响应和载荷. 本文进一步研究了超大型海上浮动机场的"振幅死亡"现象,它是非线性网络结构系统的各个振子集体性地处于一种微幅振荡抑制状态的特殊动力学现象,对于海上浮动机场的稳定性设计具有特殊意义. 文中讨论了振幅死亡的产生机理,描述了振幅死亡存在区域与连接件刚度设置和波浪周期的关系. 探讨了非线性网络动力学分析方法在海上浮动机场或大型海上浮动结构物动力响应预报中的理论意义.
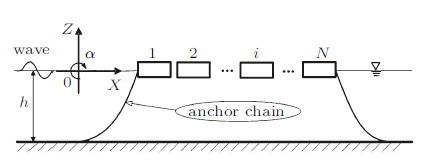
1 浮动机场网络动力学建模超大型浮动机场由$N$个浮体通过弹性连接件链式组合而成,浮动机场首尾两端浮体有锚泊缆线约束,自由漂浮于水平面,如图1所示. 系统整体坐标系定义如下: $X$轴位于未扰动自由液面,其方向沿水平面指向浮体编号增大方向; $Z$轴垂直水平面向上. 分析中,假定浮动机场周围水域为理想液体,各浮体为刚体,相邻浮体之间由线性弹性连接件连接,组成刚柔耦合模型. 仅考虑浮体在二维平面$0XZ$内的三个自由度运动: 纵荡、垂荡和纵摇,浮动机场所处的波浪环境假定为顶浪线性波.
|
图 1 多模块连接的浮动机场简化模型 Fig. 1 Sketch for the multi-module floating airport |
不同于传统建模方法所采用的铰接弹性薄板梁结构模型[32, 33, 34],本文将浮动机场视为多浮体模块相互耦合的振子网络系统,建模过程中将引入反映网络连接特性的拓扑结构矩阵. 虽然在浮体模块处理上与刚体动力学模型[20, 35]有相似之处,但本文考虑浮动刚体之间柔性连接的几何非线性力学特性. 建模过程中,首先建立单浮体动力学模型和连接件力学模型,之后依据浮体模块连接的拓扑构型形式和锚泊约束,将各子模块动力学模型集约合成浮动机场的整体网络动力学模型.
1.1 单浮体动力学模型采用线性波浪理论[40],可推导出单个浮体$i$的动力学方程
| $ \label{eq1} ({{ M}}_i + {{ \mu }}_i ){{\ddot { X}}}_i + {{ \lambda }}_i {{ \dot { X}}}_i + {{ S}}_i {{ X}}_i = {{ F}}_{i{\rm w}} $ | (1) |
其中,${{ X}}_i = \left[{x_i ,z_i ,a_i } \right]^{\rm T}$是浮体$i$的位移向量,分别代表浮体$i$的纵荡$x_i $、垂荡$z_i $和纵摇$\alpha _i$. $ M_i$为浮体$i$的质量矩阵,${{ S}}_i $为静水恢复力矩阵[41],其表达式为
| $ \label{eq2} \left.\begin{array}{l} {{ M}}_i = \left[{{\begin{array}{*{20}c} {m_i } & 0 & {m_i (z_{{\rm c}i} - z_{{\rm g}i} )} \\ 0 & {m_i } & { - m_i (x_{{\rm c}i} - x_{{\rm g}i} )} \\ {m_i (z_{{\rm c}i} - z_{{\rm g}i} )} & { - m_i (x_{{\rm c}i} - x_{{\rm g}i} )} & {I_{xxi}^\Delta + I_{zzi}^\Delta } \\ \end{array} }} \right] \\ {{ S}}_i = \left[{{\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & {\rho gA_i^{\rm W} } & { - \rho gI_{xi}^{\rm W} } \\ 0 & { - \rho gI_{xi}^{\rm W} } & {\rho g\left( {I_{xxi}^{\rm W} + I_{zzi}^{\rm W} } \right) - m_i g(z_{{\rm c}i} - z_{{\rm g}i} )} \\ \end{array} }} \right] \\ \end{array}\right\} $ | (2) |
其中$m_i $为单个浮体$i$的质量,$\rho $是水密度,$g$是重力加速度; $(x_{{\rm c}i} ,z_{{\rm c}i} )$为浮体$i$的旋转中心坐标,$(x_{{\rm g}i} ,z_{{\rm g}i} )$为其重心坐标; $A_i^{\rm W} $是浮体$i$ 的静止水面线面积,$\varDelta _i $为其排水体积且满足$\varDelta _i = L_i d_i $,其中$L_i ,d_i $分别为浮体$i$的长度和吃水深度; $I_{xi}^{\rm W} $和$I_{xxi}^{\rm W} ,I_{zzi}^{\rm W} $为浮体$i$ 水面线的一次矩和二次矩,$I_{xxi}^\Delta ,I_{zzi}^\Delta $为浮体$i$排水体积的二次矩,具体定义如下
| $ \label{eq3} \left.\begin{array}{l} A_i^{\rm W} = \displaystyle\int_{ - L_i / 2}^{L_i / 2} {{\rm{d}} x} ,\ \ I_{xi}^{\rm W} = \int_{\varGamma _{\rm W} } {(x - x_{{\rm c}i} ){\rm{d}}\varGamma } \\[3mm] I_{xxi}^{\rm W} = \displaystyle\int_{\varGamma _{\rm W} } {(x - x_{{\rm c}i} )^2{\rm{d}}\varGamma } ,\ \ I_{zzi}^{\rm W} = \displaystyle\int_{\varGamma _{\rm W} } {(z - z_{{\rm c}i} )^2{\rm{d}}\varGamma } \\[3mm] I_{xxi}^\Delta = \displaystyle\iint_{\Delta _\iota } {(x - x_{{\rm c}i} )^2{\rm{d}} V} ,\ \ I_{zzi}^\Delta = \iint_{\Delta _\iota } {(z - z_{{\rm c}i} )^2{\rm{d}} V} \\ \end{array}\right\} $ | (3) |
根据线性波浪理论,浮体所受波浪激励的速度势可以分解为入射势,散射势和辐射势. ${{ \mu }}_i$和${{ \lambda }}_i $为波浪辐射势引起的附加质量矩阵和附加阻尼矩阵,可由特征值展开匹配法[42]求得. 需要说明的是多浮体间流体散射特性极为复杂,鉴于本文重点阐述非线性网络结构动力学理论在多模块浮动机场的方法应用,故忽略散射波的影响,仅考虑入射波,则式(1)中波浪力可表达为
| $ \label{eq4} {{ F}}_{i{\rm w}} = \left[{{\begin{array}{*{20}c} {f_{i{\rm w}x}^{\rm I} } \\ {f_{i{\rm w}z}^{\rm I} } \\ {f_{i{\rm w}\alpha }^{\rm I} } \\ \end{array} }} \right]\cos (\omega t + \varphi _i ) $ | (4) |
其中,$\varphi _i $为入射波作用于浮体$i$的初相位. $f_{i{\rm w}}^{\rm I} $为波浪作用于浮体的力幅值,可由波浪理论确定
| $ \left. {\begin{array}{*{20}{l}} {f_{i{\rm{w}}x}^{\rm{I}}}& = &{\rho ga[1 - \cos (k{L_i})]\frac{{\sinh (kh) - \sinh (k(h - {d_i}))}}{{k\cosh (kh)}}}\\ {f_{i{\rm{w}}z}^{\rm{I}}}& = &{\rho ga\sin (k{L_i})\frac{{\cosh [k(h - {d_i})]}}{{k\cosh (kh)}}}\\ {f_{i{\rm{w}}\alpha }^{\rm{I}}}& = &{\rho ga\{ \frac{{\cos (k{L_i})}}{{{k^2}\cosh (kh)}}[k{d_i}\sinh [k(h - {d_i})] + }\\ {}&{}&{\cosh [k(h - {d_i})] - \cosh (kh)] - }\\ {}&{}&{\frac{{\cosh [k(h - {d_i})]}}{{{k^2}\cosh (kh)}}(2\cos \frac{{k{L_i}}}{2} + 2\cos \frac{{3k{L_i}}}{2} - }\\ {}&{}&{k{L_i}\sin \frac{{3k{L_i}}}{2})\} } \end{array}} \right\} $ | (5) |
式中,$h$为水深,$a$为波高,$k$为波数,满足色散关系式$\omega ^2 = gk\tanh (kh)$,$\omega $ 为入射波角频率. 需要说明,受到浮体尺度的影响,入射波作用于不同浮体的初相位是不同的,相邻浮体初相位的相位差为$\Delta\varphi _{i(i + 1)} =\varphi _{i + 1} - \varphi _i = {k}(L_i + L_{i+ 1} )/2$.
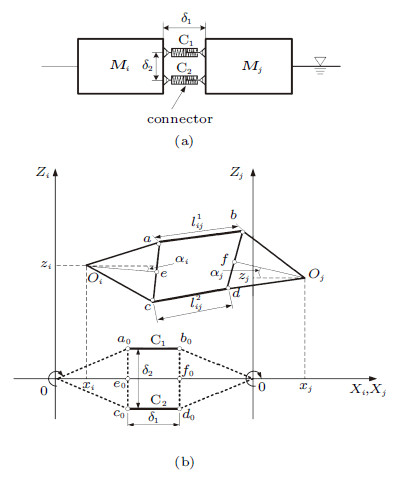
1.2 柔性连接件力学模型构成浮动机场的各个浮体模块是通过柔性连接件相互偶联. 图2(a)所示,相邻浮体间通过2个弹性连接件连接, 连接件两端分别与相 邻浮体铰接. 2个连接件平行安置,垂向间距为$\delta_2$, 连接件初始长度和浮体间初始间距均为$\delta _1 $. 这种连接件组合配置不仅能限制浮体间的水平运动, 同时也能约束浮体间的垂荡和纵摇运动.
|
图 2 (a)相邻浮体间连接件简化模型; (b)相邻浮体运动简图 Fig. 2 (a) Sketch for the connecter; (b) The position relationship for adjacent modules |
采用刚柔耦合模型,把浮体视为刚体,仅考虑浮体的纵荡、垂荡和纵摇3个自由度,则各浮体的局部坐标系$OXZ$定义如下: 以浮体旋转运动中心为坐标原点,$X$轴平行于静水面,$Z$轴垂直于静水面向上,如图2(b)所示. 图中相邻浮体$i,j$分别被简化为2个三角形,虚线三角形代表相邻浮体的初始位置, 实线三角形为相邻浮体分别经过位移$\left( {x_i ,z_i ,\alpha _i } \right)$和$\left( {x_j ,z_j ,\alpha _j } \right)$运动后的位置,$O$点为浮体旋转运动中心,图中黑色加粗线段$a_0b_0$和$c_0d_0$代表连接件C$_1$和C$_2$ 初始位置,线段$ab,cd$分别为连接件C$_1$,C$_2$经过位移运动后的位置.
连接件力学模型是描述相邻浮体运动位移与连接件的载荷关系. 连接件C$_{\rm 1}$和C$_{\rm 2}$ 的初始长度为$l_{ij}^0 = \delta _1 $,浮体位移运动后连接件C$_{\rm 1}$和C$_{\rm 2}$的形变长度为
| $ \left.\begin{array}{l} l_{ij}^1 = \sqrt {\left[{{\rm sgn}(j - i)\delta _1 + \dfrac{\delta _2 }{2}(\alpha _j - \alpha _i ) + x_j - x_i } \right]^2 + \left[{{\rm sgn}(j - i)\dfrac{L}{2}(\alpha _j + \alpha _i ) + z_j - z_i } \right]^2} \\[3mm] l_{ij}^2 = \sqrt {\left[{{\rm sgn}(j - i)\delta _1 - \dfrac{\delta _2 }{2}(\alpha _j - \alpha _i ) + x_j - x_i } \right]^2 + \left[{{\rm sgn}(j - i)\dfrac{L}{2}(\alpha _j + \alpha _i ) + z_j - z_i } \right]^2} \\ \end{array}\right\} $ | (6) |
连接件C$_{\rm 1}$和C$_{\rm 2}$的形变量分别为: $\Delta l_{ij}^1 = l_{ij}^1 - \delta _1,\Delta l_{ij}^2 = l_{ij}^2 - \delta _1 $; 连接件为线性弹性元件,其刚度为$k_{\rm c} $, 故连接件C$_{\rm 1}$和C$_{\rm 2}$所承受的载荷力为
| $ \label{eq6} \left.\begin{array}{l} F_{ij}^{{\rm c}1} = k_{\rm c} \Delta l_{ij}^1 \\[2mm] F_{ij}^{{\rm c}2} = k_{\rm c} \Delta l_{ij}^2 \\ \end{array}\right\} $ | (7) |
连接件C$_{\rm 1}$和C$_{\rm 2}$共同作用,限制浮体的纵荡、垂荡以及纵摇运动,故浮体$i$ 所受连接件作用力${{ F}}_{ij}^{\rm c} $定义如下
| $ \label{eq7} {{ F}}_{ij}^{\rm c} = k_{\rm c} [{( {\Delta l_{ij} } )_x ,( {\Delta l_{ij} } )_z ,( {\Delta l_{ij} } )_\alpha }]^{\rm T} $ | (8) |
式(8)即为连接件的力学模型,其中各方向的位移为
| $ \label{eq8} \left.\begin{array}{l} ( {\Delta l_{ij} } )_x = \Delta l_{ij}^1 ( {n_{ij}^1 } )_x + \Delta l_{ij}^2 ( {n_{ij}^2 } )_x \\[1mm] ( {\Delta l_{ij} } )_z = \Delta l_{ij}^1 ( {n_{ij}^1 } )_z + \Delta l_{ij}^2 ( {n_{ij}^2 } )_z \\[1mm] ( {\Delta l_{ij} } )_\alpha = \Delta l_{ij}^1 ( {n_{ij}^1 } )_\alpha + \Delta l_{ij}^2 ( {n_{ij}^2 } )_\alpha \\ \end{array}\right\} $ | (9) |
其中方向矢量基为
| $\begin{array}{l} {\left( {n_{ij}^1} \right)_x} = \frac{{{\rm{sgn}}(j - i){\delta _1} + \frac{{{\delta _2}}}{2}({\alpha _j} - {\alpha _i}) + {x_j} - {x_i}}}{{l_{ij}^1}}\\ {\left( {n_{ij}^1} \right)_z} = \frac{{{\rm{sgn}}(j - i)\frac{{{L_i}}}{2}({\alpha _j} + {\alpha _i}) + {z_j} - {z_i}}}{{l_{ij}^1}}\\ {\left( {n_{ij}^1} \right)_\alpha } = {\left( {n_{ij}^1} \right)_x}\left[{\frac{{{\delta _2}}}{2} - {\rm{sgn}}(j - i)\frac{{{L_i}}}{2}{\alpha _i}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;\;{\left( {n_{ij}^1} \right)_z}\left[{{\rm{sgn}}(j - i)\frac{{{L_i}}}{2} + \frac{{{\delta _2}}}{2}{\alpha _i}} \right]\\ {\left( {n_{ij}^2} \right)_x} = \frac{{{\rm{sgn}}(j - i){\delta _1} - \frac{{{\delta _2}}}{2}({\alpha _j} - {\alpha _i}) + {x_j} - {x_i}}}{{l_{ij}^2}}\\ {\left( {n_{ij}^2} \right)_z} = \frac{{{\rm{sgn}}(j - i)\frac{{{L_i}}}{2}({\alpha _j} + {\alpha _i}) + {z_j} - {z_i}}}{{l_{ij}^2}}\\ {\left( {n_{ij}^2} \right)_\alpha } = {\left( {n_{ij}^2} \right)_x}\left[{ - \frac{{{\delta _2}}}{2} - {\rm{sgn}}(j - i)\frac{{{L_i}}}{2}{\alpha _i}} \right] - \\ \;\;\;\;\;\;\;\;\;\;\;{\left( {n_{ij}^2} \right)_z} = \left[{{\rm{sgn}}(j - i)\frac{{{L_i}}}{2} - \frac{{{\delta _2}}}{2}{\alpha _i}} \right] \end{array}$ | (10) |
从式(6)和式(10)可以看出这是具有几何非线性本构关系的连接件力学模型. 由于浮体尺度与连接件尺度的巨大差异,在波浪作用下,即便当浮体产生较小的纵摇都会引起连接处的较大位移,连接件力学模型将呈现出强几何非线性特性. 在后续的分析中将会看到几何非线性特性对浮动机场的整体动力学行为产生重要作用. 传统的连接件建模方法[20, 35]仅简单假设各个方向的线性刚度连接,忽略了几何非线性本构关系的重要影响.
1.3 浮动机场动力学模型在单浮体动力学模型式(1)基础上,考虑浮体间的连接件耦合作用力,以及浮体可能受到的锚泊约束力,综合上述力学模型和各浮体间的拓扑结构连接特性,可推出$N$个浮体柔性连接的超大型海上浮动机场网络动力学模型,如下
| $\begin{array}{l} ({M_i} + {\mu _i}){{\ddot X}_i} + {\lambda _i}{{\dot X}_i} + ({S_i} + {k_i}){X_i} = \\ \qquad {F_{i{\rm{w}}}} + \varepsilon \sum\limits_{j = 1}^N {{\Phi _{ij}}G({X_i},{X_j})} {\mkern 1mu} ,\;\;i = 1,2,\cdots ,N \end{array} $ | (11) |
式(11)为非自治网络系统动力学模型[44]的典型表达式. 其特点是专设了耦合项$\varepsilon \sum_{j = 1}^N {\varPhi _{ij} G({{ X}}_i ,{{ X}}_j )} $ 来描述振子之间的耦合作用对网络系统动力学的影响. 在本文,耦合项描述浮体$i$ 受到相邻浮体$j$的耦合作用力. 其中参数$\varepsilon $为耦合强度,对应的物理意义是连接件的刚度$k_{\rm c} $,耦合函数$G({{ X}}_i ,{{ X}}_j )$ 是表征连接件在各个自由度方向上的形变函数
| $ \label{eq11} G({{ X}}_i ,{{ X}}_j ) = [{( {\Delta l_{ij} } )_x ,( {\Delta l_{ij} } )_z ,( {\Delta l_{ij} } )_\alpha }]^{\rm T} $ | (12) |
反映的是连接件几何非线性本构关系,式(12)中的参数由式(9)和(10)确定.
模型(11)中符号${{ \varPhi }}$表征浮体之间的连接关系,称之为拓扑结构矩阵. 其元素值$\varPhi _{ij} = 1$表示$i$和$j$浮体连接,$\varPhi _{ij} = 0$表示两浮体不连接. 需要指出的是浮体间连接方式形态不同, 拓扑结构矩阵${{ \varPhi }}$ 的元素赋值不同. 引入拓扑结构矩阵${{ \varPhi }}$的益处是无需改变网络动力学模型的典型表达式(11),便可对任何 拓扑构型的网络系统进行描述,具有普适性. 例如, 对环形、矩形或其他类型的海上浮体平台,建模过程仅需改变拓扑结构矩阵${{ \varPhi }}$的元素赋值. 对于本文研究的链式拓扑结构的海上浮动机场来说,其拓扑矩阵${{ \varPhi }}$为对称矩阵,其元素值$\varPhi _{ij} $定义如下
| $ \begin{array}{l} {\Phi _{ij}} = \left\{ {\begin{array}{*{20}{c}} 1&{j = i + 1}\\ 0&{其他} \end{array}} \right.\;\;\;\;i = 1,2,\cdots ,N;j = i,i + 1,\cdots ,N\\ 即\;\Phi = \left[{\begin{array}{*{20}{c}} 0&1&0&0&0&0& \ldots \\ {}&0&1&0&0&0& \cdots \\ {}&{}&0&1&0&0& \cdots \\ {}&{}&{}&0&1&0& \cdots \\ {}&{}&{}&{}&0&1& \cdots \\ {}&{}&{}&{}&{}&0& \cdots \\ {}&{}&{}&{}&{}&{}& \ddots \end{array}} \right] \end{array} $ | (13) |
本文中锚链系统约束可视为外界的环境约束,本文采用了简化的线性模型,${{ k}}_i $为锚泊刚度矩阵, 其锚泊刚度矩阵系数 可由文献[41]中的方法求得. 本模型仅考虑首尾两个浮体$1$和$N$受到锚链锚泊约束, 因此只有锚泊刚度矩阵${{ k}}_1 $和${{ k}}_N $ 的单元系数需要确定,其余锚泊刚度矩阵单元系数均为零. 值得指出的是,通过调整方程(11)中锚泊刚度矩阵的值可以调节锚泊约束的条件, 因此本模型中对锚链锚泊位置及约束力特性的设置具有较大灵活性.
在整个建模过程中,运动方程的建立仍然依据牛顿力学原理,表达方式与传统方法有所不同. 尽管避免了波浪、锚泊系统、连接 器本身的非线性因素,但由于巨大浮体的运动在柔性连接处引起的几何非线性特性, 使得多模块浮动机场网络动力学模型是个高维非线性微分方程组,具有复杂而丰富的非线性网络动力学特性.
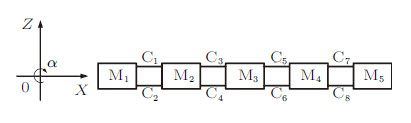
2 浮动机场非线性动力响应特性分析 2.1 计算模型计算模型选取浮体总数$N = 5$,单个浮体模块的几何参数参考文献[43]中的数据, 将其单位长度质量按二维问题换算后如表1所示. 为了不失一般性,仿真算列仅考虑普通海况,选取波高$a = 3$ m的规则波,水深$h = 50$ m,入射波浪周期$T = 10$ s. 图3是5个浮体柔性连接浮动机场模型示意图. 每个浮体依序编号从M1至M5,连接件编号从C$_{1}$至C$_{8}$. 仅M1和M5浮体受到锚泊系统约束.
| 表 1 单浮体基本参数 Table 1 Parameters of single module |
|
图 3 五浮体机场模型示意图: M1$\sim$M5是子浮体模块, C$_{1}$$\sim$C$_{8}$是连接件 Fig. 3 Sketch for the 5-module floating airport: M1--M5 indicate modules; C$_{1}$--C$_{8}$ represent connectors |
本文主要分析浮动机场的非线性动力响应特性,为了说明考虑非线性因素的必要性,特别列入了线性分析结果做对比. 线性模 型是通过对非线性网络动力学方程(11)等式右边的耦合项进行线性化处理获得的,考虑到线性化方法非常通用, 略去具体数学推导. 线性化后,连接件的刚度矩阵在各个自由度方向上解耦,不再反映力学模型中的非线性几何本构关系.
2.2 非线性响应及连接件载荷对于浮动机场的动力学问题,有两个关键参数是本文非常关心的. 其一是连接件的刚度设计如何影响系统动力学行为, 其二是 随着波浪参数的变化导致的系统动力学行为. 非线性响应会涉及各种不同类型的运动形式, 但本文关注浮体的幅频响应及连接件所承受的载荷.
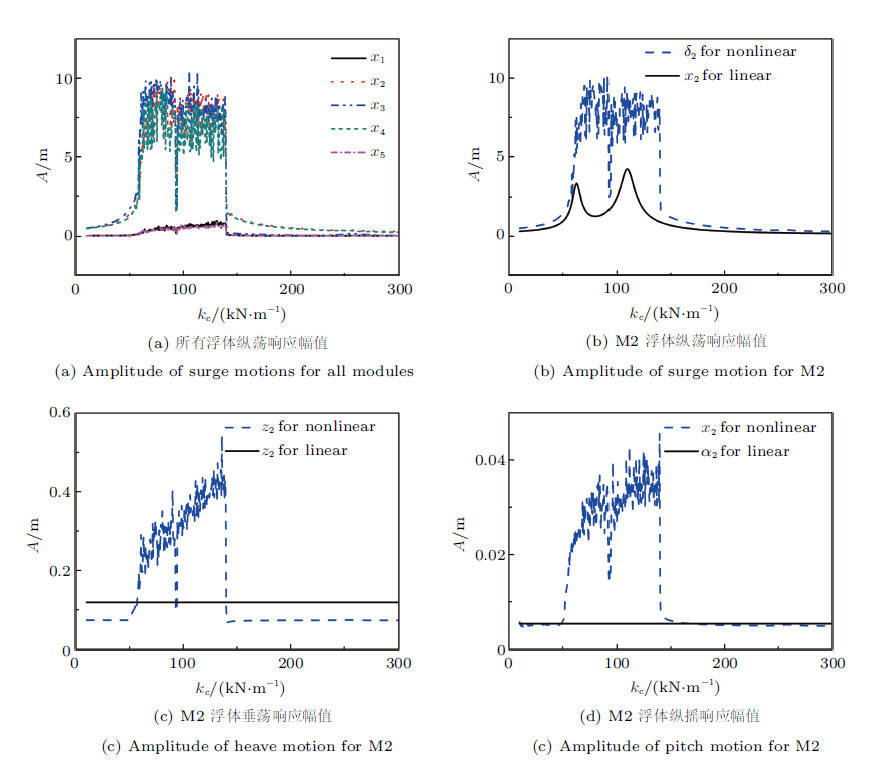
图4是浮体响应幅值随连接件刚度变化规律. 其中图4(a)描述了5个浮体的纵荡响应幅值随着连接件刚度变化的情况, 有以下几 个特点. (1)幅值随着刚度参数增加,响应逐渐增大出现一个相对大幅值振荡参数区间61 kN/m $ < k_{\rm c} < 142$ kN/m,随后会出现跳跃现象,这与非线性系统弯曲的共振支有关. (2)从幅值看, 浮体M1和M5由于受到两端锚泊约束其响应幅值相对较小; 而处于链式结构中部位置的M2,M3和M4浮体响应幅值较大, 且处于同等量级. (3)由于网络的协同效应,所有浮体响应的跳跃点具有一致性,均发生在$k_{\rm c}\approx 142$ kN/m. 为了解释非线性与线性分析结果的差异,以具体的浮体M2响应来说明. 图4(b)描述M2浮体纵荡响应幅值随刚度变化, 可以看出非线性响应(虚线)峰值区域与线性响应(实线)的共振峰区域是基本对应的,两共振峰之间, 非线性响应仍然处于大幅值振荡. 从振荡幅值看,在峰值区域非线性响应远高于线性结果,非峰值区域两者基本上一致. 图4(c)描述M2浮体垂荡响应幅值随刚度变化,非线性响应(虚线)峰值区域与图4(b)类似,但线性响应(实线)却保持不变. 仔细查验了线性化后的连 接件本构力学模型发现,水平布放的连接件刚度变化不会影响M2,M3和M4浮体垂向刚度, 线性化解耦处理截断了原 本是非线性几何本构的关系. 然而对于浮体M1和M5,由于受到锚链约束且锚链刚度矩阵为满阵, 导致该浮体的3个自由度重新耦合,故浮体间连接刚度变化会微弱地影响共振曲线,限于篇幅不在此绘图说明. 从幅值看峰值区域,非线性响应远大于线性分析结果; 垂荡响应相较于纵荡响应要小一个量级, 他们的峰值区域和跳跃点是一致的. 图4(d)描述M2浮体纵摇响应幅值随刚度变化, 非线性纵摇响应(虚线)的峰值区域和跳跃点与纵荡和垂荡是一致的;线性结果基本保持不变, 原因是线性化处理截断了纵向与其他自由度的耦合作用,连接件刚度变化仅对浮体的纵荡响应幅值影响较大.
|
图 4 浮体响应幅值随连接件刚度变化 Fig. 4 The amplitude of module responses versus change of connector stiffness |
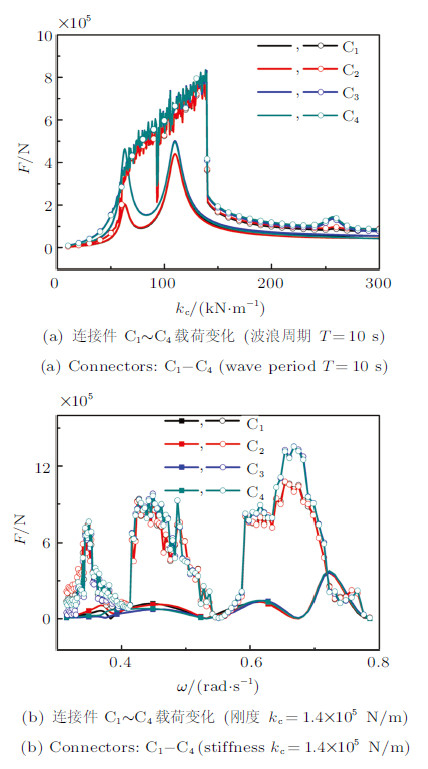
连接件是大型海上浮动机场的关键部件,评估其承受的载荷对系统安全性至关重要. 图5描述了连接件载荷随连接件刚度和入射波频率的变化. 图5(a)是关于连接件C$_{1}$$\sim$C$_{4}$载荷随刚度的变化, 在入射波周期$T = 10$ s时,非线性分析中连接件载荷(实线+空心圆)变化与浮体响应幅值是对应的,存在峰值区域. 线性分析结果(实线)与线性共振曲线接近;非线性连接件载荷明显比线性的大,基于最大载荷对比而言, 非线性载荷是线性载荷的1.6倍. 因为浮动机场浮体连接方式具有对称性, 连接件C$_{5}$$\sim$C$_{8}$载荷的变化规律与C$_{1}$$\sim$C$_{4}$相似. 值得注意的是尽管各个浮体振荡幅值明显有差异,但不同位置的连接件载荷基本相同,说明两端的锚泊约束刚度在起作用. 考虑到波浪周期对连接件载荷的影响,取$k_{\rm c} = 140$ kN/m为例, 图5(b)描述了连接件C$_{1}$$\sim$C$_{4}$载荷随波浪频率的变化,非线性连接件载荷(实线+空心圆)有明显的的3个峰值, 分布在3个波浪频段上. 在所观察的频域内,随着波浪频率增加,连接件载荷峰值增加,在波浪频率0.6$\sim $0.7\;rad/s 频段,连接件载荷峰最为明显. 与之对比的线性连接件载荷(实线)明显较小,基于最大峰值而言相差4倍有余. 非线 性峰值与线性峰值不完全对应,原因可能是非线性共振支具有弯曲性导致峰值区域向弯曲方向延伸. 理论上,不同波浪周期会影响系统的附加质量和附加阻尼,附加质量会影响系统的共振峰产生的区间,附加阻尼会影响共振峰的幅值, 所以波浪频域内的浮动机场模型具有变参数特性,其幅频响应曲线与一般意义上固定参数系统的幅频响应曲线不同.
|
图 5 连接件载荷随连接件刚度和入射波频率的变化 Fig. 5 Connector load under changes of connector stiffness and wave frequency |
分析结果表明浮动机场的纵荡响应幅值要比垂荡和纵摇响应幅值更为显著; 其连接件的载荷主要受纵荡响应的影响. 尽管本文没有涉及极端海况,仅在普通海况下讨论不同连接件刚度和波浪频率对浮动机场的动力响应的影响,其分析结果普遍性地反映这样一个事实: 浮体的非线性响应和连接件载荷均明显大于线性分析结果. 说明非线性网络结构中的耦合作用可以成倍地放大系统响应,因此基于线性分析方法会低估系统的实际响应和载荷,可能导致安全性设计过于乐观.
2.3 浮体模块响应的同步化效应为了进一步揭示浮动机场系统非线性响应特性,揭示耦合浮体间的集体动力学行为,引入一个相似函数$\varTheta$. 此函数表征两个时间序列$x_i$和$x_j $在一个时滞时间$\tau $ 时的时间平均差,定义如下[45]
| $ \label{eq12} \varTheta (\tau ) = \sqrt {\dfrac{\langle {[{x_j (t + \tau ) - x_i (t)}]^2} \rangle }{[{\langle {x_i (t)^2} \rangle \langle {x_j (t)^2} \rangle }]^{1 / 2}}} $ | (14) |
其中$\left\langle \cdot \right\rangle $表示时间的平均. 寻找它的最小值$\varTheta _{\rm m} = \min _{\tau _0 } \varTheta(\tau )$即$\varTheta _{\rm m} = \varTheta (\tau _0 )$. 从$\varTheta $的定义上看,如果响应$x_i $和$x_j $是独立的,则无论$\tau $取何值都有$\varTheta > 1$. 如果$x_i $ 和$x_j $完全同步,则当$\tau = 0$时有$\varTheta = 0$. 不同于上面的两种情况,如果对于非零的$\tau $,有相似函数$\varTheta _{\rm m} $的值小于1,则表示这两个响应间存在时间上的滞后且$\varTheta _{\rm m} $越接近零,表示两时间序列的相关性越强.
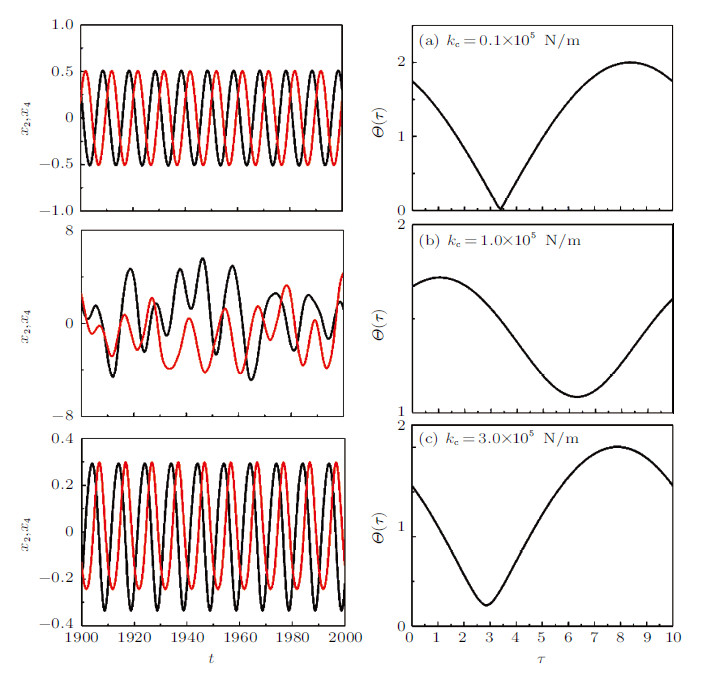
下面取图4中两次跳跃前后的3个刚度值$k_{\rm c} = 0.1\times 10^5$,$1.0\times 10^5$,$3.0\times 10^5$ N/m时的3个响应来研究系统的同步化效应. 由于浮动机场的结构对称性, 本文给出了M2和M4两个模块的纵荡响应时间历程和其对应的相似函数,如图6所示.
|
图 6 浮体模块响应同步化(响应图中黑色曲线表示$x_2 $, 红色曲线表示$x_4 $ Fig. 6 Synchronization of module response |
对于弱耦合$k_{\rm c} = 0.1\times 10^5$ N/m,图6(a)是相似函数随着时滞变化的关系,对应的左图是纵荡谐波响应时间历程. 随着时滞时间$\tau$的增大,相似函数$\varTheta $ 迅速下降并达到最小值$\varTheta _{\rm m} $又很快跃升到一个较大的值,且最小值$\varTheta _{\rm m} $几乎等于零,说明系统此时存在着广义时滞同步化效应[46]. 从相似函数的定义可以知道,此工况下两时间历程有很强的相关性只是存在一定的相位差. 从方程(14)看出,时滞时间$\tau _0 $和相位差$\varphi _{\rm d} $之间的关系为$\varphi _{\rm d} = 2\pi \tau _0 /T$并且通过验证图6(a)中的时滞时间$\tau _0 $,研究发现响应的相位差$\phi _{\rm d} $ 和作用在浮体上的波浪力的相位差$\varphi _{24} $是一致的. 类似地观察耦合强度为$k_{\rm c} = 1.0\times 10^5$ N/m时,系统响应跳跃后处于大振幅参数区间. 从对应的左图响应时间历程可以发现此时系统处于混沌运动状态. 无论时滞时间$\tau $如何变化,相似函数值$\varTheta $值均大于1,这表明两个浮体响应时间序列完全无关. 从其他的算例观察到,当系统响应涉及到复杂的混沌运动,浮体之间通常不会产生步调一致的同步化效应. 进一步观察强耦合作用$k_{\rm c}= 3.0\times 10^5$ N/m,图6(c)显示系统再一次出现类似广义时滞同步化效应. 相似函数最小值$\varTheta _{\rm m} $所对应的时滞时间$\tau _0 $较弱耦合的情况有所减小,说明随着连接件刚度的增大,浮体响应相位差减小. 此时系统运动处于谐波响应状态,其振荡频率与波浪频率一致.
浮动机场的运动模式包括基于波浪周期的单频简谐振荡,倍频振荡,其他多谐波振荡和混沌振荡. 通常当系统的运动处于简谐振荡状态,系统响应同步化协同效应就会出现. 值得指出,无论系统处于同步化状态与否,网络系统的协同效应广泛存在. 各个模块响应在所有自由度上均呈现相同的运动模式,即如果某个浮体的某个自由度运动处于混沌态,其他浮体所有自由度方向的运动必定也是混沌态. 所以,在数值仿真中,可以观察到系统的响应分叉、响应阶跃均是同时发生在所有自由度上. 这些特性可以从图4中的响应幅值曲线比较中清晰地看到.
2.4 浮动机场的振幅死亡现象浮动机场的振幅抑制现象十分重要,关乎系统的动力响应稳定性设计. 为了获得更直观认识,首先来观察图4的响应幅值曲线,在向上阶跃发生之前的$k_{\rm c} < 0.61\times 10^5$ N/m和向下阶跃发生之后$k_{\rm c} > 1.42\times 10^5$ N/m的区段,所有浮体在其三个自由度方向的振荡响应都处于明显的微幅振荡水平. 这种振幅抑制状态在非线性网络动力学中被称为振幅死亡[44]现象. 发生振幅死亡的机理是非线性系统存在多个响应解的结构,当系统参数达到某个临界值时,系统发生了霍普夫分岔或鞍结分岔导致的结果. 就海上浮动机场这个非自治系统而言,振幅抑制状态对应的是其非线性网络动力学系统的非共振支上的周期解,其特征是浮体的微幅振荡周期与波浪周期相吻合; 这个结论在作者前期研究分段非线性耦合网络动力学模型[39]时获得的,也同样适用于本文模型式(11). 由于浮体模块间的相互耦合和制约作用,当连接件的刚度参数和波浪周期参数达到某临界值时,海上浮动机场这个网络结构系统中所有的浮体模块就会呈现微幅振荡的抑制状态. 这个隶属于非线性网络结构动力学的特殊动力学性态对于海上浮动机场的整体动力学稳定性研究具有重要意义,也是传统线性分析方法无法涉及的.
关于浮动机场模型振幅死亡现象发生的临界条件,涉及到求解高维非线性微分方程的近似解析解,以及确定多参数变量情况下的解析解曲面拐点的数学条件等,推导过程十分繁杂. 本文以介绍浮动机场网络动力学建模方法和非线性动力学特性为主,对振幅死亡临界条件的数学推导,不在此详述. 下面将针对海上浮动机场模型式(11),研究其发生振幅死亡的设计参数区域. 连接件刚度参数的考察区间为10 kN/m $\leqslant k_{\rm c} \leqslant 500$ kN/m; 波浪周期参数的考察参数区间为$8$ s $\leqslant T \leqslant 20$ s,该区间基本覆盖了规则海况的波浪周期.
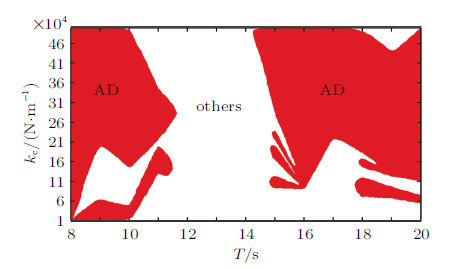
鉴于耦合的浮体模块响应具有网络协同效应,即3个自由度方向上的响应同步发生阶跃和具有相同的响应模式, 所以只需观察其 中某个自由度响应的振幅死亡特性即可. 本算例基于第三浮体的纵荡响应, 通过仿真计算来观察振幅死亡区域. 在二维参数区域内逐点扫描,纵坐标为连接件刚度,横坐标为波浪周期, 以红色标注出呈现振幅死亡现象所对应的参数值. 图7在红底色上标注的符号AD代表海上浮动机场的振幅死亡的参数区域, 在白色区域标注了"others"意味着大幅值振荡,其振荡模式有可能是混沌和高阶谐波运动态. 在红色与白色区域的交接边界上,意味着系统的动力响应幅值发生阶跃.
|
图 7 振幅死亡参数域 Fig. 7 Amplitude death parameter domains in parameter space $(k_{\rm c} ,T)$:\\ the sign $AD$ indicates amplitude death |
图7中可以看到红白界线非常不规则,局部区域会出现类似手指形的分形结构. 从全局构图来看,振幅死亡区域主要分布在左右两边. 中间 的空白部分表明无论如何调整连接件刚度设计都不可能获得振幅死亡状态, 也意味着波浪周期大约在12 s $\leqslant T \leqslant 14$ s. 区间的波段上对超大型海上浮动机场的动力响应和连接件载荷构成较严重的影响. 只有当系统的设计参数落入红色区域才能使得浮动机场获得微幅振动状态. 系统处于振幅死亡状态意味着柔性连接件所承受的载荷相对较小.
本文通过上面算例讨论了振幅死亡存在的参数区域,算例中采用的参数仅是连接件刚度和波浪周期, 作为揭示浮动机场这类网络结构 的弱振荡性态现象已足够充分. 事实上, 影响振幅死亡的参数还有波高、连接件结构设计等其它因素. 从海上浮动机场的动力响应稳定性思考, 需要分析所有参数的振幅死亡图谱,为浮动机场稳定性设计提供一个直观而简洁的参考依据,具有重要的工程应用价值.
3 结 论本文以超大型海上浮动机场为研究对象,尝试将非线性网络动力学理论拓展到超大型海上浮式结构物的动力响应预报. 详细描述了多模块海上浮动机场的非线性网络动力学建模方法,构建了具有几何非线性本构关系的浮动机场模型. 通过数值仿真分析了浮动机场的纵荡、垂荡和纵摇的非线性响应和连接件载荷,表明线性分析方法严重低估了系统的实际响应和载荷. 本文也探讨了多模块浮体之间的网络协同效应和浮动机场的振幅死亡现象这一特殊的网络动力学现象,即各浮体模块处于一种同步性的微幅振荡抑制状态. 文中简单叙述了振幅死亡产生的机理,数值仿真展示了振幅死亡区域与连接件刚度参数和波浪周期的关系,对于海上浮动机场的稳定性设计具有特殊意义.
尽管本文采用了5个浮体链式网络结构的浮动机场模型做算例,理论上,可以拓展到任何模块数量的大型浮体结构. 在作者的模拟仿真中,也对由8个浮体和10个浮体组成的链式结构浮动机场模型做了分析,从各个自由度响应幅值看较5个浮体机场模型要大,但不会有量级性的差别;从非线性响应特性看,也有响应阶跃、网络协同效应和振幅死亡现象,基本上雷同. 在网络动力学模型中特别设置了拓扑结构矩阵,使得建模方法适用于各类复杂拓扑结构的超大型海上浮式结构物; 通过改变拓扑结构矩阵的赋值,可以方便地模拟诸如矩形或其他类型的海上浮动结构平台. 值得指出的是网络动力学的研究方法与传统力学分析方法有很大差异. 网络动力学理论源自多个振子耦合系统的非线性动力学研究,探索振子间的网络协同效应及机理. 这种研究方法揭示了一系列新的动力学现象,诸如振幅死亡现象,同步化现象,局部异化现象等. 本文通过探讨海上浮动机场的非线性网络动力学特性,尝试该理论在超大型海洋工程结构动力学方面的运用,为力学界所面临的更为广泛的网络结构动力学问题,提供一个新的视角和应用范例.
| [1] | Mcallister KR. Mobile offshore bases——An overview of recent research. Journal of Marine Science and Technology, 1997, 2(3): 173-181. |
| [2] | Ohmatsu S. Overview: Research on wave loading and responses of VLFS. Marine Structures, 2005, 18(2): 149-168. |
| [3] | Wang CM, Tay ZY. Very large floating structures: Applications, research and development. Procedia Engineering, 2011, 14: 62-72. |
| [4] | Fujikubo M. Structural analysis for the design of VLFS. Marine Structures, 2005, 18(2): 201-226. |
| [5] | Yoshida K. Developments and researches on VLFS in Japan. In: Proceedings of the Second International Workshop on Very Large Floating Structures, Hayama, Japan, 1996 |
| [6] | Kyozuka Y, Kato S, Nakagawa H. A numerical study on environmental impact assessment of mega-float of Japan. Marine Structures, 2001, 14(1): 147-161 |
| [7] | Suzuki H. Overview of mega-float: Concept, design criteria, analysis, and design. Marine Structures, 2005, 18(2): 111-132. |
| [8] | Sueoka H, Sato C. Phase H research of mega-float. In: Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, USA, 2000 |
| [9] | Bhattacharya B, Basu R, Ma K. Developing target reliability for novel structures: The case of the mobile offshore base. Marine Structures, 2001, 14(1-2): 37-58 |
| [10] | Remmers G, Zueck R, Palo P, et al. Mobile offshore base. In: Proceedings of the Eighth International Offshore and Polar Engineering Conference, Montreal, Canada, 1998 |
| [11] | Zueck R, Taylor R, Palo P. Assessment of technology for mobile offshore base. In: Proceedings of the Tenth International Offshore and Polar Engineering Conference, Seattle, USA, 2000 |
| [12] | Palo P. Mobile offshore base: Hydrodynamic advancements and remaining challenges. Marine Structures, 2005, 18(2): 133-147. |
| [13] | Girard A, Hedrick KJ, Sousa DBFDTJ. A hierarchical control architecture for mobile offshore bases. Marine Structures, 2000, 13(4): 459-476 |
| [14] | Faltinsen OM. Bottom slamming on a floating airport. In: Proceedings of the Second International Workshop on Very Large Floating Structures, Hayama, Japan, 1996 |
| [15] | Rognaas G, Xu J, Lindseth S, et al. Mobile offshore base concepts: Concrete hull and steel topsides. Marine Structures, 2001, 14(1): 5-23 |
| [16] | Price WG, Inzunza MS, Temarel P. The hydroelastic behaviour of barge type structures in waves. In: Proceedings of the Second International Workshop on Very Large Floating Structures, Hayama, Japan, 1996 |
| [17] | Pinkster JA, Fauzi A. The effect of air cushions under floating offshore structures. In: Proceedings of the Eighth International Conference on the Behaviour of Offshore Structures, Delft, The Netherlands, 1997 |
| [18] | Young T, Chung JH. Introduction of barge-mounted plants project in Korea. In: Proceedings of the Second International Workshop on Very Large Floating Structures, Hayama, Japan, 1996 |
| [19] | Koh HS, Lim YB. The floating platform at the marina bay, Singapore. Structural Engineering International, 2009, 19(1): 33-37. |
| [20] | 吴有生, 杜双兴. 极大型海洋浮体结构的流固耦合分析. 舰船科学技术,1995, (1):1-9 (Wu Yousheng, Du Shuangxing. Fluid-structure interaction analysis of very large floating structures. Ship Science and Technology, 1995, (1): 1-9 (in Chinese)) |
| [21] | 崔维成, 吴有生, 李润培. 超大型海洋浮式结构物开发过程需要解决的关键技术问题.海洋工程, 2000, 18(3): 1-8 (Cui Weicheng, Wu Yousheng, Li Runpei. Technical problems in the development of very large floating structures.Ocean Engineering, 2000, 18(3): 1-8 (in Chinese)) |
| [22] | 崔维成, 吴有生, 李润培. 超大型海洋浮式结构物动力特性研究综述. 船舶力学, 2001, 5(1): 73-81 (Cui Weicheng, Wu Yousheng, Li Runpei. Recent researches on dynamic performances of very large floating structures. Journal of Ship Mechanics, 2001, 5(1): 73-81 (in Chinese)) |
| [23] | 陈国建, 杨建民, 张承懿. 箱式超大型浮体的水弹性模型试验. 海洋工程, 2003, 21(3): 1-5 (Chen Guojian, Yang Jianmin, Zhang Chengyi. Experimental research on hydroelasticity on box-typed flexible VLFS in waves. Ocean Engineering, 2003, 21(3): 1-5 (in Chinese)) |
| [24] | 韩满生. 超大型浮体结构水弹性响应的板模型分析[硕士论文]. 青岛: 中国海洋大学, 2005 (Han Mansheng. Analysis of hydroelastic responses of very large floating structure by use of plate model. [Master's Thesis]. Qingdao: Ocean University of China, 2005 (in Chinese)) |
| [25] | 胡金芝. 超大型浮体结构水弹性响应的梁板模型分析[硕士论文]. 南京: 河海大学, 2007 (Hu Jinzhi. Analysis of hydroelastic responses of very large floating structure by use of sandwich grillage model. [Master's Thesis]. Nanjing: Hohai University, 2007 (in Chinese)) |
| [26] | Bishop RED, Price WG. Hydroelasticity of Ships. Cambridge: Cambridge University Press, 1979 |
| [27] | Kashiwagi M. Research on hydroelastic responses of VLFS: Recent progress and future work. International Journal of Offshore and Polar Engineering, 2000, 10(2): 1053-5381 |
| [28] | Watanabe E, Utsunomiya T, Wang CM. Hydroelastic analysis of pontoon-type VLFS: A literature survey. Engineering Structures, 2004, 26(2): 245-256. |
| [29] | Chen XJ, Wu YS, Cui WC, et al. Review of hydroelasticity theories for global response of marine structures. Ocean Engineering, 2006, 33(3): 439-457 |
| [30] | Wang CM, Takagi K, Utsunomiya T, et al. Literature review of methods for mitigating hydroelastic response of VLFS under wave action. Applied Mechanics Reviews, 2010, 63(3): 30802. |
| [31] | Paulling JR, Tyagi S. Multi-module floating ocean structures. Marine Structures, 1993, 6(2): 187-205 |
| [32] | Gao RP, Wang CM, Koh CG. Reducing hydroelastic response of pontoon-type very large floating structures using flexible connector and gill cells. Engineering Structures, 2013, 52: 372-383. |
| [33] | Gao RP, Tay ZY, Wang CM, et al. Hydroelastic response of very large floating structure with a flexible line connection. Ocean Engineering, 2011, 38(17): 1957-1966 |
| [34] | Fu S, Moan T, Chen X, et al. Hydroelastic analysis of flexible floating interconnected structures. Ocean Engineering, 2007, 34(10): 1516-1531 |
| [35] | Maeda H, Maruyama S, Inoue R, et al. On the motions of a floating structure which consists of two or three blocks with rigid or pin joints. Journal of the Society of Naval Architects of Japan, 1979, 145: 71-78 |
| [36] | Wang D, Ertekin RC, Riggs HR. Three-dimensional hydroelastic response of a very large floating structure. International Journal of Offshore and Polar Engineering, 1991, 1(4): 1053-5381 |
| [37] | Riggs HR, Ertekin RC. Approximate methods for dynamic response of multi-module floating structures. Marine Structures, 1993, 6(2): 117-141 |
| [38] | Xu DL, Zhang HC, Lu C. On study of nonlinear network dynamics of flexibly connected multi-module very large floating structures. The Second International Conference on Vulnerability and Risk Analysis and Management, Liverpool, UK, 13-16, July, 2014 |
| [39] | Xu DL, Zhang HC, Lu C. Analytical criterion for amplitude death in non-autonomous systems with piecewise nonlinear coupling. Physical Review E, 2014, 89: 042906. |
| [40] | Stoker JJ. Water Waves: the Mathematical Theory with Applications. Hoboken: John Wiley & Sons, 1958 |
| [41] | Sannasiraj SA, Sundar V, Sundaravadivelu R. Mooring forces and motion responses of pontoon-type floating breakwaters. Ocean Engineering, 1998, 25(1): 27-48. |
| [42] | Zheng YH, You YG, Shen YM. On the radiation and diffraction of water waves by a rectangular buoy. Ocean Engineering, 2004, 31(7): 1063-1082 |
| [43] | 王志军, 李润培, 舒志. 箱式超大型浮体结构在规则波中的水弹性响应研究. 海洋工程, 2001,19(3): 9-13 (Wang Zhijun, Li Runpei, Shu Zhi. Study on hydroelastic response of box-shaped very large floating structure in regular waves. Ocean Engineering, 2001, 19(3): 9-13 (in Chinese)) |
| [44] | Resmi V, Ambika G, Amritkar RE. General mechanism for amplitude death in coupled systems. Physical Review E, 2011, 84(4): 46212. |
| [45] | Rosenblum MG, Pikovsky AS, Kurths J. From phase to lag synchronization in coupled chaotic oscillators. Physical Review Letters, 1997, 78: 4193. |
| [46] | Banerjee T, Biswas D. Amplitude death and synchronized states in nonlinear time-delay systems coupled through mean-field diffusion. Chaos, 2013, 23: 043101. |
 2015, Vol. 47
2015, Vol. 47
