2. 铁道第三勘察设计院集团有限公司, 天津 300142
作为一种天然的准脆性非均匀材料,岩石内部存在大量的微观和宏观裂隙,其破坏实际是一个损伤演化、裂纹形成与扩展、断裂贯通直 至发生运动的过程.岩石内部众多裂纹端部的应力集中是引起岩石开裂,进而发生解体破坏的原因. 在开裂的过程中,由于所受外部荷载的复杂性,裂纹可能沿着任意的路径发生扩展和演化,裂缝两侧的材料则由初始的连续状态向非连续状态转变. 研究岩石中裂纹扩展与贯通机理,对于研究岩石破坏过程具有重要的意义,同时也是解决并控制重大工程地质灾害的基础.
对于岩石裂纹扩展过程的研究,实际上经历了弹塑性力学到损伤断裂力学、连续介质到离散介质、宏观模型到微细观模型的发 展过程.随着计算技术水平的发展,采用数值方法模拟岩石在复杂荷载作用下的力学行为,是研究岩石开裂等复杂力学机制的一个有效手段. 目前,模拟岩石裂纹扩展过程的数值方法主要分为连续介质力学方法、离散介质力学方法以及连续-离散耦合方法3大类[1]. 对于连续介质力学方法和离散介质力学方法,学者们根据这些方法的各自优势提出一些适用模型,用于模拟不同岩石性状下的开裂问题[2, 3, 4]. 然而,如要对岩石由裂纹形成到解体破坏的过程进行仿真分析,建立连续与离散介质的统一模型则是关键,同时也是近年来国内外研究的重点.
连续-离散耦合分析方法的研究主要分为两大方向: (1) 裂纹扩展问题的模拟,重点在于描述连续介质中裂纹萌生的理论模型以及裂缝两侧位移非连续的方式; (2) 连续-非连续问题的求解,目的是将连续变形分析和破坏运动分析结合在统一的数值算法中. 从耦合的方式来看,包括有限元-非连续变形分析耦合、有限元-离散元耦合、有限差分-离散元耦合等.数值流形方法[5, 6, 7, 8]是将连续和非连续问题求解建立在统一的理论框架下,}应用流形覆盖技术将计算区域划分为数学网格和物理网格,通过切割数学网格实现物理网格的分离,进而模拟裂纹的形成和扩展过程. 文献[9, 10]将有限元和离散元进行耦合,在有限元中引入了损伤断裂理论,当材料破裂后利用离散元的方法在块体边界间进行接触计算. 文献[11]则在有限元网格中嵌入裂缝实现连续向非连续的转化,并用于脆性材料冲击作用下的力学行为研究. 李世海等[12]构建弹簧元模型,并嵌入CDEM[13, 14]计算程序,模拟岩石破裂以及混凝土冲击破坏过程.常晓林等[15, 16]在变形体离散元基础上,引入损伤、断裂的黏聚力模型,通过界面单元起裂、扩展和失效,实现岩体开裂. 侯艳丽[17]等在变形体离散元中引入了弥散式裂缝模型和分离式裂缝模型,分析了岩石等脆性材料的破坏过程.
本文基于变形体离散元的框架,通过单元破裂方式,建立连续-非连续单元法. 该方法在连续计算时,将单元离散为具有物 理意义的弹簧系统,在局部坐标系下求解变形和应力,连续问题计算结果与有限元一致,在继承有限元优势的同时提高了计算效率. 在此基础上,引入最大拉应力与莫尔-库伦复合准则,确定单元破坏状态和破裂方向,进而采用局部块体切割的方式实现单元内部和边界上的开裂,显示模拟裂纹的形成和扩展过程. 最后,通过数值试验模拟裂纹在拉伸、压剪等不同应力状态下的扩展问题,同时对岩石单轴压缩破坏过程进行模拟,验证连续-非连续单元法的合理性.
1 连续单元模型构建作为一种有效的非连续介质力学数值分析方法,离散元广泛应用于岩体开裂、破坏过程的模拟分析. 现有研究成果中,离散元在处理开裂问题时有以下特点: (1) 在界面单元或界面弹簧上应用准则判断破裂; (2) 裂纹只能沿着单元边界扩展.实际上,若物理问题存在宏观或微观裂隙(如节理、微裂纹等),用界面弹簧计算破裂则非常合理,为一种有效的破裂处理方法. 但若不存在裂隙,初始状态即为均匀的连续介质,界面弹簧的引入将使分析的问题并非完全连续,进而也不是真正意义上的连续-离散耦合. 此外,裂纹仅沿单元边界进行扩展,使得裂纹路径受限. 针对这两个问题,本文的连续-非连续单元法将尝试给出一种改进方式.
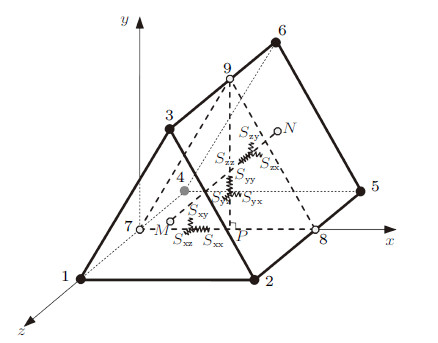
对于连续状态下单元变形和应力计算,本文采用弹簧元法(spring element method,SEM)[12, 18, 19],其思想是将单元离散为弹簧系统,在局部坐标系下由弹簧特征量求解. 弹簧系统由基本弹簧、泊松弹簧和纯剪弹簧组成. 基本弹簧包括1个法向和2个切向弹簧,泊松弹簧和纯剪弹簧为非常规意义弹簧,分别用于表述法向弹簧间相互作用、切向弹簧间相互作用. 针对拟三维情况下的连续问题计算,可构建如图1所示的三棱柱单元,记1至6为单元节点,点7,8和9分别为棱14,25和36中点,点$M$和$N$分别为面123和面456的形心. 弹簧系统的构建步骤如下: 在点7和8间建立法向弹簧$S_{xx}$和切向弹簧$S_{xy}$及$S_{xz}$; 过点9做边78的垂线9$P$,在垂线上建立法向弹簧$S_{yy}$和切向弹簧$S_{yz}$及$S_{yx}$; 在点$M$和$N$间建立法向弹簧$S_{zz}$和切向弹簧$S_{zx}$及$S_{zy}$; 在三组基本弹簧间,分别建立与两法向弹簧相关的泊松弹簧$S_{pxy}$,$S_{pyz}$和$S_{pxz}$以及与两剪切弹簧相关的纯剪弹簧$S_{sxy}$,$S_{syz}$和$S_{sxz}$. 在上述弹簧系统下,建立局部坐标系如图1所示,下文推导中单元的各个参量均是在局部坐标系下讨论.
|
图 1 三棱柱单元的离散弹簧系统 Fig.1 Spring system of triangular prism element |
对于弹簧系统中的空间点7,8,9,$M$和$N$,其位移增量可通过单元节点位移增量计算获得
| $ \label{eq1}\left.\begin{array}{l} u_{7i} = \dfrac{u_{1i} + u_{4i} }{2},\ \ u_{8i} = \dfrac{u_{2i} + u_{5i}}{2},\ \ u_{9i} = \dfrac{u_{3i} + u_{6i} }{2} \\[2mm] u_{Mi} = \dfrac{u_{1i} + u_{2i} + u_{3i} }{3},\ \ u_{Ni} = \dfrac{u_{4i} + u_{5i}+ u_{6i} }{3} \\ \end{array} \right\} $ | (1) |
式中,$i=x$,$y$,$z$; $u_{ji}$ ($j = 1,2,\cdots,6$,$i=x$,$y$,$z)$为三棱柱单元各节点在局部坐标系下的位移增量.
弹簧系统中的法向和切向弹簧的变形增量可以通过单元节点位移增量计算获得
| $ \label{eq2}\left.\begin{array}{l} \Delta u_{xi} = u_{8i} - u_{7i} \\\Delta u_{yi} = u_{9i} - mu_{7i} -nu_{8i} \\ \Delta u_{zi} = u_{Mi} - u_{Ni} \\ \end{array} \right\} $ | (2) |
式中,$m$和$n$为$P$点在边78上的线性插值系数,其计算式为
| $ \label{eq3}m = \vert 8P\vert / \vert 78\vert ,\ \ n = \vert 7P\vert / \vert78\vert $ | (3) |
对于拟三维情形下的三棱柱单元,平面上的应力应变为其核心,可先讨论空间点7,8和9构成的三角形中,$S_{xx}$,$S_{xy}$和$S_{yy}$、$S_{yx}$等4个弹簧的变形与连续单元应变之间的内在联系. 设7,8和9点在$xy$面内的位移列阵为
| $ \label{eq4} a^e = [u_{7x} u_{7y} u_{8x} u_{8y} u_{9x} u_{9y}] $ | (4) |
若三角形内的位移模式选取为一次多项式,则其位移函数可表示为
| $ u=[{{N}_{7}}{{N}_{8}}{{N}_{9}}]{{a}^{e}}=N{{a}^{e}} $ | (5) |
式中,$N_{i} = (a_{i}+b_{i}+c_{i})/2A$; $A$为三角形面积; $a_{i}$,$b_{i}$,$c_{i}$ ($i = 7,8,9$)为常数,取决于点7,8和9的坐标,可表示为
| $ \label{eq6}\left.\begin{array}{l} a_7 = x_8 y_9 - x_9 y_8 ,b_7 = y_8 - y_9 ,c_7 = - x_8 + x_9 \\ a_8 = x_9 y_7 - x_7 y_9 ,b_8 = y_9 - y_7 ,c_8 = - x_9 + x_7 \\ a_9 = x_7 y_8 - x_8 y_7 ,b_9 = y_7 - y_8 ,c_9 = - x_7 + x_8 \\ \end{array} \right\} $ | (6) |
设三角形边78长为$a$,垂线9$P$长为$b$,则7,8和9点在$xy$面内的坐标可表示为7(0,0),8 ($a$,0),9 ($na,b)$,则有
| $ \label{eq7}\left.\begin{array}{l} a_1 = ab,b_1 = - b,c_1 = - a + na \\ a_2 = 0,b_2 = b,c_2 = - na \\ a_3 = 0,b_3 = 0,c_3 = a \\ \end{array} \right\} $ | (7) |
根据弹性理论的几何方程,三角形的应变可表示为
| $ \label{eq8} \varepsilon = {Lu} = {LNa}^e = [B_7 B_8 B_9] a^e $ | (8) |
其中
| $ \label{eq9} B_i = \dfrac{1}{2A}\left[{\begin{array}{cc} b_i &0 \\ 0&c_i \\ c_i &b_i \\ \end{array}} \right]\ \ (i = 7,8,9) $ | (9) |
联立式(2),式(7)$\sim$(9)可得
| $ \label{eq10}\Delta \varepsilon _{xx} = \dfrac{\Delta u_{xx} }{a},\Delta \varepsilon_{yy} = \dfrac{\Delta u_{yy} }{b},\gamma _{xy} = \dfrac{\Delta u_{xy}}{a} + \dfrac{\Delta u_{yx} }{b} $ | (10) |
对上式进行分析可知,三角形区域的应变即等于7,8和9点间的弹簧变形除以弹簧特征长度. 同理,三棱柱单元厚度方向的应变同样可按该方式获得. 因此,整个弹簧系统中各弹簧的应变增量可表示为
| $ \label{eq11}\Delta \varepsilon_{xi} = \dfrac{\Delta u_{xi }}{a},\Delta \varepsilon _{yi} = \dfrac{\Delta u_{yi}}{b},\Delta \varepsilon _{zi} = \dfrac{\Delta u_{zi }}{c} $ | (11) |
式中,$i=x$,$y$,$z$; $c$为边$MN$的长度.
由线弹性应力-应变关系,可以求得弹簧系统的应力增量为
| $ \label{eq12}\Delta \sigma_{ij} = \lambda \Delta \varepsilon _v \delta _{ij} + 2\mu \Delta \varepsilon _{ij} $ | (12) |
式中,$\Delta \varepsilon_{v}$为体应变增量; $\lambda$,$\mu$分别为拉梅常数和剪切模量; $\delta _{ij}$为克罗内克(Kronecker) 符号. 应力增量$\Delta \sigma_{ij}$叠加到上一步的总量形成新的应力全量$\sigma_{ij}$.
在局部坐标系下,弹簧系统应力应变即可表征单元的应力应变. 通过弹簧应力乘以特征面积可求得弹簧系统中法向和切向弹簧力
| $ \label{eq13}F_{xi} = \dfrac{bc}{2}\sigma _{xi} ,\ \ F_{yi} = \dfrac{ac}{2}\sigma _{yi},\ \ F_{zi} = \dfrac{ab}{2}\sigma _{zi} $ | (13) |
式中,$i=x$,$y$,$z$; $bc/2$,$ac/2$,$ab/2$分别为3个基本弹簧的特征面积.
块体单元的节点力由弹簧力插值求得
| $ \label{eq14}\left.\begin{array}{l} F_1^i = - \dfrac{F_{xi} }{2} - \dfrac{mF_{yi} }{2} - \dfrac{F_{zi} }{3}\\[2mm] F_2^i = \dfrac{F_{xi} }{2} - \dfrac{nF_{yi} }{2} - \dfrac{F_{zi} }{3}\\[2mm]F_3^i = \dfrac{F_{yi} }{2} - \dfrac{F_{zi} }{3}\\[2mm]F_4^i= - \dfrac{F_{xi} }{2} - \dfrac{mF_{yi} }{2} + \dfrac{F_{zi} }{3} \\[2mm]F_5^i =\dfrac{F_{xi} }{2} - \dfrac{nF_{yi} }{2} + \dfrac{F_{zi} }{3} \\[2mm] F_6^i = \dfrac{F_{yi} }{2} +\dfrac{F_{zi} }{3} \\ \end{array} \right\} $ | (14) |
式中,$i=x$,$y$,$z$; $F_{j}^{i}$ ($j = 1,2,\cdots,6$) 为单元节点力.
上述内容包含了弹簧元方法的推导过程,实际计算步骤则非常简便,可概括为:
(1) 每个迭代步由单元节点位移增量,求得弹簧变形增量$\Delta u_{ij}(i,j=x,y,z)$;
(2) 由弹簧变形增量$\Delta u_{ij}$及弹簧特征长度求得单元应变增量$\Delta \varepsilon _{ij}$和应力增量$\Delta \sigma _{ij}$;
(3) 由应力全量$\sigma_{ij}$及弹簧特征面积求得弹簧力$F_{ij}$ ($i,j=x,y,z)$,通过坐标变换,插值求得单元节点力;
(4) 根据节点动力平衡方程,求得新的节点位移、速度,如此迭代求解直至收敛.
连续问题计算时,采用罚函数方法在块体单元之间建立数学弹簧作为连接,以满足单元间的变形协调条件. 将上述方法的计算结果与有限元进行对比,验证其连续计算的正确性. 如图2所示的三点弯曲梁,长度$l = 0.6$ m,高度$b = 0.15$ m,厚度$t = 0.01$ m. 数值模拟的材料参数为: 弹性模量$E = 36.5$ GPa,泊松比$\nu = 0.1$. 模型底部的两端端点$y$向约束,中心点 ($l / 2$,$b / 2$)处$x$向约束,前后面法向约束,顶部中心节点处施加$y$向荷载 $-4.8$ kN.

|
图 2 三点弯曲梁模型 Fig.2 Numerical model of three-point beam |
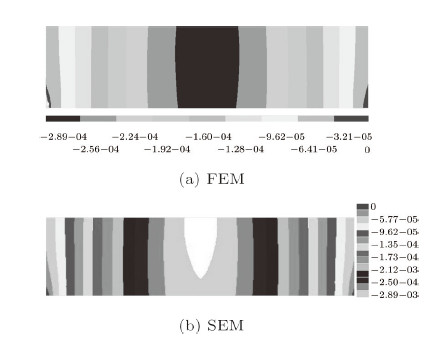
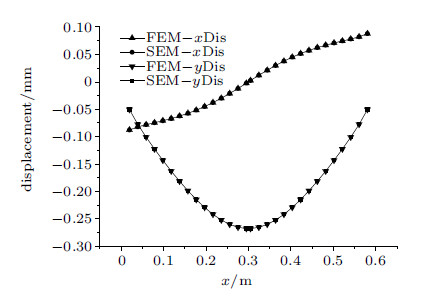
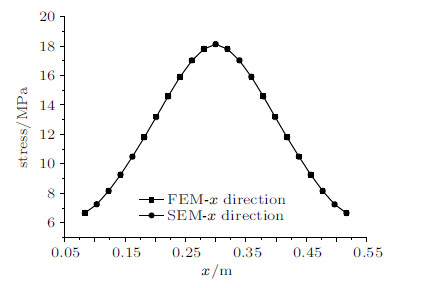
图3所示为两种方法计算的$y$向位移的云图对比,数值上完全相同. 因云图无法精确显示,可进一步在模型中选取节点数据进行 对比. 在模型底部等间距选取节点,获取节点$y$向和$x$向位移值,两种方法的计算结果对比如图4,其中横轴为节点的$x$坐标. 另 在模型底部等间距选取单元,单元$x$向应力值的计算结果对比如图5,横轴为单元中心的$x$坐标.综上,由位移曲线、应力曲线以及位移云图的对比可知,两种计算方法的计算结果一致,由此说明弹簧元模型在连续计算时的正确性.
|
图 3 有限元(a)和弹簧元(b)计算的$y$向位移云图(单位: m) Fig.3 Displacement-contour of three-point beam in y-direction by (a) FEM and(b) SEM (unit: m) |
|
图 4 两种数值方法计算的节点位移 Fig.4 Node displacement of two numerical methods |
|
图 5 两种数值方法计算的单元应力 Fig.5 Element stress of two numerical methods |
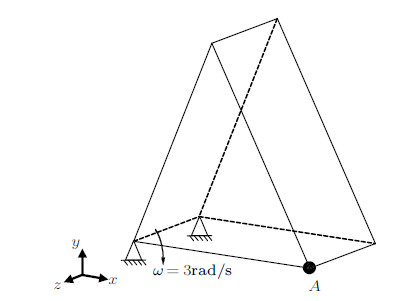
对于包含大位移和大转动问题的计算,本文所述方法需在每个迭代步更新单元节点坐标,从而更新单元局部坐标系以及弹簧系 统中弹簧长度和面积. 对于图6所示的三棱柱模型,长0.1 m,高0.1 m,厚度为0.05 m. 材料参数为: 弹性模量$E = 36.5$ GPa,泊松比$\nu = 0.1$. 模型底部左则两个节点固定约束,给初始角速度$\omega = 3$ rad/s,无阻尼情况下单元上任意点y向位移的理论表达式为
|
图 6 转动计算模型 Fig.6 Numerical model of rotation |
| $ \label{eq15}y = - r\sin (wt) $ | (15) |
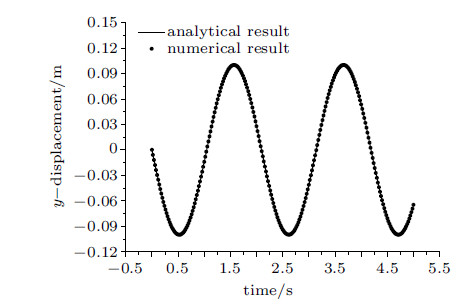
式中,$r$为该点的转动半径. 对于模型中的监测点$A$,数值计算与理论解的对比如图7所示,二者结果一 致,说明所述方法在大 位移、大转动计算时的正确性.
|
图 7 转动计算的数值结果和理论解对比 Fig.7 Comparison between numerical result and theory resolution of rotation |
连续-非连续单元法在连续计算上,继承有限元的优势,同时可计算块体大位移、大转动问题.为进一步实现连续向非连续的转变,需要实现裂纹的萌生与扩展,首先必须确定合理的起裂准则,进而确定裂纹的开裂位置和开裂路径.
2.1 单元的破裂在宏观裂纹起裂、裂纹稳定和失稳扩展的研究方面,断裂力学模型得到广泛应用. 但在实际工程中,经常面临的是多条复杂裂纹同时扩展、岩石碎裂性破坏等断裂力学较难处理的情况. 因此,本文在连续计算的基础上,应用最大拉应力和莫尔-库伦复合准则判断单元破坏状态和破裂方向.
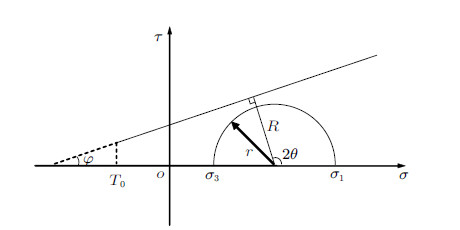
在主应力空间对单元破裂进行判断,以压应力为正,如图8所示,假设单元抗拉强度为$\sigma_{\rm t} $,若满足式
|
图 8 块体破裂的莫尔-库伦准则 Fig.8 The Mohr--Coulomb criterion for the block |
| $ \label{eq16} - \sigma _3 \geqslant \sigma _{\rm t} $ | (16) |
则单元发生拉伸破坏,裂纹方向与最小主应力$\sigma _3 $垂直. 若$ - \sigma _3 < \sigma _{\rm t} $,则考虑剪切破坏,假设单元内某一斜面的法向与$\sigma _1 $间的夹角为$\theta $,则该斜面上的法向应力可表示为
| $ \label{eq17}\sigma _{\rm n} = \dfrac{1}{2}(\sigma _1 + \sigma _3 ) + \dfrac{1}{2}(\sigma _1 -\sigma _3 )\cos 2\theta $ | (17) |
剪切应力可表示为
| $ \label{eq18}\tau = \dfrac{1}{2}(\sigma _1 - \sigma _3 )\sin 2\theta $ | (18) |
根据莫尔库伦准则,斜面上的剪切强度为
| $ \label{eq19}s = c + \sigma _{\rm n} \tan \varphi $ | (19) |
式中,$c$,$\varphi$ 分别为单元的黏聚力和内摩擦角. 发生剪切破坏的条件为
| $ \label{eq20} - \sigma _3 < \sigma _{\rm t} ,R \leqslant r $ | (20) |
对应的应力判据为
| $ \label{eq21}\sigma _1 \geqslant \sigma _3 \tan ^2(\pi / 4 + \varphi / 2) + 2c\tan (\pi / 4 + \varphi/ 2) $ | (21) |
裂纹方向与$\sigma _3 $夹角为$(\pi / 4 + \varphi / 2)$.
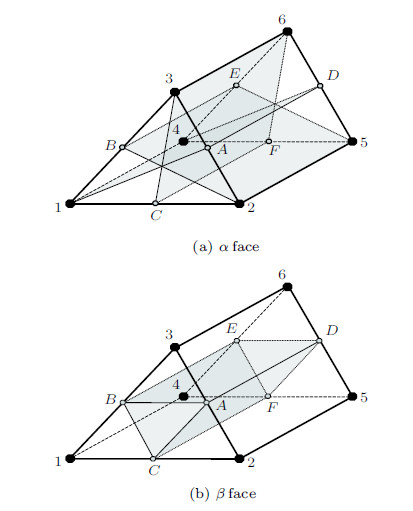
按照上述强度准则,对计算区域内的所有块体进行强度判断,可获得破裂块体的裂纹方向. 然而仅由破裂方向,块体内的裂纹位置仍无法确定. 此时若在块体内部任意位置出现裂纹,则会形成不规则单元,出现奇异性网格,这会使得计算精度大为降低,甚至会导致求解上的失败. 对于图9所示的三棱柱单元,本文假定裂纹仅在单元内部面$\alpha1AD4$,$\alpha 2BE5$,$\alpha 3CF6$,$\beta ABED$,$\beta BCFE$,$\beta CADF$和单元边界面$\gamma $1254,$\gamma $2365和$\gamma$3146上形成. 当块体发生破裂时,在6个内部面和3个边界面中,选取与理论判断的裂纹方向最为接近的面作为最终裂纹面.
|
图 9 三棱柱单元内部破裂示意图 Fig.9 Internal failure modes of triangular prism element |
采用该方法后,虽然裂纹无法精确的按照理论计算方向进行扩展,但是裂纹位置得以确定,同时网格质量也得到较好的控制.此 外,相比与界面的断裂方式(图10(a)),该方法为裂纹的扩展提供了更多可选择的路径(图10(b)、图10(c)),裂纹扩展方向更为准确.

|
图 10 节点处裂纹扩展的三种方式 Fig.10 Three modes of crack propagation on node |
上述准则中的式(16)和(21),仅用于判断单元的起裂,进而获得确定的裂缝面. 在此之后,裂缝面的力学特征描述则是重点关心的问题. 内聚力模型通过定义缝面上的应力与裂缝张开度间的软化关系,描述复合拉剪和压剪模式下损伤微裂材料的弱化力学行为[20],可表述如下.
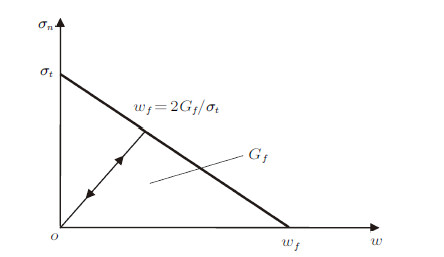
(1) 假定起裂时裂缝面的法向应力为$\sigma _{\rm t}$,即式(16)中的单元抗拉强度. 采用文献[21]建议的线性软化曲线(图11),最大裂缝张开度
|
图 11 内聚力模型线性软化曲线[21] Fig.11 Linear softening curve of cohesive model[21] |
| $ \label{eq22}w_{\rm f} = 2G_{\rm f} / \sigma _{\rm t} $ | (22) |
裂缝面上法向应力$\sigma_{\rm n}$和张开度$w$关系为
| $ \label{eq23}\sigma _{\rm n} = \left\{ {\begin{array}{ll} \sigma _{\rm t} (1 - w / w_{\rm f} ) ,\ \ & 0 \leqslant w \leqslant w_{\rm f} \\ 0,& w > w_{\rm f} \\ \end{array}} \right. $ | (23) |
式中,$G_{\rm f}$为断裂能,$w$为法向张开度.
(2)根据文献[22]假定,定义裂缝面切向刚度按法向张开度进行折减,折减系数为$\beta $,裂缝面黏聚力$c$与裂缝面抗拉强度具有相同软化模式,则有
| $ \beta ={{\sigma }_{\text{n}}}/{{\sigma }_{\text{t}}},{c}'=\beta c $ | (24) |
| $ \tau =\left\{ \begin{array}{*{35}{l}} \beta {{k}_{\text{s}}}{{u}_{\text{s}}} & (\left| \tau \right|\le -{{\sigma }_{\text{n}}}\tan \varphi +{c}') \\ \text{sign}({{{\dot{u}}}_{\text{s}}}){{\sigma }_{\text{n}}}\tan \varphi & (\left| \tau \right|>-{{\sigma }_{\text{n}}}\tan \varphi +{c}') \\ \end{array} \right. $ | (25) |
式中$k_{\rm s}$为裂缝面的切向刚度.
综上,拉剪或压剪复合模式下,裂缝面上的应力与张开度、切向位移的关系建立完成. 这里需要注意,式(16)和式(21)仅用于判断单元起裂,而确定裂缝面后,则通过式(22)$\sim$(25)描述裂缝的力学特征,裂缝面参数$\sigma _{\rm t}$,$c$,$\varphi $与单元材料一致,两者间不存在矛盾. 另外,如果裂缝面的断裂能$G_{\rm f}$ 取值为零,裂缝即表现为脆性断裂特征.
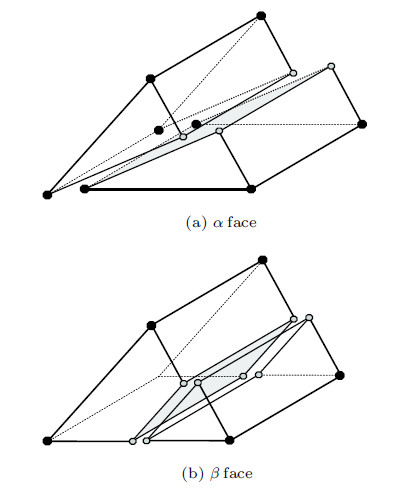
裂缝在块体内部形成后,原先的完整单元将分裂为两个子单元,同时裂缝面两侧将增加新的计算节点,子单元在裂缝面两侧可 发生分离和滑动,如图12所示.
|
图 12 裂缝面两侧的子块体发生分离或滑动 Fig.12 Sub-blocks separate or slide along the crack face |
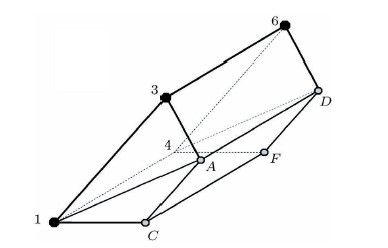
对于图12(b)中的三棱柱单元破裂形式,破裂后的两个子块体形状分别为三棱柱和六面体. 对于六面体单元,按照式(10)计算应变时,可以采用一种离散方式,将其拆分为两个三棱柱单元. 如图13所示,若裂纹沿着$AC$方向进行扩展,则六面体$1CA34FD6$可以拆分为三棱柱$1CA4FD$和三棱柱$1A34D6$进行计算.
|
图 13 子六面体单元的离散方式 Fig.13 Discrete mode of the Sub-hexahedral element |
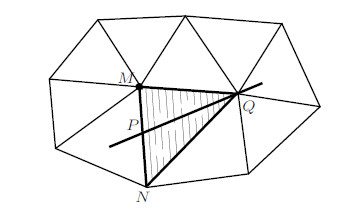
在计算区域内,单元破裂伴随着初始裂纹的形成,那么接下来的过程则是裂纹的扩展. 如图14所示,将三棱柱投影到二维平面,假设$MNQ$为破裂单元,初始裂纹为$PQ$,下面将在尖端$P$和$Q$分析裂纹的扩展路径.
|
图 14 单元内部的初始裂纹 Fig.14 Initial crack in element |
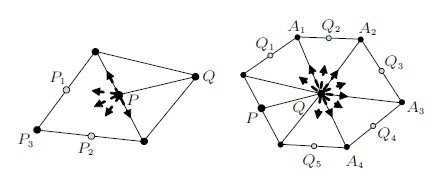
如图15所示,对于尖端$P$,裂纹扩展路径可以为单元内部面$PP_{1}$--$PP_{3}$. 在尖端$Q$处,裂纹扩展路径可以为单元边界面$QA_{1}$--$QA_{4}$,也可以为单元内部面$QQ_{1}$--$QQ_{5}$.
|
图 15 裂纹尖端的扩展路径 Fig.15 Propagation path on the crack tip |
实际判断裂纹扩展方向时,通过尖端节点应力值,按照强度准则(16)和(21)进行计算. 节点$P$和$Q$的应力可通过周围单元的应力平均求得
| $ \label{eq26}\bar {\sigma }_{ij} = \dfrac{1}{N}\sum\limits_{k = 1}^N {\sigma _{ij}^k } $ | (26) |
式中,$N$为裂纹尖端节点所连接的单元总数; $\sigma_{ij}^{k}$为相应连接单元的应力张量. 此时,若拉伸破坏式(16)满足,裂纹方向则与最小主应力$\sigma_3$垂直; 若剪切破坏式(21)满足,裂纹方向则与最小主应力$\sigma _3 $夹角为$\pi / 4 + \varphi / 2$. 因此,可以在所有的边界面、内部面中,选择与理论裂纹方向最为接近的作为最终裂纹面.
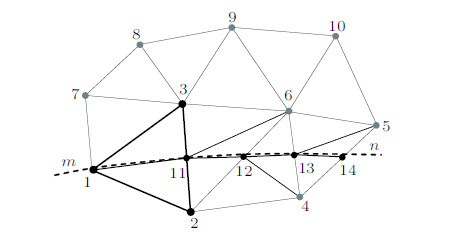
结合上述建立的破裂机制,下面通过一个简单示意,来说明本文方法在裂纹扩展问题中的实现方式. 如图16所示,初始网格由节点1$\sim$10及相应的单元组成,曲线$mn$假设为一条已知裂纹. 假定问题为: 在该网格条件下构建破裂路径,实现对裂纹$mn$的模拟. 基于本文所述的方法,裂纹可以按照如下方式扩展:
|
图 16 裂纹扩展方式示意 Fig.16 A diagram of crack propagation mode |
(1) 根据破裂准则,判断单元123沿路径1---11开裂,同时在裂纹尖端处建立新节点11;
(2) 通过尖端节点11的应力值,按强度准则获得裂纹扩展方向,进而确定开裂路径为11---12;
(3) 在节点12处判断,按此方式,可以依次建立开裂路径12---13和13---14等;
综上,本文所述的方法可以更为准确地实现对裂纹$mn$扩展过程的模拟. 相比于一般离散元的裂纹在界面上扩展方式,本文的模型 建立了单元边界和内部的联合破裂机制,从而为裂纹的扩展提供了更多可选取的路径,裂纹扩展方向更为准确.
3 数值验证及结果分析连续-非连续单元法建立了单元边界、单元内部的联合破裂机制,实现了裂纹萌生和扩展过程的模拟.为验证该方法的有效性,本 节将通过几个典型数值算例,模拟拉伸、拉剪以及压剪等各种荷载条件下的裂纹扩展问题.
3.1 三点弯曲梁试验模拟如图2所示的三点弯曲梁,文献[23]采用有限元节点松弛技术,系统研究试样中的裂纹扩展过程,并引入脆性系数$S_{\rm E}$表述 裂纹扩展过程中的力学特征,其表达式为
| $ \label{eq27}S_{\rm E} = \dfrac{G_{\rm f} }{\sigma _{\rm t} b} $ | (27) |
式中,$G_{\rm f}$为断裂能,$\sigma_{\rm t}$为抗拉强度,$b$为梁高. 试样尺寸: $l = 0.6$ m,$b = 0.15$ m,$t= 0.01$ m,其中$t$为梁的厚度. 材料参数为: 杨氏模量$E = 36.5$ GPa,泊松比$\nu= 0.1$,抗拉强度$\sigma_{\rm t}= 3.19$ MPa. 边界条件为底部两端节点$y$向约束,$(l/2,b/2)$处$x$向约束,顶部中心处施加$y$向增量位移荷载,速率为$3\times 10^{ - 7}$ mm/s.
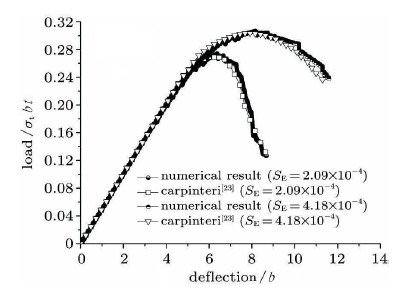
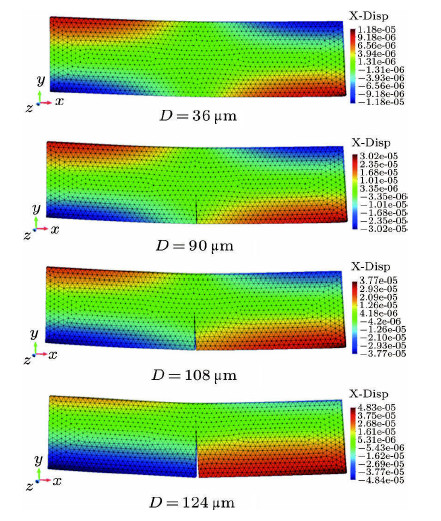
数值模拟过程中,断裂能$G_{\rm f}$ 取值为100 N/m和200 N/m两种情况进行计算,对应的系数$S_{\rm E}$的值分别为$2.09\times10^{ -4}$和$4.18\times10^{ -4}$. 图17给出了两种情况下的加载点荷载-位移关系曲线.通过荷载-位移曲线的对比可知,连续-非连续单元法的数值结果与文献[23]的结果一致.数值结果也表明: $S_{\rm E}$取值越小,裂纹扩展时表现的脆性特征越明显. 图18为$S_{\rm E}$等于$2.09\times10^{ - 4}$情况下,不同加载点位移时梁的$x$向位移云图. 由图可以分析,裂纹在单元内部萌生,扩展时穿过单元,两侧单元发生分离,模拟出裂纹显示的张开和扩展过程.
|
图 17 三点弯曲梁试样的无量纲荷载-位移曲线 Fig.17 Non-dimensional load--deflection curves for the three-point bending |
|
图 18 不同加载点位移下的试样$x$向位移云图 Fig.18 Displacement-contour of three-point bending specimen in $x$-direction |
对于图19所示的平板[24],中部存在一条初始切口,模型宽度$w = 50$ mm,高度$h =100$ mm,切口长度为$a = 12$ mm. 为模拟拉伸条件下平板中初始裂纹的扩展,在平板两端施加常速率的位移荷载,加载速率为$1\times10^{ - 6}$ mm/s. 这是典型的I型裂纹扩展问题,理论情况下初始裂纹将沿着水平方向扩展. 数值计算的材料参数为: 弹性模量$E= 80$ GPa,泊松比$\nu = 0.3$,抗拉强度$\sigma_{\rm t} = 5.0$ MPa,断裂能$G_{\rm f} = 50$ N/m. 数值网格划分如图19,节点数为4 412,单元数为4 226. 对图中所示的初始网格进行分析,可以发现其中并没有与理论结果相一致的水平路径用于裂纹的扩展.

|
图 19 几何模型和网格划分 Fig.19 Geometric model and mesh configuration |
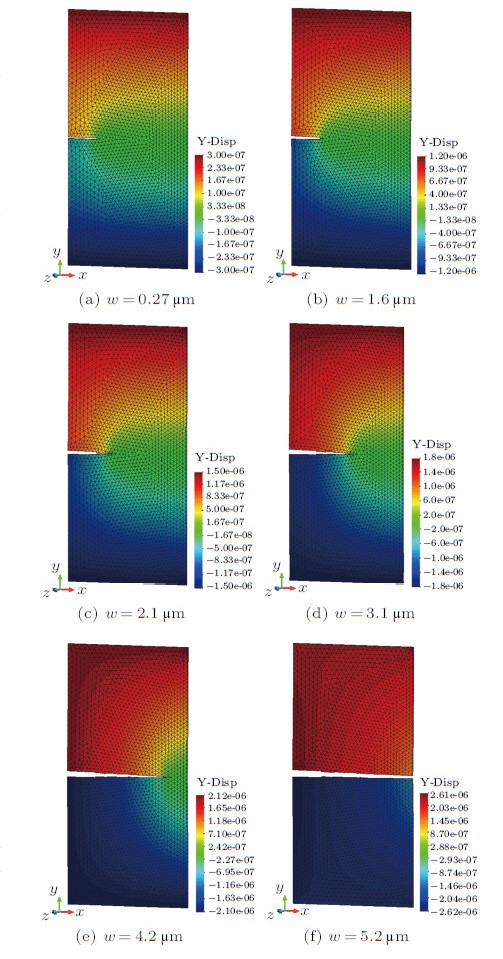
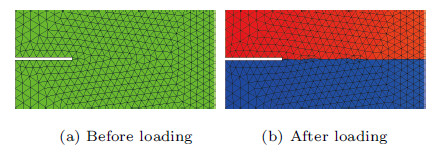
采用连续-非连续单元法的计算结果如图20所示,分别为不同切口张开位移$w$时,拉伸平板的y向位移云图.由于是显示 裂纹,此处可以直接通过位移的变化显示裂纹的形成和扩展过程. 图21所示为加载前后,裂纹附近网格的放大情况,可知该方法在裂纹扩展模拟中,通过切割单元增加了更多的扩展路径,在裂纹的扩展方向上更为精确.
|
图 20 不同切口张开位移时平板$y$向位移云图 Fig.20 Displacement-contours of $y$-direction in different CMOD |
|
图 21 加载前后网格变化局部放大图 Fig.21 Amplification of local mesh before and after loading |
对于图22所示含双切口试样,文献[25]最先通过试验研究不同加载形式下,试样中的裂纹扩展过程. 为了获得复合应力状态下的裂纹扩展模式,该试验分为两个阶段加载: (1) 在水平方向进行力加载,达到给定值后保持恒定; (2)在试样顶端进行竖向位移加载. 在此基础上,文献[26, 27]等通过数值模拟方式对该试验中的裂纹扩展模式进行研究.
|
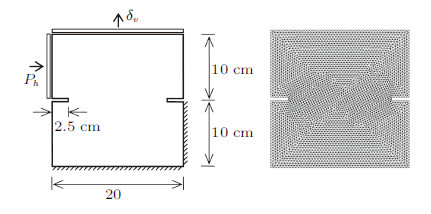
图 22 双切口试样几何模型和网格划分 Fig.22 Geometric model and mesh configuration of double-notched specimen |
采用本文所述方法对该试验进行模拟,材料参数为: 杨氏模量$E = 32$ GPa,泊松比$\nu = 0.2$,抗拉强度$\sigma_{\rm t} = 2.6$ MPa,断裂能$G_{\rm f} = 110$ N/m. 边界条件如图22所示,模型底部及右侧下半部分 固定约束,左侧水平方向荷载$P_{h} = 5$ kN,竖向位移加载速率为$3\times10^{ - 7}$ mm/s.
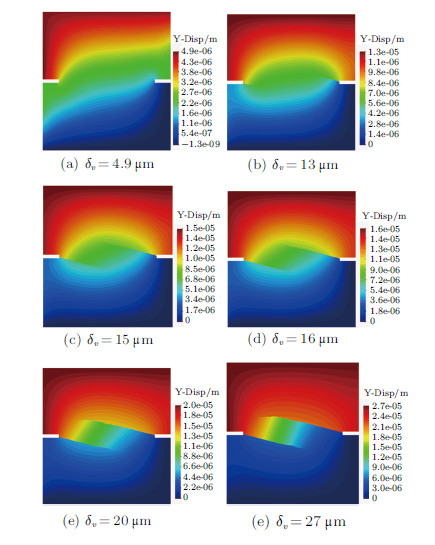
数值计算结果如图23所示,分别为不同的竖向加载位移$\delta_{v}$时试样中裂纹扩展情况,通过图中$y$向位移云图可观察裂纹两 侧的位移不连续. 图24(a)所示为单元破裂后的网格变化情况,从中可以看出裂纹的扩展路径,与文献[27]中的计算结果一致,说明了本文的连续-非连续单元法在拉剪复合应力条件下模拟裂纹扩展问题的有效性.
|
图 23 双切口试样加载过程的裂纹扩展情况 Fig.23 The crack propagation of the double-notched specimen at differentvertical displacement |

|
图 24 双切口试样裂纹模式的两种数值方法对比 Fig.24 The crack pattern of double edge-notch specimen; a for continuousdiscontinuous element method; b for Lagrange multiplier method |
压缩破坏是岩石的一种重要破坏模式,破坏过程伴随着拉伸破裂、剪切破裂及接触摩擦. 针对岩石压缩特性的实验研究已开展得比较深入,但是对其破坏机制,包括裂纹萌生、扩展贯穿以及轴向开裂、剪切破坏等过程,并未完全认识清楚. 本节将利用连续-非连续单元法,对岩石单轴压缩的裂纹形成和破裂过程进行分析.
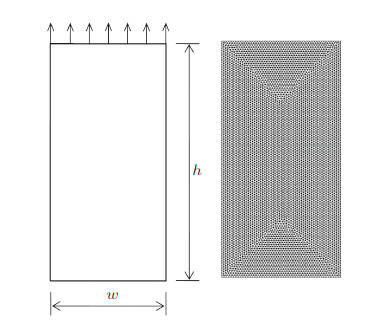
对于图25所示岩石单轴压缩试样,模型尺寸为: $w = 50$ mm,$h = 100$ mm. 材料力学参数为: 弹性模量$E = 30$ GPa,泊松比$\nu = 0.22$,黏聚力$c = 3$ MPa,内摩擦角$\varphi = 30^\circ$,抗拉强度$\sigma_{\rm t}= 3$ MPa. 该算例中设断裂能取值为0,从而裂缝表现为完全脆性的断裂特征. 模型底面$xyz$向约束,顶面$xz$向约束,前后面法向约束,采用常位移速率加载控制方式进行加载,速率为$2\times 10^{ - 7}$ mm/s. 数值计算模型的网格尺寸为1 mm,节点数为11 788,单元数为11 486.
|
图 25 几何模型和网格划分 Fig.25 Geometric model and mesh configuration |
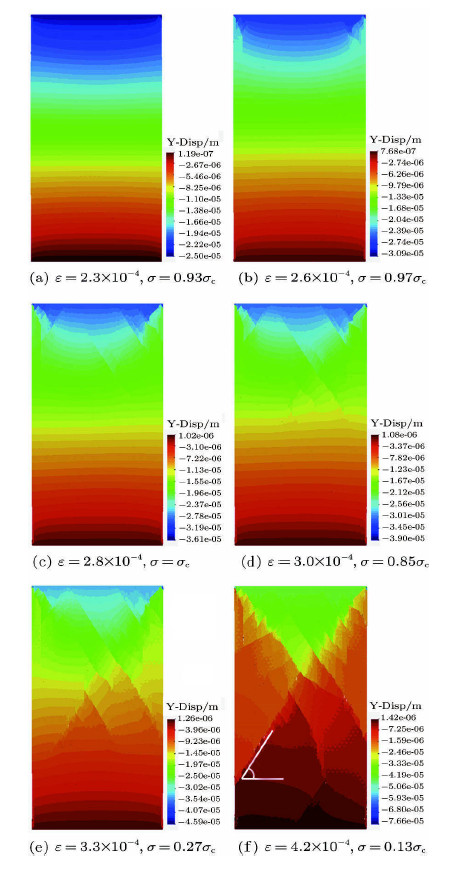
单轴压缩过程中试样的变形、开裂和裂缝演化模式如图26,选取的是加载过程中的几个典型阶段,图中所示为竖向位移云图,$\sigma _{\rm c}$为峰值应力. 由图可以观察岩石破裂的发展过程: 首先,内部裂缝缓慢发展直至优势裂缝形成,随后局部化带逐渐成型,材料破坏集中到局部化带的破裂演化上,试样沿着几条主裂缝发生明显错动,进而出现整体性破坏. 分析图26(f)可知,试样发生错动的几条主裂缝法向与最大主应力法向夹角约为59.3$^\circ$,这与莫尔库伦准则的理论解$60^\circ $几乎一致,同时可发现试样呈X状共轭斜面的剪切破坏特征,这是试验中常见的一种破坏形式.
|
图 26 单轴压缩试样加载过程的裂纹扩展情况 Fig.26 The crack propagation of the uniaxial compression specimen atdifferent stage |
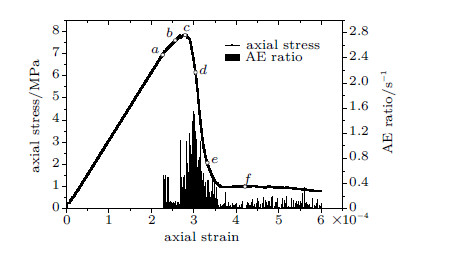
加载过程中试样的轴向应力-应变曲线如图27所示,曲线中的$a$点至$f$点分别与图26的各个破坏阶段相对应.对比分析可知,随着岩石变形和破裂的演化,应力-应变曲线经历了明显的线性、非线性和软化过程:非线性段($a$点至$c$点)表现为试样中微裂缝的萌生,同时向优势裂缝发展; 软化段($c$点至$f$点)对应局部化带的形成,试样沿着主要裂缝发生剪切错动.
|
图 27 试样轴向应力-应变曲线和声发射特征 Fig.27 The axial stress--strain curve and AE rate feature of the uniaxial compression specimen |
将试样加载过程中的声发射速率与应力-应变曲线同绘于图27中进行对比,可得如下特征:试样在非线性段开始出现微裂缝,即破裂 发生,对应声发射开始出现且速率增加; 达到峰值点后,声发射速率达到最大值,试样中大量破裂发生,对应局部化带演化,形成主裂缝,直至整体破坏. 图28所示为加载过程中,试样网格的变化情况,可以明显看出裂纹的形成和扩展过程. 综上,对于单轴压缩试验破坏过程的模拟,连续-非连续单元法在裂纹扩展模式、声发射规律、应力-应变曲线特征上能够与试验以及已有数值结果较好吻合,说明该方法在模拟岩石破坏问题中的有效性.

|
图 28 单轴压缩试样加载过程中数值网格变化图 Fig.28 The change of mesh during loading process of uniaxial compressionspecimen |
(1) 将块体单元离散为具有物理意义的弹簧系统,在局部坐标系下求解单元的变形和应力,连续问题计算结果与有限元一致,引入最大拉应力与莫尔-库伦复合准则确定单元破坏状态和破裂方向,采用局部切割块体的方式实现单元内部开裂,形成初始裂纹,进而引入内聚力模型描述裂缝特征,扩展路径可穿过单元内部和边界,可以显示模拟裂纹的形成和扩展过程.
(2) 通过单切口平板拉伸、三点弯曲梁、双切口试样等典型岩石裂纹扩展试验对所提方法进行验证分析,结果表明: 该方法可较好地解决拉伸、拉剪以及压剪复合等应力状态下的裂纹形成和扩展问题,裂纹扩展模式能够与试验以及已有数值方法吻合.
(3) 通过单轴压缩试验,对岩石的破坏过程进行分析,数值模拟结果获得了裂纹形成、声发射与应力-应变曲线各阶段之间的对应关系: 弹性阶段后微裂纹开始萌生,声发射速率增加,表现为曲线的非线性段; 峰值点后,局部带不断演化,开始出现宏观裂缝,声发射速率达到最大值,应力-应变曲线表现为软化段,数值模拟揭示的破坏机理与试验一致,说明所提方法模拟岩石裂纹扩展以及破坏问题的有效性.
(4) 本文的连续-非连续单元法是在三棱柱单元上实现,裂纹扩展分析均局限于拟三维情形,后续工作中,可进一步对真三维状态进行研究.
5 讨 论岩石裂纹扩展研究是岩石力学领域的热点问题之一. 传统离散元方法通过界面破裂形式,实现了裂纹沿着单元边界扩展,但是裂纹扩展路径受网格密度的限制较大. 本文作为变形体离散元方法的发展和延续,通过单元破裂方式,有效改善单元大小和网格密度对裂纹扩展问题的影响. 对于定量性的网格尺寸对数值结果的误差分析,由于涉及到断裂尺度和断裂能量等非连续问题,将在后续工作中进行重点研究.
| [1] | 张楚汉. 论岩石、混凝土离散-接触-断裂分析. 岩石力学与工程学报, 2008, 27(2): 217-235 (Zhang Chuhan. Discrete-contact-fracture analysis of rock and concrete. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(2): 217-235 (in Chinese)) |
| [2] | Swenson DV, Ingraffea AR. Modeling mixed-mode dynamic crack propagation using finite elements: Theory and applications. Computational Mechanics, 1988, 3: 381-397 |
| [3] | Belytschko T, Black T. Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering, 1999, 45(5): 601-620 |
| [4] | Ke TC. Simulated testing of two dimensional heterogeneous and discontinuous rock masses using discontinuous deformation analysis. [PhD Thesis]. Berkeley: University of California, 1993 |
| [5] | Shi GH. Manifold method. In: Salami MR and Banks D eds. Proceedings of the First International Forum on Discontinuous Deformation Analysis (DDA) and Simulation of Discontinuous Media. Berkeley, California, 1996. 52-204 |
| [6] | Shi GH. Numerical manifold method. In: Li JC, Wang CY, Sheng J eds. Proceedings of the First International Conference on Analysis of Discontinuous Deformation (ICADD-1). Chungli, Taiwan, China, 1995. 187-222 |
| [7] | 刘丰, 郑宏, 李春光. 基于NMM的EFG方法及其裂纹扩展模拟. 力学学报, 2014, 46(4): 582-590 (Liu Feng, Zheng Hong, Li Chunguang. The NMM-based EFG method and simulation of crack propagation. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(4): 582-590 (in Chinese)) |
| [8] | 杨永涛, 徐栋栋, 郑宏. 动载下裂纹应力强度因子计算的数值流形元法. 力学学报, 2014, 46(5): 730-738 (Yang Yongtao, Xu Dongdong, Zheng Hong. Evaluation on stress intensity factor of crack under dynamic load using numerical manifold method. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(5): 730-738 (in Chinese)) |
| [9] | Munjiza A, Owen DRJ, Bicanic N. A combined finite-discrete element method in transient dynamics of fracturing solids. Engineering Computations, 1995, 12(2): 145-174 |
| [10] | Munjiza A. The Combined Finite-Discrete Element Method. New York: John Wiley and Sons, 2004: 277-290 |
| [11] | Owen DRJ, Feng YT, De Souza Neto EA, et al. The modeling of multi-fracturing solids and particulate media. International Journal for Numerical Methods in Engineering, 2004, 60(efeq1): 317-339 |
| [12] | Li SH, Zhang YN. Feng C. A spring system equivalent to continuum model. In: The Proc. of The Fifth International Conference on Discrete Element Methods. London, 2010. 75-85 |
| [13] | 冯春, 李世海, 姚再兴. 基于连续介质力学的块体单元离散弹簧法研究. 岩石力学与工程学报, 2010, 29(增刊1): 2690-2704 (Feng Chun, Li Shihai, Yao Zaixing. Study of block-discrete-spring method based on continuum mechanics. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(Supp.1): 2690-2704 (in Chinese)) |
| [14] | 王杰, 李世海, 周东, 等. 模拟岩石破裂过程的块体单元离散弹簧模型. 岩土力学, 2013, 34(8): 2355-2362 (Wang Jie, Li Shihai, Zhou Dong, et al. A block-discrete-spring model to simulate failure process of rock. Rock and Soil Mechanics, 2013, 34(8): 2355-2362 (in Chinese)) |
| [15] | 常晓林, 胡超, 马刚, 等. 模拟岩石失效全过程的连续-非连续变形体离散元方法及应用. 岩石力学与工程学报, 2011, 30(10): 2004-2011 (Chang Xiaolin, Hu Chao, Ma Gang, et al. Continuous-discontinuous deformable discrete element method to simulate the whole failure process of rock masses and application. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2004-2011 (in Chinese)) |
| [16] | 马刚, 周创兵, 常晓林, 等. 岩石破坏全过程的连续-离散耦合分析方法. 岩石力学与工程学报, 2011, 30(12): 2444-2455 (Ma Gang, Hu Chao, Chang Xiaolin, et al. Continuous-discontinuous coupling analysis for whole failure process of rock. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(12): 2444-2455 (in Chinese)) |
| [17] | 侯艳丽, 周元德, 张楚汉. 用3D离散元实现I/II型拉剪混凝土断裂的模拟. 工程力学, 2007, 24(3): 1-7 (Hou Yanli, Zhou Yuande, Zhang Chuhan. I/II tensile shear mixed mode fracture simulation by 3D discrete element method. Engineering Mechanics, 2007, 24(3): 1-7 (in Chinese)) |
| [18] | 张青波, 李世海, 冯春. 四节点矩形弹簧元及其特性研究. 岩土力学, 2012, 33(11): 3497-3502 (Zhang Qingbo, Li Shihai, Feng Chun. Study of four-node rectangular spring element and its properties. Rock and Soil Mechanics, 2012, 33(11): 3497-3502 (in Chinese)) |
| [19] | 张青波, 李世海, 冯春, 等. 基于SEM的可变形块体离散元法研究. 岩土力学, 2013, 34(8): 2385-2392 (Zhang Qingbo, Li Shihai, Feng Chun, et al. Study of deformable block discrete element method based on SEM. Rock and Soil Mechanics, 2013, 34(8): 2385-2392 (in Chinese)) |
| [20] | 张楚汉, 金峰. 岩石和混凝土离散-接触-断裂分析. 北京: 清华大学出版社, 2008 (Zhang Chuhan, Jin Feng. Discrete-Contact-Fracture Analysis of Rock and Concrete. Beijing: Tsinghua University Press, 2008 (in Chinese)) |
| [21] | Hillerborg A, Modeer M, Petersson PE. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cement and Concrete Research, 1976, 6(6): 773-782 |
| [22] | Wells GN, Sluys LJ. A new method for modeling cohesive cracks using finite elements. International Journal for Numerical Methods in Engineering, 2001, 50(12): 2667-2682 |
| [23] | Carpinteri A, Colombo G. Numerical analysis of catastrophic softening behavior (snap-back instability). Computer & Structures, 1989, 31(4): 607-636 |
| [24] | Ning YJ, An XM, Ma GW. Footwall slope stability analysis with the numerical manifold method. International Journal of Rock Mechanics & Mining Sciences, 2001, 48(6): 964-975 |
| [25] | Nooru-Mohamed MB. Mixed-mode fracture of concrete: An experimental approach. [PhD Thesis]. Delft: University of Technology, 1992 |
| [26] | Oliver J, Huespe AE, Samaniego E, et al. Continuum approach to the numerical simulation of material failure in concrete. International Journal for Numerical and Analytical Methods in Geomechanics, 2004: 28(7-8): 609-632 |
| [27] | Zi G, Rabczuk T, Wall W. Extended meshfree methods without branch enrichment for cohesive cracks. Computational Mechanics, 2007, 40(2): 367-382 |
2. The Third Railway Survey and Design Institute Group Corporarion, Tianjin 300142, China
 2015, Vol. 47
2015, Vol. 47