引言
波动数值模拟是当前地球物理、地震学、地震工程、海洋声学、电磁波等多个学科领域广泛应用和研究的前沿热点技术. 人工边界条件为该技术的基础问题之一, 它表示有限计算模型边界上的辐射条件, 其精度和稳定性对于模拟结果能否很好地反映实际无限介质中的波动过程至关重要.
自20世纪60年代以来, 已有大量人工边界条件(artificial boundary condition, ABC)被学者和工程师们所提出, 文献[1 ,2 ]对它们作了较为系统的介绍. 对于数量众多的ABC, 如何有效掌握并在不同问题中进行选用已成为一个突出的实际问题. 一直以来关于各个特定ABC的应用及探讨较多, 而从整体上针对ABC理论与公式体系的系统性研究[3 ] 则相对较少. 这不仅导致较为复杂的新近研究成果不易被理解及吸收, 甚至对于一些简单且有着广泛应用的经典人工边界条件, 也仍然存在认识方面的不足.
廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性.
现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] .
本文工作以新提出的两个基本边界公式作为出发点, 通过公式推导证明它们的等价性并论证其与具有时空外推特点的上述各种ABC的理论联系, 建立外推型人工边界条件理论. 深入研究外推型ABC的精度控制原理, 分析并强调可调的计算波速参数对于处理复杂波动问题的价值. 最后给出基本边界公式的数值离散格式, 并通过算例验证外推型ABC理论的合理性.
1 外推型人工边界条件的基本公式
1.1 两个基本边界公式
本文提出两个基本公式作为应用和讨论外推型人工边界条件的出发点, 即
(1) $c_{\mathrm{a} j} \text { -MTF boundary : }\left[\prod_{j=1}^{N}\left(I-B\left(c_{\mathrm{a} j}\right)\right)\right] u=0$
(2) $c_{\mathrm{a} j} \text { -Higdon boundary }:\left[\prod_{j=1}^{N}\left(\frac{\partial}{\partial t}-c_{\mathrm{a} j} \frac{\partial}{\partial s}\right)\right] u=0$
这两个公式本身是最简单有效的外推型ABC, 它们奠定了以时间$\!-\!$空间外推(简称时空外推)方式计算任意时刻单个人工边界节点运动的理论和方法基础. 其他外推型ABC大多可以从这两个基本边界公式转化得到, 或者通过某种等价的中间形式与之相关联. 式(1) 为MTF引入多个人工波速$c_{{\rm a}j}$ $(j =1$, 2, $\cdots$, $N$, 这里$N$为边界阶次)得到的优化形式, 本文记为优化的MTF或$c_{{\rm a}j}$-MTF边界. 它为离散表达式, 人工边界节点的波场值由一系列参考点的波场值外推得到. 式(2)为Higdon边界在一个统一局部坐标$s$0$t$上定义并使用人工波速$c_{{\rm a}j}$作为边界参数的一般形式, 记为统一的Higdon或$c_{{\rm a}j}$-Higdon边界. 它为连续表达式, 是由多个一阶单向波动算子相乘形成的波动微分方程.
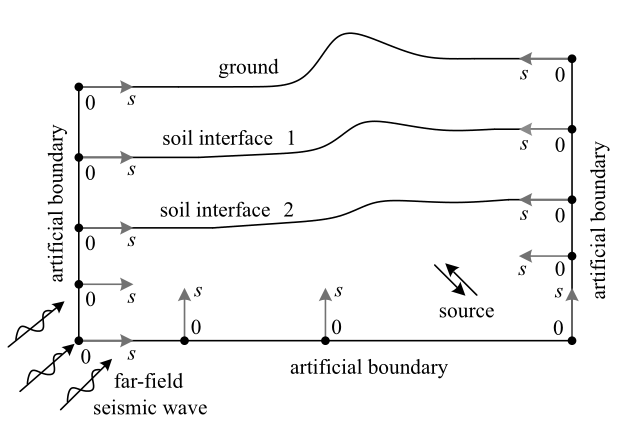
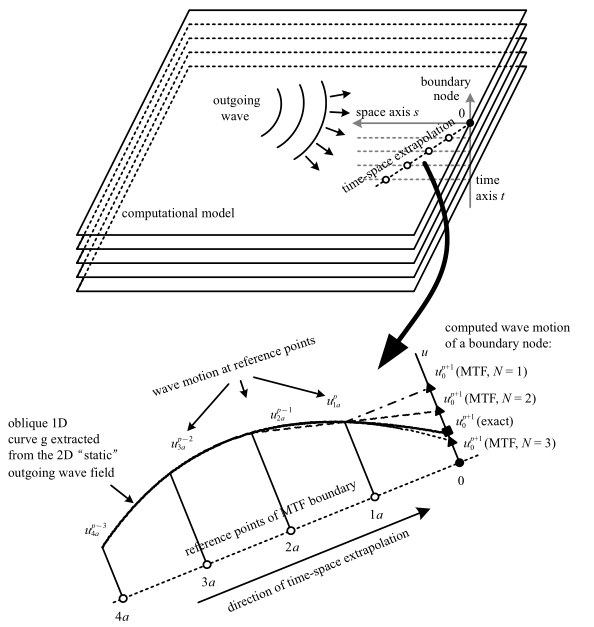
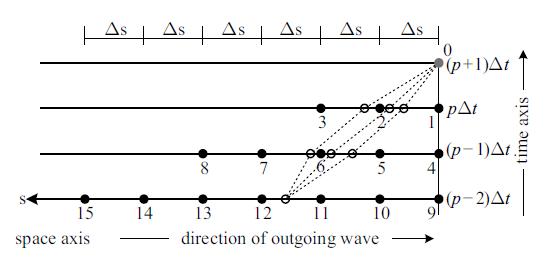
式(1)和式(2)定义在如图1 所示的以各个待求解的人工边界节点为原点的统一局部坐标$s$0$t$中, 坐标空间轴$s$位于经过人工边界节点的一条指向内域的离散网格线上(正方向向内), 时间轴$t$与整体模型一致. 式中$u=u(s,t)$为局部坐标$s$0$t$中的波场函数; $N$为边界阶次, 在式(1)中对应于离散时空外推算子($I-B(c_{{\rm a}j}))$的个数, 在式(2)中为集成的一阶单向波动微分算子($\partial $/$\partial t-c_{{\rm a}j}\partial $/$\partial s)$的个数; $c_{{\rm a}j}$ ($j = 1$, 2, $\cdots$, $N)$为一组计算波速参数称之为人工波速, 其取值具有任意性, 但较优的选择通常为等于或稍大于介质物理波速的值(后文将具体探讨); $\Delta t$为时间步长, 取值同样具有任意性, 不过为便于计算, 通常取为与内域格式一致; $I$为单位算子, 在乘积中可以略去. 在局部坐标$s$0$t$中, 离散算子$B(c_{{\rm a}j})$定义为: $B(c_{{\rm a}j}) u(s, t) = u(s+c_{{\rm a}j}\Delta t, t-\Delta t)$, 即空间上向计算区域内部、时间上向以前时刻移动($c_{{\rm a}j}\Delta t$, $-\Delta t)$, 它用于定出$c_{{\rm a}j}$-MTF边界的各个参考点的位置(相对于人工边界节点). 离散算子的求和、乘积运算法则为: [$B(c_{\rm a1})+B(c_{\rm a2})]u(s,t) = u(s+c_{\rm a1}\Delta t$, $t-\Delta t) + u(s+c_{\rm a2}\Delta t, t-\Delta t)$, $B(c_{\rm a1})B(c_{\rm a2})u(s,t) = u(s+c_{\rm a1}\Delta t+c_{\rm a2}\Delta t, t-2\Delta t)$, 依次类推. 边界表达式(1)和式(2)可直接用于处理单分量波动问题, 如声波、SH波动, 也可以分别应用于多分量波动问题的各个分量, 如弹性波、电磁波、固液两项介质波动等.
图1
图1
用于定义基本边界公式(1)和(2)的统一局部坐标示意图
Fig.1
Sketch map of the unified local coordinate used to define the basic boundary formulas (1) and (2)
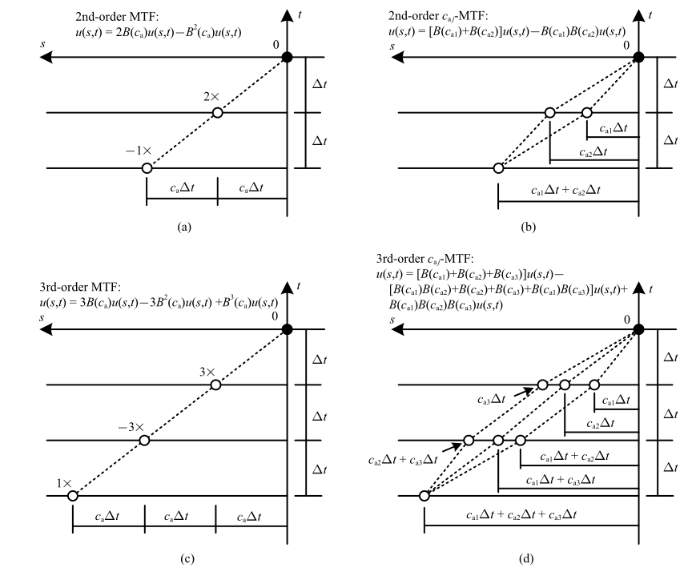
图2 给出了二阶、三阶廖氏透射边界(MTF)和本文外推型边界公式(1) ($c_{{\rm a}j}$-MTF)所涉及的离散参考点示意图. 基于单一人工波速的廖氏透射边界是边界(1)的一个特例. 利用上述离散算子廖氏透射边界可以表示为($I-B(c_{\rm a}))^{N}u = 0$. 如图2 (a)和图2 (c)所示, MTF的参考点为等距离分布且在每个$t-j\Delta t$时刻只有一个点, 各个参考点的算子表示依次为: $u(s+c_{\rm a}\Delta t$, $t-\Delta t) = B(c_{\rm a})u(s, t)$, $u(s+2c_{\rm a}\Delta t$, $t-2\Delta t) = B^{2}(c_{\rm a})u(s, t)$, $u(s+3c_{\rm a}\Delta t$, $t-3\Delta t) =B^{3}(c_{\rm a})u(s, t)$, 其余类推. 二阶MTF采用前两个参考点, 其系数分别为2和$-$1; 三阶MTF采用前3个参考点, 其系数分别为3, $-$3和1. 而从图2 (b)可以看到, 二阶$c_{{\rm a}j}$-MTF与二阶MTF相比, 2$B(c_{\rm a})u(s, t)$被优化成[$B(c_{\rm a1})+ B(c_{\rm a2})]u(s,t)$, $-B^{2}(c_{\rm a})u(s,t)$被优化成$-B(c_{\rm a1})B(c_{\rm a2})u(s, t)$. 类似地, 根据图2 (d), 三阶$c_{{\rm a}j}$-MTF与三阶MTF相比, 3$B(c_{\rm a})u(s, t)$被优化成[$B(c_{\rm a1})+ B(c_{\rm a2})+ B(c_{\rm a3})]u(s,t)$, $-3B^{2}(c_{\rm a})u(s, t)$被优化成$-[B(c_{\rm a1})B(c_{\rm a2})+ B(c_{\rm a2})B(c_{\rm a3})+ B(c_{\rm a3})B(c_{\rm a1})]u(s, t)$, $B^{3}(c_{\rm a})u(s, t)$被优化成$B(c_{\rm a1})B(c_{\rm a2})B(c_{\rm a3})u(s, t)$. 因此, $c_{{\rm a}j}$-MTF边界在各个时刻可能有一个或多个参考点, 它对传统MTF的优化是通过在各个离散时刻上由多个不同参考点的波场值代替原来单个参考点的波场值而实现的. 如果从MTF"误差波多次透射"的物理机制角度来分析$c_{{\rm a}j}$-MTF, 那么后者可以被看作是保留了"多次透射"过程, 但优化了对各阶"误差波"的描述.
图2
图2
二阶、三阶MTF和$c_{{\rm a}j}$-MTF边界的参考点示意图
Fig.2
Sketch map of the reference points in 2nd- and 3rd-order MTF and $c_{{\rm a}j}$-MTF boundaries
Higdon边界对于声波和弹性波分别具有不同形式, 它们基于整体坐标$x$, $y$或$z$给出, 且根据外行波沿坐标的正、负方向传播而有所不同. 式(2)可以视为这些现有Higdon边界公式的统一形式. 理由如下: 考虑到边界参数取值的任意性, 现有Higdon边界的声波和弹性波形式实际上是一致的[9 -10 ] ; 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$, 在推算人工边界节点运动时结果并无差异; 同样, 统一考虑$s$轴指向内域, 与考虑$s$轴指向外域亦具有相同效果, Higdon[27 ] 对此已有结论. 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$还有一个优势, 就是$s$轴可以不与整体坐标轴平行. 式(2)使得现有Higdon边界针对不同方向边界分别给出表达式再进行数值离散的做法得到大大简化, 它略去了不必要的冗余, 回归到时空外推的本质.
式(1)给出的多人工波速离散边界表达式无法单独从传统廖氏透射边界理论导出, 其借鉴了Higdon边界的计算波速设置. 式(2)给出的简洁而统一的连续边界表达式同样无法单独从现有Higdon边界导出, 其得益于廖氏透射边界思想和参数的引入. Liao[28 ] 曾指出过廖氏透射边界与Higdon边界的这种互补性.
1.2 添加小量修正的边界公式
在基本边界公式(1)和式(2)中添加一个小量对其进行修正所得到的形式,
在消除高阶外推型ABC的计算漂移失稳[29 ] 和处理强衰减外行波方面具有重要价值.
(3) $\begin{eqnarray} \label{eq3} &&\left[ {\prod\limits_{j=1}^N {\left( {I-\dfrac{1}{1+\gamma }B\left( {c_{{\rm a}j} } \right)} \right)} } \right]u=0\end{eqnarray}$
(4) $\begin{eqnarray} \label{eq4} \left[ {\prod\limits_{j=1}^N {\left( {\dfrac{\partial }{\partial t}-c_{{\rm a}j} \dfrac{\partial }{\partial s}+\varepsilon_{j} } \right)} } \right]u=0 \end{eqnarray}$
式(3)中的小量$\gamma $为一个小正数, 如0.001$\sim$0.05之间. 式(4)中的小量$\varepsilon_{j\, }(j = 1$, 2, $\cdots$, $N$)为非负数, 其中至少一个不为零.
周正华和廖振鹏[30 ] 指出添加小量在物理上考虑了介质的几何扩散特性或引入了介质的阻尼特性. 可认为这两种物理特性对应于同一种数学机制, 即考虑了波场的衰减性. 由此不难得出, 陈少林和廖振鹏[31 ] 所提出的衰减波场MTF、以及Bayliss和Turkel[32 ] 针对柱面波或 球面波扩散问题(即外行波含有显著的几何衰减)而提出的边界表达式, 分别与式(3)、式(4)在形式上具有一致性.
2 $c_{{a}j}$-MTF与$c_{{a}j}$-Higdon边界的等价性
本节证明外推型ABC理论与公式体系中的一个关键结论: 离散的$c_{{a}j}$-MTF边界与连续的$c_{{\rm a}j}$-Higdon边界是等价的. 有两种证明方法: 一是利用二元函数泰勒展开法则对$c_{{\rm a}j}$-MTF中各个参考点的波场函数在点($s, t)$处进行展开并保留至所需精度阶, 化简可得$c_{{\rm a}j}$-Higdon; 二是将$c_{{\rm a}j}$-MTF中的各个外推算子改写成某种与之等效的差分算子, 使之形成类似于$c_{{\rm a}j}$-Higdon的结构, 对差分算子取极限即得到后者.
证明1: 对于一阶$c_{{\rm a}j}$-MTF, 其具体形式为$u(s,t)=u(s+c_{\rm a1}\Delta t,t-\Delta t)$. 将等号右端项进行二元泰勒展开并保留至一阶项, 得到
(5) $\begin{eqnarray} \label{eq5} u\left( {s,t} \right)=u\left( {s,t} \right)+c_{a1} \Delta t\dfrac{\partial u}{\partial s}-\Delta t\dfrac{\partial u}{\partial t} \end{eqnarray}$
化简式(5)即得一阶$c_{{\rm a}j}$-Higdon表达式. 对于二阶$c_{{\rm a}j}$-MTF, 先写出其具体形式, 再将等号右端各项进行二元泰勒展开并保留至二阶项, 得到
(6) $\begin{array}{l}u(s, t)=u(s, t)+c_{a 1} \Delta t \frac{\partial u}{\partial s}-\Delta t \frac{\partial u}{\partial t}+ \\\frac{1}{2}\left(c_{a 1} \Delta t \frac{\partial u}{\partial s}-\Delta t \frac{\partial u}{\partial t}\right)^{2}+u(s, t)+c_{a 2} \Delta t \frac{\partial u}{\partial s}- \\\Delta t \frac{\partial u}{\partial t}+\frac{1}{2}\left(c_{a 2} \Delta t \frac{\partial u}{\partial s}-\Delta t \frac{\partial u}{\partial t}\right)^{2}- \\{\left[u(s, t)+\left(c_{a 1} \Delta t+c_{a 2} \Delta t\right) \frac{\partial u}{\partial s}-2 \Delta t \frac{\partial u}{\partial t}+\right.} \\\left.\frac{1}{2}\left(\left(c_{a 1} \Delta t+c_{a 2} \Delta t\right) \frac{\partial u}{\partial s}-2 \Delta t \frac{\partial u}{\partial t}\right)^{2}\right]\end{array}$
化简式(6)就能够得到二阶$c_{{\rm a}j}$-Higdon表达式. 对于更高阶次边界, 可用归纳法依次类推.
证明2: 考虑$c_{{\rm a}j}$-MTF的单个算子形式($I-B(c_{{\rm a}j}))u = 0$. 分别定义空间移动算子$K$和时间移动算子$Z^{-1}$: $Ku(s,t)=u(s+c_{{\rm a}j}\Delta t, t), Z^{-1}u(s,t) = u(s, t-\Delta t)$, 则式(1)的单个算子形式可以表示为($I-Z^{-1}K)u = 0$. 该式可改写为
(7) $\begin{eqnarray} \label{eq7} \left( {\dfrac{I+K}{2}\dfrac{I-Z^{-1}}{\Delta s}-\dfrac{I+Z^{-1}}{2}\dfrac{K-I}{\Delta s}} \right)u=0 \end{eqnarray}$
将式(7)中第一个$\Delta s$用$c_{{\rm a}j}\Delta t$替换然后对每一项乘以$c_{{\rm a}j}$, 得到
(8) $\begin{eqnarray} \label{eq8} \left( {\dfrac{I+K}{2}\dfrac{I-Z^{-1}}{\Delta t}-c_{{\rm a}j} \dfrac{I+Z^{-1}}{2}\dfrac{K-I}{\Delta s}} \right)u=0 \end{eqnarray}$
对式(8)中的差分算子取极限, 即可得到 ($\partial /\partial t-\partial /\partial s)u = 0$. 这表明$c_{{\rm a}j}$-MTF中每个离散形式的时空外推算子的极限形式为$c_{{\rm a}j}$-Higdon的各个单向波动微分算子, 所以这两个边界表达式等价.
由于证明1和证明2都建立在基本的数学原理之上, 证明过程中并未涉及任何波动方程, 所以$c_{{\rm a}j}$-MTF与$c_{{\rm a}j}$-Higdon边界的等价性是普遍存在的. 这远远强于已有研究所指出的Higdon边界或MTF边界与Clayton-Engquist声波边界之间的相似性[9 ,22 ] . 这种等价性将离散$c_{{\rm a}j}$-MTF边界与连续$c_{{\rm a}j}$-Higdon边界紧密联系在一起, 在讨论和应用中二者通常可以互相替换.
3 外推型ABC的理论联系
这一部分将通过公式推导来论证其他外推型ABC大多可以从基本边界公式(1)和(2)转化得到, 或通过某种等价的中间形式与之相关联.
3.1 Reynolds边界、Keys边界
Reynolds[33 ] 和Keys[34 ] 各自独立提出了一种ABC. 以外法向为$x$轴负向的边界为例, 其表达式分别为
(9) $\begin{eqnarray} \left( {\dfrac{1}{c}\dfrac{\partial }{\partial t}-\dfrac{\partial }{\partial x}} \right)\left( {\dfrac{p}{c}\dfrac{\partial }{\partial t}-\dfrac{\partial }{\partial x}} \right)u=0 \end{eqnarray}$
(10) $\begin{eqnarray} \left( {\dfrac{\partial }{\partial x}-\dfrac{\cos \theta_{1} }{c}\dfrac{\partial }{\partial t}} \right)\left( {\dfrac{\partial }{\partial x}-\dfrac{\cos \theta_{2} }{c}\dfrac{\partial }{\partial t}} \right)u=0 \end{eqnarray}$
将式(9)、式(10)与式(2)相比较可知, 它们都是式(2)的特例. 因此, $c_{{\rm a}j}$-Higdon边界已将这两种边界概括在内.
3.2 旁轴近似边界
旁轴近似边界主要为经典的Clayton-Engquist声波和弹性波边界(CE边界)[7 ] 、Halpern-Trefethen大角度 单向波动方程[8 ] 、 以及Fuyuki-Matsumoto (FM)[35 ] 、Emerman-Stephen (ES)[36 ] 、Stacey[37 ] 对CE弹性波边界的改进.
对于声波旁轴近似边界, Higdon[9 ] 已证明它们可以由Higdon边界结合声波方程来导出. 以外法向为$z$轴负向的边界为例, 考虑二阶情形, CE和Halpern-Trefethen所提出的各种二阶声波边界表达形式为
(11) $\begin{eqnarray} \label{eq11} \dfrac{\partial^{2}u}{\partial z\partial t}-\dfrac{p_{0} }{c}\dfrac{\partial ^{2}u}{\partial t^{2}}+cp_{2} \dfrac{\partial^{2}u}{\partial x^{2}}=0 \end{eqnarray}$
其中$c$为声波波速, $p_{0}$和$p_{2}$为不同边界的控制参数, 具体见文献[8 ]. 容易验证, 在式(2)的二阶形式中引入声波方程$c^{2}(\partial^{2}u/\partial x^{2}+\partial^{2}u/\partial z^{2}) = \partial ^{2}u/\partial t^{2}$, 将关于$z$的二阶偏导用关于$x$和$t$的二阶偏导所替换, 就导出了式(11). 式(2)中参数$c_{\rm a1}$, $c_{\rm a2}$与式(11)中参数$p_{0}$, $p_{2}$存在如下对应关系: $p_{0} = (1+\alpha_{1}\alpha_{2})/( \alpha_{1}+\alpha_{2})$, $p_{2} =\alpha_{1}\alpha _{2}/(\alpha_{1}+\alpha_{2})$, 其中$\alpha_{1} =c_{\rm a1}/c$, $\alpha_{2} = c_{\rm a2}/c$.
对于弹性波旁轴近似边界, 作者分析发现它们缺乏严格的理论基础, 难以达到较好的精度. 由于弹性波方程不能由其频散关系唯一地确定, 旁轴近似技术实际上无法用于推导弹性波边界. Clayton和Engquist[7 ] 仅通过粗略地模仿声波边界给出了如下弹性波边界($z$轴负向)
(12) $\begin{eqnarray} \label{eq12} \left. {\begin{array}{l} \dfrac{\partial^{2}u}{\partial t\partial z}-\dfrac{1}{c_{\rm s} }\dfrac{\partial ^{2}u}{\partial t^{2}}+\dfrac{c_{\rm s} -c_{\rm p} }{c_{\rm s} }\dfrac{\partial ^{2}w}{\partial t\partial x}-\\[2mm]\qquad\left( {\dfrac{1}{2}c_{\rm s} -c_{\rm p} } \right)\dfrac{\partial^{2}u}{\partial x^{2}}=0 \\[3mm] \dfrac{\partial^{2}w}{\partial t\partial z}-\dfrac{1}{c_{\rm p} }\dfrac{\partial ^{2}w}{\partial t^{2}}+\dfrac{c_{\rm s} -c_{\rm p} }{c_{\rm p} }\dfrac{\partial ^{2}u}{\partial t\partial x}-\\[2mm]\qquad\left( {\dfrac{1}{2}c_{\rm p} -c_{\rm s} } \right)\dfrac{\partial^{2}w}{\partial x^{2}}=0 \\ \end{array}}\ \ \right\} \end{eqnarray}$
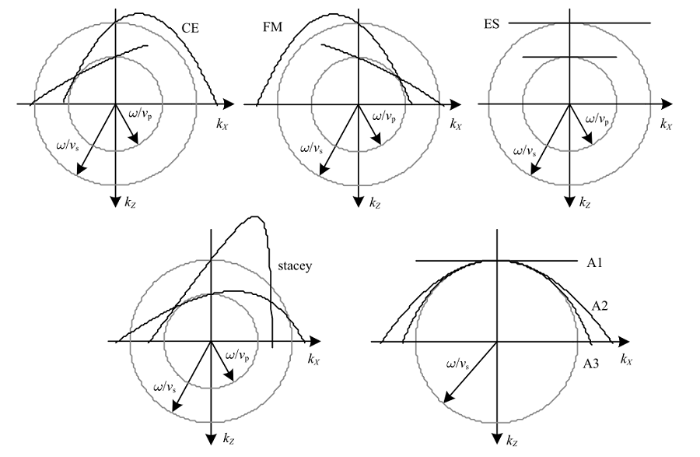
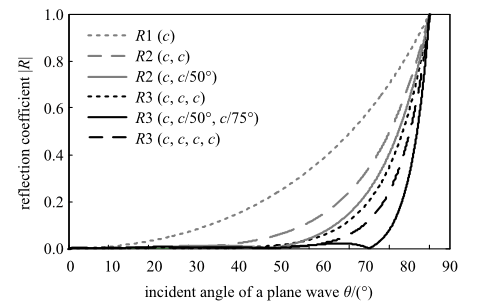
然而, 式(12)既无法从旁轴近似角度进行解释, 也无法由$c_{{\rm a}j}$-Higdon边界结合弹性波方程导出. Fuyuki和Matsumoto[35 ] 、Emerman和Stephen[36 ] 、Stacey[37 ] 在式(12)基础上所做的改进并未解决这一问题. 数值试验表明这些边界精度较差. 为了从理论上揭示所谓的旁轴近似弹性波边界的不合理性, 在波数平面上绘出了CE, FM, ES和Stacey弹性波边界的频散曲线, 如图3 所示. 作为对比, 图中还给出了声波边界(11)的频散曲线, A1, A2, A3分别表示一阶、二阶、三阶声波边界.
图3
图3
弹性波、声波旁轴近似边界的频散曲线
Fig.3
Dispersion curves of acoustic- and elastic-wave paraxial-approximation boundaries
图3 中各曲线与上半圆的接近程度反映了人工边界条件的精度. 各个弹性波边界频散曲线与上半圆的吻合度很差, 这证实了旁轴近似弹性波边界的不合理性. 与之相比, 旁轴近似声波边界精度较好, 且随着阶次上升迅速提高, 与理论结果相符.
3.3 辅助变量高阶边界
针对高阶Higdon边界数值离散比较困难的问题, Givoli-Neta等[11 -12 ] 、 Hagstrom-Warburton等[13 -14 ] 分别提出一种可顺利离散至任意阶次的辅助变量高阶边界(G-N边界和H-W边界). 这两种边界都是先给出一个与Higdon边界等价的辅助变量递推关系, 再引入声波方程将递推关系中的边界法向导数转换为切向导数, 得到只含有边界切向导数和时间导数的辅助变量递推关系, 形成实用的高阶边界. 由于声波方程的引入, 这两种为声波边界.
G-N边界表达式见文献[11 ,12 ], 它所使用的辅助变量递推关系为
(13) $\left.\begin{array}{l}\left(\frac{\partial}{\partial x}+\frac{1}{c_{1}} \frac{\partial}{\partial t}\right) u=\phi_{1} \\\left(\frac{\partial}{\partial x}+\frac{1}{c_{j+1}} \frac{\partial}{\partial t}\right) \phi_{j}=\phi_{j+1}, \quad j=1,2, \cdots, N-1\end{array}\right\}$
(14) $\begin{eqnarray} \label{eq14} &&\left( {\dfrac{\partial }{\partial x}+\dfrac{1}{c_{N} }\dfrac{\partial }{\partial t}} \right)\left( {\dfrac{\partial }{\partial x}+\dfrac{1}{c_{N-1} }\dfrac{\partial }{\partial t}} \right)\cdots\\&&\qquad \left( {\dfrac{\partial }{\partial x}+\dfrac{1}{c_{1} }\dfrac{\partial }{\partial t}} \right)u=0 \end{eqnarray}$
将式(14)与式(2)进行比较可知它们是一致的. 式(14)中的计算波速参数$c_{1},c_{2},\cdots ,c_{N} $对应于式(2)中的人工波速参数$c_{\rm a1},c_{\rm a2},\cdots ,c_{{\rm a}N} $. 所以在声波问题中, 相同参数的G-N边界与$c_{{\rm a}j}$-Higdon边界具有相同的精度.
H-W边界表达式见文献[13 ,14 ], 它基于的辅助变量递推关系为
(15) $\left.\begin{array}{l}\left(a_{0} \frac{\partial}{\partial t}+c \frac{\partial}{\partial x}\right) u=a_{0} \frac{\partial \phi_{1}}{\partial t} \\\left(a_{j} \frac{\partial}{\partial t}+c \frac{\partial}{\partial x}\right) \phi_{j}=\left(a_{j} \frac{\partial}{\partial t}-c \frac{\partial}{\partial x}\right) \phi_{j+1} \\j=1,2, \cdots, N\end{array}\right\}$
Bécache等[38 ] 经过推导, 证明式(15)的合并形式为
(16) $\begin{eqnarray} \label{eq16} &&\left( {a_{N} \dfrac{\partial }{\partial t}+c\dfrac{\partial }{\partial x}} \right)^{2}\cdots \left( {a_{1} \dfrac{\partial }{\partial t}+c\dfrac{\partial }{\partial x}} \right)^{2}\\&&\qquad\left( {a_{0} \dfrac{\partial }{\partial t}+c\dfrac{\partial }{\partial x}} \right)u=0 \end{eqnarray}$
式(16)中计算波速由声波波速$c$和任意系数$a_{0} ,a_{1} ,a_{2} ,\cdots ,a_{N} $组合而成, 为$c/a_{0}$, $c/a_{1}$, $c/a_{2}$, $\cdots$, $c/a_{N}$. 比较式(16)和式(2)可知, 在声波问题中, 1, 2, 3, $\cdots$ 阶H-W边界分别对应于3, 5, 7, $\cdots$ 阶$c_{{\rm a}j}$-Higdon边界, 即存在$2N+1$倍关系.
3.4 任意大角度波动方程
Guddati等[15 -16 ] 提出一种矩阵形式的辅助变量高阶边界AWWE, 他们通过两种方式导出这种边界: 一是将声波方程的旁轴近似递推关系按偶数阶提取出来, 将其写成矩阵形式, 再返回到时域成为人工边界条件; 二是将半无限介质分层, 利用各层动力刚度的有限单元近似, 在频域内导出矩阵关系式, 进而返回时域得到人工边界条件. 根据本文第3.2节所指出的声波旁轴近似边界可以由$c_{{\rm a}j}$-Higdon边界与声波方程相结合得到, 可以推断出1, 2, 3, $\cdots$ 阶AWWE边界分别对应于2, 4, 6, $\cdots$ 阶$c_{{\rm a}j}$-Higdon边界, 即存在2$N$倍关系. AWWE边界与$c_{{\rm a}j}$-Higdon边界的等价中间形式为
(17) $\begin{eqnarray} \label{eq17} &&\left( {\dfrac{\partial }{\partial t}+c_{N} \dfrac{\partial }{\partial z}} \right)^{2}\left( {\dfrac{\partial }{\partial t}+c_{N-1} \dfrac{\partial }{\partial z}} \right)^{2}\cdots \\&&\qquad \left( {\dfrac{\partial }{\partial t}+c_{1} \dfrac{\partial }{\partial z}} \right)^{2}u=0 \end{eqnarray}$
3.5 其他相关边界方法
Lindman[17 ] 提出一种数值优化边界, 表达式见文献[17 ]. Kausel[39 ] 证明了该边界的连续形式为一种高阶旁轴近似边界, 与Clayton-Engquist声波边界属于一个类型.
Peng-Toksöz[18 ] 提出另一种数值优化边界, 表达式为
(18) $\begin{array}{l}u^{n+1}(0, j, k)=a_{01} u^{n+1}(1, j, k)+a_{02} u^{n+1}(2, j, k)+ \\a_{10} u^{n}(0, j, k)+a_{11} u^{n}(1, j, k)+a_{12} u^{n}(2, j, k)+ \\a_{20} u^{n-1}(0, j, k)+a_{21} u^{n-1}(1, j, k)+ \\a_{22} u^{n-1}(2, j, k)\end{array}$
式中$u^{n}\left( {i,j,k} \right)=u\left( {i\Delta x,j\Delta y,k\Delta z,n\Delta t} \right)$表示离散网格中波场的节点值. 编号0为边界节点, 1和2为临近的内域节点. $a_{01} ,a_{02} ,\cdots ,a_{22} $为控制参数, 由一系列限定条件建立的方程组来确定. 显然, 式(18)借鉴了二阶Higdon边界数值离散格式所采用的3$\times$3节点组合, 只是确定计算系数的方式有所不同.
Randall[19 ] 针对弹性波边界精度不高的问题, 提出一种将弹性波场进行势分解, 对分解出来的波势函数分别使用高精度的Lindman声波边界, 再将结果合成为弹性波场的方法. 弹性波场向势函数的分解与合成分别表示为
(19) $\begin{eqnarray} \label{eq19} &&\dfrac{\partial^{2}{\varPhi }}{\partial t^{2}}=c_{\rm p}^{2} \nabla \cdot {u}, \ \ \dfrac{\partial^{2}{\varPsi }}{\partial t^{2}}=-c_{\rm s}^{2} \nabla \times {u}\end{eqnarray}$
(20) $\boldsymbol{u}=\nabla \boldsymbol{\Phi}+\nabla \times \boldsymbol{\Psi}$
式中, $u$为弹性波位移场向量, $\varPhi $和$\varPsi $分别为P波和S波势函数. $\nabla $为向量微分算子, $c_{\rm p}$和$c_{\rm s}$分别为P波和S波波速. Randall势分解方法是提高外推型ABC模拟弹性波的精度的一个有益尝试, 但由于势分解与合成过程以及Lindman边界所带来的双重复杂度, 作者未见其他学者应用或探讨该边界方法.
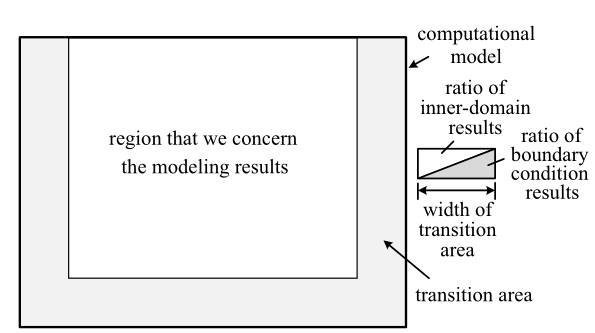
Liu和Sen[20 -21 ] 将外推型ABC与过渡区技术相结合, 发展出一套混合边界方法, 如图4 所示. 该方法在计算模型的外边界附近设置一定宽度的过渡区, 过渡区波场由内域离散格式和边界数值格式分别计算的波场进行加权和得到. 二者权系数之和始终为1, 其分配比例沿着过渡区宽度的变化如图中三角形所示.
图4
图4
Liu-Sen混合边界示意图
Fig.4
Schematic of Liu-Sen hybrid ABC
大量波动模拟实践表明Liu-Sen混合边界能够显著提高人工边界的精度, 并有效降低外推型ABC可能面临的数值失稳风险. 过渡区的引入在相当程度上阻止了反射误差向内域传播, 并延缓了不稳定结果的积累. 在数值试验中观察到过渡区内波场表现出类似完美匹配层内波场的快速衰减特征. 我们认为本文外推型ABC与Liu-Sen混合边界方法相结合, 应是解决波动数值模拟中人工边界问题一个值得重视的方向.
4 外推型ABC的精度控制原理
4.1 离散边界公式(1)的时空外推原理
离散边界公式(1)的单人工波速形式(即廖氏透射边界)存在一种明确的几何解释, 如图5 所示. 外行波沿人工边界节点所在的局部坐标空间轴$s$的传播过程, 可以在$sot$时空坐标平面上展开成一个二维"静态"波场. 在这个二维静态波场中, 沿着由单一人工波速和离散时间步距所确定的时空外推方向, 可以截取出一维波场曲线$g$. 人工边界节点运动的实际值由连续曲线$g$决定, 但在数值模拟中只能利用曲线$g$上若干个参考点的值来推算其端部人工边界节点的值. 这个推算过程的精度即为MTF边界的精度.
从图5 中可以看出, 边界阶次$N$(即参考点数目)代表基于$N-$1阶多项式的外推精度. 曲线$g$的弯曲程度则由外行波复杂程度和所选取的时空外推方向(它与人工波速有关)共同决定. 于是这种几何解释可以用一句话概括为: $N$阶MTF是以基于$N-$1阶多项式的外推精度对由人工波速所确定的时空外推方向上的外行波曲线的一种近似. 显然, 提高边界阶次$N$, 或者选取与实际视波速相接近的人工波速以获得较为平缓的曲线$g$, 都是提高MTF边界精度的有效措施.
图5
图5
MTF边界的时空外推原理
Fig.5
Time-space extrapolation of MTF boundary
MTF边界这种明确的几何解释, 加之其简洁的数学形式和"多次透射"的物理机制, 奠定了外推型人工边界理论的思想基础.
4.2 连续边界公式(2)的反射系数乘积原理
连续边界公式(2)是Higdon边界的统一形式. Higdon边界所采用的多个单向波动微分算子乘积形式是从满足边界要求的一系列离散表达式中总结而来的[9 ] . 这表明连续边界公式(2)的理论源头可以追溯到离散边界公式(1), 即上述MTF边界的时空外推原理. 因此, 外推型人工边界条件具有统一的思想基础, 它来源于离散边界. 各种微分方程形式的连续边界主要为外推型ABC提供了丰富的变化形式.
连续边界公式(2)的精度可以利用反射系数加以分析. 该边界对于入射角为$\theta$的外行平面波的反射系数为
(21) $\begin{eqnarray} \label{eq21} R\left( \theta \right)=-\prod\limits_{j=1}^N {\dfrac{ {c/c_{{\rm a}j} -\cos \theta } }{ {c/c_{{\rm a}j} +\cos \theta } }} \end{eqnarray}$
式中$c$为介质物理波速, $c_{{\rm a}j}$为边界的人工波速参数. 式(21)为多个因子的乘积, 这对应了式(2)的单向波动微分算子乘积. 图6 绘出了几种不同$N$和$c_{{\rm a}j}$取值的反射系数$R(\theta )$.
图6
图6
连续边界公式的反射系数乘积原理
Fig.6
Product of reflection coefficients of multiple first-order wave-propagation operators
在图6 中, 根据一阶边界反射系数$R$1可知单个反射因子的幅值总是小于或等于1, 所以高阶边界所具有的多个反射因子的乘积能够迅速提高边界精度. 另外, 多个反射因子如果具有不同的零反射角度(由不同人工波速取值决定), 能够在更大透射角范围内提高边界精度.
图7 绘出了$c_{{\rm a}j}$-Higdon边界(Hig)、Hagstrom-Warburton边界(HW)、AWWE边界的反射系数. 根据第3.3节和第3.4节内容可知, Givoli-Neta边界(GN)反射系数与$c_{{\rm a}j}$-Higdon边界相同, 故未在图中列出; $N$阶HW边界、AWWE边界分别对应于2$N+$1阶、2$N$阶$c_{{\rm a}j}$-Higdon边界.
图7
图7
Higdon, G-N, H-W, AWWE边界的反射系数
Fig.7
Reflection coefficients of Higdon, G-N, H-W, AWWE boundaries
图7 曲线表明相同人工波速取值下, 1, 2, 3阶HW反射系数与3, 5, 7阶Higdon相同, 1, 2, 3阶AWWE反射系数与2, 4, 6阶Higdon相同. 这证实了前文理论分析所给出的结论. 由此可见, GN、HW和AWWE 3种辅助变量高阶边界使用与$c_{{\rm a}j}$-Higdon相同数量的一阶单向波动微分算子($\partial $/$\partial t-c_{{\rm a}j}\partial $/$\partial s)$实现了与之相同的精度, 即它们提高边界精度的原理与$c_{{\rm a}j}$-Higdon并无二致.
4.3 基于视波速的多人工波速分析
基本边界公式(1)和(2)所采用的多人工波速参数$c_{{a}j}(j =1$, 2, $\cdots$, $N$)并不仅仅是形式上的优化, 它对于具有多种物理波速的复杂波动问题具有非常重要的实用价值. 这些问题包括多层介质问题、弹性波、两相介质波动、频散波动等. 上述基于透射角度$\theta $的反射系数式(21)未考虑物理波速的变化. 为同时考虑介质物理波速和透射角度的变化, 这里采用外行波的视波速$c_{n} =c/\cos \theta $作为基本变量, 得出$c_{{\rm a}j}$-Higdon边界反射系数的另一种表达形式
(22) $\begin{eqnarray} \label{eq22} R(c_{n} )=-\prod\limits_{j=1}^N {\dfrac{ {c_{{\rm a}j} -c_{n} } }{ {c_{{\rm a}j} +c_{n} } }} \end{eqnarray}$
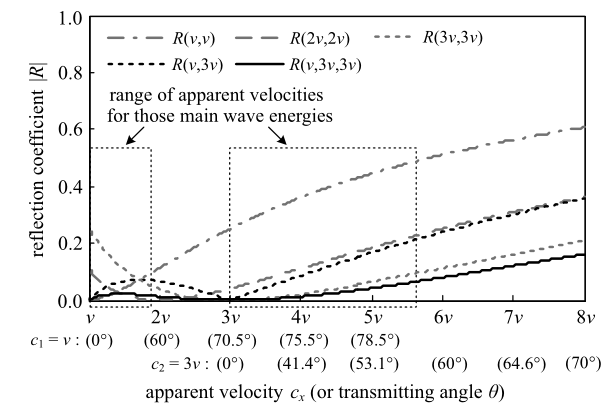
图8 所示为存在两种物理波速时$c_{{\rm a}j}$-Higdon边界的反射系数幅值与外行波视波速$c_{n}$的关系. 这里两种物理波速为$c_{1} = v$和$c_{2} =3v$, $v$表示某个可约去的波速, 它的取值不影响分析结果. 3倍的物理波速差异将对人工边界性能提出挑战.
图8
图8
多人工波速分析
Fig.8
Analysis of various artificial wave velocities
在图8 中, 主要波动能量的视波速范围有两段, 其中虽然有透射角度的影响, 但差异较大的两种物理波速起了主要作用. 理想的人工边界反射系数应当在所关心的两个区段中都处于低值. 可以看出, 采用单一人工波速的3种边界$R(v,v)$, $R(2v,2v)$和$R(3v,3v)$都不够理想, 只有采用多人工波速的二阶边界$R(v,3v)$和三阶边界$R(v,3v,3v)$较好地兼顾了对两段波动能量的吸收. 因此, 在具有多种差异较大的物理波速的波动问题中, 使用以多人工波速为参数的外推型ABC很有必要也非常实用.
5 数值算例
5.1 声波大角度透射问题
以一个均匀介质声波问题算例来检验上述外推型ABC的精度. 模型尺度为200 m$\times$500 m, 介质波速为$c = 500$ m/s. 顶面为自由边界, 左、右、底边界为人工边界. 在顶部中点施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[9 ] . 网格尺寸为2 m$\times$2 m, 时间步长满足稳定条件$c\Delta t/\Delta x \leqslant 0.71$. 人工边界分别采用本文提出的外推型ABC基本公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及现有的Clayton-Engquist (CE)旁轴近似边界[7 ] 、辅助变量高阶边界Givoli-Neta(GN)[11 ] 、Hagstrom-Warburton(HW)[13 ] 和AWWE[16 ] . 本文ABC的数值离散格式见附录.
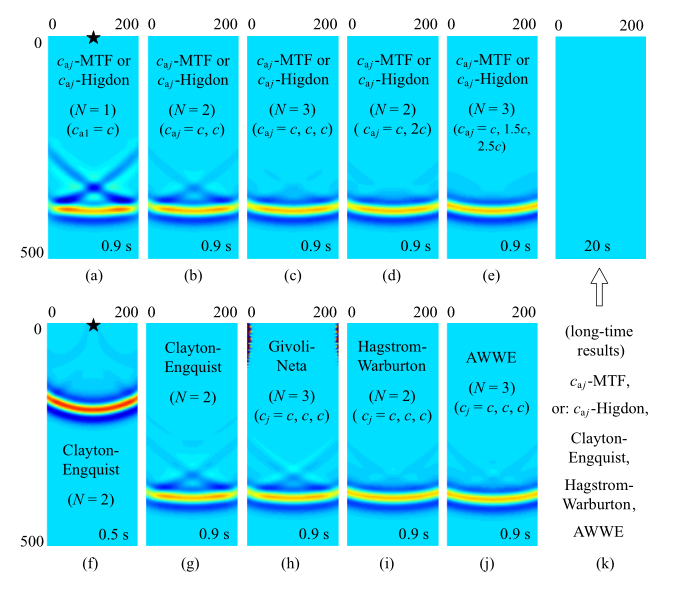
图9 给出了0.9 s时的波场快照. 此时外行波在侧边界上的透射角度约75$^\circ$, 为大角度透射, 这种情形对ABC性能要求较高. 图中括号内参数如($c$, 1.5$c$, 2.5$c)$表示所采用的人工波速参数$c_{{\rm a}j}(j =1$, 2, $\cdots$, $N)$.
图9
图9
采用不同外推型人工边界的声波模拟结果
Fig.9
Modeling results of acoustic wave propagation using different ABCs
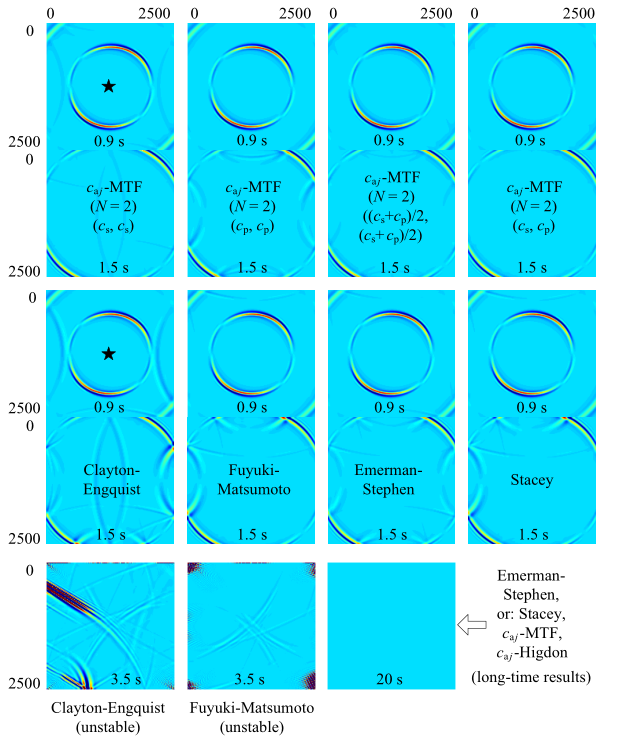
图9 中不同ABC的反射误差对比证实了前文理论分析所给出的结论, 主要包括: (1) $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon等价(见第3部分), 这在本算例中表现为尽管用于实现$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon的数值计算格式有所不同, 但只要当二者所采用的边界参数$N$和$c_{{\rm a}j}(j =1$, 2, $\cdots$, $N)$相同时, 其模拟结果就会保持一致; (2) 随着阶次$N$升高, 边界精度提高, 且多人工波速方案能够进一步改善精度(见图6 ), 图9 (a)$\sim$图9 (e)中不同边界阶次结果对比和相同阶次下多人工波速方案与单一人工波速方案结果对比证实了这个结论; (3) CE边界和辅助变量高阶边界GN, HW和AWWE具有与基本边界公式$c_{{\rm a}j}$-Higdon相同的精度控制原理(见第3.2$\sim$3.4节和图7 ), 这预示着相同边界参数下它们的模拟结果一致, 如图9 中二阶CE与二阶$c_{{\rm a}j}$-Higdon在0.9 s时的结果非常接近, 二阶HW(相当于五阶$c_{{\rm a}j}$-Higdon)和三阶AWWE(相当于六阶$c_{{\rm a}j}$-Higdon)模拟结果与三阶$c_{{\rm a}j}$-Higdon结果相似. 不同外推型ABC除了呈现出上述共同特征之外, 它们各自还有一些不同的表现, 如图中CE边界存在角点反射问题(见0.5 s快照图), GN边界出现了失稳(该失稳首先出现在边界上距离震源较近的区域, 为典型的人工边界条件失稳特征), HW和AWWE边界由于数值离散误差影响显著, 其三阶以上的高阶精度难以实现. 这些问题从侧面说明本文所提出的基本边界公式(1)和式(2)最为简单实用.
5.2 均匀介质弹性波问题
以一个均匀介质弹性波问题算例来进一步检验上述外推型ABC的性能. 模型尺度为2500 m $\times$2500 m, 介质纵、横波速为$c_{\rm p} = 2000$ m/s, $c_{\rm s} = 1000$ m/s. 四边均为人工边界. 在模型中心施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[35 ] . 网格尺寸为5 m$\times$5 m, 时间步长满足稳定条件 $\sqrt{c_{\rm s}^{2}+c_{\rm p}^{2}}\cdot$ $\Delta t/\Delta x\leqslant 1$. 人工边界分别采用$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及第3.2节提及的几种弹性波旁轴近似边界. 此时附录A中的边界离散格式分别用于人工边界节点的水平和竖向波场分量.
图10 给出了0.9 s和1.5 s时水平分量的波场快照. 此时存在两种差异较大的物理波速($c_{\rm p}$等于2倍$c_{\rm s})$, 这种情形能够凸显采用多人工波速方案的必要性及优势. $c_{{\rm a}j}$-Higdon与$c_{{\rm a}j}$-MTF结果相同, 未在图中列出. 考虑了3种单一人工波速和一种多人工波速的二阶$c_{{\rm a}j}$-MTF边界, 并以几种旁轴近似边界作为对比.
图10
图10
采用不同外推型人工边界的弹性波模拟结果
Fig.10
Modeling results of elastic wave propagation by using different ABCs
图10 中$c_{{\rm a}j}$-MTF边界模拟结果证明了对于多物理波速的复杂波动问题采用多人工波速外推型ABC的必要性及优势(第4.3节). 此时3种单一人工波速的二阶$c_{{\rm a}j}$-MTF均不能很好地实现对P波和S波的同步透射, 而多人工波速($c_{\rm s}$, $c_{\rm p})$方案几乎完美地实现了这一目标. 与基本边界$c_{{\rm a}j}$-MTF相比, 所谓的弹性波旁轴近似边界反射量很大, 这对应了图3 关于这几个弹性波边界理论上具有不合理性的分析结果. Clayton-Engquist和Fuyuki-Matsumoto (它与前者高度相似) 边界出现失稳, Emerman-Stephen和Stacey边界(文献[36 ,37 ]指出它们改善了CE弹性波边界的稳定性)以及本文提出的$c_{{\rm a}j}$-MTF边界在20 s长持时模拟结果中保持了稳定. 因此, 综合考虑精度与稳定性, 模拟弹性波的外推型ABC建议采用基本边界公式$c_{{\rm a}j}$-MTF或$c_{{\rm a}j}$-Higdon.
5.3 纵、横向不均匀介质弹性波模拟
设计如图11 所示的纵、横向不均匀介质场地模型, 检验本文边界条件的吸收效果. 该模型为右下方整块基岩与左侧、上部成层土体形成的复杂场地, 岩土体参数如图所示. 在($x, z) =$ (300 m, 100 m)处节点的竖向分量上施加中心频率为10 Hz的Ricker子波激励. 上部为自由地表, 其余3边分别采用自由边界(作为对照)或本文提出的人工边界, 进行两组模拟. 采用集中质量有限元与中心差分相结合的数值模拟方法[29 -30 ] . 单元尺寸为2.5 m$\times$2.5 m, 时间步长满足稳定条件$\sqrt {c_{\rm s}^{2} +c_{\rm p}^{2} } \Delta t/\Delta x\leqslant 1$.
图11
图11
纵、横向不均匀介质模型
Fig.11
Computational model of a longitudinal and transverse inhomogeneous media
这个模拟选用所提出的$c_{{\rm a}j}$-MTF (或$c_{{\rm a}j}$-Higdon, 与前者结果一致)边界, 边界参数为$N = 2$, $c_{{\rm a}j} = c_{\rm s}$, $c_{\rm p}$. 不考虑其他外推型ABC, 因为前文已指出: Givoli-Neta, Hagstrom-Warburton, AWWE等高阶辅助变量边界和Lindman数值优化边界只适用于声波; 算例5.2表明几种旁轴近似弹性波边界的精度和稳定性远不如$c_{{\rm a}j}$-MTF或$c_{{\rm a}j}$-Higdon; 引言中提及的Peng-Toksöz数值优化边界和Randall势分解边界十分复杂, 少有应用和讨论, 其是否有精度或稳定性方面的优势尚无定论; Liu-Sen混合边界是外推型ABC与过渡区技术相结合的综合性解决方案, 已发表大量文献, 而本文关注的仅是外推型ABC本身的性能. 模拟结果如图12 所示.
图12
图12
不均匀介质弹性波模拟结果
Fig.12
Simulation results of elastic waves in the inhomogeneous model
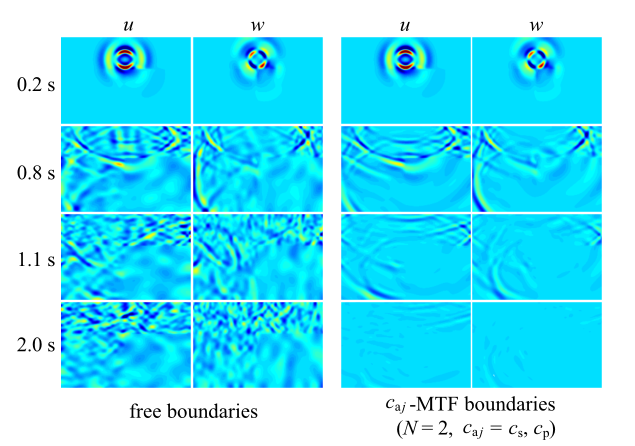
在图12 中, 由于自由边界会完全反射波动能量, 该模型像一个封闭波动能量的"盒子", 其模拟结果与实际问题中波可以无阻挡地穿过(因为原问题中此处无界面)人工边界再传向远处的过程相去甚远. $c_{{\rm a}j}$-MTF (或$c_{{\rm a}j}$-Higdon)边界则几乎看不到虚假反射波, 说明它们所推算的边界节点运动与原来无限介质中该处运动非常接近(或基本一致), 因此这个有限计算模型给出了与实际问题相符的模拟结果.
5.4 关于复杂介质模拟效果和稳定性的讨论
外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨.
数值试验表明, 本文基本边界公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon的稳定性高度一致, 且与现有MTF和Higdon边界基本没有区别. 外推型ABC的稳定性可以从所引文献及相关学者的研究成果中总结得到, 这个研究课题目前仍然活跃. 本文和相关文献数值试验表明了外推型ABC的实用性, 或者说它们一般能够在所关心的模拟时间内给出稳定结果, 这对于解决大多数持时不太长的波动问题已经足够. 对外推型ABC稳定性问题完整而详细的探讨显然不是本文所能完成的任务, 不过, 关于稳定性、边界失稳特征及其解决方法, 作者从已有研究中总结出以下几点主要认识: (1) 不同于应力型ABC (如黏弹性边界)和衰减层型ABC(如完美匹配层边界)需要附着在内域离散模型之上, 外推型ABC有着独立于内域离散模型的数值计算格式, 后者两种不同离散格式的耦合常常不如前两者的整体计算格式稳定. (2) 当边界出现某种失稳时, 其不稳定值的积累速度由边界条件的反射幅值(高阶边界大于低阶边界)和波在整个模型与所有失稳节点之间的反复反射放大共同决定, 因此三维模型(边界节点多)失稳放大最快, 二维模型次之, 一维模型最慢; 同样维度下, 小尺寸模型(来回反射距离短)比大尺寸模型失稳积累得更快; 高波速问题(来回反射所需时间少)比低波速问题失稳积累得要快; 复杂介质问题(多个界面之间反射次数多)比均匀介质问题失稳积累得快. (3) 若边界出现漂移失稳(指边界节点运动向正值或负值单方向的不正常累积), 通常采用修正的边界公式(3)或(4)来解决, 亦可考虑将高阶边界与低价边界组合使用, 或者在边界上附加弹簧和阻尼元件等. (4) 若边界出现振荡失稳, 可以考虑在整个计算模型中增加少量阻尼来解决, 或者在与一些特定的内域离散格式结合时能够避免这一问题, 此外, 增大计算模型, 或使用具有耗能特性的时间积分格式, 或采用Liu-Sen混合边界方法等都是值得考虑的选择.
6 结论
本文新提出离散形式和连续形式(即微分方程形式)两个基本边界公式, 通过证明二者的等价性并阐明其与经典的廖氏透射边界、旁轴近似边界、Higdon边界以及Givoli-Neta、Hagstrom-Warburton、AWWE辅助变量 边界等之间的理论联系, 据此建立了一种外推型人工边界条件的理论与公式体系. 主要研究结论如下:
(1) 上述经典人工边界条件可以统一地从外推型ABC角度来讨论和应用. 因为它们计算人工边界节点运动的方式都是利用边界附近一组节点的运动(不同边界使用的节点组合可能有一定差异)进行时空外推, 使用相同的控制参数(边界阶次和一组计算波速), 并且在数值模拟中表现出相似的精度和稳 定性.
(2) 本文提出的基本边界公式在精度和稳定性方面均更有优势, 是该类边界最简单实用的形式.
(3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题.
附录: $c_{{a}j}$-MTF边界的数值离散格式
在图A1所示的局部离散网格上定义空间、时间移动算子$E_{x} u_{0}^{p+1} =u_{1}^{p+1} $、$E_{t}^{-1} u_{0}^{p+1} =u_{0}^{p} $, $I$为单位算子. 对于$c_{{a}j}$-MTF边界, 采用抛物线插值公式将每个参考点的运动用临近的离散网格点的运动来代替. 这里考虑前三阶边界, 当$N = 3$时, 所得数值计算格式的算子表达式为
(A1) $\begin{eqnarray} && \Big\{ \Big[ I-E_{t}^{-1} \Big( q_{x0} +q_{x1} E_{x} +q_{x2} E_{x}^{2} \Big)\Big]\cdot \Big[ I-E_{t}^{-1} \Big( r_{x0} +r_{x1} E_{x} +r_{x2} E_{x}^{2} \Big) \Big] \cdot \\&&\qquad \Big[ I-E_{t}^{-1}\Big( s_{x0} +s_{x1} E_{x} +s_{x2} E_{x}^{2}\Big)\Big]\Big\}u_{0}^{p+1} =0 \end{eqnarray}$
图A1
图A1
$c_{{a}j}$-MTF边界数值计算格式的局部节点编号
Fig.A1
Local index numbers of the numerical scheme of $c_{{a}j}$-MTF boundaries
展开算子表达式(A1), 得到可直接用于编程的前三阶$c_{{a}j}$-MTF边界的数值计算格式如下
(A2) $s_{a 1}=c_{a 1} \cdot \Delta t / \Delta s, \quad s_{a 2}=c_{a 2} \cdot \Delta t / \Delta s, s_{a 3}=c_{a 3} \cdot \Delta t / \Delta s$
(A3) $\left.\begin{array}{l}q_{x 0}=\left(s_{a 1}-1\right)\left(s_{a 1}-2\right) / 2, \quad q_{x 1}=-s_{a 1}\left(s_{a 1}-2\right) \\q_{x 2}=s_{a 1}\left(s_{a 1}-1\right) / 2 ;\left(\boldsymbol{Q}_{v}\right)_{1 \times 3}=\left(\begin{array}{lll}q_{x 0} & q_{x 1} & q_{x 2}\end{array}\right)\end{array}\right\}$
(A4) $\left.\begin{array}{l}r_{x 0}=\left(s_{a 2}-1\right)\left(s_{a 2}-2\right) / 2, \quad r_{x 1}=-s_{a 2}\left(s_{a 2}-2\right) \\r_{x 2}=s_{a 2}\left(s_{a 2}-1\right) / 2 ;\left(\boldsymbol{R}_{v}\right)_{1 \times 3}=\left(r_{x 0} r_{x 1} r_{x 2}\right)\end{array}\right\}$
(A5) $\left.\begin{array}{l}s_{x 0}=\left(s_{a 3}-1\right)\left(s_{a 3}-2\right) / 2, s_{x 1}=-s_{a 3}\left(s_{a 3}-2\right) \\s_{x 2}=s_{a 3}\left(s_{a 3}-1\right) / 2 ;\left(\boldsymbol{S}_{v}\right)_{1 \times 3}=\left(s_{x 0} s_{x 1} s_{x 2}\right)\end{array}\right\}$
(A6) $\left(\boldsymbol{T}_{1}\right)_{1 \times 3}=\boldsymbol{Q}_{v}$
(A7) $\left.\begin{array}{l}\left.\left(\boldsymbol{T}_{2_{-} 1}\right)_{1 \times 3}=\boldsymbol{Q}_{v}+\boldsymbol{R}_{v}, \quad\left(\boldsymbol{T}_{2_{-} 2}\right)_{1 \times 5}=\boldsymbol{R}_{v} \cdot\left(\begin{array}{ccc}\boldsymbol{Q}_{v} & 0 & 0 \\0 & \boldsymbol{Q}_{v} & 0 \\0 & 0 & \boldsymbol{Q}_{v}\end{array}\right)\right\} \\\left(\boldsymbol{T}_{2}\right)_{1 \times 8}=\left[\begin{array}{ll}\boldsymbol{T}_{2_{-} 1}-\boldsymbol{T}_{2_{-} 2}\end{array}\right]\end{array}\right\}$
(A8) $\begin{array}{l}\left(\boldsymbol{T}_{3_{-} 1}\right)_{1 \times 3}=\boldsymbol{Q}_{v}+\boldsymbol{R}_{v}+\boldsymbol{S}_{v} \\\left(\boldsymbol{T}_{3-2}\right)_{1 \times 5}=\boldsymbol{T}_{2_{-} 2}+\boldsymbol{S}_{v} \cdot\left(\begin{array}{ccc}\boldsymbol{T}_{2-1} & 0 & 0 \\0 & \boldsymbol{T}_{2-1} & 0 \\0 & 0 & \boldsymbol{T}_{2_{-1}}\end{array}\right) \\\left(\boldsymbol{T}_{3_{-} 3}\right)_{1 \times 7}=\boldsymbol{S}_{v} \cdot\left(\begin{array}{ccc}\boldsymbol{T}_{2-2} & 0 & 0 \\0 & \boldsymbol{T}_{2-2} & 0 \\0 & 0 & \boldsymbol{T}_{2_{2}-2}\end{array}\right) \\\left(\boldsymbol{T}_{3}\right)_{1 \times 15}=\left[\begin{array}{lll}\boldsymbol{T}_{3_{-} 1} & -\boldsymbol{T}_{3_{-2}} & \boldsymbol{T}_{3_{-} 3}\end{array}\right]\end{array}$
(A9) $\left.\begin{array}{l}\left(\boldsymbol{u}_{t 1}\right)_{3 \times 1}=\left(u_{1} u_{2} u_{3}\right)^{\mathrm{T}}, \quad\left(\boldsymbol{u}_{t 2}\right)_{8 \times 1}=\left(u_{1} u_{2} \cdots u_{8}\right)^{\mathrm{T}} \\\left(\boldsymbol{u}_{t 3}\right)_{15 \times 1}=\left(u_{1} u_{2} \cdots u_{15}\right)^{\mathrm{T}}\end{array}\right\}$
(A10) $\text { first order } c_{\mathrm{a} j^{-}} \cdot \mathrm{MTF}: u_{0}^{p+1}=\boldsymbol{T}_{1} \cdot \boldsymbol{u}_{t 1}$
(A11) $\text { second order } c_{\mathrm{a} j}-\mathrm{MTF}: u_{0}^{p+1}=\boldsymbol{T}_{2} \cdot \boldsymbol{u}_{t 2}$
(A12) $\text { third order } c_{\mathrm{a} j} \text { -MTF }: u_{0}^{p+1}=\boldsymbol{T}_{3} \cdot \boldsymbol{u}_{t 3}$
这里, 式(A3)$\sim$(A9)中的括号下标()$_{1\times 3}$, ()$_{1\times 8}$, ()$_{15\times 1}$等用于指示行向量或列向量的维度, 在实际编程时可以忽略. 式(A9)中涉及的局部节点编号$u_{1}$, $u_{2}$, $\ldots$, $u_{15}$由图A1给出.
参考文献
View Option
[1]
谢志南 , 郑永路 , 章旭斌 等 . 弱形式时域完美匹配层 —— 滞弹性近场波动数值模拟
地球物理学报 , 2019 ,62 (8 ):3140 -3154
[本文引用: 2]
(Xie Zhinan Zheng Yonglu Zhang Xubin , et al . Weak-form time-domain perfectly matched layer for numerical simulation of viscoelastic wave propagation in infinite-domain
Chinese Journal of Geophysics 2019 ,62 (8 ):3140 -3154 (in Chinese))
[本文引用: 2]
[2]
Zhao M Wu LH Du XL , et al . Stable high-order absorbing boundary condition based on new continued fraction for scalar wave propagation in unbounded multilayer media
Computer Methods in Applied Mechanics and Engineering 2018 ,334 :111 -137
[本文引用: 2]
[3]
Gao YJ Song HJ Zhang JH , et al . Comparison of artificial absorbing boundaries for acoustic wave equation modeling
Exploration Geophysics 2017 ,48 :76 -93
DOI
URL
[本文引用: 1]
[4]
Huang JJ . An incrementation-adaptive multi-transmitting boundary for seismic fracture analysis of concrete gravity dams
Soil Dynamics and Earthquake Engineering 2018 ,110 :145 -158
DOI
URL
[本文引用: 2]
[5]
Xing HJ Li XJ Li HJ , et al . Spectral-element formulation of multi-transmitting formula and its accuracy and stability in 1D and 2D seismic wave modeling
Soil Dynamics and Earthquake Engineering 2021 ,140 :1 -15
[6]
邢浩洁 , 李鸿晶 . 透射边界条件在波动谱元模拟中的实现: 二维波动
力学学报 , 2017 ,49 (4 ):894 -906
[本文引用: 1]
(Xing Haojie Li Hongjing . Implementation of multi-transmitting boundary condition for wave motion simulation by spectral element method: Two dimension case
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (4 ):894 -906 (in Chinese))
[本文引用: 1]
[7]
Levin T Turkel E Givoli D . Obstacle identification using the TRAC algorithm with a second order ABC
International Journal for Numerical Methods in Engineering 2019 ,118 (2 ):61 -92
[本文引用: 4]
[8]
Halpern L Trefethen LN . Wide-angle one-way wave equations
Journal of the Acoustical Society of America 1988 ,84 (4 ):1397 -1404
PMID
[本文引用: 3]
A one-way wave equation, also known as a paraxial or parabolic wave equation, is a differential equation that permits wave propagation in certain directions only. Such equations are used regularly in underwater acoustics, in geophysics, and as energy-absorbing numerical boundary conditions. The design of a one-way wave equation is connected with the approximation of (1-s2)1/2 on [-1,1] by a rational function, which has usually been carried out by Padé approximation. This article presents coefficients for L2, L infinity, and other alternative classes of approximants that have better wide-angle behavior. For theoretical results establishing the well posedness of these wide-angle equations, see the work of Trefethen and Halpern ["Well-posedness of one-way wave equations and absorbing boundary conditions," Math. Comput. 47, 421-435 (1986)].
[9]
Higdon RL . Absorbing boundary conditions for difference approximations to the multi-dimensional wave equation
Mathematics of Computation 1986 ,47 (176 ):437 -459
[本文引用: 7]
[10]
Higdon RL . Radiation boundary conditions for elastic wave propagation
SIAM Journal on Numerical Analysis 1990 ,27 (4 ):831 -870
DOI
URL
[本文引用: 2]
[11]
Givoli D Neta B . High-order non-reflecting boundary scheme for time-dependent waves
Journal of Computational Physics 2003 ,186 :24 -46
DOI
URL
[本文引用: 5]
[12]
Givoli D Neta B Patlashenko I . Finite-element analysis of time-dependent semi-infinite wave-guides with high-order boundary treatment
International Journal for Numerical Methods in Engineering 2003 ,58 :1955 -1983
DOI
URL
[本文引用: 3]
[13]
Hagstrom T Warburton T . A new auxiliary variable formulation of high-order local radiation boundary conditions: Corner compatibility conditions and extensions to first-order systems
Wave Motion 2004 ,39 :327 -338
DOI
URL
[本文引用: 4]
[14]
Hagstrom T Mar-Or A Givoli D . High-order local absorbing conditions for the wave equation: Extensions and improvements
Journal of Computational Physics 2008 ,227 :3322 -3357
DOI
URL
[本文引用: 3]
[15]
Guddati MN Tassoulas JL . Continued-fraction absorbing boundary conditions for the wave equation
Journal of Computational Acoustics 2000 ,8 (1 ):139 -156
DOI
URL
[本文引用: 2]
[16]
Guddati MN Heidari AH . Migration with arbitrary wide-angle wave equations
Geophysics 2005 ,70 (3 ):1 -10
[本文引用: 4]
[17]
Lindman EL . "Free-space" boundary conditions for the time dependent wave equation
Journal of Computational Physics 1975 ,18 :66 -78
DOI
URL
[本文引用: 3]
[18]
Peng CB Toksöz MN . An optimal absorbing boundary condition for finite-difference modeling of acoustic and elastic wave propagation
Journal of the Acoustical Society of America 1994 ,95 (2 ):733 -745
DOI
URL
[本文引用: 2]
[19]
Randall CJ . Absorbing boundary condition for the elastic wave equation
Geophysics 1988 ,53 (5 ):611 -624
DOI
URL
[本文引用: 2]
[20]
Liu Y Sen MK . An improved hybrid absorbing boundary condition for wave equation modeling
Journal of Geophysics and Engineering 2018 ,15 :2602 -2613
DOI
URL
[本文引用: 2]
[21]
徐世刚 , 刘洋 . 基于优化有限差分和混合吸收边界条件的三维VTI介质声波和弹性波数值模拟
地球物理学报 , 2018 ,61 (7 ):2950 -2968
[本文引用: 3]
(Xu Shigang Liu Yang . 3D acoustic and elastic VTI modeling with optimal finite-difference schemes and hybrid absorbing boundary conditions
Chinese Journal of Geophysics 2018 ,61 (7 ):2950 -2968 (in Chinese))
[本文引用: 3]
[22]
Cheng NY Cheng CH . Relationship between Liao and Clayton-Engquist absorbing boundary conditions: Acoustic case
Bulletin of the Seismological Society of America 1995 ,85 (3 ):954 -956
[本文引用: 2]
[23]
高毅超 , 徐艳杰 , 金峰 . 基于高阶双渐近透射边界的重力坝-层状地基动力相互作用分析
地球物理学报 , 2019 ,62 (7 ):2582 -2590
[本文引用: 1]
(Gao Yichao Xu Yanjie Jin Feng . The dynamic analysis of gravity dam-layered foundation interaction based on a high-order double asymptotic open boundary
Chinese Journal of Geophysics 2019 ,62 (7 ):2582 -2590 (in Chinese))
[本文引用: 1]
[24]
吴利华 , 赵密 , 杜修力 . 黏弹性多层介质中SH波动的一种吸收边界条件
力学学报 , 2020 ,52 (2 ):480 -490
[本文引用: 1]
(Wu Lihua Zhao Mi Du Xiuli . An absorbing boundary condition for SH wave propagation in viscoelastic multilayered media
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (2 ):480 -490 (in Chinese))
[本文引用: 1]
[25]
Cerjan C Kosloff D Kosloff R , et al . A nonreflecting boundary condition for discrete acoustic and elastic wave equations
Geophysics 1985 ,50 (4 ):705 -708
DOI
URL
[本文引用: 2]
[26]
Yang JB Yu FM Michael K , et al . The Perfectly Matched Layer absorbing boundary for fluid--structure interactions using the Immersed Finite Element Method
Journal of Fluids and Structures 2018 ,76 :135 -152
DOI
URL
[本文引用: 2]
[27]
Higdon RL . Absorbing boundary conditions for elastic waves
Geophysics 1991 ,56 (2 ):231 -241
DOI
URL
[本文引用: 1]
[28]
Liao ZP . Extrapolation non-reflecting boundary conditions
Wave Motion 1996 ,24 :117 -138
DOI
URL
[本文引用: 1]
[29]
李小军 , 廖振鹏 . 时域局部透射边界的计算飘移失稳
力学学报 , 1996 ,28 (5 ):627 -632
[本文引用: 2]
(Li Xiaojun Liao Zhenpeng . The drift instability of local transmitting boundary in time domain
Chinese Journal of Theoretical and Applied Mechanics 1996 ,28 (5 ):627 -632 (in Chinese))
[本文引用: 2]
[30]
周正华 , 廖振鹏 . 消除多次透射公式飘移失稳的措施
力学学报 , 2001 ,33 (4 ):550 -554
[本文引用: 2]
(Zhou Zhenghua Liao Zhenpeng . A measure for eliminating drift instability of the multi-transmitting formula
Chinese Journal of Theoretical and Applied Mechanics 2001 ,33 (4 ):550 -554 (in Chinese))
[本文引用: 2]
[31]
陈少林 , 廖振鹏 . 多次透射公式在衰减波场中的实现
地震学报 , 2003 ,25 (3 ):272 -280
[本文引用: 2]
(Chen Shaolin Liao Zhenpeng . Multi-transmitting formula for attenuating waves
Acta Seismologica Sinica 2003 ,25 (3 ):272 -280 (in Chinese))
[本文引用: 2]
[32]
Bayliss A Turkel E . Radiation boundary conditions for wave-like equations
Communications on Pure and Applied Mathematics 1980 ,XXXIII :707 -725
[本文引用: 1]
[33]
Reynolds AC . Boundary conditions for the numerical solution of wave propagation problems
Geophysics 1978 ,43 (6 ):1099 -1110
DOI
URL
[本文引用: 1]
[34]
Keys RG . Absorbing boundary conditions for acoustic media
Geophysics 1985 ,50 (6 ):892 -902
DOI
URL
[本文引用: 1]
[35]
Fuyuki M Matsumoto Y . Finite difference analysis of Rayleigh wave scattering at a trench
Bulletin of the Seismological Society of America 1980 ,70 (6 ):2051 -2069
[本文引用: 4]
[36]
Emerman SH Stephen RA . Comment on "Absorbing boundary conditions for acoustic and elastic wave equations," by R. Clayton and E. Engquist
Bulletin of the Seismological Society of America 1983 ,73 (2 ):661 -665
[本文引用: 3]
[37]
Stacey R . Improved transparent boundary formulations for the elastic-wave equation
Bulletin of the Seismological Society of America 1988 ,78 (6 ):2089 -2097
[本文引用: 3]
[38]
Bécache E Givoli D Hagstrom T . High-order absorbing boundary conditions for anisotropic and convective wave equations
Journal of Computational Physics 2010 ,229 :1099 -1129
DOI
URL
[本文引用: 1]
[39]
Kausel E . Local transmitting boundaries
Journal of Engineering Mechanics 1988 ,114 (6 ):1011 -1027
DOI
URL
[本文引用: 1]
[40]
吴利华 , 赵密 , 杜修力 . 黏弹性多层介质中SH波动的一种吸收边界条件
力学学报 , 2020 ,52 (2 ):480 -490
[本文引用: 1]
(Wu Lihua Zhao Mi Du Xiuli . An absorbing boundary condition for SH wave propagation in viscoelastic multilayered media
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (2 ):480 -490 (in Chinese))
[本文引用: 1]
[41]
李述涛 , 刘晶波 , 宝鑫 . 采用黏弹性人工边界单元时显式算法稳定性的改善研究
力学学报 , 2020 ,52 (6 ):1838 -1849
[本文引用: 1]
(Li Shutao Liu Jingbo Bao Xin . Improvement of explicit algorithms stability with visco-elastic artificial boundary elements
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (6 ):1838 -1849 (in Chinese))
[本文引用: 1]
[42]
陈少林 , 柯小飞 , 张洪翔 . 海洋地震工程流固耦合问题统一计算框架
力学学报 , 2019 ,51 (2 ):594 -606
[本文引用: 1]
(Chen Shaolin Ke Xiaofei Zhang Hongxiang . A unified computational framework for fluid-solid coupling in marine earthquake engineering
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):594 -606 (in Chinese))
[本文引用: 1]
[43]
陈少林 , 孙杰 , 柯小飞 . 平面波输入下海水-海床-结构动力相互作用分析
力学学报 , 2020 ,52 (2 ):578 -590
[本文引用: 1]
(Chen Shaolin Sun Jie Ke Xiaofei . Analysis of water-seabed-structure dynamic interaction excited by plane waves
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (2 ):578 -590 (in Chinese))
[本文引用: 1]
弱形式时域完美匹配层 —— 滞弹性近场波动数值模拟
2
2019
... 自20世纪60年代以来, 已有大量人工边界条件(artificial boundary condition, ABC)被学者和工程师们所提出, 文献[1 ,2 ]对它们作了较为系统的介绍. 对于数量众多的ABC, 如何有效掌握并在不同问题中进行选用已成为一个突出的实际问题. 一直以来关于各个特定ABC的应用及探讨较多, 而从整体上针对ABC理论与公式体系的系统性研究[3 ] 则相对较少. 这不仅导致较为复杂的新近研究成果不易被理解及吸收, 甚至对于一些简单且有着广泛应用的经典人工边界条件, 也仍然存在认识方面的不足. ...
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
弱形式时域完美匹配层 —— 滞弹性近场波动数值模拟
2
2019
... 自20世纪60年代以来, 已有大量人工边界条件(artificial boundary condition, ABC)被学者和工程师们所提出, 文献[1 ,2 ]对它们作了较为系统的介绍. 对于数量众多的ABC, 如何有效掌握并在不同问题中进行选用已成为一个突出的实际问题. 一直以来关于各个特定ABC的应用及探讨较多, 而从整体上针对ABC理论与公式体系的系统性研究[3 ] 则相对较少. 这不仅导致较为复杂的新近研究成果不易被理解及吸收, 甚至对于一些简单且有着广泛应用的经典人工边界条件, 也仍然存在认识方面的不足. ...
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
Stable high-order absorbing boundary condition based on new continued fraction for scalar wave propagation in unbounded multilayer media
2
2018
... 自20世纪60年代以来, 已有大量人工边界条件(artificial boundary condition, ABC)被学者和工程师们所提出, 文献[1 ,2 ]对它们作了较为系统的介绍. 对于数量众多的ABC, 如何有效掌握并在不同问题中进行选用已成为一个突出的实际问题. 一直以来关于各个特定ABC的应用及探讨较多, 而从整体上针对ABC理论与公式体系的系统性研究[3 ] 则相对较少. 这不仅导致较为复杂的新近研究成果不易被理解及吸收, 甚至对于一些简单且有着广泛应用的经典人工边界条件, 也仍然存在认识方面的不足. ...
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
Comparison of artificial absorbing boundaries for acoustic wave equation modeling
1
2017
... 自20世纪60年代以来, 已有大量人工边界条件(artificial boundary condition, ABC)被学者和工程师们所提出, 文献[1 ,2 ]对它们作了较为系统的介绍. 对于数量众多的ABC, 如何有效掌握并在不同问题中进行选用已成为一个突出的实际问题. 一直以来关于各个特定ABC的应用及探讨较多, 而从整体上针对ABC理论与公式体系的系统性研究[3 ] 则相对较少. 这不仅导致较为复杂的新近研究成果不易被理解及吸收, 甚至对于一些简单且有着广泛应用的经典人工边界条件, 也仍然存在认识方面的不足. ...
An incrementation-adaptive multi-transmitting boundary for seismic fracture analysis of concrete gravity dams
2
2018
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
Spectral-element formulation of multi-transmitting formula and its accuracy and stability in 1D and 2D seismic wave modeling
0
2021
透射边界条件在波动谱元模拟中的实现: 二维波动
1
2017
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
透射边界条件在波动谱元模拟中的实现: 二维波动
1
2017
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
Obstacle identification using the TRAC algorithm with a second order ABC
4
2019
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 旁轴近似边界主要为经典的Clayton-Engquist声波和弹性波边界(CE边界)[7 ] 、Halpern-Trefethen大角度 单向波动方程[8 ] 、 以及Fuyuki-Matsumoto (FM)[35 ] 、Emerman-Stephen (ES)[36 ] 、Stacey[37 ] 对CE弹性波边界的改进. ...
... 对于弹性波旁轴近似边界, 作者分析发现它们缺乏严格的理论基础, 难以达到较好的精度. 由于弹性波方程不能由其频散关系唯一地确定, 旁轴近似技术实际上无法用于推导弹性波边界. Clayton和Engquist[7 ] 仅通过粗略地模仿声波边界给出了如下弹性波边界($z$轴负向) ...
... 以一个均匀介质声波问题算例来检验上述外推型ABC的精度. 模型尺度为200 m$\times$500 m, 介质波速为$c = 500$ m/s. 顶面为自由边界, 左、右、底边界为人工边界. 在顶部中点施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[9 ] . 网格尺寸为2 m$\times$2 m, 时间步长满足稳定条件$c\Delta t/\Delta x \leqslant 0.71$. 人工边界分别采用本文提出的外推型ABC基本公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及现有的Clayton-Engquist (CE)旁轴近似边界[7 ] 、辅助变量高阶边界Givoli-Neta(GN)[11 ] 、Hagstrom-Warburton(HW)[13 ] 和AWWE[16 ] . 本文ABC的数值离散格式见附录. ...
Wide-angle one-way wave equations
3
1988
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 旁轴近似边界主要为经典的Clayton-Engquist声波和弹性波边界(CE边界)[7 ] 、Halpern-Trefethen大角度 单向波动方程[8 ] 、 以及Fuyuki-Matsumoto (FM)[35 ] 、Emerman-Stephen (ES)[36 ] 、Stacey[37 ] 对CE弹性波边界的改进. ...
... 其中$c$为声波波速, $p_{0}$和$p_{2}$为不同边界的控制参数, 具体见文献[8 ]. 容易验证, 在式(2)的二阶形式中引入声波方程$c^{2}(\partial^{2}u/\partial x^{2}+\partial^{2}u/\partial z^{2}) = \partial ^{2}u/\partial t^{2}$, 将关于$z$的二阶偏导用关于$x$和$t$的二阶偏导所替换, 就导出了式(11). 式(2)中参数$c_{\rm a1}$, $c_{\rm a2}$与式(11)中参数$p_{0}$, $p_{2}$存在如下对应关系: $p_{0} = (1+\alpha_{1}\alpha_{2})/( \alpha_{1}+\alpha_{2})$, $p_{2} =\alpha_{1}\alpha _{2}/(\alpha_{1}+\alpha_{2})$, 其中$\alpha_{1} =c_{\rm a1}/c$, $\alpha_{2} = c_{\rm a2}/c$. ...
Absorbing boundary conditions for difference approximations to the multi-dimensional wave equation
7
1986
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
... Higdon边界对于声波和弹性波分别具有不同形式, 它们基于整体坐标$x$, $y$或$z$给出, 且根据外行波沿坐标的正、负方向传播而有所不同. 式(2)可以视为这些现有Higdon边界公式的统一形式. 理由如下: 考虑到边界参数取值的任意性, 现有Higdon边界的声波和弹性波形式实际上是一致的[9 -10 ] ; 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$, 在推算人工边界节点运动时结果并无差异; 同样, 统一考虑$s$轴指向内域, 与考虑$s$轴指向外域亦具有相同效果, Higdon[27 ] 对此已有结论. 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$还有一个优势, 就是$s$轴可以不与整体坐标轴平行. 式(2)使得现有Higdon边界针对不同方向边界分别给出表达式再进行数值离散的做法得到大大简化, 它略去了不必要的冗余, 回归到时空外推的本质. ...
... 由于证明1和证明2都建立在基本的数学原理之上, 证明过程中并未涉及任何波动方程, 所以$c_{{\rm a}j}$-MTF与$c_{{\rm a}j}$-Higdon边界的等价性是普遍存在的. 这远远强于已有研究所指出的Higdon边界或MTF边界与Clayton-Engquist声波边界之间的相似性[9 ,22 ] . 这种等价性将离散$c_{{\rm a}j}$-MTF边界与连续$c_{{\rm a}j}$-Higdon边界紧密联系在一起, 在讨论和应用中二者通常可以互相替换. ...
... 对于声波旁轴近似边界, Higdon[9 ] 已证明它们可以由Higdon边界结合声波方程来导出. 以外法向为$z$轴负向的边界为例, 考虑二阶情形, CE和Halpern-Trefethen所提出的各种二阶声波边界表达形式为 ...
... 连续边界公式(2)是Higdon边界的统一形式. Higdon边界所采用的多个单向波动微分算子乘积形式是从满足边界要求的一系列离散表达式中总结而来的[9 ] . 这表明连续边界公式(2)的理论源头可以追溯到离散边界公式(1), 即上述MTF边界的时空外推原理. 因此, 外推型人工边界条件具有统一的思想基础, 它来源于离散边界. 各种微分方程形式的连续边界主要为外推型ABC提供了丰富的变化形式. ...
... 以一个均匀介质声波问题算例来检验上述外推型ABC的精度. 模型尺度为200 m$\times$500 m, 介质波速为$c = 500$ m/s. 顶面为自由边界, 左、右、底边界为人工边界. 在顶部中点施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[9 ] . 网格尺寸为2 m$\times$2 m, 时间步长满足稳定条件$c\Delta t/\Delta x \leqslant 0.71$. 人工边界分别采用本文提出的外推型ABC基本公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及现有的Clayton-Engquist (CE)旁轴近似边界[7 ] 、辅助变量高阶边界Givoli-Neta(GN)[11 ] 、Hagstrom-Warburton(HW)[13 ] 和AWWE[16 ] . 本文ABC的数值离散格式见附录. ...
Radiation boundary conditions for elastic wave propagation
2
1990
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Higdon边界对于声波和弹性波分别具有不同形式, 它们基于整体坐标$x$, $y$或$z$给出, 且根据外行波沿坐标的正、负方向传播而有所不同. 式(2)可以视为这些现有Higdon边界公式的统一形式. 理由如下: 考虑到边界参数取值的任意性, 现有Higdon边界的声波和弹性波形式实际上是一致的[9 -10 ] ; 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$, 在推算人工边界节点运动时结果并无差异; 同样, 统一考虑$s$轴指向内域, 与考虑$s$轴指向外域亦具有相同效果, Higdon[27 ] 对此已有结论. 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$还有一个优势, 就是$s$轴可以不与整体坐标轴平行. 式(2)使得现有Higdon边界针对不同方向边界分别给出表达式再进行数值离散的做法得到大大简化, 它略去了不必要的冗余, 回归到时空外推的本质. ...
High-order non-reflecting boundary scheme for time-dependent waves
5
2003
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 针对高阶Higdon边界数值离散比较困难的问题, Givoli-Neta等[11 -12 ] 、 Hagstrom-Warburton等[13 -14 ] 分别提出一种可顺利离散至任意阶次的辅助变量高阶边界(G-N边界和H-W边界). 这两种边界都是先给出一个与Higdon边界等价的辅助变量递推关系, 再引入声波方程将递推关系中的边界法向导数转换为切向导数, 得到只含有边界切向导数和时间导数的辅助变量递推关系, 形成实用的高阶边界. 由于声波方程的引入, 这两种为声波边界. ...
... G-N边界表达式见文献[11 ,12 ], 它所使用的辅助变量递推关系为 ...
... 以一个均匀介质声波问题算例来检验上述外推型ABC的精度. 模型尺度为200 m$\times$500 m, 介质波速为$c = 500$ m/s. 顶面为自由边界, 左、右、底边界为人工边界. 在顶部中点施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[9 ] . 网格尺寸为2 m$\times$2 m, 时间步长满足稳定条件$c\Delta t/\Delta x \leqslant 0.71$. 人工边界分别采用本文提出的外推型ABC基本公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及现有的Clayton-Engquist (CE)旁轴近似边界[7 ] 、辅助变量高阶边界Givoli-Neta(GN)[11 ] 、Hagstrom-Warburton(HW)[13 ] 和AWWE[16 ] . 本文ABC的数值离散格式见附录. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
Finite-element analysis of time-dependent semi-infinite wave-guides with high-order boundary treatment
3
2003
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 针对高阶Higdon边界数值离散比较困难的问题, Givoli-Neta等[11 -12 ] 、 Hagstrom-Warburton等[13 -14 ] 分别提出一种可顺利离散至任意阶次的辅助变量高阶边界(G-N边界和H-W边界). 这两种边界都是先给出一个与Higdon边界等价的辅助变量递推关系, 再引入声波方程将递推关系中的边界法向导数转换为切向导数, 得到只含有边界切向导数和时间导数的辅助变量递推关系, 形成实用的高阶边界. 由于声波方程的引入, 这两种为声波边界. ...
... G-N边界表达式见文献[11 ,12 ], 它所使用的辅助变量递推关系为 ...
A new auxiliary variable formulation of high-order local radiation boundary conditions: Corner compatibility conditions and extensions to first-order systems
4
2004
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 针对高阶Higdon边界数值离散比较困难的问题, Givoli-Neta等[11 -12 ] 、 Hagstrom-Warburton等[13 -14 ] 分别提出一种可顺利离散至任意阶次的辅助变量高阶边界(G-N边界和H-W边界). 这两种边界都是先给出一个与Higdon边界等价的辅助变量递推关系, 再引入声波方程将递推关系中的边界法向导数转换为切向导数, 得到只含有边界切向导数和时间导数的辅助变量递推关系, 形成实用的高阶边界. 由于声波方程的引入, 这两种为声波边界. ...
... H-W边界表达式见文献[13 ,14 ], 它基于的辅助变量递推关系为 ...
... 以一个均匀介质声波问题算例来检验上述外推型ABC的精度. 模型尺度为200 m$\times$500 m, 介质波速为$c = 500$ m/s. 顶面为自由边界, 左、右、底边界为人工边界. 在顶部中点施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[9 ] . 网格尺寸为2 m$\times$2 m, 时间步长满足稳定条件$c\Delta t/\Delta x \leqslant 0.71$. 人工边界分别采用本文提出的外推型ABC基本公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及现有的Clayton-Engquist (CE)旁轴近似边界[7 ] 、辅助变量高阶边界Givoli-Neta(GN)[11 ] 、Hagstrom-Warburton(HW)[13 ] 和AWWE[16 ] . 本文ABC的数值离散格式见附录. ...
High-order local absorbing conditions for the wave equation: Extensions and improvements
3
2008
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... 针对高阶Higdon边界数值离散比较困难的问题, Givoli-Neta等[11 -12 ] 、 Hagstrom-Warburton等[13 -14 ] 分别提出一种可顺利离散至任意阶次的辅助变量高阶边界(G-N边界和H-W边界). 这两种边界都是先给出一个与Higdon边界等价的辅助变量递推关系, 再引入声波方程将递推关系中的边界法向导数转换为切向导数, 得到只含有边界切向导数和时间导数的辅助变量递推关系, 形成实用的高阶边界. 由于声波方程的引入, 这两种为声波边界. ...
... H-W边界表达式见文献[13 ,14 ], 它基于的辅助变量递推关系为 ...
Continued-fraction absorbing boundary conditions for the wave equation
2
2000
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Guddati等[15 -16 ] 提出一种矩阵形式的辅助变量高阶边界AWWE, 他们通过两种方式导出这种边界: 一是将声波方程的旁轴近似递推关系按偶数阶提取出来, 将其写成矩阵形式, 再返回到时域成为人工边界条件; 二是将半无限介质分层, 利用各层动力刚度的有限单元近似, 在频域内导出矩阵关系式, 进而返回时域得到人工边界条件. 根据本文第3.2节所指出的声波旁轴近似边界可以由$c_{{\rm a}j}$-Higdon边界与声波方程相结合得到, 可以推断出1, 2, 3, $\cdots$ 阶AWWE边界分别对应于2, 4, 6, $\cdots$ 阶$c_{{\rm a}j}$-Higdon边界, 即存在2$N$倍关系. AWWE边界与$c_{{\rm a}j}$-Higdon边界的等价中间形式为 ...
Migration with arbitrary wide-angle wave equations
4
2005
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Guddati等[15 -16 ] 提出一种矩阵形式的辅助变量高阶边界AWWE, 他们通过两种方式导出这种边界: 一是将声波方程的旁轴近似递推关系按偶数阶提取出来, 将其写成矩阵形式, 再返回到时域成为人工边界条件; 二是将半无限介质分层, 利用各层动力刚度的有限单元近似, 在频域内导出矩阵关系式, 进而返回时域得到人工边界条件. 根据本文第3.2节所指出的声波旁轴近似边界可以由$c_{{\rm a}j}$-Higdon边界与声波方程相结合得到, 可以推断出1, 2, 3, $\cdots$ 阶AWWE边界分别对应于2, 4, 6, $\cdots$ 阶$c_{{\rm a}j}$-Higdon边界, 即存在2$N$倍关系. AWWE边界与$c_{{\rm a}j}$-Higdon边界的等价中间形式为 ...
... 以一个均匀介质声波问题算例来检验上述外推型ABC的精度. 模型尺度为200 m$\times$500 m, 介质波速为$c = 500$ m/s. 顶面为自由边界, 左、右、底边界为人工边界. 在顶部中点施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[9 ] . 网格尺寸为2 m$\times$2 m, 时间步长满足稳定条件$c\Delta t/\Delta x \leqslant 0.71$. 人工边界分别采用本文提出的外推型ABC基本公式$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及现有的Clayton-Engquist (CE)旁轴近似边界[7 ] 、辅助变量高阶边界Givoli-Neta(GN)[11 ] 、Hagstrom-Warburton(HW)[13 ] 和AWWE[16 ] . 本文ABC的数值离散格式见附录. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
"Free-space" boundary conditions for the time dependent wave equation
3
1975
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Lindman[17 ] 提出一种数值优化边界, 表达式见文献[17 ]. Kausel[39 ] 证明了该边界的连续形式为一种高阶旁轴近似边界, 与Clayton-Engquist声波边界属于一个类型. ...
... 提出一种数值优化边界, 表达式见文献[17 ]. Kausel[39 ] 证明了该边界的连续形式为一种高阶旁轴近似边界, 与Clayton-Engquist声波边界属于一个类型. ...
An optimal absorbing boundary condition for finite-difference modeling of acoustic and elastic wave propagation
2
1994
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Peng-Toksöz[18 ] 提出另一种数值优化边界, 表达式为 ...
Absorbing boundary condition for the elastic wave equation
2
1988
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Randall[19 ] 针对弹性波边界精度不高的问题, 提出一种将弹性波场进行势分解, 对分解出来的波势函数分别使用高精度的Lindman声波边界, 再将结果合成为弹性波场的方法. 弹性波场向势函数的分解与合成分别表示为 ...
An improved hybrid absorbing boundary condition for wave equation modeling
2
2018
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Liu和Sen[20 -21 ] 将外推型ABC与过渡区技术相结合, 发展出一套混合边界方法, 如图4 所示. 该方法在计算模型的外边界附近设置一定宽度的过渡区, 过渡区波场由内域离散格式和边界数值格式分别计算的波场进行加权和得到. 二者权系数之和始终为1, 其分配比例沿着过渡区宽度的变化如图中三角形所示. ...
基于优化有限差分和混合吸收边界条件的三维VTI介质声波和弹性波数值模拟
3
2018
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Liu和Sen[20 -21 ] 将外推型ABC与过渡区技术相结合, 发展出一套混合边界方法, 如图4 所示. 该方法在计算模型的外边界附近设置一定宽度的过渡区, 过渡区波场由内域离散格式和边界数值格式分别计算的波场进行加权和得到. 二者权系数之和始终为1, 其分配比例沿着过渡区宽度的变化如图中三角形所示. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
基于优化有限差分和混合吸收边界条件的三维VTI介质声波和弹性波数值模拟
3
2018
... 廖氏透射边界[4 -6 ] 是中国学者在人工边界领域做出的重要成果. 它采用等距离散点的外推公式(Newton-Gregory公式)来推算任意人工边界节点在各个时刻的运动. 廖振鹏等将该边界条件与"误差波多次透射"的物理机制联系起来, 据此命名为"多次透射公式" (multi-transmitting formula, MTF), 也可称为廖氏透射边界. MTF以简洁的离散表达式来描述任意外行波的一般传播过程, 完美地将严格的数学公式和清楚的物理机制融合在一起, 其基本思想和表达形式均具有普适性. 在廖振鹏等的工作基础上, 作者经过理论分析和波动模拟实践发现, MTF边界的上述特征实际上奠定了一大类人工边界条件的思想和公式基础. 本文将这类边界称为外推型人工边界条件, 其特点是人工边界节点在每一时刻的运动, 直接由一组临近离散网格点在前若干时刻的运动进行时空外推得到. 具有时空外推特点的人工边界条件除了MTF之外, 主要包括经典的旁轴近似边界[7 -8 ] 、Higdon边界[9 -10 ] 、 Givoli-Neta等[11 -12 ] 的辅助变量高阶边界、Hagstrom等[13 -14 ] 的辅助变量高阶边界、 Guddati等[15 -16 ] 的任意大角度波动方程(arbitrarily wide-angle wave equations, AWWE)、Lindman数值优化边界[17 ] 、Peng-Toksöz数值优化边界[18 ] , 以及Randall势分解方法[19 ] 、Liu-Sen混合边界方法[20 -21 ] 等. 这些边界使用相同的控制参数(边界阶次和一组计算波速), 通过某种等价的中间形式相联系, 并且在数值模拟中表现出相似的精度和稳定性. ...
... Liu和Sen[20 -21 ] 将外推型ABC与过渡区技术相结合, 发展出一套混合边界方法, 如图4 所示. 该方法在计算模型的外边界附近设置一定宽度的过渡区, 过渡区波场由内域离散格式和边界数值格式分别计算的波场进行加权和得到. 二者权系数之和始终为1, 其分配比例沿着过渡区宽度的变化如图中三角形所示. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
Relationship between Liao and Clayton-Engquist absorbing boundary conditions: Acoustic case
2
1995
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
... 由于证明1和证明2都建立在基本的数学原理之上, 证明过程中并未涉及任何波动方程, 所以$c_{{\rm a}j}$-MTF与$c_{{\rm a}j}$-Higdon边界的等价性是普遍存在的. 这远远强于已有研究所指出的Higdon边界或MTF边界与Clayton-Engquist声波边界之间的相似性[9 ,22 ] . 这种等价性将离散$c_{{\rm a}j}$-MTF边界与连续$c_{{\rm a}j}$-Higdon边界紧密联系在一起, 在讨论和应用中二者通常可以互相替换. ...
基于高阶双渐近透射边界的重力坝-层状地基动力相互作用分析
1
2019
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
基于高阶双渐近透射边界的重力坝-层状地基动力相互作用分析
1
2019
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
黏弹性多层介质中SH波动的一种吸收边界条件
1
2020
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
黏弹性多层介质中SH波动的一种吸收边界条件
1
2020
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
A nonreflecting boundary condition for discrete acoustic and elastic wave equations
2
1985
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
The Perfectly Matched Layer absorbing boundary for fluid--structure interactions using the Immersed Finite Element Method
2
2018
... 现有研究虽然早已指出MTF边界和经典的Clayton-Engquist旁轴近似边界以及Higdon边界存在密切联系[9 ,22 ] , 但是在讨论和应用中仍然将它们视作不同的人工边界条件. 由于上述边界至今尚未被归并到一个理论框架当中, 导致对于它们的理论联系以及与精度和稳定性相关的诸多应用问题还缺乏系统性认识, 如: 表达形式与波动类型、内域离散格式、几何构型的无关性, 边界阶次和计算波速参数对边界精度的控制原理, 独立的边界离散格式所导致的稳定性问题等. 这不利于该类人工边界条件的研究成果的相互借鉴和进一步发展与应用. 另外值得指出的是, 真正与上述边界在表达形式、数值离散格式、精度控制原理以及稳定性各个方面都存在显著不同的是另外两大类人工边界条件, 分别为以黏性边界、黏弹性边界等为代表的应力型边界[2 ,23 -24 ] 和以函数衰减层、完美匹配层等为代表的衰减层型边界[1 ,25 -26 ] . ...
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
Absorbing boundary conditions for elastic waves
1
1991
... Higdon边界对于声波和弹性波分别具有不同形式, 它们基于整体坐标$x$, $y$或$z$给出, 且根据外行波沿坐标的正、负方向传播而有所不同. 式(2)可以视为这些现有Higdon边界公式的统一形式. 理由如下: 考虑到边界参数取值的任意性, 现有Higdon边界的声波和弹性波形式实际上是一致的[9 -10 ] ; 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$, 在推算人工边界节点运动时结果并无差异; 同样, 统一考虑$s$轴指向内域, 与考虑$s$轴指向外域亦具有相同效果, Higdon[27 ] 对此已有结论. 用统一局部坐标的空间轴$s$代替整体坐标$x$, $y$或$z$还有一个优势, 就是$s$轴可以不与整体坐标轴平行. 式(2)使得现有Higdon边界针对不同方向边界分别给出表达式再进行数值离散的做法得到大大简化, 它略去了不必要的冗余, 回归到时空外推的本质. ...
Extrapolation non-reflecting boundary conditions
1
1996
... 式(1)给出的多人工波速离散边界表达式无法单独从传统廖氏透射边界理论导出, 其借鉴了Higdon边界的计算波速设置. 式(2)给出的简洁而统一的连续边界表达式同样无法单独从现有Higdon边界导出, 其得益于廖氏透射边界思想和参数的引入. Liao[28 ] 曾指出过廖氏透射边界与Higdon边界的这种互补性. ...
时域局部透射边界的计算飘移失稳
2
1996
... 在消除高阶外推型ABC的计算漂移失稳[29 ] 和处理强衰减外行波方面具有重要价值. ...
... 设计如图11 所示的纵、横向不均匀介质场地模型, 检验本文边界条件的吸收效果. 该模型为右下方整块基岩与左侧、上部成层土体形成的复杂场地, 岩土体参数如图所示. 在($x, z) =$ (300 m, 100 m)处节点的竖向分量上施加中心频率为10 Hz的Ricker子波激励. 上部为自由地表, 其余3边分别采用自由边界(作为对照)或本文提出的人工边界, 进行两组模拟. 采用集中质量有限元与中心差分相结合的数值模拟方法[29 -30 ] . 单元尺寸为2.5 m$\times$2.5 m, 时间步长满足稳定条件$\sqrt {c_{\rm s}^{2} +c_{\rm p}^{2} } \Delta t/\Delta x\leqslant 1$. ...
时域局部透射边界的计算飘移失稳
2
1996
... 在消除高阶外推型ABC的计算漂移失稳[29 ] 和处理强衰减外行波方面具有重要价值. ...
... 设计如图11 所示的纵、横向不均匀介质场地模型, 检验本文边界条件的吸收效果. 该模型为右下方整块基岩与左侧、上部成层土体形成的复杂场地, 岩土体参数如图所示. 在($x, z) =$ (300 m, 100 m)处节点的竖向分量上施加中心频率为10 Hz的Ricker子波激励. 上部为自由地表, 其余3边分别采用自由边界(作为对照)或本文提出的人工边界, 进行两组模拟. 采用集中质量有限元与中心差分相结合的数值模拟方法[29 -30 ] . 单元尺寸为2.5 m$\times$2.5 m, 时间步长满足稳定条件$\sqrt {c_{\rm s}^{2} +c_{\rm p}^{2} } \Delta t/\Delta x\leqslant 1$. ...
消除多次透射公式飘移失稳的措施
2
2001
... 周正华和廖振鹏[30 ] 指出添加小量在物理上考虑了介质的几何扩散特性或引入了介质的阻尼特性. 可认为这两种物理特性对应于同一种数学机制, 即考虑了波场的衰减性. 由此不难得出, 陈少林和廖振鹏[31 ] 所提出的衰减波场MTF、以及Bayliss和Turkel[32 ] 针对柱面波或 球面波扩散问题(即外行波含有显著的几何衰减)而提出的边界表达式, 分别与式(3)、式(4)在形式上具有一致性. ...
... 设计如图11 所示的纵、横向不均匀介质场地模型, 检验本文边界条件的吸收效果. 该模型为右下方整块基岩与左侧、上部成层土体形成的复杂场地, 岩土体参数如图所示. 在($x, z) =$ (300 m, 100 m)处节点的竖向分量上施加中心频率为10 Hz的Ricker子波激励. 上部为自由地表, 其余3边分别采用自由边界(作为对照)或本文提出的人工边界, 进行两组模拟. 采用集中质量有限元与中心差分相结合的数值模拟方法[29 -30 ] . 单元尺寸为2.5 m$\times$2.5 m, 时间步长满足稳定条件$\sqrt {c_{\rm s}^{2} +c_{\rm p}^{2} } \Delta t/\Delta x\leqslant 1$. ...
消除多次透射公式飘移失稳的措施
2
2001
... 周正华和廖振鹏[30 ] 指出添加小量在物理上考虑了介质的几何扩散特性或引入了介质的阻尼特性. 可认为这两种物理特性对应于同一种数学机制, 即考虑了波场的衰减性. 由此不难得出, 陈少林和廖振鹏[31 ] 所提出的衰减波场MTF、以及Bayliss和Turkel[32 ] 针对柱面波或 球面波扩散问题(即外行波含有显著的几何衰减)而提出的边界表达式, 分别与式(3)、式(4)在形式上具有一致性. ...
... 设计如图11 所示的纵、横向不均匀介质场地模型, 检验本文边界条件的吸收效果. 该模型为右下方整块基岩与左侧、上部成层土体形成的复杂场地, 岩土体参数如图所示. 在($x, z) =$ (300 m, 100 m)处节点的竖向分量上施加中心频率为10 Hz的Ricker子波激励. 上部为自由地表, 其余3边分别采用自由边界(作为对照)或本文提出的人工边界, 进行两组模拟. 采用集中质量有限元与中心差分相结合的数值模拟方法[29 -30 ] . 单元尺寸为2.5 m$\times$2.5 m, 时间步长满足稳定条件$\sqrt {c_{\rm s}^{2} +c_{\rm p}^{2} } \Delta t/\Delta x\leqslant 1$. ...
多次透射公式在衰减波场中的实现
2
2003
... 周正华和廖振鹏[30 ] 指出添加小量在物理上考虑了介质的几何扩散特性或引入了介质的阻尼特性. 可认为这两种物理特性对应于同一种数学机制, 即考虑了波场的衰减性. 由此不难得出, 陈少林和廖振鹏[31 ] 所提出的衰减波场MTF、以及Bayliss和Turkel[32 ] 针对柱面波或 球面波扩散问题(即外行波含有显著的几何衰减)而提出的边界表达式, 分别与式(3)、式(4)在形式上具有一致性. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
多次透射公式在衰减波场中的实现
2
2003
... 周正华和廖振鹏[30 ] 指出添加小量在物理上考虑了介质的几何扩散特性或引入了介质的阻尼特性. 可认为这两种物理特性对应于同一种数学机制, 即考虑了波场的衰减性. 由此不难得出, 陈少林和廖振鹏[31 ] 所提出的衰减波场MTF、以及Bayliss和Turkel[32 ] 针对柱面波或 球面波扩散问题(即外行波含有显著的几何衰减)而提出的边界表达式, 分别与式(3)、式(4)在形式上具有一致性. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
Radiation boundary conditions for wave-like equations
1
1980
... 周正华和廖振鹏[30 ] 指出添加小量在物理上考虑了介质的几何扩散特性或引入了介质的阻尼特性. 可认为这两种物理特性对应于同一种数学机制, 即考虑了波场的衰减性. 由此不难得出, 陈少林和廖振鹏[31 ] 所提出的衰减波场MTF、以及Bayliss和Turkel[32 ] 针对柱面波或 球面波扩散问题(即外行波含有显著的几何衰减)而提出的边界表达式, 分别与式(3)、式(4)在形式上具有一致性. ...
Boundary conditions for the numerical solution of wave propagation problems
1
1978
... Reynolds[33 ] 和Keys[34 ] 各自独立提出了一种ABC. 以外法向为$x$轴负向的边界为例, 其表达式分别为 ...
Absorbing boundary conditions for acoustic media
1
1985
... Reynolds[33 ] 和Keys[34 ] 各自独立提出了一种ABC. 以外法向为$x$轴负向的边界为例, 其表达式分别为 ...
Finite difference analysis of Rayleigh wave scattering at a trench
4
1980
... 旁轴近似边界主要为经典的Clayton-Engquist声波和弹性波边界(CE边界)[7 ] 、Halpern-Trefethen大角度 单向波动方程[8 ] 、 以及Fuyuki-Matsumoto (FM)[35 ] 、Emerman-Stephen (ES)[36 ] 、Stacey[37 ] 对CE弹性波边界的改进. ...
... 然而, 式(12)既无法从旁轴近似角度进行解释, 也无法由$c_{{\rm a}j}$-Higdon边界结合弹性波方程导出. Fuyuki和Matsumoto[35 ] 、Emerman和Stephen[36 ] 、Stacey[37 ] 在式(12)基础上所做的改进并未解决这一问题. 数值试验表明这些边界精度较差. 为了从理论上揭示所谓的旁轴近似弹性波边界的不合理性, 在波数平面上绘出了CE, FM, ES和Stacey弹性波边界的频散曲线, 如图3 所示. 作为对比, 图中还给出了声波边界(11)的频散曲线, A1, A2, A3分别表示一阶、二阶、三阶声波边界. ...
... 以一个均匀介质弹性波问题算例来进一步检验上述外推型ABC的性能. 模型尺度为2500 m $\times$2500 m, 介质纵、横波速为$c_{\rm p} = 2000$ m/s, $c_{\rm s} = 1000$ m/s. 四边均为人工边界. 在模型中心施加中心频率为10 Hz的Ricker子波激励. 计算模型的空间、时间离散均采用标准的二阶中心差分格式[35 ] . 网格尺寸为5 m$\times$5 m, 时间步长满足稳定条件 $\sqrt{c_{\rm s}^{2}+c_{\rm p}^{2}}\cdot$ $\Delta t/\Delta x\leqslant 1$. 人工边界分别采用$c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon, 以及第3.2节提及的几种弹性波旁轴近似边界. 此时附录A中的边界离散格式分别用于人工边界节点的水平和竖向波场分量. ...
... 外推型ABC模拟复杂介质的效果已被现有文献给出的各种波动问题模拟结果所证实, 如文献[4 ]混凝土坝开裂模拟中的边界处理, 文献[11 ]中频散介质波动模拟, 文献[16 ]对力学性质渐变介质的反演, 文献[21 ]对三维VTI介质的波动过程正演, 文献[31 ]中适用于两相介质波动问题的边界, 文献[35 ]对Rayleigh波边界的探讨等. 在本文建立的外推型人工边界条件理论与公式体系中, 这些复杂波动过程的绝大多数特征已得到充分考虑, 具体为: (1) 多种人工波速的参数配置能够很好地考虑由多种物理波速 (包括弹性波、两相介质波动、频散波动、介质交界面等)以及不同透射角度所决定的沿外推型ABC计算方向视传播速度的复杂性; (2) 由几何扩散、阻尼效应或其他原因引起的波场的衰减性, 可以由添加小量修正的边界表达式(3)和式(4)很好地模拟, 或者只是单纯地将边界(1)和边界(2)的阶次提得足够高, 也能够达到满意精度(其原理参考图5 ); (3) 对于角点、介质交界面、曲线边界等不同几何构型的适应性, $c_{{\rm a}j}$-MTF和$c_{{\rm a}j}$-Higdon可以无差别地应用, 因为它们只涉及到一条由边界节点指向内域的离散网格线上的信息, 与边界形状无关, 而其他外推型ABC若涉及到边界本身的信息, 则会受到边界几何构型的制约. 除了上述特征之外, 在不同复杂波动问题中是否还存在其他影响边界精度的重要因素, 如多种波动成分之间的耦合效应等, 将在后续工作中具体探讨. ...
Comment on "Absorbing boundary conditions for acoustic and elastic wave equations," by R. Clayton and E. Engquist
3
1983
... 旁轴近似边界主要为经典的Clayton-Engquist声波和弹性波边界(CE边界)[7 ] 、Halpern-Trefethen大角度 单向波动方程[8 ] 、 以及Fuyuki-Matsumoto (FM)[35 ] 、Emerman-Stephen (ES)[36 ] 、Stacey[37 ] 对CE弹性波边界的改进. ...
... 然而, 式(12)既无法从旁轴近似角度进行解释, 也无法由$c_{{\rm a}j}$-Higdon边界结合弹性波方程导出. Fuyuki和Matsumoto[35 ] 、Emerman和Stephen[36 ] 、Stacey[37 ] 在式(12)基础上所做的改进并未解决这一问题. 数值试验表明这些边界精度较差. 为了从理论上揭示所谓的旁轴近似弹性波边界的不合理性, 在波数平面上绘出了CE, FM, ES和Stacey弹性波边界的频散曲线, 如图3 所示. 作为对比, 图中还给出了声波边界(11)的频散曲线, A1, A2, A3分别表示一阶、二阶、三阶声波边界. ...
... 图10 中$c_{{\rm a}j}$-MTF边界模拟结果证明了对于多物理波速的复杂波动问题采用多人工波速外推型ABC的必要性及优势(第4.3节). 此时3种单一人工波速的二阶$c_{{\rm a}j}$-MTF均不能很好地实现对P波和S波的同步透射, 而多人工波速($c_{\rm s}$, $c_{\rm p})$方案几乎完美地实现了这一目标. 与基本边界$c_{{\rm a}j}$-MTF相比, 所谓的弹性波旁轴近似边界反射量很大, 这对应了图3 关于这几个弹性波边界理论上具有不合理性的分析结果. Clayton-Engquist和Fuyuki-Matsumoto (它与前者高度相似) 边界出现失稳, Emerman-Stephen和Stacey边界(文献[36 ,37 ]指出它们改善了CE弹性波边界的稳定性)以及本文提出的$c_{{\rm a}j}$-MTF边界在20 s长持时模拟结果中保持了稳定. 因此, 综合考虑精度与稳定性, 模拟弹性波的外推型ABC建议采用基本边界公式$c_{{\rm a}j}$-MTF或$c_{{\rm a}j}$-Higdon. ...
Improved transparent boundary formulations for the elastic-wave equation
3
1988
... 旁轴近似边界主要为经典的Clayton-Engquist声波和弹性波边界(CE边界)[7 ] 、Halpern-Trefethen大角度 单向波动方程[8 ] 、 以及Fuyuki-Matsumoto (FM)[35 ] 、Emerman-Stephen (ES)[36 ] 、Stacey[37 ] 对CE弹性波边界的改进. ...
... 然而, 式(12)既无法从旁轴近似角度进行解释, 也无法由$c_{{\rm a}j}$-Higdon边界结合弹性波方程导出. Fuyuki和Matsumoto[35 ] 、Emerman和Stephen[36 ] 、Stacey[37 ] 在式(12)基础上所做的改进并未解决这一问题. 数值试验表明这些边界精度较差. 为了从理论上揭示所谓的旁轴近似弹性波边界的不合理性, 在波数平面上绘出了CE, FM, ES和Stacey弹性波边界的频散曲线, 如图3 所示. 作为对比, 图中还给出了声波边界(11)的频散曲线, A1, A2, A3分别表示一阶、二阶、三阶声波边界. ...
... 图10 中$c_{{\rm a}j}$-MTF边界模拟结果证明了对于多物理波速的复杂波动问题采用多人工波速外推型ABC的必要性及优势(第4.3节). 此时3种单一人工波速的二阶$c_{{\rm a}j}$-MTF均不能很好地实现对P波和S波的同步透射, 而多人工波速($c_{\rm s}$, $c_{\rm p})$方案几乎完美地实现了这一目标. 与基本边界$c_{{\rm a}j}$-MTF相比, 所谓的弹性波旁轴近似边界反射量很大, 这对应了图3 关于这几个弹性波边界理论上具有不合理性的分析结果. Clayton-Engquist和Fuyuki-Matsumoto (它与前者高度相似) 边界出现失稳, Emerman-Stephen和Stacey边界(文献[36 ,37 ]指出它们改善了CE弹性波边界的稳定性)以及本文提出的$c_{{\rm a}j}$-MTF边界在20 s长持时模拟结果中保持了稳定. 因此, 综合考虑精度与稳定性, 模拟弹性波的外推型ABC建议采用基本边界公式$c_{{\rm a}j}$-MTF或$c_{{\rm a}j}$-Higdon. ...
High-order absorbing boundary conditions for anisotropic and convective wave equations
1
2010
... Bécache等[38 ] 经过推导, 证明式(15)的合并形式为 ...
Local transmitting boundaries
1
1988
... Lindman[17 ] 提出一种数值优化边界, 表达式见文献[17 ]. Kausel[39 ] 证明了该边界的连续形式为一种高阶旁轴近似边界, 与Clayton-Engquist声波边界属于一个类型. ...
黏弹性多层介质中SH波动的一种吸收边界条件
1
2020
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
黏弹性多层介质中SH波动的一种吸收边界条件
1
2020
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
采用黏弹性人工边界单元时显式算法稳定性的改善研究
1
2020
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
采用黏弹性人工边界单元时显式算法稳定性的改善研究
1
2020
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
海洋地震工程流固耦合问题统一计算框架
1
2019
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
海洋地震工程流固耦合问题统一计算框架
1
2019
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
平面波输入下海水-海床-结构动力相互作用分析
1
2020
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...
平面波输入下海水-海床-结构动力相互作用分析
1
2020
... (3) 真正与外推型ABC不同类型的是以黏性边界、黏弹性边界等为代表的应力型边界[40 -41 ] 和以函数衰减层、完美匹配层等为代表的衰减层 型边界[25 -26 ] . 在后续研究和应用中, 外推型ABC[42 -43 ] 的稳定性、高阶应力型边界或完美匹配层边界应用于不同波动问题的实现方式与计算效率、融合不同方法的人工边界 问题综合性解决方案等, 都是值得继续探讨并更好地解决的重要问题. ...