引言
拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] .
但由于制造方式、加工过程及环境、设备和操作等因素的影响, 通过增材制造成型的结构件易出现制造缺陷[12 -14 ] . 制造缺陷使得结构件成型精度降低、表面粗糙度大, 进而导致结构件表面材料分布不均匀, 引起表面层异质[15 ] . 表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性, 致使结构性能偏离设计、达不到预期目标. 然而, 当前大多数拓扑优化方法的研究是基于确定性的参数开展, 忽略了不确定因素对结构性能的影响, 导致优化后的构型不一定是最优的或者不符合实际, 严重影响结构的安全性. 因此在拓扑优化设计中, 考虑不确定因素对结构构型的影响是十分重要的.
一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差.
研究结构表面层异质引起的表面层厚度不确定性, 需要解决两个关键问题: (1)准确识别结构表面层; (2)对不确定性进行传播分析和随机响应估计. 本文建立了考虑表面层厚度不确定性的拓扑优化模型, 采用基于腐蚀操作的表面层识别技术, 实现了表面层异质等效模型的建立. 基于摄动有限元法开展了不确定性传播的分析和系统随机响应的预测, 并推导了目标函数关于设计变量的敏度信息. 通过数值算例证实了考虑表面层厚度不确定性的必要性及本方法的有效性.
1 基于腐蚀操作的结构表面层识别技术
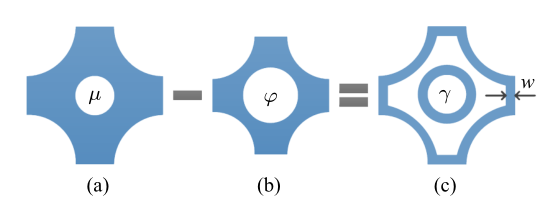
如何准确地对结构表面层进行建模, 通常是基于密度的拓扑优化方法中较为困难的问题. Clausen等[25 ] 采用基于两步过滤的操作, 以较大的空间密度梯度识别了结构的表面层, 并成功应用于基于密度的拓扑优化问题[26 -27 ] . 本文采用一种基于腐蚀操作的表面层识别技术[28 ] 建立表面层异质的等效模型. 其主要思想是: 首先对图1 (a)所示的初始结构进行腐蚀操作, 得到图1 (b)所示规模缩减后的被腐蚀结构; 然后将初始结构与被腐蚀结构的不同部分, 即图1 (c)所示的被腐蚀掉的部分, 定义为结构表面层.
图1
图1
基于腐蚀操作的表面层识别方法的基本思想
Fig.1
Basic idea of the erosion-based interface identification method
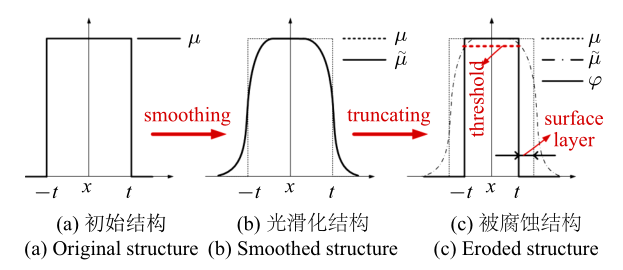
腐蚀操作通过光滑过滤和离散映射两个过程来实现. 其中, 光滑过滤使得初始结构场光滑连续; 离散映射使用一个较大的阈值, 将光滑化的结构场进行截断, 得到被腐蚀后的结构, 进而识别出结构表面层. 图2 给出了一维情况下腐蚀操作的一般过程(文中腐蚀操作的所有参数都用下标e标记).
图2
图2
一维情况下腐蚀操作的一般过程
Fig.2
1D example of the general process of the erosion operation
本文中, 首先使用基于Helmholtz偏微分方程的密度过滤[29 -30 ] —— PDE技术[31 ] , 对初始结构场$\mu $进行光滑化处理
(1) $\begin{eqnarray} \label{eq1} -r_{\rm e}^{2} \nabla^{2}\tilde{{\mu }}+\tilde{{\mu }}=\mu \end{eqnarray}$
式中 $\tilde{{\mu }}$表示经过光滑化后的结构场, $r_{\rm e} $是长度参数, 且与标准的过滤半径$R_{\rm e} $之间满足: $r_{\rm e} =R_{\rm e} /2\sqrt 3 $.
然后, 选取一个较大的阈值$\eta_{\rm e} $, 采用基于Heaviside过滤[20 ,32 ] 和tanh函数的离散映射[33 ] 对光滑化后的结构场$\tilde{{\mu }}$进行截断,得到被腐蚀后的结构场$\varphi $
(2) $\begin{eqnarray} \label{eq2} \varphi =\frac{\tanh (\beta_{\rm e} \eta_{\rm e} )+\tanh [\beta_{\rm e} (\tilde{{\mu }}-\eta_{\rm e} )]}{\tanh (\beta_{\rm e} \eta_{\rm e} )+\tanh [\beta_{\rm e} (1-\eta _{\rm e} )]} \end{eqnarray}$
式中 $\beta_{\rm e} $为映射函数的锐度, 阈值$\eta_{\rm e} =0.5+\Delta \eta _{\rm e} $通过引入$\Delta \eta_{\rm e} \in (0,0.5)$来定义.
基于上述光滑过滤和离散映射的腐蚀操作, 可以将厚度均匀可控的结构表面层$\gamma $识别出来. 表面层厚度$w$与过滤半径$R_{\rm e} $、阈值$\Delta \eta_{\rm e} $之间满足如下关系
(3) $\begin{eqnarray} \label{eq3} w=-\frac{R_{\rm e} }{2\sqrt 3 }\ln (1-2\Delta \eta_{\rm e} ) \end{eqnarray}$
式中, 通过合理选取$R_{\rm e} $和$\Delta \eta_{\rm e}$的值即可实现对表面层厚度$w$的精确控制. 本文采取的策略是固定$\Delta \eta _{\rm e} $的值, 通过改变$R_{\rm e} $的值来控制$w$. 为了得到$w$和$R_{\rm e} $更规整的近似关系, 文中算例依据经验$\Delta \eta_{\rm e} $均取值为0.45, 此时$R_{\rm e} \approx 1.50w$. (3)式的详细理论推导参见文献[28 ]. 在此基础上, 物理密度和刚度的插值函数可以定义为
(4) $\begin{eqnarray} \label{eq4} &&\rho (\mu ,\varphi )=\mu [\varphi \rho_{\rm b} +(1-\varphi )\rho_{\rm s} ] \end{eqnarray}$
(5) $\begin{eqnarray} \label{eq5} E(\mu ,\varphi )=\mu^{p}[\varphi^{p}E_{\rm b} +(1-\varphi^{p})E_{\rm s} ] \end{eqnarray}$
式中 $\rho_{\rm b} $, $E_{\rm b} $, $\rho_{\rm s} $, $E_{\rm s} $分别表示基体和表面层的材料性质, $p$为惩罚因子, 一般取值为3. 当$\mu =1$且$\varphi =1$时, 描述结构的基体部分; 当$\mu =1$且$\varphi =0$时, 描述结构表面层; 当$\mu =0$时, 表示结构为空.
2 基于摄动有限元的稳健性拓扑优化设计
2.1 摄动有限元法及系统随机响应估计
随机有限元法是将随机分析理论与有限元方法相结合的数值分析方法. 其中, 基于摄动开展的随机有限元法得到了广泛的应用[18 ,34 -35 ] . 其基本思想是: 引入一个零均值的微小摄动量$\Delta \xi $, 来描述随机变量$\xi $在其均值$\xi_{0} $处产生微小摄动所引起的不确定性, 那么随机变量$\xi $可以表示为
(6) $\begin{eqnarray} \xi =\xi_{0} +\Delta \xi \end{eqnarray}$
若假设系统发生准静态线弹性行为, 且不确定性仅存在于某些结构参数(如几何形状、材料性质)中, 而外荷载是确定的, 那么有限元平衡方程可以写作
(7) $\begin{eqnarray} \label{eq7} K(\xi )u(\xi )=f \end{eqnarray}$
式中$K(\xi )$和$u(\xi )$分别表示与随机变量$\xi$相关的刚度矩阵和位移响应向量. 在$\xi_{0} $处对$K(\xi )$和$u(\xi )$进行二阶Taylor展开
(8) $\begin{eqnarray} \label{eq8} &&K(\xi )=K_{0} +\sum\limits_i {K_{i} } \Delta \xi_{i} +\frac{1}{2}\sum\limits_i {\sum\limits_j {K_{ij} } } \Delta \xi_{i} \Delta \xi_{j}\end{eqnarray}$
(9) $\boldsymbol{u}(\xi)=\boldsymbol{u}_{0}+\sum_{i} \boldsymbol{u}_{i} \Delta \xi_{i}+\frac{1}{2} \sum_{i} \sum_{j} \boldsymbol{u}_{i j} \Delta \xi_{i} \Delta \xi_{j}$
式中$K_{0} =K(\xi_{0} )$, $u_{0} =u(\xi_{0} )$且$K_{i} $, $K_{ij}$, $u_{i} $, $u_{ij}$为$K$和$u$在$\xi_{0} $处对随机变量$\xi$的一阶、二阶偏导数. 将式(8)、式(9)代入式(7), 忽略$\Delta \xi $的高阶小量同时合并同阶项, 可以得到
(10) $\left.\begin{array}{l}\boldsymbol{K}_{0} \boldsymbol{u}_{0}=\boldsymbol{f} \\\boldsymbol{K}_{0} \boldsymbol{u}_{i}=-\boldsymbol{K}_{i} \boldsymbol{u}_{0} \\\boldsymbol{K}_{0} \boldsymbol{u}_{i j}=-\boldsymbol{K}_{i} \boldsymbol{u}_{j}-\boldsymbol{K}_{j} \boldsymbol{u}_{i}-\boldsymbol{K}_{i j} \boldsymbol{u}_{0}\end{array}\right\}$
通过按自上而下的顺序求解方程组(10), 可以得到由式(9)表示的位移响应$u$的二阶近似表达. 若$\Delta \xi $服从正态分布, 那么位移响应$u$的均值及协方差的二阶近似估计表示为
(11) $\begin{eqnarray} \label{eq11} &&E[u]=\bar{{u}}=u_{0} +\frac{1}{2}\sum\limits_i {\sum\limits_j {u_{ij} } } \sigma_{ij}\end{eqnarray}$
(12) $\begin{array}{l}\operatorname{Cov}[\boldsymbol{u}]=\sum_{i} \sum_{j} \boldsymbol{u}_{i} \boldsymbol{u}_{j}^{\mathrm{T}} \sigma_{i j}+ \\\frac{1}{4} \sum_{i} \sum_{j} \sum_{k} \sum_{l} \boldsymbol{u}_{i j} \boldsymbol{u}_{k l}^{\mathrm{T}}\left(\sigma_{i k} \sigma_{j l}+\sigma_{i l} \sigma_{j k}\right)\end{array}$
式中 $\sigma_{ij} =E[\Delta \xi_{i} \Delta \xi_{j} ]$表示$\Delta \xi $的二阶统计矩.
2.2 考虑表面层厚度不确定的稳健性拓扑优化方法
本文考虑静力学拓扑优化中的最小柔顺性设计问题, 即在确定的外载荷下, 给定有限体积的材料, 设计得到储存应变能最小的结构拓扑, 优化列式可以描述为
(13) $\left.\begin{array}{cc}\min\limits _{\rho_{e}} & c=u^{\mathrm{T}} \boldsymbol{K} \boldsymbol{u} \\\text { s.t. } & \boldsymbol{K} u=f \\& V-\nabla \leqslant 0 \\& 0 \leqslant \rho_{\mathrm{e}} \leqslant 1\end{array}\right\}$
式中, 设计变量$\rho_{\rm e} $是表示每个单元的密度, $c$表示结构的柔顺性, $K$, $u$, $f$分别表示结构的总体刚度矩阵、位移向量和外载荷向量, $V$和$\bar{{V}}$分别表示结构所用材料的体积和给定的体积上限.
本文第1节中, 通过基于腐蚀操作的表面层识别技术, 对厚度为$w$的结构表面层进行了建模. 本节中以表面层厚度$w$为随机变量, 根据摄动有限元法的思想, 引入一个均值为、标准差为$\sigma $且服从高斯分布的微小摄动量$\delta $, 对表面层厚度的不确定性进行建模. 稳健性拓扑优化设计旨在优化结构的性能, 并且最小化其对不确定因素的敏感程度. 那么, 考虑表面层厚度不确定性的稳健性拓扑优化列式可以描述为
(14) $\left.\begin{array}{ll}\min\limits _{\rho_{\mathrm{e}}} & \hat{c}=E[c]+\alpha S t d[c] \\\text { s.t. } & K(\delta) u(\delta)=f \\& \sum\limits_{i=1}^{\text {Nele }} \rho_{i} v_{\mathrm{e}} \leqslant f r a c \sum \limits_{i=1}^{\text {Nele }} v_{\mathrm{e}} \\& 0 \leqslant \rho_{\mathrm{e}} \leqslant 1\end{array}\right\}$
式中 $\hat{{c}}$是稳健性拓扑优化问题的目标函数, 表示为结构柔顺性的均值$E[c]$和标准差$Std[c]$的加权和形式, $\alpha $为权系数. $K(\delta )$和$u(\delta )$分别为与微小摄动量$\delta $相关的刚度矩阵和位移响应向量, $Nele$为单元数量, $v_{\rm e} $为每个单元的体积, $frac$为体积分数.
那么, 结构柔顺性均值$E[c]$、方差$Var[c]$的近似估计可以表示为
(15) $\begin{eqnarray} \label{eq14} && E[c]=f^{\rm T}E[u]=f^{\rm T}u^{(0)}+\sigma u^{(1)\rm T}K^{(0)}u^{(1)}- \\&&\qquad\frac{1}{2}\sigma u^{(0)\rm T}K^{(2)}u^{(0)}\end{eqnarray}$
(16) $\begin{eqnarray} \label{eq15} Var[c]=Var[f^{\rm T}u]=f^{\rm T}Cov[u]f=\sigma f^{\rm T}u^{(1)}u^{(1)\rm T}f \end{eqnarray}$
式中 $[\cdot ]^{(0)}$, $[\cdot ]^{(1)}$, $[\cdot ]^{(2)}$分别表示变量$[\cdot]$经过摄动分析后所获得的零阶、一阶及二阶信息.
而结构柔顺性的标准差$Std[c]$与方差$Var[c]$之间满足$Std[c]=\sqrt {Var[c]} $. 本文采用梯度类算法MMA[36 ] 求解优化问题, 基于伴随法求解敏度, 通过选择合适的伴随向量, 可以消除敏度信息中含${\partial u^{(0)}}/{\partial \rho_{\rm e} }$和${\partial u^{(1)}}/{\partial \rho_{\rm e}}$的项[18 ] . 那么, 目标函数关于设计变量的敏度信息可以表示为
(17) $\begin{eqnarray} \label{eq17} \frac{\partial \hat{{c}}}{\partial \rho_{\rm e} }=\frac{\partial E[c]}{\partial \rho_{\rm e} }+\alpha \frac{\partial Std[c]}{\partial \rho_{\rm e} } \end{eqnarray}$
(18) $\frac{\partial E[c]}{\partial \rho_{\mathrm{e}}}=-u_{\mathrm{e}}^{(0) \mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(0)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(0)}-\zeta_{\mathrm{e}}^{\mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(0)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(0)}-\sigma * \\ \begin{array}{l}\left(u_{\mathrm{e}}^{(1) \mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(0)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(1)}+2 u_{\mathrm{e}}^{(1) \mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(1)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(0)}+\right. \\\left.\frac{1}{2} u_{\mathrm{e}}^{(0) \mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(2)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(0)}\right)\end{array}$
(19) $\begin{array}{c}\frac{\partial S t d[c]}{\partial \rho_{\mathrm{e}}}=-\frac{1}{S t d[c]} \sigma f^{\mathrm{T}} \boldsymbol{u}^{(1)} * \\\left(2 u_{\mathrm{e}}^{(0) \mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(0)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(1)}+u_{\mathrm{e}}^{(0) \mathrm{T}} \frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(1)}}{\partial \rho_{\mathrm{e}}} u_{\mathrm{e}}^{(0)}\right)\end{array}$
式中 $\zeta $为对位移向量进行摄动展开时二阶系数的总和, 满足关系$K_{\rm e}^{(0)} \zeta_{\rm e} =-\sigma \left( {2K_{\rm e}^{(1)} u_{\rm e}^{(1)} +K_{\rm e}^{(2)} u_{\rm e}^{(0)} } \right)$. 而${\partial K_{\rm e}^{(0)} }/{\partial \rho_{\rm e} }$, ${\partial K_{\rm e}^{(1)} }/{\partial \rho_{\rm e} }$, ${\partial K_{\rm e}^{(2)} }/{\partial \rho_{\rm e} }$可分别表示为
(20) $\left.\begin{array}{l}\frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(0)}}{\partial \rho_{\mathrm{e}}}=\sum_{i} \frac{\partial E_{i}^{(0)}}{\partial \rho_{\mathrm{e}}} \boldsymbol{k}^{0} \\\frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(1)}}{\partial \rho_{\mathrm{e}}}=\sum_{i} \frac{\partial E_{i}^{(1)}}{\partial \rho_{\mathrm{e}}} \boldsymbol{k}^{0}=\sum_{i} \frac{\partial}{\partial \rho_{\mathrm{e}}}\left(\frac{\partial E_{i}^{(0)}}{\partial \delta}\right) \boldsymbol{k}^{0} \\\frac{\partial \boldsymbol{K}_{\mathrm{e}}^{(2)}}{\partial \rho_{\mathrm{e}}}=\sum_{i} \frac{\partial E_{i}^{(2)}}{\partial \rho_{\mathrm{e}}} \boldsymbol{k}^{0}=\sum_{i} \frac{\partial}{\partial \rho_{\mathrm{e}}}\left(\frac{\partial^{2} E_{i}^{(0)}}{\partial \delta^{2}}\right) \boldsymbol{k}^{0}\end{array}\right\}$
式中$k^{0}$表示单位杨氏模量下的单元刚度阵. 而刚度插值函数对设计变量及摄动量的偏导数${\partial E_{i}^{(0)} }/{\partial \rho_{\rm e} }$, ${\partial E_{i}^{(0)} }/{\partial \delta }$, ${\partial^{2}E_{i}^{(0)} }/{\partial \delta^{2}}$可进一步表示为
(21) $\left.\begin{array}{l}\frac{\partial E_{i}^{(0)}}{\partial \rho_{\mathrm{e}}}=p \mu_{i}^{p-1}\left[\varphi_{i}^{p} E_{\mathrm{b}}+\left(1-\varphi_{i}^{p}\right) E_{\mathrm{s}}\right] \frac{\partial \mu_{i}}{\partial \rho_{\mathrm{e}}}+ \\p \mu_{i}^{p} \varphi_{i}^{p-1}\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \frac{\partial \varphi_{i}}{\partial \rho_{\mathrm{e}}} \\\frac{\partial E_{i}^{(0)}}{\partial \delta}=p \mu_{i}^{p} \varphi_{i}^{p-1}\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \frac{\partial \varphi_{i}}{\partial \delta} \\\frac{\partial^{2} E_{i}^{(0)}}{\partial \delta^{2}}=p \mu_{i}^{p}\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) * \\{\left[(p-1) \varphi_{i}^{p-2}\left(\frac{\partial \varphi_{i}}{\partial \delta}\right)^{2}+\varphi_{i}^{p-1} \frac{\partial^{2} \varphi_{i}}{\partial \delta^{2}}\right]}\end{array}\right\}$
将式(21)代入式(20)中, 可得刚度插值函数对摄动量偏导数的最终表达
(22) $\begin{eqnarray} \label{eq22} && \dfrac{\partial }{\partial \rho_{\rm e} }\left( {\dfrac{\partial E_{i}^{(0)} }{\partial \delta }} \right)= p\left( {E_{\rm b} -E_{\rm s} } \right)\dfrac{\partial \left( {\mu_{i}^{p} \varphi_{i}^{p-1} \dfrac{\partial \varphi_{i} }{\partial \delta }} \right)}{\partial \rho_{\rm e} } =\\&&\qquad p\left( {E_{\rm b} -E_{\rm s} } \right)\mu_{i}^{p} \varphi_{i}^{p-1} \dfrac{\partial }{\partial \rho_{\rm e} }(\dfrac{\partial \varphi_{i} }{\partial \delta })+p\left( {E_{\rm b} -E_{\rm s} } \right)\ast \\&&\qquad [P\mu_{i}^{p-1} \varphi_{i}^{p-1} \dfrac{\partial \mu_{i} }{\partial \rho_{\rm e} }+(p-1)\mu_{i}^{p} \varphi_{i}^{p-2} \dfrac{\partial \varphi_{i} }{\partial \rho_{\rm e} }]\dfrac{\partial \varphi_{i} }{\partial \delta }\end{eqnarray}$
(23) $\begin{array}{l}\frac{\partial}{\partial \rho_{\mathrm{e}}}\left(\frac{\partial^{2} E_{i}^{(0)}}{\partial \delta^{2}}\right)=p\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) . \frac{\partial\left(\mu_{i}^{p}\left[(p-1) \varphi_{i}^{p-2}\left(\frac{\partial \varphi_{i}}{\partial \delta}\right)^{2}+\varphi_{i}^{p-1} \frac{\partial^{2} \varphi_{i}}{\partial \delta^{2}}\right]\right)}{\partial \rho_{\mathrm{e}}}= \\p^{2}(p-1)\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \mu_{i}^{p-1} \varphi_{i}^{p-2}\left(\frac{\partial \varphi_{i}}{\partial \delta}\right)^{2} \frac{\partial \mu_{i}}{\partial \rho_{\mathrm{e}}}+ \\p^{2}\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \mu_{i}^{p-1} \varphi_{i}^{p-1} \frac{\partial^{2} \varphi_{i}}{\partial \delta^{2}} \frac{\partial \mu_{i}}{\partial \rho_{\mathrm{e}}}+ \\p(p-1)(p-2)\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \mu_{i}^{p} \varphi_{i}^{p-3}\left(\frac{\partial \varphi_{i}}{\partial \delta}\right)^{2} \frac{\partial \varphi_{i}}{\partial \rho_{\mathrm{e}}}+ \\2 p(p-1)\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \mu_{i}^{p} \varphi_{i}^{p-2} \frac{\partial \varphi_{i}}{\partial \delta} \frac{\partial}{\partial \rho_{\mathrm{e}}}\left(\frac{\partial \varphi_{i}}{\partial \delta}\right)+ \\p(p-1)\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \mu_{i}^{p} \varphi_{i}^{p-2} \frac{\partial^{2} \varphi_{i}}{\partial \delta^{2}} \frac{\partial \varphi_{i}}{\partial \rho_{\mathrm{e}}}+ \\p\left(E_{\mathrm{b}}-E_{\mathrm{s}}\right) \mu_{i}^{p} \varphi_{i}^{p-1} \frac{\partial}{\partial \rho_{\mathrm{e}}}\left(\frac{\partial^{2} \varphi_{i}}{\partial \delta^{2}}\right)\end{array}$
式中, ${\partial \mu_{i} }/{\partial \rho_{\rm e} }$和${\partial \varphi_{i} }/{\partial \rho_{\rm e} }$的推导可参照参考文献[28 ], ${\partial \varphi_{i} }/{\partial \delta }$和${\partial ^{2}\varphi_{i}}/{\partial \delta^{2}}$的推导则同理可得, 此处不做赘述.
3 数值算例
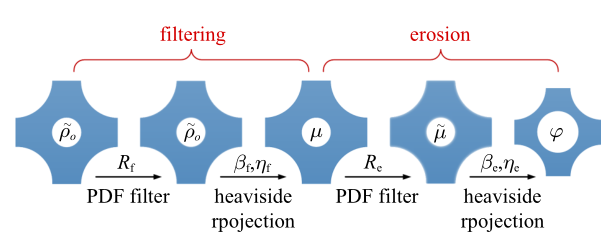
为了避免棋盘效应和网格依赖性对优化结果的影响, 并保证得到0-1分布的结构场, 在识别结构表面层之前, 先后对初始结构场应用了PDE过滤、基于Heaviside过滤和tanh函数的离散映射. 这一过程与基于腐蚀操作的表面层识别几乎相同, 但却实现了不同的功能. 文中将这一过程定义为过滤过程(所有参数都用下标$f$标记),将表面层识别的过程定义为腐蚀过程, 并将过滤过程和腐蚀过程统称为改进的两步过滤法, 其实现流程及控制参数见图3 . 此外, 所有算例都使用鲁棒公式[19 ,21 -22 ] 来实现结构最小尺寸的控制, 控制参数[28 ] 为$\Delta \eta_{\rm f} $; 同时通过域扩展方法[37 ] 保证在结构边界处获得相同的腐蚀厚度.
图3
图3
改进的两步过滤法识别结构表面层
Fig.3
Improved two-step filter process for structure surface layer identification
本文算例中数值为常量的控制参数如下: 惩罚系数$p=3$;
当计算收敛时或每50个迭代步后, 投影锐度$\beta_{\rm e} =\beta_{\rm f} \in (1,20)$变为当前值的1.5倍.
3.1 简支梁算例
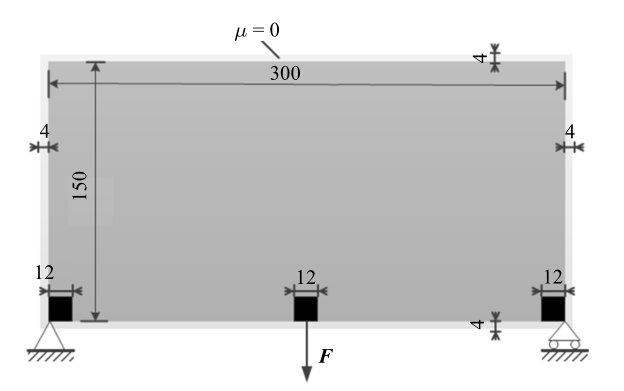
图4 所示为简支梁算例的设计域及边界条件, 结构的几何尺寸为$300\times 150$, 集中力$F=1$. 表面层结构和基体结构的材料属性分别为$\rho_{\rm s} =1$, $E_{\rm s} =1$, $\rho_{\rm b} =0.8$, $E_{\rm b} =0.5$, 即表面层为硬材料, 基体为软材料. 表面层厚度为$w=2$, 其标准差$\sigma =0.3 w$. 过滤过程和腐蚀过程的过滤半径分别取值为$R_{\rm f} =8$, $R_{\rm e} \approx 1.5 w$, 最小尺寸的控制参数$\Delta \eta_{\rm f} =0.1$. 体积分数为40%且每10个迭代步进行一次更新[28 ] . 目标函数中的权系数$\alpha $选取值为4.
图4
图4
简支梁算例的设计域及边界条件
Fig.4
Design domain and boundary conditions of MBB example
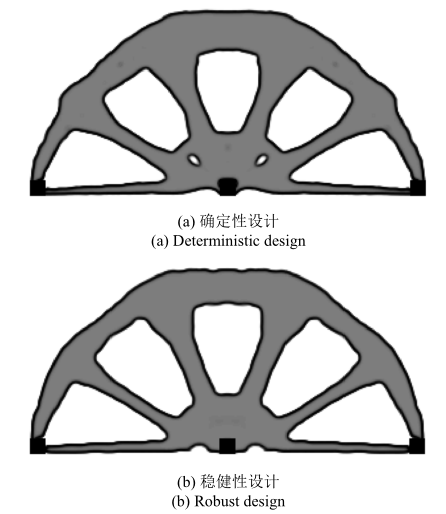
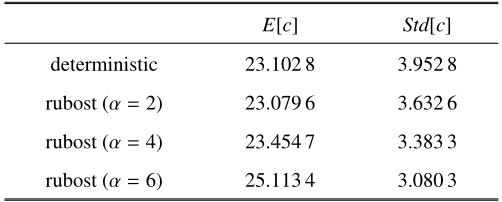
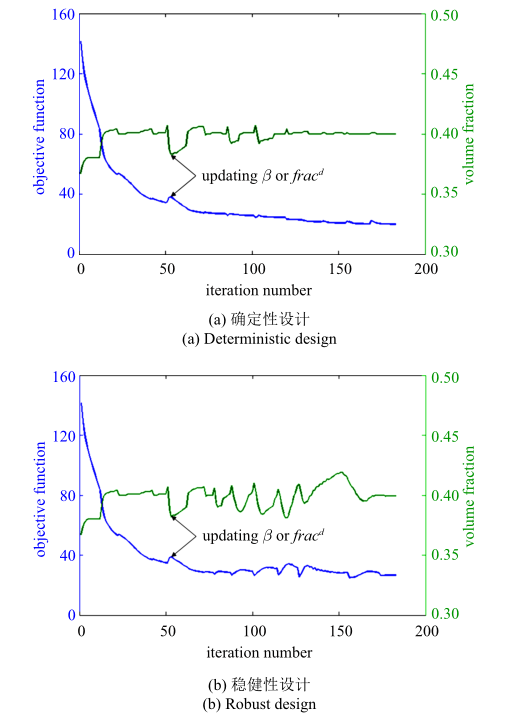
如图5 所示, 简支梁结构的确定性和稳健性拓扑优化结果有着不同的拓扑构型, 相比于确定性设计, 稳健性设计去除了细小孔洞的存在. 不同结果对应的结构柔顺性均值和标准差数值, 列入表1 . 与确定性设计相比($\sigma =3.952\,8$), 稳健性设计($\sigma =3.383\,3$)的标准差较小, 这表明稳健性拓扑优化结果对表面层厚度变化的敏感性更低. 图6 给出了确定性设计和稳健性设计在优化过程中目标函数和体积分数的迭代历史, 最后都达到了稳定收敛.
图5
图5
简支梁算例的拓扑优化结果
Fig.5
Topology optimization results of MBB example
图6
图6
简支梁算例目标函数和体积分数的迭代历史
Fig.6
Convergence history of objective function and volume fraction of MBB example
为了研究目标函数中权系数$\alpha $的取值对拓扑优化结果的影响, 本文比较了当$\alpha $分别取值为2、4、6时, 表1 中列出了稳健性设计下结构柔顺性的均值和标准差的数值, 图7 所示为相对应$\alpha $取不同值时结构柔顺性的均值与标准差的变化趋势. 可以看出结构柔顺性的均值随着权系数$\alpha $的增大而增大, 但其标准差却呈现出相反的变化趋势, 这与双准则优化问题帕累托解的基本特征是吻合的. 同时, 标准差越小反映出结构对不确定因素的敏感程度越低.
图7
图7
权系数$\alpha $取不同值时结构柔顺性的均值与标准差
Fig.7
Mean and standard deviations of compliance for different weighing factor
3.2 悬臂梁算例
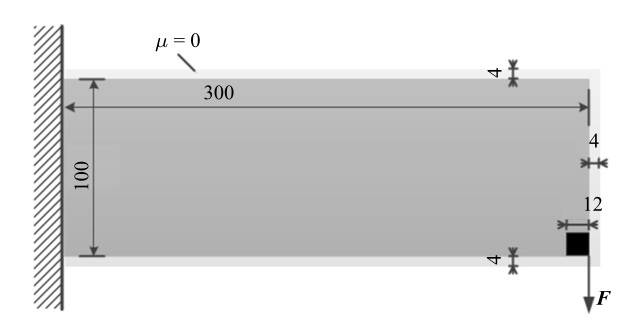
图8 所示为悬臂梁算例的设计域及边界条件, 结构的几何尺寸为$300\times 100$, 集中力$F=1$. 表面层结构和基体结构的材料属性分别为$\rho_{\rm s} =0.7$, $E_{\rm s} =0.4$, $\rho_{\rm b} =1$, $E_{\rm b} =1$, 即表面层为软材料, 基体为硬材料. 表面层厚度为$w=2$, 其标准差$\sigma =0.05 w$. 过滤过程和腐蚀过程的过滤半径分别取值为$R_{\rm f} =8$, $R_{\rm e} \approx 1.5 w$, 最小尺寸的控制参数$\Delta \eta_{\rm f} =0.1$. 体积分数为40%且每10个迭代步进行一次更新. 目标函数中的权系数$\alpha $选取为1.
图8
图8
悬臂梁算例的设计域及边界条件
Fig.8
Design domain and boundary conditions of cantilever beam example
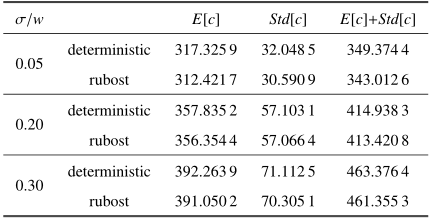
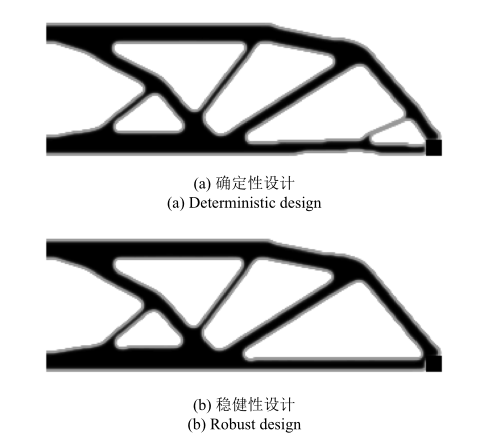
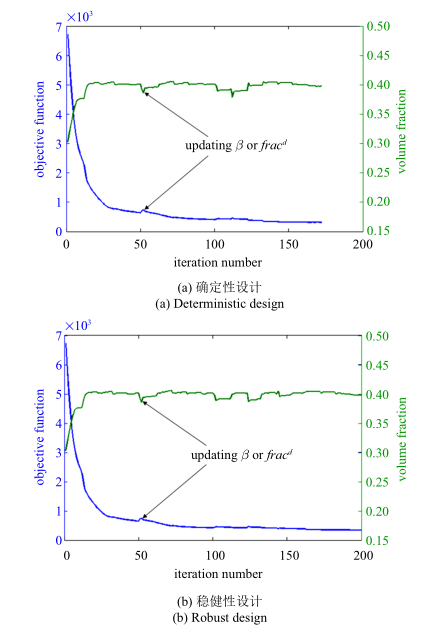
结构的确定性和稳健性拓扑优化结果如图9 所示, 相比于确定性结果, 稳健性结果去除了细小杆件的存在, 且结构表面更为平滑. 表2 所示为$\sigma$取不同值时确定性设计和稳健性设计结果对比. 从表2 可以看出, 稳健性设计的标准差较小, 其均值和标准差的加权和值也更低, 再次验证了稳健性结果在结构整体刚度较高的同时具有更好的抵抗不确定性的能力. 优化过程中目标函数和体积分数的迭代历史如图10 所示, 都达到了稳定收敛.
图9
图9
悬臂梁算例的拓扑优化结果
Fig.9
Topology optimization results of cantilever beam example
本文研究了当表面层厚度标准差取不同值时, 对稳健性拓扑优化结果的影响. 在其他参数保持不变的情况下, $\sigma =0.05w$, $\sigma =0.2w$, $\sigma =0.3w$所对应的稳健性拓扑优化结果分别如图9 (b)、图11 (a)、图11 (b)所示. 可以看出, 当不确定性相对较小($\sigma =0.05w)$时, 稳健性设计与确定性设计有着相似的结构; 而在$\sigma =0.2 w$, $\sigma =0.3 w$的情况下, 稳健性结果与确定性结果在杆件数量、布局等方面具有一定的差异. 3种情况下结构柔顺性的均值和标准差的数据比较见表2 . 数据表明, 任一情况下稳健性设计结果的标准差值、均值和标准差的和值都小于确定性结果, 进一步验证了本文所提出方法的有效性.
图10
图10
悬臂梁算例目标函数和体积分数的迭代历史
Fig.10
Convergence history of objective function and volume fraction of cantilever beam example
图11
图11
$\sigma $取不同值时悬臂梁算例的稳健性拓扑优化结果
Fig.11
Robust topology optimization results of cantilever beam example for different $\sigma $
4 结论
针对增材制造工艺在制备过程中出现的结构表面层异质现象, 本文以结构柔顺性均值和标准差的加权和作为优化目标, 建立了考虑结构表面层厚度不确定的稳健性拓扑优化模型. 采用一种基于腐蚀操作的表面层识别技术对表面层异质进行了等效建模, 并将表面层厚度视为具有给定概率分布特征的随机变量, 通过随机摄动理论开展了不确定性传播分析和系统随机响应预测. 数值算例表明, 所提出的方法能够得到对结构表面层厚度变化不敏感的合理结构, 具有更强的抵抗不确定性的能力. 因此, 对增材制造结构而言, 在拓扑优化设计中考虑表面层厚度不确定性对结构性能的影响具有重要意义.
参考文献
View Option
[1]
Bendsøe MP Kikuchi N . Generating optimal topologies in structural design using a homogenization method
Computer Methods in Applied Mechanics and Engineering 1988 ,71 (2 ):197 -224
DOI
URL
[本文引用: 1]
[2]
Mei YL Wang XM . A level set method for structural topology optimization
Computer Methods in Applied Mechanics and Engineering 2004 ,35 (7 ):415 -441
[本文引用: 1]
[3]
Zuo ZH Xie YM Huang X . Evolutionary topology optimization of structures with multiple displacement and frequency constraints
Advances in Structural Engineering 2012 ,15 (2 ):385 -398
[4]
Zhang WS Yuan J Zhang J , et al . A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model
Structural and Multidisciplinary Optimization 2016 ,53 (6 ):1243 -1260
DOI
URL
[5]
Luo YF Chen WJ Liu ST , et al . A discrete-continuous parameterization (DCP) for concurrent optimization of structural topologies and continuous material orientations
Composite Structures 2020 ,236 :111900
DOI
URL
[本文引用: 1]
[6]
卢秉恒 , 李涤尘 . 增材制造(3D打印)技术发展
机械制造与自动化 , 2013 ,42 (4 ):1 -4
[本文引用: 1]
(Lu Bingheng Li Dichen . Development of the Additive Manufacturing (3D printing) Technology
Machine Building and Automation 2013 ,42 (4 ):1 -4 (in Chinese))
[本文引用: 1]
[7]
汤慧萍 , 王建 , 逯圣路 等 . 电子束选区熔化成形技术研究进展
中国材料进展 , 2015 ,34 (3 ):225 -235
(Tang Huiping Wang Jian Lu Shenglu , et al . Research Progress in Selective Electron Beam Melting
Materials China 2015 ,34 (3 ):225 -235 (in Chinese))
[8]
Javaid M Haleem A . Additive manufacturing applications in medical cases: A literature based review
Alexandria Journal of Medicine 2017 ,54 (4 ):411 -422
DOI
URL
[9]
卢秉恒 . 增材制造技术 —— 现状与未来
中国机械工程 , 2020 ,31 (1 ):19 -23
[本文引用: 1]
(Lu Bingheng . Additive manufacturing - Current situation and future
China Machine Engineering 2020 ,31 (1 ):19 -23 (in Chinese))
[本文引用: 1]
[10]
Meng L Zhang W Quan D , et al . Correction to: From topology optimization design to additive manufacturing: Today's success and tomorrow's roadmap
Archives of Computational Methods in Engineering 2021 ,21 :269
[本文引用: 1]
[11]
Luo YF Sigmund O Li QH , et al . Additive manufacturing oriented topology optimization of structures with self-supported enclosed voids
Computer Methods in Applied Mechanics and Engineering 2020 ,372 :113385
DOI
URL
[本文引用: 1]
[12]
顾冬冬 , 沈以赴 . 基于选区激光融化的金属材料零件快速成形现状与技术展望
航空制造技术 , 2012 (8 ):32 -37
[本文引用: 1]
(Gu Dongdong Shen Yifu . Research status and technical prospect of rapid manufacturing of metallic part by sdective laser meIting
Aeronautical Manufacturing Technology 2012 (8 ):32 -37 (in Chinese))
[本文引用: 1]
[13]
Du W Bai Q Wang Y , et al . Eddy current detection of subsurface defects for additive/subtractive hybrid manufacturing
International Journal of Advanced Manufacturing Technology 2017 ,95 (5-8 ):1 -11
DOI
URL
[14]
Wang JC Cui YN Liu CM , et al . Understanding internal defects in Mo fabricated by wire arc additive manufacturing through 3D computed tomography
Journal of Alloys and Compounds 2020 ,840 :155753
DOI
URL
[本文引用: 1]
[15]
范慧茹 . 考虑表面层异质及其不确定性的增材制造结构拓扑优化方法. [硕士论文]
大连: 大连理工大学 , 2018
[本文引用: 1]
(Fan Huiru . Topology optimization method of additive manufacture structures with surface layer heterogeneity and uncertainty considered. [Master Thesis]
Dalian: Dalian University of Technology , 2018 (in Chinese))
[本文引用: 1]
[16]
Du J Sun C . Reliability-based vibro-acoustic microstructural topology optimization
Structural & Multidiplinary Optimization 2016 ,55 (4 ):1 -21
[本文引用: 1]
[17]
Wang L Xia HJ Zhang XY , et al . Non-probabilistic reliability-based topology optimization of continuum structures considering local stiffness and strength failure
Computer Methods in Applied Mechanics and Engineering 2019 ,346 :788 -809
DOI
[本文引用: 1]
This study presents a novel non-probabilistic reliability-based topology optimization (NRBTO) framework to determine optimal material configurations for continuum structures under local stiffness and strength limits. Uncertainty quantification (UQ) analysis under unknown-but-bounded (UBB) inputs is conducted to determine the feasible bounds of structural responses by combining a material interpolation model with stress aggregation function and interval mathematics. For safety reasons, improved interval reliability indexes that correspond to displacement and stress constraints are applied in topological optimization issues. Meanwhile, an adjoint-vector based sensitivity analysis is further discussed from which the gradient features between reliability measures and design variables are mathematically deduced, and the computational difficulties in large-scale variable updating can be effectively overcome. Numerical examples are eventually given to demonstrate the validity of the developed NRBTO methodology. (C) 2018 Elsevier B.V.
[18]
Asadpoure A Tootkaboni M Guest JK . Robust topology optimization of structures with uncertainties in stiffness-Application to truss structures
Computers and Structures 2011 ,89 (11-12 ):1131 -1141
DOI
URL
[本文引用: 3]
[19]
Sigmund O . Manufacturing tolerant topology optimization
Acta Mechanica Sinica 2009 ,25 (2 ):227 -239
DOI
URL
[本文引用: 2]
[20]
Sigmund O . Morphology-based black and white filters for topology optimization
Structural & Multidisciplinary Optimization 2007 ,33 (4 ):401 -424
[本文引用: 2]
[21]
Wang FW Jensen JS Sigmund O . Robust topology optimization of photonic crystal waveguides with tailored dispersion properties
Journal of the Optical Society of America, B, Optical physics 2011 ,28 (3 ):387 -397
DOI
URL
[本文引用: 2]
[22]
Schevenels M Lazarov BS Sigmund O . Robust topology optimization accounting for spatially varying manufacturing errors
Computer Methods in Applied Mechanics and Engineering 2011 ,200 (49-52 ):3613 -3627
DOI
URL
[本文引用: 2]
[23]
Kang Z Wu CL Luo YJ , et al . Robust topology optimization of multi-material structures considering uncertain graded interface
Composite Structures 2019 ,208 :395 -406
DOI
URL
[本文引用: 1]
[24]
Zheng J Luo Z Jiang C , et al . Robust topology optimization for concurrent design of dynamic structures under hybrid uncertainties
Mechanical Systems and Signal Processing 2019 ,120 :540 -559
DOI
[本文引用: 1]
A new robust topology optimization method based on level sets is developed for the concurrent design of dynamic structures composed of uniform periodic microstructures subject to random and interval hybrid uncertainties. A Hybrid Dimensional Reduction (HDR) method is proposed to estimate the interval mean and the interval variance of the uncertain objective function based on a bivariate dimension reduction scheme. The robust objective function is defined as a weighted sum of the mean and standard variance of the dynamic compliance under the worst case. The sensitivity information of the robust objective function with respect to the macro and micro design variables can then be obtained after the uncertainty analysis. Several examples are used to validate the effectiveness of the proposed robust topology optimization method. (C) 2018 Elsevier Ltd.
[25]
Clausen A Aage N Sigmund O . Topology optimization of coated structures and material interface problems
Computer Methods in Applied Mechanics and Engineering 2015 ,290 :524 -541
DOI
URL
[本文引用: 1]
[26]
Chu S Xiao M Gao L , et al . Topology optimization of multi-material structures with graded interfaces
Computer Methods in Applied Mechanics and Engineering 2019 ,346 :1096 -1117
DOI
URL
[本文引用: 1]
[27]
Luo YF Li QH Liu ST . A projection-based method for topology optimization of structures with graded surfaces
International Journal for Numerical Methods in Engineering 2019 ,118 (11 ):654 -677
DOI
URL
[本文引用: 1]
[28]
Luo YF Li QH Liu ST . Topology optimization of shell-infill structures using an erosion-based interface identification method
Computer Methods in Applied Mechanics and Engineering 2019 ,355 :94 -112
DOI
URL
[本文引用: 5]
[29]
Bourdin B . Filters in topology optimization
International Journal for Numerical Methods in Engineering 2001 ,50 (9 ):2143 -2158
DOI
URL
[本文引用: 1]
[30]
Bruns TE Tortorelli DA . Topology optimization of non-linear elastic structures and compliant mechanisms
Computer Methods in Applied Mechanics & Engineering 2001 ,190 (26-27 ):3443 -3459
[本文引用: 1]
[31]
Lazarov BS Sigmund O . Filters in topology optimization based on Helmholtz-type differential equations
International Journal for Numerical Methods in Engineering 2011 ,86 (6 ):765 -781
DOI
URL
[本文引用: 1]
[32]
Guest JK Prevost J Belytschko T . Achieving minimum length scale in topology optimization using nodal design variables and projection functions
International Journal for Numerical Methods in Engineering 2004 ,61 (2 ):238 -254
DOI
URL
[本文引用: 1]
[33]
Wang FW Lazarov BS Sigmund O . On projection methods, convergence and robust formulations in topology optimization
Structural and Multidisciplinary Optimization 2011 ,43 (6 ):767 -784
DOI
URL
[本文引用: 1]
[34]
亢战 , 程耿东 . 基于随机有限元的非线性结构稳健性优化设计
计算力学学报 , 2006 ,23 (2 ):129 -135
[本文引用: 1]
(Kang Zhan Cheng Gengdong . Structural robust design based on perturbation stochastic finite element method
Chinese Journal of Computational Mechanics 2006 ,23 (2 ):129 -135 (in Chinese))
[本文引用: 1]
[35]
Da Silva GA Cardoso EL . Stress-based topology optimization of continuum structures under uncertainties
Computer Methods in Applied Mechanics and Engineering 2017 ,313 :647 -672
DOI
URL
[本文引用: 1]
[36]
Svanberg K . The method of moving asymptotes — A new method for structural optimization
International journal for numerical methods in engineering 1987 ,24 (2 ):359 -373
DOI
URL
[本文引用: 1]
[37]
Clausen A Andreassen E . On filter boundary conditions in topology optimization
Structural and Multidisciplinary Optimization 2017 ,56 (5 ):1147 -1155
DOI
URL
[本文引用: 1]
Generating optimal topologies in structural design using a homogenization method
1
1988
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
A level set method for structural topology optimization
1
2004
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
Evolutionary topology optimization of structures with multiple displacement and frequency constraints
0
2012
A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model
0
2016
A discrete-continuous parameterization (DCP) for concurrent optimization of structural topologies and continuous material orientations
1
2020
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
增材制造(3D打印)技术发展
1
2013
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
增材制造(3D打印)技术发展
1
2013
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
Additive manufacturing applications in medical cases: A literature based review
0
2017
增材制造技术 —— 现状与未来
1
2020
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
增材制造技术 —— 现状与未来
1
2020
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
Correction to: From topology optimization design to additive manufacturing: Today's success and tomorrow's roadmap
1
2021
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
Additive manufacturing oriented topology optimization of structures with self-supported enclosed voids
1
2020
... 拓扑优化[1 ] 是一种基于给定载荷和约束, 在特定的域内寻找结构最优传力路径及材料分布的设计方法, 具有不依赖于初始构型、设计自由度高及性能驱动的特点, 已成为结构与材料创新设计的重要工具[2 -5 ] . 但由于几何构型较复杂, 采用传统的制造工艺往往加工困难. 增材制造技术[6 -9 ] 是一种通过逐点打印、逐层累积材料来制备结构的新兴技术, 可实现高度复杂结构的制备. 将拓扑优化方法与增材制造技术相融合, 在实现拓扑优化设计价值最大化的同时, 还可以充分发挥增材制造的制造潜力, 是目前研究的重要趋势[10 -11 ] . ...
基于选区激光融化的金属材料零件快速成形现状与技术展望
1
2012
... 但由于制造方式、加工过程及环境、设备和操作等因素的影响, 通过增材制造成型的结构件易出现制造缺陷[12 -14 ] . 制造缺陷使得结构件成型精度降低、表面粗糙度大, 进而导致结构件表面材料分布不均匀, 引起表面层异质[15 ] . 表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性, 致使结构性能偏离设计、达不到预期目标. 然而, 当前大多数拓扑优化方法的研究是基于确定性的参数开展, 忽略了不确定因素对结构性能的影响, 导致优化后的构型不一定是最优的或者不符合实际, 严重影响结构的安全性. 因此在拓扑优化设计中, 考虑不确定因素对结构构型的影响是十分重要的. ...
基于选区激光融化的金属材料零件快速成形现状与技术展望
1
2012
... 但由于制造方式、加工过程及环境、设备和操作等因素的影响, 通过增材制造成型的结构件易出现制造缺陷[12 -14 ] . 制造缺陷使得结构件成型精度降低、表面粗糙度大, 进而导致结构件表面材料分布不均匀, 引起表面层异质[15 ] . 表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性, 致使结构性能偏离设计、达不到预期目标. 然而, 当前大多数拓扑优化方法的研究是基于确定性的参数开展, 忽略了不确定因素对结构性能的影响, 导致优化后的构型不一定是最优的或者不符合实际, 严重影响结构的安全性. 因此在拓扑优化设计中, 考虑不确定因素对结构构型的影响是十分重要的. ...
Eddy current detection of subsurface defects for additive/subtractive hybrid manufacturing
0
2017
Understanding internal defects in Mo fabricated by wire arc additive manufacturing through 3D computed tomography
1
2020
... 但由于制造方式、加工过程及环境、设备和操作等因素的影响, 通过增材制造成型的结构件易出现制造缺陷[12 -14 ] . 制造缺陷使得结构件成型精度降低、表面粗糙度大, 进而导致结构件表面材料分布不均匀, 引起表面层异质[15 ] . 表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性, 致使结构性能偏离设计、达不到预期目标. 然而, 当前大多数拓扑优化方法的研究是基于确定性的参数开展, 忽略了不确定因素对结构性能的影响, 导致优化后的构型不一定是最优的或者不符合实际, 严重影响结构的安全性. 因此在拓扑优化设计中, 考虑不确定因素对结构构型的影响是十分重要的. ...
考虑表面层异质及其不确定性的增材制造结构拓扑优化方法. [硕士论文]
1
2018
... 但由于制造方式、加工过程及环境、设备和操作等因素的影响, 通过增材制造成型的结构件易出现制造缺陷[12 -14 ] . 制造缺陷使得结构件成型精度降低、表面粗糙度大, 进而导致结构件表面材料分布不均匀, 引起表面层异质[15 ] . 表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性, 致使结构性能偏离设计、达不到预期目标. 然而, 当前大多数拓扑优化方法的研究是基于确定性的参数开展, 忽略了不确定因素对结构性能的影响, 导致优化后的构型不一定是最优的或者不符合实际, 严重影响结构的安全性. 因此在拓扑优化设计中, 考虑不确定因素对结构构型的影响是十分重要的. ...
考虑表面层异质及其不确定性的增材制造结构拓扑优化方法. [硕士论文]
1
2018
... 但由于制造方式、加工过程及环境、设备和操作等因素的影响, 通过增材制造成型的结构件易出现制造缺陷[12 -14 ] . 制造缺陷使得结构件成型精度降低、表面粗糙度大, 进而导致结构件表面材料分布不均匀, 引起表面层异质[15 ] . 表面层异质会带来结构表面材料属性的不确定性和表面层厚度的不确定性, 致使结构性能偏离设计、达不到预期目标. 然而, 当前大多数拓扑优化方法的研究是基于确定性的参数开展, 忽略了不确定因素对结构性能的影响, 导致优化后的构型不一定是最优的或者不符合实际, 严重影响结构的安全性. 因此在拓扑优化设计中, 考虑不确定因素对结构构型的影响是十分重要的. ...
Reliability-based vibro-acoustic microstructural topology optimization
1
2016
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
Non-probabilistic reliability-based topology optimization of continuum structures considering local stiffness and strength failure
1
2019
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
Robust topology optimization of structures with uncertainties in stiffness-Application to truss structures
3
2011
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
... 随机有限元法是将随机分析理论与有限元方法相结合的数值分析方法. 其中, 基于摄动开展的随机有限元法得到了广泛的应用[18 ,34 -35 ] . 其基本思想是: 引入一个零均值的微小摄动量$\Delta \xi $, 来描述随机变量$\xi $在其均值$\xi_{0} $处产生微小摄动所引起的不确定性, 那么随机变量$\xi $可以表示为 ...
... 而结构柔顺性的标准差$Std[c]$与方差$Var[c]$之间满足$Std[c]=\sqrt {Var[c]} $. 本文采用梯度类算法MMA[36 ] 求解优化问题, 基于伴随法求解敏度, 通过选择合适的伴随向量, 可以消除敏度信息中含${\partial u^{(0)}}/{\partial \rho_{\rm e} }$和${\partial u^{(1)}}/{\partial \rho_{\rm e}}$的项[18 ] . 那么, 目标函数关于设计变量的敏度信息可以表示为 ...
Manufacturing tolerant topology optimization
2
2009
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
... 为了避免棋盘效应和网格依赖性对优化结果的影响, 并保证得到0-1分布的结构场, 在识别结构表面层之前, 先后对初始结构场应用了PDE过滤、基于Heaviside过滤和tanh函数的离散映射. 这一过程与基于腐蚀操作的表面层识别几乎相同, 但却实现了不同的功能. 文中将这一过程定义为过滤过程(所有参数都用下标$f$标记),将表面层识别的过程定义为腐蚀过程, 并将过滤过程和腐蚀过程统称为改进的两步过滤法, 其实现流程及控制参数见图3 . 此外, 所有算例都使用鲁棒公式[19 ,21 -22 ] 来实现结构最小尺寸的控制, 控制参数[28 ] 为$\Delta \eta_{\rm f} $; 同时通过域扩展方法[37 ] 保证在结构边界处获得相同的腐蚀厚度. ...
Morphology-based black and white filters for topology optimization
2
2007
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
... 然后, 选取一个较大的阈值$\eta_{\rm e} $, 采用基于Heaviside过滤[20 ,32 ] 和tanh函数的离散映射[33 ] 对光滑化后的结构场$\tilde{{\mu }}$进行截断,得到被腐蚀后的结构场$\varphi $ ...
Robust topology optimization of photonic crystal waveguides with tailored dispersion properties
2
2011
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
... 为了避免棋盘效应和网格依赖性对优化结果的影响, 并保证得到0-1分布的结构场, 在识别结构表面层之前, 先后对初始结构场应用了PDE过滤、基于Heaviside过滤和tanh函数的离散映射. 这一过程与基于腐蚀操作的表面层识别几乎相同, 但却实现了不同的功能. 文中将这一过程定义为过滤过程(所有参数都用下标$f$标记),将表面层识别的过程定义为腐蚀过程, 并将过滤过程和腐蚀过程统称为改进的两步过滤法, 其实现流程及控制参数见图3 . 此外, 所有算例都使用鲁棒公式[19 ,21 -22 ] 来实现结构最小尺寸的控制, 控制参数[28 ] 为$\Delta \eta_{\rm f} $; 同时通过域扩展方法[37 ] 保证在结构边界处获得相同的腐蚀厚度. ...
Robust topology optimization accounting for spatially varying manufacturing errors
2
2011
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
... 为了避免棋盘效应和网格依赖性对优化结果的影响, 并保证得到0-1分布的结构场, 在识别结构表面层之前, 先后对初始结构场应用了PDE过滤、基于Heaviside过滤和tanh函数的离散映射. 这一过程与基于腐蚀操作的表面层识别几乎相同, 但却实现了不同的功能. 文中将这一过程定义为过滤过程(所有参数都用下标$f$标记),将表面层识别的过程定义为腐蚀过程, 并将过滤过程和腐蚀过程统称为改进的两步过滤法, 其实现流程及控制参数见图3 . 此外, 所有算例都使用鲁棒公式[19 ,21 -22 ] 来实现结构最小尺寸的控制, 控制参数[28 ] 为$\Delta \eta_{\rm f} $; 同时通过域扩展方法[37 ] 保证在结构边界处获得相同的腐蚀厚度. ...
Robust topology optimization of multi-material structures considering uncertain graded interface
1
2019
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
Robust topology optimization for concurrent design of dynamic structures under hybrid uncertainties
1
2019
... 一般来说, 考虑不确定性的拓扑优化模型包括基于可靠度的拓扑优化[16 -17 ] 和稳健性拓扑优化. 其中, 基于可靠度的拓扑优化关心的是结构在极端条件下的可靠性, 而稳健性拓扑优化则关心的是结构性能在其均值处的变异程度, 旨在降低结构性能对不确定因素的敏感程度. 近年来, 一批学者开展了针对稳健性拓扑优化问题的研究. Asadpoure等[18 ] 针对桁架结构的随机问题, 采用摄动技术对桁架刚度的不确定性进行了建模和随机响应分析. Sigmund[19 ] 基于图像形态学中的腐蚀、扩散操作[20 ] 对制备过程中均匀变化的过刻蚀、欠刻蚀进行了模拟, 并在光子晶体波导的稳健性拓扑优化设计中得以验证[21 ] . 随后, Schevenels等[22 ] 通过把离散映射的控制阈值作为随机变量, 将该研究扩展到考虑非均匀制造误差的情况. Kang等[23 ] 基于水平集方法跟踪多材料结构界面的演化, 利用级数最优线性估计(EOLE)结合多项式混沌(PCE)技术对材料界面宽度的不确定性进行了建模、离散及随机响应分析, 建立了考虑多材料结构界面不确定性的稳健性形状和拓扑优化方法. 针对具有随机和区间混合不确定的均匀周期性微结构动力及结构并行设计问题, Zheng等[24 ] 提出了一种基于水平集的稳健拓扑优化方法, 采用基于二元降维方案的混合降维方法来估计不确定目标函数的区间均值和区间方差. ...
Topology optimization of coated structures and material interface problems
1
2015
... 如何准确地对结构表面层进行建模, 通常是基于密度的拓扑优化方法中较为困难的问题. Clausen等[25 ] 采用基于两步过滤的操作, 以较大的空间密度梯度识别了结构的表面层, 并成功应用于基于密度的拓扑优化问题[26 -27 ] . 本文采用一种基于腐蚀操作的表面层识别技术[28 ] 建立表面层异质的等效模型. 其主要思想是: 首先对图1 (a)所示的初始结构进行腐蚀操作, 得到图1 (b)所示规模缩减后的被腐蚀结构; 然后将初始结构与被腐蚀结构的不同部分, 即图1 (c)所示的被腐蚀掉的部分, 定义为结构表面层. ...
Topology optimization of multi-material structures with graded interfaces
1
2019
... 如何准确地对结构表面层进行建模, 通常是基于密度的拓扑优化方法中较为困难的问题. Clausen等[25 ] 采用基于两步过滤的操作, 以较大的空间密度梯度识别了结构的表面层, 并成功应用于基于密度的拓扑优化问题[26 -27 ] . 本文采用一种基于腐蚀操作的表面层识别技术[28 ] 建立表面层异质的等效模型. 其主要思想是: 首先对图1 (a)所示的初始结构进行腐蚀操作, 得到图1 (b)所示规模缩减后的被腐蚀结构; 然后将初始结构与被腐蚀结构的不同部分, 即图1 (c)所示的被腐蚀掉的部分, 定义为结构表面层. ...
A projection-based method for topology optimization of structures with graded surfaces
1
2019
... 如何准确地对结构表面层进行建模, 通常是基于密度的拓扑优化方法中较为困难的问题. Clausen等[25 ] 采用基于两步过滤的操作, 以较大的空间密度梯度识别了结构的表面层, 并成功应用于基于密度的拓扑优化问题[26 -27 ] . 本文采用一种基于腐蚀操作的表面层识别技术[28 ] 建立表面层异质的等效模型. 其主要思想是: 首先对图1 (a)所示的初始结构进行腐蚀操作, 得到图1 (b)所示规模缩减后的被腐蚀结构; 然后将初始结构与被腐蚀结构的不同部分, 即图1 (c)所示的被腐蚀掉的部分, 定义为结构表面层. ...
Topology optimization of shell-infill structures using an erosion-based interface identification method
5
2019
... 如何准确地对结构表面层进行建模, 通常是基于密度的拓扑优化方法中较为困难的问题. Clausen等[25 ] 采用基于两步过滤的操作, 以较大的空间密度梯度识别了结构的表面层, 并成功应用于基于密度的拓扑优化问题[26 -27 ] . 本文采用一种基于腐蚀操作的表面层识别技术[28 ] 建立表面层异质的等效模型. 其主要思想是: 首先对图1 (a)所示的初始结构进行腐蚀操作, 得到图1 (b)所示规模缩减后的被腐蚀结构; 然后将初始结构与被腐蚀结构的不同部分, 即图1 (c)所示的被腐蚀掉的部分, 定义为结构表面层. ...
... 式中, 通过合理选取$R_{\rm e} $和$\Delta \eta_{\rm e}$的值即可实现对表面层厚度$w$的精确控制. 本文采取的策略是固定$\Delta \eta _{\rm e} $的值, 通过改变$R_{\rm e} $的值来控制$w$. 为了得到$w$和$R_{\rm e} $更规整的近似关系, 文中算例依据经验$\Delta \eta_{\rm e} $均取值为0.45, 此时$R_{\rm e} \approx 1.50w$. (3)式的详细理论推导参见文献[28 ]. 在此基础上, 物理密度和刚度的插值函数可以定义为 ...
... 式中, ${\partial \mu_{i} }/{\partial \rho_{\rm e} }$和${\partial \varphi_{i} }/{\partial \rho_{\rm e} }$的推导可参照参考文献[28 ], ${\partial \varphi_{i} }/{\partial \delta }$和${\partial ^{2}\varphi_{i}}/{\partial \delta^{2}}$的推导则同理可得, 此处不做赘述. ...
... 为了避免棋盘效应和网格依赖性对优化结果的影响, 并保证得到0-1分布的结构场, 在识别结构表面层之前, 先后对初始结构场应用了PDE过滤、基于Heaviside过滤和tanh函数的离散映射. 这一过程与基于腐蚀操作的表面层识别几乎相同, 但却实现了不同的功能. 文中将这一过程定义为过滤过程(所有参数都用下标$f$标记),将表面层识别的过程定义为腐蚀过程, 并将过滤过程和腐蚀过程统称为改进的两步过滤法, 其实现流程及控制参数见图3 . 此外, 所有算例都使用鲁棒公式[19 ,21 -22 ] 来实现结构最小尺寸的控制, 控制参数[28 ] 为$\Delta \eta_{\rm f} $; 同时通过域扩展方法[37 ] 保证在结构边界处获得相同的腐蚀厚度. ...
... 图4 所示为简支梁算例的设计域及边界条件, 结构的几何尺寸为$300\times 150$, 集中力$F=1$. 表面层结构和基体结构的材料属性分别为$\rho_{\rm s} =1$, $E_{\rm s} =1$, $\rho_{\rm b} =0.8$, $E_{\rm b} =0.5$, 即表面层为硬材料, 基体为软材料. 表面层厚度为$w=2$, 其标准差$\sigma =0.3 w$. 过滤过程和腐蚀过程的过滤半径分别取值为$R_{\rm f} =8$, $R_{\rm e} \approx 1.5 w$, 最小尺寸的控制参数$\Delta \eta_{\rm f} =0.1$. 体积分数为40%且每10个迭代步进行一次更新[28 ] . 目标函数中的权系数$\alpha $选取值为4. ...
Filters in topology optimization
1
2001
... 本文中, 首先使用基于Helmholtz偏微分方程的密度过滤[29 -30 ] —— PDE技术[31 ] , 对初始结构场$\mu $进行光滑化处理 ...
Topology optimization of non-linear elastic structures and compliant mechanisms
1
2001
... 本文中, 首先使用基于Helmholtz偏微分方程的密度过滤[29 -30 ] —— PDE技术[31 ] , 对初始结构场$\mu $进行光滑化处理 ...
Filters in topology optimization based on Helmholtz-type differential equations
1
2011
... 本文中, 首先使用基于Helmholtz偏微分方程的密度过滤[29 -30 ] —— PDE技术[31 ] , 对初始结构场$\mu $进行光滑化处理 ...
Achieving minimum length scale in topology optimization using nodal design variables and projection functions
1
2004
... 然后, 选取一个较大的阈值$\eta_{\rm e} $, 采用基于Heaviside过滤[20 ,32 ] 和tanh函数的离散映射[33 ] 对光滑化后的结构场$\tilde{{\mu }}$进行截断,得到被腐蚀后的结构场$\varphi $ ...
On projection methods, convergence and robust formulations in topology optimization
1
2011
... 然后, 选取一个较大的阈值$\eta_{\rm e} $, 采用基于Heaviside过滤[20 ,32 ] 和tanh函数的离散映射[33 ] 对光滑化后的结构场$\tilde{{\mu }}$进行截断,得到被腐蚀后的结构场$\varphi $ ...
基于随机有限元的非线性结构稳健性优化设计
1
2006
... 随机有限元法是将随机分析理论与有限元方法相结合的数值分析方法. 其中, 基于摄动开展的随机有限元法得到了广泛的应用[18 ,34 -35 ] . 其基本思想是: 引入一个零均值的微小摄动量$\Delta \xi $, 来描述随机变量$\xi $在其均值$\xi_{0} $处产生微小摄动所引起的不确定性, 那么随机变量$\xi $可以表示为 ...
基于随机有限元的非线性结构稳健性优化设计
1
2006
... 随机有限元法是将随机分析理论与有限元方法相结合的数值分析方法. 其中, 基于摄动开展的随机有限元法得到了广泛的应用[18 ,34 -35 ] . 其基本思想是: 引入一个零均值的微小摄动量$\Delta \xi $, 来描述随机变量$\xi $在其均值$\xi_{0} $处产生微小摄动所引起的不确定性, 那么随机变量$\xi $可以表示为 ...
Stress-based topology optimization of continuum structures under uncertainties
1
2017
... 随机有限元法是将随机分析理论与有限元方法相结合的数值分析方法. 其中, 基于摄动开展的随机有限元法得到了广泛的应用[18 ,34 -35 ] . 其基本思想是: 引入一个零均值的微小摄动量$\Delta \xi $, 来描述随机变量$\xi $在其均值$\xi_{0} $处产生微小摄动所引起的不确定性, 那么随机变量$\xi $可以表示为 ...
The method of moving asymptotes — A new method for structural optimization
1
1987
... 而结构柔顺性的标准差$Std[c]$与方差$Var[c]$之间满足$Std[c]=\sqrt {Var[c]} $. 本文采用梯度类算法MMA[36 ] 求解优化问题, 基于伴随法求解敏度, 通过选择合适的伴随向量, 可以消除敏度信息中含${\partial u^{(0)}}/{\partial \rho_{\rm e} }$和${\partial u^{(1)}}/{\partial \rho_{\rm e}}$的项[18 ] . 那么, 目标函数关于设计变量的敏度信息可以表示为 ...
On filter boundary conditions in topology optimization
1
2017
... 为了避免棋盘效应和网格依赖性对优化结果的影响, 并保证得到0-1分布的结构场, 在识别结构表面层之前, 先后对初始结构场应用了PDE过滤、基于Heaviside过滤和tanh函数的离散映射. 这一过程与基于腐蚀操作的表面层识别几乎相同, 但却实现了不同的功能. 文中将这一过程定义为过滤过程(所有参数都用下标$f$标记),将表面层识别的过程定义为腐蚀过程, 并将过滤过程和腐蚀过程统称为改进的两步过滤法, 其实现流程及控制参数见图3 . 此外, 所有算例都使用鲁棒公式[19 ,21 -22 ] 来实现结构最小尺寸的控制, 控制参数[28 ] 为$\Delta \eta_{\rm f} $; 同时通过域扩展方法[37 ] 保证在结构边界处获得相同的腐蚀厚度. ...