引言
几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] .
已有研究表明, 在局部标架思想下, 可构造出一类SE(3)几何精确梁单元[11 ] 以及绝对节点坐标梁单元. 局部标架梁单元能够规避刚体运动带来的几何非线性问题, 离散数值模型中广义质量矩阵与切线刚度矩阵满足刚体变换的不变性, 可明显地提高柔性多体系统动力学问题的计算效率. 在有限元方法中, 梁、板/壳单元普遍存在剪切、薄膜以及泊松闭锁问题. 多年来, 有限元领域学者提出了许多单元技术来有效地缓解闭锁. 本文主要关注如何提高局部标架梁单元的收敛性, 关于李群局部标架建模与计算方法涉及的其它细节本文不再赘述, 可参见作者的相关研究工作.
缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性".
混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的.
ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能.
本文研究局部标架下几类梁单元的闭锁缓解方法. 采用Hu-Washizu三场变分原理缓解局部标架下李群SE(3)几何精确梁的剪切闭锁, 采用应变分解法缓解局部标架下ANCF全参数梁的泊松闭锁. 通过对比几何精确与绝对节点坐标两类建模方法, 分析基于局部标架的李群SE(3)几何精确梁在计算精度与效率方面的优势. 本文中的李群SE(3)几何精确梁与ANCF梁单元均基于局部标架, 为了方便起见, 下文省去"基于局部标架"几个字.
1 基于李群SE(3)局部标架的几何精确梁理论
1.1 梁的运动学描述及本构模型
基于经典的Timoshenko梁假设, 李群几何精确梁理论融合非线性有限元方法与几何力学思想, 在李群SE(3)内建立系统的平衡方程, 可精确地描述柔性梁的大转动、大变形刚柔耦合动力学特性, 同时可规避刚体运动带来的几何非线性[31 ] .
梁的初始构型和当前构型如图1 所示. 引入参考坐标系{$O$; $ e_{1}$, $ e_{2}$, $ e_{3}$}. 在当前构型中, 在梁中线的每一点定义随体基矢量($ t$, $ n$, $ b$), 引入梁中线位置矢量$ x$和截面旋转矩阵$ R$, 初始构型对应的量为($\cdot$)$^{0}$.
图1
图1
几何精确梁初始构型与当前构型
Fig.1
Initial and current configurations of the geometrically exact beam
在梁的当前构型中, 截面上任意一点$p$的位置矢量为
(1) $\begin{eqnarray} \label{eq1} { x}_{p} (\xi_{1} ,\xi_{2} ,\xi_{3} )={ x}(\xi_{1} )+{ R}(\xi_{1} ){ y}_{p} (\xi_{2} ,\xi_{3} ) \end{eqnarray}$
式中, $\xi_{1}\in [0, L]$表示初始构型中$p$点所在截面对应的弧长坐标, $\xi _{2}$和$\xi_{3}$为$p$点在局部坐标系中的坐标分量, $L$为梁单元的长度, $ y_{p} = [0 \ \ \xi_{2} \ \ \xi_{3}]^{\rm T}$. 基于小应变假设, 当前构型的应变度量可以表示为
(2) $\begin{eqnarray} \label{eq2} { f}=\left[ {{\begin{array}{*{20}c} {{ f}_{u} }\\ {{ f}_{\omega } }\\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {{ R}^{\rm T}{ {x}'}}\\ {\mbox{axial}({ R}^{\rm T}{ {R}'})}\\ \end{array} }} \right] \end{eqnarray}$
式中, $ f_{u}$和$ f_{\omega}$分别为应变度量$ f$的平动和转动部分, 记号$(\cdot )' = \partial (\cdot )/\partial \xi_{1} $, axial$(\cdot )$表示反对称矩阵$\cdot$的轴矢量. 初始构型的应变度量$ f^{0}$可以表示为
(3) $\begin{eqnarray} \label{eq3} { f}^{0}=\left[ {{\begin{array}{*{20}c} {{ R}^{\rm 0T}{ x}^{0'}}\\ {\mbox{axial}({ R}^{\rm 0T}{ R}^{0'})}\\ \end{array} }} \right] \end{eqnarray}$
引入记号$\widehat{(\cdot )}$和$\check{(\cdot )}$, 它们的定义如下
(4) $\begin{eqnarray} \label{eq4} {\hat{{ f}}}=\left[ {{\begin{array}{c@{\quad }c} {{\tilde{{ f}}}_{\omega } }& {{\tilde{{ f}}}_{u} } \\ {{\bf 0}_{3} }& {{\tilde{{ f}}}_{\omega } }\\ \end{array} }} \right], \ \ \check{ f}=\left[ {{\begin{array}{c@{\quad }c} {{\bf 0}_{3} }& {{\tilde{{ f}}}_{u} }\\ {{\tilde{{ f}}}_{u} }& {{\tilde{{ f}}}_{\omega } }\\ \end{array} }} \right] \end{eqnarray}$
式中, 记号$\tilde{{\cdot }}$表示矢量$\cdot $的反对称矩阵, ${\bf0}_{3}$表示3 $\times$ 3的零矩阵. 应变可以表示为
(5) $\begin{eqnarray} \label{eq5} { \varepsilon }={ f}-{ f}^{0}=\left[ {{\begin{array}{*{20}c} {{ \gamma }}\\ {{ \kappa }}\\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {{ R}^{\rm T}{ x'}-{ R}^{\rm 0T}{ x}^{0'}}\\ {\mbox{axial}({ R}^{\rm T}{ R'}-{ R}^{\rm 0T}{ R}^{0'})}\\ \end{array} }} \right] \end{eqnarray}$
式中, $ \gamma = [\gamma_{1} \ \ \gamma_{2} \ \ \gamma_{3}]^{\rm T}$, $\gamma_{1}$表示梁中线的拉伸应变, $\gamma_{2}$和$\gamma_{3}$表示横向剪切应变, $ \kappa = [\kappa _{1} \ \ \kappa_{2} \ \ \kappa_{3}]^{\rm T}$, $\kappa_{1}$表示截面的扭转应变, $\kappa_{2}$和$\kappa_{3}$表示截面绕$ n$轴和$ b$轴的弯曲应变. 应力可以表示为
(6) $\begin{eqnarray} \label{eq6} { S}={ D}{ \varepsilon } \end{eqnarray}$
式中, 弹性系数矩阵$ D = {\rm diag} (EA$, $k_{\rm s2}GA$, $k_{\rm s3}GA$, $GJ_{\rm s}$, $EI_{2}$, $EI_{3})$, 其中$E$和$G$分别为杨氏模量和剪切模量, $A$, $I_{2}$和$I_{3}$分别表示梁初始构型的截面面积和截面惯性矩, $J_{\rm s}$表示圣维南扭转常数, $k_{\rm s2}$和$k_{\rm s3}$为截面的剪切修正系数.
1.2 SE3几何精确梁控制方程及线性化
(7) $\begin{eqnarray} \label{eq7} \delta {\cal W}_{\rm int} -\delta {\cal W}_{\rm ext} +\delta {\cal W}_{\rm ine} = {0} \end{eqnarray}$
式中, $\delta {\cal W}_{\rm int} $为内力所做的虚功, $\delta {\cal W}_{\rm ext} $为外载荷所做的虚功, $\delta {\cal W}_{\rm ine} $为惯性力所做的虚功.
为获得一个对称的切线刚度矩阵, 本文在前一个收敛步所在切平面进行物理量的一次与二次变分. 因此, 应变的变分可以表示为
(8) $\begin{eqnarray} \label{eq8} \delta { \varepsilon }=\lt({\rm T}'+{\rm T}\frac{\rm d}{{\rm d}\xi_{1} }+{\hat{{ f}}{\rm T}})\delta { h} \triangleq {\rm B}\delta { h} \end{eqnarray}$
式中, T为SE(3)群的切空间算符, $\delta h= [\delta d^{\rm T}\ \ \delta \eta^{\rm T}]^{\rm T}$, $\delta d$和$\delta \eta $分别为局部标架下的虚位移和虚转角, B为应变算符. 内部虚功可以表示为
(9) $\begin{eqnarray} \label{eq9} \delta {\cal W}_{\rm int} =\int_L {(\delta { \varepsilon })^{\rm T} D{ \varepsilon} {\rm d}\xi_{1} } =\int_L \delta h^{\rm T}{\rm B}^{\rm T} D{ \varepsilon }{\rm d}\xi _{1} \end{eqnarray}$
(10) $\begin{eqnarray} \label{eq10} \delta {\cal W}_{\rm ext} =\int_L {\delta { x}_{p}^{\rm T} { p}^{\rm ext}{\rm d}\xi_{1}} \end{eqnarray}$
式中, $ p^{\rm ext}$为作用于$p$点的外载荷. 惯性虚功可以表示为
(11) $\begin{eqnarray} \label{eq11} \delta {\cal W}_{\rm ine} =\int {\delta{ h}^{\rm T}\left( {{ C\dot{{ v}}}-{\hat{{ v}}}^{\rm T}{ C v}} \right){\rm d}\xi_{1} }, \ \ { C}=\left[ {{\begin{array}{c@{\ \ }c} {\rho_{A} { I}_{3} }& {{\bf 0}_{3} }\\ {{\bf 0}_{3} }& {{ J}}\\ \end{array} }} \right]\quad \end{eqnarray}$
式中, $ v= [ U^{\rm T}\ \ \omega^{\rm T}]^{\rm T}$, $ U$和 $ \omega $分别为局部标架下的线速度与角速度, 顶标 $\cdot$ 表示变量对时间$t$的全导数, $\rho_{A}$为单位长度的材料密度, $ I_{3}$表示3 $\times$ 3的单位矩阵, $ J$为截面形心惯性矩阵.
(12) $\begin{eqnarray} \label{eq12} &&\Delta (\delta {\cal W}_{\rm int} )=\int_L {\Big(\delta { h}^{\rm T}{\rm B}^{\rm T}{ D}\Delta { \varepsilon }+\delta { h}^{\rm T}\Delta {\rm B}^{\rm T}{ S}\Big){\rm d}\xi_{1} } =\\&&\qquad \int_L {\Big(\delta { h}^{\rm T}{\rm B}^{\rm T}{ D{\rm B}}\Delta { h}+\delta { h}^{\rm T}\Delta {\rm B}^{\rm T}{ S}\Big){\rm d}\xi_{1} } \end{eqnarray}$
(13) $\begin{eqnarray} \label{eq13} \Delta {\rm B}^{\rm T}=\Delta {\rm T'}^{\rm T}+\frac{\rm d}{{\rm d}\xi_{1} }\Delta {\rm T}^{\rm T}+\Delta {\rm T}^{\rm T}{\hat{{ f}}}^{\rm T}+{\rm T}^{\rm T}\Delta {\hat{{ f}}}^{\rm T} \end{eqnarray}$
为了进一步简化$\Delta (\delta {\cal W}_{\rm int} )$的几何部分, 引入两个矩阵$\varXi_{{\rm T}}$和$\varXi_{\rm T'}$, 它们的定义如下
(14) $\left.\begin{array}{l}\Delta \boldsymbol{T}^{\mathrm{T}} \boldsymbol{A}=\boldsymbol{\Xi}_{\mathrm{T}}(\boldsymbol{A}) \Delta \boldsymbol{h} \\\Delta \boldsymbol{T}^{\prime \mathrm{T}} \boldsymbol{A}=\boldsymbol{\Xi}_{\mathrm{T}^{\prime}}(\boldsymbol{A})\left[\begin{array}{c}\Delta \boldsymbol{h} \\\Delta \boldsymbol{h}^{\prime}\end{array}\right]=\left[\begin{array}{lll}\boldsymbol{\Xi}_{\mathrm{T}^{\prime}}^{(1)}(\boldsymbol{A}) & \boldsymbol{\Xi}_{\mathrm{T}^{\prime}}^{(2)}(\boldsymbol{A})\end{array}\right]\left[\begin{array}{l}\Delta \boldsymbol{h} \\\Delta \boldsymbol{h}^{\prime}\end{array}\right]\end{array}\right\}$
式中, $ A$为一个任意的6 $\times$ 1的矢量, 记号${\Xi }_{\rm T'}^{(1)} $和${\Xi }_{\rm T'}^{(2)} $分别是矩阵${\varXi }_{\rm T'} $的前半部分和后半部分, 其具体形式可参见文献[11 ]. 因此, 几何部分为
(15) $\begin{eqnarray} \label{eq15} \Delta {\rm B}^{\rm T}{ S}=\varUpsilon ({ S})\Delta { h} \end{eqnarray}$
(16) $\begin{eqnarray} \label{eq16} &&\varUpsilon ({ S})={\varXi }_{\rm T'}^{(1)} ({ S})+{\varXi }_{{\rm T}} \Big( {\hat{{ f}}}^{\rm T}{ S}\Big)+{\rm T}^{\rm T}\check{ S}\Big({ {T}'}+{\hat{{ f}}T}\Big) +\\&&\qquad\Big[{\varXi }_{\rm T'}^{(2)} ({ S})+{\rm T}^{\rm T}\check{ S} {\rm T}\Big]\frac{\rm d}{{\rm d}\xi_{1} }+\frac{\rm d}{{\rm d}\xi _{1} }{\varXi }_{{\rm T}} ({ S}) \end{eqnarray}$
(17) $\begin{eqnarray} \label{eq17} \Delta (\delta {\cal W}_{\rm int} )=\delta { h}^{\rm T}\int_L {\Big[{\rm B}^{\rm T}{ D{\rm B}}+\varUpsilon ({ S})\Big]{\rm d}\xi_{1} } \Delta { h} \end{eqnarray}$
需要指出的是, 由于$\delta h$为局部标架下的平动与转动虚位移, $\Delta h$为局部标架下的平动与转动无限小位移, 它们均与该点的任意刚体位移无关. 因此, 单元的弹性力及其切线刚度矩阵均满足刚体变换的不变性. 对于广义惯性力及其广义质量矩阵也同时具有类似的形式.
1.3 SE3几何精确梁有限元离散格式
对梁中线位置矢量$ x$和截面相对旋转伪矢量$\varTheta^{r}$[11 ] 进行空间离散
(18) $\begin{eqnarray} \label{eq18} { x}=N_{I} { x}_{I},\ \ \varTheta ^{r}=N_{I} \lg ({ R}_{r}^{-1} { R}_{I} ) \end{eqnarray}$
式中, $N_{I}$是节点$I$的形函数, $ x_{I}$是梁中线上节点$I$的位置矢量, $ R_{r}$是参考点所在截面的旋转矩阵, $ R_{I}$是节点$I$所在截面的旋转矩阵, 旋转伪矢量为转轴单位矢量与转角的乘积.
离散应变算符B得到应变$\!-\!$位移矩阵$ B_{I}$, 它的表达式为
(19) $\begin{eqnarray} \label{eq19} { B}_{I} ={\rm T'}N_{I} +{\rm T}{N}'_{I} +{\hat{{ f}}\rm T}N_{I} \end{eqnarray}$
(20) $\begin{eqnarray} \label{eq20} { F}_{\rm int} =\int_L {{ B}_{I}^{\rm T} { S}{\rm d}\xi_{1} } \end{eqnarray}$
(21) $\begin{eqnarray} \label{eq21} { K}_{\rm mat} =\int_L {{ B}_{I}^{\rm T} { D{\rm B}}_{I} {\rm d}\xi_{1}}, \ \ { K}_{\rm geo} =\int_L {N_{I}^{\rm T} \varUpsilon ({ S})N_{I} {\rm d}\xi_{1} } \end{eqnarray}$
对于非常细长的梁结构, 采用一阶插值描述几何精确梁弯曲时将会产生剪切闭锁. 由于梁非常细长, 截面内横向剪切应变处处接近于0. 而由于平动参数$ x$和转动参数 $ \theta $采用了相同的插值函数, 使式(5)中横向剪切应变$ \gamma_{s}$中的$ R$ ($\theta)$和$ x'$两项具有不同阶次, $ \gamma_{s} = {\bf 0}$ 不可能处处满足, 导致能量泛函中剪切变形能项的量级不正确, 由此带来了剪切闭锁. 此时, 单元表现得十分刚硬, 即计算出来的位移值远小于参考解, 总体刚度矩阵很大.
2 基于局部标架的绝对节点坐标方法的三维全参数梁理论
本节简要介绍基于局部标架的绝对节点坐标全参数梁单元建模方法. 某质点从初始位置$ X$运动到当前位置$ r$, 变形梯度可以表示为
(22) $\begin{eqnarray} \label{eq22} { J}=\frac{\partial { r}}{\partial { X}} \end{eqnarray}$
(23) $\begin{eqnarray} \label{eq23} { \varepsilon }=\frac{1}{2}({ J}^{\rm T}{ J}-{ I}) \end{eqnarray}$
(24) $\begin{eqnarray} \label{eq24} U=\frac{1}{2}\int_{{V}} {{ \varepsilon }^{\rm T} D{ \varepsilon}{\rm d}V} \end{eqnarray}$
式中, $ D$为弹性矩阵, $V$为梁的体积. 应变能对广义坐标$ e$求偏导得弹性力为
(25) $\begin{eqnarray} \label{eq25} { F}^{\rm int}=\frac{\partial U}{\partial { e}}=\int_V { \varepsilon ^{{\rm T}} D\frac{\partial \varepsilon }{\partial { e}}{\rm d}V} \end{eqnarray}$
(26) $\begin{eqnarray} \label{eq26} { K}=\frac{\partial { F}^{\rm int}}{\partial { e}}=\int_V \left[ \left( \frac{\partial \varepsilon }{\partial { e}} \right)^{\rm T} D\frac{\partial \varepsilon }{\partial { e}}+ \varepsilon^{\rm T} D\frac{\partial^{2} \varepsilon }{\partial { e}^{2}} \right]{\rm d}V \end{eqnarray}$
相比于几何精确梁单元, ANCF单元没有转动参数, 不能直接定义局部标架, 需要通过平动位移场定义转动场. 此处采用ANCF斜率矢量定义该点的局部标架基矢量
(27) $\left. \begin{array} \\ { R}=[{ i}_{1}\ \ { i}_{2}\ \ { i}_{3}], \ \ { i}_{1} =\dfrac{{ r}_{X} }{\left\| {{ r}_{X} } \right\|} \\ { i}_{2} ={ i}_{3} \times { i}_{1} , \ \ { i}_{3} =\dfrac{{ r}_{X} \times { r}_{Y} }{\left\| {{ r}_{X} \times { r}_{Y} } \right\|} \end{array} \right\}$
式中, $ r_{X}$和$ r_{Y}$为当前位置矢量$ r$对物质坐标的偏导数. 由于平动位移场在局部标架中描述, 单元的刚体运动可自然被消除. 因此, 系统质量矩阵以及切线刚度矩阵满足刚体运动的不变性, 从而可极大地减少系统质量矩阵与刚度矩阵在仿真过程中的更新次数.
ANCF全参数梁单元会遇到泊松闭锁问题, 闭锁产生的原因如下. 由于ANCF全参数梁是连续介质单元, 梁的中线为三阶Hermite插值, 在泊松效应的作用下, 截面应该变形为曲面. 然而横截面为一阶插值, 不能描述截面的曲面变形模式, 因此导致泊松闭锁.
3 两类局部标架梁单元的闭锁缓解方法
3.1 基于Hu-Washizu三场变分原理的剪切闭锁缓解方法
Hu-Washizu三场变分原理不仅假设位移场, 同时假设应力和应变场, 且三类场变量的插值相互独立. 假设剪切应变$\bar{ \gamma}$和假设剪切应力$\bar{ \tau }$的分布为
(28) $\begin{eqnarray} \label{eq28} \bar{ \gamma}={ N}_{\gamma }{ \alpha }_{e} ,\ \ {\bar{{ \tau }}}={ N}_{\tau } {\beta }_{e} \end{eqnarray}$
式中, $ N_{\gamma } = N_{\tau } =[1, \xi ,\cdots, \xi^{n-2}]$, $ \alpha_{e} = [\alpha_{1}, \alpha_{2}$, $\cdots$, $\alpha_{n-1}]^{\rm T}$, $ \beta_{e}= [\beta_{1}, \beta_{2}, ..., \beta_{n-1}]^{\rm T}$, $n$为单元节点数. 剪切部分的泛函可以表示为
(29) $\begin{eqnarray} \label{eq29} \varPi_{s} =\int_L \left[ \frac{1}{2}\bar{{ \gamma }}_{s}^{\rm T} D_{\rm s} \bar{ \gamma}_{\rm s} +\bar{ \tau }^{\rm T}( \gamma _{\rm s} -\bar{ \gamma}_{\rm s}) \right]{\rm d}\xi_{1} \end{eqnarray}$
式中, $ \gamma_{\rm s}$代表由等参插值产生的剪切应变, 弹性系数矩阵$ D_{\rm s} = {\rm diag} (k_{\rm s2}GA$, $k_{\rm s3}GA$). 对剪切部分的泛函$\varPi _{\rm s}$求变分得
(30) $\begin{eqnarray} \label{eq30} &&\hspace{-2mm} \delta \varPi_{\rm s}\!=\!\int_L {\left[ {{\bar{{ \gamma }}}_{\rm s}^{\rm T} D_{\rm s} \delta {\bar{{ \gamma }}}_{\rm s} +\delta {\bar{{ \tau }}}^{\rm T}({ \gamma }_{\rm s} -{\bar{{ \gamma }}}_{\rm s} )+\delta ({ \gamma }_{\rm s}^{\rm T} -{\bar{{ \gamma }}}_{\rm s}^{\rm T} ){\bar{{ \tau }}}} \right]{\rm d}\xi_{1} }=\\&&\qquad\hspace{-4mm} \int_L {\left[ {\delta {\bar{{ \gamma }}}_{\rm s}^{\rm T} D_{\rm s} {\bar{{ \gamma }}}_{\rm s} +\delta {\bar{{ \tau }}}^{\rm T}({ \gamma }_{\rm s} -{\bar{{ \gamma }}}_{\rm s} )+(\delta h^{\rm T}{\rm B}^{\rm 23T}-\delta {\bar{{ \gamma }}}_{\rm s}^{\rm T} ){\bar{{ \tau}}}} \right]{\rm d}\xi_{1} }\\&&\qquad \end{eqnarray}$
式中, B$^{23}$为应变算符B的第2和第3行. 对$\delta \varPi_{\rm s}$线性化得
(31) $\begin{eqnarray} \label{eq31} &&\Delta (\delta \varPi_{s} )=\int_L \Big[\delta {\bar{{ \gamma }}}_{\rm s}^{\rm T} D_{\rm s} \Delta {\bar{{ \gamma }}}_{\rm s} +\delta {\bar{{ \tau }}}^{\rm T}(\Delta { \gamma }_{\rm s} -\Delta {\bar{{ \gamma }}}_{\rm s} )+\\&&\qquad (\delta h^{\rm T}{\rm B}^{\rm 23T}-\delta {\bar{{ \gamma }}}_{\rm s}^{\rm T} )\Delta {\bar{{ \tau }}}+\delta h^{\rm T}\Delta {\rm B}^{\rm 23T}{\bar{{ \tau }}}\Big]{\rm d}\xi_{1} =\\&&\qquad\int_L \Big[\delta {\bar{{ \gamma }}}_{\rm s}^{\rm T} D_{\rm s} \Delta {\bar{{ \gamma }}}_{\rm s} +\delta {\bar{{ \tau }}}^{\rm T}{\rm B}^{23}\Delta h-\delta {\bar{{ \tau }}}^{\rm T}\Delta {\bar{{ \gamma }}}_{\rm s} +\\&&\qquad\delta h^{\rm T}{\rm B}^{\rm 23T}\Delta {\bar{{ \tau }}}-\delta {\bar{{ \gamma }}}_{\rm s}^{\rm T} \Delta {\bar{{ \tau }}}+\delta h^{\rm T}\varUpsilon ( S_{\rm s} )\Delta h \Big]{\rm d}\xi_{1} \end{eqnarray}$
式中, $ S_{\rm s}= [{0}, {\bar{{ \tau }}}, {0}, {0}, {0}]^{\rm T}$. 剪切部分的弹性力可以表示为
(32) $\begin{eqnarray} \label{eq32} { F}_{\rm s}^{\rm int} =\int_L {\left[ {\begin{array}{c} {\rm B}^{\rm 23T}\bar{{\tau }} \\ { N}_{\gamma }^{\rm T} ({ D}_{\rm s} \bar{{\gamma }}-\bar{{\tau }}) \\ { N}_{\tau }^{\rm T} (\gamma_{\rm s} -\bar{{\gamma }}_{\rm s} ) \\ \end{array}} \right]{\rm d}\xi_{1} } \end{eqnarray}$
(33) $\begin{eqnarray} \label{eq33} { K}_{\rm s} =\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c} {{ K}_{\rm s}^{\rm geo} }& {\bf 0}& {{ A}^{\rm T}} \\ {\bf 0}& {{ W}}& {-{ C}^{\rm T}}\\ {{ A}}& {-{ C}}& {\bf 0}\\ \end{array} }} \right] \end{eqnarray}$
(34) $\left. \begin{array} \\ { K}_{\rm s}^{\rm geo} =\int_L {N_{I}^{\rm T} \varUpsilon ({ S}_{\rm s} )N_{I} {\rm d}\xi_{1} } , \ \ { A}=\int_L {{ N}_{\tau }^{\rm T}{\rm B}^{23}{\rm d}\xi_{1} } \\ { C}=\int_L {{ N}_{\tau }^{\rm T} { N}_{\gamma } {\rm d}\xi_{1}}, \ \ { W}=\int_L {{ N}_{\gamma }^{\rm T} { D}_{\rm s}{ N}_{\gamma } {\rm d}\xi_{1} } \\ \end{array} \right\}$
(35) $\begin{eqnarray} \label{eq35} \left[ {{\begin{array}{ccc} {{ K}_{\rm m} +{ K}_{\rm b} +{ K}_{\rm s}^{\rm geo} }& {\bf 0}& {{ A}^{\rm T}}\\ {\bf 0}& {{ W}}& {-{ C}^{\rm T}}\\ {{ A}}& {-{ C}}& {\bf 0}\\ \end{array} }} \right]\left[ {\begin{array}{l} \Delta { h}^{N} \\ \Delta \alpha_{e} \\ \Delta \beta_{e} \\ \end{array}} \right]=-{ R e s} \end{eqnarray}$
式中, $ K_{\rm m}$和$ K_{\rm b}$分别为薄膜和弯曲部分的刚度矩阵, $\Delta h^{N}$为节点运动矢量的增量, $ R e s$为残差. 将上式静力缩聚化为单场形式
(36) $\begin{eqnarray} \label{eq36} \Big({ K}_{\rm m} +{ K}_{\rm b} +{ K}_{\rm s}^{\rm geo} +{ A}^{\rm T}{ C}^{\rm -T}{ W C}^{-1}{ A}\Big)\Delta { h}^{N}=-{ R e s} \end{eqnarray}$
一阶插值的几何精确梁会产生严重的剪切闭锁, 二阶及二阶以上插值的几何精确梁剪切闭锁较轻. 因此, 本文关于几何精确梁剪切闭锁处理方法着重于一阶梁单元. Hu-Washizu三场变分原理中, 位移场、应变场和应力场均独立插值. 式(28)假设横向剪切应变为常数, 可避免产生过大的剪切应变能, 有效缓解了剪切闭锁.
此外, 对于梁单元, 缩减积分技术也是缓解剪切闭锁的有效手段. 数值算例展示了采用Hu-Washizu三场变分原理与缩减积分技术缓解梁单元剪切闭锁的效果. 相比较而言, 缩减积分技术由于其简便性在梁单元中应用较为广泛, 但用在板壳单元中会产生沙漏变形模式. 进一步, 上述Hu-Washizu三场变分原理的研究将为低阶几何精确板壳单元的闭锁缓解起到一定的借鉴作用.
3.2 基于应变分解法的泊松闭锁缓解方法
(37) $\begin{eqnarray} \label{eq37} \left. {\begin{array}{l} { r}={ r}^{\rm c}+Y{ r}_{Y} +Z{ r}_{Z} \\ { r}_{X} ={ r}_{X}^{\rm c} +Y{ r}_{YX} +Z{ r}_{ZX} \\ { r}_{Y} ={ r}_{Y} , \ \ { r}_{Z} ={ r}_{Z} \\ \end{array}} \right\} \end{eqnarray}$
式中, 上标c代表中线. 于是, 位置矢量梯度矩阵可以写为
(38) $\begin{eqnarray} \label{eq38} { J}=[{ r}_{X}^{\rm c} +Y{ r}_{YX} +Z{ r}_{ZX}\ \ { r}_{Y}\ \ { r}_{Z} ]={ J}^{\rm c}(X)+{ J}^{k}(Y,Z) \end{eqnarray}$
式中, ${ J}^{\rm c}=[{ r}_{X}^{\rm c}\ \ { r}_{Y}\ \ { r}_{Z} ]$仅与中线参数$X$相关, ${ J}^{k}=[Y{ r}_{YX}+Z{ r}_{ZX}\ \ {\bf 0}_{3\times 1}\ \ {\bf 0}_{3\times 1} ]$与单元的剪切、扭转和弯曲变形相关. 因此, Green-Lagrange应变张量可以写为
(39) $\begin{eqnarray} \label{eq39} &&{ \varepsilon }=\frac{1}{2}\Big({ J}^{\rm T}{ J}-{ I}\Big)=\frac{1}{2}\Big({ J}^{\rm cT}{ J}^{\rm c}+{ J}^{\rm cT}{ J}^{k}+{ J}^{k\rm T}{ J}^{\rm c}+\\&&\qquad{ J}^{k\rm T}{ J}^{k}-{ I}\Big) \end{eqnarray}$
将$ J^{\rm c}$和$ J^{k}$代入上式得Green-Lagrange应变张量的分量为
(40) $\left. \begin{array} \\ { \varepsilon }=\dfrac{1}{2}\left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c} {\varepsilon_{11} }&& {\rm sym}\\ {{ r}_{X}^{\rm cT} { r}_{Y} +Y{ r}_{YX}^{\rm T} { r}_{Y} +Z{ r}_{ZX}^{\rm T} { r}_{Y} }& {{ r}_{Y}^{\rm T} { r}_{Y}-1}&\\ {{ r}_{X}^{\rm cT} { r}_{Z} +Y{ r}_{YX}^{\rm T} { r}_{Z} +Z{ r}_{ZX}^{\rm T} { r}_{Z} }& {{ r}_{Y}^{\rm T} { r}_{Z} }& {{ r}_{Z}^{\rm T} { r}_{Z} -1}\\ \end{array} }} \right] \\ \varepsilon_{11} ={ r}_{X}^{\rm cT} { r}_{X}^{\rm c}+2Y{ r}_{X}^{\rm cT} { r}_{YX} +2Z{ r}_{X}^{\rm cT} { r}_{ZX} +2YZ{ r}_{YX}^{\rm T} { r}_{ZX}+\\\qquad Y^{2}{ r}_{YX}^{\rm T} { r}_{YX}+Z^{2}{ r}_{ZX}^{\rm T} { r}_{ZX} -1 \\ \end{array} \right\}$
Green-Lagrange应变张量可以分解为两部分$ \varepsilon = \varepsilon^{\rm c} + \varepsilon^{k}$[30 ] , 式中,
(41) $\left. \begin{array} \\ { \varepsilon}^{\rm c}\!=\!\dfrac{1}{2}\Big({ J}^{\rm cT}{ J}^{\rm c}-{ I}\Big)\!=\!\dfrac{1}{2}\left[ {{\begin{array}{ccc} {{ r}_{X}^{\rm cT} { r}_{X}^{\rm c} -1}& {{ r}_{X}^{\rm cT} { r}_{Y} }& {{ r}_{X}^{\rm cT} { r}_{Z} }\\ & {{ r}_{Y}^{\rm T} { r}_{Y} -1}& {{ r}_{Y}^{\rm T} { r}_{Z} }\\ {\rm sym}&& {{ r}_{Z}^{\rm T} { r}_{Z} -1}\\ \end{array} }} \right] \\ { \varepsilon}^{k}=\dfrac{1}{2}\Big({ J}^{\rm cT}{ J}^{k}+{ J}^{k\rm T}{ J}^{\rm c}+{ J}^{k\rm T}{ J}^{k}\Big) =\\\qquad\dfrac{1}{2}\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c} {\varepsilon_{11}^{k}}& {Y{ r}_{YX}^{\rm T} { r}_{Y} +Z{ r}_{ZX}^{\rm T} { r}_{Y} }& {Y{ r}_{YX}^{\rm T} { r}_{Z}+Z{ r}_{ZX}^{\rm T} { r}_{Z} }\\ & 0& 0\\ {\rm sym}&& 0\\ \end{array} }} \right] \\ \varepsilon_{11}^{k} =2Y{ r}_{X}^{\rm cT} { r}_{YX} +2Z{ r}_{X}^{\rm cT} { r}_{ZX} +2YZ{ r}_{YX}^{\rm T} { r}_{ZX} +\\\qquad Y^{2}{ r}_{YX}^{\rm T} { r}_{YX} +Z^{2}{ r}_{ZX}^{\rm T} { r}_{ZX} \\ \end{array} \right\}$
$ \varepsilon^{\rm c}$中只有低阶应变, 且$ \varepsilon^{\rm c}$仅与梁中线参数$X$相关; $ \varepsilon^{k}$中包含高阶应变, 这些高阶应变会导致截面变形和弯曲变形. 为了缓解闭锁, 泊松耦合只用在正应变的低阶项中, 即仅在$ \varepsilon^{\rm c}$中考虑泊松效应, 忽略正应变的高阶项的泊松效应. 因此, 梁截面不会变形为曲面, 缓解了泊松闭锁. 第二类Piola-Kirchhoff应力的Voigt形式可以写为
(42) $\begin{eqnarray} \label{eq42} { \sigma }_{v} ={ D}^{\rm c}{ \varepsilon }_{v}^{\rm c} +{ D}^{k}{ \varepsilon }_{v}^{k} \end{eqnarray}$
式中, 应变也是Voigt形式. 基于平面应变假设, 弹性系数矩阵可以被定义为
(43) $\left. \begin{array} \\ { D}^{\rm c}=\left[ {{\begin{array}{*{20}c} {\lambda +2\mu }& \lambda& \lambda& 0& 0 & 0\\ & {\lambda +2\mu }& \lambda& 0& 0& 0 \\ && {\lambda +2\mu }& 0& 0& 0\\ &&& \mu& 0& 0\\ & {\rm sym}&&& {\mu k_{\rm s2} }& 0\\ &&&&& {\mu k_{\rm s3} }\\ \end{array} }} \right] \\ { D}^{k}=\mbox{diag}(E,E,E,\mu ,\mu k_{\rm s2} ,\mu k_{\rm s3} ) \\ \end{array} \right\}$
式中, $\lambda=E\nu /[(1+\nu )(1-2\nu )]$和$\mu =E/[2(1+\nu )]$为拉梅常数, $E$和$\nu $分别为杨氏模量和泊松比. 应变能可以表示为
(44) $\begin{eqnarray} \label{eq44} U=\frac{1}{2}\int_V {\left( {{ \varepsilon }_{v}^{\rm cT} { D}^{\rm c}{ \varepsilon }_{v}^{\rm c} +{ \varepsilon }_{v}^{k\rm T} D^{k}{ \varepsilon }_{v}^{k} } \right)} {\rm d}{V} \end{eqnarray}$
(45) $\begin{eqnarray} \label{eq45} F^{\rm int }=\int_{V}\left[\left(\frac{\partial \varepsilon _{v}^{\rm c}}{\partial e }\right)^{\rm T} D^{\rm c} \varepsilon _{v}^{\rm c}+\left(\frac{\partial \varepsilon _{v}^{k}}{\partial e }\right)^{\rm T} D^{k} \varepsilon _{v}^{k}\right]{\rm d} V \end{eqnarray}$
(46) $\left. \begin{array} \\ K _{\rm mat}=\int_{V}\left[\left(\dfrac{\partial \varepsilon _{v}^{\rm c}}{\partial e }\right)^{\rm T} D ^{\rm c} \dfrac{\partial \varepsilon _{v}^{\rm c}}{\partial e }+\left(\dfrac{\partial \varepsilon _{v}^{k}}{\partial e }\right)^{\rm T } D ^{k} \dfrac{\partial \varepsilon _{v}^{k}}{\partial e }\right] {\rm d} V \\ K _{\rm geo}=\int_{V}\left( \sigma _{v}^{\rm cT} \dfrac{\partial^{2} \varepsilon _{v}^{\rm c}}{\partial e ^{2}}+ \sigma _{v}^{k\rm T } \dfrac{\partial^{2} \varepsilon _{v}^{k}}{\partial e ^{2}}\right) {\rm d} V \end{array} \right\}$
4 三类常用的有限元插值方法
本节简要介绍三类有限元插值方法, 包括Lagrange插值、Hermite插值以及非均匀有理B-样条(NURBS). 其中, Lagrange插值在有限元中应用最为广泛; 绝对节点坐标方法则采用Hermite插值, 以保证位移场的C$^{1}$连续; NURBS的基函数可以构造任意阶连续的近似函数, 建立了计算机辅助设计(CAD)与计算机辅助工程(CAE)间的桥梁, 该方法被称为等几何分析.
为对比分析不同插值方法的优劣势, 本文涉及一阶与三阶Lagrange插值、三阶Hermite插值以及三阶NURBS插值.
4.1 Lagrange插值
给定函数$f(x)$在$n+1$个互不相同的点$x_{i}$ ($i=0$, 1, 2, $\cdots$, $n)$上的函数值$f(x_{i}) = y_{i}$, $n$次Lagrange插值多项式可以表示为
(47) $\begin{eqnarray} \label{eq47} P_{n} (x)=\sum\limits_{i=0}^n {\left( {\prod\limits_{j=1,j\ne i}^n {\frac{x-x_{j} }{x_{i} -x_{j} }} } \right)} y_{i} \end{eqnarray}$
4.2 Hermite插值
给定函数$f(x)$在$n+1$个互不相同的点$x_{i}$ ($i = 0$, 1, 2, $\cdots$, $n)$上的函数值$y_{i}$及一阶导数值${y}'_{i} $, Hermite插值多项式可以表示为
(48) $\begin{eqnarray} \label{eq48} H_{2n+1} (x)=\sum\limits_{i=0}^n {\Big[y_{i} A_{i} (x)+{y}'_{i} B_{i} (x)\Big]} \end{eqnarray}$
Hermite插值基函数$A_{i}(x)$和$B_{i}(x)$为
(49) $\left. \begin{array} \\ A_{i} (x)=\Big[1-2(x-x_{i} ){l}'_{i} (x_{i} )\Big]l_{i}^{2} (x) \\ B_{i} (x)=(x-x_{i} )l_{i}^{2} (x) \\ \end{array} \right\}$
式中, $l_{i} (x)=\prod\limits_{j=0,j\ne i}^n {(x-x_{j} )/(x_{i} -x_{j} )} $.
4.3 非均匀有理B-样条
在区间[$a$, $b$]内, 设$U =\{u_{0},u_{1}, u_{2}, \cdots, u_{m}\}$ 是一不减的实数序列. 以$U$作为样条结点, $p$次的第$i$个B-样条基函数$N_{i,p}(u)$定义为
(50) $\left. \begin{array} \\ N_{i,0} (u)=\left\{\begin{array}{l@{\quad }l} 1, & u_{i} \leqslant u<u_{i+1} \\ 0, & {\rm else}\\ \end{array} \right. \\ N_{i,p} (u)=\dfrac{u-u_{i} }{u_{i+p} -u_{i} }N_{i,p-1} (u)+\\ \qquad \dfrac{u_{i+p+1} -u}{u_{i+p+1} -u_{i+1} }N_{i+1,p-1} (u) \\ \end{array} \right\}$
(51) $\begin{eqnarray} \label{eq51} { C}(u)=\frac{\sum\limits_{i=0}^n {N_{i,p} (u)\omega_{i} { P}_{i} } }{\sum\limits_{i=0}^n {N_{i,p} (u)\omega_{i} } }, \ \ a\leqslant u\leqslant b \end{eqnarray}$
式中, $ P_{i}$是控制点, $\omega_{i}$是权系数.
5 直/曲梁结构大变形静力学分析
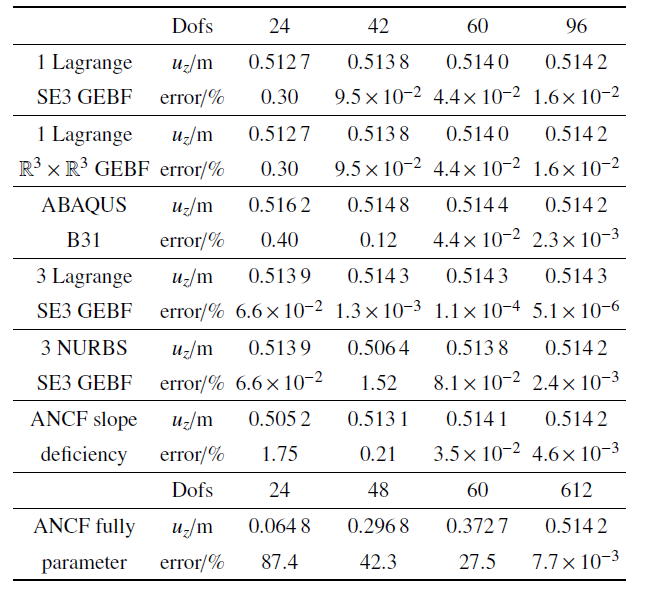
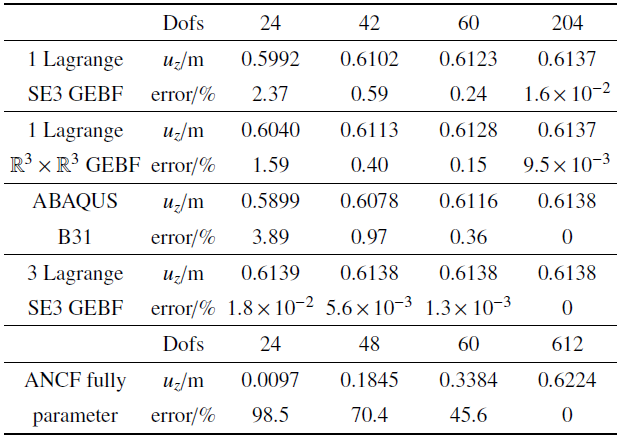
本节考察$XOY$平面内的直梁与曲梁模型, 验证上述闭锁处理方法的有效性. 其中, 悬臂直梁长$L = 1$ m; 悬臂曲梁半径$R = 1$ m, 初始构型为1/4圆. 梁的截面均为矩形, 宽和高为0.01 m; 材料的杨氏模量为$E = 2.1$ $\times$ 10$^{11}$ Pa, 泊松比为$\nu = 0.3$. 首先, 在直梁和曲梁末端分别施加集中力(30, 20, 400) N (直梁)、(30, 20, 100) N (曲梁), 用ABAQUS计算得到梁端点沿$z$方向的位移分别为0.5143 m (直梁)、0.6138 m (曲梁). 计算的过程中, 上述两类载荷均分为10个加载步均匀加载. 此外, 对直梁与曲梁进行纯弯曲测试. 在直梁和曲梁末端均施加$z$方向的力矩$M_{z}=-\pi EI/2L$, 由材料力学解答知, 梁端沿$z$方向转角位移的解析解为$\theta_{z}=-\pi /2$.
5.1 悬臂直梁和曲梁低阶单元闭锁缓解方法数值测试
本节考查SE(3)几何精确一阶直梁与曲梁单元在三维复杂应力状态下, 缩减积分技术和Hu-Washizu三场变分原理缓解剪切闭锁的能力.
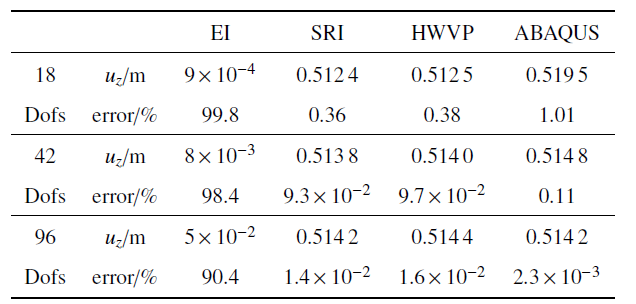
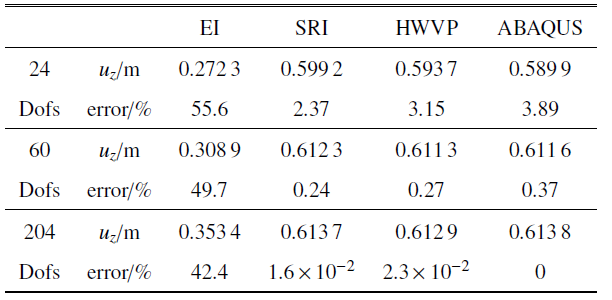
悬臂直梁和曲梁末端受集中力的作用, 变形如图2 所示. 单元位移场采用一阶Lagrange插值. 对比分析完全积分(exact integration, EI)、缩减积分(reduced integration, RI)和Hu-Washizu三场变分原理(Hu-Washizu variational principle, HWVP)三种情况, 在不同自由度(degrees of freedom, Dofs)下悬臂梁末端点$z$方向的位移$u_{z}$, 计算相对误差, 将结果列于表1 和表2 中. 同时, 采用ABAQUS软件中B31梁单元(该单元为三维二节点一阶梁单元, 每个节点6个广义坐标, 分别是3个平移和3个转动参数)对本算例进行仿真计算.
图2
图2
(a)直梁和(b)曲梁变形前后示意图
Fig.2
Initial and deformed configurations of (a) the straight beam and (b) the curved beam
表1 和表2 的数值结果表明: 采用缩减积分技术的SE(3)几何精确梁与ABAQUS中B31单元收敛结果基本一致. 采用Hu-Washizu三场变分原理缓解闭锁的SE(3)几何精确梁与其他两类方法的收敛结果不同, 其中, 直梁模型收敛值偏大, 曲梁模型收敛值偏小. 在三维复杂应力状态下, 一阶直梁和曲梁均有剪切闭锁问题. 缓解闭锁后, 直梁的计算精度提高了98%以上, 曲梁的计算精度提高了52%以上, 效果十分显著. 对于一阶直梁, 以上两种缓解闭锁的方法计算精度无明显差别. 对于一阶曲梁, 缩减积分技术的计算精度略高于Hu-Washizu三场变分原理.
5.2 悬臂直梁和曲梁纯弯曲测试
本节考查SE(3)几何精确一阶直梁与曲梁单元在纯弯曲应力状态下, 缩减积分技术和Hu-Washizu三场变分原理缓解剪切闭锁的能力, 同时评价单元描述纯弯曲的能力.
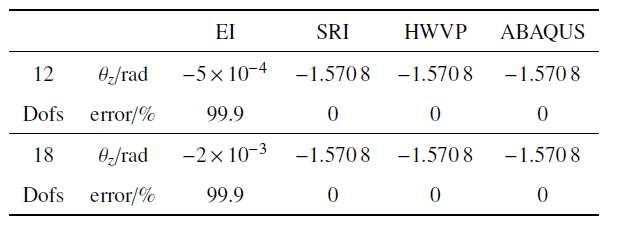
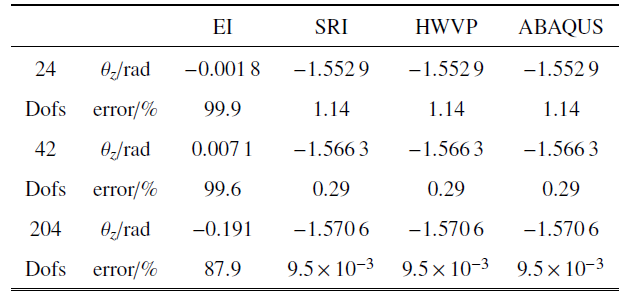
在悬臂直梁和曲梁末端施加集中弯矩, 此时, 悬臂梁发生纯弯曲, 处于简单应力状态. 单元位移场采用一阶Lagrange插值. 对比分析完全积分、缩减积分和Hu-Washizu三场变分原理三种情况下, 悬臂梁末端点$z$方向的转角位移$\theta_{z}$, 计算相对误差, 将结果列于表3 和表4 中. 同时, 采用ABAQUS软件中B31梁单元对本算例进行仿真计算.
表3 和表4 的数值结果表明: 在纯弯曲应力状态下, 一阶直梁和曲梁均有剪切闭锁问题. 缓解闭锁后, 直梁和曲梁模型的计算精度均提高了98%以上, 效果十分显著. 而且, 以上两种缓解闭锁的方法和ABAQUS中B31单元的计算精度完全一致. 表3 中, 一阶直梁在任意单元数目下, 转角与解析解的相对误差均为零. 这是由于SE(3)几何精确直梁模型能够精确地构造一个常弯曲单元, 因此仅用1个单元就能够精确模拟纯弯曲状态下的转动场. 表4 中, 一阶曲梁模型的转角渐近收敛, 这是由于一阶插值函数无法精确地描述一段圆弧.
同时, 采用三阶Lagrange插值构造了高阶几何精确直梁与曲梁单元. 通过上述悬臂直梁与曲梁算例, 测试了单元收敛精度, 其中同样采用Hu-Washizu三场变分原理处理剪切闭锁. 数值结果表明: 处理闭锁不会提升单元收敛性能, 进一步说明了高阶直梁与曲梁单元不存在剪切闭锁. 在5.3节中, 将进一步对比处理闭锁后的一阶单元与高阶单元的收敛性.
5.3 几类局部标架梁单元收敛性对比分析
本节对比一阶和三阶SE(3)几何精确梁单元、一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁、ANCF缩减(slope deficiency)梁、ANCF全参数梁与ABAQUS软件中B31梁单元的收敛性. 其中, 一阶几何精确梁与ANCF全参数梁单元均已处理闭锁.
在悬臂直梁和曲梁末端施加集中力. 计算以上几类建模方法在不同自由度下悬臂梁末端点$z$方向的位移$u_{z}$和相对误差, 将结果列于表5 和表6 中. ANCF缩减曲梁单元无算进行本算例的计算。
表5 和表6 的数值结果表明: 直梁模型的五种建模方法收敛结果基本一致. 对于曲梁模型, SE(3)几何精确梁、$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁和ABAQUS中B31单元收敛结果基本一致, ANCF全参数梁单元收敛结果略大于其他三类方法的收敛值. 需要指出的是, 表5 中三阶NURBS插值的SE(3)几何精确梁单元在24个自由度时, 虽然计算结果的相对误差为6.6 $\times$ 10$^{-4}$, 但此时单元还没有收敛, 60个自由度时, 单元才收敛. 对于高阶单元, 三阶Lagrange比三阶NURBS插值的SE(3)几何精确梁的计算精度高, 几类几何精确梁均比ANCF梁单元的计算精度高. ANCF缩减梁比ANCF全参数梁单元的计算精度高.
对于一阶直梁单元, 两类几何精确梁具有完全相同的计算精度. 对于一阶曲梁单元, $\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁的计算精度略高于SE(3)几何精确梁. 对于一阶直梁和曲梁单元, 两类几何精确方法均比ABAQUS中B31单元的计算精度高. 显然高阶单元比低阶单元精度高, 但是高阶单元计算效率低, 即自由度相同时, 高阶单元刚度矩阵内非零元素的个数多.
6 高转速/大变形柔性多体系统动力学验证算例
本节通过高转速曲柄滑块机构以及空间双摆的动力学仿真, 分析局部标架下的梁单元在动力学仿真中的计算精度差异, 以及消除刚体运动带来的几何非线性后梁单元的数值特性. 由于商业软件无法直接进行大变形柔性多体系统动力学仿真, 因此本节不再采用商业软件进行仿真对比. 为了设计特定的小变形或大变形的柔性多体系统动力学模型, 本节算例中部分材料参数未与真实材料对应.
本节数值算例共涉及如下3类建模方法: (1)一阶和三阶Lagrange插值的SE(3)几何精确梁单元; (2)一阶Lagrange插值的$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁单元; (3) ANCF全参数梁单元. 需要指出的是, 除了三阶SE(3)几何精确梁单元, 其他单元均已处理闭锁.
6.1 发生小变形和中等变形的高速旋转的平面曲柄滑块机构
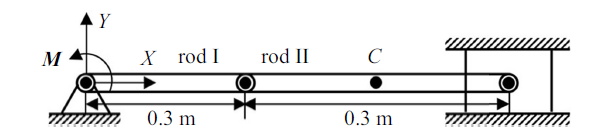
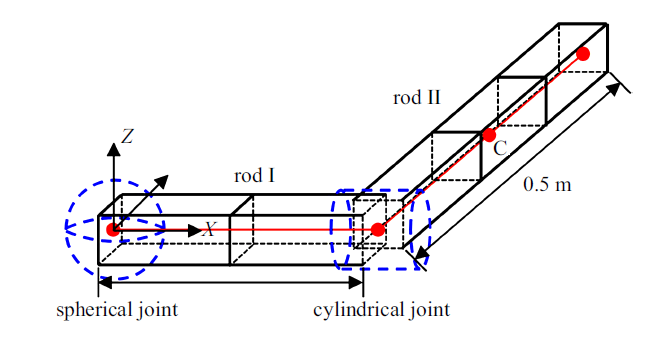
本节对一个典型的多体系统————曲柄滑块机构进行动力学仿真. 如图3 所示, 平面曲柄滑块机构由两根杆与一个滑块组成, 杆I一端与地面采用球铰相连接, 另一端与杆II一端也通过球铰连接, 杆II末端与一个仅能在$X$轴上运动的刚体滑块铰接.
图3
图3
曲柄滑块机构本
Fig.3
A crank-slider mechanism
算例中, 通过杆II中点$C$到其首尾连线的距离$d$度量杆II的弹性变形, 变形率为$d$与杆原长之间的比值. 同时, 以1944个自由度的$\mathbb{R}^{3}$空间ANCF全参数梁单元所得到的数值结果作为参考值, 建模方法数值结果收敛标准设为变形场最大值与参考解的相对误差在1%以内.
杆I与杆II的长度分别为0.3 m和0.5 m, 两杆的截面均为矩形, 宽与高为0.05 m, 材料参数设为: $\rho = 2000$ kg/m$^{3}$, $E = 8.2$ $\times$ 10$^{12}$ Pa, $\nu = 0.3$. 杆II末端滑块的质量为0.1 kg. 系统初始静止放置于$XOY$水平面内, 杆I与$X$轴夹角为0$^\circ$. 在曲柄上施加$Z$方向力矩900 N$\cdot$m, 持续时间为0.2 s, 杆I的最大转速约为1033 rad/s. 时间积分算法采用广义$\alpha $方法, 仿真时间为0.2 s, 时间步长设为1.0 $\times$ 10$^{-4}$ s, 算法参数谱半径设为0.8.
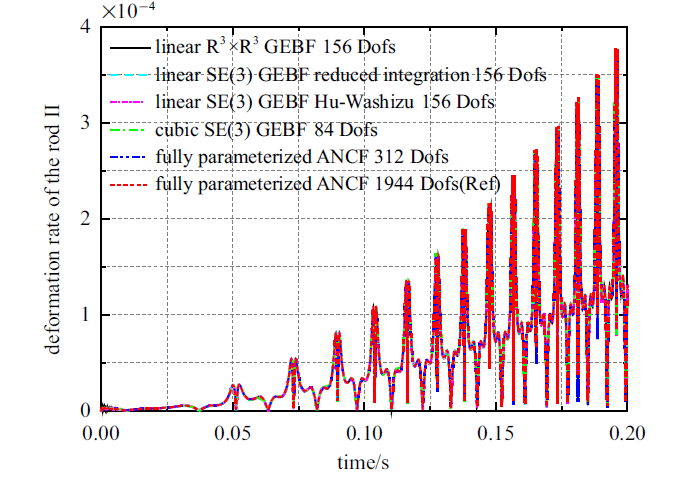
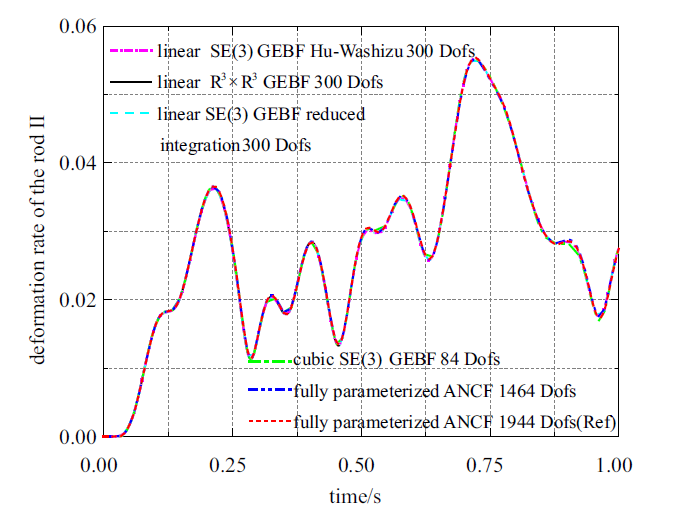
通过试算, 三阶SE(3)几何精确梁84个自由度收敛, 采用缩减积分技术和Hu-Washizu三场变分原理的一阶SE(3)几何精确梁与一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁均在156个自由度收敛, ANCF全参数梁312个自由度收敛. 图4 给出了上述三类建模方法收敛时杆II变形率随时间的变化曲线. 随着转速增大, 杆II的变形逐渐增大, 最大变形能够达到杆长度的0.04%.
图4
图4
杆II变形率随时间变化曲线
Fig.4
Deformation rate of the rod II
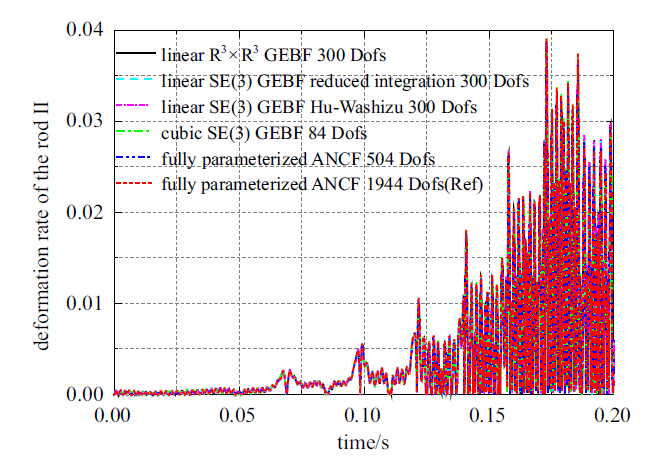
杆I与杆II的长度分别为0.3 m和0.5 m, 两杆的截面均为矩形, 宽与高为0.03 m, 材料参数设为: $\rho = 5600$ kg/m$^{3}$, $E = 4.1$ $\times$ 10$^{11}$ Pa, $\nu = 0.3$. 杆II末端滑块质量为0.1 kg. 系统初始静止放置于$XOY$水平面内, 杆I与$X$轴夹角为0$^\circ$. 在曲柄上施加$Z$方向力矩500 N$\cdot$m, 持续时间为0.2 s, 杆I的最大转速约为518 rad/s. 时间积分算法采用广义$\alpha$方法, 仿真时间为0.2 s, 时间步长设为3.0 $\times$ 10$^{-5}$ s, 算法参数谱半径设为0.8.
通过试算, 三阶SE(3)几何精确梁84个自由度收敛, 采用缩减积分技术和Hu-Washizu三场变分原理的一阶SE(3)几何精确梁与一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁均在300个自由度收敛, ANCF全参数梁504个自由度收敛. 图5 给出了上述三类建模方法收敛时杆II变形率随时间的变化曲线. 随着转速增大, 杆II的变形逐渐增大, 最大变形能够达到杆长度的4%.
图5
图5
杆II变形率随时间变化曲线
Fig.5
Deformation rate of the rod II
由图4 和图5 可知, SE(3)几何精确梁、$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁和ANCF全参数梁均能达到收敛的数值结果, 验证了这三类建模方法在描述高转速、小变形以及中等变形多体系统动力学问题时的正确性. 采用缩减积分技术与Hu-Washizu三场变分原理可以缓解动力学问题中的剪切闭锁, 两种方法的收敛速度无明显差别. 一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁与一阶SE(3)几何精确梁收敛速度无明显差别.
在一个牛顿迭代步中, 最耗时的两个部分包括计算系统刚度矩阵与迭代矩阵的LU分解/回代. 由于本文中的梁单元均采用局部标架建模方法, 刚度矩阵更新次数大幅降低. 因此, 可通过计算迭代矩阵中非零元素的个数来评价一个牛顿迭代步的计算速度. 对于模型I, 几类一阶几何精确梁迭代矩阵非零元素的个数均为2808, 三阶SE(3)几何精确梁和ANCF全参数梁迭代矩阵非零元素的个数分别为3528和11 232. 对于模型II, 几类一阶几何精确梁迭代矩阵非零元素的个数均为5400, 三阶SE(3)几何精确梁和ANCF全参数梁迭代矩阵非零元素的个数分别为3528和18 144. 由以上数据可知, 在达到相同的计算精度时, 几类一阶几何精确梁计算效率相同, SE(3)和$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁的计算效率明显高于ANCF全参数梁.
其次, 通过分析系统质量矩阵和刚度矩阵更新情况, 验证基于局部标架的SE(3)几何精确方法能够有效地减轻刚体运动带来的非线性问题. 若忽略外力对应的Jacobian矩阵, 系统迭代矩阵的表达式为
(52) $\begin{eqnarray} \label{eq52} { J}_{\rm iter} =\left[\begin{array}{c@{\quad }c} h^{2}\beta ({ M}+{ K}) & \varPhi_{q}^{\rm T}\\ \varPhi_{q} & {\bf 0} \\ \end{array} \right] \end{eqnarray}$
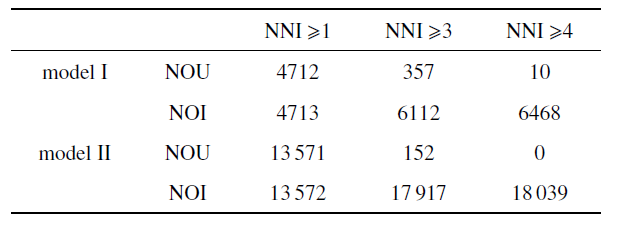
式中, $h$为积分步长, $\beta $为广义$\alpha $方法算法参数, $ M$为广义质量矩阵, $ K$为切线刚度矩阵, $ \varPhi_{q}$为约束方程的Jacobian矩阵. 本算例中, 牛顿迭代收敛标准设为广义坐标修正量$||\varDelta||^{2}< 1.0$ $\times$ 10$^{-6}$.表7 给出了一阶SE(3)几何精确梁迭代矩阵的主要部分$ J_{q} = h^{2}\beta ( M+ K)$的更新次数(number of update, NOU)以及仿真过程中牛顿迭代总次数(number of iterations, NOI). 表7 中"NNI $\geqslant i$"表示一个时间步内, 牛顿迭代次数大于等于$i$步时, $ J_{q}$强制更新.
模型I的数值结果表明: 对于基于局部标架的SE(3)几何精确梁模型, 若每个牛顿迭代步中$ J_{q}$均更新, 则整个仿真过程共需要进行4713次牛顿迭代步, 同时$ J_{q}$也需要更新4712次. 当NNI $\geqslant 3$时(即每个时间步中牛顿迭代达到三步时更新一次$ J_{q})$, $ J_{q}$需要更新357次, 总迭代次数增加了30%左右. 当NNI $\geqslant 4$时(即每个时间步中牛顿迭代达到四步时更新一次$ J_{q})$, $ J_{q}$需要更新10次, 总迭代次数增加了37%左右. 模型II与模型I情况类似, 这里不再赘述. 由此可得, 对于此类高速转动的多体动力学问题, 基于局部标架的SE(3)几何精确梁能够极大地降低刚体运动带来的几何非线性.
6.2 发生中等变形和超大变形的空间双摆
本节对空间双摆模型进行动力学仿真. 如图6 所示, 空间双摆模型初始放置于$XOY$水平面上, 并在重力作用下开始运动. 与算例6.1一致, 本算例通过杆II中点$C$到其首尾连线的距离$d$度量杆II的弹性变形, 变形率为$d$与杆原长之间的比值. 同时, 以1944个自由度的$\mathbb{R}^{3}$空间ANCF全参数梁单元所得到的数值结果作为参考值, 建模方法数值结果收敛标准设为变形场最大值与参考解的相对误差在1%以内.
图6
图6
空间双摆
Fig.6
A spatial double pendulum
双摆两个摆臂的长度分别为0.3 m和0.5 m, 两个摆臂的截面均为矩形, 宽与高为0.5 mm, 材料参数设为: $\rho = 2700$ kg/m$^{3}$, $E = 2.1$ $\times$ 10$^{10}$ Pa, $\nu = 0.3$, 重力加速度为$g = 9.81$ m/s$^{2}$. 时间积分算法采用广义$\alpha $方法, 仿真时间1 s, 时间步长设为5.0 $\times$ 10$^{-4}$ s, 算法参数谱半径设为0.8.
通过试算, 三阶SE(3)几何精确梁84个自由度收敛, 采用缩减积分技术和Hu-Washizu三场变分原理的一阶SE(3)几何精确梁均在300个自由度收敛, ANCF全参数梁1464个自由度收敛. 300个自由度的一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁在$t = 0.457 5$ s发散. 图7 给出了上述三类建模方法收敛时杆II变形率随时间的变化曲线, 最大变形能够达到杆长度的5.5%.
图7
图7
杆II变形率随时间变化曲线
Fig.7
Deformation rate of the rod II
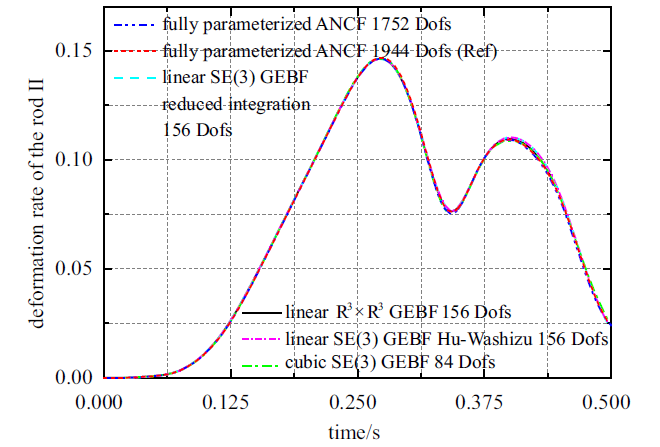
双摆两个摆臂的长度分别为0.3 m和0.5 m, 两个摆臂的截面均为矩形, 宽与高为0.3 mm, 材料参数设为: $\rho = 2700$ kg/m$^{3}$, $E = 1.5$ $\times$ 10$^{10}$ Pa, $\nu = 0.3$, 重力加速度为$g = 9.81$ m/s$^{2}$. 时间积分算法采用广义$\alpha $方法, 仿真时间0.5 s, 时间步长设为5.0 $\times$ 10$^{-4}$s, 算法参数谱半径设为0.8.
通过试算, 三阶SE(3)几何精确梁84个自由度收敛, 采用缩减积分技术和Hu-Washizu三场变分原理的一阶SE(3)几何精确梁156个自由度收敛, ANCF全参数梁1752个自由度收敛. 156个自由度的一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁在$t = 0.444 5$ s发散. 图8 给出了上述三类建模方法收敛时杆II变形率随时间的变化曲线, 最大变形能够达到杆长度的15%.
图8
图8
杆II变形率随时间变化曲线
Fig.8
Deformation rate of the rod II
由图7 和图8 可知, SE(3)几何精确梁、$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁和ANCF全参数梁均能达到收敛的数值结果, 验证了这三类建模方法在描述中等变形和超大变形多体系统动力学问题时的正确性. 采用缩减积分技术与Hu-Washizu三场变分原理均可有效缓解动力学中的剪切闭锁问题, 两种方法的收敛速度无明显差别.
下面通过计算迭代矩阵中非零元素的个数来评价一个牛顿迭代步的计算速度. 对于模型III, 几类一阶几何精确梁迭代矩阵非零元素的个数均为5400, 三阶SE(3)几何精确梁和ANCF全参数梁迭代矩阵非零元素的个数分别为3528和52 704. 对于模型IV, 几类一阶几何精确梁迭代矩阵非零元素的个数均为2808, 三阶SE(3)几何精确梁和ANCF全参数梁迭代矩阵非零元素的个数分别为3528和63 072. 由以上数据可知, 在达到相同的计算精度时, 几类一阶几何精确梁计算效率相同, SE(3)几何精确梁的计算效率明显高于ANCF全参数梁.
通过与6.1节中等变形的平面多体系统对比, 可以发现, 随着柔性体变形的增大, SE(3)几何精确梁比ANCF全参数梁单元优势更明显. 一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁在仿真计算的过程中发散, 是由于本文仅采用Rescaling技术[32 ] 处理转动参数, 没有进一步采用其他方法避免转动参数的奇异性. 相比较而言, 本文提出的局部标架建模方法则可自然地避免转动参数的奇异性问题.
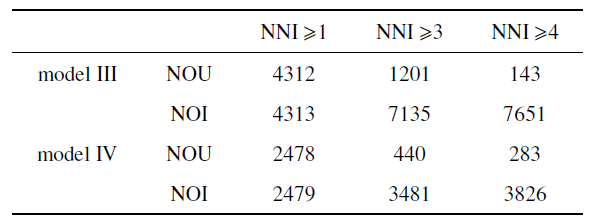
与6.1节统计方法类似, 通过分析系统质量矩阵和刚度矩阵更新情况, 以说明基于局部标架的SE(3)几何精确建模方法描述大转动、大变形非线性运动的能力. 本算例中, 牛顿迭代收敛标准设为广义坐标修正量$||\varDelta||^{2}<1.0$ $\times$ 10$^{-6}$. 表8 中给出了一阶SE(3)几何精确梁$ J_{q}$的更新次数以及仿真过程中的牛顿迭代总次数.
模型IV的数值结果表明: 对于基于局部标架的SE(3)几何精确梁模型, 若每个牛顿迭代步中$ J_{q}$均更新, 则整个仿真过程共需要进行2479次牛顿迭代步, 同时$ J_{q}$也需要更新2478次. 当NNI $\geqslant 3$时(即每个时间步中牛顿迭代达到三步时更新一次$ J_{q})$, $ J_{q}$需更新440次, 总迭代次数增加了40%左右. 当NNI $\geqslant4$时(即每个时间步中牛顿迭代达到四步时更新一次$ J_{q})$, $ J_{q}$需要更新283次, 总迭代次数增加了54%左右. 模型III与模型IV情况类似, 这里不再赘述. 由此可得, 对于此类大变形多体动力学问题, 基于局部标架的SE(3)几何精确梁仍然能够明显地降低刚体运动带来的几何非线性.
7 结论
本文基于李群SE(3)局部标架, 研究几类梁单元的闭锁缓解方法. 采用Hu-Washizu三场变分原理缓解了SE(3)几何精确梁单元中的剪切闭锁, 采用应变分解法缓解了ANCF全参数梁单元中的泊松闭锁, 并对SE(3)几何精确梁、$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁和ANCF全参数梁的单元性能进行了算例对比. 静力学与动力学算例结果均表明, 缓解闭锁后的SE(3)几何精确梁计算精度高. 在进行大转动、大变形动力学计算时, $\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁单元会出现转动参数奇异问题, 若处理不当则会不收敛, 而SE(3)几何精确梁单元可避免转动参数奇异性问题. SE(3)几何精确梁的广义质量矩阵主项为常数, 与转动参数相关的切线刚度矩阵满足刚体转动的不变性, 在计算中无须更新, 可极大地减少迭代矩阵的更新次数, 有效地提高计算效率. 基于SE(3)群局部标架的几何精确建模方法更适合用于描述梁结构的大转动、大变形运动.
参考文献
View Option
[1]
Meier C Popp A Wall WA . Geometrically exact finite element formulations for slender beams: Kirchhoff-Love theory versus Simo-Reissner theory
Archives of Computational Methods in Engineering 2019 ,26 (1 ):163 -243
[本文引用: 1]
[2]
孙加亮 , 田强 , 胡海岩 . 多柔体系统动力学建模与优化研究进展
力学学报 , 2019 ,51 (6 ):1565 -1586
[本文引用: 1]
( Sun Jialiang Tian Qiang Hu Haiyan . Advances in dynamic modeling and optimization of flexible multibody systems
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1565 -1586 (in Chinese))
[本文引用: 1]
[3]
Schulz M Böl M . A finite element formulation for a geometrically exact Kirchhoff-Love beam based on constrained translation
Computational Mechanics 2019 : 1 -21
[本文引用: 1]
[4]
Choi MJ Cho S . Isogeometric configuration design sensitivity analysis of geometrically exact shear-deformable beam structures
Computer Methods in Applied Mechanics and Engineering 2019 ,351 :153 -183
[本文引用: 1]
[5]
Duan LP Zhao JC . A geometrically exact cross-section deformable thin-walled beam finite element based on generalized beam theory
Computers and Structures 2019 ,218 :32 -59
[本文引用: 1]
[6]
Lestringant C Audoly B Kochmann DM . A discrete, geometrically exact method for simulating nonlinear, elastic and inelastic beams
Computer Methods in Applied Mechanics and Engineering 2020 ,361 :112741
[本文引用: 1]
[7]
Shabana AA . An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies
Chicago: University of Illinois at Chicago , 1996
[本文引用: 1]
[8]
范纪华 , 章定国 , 谌宏 . 基于绝对节点坐标法的弹性线方法研究
力学学报 , 2019 ,51 (5 ):1455 -1465
[本文引用: 1]
( Fan Jihua Zhang Dingguo Shen Hong . Research on elastic line method based on absolute nodal coordinate method
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (5 ):1455 -1465 (in Chinese))
[本文引用: 1]
[9]
吴吉 , 章定国 , 黎亮 等 . 带集中质量的旋转柔性曲梁动力学特性分析
力学学报 , 2019 ,51 (4 ):1134 -1147
[本文引用: 1]
( Wu Ji Zhang Dingguo Li Liang , et al . Dynamic characteristics analysis of a rotating flexible curved beam with a concentrated mass
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):1134 -1147 (in Chinese))
[本文引用: 1]
[10]
Liu C Tian Q Yan D . et al . Dynamic analysis of membrane systems undergoing overall motions, large deformations and wrinkles via thin shell elements of ANCF
Computer Methods in Applied Mechanics and Engineering 2013 ,258 :81 -95
[本文引用: 1]
[11]
Rong JL Wu ZP Liu C . et al . Geometrically exact thin-walled beam including warping formulated on the special Euclidean group SE(3)
Computer Methods in Applied Mechanics and Engineering 2020 ,369 :113062
[本文引用: 3]
[12]
Zienkiewicz OC Taylor R Too JM . Reduced integration technique in general analysis of plates and shells
International Journal for Numerical Methods in Engineering 1971 ,3 (2 ):275 -290
[本文引用: 1]
[13]
Zienkiewicz OC Owen DRJ Lee KN . Least square-finite element for elasto-static problems. Use of 'reduced' integration
International Journal for Numerical Methods in Engineering 1974 ,8 (2 ):341 -358
[本文引用: 1]
[14]
Hughes TJR Taylor RL Kanoknukulchai W . A simple and efficient finite element for plate bending
International Journal for Numerical Methods in Engineering 1977 ,11 (10 ):1529 -1543
[本文引用: 1]
[15]
Simo JC Vu-Quoc L . A three-dimensional finite-strain rod model. Part II: Computational aspects
Computer Methods in Applied Mechanics and Engineering 1986 ,58 (1 ):79 -116
[本文引用: 1]
[16]
Malkus DS Hughes TJR . Mixed finite element methods-reduced and selective integration techniques: A unification of concepts
Computer Methods in Applied Mechanics and Engineering 1978 ,15 (1 ):63 -81
[本文引用: 1]
[17]
Noor AK Peters JM . Mixed models and reduced/selective integration displacement models for nonlinear analysis of curved beams
International Journal for Numerical Methods in Engineering 1981 ,17 (4 ):615 -631
[本文引用: 1]
[18]
Pian THH . Finite elements based on consistently assumed stresses and displacements
Finite Elements in Analysis and Design 1985 ,1 (2 ):135 -140
[本文引用: 1]
[19]
Liu WK Belytschko T Chen J . Nonlinear versions of flexurally super convergent elements
Computer Methods in Applied Mechanics and Engineering 1988 ,71 (3 ):241 -258
[本文引用: 1]
[20]
Dorfi HR Busby HR . An effective curved composite beam finite element based on the hybrid-mixed formulation
Computers and Structures 1994 ,53 (1 ):43 -52
[本文引用: 1]
[21]
Simo JC Rifai MS . A class of mixed assumed strain methods and the method of incompatible modes
International Journal for Numerical Methods in Engineering 1990 ,29 (8 ):1595 -1638
[本文引用: 1]
[22]
Simo JC Armero F . Geometrically non-linear enhanced strain mixed methods and the method of incompatible modes
International Journal for Numerical Methods in Engineering 1992 ,33 (7 ):1413 -1449
[本文引用: 1]
[23]
Andelfinger U Ramm E . EAS-elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-elements
International Journal for Numerical Methods in Engineering 1993 ,36 (8 ):1311 -1337
[本文引用: 1]
[24]
Pian THH Sumihara K . Rational approach for assumed stress finite elements
International Journal for Numerical Methods in Engineering 1984 ,20 (9 ):1685 -1695
[本文引用: 1]
[25]
Gerstmayr J Shabana AA . Analysis of thin beams and cables using the absolute nodal co-ordinate formulation
Nonlinear Dynamics 2006 ,45 (1-2 ):109 -130
[本文引用: 1]
[26]
Gerstmayr J Matikainen MK . Analysis of stress and strain in the absolute nodal coordinate formulation
Mechanics Based Design of Structures and Machines 2006 ,34 (4 ):409 -430
[本文引用: 1]
[27]
Kerkkaenen KS Sopanen JT Mikkola AM . A linear beam finite element based on the absolute nodal coordinate formulation
Journal of Mechanical Design 2005 ,127 (4 ):621 -630
[本文引用: 1]
[28]
Gerstmayr J Matikainen MK Mikkola A . A geometrically exact beam element based on the absolute nodal coordinate formulation
Multibody System Dynamics 2008 ,20 (4 ):359 -384
[本文引用: 1]
[29]
Matikainen MK Dmitrochenko O Mikkola A . Beam elements with trapezoidal cross section deformation modes based on the absolute nodal coordinate formulation//International Conference on Numerical Analysis and Applied Mathematics,
Greece , 2010 : 1266 -1270
[本文引用: 1]
[30]
Patel M Shabana AA . Locking alleviation in the large displacement analysis of beam elements: The strain split method
Acta Mechanica 2018 ,229 (7 ):2923 -2946
[本文引用: 2]
[31]
[本文引用: 1]
( Liu Cheng Hu Haiyan . Dynamic modeling and computation for flexible multibody systems based on the local frame of Lie group
Chinese Journal of Theoretical and Applied Mechanics 2021 ,53 (1 ), doi: 10.6052/0459-1879-20-292 (in Chinese))
[本文引用: 1]
[32]
Olivier AB . Flexible Multibody Dynamics
Springer Netherlands , 2011 : 534 -537
[本文引用: 1]
Geometrically exact finite element formulations for slender beams: Kirchhoff-Love theory versus Simo-Reissner theory
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
多柔体系统动力学建模与优化研究进展
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
多柔体系统动力学建模与优化研究进展
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
A finite element formulation for a geometrically exact Kirchhoff-Love beam based on constrained translation
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
Isogeometric configuration design sensitivity analysis of geometrically exact shear-deformable beam structures
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
A geometrically exact cross-section deformable thin-walled beam finite element based on generalized beam theory
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
A discrete, geometrically exact method for simulating nonlinear, elastic and inelastic beams
1
2020
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies
1
1996
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
基于绝对节点坐标法的弹性线方法研究
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
基于绝对节点坐标法的弹性线方法研究
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
带集中质量的旋转柔性曲梁动力学特性分析
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
带集中质量的旋转柔性曲梁动力学特性分析
1
2019
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
Dynamic analysis of membrane systems undergoing overall motions, large deformations and wrinkles via thin shell elements of ANCF
1
2013
... 几何精确方法[1 ] (geometrically exact formulation, GEF)与绝对节点坐标方法[2 ] (absolute nodal coordinate formulation, ANCF)是描述大转动、大变形柔性多体系统的两类常用的建模方法. 20世纪80年中期, 李群/李代数基本理论逐渐与非线性有限元方法融合, 以解决梁、板/壳结构的大转动、大变形动力学问题. 几何精确建模方法在有限元理论框架下利用节点位置矢量与转动伪矢量作为节点参数描述三维梁大转动、大变形运动, 对位置矢量与转动伪矢量独立插值[3 ] . 其中涉及的两个核心算法在于: 第一、刚体旋转矩阵在李群SO(3)内采用乘法更新, 对应的转动伪矢量由对数映射确定, 满足刚体转动合成的几何意义[4 ] . 第二、通过转动参数定义梁截面局部标架, 并在局部标架下研究梁微元的动能与弹性势能, 即拉伸、剪切、扭转、弯曲应变以及截面角速度均定义在局部标架内[5 -6 ] . 在多体系统动力学领域, Shabana[7 ] 于1996年提出了绝对节点坐标方法, 其本质上也属于一种非线性有限元方法[8 ] . 该方法在处理物体转动问题上, 摒弃复杂的转动参数, 采用节点位置矢量以及沿物质坐标的斜率矢量来描述物体转动, 可方便地建立大转动、大变形柔性多体系统动力学模型[9 -10 ] . ...
Geometrically exact thin-walled beam including warping formulated on the special Euclidean group SE(3)
3
2020
... 已有研究表明, 在局部标架思想下, 可构造出一类SE(3)几何精确梁单元[11 ] 以及绝对节点坐标梁单元. 局部标架梁单元能够规避刚体运动带来的几何非线性问题, 离散数值模型中广义质量矩阵与切线刚度矩阵满足刚体变换的不变性, 可明显地提高柔性多体系统动力学问题的计算效率. 在有限元方法中, 梁、板/壳单元普遍存在剪切、薄膜以及泊松闭锁问题. 多年来, 有限元领域学者提出了许多单元技术来有效地缓解闭锁. 本文主要关注如何提高局部标架梁单元的收敛性, 关于李群局部标架建模与计算方法涉及的其它细节本文不再赘述, 可参见作者的相关研究工作. ...
... 式中, $ A$为一个任意的6 $\times$ 1的矢量, 记号${\Xi }_{\rm T'}^{(1)} $和${\Xi }_{\rm T'}^{(2)} $分别是矩阵${\varXi }_{\rm T'} $的前半部分和后半部分, 其具体形式可参见文献[11 ]. 因此, 几何部分为 ...
... 对梁中线位置矢量$ x$和截面相对旋转伪矢量$\varTheta^{r}$[11 ] 进行空间离散 ...
Reduced integration technique in general analysis of plates and shells
1
1971
... 缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性". ...
Least square-finite element for elasto-static problems. Use of 'reduced' integration
1
1974
... 缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性". ...
A simple and efficient finite element for plate bending
1
1977
... 缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性". ...
A three-dimensional finite-strain rod model. Part II: Computational aspects
1
1986
... 缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性". ...
Mixed finite element methods-reduced and selective integration techniques: A unification of concepts
1
1978
... 缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性". ...
Mixed models and reduced/selective integration displacement models for nonlinear analysis of curved beams
1
1981
... 缩减积分是解决闭锁问题最广泛使用的技术之一. Zienkiewicz等[12 ] 最早将缩减积分应用于壳单元、等参四边形单元和梁单元[13 ] , 提高了单元精度. Hughes等[14 ] 将选择缩减积分应用于板单元, 缓解了薄板的剪切闭锁. Simo等[15 ] 采用缩减积分技术缓解了几何精确梁中的剪切闭锁. Malkus和Hughes[16 ] 证明了某些混合列式与使用缩减积分的位移公式的等价性, 并且表明缩减积分单元可以达到多变量有限元的性能. Noor和Peters[17 ] 在曲梁中应用选择缩减积分, 并通过比较刚度矩阵讨论了混合列式和位移列式的等价性和"近等价性". ...
Finite elements based on consistently assumed stresses and displacements
1
1985
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
Nonlinear versions of flexurally super convergent elements
1
1988
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
An effective curved composite beam finite element based on the hybrid-mixed formulation
1
1994
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
A class of mixed assumed strain methods and the method of incompatible modes
1
1990
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
Geometrically non-linear enhanced strain mixed methods and the method of incompatible modes
1
1992
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
EAS-elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-elements
1
1993
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
Rational approach for assumed stress finite elements
1
1984
... 混合法不仅假设位移场, 同时假设应力场或应变场, 是一种高性能的多变量有限元方法, 已被广泛用于解决体积闭锁、剪切闭锁和薄膜闭锁等问题. 1985年, Pian[18 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合单元, 采用假设应力和位移场改善了梁和板的弯曲性能. 1988年, Liu等[19 ] 提出了基于Hu-Washizu三场变分原理的弯曲超收敛单元, 该单元在粗网格中显示出良好的精度. 1994年, Dorfi和Busby[20 ] 提出了一种基于Hellinger-Reissner两场变分原理的混合曲梁单元, 该单元的位移和应力具有良好的收敛性. 1990年, Simo和Rifai[21 ] 提出了增强假设应变法, 该方法是一种具有变分基础的闭锁缓解技术. 随后, Simo和Armero[22 ] 将增强应变法推广到了几何非线性问题中. 1993年, Andelfinger和Ramm[23 ] 利用增强应变法开发了二维和三维板和壳单元, 并证明了该方法与基于Hellinger-Reissner两场变分原理的假设应力法[24 ] 是等价的. ...
Analysis of thin beams and cables using the absolute nodal co-ordinate formulation
1
2006
... ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能. ...
Analysis of stress and strain in the absolute nodal coordinate formulation
1
2006
... ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能. ...
A linear beam finite element based on the absolute nodal coordinate formulation
1
2005
... ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能. ...
A geometrically exact beam element based on the absolute nodal coordinate formulation
1
2008
... ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能. ...
Beam elements with trapezoidal cross section deformation modes based on the absolute nodal coordinate formulation//International Conference on Numerical Analysis and Applied Mathematics,
1
2010
... ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能. ...
Locking alleviation in the large displacement analysis of beam elements: The strain split method
2
2018
... ANCF全参数(fully parameterized)梁单元基于三维连续介质力学方法计算广义弹性力, 当泊松比不为零时, 其计算结果不能收敛到正确解. 该问题即为泊松闭锁[25 ] . 起初, 学者们令泊松比为零[26 ] 或通过简化应力张量[27 ] 除去泊松效应, 缓解了泊松闭锁. 随后, Gerstmayr等[28 ] 采用选择缩减积分技术缓解了泊松闭锁, 同时在单元的变形模式中保留了泊松效应. 2010年, Matikainen等[29 ] 提出了一种高阶三维ANCF梁单元, 该单元对截面进行二次插值, 有效地缓解了泊松闭锁, 但是单元自由度过多. 2018年, Patel和Shabana[30 ] 提出了一种新型闭锁缓解技术——应变分解法(strain split method, SSM). 该方法通过分解Green-Lagrange应变张量并修改本构模型, 假设仅与梁中线变形相关的低阶应变具有泊松效应, 忽略正应变的高阶项的泊松效应, 显著改善了梁的弯曲性能. ...
... Green-Lagrange应变张量可以分解为两部分$ \varepsilon = \varepsilon^{\rm c} + \varepsilon^{k}$[30 ] , 式中, ...
基于李群局部标架的多柔体系统动力学建模与计算
1
2021
... 基于经典的Timoshenko梁假设, 李群几何精确梁理论融合非线性有限元方法与几何力学思想, 在李群SE(3)内建立系统的平衡方程, 可精确地描述柔性梁的大转动、大变形刚柔耦合动力学特性, 同时可规避刚体运动带来的几何非线性[31 ] . ...
基于李群局部标架的多柔体系统动力学建模与计算
1
2021
... 基于经典的Timoshenko梁假设, 李群几何精确梁理论融合非线性有限元方法与几何力学思想, 在李群SE(3)内建立系统的平衡方程, 可精确地描述柔性梁的大转动、大变形刚柔耦合动力学特性, 同时可规避刚体运动带来的几何非线性[31 ] . ...
Flexible Multibody Dynamics
1
2011
... 通过与6.1节中等变形的平面多体系统对比, 可以发现, 随着柔性体变形的增大, SE(3)几何精确梁比ANCF全参数梁单元优势更明显. 一阶$\mathbb{R}^{3}$ $\times$ $\mathbb{R}^{3}$几何精确梁在仿真计算的过程中发散, 是由于本文仅采用Rescaling技术[32 ] 处理转动参数, 没有进一步采用其他方法避免转动参数的奇异性. 相比较而言, 本文提出的局部标架建模方法则可自然地避免转动参数的奇异性问题. ...