引言
自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献.
各种连续体结构拓扑优化方法基本上集中在 建模途径和求解效率上,而对于优化模型是否合理以及模型之 间的相互关系则缺乏注意. 研究优化模型的合理性始于隋允康等将 MCVC (minimumcompliances with a volume constraint) 模型同 MVDC (minimum volume with displacementconstraints) 模型进行比较[19 -21 ] ,说明 MCVC 模型约束条件值的选取和多工况时目标函数的不合理性.
需要指出的是 (1)"合理与否"是各个层次的"结构优化模型"中的共同问题,只是在结构拓扑优化中显得更加突出.(2)"优化 模型的合理与否"不同于"结论的正确与否".结论的正确与否证明即可,而优化模型的合理与否需要花费较多的篇幅阐述.
为了节省读者查阅文献[19 ,20 ,21 ] 时间,这里给出"结构优化设计模型合理与否"的诠释.
在结构优化设计的模型中,常常存在如下特点的问题:(1) 本来可以建立单目标函数最优的问题却不适当处理成多目标最优的问题;(2)需要先验、无根据地预先给出一些约束值,从而导致最优点不恰当地依赖于约束值而变成为难以从最优解集中确定出有限个解;(3)多层次的优化问题不能按同一个标准建立模型,以至于有些不同层次选取的目标函数与约束函数是不同的,甚至出现关注没有工程意义的力学性能的情况;(4)本来应该追求满足工程规范或力学性能的经济指标最小,却不必要的追求工程规范或力学性能的最佳而很难预先设定经济指标约束限.
如果上述模型经过对于目标函数与约束条件的对调,其中的任何一个问题都不再出现,那么,就可以把原来的问题称为一个"不合理的模型",相应地,调整后的问题成为"合理的模型".
在连续体结构拓扑优化的背景下,作者团队进一步研究模型合理化与否,同运筹学中数学规划论的对偶规划[22 -25 ] 比对,从而提出了互逆规划的概念[26 ] .
互逆规划的两方具有目标函数与约束条件相互交换位置的对应关系,它的意义在于:揭示了数学规划领域里,除了存在对偶理论,还存在与之表面相似却不同的互逆规划理论,也就是说,对于数学规划补充了新的理论内容;利用该理论审视结构拓扑优化的模型,揭示了不合理的模型是因为相关的研究者没有采用互逆规划的 s 方 (单目标函数) 建模,而是采用了 m 方 (多目标函数) 建模. 研究表明,互逆规划在结构拓扑优化研究中具有明确的力学背景和广泛的应用价值.
基于文献[26 ] 提出的互逆规划,本文发展了相关定义及理论,内容如下:
(1) 把 s-m 型互逆规划拓宽出 s-s 型互逆规划和 m-m 型互逆规划,从而得到 3 种类型的互逆规划.
(2) 对于 3 种互逆规划分别推导出各自两方面的 KKT 条件关系,并且揭示了两方关系的本质,提出了 3 个定理.
1 将互逆规划由 1 种推广为 3 种
文献[26 ] 提出了 s-m 型互逆规划,由 s 方和 m 方两个问题数学规划问题组成:(1) s 方——取单个目标函数和多个约束条件;(2) m 方——取 s 方的多个约束条件作为该方的目标函数,取 s 方的目标函数作为该方的约束条件.
为了完善互逆规划的理论,本文把单目标和单约束构成的一对互逆规划定义为 s-s 型互逆规划,把多目标和多约束构成的一对互逆规划定义为 m-m 型互逆规划.
从表达方便出发,将各种互逆规划的两方按表示的顺序分别称为正向问题 (forward problem, FP)、反向问题 (reverse problem, RP). 若交换表示的顺序,也就将一对互逆规划的 FP 问题和 RP 问题换位,两种表达的本质是一样的.
这是 FP 问题和 RP 问题皆为单目标函数的互逆规划. 也就是说,其 FP 问题和 RP 问题都只有单个约束条件.
(1a) ${FP}: \ \left\{ \!\!\begin{array}{l} {find}: x \in E^N \\ \min : H(x) \\ {s.t.} G(x) = \overline G \end{array} \right. $
(1b) ${RP}: \ \left\{ \!\!\begin{array}{l} {find}: x \in E^N \\ \min : G(x) \\ {s.t.} H(x) = \overline H \end{array} \right.$
这是 FP 问题和 RP 问题分别为多目标函数和单目标函数的互逆规划. 也就是说,其 FP 问题和 RP 问题分别具有个单约束条件和多个约束条件.
(2a) ${FP}: \ \left\{ \!\!\begin{array}{l} {find}: x \in E^N \\ \min : H_i (x) \ (i = 1,2,\cdots,L) \\ {s.t.} G(x) \leqslant \overline G \end{array} \right.$
(2b) ${RP}: \ \left\{ \!\!\begin{array}{l} {find}: x \in E^N \\ \min : G(x) \\ {s.t.} H_i (x) \leqslant \overline {H_i } \ (i = 1,2,\cdots,L) \end{array} \right.$
FP 问题和 RP 问题孰在前、孰在后,只是顺序的不同,并不影响问题的本质,因而 m-s 型互逆规划同文献[26 ] 提出的 s-m 型互逆规划实际是同一个事物.
这是 FP 问题和 RP 问题皆为多目标函数的互逆规划. 也就是说,其 FP 问题和 RP 问题也都具有多个约束条件.
(3a) ${FP}: \ \left\{ \!\!\begin{array}{l} {find}: x \in E^N \\ \min : H_i (x) \ (i = 1,2,\cdots,L) \\ {s.t.} G_j (x) \leqslant \overline {G_j } \ (j = 1,2,\cdots,M) \end{array} \right.$
(3b) ${RP}: \ \left\{ \!\!\begin{array}{l} {find}: x \in E^N \\ \min : G_j (x) \ (j = 1,2,\cdots,M) \\ {s.t.} H_i (x) \leqslant \overline {H_i } \ (i = 1,2,\cdots,L) \end{array} \right.$
以上提出的 s-s 型互逆规划和 m-m 型互逆规划,是对文献[26 ] 提出的互逆规划的推广. 推广之后的互逆规划共分上述 3 类.
2 互逆规划基于 KKT 条件的 3 个定理
一对互逆规划,由于双方的约束条件不同,二者的可行域是不同的,一般说来,不能保证两个可行域有交集,更不可能期望这对互逆规划的解相同. 本文的研究得到两个结论:其一、发掘出一对互逆规划两个 KKT 条件内在关连的 3 个定理;其二、利用一对互逆规划任一方的最优解调整另一方的约束条件,可以求出拟相同的最优解.
下面分别叙述 s-s 型、s-m 型和 m-m 型互逆规划问题的上述两个结论. 限于篇幅,本文只给出定理 2 的证明,略掉了相对容易的定理 1 与 3 的证明.
2.1 s-s 型互逆规划的两方 KKT 条件及其关系
定理 1 对于 s-s 型互逆规划的双方,其一、两个 KKT 条件在形式上相像,称为拟同构;其二、部分调整参数后的互逆规划双方在数值上拟同解,即取一方的最优解或 KKT 点的目标函数值,作为另一方面的约束限值,则该最优解也满足调整了上述参数后的另一方的 KKT 条件.
2.2 s-m 型互逆规划的两方 KKT 条件及其关系
对于 s-m 型互逆规划,也有同定理 1 类似却不同的定理,为了方便予以叙述和论证,首先定义多目标规划 FP 问题式 (2a) 和单目标 RP 问题式 (2b) 的两方 Lagrange 函数如下
(4) $L(x,\lambda ,\mu ) = \sum_{i = 1}^L {\lambda _i H_i (x)} + \mu (G(x) -\overline G )$
(5) $\hat {L}({\pmb x},\hat {\mu }, \hat{\pmb \lambda }) = \hat {\mu }G({\pmb x}) + \sum_{i = 1}^L {\hat {\lambda }_i (H_i ({\pmb x}) - \bar {H}_i )}$
其中 $\mu $ 与 $\hat {\mu }$ 分别为 Lagrange 乘子和常数,且 $\hat {\mu } = 1 $;$\lambda_i (i = 1,2,\cdots,L)$ 为 $H_i (x) (i = 1,2, \cdots,L)$ 的权系数,且 $\lambda _i > 0$;而 $ \hat{\lambda }_i (i = 1,2, \cdots, L)$ 为 Lagrange 乘子向量的分量.
需要说明一下:一般的多目标权系数都有归一化条件 $\lambda _{1} + \lambda _{2} + \cdots + \lambda _L = 1$,$\lambda _i \in(0,1)$,为了推导的方便,忽略这个不影响求解的条件,因为只要将每个权系数除以权系数之和,即可满足归一化条件.
若函数 $H_i (x) (i=1,2,\cdots,L)$ 和 $G(x)$ 是可微函数,且 $x^{\ast }$ 和 $\hat {x}^{\ast}$ 依次是式 (2a) 的帕累托最优解和式 (2b) 的最优解,则可以给出 s-m 型互逆规划的如下定理.
定理 2 对于 m-s 型或 s-m 型互逆规划的双方,其一、两个 KKT 条件拟同构;其二、两种情况下互逆规划双方拟同解:情况 1、先求解 m 方,取其帕累托最优解的多目标函数值,作为 s 方的多约束条件限值,然后求解调整上述参数后的 s 方,则 s 方与 m 方拟同解;情况 2、先求解 s 方,取其最优解的单目标函数值,作为 m 方的单约束条件限值,且取 s 方的最优的 Lagrange 乘子向量值作为 m 方的多目标的权系数向量值 (可以不满足归一化条件),然后求解调整上述参数后的 m 方,则 m 方与 s 方拟同解.
注:本定理中拟同构和拟同解的概念与定理 1 中的叙述相同.
记 $\lambda _i^\ast = \lambda _i $,$\hat {\mu }^{\ast} = \hat {\mu } = 1$ 则借助式 (4) 与式 (5),写出式 (2a) 与式 (2b) 的 KKT 条件,分别为
(6) $\left.\begin{array}{l} \dfrac{\partial L(x^{\ast },\lambda^{\ast },\mu^{\ast })}{\partial x_k } = \sum_{i = 1}^L {\lambda _i^{\ast }\dfrac{\partial H_i (x^{\ast })}{\partial x_k }} + \mu^{\ast }\dfrac{\partial G(x^{\ast })}{\partial x_k } = 0 \\ (k = 1,2,\cdots,N) \\ G(x^{\ast }) \leqslant \overline G \\ \mu^{\ast} ( G(x^{\ast }) - \overline G ) = 0 \\ \mu^{\ast} > 0 \end{array}\right\}$
(7) $\left.\begin{array}{l} \dfrac{\partial L(\hat {x}^{\ast },\hat {\mu }^{\ast },\hat {\lambda }^{\ast })}{\partial x_k } = \hat {\mu }^{\ast }\dfrac{\partial G(\hat {x}^{\ast })}{\partial x_k } + \sum_{i = 1}^L {\hat {\lambda }_i^{\ast }\dfrac{\partial H_i (\hat {x}^{\ast })}{\partial x_k }} = 0 \\ (k = 1,2,\cdots,N) \\ H_i (\hat {x}^{\ast }) \leqslant \overline {H_i } \\ \hat {\lambda }_i^\ast ( H(\hat {x}^{\ast }) - \overline H ) = 0 \\ \hat {\lambda }_i^\ast \geqslant 0 \ (i = 1, 2, \cdots ,L) \end{array}\right\}$
对于式 (6),将单约束 $G(x^{\ast }) \leqslant \overline G$ 视为起作用约束即 $G(x^{\ast }) = \overline G $,且 $\mu^{\ast }> 0 $;记 $H_i (x^{\ast }) = H_i^\ast $,当 $\lambda _i^\ast > 0 $ 时有 $\lambda _i^\ast ( H_i (x^{\ast }) - H_i^\ast ) = 0 $,故式 (6) 可以扩展为
(8) $\left.\begin{array}{l} \dfrac{\partial L(x^{\ast },\lambda^{\ast },\mu^{\ast})}{\partial x_k } = \sum_{i = 1}^L {\lambda _i^{\ast}\dfrac{\partial H_i (x^{\ast })}{\partial x_k }} + \mu^{\ast}\dfrac{\partial G(x^{\ast })}{\partial x_k } = 0 \\ H_i (x^{\ast }) \leqslant H_i ^{\ast } \\ \lambda _i^\ast (H_i (x^{\ast }) - H_i ^{\ast }) = 0 \\ \lambda _i^\ast > 0 \ (k = 1,2, \cdots ,N ; \ i = 1,2, \cdots ,L) \\ G(x^{\ast }) \leqslant \overline G \\ \mu^{\ast} ( G(x^{\ast }) - \overline G ) = 0 \\ \mu^{\ast} > 0\end{array}\!\! \right\}$
记 $G(x^{\ast }) = G^{\ast }$,同样式 (7) 也可以扩展为
(9) $\left.\begin{array}{l} \dfrac{\partial L(\hat {x}^{\ast },\hat {\mu }^{\ast },\hat {\lambda }^{\ast })}{\partial x_k } = \hat {\mu }^{\ast }\dfrac{\partial G(\hat {x}^{\ast })}{\partial x_k } + \sum_{i = 1}^L {\hat {\lambda }_i^{\ast }\dfrac{\partial H_i (\hat {x}^{\ast })}{\partial x_k }} = 0 \\ G(\hat {x}^{\ast }) \leqslant G^{\ast }\\ \hat {\mu }^{\ast} ( G(\hat {x}^{\ast }) - G^{\ast }) = 0 \\ \hat {\mu }^{\ast } = 1 \\ H_i (\hat {x}^{\ast }) \leqslant \overline {H_i } \\ \hat {\lambda }_i^\ast ( H(\hat {x}^{\ast }) - \overline H ) = 0 \\ \hat {\lambda }_i^\ast \geqslant {0} \ (k = 1,2, \cdots ,N ; \ i = 1,2, \cdots ,L) \end{array} \right\}$
比对式 (8) 与式 (9),将 $\lambda _i^{\ast }$ 与 $\hat {\lambda }_i^{\ast}$ 作为对应 量,$\mu _i^{\ast }$与$\hat {\mu }_i^{\ast }$ 作为对应量,$x^{\ast }$ 与 $\hat {x}_i^{\ast }$ 作为对 应量,不难证明定理 2 的前半部分:两组 KKT 条件具有形式上的同构性,称为拟同构. 不过有两点需注意:其 一, $\lambda _i^{\ast }$ 在式 (6) 中是预先确定的权系数且 $\lambda _i^{\ast} > 0 $, 而 $\hat {\lambda }_i^{\ast } (i = 1,2,\cdots,L)$ 是有待求解出来的未知数, 且 $\hat {\lambda }_i^{\ast } \geqslant {0}$. 其二,$\mu^{\ast }$ 是有待求解出来的 未知数且 $\mu^{\ast} > 0 $,而 $\hat {\mu }^{\ast }$ 是预先确定的已知数且 $\hat {\mu }^{\ast }= 1 $.
下面证明定理 2 的后半部分,具体可以分成两种情况:
情况 1:从式 (2a) 的解到式 (2b) 的解.
与式 (8) 同样记式 (2a) 的最优目标值为 $H_i (x^{\ast }) = H_i^{\ast } (i = 1,2, \cdots ,L)$,用此来调整式 (2b) 的约束值,即取 $\bar {H}_i = H_i ^{\ast } (i = 1, 2,\cdots ,L)$. 为了进一步的证明,把式 (8) 与式 (9) 分别写为
(10) $\left.\begin{array}{l} \dfrac{\partial L ({\pmb x}^*, {\pmb \lambda}^*, \mu^*)}{\partial x_k}=um^L_{i=1} \dfrac{\lambda_i^*}{\mu^*} \dfrac{\partial H_i({\pmb x}^*)}{\partial x_k} +\dfrac{\partial G({\pmb x}^*)}{\partial x_k}=0\\ H_i ({\pmb x}^*) \leq H^*_i \\ \dfrac{\lambda_i^*}{\mu^*} (H_i({\pmb x}^*)-H^*_i) =0 \\ G({\pmb x}^*)=\bar G \\ \dfrac{\lambda_i^*}{\mu^*} >0 \\ \mu^*>0 \\ (k=1,2,\cdots,N ; \ i=1,2,\cdots,L)\end{array} \right\}$
(11) $\left.\begin{array}{l} \dfrac{\partial G(\hat {x}^{\ast })}{\partial x_k } + \sum_{i = 1}^L {\hat {\lambda }_i^{\ast }\dfrac{\partial H_i (\hat {x}^{\ast })}{\partial x_k }} = 0 \\ G(\hat {x}^{\ast }) = \hat {G}^{\ast } \\ H_i (\hat {x}^{\ast }) \leqslant H_i^\ast \\ \hat {\lambda }_i^\ast ( H_i (\hat {x}^{\ast }) - H_i^\ast ) = 0 \\ \hat {\lambda }_i^\ast \geqslant {0} \ (k = 1,2, \cdots ,N ; \ i = 1,2, \cdots ,L) \end{array}\!\! \right\}$
在式 (11) 的求解中,第 2 式不需要求解,因它只表明 $G(\hat {x}^{\ast }) = \hat {G}^{\ast}$,欲从式 (11) 的其余式子中解出 $\hat {x}^{\ast }$ 和 $\hat {\lambda }_i^\ast (i = 1,2,\cdots,L)$,对比式 (10),可看出,$\dfrac{\lambda _i^{\ast }}{\mu^{\ast }}$ 与 $\hat {\lambda }_i^\ast $,$x^{\ast }$ 与 $\hat {x}_i^{\ast }(i = 1,2, \cdots ,L)$ 是两种对应的形式参数,可取式 (11) 的解为 $\hat{\lambda }_i^\ast = \dfrac{\lambda _i^{\ast }}{\mu^{\ast }} (i = 1,2, \cdots ,L)$,$\hat {x}_i^{\ast }=x^{\ast }$.
结论是:由式 (2a) 的解调整式 (2b) 的约束值之后,式 (2a) 的 Pareto 最优解是式 (2b) 的 KKT 点,或称为两方拟同解.
情况 2:从式 (2b) 的解到式 (2a) 的解.
记式 (2b) 的最优目标值为 $\hat {G}_i (x^{\ast }) = \hat {G}_i^{\ast } (i = 1, 2, \cdots ,L)$,Lagrange 乘子的最优值为 $\hat {\lambda }_i^\ast (i = 1$, $2, \cdots,L)$,用它们调整式 (2a) 的参数,取 $\bar {G} = \hat {G}^\ast $,$\lambda _i = \lambda _i^\ast = \hat {\lambda }_i^\ast\geqslant 0 (i = 1,2, \cdots ,L)$,此时式 (8) 与式 (9) 分别可以写为
(12) $\left.\begin{array}{l} \sum^L_{i=1} \hat \lambda_i^* \dfrac{\partial H_i ({\pmb x}^*)}{\partial x_k} +\mu^* \dfrac{\partial G ({\pmb x}^*)}{\partial x_k} =0 \\ H_i ({\pmb x}^*) \leq H^*_i \\ \hat \lambda_i^* (H_i ({\pmb x}^*)-H^*_i ) =0 \\ G ({\pmb x}^*)=\hat G^* \\ \hat\lambda^*_i \geq 0 , \ \ \mu^* \geq 0 \\ (k=1,2,\cdots,N ; \ i=1,2,\cdots,L)\end{array} \right\}$
(13) $\left.\begin{array}{l} \dfrac{\partial G(\hat {x}^{\ast })}{\partial x_k } + \sum_{i = 1}^L {\hat {\lambda }_i^{\ast }\dfrac{\partial H_i (\hat {x}^{\ast })}{\partial x_k }} = 0 \\ H_i (\hat {x}^{\ast }) \leqslant H_i ^{\ast }\\ \hat {\lambda }_i^{\ast} ( H_i (\hat {x}^{\ast }) - H_i ^{\ast }) = 0 \\ G(\hat {x}^{\ast }) = \hat {G}^{\ast } \\ \hat {\lambda }_i^\ast \geqslant {0} \\ (k = 1, 2,\cdots ,N ; \ i = 1, 2, \cdots ,L) \end{array} \!\! \right\}$
在式 (12) 的求解中,其中第 2,3 式不需要求解,因它们只表示 $H_i (x^{\ast }) = H_i ^{\ast } (i = 1, 2,\cdots ,L)$. 欲从式 (12) 的其余式子中求解,只需将 (12) 和 (13) 进行比较,可看出 $x^{\ast}$ 与 $\hat {x}^{\ast }$ 是对应的形式参数,由此解得 $\hat {\mu }^{\ast } = 1$,$\hat {x}^{\ast} = x^{\ast}$.
结论是:由式 (2b) 的最优解对式 (2a) 的两个参数予以调整,其一是用 (2b) 的最优化目标代替 (2a) 的约束值,其二是用 (2b) 的最优的 Lagrange 乘子代替 (2a) 的目标函数权系数的若干倍,此时的式 (2b) 单目标最优解是式 (2a) 的带权重系数的多目标规划的 KKT 点,称为拟同解.
两种情况可以概括为定理 2 的后半部分,根据任一方的最优解调整第二方的约束限并取为约束式,以及在第二方为多目标时,用第一方的 Lagrange 乘子代替多目标的权系数的若干倍,此时两个互逆规划拟同解.
2.3 m-m 型互逆规划的两方 KKT 条件及其关系
定理 3 对于 m-m 型互逆规划的双方,表达Pareto 最优解须满足的 KKT 条件,其一、双方的 KKT 条件是拟同构;其二、部分调整参数后的互逆规划与另一方是拟同解,即取任一方最优点时多目标函数值作为另一方的多约束限值,且取第一方最优的 Lagrange 乘子向量值作为第二方的多目标函数权系数向量值 (可以不满足归一化条件),则按上述调整参数后的第二方与另一方拟同解.
注:本定理中拟同构和拟同解的概念与定理 1 中的叙述相同.
3 互逆规划的应用和求解
3.1 互逆规划的应用
文献[26 ] 应用互逆规划揭示了结构优化中存在有不合理模型,例如:结构拓扑优化结构体积约束下多工况柔顺度最小问题,属于不合理的多目标模型,依照本文发展的互逆规划理论予以剖析,是 m-s 型问题的 FP (正向问题) 方.
尽管上述 m-s 型问题的 FP 方属于不合理的多目标模型,但是基于互逆规划,取其 RP (反向问题) 方可以得到单目标模型,是合理的模型. 于是,本来在 FP 问题必须面对的多目标函数和体积约束限难以选取的两个致命困难,在 RP 问题中就不复存在了.
单工况下,若目标函数取柔顺度最小,鉴于其结构体积约束值很难预先确定,也属于不合理问题. 按照本文拓宽出的 s-s 类模型互逆规划去理解和处理,取其对应的另一方,就可以得到合理的模型了.
本文完善的互逆规划理论不仅对于建立模型的合理化有裨益,而且采用 3 个定理,对于已经建立起的模型,可以提供有效的解法. 这就是后续即将叙述的互逆规划的求解策略和具体解法.
多目标规划问题的求解,在数学规划中发展得比较缓慢,尤其寻求 Pareto 最优解集时,前提是要选定恰当的权系数,这是较难操作的. 本文提出了预选权系数的新途径,即按涉及 m-m 型问题的定理 3 予以处理,详细做法将在 3.3 小节叙述.
总之,文献[26 ] 揭示了存在互逆规划的两方,而本文则扩充了互逆规划的类型,并且揭示了互逆规划双方的内在关连. 前者有助于识别出不合理的状态,并且将其转化为合理的问题,后者则依靠互逆规划的双方关连性补充了求解的方法.
3.2 互逆规划的求解策略和具体做法
首先从工程实际或物理问题的自身背景角度,审视该问题是否合理?如果是合理的,就进入求解阶段;如果属于不合理的问题,建议从互逆规划出发,考虑其另一方,那可能就是一个合理的模型.
对于合理的规划问题,如果是单目标函数,就按以往的有效算法;如果是多目标函数,3.3 小节将予以阐述.
对于必须求解的不合理规划问题,首先按互逆规划理论建立其对应的合理问题,然后按合理的一方求解,从而确定不合理规划一方难以确定的参数,最后就可以求解不合理规划问题了,3.4 小节将予以阐述.
存在 2 种情况:其一是,待求解的一方是合理的,直接求解即可;待求解的一方是不合理的,则先求解其互逆对应的合理一方,然后借鉴定理1调整不合理一方的参数后,再予以求解.
存在 4 种情况:其一是,待求解的 s 方是合理的,直接求解这个单目标、多约束的问题即可;其二是,待求解的 s 方是不合理的、而 m 方是合理的规划,按 3.3 小节介绍的凝聚函数方法处理目标函数,先求解 m 方,用其解调整 s 方的参数,最后予以求解;其三是,待求解的 m 方是合理的规划,按凝聚函数方法处理目标函数,然后求解;其四是,待求解的 m 方是不合理的、而 s 方是合理的规划,先求解 s 方,用其解调整 m 方的参数,按帕累托模型求解 m 方.
存在 2 种情况:其一是,待求解的一方是合理的,直接求解即可,其中多目标按凝聚函数方法处理;其二是,待求解的一方是不合理的,则先按凝聚函数处理其互逆对应的合理一方的目标函数,接着求解,然后借鉴定理 3,用合理方的结果调整不合理方的参数后,最后求解其帕累托模型.
3.3 多目标问题的两种解法
定理 2 与定理 3 都涉及到多目标规划的求解问题,本文建议如下两种解法:
对于一个多目标优化问题,可以引用隋允康提出的统一的凝聚函数方法以及铁军、隋允康提出的抛物线凝聚函数方法[27 -28 ] ,通过适当简化以便于数值计算的方法将多目标化为一个凝聚的单目标函数. 需要指出,统一的凝聚函数方法统一了模优化 (norm optimization) 和 K-S 函数,即
(14) $F_{agg} ( a_i, p ) = \Big [ {log}_C \Big (\sum_{i = 1}^M C^{a_i^P } \Big ) \Big]^{\tfrac{1}{p}} \ \ (P > 0 , \ C > 0 , \ a_i > 0)$
(b) 模优化 (norm optimization)
(15) $F_{agg} ( a_i ,p ) = \Big (\sum_{i = 1}^M a_i^p \Big )^{\tfrac{1}{p}} , \ \ (a_i > 0 \ p > 0)$
(16) $ F_{agg} ( a_i, p ) = \dfrac{1}{P} {log}_C \Big (\sum_{i = 1}^M C^{Pa_i } \Big ) \ \ (P > 0 , \ C = e)$
(17) $ F_{agg} ( f_i ,p ) = \dfrac{1}{p} \Big [\ln \Big (\sum_{i = 1}^n {e}^{p^2f_i^2 (x)} \Big ) \Big]^{\tfrac{1}{2}} \ \ (p > 0 , \ f_i (x) \geqslant 0)$
利用凝聚函数,多目标优化问题可以转化为单目标优化问题. 凝聚函数 $H_{agg} (H_i(x),p)$ 代替式 (3a) 的多个目标函数的原因在于:凝聚函数有一个珍贵的性质,对于适当选择的拉伸因子 $P$,随着 $P$ 的增大,凝聚函数趋于 $\overline H =\max H_i (x) (i = 1,2,\cdots,L)$. 由此式得
(18) $ \min H_i (x)(i = 1,2,\cdots,L) \leqslant \min \overline H = \min \mathop {\max}\limits_{i = 1, 2,\cdots,L} H_i (x)$
式 (18) 左边表达了 $L$ 个多目标函数,右边表达了 1 个单目标函数.式 (18) 的本质是:它表述了多目标优化的 minimax 解法,而凝聚函数则是实施该解法的途径之一.
将式 (18) 和凝聚函数代入式 (3a) 中,得到了用单目标函数求解多目标优化式 (3a) 的如下问题
(19) $ \left.\begin{array}{l} {find}: {\pmb x} \in E^N \\ \min: H_{agg} (H_i ({\pmb x} ),p) \\ {s.t.} G_j ({\pmb x} ) \leqslant \overline G _j (j = 1,2,\cdots,M) \end{array} \!\! \right \}$
特别需要指出的是,在采用式 (14) $\sim$ 式 (17) 把多目标处理为一个凝聚函数时,为了满足被凝聚的每个函数都大于 0 的条件,可以对于每一可能会小于 0 的函数加上适合自己的充分大正数.
往下的具体求解可以采用研究者青睐的各种行之有效的约束规划算法,本文倾向于应用 DSQP (对偶序列二次规划) 算法[29 ] 或 DP-EM 方法[30 -31 ] .
一般地,多目标规划问题并不存在唯一的最优解,故以往解决多目标规划问题通常多依赖于寻求解帕累托模型的过程. 该解法的前提是,设取 $L$ 个目标函数的权系数,其本质也是将多个目标函数化为单个目标函数. 众所周知,权系数绝非是理性的预判,而是感性偏好的预设,最多也只能说是以往经验的积累.
顺便阐述帕累托解法与 minimax 解法的关系. 由 $ \overline H = \max H_i (x) (i= 1,2,\cdots,L)$ 得
(20) $ \sum_{i = 1}^L \lambda _i H_i (x) \leqslant \sum_{i = 1}^L \lambda _i \overline H = \overline H$
(21) $ \min \sum_{i = 1}^L \lambda _i H_i (x) \leqslant \min \overline H = \min \mathop {\max}\limits_{i = 1,2,\cdots,L} H_i (x)$
式 (21) 与式 (18) 比较,表明 minimax 解与帕累托解的关系,类似于 minimax 解与一般多目标解的关系.二者的区别在于:前者落脚于右式的单目标的选取方式,后者落脚于左式的多目标的权系数的选取上.
利用帕累托解法求解一般多目标问题解的前提是恰当地选取权系数,为了提出解决这一关键问题的新方法,前面在 3.2 小节介绍具体做法时已经提及,这里再详细阐明其中的两种途径.
3.2小节的具体做法 (2) 对应于 m-s 型或 s-m 型互逆规划,其中情况四是:待求解的 m 方是不合理的模型,而它对应的 s 方是合理的模型.
此时先求解 s 方问题 (2b),根据定理 2,用其解来调整 m 方的参数:取问题 (2b) 的 Lagrange 乘子的最优值作为式 (2a) 的多目标权系数,取问题 (2b) 的最优目标值作为式 (2a) 的约束限.此时作为 m 方的式 (2a) 就可 以按帕累托模型进行求解.
3.2小节的具体做法 (3) 对应于 m-m 型互逆规划,其中情况二是:待求解的一方是不合理的模型,而它对应的另一方是合理的模型,不妨假定它们依次为问题 (3a) 和问题 (3b).
此时先着手合理方对应的问题 (3b),先按凝聚函数处理式 (3b) 目标函数为单目标函数,接着求解. 接着根据定理 3,用式 (3b) 的解来调整式 (3a) 的参数:取问题 (3b) 的 Lagrange 乘子的最优值作为问题 (3a) 的多目标权系数,问题 (3b) 的最优的多目标值取作问题 (3a) 的多约束限. 此时的式 (3a) 可按帕累托模型进行求解.
上述两个途径的共性是:利用各自先求解的互逆规划第一方的最优 Lagrange 乘子向量取作第二方的多目标权系数向量,这是本文对于帕累托模型的贡献. 两个途径的个性只是在于第一方模型不同而造成的第一方求解差异.
另外,处理后的每一个单目标问题均可以利用 DSQP 算法求解.
3.4 利用互逆规划理论求出不合理问题的"合理结果"
文献[26 ] 从互逆规划的角度,揭示了结构拓扑优化里存在有不合理模型的情况,例如给定体积约束求柔顺度最小化的 MCVC 问题,本文 3.2 小节的求解策略和具体做法也提到不合理模型的情况,并且在具体做法里从 3 种类型互逆规划逐一进行了讨论.
本文作者一如既往的观点是:尽量建立和求解合理的规划;不过,也有不得不遭遇计算不合理模型的尴尬,例如:为了呼吁学者们抛弃不合理模型,采用合理的模型,就需要耐心地进行数值比较,既要计算出合理的结果,也要计算出不合理的结果.
为此,本文进行如下的工作:首先,在多工况条件下,取式 (2a) 代表给定体积约束的多个柔顺度皆最小化的 MCVC 问题,取式 (2b) 代表多个柔顺度约束的体积最小化 MVCC 问题. 利用 ICM 方法分别对于这个互逆规划的双方建立起优化模型.
设单元刚度矩阵和单元体积的过滤函数分别为 $f_k (x_i ) = x_i^3 $ 和 $f_v (x_i ) =x_i $ ($i = 1,2,\cdots, N)$.
(22) $ \left.\begin{array}{l} {find}: {\pmb x} \in E^N \\ \min: C_j = \sum_{i = 1}^N f_k (x_i ){\pmb u}_{ij}^{T} {\pmb k }_{ij}^0 {\pmb u }_{ij} \\ {s.t.}: V = \sum_{i = 1}^N f_v (x_i )v_i^0 \leqslant \bar{V} \end{array} \!\! \right \}$
其中,${\pmb x}$ 为设计变量向量,$C_j $,$K_j $,$F_j $ 和 $ U_j$ 分别为第 $j$ 号载荷工况的结构柔顺度、结构刚度矩阵、总载荷向量和总位移向量,$k_{ij} $ 和 $u_{ij}$ 分别为第$j$号载荷工况的单元位移列向量和单元刚度矩阵,$v_i$ 为单元 $i$ 的体积,$V$为结构总体积,$\overline V $ 为指定的体积上限约束.
(23) $ \left.\begin{array}{l} {find}: {\pmb x } \in E^N \\ \min : V = \sum_{i = 1}^N {f_v (x_i )v_i^0 } \\ {s.t.}: C_j = \sum_{i = 1}^N {f_k (x_i ){\pmb u }_{ij}^{T} {\pmb k }_{ij}^0 {\pmb u }_{ij} } \leqslant \bar {C}_j \end{array} \!\! \right \}$
其中,$\overline {C_j } $ 是结构柔顺度约束值.
式 (22) 相比式 (23),是不合理的. 原因不仅在于多目标上,更在于所给出作为结构体积上限 $\overline V$ 为指定的值,不具有理性的根据.因此,本文作者多次呼吁以 MVCC 问题替代 MCVC 问题,而且文献[26 ] 给出了结构柔顺度约束值的物理意义和计算公式.
从学术角度考虑,应当与同行作者的 MCVC 问题结果进行比较,导致本文作者不得不求解式 (22),从而探究不合理一方解法,进而利用互逆规划的定理 2,计算出不合理问题的"合理结果".亦即给出如下的建议:
首先求出式 (23) 的解 $V^\ast $,然后取式 (22) 的 $\overline V = V^\ast$,且取式 (23) 最优的 Lagrange 乘子向量作为式 (22) 的多目标权系数向量,加权求和使之成为单目标问题,当然也可以采用凝聚函数将式 (22) 化为单目标问题.也就是说,经过这一番由式 (23) 的解调整式 (22) 的参数,最后才有可能求解计算出不合理问题的"合理结果".
上面探讨了对于 m-s 型 (或 s-m 型) 互逆规划,借助于定理 2,从求解合理的 s 方的途径得到不合理的 m 方的"合理解"的过程. 类似地,对于 m-m 型互逆规划,借助于定理 3,也可以从求解合理的 m 方的途径,调整不合理的 m 方的参数,最后求出"合理解". 具体做法相似,此处不再赘述了.
4 数值算例
这里以两个数学问题和两个结构拓扑优化问题,作为本文应用的数值算例.
4.1 算例 1: 简单的 s-s 型数学规划问题
一对 s-s 型互逆规划如式 (24) 所示,其中式(20b) 中 $\langle$RP 问题 $\rangle$ 中的约束值,有待根据定理 1,由式 (24a) 即 $\langle$FP 问题 $\rangle$ 中的最优目标值确定.
(24a) ${FP}: \ \left\{ \!\! \begin{array}{l} \min : \ H = x_1^2 - 6x_1 + x_2^2 - 4x_2 \\ {s.t.} \ G = x_1 + x_2 = 4 \end{array} \right.$
(24b) ${RP}: \ \left\{ \!\!\begin{array}{l} \min :G = x_1 + x_2 \\ {s.t.} \ H = x_1^2 - 6x_1 + x_2^2 - 4x_2 = \bar {H} \end{array} \right.$
(25) $ L(x_1 ,x_2 ,\lambda ) = (x_1^2 - 6x_1 + x_2^2 - 4x_2 )+ \\ \lambda (x_1 + x_2 - 4)$
(26) $ \left.\begin{array}{l} \dfrac{\partial L}{\partial x_1 } = 2x_1 - 6 + \lambda\\ \dfrac{\partial L}{\partial x_2 } = 2x_2 - 4 + \lambda \\ \dfrac{\partial L}{\partial \lambda } = x_1 + x_2 - 4 = 0 \end{array} \!\! \right \}$
解出$x_1^\ast = 2.5$,$x_2^\ast = 1.5$,$\lambda^\ast = 1$,$H^\ast = -12.5$.
取 $\bar {H} = H^\ast = - 12.5$,求解 RP,构造 Lagrange 函数
(27) $ \hat {L}(x_1 ,x_2 ,\beta ) = (x_1 + x_2 ) +\\ \beta (x_1^2 - 6x_1 + x_2^2 - 4x_2 + 12.5)$
(28) $ \left.\begin{array}{l} \dfrac{\partial \hat {L}}{\partial x_1 } = 1 + \beta (2x_1 - 6) \\ \dfrac{\partial \hat {L}}{\partial x_2 } = 1 + \beta (2x_2 - 4) \\ \dfrac{\partial \hat {L}}{\partial \beta } = x_1^2 - 6x_1 + x_2^2 - 4x_2 + 12.5 = 0 \end{array}\!\! \right \}$
解出 $x_1^\ast = 2.5$,$x_2^\ast = 1.5$,$\beta ^\ast = 1$,$G^\ast =4$.
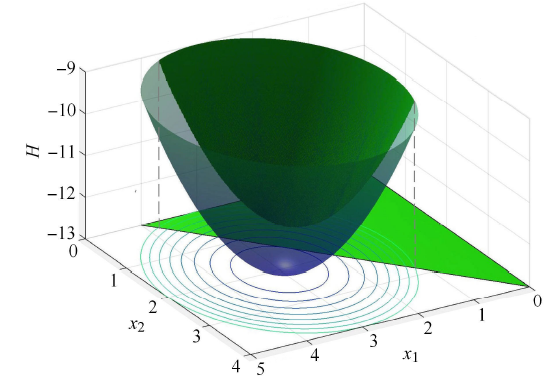
图1
图1
G 与 H 函数关系
Fig. 1
Relationship between G and H function
为了从直观上把握互逆规划,从 3 个方面进行如下讨论.
(29) $ {FP}: \ \left\{ \!\!\begin{array}{l} \min : \ H = x_1^2 - 6x_1 + x_2^2 - 4x_2 \\ {s.t.} \ G = x_1 + x_2 \leqslant 4 \end{array} \right.$
单约束问题若不退化为无约束问题,约束必定取等式. 按 KKT 条件叙述,即 Lagrange 乘子必不为 0,而为 正数.因此,式 (29) 是式 (24a) 的更一般情况.
目标函数是由大圆向圆心下降的等值圆族,这个结论可以由式 (29) 的目标函数负梯度的指向得出,也可以 从点 (3,0), (2.5, 1.5) 和 (3, 2) 目标函数值 $-9$, $-12.5$ 和 $-13$ 看到,它们分别是棕色圆、紫色圆和圆心的目标值.
最优点是在紫色圆与绿色直线的相切点,最优目标值等于 $-12.5$. 想象在设计变量-目标函数的里,目标函数构成了一个倒置的旋转面,旋转面的锥点高度为 $-13$,在高度为 $-12.5$ 处的旋转面的水平截线圆上一点,有一直线过该点,而这个直线的投影与过 (4, 4) 点,该直线就是可行域的边线.
顺便指出:式 (29) 的半无穷大可行域退化式 (24a) 等式表示的直线.
(30) $ {RP}: \ \left\{ \!\!\begin{array}{l} \min : \ G = x_1 + x_2 \\ {s.t.} \ H = x_1^2 - 6x_1 + x_2^2 - 4x_2 \leqslant - 12.5 \end{array} \right.$
图2
图2
FP 问题的几何直观
Fig. 2
Geometry of the FP program
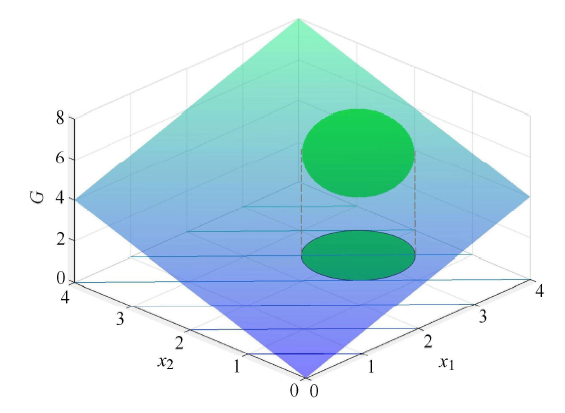
目标函数等值线是由与绿色直线平行的直线族组成,垂直于平行直线向左下方下降;可行域是包括紫色圆边线的圆区域.
最优点是在紫色圆与绿色直线的相切点,最优目标值等于 4.
在设计变量-目标函数的里,目标函数等值线构成了过 (0,0,0), (4,0,4) 和 (0,4,4) 三个点的无限大的平面.
图3
图3
RP 问题的几何直观
Fig. 3
Geometry of the RP program
顺便指出:式 (29) 的圆面积可行域退化式 (24b) 等式表示的圆周线可行域.
当 $H^\ast = - 12.5$ 时,求解式 (24b),可以得到如下结论:
① 若 $\bar {H} > H^\ast$,求解 RF 得到的 $G^\ast < 4$;
② 若 $\bar {H} = H^\ast$,求解 RF 得到的 $G^\ast = 4$;
③ 若 $\bar {H} < H^\ast$,求解 RF 得到的 $G^\ast > 4$.
该结论可如下推证. 取 $R$ 为圆心坐标为 (3, 2) 的圆的半径,令
$ x_1^2 - 6x_1 + x_2^2 - 4x_2 - \bar {H} = (x_1 - 3)^2 + (x_2 - 2)^2 - R^2 $
$ \bar {H} - H^\ast = R^2 - (H^\ast + 13) $
① 若 $\bar {H} > H^\ast$,则 $R^2 > H^\ast + 13$,该圆跨过了直线 $x_1 + x_2 =4$,求解 RF 得到的 $G^\ast < 4$;
② 若 $\bar {H} = H^\ast$,则 $R^2 = H^\ast + 13$,该圆相切于直线 $x_1 + x_2 =4$,求解 RF 得到的 $G^\ast = 4$;
③ 若 $\bar {H} < H^\ast$,则 $R^2 < H^\ast + 13$,该圆在直线 $x_1 + x_2 =4$ 的上方,求解 RF 得到的 $G^\ast > 4$.
4.2 算例 2: 简单的 m-s 型数学规划问题
(31a) ${FP}: \ \left\{ \!\!\begin{array}{l} \min : \ H = x_1^2 + x_2^2 \\ {s.t.} \ G_1 = - x_1 - 2x_2 \leqslant - 3 \\ \quad G_2 = - 2x_1 - x_2 \leqslant - 3 \end{array} \right.$
(31b) ${RP}: \ \left\{ \!\!\begin{array}{l} \min : \ G_1 = - x_1 - 2x_2 \\ {min}: \ G_2 = - 2x_1 - x_2 \\ {s.t.} \ x_1^2 + x_2^2 \leqslant \bar {H} \end{array} \right.$
(32) $ L(x_1 ,x_2 ,\lambda ) = (x_1^2 + x_2^2 )+\\ \lambda _1 ( - x_1 - 2x_2 + 3) + \lambda _2 ( - 2x_1 - x_2 + 3) $
(33) $ \left.\begin{array}{l} \dfrac{\partial L}{\partial x_1 } = 2x_1 - \lambda _1 - 2\lambda _2 = 0 \\ \dfrac{\partial L}{\partial x_2 } = 2x_2 - 2\lambda _1 - \lambda _2 = 0 \\ - x_1 - 2x_2 + 3 \leqslant 0 \\ - 2x_1 - x_2 + 3 \leqslant 0 \\ \lambda _1 ( - x_1 - 2x_2 + 3) = 0 \\ \lambda _2 ( - 2x_1 - x_2 + 3) = 0 \\ \lambda _1 \geqslant 0 \\ \lambda _2 \geqslant 0 \end{array} \right\}$
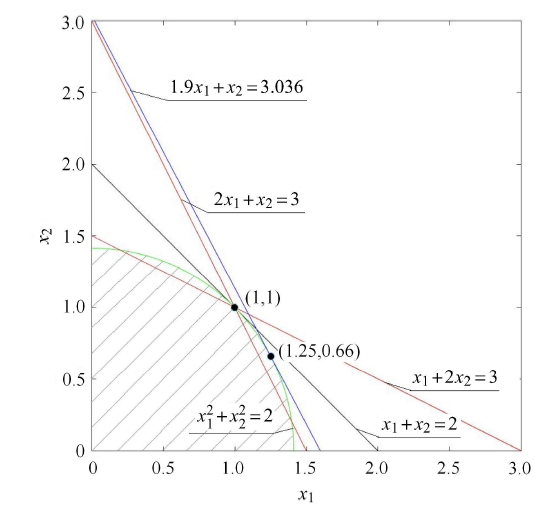
解出:$x_1^\ast = 1$,$x_2^\ast = 1$,$\lambda _1^\ast = 2 / 3$,$\lambda _2^\ast = 2 / 3$,$H^\ast = 2$.
图4
图4
FP 问题的目标函数及可行域
Fig. 4
Objective function and feasible region of the FP program
根据定理 2,取 Lagrange 乘子向量 $[\lambda _1^\ast$, $\lambda _2^\ast ] = [2 /3, 2 / 3]$ 作为 RF 模型的多目标权系数,进行归一化,得 $[w_1, w_2] =[0.5, 0.5]$,并取 $\overline H = H^\ast = 2$ 由此得到 RF 模型为
(34) $ \left.\begin{array}{l} \min : \ G = 0.5( - x_1 - 2x_2 ) + 0.5( - 2x_1 - x_2 ) =\\ - 1.5(x_1 + x_2 ) \\ {s.t.} \ H = x_1^2 + x_2^2 \leqslant 2 \end{array} \right \}$
因式 (28) 中仅一个约束,也可以按等式约束处理. 为了求解 FP,构造 Lagrange 函数
(35) $ \hat {L}(x_1 ,x_2 ,\beta ) = - 1.5(x_1 + x_2 ) + \beta [(x_1^2 + x_2^2 ) - 2]$
(36) $ \left.\begin{array}{l} \dfrac{\partial \hat {L}}{\partial x_1 } = - 1.5 + 2\beta x_1 = 0 \\ \dfrac{\partial \hat {L}}{\partial x_2 } = - 1.5 + 2\beta x_2 = 0 \\ \dfrac{\partial \hat {L}}{\partial \beta } = x_1^2 + x_2^2 - 2 = 0 \\ \beta (x_1^2 + x_2^2 - 2) = 0 \\ \beta \geqslant 0 \end{array} \!\! \right \}$
解出 $x_1^\ast = 1$,$x_2^\ast = 1$,$\beta ^\ast = 3 / 4$,$G^\ast = - 3$.
为了方便比较结果,图5 中画了式 (31b) 中的两个目标函数 $G_{1}$ 及 $G_{2}$ 最优点对应的直线线,它们对应的目标函数最优值分别为 $G_1^\ast= - 3$ 及 $G_2^\ast = - 3$. 还画了 $[w_1 ,w_2 ] = [0.1,0.9]$ 情况下最优点 (1.25,0.66) 对应的直线,其对应的目标函数最优值为 $G^\ast = - 3.036$.它们的最优点与式 (28) 的最优点在图5 上以 2 个黑点表示.
图5
图5
RP 问题的目标函数及可行域
Fig. 5
Objective function and feasible region of the RP program
4.3 算例 3: 单工况 MBB 梁问题拓扑优化
材料弹性模量 $E =2.1 \times 10^{5}$ MPa,泊松比为 0.3. 基结构宽为 300 mm、高 50 mm,取一半结构进行分析,左、右下角分别为铰支和滑动铰支约束,计算简图如图6 所示,采用 150$\times $50 网格.一个集中载荷 200 N 载荷工况,作用于跨中顶点,为避免应力集中,$F=100$ N 分散作用在相邻的 4 个结点上,右下角竖向约束也分散在 2 个结点上. 过滤半径为 3 mm,收敛精度取 0.001. 为了进行结果的比较,涉及到 MCVC 模型,惩罚 因子取 $p=3$, 分 别采用 20% 与 60% 的体积比约束值,进行两种情况的计算;涉及到 MVCC 模型,采用许用应力 $[\sigma ] =125$ MPa,对应的结构应变能约束值为 $\overline C = 10.012$ N$\cdot$mm[26 ] . 此例计算按如下 3 步进行.
图6
图6
MBB 梁问题取一半结构进行分析及优化的模型
Fig. 6
Half of structure for analysis and optimization of the MBB beam
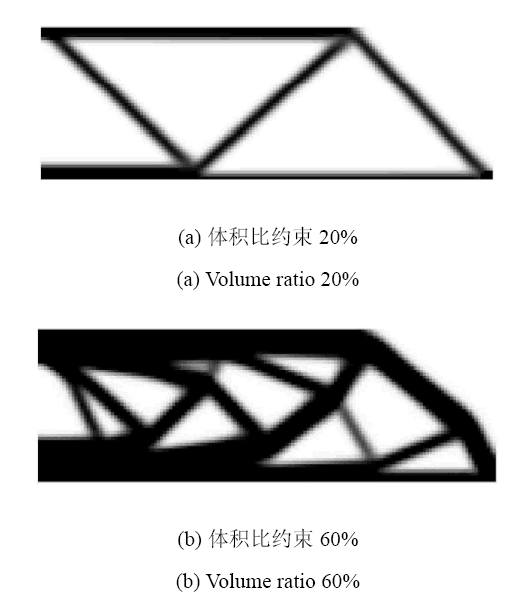
分别采用 20% 和 60% 的体积比约束值,最优拓扑图如图7 所示. 体积比约束 20% 时,最大应力 148.71 MPa,最优柔顺度 13.242 N$\cdot$mm;体积比约束 60% 时,最大应力 77.60 MPa,最优柔顺度 3.889 N$\cdot$mm.
图7
图7
MCVC 模型得到的最优拓扑
Fig. 7
Optimized topology obtained by the MCVC model
可以看到 MCVC 模型对不同的体积比约束值,不仅各自对应的最大 Mises 应力不同,而且更重要的是二者最优拓扑构型也不一样. 拓扑构型的不同与最大应力的差别皆源于体积比约束值各异. 究竟如何做,才能避免难以选取适当体积比约束值的困扰?为此,进行第二步计算.
以体积极小为目标、全局应变能约束计算所得最优拓扑如图8 (a) 所示. 对应的 Mises 应力分布如图8 (b) 所示. 最优体积比为 23.88%. 最大应力为 125.07 MPa,满足应力约束条件[26 ] . 为了便于第三步的数值比较,算出最优点处结构柔顺度为 $\overline C = 10.012$ N$\cdot$mm.
图8
图8
MVCC 模型得到的结果
Fig. 8
The results obtained by the MVCC model
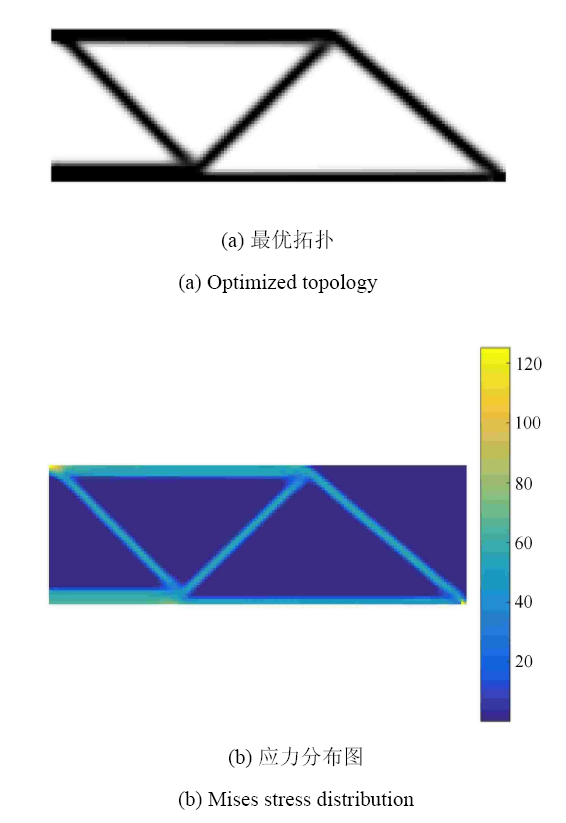
依据定理 1,将 MVCC 模型得到的最优体积比 23.88%,作为修正的 MCVC 模型的体积约束,再计算得到最优点结构柔顺度 $\overline C =10.121$ N$\cdot$mm,最优拓扑与 Mises 应力分布如图9 所示,最大应力为 124.75 MPa.
图9
图9
体积比 23.88% 时 MCVC 模型得到的结果
Fig. 9
The results obtained by the MCVC model with 23.88% volume ratio constraint
计算结果的拓扑构型、最大应力和结构柔顺度,都接近 MVCC 模型得到的结果. 以上三步计算,从 MVCC 模型--MVCC 模型--MCVC 模型,恰似一个否定之否定的过程.这个过程与依据"以往 MCVC 模型"求解的不同,在于"新 MCVC 模型"插入了上述的第二步.可见,依据 MVCC 模型可以确定 MCVC 模型一个恰当的体积比约束值.也就是说,经过定理 1 的改造,不合理的模型求出了合理的结果. 可见,这是本文对于 MCVC 模型求解的一个贡献.
4.4 算例 4: 多工况正方形平板问题拓扑优化
材料弹性模量 $E =2.1 \times 10^{5}$ MPa,泊松比为 0.3. 基结构宽为 100 mm、高 50 mm,结构左边为固定约束,计算简图如图10 所示,采用 100 $\times $ 50 网格. 工况 1 为一集中载荷 $F_{1}=200$ N 竖直向上作用于上边中点,工况 2 为一集中载荷 $F_{2} =150$ N 竖直向上作用于上边右角,为避免应力集中,$F_{1}$ 分散作用在相邻的 4 个结点上,$F_{2}$ 分散作用在相邻的 3 个结点上.过滤半径为 3 mm,收敛精度取 0.001. 为了进行结果的比较,涉及到 MCVC 模型,惩罚因子取 $p=3$;涉及到 MVCC 模型,采用许用应力 $[\sigma ] =125$ MPa,对应于两个工况的结构应变能约束值为 $\overline {C_1} =3.841 4$ N$\cdot$mm 和 $\overline {C_2}= 7.412 3$ N$\cdot$mm[26 ] . 此例计算按如下三步进行.
图10
图10
正方形平板拓扑优化问题模型
Fig. 10
Definition of the topology optimization problem of a square plate
MCVC 模型因工况不同产生的多目标,其加权系数按载荷大小的比值 4:3 计算,得到归一化的权系 数 $w_1 =0.571 4$ 和 $w_2 = 0.428 6$,分别计算 20% 和 60% 的体积比约束值两种情况. 体积比约束 20% 时,两工况下最大应力分别为 $\sigma _1^\ast =163.34$ MPa 和 $\sigma _2^\ast = 195.40$ MPa,均不满足应力约束条件. 最优 点处结构柔顺度为 $C_1^\ast = 5.902 6$ N$\cdot$mm 和 $C_2^\ast = 18.688 5 $N$\cdot$mm.体积比约束 60% 时,两工况下最大应 力分别为 $\sigma _1^\ast = 56.39$ MPa 和 $\sigma _2^\ast =80.58$ MPa,均比应力约束值小很多,未 能充分发挥材料的强度性能. 最优点处结构柔顺度为 $C_1^\ast =1.157 7$ N$\cdot$mm 和 $C_2^\ast = 3.297 4$ N$\cdot$mm. 最优拓扑如图11 所示.
图11
图11
MCVC 模型得到的最优拓扑
Fig. 11
Optimized topology obtained by the MCVC model
为了比较,再计算一种情况:保持 60% 的体积比约束,使两工况的加权系数相同 $w_1 = 0.5$ 及 $w_2 = 0.5$,计算得到两工况下最大应力为 $\sigma _1^\ast = 58.60$ MPa 和 $\sigma _2^\ast =80.58$ MPa,同样比应力约束值小 很多. 最优点处结构柔顺度为 $C_1^\ast =1.206 0$ N$\cdot$mm 和 $C_2^\ast = 3.264 1$ N$\cdot$mm.
可见,MCVC 模型对不同的体积比约束值,对应与不同的工况的权系数,不仅各自对应的最大 Mises 应力不同,而且最优拓扑构型也不一样. 原因在于,体积比约束值和多目标加权系数的预估,都没有找到理性的取值方法. 为此,导致下一步计算.
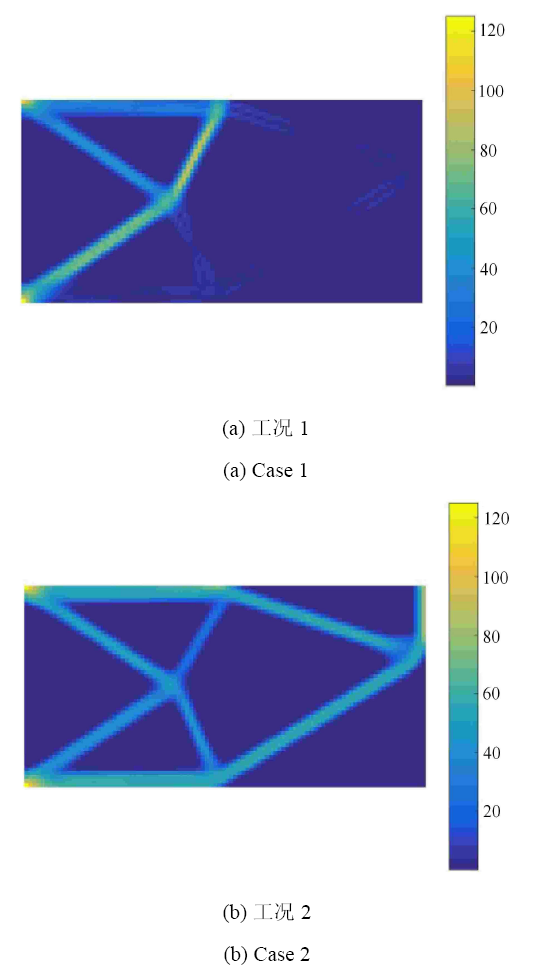
取结构体积极小化为目标、应力约束对应的全局应变能上限为约束条件[26 ] ,计算所得最优拓扑如图12 所示.对应的 Mises 应力分布如图13 所示. 最优解的体积比为 29.44%.两工况下最优点处结构柔顺度皆正好满足各自的应变能约束条件为 $\overline {C_{1} } =3.841 4$ N$\cdot$mm 和 $\overline {C_{2} } = 7.412 3$ N$\cdot$mm;对应的最大应力为 $\sigma _1^\ast =125.00$ MPa 和 $\sigma _2^\ast = 125.00$ MPa,恰好满足应力约束条件[26 ] .此时两工况约束对应的 Lagrange 乘子为 $\lambda _1^\ast =22.2135$ 和 $\lambda _2^\ast =67.318 4$.
图12
图12
MVCC 模型得到最优拓扑
Fig. 12
Optimized topology obtained by the MVCC model
图13
图13
MVCC 模型得到最优拓扑的 Mises 应力分布
Fig. 13
Mises stress distribution of the optimized topology obtained by the MVCC model
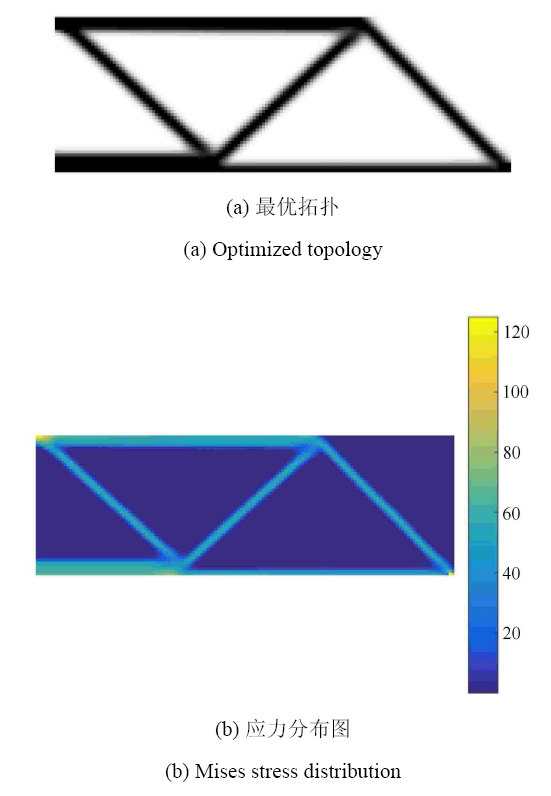
依据定理 2,确定再计算的 MCVC 模型体积约束值和多目标的权系数值:将 MVCC 模型得到的最优体积比 29.44%,作为 MCVC 模型的体积约束;依据上述得到的 Lagrange 乘子进行归一化处理,得到多目标的权系数 $w_1 = 0.248 1$ 和 $w_2 = 0.751 9$.再进行寻优计算,得到两工况下最大应力为 $\sigma _1^\ast =120.65$ MPa 和 $\sigma _2^\ast =125.12$ MPa,基本满足应力约束条件. 最优点处结构柔顺度为 $C_1^\ast = 3.777 6$ N$\cdot$mm 和 $C_2^\ast =7.381 0$ N$\cdot$mm,与 MVCC 模型的约束值接近.最优拓扑如图14 所示,与 MVCC 模型得到的最优拓扑构型相同. 对应的 Mises 应力分布如图15 所示.
图14
图14
MCVC 模型得到最优拓扑
Fig. 14
Optimized topology obtained by the MCVC model
图15
图15
MCVC 模型得到最优拓扑的 Mises 应力分布
Fig. 15
Mises stress distribution of the optimized topology obtained by the MCVC model
特别应当提醒一下,根据载荷大小的比值得到的多目标权系数为 $w_1 = 0.571 4$ 和 $w_2 =0.428 6$,而根据 MVCC 模型最优的 Lagrange 乘子得到的权系数为 $w_1 = 0.248 1$ 和 $w_2 = 0.751 9$.二者正好呈现相反的趋向,可见感性准则有时并不可靠.
可以看到,对 s-m 型问题,经过定理 2 的改造,不合理的模型求出了合理的结果.
5 结语
(1) 根据互逆规划的目标函数和约束条件各自单函数或多函数,相互进行组合,从原有一种的互逆规划出发,扩展得到了使互逆规划完备的 3 种类型.
(2) 依据数学规划的 KKT 条件理论,审视 3 种类型的互逆规划,对于每种互逆规划,提出和证明了各自双方关于拟同构和拟同解的 3 个定理.
(3) 提出了 3 种互逆规划的求解策略,阐述了具体的求解做法. 其中的要点是按一方解调整另一方的相关参数后,互逆规划双方在拟同解中得到了 借鉴.
(4) 对于多目标规划的帕累托模型,提出了 求解的一个新方法:取互逆规划第一方的最优Lagrange 乘子向量,作为第二方的多目标权系数向量,然后寻优.
(5) 对于不合理的结构拓扑优化模型,提出了得到 "合理结果" 的求解途径,亦即:基于 ICM 方法建模,借助 MVCC 模型,迂回地求解了 MCVC 模型.
(6) 给出了两个 2 维数学问题,图示了互逆规划双方关系;用 Matlab 编程,计算了多个结构拓扑优化个案;数值结果均支持了本文提出的互逆规划理论.
参考文献
View Option
[1]
Bendsoe MP Kikuchi N . Generating optimal topologies in structural design using a homogenization method
Computer Methods in Applied Mechanics and Engineering 1988 ,71 (2 ):197 -224
DOI
URL
[本文引用: 1]
[2]
Mlejnek HP . Some aspects of the genesis of structures
Structural Optimization 1992 ,5 (1-2 ):64 -69
DOI
URL
[本文引用: 1]
[3]
Bendsoe MP Sigmund O . Topology Optimization: Theory, Methods and Applications
NewYork: Springer-Berlin-Heidelberg , 2003
[本文引用: 1]
[4]
隋允康 . 建模$\cdot $变换$\cdot $优化: 结构综合方法新进展 . 大连 : 大连理工大学出版社 , 1996
[本文引用: 1]
( Sui Yunkang . Modeling, Transformation and Optimization - New Development of Structural Synthesis Method . Dalian : Dalian University of Technology Press , 1996 (in Chinese))
[本文引用: 1]
[5]
隋允康 , 叶红玲 . 连续体结构拓扑优化的 ICM 方法 . 北京 : 科学出版社 , 2013
( Sui Yunkang Ye Hongling . Continuum Topology Optimization ICM Method . Beijing : Science Press , 2013 (in Chinese))
[6]
Sui YK Peng XR . Modeling, Solving and Application for Topology Optimization of Continuum Structures, ICM Method Based on Step Function
Elsevier , 2018
[本文引用: 1]
[7]
Xie YM Steven GP . A simple evolutionary procedure for structural Optimization
Computers and Structure 1993 ,49 (5 ):885 -896
DOI
URL
[本文引用: 1]
[8]
Osher S Sethian J . Fronts propagating with curvature dependent speed-algorithms based on hamilton-jacobi formulations
J Comput Phys 1988 ,79 (1 ):12 -49
DOI
URL
[本文引用: 1]
[9]
Wei P Li ZY Li XP , et al . An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions
Structural and Multidisciplinary Optimization 2018 ,58 (2 ):831 -849
DOI
URL
[本文引用: 1]
[10]
Norato J Bendsøe M Haber R , et al . A topological derivative method for topology optimization
Structural and Multidisciplinary Optimization 2007 ,33 (4-5 ):375 -386
DOI
URL
[本文引用: 1]
We propose a fictitious domain method for topology optimization in which a level set of the topological derivative field for the cost function identifies the boundary of the optimal design. We describe a fixed-point iteration scheme that implements this optimality criterion subject to a volumetric resource constraint. A smooth and consistent projection of the region bounded by the level set onto the fictitious analysis domain simplifies the response analysis and enhances the convergence of the optimization algorithm. Moreover, the projection supports the reintroduction of solid material in void regions, a critical requirement for robust topology optimization. We present several numerical examples that demonstrate compliance minimization of fixed-volume, linearly elastic structures.]]>
[11]
Cai SY Zhang WH . An adaptive bubble method for structural shape and topology optimization
Computer Methods in Applied Mechanics and Engineering 2020 ,360 :1 -25
[本文引用: 1]
[12]
Bourdin B Chambolle A . Design-dependent loads in topology optimization
ESAIM: Control, Optimisation and Calculus of Variations 2003 ,9 (8 ):19 -48
DOI
URL
[本文引用: 1]
[13]
Guo X Zhang WS Zhang J . Explicit structural topology optimization based on moving morphable components (MMC) with curved skeletons
Computer Methods in Applied Mechanics and Engineering 2016 ,310 (10 ):711 -748
DOI
URL
[本文引用: 1]
[14]
Bourdin B Chambolle A Zhang WS , et al . A new three-dimensional topology optimization method based on moving morphable components (MMCs)
Computational Mechanics 2017 ,59 (4 ):647 -665
DOI
URL
[本文引用: 1]
[15]
Zhang WH Zhao LY Gao T , et al . Topology optimization with closed B-splines and Boolean operations
Computer Methods in Applied Mechanics and Engineering 2017 ,315 (3 ):652 -670
DOI
URL
[本文引用: 1]
[17]
Rozvany GIN . A critical review of established methods of structural topology optimization
Structural and Multidisciplinary Optimization 2009 ,37 (3 ):217 -237
DOI
URL
[本文引用: 1]
The aim of this article is to evaluate and compare established numerical methods of structural topology optimization that have reached the stage of application in industrial software. It is hoped that our text will spark off a fruitful and constructive debate on this important topic.]]>
[18]
Sigmund O Maute K . Topology optimization approaches
Structural and Multidisciplinary Optimization 2013 ,48 (6 ):1031 -1055
DOI
URL
[本文引用: 1]
[19]
Yi GL Sui YK . Different effects of economic and structural performance indicators on model construction of structural topology optimization
Acta Mechanica Sinia 2015 ,31 (9 ):1 -12
[本文引用: 2]
[20]
彭细荣 , 隋允康 . 应该为结构拓扑优化的设计变量正名和处理方法顺言
北京工业大学学报 , 2016 ,42 (12 ):27 -37
[本文引用: 1]
( Peng Xirong Sui Yunkang . Name correction for design variable of structural topology optimization and presentation of its corresponding treatment method
Journal of Beijing University of Techology 2016 ,42 (12 ):27 -37 (in Chinese))
[本文引用: 1]
[21]
彭细荣 , 隋允康 . 对连续体结构拓扑优化合理模型的再探讨
固体力学学报 , 2016 ,37 (1 ):1 -11
[本文引用: 2]
( Peng Xirong Sui Yunkang . A further discussion on rational topology optimization models for continuum structures
Chinese Journal of Solid Mechanics 2016 ,37 (1 ):1 -11 (in Chinese))
[本文引用: 2]
[22]
Fleury C . Structural weight optimization by dual methods of convex programming
International Journal for Numerical Methods in Engineering 1979 ,14 (2 ):1761 -1783
DOI
URL
[本文引用: 1]
[23]
Fleury C . Primal and dual methods in structural optimization
Journal of the Structural Division 1980 ,106 (5 ):1117 -1133
[24]
Fleury C Braibant V . Structural optimization: A new dual method using mixed variables
International Journal for Numerical Methods in Engineering 1986 ,23 (3 ):409 -428
DOI
URL
[25]
黄红选 , 韩继业 . 数学规划 . 北京 : 清华大学出版社 , 2006
[本文引用: 1]
( Huang Hongxuan Han Jiye . Mathematical Programming . Beijing : Tsinghua University Press , 2006 (in Chinese))
[本文引用: 1]
[26]
隋允康 , 彭细荣 , 叶红玲 等 . 互逆规划理论及其用于建立结构拓扑优化的合理模型
力学学报 , 2019 ,51 (6 ):1940 -1948
[本文引用: 14]
( Sui Yunkang Peng Xirong Ye Hongling , et al . Reciprocal programming theory and its application to establish a reasonable model of structural topology optimization
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (6 ):1940 -1948 (in Chinese))
[本文引用: 14]
[27]
隋允康 , 于新 . K-S 函数与模函数法的统一
大连理工大学学报 , 1998 ,38 (5 ):502 -505
[本文引用: 1]
( Sui Yunkang Yu Xing . Uniform of K-S function and norm function
Journal of Dalian University of Technology 1998 ,38 (5 ):502 -505 (in Chinese))
[本文引用: 1]
[28]
Jun T Sui YK . Topology optimization using parabolic aggregation function with independent-continuous-mapping method
Mathematical Problems in Engineering 2013 ,2013 (3 ):1 -18
[本文引用: 1]
[29]
钱令希 , 钟万勰 , 程耿东 等 . 工程结构优化设计的一个新途径——序列二次规划 SQP
计算结构力学及其应用 , 1984 ,1 (1 ):7 -20
[本文引用: 1]
( Qian Lingxi Zhong Wanxie Cheng Gendong , et al . An approach to structural optimization--sequential quadratic programming, SQP
Computational Structural Mechanics and Applications 1984 ,1 (1 ):7 -20 (in Chinese))
[本文引用: 1]
[30]
隋允康 , 彭细荣 . 求解一类可分离凸规划的对偶显式模型 DP-EM 方法
力学学报 , 2017 ,49 (5 ):1135 -1144
[本文引用: 1]
( Sui Yunkang Peng Xirong . A dual explicit model based DP-EM method for solving a class of separable convex programming
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (5 ):1135 -1144 (in Chinese))
[本文引用: 1]
[31]
Sui YK Peng XR . Explicit model of dual programming and solving method for a class of separable convex programming problems
Engineering Optimization 2019 ,51 (7-9 ):1604 -1625
DOI
URL
[本文引用: 1]
Generating optimal topologies in structural design using a homogenization method
1
1988
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Some aspects of the genesis of structures
1
1992
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Topology Optimization: Theory, Methods and Applications
1
2003
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
1
1996
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
1
1996
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Modeling, Solving and Application for Topology Optimization of Continuum Structures, ICM Method Based on Step Function
1
2018
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
A simple evolutionary procedure for structural Optimization
1
1993
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Fronts propagating with curvature dependent speed-algorithms based on hamilton-jacobi formulations
1
1988
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
An 88-line MATLAB code for the parameterized level set method based topology optimization using radial basis functions
1
2018
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
A topological derivative method for topology optimization
1
2007
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
An adaptive bubble method for structural shape and topology optimization
1
2020
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Design-dependent loads in topology optimization
1
2003
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Explicit structural topology optimization based on moving morphable components (MMC) with curved skeletons
1
2016
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
A new three-dimensional topology optimization method based on moving morphable components (MMCs)
1
2017
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Topology optimization with closed B-splines and Boolean operations
1
2017
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
A material-field series-expansion method for topology optimization of continuum structures
1
2019
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
A critical review of established methods of structural topology optimization
1
2009
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Topology optimization approaches
1
2013
... 自 1988 年 Bendsoe 与 Kikuchi[1 ] 提出均匀化方法以来,连续体结构拓扑优化得到了快速发展,同时涌现出许多方法,包括变密度方法[2 -3 ] 、 独立连续映射 (independent, continuous andmapping,ICM) 方法[4 -6 ] 、ESO (evolutionary structural optimization)方法[7 ] 、水平集方法[8 -9 ] 、拓扑导数法[10 -11 ] 、相场 法[12 ] 、 MMC (movingmorphable components) 方法[13 -14 ] 、CBS (closedB-splines) 方法[15 ] 、材料场序列展开法[16 ] 等. 对各类方法的综述可参阅 Rozvany[17 ] 及 Sigmund[18 ] 等的文献. ...
Different effects of economic and structural performance indicators on model construction of structural topology optimization
2
2015
... 各种连续体结构拓扑优化方法基本上集中在 建模途径和求解效率上,而对于优化模型是否合理以及模型之 间的相互关系则缺乏注意. 研究优化模型的合理性始于隋允康等将 MCVC (minimumcompliances with a volume constraint) 模型同 MVDC (minimum volume with displacementconstraints) 模型进行比较[19 -21 ] ,说明 MCVC 模型约束条件值的选取和多工况时目标函数的不合理性. ...
... 为了节省读者查阅文献[19 ,20 ,21 ] 时间,这里给出"结构优化设计模型合理与否"的诠释. ...
应该为结构拓扑优化的设计变量正名和处理方法顺言
1
2016
... 为了节省读者查阅文献[19 ,20 ,21 ] 时间,这里给出"结构优化设计模型合理与否"的诠释. ...
应该为结构拓扑优化的设计变量正名和处理方法顺言
1
2016
... 为了节省读者查阅文献[19 ,20 ,21 ] 时间,这里给出"结构优化设计模型合理与否"的诠释. ...
对连续体结构拓扑优化合理模型的再探讨
2
2016
... 各种连续体结构拓扑优化方法基本上集中在 建模途径和求解效率上,而对于优化模型是否合理以及模型之 间的相互关系则缺乏注意. 研究优化模型的合理性始于隋允康等将 MCVC (minimumcompliances with a volume constraint) 模型同 MVDC (minimum volume with displacementconstraints) 模型进行比较[19 -21 ] ,说明 MCVC 模型约束条件值的选取和多工况时目标函数的不合理性. ...
... 为了节省读者查阅文献[19 ,20 ,21 ] 时间,这里给出"结构优化设计模型合理与否"的诠释. ...
对连续体结构拓扑优化合理模型的再探讨
2
2016
... 各种连续体结构拓扑优化方法基本上集中在 建模途径和求解效率上,而对于优化模型是否合理以及模型之 间的相互关系则缺乏注意. 研究优化模型的合理性始于隋允康等将 MCVC (minimumcompliances with a volume constraint) 模型同 MVDC (minimum volume with displacementconstraints) 模型进行比较[19 -21 ] ,说明 MCVC 模型约束条件值的选取和多工况时目标函数的不合理性. ...
... 为了节省读者查阅文献[19 ,20 ,21 ] 时间,这里给出"结构优化设计模型合理与否"的诠释. ...
Structural weight optimization by dual methods of convex programming
1
1979
... 在连续体结构拓扑优化的背景下,作者团队进一步研究模型合理化与否,同运筹学中数学规划论的对偶规划[22 -25 ] 比对,从而提出了互逆规划的概念[26 ] . ...
Primal and dual methods in structural optimization
0
1980
Structural optimization: A new dual method using mixed variables
0
1986
1
2006
... 在连续体结构拓扑优化的背景下,作者团队进一步研究模型合理化与否,同运筹学中数学规划论的对偶规划[22 -25 ] 比对,从而提出了互逆规划的概念[26 ] . ...
1
2006
... 在连续体结构拓扑优化的背景下,作者团队进一步研究模型合理化与否,同运筹学中数学规划论的对偶规划[22 -25 ] 比对,从而提出了互逆规划的概念[26 ] . ...
互逆规划理论及其用于建立结构拓扑优化的合理模型
14
2019
... 在连续体结构拓扑优化的背景下,作者团队进一步研究模型合理化与否,同运筹学中数学规划论的对偶规划[22 -25 ] 比对,从而提出了互逆规划的概念[26 ] . ...
... 基于文献[26 ] 提出的互逆规划,本文发展了相关定义及理论,内容如下: ...
... 文献[26 ] 提出了 s-m 型互逆规划,由 s 方和 m 方两个问题数学规划问题组成:(1) s 方——取单个目标函数和多个约束条件;(2) m 方——取 s 方的多个约束条件作为该方的目标函数,取 s 方的目标函数作为该方的约束条件. ...
... FP 问题和 RP 问题孰在前、孰在后,只是顺序的不同,并不影响问题的本质,因而 m-s 型互逆规划同文献[26 ] 提出的 s-m 型互逆规划实际是同一个事物. ...
... 以上提出的 s-s 型互逆规划和 m-m 型互逆规划,是对文献[26 ] 提出的互逆规划的推广. 推广之后的互逆规划共分上述 3 类. ...
... 文献[26 ] 应用互逆规划揭示了结构优化中存在有不合理模型,例如:结构拓扑优化结构体积约束下多工况柔顺度最小问题,属于不合理的多目标模型,依照本文发展的互逆规划理论予以剖析,是 m-s 型问题的 FP (正向问题) 方. ...
... 总之,文献[26 ] 揭示了存在互逆规划的两方,而本文则扩充了互逆规划的类型,并且揭示了互逆规划双方的内在关连. 前者有助于识别出不合理的状态,并且将其转化为合理的问题,后者则依靠互逆规划的双方关连性补充了求解的方法. ...
... 文献[26 ] 从互逆规划的角度,揭示了结构拓扑优化里存在有不合理模型的情况,例如给定体积约束求柔顺度最小化的 MCVC 问题,本文 3.2 小节的求解策略和具体做法也提到不合理模型的情况,并且在具体做法里从 3 种类型互逆规划逐一进行了讨论. ...
... 式 (22) 相比式 (23),是不合理的. 原因不仅在于多目标上,更在于所给出作为结构体积上限 $\overline V$ 为指定的值,不具有理性的根据.因此,本文作者多次呼吁以 MVCC 问题替代 MCVC 问题,而且文献[26 ] 给出了结构柔顺度约束值的物理意义和计算公式. ...
... 材料弹性模量 $E =2.1 \times 10^{5}$ MPa,泊松比为 0.3. 基结构宽为 300 mm、高 50 mm,取一半结构进行分析,左、右下角分别为铰支和滑动铰支约束,计算简图如图6 所示,采用 150$\times $50 网格.一个集中载荷 200 N 载荷工况,作用于跨中顶点,为避免应力集中,$F=100$ N 分散作用在相邻的 4 个结点上,右下角竖向约束也分散在 2 个结点上. 过滤半径为 3 mm,收敛精度取 0.001. 为了进行结果的比较,涉及到 MCVC 模型,惩罚 因子取 $p=3$, 分 别采用 20% 与 60% 的体积比约束值,进行两种情况的计算;涉及到 MVCC 模型,采用许用应力 $[\sigma ] =125$ MPa,对应的结构应变能约束值为 $\overline C = 10.012$ N$\cdot$mm[26 ] . 此例计算按如下 3 步进行. ...
... 以体积极小为目标、全局应变能约束计算所得最优拓扑如图8 (a) 所示. 对应的 Mises 应力分布如图8 (b) 所示. 最优体积比为 23.88%. 最大应力为 125.07 MPa,满足应力约束条件[26 ] . 为了便于第三步的数值比较,算出最优点处结构柔顺度为 $\overline C = 10.012$ N$\cdot$mm. ...
... 材料弹性模量 $E =2.1 \times 10^{5}$ MPa,泊松比为 0.3. 基结构宽为 100 mm、高 50 mm,结构左边为固定约束,计算简图如图10 所示,采用 100 $\times $ 50 网格. 工况 1 为一集中载荷 $F_{1}=200$ N 竖直向上作用于上边中点,工况 2 为一集中载荷 $F_{2} =150$ N 竖直向上作用于上边右角,为避免应力集中,$F_{1}$ 分散作用在相邻的 4 个结点上,$F_{2}$ 分散作用在相邻的 3 个结点上.过滤半径为 3 mm,收敛精度取 0.001. 为了进行结果的比较,涉及到 MCVC 模型,惩罚因子取 $p=3$;涉及到 MVCC 模型,采用许用应力 $[\sigma ] =125$ MPa,对应于两个工况的结构应变能约束值为 $\overline {C_1} =3.841 4$ N$\cdot$mm 和 $\overline {C_2}= 7.412 3$ N$\cdot$mm[26 ] . 此例计算按如下三步进行. ...
... 取结构体积极小化为目标、应力约束对应的全局应变能上限为约束条件[26 ] ,计算所得最优拓扑如图12 所示.对应的 Mises 应力分布如图13 所示. 最优解的体积比为 29.44%.两工况下最优点处结构柔顺度皆正好满足各自的应变能约束条件为 $\overline {C_{1} } =3.841 4$ N$\cdot$mm 和 $\overline {C_{2} } = 7.412 3$ N$\cdot$mm;对应的最大应力为 $\sigma _1^\ast =125.00$ MPa 和 $\sigma _2^\ast = 125.00$ MPa,恰好满足应力约束条件[26 ] .此时两工况约束对应的 Lagrange 乘子为 $\lambda _1^\ast =22.2135$ 和 $\lambda _2^\ast =67.318 4$. ...
... [26 ].此时两工况约束对应的 Lagrange 乘子为 $\lambda _1^\ast =22.2135$ 和 $\lambda _2^\ast =67.318 4$. ...
互逆规划理论及其用于建立结构拓扑优化的合理模型
14
2019
... 在连续体结构拓扑优化的背景下,作者团队进一步研究模型合理化与否,同运筹学中数学规划论的对偶规划[22 -25 ] 比对,从而提出了互逆规划的概念[26 ] . ...
... 基于文献[26 ] 提出的互逆规划,本文发展了相关定义及理论,内容如下: ...
... 文献[26 ] 提出了 s-m 型互逆规划,由 s 方和 m 方两个问题数学规划问题组成:(1) s 方——取单个目标函数和多个约束条件;(2) m 方——取 s 方的多个约束条件作为该方的目标函数,取 s 方的目标函数作为该方的约束条件. ...
... FP 问题和 RP 问题孰在前、孰在后,只是顺序的不同,并不影响问题的本质,因而 m-s 型互逆规划同文献[26 ] 提出的 s-m 型互逆规划实际是同一个事物. ...
... 以上提出的 s-s 型互逆规划和 m-m 型互逆规划,是对文献[26 ] 提出的互逆规划的推广. 推广之后的互逆规划共分上述 3 类. ...
... 文献[26 ] 应用互逆规划揭示了结构优化中存在有不合理模型,例如:结构拓扑优化结构体积约束下多工况柔顺度最小问题,属于不合理的多目标模型,依照本文发展的互逆规划理论予以剖析,是 m-s 型问题的 FP (正向问题) 方. ...
... 总之,文献[26 ] 揭示了存在互逆规划的两方,而本文则扩充了互逆规划的类型,并且揭示了互逆规划双方的内在关连. 前者有助于识别出不合理的状态,并且将其转化为合理的问题,后者则依靠互逆规划的双方关连性补充了求解的方法. ...
... 文献[26 ] 从互逆规划的角度,揭示了结构拓扑优化里存在有不合理模型的情况,例如给定体积约束求柔顺度最小化的 MCVC 问题,本文 3.2 小节的求解策略和具体做法也提到不合理模型的情况,并且在具体做法里从 3 种类型互逆规划逐一进行了讨论. ...
... 式 (22) 相比式 (23),是不合理的. 原因不仅在于多目标上,更在于所给出作为结构体积上限 $\overline V$ 为指定的值,不具有理性的根据.因此,本文作者多次呼吁以 MVCC 问题替代 MCVC 问题,而且文献[26 ] 给出了结构柔顺度约束值的物理意义和计算公式. ...
... 材料弹性模量 $E =2.1 \times 10^{5}$ MPa,泊松比为 0.3. 基结构宽为 300 mm、高 50 mm,取一半结构进行分析,左、右下角分别为铰支和滑动铰支约束,计算简图如图6 所示,采用 150$\times $50 网格.一个集中载荷 200 N 载荷工况,作用于跨中顶点,为避免应力集中,$F=100$ N 分散作用在相邻的 4 个结点上,右下角竖向约束也分散在 2 个结点上. 过滤半径为 3 mm,收敛精度取 0.001. 为了进行结果的比较,涉及到 MCVC 模型,惩罚 因子取 $p=3$, 分 别采用 20% 与 60% 的体积比约束值,进行两种情况的计算;涉及到 MVCC 模型,采用许用应力 $[\sigma ] =125$ MPa,对应的结构应变能约束值为 $\overline C = 10.012$ N$\cdot$mm[26 ] . 此例计算按如下 3 步进行. ...
... 以体积极小为目标、全局应变能约束计算所得最优拓扑如图8 (a) 所示. 对应的 Mises 应力分布如图8 (b) 所示. 最优体积比为 23.88%. 最大应力为 125.07 MPa,满足应力约束条件[26 ] . 为了便于第三步的数值比较,算出最优点处结构柔顺度为 $\overline C = 10.012$ N$\cdot$mm. ...
... 材料弹性模量 $E =2.1 \times 10^{5}$ MPa,泊松比为 0.3. 基结构宽为 100 mm、高 50 mm,结构左边为固定约束,计算简图如图10 所示,采用 100 $\times $ 50 网格. 工况 1 为一集中载荷 $F_{1}=200$ N 竖直向上作用于上边中点,工况 2 为一集中载荷 $F_{2} =150$ N 竖直向上作用于上边右角,为避免应力集中,$F_{1}$ 分散作用在相邻的 4 个结点上,$F_{2}$ 分散作用在相邻的 3 个结点上.过滤半径为 3 mm,收敛精度取 0.001. 为了进行结果的比较,涉及到 MCVC 模型,惩罚因子取 $p=3$;涉及到 MVCC 模型,采用许用应力 $[\sigma ] =125$ MPa,对应于两个工况的结构应变能约束值为 $\overline {C_1} =3.841 4$ N$\cdot$mm 和 $\overline {C_2}= 7.412 3$ N$\cdot$mm[26 ] . 此例计算按如下三步进行. ...
... 取结构体积极小化为目标、应力约束对应的全局应变能上限为约束条件[26 ] ,计算所得最优拓扑如图12 所示.对应的 Mises 应力分布如图13 所示. 最优解的体积比为 29.44%.两工况下最优点处结构柔顺度皆正好满足各自的应变能约束条件为 $\overline {C_{1} } =3.841 4$ N$\cdot$mm 和 $\overline {C_{2} } = 7.412 3$ N$\cdot$mm;对应的最大应力为 $\sigma _1^\ast =125.00$ MPa 和 $\sigma _2^\ast = 125.00$ MPa,恰好满足应力约束条件[26 ] .此时两工况约束对应的 Lagrange 乘子为 $\lambda _1^\ast =22.2135$ 和 $\lambda _2^\ast =67.318 4$. ...
... [26 ].此时两工况约束对应的 Lagrange 乘子为 $\lambda _1^\ast =22.2135$ 和 $\lambda _2^\ast =67.318 4$. ...
K-S 函数与模函数法的统一
1
1998
... 对于一个多目标优化问题,可以引用隋允康提出的统一的凝聚函数方法以及铁军、隋允康提出的抛物线凝聚函数方法[27 -28 ] ,通过适当简化以便于数值计算的方法将多目标化为一个凝聚的单目标函数. 需要指出,统一的凝聚函数方法统一了模优化 (norm optimization) 和 K-S 函数,即 ...
K-S 函数与模函数法的统一
1
1998
... 对于一个多目标优化问题,可以引用隋允康提出的统一的凝聚函数方法以及铁军、隋允康提出的抛物线凝聚函数方法[27 -28 ] ,通过适当简化以便于数值计算的方法将多目标化为一个凝聚的单目标函数. 需要指出,统一的凝聚函数方法统一了模优化 (norm optimization) 和 K-S 函数,即 ...
Topology optimization using parabolic aggregation function with independent-continuous-mapping method
1
2013
... 对于一个多目标优化问题,可以引用隋允康提出的统一的凝聚函数方法以及铁军、隋允康提出的抛物线凝聚函数方法[27 -28 ] ,通过适当简化以便于数值计算的方法将多目标化为一个凝聚的单目标函数. 需要指出,统一的凝聚函数方法统一了模优化 (norm optimization) 和 K-S 函数,即 ...
工程结构优化设计的一个新途径——序列二次规划 SQP
1
1984
... 往下的具体求解可以采用研究者青睐的各种行之有效的约束规划算法,本文倾向于应用 DSQP (对偶序列二次规划) 算法[29 ] 或 DP-EM 方法[30 -31 ] . ...
工程结构优化设计的一个新途径——序列二次规划 SQP
1
1984
... 往下的具体求解可以采用研究者青睐的各种行之有效的约束规划算法,本文倾向于应用 DSQP (对偶序列二次规划) 算法[29 ] 或 DP-EM 方法[30 -31 ] . ...
求解一类可分离凸规划的对偶显式模型 DP-EM 方法
1
2017
... 往下的具体求解可以采用研究者青睐的各种行之有效的约束规划算法,本文倾向于应用 DSQP (对偶序列二次规划) 算法[29 ] 或 DP-EM 方法[30 -31 ] . ...
求解一类可分离凸规划的对偶显式模型 DP-EM 方法
1
2017
... 往下的具体求解可以采用研究者青睐的各种行之有效的约束规划算法,本文倾向于应用 DSQP (对偶序列二次规划) 算法[29 ] 或 DP-EM 方法[30 -31 ] . ...
Explicit model of dual programming and solving method for a class of separable convex programming problems
1
2019
... 往下的具体求解可以采用研究者青睐的各种行之有效的约束规划算法,本文倾向于应用 DSQP (对偶序列二次规划) 算法[29 ] 或 DP-EM 方法[30 -31 ] . ...