引言
输流管的振动行为是一种典型的流固耦合振动现象, 同时作为一种典型的细长结构,它广泛应用于海洋工程、核工业、航空航天以及石油化工等工程领域. 因此,输流管动力学的研究具有重要的工程意义与学术价值[1 -2 ] .著名动力学专家Paidoussis教授曾经指出,输流管振动仍是当今动力学研究的重要课题之一,主要因为(1)输流管振动能表现出有趣且复杂的非线性动力学行为;(2)可为现代动力学的发展提供重要的理论依据[1 -2 ] .
输流管按照其边界条件可分为两端支撑管以及悬臂管. 其中,悬臂管是一种非保守系统, 当内流流速达到一定值时, 会发生颤振行为.其丰富的动力学行为吸引大量的学者对其进行研究.关于输流管非线性振动控制方程大多是基于Hamilton原理推导得到. 比如1994年,Selmer等[3 ] 基于Hamilton方程所给出的输流管二维非线性振动微分方程,是如今运用最广泛的悬臂输流管控制方程. 2007年,Wadham等[4 ] 基于修正的Hamilton原理将悬臂输流管由二维的动力学方程扩展至三维构型.
随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型.
在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照.
本文主要从理论和实验上研究集中质量对悬臂输流管系统临界流速、失稳模态和振动幅值等动力学特性的影响规律,为输流管振动控制提供一种可控性策略和实验数据. 鉴于此,首先基于扩展Hamilton原理建立了含集中质量悬臂输流管的非线性动力学控制方程;然后借助Galerkin技术将偏微分控制方程离散为常微分方程进行数值求解;再通过线性分析和非线性分析方法研究集中质量对输流管振动特性的影响规律; 最后,通过搭建相关实验对理论计算结果进行了验证对比.
1 动力学建模与求解
考虑图1 (a)所示的含集中质量悬臂输流管模型, $U$表示管道内流流速;$s$为管道横截面位置坐标; $G$表示重力加速度方向; 右下角给出全局坐标系,$x$代表管道轴向方向, $y$代表管道横向方向.坐标附加集中质量可以沿管道轴向方向进行变化,假设集中质量在沿管道轴向$x_{j}$处.
图1
图1
(a)考虑集中质量悬臂输流管构型的模型图(静止状态);(b)考虑集中质量悬臂输流管构型的模型图(振动状态)
Fig. 1
(a) Model diagram considering the configuration of the cantilevered fluid-conveying pipe attached with the lumped mass (rest state); (b) model diagram considering the configuration of the cantilevered fluid-conveying pipe attached with the lumped mass (vibration state)
为方便研究, 对输流管结构和流体属性做如下假设: (1)流体为定常流且不可压缩;(2)将具有细长特征(长径比大)的管视为二维平面上的Euler-Bernoulli梁模型,不考虑管的转动惯量和剪切变形; (3)忽略了管材的黏弹性阻尼,只考虑实验中产生的机械阻尼; (4)管道轴线不可伸长且考虑小应变.基于以上假设条件,关于含集中质量输流管系统的非线性动力学方程可以通过Hamilton原理进行推导
(1) $\delta \int_{t_{1}}^{t_{2} } {(T_{tot} -V_{tot} )} =\int_{t_{1}}^{t_{2}} [MU(\frac{\partial r}{\partial t}+U\tau )\delta r]\text{d}t$
其中, $T_{tot}$为系统的总动能, $V_{tot}$为系统总的势能, $M$为单位流体质量,$u$为管内流体流速. 公式右边是管道自由端流体流出时作的虚功. $r$和$\tau$为管道的位置矢量和切矢量. 输流管系统的总动能分为两部分
(2) $T_{tot} =T_{p} +T_{f} =\frac{1}{2}m\int_{0}^{{L}} v_{p} ^{2}\text{d}s +\frac{1}{2}m_{j} (v_{p} \vert x=x_{j} )^{2}+\\ \frac{1}{2}M\int_{0}^{{L}}v_{f}^{2}\text{d}s$
式中, p和f分别代表管与流体, $v$代表速度, $m$代表管道单位长度质量, $m_{j}$代表附加集中质量, $x_{j}$表示集中质量的位置坐标,$s$为管道横截面位置坐标, 有$s\approx x$. 考虑重力的影响, 系统总势能分为管道应变能和重力势能. 在小应变假设下,管道应变能$V_{s}$可写为[30 ]
(3) $V_{s} =\frac{1}{2}\int_0^L EI\kappa^{2}\text{d}s$
其中, $\kappa $为曲率表示为$({{{\partial^{2}w}/{\partial^{2}s}}})/{\sqrt {1-({{\partial w}/{\partial s}})^{2}} }$, $EI$为弯曲刚度. 重力势能表示为
(4) $V_{g} =-[m+\frac{m_{j} }{L}\delta (s-x_{j} )+M]g\int_0^L x\text{d}s$
将方程(2) $\sim$ (4)代入方程(1)中, 基于变分法, 可得到控制方程
(5) $\begin{array}{l}\left[ m+\frac{m_{j} }{L}\delta (x-x_{j} )+M \right]\ddot{{w}}+2MU{\dot{{w}}}'\left( {1+{w}'^{2}} \right) +\\ \left[ {m+\frac{m_{j} }{L}\delta (x-x_{j} )+M} \right]g{w}'\left( {1+\frac{1}{2}{w}'^{2}} \right) +\\ {w}"\bigg\{ MU^{2}(1+{w}'^{2})+\bigg[ M\dot{{U}}-\bigg( m+\frac{m_{j} }{L}\delta (x-x_{j} )+ \\ M \bigg)g \bigg]\left( {L-s} \right)(1+\frac{3}{2}{w}'^{2})\bigg\}+ EI\Big[ {{w}"}"\left( {1+{w}'^{2}} \right)+\\ 4{w}'{w}"{w}"'+{w}"^{3}\Big]- {w}"\bigg\{ \int_s^L \int_0^s \bigg[ m+ \\ \frac{m_{j} }{L}\delta (x-x_{j} )+M \bigg] \left( {{\dot{{w}}}'^{2}+{w}'{\ddot{{w}}}'} \right)\text{d}s\text{d}s +\\ \int_s^L {\left( {\frac{1}{2}MU{w}'^{2}+2MU{w}'{\dot{{w}}}'+MU^{2}{w}'{w}"} \right)}\text{d}s\bigg\}+\\ {w}'\int_0^s \left[ {m+\frac{m_{j} }{L}\delta (x-x_{j} )+M} \right]\cdot\\ \left( {{\dot{{w}}}'^{2}+{w}'{\ddot{{w}}}'} \right)\text{d}s=0\end{array}$
其中, $w$表示管的横向位移, $L$为管的长度, $M$和$m$分别为流体和管道单位长度的质量,$\delta (x)$表示Dirac delta函数. 为计算方便, 引入以下无量纲参数
(6) $\left.\begin{array}{l} \xi =\dfrac{x}{L}, \ \ \eta =\dfrac{w}{L}, \ \ \tau =\sqrt {\dfrac{EI}{m+M}} \dfrac{t}{L^{2}}\\ u=\sqrt {\dfrac{M}{EI}} UL, \ \ \beta =\dfrac{M}{m+M+{{m_{j} }/L}}\\ \mu =\dfrac{m_{j} }{(m+M)L},\ \ \gamma =\dfrac{m+M+{{m_{j} }/L}}{EI}L^{3}g, \ \ \xi_{j} =\dfrac{x_{j} }{L} \end{array}\right\}$
(7) $\begin{array}{l}\left[ {1+\mu \delta \left( {\xi -\xi_{j} } \right)} \right]\ddot{{\eta }}+\eta ""+2u\sqrt \beta \dot{{{\eta }'}} + u^{2}\eta "+\\ \gamma \left[ {1+\mu \delta \left( {\xi -\xi_{j} } \right)} \right]{\eta }' -\\ \gamma \int_\xi^1 {\left[ {1+\mu \delta \left( {\xi -\xi_{j} } \right)} \right]\text{d}\xi } \eta " +\\ \frac{1}{2}\gamma [1+\mu \delta \left( {\xi -\xi_{j} } \right)]{\eta }'^{3} -\\ \frac{3}{2}\gamma \int_\xi^1 {\left[ {1+\mu \delta \left( {\xi -\xi_{j} } \right)} \right]\text{d}\xi } {\eta }'^{2}\eta " +\\ 2u\sqrt \beta \left[ {{\eta }'^{2}\dot{{{\eta }'}}-\eta "\int_\xi^1 {{\eta }'\dot{{{\eta }'}}\text{d}\xi } } \right] +\\ u^{2}\left[ {\left( {{\eta }'^{2}\eta "-\eta "\int_\xi^1 {{\eta }'\eta "\text{d}\xi } } \right)} \right] +\\ \left( {\eta "^{3}+4{\eta }'\eta "\eta "'+{\eta }'^{2}\eta ""} \right) +\\ {\eta }'\left[ {1+\mu \delta \left( {\xi -\xi_{j} } \right)} \right]\int_0^\xi {\left( {\dot{{{\eta }'}}^{2}+{\eta }'{\ddot{{\eta }}}'} \right)\text{d}\xi } - \\ \eta "\int_\xi^1 \left[ {1+\mu \delta \left( {\xi -\xi_{j} } \right)} \right]\cdot\\ \int_0^\xi {\left( {\dot{{{\eta }'}}^{2}+{\eta }'{\ddot{{\eta }}}'} \right)\text{d}\xi } \text{d}\xi =0\end{array}$
首先采用Galerkin法对动力学方程(7)进行离散, 将偏微分方程(PDE)可转化为常微分方程(ODE)进行数值求解. 将振动幅值$\eta(\xi,\tau )$表示为
(8) $\eta \left( {\xi ,\tau } \right)=\sum\limits_{j=1}^N {\varphi_{j} \left( \xi \right)q_{j} \left( \tau \right)} ={\varphi q}$
其中, $\varphi_{j}(\xi )$为经典的悬臂梁的模态函数, $q_{j}(\tau)$则为离散系统对应的广义坐标.
将方程(8)代入方程(7), 然后在方程左端乘上 $\varphi^{{T}}$, 并从0到1积分,则可以得到以下关于质量、阻尼和刚度矩阵的离散方程形式
(9) $(M_{L} + M_{N})\ddot{q} +(C_{L} +C_{N} )\dot{q}+(K_{L} + K_{N} )q=0$
其中, ${q}=\left[ {q_{1}, q_{2}, \cdots, q_{N} } \right]$, ${\dot{{q}}}=\left[ {\dot{{q}}_{1},\dot{{q}}_{2}, \cdots, \dot{{q}}_{N} } \right]$和${\ddot{{q}}}=\left[ {\ddot{{q}}_{1}, \ddot{{q}}_{2}, \cdots, \ddot{{q}}_{N} }\right]$分别为输流管发生各阶模态振动时所对应的振幅、速度以及加速度. $M_{{L}}$, $M_{{N}}$; $C_{{L}}$, $C_{{N}}$; $K_{{L}}$, $K_{{N}}$分别表示质量矩阵、阻尼矩阵、刚度矩阵. 下标L代表其为线性项, 下标N代表为非线性项. 最后, 借助高阶的龙格库塔数值法来求解方程(9),就可以得到输流管系统在内流速激励和外部集中质量边界条件下的振动响应以及动力学行为.
2 输流管振动实验设计
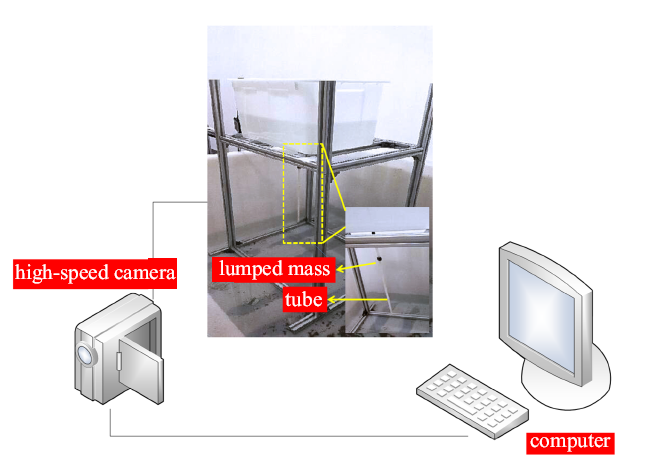
如图2 所示, 本实验由自主搭建的悬臂输流管装置、高速摄像机以及计算机配合完成.悬臂输流管装置中, 输流管内流体由水泵提供, 水泵入水口连接上方水槽,出水口连接输流管道, 通过调节水泵的功率来实现管内流速的变化.管道材料为硅橡胶, 其具体参数为: 密度$\rho =1574.5$ kg/m$^{3}$,弹性模量$E=8$ MPa, 长度$L=0.4$ m, 外径$D=0.008$ m, 内径$d=0.006$ m.集中质量采用体积为$2.826\times10^{-7}$ m$^{3}$的金属螺母代替,其质量大小$m_{j}=0.011$ kg. 水泵可调节的流速范围为0 $\sim$ 5.72 m/s,转化为无量纲的流速范围为0 $\sim$ 11.61. 当管内流速达到临界流速时,则会引起悬臂输流管颤振, 此时使用高速摄像机录下输流管的振动过程.对录下的视频文件进行图像处理以得到输流管道的振动幅值.首先将图像进行二值化处理, 即将输流管标记为白色, 背景标记为黑色,之后标记出最大连通域图像. 整个图像可视作一个坐标系. 在输流管自由端添加标记,即可通过标记的坐标变化来获取信号、采样频率与时间序列数据, 并以此绘制曲线.
图2
图2
实验装置示意图
Fig. 2
Schematic diagram of the experimental apparatus
结构系统的阻尼可以通过自由振动实验[30 ] 得到.通过以上图像处理方法获得系统的自由振动幅值,通过结构振动的衰减趋势以得到衰减系数$\eta $, 再由公式$\ln \eta =2\pi /\sqrt{1-\zeta^{2}} $得出阻尼比$\zeta $, 进一步由公式$\zeta =c/2\sqrt {KM}$得到结构系统的阻尼$c$.
通过上述实验过程, 可得到含集中质量输流管的动力学特性.基于上述输流管的材料参数, 得到系统参数$\beta =0.313$, $\gamma =51.69$,$\mu =0.437$, 以此作为理论计算的系统参数, 即可与本实验进行对比,以验证理论计算的准确性.
3 线性动力学特征分析
为研究含集中质量输流管结构的稳定性, 首先进行线性动力学特征分析.通过临界流速, 固有频率和失稳模态等特性来表征输流管系统的稳定性.针对矩阵方程(9), 去掉非线性项后, 得到的线性矩阵方程可以写成如下形式
(10) ${M}_{L} {\ddot{{q}}}+C_{L} {\dot{{q}}}+ K_{L} {q}={\bf0}$
通过Galerkin前四阶模态截断, $M_{{L}}$, $C_{{L}}$, $K_{{L}}$无量纲形式可以表示为
(11) ${M}_{L} =\int_0^1 {{\varphi }^{T}} {\varphi }\text{d}\xi +\mu [{\varphi }^{T}{\varphi }]_{\xi =\xi_{j} }$
(12) ${C}_{L} =2u\sqrt \beta \int_0^1 {{\varphi }^{T}{\varphi'}} \text{d}\xi$
(13) ${K}_{L} =\int_0^1{\varphi }^{T}\varphi ""\text{d}\xi +\left( {u^{2}-\gamma \mu } \right)\int_0^1 {\varphi }^{T}{{\varphi }"}\text{d}\xi -\\ \gamma \int_0^1 {\left( {1-\xi } \right){\varphi }^{T}{ {\varphi }"}\text{d}\xi } +\gamma \int_0^1 {{\varphi }^{T}{{\varphi }'}\text{d}\xi } + \\ \gamma \mu \left[ {{\varphi }^{T}{{\varphi }'}} \right]_{\xi =\xi_{j} }$
从上式中可以明显看出集中质量对$M_{{L}}$和$K_{{L}}$矩阵带来的影响. 其中 $\varphi$为悬臂输流管的模态函数, 可以表示为
(14) ${\varphi }={sh}\left( {\lambda_{i} \xi } \right)-\sin\left( {\lambda_{i} \xi } \right)+\sigma \left[ {{ch}\left( {\lambda_{i} \xi } \right)-\cos\left( {\lambda_{i} \xi } \right)} \right]$
(15) $\sigma =\left[ {\cos\left( {\lambda_{i} \xi } \right)+\cos\left( {\lambda _{i} \xi } \right)} \right]/\left[ {\sin\left( {\lambda_{i} \xi } \right)-{sh}\left( {\lambda_{i} \xi } \right)} \right]$
其中$i=1$, 2, 3, 4; 即 $\varphi $为4乘1的向量. $\varphi^{{T}}$ $\varphi $则为4乘4的矩阵, 所以$M_{{L}}$, $C_{{L}}$, $K_{{L}}$也分别为4乘4的矩阵. 可以定义以下矩阵和向量
(16) ${B}=\left[ {{\begin{array}{*{20}c} {{0}} & {{M}} \\[-1mm] {{M}} & {{C}} \\ \end{array} }} \right], \quad {E=}\left[ {{\begin{array}{*{20}c} {{-M}} & {{0}} \\[-1mm] {{0}} & {{K}} \\ \end{array} }} \right], \quad {Z=}\left\{ {{\begin{array}{*{20}c} {{\dot{{q}}}} \\[-1mm] {{q}} \\ \end{array} }} \right\}$
(17) $B\dot{{Z}}+EZ=0$
令${Z}={A}{e}^{\lambda_{i} t}={A}{e}^{{i}\omega_{i} t}$, $\lambda_{i} ={i}\omega_{i} $.则矩阵方程(17)转化为特征值问题
(18) $\left( {{\lambda I-Y}} \right)A={\bf0}$
其中, $Y=-\dfrac{{E}}{{B}} =\left[\begin{array}{cc} {{0}} & {{I}} \\ -\dfrac{{M}_{L} }{{K}_{L} } & -\dfrac{{M}_{L} }{{C}_{L} } \\\end{array}\right]$, $I$为单位矩阵. 则需解出矩阵$Y$的特征值$\lambda $. 随着附加集中质量的变化, $M_{{L}}$和 $K_{{L}}$矩阵均受到矩阵$\mu \left[ {{\varphi }^{{T}}{{\varphi }'}} \right]_{\xi =\xi_{j} } $的影响. 导致了特征值$ \lambda $也发生相应变化. 由$\lambda_{i}={i}\omega _{i}$的关系可知, 特征值$\lambda $虚部为振动频率,实部为阻尼. 通过频率和阻尼绘制出管道系统的前四阶复频率随流速变化的Argand图,临界流速即可通过Argand图得到.
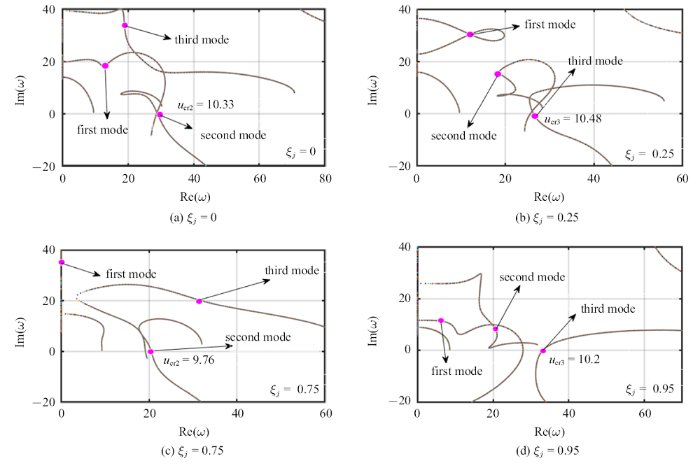
在计算过程中, 如上节所述, 取系统参数值$\beta =0.313$, $\gamma =51.69$,$\mu =0.437$. 图3 给出的当集中质量被安装在输流管不同位置时,管道系统的前四阶复频率随流速变化的Argand图. 横坐标是复频率的实部,代表的输流管结构的固有频率. 纵坐标是复频率的虚部, 代表的是结构的阻尼.随着内流速的增大, 实部和虚部值会发生变化, 当虚部由正值变为负值时,系统发生失稳. 此时内流速为系统的临界流速. 选取的位置为$\xi_{j}=0$,0.25, 0.75和0.95处. 显然, 当$\xi_{j}=0$时相当于输流管不含有集中质量.从图3 的计算结果可以看出, 随着集中质量所处位置的变化,管道系统的临界流速以及对应失稳模态也发生了较大的变化. 比如, 当$\xi_{j}=0$时, 即, 输流管不含有集中质量, 此时输流管结构的临界流速为10.33,且发生的是二阶模态失稳. 当$\xi_{j}=0.25$时, 由于集中质量的影响,输流管结构的临界流速增大到10.48, 且对应的失稳模态阶数为三阶.这说明引入集中质量可以增大临界流速从而提高输流管系统的稳定性. 比较有趣的是,当集中质量位于0.75处时, 输流管系统的临界流速有所降低, 变为9.76,失稳模态变为二阶. 当集中质量在0.95处时, 此时临界流速又增大到10.2,且对应的失稳模态转迁为三阶. 这说明,当集中质量的安装位置从输流管固定端变化到自由端时,管道系统的临界流速呈现出复杂的非线性变化趋势,这与失稳模态的转迁有很大的关系.
图3
图3
集中质量处于不同位置时, 管道系统的前四阶复频率随流速变化的Argand图
Fig. 3
Argand diagram of the first four order complex frequencies varying with the flow velocity of the pipe system when the lumped mass is at different positions
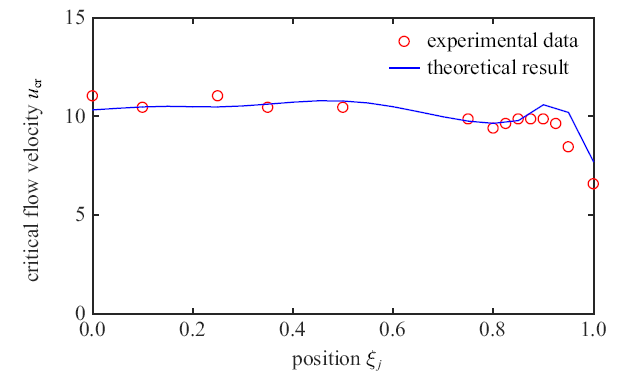
为了进一步了解集中质量位置对输流管系统临界流速的影响规律,图4 给出了临界流速随位置变化关系曲线. 蓝色的线是理论计算的结果, 可以看出,当集中质量位置从固定端($\xi_{j}=0$)调节到自由端($\xi_{j}=1$)时,临界流速大小呈现出先增大后减小, 再增大再减小的趋势. 比如,当集中质量位置在$\xi_{j}=0.5$之前时, 系统的临界流速随$\xi_{j}$增大表现出小幅增加趋势. 当$\xi_{j}$ 从0.5增大到0.75时,临界流速开始逐渐降低, 大约在$\xi_{j}=0.75$处, 临界流速降到低谷. 随后,当$\xi_{j}$ 从0.75增大到0.9时, 临界流速反而表现出增大的趋势. 最后,随着位置越来越靠近自由端, 输流管系统的临界流速再次逐渐下降并降到最低.
图4
图4
管道系统失稳临界流速随集中质量位置变化曲线
Fig. 4
curve graph of the critical velocity of the pipe system instability varying with the lumped mass position
将理论计算结果与实验测试进行了对比, 红色圆圈代表实验测试结果. 在实验中,随着流速的增大, 当输流管将要或刚发生振动时, 记录此时的流速为临界流速.从实验可以看出, 当集中质量位于$\xi_{j}=0.5$之前时,临界流速基本不发生变化. 当集中质量的位置大于$\xi_{j}=0.5$时,实验测得的临界流速同样表现出先减小后增大, 然后再次减小的趋势.这与理论预测结果是一致的, 且从对比中可以看出, 临界流速值大小相差不大.需要指出的是, 在靠近自由端时, 理论与实验得到的临界流速大小有所差异,这是因为, 一是集中质量在输流管上占据了一定的体积,导致在自由端位置的测试不够准确; 二是集中质量靠近自由端时,输流管可能发生非平面等复杂动力学行为,与本文采用的平面振动假设理论有一定偏差. 因此,从理论上预测临界流速时与实验测试存在一定的误差.
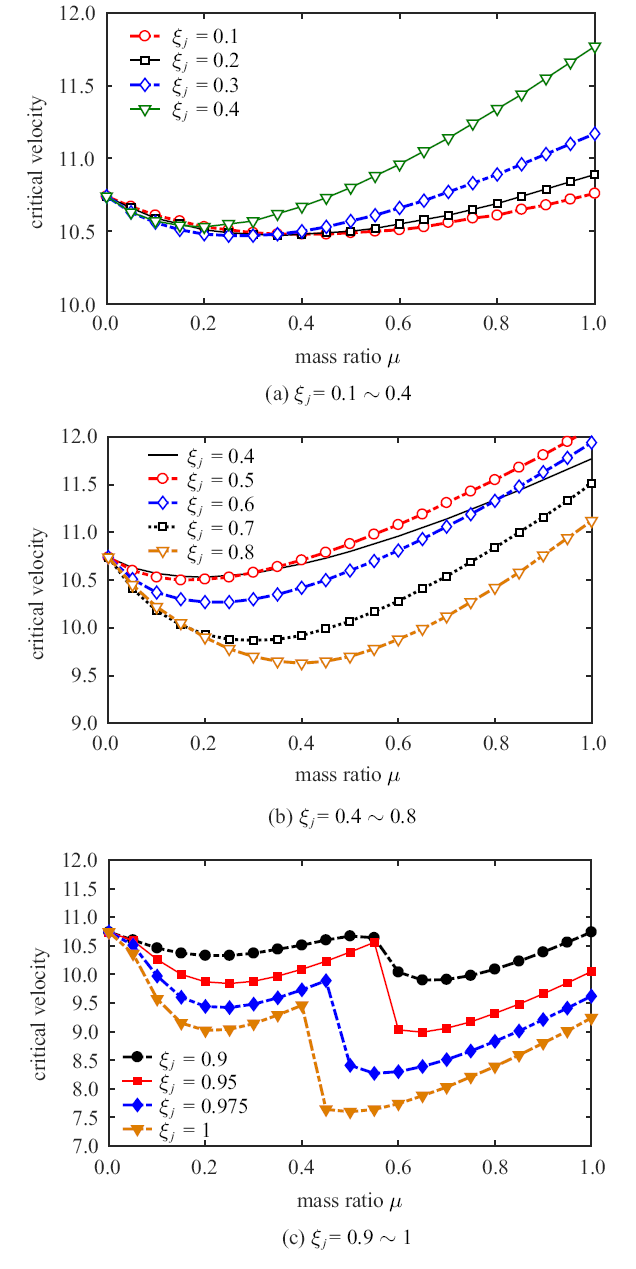
图5 给出的是集中质量的质量比对输流管系统临界流速的影响,质量比表示的是集中质量与管道系统的质量之比. 可以发现,当集中质量处于不同位置时, 其质量比对临界流速影响的变化趋势也不尽相同. 比如,当安装位置$\xi_{j}$从0.1变化到0.5时, 如图5 (a)和图5 (b)所示, 随着质量比$\mu$从0增大到1, 临界流速先减小后增大. 当质量比$\mu<0.2$时,集中质量所处的位置($\xi_{j})$对临界流速几乎没有影响; 质量比$\mu>0.2$时, 可以看到, $\xi_{j}$越大, 临界流速也越大. 然而,当安装位置$\xi_{j}$从0.5增大到0.8时, 虽然随着质量比$\mu $从0增大到1,临界流速也表现出先减小后增大的趋势, 但是$\xi_{j}$越大, 临界流速却越小,这与安装位置在0.1到0.5之间的临界流速变化情况有所不同. 随着安装位置$\xi_{j}$的进一步增大(越靠近自由端), 从图4 (c)可以得到,临界流速随质量比增大表现出的变化趋势越来越复杂. 具体表现为,随着质量比从0增大到1, 临界流速先减小再增大; 然后存在一个转折点,此时临界流速值急剧下降, 最后逐渐增大. 当集中质量离自由端越来越近($\xi_{j}$越来越大), 这个转折点会逐渐左移. 且随着$\xi_{j}$从0.9增大到1,输流管系统的临界流速是逐渐降低的.这种临界流速的变化与振动模态的转迁有很大的关系,也说明集中质量的安装位置($\xi_{j})$和质量比($\mu)$对输流管系统的振动模态有很大的影响.
图5
图5
集中质量置于不同位置时,管道系统失稳临界流速随集中质量比变化曲线
Fig. 5
curve graph of the critical velocity of the pipe system instability varying with the lumped mass ratio at different lumped mass position
4 非线性振动特征分析
通过前面的分析可知, 引入集中质量可以改变输流管系统的临界流速和失稳模态,从而影响系统的非线性振动行为. 因此,本节研究了集中质量对输流管系统非线性振动特性的影响规律.主要分析了集中质量位置对输流管振动模态和振动幅值的影响,并将理论计算结果与实验测试进行了对比. 取集中质量安装在0.25,0.75和0.95位置处, 无量纲内流速取11.03. 根据图6 可知,当集中质量在0.25位置处时, 输流管结构发生了二阶模态的颤振行为.图6 (a)和图6 (b)分别代表理论计算出的不同时刻输流管振动构型,图6 (c)表示理论计算得到的输流管的振动轨迹,图6 (d)为实验中观测的输流管振动构型. 可知, 对输流管振动模态的研究,理论预测与实验观察具有一致性. 同样, 当$\xi_{j}=0.75$时,理论计算输流管结构发生的是二阶模态颤振,实验中输流管振动也表现为很明显的二阶模态振动行为, 如图7 所示. 而当$\xi_{j}=0.95$时, 输流管的振动模态由二阶转迁为三阶,理论和实验对比结果如图8 所示. 在同一流速下, 对比图6 ~图8 可以看出,无论是理论计算还是实验测试结果, 输流管自由端部($\xi =1$)的振动幅值随着安装位置($\xi_{j})$的不同发生了较大的变化. 当$\xi_{j}=0.75$时, 输流管振动幅值明显要高于在0.25和0.95处时的振幅.
图6
图6
集中质量处于0.25位置时, 输流管结构的振动行为
Fig. 6
The vibration behavior of the fluid-conveying pipe structure at the lumped position 0.25
图7
图7
集中质量处于0.75位置, 输流管结构的振动行为
Fig. 7
The vibration behavior of the fluid-conveying pipe structure at the lumped position 0.75
图8
图8
集中质量处于0.95位置, 输流管结构振动行为
Fig. 8
The vibration behavior of the fluid-conveying pipe structure at the lumped position 0.95
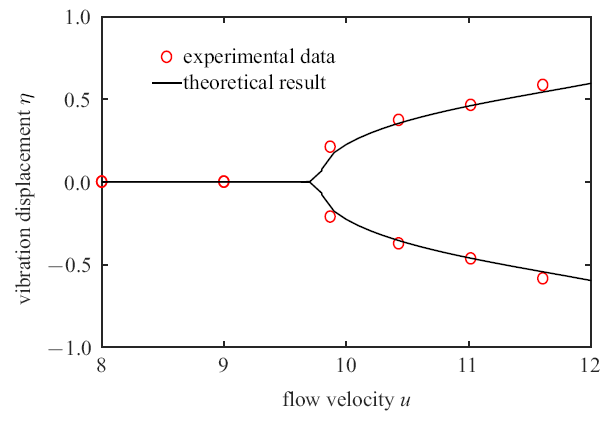
为了进一步研究集中质量位置对输流管振动幅值的影响规律, 取$\xi_{j}=0$, 0.35, 0.55, 0.75和0.95五种情况, 理论计算结果与实验测试数据进行了对比,如表1 所示. 由于实验中所用水泵的流速范围较窄,只选取了两种流速分别为$u=11.03$和11.61进行实验. 实验结果表明,当集中质量位置从0增大到0.95时, 对于给定的流速, 输流管振动幅值会先增大后减小.在$\xi_{j}=0.75$处时, 输流管振幅有最大值. 随着流速从11.03增大到11.61,输流管的振动幅值也有所增大. 从表1 中得出,理论计算结果与实验测试数据的误差大多都在10%左右,由此证明理论模型的准确性. 根据计算结果和实验测试数据可知,当集中质量安装在0到0.75位置范围内时, 输流管振动主要表现出二阶模态颤振行为,且随着$\xi_{j}$的增大, 振幅越来越大.当集中质量位置越靠近自由端时(比如$\xi_{j}>0.75$),输流管振动模态由二阶转迁为三阶, 振幅会有所下降. 图9 给出了当$\xi_{j}=0.75$时, 输流管道自由端的振动幅值随流速变化的分岔图,理论计算结果与实验测试数据进行了对比. 可知, 当流速超过临界值时,随着流速的增大, 输流管振动幅值逐渐增大. 图10 给出的是当流速分别为9.87和11.03时输流管振动的时间历程曲线.
图9
图9
当$\xi_{j}=0.75$时, 输流管自由端的位移随流速变化分岔图
Fig. 9
Bifurcation diagram of the tip displacement of the fluid-conveying pipe varying with the velocity when the model at $\xi_{j} =0.75$
图10
图10
$\xi_{j} =0.75$, (a)和(b)无量纲内流速为9.87,(c)和(d)无量纲内流速为11.03时输流管结构振动的时间历程曲线;(a)和(c)理论预测结果曲线; (b)和(d)实验测得结果曲线
Fig. 10
Time history curves of the fluid-conveying pipe structure vibrationwith a dimensionless velocity of (a) , (b) 9.87; (c), (d) 11.03 at $\xi_{j}=0.75$; (a) and (c) are the resulting curves of theoreticalpredictions; (b) and (d) are experimental results
5 结论
本文基于哈密顿原理对附加集中质量的悬臂输流管系统进行了数学建模,推导出了附加集中质量悬臂输流管系统的非线性动力学方程.通过数值求解以及实验的方法对该理论模型进行验证,并对附加集中质量的悬臂输流管系统的稳定性与非线性动力学行为进行了研究.揭示了附加集中质量对悬臂输流管系统所带来的动力学影响. 可以得到如下结论:
(1)附加集中质量会导致悬臂输流管结构失稳临界流速的降低, 以及振幅的增大.
(2)集中质量的放置位置与质量比是影响悬臂输流管系统稳定性以及非线性响应的重要因素.悬臂输流管结构的失稳临界流速随集中质量的放置位置与质量比的变化而变化. 同时,集中质量的位置对悬臂输流管结构的振动幅值也有较大影响. 当$\xi_{j}=0.75$时, 悬臂输流管系统的失稳临界流速最低, 且振动幅值最大.
(3) 当集中质量接近自由端时, 悬臂输流管结构的振动模态会发生转迁;质量比足够大时也会导致悬臂输流管结构的振动模态转迁. 当集中质量位于$\xi_{j}=0.95$时, 悬臂输流管结构的振动模态由二阶转变为三阶,其失稳临界流速进一步降低, 振动幅值反而减小.由此推断振动模态的变化导致了失稳临界流速与振幅的减小. 当$\xi_{j}=1$,即集中质量位于自由端时, 悬臂输流管结构的失稳临界流速达到最低.
参考文献
View Option
[1]
Paidoussis MP . Fluid-Structure Interactions: Slender Structures and Axial Flow (Vol.1) London : Academic Press , 1998
[本文引用: 2]
[2]
Paidoussis MP Li GX . Pipes conveying fluid: A model dynamical problem
Journal of Fluids and Structures 1993 ,7 :137 -204
[本文引用: 2]
[3]
Semler C Li GX Paidoussis MP . The non-linear equations of motion of pipes conveying fluid
Journal of Sound and Vibration 1994 ,169 (5 ):577 -599
[本文引用: 1]
[4]
Wadham-Gagnon M Paidoussis MP Semler C . Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion
Journal of Fluids and Structures 2007 ,23 (4 ):545 -567
DOI
URL
[本文引用: 1]
[5]
Yoon H Son IS . Dynamic response of rotating flexible cantilever pipe conveying fluid with tip mass
International Journal of Mechanical Sciences 2007 ,49 :878 -887
DOI
URL
[本文引用: 2]
AbstractIn this study the vibration system is consisted of a rotating cantilever pipe conveying fluid and a tip mass. The equation of motion is derived by using the Lagrange's equation. Also, the equation of motion is derived applying a modeling method that employs hybrid deformation variables. The influences of the rotating angular velocity and the velocity of fluid flow on the dynamic behavior of a cantilever pipe are studied by the numerical method. The effects of a tip mass on the dynamic behavior of a rotating cantilever pipe are also studied. The influences of a tip mass, the velocity of fluid, the angular velocity of a cantilever pipe and the coupling of these factors on the dynamic behavior of a cantilever pipe are analytically clarified. The natural frequencies of a cantilever pipe conveying fluid are proportional to the angular velocity of the pipe and a tip mass in both axial direction and lateral direction.]]>
[6]
Dai HL Wang L Ni Q . Dynamics of a fluid-conveying pipe composed of two different materials
International Journal of Engineering Science 2013 ,73 :67 -76
DOI
URL
[本文引用: 1]
The dynamics of fluid-conveying cantilevered pipe consisting of two segments made of different materials is studied, focusing on the effects induced by different length ratios between the two segments. Two kinds of hybrid pipes are considered: one is made of steel and aluminum and the other is made of aluminum and epoxy. The complex frequency of the four lowest modes of the hybrid system is calculated in two representative cases for successively increasing values of the flow velocity to demonstrate how transition from stability to instability takes place. Compared with a uniform pipe conveying fluid, it is found that the hybrid pipe is capable of displaying more complex and sometimes unexpected dynamical behaviors. The numerical results show that in such a hybrid pipe system, an instability-restabilization-instability sequence would occur as the flow velocity is successively increasing. When the length ratio between the two segments is successively increased, the lowest order of unstable modes may frequently shift from one to another. It is also demonstrated that with increasing flow velocity, the flutter instability first occurring in the fourth mode is possible and a certain unstable mode may suddenly regain stability, which has not been reported before. Furthermore, when the segment made of softer material is placed at the clamped end, the system is much easier to lose stability. Some of these new results observed in the hybrid pipe system are also expected to be helpful in controlling the dynamical behaviors of fluid-conveying pipes. (C) 2013 Elsevier Ltd.
[7]
Zhou K Xiong FR Jiang NB , et al . Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink
Nonlinear Dynamics 2019 ,95 :1435 -1456
[本文引用: 1]
[8]
Liu ZY Wang L Dai HL , et al . Nonplanar vortex-induced vibrations of cantilevered pipes conveying fluid subjected to loose constraints
Ocean Engineering 2019 ,178 :1 -19
[本文引用: 1]
[9]
Ni Q Wang Y Tang M , et al . Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints
Nonlinear Dynamics 2015 ,81 (1-2 ):893 -906
[本文引用: 1]
[10]
Yan H Dai H Ni Q , et al . Nonlinear dynamics of a sliding pipe conveying fluid
Journal of Fluids and Structures 2018 ,81 :36 -57
[本文引用: 1]
[11]
周坤 , 倪樵 , 代胡亮 等 . 周期性输流管道的非线性动力学特性研究
振动与冲击 , 2020 ,39 (10 ):75 -80
[本文引用: 2]
( Zhou Kun Ni Qiao Dai Huliang , et al . Analysis of nonlinear dynamic characteristics of periodic pipe conveying fluid
Journal of Vibration and Shock 2020 ,39 (10 ):75 -80 (in Chinese))
[本文引用: 2]
[12]
Yu D Païdoussis MP Shen H , et al . Dynamic stability of periodic pipes conveying fluid
Journal of Applied Mechanics 2014 ,81 (1 ):011008
[本文引用: 1]
[13]
Najjar J Daneshmand F . Stability of horizontal and vertical pipes conveying fluid under the effects of additional point masses and springs
Ocean Engineering 2020 ,206
[本文引用: 1]
[14]
Li Q Liu W Zhang Z , et al . Parametric resonance of pipes with soft and hard segments conveying pulsating fluids
International Journal of Structural Stability and Dynamics 2018 ,18 (10 ):1850119
DOI
URL
[15]
Stangl M Gerstmayr J Irschik H . A large deformation planar finite element for pipes conveying fluid based on the absolute nodal coordinate formulation
Journal of Computational and Nonlinear Dynamics 2009 ,4 (3 ):031009
DOI
URL
[16]
Modarres-Sadeghi Y Paidoussis MP Semler C . Three-dimensional oscillations of a cantilever pipe conveying fluid
International Journal of Non-Linear Mechanics 2008 ,43 (1 ):18 -25
DOI
URL
AbstractThe aim of the study described in this paper is to investigate the two-dimensional (2-D) and three-dimensional (3-D) flutter of cantilevered pipes conveying fluid. Specifically, by means of a complete set of non-linear equations of motion, two questions are addressed: (i) whether for a system losing stability by either 2-D or 3-D flutter the motion remains of the same type as the flow velocity is increased substantially beyond the Hopf bifurcation precipitating the flutter; (ii) whether the bifurcational behaviour of a horizontal system and a vertical one (sufficiently long for gravity to have an important effect on the dynamics) are substantially similar. Stability maps and tables are used to delineate areas in a flow velocity versus mass parameter plane where 2-D or 3-D motions occur, and limit-cycle motions are illustrated by phase–plane plots, PSDs and cross-sectional diagrams showing whether the motion is circular (3-D) or planar (2-D).]]>
[17]
Giacobbi DB Semler C Païdoussis MP . Dynamics of pipes conveying fluid of axially varying density
Journal of Sound and Vibration 2020 ,473
[18]
金基铎 , 邹光胜 , 张宇飞 . 悬臂输流管道的运动分岔现象和混沌运动
力学学报 , 2002 ,34 (6 ):863 -873
( Jin Jiduo Zou Guangsheng Zhang Yufei . Bifurcations and chaotic motions of a cantilevered pipe conveying fluid
Chinese Journal of Theoretical and Applied Mechanics 2002 ,34 (6 ):863 -873 (in Chinese))
[19]
王乙坤 , 王琳 . 分布式运动约束下悬臂输液管的参数共振研究
力学学报 , 2019 ,51 (2 ):558 -568
[本文引用: 1]
( Wang Yikun Wang Lin . Parametricresonance of a cantilevered pipe conveying fluid subjected to distributed motion constraints
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):558 -568 (in Chinese))
[本文引用: 1]
[20]
王乙坤 , 倪樵 , 王琳 等 . 具有松动约束悬臂输液管的三维非线性振动
科学通报 , 2017 ,62 (36 ):4270 -4277
( Wang Yikun Ni Qiao Wang Lin , et al . Three-dimensional nonlinear dynamics of a cantilevered pipe conveying fluid subjected to loose constraints
Chinese Science Bulletin 2017 ,62 (36 ):4270 -4277 (in Chinese))
[21]
Stangl M Gerstmayr J Irschik H . An alternative approach for the analysis of nonlinear vibrations of pipes conveying fluid
Journal of Sound and Vibration 2008 ,310 (3 ):493 -511
DOI
URL
[22]
徐鉴 , 王琳 . 输流管动力学分析和控制 . 北京 : 科学出版社 , 2015
( Xu Jian Wang Lin . Dynamics and Control of Fluid-conveying Pipe Systems . Beijing : Science Press , 2015 (in Chinese))
[23]
张艳雷 , 黄慧春 , 陈立群 . 振荡流作用下受约束的悬臂输流管的分岔特性
噪声与振动控制 , 2012 ,32 (5 ):46 -48, 167
( Zhang Yanlei Huang Huichun Chen Liqun . Bifurcation analysis of a constrained cantilevered pipe conveying fluid under the harmonic parametric excitations
Noise and Vibration Control 2012 ,32 (5 ):46 -48, 167 (in Chinese))
[24]
黄茜 , 臧峰刚 , 张毅雄 等 . 带滞变支撑悬臂输流管的动力响应分析
振动与冲击 , 2011 ,30 (11 ):8 -12
URL
[本文引用: 1]
将滞变支撑所做的虚功引入到管道的能量方程中,利用Hamilton体系的变分原理,导出了带滞变支撑悬臂输流管的非线性运动方程。进而利用Galerkin法对偏微分方程进行离散,以Matlab为平台编制了带滞变支撑悬臂输流管流致振动的计算程序。通过滞变支撑退化模型与现有文献结果比较,验证了本文模型的有效性;随后,考察了该系统的动力学行为,并分析了滞变支撑刚度对悬臂输流管稳定性的影响。结果表明,滞变支撑悬臂输流管表现出丰富的动力学行为,刚度的变化不仅使使得系统的分叉类型、分叉方式与分叉路径发生了的显著变化,也改变了周期运动的周期数,并使其出现复杂响应的参数范围发生了改变。]]>
( Huang Qian Zang Fenggang Zhang Yixiong , et al . Nonlinear dynamic analysis of cantilevered pipes conveying fluid with hysteretic supports
Journal of Vibration and Shock 2011 ,30 (11 ):8 -12 (in Chinese))
URL
[本文引用: 1]
By introducing the hysteretic forces acting on the pipe into Hamilton’s principle through the principle of virtual work, the nonlinear equations of motion of cantilevered pipes conveying fluid with hysteretic supports are derived. Galerkin’s discretization method is applied to the motion equations, numerical simulation of dynamic responses are performed based on the platform of MATLAB, First,the reasonableness of the hysteretic model has been proved by comparing the results of its degenerate model and the results by other researchers. Then, numerical simulations of dynamic response of system and parametric researches about structural nondimensional stiffness are conducted. Results show abundant dynamic phenomenon of the system, the variety of nondimensional stiffness can lead to the changes of bifurcation style, bifurcation path, period number and parameter range.]]>
[25]
何涛 . 基于 ALE 有限元法的流固耦合强耦合数值模拟
力学学报 , 2018 ,50 (2 ):395 -404
[本文引用: 1]
( He Tao . A partitioned strong coupling algorithm for fluid-structure interaction using arbitrary lagrangian-eulerian finite element formulation
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):395 -404 (in Chinese))
[本文引用: 1]
[26]
胡璐 , 闫寒 , 张文明 等 . 黏性流体环境下 V 型悬臂梁结构流固耦合振动特性研究
力学学报 , 2018 ,50 (3 ):643 -653
[本文引用: 1]
( Hu Lu Yan Han Zhang Wenming , et al . Analysis of flexural vibration of V-shaped beams immersed in viscous fluids
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (3 ):643 -653 (in Chinese))
[本文引用: 1]
[27]
邹光胜 , 金基铎 , 沙云东 . 简谐激励下输流管动态响应特性的实验研究
振动、测试与诊断 , 2001 (1 ):28 -31
[本文引用: 1]
( Zou Guangsheng Jin Jiduo Sha Yundong . Experimental study on vibration of pipes conveying fluid under harmonic excitation
Journal of Vibration, Measurement & Diagnosis 2001 (1 ):28 -31 (in Chinese))
[本文引用: 1]
[28]
高培鑫 . 多源激励下航空液压管路系统振动分析及其约束层阻尼减振技术研究. [博士论文]
大连: 大连理工大学 , 2017
[本文引用: 1]
( Gao Peixin . Vibration analysis of aviation hydraulic pipeline system under multi-source excitation and study on damping and vibration reduction technology of constrained layer. [PhD Thesis]
Dalian: Dalian University of Technology , 2017 (in Chinese))
[本文引用: 1]
[29]
郭世豪 , 李晔 . 柔性输流管泄流效应实验研究
应用数学和力学 , 2019 ,40 (8 ):866 -879
[本文引用: 1]
( Guo Shihao Li Ye . Experimental study on discharge effect of flexible pipe conveying fluid
Journal Applied Mathematics and Mechanics 2019 ,40 (8 ):866 -879 (in Chinese))
[本文引用: 1]
[30]
代胡亮 , 林时想 , 张岚斌 等 . 基于人体运动的压电-电磁混合式振动能量采集研究
固体力学学报 , 2019 ,40 (5 ):427 -440
[本文引用: 2]
( Dai Huliang Lin Shixiang Zhang Lanbin , et al . Chinese Journal of Solid Mechanics 2019 ,40 (5 ):427 -440 (in Chinese))
[本文引用: 2]
2
1998
... 输流管的振动行为是一种典型的流固耦合振动现象, 同时作为一种典型的细长结构,它广泛应用于海洋工程、核工业、航空航天以及石油化工等工程领域. 因此,输流管动力学的研究具有重要的工程意义与学术价值[1 -2 ] .著名动力学专家Paidoussis教授曾经指出,输流管振动仍是当今动力学研究的重要课题之一,主要因为(1)输流管振动能表现出有趣且复杂的非线性动力学行为;(2)可为现代动力学的发展提供重要的理论依据[1 -2 ] . ...
... [1 -2 ]. ...
Pipes conveying fluid: A model dynamical problem
2
1993
... 输流管的振动行为是一种典型的流固耦合振动现象, 同时作为一种典型的细长结构,它广泛应用于海洋工程、核工业、航空航天以及石油化工等工程领域. 因此,输流管动力学的研究具有重要的工程意义与学术价值[1 -2 ] .著名动力学专家Paidoussis教授曾经指出,输流管振动仍是当今动力学研究的重要课题之一,主要因为(1)输流管振动能表现出有趣且复杂的非线性动力学行为;(2)可为现代动力学的发展提供重要的理论依据[1 -2 ] . ...
... -2 ]. ...
The non-linear equations of motion of pipes conveying fluid
1
1994
... 输流管按照其边界条件可分为两端支撑管以及悬臂管. 其中,悬臂管是一种非保守系统, 当内流流速达到一定值时, 会发生颤振行为.其丰富的动力学行为吸引大量的学者对其进行研究.关于输流管非线性振动控制方程大多是基于Hamilton原理推导得到. 比如1994年,Selmer等[3 ] 基于Hamilton方程所给出的输流管二维非线性振动微分方程,是如今运用最广泛的悬臂输流管控制方程. 2007年,Wadham等[4 ] 基于修正的Hamilton原理将悬臂输流管由二维的动力学方程扩展至三维构型. ...
Dynamics of cantilevered pipes conveying fluid. Part 1: Nonlinear equations of three-dimensional motion
1
2007
... 输流管按照其边界条件可分为两端支撑管以及悬臂管. 其中,悬臂管是一种非保守系统, 当内流流速达到一定值时, 会发生颤振行为.其丰富的动力学行为吸引大量的学者对其进行研究.关于输流管非线性振动控制方程大多是基于Hamilton原理推导得到. 比如1994年,Selmer等[3 ] 基于Hamilton方程所给出的输流管二维非线性振动微分方程,是如今运用最广泛的悬臂输流管控制方程. 2007年,Wadham等[4 ] 基于修正的Hamilton原理将悬臂输流管由二维的动力学方程扩展至三维构型. ...
Dynamic response of rotating flexible cantilever pipe conveying fluid with tip mass
2
2007
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
... [5 ]针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Dynamics of a fluid-conveying pipe composed of two different materials
1
2013
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Nonlinear vibration control of a cantilevered fluid-conveying pipe using the idea of nonlinear energy sink
1
2019
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Nonplanar vortex-induced vibrations of cantilevered pipes conveying fluid subjected to loose constraints
1
2019
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Nonlinear impacting oscillations of a fluid-conveying pipe subjected to distributed motion constraints
1
2015
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Nonlinear dynamics of a sliding pipe conveying fluid
1
2018
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
周期性输流管道的非线性动力学特性研究
2
2020
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
... [11 ]基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
周期性输流管道的非线性动力学特性研究
2
2020
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
... [11 ]基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Dynamic stability of periodic pipes conveying fluid
1
2014
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Stability of horizontal and vertical pipes conveying fluid under the effects of additional point masses and springs
1
2020
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
Parametric resonance of pipes with soft and hard segments conveying pulsating fluids
0
2018
A large deformation planar finite element for pipes conveying fluid based on the absolute nodal coordinate formulation
0
2009
Three-dimensional oscillations of a cantilever pipe conveying fluid
0
2008
Dynamics of pipes conveying fluid of axially varying density
0
2020
悬臂输流管道的运动分岔现象和混沌运动
0
2002
悬臂输流管道的运动分岔现象和混沌运动
0
2002
分布式运动约束下悬臂输液管的参数共振研究
1
2019
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
分布式运动约束下悬臂输液管的参数共振研究
1
2019
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
具有松动约束悬臂输液管的三维非线性振动
0
2017
具有松动约束悬臂输液管的三维非线性振动
0
2017
An alternative approach for the analysis of nonlinear vibrations of pipes conveying fluid
0
2008
振荡流作用下受约束的悬臂输流管的分岔特性
0
2012
振荡流作用下受约束的悬臂输流管的分岔特性
0
2012
带滞变支撑悬臂输流管的动力响应分析
1
2011
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
带滞变支撑悬臂输流管的动力响应分析
1
2011
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
1
2018
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
1
2018
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
黏性流体环境下 V 型悬臂梁结构流固耦合振动特性研究
1
2018
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
黏性流体环境下 V 型悬臂梁结构流固耦合振动特性研究
1
2018
... 随着对悬臂输流管非线性动力学方程的不断完善,又涌现出了一系列基于不同构型悬臂输流管系统的研究[5 -24 ] ,以达到控制和利用悬臂输流管非线性振动的目的.关于流固耦合结构系统的建模与分析,主要有数值模拟和理论模型两种研究方法[25 -26 ] .而在研究输流管流固耦合问题时, 大多采用理论模型来建立动力学控制方程. 比如,2006年, Yoon和Son[5 ] 针对含尖端质量的旋转柔性悬臂输流管进行了研究,发现尖端质量对稳定性有重要影响. 后来,Dai等[6 ] 提出了双材料组合构型的悬臂输流管结构,发现材料的刚度比值对输流管的颤振失稳临界流速有很大影响. 最近,Zhou等[7 ] 提出了非线性能量汇(NES)的被动控制方法. 研究发现,NES的质量、阻尼、刚度和安装位置对管道临界流速和振动幅值有重要影响. 此外,Liu等[8 ] 还研究了松动约束下的悬臂输流管的非线性振动特性,发现约束间隙能导致输流管发生混沌等复杂动力学行为.Ni等[9 ] 研究了悬臂输流管与两侧支撑壁面相互作用的非线性动力学关系,使用三次弹簧来模拟冲击力.Yan等[10 ] 研究了滑动输流管道的非线性动力学特征,详细讨论了流速、滑动速率和质量比、重力两个关键参数对管道动态特性的影响.周期性输流管道也成为学者们研究的热点之一[11 -12 ] , 周坤等[11 ] 基于绝对节点坐标法,推导出不同材料组成的周期性悬臂输流管道在定常内流作用下的非线性动力学方程,对铝-钢及钢-铝周期性悬臂输流管道的稳定性和非线性动力学行为进行了研究.值得一提的是,Najjar等[13 ] 最近研究了附加集中质量和弹簧分别对悬臂输流管失稳特性的影响.他们主要研究了集中质量条件下管道质量比对失稳临界流速的影响规律,仅限于线性动力学的分析, 且没有开展实验研究.王乙坤等[19 ] 在悬臂输流管的碰撞振动方面做了更深入的研究,基于非光滑理论建立了具有刚性间隙约束简支输流管的非线性碰撞振动模型. ...
简谐激励下输流管动态响应特性的实验研究
1
2001
... 在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照. ...
简谐激励下输流管动态响应特性的实验研究
1
2001
... 在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照. ...
多源激励下航空液压管路系统振动分析及其约束层阻尼减振技术研究. [博士论文]
1
2017
... 在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照. ...
多源激励下航空液压管路系统振动分析及其约束层阻尼减振技术研究. [博士论文]
1
2017
... 在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照. ...
柔性输流管泄流效应实验研究
1
2019
... 在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照. ...
柔性输流管泄流效应实验研究
1
2019
... 在输流管系统实验研究方面,邹光胜等[27 ] 对两端受扭转弹簧约束的简支输流管在简谐运动激励下的振动特性问题进行了实验研究,发现在某些频率段上管道会发生多周期的复杂运动, 并通过倍周期分岔而进入混沌运动. 此外,高培鑫[28 ] 用解析分析、数值计算与试验测试相结合的方法, 系统研究了航空液压管路系统的振动特性、泵源脉动激励和基础激励综合作用下的管路系统动力学特性以及附加黏弹性约束层阻尼材料的管路系统阻尼减振特性的研究.郭世豪等[29 ] 基于模型试验研究了柔性输流管在恒定内流速度下由泄漏孔引入的泄流效应,研究发现了泄流效应对输流管系统振动响应的影响, 并为数值模拟提供了实验参照. ...
基于人体运动的压电-电磁混合式振动能量采集研究
2
2019
... 式中, p和f分别代表管与流体, $v$代表速度, $m$代表管道单位长度质量, $m_{j}$代表附加集中质量, $x_{j}$表示集中质量的位置坐标,$s$为管道横截面位置坐标, 有$s\approx x$. 考虑重力的影响, 系统总势能分为管道应变能和重力势能. 在小应变假设下,管道应变能$V_{s}$可写为[30 ] ...
... 结构系统的阻尼可以通过自由振动实验[30 ] 得到.通过以上图像处理方法获得系统的自由振动幅值,通过结构振动的衰减趋势以得到衰减系数$\eta $, 再由公式$\ln \eta =2\pi /\sqrt{1-\zeta^{2}} $得出阻尼比$\zeta $, 进一步由公式$\zeta =c/2\sqrt {KM}$得到结构系统的阻尼$c$. ...
基于人体运动的压电-电磁混合式振动能量采集研究
2
2019
... 式中, p和f分别代表管与流体, $v$代表速度, $m$代表管道单位长度质量, $m_{j}$代表附加集中质量, $x_{j}$表示集中质量的位置坐标,$s$为管道横截面位置坐标, 有$s\approx x$. 考虑重力的影响, 系统总势能分为管道应变能和重力势能. 在小应变假设下,管道应变能$V_{s}$可写为[30 ] ...
... 结构系统的阻尼可以通过自由振动实验[30 ] 得到.通过以上图像处理方法获得系统的自由振动幅值,通过结构振动的衰减趋势以得到衰减系数$\eta $, 再由公式$\ln \eta =2\pi /\sqrt{1-\zeta^{2}} $得出阻尼比$\zeta $, 进一步由公式$\zeta =c/2\sqrt {KM}$得到结构系统的阻尼$c$. ...