引言
目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星.
早期在质量矩技术方面的研究主要集中在移动质量姿态控制技术[6 -13 ] .Childs[6 ] 和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义.
相关学者还研究了结合环境合外力的质量矩技术[14 -21 ] ,该技术通过移动滑块改变系统质心位置从而主动将环境干扰力作为姿态控制力矩.Shahin和Gong[14 ] 基于解析法分析了在太阳帆卫星上使用质量矩技术的可控性问题.Wie[16 ] 设计了双滑块质量矩姿态控制系统,并以此实现了太阳帆卫星俯仰角和偏航角的控制. Petsopoulos和Regan[21 ] 提出使用质量矩姿态控制装置取代传统再入飞行器舵面控制方式从而避免舵面烧蚀问题.
对于500 km以下的低轨纳卫星,可通过主动控制气动力矩从而控制卫星姿态的稳定和机动[22 -27 ] .由于气动力矩定垂直于大气来流方向, 故单质量矩姿态控制属于欠驱动控制方式.陆正亮[22 ] 探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题.
本文针对由质量移动产生的附加干扰力矩、卫星系统质心位置不确定和由气动力不确定引起的气动控制力矩误差等实际工程问题做出研究.针对质量矩和磁力矩的合力矩设计控制律,并研究最优力矩分配方法实现双执行机构的控制.利用干扰观测器有效观测系统慢时变干扰,并通过控制周期延长和最优力矩分配策略大幅减小由滑块运动引起的快时变附加干扰.为双执行机构搭建半物理仿真平台, 进一步验证质量矩技术的可行性.
1 系统建模
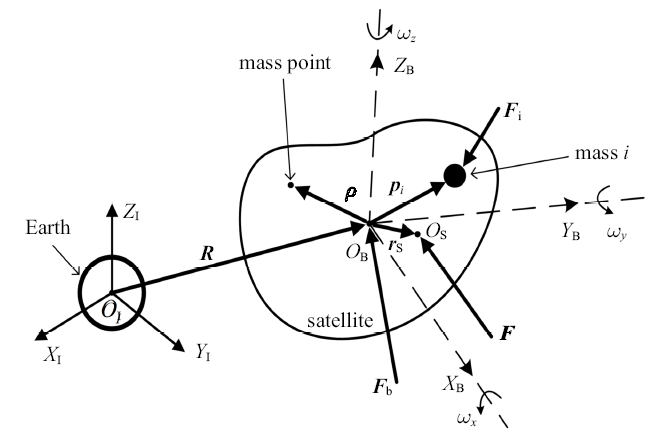
本文以低轨纳卫星为研究对象, 利用质量矩和磁力矩双执行机构进行姿态机动控制, 质量矩执行机构为$n$个可移动滑块, 系统模型如图1 所示.
图1
图1
质量矩卫星系统受力示意图
Fig. 1
Force diagram of the satellite system
(1) $O_{I} X_{I}Y_{I}Z_{I}$为地球惯性坐标系; $O_{B} X_{B} Y_{B} Z_{B}$为建立在卫星本体(除去滑块)质心$O_{B}$的本体坐标系; $O_{S}$为卫星系统(包括滑块)质心位置矢量;
(2) ${R}$表示本体系相对惯性系位置矢量在本体下的表达; ${\rho }$表示卫星本体质点在本体系下的位置矢量; ${p}_i$表示滑块$i$在本体系下的位置矢量; ${r}_{s}$表示系统质心在本体系下的位置矢量;
(3) ${F}_{b} $表示卫星本体受到合外力; ${F}_{i}$表示滑块$i$受到合外力; ${F}$表示卫星系统受到合外力;
(4) 任一矢量${x}$对惯性系的二阶导数表示为${\hat{{\ddot{{x}}}}}$, 对本体系的一阶和二阶导数分别表示为${\dot{{x}}}$和${\ddot{{x}}}$;
(5) ${\omega }$和${\dot{{\omega}}}$分别为卫星本体系相对惯性系的角速度和角加速度在本体系下的表达;
(6) $M$为卫星本体质量; $m_i $为滑块$i$质量; ${J}_{B}$为卫星本体转动惯量;
(7) $[\cdot ]^\times $表示矢量的斜对称矩阵.
1.1 质量矩卫星系统动力学
可移动滑块尺寸相对卫星较小, 被简化为质点处理, 如图1 所示, 卫星本体、滑块$i$以及卫星系统受力为
(1) ${F}_{b} =\int_{M} {\left( {{\hat{{\ddot{{R}}}}}+{\hat{{\ddot{{\rho}}}}}} \right)} \text{d}m$
(2) ${F}_i =m_i \left( {{\hat{{\ddot{{R}}}}}+{\hat{{\ddot{{p}}}}}_i }\right)$
(3) ${F}={G}+{F}_{e} ={F}_{b} +\sum\limits_{i=1}^n {{F}_i }=\\ \int_{M} {\left( {{\hat{{\ddot{{R}}}}}+{\hat{{\ddot{{\rho }}}}}} \right)} \text{d}m+\sum\limits_{i=1}^n {m_i \left( {{\hat{{\ddot{{R}}}}}+{\hat{{\ddot{{p}}}}}_i } \right)}$
其中, ${G}$为卫星系统所受重力, ${F}_{e} $为卫星系统除重力外所受合外力.
(4) ${\hat{{\ddot{{p}}}}}_i ={\ddot{{p}}}_i +2{\omega }\times {\dot{{p}}}_i +{\dot{{\omega }}}\times {p}_i +{\omega }\times \left( {{\omega }\times {p}_i } \right)$
(5) ${\hat{{\ddot{{\rho }}}}}={\dot{{\omega }}}\times {\rho }+{\omega }\times \left( {{\omega }\times {\rho }} \right)$
定义本体系原点$O_{B} $在卫星本体质心, 可知
(6) $\int_{M} {\rho } \text{d}m={\bf0}$
假定低轨纳卫星轨道近似为圆轨道, 则重力和径向加速度引起的惯性力处于平衡状态, 即
(7) ${G}=\left( {M+\sum\limits_{i=1}^n {m_i } } \right){\hat{{\ddot{{R}}}}}$
其中, ${\hat{{\ddot{{R}}}}}$表示卫星所在位置的重力加速度. 将式(5)~式(7)代入式(3),
(8) ${F}_{e} =\left( {M+\sum\limits_{i=1}^n {m_i } } \right)\delta {\hat{{\ddot{{R}}}}}+\sum\limits_{i=1}^n {m_i {\hat{{\ddot{{p}}}}}_i }$
(9) $\delta {\hat{{\ddot{{R}}}}}=\frac{{F}_{e} -\sum\limits_{i=1}^n {m_i{\hat{{\ddot{{p}}}}}_i } }{M+\sum\limits_{i=1}^n {m_i } }$
式中$\delta {\hat{{\ddot{{R}}}}}={\hat{{\ddot{{R}}}}}-{\hat{{\ddot{{R}}}}}$, 表示卫星系统质心除去重力影响的惯性加速度在本体系下的表达. 滑块$i$受到重力和卫星本体的作用力, 来自卫星本体的作用力可表示为
(10) ${f}_i =m_i \left( {\delta {\hat{{\ddot{{R}}}}}+{\hat{{\ddot{{p}}}}}_i } \right)$
因此, 滑块对本体作用力相对本体质心的矩${T}_{m} $可计算得到
(11) ${T}_{m} =-\sum\limits_{i=1}^n {{p}_i \times {f}_i }$
卫星本体受到磁控力矩${T}_{B} $、环境力相对本体质心的矩${T}_{e} $以及滑块对本体作用力相对本体质心的矩${T}_{m} $, 代入标准卫星动力学方程
(12) ${J}_{B} {\dot{{\omega }}}+{\omega }\times {J}_{B} {\omega }={T}_{B} +{T}_{e} +{T}_{m}$
其中, ${T}_{B} ={m}_{mag} \times {B}$, ${m}_{mag}$表示磁力矩器产生的磁矩控制量, ${B}$是卫星所在位置本体系下地磁矢量.
(13) ${T}_{m} =-{r}_{s} \times {F}_{e} +\left[ {{r}_{s} \times \sum\limits_{i=1}^n {m_i {\hat{{\ddot{{p}}}}}_i } -\sum\limits_{i=1}^n {\left( {m_i {p}_i \times {\hat{{\ddot{{p}}}}}_i } \right)} } \right]$
(14) ${r}_{s} =\frac{\sum\limits_{i=1}^n {m_i {p}_i }}{M+\sum\limits_{i=1}^n {m_i } }$
式中, ${r}_{s} $为在本体系下系统质心位置; 等号右边第一项是气动控制力矩, 通过调整滑块位置矢量${p}_i $,可改变系统质心位置${r}_{s} $, 从而输出理想气动控制力矩; 等号右边第二项是由滑块位置变化引起的系统转动惯量变化以及由滑块运动引起的附加力矩.
(15) ${r}_{s} \times \sum\limits_{i=1}^n {m_i {\hat{{\ddot{{p}}}}}_i } -\sum\limits_{i=1}^n {\left( {m_i {p}_i \times {\hat{{\ddot{{p}}}}}_i } \right)} ={M}_{xt} -{J}_{M} {\dot{{\omega}}}$
(16) $\left. \begin{array}{l} {{J}_{M} =\left[ {{r}_{s} } \right]^\times \left[ {\sum\limits_{i=1}^n {m_i {p}_i } } \right]^\times -\sum\limits_{i=1}^n {m_i \left[ {{ p}_i } \right]^\times \left[ {{p}_i } \right]^\times } } \\ {{M}_{xt} ={M}_{a} +{M}_{c} +{M}_{g} } \\ {{M}_{a} ={r}_{s} \times \sum\limits_{i=1}^n {m_i {\ddot{{p}}}_i } -\sum\limits_{i=1}^n {m_i {p}_i \times {\ddot{{p}}}_i } } \\ {M}_{c} ={r}_{s} \times \left( {2{\omega }\times \sum\limits_{i=1}^n {m_i {\dot{{p}}}_i } } \right)-\\ \sum\limits_{i=1}^n {2m_i {p}_i \times \left( {{\omega }\times {\dot{{p}}}_i } \right)} \\ {M}_{g} ={r}_{s} \times \left[ {{\omega }\times \left( {{\omega }\times \sum\limits_{i=1}^n {m_i {p}_i } } \right)} \right] -\\ \sum\limits_{i=1}^n {m_i {p}_i \times \left[ {{\omega }\times \left( {{\omega }\times {p}_i } \right)} \right]} \end{array}\right\}$
式中, ${J}_{M} $是与滑块位置有关的附加转动惯量, ${M}_{xt} $是由滑块运动引起的附加力矩, 包括与加速度${\ddot{{p}}}_i $有关的附加惯性力矩${M}_{a} $、与速度${\dot{{p}}}_i$有关的附加哥式力矩${M}_{c} $、与位置${p}_i $有关的附加陀螺力矩${M}_{g} $.
将式(13)和式(15)代入式(12), 得到质量矩系统完整动力学方程为
(17) $\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}+{\omega }\times {J}_{B} {\omega }=\\ {T}_{e} +{T}_{B} -{r}_{s} \times {F}_{e} +{M}_{xt}$
其中, 由于低轨卫星气动阻力远大于其他环境力, 同时, 真实大气环境存在不确定性, 难以建模, 故将环境力${F}_{e}$简化为大小和方向上存在误差的理想大气阻力${F}_{aero}^{b} $. 参考文献[23 ] ,理想气动力模型为${F}_{aero}^{b} =0.5\rho \left\| {{v}_{a}^{b} }\right\|^2C_{D} A_{p} \cdot {\hat{{v}}}_{a}^{b} $, $\rho $为大气平均密度, $C_{D}$为阻力系数, ${v}_{a}^{b} $为大气来流速度矢量, $A_{p} $为卫星在矢量${v}_{a}^{b} $方向上的投影面积, ${\hat{{v}}}_{a}^{b} $为本体系下来流速度单位矢量.
1.2 相对轨道系的运动学和动力学方程
定义角速度${\omega }_{bo}$为卫星本体系相对于轨道系的姿态角速度在本体系下的表达, 可表示为
(18) ${\omega }_{bo} ={\omega }-{A}_{bo} {\omega }_{oi}$
其中, ${\omega }_{oi} $是轨道角速度, ${A}_{bo}$是轨道系到本体系的姿态转换矩阵, 可展开为
(19) ${A}_{bo} ={I}_{3\times 3} -\frac{4\left( {1-{\sigma }_{bo} ^{T}{\sigma }_{bo}} \right)}{\left( {1+{\sigma }_{bo} ^{T}{\sigma }_{bo} } \right)^2}\left[ {{\sigma } } \right]^\times+\\ \frac{8}{\left( {1+{\sigma }_{bo} ^{T}{\sigma }_{bo} } \right)^2}\left[ {{\sigma }_{bo} } \right]^{\times2}$
利用修正罗德里格参数${\sigma }_{bo} $描述卫星本体系相对于轨道系$O_O X_OY_O Z_O $的姿态, 则相对轨道系的姿态运动学方程为
(20) ${\dot{{\sigma }}}_{bo} ={G}\left( {{\sigma }_{bo} } \right){\omega }_{bo}$
(21) ${G}\left( {{\sigma }_{bo} } \right)=\frac{1}{2}\Bigg( { I}_{3\times 3} +\left[ {{\sigma }_{bo} } \right]^\times +{\sigma }_{bo} {\sigma }_{bo} ^{T}- \frac{1+{\sigma }_{bo} ^{T}{\sigma }_{bo} }{2}{I}_{3\times 3} \Bigg)$
(22) ${\dot{{\omega }}}_{bo} ={\dot{{\omega }}}+{\omega }_{bo} \times {A}_{bo} {\omega }_{oi}$
将式(22)代入式(17)得到相对轨道系的姿态动力学方程为
(23) $\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}_{bo} =-{ \omega }\times {J}_{B} {\omega }+\left( {{J}_{B} +{J}_{M} } \right)\cdot \\ \left( {{\omega }_{bo} \times {A}_{bo} {\omega }_{oi} } \right)+{ T}_{e} +{T}_{B} -\\ {r}_{s} \times {F}_{aero} +{M}_{xt}$
2 滑模控制律设计
本文采用质量矩与磁力矩相结合的姿态控制方法, 将单使用质量矩或者单使用磁力矩的欠驱动控制方式转化为三轴全驱动控制方式.参考文献[28 ,29 ] , 针对三轴理想合力矩设计了基于干扰观测器的滑模控制律. 理想控制合力矩${u}_{t} $为
(24) ${u}_{t} ={m}_{mag} \times {B}-{r}_{s} \times {F}_{aero}$
(2)环境力相对本体质心的矩${T}_{e} $;
(3)滑块运动引起的附加力矩${M}_{xt} $;
(4)由理想气动模型误差引起的气动控制力误差${F}_{aero} $;
注意到附加干扰力矩${M}_{xt} $与滑块的速度与加速度有关, 属于快时变干扰, 作用在卫星系统上使得卫星姿态出现抖动. 其余干扰力矩属于慢时变干扰, 可通过干扰观测器有效跟踪并补偿.
将式(24)及上述干扰项代入系统动力学方程式(23), 得到
(25) $\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}_{bo} =-{ \omega }\times {J}_{B} {\omega }+\\ \left( {{J}_{B} +{J}_{M} } \right)\left( {{\omega }_{bo} \times {A}_{bo} {\omega }_{oi} } \right)+{u}_{t} +{d}$
(26) ${d}={m}_{rsd} \times {B}+\left[ {-{r}_{s} \times {F}_{aero} -{r}_{s} \times ({F}_{aero}+{F}_{aero} )} \right]+\\ {d}_{s} +{M}_{xt}$
式中等号右边第一项是剩磁干扰力矩,第二项是气动控制力误差与卫星本体质心偏差共同作用的气动力矩误差.
2.1 指数收敛干扰观测器设计
取${\dot{{\hat{{d}}}}}=K\left( {{d}-{\hat{{d}}}} \right)$, 其中$K>0$与观测器收敛速率有关. 定义辅助参数向量
(27) ${z}={\hat{{d}}}-K\left( {{J}_{B} +{J}_{M} } \right){\omega }_{bo}$
(28) ${\dot{{z}}}={\dot{{\hat{{d}}}}}-K\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}_{bo}$
(29) ${\dot{{\hat{{d}}}}}=K\left( {{d}-{\hat{{d}}}} \right)=K\left[ {\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}_{bo} +{\omega }\times {J}_{B} {\omega }-{u}_{t} } \right]-\\ K\left( {{J}_{B} +{J}_{M} } \right)\left( {{\omega }_{bo} \times {A}_{bo} {\omega }_{oi} } \right)-K{\hat{{d}}}$
(30) $\left.\begin{array}{l} {\dot{{z}}}=K\left[ {\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}_{bo} +{\omega }\times {J}_{B} {\omega }-} \right]-\\ K\left[ {\left( {{J}_{B} +{J}_{M} } \right)\left( {{\omega }_{bo} \times {A}_{bo} {\omega }_{oi} } \right)+{u}_{t} } \right]-\\ K{\hat{{d}}}-K\left( {{J}_{B} +{J}_{M} } \right){\dot{{\omega }}}_{bo}=\\ K\left[ {{\omega }\times {J}_{B} {\omega }-\left( {{ J}_{B} +{J}_{M} } \right)\left( {{\omega }_{bo} \times {A}_{bo} { \omega }_{oi} } \right)} \right]-\\ K{u}_{t} -K{\hat{{d}}}\\ {{\hat{{d}}}={z}+K\left( {{J}_{B} +{J}_{M} } \right){\omega }_{bo} } \end{array}\right\}$
由于质量矩系统干扰变化远慢于观测器的更新动态, 故可视为慢时变干扰, 即${\dot{{d}}}={\bf 0}$. 令观测误差为${\tilde{{d}}}={d}-{\hat{{d}}}$, 因而得到观测器误差方程为
(31) ${\dot{{\tilde{{d}}}}}+K{\tilde{{d}}}={\bf0}$
(32) ${\tilde{{d}}}\left( t \right)={\tilde{{d}}}\left( {t_0 } \right){e}^{-Kt}$
由于${\tilde{{d}}}\left( {t_0 } \right)$的值是确定的, 可见, 观测器指数收敛于干扰${d}$.
2.2 滑模控制器设计
卫星姿态机动目标为${\sigma }_{bo} \to {\sigma }_{bo}^{d} $, ${\omega }_{bo} \to {\omega }_{bo}^{d} $. 定义误差参数${e}_1 ={\sigma }_{bo} -{\sigma }_{bo}^{d} $和${e}_2 ={\omega }_{bo} -{\omega }_{bo}^{d} $, 设计滑模函数为
(33) ${s}={ce}_1 +{e}_2$
其中, ${c}=\mbox{diag}(c_1\ \ c_2\ \ c_3)$且$c_1 ,c_2 ,c_3 >0$. 由文献[30 ] 可知,考虑卫星运动学方程(20)和动力学方程(25), 如果滑模函数${s}\left( t \right)$满足$\lim\limits_{t\to \infty } s\left( t\right)=0$, 那么可以得到$\lim\limits_{t\to \infty } {e}_1 \left( t \right)=0$和$\lim\limits_{t\to \infty } {e}_2 \left( t \right)=0$.
(34) $\begin{array}{l}{\dot{{s}}}={c\dot{{e}}}_1 +{\dot{{e}}}_2 ={c}\left( {{\dot{{\sigma }}}_{bo} -{\dot{{\sigma }}}_{bo}^{d} } \right)+{\dot{{\omega }}}_{bo} -{\dot{{\omega }}}_{bo}^{d}=\\ {c}\left( {{G}\left( {{\sigma }_{bo} } \right){\omega }_{bo} -{\dot{{\sigma }}}_{bo}^{d} } \right)+{\omega }_{bo} \times {A}_{bo} {\omega }_{oi}+\\ \left( {{J}_{B} +{J}_{M} } \right)^{-1}\left( {-{\omega }\times {J}_{B} {\omega }+{u}_{t} +{d}} \right)\end{array}$
(35) ${u}_{t} =\left( {{J}_{B} +{J}_{M} } \right)\Big[ -{c}\left( {{G}\left( {{\sigma }_{bo} } \right){\omega }_{bo} -{\dot{{\sigma }}}_{bo}^{d} } \right) -{\omega }_{bo} \times\\ {A}_{bo} {\omega }_{oi} -{ks}-{\eta }{sgn}\left( {s} \right) \Big]+{\omega }\times{J}_{B} {\omega }-{\hat{{d}}}$
其中, ${k}=\mbox{diag}(k_1\ \ k_2\ \ k_3 )$且$k_1 ,k_2 ,k_3 >0$.
(36) $V=\frac{1}{2}{s}^{T}{s}+\frac{1}{2}{\tilde{{d}}}^{T}{\tilde{{d}}}$
结合式(31)、式(34)和式(35), 则Lyapunov函数的导数为
(37) $\begin{array}{l}\dot{{V}}={s}^{T}{\dot{{s}}}+{\tilde{{d}}}^{T}{\dot{{\tilde{{d}}}}} =\\ {s}^{T}\left[ {{c}\left( {{G}\left( {{\sigma }_{bo} } \right){\omega }_{bo} -{\dot{{\sigma }}}_{bo}^{d} } \right)+{ \omega }_{bo} \times {A}_{bo} {\omega }_{oi} } \right]+\\ {s}^{T}\left[ {\left( {{J}_{B} +{J}_{M} } \right)^{-1}\left( {-{\omega }\times {J}_{B} {\omega }+{u}_{t} +{d}} \right)} \right]+\\ {\tilde{{d}}}^{T}\left( {-K{\tilde{{d}}}} \right)={s}^{T}\Big[ -{ks}-{\eta}{sgn}\left( {s} \right)-\\ \left( {{J}_{B} +{J}_{M} } \right)^{-1}{\tilde{{d}}} \Big]-K\left\| {{\tilde{{d}}}} \right\|^2 =-\sum\limits_{i=1}^3 {\left( {k_i s_i^2 +\eta _i \left| {s_i } \right|} \right)} -\\ {s}^{T}\left( {{J}_{B} +{J}_{M} } \right)^{-1}{\tilde{{d}}}-K\left\| {{\tilde{{d}}}} \right\|^2\leqslant 0\end{array}$
其中, 定义${D}={s}^{T}\left( {{J}_{B} +{J}_{M} } \right)^{-1}{\tilde{{d}}}=[D_1\ \ D_2\ \ D_3]^{T}$, 则取参数$\eta _i \geqslant \left| {D_i } \right|_{\max }$, $i=1,2,3$. 由于
(38) $\begin{array}{l}\dot{{V}}=-\sum\limits_{i=1}^3 {\left( {k_i s_i^2 +\eta _i \left| {s_i } \right|} \right)} -{s}^{T}\left( {{J}_{B} +{J}_{M} } \right)^{-1}{\tilde{{d}}}-K\left\| {{\tilde{{d}}}} \right\|^2\leqslant\\ -\sum\limits_{i=1}^3 {k_i s_i^2 } -K\left\| {{\tilde{{d}}}} \right\|^2\leqslant -k_1 \left( {\frac{1}{2}{s}^{T}{s}+\frac{1}{2}{\tilde{{d}}}^{T}{\tilde{{d}}}} \right)=\\ -k_{m} V\end{array}$
其中$k_{m} =2\min \left\{ {k_1 ,k_2 ,k_3 ,K} \right\}$. 根据文献[31 ] , 不等式$\dot{{V}}\leqslant -k_{m} V$的解析解为$V\left( t \right)\leqslant {e}^{-k_{m} \left({t-t_0 } \right)}V\left( {t_0 } \right)$, 可见, 控制系统呈指数收敛, 收敛精度取决于参数$k_{m} $的值.
为防止系统抖振, 采用双曲正切函数取代控制律(35)中符号函数, 相较于饱和函数, 双曲正切函数曲线更加平滑,避免滑块运动的突变引起过大的附加干扰力矩. 基于双曲正切函数的滑模控制律为
(39) ${u}_{t} =\left( {{J}_{B} +{J}_{M} } \right)\Big[ -{c}\left( {G}\left( {{\sigma }_{bo} } \right){\omega }_{bo} -{\dot{{\sigma }}}_{bo}^{d}\right)-\\ {\omega }_{bo} \times {A}_{bo} {\omega }_{oi}\Big]-\left( {{J}_{B} +{J}_{M} } \right)\left[ {{ks}+{ \eta }\tanh \left( {\frac{{s}}{{\varepsilon }_{m} }} \right)} \right]+\\ {\omega }\times {J}_{B} {\omega }-{\hat{{d}}}$
其中, ${\varepsilon }_{m} =[\varepsilon _{m1}\ \ \varepsilon _{m2}\ \ \varepsilon_{m3}]$且$\varepsilon _{m1} ,\varepsilon _{m2} ,\varepsilon _{m3} >0$.
3 最优控制力矩分配
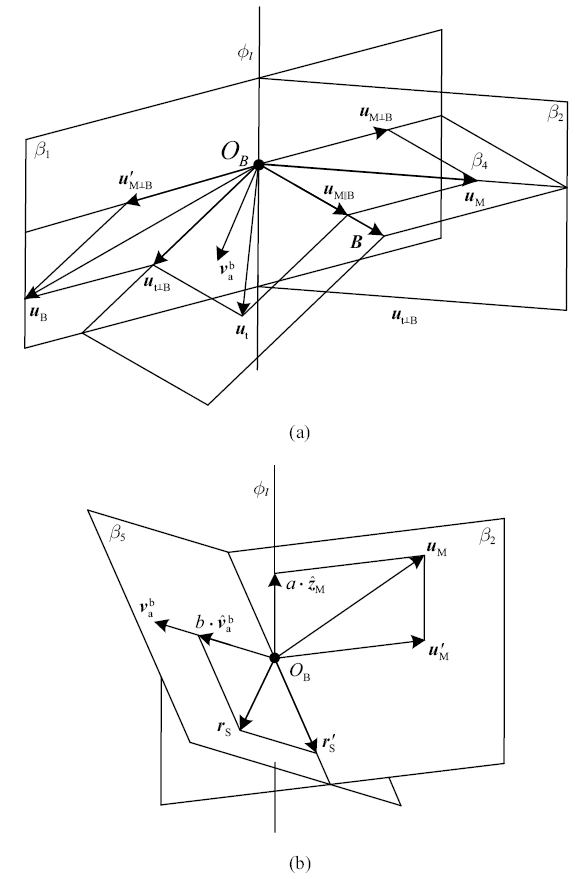
本文控制律针对三轴理想合力矩设计, 实际控制量是滑块位置和磁力矩器输出磁矩, 因此需要配合力矩分配策略将合力矩转为执行机构实际控制量. 理想控制力矩分配方法见图2 .
图2
图2
力矩分配示意图
Fig. 2
Allocation of the ideal control torque
图2 (a)中, 平面${\beta }_1 $垂直于地磁矢量${B}$, 平面${\beta }_2 $垂直于来流速度矢量${v}_{a}^{b}$, 平面${\beta }_4$是矢量${B}$和气动力矩矢量${u}_{M} $所在平面, 平面${\beta }_1$和平面${\beta }_2 $的交线为$\phi _l $.
将理想控制力矩${u}_{t} $在平面${\beta }_3 $上分解为平行于矢量${B}$的力矩${u}_{t\parallel B} $和垂直于矢量${B}$的力矩${u}_{t\bot B}$, 矢量${u}_{t\bot B} $在平面${\beta }_1 $上. 根据投影定理可得
(40) ${u}_{t\parallel B} ={\hat{{B}}}\left[ {\left( {{\hat{{B}}}} \right)^{T}{u}_{t} } \right]$
(41) ${u}_{t\bot B} ={u}_{t} -{u}_{t\parallel B}$
由于磁力矩${u}_{B} $垂直于矢量${B}$, 故${u}_{t\parallel B}$是矢量${u}_{M} $在矢量${\hat{{B}}}$方向上的投影. 根据文献[27 ] , 若平面${\beta }_4 $与平面${\beta }_2 $垂直, 此时气动力矩$u'_{M} $为
(42) $u'_{M} =\frac{{u}_{t} ^{T}{\hat{{B}}}}{\left( {{ Pu}_{t\parallel B} } \right)^{T}{\hat{{B}}}}\left( {{Pu}_{t\parallel B} } \right)$
式中${P}={I}_{3\times 3} -{\hat{{v}}}_{a}^{b} \left( {{\hat{{v}}}_{a}^{b} } \right)^{T}$. 然而平面${\beta }_4 $与平面${\beta }_2$并不一定垂直, 即矢量${u}_{M} $并不唯一, 如图2 (b)所示, 在平面${\beta }_2 $上定义单位方向矢量${\hat{{z}}}_{M} $为
(43) ${\hat{{z}}}_{M} =\frac{{v}_{a}^{b} \times {B}}{\left\| {{v}_{a}^{b} \times {B}} \right\|}$
式中单位矢量${\hat{{z}}}_{M} $垂直于矢量${v}_{a}^{b}$和矢量${B}$所在平面. 则气动力矩${u}_{M} $可表示为
(44) ${u}_{M} =u'_{M} +a\cdot {\hat{{z}}}_{M}$
平面${\beta }_5 $垂直于矢量${u}_{M} $, 由式(24)可知, 若矢量${u}_{M} $与矢量${F}_{aero}^{b} $一定, 矢量${r}_{s} $在平面${\beta }_5 $上不唯一. 根据文献[24 ] , 在平面${\beta }_2 $上的矢量$r'_{s} $为
(45) $r'_{s} =-\frac{{F}_{aero}^{b} \times {u}_{M} }{\left\| {{ F}_{aero}^{b} } \right\|^2}$
如图2 (b)所示, 定义单位方向矢量${\hat{{z}}}_{B} ={\hat{{v}}}_{a}^{b} $, 则质心位置矢量${r}_{s} $可表示为
(46) ${r}_{s} =r'_{s} +b\cdot {\hat{{z}}}_{B}$
由式(44)和式(46)可知, 力矩分配策略的不唯一性主要体现在质心位置矢量${r}_{s}$表达式中系数$a$和$b$可以在一定范围内变化, 这为优化滑块位移提供了可能.
(47) ${u}_{B} ={u}_{t} -{u}_{M}$
(48) ${m}_{mag} =\frac{{B}\times {u}_{B} }{\left\| {B} \right\|^2}$
可以利用理想力矩分配方法的不唯一性优化滑块位移,通过优化系数$a$和$b$减小滑块运动附加干扰力矩.此优化属于标准的非线性优化问题,可借助传统非线性优化算法或者智能优化算法求解此问题. 同时,为减小姿态机动过程中附加力矩的影响, 还可通过减缓滑块运动实现,即减小控制律增益以减小滑块位移量, 或者拉长控制周期以增大滑块运动时间.
4 仿真分析
本文以正交三滑块和三轴磁力矩器为姿态控制执行机构. 如图3 所示,正交三滑块可沿平行于卫星本体系各轴方向移动.采用德国FAULHABER公司的LM0830-040-01系列直线电机驱动滑块,加装铜制配重以达到滑块设计质量,该电机能以300Hz频率通过串口返回位置和速度信息.三轴磁力矩器由两个带铁芯的线圈和一个空心盘状线圈组成,可通过采集各线圈电流大小间接测量磁力矩器三轴输出磁矩.
图3
图3
半物理仿真平台
Fig. 3
Semi-physical simulation platform for two actuators
本文为验证所设计的观测器和滑模控制律的有效性,并由此说明在低轨纳卫星上主动利用气动力矩控制姿态的可行性,搭建针对双执行机构的半物理仿真平台. 由图3 可见, 为避免重力影响,将三滑块水平布置,并利用采集计算机采集各滑块运动信息和磁力矩器三轴的输出磁矩.
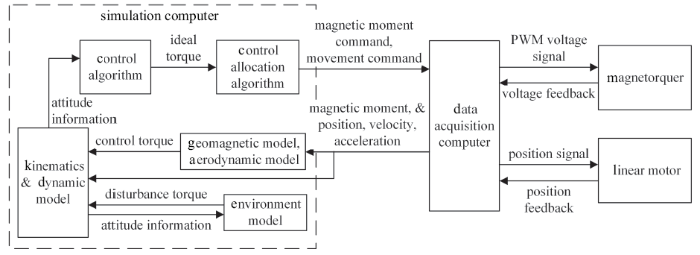
如图4 所示, 半物理仿真平台包括仿真计算机、采集计算机和双执行机构. 仿真计算机利用MATLAB软件计算控制律和动力学, 并更新姿态信息, 动力学计算周期为200 ms, 控制周期为10 s.
图4
图4
半物理仿真流程图
Fig. 4
The flow diagram of the semi-physical simulation process
所选用两单元立方星尺寸为110 mm $\times $ 110 mm $\times $ 230 mm,给定本体系下三滑块的位置矢量${p}_1 =[l_1 ,0.01,-0.01]^{T}$ cm, ${p}_2 =[-0.01,l_2 ,0.01]^{T}$ cm, ${p}_3 =[0.01,-0.01,l_3]^{T}$ cm, 卫星系统质心在本体系下三方向可调整范围为$\pm $1.35mm.其余系统参数及控制参数如表1 所示.
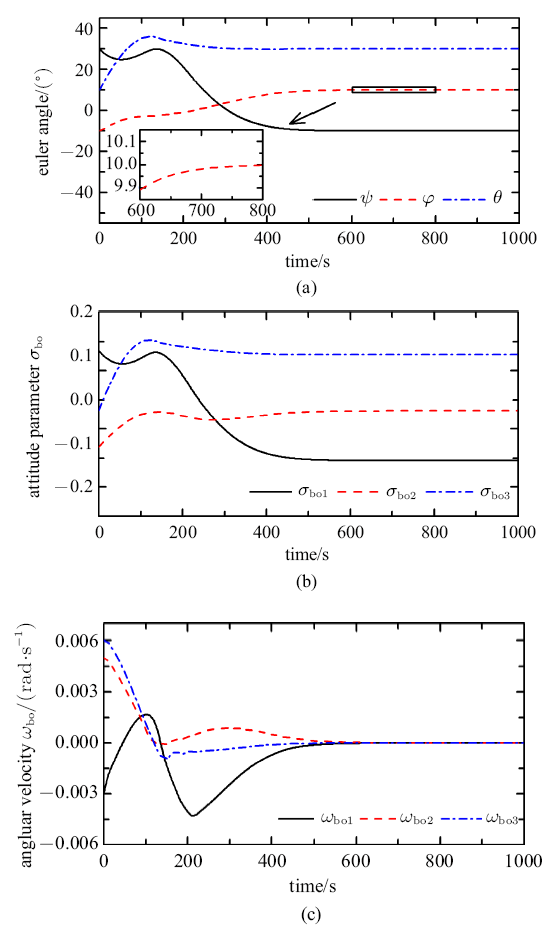
仿真中初始姿态(3-1-2转动顺序)为滚动角$\varphi =-10^{\circ}$, 俯仰角$\theta=10^{\circ}$, 偏航角$\psi =30^{\circ}$, 初始角速度${\omega }_{bo0}=[-0.003,0.005,0.006]$ rad/s. 机动目标姿态为$\varphi =10^{\circ}$,$\theta =30^{\circ}$, $\psi =-10^{\circ}$, 目标角速度为${\omega }_{bod} =[0,0,0]$ rad/s. 仿真曲线如图5 ~图8 所示.
图5
图5
姿态参数变化曲线
Fig. 5
Curves of attitude parameters
图6
图6
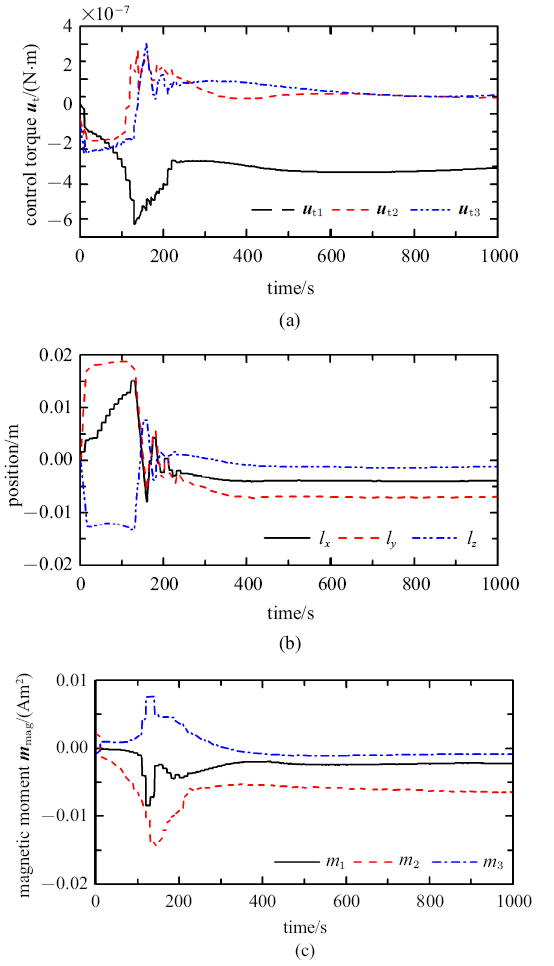
控制输入变化曲线
Fig. 6
Curves of control inputs
图7
图7
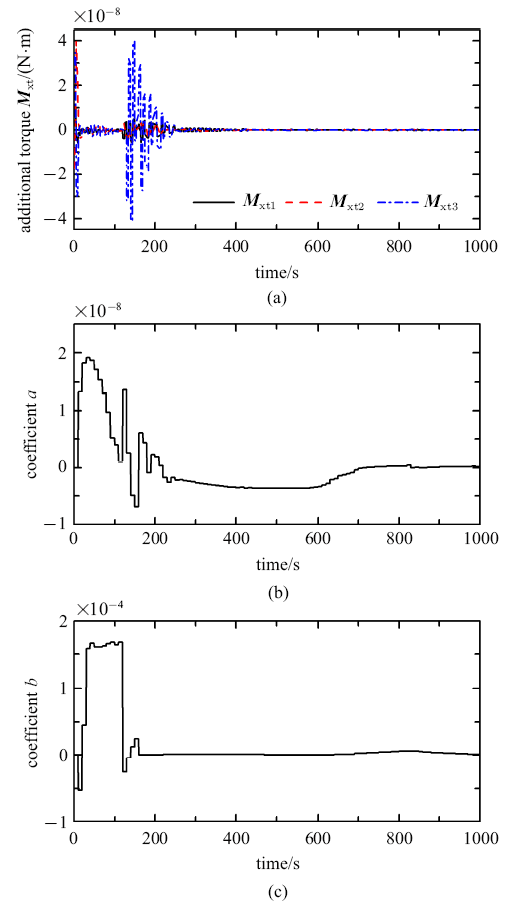
附加干扰力矩及力矩分配系数变化曲线
Fig. 7
Curves of additional torque and coefficients $a$, $b$
图8
图8
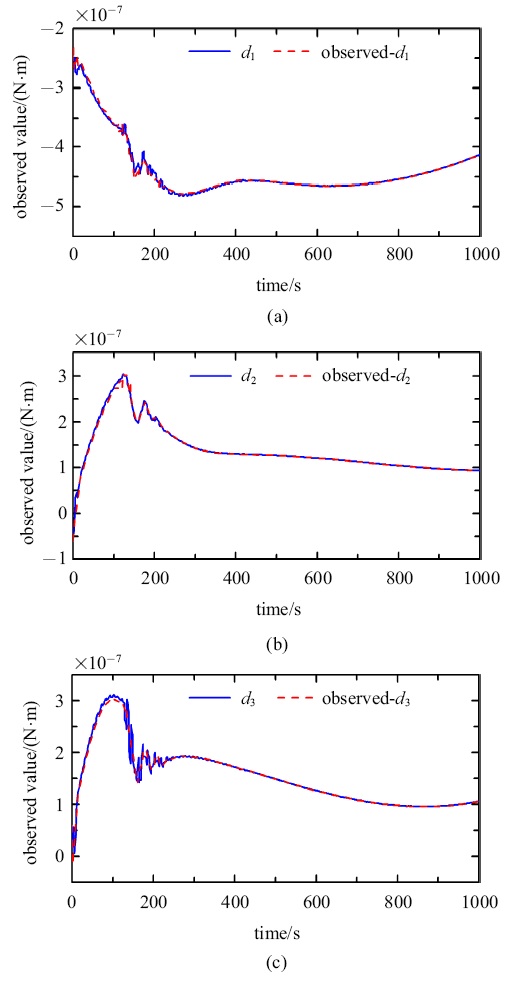
系统误差及观测值变化曲线
Fig. 8
Curves of system disturbance and observed value
由图5 可看出, 卫星在600 s逼近至目标姿态, 姿态角收敛精度达到$\pm $0.1$^\circ$,完成姿态机动,验证了利用质量矩执行机构主动控制气动力矩实现姿态机动方法的可行性.虽然可以通过增大控制系统的增益值来加快姿态收敛速度,但势必会造成超调增大、执行机构过载等情况出现, 故需综合考虑. 由图6 可看出,理想控制力矩在300 s之前存在波动,这主要是由于滑块位置缓慢变化导致的控制输入误差引起的,最终控制力矩为抵消系统所受干扰力矩未能收敛至0. 在姿态机动过程中,仿真中将控制周期延长至10 s, 因而滑块的位移变化曲线趋于平缓,能大幅减小滑块附加干扰.
由图7 和图8 可看出, 由于气动力模型误差、卫星参数不确定、环境干扰等因素,低轨质量矩纳卫星姿态控制存在不可忽略的系统干扰,达到$10^{-7}~\mbox{N$\cdot$m}$的量级. 相较于此,由于延长了滑块的运动时间以及设计了最优力矩分配策略,滑块附加干扰力矩被减小至$10^{-8}~\mbox{N$\cdot$m}$的量级, 远小于系统其他干扰.本文所设计的指数收敛干扰观测器能有效跟踪系统干扰力矩, 大幅提高姿态收敛精度,减小控制输入的震荡.
5 结论
本文在低轨纳卫星大规模应用, 任务日趋多样化的背景下,探索了利用质量矩技术实现姿态机动控制的方法.通过延长控制周期以减小滑块运动速度和加速度,从而减小由滑块运动引起的附加干扰力矩,并为此设计了针对理想控制力矩基于干扰观测器的滑模控制器,以及基于优化算法的控制力矩最优分配策略.搭建了针对双执行机构的半物理仿真平台, 通过仿真,干扰观测器能有效观测系统干扰, 提高滑模控制律的姿态控制精度,姿态角收敛误差小于$\pm $0.1$^\circ$, 减弱了系统控制输入抖振现象.本研究不足之处在于设计控制律的过程中没有考虑到执行机构饱和的问题,且直接延长控制周期有可能会导致控制律不收敛,后续将针对先进姿态机动控制律展开研究.
参考文献
View Option
[1]
曹登庆 , 白坤朝 , 丁虎 , 等 . 大型柔性航天器动力学与振动控制研究进展
力学学报 , 2019 ,51 (1 ):9 -21
[本文引用: 1]
( Cao Dengqing Bai Kunchao Ding Hu , et al . Research progress in dynamics and vibration control of large flexible spacecraft
Acta Mechanica Sinica 2019 ,51 (1 ):9 -21 (in Chinese))
[本文引用: 1]
[2]
Zhang XH Zhang X Lu ZL , et al . Optimal path planning-based finite-time control for agile CubeSat attitude maneuver
IEEE Access 2019 ,7 :102186 -102198
DOI
URL
[本文引用: 1]
[3]
魏鹏鑫 , 高长生 , 荆武兴 . 质量矩控制飞行器的压心不确定性问题研究
航天控制 , 2012 ,30 (2 ):39 -45
[本文引用: 1]
( Wei Pengxin Gao Changsheng Jing Wuxing . The research on the uncertainty of pressure center for moving mass actuated vehicle
Aerospace Control 2012 ,30 (2 ):39 -45 (in Chinese))
[本文引用: 1]
[4]
朱安 , 陈力 . 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
力学学报 , 2019 ,51 (4 ):1156 -1169
[本文引用: 1]
( Zhu An Chen Li . Mechanical simulation and full order sliding mode collision avoidance compliant control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):1156 -1169 (in Chinese))
[本文引用: 1]
[5]
Firuzi S Gong S . Attitude control of a flexible solar sail in low Earth orbit
Journal of Guidance, Control, and Dynamics 2018 ,41 :1715 -1730
DOI
URL
[本文引用: 1]
[6]
Childs DW . A movable-mass attitude-stabilization system for artificial-g space stations
Journal of Spacecraft Rockets 1971 ,8 (8 ):829 -834
DOI
URL
[本文引用: 2]
[7]
Edwards TL . Automatic spacecraft detumbling by internal mass motion
AIAA Journal 1974 ,12 (4 ):496 -502
DOI
URL
[本文引用: 1]
[8]
Bainum PM Sellappan R . The use of a movable telescoping end mass system for the time-optimal control of spinning spacecraft
Acta Astronautica 1978 ,5 (1 ):781 -795
[9]
Kunciw BG Kaplan MH . Optimal space station detumbling by internal mass motion
Automatica 1976 ,12 :417 -425
DOI
URL
[10]
Guo P Zhao L . Modeling and attitude control of a spinning spacecraft with internal moving mass
Advanced Materials Research 2013 ,760 :1216 -1220
[本文引用: 1]
[11]
Kumar KD Zhou AM . Attitude control of miniature satellites using movable masses
// SpaceOps 2010 Conf. , Huntsville, Alabama, USA , Apr. 2010, Paper AIAA 2010-1982
[本文引用: 1]
[12]
Atkins BM Henderson TA . Under-actuated moving mass attitude control for a 3U CubeSat mission
// 22nd Spaceflight mechanics., Charleston, South Carolina , Jan. 2012 , vol. 143 , pp. 2083 -2094
[13]
Daniel EH . Dynamics and control of spinning spacecraft using translating masses with friction conpensation
Journal of Spacecraft and Rockets 2017 ,54 (6 ):1376 -1381
DOI
URL
[本文引用: 1]
[14]
Shahin F Gong S . Attitude control of a flexible solar sail in low earth orbit
Journal of Guidance Control and Dynamics 2018 , 1715 -1729
[本文引用: 2]
[15]
Thomas S Paluszek M Wie B . Design and simulation of sailcraft attitude control systems using the solar sail control toolbox
// AIAA Guidance, Navigation, and Control Conference and Exhibit, AIAA Paper 2004 ,4890 :16 -19
[16]
Wie B . Solar sail attitude control and dynamics, part two
Journal of Guidance, Control, and Dynamics 2004 ,27 (4 ):536 -544
DOI
URL
[本文引用: 1]
[17]
Wie B Murphy D . Solar-sail attitude control design for a flight validation mission
Journal of Spacecraft and Rockets 2007 ,44 (4 ):809 -821
[18]
尹婷婷 , 邓子辰 , 胡伟鹏 等 . 空间刚性杆弹簧组合结构轨道、姿态耦合动力学分析
力学学报 , 2018 ,5 (1 ):87 -98
( Yin Tingting Deng Zichen Hu Weipeng , et al . Dynamic modelling and simulation of orbit and attitude coupling problems for structure combined of spatial rigid rods and spring
Acta Mechanica Sinica 2018 ,50 (1 ):87 -98 (in Chinese))
[19]
陆正亮 , 张翔 , 于永军 等 . 立方体卫星质量矩姿态控制建模和布局优化
系统工程与电子技术 , 2017 ,39 (3 ):599 -605
( Lu Zhengliang Zhang Xiang Yu Yongjun , et al . Modeling and layout optimization of mass moment attitude control for cube satellite
Systems Engineering and Electronics 2017 ,39 (3 ):599 -605 (in Chinese))
[20]
陆正亮 , 张翔 , 于永军 等 . 纳卫星变轨段质量矩姿态控制系统设计
宇航学报 , 2017 , 38 (6 ): 320778(1 -9 )
( Lu Zhengliang Zhang Xiang Yu Yongjun , et al . Design of attitude control system of mass moment in orbit changing section of nanosatellite
Acta Aeronautica et Astrinautica Sinica 2017 , 38 (6 ): 320778(1 -9 )(in Chinese))
[21]
Petsopoulos T Regan FJ Barlow J . Moving-mass roll control system for fixed-trim re-entry vehicle
Journal of Spacecraft and Rockets 1996 ,33 (1 ):56 -60
[本文引用: 2]
[22]
陆正亮 . 快速机动卫星质量矩姿态控制技术研究. [博士论文]
南京: 南京理工大学 , 2017
[本文引用: 2]
( Lu Zhengliang . Research on attitude control technology of mass moment for fast maneuvering satellite. [PhD Thesis]
Nanjing: Nanjing University of Science and Technology , 2017 (in Chinese))
[本文引用: 2]
[23]
Chesi S . Attitude control of nanosatellites using shifting masses. [PhD Thesis]
Santa Cruz: University of California , 2015
[本文引用: 2]
[24]
Chesi S Gong Q Romano M . Aerodynamic three-axis attitude stabilization of a spacecraft by center-of-mass shifting
Journal of Guidance, Control and Dynamics 2017 ,40 (07 ):1613 -1626
DOI
URL
[本文引用: 1]
[25]
Virgili-Llop J Polat H . Using shifting masses to reject aerodynamic perturbations and to maintain a stable attitude in very low earth orbit
// 26th AAS/AIAA Space Flight Mechanics Meeting, Napa, CA , 2016 , AAS 16-354 , 2129 -2148
[本文引用: 1]
[26]
Polat H . Prototype design and mission analysis for a small satellite exploiting environment disturbances for attitude stabilization. [PhD Thesis]
Monterey: Naval Postgraduate School , 2016
[27]
Virgili-Llop J Polat H Romano M . Attitude stabilization of spacecraft in very low earth orbit by center-of-mass shifting
Frontiers in Robotics and AI 2019 ,6 (7 ):1 -19
DOI
URL
[本文引用: 2]
[28]
刘金琨 . 滑模变结构控制MATLAB仿真: 基本理论与设计方法 . 北京 : 清华大学出版社 , 2015
[本文引用: 1]
( Liu Jinkun . Sliding Mode Control Design and MATLAB Simulation: The Basic Theory and Design Method . Beijing : Tsinghua University Press , 2015 (in Chinese))
[本文引用: 1]
[29]
刘金琨 . 滑模变结构控制MATLAB仿真: 先进控制系统设计方法 . 北京 : 清华大学出版社 , 2015
[本文引用: 1]
( Liu Jinkun . Sliding Mode Control Design and MATLAB Simulation: The Design Method of Advanced Control System . Beijing : Tsinghua University Press , 2015 (in Chinese))
[本文引用: 1]
[30]
Hu Q Li B Qi M . Disturbance observer based finite-time attitude control for rigid spacecraft under input saturation
Aerospace Science and Technology 2014 ,39 (1 ):13 -21
DOI
URL
[本文引用: 1]
[31]
Petros AI Jing S . Robust Adaptive Control
PTR Prentice-Hall , 1996 : 75 -76
[本文引用: 1]
大型柔性航天器动力学与振动控制研究进展
1
2019
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
大型柔性航天器动力学与振动控制研究进展
1
2019
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
Optimal path planning-based finite-time control for agile CubeSat attitude maneuver
1
2019
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
质量矩控制飞行器的压心不确定性问题研究
1
2012
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
质量矩控制飞行器的压心不确定性问题研究
1
2012
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
1
2019
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
Attitude control of a flexible solar sail in low Earth orbit
1
2018
... 目前, 低轨纳卫星姿态机动主要是依靠基于飞轮的零动量控制方式[1 -2 ] , 飞轮工作过程中转速饱和以及高速转动引起的姿态抖动是不可避免的问题[3 -4 ] . 同时, 由于气动力严重影响着姿态控制效果, 卫星需要主动补偿此干扰力矩, 无疑增加了系统的功耗. 相较于此, 质量矩技术通过调整系统质心改变外力作用力臂[5 ] ,能够将环境干扰力矩作为控制力矩, 实现姿态平缓机动, 姿态指向精度更高, 更加适用于受到气动力矩干扰、对姿态指向精度要求高的低轨纳卫星. ...
A movable-mass attitude-stabilization system for artificial-g space stations
2
1971
... 早期在质量矩技术方面的研究主要集中在移动质量姿态控制技术[6 -13 ] .Childs[6 ] 和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义. ...
... [6 ]和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义. ...
Automatic spacecraft detumbling by internal mass motion
1
1974
... 早期在质量矩技术方面的研究主要集中在移动质量姿态控制技术[6 -13 ] .Childs[6 ] 和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义. ...
The use of a movable telescoping end mass system for the time-optimal control of spinning spacecraft
0
1978
Optimal space station detumbling by internal mass motion
0
1976
Modeling and attitude control of a spinning spacecraft with internal moving mass
1
2013
... 早期在质量矩技术方面的研究主要集中在移动质量姿态控制技术[6 -13 ] .Childs[6 ] 和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义. ...
Attitude control of miniature satellites using movable masses
1
2010-1982
... 早期在质量矩技术方面的研究主要集中在移动质量姿态控制技术[6 -13 ] .Childs[6 ] 和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义. ...
Under-actuated moving mass attitude control for a 3U CubeSat mission
0
2012
Dynamics and control of spinning spacecraft using translating masses with friction conpensation
1
2017
... 早期在质量矩技术方面的研究主要集中在移动质量姿态控制技术[6 -13 ] .Childs[6 ] 和Edwards[7 ] 利用广义动量矩定理推导了单滑块系统的完整动力学方程,并利用内部单滑块产生控制力矩稳定了失控空间站,文献中系统建模方法是本文动力学建模的重要参考依据.郭平等[10 ] 为了消除环境力矩对自旋卫星的干扰,利用垂直布置的双滑块系统实现卫星的自旋稳定控制.Kumar等[11 ] 首次提出直接利用卫星本体与滑块间的相互作用力控制卫星姿态,但是受限于卫星系统动量矩模值守恒, 该方法只能实现两轴姿态的控制.由于移动质量姿态控制技术直接忽略了合外力对卫星姿态的影响,本质上不属于质量矩技术, 并不适用于受环境合外力影响的卫星,但是在建模方法、控制机理分析等方面对质量矩技术有着重要借鉴意义. ...
Attitude control of a flexible solar sail in low earth orbit
2
2018
... 相关学者还研究了结合环境合外力的质量矩技术[14 -21 ] ,该技术通过移动滑块改变系统质心位置从而主动将环境干扰力作为姿态控制力矩.Shahin和Gong[14 ] 基于解析法分析了在太阳帆卫星上使用质量矩技术的可控性问题.Wie[16 ] 设计了双滑块质量矩姿态控制系统,并以此实现了太阳帆卫星俯仰角和偏航角的控制. Petsopoulos和Regan[21 ] 提出使用质量矩姿态控制装置取代传统再入飞行器舵面控制方式从而避免舵面烧蚀问题. ...
... [14 ]基于解析法分析了在太阳帆卫星上使用质量矩技术的可控性问题.Wie[16 ] 设计了双滑块质量矩姿态控制系统,并以此实现了太阳帆卫星俯仰角和偏航角的控制. Petsopoulos和Regan[21 ] 提出使用质量矩姿态控制装置取代传统再入飞行器舵面控制方式从而避免舵面烧蚀问题. ...
Design and simulation of sailcraft attitude control systems using the solar sail control toolbox
0
2004
Solar sail attitude control and dynamics, part two
1
2004
... 相关学者还研究了结合环境合外力的质量矩技术[14 -21 ] ,该技术通过移动滑块改变系统质心位置从而主动将环境干扰力作为姿态控制力矩.Shahin和Gong[14 ] 基于解析法分析了在太阳帆卫星上使用质量矩技术的可控性问题.Wie[16 ] 设计了双滑块质量矩姿态控制系统,并以此实现了太阳帆卫星俯仰角和偏航角的控制. Petsopoulos和Regan[21 ] 提出使用质量矩姿态控制装置取代传统再入飞行器舵面控制方式从而避免舵面烧蚀问题. ...
Solar-sail attitude control design for a flight validation mission
0
2007
空间刚性杆弹簧组合结构轨道、姿态耦合动力学分析
0
2018
空间刚性杆弹簧组合结构轨道、姿态耦合动力学分析
0
2018
立方体卫星质量矩姿态控制建模和布局优化
0
2017
立方体卫星质量矩姿态控制建模和布局优化
0
2017
Moving-mass roll control system for fixed-trim re-entry vehicle
2
1996
... 相关学者还研究了结合环境合外力的质量矩技术[14 -21 ] ,该技术通过移动滑块改变系统质心位置从而主动将环境干扰力作为姿态控制力矩.Shahin和Gong[14 ] 基于解析法分析了在太阳帆卫星上使用质量矩技术的可控性问题.Wie[16 ] 设计了双滑块质量矩姿态控制系统,并以此实现了太阳帆卫星俯仰角和偏航角的控制. Petsopoulos和Regan[21 ] 提出使用质量矩姿态控制装置取代传统再入飞行器舵面控制方式从而避免舵面烧蚀问题. ...
... [21 ]提出使用质量矩姿态控制装置取代传统再入飞行器舵面控制方式从而避免舵面烧蚀问题. ...
快速机动卫星质量矩姿态控制技术研究. [博士论文]
2
2017
... 对于500 km以下的低轨纳卫星,可通过主动控制气动力矩从而控制卫星姿态的稳定和机动[22 -27 ] .由于气动力矩定垂直于大气来流方向, 故单质量矩姿态控制属于欠驱动控制方式.陆正亮[22 ] 探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
... [22 ]探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
快速机动卫星质量矩姿态控制技术研究. [博士论文]
2
2017
... 对于500 km以下的低轨纳卫星,可通过主动控制气动力矩从而控制卫星姿态的稳定和机动[22 -27 ] .由于气动力矩定垂直于大气来流方向, 故单质量矩姿态控制属于欠驱动控制方式.陆正亮[22 ] 探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
... [22 ]探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
Attitude control of nanosatellites using shifting masses. [PhD Thesis]
2
2015
... 对于500 km以下的低轨纳卫星,可通过主动控制气动力矩从而控制卫星姿态的稳定和机动[22 -27 ] .由于气动力矩定垂直于大气来流方向, 故单质量矩姿态控制属于欠驱动控制方式.陆正亮[22 ] 探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
... 其中, 由于低轨卫星气动阻力远大于其他环境力, 同时, 真实大气环境存在不确定性, 难以建模, 故将环境力${F}_{e}$简化为大小和方向上存在误差的理想大气阻力${F}_{aero}^{b} $. 参考文献[23 ] ,理想气动力模型为${F}_{aero}^{b} =0.5\rho \left\| {{v}_{a}^{b} }\right\|^2C_{D} A_{p} \cdot {\hat{{v}}}_{a}^{b} $, $\rho $为大气平均密度, $C_{D}$为阻力系数, ${v}_{a}^{b} $为大气来流速度矢量, $A_{p} $为卫星在矢量${v}_{a}^{b} $方向上的投影面积, ${\hat{{v}}}_{a}^{b} $为本体系下来流速度单位矢量. ...
Aerodynamic three-axis attitude stabilization of a spacecraft by center-of-mass shifting
1
2017
... 平面${\beta }_5 $垂直于矢量${u}_{M} $, 由式(24)可知, 若矢量${u}_{M} $与矢量${F}_{aero}^{b} $一定, 矢量${r}_{s} $在平面${\beta }_5 $上不唯一. 根据文献[24 ] , 在平面${\beta }_2 $上的矢量$r'_{s} $为 ...
Using shifting masses to reject aerodynamic perturbations and to maintain a stable attitude in very low earth orbit
1
2016
... 对于500 km以下的低轨纳卫星,可通过主动控制气动力矩从而控制卫星姿态的稳定和机动[22 -27 ] .由于气动力矩定垂直于大气来流方向, 故单质量矩姿态控制属于欠驱动控制方式.陆正亮[22 ] 探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
Prototype design and mission analysis for a small satellite exploiting environment disturbances for attitude stabilization. [PhD Thesis]
0
2016
Attitude stabilization of spacecraft in very low earth orbit by center-of-mass shifting
2
2019
... 对于500 km以下的低轨纳卫星,可通过主动控制气动力矩从而控制卫星姿态的稳定和机动[22 -27 ] .由于气动力矩定垂直于大气来流方向, 故单质量矩姿态控制属于欠驱动控制方式.陆正亮[22 ] 探索了利用双对称布置的可移动滑块实现姿态三轴稳定欠驱动控制.针对单质量矩控制欠驱动问题,Chesi[23 ] 首次提出质量矩与磁力矩相结合的姿态控制方法,为理想三轴全驱动合力矩设计控制律, 并设计力矩分配算法控制两执行机构.Virgili-Liop和Polat[25 ] 在该方法基础上详细分析了理想气动力矩模型的干扰来源.然而先前学者只是在理论上说明了利用质量矩技术的可行性,未能综合考虑到移动质量执行机构在工程应用中的实际问题. ...
... 由于磁力矩${u}_{B} $垂直于矢量${B}$, 故${u}_{t\parallel B}$是矢量${u}_{M} $在矢量${\hat{{B}}}$方向上的投影. 根据文献[27 ] , 若平面${\beta }_4 $与平面${\beta }_2 $垂直, 此时气动力矩$u'_{M} $为 ...
1
2015
... 本文采用质量矩与磁力矩相结合的姿态控制方法, 将单使用质量矩或者单使用磁力矩的欠驱动控制方式转化为三轴全驱动控制方式.参考文献[28 ,29 ] , 针对三轴理想合力矩设计了基于干扰观测器的滑模控制律. 理想控制合力矩${u}_{t} $为 ...
1
2015
... 本文采用质量矩与磁力矩相结合的姿态控制方法, 将单使用质量矩或者单使用磁力矩的欠驱动控制方式转化为三轴全驱动控制方式.参考文献[28 ,29 ] , 针对三轴理想合力矩设计了基于干扰观测器的滑模控制律. 理想控制合力矩${u}_{t} $为 ...
1
2015
... 本文采用质量矩与磁力矩相结合的姿态控制方法, 将单使用质量矩或者单使用磁力矩的欠驱动控制方式转化为三轴全驱动控制方式.参考文献[28 ,29 ] , 针对三轴理想合力矩设计了基于干扰观测器的滑模控制律. 理想控制合力矩${u}_{t} $为 ...
1
2015
... 本文采用质量矩与磁力矩相结合的姿态控制方法, 将单使用质量矩或者单使用磁力矩的欠驱动控制方式转化为三轴全驱动控制方式.参考文献[28 ,29 ] , 针对三轴理想合力矩设计了基于干扰观测器的滑模控制律. 理想控制合力矩${u}_{t} $为 ...
Disturbance observer based finite-time attitude control for rigid spacecraft under input saturation
1
2014
... 其中, ${c}=\mbox{diag}(c_1\ \ c_2\ \ c_3)$且$c_1 ,c_2 ,c_3 >0$. 由文献[30 ] 可知,考虑卫星运动学方程(20)和动力学方程(25), 如果滑模函数${s}\left( t \right)$满足$\lim\limits_{t\to \infty } s\left( t\right)=0$, 那么可以得到$\lim\limits_{t\to \infty } {e}_1 \left( t \right)=0$和$\lim\limits_{t\to \infty } {e}_2 \left( t \right)=0$. ...
Robust Adaptive Control
1
1996
... 其中$k_{m} =2\min \left\{ {k_1 ,k_2 ,k_3 ,K} \right\}$. 根据文献[31 ] , 不等式$\dot{{V}}\leqslant -k_{m} V$的解析解为$V\left( t \right)\leqslant {e}^{-k_{m} \left({t-t_0 } \right)}V\left( {t_0 } \right)$, 可见, 控制系统呈指数收敛, 收敛精度取决于参数$k_{m} $的值. ...