引言
两种方式的建模所得到的数学模型是等价的, 相比于第一类建模方式来讲, 第二类更具有普适性, 因为既可以根据极值问题的必要性条件得到对应的微分(代数)类方程, 同时也可以直接将问题作为优化问题, 从而利用各种数学规划的方法进行求解[5].
高斯原理往往被认为更具普适性的变分原理, 它也被称作是高斯最小拘束原理, 提出了将真实运动(或真实平衡状态)与在同样条件下的可能运动(或可能平衡状态)区分出来的准则, 可叙述为: 在任意时刻, 系统的真实运动与位置和速度相同、但加速度不同的可能运动相比较, 其拘束函数取极小值[6].
上述关于高斯原理的研究工作主要集中在约束的相互作用可以通过约束方程所表达的理想系统, 但在大量的实际条件下需要考虑含干摩擦等的非理想因素, 这些非理想的相互作用不能完全通过适当的约束方程来表达[25], 因此原有的针对理想系统的高斯拘束失去了极值特性. 关于非理想情况下的高斯原理的理论及应用方面的研究工作并不多, Pfeiffer[26]将无摩擦的单边及双边约束的线性互补模型(linear complementary problem, LCP)等价为高斯最小拘束原理表达的最小值问题, 但他认为滑动接触的摩擦系数的出现破坏了最优性条件, 从而针对含摩擦的情况没有严格凸的最优化模型; Udwadia[27]讨论了约束力做功不为零的非理想约束系统的最小值原理, 文中的这个原理以笛卡尔坐标形式的高斯原理表达, 姚文莉等[28-30]对高斯原理在碰撞问题、单边约束及非理想系统中的应用进行了讨论.
当做功的非理想约束力只与位置、速度及时间相关, 而与相应的理想约束力无关时, 比如为了强制非完整系统的约束实现所施加的做功的控制力等, 文献[27]中给出的极值原理是可用的, 但当非理想约束力与相应的理想约束力相关, 如工程中通常需要考虑以库仑摩擦定律表征的摩擦现象时, 上述极值原理失效.
本文旨在从基本的动力学原理出发, 研究高斯原理在非理想系统中的应用, 从而得到以函数极值形式表达的非理想多体系统的优化模型.
本文所做的工作主要分为5个部分: (1) 建立高斯意义上的受约束多体系统基本变分方程; (2) 推导及证明非理想系统的高斯最小拘束原理; (3) 建立含库仑摩擦的单边接触系统的动力学优化模型; (4) 例证: 考虑摩擦的杆件滑动的单点及多点接触的两个例子; (5) 结语.
1 受约束系统高斯类动力学变分方程
1.1 笛卡尔坐标形式的高斯类变分方程[6]
考虑$N$个质点组成的系统, 假定已知质点系受到主动力${F}=[F_{\rm 1}\ \ F_{\rm 2}\ \ \cdots \ \ F_{3N} ]^{\rm T}$作用, 系统的位形由笛卡尔坐标矢量${u}=[u_1\ \ u_2\ \ \cdots \ \ u_{3N}]^{\rm T}$来表达, 假设系统受到如下约束组的作用
则系统的理想约束力矢量可以表达如下[6]
式中, $M'=\left[\begin{array}{c} m_{\rm 1} && & \\ & m_{\rm 2}& &\\ & &\ddots & \\ & && m_{3N} \\ \end{array}\right]$为系统质量矩阵, 其中$m_{3i-2} =m_{3i-1} =m_{3i} =m_i$ $(i=1,2,\cdots, N)$为质点$i$的质量; $F^{Ci}=[F_1^{Ci}\ \ F_2^{Ci} \ \ \cdots \ \ F_{3N}^{Ci}]^{\rm T}$及$F^{Cn}=[F_1^{Cn} \ \ F_2^{Cn} \ \ \cdots \ \ {F_{3N}^{Cn}}]^{\rm T}$分别为作用在质点系上的理想约束力及非理想约束力矢量.
代入理想约束力矢量的条件, 有
上式表示在给定的时间$t$和状态下, 理想约束力矢量及基本动力学矢量与高斯意义上的加速度变分正交.
1.2 广义坐标形式的高斯类变分方程
若多体系统的位形由$n$个广义坐标${q}=[q_1$, $q_2$, $q_3$, $\cdots$, $q_{n}]^{\rm T}$表达, 且假设系统受到如下类型的约束
其中, $\varPhi'_1$, $\varPhi'_2$, $\varPsi'_{1}$, $\varPsi'_{2}$分别是$h$维、l维、$s$维及$g$维矢量. 假定初始条件满足约束.
假定约束足够光滑, 对时间微分式(4)和式(6)两次, 而微分式(5)和式(7)一次得到如下方程
其中, ${A}_1 $及${A}_2 $分别是$(h+l)\times n$阶及$(s+g)\times n$阶的约束雅可比矩阵, 而${b}_1$及$b_2$分别是由微分得到的$(h+s)$维及$g$维矢量.
则类似于方程(1), 可将广义坐标形式的动力学微分方程写作如下形式
其中, $M$是$n\times n$阶的正定的广义质量矩阵, ${Q}^{Ci}={GF}^{Ci}$代表广义理想约束力矢量, ${Q}^{Cn}={HF}^{Cn}$代表做功不为零的广义非理想约束力矢量, $G$及$H$为相应的约束雅可比矩阵.
由方程(10)可以得到
同时可由式(10)得到由广义加速度及非理想约束力表示的理想约束力表达式
由理想约束力矢量的定义, 可得到
式中, $\delta {\ddot{{q}}}$为高斯意义上的广义加速度变分, 式(13)可以看作为变分形式的针对非理想约束系统的高斯原理.
由方程(3)及式(13)可见, 当将广义坐标体系取作笛卡尔坐标时, 二者形式相同, 故下面将以广义坐标表达的方程(13)来讨论非理想系统的极值原理.
2 非理想系统极值形式的高斯原理的推导及证明
2.1 非理想系统高斯拘束及限制条件的推导
2.1.1 非理想约束力矢量与理想约束力无明显关联
当非理想约束力与理想约束力无明显关联, 只与时间及系统状态有关时, 由方程(11)可以得到高斯意义上的广义加速度变分与理想约束力变分之间的关系式
故极值形式的高斯最小拘束原理的拘束可取作以广义加速度以及以理想约束力为变量的两种形式
将式(11)代入式(8)和式(9)之后得到
2.1.2 非理想约束力矢量可以表达为理想约束力矢量的函数
当非理想约束力矢量与理想约束力有明显的函数关系, 即$F^{Cn}={f}(F^{Ci})$, 则它的高斯变分与广义加速度及理想约束力相关.
对式(11)两边取高斯变分, 得到
故由式(13)的第一项, 可以得到
故取此种情况下的高斯拘束为
同样将式(11)及关于非理想约束力的函数式代入式(8)和式(9), 可以得到关于理想约束力所受到的等式及不等式限制条件
通过下面的变换可以得到关于广义加速度的高斯拘束.
通过求解代数方程${\ddot{{q}}}=M^{-1}{Q}+M^{-1}{GF}^{Ci}+M^{-1}{f}(F^{Ci})$, 可以得到以广义加速度表达的关于理想约束力的显式函数, 即$F^{Ci}={F}({\ddot{{q}}})$, 因此$F^{Cn}={Y}({\ddot{{q}}})={f}({F}({\ddot{{q}}}))$, 则可以得到关于广义加速度的变分形式的高斯原理
若${Y}({\ddot{{q}}})$为${\ddot{{q}}}$的线性表达式, 则高斯拘束可表示为广义加速度的二次函数.
当非理想约束力与理想约束力有明显的函数关系时, 其理想约束力表达的高斯拘束可以写作式(20). 由式(20)可以看出, 若非理想约束力与理想约束力没有明显的关联, 则${f}_{Ci} ={\partial {f}}/{\partial F^{Ci}}={\bf0}$ , 将其代入式(20), 可以得到$G_{ni} (F^{Ci})=(F^{Ci})^{\rm T}G^{\rm T}M^{-1}{GF}^{Ci}/2$, 恰好与式(16)相同, 因此针对两种情况, 可以采用统一的形式(20)来表示高斯极值原理的拘束.
2.2 非理想系统的高斯拘束取得最小值的条件及证明
在时刻$t$, 保持系统的状态(位置及速度)相同, 当理想约束力有微小变更$\Delta F^{Ci}$时, 相应的高斯拘束的差值为
$\Delta G_{ni} (F^{Ci})=\\ \qquad\frac{1}{2}(F^{Ci}+\Delta F^{Ci})^{\rm T}G^{\rm T}M^{-1}(G+Hf_{Ci})(F^{Ci}+\Delta F^{Ci}) -\\ \qquad\frac{1}{2}(F^{Ci})^{\rm T}G^{\rm T}M^{-1}(G+Hf_{Ci})(F^{Ci}) =\\ \qquad(\Delta F^{Ci})^{\rm T}G^{\rm T}M^{-1}(G+Hf_{Ci})(F^{Ci}) +\\ \qquad\frac{1}{2}(\Delta F^{Ci})^{\rm T}G^{\rm T}M^{-1}(G+Hf_{Ci})(\Delta F^{Ci}) =\\ \qquad\frac{1}{2}(\Delta F^{Ci})^{\rm T}G^{\rm T}M^{-1}(G+Hf_{Ci})(\Delta F^{Ci}) =\\ \qquad\frac{1}{2}(\Delta F^{Ci})^{\rm T}M^{-1}(G+Hf_{Ci})(\Delta F^{Ci}) =\\ \qquad\frac{1}{2}(\Delta F^{Ci})^{\rm T}G^{\rm T}M^{-1}(G+Hf_{Ci})(\Delta F^{Ci}) $
当式中$G^{\rm T}M^{-1}(G+Hf_{Ci} )$是正定矩阵时, $(\Delta F^{Ci})^{\rm T}$ $G^{\rm T}M^{-1}(G+{Hf}_{Ci})$ $(\Delta F^{Ci})/2$为关于$\Delta F^{Ci}$的正定二次型, 因此在该条件下, $\Delta G_{ni} (F^{Ci})$总大于零, 则以方程(20)所表达的高斯拘束总会取得最小值. 可得到下列针对非理想系统的高斯原理的表达形式.
非理想系统的高斯极值原理如下.
当系统满足$G^{\rm T}M^{-1}(G+Hf_{Ci})$为正定矩阵时, 在时刻$t$及给定的状态下, 在所有的可能理想约束力$F^{Ci*}$(即满足约束方程(21))中, 实际理想约束力$F^{Ci}$使得高斯拘束最小, 即
若非理想约束力预先给定, 则可采用式(25)所表达的以广义加速度为变量的高斯拘束
可以将式(24)描述为: 在时刻$t$及给定的状态下, 在所有的可能广义加速度${\ddot{{q}}}^* $[即满足约束方程(8)和(9)]中, 实际广义加速度${\ddot{{q}}}$使得高斯拘束最小.
证明过程类似式(23)的证明, 故略.
3 考虑库仑摩擦的单边约束的多体系统动力学的优化模型
对于考虑库仑摩擦的接触问题可以看作为单边约束的非理想多体系统动力学问题, 采用下列的单边约束表示系统的接触-分离两种状态
代表接触物体间的相对法向距离始终大于等于零, 对上式求一阶及二阶导数为
其中, $W_{\rm N}$为接触相对法向距离的雅可比矩阵, ${\widetilde{{W}}}_{\rm N}$为与广义坐标及时间有关的量, $\overline{{W}}_{\rm N}$为与广义坐标、广义速度及时间有关的量.
则动力学方程可以写作
其中, ${\lambda}$为法向约束力矢量, ${W}_{\rm t}$为接触点相对切向滑动距离的雅可比矩阵.
对应高斯拘束式(23)中的各项, $G={W}_{\rm N}^{\rm T}$, ${H}={W}_{\rm t}^{\rm T}$, ${f}_{Ci} ={sU}$, 其中$s$是对角线元素为接触点切向相对速度的符号函数对角矩阵, $U$为对角线元素是接触点动滑动摩擦系数的对角矩阵.
当${A}={W}_{\rm N} M^{-1}(W_{\rm N}^{\rm T} +{W}_{\rm t}^{\rm T} {sU})$为正定矩阵时, 在时刻$t$, 广义坐标及广义速度不变的情况下, 真实的法向约束力矢量满足下列条件
其中, ${B}={W}_{\rm N} M^{-1}{Q}+{\bar{{W}}}_{\rm N} $.
因此, 在$A$为正定矩阵的条件下, 含摩擦的多体系统的接触问题存在严格凸的最优化模型, 这一点与文献[14]的论述有所不同.
4 例子
4.1 含摩擦的单点接触问题
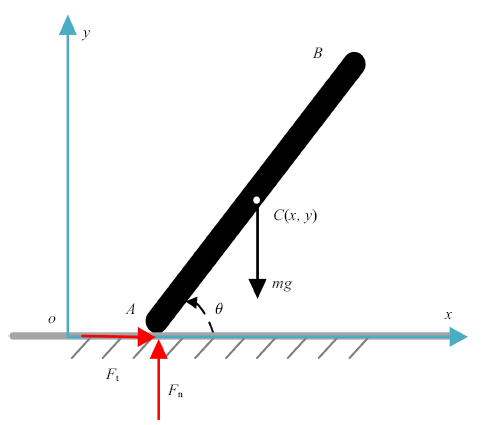
如图1所示. 地面上有一刚性均匀细杆, 长$2l$, 质量为$m$, 杆的一端$A$与地面接触做平面运动, 接触处有库仑干摩擦作用. 研究$A$点维持接触并向左滑行的状况, 此时$y_A =0$, $\dot{{y}}_A =0$, $\dot{{x}}_A <0$, 并有库仑干摩擦定律成立.
图1
4.1.1 杆件运动学与动力学方程
杆的动力学方程可以表示为
单边约束方程为
$g_{\rm N} =y_A =y-l\sin \theta \geqslant 0 $
根据运动学关系
$\ddot{{y}}=\ddot{{y}}_A +l\ddot{{\theta }}\cos \theta -l\dot{{\theta }}^2\sin \theta $
可以得到接触点法向加速度和法向接触力之间的关系
其中
$A=\frac{1}{m}[1+3\cos \theta (\cos \theta -\mu \sin \theta )]\\ B=l\dot{{\theta }}^2\sin \theta -g $
同时可以计算得到方程(29)中的矩阵
$M=\left[ {{\begin{array}{c} {m} & \\ & m & \\ && {\frac{1}{3}ml^2} \\ \end{array} }} \right], Q=\left[ {{\begin{array}{c} 0 \\ {-mg} \\ 0 \\ \end{array} }} \right]\\ {W}_{\rm N} =\left[ 0 \ 1\ {-l\cos\theta } \right] \ \ {W}_{\rm t} =\left[ 1 \ 0 \ {l\sin\theta } \right] \\ {s}=[1], \ \ {U}=\left[ \mu \right] $
则
${A}={W}_{\rm N} M^{-1}(W_{\rm N}^{\rm T} +{W}_{\rm t}^{\rm T} {sU})= [m^{-1}(1+3\cos^2\theta -3\mu\sin \theta \cos \theta )]=\left[A \right]\\ {B}={W}_{\rm N} M^{-1}{Q}+{\bar{{W}}}_{\rm N} =\left[ l\sin \theta \dot{\theta}^2-g\right]=\left[ B \right] $
可见, 通过矩阵计算的结果与通过运动学及动力学方程计算的结果相吻合.
下面将通过两种方法来分析本问题中含摩擦的单边约束问题.
4.1.2 接触模型及对比分析
(1)单边接触的线性互补模型 (linear complementary problem, LCP)
当$y=0$且$\dot{{y}}=0$时, 应有
即
由线性互补性问题的解的唯一性判别方法, 当$A>0$时, 不管$B$为何值, 上述关于法向约束力的LCP问题均有唯一解存在.
(2) 单边接触的高斯优化模型
由式(29)所给出的极值原理计算可知: 对于本问题, 当 $A>0$时, 总会有
可见, 当$A>0$时, 关于法向约束力的线性互补模型及高斯优化模型同时对应系统的唯一解.
(3) 两种模型之间的对比分析
① 由高斯优化模型可以推导得出LCP模型
根据式(34)所代表的约束最优化问题, 其可行域为$\{\lambda|A\lambda +B\geqslant 0\}$, 设其非空, 则实际法向约束力$F_{\rm n} $为函数$f(\lambda )=(\lambda)^{\rm T}A{\lambda}/2$极小值点的K-T条件是
式(35)与直接建立的LCP模型(33)吻合.
② 由LCP模型可推出高斯优化模型
LCP模型与二次型优化问题紧密相连, 式(33)所代表的LCP模型可转化为二次型优化问题
最优化问题(36)的对偶问题为
将符号$F_{\rm n} $由$\lambda $代替, 则得到了与高斯优化模型式(34)吻合的优化模型.
由此可见, 本文中得到的高斯优化模型与LCP模型是分别通过不同的方法得到的, 但同时又可以根据最优化理论相互推导得到, 因此可以有效证明两种方法的可靠性.
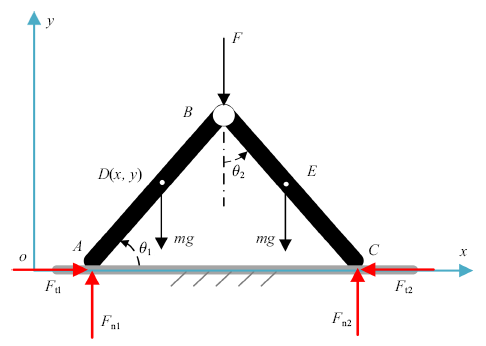
4.2 双杆系统的多点接触问题
如图2所示两根相同的均质杆$AB$和$BC$, 长为$l$, 质量为$m$, 在端点$B$用光滑铰链连接, 且受到外力$F$作用, $A$和$C$两端放在非光滑的水平面上, 杆与地面间动滑动摩擦系数为$\mu $.
图2
4.2.1 多点接触系统高斯优化模型
系统的广义坐标矢量可取为${q}=[x\ \ y \ \ \theta _1\ \ \theta _2]^{\rm T}$, 其中$(x,y)$为$AB$杆的质心坐标, $\theta_{\rm 1}$为$AB$杆与水平线的夹角, $\theta _2 $为$BC$杆与铅直线的夹角, 则$A$点与$C$点的单边接触方程为
则可以计算得到优化模型(29)中的各矩阵项
$M= {{\begin{bmatrix} {2m} & 0 & {-\dfrac{1}{\mbox{2}}ml\sin \theta _1 } & {\dfrac{1}{\mbox{2}}ml\cos \theta _2 }\\ 0 & {2m} & {\dfrac{1}{\mbox{2}}ml\cos \theta _1 } & {\dfrac{1}{\mbox{2}}ml\sin \theta _2 }\\ {-\dfrac{1}{\mbox{2}}ml\sin \theta _1 } & {\dfrac{1}{\mbox{2}}ml\cos \theta _1 } & {\dfrac{1}{3}ml^2} & {-\dfrac{1}{\mbox{4}}ml^2\sin (\theta _1 -\theta _2 )}\\ {\dfrac{1}{\mbox{2}}ml\cos \theta _2 } & {\dfrac{1}{\mbox{2}}ml\sin \theta _2 } & {-\dfrac{1}{\mbox{4}}ml^2\sin (\theta _1 -\theta _2 )} & {\dfrac{1}{3}ml^2} \\ \end{bmatrix} }} $
$Q= {{\begin{bmatrix} 0 & F & {\dfrac{1}{2}Fl\cos \theta _1 } & 0 \\ \end{bmatrix} }} ^{\rm T} \\ {\bar{{W}}}_{\rm N} = {{\begin{bmatrix} {\dfrac{l}{2}\cos \theta _1 \dot{{\theta }}_1^2 +\dfrac{l}{2}\sin \theta _2 \dot{{\theta }}_2^2 } \\ {-\dfrac{l}{2}\sin \theta _1 \dot{{\theta }}_1^2 +\dfrac{l}{2}\cos \theta _2 \dot{{\theta }}_2^2 } \\ \end{bmatrix} }} \\ {W}_{\rm t} = {{\begin{bmatrix} 1 & 0 & {\dfrac{l}{2}\mbox{sin}\theta _1 } & 0 \\ 1 & 0 & {-\dfrac{l}{2}\mbox{sin}\theta _1 } & {l\mbox{cos}\theta _2 } \end{bmatrix} }} \\ {W}_{\rm N} = {{\begin{bmatrix} 0 & l & {-\dfrac{l}{2}\cos \theta _1 } & 0 \\ 1 & 0 & {\dfrac{l}{2}\mbox{sin}\theta _1 } & {l\sin \theta _2 } \\ \end{bmatrix} }} \\ {U}= {{\begin{bmatrix}{c} \mu & \\ & \mu \\ \end{bmatrix} }} ,\ \ \ {S}= {{\begin{bmatrix}{c} {sgn(\dot{{x}}_A )} & \\ & {sgn(\dot{{x}}_{\rm C} )} \\ \end{bmatrix} }} $
则将上述矩阵代入, 便可以确定关于法向约束力矢量的优化模型
其中, ${A}={W}_{\rm N} M^{-1}(W_{\rm N}^{\rm T} +{W}_{\rm t}^{\rm T} {sU})$; ${B}={W}_{\rm N} M^{-1}{Q}+{\bar{{W}}}_{\rm N}$.
4.2.2 基于优化模型的动力学的计算过程及数值模拟
算法流程如下:
(1)输入初始条件${q}_0$, ${\dot{{q}}}_0 $, 积分区间为$[0,T]$, 步长$\Delta t$以及系统的物理、几何参数;
(2)计算优化模型(39)中的各系数矩阵;
(3)计算法向约束力矢量${\lambda }$:
解决上述优化问题(39)的计算方法很多, 本例选择了比较成熟的传统优化算法: 牛顿法来计算法向约束力矢量[18].
(4) 计算广义加速度矢量${\ddot{{q}}}$:
采用下列公式计算广义加速度矢量
(5)根据步骤4所得到的广义加速度, 积分得到下一时刻广义坐标的速度和位移: $\dot{{q}}_{t+\Delta t} $, $q_{t+\Delta t} $;
(6)判断此时$t$是否满足终止条件$t\leqslant T$:
(a)如果满足, 程序终止并输出;
(b)如果不满足, 令$t=t+\Delta t$ 转到步骤2继续运行.
依据上述算法流程, 选取下列参数及初始条件对系统进行动力学数值模拟
$m=2 \mbox{kg}, \ \ l=2 \mbox{m},\ \ \mu =0.2;\\ \theta _1 =\theta _2 =\frac{\pi}{4},\ \ x=y=l\sin \frac{\pi }{4} \mbox{m},\\ \dot{{x}}=-1 \mbox{m}/\mbox{s},\ \ \dot{{y}}=1 \mbox{m}/\mbox{s},\ \ \dot{{\theta }}_2 =0.1 {\mbox{rad}}/\mbox{s},\\ \dot{{\theta }}_1 =-0.1 {\mbox{rad}}/\mbox{s}. $
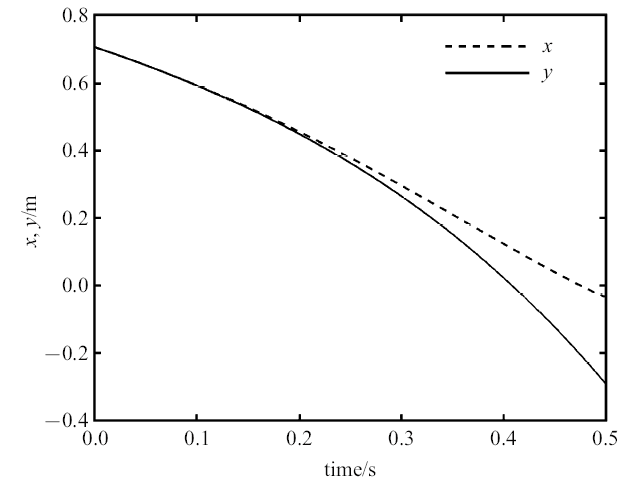
图3
图3
杆$AB$的质心坐标的时间历程图
Fig. 3
Time history of barycentric coordinates of bar $AB$
图4
图5
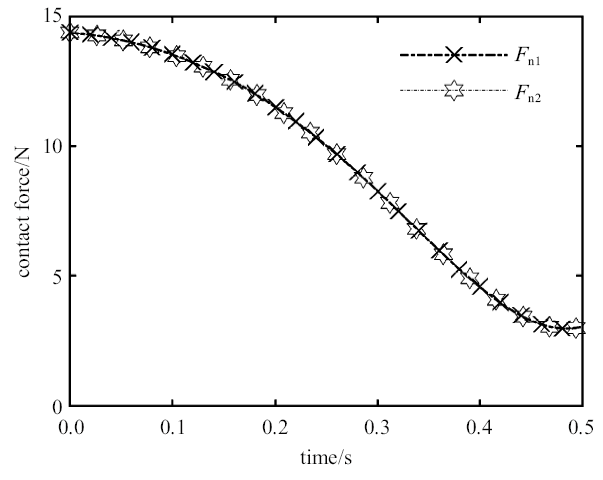
图5
接触点的法向约束力的时间历程图
Fig. 5
Time history diagram of normal binding force of contact point
5 结语
本文在从基本的动力学原理——高斯原理出发, 研究了高斯原理在非理想系统中的应用, 推导并证明了非理想系统中高斯拘束的函数表达式, 从而得到了以函数极值形式表达的非理想多体系统的优化模型. 该工作的意义在于:
(1) 借助于高斯原理, 非光滑的多体系统动力学的求解过程可以从求解含互补条件的微分代数方程变为自然寻优的过程, 其寻优的过程非借助于互补性及最优化理论之间的关系, 而是使得目标函数的选择更加符合自然哲学的思想;
(2)因为原理本身所具有的极值形式可以将非理想系统的动力学问题引入求解优化问题的框架内, 从而可以尝试探索现代智能优化算法在非理想多体系统中的应用; 同时对于带控制的多体系统, 可以根据技术需要将动力学分析与系统的优化结合进行.
参考文献
探讨用最优控制方法解力学问题
//
The discussion about using optimal control method solve mechanical problems
//
Nonsmooth Mechanics: Models, Dynamics and Control (3rd edition)
An important chapter in the history of multibody system dynamics
Dynamic analysis of multirigid-body system based on the Gauss principle
杆网系统基于高斯原理的动力学建模
Dynamic modeling of pole net system based on gauss principle
基于高斯原理的Cosserat弹性杆动力学模型
Based on the generalized principles of dynamics, the feature of Gauss principle of least constraint is that the motion law can be directly obtained by using the variation method of seeking the minimal value of the constraint function without establishing any dynamic differential equations. According to the Kirchhoff's dynamic analogy, the configuration of an elastic rod can be described by the rotation of rigid cross section of the rod along the centerline. Since the local small change of the attitude of cross section can be accumulated infinitely along the arc-coordinate, the Kirchhoff's model is suited to describe the super-large deformation of elastic rod. Therefore the analytical mechanics of elastic rod with arc-coordinate s and time t as double arguments has been developed. The Cosserat model of elastic rod takes into consideration the factors neglected by the Kirchhoff model, such as the shear deformation of cross section, the tensile deformation of centerline, and distributed load, so it is more suitable to modeling a real elastic rod. In this paper, the model of the Cosserat rod is established based on the Gauss principle, and the constraint function of the rod is derived in the general form. The plane motion of the rod is discussed as a special case. As regards the special problem that different parts of the rod in space are unable to self-invade each other, a constraint condition is derived to restrict the possible configurations in variation calculation so as to avoid the invading possibility.
Dynamic model of Coserat elastic rod based on Gauss principle
Based on the generalized principles of dynamics, the feature of Gauss principle of least constraint is that the motion law can be directly obtained by using the variation method of seeking the minimal value of the constraint function without establishing any dynamic differential equations. According to the Kirchhoff's dynamic analogy, the configuration of an elastic rod can be described by the rotation of rigid cross section of the rod along the centerline. Since the local small change of the attitude of cross section can be accumulated infinitely along the arc-coordinate, the Kirchhoff's model is suited to describe the super-large deformation of elastic rod. Therefore the analytical mechanics of elastic rod with arc-coordinate s and time t as double arguments has been developed. The Cosserat model of elastic rod takes into consideration the factors neglected by the Kirchhoff model, such as the shear deformation of cross section, the tensile deformation of centerline, and distributed load, so it is more suitable to modeling a real elastic rod. In this paper, the model of the Cosserat rod is established based on the Gauss principle, and the constraint function of the rod is derived in the general form. The plane motion of the rod is discussed as a special case. As regards the special problem that different parts of the rod in space are unable to self-invade each other, a constraint condition is derived to restrict the possible configurations in variation calculation so as to avoid the invading possibility.
基于高斯原理的多体系统动力学建模
Based on the Gauss's principle of least constraint, the dynamic modeling of a multi-body system connected by an elastic cable with varied lengths and large deformation in gravitational field of the earth was proposed in this paper. The practical background of the topic is the release process of a tethered satellite. The Kirchhoff's method was applied to transform the deformation of the elastic cable to rotation of rigid cross section along the centerline of the cable. Since the local small deformation of the cable can be accumulated limitlessly along the arc-coordinate, the Kirchhoff's model is suitable to describe the super-large deformation of elastic rod. In present paper the Gauss's constraint function of the system of rigid-flexible bodies in gravitational field of the earth was derived, and the geometric constraint conditions concerning relative position of bodies in space were considered using the Lagrange's multipliers. Therefore the dynamical model of the system was established in the form of conditional extremum problem. Applying the approach of Gauss's principle the real motion of the system can be obtained by the variation method directly through seeking the minimal value of constraint function without differential equations. The unified form of the model does not changed for different topologic constructions of the system, and it is unnecessary to distinct the tree system or system with loops. In the case of multi-body system with automatic control, the dynamic analysis can be combined with the optimization for different technique objectives.
Dynamic modeling of multibody system based on Gauss principle
Based on the Gauss's principle of least constraint, the dynamic modeling of a multi-body system connected by an elastic cable with varied lengths and large deformation in gravitational field of the earth was proposed in this paper. The practical background of the topic is the release process of a tethered satellite. The Kirchhoff's method was applied to transform the deformation of the elastic cable to rotation of rigid cross section along the centerline of the cable. Since the local small deformation of the cable can be accumulated limitlessly along the arc-coordinate, the Kirchhoff's model is suitable to describe the super-large deformation of elastic rod. In present paper the Gauss's constraint function of the system of rigid-flexible bodies in gravitational field of the earth was derived, and the geometric constraint conditions concerning relative position of bodies in space were considered using the Lagrange's multipliers. Therefore the dynamical model of the system was established in the form of conditional extremum problem. Applying the approach of Gauss's principle the real motion of the system can be obtained by the variation method directly through seeking the minimal value of constraint function without differential equations. The unified form of the model does not changed for different topologic constructions of the system, and it is unnecessary to distinct the tree system or system with loops. In the case of multi-body system with automatic control, the dynamic analysis can be combined with the optimization for different technique objectives.
Quadratic programming in mechanics: Dynamics of one-sided constraints
高斯最小拘束原理在一类刚柔耦合系统分析中的应用
Applying the Gauss minimum constraint theory,a finite segment modeling method is presented for a rigid-flexible coupled system. The cantilever beam’s movement with considerable range is synthesized in the model,and the system’s dynamic characteristic is expressed integrally. The simulation results and error analysis are given,which shows that the method has considerable preci?sion. The Gauss minimum constraint theory has its uniform expression,and it can reflect the system’s inertia effect. It is suitable for use in the modeling and analysis of a rigid- flexible coupled system.
The application of Gauss minimum restraint principle in the analysis of a kind of rigid flexible coupling system
Applying the Gauss minimum constraint theory,a finite segment modeling method is presented for a rigid-flexible coupled system. The cantilever beam’s movement with considerable range is synthesized in the model,and the system’s dynamic characteristic is expressed integrally. The simulation results and error analysis are given,which shows that the method has considerable preci?sion. The Gauss minimum constraint theory has its uniform expression,and it can reflect the system’s inertia effect. It is suitable for use in the modeling and analysis of a rigid- flexible coupled system.
单柔体与多柔体动力学的高斯最小拘束原理
Gauss' principle of least constraint of single flexible body and multi-flexible body dynamics
Cosserat生长弹性杆动力学的 Gauss 最小拘束原理
Gauss minimum restraint principle for the dynamics of Coserat growing elastic rod
高斯最小拘束原理在火炮振动分析中的应用
Application of Gauss minimum constraint principle in gun vibration analysis
多柔体系统动力学建模与优化研究进展
Advances in dynamic modeling and optimization of flexible multibody systems
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
Mechanical simulation and full order sliding mode collision avoidance compliant control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Modeling and algorithm on a class of mechanical systems with unilateral constraints
In the present paper, the cable-structures are considered as a class of mechanical complementary-slackness systems. Based on the optimization algorithms used for multi-body dynamics with unilateral contacts, an algorithm by means of artificial neural network (NNW) is developed. The following two classes of cable-structures have been considered force-elongation of cable member follows elastic behavior and work-hardening assumption. Due to simplicity the former is used to prove the method reliability, and the latter, as general cable-structure problem is handled. First, the complementarity problems for those structures have been formulated; then using generalized Gaussian‘ least action principle they are summarized as an optimization problem. Based on Hopfield’s work, an artificial NNW has been designed and used to decide combination of possible constraints at each step in simulation. As examples, two cable-structures have been investigated. The calculated results for a simple suspension structure evidence the reliability and time-economization of the proposed method. An example of guyed mast shows the suitability of the proposed method for practical cable-structures.
Gauss principle and the dynamics of redundant and constrained manipulators
//
A new perspective on constrained motion
Equations of motion for nonholonomic, constrained dynamical systems via Gauss's principle
An extension of Gauss's principle of least constraint
Reflections on the Gauss principle of least constraint
The Gauss principle of least constraint is derived from a new point of view. Then, an extended principle of least constraint is derived to cover the case of nonideal constraints. Finally, a version of the principle for general underdetermined systems is adumbrated. Throughout, the notion of generalized inverses of matices plays a prominent role.
分析动力学中的基本方程与非完整约束
Analytical mechanics is established based on d'Almbert-Lagrange Principle, Gauss principle, Jourdian principle and Hamilton principle, to deal with the dynamics of mechanical systems subject to holonomic or nonholonomic constraints. The governing equation of the systems are derived either by introducing Lagrange's multipliers to adjoin with the limitation equations for the virtual displacements, or by directly eliminating the constraint equations to achieve minimal formulations. The author presents a survey for the history of analytical mechanics, and explains some basic concepts, such as virtual displacement, ideal constraint, and the correlations between the Lagrange multipliers and the real constraint forces.
The fundamental equations in analytical mechanics for nonholonomic systems
Analytical mechanics is established based on d'Almbert-Lagrange Principle, Gauss principle, Jourdian principle and Hamilton principle, to deal with the dynamics of mechanical systems subject to holonomic or nonholonomic constraints. The governing equation of the systems are derived either by introducing Lagrange's multipliers to adjoin with the limitation equations for the virtual displacements, or by directly eliminating the constraint equations to achieve minimal formulations. The author presents a survey for the history of analytical mechanics, and explains some basic concepts, such as virtual displacement, ideal constraint, and the correlations between the Lagrange multipliers and the real constraint forces.
Multibody Dynamics with Unilateral Contacts
New general principle of mechanics and its application to general nonideal nonholonomic systems
广义坐标形式的高斯最小拘束原理及其推广
当采用广义坐标描述系统的运动时,相比质点形式的高斯最小拘束原理,通过广义坐标形式的高斯最小拘束原理来建立动力学优化模型,计算效率更高. 从高斯原理的变分形式出发推导了广义坐标形式的高斯最小拘束原理,并研究了非理想约束、单边约束及刚体碰撞情形下的高斯最小拘束原理的形式. 研究认为:对刚体碰撞情形下,高斯最小拘束原理不能取代碰撞恢复定律,碰撞恢复定律以碰撞后广义速度的约束方程形式起作用.
Gauss principle of least constraint in generalized coordinates and its generalization
当采用广义坐标描述系统的运动时,相比质点形式的高斯最小拘束原理,通过广义坐标形式的高斯最小拘束原理来建立动力学优化模型,计算效率更高. 从高斯原理的变分形式出发推导了广义坐标形式的高斯最小拘束原理,并研究了非理想约束、单边约束及刚体碰撞情形下的高斯最小拘束原理的形式. 研究认为:对刚体碰撞情形下,高斯最小拘束原理不能取代碰撞恢复定律,碰撞恢复定律以碰撞后广义速度的约束方程形式起作用.
基于广义坐标形式的高斯最小拘束原理的多刚体系统动力学建模
By variational Gauss principle in the form of kinetic energy and explicit express, the meaning of items in Gauss constraints is confirmed. The optimization model of dynamics of multi-rigid-body system in the form of Descartes generalized coordinates is established based on Gauss principle of least constraint in generalized coordinates. The method to write the Gauss constraints in other coordinate system according to the above model is studied. The dynamical problem of multi-rigid-body system can be turned into a problem for a minimum, and provided by the relation between the Descartes generalized coordinates and other coordinates system, the Gauss constraint in this kind of coordinates system is easy to be obtained. The modeling method is more convenient and is of universality. The dynamical models are established for planar motion and fixed axis rotation by Descartes generalized coordinate and Lagrange coordinate, and the validity of this method is proved.
Dynamical modeling of multi-rigid-body system based on Gauss principle of least constraint in generalized coordinates
By variational Gauss principle in the form of kinetic energy and explicit express, the meaning of items in Gauss constraints is confirmed. The optimization model of dynamics of multi-rigid-body system in the form of Descartes generalized coordinates is established based on Gauss principle of least constraint in generalized coordinates. The method to write the Gauss constraints in other coordinate system according to the above model is studied. The dynamical problem of multi-rigid-body system can be turned into a problem for a minimum, and provided by the relation between the Descartes generalized coordinates and other coordinates system, the Gauss constraint in this kind of coordinates system is easy to be obtained. The modeling method is more convenient and is of universality. The dynamical models are established for planar motion and fixed axis rotation by Descartes generalized coordinate and Lagrange coordinate, and the validity of this method is proved.
优化形式的刚体系统动力学模拟
基于广义坐标形式的高斯最小拘束原理来研究刚体系统的动力学问题的优化方法. 相比目前动力学建模普遍采用的质点形式的高斯最小拘束原理,广义坐标形式的高斯最小拘束原理因对所选择的广义坐标没有要求,而使得建模过程更简单及具有更强的通用性. 本文分别建立了有约束和无约束条件下问题的优化动力学模型,对问题进行了动力学数值模拟,并与用拉格朗日微分方程处理的模型进行了对比分析,从而验证了所提方法的有效性.
Simulation of body dynamics with optimization
基于广义坐标形式的高斯最小拘束原理来研究刚体系统的动力学问题的优化方法. 相比目前动力学建模普遍采用的质点形式的高斯最小拘束原理,广义坐标形式的高斯最小拘束原理因对所选择的广义坐标没有要求,而使得建模过程更简单及具有更强的通用性. 本文分别建立了有约束和无约束条件下问题的优化动力学模型,对问题进行了动力学数值模拟,并与用拉格朗日微分方程处理的模型进行了对比分析,从而验证了所提方法的有效性.