引言
随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] .
过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法.
近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用.
本文主要研究空间双臂机器人的协调路径规划问题,基于 RRT* 算法分别规划双臂的末端执行器在笛卡尔空间中的初始可行路径,并利用四次样条曲线对由 RRT* 算法生成的初始路径进行平滑处理,通过满足样条曲线的一阶、二阶及三阶微分连续约束,保证机械臂末端执行器的初末速度、加速度约束条件,得到适合于机器人执行的平滑路径. 本工作采用 RRT* 和四次样条曲线方法,研究了空间多臂机器人的快速路径规划问题,考虑双臂规划过程中的协调性操作和路径平滑处理,以期为空间多臂机器人协调运动规划问题以及多智能体协调运动规划问题提供参考数据.
1 自由漂浮双臂空间机器人建模
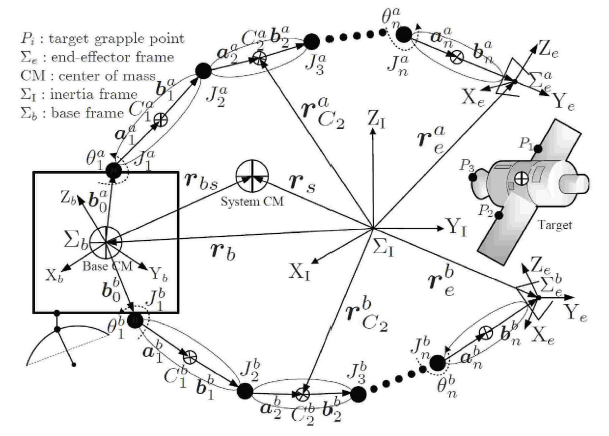
如图 1 所示,双臂空间机器人系统由 1 个基座和 2 个 $n$ 自由度的机械臂构成,共计 $2n +1$ 个刚体,且系统不受任何外力作用 (本文研究中 $n =7$).
图1
图1
自由漂浮双臂空间机器人系统示意图
Fig.1
Sketch of a dual-arm free-floating space robot
空间机器人建模方面的现有研究很成熟,根据泊松公式[30 ] ,空间机器人的运动学方程表示如下
(1) $\left [\!\!\begin{array}{c} \dot{\pmb x}^a_{\rm e} \\ \dot{\pmb x}^b_{\rm e} \end{array}\!\!\right] =\left[\!\!\begin{array}{l} {\pmb J}^a_{\rm b} \dot{\pmb x}_{\rm b}+{\pmb J}^a_{\rm e}\dot{\pmb \theta}^a \\ {\pmb J}^b_{\rm b} \dot{\pmb x}_{\rm b}+{\pmb J}^b_{\rm e}\dot{\pmb \theta}^b \end{array}\!\!\right]$
其中,上标 $a$ 和 $b$ 分别表示变量属于机械臂 $a$ 和 $b$. 下标 ${\rm b}$ 和 ${\rm e}$ 分别表示变量属于基座 (base) 和末端执行 器 (end-effector). $\dot {\pmb x}_{\rm b} \in {\bf R}^{6\times 1},\dot {\pmb x}_{\rm e}^a \in {\bf R}^{6\times 1},\dot {\pmb x}_{\rm e}^b \in {\bf R}^{6\times 1}$ 分别为基座和末端执行器的线速度、角速度合矢量,$\dot {\pmb \theta }^a \in {\bf R}^{7\times 1},\dot {\pmb \theta }^b \in {\bf R}^{7\times 1}$ 为各机械臂关节角速度. 若无特别说明,文中矢量 (除姿态相关矢量) 选择向惯性坐标系投影,其他矢量已在表 1 中列举.
根据第二类拉格朗日方程[31 ] ,空间机器人的动力学方程表示如下
(2) $\left[\!\!\begin{array}{c} {\pmb H}_{\rm b} & {\pmb H}^a_{\rm bm} &{\pmb H}^b_{\rm bm} \\ {\pmb H}^{a{\rm T}}_{\rm bm} & {\pmb H}^a_{\rm m} & {\bf 0}_{\rm n} \\ {\pmb H}^{b{\rm T}}_{\rm bm} & {\bf 0}_{\rm n} & {\pmb H}^b_{\rm m} \end{array}\!\! \right] \left[\!\!\begin{array}{c} \ddot{\pmb x}_{\rm b} \\ \ddot{\pmb\theta}^a \\ \ddot{\pmb\theta}^b \end{array}\!\! \right] + \left [\!\!\begin{array}{c} {\pmb c}_{\rm b}\\ {\pmb c}^a_{\rm m} \\ {\pmb c}^b_{\rm m} \end{array}\!\!\right]= \\ \qquad \left[\!\!\begin{array}{c} {\pmb f}_{\rm b} \\ {\pmb\tau}^a_{\rm m} \\ {\pmb \tau}^b_{\rm m} \end{array} \!\!\right] +\left[\!\!\begin{array}{cc} {\pmb J}^{a{\rm T}}_{\rm b} &{\pmb J}^{b{\rm T}}_{\rm b}\\ {\pmb J}^{a{\rm T}}_{\rm e} & {\bf 0}_{n\times 6} \\ {\bf 0}_{n\times 6} & {\pmb J}^{b{\rm T}}_{\rm e} \end{array} \!\!\right] \left[\!\!\begin{array}{c} {\pmb f}^a_{\rm e} \\ {\pmb f}^b_{\rm e} \end{array} \!\!\right]$
式中,$\ddot {\pmb x}=\left[\!\!\begin{array}{c} {\ddot {\pmb r}_{\rm b} } \\ {\dot {\pmb \omega }_{\rm b} } \end{array}\!\! \right]$ 为基座的线加速度、角加速度合矢量,$\ddot{\pmb\theta}^a $ 和 $\ddot{\pmb\theta}^b $ 分别是各机械臂的关节角加速度矢量. 在自由漂浮模式下,基座和末端执行器不受外力和外力矩,即有 ${\pmb f}_{\rm b}={\pmb f}^a_{\rm e}={\pmb f}^b_{\rm e}={\bf 0}$,机械臂的运动仅受关节内力影响. 系统满足动量守恒,故其运动学方程可写为
(3) $\left[\!\! \begin{array}{c} {\pmb P}_0 \\ {\pmb L}_0 \end{array} \!\! \right] = H_{\rm b} \left[\!\! \begin{array}{l} \dot{\pmb r}_{\rm b} \\ {\pmb \omega}_{\rm b} \end{array} \!\! \right] + {\pmb H}_{\rm bm}^a \dot {\pmb \theta }^a + {\pmb H}_{\rm bm}^b \dot{\pmb \theta }^b = \\ \qquad \left[ \!\! \begin{array}{l} m_{\rm b} \dot {\pmb r}_{\rm b} + \sum_{i = 1}^{2n} m_i \dot {\pmb r}_{C_i } \\ {\pmb I}_{\rm b} {\pmb \omega}_{\rm b} + m_{\rm b} {\pmb r}_{\rm b} \times \dot {\pmb r}_{\rm b} + \sum_{i = 1}^{2n} (m_i {\pmb r}_{C_i } \times \dot {\pmb r}_{C_i } ) \end{array} \!\! \right] $
式中,${\pmb M}_0=[{\pmb P}_0 \ {\pmb L}_0]^{\rm T}$ 为系统的初始线动量、角动量. 由于矩阵 ${\pmb H}_{\rm b}$ 可逆,可以将基座的运动方程改写如下
(4) $\left[ \begin{array}{l} \dot {\pmb r}_{\rm b} \\ {\pmb \omega}_{\rm b} \end{array} \right] = \left[ \begin{array}{cc} { - {\pmb H}_{\rm b}^{ - 1} {\pmb H}_{\rm bm}^a } & { - {\pmb H}_{\rm b}^{ - 1} {\pmb H}_{\rm bm}^b } \end{array} \right]\left[ \begin{array}{l} \dot {\pmb \theta }^a \\ \dot {\pmb \theta }^b \end{array} \right] - {\pmb H}_{\rm b}^{ - 1} {\pmb M}_0$
将式 (2) 代入式 (1),那么末端执行器的运动表达如下
(5) $\left[ \!\! \begin{array}{l} \dot{\pmb x}_{\rm e}^a + {\pmb J}_{\rm d}^a {\pmb M}_0 \\ \dot{\pmb x}_{\rm e}^b + {\pmb J}_{\rm d}^b {\pmb M}_0 \end{array} \!\! \right] = \left[\!\!\begin{array}{l} {\pmb J}_{\rm g}^a\\ {\pmb J}_{\rm g}^b \end{array} \!\! \right]\dot {\pmb \theta } = \\ \qquad \left[\!\! \begin{array}{cc} {\pmb J}_{\rm e}^a - {\pmb J}_{\rm b}^a {\pmb H}_{\rm b}^{ - 1} {\pmb H}_{bm}^a & - {\pmb J}_{\rm b}^a {\pmb H}_{\rm b}^{ - 1} {\pmb H}_{\rm bm}^b \\ - {\pmb J}_{\rm b}^b {\pmb H}_{\rm b}^{ - 1} {\pmb H}_{\rm bm}^a & {\pmb J}_{\rm e}^b - {\pmb J}_{\rm b}^b {\pmb H}_{\rm b}^{ - 1} {\pmb H}_{\rm bm}^b \end{array} \!\! \right]\left[\!\! \begin{array}{l} \dot {\pmb \theta }^a \\ \dot {\pmb \theta }^b \end{array} \!\!\right] $
式中,${\pmb J}_{\rm g}$ 为系统的广义雅克比矩阵,${\pmb J}_{\rm d}$ 为系统初始动量 ${\pmb M}_0$ 引起的耦合矩阵.
2 协调 RRT* 结合四次样条的路径规划
2.1 RRT* 协调路径规划
基于随机采样原理的快速搜索随机树方法具有概率完备性、计算量小、计算难度低等特点,非常适合空间自主航天器完成复杂空间的近距离操作服务任务. 此外,它对解决高维状态规划问题有着较强的适应性,这一能力是目前很多规划算法所不具备的,因此它非常适合空间机器人高维运动状态规划的实际情况. 鉴于 RRT* 算法不仅加快了原 RRT 算法的收敛速度,还增强了算法的最优性能,因此本文选取 RRT* 作为空间机器人路径规划的主要方法,这里简单给出 RRT* 算法的基本流程,关于 RRT* 算法的细则可以参考文献[32 ] .
本文研究中,利用 RRT* 规划算法生成机械臂末端执行器在笛卡尔空间下的期望路径,具体工作流程如下:
(1) 将系统的初始状态 (末端执行器的位置信息) 作为树的第一个顶点;
(2) 当无障碍环境时在状态空间中随机生成一个采样点;
(3) 在原树与该采样点最近点处延伸固定步长 (初始时即为顶点);
(4) 对采样点周围的点进行检测与优化,若有更短的航迹,则用新节点替代旧节点;
(5) 考虑障碍物等运动学约束,进行碰撞检测,以保证生成路径的安全性;
(6) 经过有限次迭代优化求解,直至达到目标状态.
通过以上步骤,可以在非结构环境中快速搜索到一条无碰撞的从初始状态到期望状态的优化运动路径.
然而,将 RRT* 算法直接应用于双臂空间机器人的末端执行器在任务空间下的路径规划,双末端执行器在规划的过程中由于随机采样极有可能会发生碰撞. 因此本文针对原有 RRT* 算法进行改进,提出一种适用于多臂路径规划的协调 RRT* 算法,改进的 RRT* 算法同样适用于其它多智能体系统的协调路径规划问题.
基于原有 RRT* 算法框架,在设置双臂的采样空间时,本文对双臂各自采样空间预留了约 0.1m 宽度的欧氏距离,通过在不同的采样空间中分别进行各末端执行器的路径搜索,这相当于对双末端施加了具有一定边界范围的笛卡尔空间约束. 值得注意的是,此空间约束不是固定的,应随着末端执行器的运动而连续变化. 此空间约束可以保证整个规划执行过程中双臂空间机器人不发生自身碰撞,包括两个末端执行器不发生碰撞,以及双臂各连杆不发生自身碰撞. 改进的协调RRT*路径规划算法流程如下:
(5) 判断是否有更少代价的航迹,若有则替代原航迹;
注意,由上述 RRT* 算法得到的末端初始路径十分不平滑,不能直接施加于空间机器人,需要对得到的初始路径进行平滑处理. 常见的平滑处理技巧分为两类,一类是基于优化方法,例如,共轭梯度法、凸优化方法等. 但此类方法比较耗时,因此本文采用第二类方法:曲线拟合技巧.
2.2 四次样条平滑
样条曲线被认为是平滑机器人路径的最有效的手段之一,在机器人规划中也得到了很多应用,包括关节规划和末端规划. 实际应用中最常见的样条曲线是三次样条曲线,本文研究表明,为了满足路径的三阶导数连续条件,针对末端的路径规划至少需要用到四次及以上的样条曲线.
首先,回顾样条曲线的基本知识. 假设有 $n +1$ 个时间位置相关的路径点如下
(6) $(t_0 ,x_0 ),(t_1 ,x_1 ), \cdots ,(t_n ,x_n )$
其中,$x_i $ 表示机器人末端执行器在时间 $t_i $ 的期望位置.
给定这些路径点,四次样条曲线可以平滑地衔接这些路径点,且保证在曲线衔接处满足一阶、二阶微分连续约束等. 四次条件曲线的基本形式表达如下
(7) $x_i (t) = a_i + b_i (t - t_i ) + c_i (t - t_i )^2 + d_i (t - t_i )^3 + e_i (t - t_i )^4$
其中,$a_i ,b_i ,c_i ,d_i ,e_i $ 分别是四次样条曲线的参数. 最终的路径由若干段四次样条曲线级联而成. 给定路径点,存在唯一的样条参数集合,使得规划的路径通过各个路径点,且在各个路径点处满足特定的速度连续,加速度连续等约束条件. 针对机器人运动而言,还需要保持加加速度连续,以防机械臂产生抖振现象.
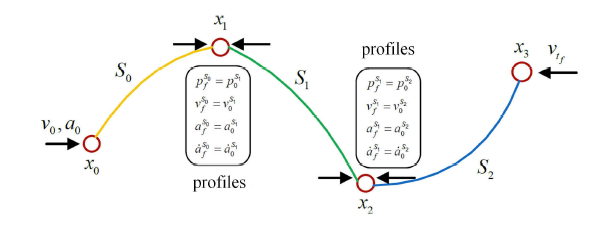
如图 2 所示,给定一系列末端执行器的期望路径点(本文研究中,这些路径点由 RRT* 算法给出),假设 $i =3$,那么则有 4 个路径点,即需要级联 3 段四次样条曲线,共计 15 个未知参数.
图2
图2
四次样条曲线示意图
Fig.2
Sketch of quartic splines
通过保证各个路径点位置约束 (6 个约束);中间路径点还需满足速度、加速度、加加速度连续约束 (6 个约束),以保证机器人能够平滑地执行全部路径;此外,本文对末端的初始速度、加速度和终止速度施加限制 (3 个约束). 由上述 15 个约束构建方程组,可以求解 15 个未知的样条参数. 构建的约束方程组具体表达如下
(8a) $\left.\!\! \begin{array}{l} a_0 = x_0 , \ \ a_2 = x_2 \\ a_0 + b_0 h_0 + c_0 h_0^2 + d_0 h_0^3 + e_0 h_0^4 = x_1 \\ a_1 + b_1 h_1 + c_1 h_1^2 + d_1 h_1^3 + e_1 h_1^4 = x_2 \\ a_2 + b_2 h_2 + c_2 h_2^2 + d_2 h_2^3 + e_2 h_2^4 = x_3 \\ b_0 + 2c_0 h_0 + 3d_0 h_0^2 + 4e_0 h_0^3 - b_1 = 0 \\ b_1 + 2c_1 h_1 + 3d_1 h_1^2 + 4e_1 h_1^3 - b_2 = 0 \end{array} \!\! \right\} $
(8b) $\left.\!\! \begin{array}{l} c_0 + 3d_0 h_0 + 6e_0 h_0^2 - c_1 = 0 \\ c_1 + 3d_1 h_1 + 6e_1 h_1^2 - c_2 = 0 \\ d_0 + 4e_0 h_0 - d_1 = 0 \\ d_1 + 4e_1 h_1 - d_2 = 0 \\ \dot {S}_0 (x_0 ) = b_0 , \ \ \ddot {S}_0 (x_0 ) = 2c_0 \\ \dot {S}_2 (x_3 ) = b_2 + 2c_2 h_2 + 3d_2 h_2^2 + 4e_2 h_2^3 \end{array} \!\! \right\} $
其中,$h_0, h_1, h_2$是仅与时间相关的常量,取决于时间序列$t_0, t_1, t_2, t_3$. 通过上述方程组即可求解样条参数,进而得到机器人末端的运动轨迹.
综上所述,自由漂浮双臂空间机器人的路径规划问题可描述为以下形式
(9) $\left.\begin{array}{ll} \min : \!\!& f({\pmb x}_{\rm e} ) \\ {\rm s.t.}: \!\!& {\pmb x}_{\rm e} (t = 0) = {\pmb x}_{\rm e}^s , \ {\pmb x}_{\rm e} (t = t_{\rm f} ) = {\pmb x}_{\rm e}^{\rm f} \\ & \dot{\pmb x}_{\rm e} (t = 0) = \dot {\pmb x}_{\rm e}^s, \ \dot{\pmb x}_{\rm e} (t = t_{\rm f} ) = \dot{\pmb x}_{\rm e}^{\rm f} \\ & \ddot{\pmb x}_{\rm e} (t = 0) = \ddot{\pmb x}_{\rm e}^s\\& {\pmb \theta }(t = 0) = {\pmb \theta}^s, \ \dot {\pmb \theta }(t = 0) = \dot {\pmb \theta }^s, \ddot {\pmb \theta }(t = 0) = \ddot{\pmb \theta }^s \\ & \dot{\pmb \theta }_{\min } \leqslant \dot {\pmb \theta } \leqslant \dot{\pmb \theta }_{\max } , \ \ddot{\pmb \theta }_{\min } \leqslant \ddot{\pmb \theta } \leqslant \ddot{\pmb \theta }_{\max } \end{array}\!\!\right\}$
式中,目标函数 $f({\pmb x}_{\rm e} )$ 为由 RRT* 算法给出的路径点的位置函数,保证路径点位置与样条曲线中的位置匹配. 规划过程中,还需要满足末端执行器的初末状态约束,以及机械臂关节物理极限约束.
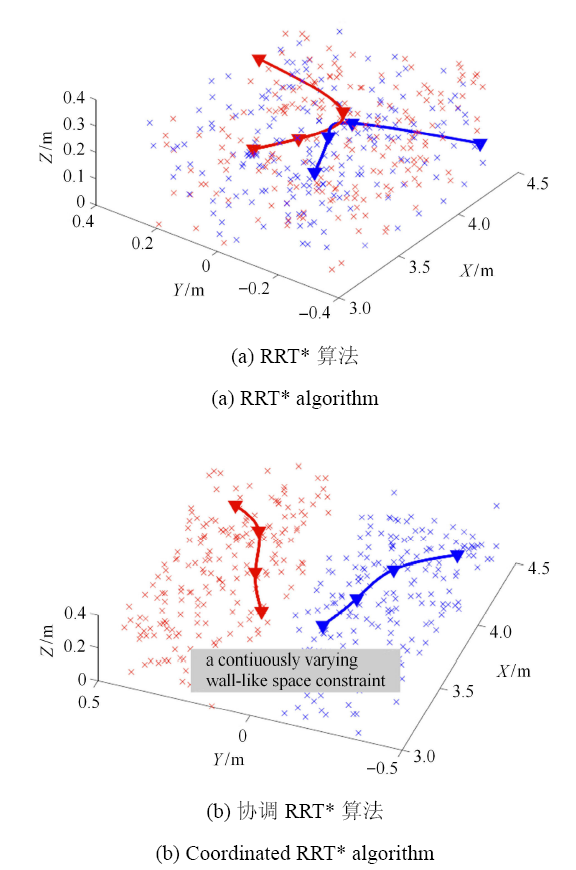
基于 RRT* 算法,在非结构化环境中生成若干可行路径点,再由四次样条曲线拟合这些路径点,即可得到平滑可行的机器人路径,本文所提的路径规划算法,效果如图 3 所示. 其中,红色曲线是原始 RRT* 算法生成的路径,蓝色曲线是由 RRT* 结合 样条设计生成的路径,可以明显看出所提算法生成的路径不仅平滑,而且极大地保留了原 RRT* 生成路径的最优性.此外,图 4 验证了所提路径规划算法的协调性,基于分离的采样空间,有效地避免了可能发生的碰撞.
图3
图3
RRT* 结合四次样条路径规划示意图
Fig.3
Sketch of spline-RRT* algorithm
图4
图4
协调 RRT* 路径规划示意图
Fig.4
Sketch of coordinated RRT* algorithm
3 仿真结果
为验证所提协调路径规划方法的有效性,本章给出了采用运动学冗余双机械臂抓捕空间目标的演 示实例,如图 5 所示.表 2 给出了本文所用双臂空间机器人的运动学和动力学参数,两机械臂参数相同.
图5
图5
空间机器人抓捕目标示意图
Fig.5
Sketch of capturing task by space robot
假设基座的初始位姿是 0,末端执行器的初始位姿分别为
$\begin{array}{l} x_{\rm e}^{\rm as} = \Big (3.556, - 0.101,0.168, - \dfrac{\pi }{2},0,\dfrac{\pi }{4}\Big ) \\ x_{\rm e}^{\rm bs} = \Big (3.556,0.101,0.168,\dfrac{\pi }{2},0, - \dfrac{\pi }{4}\Big ) \\ \end{array} $
$\begin{array}{l} x_{\rm e}^{\rm af} = \Big (4.271, - 0.365, 0.168, - \dfrac{\pi }{2}, 0, \dfrac{\pi }{6} \Big) \\ x_{\rm e}^{\rm bf} = \Big (4,271,0.365,0.168,\dfrac{\pi }{2},0, - \dfrac{\pi }{6} \Big) \end{array} $
注意,本文所提的基于 RRT* 路径规划方法只用于末端执行器的位置规划,对于其姿态规划,仍采用前期工作中[33 ] 的用到的 Bézier 曲线. 基于五阶 Bézier 曲线,规划末端执行器在笛卡尔空间下的姿态路径 ${\pmb x}(t)$,描述如下
(10) $x_i (\tau ) = \sum_{j = 0}^m b_{j,m} (\tau )P_{ij} = \sum_{j = 0}^m \left(\!\!\begin{array}{c} m \\ j \end{array} \!\! \right)(1 - \tau )^{m - j}\tau ^jP_{ij}$
其中,多项式 $ b_{j,m} (\tau ) $ 是 $m$ 阶 Bernstein 基本多项式,$\left(\!\! \begin{array}{c} m \\ j \end{array} \!\! \right) $是二项式系数. $P_{ij}$ 是给定构建 Bézier 曲线的控制点.
给定末端的初末位姿,考虑机械臂的速度以及加速度限制条件,可以计算出规划路径的执行时间
(11) $T \geq \max \Bigg ( \dfrac{| \dot{\bar{\pmb x}}_{\max} |} {\dot{\pmb x}_{\max}} , \ \sqrt{\dfrac{| \ddot{\bar{\pmb x}}_{\max} | } {\ddot{\pmb x}_{\max}}} \Bigg )$
图 6 给出了由规划的末端执行器的路径,以及路径的执行速度. 可以看出,规划的末端路径较为平滑,且速度保持在机器人末端执行速度的最大限制范围 (0.1m/s) 内,且路径的初始速度、加速度和终止速度都为零,符合所 设计的情况,由此说明了规划路径的有效性.
图6
图6
规划的末端执行器的路径及其速度
Fig.6
Planned path and velocity for end-effectors
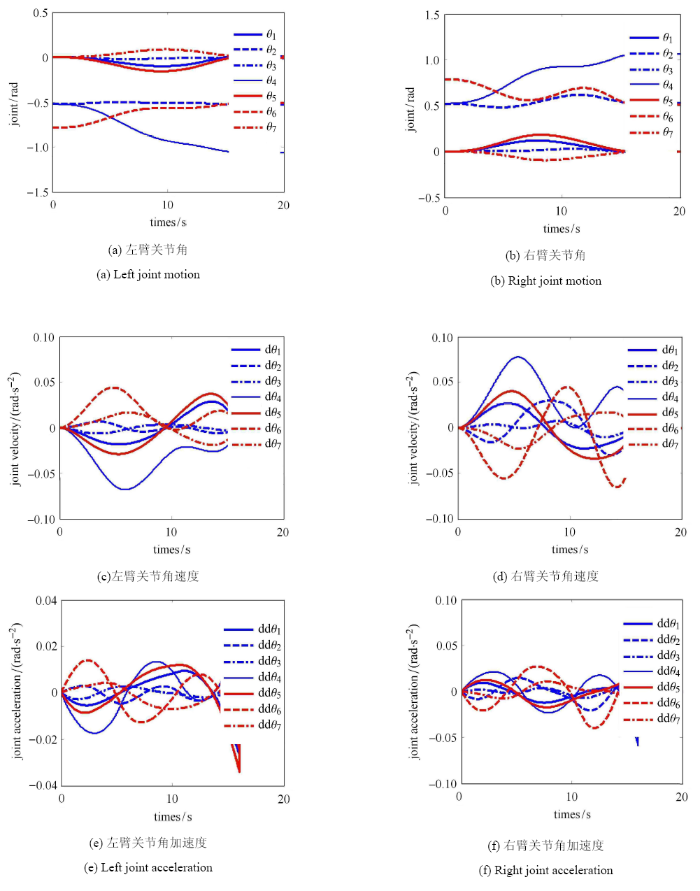
图 7 给出了机械臂执行所规划路径过程中,机械臂关节角、关节角速度以及关节角加速度的变化曲线. 可以看出,各机械臂的关节角、关节角速度以 及关节角加速度变化平滑,且速度和加速度大小均被限制在给定范围内,分别是 0.1rad/s 和 0.1rad/s$^{2}$,且关节角速度和关节角加速度初始为零,符合实际情况.
图7
图7
各机械臂关节变化曲线
Fig.7
Joint angle, velocity and acceleration
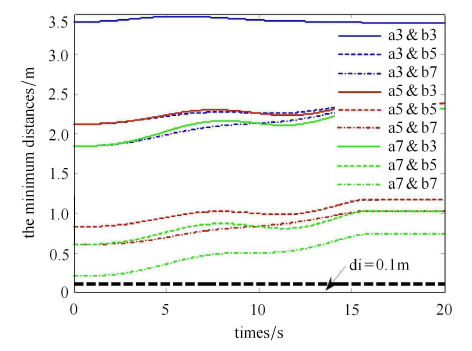
图 8 给出了机械臂末端执行器的实际跟踪误差曲线. 可以看出,整个执行过程中,末端执行器的实际跟踪误差保持在 10$^{-4}$ 量级,由此说明,末端能够跟踪上规划的路径,证明了所设计的规划算法的正确性.此外,机械臂各连杆在执行过程中亦未发生碰撞,各部件均保持在安全距离 ($d_{i} =0.1$m) 以外,如图 9 所示.
图8
图8
末端执行器的跟踪误差
Fig.8
Tracking error of end-effectors
图9
图9
机械臂各连杆之间的相对距离
Fig.9
The minimum distance between robot links
4 结论
考虑到安全性和最优性因素,本文提出了一种双臂空间机器人协调路径规划方法. 基于 RRT* 算法在非结构化环境中快速生成末端执行器安全可行的初始路径,并利用四次样条曲线,平滑了由 RRT* 生成的初始路径,保证机器人以良好的状态执行规划的路径,同时考虑了机械臂末端以及关节的物理极限约束. 仿真结果说明了所提协调路径规划方法的有效性.
附录 A 双臂空间机器人运动学建模
双臂空间机器人各连杆质心和末端执行器的位置矢量可以表示为
(A1) ${\pmb r}_i^k = {\pmb p}_i^k + {\pmb a}_i^k = {\pmb r}_{\rm b} + {\pmb b}_{\rm b}^k + \sum_{j = 1}^{i - 1} ({\pmb a}_j^k + {\pmb b}_j^k ) + {\pmb a}_i^k $
(A2) ${\pmb p}_{\rm e}^k = {\pmb r}_{n_k }^k + {\pmb b}_{n_k }^k = {\pmb r}_{\rm b} + {\pmb b}_{\rm b}^k + \sum_{j = 1}^{n_k } ({\pmb a}_j^k + {\pmb b}_j^k )$
利用泊松公式 $\dot{\pmb r}={\pmb v}+{\pmb\omega}\times {\pmb r}$,空间机器人各连杆质心和末端执行器的线速度可以表示为
(A3) ${\pmb \upsilon}_i^k = \dot{\pmb r}_i^k = {\pmb \upsilon}_{\rm b} + {\pmb \omega}_{\rm b} \times \left( {{\pmb r}_i^k - {\pmb r}_{\rm b} } \right) + \sum_{j = 1}^i {\left[ {{\pmb k}_j^k \times \left( {{\pmb r}_i^k -{\pmb p}_j^k } \right)} \right]\dot{\pmb \theta }_j^k } $
(A4) $ {\pmb \upsilon}_{\rm e}^k = \dot{\pmb p}_{\rm e}^k = {\pmb \upsilon}_{\rm b} + {\pmb \omega}_{\rm b} \times \left( {{\pmb p}_{\rm e}^k - {\pmb r}_{\rm b} } \right) + \sum_{j = 1}^{n_k } {\left[ {{\pmb k}_j^k \times \left( {{\pmb p}_{\rm e}^k - {\pmb p}_j^k } \right)} \right]\dot{\pmb \theta }_j^k } $
(A5) ${\pmb \omega} _i^k = {\pmb \omega} _{\rm b}+ \sum_{j = 1}^i {\pmb k}_j^k \dot {\pmb \theta }_j^k $
(A6) ${\pmb \omega }_{\rm e}^k = {\pmb \omega }_{\rm b} + \sum_{j = 1}^{n_k } {\pmb k}_j^k \dot {\pmb \theta }_j^k $
(A7) $\left[ \!\! \begin{array}{l} {\pmb \upsilon }_{\rm e}^k \\ {\pmb \omega }_{\rm e}^k \end{array} \!\! \right] = J_{\rm b}^k \left[\!\! \begin{array}{l} {\pmb \upsilon }_{\rm b} \\ {\pmb \omega }_{\rm b} \end{array} \!\! \right] + J_{\rm e}^k \dot {\theta }^k$
$\begin{array}{l} {\pmb J}_{\rm b}^k = \left[ \begin{array}{c} {\pmb J}_{\rm bv}^k \\ {\pmb J}_{\rm b\omega }^k \end{array} \right] = \left[ \begin{array}{cc} {\pmb E}_3 & - \tilde{\pmb p}_{\rm be}^k \\ 0 & {\pmb E}_3 \end{array} \right] \in {\pmb R}^{ 6\times 6} \\ {\pmb p}_{\rm be}^k = {\pmb p}_{\rm e}^k - {\pmb r}_{\rm b} \\ {\pmb J}_{\rm e}^k = \left[ \begin{array}{c} {\pmb J}_{\rm ev}^k \\ {\pmb J}_{\rm e\omega }^k \end{array} \right] \in {\pmb R }^{6\times n_k } \end{array} $
${\pmb J}_{\rm b}^k $ 为与基座运动相关的雅可比矩阵,${\pmb J}_{\rm bv}^k $, ${\pmb J}_{\rm b\omega }^k $ 为 ${\pmb J}_{\rm b}^k $ 的分块矩阵,分别对应基座的线速度和角速度. ${\pmb J}_{\rm e}^k $ 为与机械臂运动相关的雅克比矩阵,类似地, ${\pmb J}_{\rm ev}^k $,${\pmb J}_{\rm e\omega }^k $ 为矩阵 ${\pmb J}_{\rm e}^k $ 的分块矩阵.
记$\dot{\pmb x}_{\rm e}^k = \left[\!\! \begin{array}{l} {\pmb \upsilon}_{\rm e}^k \\ {\pmb \omega}_{\rm e}^k \end{array} \!\! \right]$, $\dot {\pmb x}_{\rm b} = \left[\!\! \begin{array}{l} {\pmb \upsilon }_{\rm b} \\ {\pmb \omega} _{\rm b} \end{array} \!\! \right]$,当 $k=2$ 时 (即双臂情形),式 (A7) 表达如下
(A8) $\left[\begin{array}{c} \dot{\pmb x}^a_{\rm e} \\ \dot{\pmb x}^b_{\rm e} \end{array} \right]= \left[\begin{array}{c} {\pmb J}^a_{\rm b}+ {\pmb J}^a_{\rm e} \dot{\pmb\theta}^a \\ {\pmb J}^b_{\rm b}+ {\pmb J}^b_{\rm e} \dot{\pmb\theta}^b \end{array} \right] $
其中,上标 $a$ 和 $b$ 分别表示变量属于机械臂 $a$ 和 $b$.
附录B 双臂空间机器人动力学建模
基于拉格朗日方程进行自由漂浮双臂空间机器人的动力学建模,第二类拉格朗日方程如下式所示
(B1) $\dfrac{\text{d}}{\text{d}t} \Big ( \dfrac{\partial L}{\partial \dot q_i} \Big )-\dfrac{\partial L}{\partial q_i}=0 \ \ (i=1,2,\cdots,k) $
其中,$q_i$ 为描述系统位形的独立的广义坐标,$L$ 称为拉格朗日函数,与系统的动能 $T$ 以及势能 $V$ 满足关系
(B2) L=T-V
双臂空间机器人系统处于空间微重力环境中,因此 $V=0$,双臂空间机器人系统的动能包括基座和各连杆运动产生的动能
(B3) $ T = \sum_{i = 0}^{n_{\rm a} + n_{\rm b} } T_i = \sum_{i = 0}^{n_{\rm a} + n_{\rm b} } \Big(\dfrac{1}{2}m_i \dot {\pmb r}_i \cdot \dot {\pmb r}_i + \dfrac{1}{2}\omega _i \cdot {\pmb I}_i \cdot {\pmb \omega }_i \Big ) =\\ \qquad \dfrac{1}{2}m_{\rm b} \dot{\pmb r}_{\rm b}^{\rm T}\dot{\pmb r}_{\rm b} + \dfrac{1}{2}{\pmb \omega }_{\rm b}^{\rm T}{\pmb I}_{\rm b} {\pmb \omega}_{\rm b} + \\ \qquad \sum_{i = 1}^{n_{\rm a} } \left( {\dfrac{1}{2}m_i^a \left( {\dot{\pmb r}_i^a } \right)^ {\rm T}\dot{\pmb r}_i^a + \dfrac{1}{2}\left( {{\pmb \omega}_i^a } \right)^T{\pmb I}_i^a {\pmb \omega}_i^a } \right) + \\ \qquad \sum_{i = 1}^{n_{\rm b} } \left( {\dfrac{1}{2}m_i^b \left( {\dot {\pmb r}_i^b } \right)^{\rm T}\dot{\pmb r}_i^b + \dfrac{1}{2}\left( {{\pmb \omega} _i^b } \right)^{\rm T}{\pmb I}_i^b {\pmb \omega}_i^b } \right) $
$将式 (A3) 和式 (A5) 代入上式,得到紧凑形式的双臂空间机器人动能表达式
(B4) $ T = \dfrac{1}{2}\left[ {\pmb v}_{\rm b}^{\rm T} \ \ {\pmb \omega}_{\rm b}^{\rm T} \ \ \left( {\dot {\pmb\theta}^a} \right)^{\rm T} \ \ \left( {\dot {\pmb\theta }^b} \right)^ {\rm T} \right]\cdot \\ \qquad \left[ \begin{array}{cccc} M {\pmb E}_3 & M \tilde {\pmb r}_{0s}^{\rm T} & {\pmb J}_{\rm T\omega }^a & {\pmb J}_{\rm T\omega }^b \\ M \tilde {\pmb r}_{0s} & {\pmb H}_\omega & {\pmb H}_{\omega \phi }^a & {\pmb H}_{\omega \phi }^b \\ {\pmb J}_{T\omega }^{a\rm T} & {\pmb H}_{\omega \phi }^{a\rm T} & {\pmb H}_{\rm m}^a & {\bf 0}_{\rm n} \\ {\pmb J}_{\rm T\omega }^{b\rm T} & {\pmb H}_{\omega \phi }^{b\rm T} & {\bf 0}_{\rm n} & {\pmb H}_{\rm m}^b \end{array} \right]\left[ \begin{array}{c} {{\pmb v}_{\rm b} } \\ {{\pmb\omega}_{\rm b} } \\ {\dot {\theta }^a} \\ {\dot {\theta }^b} \end{array} \right] =\\ \qquad \dfrac{1}{2}\left[ { \dot {\pmb x}_{\rm b}^{\rm T} } \ \ {\left( {\dot {\pmb \theta }^a} \right)^ {\rm T} } \ \ {\left( {\dot {\pmb \theta }^b} \right)^{\rm T}} \right] \left[ \begin{array}{ccc} {\pmb H}_{\rm b } & {\pmb H}_{\rm bm}^a & {\pmb H}_{\rm bm}^b \\ {{\pmb H}_{\rm bm}^{a\rm T} } & {{\pmb H}_{\rm m}^a } & {{\pmb 0}_{\rm n} } \\ {{\pmb H}_{\rm bm}^{b\rm T} } & {{\pmb 0}_{\rm n} } & {{\pmb H}_{\rm m}^b } \end{array} \right]\left[ \begin{array}{c} { \dot {\pmb x}_{\rm b} } \\ {\dot {\pmb \theta }^a} \\ {\dot {\pmb \theta }^b} \end{array} \right] $
对于空间机器人系统,$L=T$,代入式 (B3) 表示的拉格朗日方程,可以得到双臂空间机器人的一般动力学方程
(B5) $ \left[\!\!\begin{array}{ccc} {\pmb H}_{\rm b} & {\pmb H}_{\rm bm}^a & {\pmb H}_{\rm bm}^b \\ {\pmb H}_{\rm bm}^{a\rm T} & {\pmb H}_{\rm m}^a & {\bf 0}_{\rm n} \\ {\pmb H}_{\rm bm}^{b\rm T} & {\bf 0}_{\rm n} & {\pmb H}_{\rm m}^b \end{array} \!\!\right] \left [ \!\!\begin{array}{ccc} \ddot{\pmb x}_{\rm b} \\ \ddot{\pmb \theta}^a \\ \ddot{\pmb\theta}^b \end{array}\!\!\right] +\left[\!\! \begin{array}{ccc}{\pmb c}_{\rm b} \\ {\pmb c}_{\rm m}^a \\ {\pmb c}_{\rm m}^b \end{array}\!\!\right]= \\ \qquad \left[ \begin{array}{ccc} {\pmb f}_{\rm b} \\ {\pmb\tau}^a_{\rm m} \\ {\pmb\tau}^b_{\rm m} \end{array}\!\!\right]+ \left[\!\!\begin{array}{cc} {\pmb J}^{ aT}_{\rm b} & {\pmb J}^{ bT}_{\rm b} \\ {\pmb J}^{ a\rm T}_{\rm e} & {\bf 0}_{n\times 6} \\ {\bf 0}_{n\times 6} & {\pmb J}^{ b\rm T}_{\rm e} \end{array}\!\! \right] \left[\!\!\begin{array}{ccc} {\pmb f}^a_{\rm e} \\ {\pmb f}^b_{\rm e} \end{array}\!\!\right] $
其中,${\pmb c}_{\rm b}, {\pmb c}_{\rm m}^a, {\pmb c}_{\rm m}^b \in {\bf R}^6$ 分别为与基座、机械臂运动相关的非线性力,包括向心力和哥氏力;${\pmb f}_{\rm b} \in {\bf R}^6$为作用在基座上的外力和外力矩; ${\pmb\tau}^a_{\rm m}, {\pmb\tau}^b_{\rm m} \in {\bf R}^n$为机械臂关节的输入力矩;当机械臂末端执行器和目标发生碰撞时,${\pmb f}_{\rm e}^a , {\pmb f}_{\rm e}^b \in {\bf R}^6$为碰撞产生的外力和外力矩.
参考文献
View Option
[1]
Oda M Kibe K Yamagata F . Ets-vii, space robot in-orbit experiment satellite
// Proceedings of the 1996 IEEE International Conference on Robotics and Automation, Minnesota, USA , 1996 : 22 -28
[本文引用: 1]
[2]
Ogilvie A Allport J Hannah M , et al . Autonomous satellite serving using the orbital express demonstration manipulator system
// Proceedings of the 9th International Symposium on Artificial Intelligence, Robotics and Automation in Space , 2008
[本文引用: 1]
[3]
王明明 , 罗建军 , 余敏 等 . 冗余空间机械臂抓捕自旋卫星后的消旋控制
宇航学报 , 2018 ,39 (5 ):84 -95
[本文引用: 1]
( Wang Mingming Luo Jianjun Yu Min , et al . Detumbling control for kinematic redundant space manipulator post-grasping a rotational satellite
Journal of Astronautica 2018 ,39 (5 ):84 -95 (in Chinese))
[本文引用: 1]
[4]
宗立军 , 罗建军 , 王明明 等 . 自由漂浮空间机器人多约束混合整数预测控制
宇航学报 , 2016 ,37 (8 ):992 -1000
DOI
URL
针对空间机器人完成任务时需要躲避障碍物的问题,提出一种自由漂浮空间机器人的混合整数预测控制方法。首先,在模型预测控制方法框架下,机械臂关节的物理限制,躲避障碍物的要求被统一描述为最优控制问题下的不等式约束,可以得到自由漂浮空间机器人具有线性二次规划形式的最优控制律。其次,基于命题逻辑建立控制问题中各约束的优先级,保证在最大程度地满足约束的情形下得到控制问题的解,有效弥补了模型预测控制方法用于空间机器人控制时,多约束可能导致最优控制问题不可行的不足。最后,仿真结果校验了所设计控制律的有效性。
( Zong Lijun Luo Jianjun Wang Mingming , et al . A mixed integer predictive controller with multi-constraint for free-floating space robots
Journal of Astronautica 2016 ,37 (8 ):992 -1000 (in Chinese))
DOI
URL
针对空间机器人完成任务时需要躲避障碍物的问题,提出一种自由漂浮空间机器人的混合整数预测控制方法。首先,在模型预测控制方法框架下,机械臂关节的物理限制,躲避障碍物的要求被统一描述为最优控制问题下的不等式约束,可以得到自由漂浮空间机器人具有线性二次规划形式的最优控制律。其次,基于命题逻辑建立控制问题中各约束的优先级,保证在最大程度地满足约束的情形下得到控制问题的解,有效弥补了模型预测控制方法用于空间机器人控制时,多约束可能导致最优控制问题不可行的不足。最后,仿真结果校验了所设计控制律的有效性。
[5]
付晓东 , 陈力 . 全柔性空间机器人运动振动一体化输入受限重复学习控制
力学学报 , 2020 ,52 (1 ):171 -183
( Fu Xiaodong Chen Li . An input limited repetitive learning control of flexible-base two-flexible-link and two-flexible-joint space robot with integration of motion and vibration
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):171 -183 (in Chinese))
[6]
朱安 , 陈力 . 配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
力学学报 , 2019 ,51 (2 ):1156 -1169
( Zhu An Chen Li . Mechanical simulation and full ordered sliding mode collision avoidance compliant control based on neural network of dual-arm space robot with compliant mechanism capturing satellite
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):1156 -1169 (in Chinese))
[7]
葛一敏 , 袁海辉 . 基于步态切换的欠驱动双足机器人控制方法
力学学报 , 2018 ,50 (2 ):871 -879
[本文引用: 1]
( Ge Yimin Yuan Haihui . Control method of an underactuated biped robot based on gait transition
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):871 -879 (in Chinese))
[本文引用: 1]
[8]
Yoshida K Hashizume K Abiko S . Zeros reaction maneuver: flight validation with ets-vii space robot and extension to kinematically redundant arm
// Proceedings of the 2001 IEEE International Conference on Robotics and Automation. Seoul, Korea , 2001 : 21 -26
[本文引用: 1]
[9]
Wang MM Luo JJ Walter U . Novel synthesis method for minimizing attitude disturbance of the free-floating space robots
Journal of Guidance, Control, and Dynamics 2016 ,39 (1 ):695 -704
[本文引用: 1]
[10]
Wang MM Luo JJ Yuan JP , et al . Detumbling strategy and coordination control of kinematically redundant space robot after capturing a tumbling target
Nonlinear Dynamics 2018 ,92 (1 ):1023 -1043
[11]
Wang MM Luo JJ Yuan JP , et al . An integrated control scheme for space robot after capturing non-cooperative target
Acta Astronautica 2018 ,147 :350 -363
[12]
Wang MM Luo JJ Yuan JP , et al . Coordinated trajectory planning of dual-arm space robot using constrained particle swarm pptimization
Acta Astronautica 2018 ,146 :259 -272
DOI
URL
[13]
Wang MM Luo JJ Fang J , et al . Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm
Advances in Space Research 2018 ,61 (4 ):1525 -1536
DOI
URL
[本文引用: 1]
[14]
罗建军 , 薛爽爽 , 马卫华 等 . 空间机器人抓捕目标后动力学参数辨识研究
宇航学报 , 2016 ,37 (12 ):1411 -1418
URL
[本文引用: 1]
( Luo Jianjun Xue Shuangshuang Ma Weihua , et al . Dynamic parameter identification of free-floating space robots after capturing targets
Journal of Astronautica 2016 ,37 (12 ):1411 -1418 (in Chinese))
URL
[本文引用: 1]
[15]
Xu WF Li C Wang X , et al . Study on non-holonomic cartesian path planning of a free-floating space robotic system
Advanced Robot 2009 ,23 (12 ):113 -143
DOI
URL
[本文引用: 1]
[16]
Nakamura Y Hanafusa H Yoshikawa T . Task-priority based redundancy control of robot manipulators
International Journal of Robotics Research 1987 ,6 (2 ):3 -15
[本文引用: 1]
[17]
戈新生 , 陈凯捷 . 自由漂浮空间机器人路径优化的 Legendre 伪谱法
力学学报 , 2016 ,48 (2 ):823 -831
[本文引用: 1]
( Ge Xinsheng Chen Kaijie . Path planning of free floating space robot using legendre pseudospectral method
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (2 ):823 -831 (in Chinese))
[本文引用: 1]
[18]
程靖 , 陈力 . 空间机器人双臂捕获卫星力学分析及镇定控制
力学学报 , 2016 ,48 (2 ):832 -842
[本文引用: 1]
( Cheng Jing Chen Li . Mechanical analysis and calm control of dual-arm space robot for capturing a satellite
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (2 ):832 -842 (in Chinese))
[本文引用: 1]
[19]
Salehian SSM Figueroa N Billard A . A unified framework for coordinated multi-arm motion planning
The International Journal of Robotics Research 2018 ,37 (7 ):1 -25
[本文引用: 1]
[20]
杨冬 , 李继强 , 董跃巍 等 . 冗余双臂机器人实时协调避碰方法研究
机械设计与制造 , 2019 ,337 (3 ):43 -47
[本文引用: 1]
( Yang Dong Li Jiqiang Dong Yuewei , et al . Research on real-time coordinating collision-avoidance of redundant dual-arm robot
Machinery Design and Manufacture 2019 ,337 (3 ):43 -47 (in Chinese))
[本文引用: 1]
[21]
方健 . 冗余双臂机器人在线运动规划与协调操作方法研究
[博士论文]. 合肥:中国科学技术大学 , 2016
[本文引用: 1]
( Fang Jian . Research on online motion planning and cooperative operation method for the redundant dual-arm manipulator
[PhD Thesis]. Hefei: University of Science and Technology of China , 2016 (in Chinese))
[本文引用: 1]
[22]
LaValle SM . Rapidly-exploring random trees: A new tool for path planning
Computer Science 1998 ,98 (11 ):1 -4
[本文引用: 1]
[23]
Vahrenkamp N Do M Asfour T , et al . Integrated grasp and motion planning
// IEEE International Conference on Robotics and Automation , 2010
DOI
URL
PMID
[本文引用: 1]
This paper presents algorithms for optimal selection of needle grasp, for autonomous robotic execution of the minimally invasive surgical suturing task. In order to minimize the tissue trauma during the suturing motion, the best practices of needle path planning that are used by surgeons are applied for autonomous robotic surgical suturing tasks. Once an optimal needle trajectory in a well-defined suturing scenario is chosen, another critical issue for suturing is the choice of needle grasp for the robotic system. Inappropriate needle grasp increases operating time requiring multiple re-grasps to complete the desired task. The proposed methods use manipulability, dexterity and torque metrics for needle grasp selection. A simulation demonstrates the proposed methods and recommends a variety of grasps. Then a realistic demonstration compares the performances of the manipulator using different grasps.
[24]
James F Shah SV Singh AK , et al . Reactionless maneuvering of a space robot in pre-capture phase
Journal of Guidance, Control, and Dynamics 2016 ,39 (7 ):2419 -2425
DOI
URL
[本文引用: 1]
[25]
Lin CS Chang PR Luh J . Formulation and optimization of cubic polynomial joint trajectories for industrial robots
IEEE Transactions on Automatic Control 1983 ,28 (12 ):1066 -1074
[本文引用: 1]
[26]
Kolter JZ Ng AY . Task-space trajectories via cubic spline optimization
// IEEE International Conference on Robotics and Automation , 2009
URL
PMID
[本文引用: 1]
[27]
Vaz AIF Fernandes EM . Tools for robotic trajectory planning using cubic splines and semi-infinite programming
Recent Advances in Optimization 2006 : 399 -413
[本文引用: 1]
[28]
赵皓 , 刘满禄 , 张华 . 基于三次非均匀B样条的 6DOF 机械臂轨迹规划
机器人技术与应用 , 2016 ,(6 ):43 -48
[本文引用: 1]
( Zhao Hao Liu Manlu Zhang Hua . Cubic non-uniform B-spline method for 6DOF manipulator trajectory planning
Robotic Technology and Application 2016 ,(6 ):43 -48 (in Chinese))
[本文引用: 1]
[29]
赖永林 , 林茂松 , 梁艳阳 . 基于三次非均匀 B 样条曲线的机器人轨迹规划算法研究
科学技术与工程 , 2013 ,13 (35 ):10511 -10517
[本文引用: 1]
( Lai Yongsong Lin Maosong Liang Yanyang . Research on robotic trajectory planning by using cubic non-uniform B-spline method
Science Technology and Engineering 2013 ,13 (35 ):10511 -10517 (in Chinese))
[本文引用: 1]
[30]
Xu W Hu Z Zhang Y , et al . On-orbit identifying the inertia parameters of space robotic systems using simple equivalent dynamics
Acta Astronautica 2017 ,132 :131 -142
DOI
URL
[本文引用: 1]
[31]
支希哲 . 理论力学 . 北京 : 高等教育出版社 , 2010
[本文引用: 1]
( Zhi Xizhe . Theoretical Mechanics . Beijing : Higher Education Press , 2010 (in Chinese))
[本文引用: 1]
[32]
Karaman S Frazzoli E . Sampling-based algprothms for optimal motion planning
The International Journal of Robotics Research 2011 ,30 (5 ):846 -894
DOI
URL
[本文引用: 1]
[33]
Luo JJ Yu M Wang MM , et al . A fast trajectory planning framework with task-priority for space robot
Acta Astronautica 2018 ,152 :823 -835
DOI
URL
[本文引用: 1]
Ets-vii, space robot in-orbit experiment satellite
1
1996
... 随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] . ...
Autonomous satellite serving using the orbital express demonstration manipulator system
1
2008
... 随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] . ...
冗余空间机械臂抓捕自旋卫星后的消旋控制
1
2018
... 随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] . ...
冗余空间机械臂抓捕自旋卫星后的消旋控制
1
2018
... 随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] . ...
自由漂浮空间机器人多约束混合整数预测控制
2016
自由漂浮空间机器人多约束混合整数预测控制
2016
全柔性空间机器人运动振动一体化输入受限重复学习控制
2020
全柔性空间机器人运动振动一体化输入受限重复学习控制
2020
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
2019
配置柔顺机构空间机器人双臂捕获卫星操作力学模拟及基于神经网络的全阶滑模避撞柔顺控制
2019
基于步态切换的欠驱动双足机器人控制方法
1
2018
... 随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] . ...
基于步态切换的欠驱动双足机器人控制方法
1
2018
... 随着在轨维修、空间装配等任务需求的与日俱增,空间机器人技术被验证是执行特殊恶劣空间环境下任务最有效的手段之一. 典型实例有 "工程试验卫星 (engineering test satellite VII, ETS-VII)"[1 ] 和 "轨道快车 (orbit express, OE)"[2 ] . 空间机器人在轨服务任务中最具挑战性的工作之一是其抓捕过程中的运动规划问题[3 -7 ] . ...
Zeros reaction maneuver: flight validation with ets-vii space robot and extension to kinematically redundant arm
1
2001
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
Novel synthesis method for minimizing attitude disturbance of the free-floating space robots
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
Detumbling strategy and coordination control of kinematically redundant space robot after capturing a tumbling target
2018
An integrated control scheme for space robot after capturing non-cooperative target
2018
Coordinated trajectory planning of dual-arm space robot using constrained particle swarm pptimization
2018
Optimal trajectory planning of free-floating space manipulator using differential evolution algorithm
1
2018
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
空间机器人抓捕目标后动力学参数辨识研究
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
空间机器人抓捕目标后动力学参数辨识研究
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
Study on non-holonomic cartesian path planning of a free-floating space robotic system
1
2009
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
Task-priority based redundancy control of robot manipulators
1
1987
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
自由漂浮空间机器人路径优化的 Legendre 伪谱法
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
自由漂浮空间机器人路径优化的 Legendre 伪谱法
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
空间机器人双臂捕获卫星力学分析及镇定控制
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
空间机器人双臂捕获卫星力学分析及镇定控制
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
A unified framework for coordinated multi-arm motion planning
1
2018
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
冗余双臂机器人实时协调避碰方法研究
1
2019
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
冗余双臂机器人实时协调避碰方法研究
1
2019
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
冗余双臂机器人在线运动规划与协调操作方法研究
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
冗余双臂机器人在线运动规划与协调操作方法研究
1
2016
... 过去的文献中已提出过多种空间机器人运动规划方法. 基于零作用空间,Yoshida 等[8 ] 提出了无反作用机械臂,解决了运动学非冗余臂和冗余臂考虑时间最少和机械臂速度限制的规划问题. 基于零反作用空间的概念,Wang 等[9 -13 ] 提出了一种考虑任务优先级的运动学冗余机械臂路径规划方法,并基于 Bézier 曲线提出抓捕自旋卫星后的最优消旋与路径规划策略. 罗建军等[14 ] 提出了一种利用傅里叶级数对空间机械臂关节运动轨迹进行参数化的规划方法. Xu 等[15 ] 利用自由漂浮空间机器人非完整特性提出了一种点到点的路径规划方法,同时调节基座姿态和末端的位姿. Nakamura 等[16 ] 最早在机器人学中引入了任务优先级的概念,基于二次规划框架,仅考虑两个优先级水平,解决了冗余机械臂关节轨迹优 化问题. 戈新生等[17 ] 基于 Legendre 伪谱法研究自由漂浮空间机器人非完整路径规划的最 优控制问题. 程靖等[18 ] 分析了双臂空间机器人捕获卫星的力学,并研究其镇定控 制问题. Salehian 等[19 ] 研究了双臂机器人的协调操作机制与自碰撞规避策略. 杨冬等[20 ] 研究了冗余双臂机器人的实时协调避碰方法. 方健[21 ] 研究双臂机器人的在线运动规划与协调操作方法. ...
Rapidly-exploring random trees: A new tool for path planning
1
1998
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
Integrated grasp and motion planning
1
2010
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
Reactionless maneuvering of a space robot in pre-capture phase
1
2016
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
Formulation and optimization of cubic polynomial joint trajectories for industrial robots
1
1983
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
Task-space trajectories via cubic spline optimization
1
2009
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
Tools for robotic trajectory planning using cubic splines and semi-infinite programming
1
2006
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
基于三次非均匀B样条的 6DOF 机械臂轨迹规划
1
2016
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
基于三次非均匀B样条的 6DOF 机械臂轨迹规划
1
2016
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
基于三次非均匀 B 样条曲线的机器人轨迹规划算法研究
1
2013
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
基于三次非均匀 B 样条曲线的机器人轨迹规划算法研究
1
2013
... 近年来,非结构化环境下的机器人自主导航控制技术成为亟需. 基于随机采样的规划方法在机器人领域中兴起,它适合于解决高自由度机器人在复杂环境中的规划问题,而且对带有微分约束的规划问题也具有较强的解 决能力. 例如,RRT 算法[22 ] ,其本质上是单一查询的规划方法,其基本算法的主要思想是:由起始位形点出发构造搜索树,而后再从整个位形空间中随机选择一个位形点,找出与该点在搜索树中最近的位形点,以此不断的产生新位形状态,直到到达目标,搜索树构造结束. 由于在搜索树构造过程中可以考虑多种微分约束 (如非完整约束、运动学及动力学约束等),因而获得的规划结果合理性较强. Vahrenkamp 等[23 ] 基于 RRT 算法,提出一种适用于地面双臂机器人的抓捕和运动规划策略. James 等[24 ] 将 RRT 方法应用于双臂空间机器人抓捕前阶段的路径规划过程中. 然而,基于 RRT 算法的运动规划方法产生的初始轨迹不平滑,不能直接应用于机器人运动规划过程中. 常见的平滑处理技巧有优化方法和样条曲线拟合技巧[25 ] 等,然而采用优化方法较为耗时. Kolter 等[26 ] 利用三次样条曲线设计四足机器人的在任务空间下的运动轨迹. Vaz 等[27 ] 结合三次样条和半无限规划方法进行机器人的轨迹规划. 基于三次非均匀 B 样条曲线,赵皓等[28 ] 和赖永林等[29 ] 分别进行 6DOF 机械臂和工业机器人的轨迹规划. 上述研究表明,样条函数是最有效的平滑处理技巧之一,且在机器人运动规划中得到广泛的成功应用. ...
On-orbit identifying the inertia parameters of space robotic systems using simple equivalent dynamics
1
2017
... 空间机器人建模方面的现有研究很成熟,根据泊松公式[30 ] ,空间机器人的运动学方程表示如下 ...
1
2010
... 根据第二类拉格朗日方程[31 ] ,空间机器人的动力学方程表示如下 ...
1
2010
... 根据第二类拉格朗日方程[31 ] ,空间机器人的动力学方程表示如下 ...
Sampling-based algprothms for optimal motion planning
1
2011
... 基于随机采样原理的快速搜索随机树方法具有概率完备性、计算量小、计算难度低等特点,非常适合空间自主航天器完成复杂空间的近距离操作服务任务. 此外,它对解决高维状态规划问题有着较强的适应性,这一能力是目前很多规划算法所不具备的,因此它非常适合空间机器人高维运动状态规划的实际情况. 鉴于 RRT* 算法不仅加快了原 RRT 算法的收敛速度,还增强了算法的最优性能,因此本文选取 RRT* 作为空间机器人路径规划的主要方法,这里简单给出 RRT* 算法的基本流程,关于 RRT* 算法的细则可以参考文献[32 ] . ...
A fast trajectory planning framework with task-priority for space robot
1
2018
... 注意,本文所提的基于 RRT* 路径规划方法只用于末端执行器的位置规划,对于其姿态规划,仍采用前期工作中[33 ] 的用到的 Bézier 曲线. 基于五阶 Bézier 曲线,规划末端执行器在笛卡尔空间下的姿态路径 ${\pmb x}(t)$,描述如下 ...