引言
运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] .
猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似.
火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣.
基于能量的方法具有简洁、对精细化的动力学模型依赖较少的优点,但是其结论较为保守,尤其是能量法将触地时所有动能均视为翻倒能,但动力学仿真表明,当着陆腿中含有塑性缓冲吸能材料时,着陆时竖直方向速度的大小对不翻倒对应的参数边界的影响较小[13 ] . 基于动力学仿真的方法及实验的方法结论更为准确,但是其分析过程对精细化的动力学模型较为依赖,而在重复使用火箭的方案设计初期确定着陆腿的几何参数时,由于对象尚未确定,往往难以建立精细的动力学模型,所以难以采用动力学仿真或实验的方法. 火箭着陆问题为含摩擦的多点碰撞问题,基于广义碰撞定律 (generalized impact law) 的运动学研究可以在方案设计初期,对着陆稳定性分析提供借鉴. 目前基于运动学方法对着陆器着陆稳定性的研究较少,Brogliato 等[27 ] 曾将广义碰撞定律应用于 Rocking Block 问题,讨论了黏滞和无摩擦状态下二维 Rocking Block 问题中碰撞后速度的取值范围.
Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性.
本文采用广义碰撞定律,根据单边约束条件和碰撞中的机械能损失,对平面运动着陆模式下火箭与平台碰撞中广义恢复系数的值域进行了探讨. 本文首先对火箭和平台建立刚体平面运动模型,将该种着陆模式下空间的四点碰撞问题简化为平面的两点碰撞问题,然后根据动力学方程和单边约束条件,给出了广义恢复系数的值域,然后讨论了黏滞、光滑和滑动摩擦条件下,Free Rocking 和 Half Rocking 两种碰撞后运动模式广义运动学恢复系数的值域,对于箭体与着陆平台完全非弹性碰撞的情况,给出了由其几何构型所决定的广义运动学恢复系数,最终提出了一种基于广义碰撞定律的着陆稳定性判别方法,简称 GKILSC 法 (generalized impact law based stable criterion method).
1 系统动力学模型
对于重复使用运载火箭的着陆过程,依据四条着陆腿是否存在同时落地,可以分为 4,2-2,1-2-1,1-1-1-1 共 4 种着陆模式,其中 4 模式表示 4 条着陆腿同时落地;2-2 模式表示先有两条腿同时落地,再有两条腿同时落地;1-2-1 模式表示先有 1 条腿落地,然后两条腿同时着地,最后再有 1 条腿落地,这里考虑了着陆腿的形变导致着陆过程中 4 条腿的着陆点不恒共面;1-1-1-1 模式表示 4 条腿不同时依次落地;其中 2-2 模式和 1-2-1 模式均为平面运动着陆模式,有研究通过三维动力学仿真表明,2-2 模式较 1-2-1 模式的稳定性更差[25 ] . 本文将针对 2-2 模式,基于刚体动力学研究其着陆的稳定性.
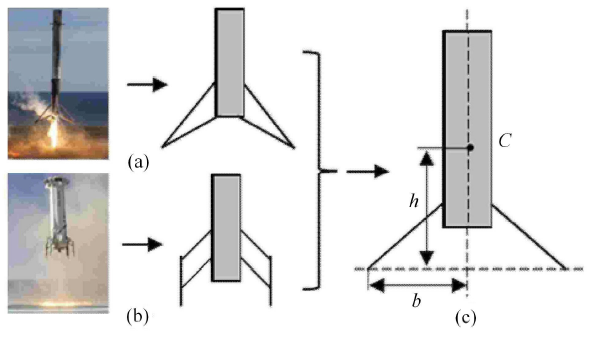
如图 1 所示,在 2-2 着陆模式下,形如太空探索技术公司的猎鹰 9 号火箭的倒三角式着陆腿 (a) 和型如蓝色起源太空公司的新谢泼德火箭的平行四边形式着陆腿 (b) 均可简化为图 1 中部所示的平面动力学模型,在采用刚体动力学分析时,两种模型可进一步简化为 (c) 所示的刚体平面运动的通用等效模型. 其质心 $C$ 距离着陆腿底部的轴向距离为 $h$,着陆腿跨距为 $2b$,质量为 $m$,绕过质心且垂直于运动平面的轴的转动惯量为 $J_{\rm c}$.
图1
图1
2-2 着陆模式的通用等效模型
Fig.1
Universal equivalent model of 2-2 landing mode
1.1 着陆过程动力学模型
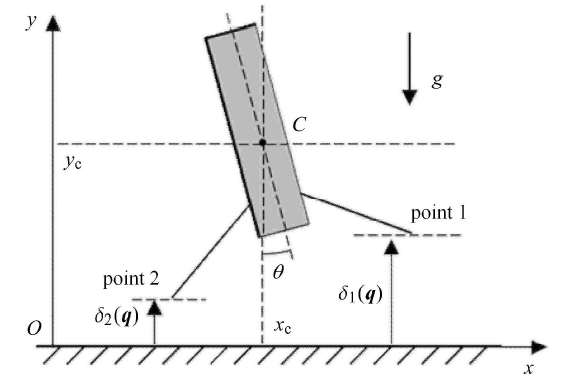
箭体与着陆平台的动力学模型如图 2 所示,其质心水平坐标为 $x_{\rm c} $,质心距着陆平台高 度为 $y_{\rm c}$,箭体倾角为 $\theta $,取描述系统的广义坐标 ${\pmb q} = \{x_{\rm c} ,y_{\rm c} ,\theta \}$,1 点、2 点与着陆平台的距离分别为 $\delta _1 ({\pmb q})$,$\delta _2 ({\pmb q})$.
图2
图2
运载火箭着陆的动力学模型
Fig.2
Dynamics model of RLV landing
(1) $\left.\!\!\begin{array}{l} \delta _1 ({\pmb q}) = y_{\rm c} - h\cos \theta + b\sin \theta \geqslant 0 \\ \delta _2 ({\pmb q}) = y_{\rm c} - h\cos \theta - b\sin \theta \geqslant 0 \end{array} \!\! \right\}$
箭体可能在 1 点和 2 点受到约束面的作用力,设 1 和 2 两点处的支 撑力为 $F_{{\rm n},1}$ 和 $F_{{\rm n},2} $,摩擦力为 $F_{{\rm f},1} $ 和 $F_{{\rm f},2}$,则系统的动力学方程为
(2) $\left.\begin{array}{l} m\ddot {x}_{\rm c} = F_{{\rm f},1} + F_{{\rm f},2} \\ m\ddot {y}_{\rm c} = F_{{\rm n},1} + F_{{\rm n},2} - m{\rm g} \\ J_{\rm c} \ddot {\theta } = (b\cos \theta + h\sin \theta )F_{{\rm n},1} + ( - b\cos \theta + h\sin \theta )F_{{\rm n},2} +\\ \qquad ( - b\sin \theta + h\cos \theta )F_{{\rm f},1} + (b\sin \theta + h\cos \theta )F_{{\rm f},2} \end{array} \!\!\right\}$
同时约束面作用力 $ F_{{\rm n},1}$ 和 $F_{{\rm n},2}$ 与 $\delta _1 $ 和 $\delta _2 $ 满足线性互补条件[32 -35 ]
(3) $0 \leqslant F_{{\rm n},i} \bot \delta _i \geqslant 0, \ \ i = 1,2$
1.2 切向力模型
诸多研究人员对碰撞中的摩擦现象提出了多种摩擦模型,例如库伦摩擦模型、库伦摩擦+黏性摩擦模型、Stribeck 摩擦模型等[40 ] ,本文采用经典库伦干摩擦模型,其摩擦力 $F_{{\rm f},i} $ 为
(4) $F_{{\rm f},i} \in - {\mu }F_{{\rm n},i} {\rm Sgn} (v_{\tau , i})$
其中,$F_{{\rm n},i } $ 为该点支撑力;$\mu $ 为摩擦系数;$v_{{\tau},i} $ 为碰撞两点切向的相对速度;$ {\rm Sgn}( \cdot )$ 为集值函数[35 ] .
对于碰撞过程中的切向冲量 $I_{{\tau}, i} = \int_{t - }^{t^ + } F_{{\rm f},i } \text{d}t $,在这里对碰撞过程中引入假设.
假设 1: 若碰撞结束后 $v_{{\tau}, i} (t^ +) \ne 0$,则在碰撞过程中 $v_ {{\tau}, i}$ 不连续为 0,且碰撞过程中始终有
$$F_{{\rm f},i} \in - \mu F_{{\rm n},i} {\rm Sgn} \left( v_{{\tau},i}(t^ + ) \right) $$
(5) $I_{{\tau},i} \in - \mu I_{{\rm n},i} {\rm Sgn}\left( {v_{{\tau},i} ( t^ + ) } \right)$
在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号.
2 基于广义碰撞定律的分析
2.1 广义碰撞定律
对于受到 $l$ 个单边约束的 $n$ 维 Lagrange 系统,该系统的广义坐标为 ${\pmb q}$,每个单边约束为 $\phi_i ({\pmb q}) \geqslant 0$, $1 \leqslant i \leqslant l$,同时系统具有对称正定的广义质量矩阵 ${\pmb M} ({\pmb q})$. 同时在该空间下对任意向量 ${\pmb \nu }_1 $,${\pmb \nu }_2 $ 定义内积 $\left\langle {{ \pmb \nu }_1 , {\pmb \nu }_2 } \right\rangle = {\pmb \nu }_1 ^{\rm T} {\pmb M}({\pmb q}){\pmb \nu }_2 $,则可定义每个单边约束的单位法向量
(6) ${\pmb n}_i = \dfrac{{\pmb M}({\pmb q})^{ - 1}\nabla \phi _i ({\pmb q})} {\sqrt {\nabla \phi _i ({\pmb q})^{\rm T}{\pmb M}({\pmb q})^{ - 1}\nabla \phi _i ({\pmb q})} }$
若这 $l$ 个单边约束互相独立,则在该 Lagrange 系统中共有 $l$ 个约束面的法 向量 $\{ {\pmb n}_1,{\pmb n}_2, \cdots , {\pmb n}_l \}$,且线性无关. 同时可找到 $n-l$ 个单位向量 ${\pmb t}_j $,满足正交性 ${\pmb n}_i ^{\rm T}{\pmb M}({\pmb q}){\pmb t}_j = 0$ 和单位性 ${\pmb t}_i ^{\rm T}{\pmb M}({\pmb q}){\pmb t}_j = \delta _{ij} $. 则可构造一组该 Lagrange 系统的基向量 $\{ {\pmb n}_1 , {\pmb n}_2,\cdots ,$${\pmb n}_l ,{\pmb t}_1 , {\pmb t}_2 , \cdots ,{\pmb t}_{n - l} \}$,对于该系统中的任意状态 $ {\pmb p}$,可由该组基表出 ${\pmb p} = c_1 {\pmb n}_1 + c_2 {\pmb n}_2 +\cdots + c_l {\pmb n}_l+ $ $d_1 {\pmb t}_1 + d_2 {\pmb t}_2+ \cdots + d_{n - l} {\pmb t}_{n - l} $,其中 $c_1 , c_2 , \cdots ,c_l \geqslant 0$,即该 Lagrange 系统为 $n$ 维空间的一个广义锥面. 定义原坐标到 $\{ {\pmb n}_1, {\pmb n}_2,\cdots ,{\pmb n}_l ,{\pmb t}_1 , {\pmb t}_2 , \cdots ,{\pmb t}_{n - l} \}$ 的坐标变换矩阵 $\varXi ({\pmb q})=({\pmb n}_1 , {\pmb n}_2 , \cdots ,{\pmb n}_l ,{\pmb t}_1 , {\pmb t}_2, \cdots ,{\pmb t}_{n - l} )^{\rm T}$,进一步定义广义法向速度 $ \dot{\pmb q}_{\rm n} $、广义切向速度 $\dot{\pmb q}_{\tau } $
(7) $\left( \!\! \begin{array}{c} \dot{\pmb q}_{\rm n} \\ \dot{\pmb q}_{\rm \tau } \end{array} \!\! \right) = {\pmb \varXi }({\pmb q}){\pmb M}({\pmb q})\dot{\pmb q}$
当约束面无摩擦时约束面无法提供切向力,设第 $i$ 个单边约束的法向约束力为 $F_{{\rm n},i} $,其虚功为 $\delta W_i = F_{{\rm n},i} \delta \phi _i ({\pmb q})$,进一步得系统受到的约束力的虚功 $\delta W = \delta {\pmb q}^{\rm T}\nabla \phi ({\pmb q}){\pmb F}_{\rm n} $ 和广义力 ${\pmb Q}_{\rm n} = \nabla \phi ({\pmb q}){\pmb F}_{\rm n} $. 其中 $\nabla \phi ({\pmb q})$ 为一个 $n\times l$ 维的矩阵,此外系统受到广义常规力 ${\pmb F}({\pmb q},\dot {\pmb q})$,如重力等. 则广义坐标下系统的动力学方程为 ${\pmb M}({\pmb q}) \ddot {\pmb q} = \nabla \phi ({\pmb q}){\pmb F}_{\rm n} + {\pmb F}({\pmb q},\dot {\pmb q})$. 在 $t$ 时刻系统发生碰撞,$t^{-}$ 表示碰撞开始时刻,$t^{ + }$ 表示碰撞结束时刻,则碰撞过程中有
(8) $\int_{t^ - }^{t^ + } {\pmb M}({\pmb q}) \ddot{\pmb q} \text{d}t = \int_{t - }^{t^ + } \left[ {\nabla \phi ({\pmb q}){\pmb F}_{\rm n} + {\pmb F}({\pmb q}, \dot{\pmb q})} \right] \text{d}t$
假设 2: 碰撞过程中,由于碰撞时间很短且广义速度 $ \dot {\pmb q}$ 有限,故系统构型 ${\pmb q}$ 碰撞前后变化很小,认为在碰撞过程中 ${\pmb q}$ 为定值,则在碰撞过程中 ${\pmb M}({\pmb q})$ 和 $\nabla \phi ({\pmb q})$ 在也为定值.
假设 3: 由于接触点处广义碰撞力 $\nabla \phi ({\pmb q}){\pmb F}_{\rm n} $ 远大于广义常规力 ${\pmb F}({\pmb q}, \dot {\pmb q})$,且在单边约束下各点碰撞力 $F_{{\rm n},i} \geqslant 0$, $1 \leqslant i \leqslant l$,则碰撞过程中常规力的冲量远小于碰撞力的冲量,认为常规力冲量可忽略.
进一步,将上述假设代入式 (8) 得到其简化的 方程 ${\pmb M}({\pmb q})\left( { \dot {\pmb q} (t^ + ) - \dot {\pmb q} (t^ - )} \right) = \nabla \phi ( {\pmb q})\int_{t - }^{t^ + } {\pmb F}_{\rm n} \text{d}t$. 定义法向冲量 $I_{{\rm n},i} = \int_{t - }^{t^ + } F_{{\rm n},i} \text{d}t $,${\pmb I}_{\rm n} = \left( {I_{{\rm n},1} , I_{{\rm n},2} , \cdots , I_{{\rm n},l} } \right)^{\rm T}$,可得碰撞的冲量定理 ${\pmb M}({\pmb q})\left( { \dot{\pmb q} (t^ + ) - \dot {\pmb q} (t^ -) } \right) = \nabla \phi ({\pmb q}){\pmb I}_{\rm n} $. 由式 (7) 将 $ \dot{\pmb q}$ 转换为 $ \dot{\pmb q}_{\rm n} $ 和 $ \dot{\pmb q}_{\tau } $,由于约束面无摩擦,碰撞过程中约束面无法提供切向冲量,由正交性可知 $\dot{\pmb q}_{\tau } $ 与约束面法向正交,则在碰撞前后 $\dot{\pmb q}_{\tau } $ 不发生变化,由冲量定理得
(9) $\left( \!\!\begin{array}{c} \dot{\pmb q}_{\rm n} ( t^ + ) - \dot{\pmb q}_{\rm n} ( t^ - ) \\ \dot{\pmb q}_{\tau } ( t^ + ) -\dot{\pmb q}_{\tau } ( t^ - ) \end{array} \!\! \right) = \left(\!\! \begin{array}{c} {\pmb n}^{\rm T}\nabla \phi ({\pmb q}){\pmb I}_{\rm n} \\ 0 \end{array}\!\! \right)$
其中 ${\pmb n} = ({\pmb n}_1 , {\pmb n}_2 , \cdots ,{\pmb n}_l )^{\rm T}$,即 ${\pmb n}$ 为 $\Xi ({\pmb q})$ 的前 $l$ 行.
定义广义运动学恢复系数 $\varepsilon $,在碰撞过程中有广义 碰撞定律:$\dot {\pmb q}_{\rm n} ( t^ + ) = - \varepsilon \dot {\pmb q}_{\rm n} ( t^ - ) $.
对于含摩擦的碰撞,可定义一个切向恢复系数矩阵 $\varepsilon _{\tau } $,其元素 $e_{{\tau}, ii} = - \dot{\pmb q}_{{\tau}, i} (t^+ )/ \dot {\pmb q}_{{\tau},i} (t^ - )$,即为 碰撞前后速度之比. 则其广义碰撞定律为
(10) $\dot {\pmb q}(t^ + ) = - \varepsilon \dot {\pmb q}(t^ - ), \quad {\pmb \varepsilon } = \left( \begin{array}{cc} \varepsilon _{\rm n} & 0 \\ 0 & \varepsilon _{\tau } \end{array} \right)$
系统无摩擦时其切向恢复系 ${\pmb \varepsilon }_{\tau } = - {\pmb I}_{n - l} $,这里 ${\pmb I}_{n - l} $ 表示 $n - l$ 维单位矩阵.
2.2 一般情况碰撞后速度分析
(11) ${\pmb M}({\pmb q}) = \left( \!\!\begin{array}{ccc} m & 0 & 0 \\ 0 & m 0 & 0 \\ 0 & 0 & {J_{\rm c} } \end{array}\!\! \right)$
约束方程为式 (1),即 $\phi _1 ({\pmb q}) = \delta _1 ({\pmb q}) \geqslant 0$,$\phi _2 ({\pmb q}) = \delta _2 ({\pmb q}) \geqslant 0$,由式 (6) 得正交化的单位向量
(12) $\left.\begin{array}{l} {\pmb n}_1 = \dfrac{1}{\sqrt {\dfrac{1}{m} + \dfrac{(h\sin \theta + b\cos \theta )^2}{J_{\rm c} }} } \left( \!\!\begin{array}{c} 0 \\ {1}/{m} \\ \dfrac{(h\sin \theta + b\cos \theta )^2}{J_{\rm c} } \end{array} \!\! \right) \\ {\pmb n}_2 = \dfrac{1}{\sqrt {\dfrac{1}{m} + \dfrac{(h\sin \theta - b\cos \theta )^2}{J_{\rm c} }} } \left(\!\! \begin{array}{c} 0 \\ {1}/{m} \\ {\dfrac{(h\sin \theta - b\cos \theta )^2}{J_{\rm c} }} \end{array} \!\! \right) \\ {\pmb t} = \dfrac{1}{\sqrt m }\left(\!\! \begin{array}{c} 1 \\ 0 \\ 0 \end{array} \!\! \right) \end{array}\!\!\right\}$
(13) $\left. \!\!\begin{array}{l} \dot {q}_{{\rm n},1} = \dfrac{\dot {y}_{\rm c} + (h\sin \theta + b\cos \theta )\dot {\theta }}{\sqrt {\dfrac{1}{m} + \dfrac{(h\sin \theta + b\cos \theta )^2}{J_{\rm c} }} } \\ \dot {q}_{{\rm n},2} = \dfrac{\dot {y}_{\rm c} + (h\sin \theta - b\cos \theta )\dot {\theta }}{\sqrt {\dfrac{1}{m} + \dfrac{(h\sin \theta - b\cos \theta )^2}{J_{\rm c} }} } \\ \dot {q}_{\tau } = \sqrt m \dot {x}_{\rm c} \end{array}\!\! \right\}$
(14) $\left\{ \!\! \begin{array}{c} {\dot {q}_{{\rm n},1} ( t^ + ) } \\ {\dot {q}_{{\rm n},2} ( t^ + ) } \\ {\dot {q}_{\tau } ( t^ + ) } \end{array} \!\! \right\} = - \left[\!\! \begin{array}{ccc} {e_{{\rm n},1} } & {e_{{\rm n},12} } & 0 \\ {e_{{\rm n},21} } & {e_{{\rm n},2} } & 0 \\ 0 & 0 & {e_{\tau } } \end{array} \!\! \right]\left\{ \!\! \begin{array}{c} {\dot {q}_{{\rm n},1} ( t^ - ) } \\ {\dot {q}_{{\rm n},2} ( t^ - ) } \\ {\dot {q}_{\tau } ( t^ - ) } \end{array} \!\! \right\}$
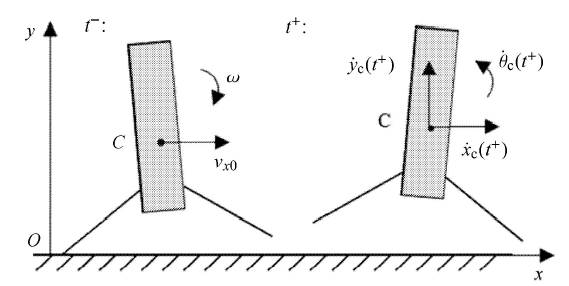
在运动平面内,考察 2 点与地面碰撞后保持与地面接触 $q_{{\rm n},2} = 0$,$\dot {q}_{{\rm n},2} = 0$,1 点悬空且 $\dot {q}_{{\rm n},1} < 0$,如图 3 左侧所示.
图3
图3
箭体与平台的两点碰撞过程
Fig.3
Impact procedure between rocket and platform
在 $t$ 时刻 1 点与地面发生碰撞,即 $q_{{\rm n},1} (t) = 0$, $\theta (t) = 0$,则在 $t$ 时刻箭体与地面发生多点碰撞,在空间中为四条着陆腿与地面的四点碰撞,在简化的平面运动模型中为两点碰撞,碰撞后运动如图 3 右侧所示. 碰撞前的速度为
(15) $\dot {x}_{\rm c} ( t^ - ) = v_{x0} , \ \ \dot {y}_{\rm c} ( t^ - ) = - b\omega , \ \ \dot {\theta } ( t^ - ) = - \omega$
(16) $\left. \!\! \begin{array}{l} \dot {q}_{{\rm n},1} ( t^ - ) = \dfrac{ - 2b\omega }{\sqrt { {1}/{m} + {b^2}/{J_{\rm c} }} } \\ \dot {q}_{{\rm n},2} ( t^ - ) = 0 \\ \dot {q}_{\tau } ( t^ - ) = \sqrt{ m} v_{x0} \end{array} \!\! \right\}$
由于碰撞前有 $\dot {q}_{{\rm n},2} (t^{ - }) = 0$,故在此问题中 $e_{{\rm n},21} $ 和 $e_{{\rm n},2} $ 没有作用. 由式 (14) 和式 (16) 得碰撞后的广义速度
(17) $\left. \begin{array}{l}\dot {q}_{{\rm n},1} ( t^ + ) = \dfrac{2b\omega e_{{\rm n},1} }{\sqrt {{1}/{m} + {b^2}/{J_{\rm c} }} }\\ \dot {q}_{{\rm n},2} ( t^ + ) = \dfrac{2b\omega e_{{\rm n},21} }{\sqrt { {1}/{m} + {b^2}/{J_{\rm c} }} }\\ \dot {q}_{\tau } ( t^ + ) = - e_{\tau } \sqrt m v_{x0} \end{array} \!\!\right\}$
由式 (13) 和式 (17) 得碰撞后箭体的速度
(18) $\left.\begin{array}{l} \dot {x}_{\rm c} ( t^ + ) = - e_{\tau } v_{x0} \\ \dot {y}_{\rm c} ( t^ + ) = \left( {e_{{\rm n},1} + e_{{\rm n},21} } \right)b\omega \\ \dot {\theta } ( t^ + ) = \left( {e_{{\rm n},1} - e_{{\rm n},21} } \right)\omega \end{array} \!\! \right\}$
$\dot{\delta }_1 ( t^ + ) = e_{{\rm n},1} \cdot 2b\omega $, $\dot {\delta }_2 ( t^ + ) = e_{{\rm n},21} \cdot 2b\omega $. 由单边运动约束可知碰撞后有运动约束 $\dot {\delta }_1 ( t^ + ) \geqslant 0$,$\dot {\delta }_2 ( t^ + ) \geqslant 0$,即
(19) $e_{{\rm n},1} \geqslant 0, \quad e_{{\rm n},21} \geqslant 0$
系统的动能 $T = \dfrac{1}{2}m\dot {x}_{\rm c} ^2 + \dfrac{1}{2}m {\dot {y}}_{\rm c} ^2 + \dfrac{1}{2}J_{\rm c} \dot {\theta }^2$. 在碰撞过程中机械能不增加,又由于在碰撞前后火箭的质心高度没有发生变化,则机械能的变化即动能的变化,即系统的动能满足$T ( t^ - ) - T ( t^ + ) \geqslant 0$,得机械能约束的不等式
(20) $e_{\tau }^2 \left( {\dfrac{v_{x0} }{\omega }} \right)^2 + \left( {e_{{\rm n},1} + e_{{\rm n},21} } \right)^2b^2 + \left( {e_{{\rm n},1} - e_{{\rm n},21} } \right)^2\dfrac{J_{\rm c} }{m} \leqslant \\ \qquad \left( {\dfrac{v_{x0} }{\omega }} \right)^2 + b^2 + \dfrac{J_{\rm c} }{m}$
(21) $\left.\begin{array}{l} m\left( \dot {x}_{\rm c} ( t^ + ) - \dot {x}_{\rm c} ( t^ - ) \right) = I_{\tau,1} + I_{\tau,2 } \\ m\left( \dot {y}_{\rm c} ( t^ + ) - \dot {y}_{\rm c} ( t^ - ) \right) = I_{{\rm n},1} + I_{{\rm n},2} \\ J_{\rm c} \left( \dot {\theta } ( t^ + ) - \dot {\theta } ( t^ - ) \right) = \left( I_{{\rm n},1} - I_{{\rm n},2} \right)b + \left( {I_{{\tau },1} + I_{{\tau },1} } \right)h \end{array} \!\! \right\}$
由于在碰撞中 $ I_{\tau,1}$ 与 $ I_{\tau,2}$ 方向相同、作用在同一条直 线上,且 $v_{\tau ,1} = v_{\tau ,2}$,故 $I_{\tau,1} $ 与 $I_{\tau,2} $ 对箭体的影响为耦合的,令 $I_{\tau } = I_{\tau,1} + I_{\tau,2} $,由式 (15)、式 (18)、式 (21),得到 3 个冲量
(22) $\left.\begin{array}{l} I_{{\rm n},1} = \dfrac{\left( {1 + e_{\tau } } \right)mhv_{x0} }{2b}+\\ \qquad \dfrac{\left( {1 + e_{{\rm n},1} + e_{{\rm n},21} } \right)mb^2\omega + \left( {1 + e_{{\rm n},1} - e_{{\rm n},21} } \right)J_{\rm c} \omega }{2b} \\ I_{{\rm n},2} = \dfrac{ - \left( {1 + e_{\tau } } \right)mhv_{x0} }{2b} +\\ \qquad \dfrac{\left( {1 + e_{{\rm n},1} + e_{{\rm n},21} } \right)mb^2\omega - \left( {1 + e_{{\rm n},1} - e_{{\rm n},21} } \right)J_{\rm c} \omega }{2b} \\ I_{tau } = \left( {1 + e_{\tau } } \right)mv_{x0} \end{array}\!\!\right\}$
单边约束要求 $I_{{\rm n},1} \geqslant 0$,$I_{{\rm n},2} \geqslant 0$,得不等式
(23) $\left.\begin{array}{l} \left( {1 + e_{{\rm n},1} + e_{{\rm n},21} } \right) b^2 + \left( {1 + e_{{\rm n},1} - e_{{\rm n},21} } \right)\dfrac{J_{\rm c} }{m} + \\ \qquad \left( {1 + e_{\tau } } \right)\dfrac{v_{x0} h}{\omega } \geqslant 0 \\ \left( {1 + e_{{\rm n},1} + e_{{\rm n},21} } \right) b^2 - \left( {1 + e_{{\rm n},1} - e_{{\rm n},21} } \right)\dfrac{J_{\rm c} }{m} -\\ \qquad \left( {1 + e_{\tau } } \right)\dfrac{v_{x0} h}{\omega } \geqslant 0 \end{array}\!\!\right\}$
摩擦冲量如式 (5) 所示,由于碰撞时刻 $\theta (t) = 0$,令 $v_{\tau } (t) = v_{{\tau },1 } (t) = v_{{\tau},2} (t)$,有
(24) $I_{\tau } \in {\rm Sgn}\left( {v_{\tau } ( t^ + ) } \right) {\mu }\left( {I_{{\rm n},1} + I_{{\rm n},2} } \right)$
由式 (15)、式 (18) 得碰撞前后接触点的切向速度
(25) $\left. \begin{array}{l} v_{\tau } ( t^ - ) = v_{x0} - \omega h \\ v_{\tau } ( t^ + ) = e_{\tau } v_{x0} + (e_{{\rm n},1} - e_{{\rm n},21} )\omega h \end{array} \!\! \right\}$
若碰撞过程为滑动摩擦,即 $v_{\tau } ( t^ + ) \ne {0}$,切向恢复系数
(26) $e_{\tau } = {\rm Sgn}\left( {v_{\tau } ( t^ + ) } \right) {\mu }(1 + e_{{\rm n},1} + e_{{\rm n},21} )\dfrac{v_{x0} }{\omega b}-1$
同时 $v_{\tau } ( t^+) \ne {0}$ 对 $\mu $ 的上限有约束,按照$v_{\tau } ( t^ + ) > 0$ 和 $v_{\tau } ( t^ + ) < 0$ 两种情况进行讨论.
当 $v_{\tau } ( t^ + ) > 0$,由式 (25)、式 (21)、式 (24) 得碰撞后接触点的切 向速度 $v_{\tau } ( t^ + ) = v_{x0} - \mu (1+e_{{\rm n},1} +e_{{\rm n},21} ) \omega b+ (e_{{\rm n},1} - e_{{\rm n},21} ) \omega h > 0$,即要求 $\mu $ 满足
(27) ${\mu } < \dfrac{v_{x0} + (e_{{\rm n},1} - e_{{\rm n},21} )\omega h}{(1 + e_{{\rm n},1} + e_{{\rm n},21} )\omega b}$
当 $v_{\tau } ( t^ + ) < 0$,同理可得 $v_{\tau } ( t^ + ) = v_{x0} + \mu (1+ e_{{\rm n},1} +e_{{\rm n},21} ) \omega b + (e_{{\rm n},1} - e_{{\rm n},21} ) \omega h < 0$,即要求 $\mu $ 满足
(28) ${\mu } < - \dfrac{v_{x0} + (e_{{\rm n},1} - e_{{\rm n},21} )\omega h}{(1 + e_{{\rm n},1} + e_{{\rm n},21} )\omega b}$
若为静摩擦,碰撞后箭体与地面相对滑移速度为 0,则有 $v_{\tau } ( t^ + ) = 0$,由式 (25) 得几何约束
(29) $e_{\tau } = (e_{{\rm n},1} - e_{{\rm n},21} )\dfrac{\omega h}{v_{x0} }$
又由于 $v_{\tau } ( t^ + ) = 0$,则 ${\rm Sgn}\left( {v_{\tau } ( t^ + ) } \right) \in \left[ { - 1, 1} \right]$. 将式 (24)、式 (29) 代入式 (22),得恢复系数 $e_{{\rm n},1} $,$e_{{\rm n},21} $ 与 $\mu $ 间需满足的关系
(30) $\vert v_{x0} + (e_{{\rm n},1} - e_{{\rm n},21} )\omega h\vert \leqslant {\mu }(1 + e_{{\rm n},1} + e_{{\rm n},21} )\omega b$
(4) 摩擦条件,对于滑动摩擦,其切向恢复系数满足式 (26),同时 $\mu $ 需满足要求式 (27)、式 (28);对于静摩擦,需满足式 (29) 和式 (30).
3 典型运动模式分析
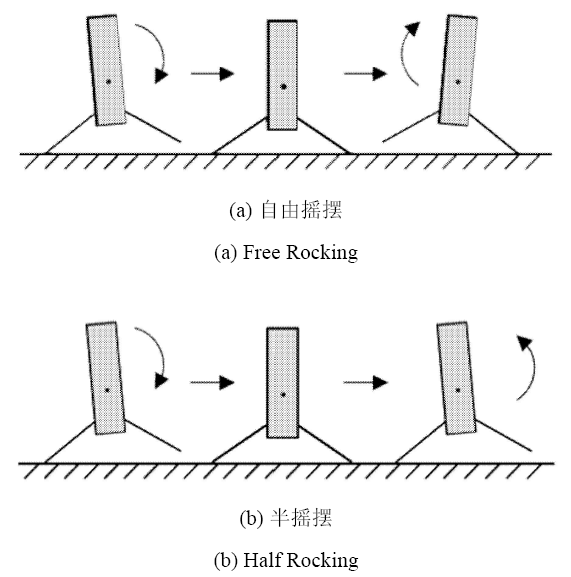
上文讨论了无附加约束下恢复系数的值域,为碰撞后运动的一般情况,诸多分析和试验表明发生如图 3 所示的碰撞后,箭体通常有一条腿与着陆平台保持接触[27 -31 ,35 ] . 若碰撞后 1 点与平台保持接触,即 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} \geqslant 0$,该运动模式称为 Free Rocking;若碰撞后 2 点与平台保持接触,即 $e_{{\rm n},1} \geqslant 0$,$e_{{\rm n},21} = 0$,该运动模式称为 Half Rocking. 两种运动模式如图 4 所示. 下面,本文将分别讨论这两种运动模式在碰撞前后保持黏滞、无摩擦、碰撞前滑动碰 撞后黏滞、碰撞前后保持滑动摩擦 4 种情况下其恢复系数、几何参数、摩擦系数需满足的条件.
图4
图4
两种典型运动模式
Fig.4
The two typical motion
3.1 Free Rocking 模式,碰撞前后保持黏滞
由于碰撞前后均为黏滞状态 $v_{\tau } ( t^ - ) \!=\!v_{\tau } ( t^ + ) \!=\! 0$, 摩擦为静摩擦,由式 (25) 得 $e_{\tau } = - e_{{\rm n},21} $.
由式 (19) 碰撞后单边运动约束和式 (20) 机械能约束、式 (23) 冲量的单边约束条件、式 (30) 静摩擦条件得
(31) $\left.\begin{array}{l} 0 \leqslant e_{{\rm n},21} \leqslant 1 \\ e_{{\rm n},21} \geqslant e_{{\rm c1},1} \triangleq \dfrac{ {J_{\rm c} }/{m} + h^2 - b^2}{ {J_{\rm c} }/{m} + h^2 + b^2} \\ {\mu } \geqslant {\mu }_{{\rm c}1} \triangleq \dfrac{\left( {1 - e_{{\rm n},21} } \right)h}{\left( {1 + e_{{\rm n},21} } \right)b} \end{array}\!\!\right\}$
综上所述有 $e_{{\rm n},21} \in [\max(0 ,e_{{\rm c1},1} ) , 1]$. 需要注意,若 $e_{{\rm c1},1} > 0$,即 $b^2 < {J_{\rm c} } / m + h^2$,则无论如何设计缓冲机构均无法使箭体在该次碰撞后静止.
3.2 Free Rocking 模式,无摩擦
无摩擦时认为保持滑动且 $\mu = 0$,$I_{\tau } = 0$,由式 (19) 和式 (20)、式 (23)、式 (26) 得
(32) $\left. \begin{array}{l} 0 \leqslant e_{{\rm n},21} \leqslant 1 \\ e_{{\rm n},21} \geqslant e_{{\rm c2},1} \triangleq \dfrac{ {J_{\rm c} }/{m} - b^2}{ {J_{\rm c} }/{m} + b^2} \\ e_{\tau } = - 1 \end{array} \right\}$
综上所述有 $e_{{\rm n},21} \!\in\! [\max(0,e_{{\rm c2},1} ), 1]$. 若 $e_{{\rm c2},1} \! >\! 0$,即 $b^2 < {J_{\rm c} }/ m$,则无论如何设计缓冲机构均无法使箭体在该次碰撞后静止.
3.3 Free Rocking 模式,碰撞前滑动、碰撞后黏滞
由于碰撞后为黏滞状态,故摩擦为静摩擦,且有 $v_{\tau } ( t^ + ) = 0$,由式 (25)、式 (19) 和式 (20)、式 (23)、式 (30) 得
(33) $\left. \begin{array}{l} e_{{\rm n},21} \geqslant e_{{\rm c3},1} \triangleq \dfrac{ {J_{\rm c} }/{m} + \dfrac{v_{x0} h}{\omega } - b^2}{ {J_{\rm c} }/{m} + h^2 + b^2} \\ e_{{\rm n},21} \leqslant e_{{\rm c3},2} \triangleq \dfrac{ {J_{\rm c} }/{m} + b^2 + \left( {\dfrac{v_{x0} }{\omega }} \right)^2}{ {J_{\rm c} }/{m} + h^2 + b^2} \\ e_{\tau } = - e_{{\rm n},21} \dfrac{\omega h}{v_{x0} } \\ {\mu } > {\mu }_{{\rm c}3} \triangleq \left| {\dfrac{v_{x0} - e_{{\rm n},21} \omega h}{\left( {1 + e_{{\rm n},21} } \right)\omega b}} \right| \end{array} \!\! \right\}$
综上所述有 $e_{{\rm n},21} \in [ \max(0,e_{{\rm c3},1} ),e_{{\rm c3},2} ]$. 若 $e_{{\rm c3},1} > 0$,即 $b^2 < {J_{\rm c} }/ m + {v_{x0} h} / \omega $,则无论如何设计缓冲机构均无法使箭体在该次碰撞后静止.
3.4 Free Rocking 模式,碰撞前后保持滑动摩擦
对于滑动摩擦,需要考虑 $v_{\tau } ( t^ + ) $ 正负两种情况.
当 $v_\tau (t^ + ) > 0$,由式 (19) 和式 (20)、式 (23) 及 $v_\tau (t^ + ) > 0$ 的条件式 (26)、式 (27) 得
(34) $\left.\!\!\begin{array}{l} e_{{\rm n},21} \geqslant e_{{\rm c}4,1} \triangleq \dfrac{ {J_{\rm c} }/{m} - b^2 + {\mu }bh}{ {J_{\rm c} }/{m} + b^2 - {\mu }bh}\\ e_{{\rm n},21} \leqslant e_{{\rm c}4,2} \triangleq \dfrac{\left( {1 - {\mu }^2} \right)b^2 + {J_{\rm c} }/{m} + 2 {\mu }b \cdot {v_{x0} }/{\omega }}{\left( {1 + {\mu }^2} \right)b^2 + {J_{\rm c} }/{m}}\\ e_{\tau } = {\mu }\left( {1 + e_{{\rm n},21} } \right)\dfrac{\omega b}{v_{x0} } - 1 \\ {\mu } < {\mu }_{{\rm c}4,1} \triangleq \dfrac{v_{x0} - e_{{\rm n},21} \omega h} {\left( {1 + e_{{\rm n},21} } \right)\omega b} \end{array} \right\}$
需证明 $e_{{\rm c}4,1} \leqslant e_{{\rm c}4,2} $ 且 $e_{{\rm c}4,2} \geqslant 0$ 恒成立. 由式 (34) 可知 $v_{x0} > e_{{\rm n},21} \omega h + \mu (1+ e_{{\rm n},21} ) \omega b$,进一步得
$$e_{{\rm c}4,2} \geqslant 1 + \dfrac{2 {\mu }b\left( {h + {\mu }b} \right)e_{{\rm c}4,1} }{\left( {1 + {\mu }^2} \right)b^2 + {J_{\rm c} } / m} \geqslant e_{{\rm c}4,1} $$
即恒有 $e_{{\rm c}4,1} < e_{{\rm c}4,2} $. 同时 $e_{{\rm c}4,2} \geqslant 0$ 对 $\mu $ 有限制
$$ {\mu } \leqslant {\mu }_{{\rm c}4,2} = \dfrac{v_{x0} }{\omega b} + \sqrt {1 + \dfrac{J_{\rm c} }{mb^2} + \left( {\dfrac{v_{x0} }{\omega b}} \right)^2} $$
由式 (34) 可知 $ {\mu }_{{\rm c}4,1} \leqslant {v_{x0} } / {\omega b} \leqslant {\mu }_{{\rm c}4,2} $. 故 $\forall {\mu } \leqslant {\mu }_{{\rm c}4,1} $ 均有 $ {\mu }_{{\rm c}4,1} < {\mu }_{{\rm c}4,2} $.
综上所述有 $e_{{\rm n},21} \!\in\! [\max(0 , e_{c4,1}),e_{{\rm c}4,2} ]$. 若 $e_{{\rm c}4,1} \! >\! 0$,即 $b^2 < {J_{\rm c} } /m + {\mu }bh$,则无论如何设计缓冲机构均无法使箭体在该次碰撞后静止.
当 $v_\tau (t^ + ) < 0$,同理可得
(35) $\left.\begin{array}{l} e_{{\rm n},21} \geqslant e_{{\rm c}4,3} \triangleq \dfrac{ {J_{\rm c} }/{m} - b^2 - {\mu }bh}{ {J_{\rm c} }/{m} + b^2 + {\mu }bh} \\ e_{{\rm n},21} \leqslant e_{{\rm c}4,4} \triangleq \dfrac{\left( {1 - {\mu }^2} \right)b^2 + {J_{\rm c} }/{m} - 2 {\mu }b \cdot {v_{x0} }/{\omega }}{\left( {1 + {\mu }^2} \right)b^2 + {J_{\rm c} }/{m}} \\ e_{\tau } = - {\mu }\left( {1 + e_{{\rm n},21} } \right) \dfrac{\omega b}{v_{x0} }- 1 \\ {\mu } < {\mu }_{{\rm c}4,3} \triangleq - \dfrac{v_{x0} - e_{{\rm n},21} \omega h}{\left( {1 + e_{{\rm n},21} } \right)\omega b} \end{array}\!\!\right\}$
同时,可证恒有 $e_{{\rm c}4,3} < e_{{\rm c}4,4}$且$e_{{\rm c}4,4 } \geqslant 0$.
综上所述有 $e_{{\rm n},21} \in [\max(0,e_{{\rm c}4,3} ),e_{{\rm c}4,4} ]$. 若 $e_{{\rm c}4,3} > 0$,即 $b^2 < {J_{\rm c} } / m - {\mu }bh$,则无论如何设计缓冲机构均无法使箭体在该次碰撞后静止.
3.5 Half Rocking 模式,碰撞前后保持黏滞
由于碰撞前后均为黏滞状态,故摩擦为静摩擦,且有 $v_{\tau } ( t^ - ) = v_{\tau } ( t^ + ) = 0$,由式 (19) 和式 (20)、式 (23)、式 (25)、式 (30) 得
(36) $\left.\!\begin{array}{l} 0 \leqslant e_{{\rm n},21} \leqslant 1 \\ b^2 > \dfrac{J_{\rm c} }{m} + h^2 \\ e_{\tau } = e_{{\rm n},1} \\ {\mu } \geqslant {\mu }_{{\rm c}5} \triangleq \dfrac{h}{b} \end{array} \right\}$
由式 (36) 的第 2 式可知,Half Rocking 模式仅跨距较大时可能发生.
3.6 Half Rocking 模式,无摩擦状态
无摩擦时认为保持滑动且 $\mu = 0$, $I_{\tau } =0$,由式 (19) 和式 (20)、式 (23)、式 (26) 得
(37) $\left. \begin{array}{l} 0 \leqslant e_{{\rm n},21} \leqslant 1 \\ b^2 > \dfrac{J_{\rm c} }{m} \\ e_{\tau } = - 1 \end{array} \right\}$
与 3.5 结论相似,由式 (37) 的第 2 式可知,Half Rocking 模式仅在跨距较大时才可能发生.
3.7 Half Rocking 模式,碰撞前滑动、碰撞后黏滞
由于碰撞后为黏滞状态 $v_{\tau } ( t^ + ) = 0$,故摩擦为静摩擦,由式 (19) 和式 (20)、式 (23)、式 (25)、式 (30) 得
(38) $\left.\begin{array}{l} \!\! 0 \leqslant e_{{\rm n},1} \leqslant e_{{\rm c7},1} \triangleq \dfrac{ {J_{\rm c} }/{m} + b^2 + \left( { {v_{x0} }/{\omega }} \right)^2}{ {J_{\rm c} }/{m} + h^2 + b^2} \\ \left( {b^2 - \dfrac{J_{\rm c} }{m} - h^2} \right)\left( {1 + e_{{\rm n},1} } \right) + \left( {h - \dfrac{v_{x0} }{\omega }} \right)h \geqslant 0 \\ e_{\tau } = e_{{\rm n},1} \dfrac{\omega h}{v_{x0} } \\ {\mu } \geqslant {\mu }_{{\rm c}7} \triangleq \left| {\dfrac{v_{x0} + e_{{\rm n},1} \omega h}{\left( {1 + e_{{\rm n},1} } \right)\omega b}} \right| \end{array}\!\!\right\}$
与 3.5 节碰撞中保持黏滞相比,若碰撞前向左侧滑动 $v_{x0} - \omega h < 0$,Half Rocking 运动模式对跨距的要求更低;若碰撞前向右侧滑动 $v_{x0} - \omega h > 0$,Half Rocking 运动模式对跨距的要求更高.
3.8 Half Rocking 模式,碰撞前后保持滑动摩擦
对于滑动摩擦,需要考虑 $v_{\tau } ( t^ + ) $ 正负两种情况.
当 $v_\tau (t^ + ) > 0$,由式 (19) 和式 (20)、式 (23)、式 (26)、式 (27) 得
(39) $\left.\begin{array}{l} 0 \leqslant e_{{\rm n},1} \leqslant e_{{\rm c}8,1} \triangleq \dfrac{\left( {1 - {\mu }^2} \right)b^2 + {J_{\rm c} }/{m} + 2 {\mu }b \cdot {v_{x0} }/{\omega }}{\left( {1 + {\mu }^2} \right)b^2 + {J_{\rm c} }/{m}} \\ b^2 \geqslant \dfrac{J_{\rm c} }{m} + {\mu }bh \\ e_{\tau } = {\mu }\left( {1 + e_{{\rm n},1} } \right) \cdot \dfrac{\omega b}{v_{x0} } - 1 \\ {\mu } < {\mu }_{{\rm c}8,1} \triangleq \dfrac{v_{x0} + e_{{\rm n},1} \omega h}{\left( {1 + e_{{\rm n},1} } \right)\omega b} \end{array}\!\!\right\}$
需证明 $e_{{\rm c}8,1} \geqslant 0$ 恒成立. 由 $ {\mu } < {\mu }_{{\rm c}8,1} $ 得 ${v_{x0} } /{\omega h} > (1+ e_{{\rm n},1} ){ {\mu }b}/ h - e_{{\rm n},1} $,进一步得
$$e_{{\rm c}8,1} \geqslant 1 + \dfrac{2 {\mu }b( {\mu }b - h)e_{{\rm n},1} }{\left( {1 + {\mu }^2} \right)b^2 + {J_{\rm c} } / m} $$
由 $e_{{\rm n},1} \geqslant 0$ 可证不等式右侧 $ \geqslant 0$,则 $e_{{\rm c}8,1} \geqslant 0$. 故有 $e_{{\rm n},1} \in [0, e_{{\rm c}8,1} ]$.
当 $v_\tau (t^ + ) < 0$,同理可得
(40) $\left.\begin{array}{l} 0 \leqslant e_{{\rm n},1} \leqslant e_{{\rm c}8,2} \triangleq \dfrac{\left( {1 - {\mu }^2} \right)b^2 + {J_{\rm c} }/{m}-2 {\mu }b \cdot {v_{x0} }/{\omega }}{\left( {1 + {\mu }^2} \right)b^2 + {J_{\rm c} }/{m}} \\ b^2 \geqslant \dfrac{J_{\rm c} }{m} - {\mu }bh \\ e_{\tau } = - {\mu }\left( {1 + e_{{\rm n},1} } \right) \cdot \dfrac{\omega b}{v_{x0} } - 1 \\ {\mu } < {\mu }_{{\rm c}8,2} \triangleq - \dfrac{v_{x0} + e_{{\rm n},1} \omega h}{\left( {1 + e_{{\rm n},1} } \right)\omega b} \end{array}\!\!\right\}$
同时可证恒有 $e_{{\rm c}8,2} \geqslant 0$,此 $e_{{\rm n},1} \in [0, e_{{\rm c}8,2} ]$.
由上述分析可知,在 Half Rocking 运动中单边约束式 (23) 将简化为几何约束,且该种运动模式仅在跨距较大时才可能发生.
4 基于完全非弹性碰撞假设的箭体着陆
在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数.
4.1 不同速度组合下的运动学恢复系数
当 $\mu $ 较大、碰撞时水平速度 $v_{x0} $ 绝对值较小,碰撞后可出现黏滞 状态,即 $v_{\tau } ( t^ + ) = 0$. 当 $v_{x0} $ 沿负向增大,则会出现 $v_{\tau } ( t^ + ) < 0$ 的运动状态,即在图 2 所示的坐标系下,接触点向左滑动;反之当 $v_{x0} $ 沿正向增大,则 $v_{\tau } ( t^ + ) > 0$ 接触点向右滑动,接下来分别讨论 3 种运动状态及其临界情况.
对碰撞后接触点向左滑动和黏滞的临界情况,$\mu $ 与速度需满足式 (41),定义此时的临界速 度比 $({v_{x0} } / {\omega h})_{{\rm ch}1} $ 如式 (42),其中 $e_{{\rm c}4,3} $ 由式 (35) 给出
(41) ${\mu}= \dfrac{e_{{\rm c}4,3} \omega h - v_{x0} }{(1 + e_{{\rm c}4,3} )\omega b}$
(42) $\left( {\dfrac{v_{x0} }{\omega h}} \right)_{ {\rm ch1}} = e_{{\rm c}4,3} - {\mu }\left( {1 + e_{{\rm c}4,3} } \right)\dfrac{b}{h}$
若 ${v_{x0} } / {\omega h} < ({v_{x0} } /{\omega h})_{{\rm ch}1} $,运动状态为碰撞后接触点向左滑动,$e_{{\rm n},21} = e_{{\rm c}4,3} $,$e_{\tau } $ 由式 (35) 给出. 对碰撞后接触点黏滞与向右滑动的临界情况,$\mu $ 与速度需满足式 (43),临界速度比 $({v_{x0} } /{\omega h})_{{\rm ch}2} $ 如式 (44)
(43) ${\mu } = \dfrac{v_{x0} - e_{{\rm c}4,1} \omega h}{(1 + e_{{\rm c}4,1} )\omega b}$
(44) $\left( {\dfrac{v_{x0} }{\omega h}} \right)_{ {\rm ch2}} = e_{{\rm c}4,1} + {\mu }\left( {1 + e_{{\rm c}4,1} } \right)\dfrac{b}{h}$
若 ${v_{x0} } /{\omega h} > ({v_{x0} }/{\omega h})_{{\rm ch2}} $,运动状态为碰撞后 接触点向右滑动,$e_{{\rm n},21} = e_{{\rm c}4,1} $,$e_{\tau } $ 由式 (34) 给出.
若 $({v_{x0} }/{\omega h})_{{\rm ch1}} \leqslant {v_{x0} } /{\omega h} \leqslant ({v_{x0} } /{\omega h})_{{\rm ch2}} $,运动状态为碰撞 后黏滞,$e_{{\rm n},21} = e_{{\rm c3},1} $,$e_{\tau } $ 由式 (33) 给出. 由 $e_{{\rm c3},1} $,$e_{{\rm c}4,1} $,$e_{{\rm c}4,3} $ 的表达式可知 $e_{{\rm c}4,3} \leqslant e_{{\rm c3},1} \leqslant e_{{\rm c}4,1} $,即 $e_{{\rm c}4,3} $ 和 $e_{{\rm c}4,1} $ 分别为 $e_{{\rm n},21} $ 的下界和上界.
3.1 中所分析的箭体与平台碰撞前后接触点均保持黏滞所示的运动状态,为当 $({v_{x0} } /{\omega h})_{{\rm ch2}} \geqslant 1$ 时,3.3 所分析的碰撞后黏滞的运动状态在 ${v_{x0} } / {\omega h} = 1$ 时的特殊情况;3.2 所分析的无摩擦的运动状态,为当 $\mu = 0$ 时,3.4 滑动摩擦的特殊情况.
根据上述分析,考虑单边运动约束 $e_{{\rm n},21} \geqslant 0$,$e_{{\rm n},21} $ 与碰撞前速度比 ${v_{x0} }/ {\omega h}$ 的关系可总结如表 2 .
由式 (34) 可知,当 $ {\mu }h \geqslant b$ 时 $e_{{\rm c}4,1} > 1$,即在向右滑动时碰撞后角速度增大,即虽然碰撞后总机械能降低,但是在摩擦的作用下,使得箭体的角速度增大,进而增大了箭体翻倒的可能,该种情况仅可能发生在摩擦冲量向左时. 由式 (35) 可知恒有 $e_{{\rm c}4,3} < 1$,即当运动状态为箭体与平台碰撞后向左滑动时,碰撞后箭体的角速度必然降低.
本文虽然没有对碰撞过程中接触点黏滞-滑移的状态切换过程进行判断,但在经典库伦干摩擦模型描述摩擦力的前提下 $\vert I_{{\tau ,}i} \vert \leqslant {\mu }I_{{\rm n,}i} $ 恒成立,由上述分析可知,结论 $e_{{\rm c}4,3} \leqslant e_{{\rm n},21} \leqslant e_{{\rm c}4,1} $ 及 $e_{{\rm c}4,3} $,$e_{{\rm c}4,1} $ 的取值与碰撞过程中对黏滞-滑移状态的判断方法无关,仅影响 $({v_{x0} } /{\omega h})_{{\rm ch2}} $和$e_{{\rm c3},1} $ 的取值. 若对上述切换过程进行动态判断,当 $0 < {v_{x0} } / {\omega h} < 1$ 且碰撞后向右滑动时,$\vert I_{\tau } \vert $ 低于式 (5) 的结果,该情况下 $I_{\tau } $ 方向向左,故本文的分析较真实情况更为保守.
特别地,若希望与地面碰撞后箭体在纵向静止,$\dot {\delta }_1 (t^ + ) = 0$,$\dot {\delta }_2 (t^ + ) = 0$,即 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} = 0$,由上文的分析可知,这不仅为一个能量耗散的问题还受到运动学约束,即要求上述分析中 $e_{{\rm n},21} $ 的下界为 0. 从碰撞后停止、向左滑动和向右滑动 3 种工况出发,实现该目标箭体几何尺寸和 $\mu $ 的必要条件见表 3 .
可见 ${v_{x0} } / \omega $ 较小,甚至为负,更有利于着陆稳定,由于 $\dot {\theta }(t^ - ) = - \omega $,$\dot {x}_{\rm c} (t^ - ) = v_{x0} $,故 $\dot {\theta }(t^ - )$ 与 $\dot {x}_{\rm c} (t^ - )$ 在图 3 所示的坐标系下同号更有利于着陆稳定.
4.2 翻倒评价准则
本节讨论当 1 点接触平台且 $\dot {\theta } < 0$ 时,箭体是否向右侧翻倒的问题. 在碰撞结束到翻倒过程中,1 点与地面保持接触,接触状态可能为黏滞、保持滑动、先滑动后黏滞,同时滑动需考虑两个方向. 本节基于能量法提出一种考虑摩擦的不翻倒的判断方法. 首先,不翻倒的充分条件为其的动能小于翻倒所需的重力势能 $E_{{\rm cri}} = g( \sqrt {b^2 + h^2} - h)$,如式 (45). 这里为讨论方便,动能和和重力势能均除以质量
(45) $\dfrac{1}{2}\left( {\dfrac{J_{\rm c} }{m} + b^2} \right)\dot {\theta }^2 + \dfrac{1}{2}\dot {x}_{\rm c}^2 < E_{{\rm cri}}$
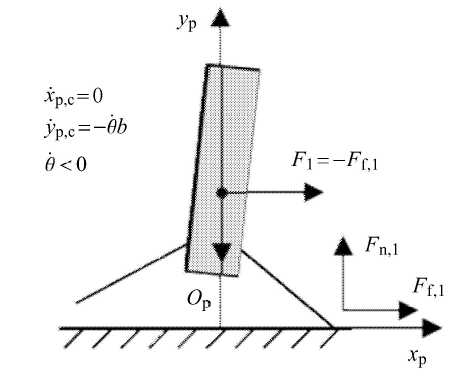
为便于分析,设一直线平移坐标系 $P$ 系 (非惯性系),其 $y$ 轴固连于质心,$x$ 轴与大地坐标系重合,如图 5 所示. 在该系中质心水平速度 $\dot {x}_{{\rm p,c}} = 0$,箭体受过质心的重力、惯性力 $F_{\rm I} $,过 1 点的支撑力 $F_{{\rm n,1}} $、摩擦力 $F_{{\rm f,1}} $,翻倒过程中仅重力和 $F_{{\rm f,1}} $ 做功.
图5
图5
直线平移坐标系
Fig.5
Straight-line translation coordinate
若不考虑摩擦,$F_{{\rm f,1}} = 0$,不翻倒的条件为
(46) $\dfrac{1}{2}\left( {\dfrac{J_{\rm c} }{m} + b^2} \right)\dot {\theta }^2 < E_{{\rm cri}}$
考虑存在摩擦的情况. 当 $\dot {x}_{\rm c} < 0$,$\dot {\theta } < 0$,1 点相对着陆平台向左滑动,$F_{{\rm f,1}} > 0$,在翻倒过程中摩擦力做负功,若式 (46) 成立,该箭体也不会翻倒.
定义摩擦角 $\varphi _{\mu } = \arctan ( {\mu })$. 当 $\dot {x}_{\rm c} > 0$ 且翻倒过程中 1 点相对着陆平台始终向右滑动,$F_{{\rm f,1}} < 0$,在 $P$ 系中摩擦力做正功,且若箭体质心与 1 点连线与竖直方向夹角 $\alpha _{{\rm c}1} < \varphi _{\mu } $ 便会翻 倒. 当 $\alpha _{{\rm c}1} > \varphi _{\mu } $ 箭体质心加速度具有向下的 分量,则 $F_{{\rm n,1}} \leqslant mg$,故翻倒过程中 $\vert F_{{\mu ,1}} \vert \leqslant {\mu }m{\rm g}$. 在 $P$ 系中考察箭体从 $\theta = 0$ 转动到跨过摩擦角的过程,若初始动能和摩擦力做功小于重力势能变化,则不会翻倒,不翻倒的条件为
(47) $\dfrac{1}{2}\left( {\dfrac{J_{\rm c} }{m} + b^2} \right)\dot {\theta }^2 + \mu g\left( {b - \sqrt {b^2 + h^2} \sin \varphi _\mu } \right) < \\ \qquad {g}\left( {\sqrt {b^2 + h^2} \cos \varphi _\mu - h} \right) <\\ \qquad {g}\left( {\sqrt {b^2 + h^2} \cos \varphi _{\mu } - h} \right)$
式 (45)$\sim$ 式 (47) 为不翻倒的充分条件,定义翻倒能量 $E_{\rm fall}$ 和无量纲的稳定系数 $\gamma _{\rm stable} $,不翻倒需满足式 (48),静止时 $\gamma_{\rm stable} = 1$.
(48) $\gamma _{{\rm stable}} = \dfrac{E_{{\rm cri }} - E_{{\rm fall }} }{E_{{\rm cri }} } > 0$
(49) $E_{{\rm fall }} = \left\{ \begin{array}{ll} \dfrac{1}{2}\left( {\dfrac{J_{\rm c} }{m} + b^2} \right)\dot {\theta }^2 , & \dot {x}_{\rm c} \leqslant 0 \\ \dfrac{1}{2}\left( {\dfrac{J_{\rm c} }{m} + b^2} \right)\dot {\theta }^2 + \min \left\{ {\dfrac{\dot {x}_{\rm c}^2 }{2},E_1 } \right\} , & \dot {x}_{\rm c} > 0 \end{array} \right.$
其中 $E_{1} = {\mu }{g}b - {g}\sqrt {b^2 + h^2} ( \sqrt {1 + {\mu }^2} - 1)$.
4.3 静止平台着陆稳定性判别方法
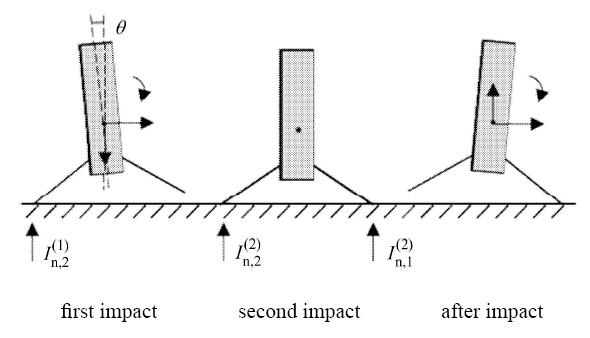
第三章的分析均为分析火箭以 2-2 模式着陆时箭体与着陆平台的第二次碰撞,在本节中将考虑在 2-2 着陆模式下箭体与着陆平台的第一次和第二次碰撞,以碰撞后不翻倒为稳定条件给出一种小姿态角下着陆稳定性判别方法,碰撞均视为完全非弹性碰撞,其碰撞过程如图 6 所示,坐标系与图 2 一致,其中 $I_{{\rm n},i}^{(j)} $ 表示第 $j$ 次碰撞中 $i$ 点的法向冲量.
图6
图6
箭体着陆碰撞过程
Fig.6
Landing impact procedure of the rocket
设第一次碰撞前的速度为 $\dot {x}_{\rm c}^{(0)} $,$\dot {y}_{\rm c}^{(0)} $,$\dot {\theta }^{(0)}$,碰撞时的姿态角为 $\theta $,假定 $\theta \approx 0$,即姿态角较小. 要求 $\dot {\delta }_2^{(0)} = \dot {y}_{\rm c}^{(0)} - \dot {\theta }^{(0)}b < 0$. 2 点首先与着陆平台发生单点碰撞,碰撞冲量为 $I_{{\rm n}, 2}^{(1)} $,碰撞后 2 点与着陆 平台保持接触,即 $\delta _{2} = 0$,$\dot {\delta }_{2} = 0$,$\dot {\delta }_{1} < 0$,设该次碰撞后水平方向速度为 $\dot {x}_{\rm c}^{(1)} $,角速度为 $\dot {\theta }^{(1)}$,若 $\dot {\theta }^{(1)} > 0$,则不发生第二次碰撞,需对随后箭体是否翻倒进行判断. 若 $\dot {\theta }^{(1)} < 0$,则随后 1 点与地面保持接触并发生第二次碰撞,由于着陆前有 $\theta \approx 0$,故第一次碰撞后到第二次碰撞前速度的变化可忽略. 第二次碰撞为 1 点、2 点与着陆平台的两点碰撞,由第 4.1 节中分析可知,第二次碰撞后为 Free Rocking 运动,碰撞后1点与地面保持接触,设第二次碰撞后的水平速度为 $\dot {x}_{\rm c}^{(2)} $,角速度为 $\dot {\theta }^{(2)} < 0$,设 $\omega ^{(2)} = - \dot {\theta }^{(2)}$.
首先假定第一次碰撞保持黏滞,碰撞时的切向冲量与法向冲量为
(50) $\left. \begin{array}{l} I_{{\tau , 2}}^{(1)} = - \left[ {\dfrac{J_{\rm c} }{m}h\dot {\theta }^{(0)} + \left( {\dfrac{J_{\rm c} }{m} + b^2} \right)\dot {x}_{\rm c}^{(0)} + bh\dot {y}_{\rm c}^{(0)} } \right] \\ I_{{\rm n, 2}}^{(1)} = \dfrac{J_{\rm c} }{m}h\dot {\theta }^{(0)} - bh\dot {x}_{\rm c}^{(0)} - \left( {\dfrac{J_{\rm c} }{m} + h^2} \right)\dot {y}_{\rm c}^{(0)} \end{array} \right\}$
定义 $\mu _{{\rm 1,stick}} \triangleq I_{{\tau , 2}}^{(1)} / I_{{\rm n, 2}}^{(1)} $,保持黏滞要求 $\vert \mu _{\rm 1,stick} \vert \leqslant {\mu }$ 且 $I_{\rm n, 2}^{(1)} > 0$. 若保持黏滞,此时碰撞后速度为
(51) $\left. \begin{array}{l} \dot {\theta }^{(1)} = \dfrac{\dot {y}_{\rm c}^{(0)} b - \dot {x}_{\rm c}^{(0)} h + {J_{\rm c} }/{m}\dot {\theta }^{(0)}}{ {J_{\rm c} }/{m} + b^2 + h^2} \\ \dot {x}_{\rm c}^{(1)} = - \dot {\theta }^{(1)}h \end{array} \!\! \right\}$
若无法保持黏滞且 $I_{\tau , 2}^{(1)} > 0$,则碰撞后向左滑动,$v_{\tau }^{(1)} < 0$,碰撞后速度为
(52) $\left. \begin{array}{l} \dot {\theta }^{(1)} = \dfrac{\left( {b - {\mu }h} \right)\dot {y}_{\rm c}^{(0)} + {J_{\rm c} }/{m}\dot {\theta }^{(0)}}{ {J_{\rm c} }/{m} + b^2 - {\mu }bh} \\ \dot {x}_{\rm c}^{(1)} = \dot {x}_{\rm c}^{(0)} + \dfrac{ {\mu } {J_{\rm c} }/{m}\left( {\dot {\theta }^{(0)}b - \dot {y}_{\rm c}^{(0)} } \right)}{ {J_{\rm c} }/{m} + b^2 - {\mu }bh} \end{array}\!\! \right\}$
若无法保持黏滞且 $I_{\tau , 2}^{(1)} < 0$,则碰撞后向由滑动,$v_{\tau }^{ (1)} > 0$,碰撞后速度为
(53) $\left. \begin{array}{l} \dot {\theta }^{(1)} = \dfrac{\left( {b + {\mu }h} \right)\dot {y}_{\rm c}^{(0)} + {J_{\rm c} }/{m}\dot {\theta }^{(0)}}{ {J_{\rm c} }/{m} + b^2 + {\mu }bh} \\ \dot {x}_{\rm c}^{(1)} = \dot {x}_{\rm c}^{(0)} - \dfrac{ {\mu } {J_{\rm c} }/{m}\left( {\dot {\theta }^{(0)}b - \dot {y}_{\rm c}^{(0)} } \right)}{ {J_{\rm c} }/{m} + b^2 + {\mu }bh} \end{array} \right\}$
即对于第一次碰撞,首先由式 (50) 计算 $I_{\tau , 2}^{(1)} $,$I_{\rm n, 2}^{(1)} $,$\mu _{\rm 1,stick} $, 若 $\vert \mu _{\rm 1,stick} \vert \leqslant {\mu }$ 且 $I_{\rm n, 2 }^{(1)} > 0$,运动状态为碰撞后在 2 点 保持黏滞,碰撞后速度见式 (51);否则若 $I_{\tau , 2}^{(1)} > 0$,运动为碰撞后在 2 点向左滑动,碰撞后速度 见式 (52);否则若 $I_{\tau , 2}^{(1)} < 0$,运动为碰撞后在 2 点向右滑动,碰撞后速度见式 (53). 由于保持接触,式 (51)$\sim$式 (53) 均有 $\dot {y}_{\rm c}^{(1)} = \dot {\theta }^{(1)}b$.
若 $\dot {\theta }^{(1)} > 0$,则不会发生第二次碰撞,通过 4.2 所述的评价准则式 (48) 对是否翻倒进行判断,需要注意这里的翻倒模式为绕 2 点向左侧翻倒,故需要将 $\dot {x}_{\rm c} $ 反号再代入式 (49). 若 $\dot {\theta }^{(1)} < 0$,则将发生第二次碰撞,碰撞过程分析如 4.1 所示,通过表 2 得到碰撞后速度后,通过式 (49) 进行判断.
在前期设计时,在小姿态角着陆情况下难以判断第一次碰撞发生在 1 点还是 2 点,故应考虑两种情况并取不利的情况作为着陆速度的限制.
5 算例
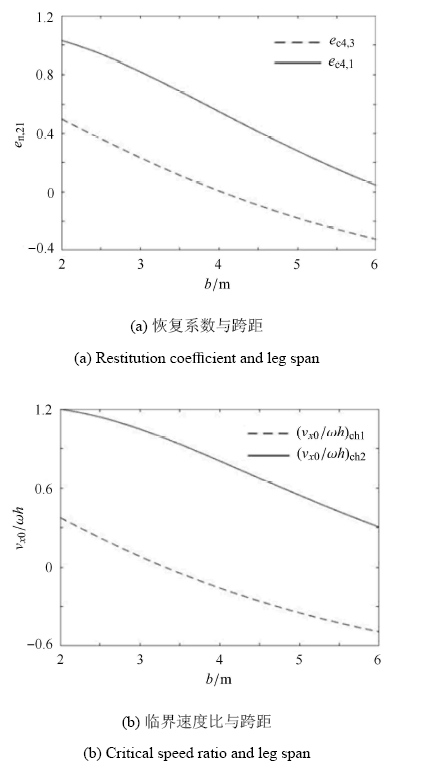
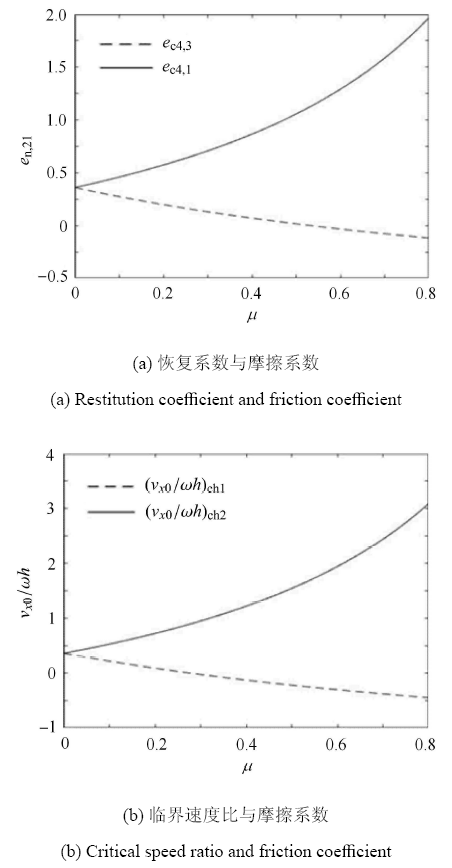
以文献[10 ] 中采用的四腿式火箭垂直着陆原理样机为例,考察完全非弹性碰撞下火箭的着陆过程. 该样机在 2-2 着陆模式下 $b = 3.43$m,着陆腿展开后质心高度 $h = 7.27$m,着陆体总质量 $m = 5400$kg,其中着陆腿重 200kg,$ {\mu } = 0.3$,绕质心转动惯量 $J_{\rm c} = 1.354\times 10^5$kg$\cdot $m$^2$. 由式 (42)、式 (44) 得
$$ (v_{x0} /\omega h)_{ {\rm ch1}} = - 0.028649, \ \ e_{{\rm c4,3}} = 0.131505 \\ (v_{x0} / \omega h)_{ {\rm ch2}} = 0.949923, \ \ e_{{\rm c4,1}} = 0.708150 $$
对于上述参数,由表 2 得 $e_{{\rm n},21} $与${v_{x0} } /{\omega h}$ 的关系如图 7 所示. 对其跨距进行调整,分析跨距对恢复系数 $e_{{\rm c}4,3} $,$e_{{\rm c}4,1} $ 及其对应的临界速度比 $({v_{x0} }/{\omega h})_{{\rm ch}1} $,$({v_{x0} } /{\omega h})_{{\rm ch2}} $ 影响,半跨距 $b$ 取 2$\sim$6m,由于着陆腿质量仅为 200kg,故可近似忽略跨距变化对转动惯量的影响,结果如图 8 所示. 对 $\mu $ 进行调整,分析 $\mu $ 对恢复系数 $e_{{\rm c}4,1} $,$e_{{\rm c}4,3} $ 及其对应的临界速度比影响,同样保持其他参数与文献[10 ] 一致,$\mu $ 取 0 到 0.8,结果如图 9 所示.
图7
图7
恢复系数与速度比
Fig.7
Restitution coefficient and speed ratio
图8
图8
着陆腿跨距的影响
Fig.8
Result of leg span
图9
图9
摩擦系数的影响
Fig.9
Result of friction coefficient
由图 8 (a) 可见 $e_{{\rm c}4,1} $,$e_{{\rm c}4,3} $ 均随跨距增大而减小,即随跨距增大着陆过程更稳定. 由于,故当 $e_{{\rm c}4,3} \leqslant 0$ 时表示当 ${v_{x0} } / {\omega h}$ 小于某个临界速度比时 $e_{{\rm n},21} = 0$,即箭体停止摇晃. 当 $e_{{\rm c}4,1} \leqslant 0$ 时表示无论何种速度比碰撞后均停止摇晃. 由图 8 (b) 可见两个临界速度比均随跨距增大而减小,说明随跨距增大,发生碰撞后向右滑动对速度比的要求降低,发生碰撞后向左滑动对速度比要求升高. 同时,在同样的 ${v_{x0}} /{\omega h}$ 下,$e_{{\rm n},21} $ 随着 $b$ 的增大而减小,直到 $e_{{\rm n},21} = 0$.
由图 9 (a) 可见,$\mu = 0$ 时 $e_{{\rm c}4,1} = e_{{\rm c}4,3} = 0.3613$,即 $e_{{\rm c}2,1} $. 随 着 $\mu $ 增大, $e_{{\rm c}4,3} $ 和 $({v_{x0} }/ {\omega h})_{{\rm ch}1} $ 减小,$e_{{\rm c}4,1} $和 $({v_{x0} } /{\omega h})_{{\rm ch2}} $ 增大,即摩擦力对转动角速度的影响增大,在摩擦较大的情况下应尽量使得着陆前 $\dot {x}_{\rm c} (t^ - )$ 与 $\dot {\theta }(t^ - )$ 同号. 由图 9 (b) 可见随着 $\mu $ 增大,发生碰撞后黏滞的可能性增大.
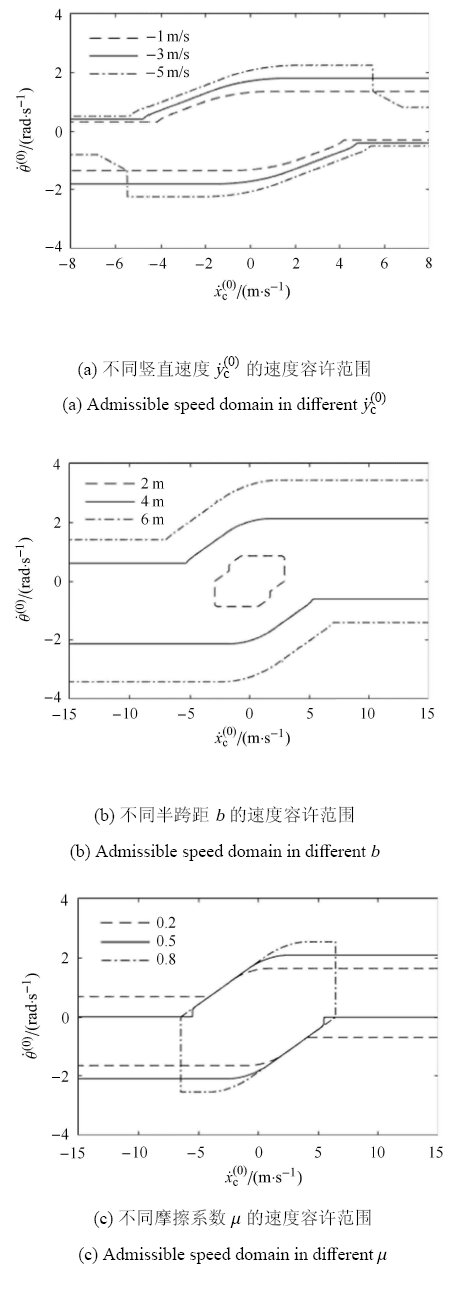
采用上述稳定性判别方法对上述模型计算其着陆的速度容许范围,即 $\gamma _{\rm stable} = 0$ 对应的着陆速度. 不同下落速度 $\dot {y}_{\rm c}^{(0)} $的速度容许范围见图 9 (a);取不同跨距,$\dot {y}_{\rm c}^{(0)} = - 3$m/s,其他参数不变,速度容许范围见图 9 (b);取不同的摩擦系数,$\dot {y}_{\rm c}^{(0)} = - 3$m/s,其他参数不变,速度容许范围见图 9 (c).
在小姿态角着陆时需要考虑第一次碰撞发生在 1 点或 2 点两种情况并分别计算其 $\gamma _{\rm stable} $ 并对二者取不利情况,即取两种情况 $\gamma _{\rm stable} $ 的较小值. 则对任意着陆速度 $ \{ \dot {x}_{\rm c}^{(0)}$, $\dot {y}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} \}$ 在着陆稳定分析中其 $\gamma _{\rm stable} $ 与 $ \{ - \dot {x}_{\rm c}^{(0)}$, $\dot {y}_{\rm c}^{(0)}$, $ - \dot {\theta }^{(0)} \}$ 对应的 $\gamma _{\rm stable} $ 相等,可见图 9 所示的稳定速度边界也具有这种对称性. 由图 9 (a) 可见,在图 2 所建立的坐标系下着陆前角速度与切向速度同号时着陆更稳定,竖直下降速度 $ - \dot {y}_{\rm c}^{(0)} $ 对稳定性的影响较为复杂,但稳定区间差别较小,与动力学仿真的结论相似[12 ] . 同时 $\dot {y}_{\rm c}^{(0)} = - 5$m/s 与 $ - 1$m/s 和 $ - 3$m/s 两种速度在角速度与切向速度同号且 $\vert \dot {x}_{\rm c}^{(0)} \vert $ 较大时速度容许范围边界的趋势不同,是由于其翻倒模式不同. 以 $\dot {x}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} > 0$ 为例,$\dot {y}_{\rm c}^{(0)} = - 5$m/s 时其翻倒模式为首先在 1 点发生碰撞后再发生第二次碰撞,随后绕 2 点翻倒;而 $\dot {y}_{\rm c}^{(0)} = - 1$m/s 或 $ - 3$m/s 时其翻倒模式为在 2 点发生碰撞后绕 2 点翻倒,不发生第二次碰撞. 对于图 9 (b) $b = 2$m 时,$\dot {x}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} > 0$ 且 $\dot {x}_{\rm c}^{(0)} $ 较大时翻倒模式与图 9 (a) $\dot {y}_{\rm c}^{(0)} = - 5$m/s 时相同,同时由图 9 (b) 可见随着陆腿跨距增大稳定性增强. 由图 9 (c) 可见随着 $\mu $ 增大在 $\dot {\theta }^{(0)}$ 较大、$\dot {x}_{\rm c}^{(0)} $ 较小时着陆更稳定,在 $\dot {\theta }^{(0)}$ 较小、$\dot {x}_{\rm c}^{(0)} $ 较大时着陆更不稳定,考虑到垂直着陆时水平速度通常较小,故 $\mu $ 增大有利于着陆稳定. 若干算例对应的容许速度范围的边界沿水平轴 $\dot {x}_{\rm c}^{(0)} $ 无限延伸,此时为判据式 (47) 所示的情况,即始终保持滑动也不会翻倒.
图10
图10
参数对速度容许范围的影响
Fig.10
Admissible speed domain in different parameters
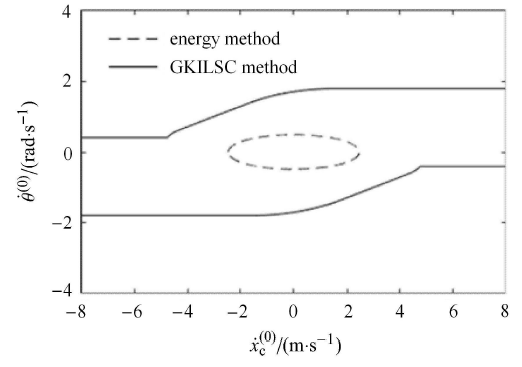
保持上述参数不变,取 $\dot {y}_{\rm c}^{(0)} = - 3$m/s,分别采用 GKILSC 法和能量法[17 ] 对能量法稳定的速度边界进行对比如图 11 所示,可见 GKILSC 法相较于能量法,其速度容许范围区域更大,且考虑了水平速度和角速度方向的影响,故更为精确.
图11
图11
能量法与本文方法速度容许范围的对比
Fig.11
Admissible domain of speed comparison between Energy method and GKILSC method
6 结论
本文基于广义碰撞定律,对重复使用运载火箭在 2-2 着陆模式下的着陆稳定性问题进行了研究,本文首先将该种着陆模式下火箭与平台的碰撞简化为平面运动两点碰撞问题,采用单边约束条件刻画竖直方向上的速度和冲量,采用经典库伦干摩擦模型刻画切向冲量. 同时考虑机械能的约束,给出了该着陆模式下火箭与平台发生多点碰撞后速度的值域.
对于浮放物体实验中观测到的 Free Rocking 和 Half Rocking 碰撞后两种运动模式,分别考虑了滑动摩擦和静摩擦状态下,给出了碰撞过程中恢复系数的值域. 最后基于实际工程中碰撞为接近完全非弹性碰撞的情况,给出了碰撞后切向速度和角速度与碰撞前切向速度和角速度的表达式,并提出了一种着陆稳定性的判别方法,该法形式较为简单,通过近似和简化避免了积分过程,适用于前期着陆稳定性估计. 随后通过算例分析了着陆腿跨距、摩擦系数对第二次碰撞中的广义运动学恢复系数和着陆稳定的速度容许范围的影响,以及不同竖直速度、着陆腿跨距、摩擦系数在水平速度-角速度剖面上对应的稳定要求的速度容许范围.
结论表明:稳定性随着着陆腿跨距增大而提高,摩擦系数越大稳定性受水平速度的影响越大,在水平速度的较小时稳定性随着摩擦系数增大而提高,竖直速度对稳定性的影响较小. 在图 2 所建立的坐标系下,角速度与切向速度同号时,着陆稳定性更好;当角速度与切向速度异号时,第二次碰撞过程中存在摩擦冲量使得箭体转动速度增大的风险,使得稳定性降低.
本文对碰撞过程中摩擦的分析为基于冲量的,没有对接触碰撞过程中接触点的黏滞-滑移的状态切换过程进行判断. 但由于着陆过程中的最不利工况出现在碰撞后向左或向右滑动,且由 4.1 的分析可知本文的假设更为保守,故本文的研究工作适用于实际工程的运载火箭着陆稳定性分析,可用于指导工程设计.
参考文献
View Option
[1]
余梦伦 . 两级入轨重复使用运载器的方案探讨
装备指挥技术学院学报 , 2006 ,17 (1 ):1 -5
[本文引用: 1]
( Yu Menglun . A study of the two-stage-to-orbit re-usable launch vehicle scheme
Journal of the Academy of Equipment Command & Technology 2006 ,17 (1 ):1 -5 (in Chinese))
[本文引用: 1]
[2]
杨勇 , 王小军 , 唐一华 等 . 重复使用运载器发展趋势及特点
导弹与航天运载技术 , 2002 , (5 ):15 -19
URL
[本文引用: 1]
自从上个世纪五六十年代人们提出重复使用运载器的概念,到现在的四五十年里,重复使用运载器的发展取得了很大的成就,同时也历经了不少挫折与失败.由于重复使用运载器具有极高的军事和民用价值,因此越来越受到世界各国的高度重视,当前又掀起了一股新的重复使用运载器研究热潮.本文综合分析了世界各国重复使用运载器的发展趋势、特点及从中得到的一些经验教训,值得我国发展重复使用运载器时借鉴和参考.
( Yang Yong Wang Xiaojun Tang Yihua , et al . Development trends and characteristics of reusable launch vehicles
Missiles and Space Vehicles 2002 , (5 ):15 -19 (in Chinese))
URL
[本文引用: 1]
自从上个世纪五六十年代人们提出重复使用运载器的概念,到现在的四五十年里,重复使用运载器的发展取得了很大的成就,同时也历经了不少挫折与失败.由于重复使用运载器具有极高的军事和民用价值,因此越来越受到世界各国的高度重视,当前又掀起了一股新的重复使用运载器研究热潮.本文综合分析了世界各国重复使用运载器的发展趋势、特点及从中得到的一些经验教训,值得我国发展重复使用运载器时借鉴和参考.
[3]
徐大富 , 张哲 , 吴克 等 . 垂直起降重复使用运载火箭发展趋势与关键技术研究进展
科学通报 , 2016 ,61 (32 ):3453 -3463
DOI
URL
[本文引用: 2]
( Xu Dafu Zhang Zhe Wu Ke , et al . Recent progress on development trend and key technologies of vertical take-off vertical landing reusable launch vehicle
Chin Sci Bull 2016 ,61 (32 ):3453 -3463 (in Chinese))
DOI
URL
[本文引用: 2]
[4]
Ralph E . SpaceX's successful debut of Falcon 9 Block 5 heralds the future of reusable rocketry
https://www.teslarati.com/spacex-successful-block-5-bangabandhu-launch-landing/. 2018 -05 -11
URL
[本文引用: 1]
[5]
Peter B . SpaceX's reusable Falcon 9: What are the real cost savings for customers
https://spacenews.com/spacexs-reusable-falcon-9-what-are-the-real-cost-savings-for-customers/. 2016 -4 -25
URL
[本文引用: 1]
[6]
王辰 , 王小军 , 张宏剑 等 . 可重复使用运载火箭发展研究
飞航导弹 , 2018 , (9 ):18 -26
[本文引用: 1]
( Wang Chen Wang Xiaojun Zhang Hongjian , et al . Research on development of reusable rocket
Aerodynamic Missile Journal 2018 , (9 ):18 -26 (in Chinese))
[本文引用: 1]
[7]
Blase WP . The first reusable SSTO spacecraft
Spaceflight 1994 ,35 (3 ):90 -94
[本文引用: 1]
[8]
崔乃刚 , 吴荣 , 韦常柱 等 . 垂直起降可重复使用运载器发展现状与关键技术分析
宇航总体技术 , 2018 ,2 (2 ):27 -42
[本文引用: 1]
( Cui Naigang Wu Rong Wei Changzhu , et al . Development and key technologies of vertical takeoff vertical landing reusable launch vehicle
Astronautical Systems Engineering Technology 2018 ,2 (2 ):27 -42 (in Chinese))
[本文引用: 1]
[9]
夏元明 , 张威 , 崔天宁 等 . 金属多级类蜂窝的压溃行为研究
力学学报 , 2019 ,51 (3 ):873 -883
[本文引用: 2]
( Xia Yuanming Zhang Wei Cui Tianning , et al . Investigation on crushing behavior of metal honeycomb-like hierarchical structure
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):873 -883 (in Chinese))
[本文引用: 2]
[10]
岳帅 , 聂宏 , 张明 等 . 一种用于垂直降落重复使用运载器的缓冲器性能分析
宇航学报 , 2016 ,37 (6 ):646 -656
DOI
URL
[本文引用: 4]
Based on a new type of oilhoneycomb multistage damper, a softlanding dynamic model is established for a vertical landing reusable launch vehicle with four symmetricallydistributed struts. This dynamic model takes account of the ground elasticoplastic deformation. Five kinds of critical landing working conditions are proposed, and coordinated analysis of the oilhoneycomb multistage damping parameters on the foundation of the first four conditions is carried out. After that, the effects of damping parameters on the landing stability on the basis of the turnover limit working conditions are studied. The research shows that the hydraulic damping parameters including orifice size, piston rod diameter and preload of the orifice valve's spring exert a great influence on the honeycomb crushing load, and a balanced combination of previous four parameters can boost vehicle's landing stability drastically.
( Yue Shuai Nie Hong Zhang Ming , et al . Analysis on performance of a damper used for vertical landing reusable launch vehicle
Journal of Astronautics 2016 ,37 (6 ):646 -656 (in Chinese))
DOI
URL
[本文引用: 4]
Based on a new type of oilhoneycomb multistage damper, a softlanding dynamic model is established for a vertical landing reusable launch vehicle with four symmetricallydistributed struts. This dynamic model takes account of the ground elasticoplastic deformation. Five kinds of critical landing working conditions are proposed, and coordinated analysis of the oilhoneycomb multistage damping parameters on the foundation of the first four conditions is carried out. After that, the effects of damping parameters on the landing stability on the basis of the turnover limit working conditions are studied. The research shows that the hydraulic damping parameters including orifice size, piston rod diameter and preload of the orifice valve's spring exert a great influence on the honeycomb crushing load, and a balanced combination of previous four parameters can boost vehicle's landing stability drastically.
[11]
陶海峰 . 垂直起降重复使用运载器软着陆系统研究
[硕士论文]. 南京: 南京航空航天大学 , 2017
[本文引用: 2]
( Tao Haifeng . Research on system of a damper used for vertical landing reusable launch vehicle
[Master Thesis]. Nanjing: Nanjing University of Aeronautics and Astronautics , 2017 (in Chinese))
[本文引用: 2]
[12]
杨文淼 , 刘志 , 时军委 . 可重复使用垂直起降运载火箭软着陆动力学仿真研究
科学技术与工程 , 2017 ,17 (21 ):329 -334
[本文引用: 3]
( Yang Wenmiao Liu Zhi Shi Junwei Dynamic simulation of VTOL reusable launch vehicle soft-landing
Science Technology and Engineering 2017 ,17 (21 ):329 -334 (in Chinese))
[本文引用: 3]
[13]
毕春莹 . 可回收火箭平行四边形式着陆机构设计及稳定性分析
[硕士论文]. 哈尔滨:哈尔滨工业大学 , 2016
[本文引用: 3]
( Bi Chunying . Design and stability analysis of landing mechanism with parallelogram structure for recyclable rocket
[Master Thesis]. Harbin: Harbin Institute of Technology , 2016 (in Chinese))
[本文引用: 3]
[14]
Herr RW Leonard HW . Dynamic model investigation of touchdown stability of lunar landing vehicles
NASA TN D-4215 , 1967
[本文引用: 1]
[15]
Zupp GA Doiron HH . A mathematical procedure for predicting the touchdown dynamics of a soft-landing vehicle
NASA TN-D-7045 , 1971
[本文引用: 1]
[16]
Black RJ . Quadrupedal landing gear systems for spacecraft
Journal of Spacecraft and Rockets 1964 ,1 (2 ):196 -203
DOI
URL
[本文引用: 1]
[17]
Doiron HH Zupp GA . Apollo lunar module landing dynamics
41st Structures, Structural Dynamics, and Materials Conference and Exhibit, Atlanta, USA, 2000-4-3-6 , 1 -11
[本文引用: 2]
[18]
杨建中 , 曾福明 , 满剑锋 等 . 嫦娥三号着陆器着陆缓冲系统设计与验证
中国科学: 技术科学 , 2014 ,44 (5 ):440 -449
DOI
URL
[本文引用: 2]
( Yang Jianzhong Zeng Fuming Man Jianfeng , et al . Design and verification of the landing impact attenuation system for Chang' E-3 lander
Sci Sin Tech 2014 ,44 (5 ):440 -449 (in Chinese))
DOI
URL
[本文引用: 2]
[19]
朱汪 , 杨建中 . 月球着陆器软着陆机构着陆稳定性仿真分析
宇航学报 , 2009 ,30 (5 ):1792 -1796
DOI
URL
[本文引用: 1]
介绍了软着陆机构仿真模型,提出了着陆稳定性判据和稳定性边界的离散化搜寻策略,并以实际算例给出了由着陆器着陆瞬时的竖直速度、水平速度、偏航角和月面倾角等主要影响因素确定的着陆稳定性边界。分析结果表明:对称着陆比非对称着陆更稳定;横向速度较大时支柱联接点容易发生强度破坏;当着陆面存在坡度时,横向速度沿下坡方向相对于沿上坡方向而言,着陆器更容易翻倒。
( Zhu Wang Yang Jianzhong . Touchdown stability simulation of landing gear system for lunar lander
Journal of Astronautics 2009 ,30 (5 ):1792 -1796 (in Chinese))
DOI
URL
[本文引用: 1]
介绍了软着陆机构仿真模型,提出了着陆稳定性判据和稳定性边界的离散化搜寻策略,并以实际算例给出了由着陆器着陆瞬时的竖直速度、水平速度、偏航角和月面倾角等主要影响因素确定的着陆稳定性边界。分析结果表明:对称着陆比非对称着陆更稳定;横向速度较大时支柱联接点容易发生强度破坏;当着陆面存在坡度时,横向速度沿下坡方向相对于沿上坡方向而言,着陆器更容易翻倒。
[20]
朱汪 , 杨建中 . 月球探测器软着陆机构着陆腿模型与仿真分析
宇航学报 , 2008 ,29 (6 ):1723 -1728
DOI
URL
[本文引用: 1]
给出了着陆动力学分析的数学模型,并在分析铝蜂窝材料缓冲特性的基础上,建立了 铝蜂窝缓冲器模型,将其应用于软着陆机构单条着陆腿冲击仿真。仿真结果表明,该模型在 缓冲行程、能量吸收及缓冲后加速度响应峰值等方面与试验结果基本一致。为软着陆机构着 陆冲击动力学分析时铝蜂窝建模提供参考。
( Zhu Wang Yang Jianzhong . Modeling and simulation of landing leg for the lunar landing gear system
Journal of Astronautics 2008 ,29 (6 ):1723 -1728 (in Chinese))
DOI
URL
[本文引用: 1]
给出了着陆动力学分析的数学模型,并在分析铝蜂窝材料缓冲特性的基础上,建立了 铝蜂窝缓冲器模型,将其应用于软着陆机构单条着陆腿冲击仿真。仿真结果表明,该模型在 缓冲行程、能量吸收及缓冲后加速度响应峰值等方面与试验结果基本一致。为软着陆机构着 陆冲击动力学分析时铝蜂窝建模提供参考。
[21]
Lin Q Nie H Chen J , et al . Research on stability of lunar lander soft landing based on flexible models
2010 International Conference on Computer Application and System Modeling (ICCASM 2010), Taiyuan, China, 2010-10-22-24 .
[本文引用: 1]
[22]
Wei X Lin Q Nie H , et al . Investigation on soft-landing dynamics of four-legged lunar lander
Acta Astronautica 2014 ,101 (1 ):55 -66
DOI
URL
[本文引用: 1]
[23]
王闯 , 刘荣强 , 邓宗全 等 . 月球着陆器着陆过程动力学分析
北京航空航天大学学报 , 2008 ,34 (4 ):381 -385
URL
[本文引用: 2]
The prototype of spatial trussed lunar lander was taken as a researching object. It was designed and manufactured by RCAMC HIT(Research Center of Aerospace Mechanism and Control, Harbin Institute of Technology). The simplified model of the lunar lander construction was given. Then, the location coordinate equations of every lunar lander foot and center of mass in inertial coordinate system were deduced. Based on these location coordinate equations, the lunar-s quasi-static stability condition was gotten. By analyzing the lunar lander-s transient dynamics behavior during the landing time, the formulas to calculate the transient dynamic parameters of the lunar lander during the landing time were derived; Through scattering time variables, the calculating procedures that can be imitated dynamic characters of the whole landing process were put forward, which laid a foundation for further research on the lunar lander-s landing dynamics behavior.
( Wang Chuang Liu Rongqiang Deng Zongquan , et al . Dynamics analysis of lunar lander's landing process
Journal of Beijing University of Aeronautics and Astronautics 2008 ,34 (4 ):381 -385 (in Chinese))
URL
[本文引用: 2]
The prototype of spatial trussed lunar lander was taken as a researching object. It was designed and manufactured by RCAMC HIT(Research Center of Aerospace Mechanism and Control, Harbin Institute of Technology). The simplified model of the lunar lander construction was given. Then, the location coordinate equations of every lunar lander foot and center of mass in inertial coordinate system were deduced. Based on these location coordinate equations, the lunar-s quasi-static stability condition was gotten. By analyzing the lunar lander-s transient dynamics behavior during the landing time, the formulas to calculate the transient dynamic parameters of the lunar lander during the landing time were derived; Through scattering time variables, the calculating procedures that can be imitated dynamic characters of the whole landing process were put forward, which laid a foundation for further research on the lunar lander-s landing dynamics behavior.
[24]
罗昌杰 , 邓宗全 , 刘荣强 等 . 基于零力矩点理论的腿式着陆器着陆稳定性研究
机械工程学报 , 2010 ,46 (9 ):38 -45
( Luo Changjie Deng Zongquan Liu Rongqiang , et al . Landing stability investigation of legged-type spacecraft lander based on zero moment point theory
Journal of Mechanical Engineering 2010 ,46 (9 ):38 -45 (in Chinese))
[25]
Li K Liu R Deng Z , et al . Research on the lander stability during lunar rover unloading base on the theory of ZMP
Advanced Materials Research 2012 , 457-458 :1264 -1270
DOI
URL
[本文引用: 2]
[26]
龙铝波 , 卿启湘 , 文桂林 等 . 基于的着陆器软着陆稳定性仿真分析
工程设计学报 , 2010 ,17 (5 ):334 -338
[本文引用: 2]
( Long Lubo Qing Qixiang Wen Guilin , et al . Simulation analysis of lander soft landing's stability based on ADAMS
Journal of Engineering Design 2010 ,17 (5 ):334 -338 (in Chinese))
[本文引用: 2]
[27]
Brogliato B Zhang H Liu C . Analysis of a generalized kinematic impact law for multibody-multicontact systems, with application to the planar rocking block and chains of balls
Multibody System Dynamics 2012 ,27 (3 ):351 -382
DOI
URL
[本文引用: 4]
In this paper, we analyze the capabilities of a generalized kinematic (Newton's like) restitution law for the modeling of a planar rigid block that impacts a rigid ground. This kinematic restitution law is based on a specific state transformation of the Lagrangian dynamics, using the kinetic metric on the configuration space. It allows one to easily derive a restitution rule for multiple impacts. The relationships with the classical angular velocity restitution coefficient r for rocking motion are examined in detail. In particular, it is shown that r has the interpretation of a tangential restitution coefficient. The case when Coulomb's friction is introduced at the contact impulse level together with an angular velocity restitution is analyzed. A simple chain of aligned balls is also examined, illustrating that the impact law applies to various types of multibody systems.
[28]
Housner GW . The behavior of inverted pendulum structures during earthquakes
Bulletin of the Seismological Society of America 1963 ,53 (2 ):403 -417
[本文引用: 1]
[29]
Shenton HW Jones NP . Base excitation of rigid bodies. I: Formulation
Journal of Engineering Mechanics 1991 ,117 (10 ):2286 -2306
DOI
URL
[本文引用: 1]
[30]
Shenton HW Jones NP . Base excitation of rigid bodies. II: Periodic slide-rock response
Journal of Engineering Mechanics 1991 ,117 (10 ):2307 -2328
DOI
URL
[本文引用: 1]
[31]
Lipscombe PR Pellegrino S . Free rocking of prismatic blocks
Journal of Engineering Mechanics 1993 ,119 (7 ):1387 -1410
DOI
URL
[本文引用: 2]
[32]
Zhuang F Wang Q . Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints
Multibody System Dynamics 2013 ,29 (4 ):403 -423
DOI
URL
[本文引用: 3]
The main purpose of this paper is to present a modeling and simulation method for the rigid multibody system with frictional translational joints. The small clearance between a slider and guide is considered. The geometric constraints of the translational joints are treated as bilateral constraints and the impacts between sliders and guides are neglected when the clearance sizes of the translational joints are very small. The contact situations of the normal forces acting on the sliders are described by inequalities and complementarity conditions, while the frictional contacts are characterized by a set-valued force law of the type of Coulomb's law for dry friction. The dynamic equations of the multibody systems with normal and tangential contact forces are written on the acceleration-force level using the Lagrange multiplier technique. The problem of the transitions of the contact situation of the normal forces acting on sliders and the transitions of the stick-slip of the sliders in the system is formulated as a horizontal linear complementarity problem (HLCP), which is solved by event-driven method. Baumgarte's stabilization method is used to decrease the constraint drift. Finally, two typical mechanisms are considered as demonstrative application examples. The numerical results obtained show some dynamical behaviors of the systems with frictional translational joints and constraint stabilization effect.
[33]
Zhuang F Wang Q . Modeling and analysis of rigid multibody systems with driving constraints and frictional translation joints
Acta Mechanica Sinica 2014 ,30 (3 ):437 -446
DOI
URL
An approach is proposed for modeling and analyses of rigid multibody systems with frictional translation joints and driving constraints. The geometric constraints of translational joints with small clearance are treated as bilateral constraints by neglecting the impact between sliders and guides. Firstly, the normal forces acting on sliders, the driving constraint forces (or moments) and the constraint forces of smooth revolute joints are all described by complementary conditions. The frictional contacts are characterized by a setvalued force law of Coulomb's dry friction. Combined with the theory of the horizontal linear complementarity problem (HLCP), an event-driven scheme is used to detect the transitions of the contact situation between sliders and guides, and the stick-slip transitions of sliders, respectively. And then, all constraint forces in the system can be computed easily. Secondly, the dynamic equations of multibody systems are written at the acceleration-force level by the Lagrange multiplier technique, and the Baumgarte stabilization method is used to reduce the constraint drift. Finally, a numerical example is given to show some non-smooth dynamical behaviors of the studied system. The obtained results validate the feasibility of algorithm and the effect of constraint stabilization.
[34]
王晓军 , 吕敬 , 王琪 . 含摩擦滑移铰平面多刚体系统动力学的数值算法
力学学报 , 2019 ,51 (1 ):209 -217
URL
( Wang Xiaojun Lü Jing Wang Qi . A numerical method for dynamics of planar multi-rigid-body system with frictional translational joints based on LuGre friction model
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):209 -217 (in Chinese))
URL
[35]
张润森 , 王琪 . 浮放物体平面多刚体动力学建模与算法研究
力学学报 , 2017 ,49 (6 ):1370 -1379
URL
[本文引用: 5]
( Zhang Runsen Wang Qi . Research on modeling and numerical method of free standing body on planar rigid multibody dynamics
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (6 ):1370 -1379 (in Chinese))
URL
[本文引用: 5]
[36]
Zhang H Brogliato B Liu C . Study of the Planar Rocking-Block Dynamics With Coulomb Friction: Critical Kinetic Angles
Journal of Computational and Nonlinear Dynamics 2012 ,8 :021002
DOI
URL
[本文引用: 2]
[37]
张宏剑 , 庄方方 , 王辰 等 . 线碰撞离散化研究
动力学与控制学报 , 2017 ,15 (4 ):330 -334
[本文引用: 2]
( Zhang Hongjian Zhuang Fangfang Wang Chen , et al . Research on discretization of line impact in rocking block
Journal of Dynamics and Control 2017 ,15 (4 ):330 -334 (in Chinese))
[本文引用: 2]
[38]
Liu C Zhao Z Brogliato B . Frictionless multiple impacts in multibody systems, I, Theoretical framework
Proc R Soc A 2008 ,464 :3193 -3211
DOI
URL
[本文引用: 3]
[39]
Liu C Zhao Z Brogliato B . Frictionless multiple impacts in multibody systems. II, Numerical algorithm and simulation results
Proc R Soc A 2009 ,465 :2267 -2292
DOI
URL
[本文引用: 3]
[40]
刘丽兰 , 刘宏昭 , 吴子英 等 . 机械系统中摩擦模型的研究进展
力学进展 , 2008 ,38 (2 ):201 -213
URL
[本文引用: 1]
The friction inmechanical systems plays an increasingly prominent role. It isimportant to reduce friction in mechanical systems, especially the nonlinear friction. Because of its complicated nature, it is very difficult for a single model to account for various mechanisms of friction, and dozens offriction models have been put forward so far. With respect to thedevelopment of the friction modeling in mechanical systems, some important friction phenomena are first described in this paper, suchas Coulomb friction, viscous friction, Stribeck friction,presliding displacement, varying static force and friction lag,etc. Next, a few important friction models in common use are discussed, including six static and seven dynamic friction models. The forms, characteristics andapplicability of these models are discussed in detail. The formsand the parameter identification of the static friction models aresimple and easy, but they cannot be used to simulate the dynamiccharacteristics of friction. Comparatively, the dynamic frictionmodels can describe the friction more completely, with their complicated forms, which makes it difficult to identify related parameters.Then, the influence of friction modeling on the mechanical systemdynamics is briefly discussed as well as the applications offriction models to the control of high precision mechanicalsystems. Lastly, several problems to be further studied arepointed out. This paper provides some guidance in the selection of friction models in applications.
( Liu Lilan Liu Hongzhao Wu Ziying , et al . An overview of friction models in mechanical systems
Advances in Mechanics 2008 ,38 (2 ):201 -213 (in Chinese))
URL
[本文引用: 1]
The friction inmechanical systems plays an increasingly prominent role. It isimportant to reduce friction in mechanical systems, especially the nonlinear friction. Because of its complicated nature, it is very difficult for a single model to account for various mechanisms of friction, and dozens offriction models have been put forward so far. With respect to thedevelopment of the friction modeling in mechanical systems, some important friction phenomena are first described in this paper, suchas Coulomb friction, viscous friction, Stribeck friction,presliding displacement, varying static force and friction lag,etc. Next, a few important friction models in common use are discussed, including six static and seven dynamic friction models. The forms, characteristics andapplicability of these models are discussed in detail. The formsand the parameter identification of the static friction models aresimple and easy, but they cannot be used to simulate the dynamiccharacteristics of friction. Comparatively, the dynamic frictionmodels can describe the friction more completely, with their complicated forms, which makes it difficult to identify related parameters.Then, the influence of friction modeling on the mechanical systemdynamics is briefly discussed as well as the applications offriction models to the control of high precision mechanicalsystems. Lastly, several problems to be further studied arepointed out. This paper provides some guidance in the selection of friction models in applications.
[41]
王东 , 徐超 , 胡杰 等 . 连接结构接触界面非线性力学建模研究
力学学报 , 2018 ,50 (1 ):44 -57
URL
[本文引用: 1]
( Wang Dong Xu Chao Hu Jie , et al . Nonlinear mechanics modeling for joint interface of assembled structure
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (1 ):44 -57 (in Chinese))
URL
[本文引用: 1]
[42]
赵振 , 刘才山 , 陈滨 . Painlevé疑难的理论分析和实验验证
力学学报 , 2013 ,45 (1 ):37 -44
DOI
URL
[本文引用: 1]
Painlevé paradox may appear in multi-rigid-body systems subjected to Coulomb' friction. No solution or multiple solutions make the systems inconsistent or indeterminate. It is worth investigating how the subsequent motions of the systems in inconsistent states evolve since the actual systems will always move on. The theoretical analysis and the experimental verification are carried out to confirm the tangential impact in the inconsistent case of the systems. The characteristic of the stick motions are confirmed during tangential impact.
( Zhao Zhen Liu Caishan Chen Bin . Theoretical analysis and experimental verification for Painlevé paradox
Chinese Journal of Theoretical and Applied Mechanics 2013 ,45 (1 ):37 -44 (in Chinese))
DOI
URL
[本文引用: 1]
Painlevé paradox may appear in multi-rigid-body systems subjected to Coulomb' friction. No solution or multiple solutions make the systems inconsistent or indeterminate. It is worth investigating how the subsequent motions of the systems in inconsistent states evolve since the actual systems will always move on. The theoretical analysis and the experimental verification are carried out to confirm the tangential impact in the inconsistent case of the systems. The characteristic of the stick motions are confirmed during tangential impact.
两级入轨重复使用运载器的方案探讨
1
2006
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
两级入轨重复使用运载器的方案探讨
1
2006
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
重复使用运载器发展趋势及特点
1
2002
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
重复使用运载器发展趋势及特点
1
2002
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
垂直起降重复使用运载火箭发展趋势与关键技术研究进展
2
2016
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
垂直起降重复使用运载火箭发展趋势与关键技术研究进展
2
2016
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
SpaceX's successful debut of Falcon 9 Block 5 heralds the future of reusable rocketry
1
2018
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
SpaceX's reusable Falcon 9: What are the real cost savings for customers
1
2016
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
可重复使用运载火箭发展研究
1
2018
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
可重复使用运载火箭发展研究
1
2018
... 运载火箭作为人类进入太空的主要工具,高昂的发射费用限制了人类对太空的开发和利用,运载火箭的一次性使用是导致发射成本高昂的主要原因之一. 因此对运载器的重复使用,对于降低发射成本、提升人类进入太空能力具有十分重要的意义. 余梦伦[1 ] 指出在现有的动力、结构等技术水平下,两级入轨的重复使用运载器较单级入轨的重复使用运载器具有更高的可行性. 美国、日本、欧洲等多个国家和地区对运载器重复使用的多种技术方案进行了诸多尝试[2 ] . 美国的航天飞机是第一种实用化的重复使用运载器,采用一级半入轨、轨道器水平返回的设计方案,但是其发射费用远超预期,单次发射费用高达 3$\sim$4 亿美元[3 ] . 美国的太空探索技术公司 (SpaceX) 的猎鹰 9 号 (Falcon-9) 火箭为一种两级入轨的运载火箭,2015 年以垂直着陆的方式实现了一子级回收,并于 2017 年成功实现了回收的火箭一子级的重复使用[4 ] ,实现一子级重复使用后,其单次发射费用从 6120 万美元降低至 4280 万美元[5 ] . 猎鹰 9 号火箭在技术和经济上取得的成功,证明了两级入轨、一子级垂直返回是一种实现运载器重复使用的可行方案[6 ] . ...
The first reusable SSTO spacecraft
1
1994
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
垂直起降可重复使用运载器发展现状与关键技术分析
1
2018
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
垂直起降可重复使用运载器发展现状与关键技术分析
1
2018
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
金属多级类蜂窝的压溃行为研究
2
2019
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
金属多级类蜂窝的压溃行为研究
2
2019
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
一种用于垂直降落重复使用运载器的缓冲器性能分析
4
2016
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
... 以文献[10 ] 中采用的四腿式火箭垂直着陆原理样机为例,考察完全非弹性碰撞下火箭的着陆过程. 该样机在 2-2 着陆模式下 $b = 3.43$m,着陆腿展开后质心高度 $h = 7.27$m,着陆体总质量 $m = 5400$kg,其中着陆腿重 200kg,$ {\mu } = 0.3$,绕质心转动惯量 $J_{\rm c} = 1.354\times 10^5$kg$\cdot $m$^2$. 由式 (42)、式 (44) 得 ...
... 对于上述参数,由表 2 得 $e_{{\rm n},21} $与${v_{x0} } /{\omega h}$ 的关系如图 7 所示. 对其跨距进行调整,分析跨距对恢复系数 $e_{{\rm c}4,3} $,$e_{{\rm c}4,1} $ 及其对应的临界速度比 $({v_{x0} }/{\omega h})_{{\rm ch}1} $,$({v_{x0} } /{\omega h})_{{\rm ch2}} $ 影响,半跨距 $b$ 取 2$\sim$6m,由于着陆腿质量仅为 200kg,故可近似忽略跨距变化对转动惯量的影响,结果如图 8 所示. 对 $\mu $ 进行调整,分析 $\mu $ 对恢复系数 $e_{{\rm c}4,1} $,$e_{{\rm c}4,3} $ 及其对应的临界速度比影响,同样保持其他参数与文献[10 ] 一致,$\mu $ 取 0 到 0.8,结果如图 9 所示. ...
一种用于垂直降落重复使用运载器的缓冲器性能分析
4
2016
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
... 以文献[10 ] 中采用的四腿式火箭垂直着陆原理样机为例,考察完全非弹性碰撞下火箭的着陆过程. 该样机在 2-2 着陆模式下 $b = 3.43$m,着陆腿展开后质心高度 $h = 7.27$m,着陆体总质量 $m = 5400$kg,其中着陆腿重 200kg,$ {\mu } = 0.3$,绕质心转动惯量 $J_{\rm c} = 1.354\times 10^5$kg$\cdot $m$^2$. 由式 (42)、式 (44) 得 ...
... 对于上述参数,由表 2 得 $e_{{\rm n},21} $与${v_{x0} } /{\omega h}$ 的关系如图 7 所示. 对其跨距进行调整,分析跨距对恢复系数 $e_{{\rm c}4,3} $,$e_{{\rm c}4,1} $ 及其对应的临界速度比 $({v_{x0} }/{\omega h})_{{\rm ch}1} $,$({v_{x0} } /{\omega h})_{{\rm ch2}} $ 影响,半跨距 $b$ 取 2$\sim$6m,由于着陆腿质量仅为 200kg,故可近似忽略跨距变化对转动惯量的影响,结果如图 8 所示. 对 $\mu $ 进行调整,分析 $\mu $ 对恢复系数 $e_{{\rm c}4,1} $,$e_{{\rm c}4,3} $ 及其对应的临界速度比影响,同样保持其他参数与文献[10 ] 一致,$\mu $ 取 0 到 0.8,结果如图 9 所示. ...
垂直起降重复使用运载器软着陆系统研究
2
2017
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
垂直起降重复使用运载器软着陆系统研究
2
2017
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
可重复使用垂直起降运载火箭软着陆动力学仿真研究
3
2017
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
... 在小姿态角着陆时需要考虑第一次碰撞发生在 1 点或 2 点两种情况并分别计算其 $\gamma _{\rm stable} $ 并对二者取不利情况,即取两种情况 $\gamma _{\rm stable} $ 的较小值. 则对任意着陆速度 $ \{ \dot {x}_{\rm c}^{(0)}$, $\dot {y}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} \}$ 在着陆稳定分析中其 $\gamma _{\rm stable} $ 与 $ \{ - \dot {x}_{\rm c}^{(0)}$, $\dot {y}_{\rm c}^{(0)}$, $ - \dot {\theta }^{(0)} \}$ 对应的 $\gamma _{\rm stable} $ 相等,可见图 9 所示的稳定速度边界也具有这种对称性. 由图 9 (a) 可见,在图 2 所建立的坐标系下着陆前角速度与切向速度同号时着陆更稳定,竖直下降速度 $ - \dot {y}_{\rm c}^{(0)} $ 对稳定性的影响较为复杂,但稳定区间差别较小,与动力学仿真的结论相似[12 ] . 同时 $\dot {y}_{\rm c}^{(0)} = - 5$m/s 与 $ - 1$m/s 和 $ - 3$m/s 两种速度在角速度与切向速度同号且 $\vert \dot {x}_{\rm c}^{(0)} \vert $ 较大时速度容许范围边界的趋势不同,是由于其翻倒模式不同. 以 $\dot {x}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} > 0$ 为例,$\dot {y}_{\rm c}^{(0)} = - 5$m/s 时其翻倒模式为首先在 1 点发生碰撞后再发生第二次碰撞,随后绕 2 点翻倒;而 $\dot {y}_{\rm c}^{(0)} = - 1$m/s 或 $ - 3$m/s 时其翻倒模式为在 2 点发生碰撞后绕 2 点翻倒,不发生第二次碰撞. 对于图 9 (b) $b = 2$m 时,$\dot {x}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} > 0$ 且 $\dot {x}_{\rm c}^{(0)} $ 较大时翻倒模式与图 9 (a) $\dot {y}_{\rm c}^{(0)} = - 5$m/s 时相同,同时由图 9 (b) 可见随着陆腿跨距增大稳定性增强. 由图 9 (c) 可见随着 $\mu $ 增大在 $\dot {\theta }^{(0)}$ 较大、$\dot {x}_{\rm c}^{(0)} $ 较小时着陆更稳定,在 $\dot {\theta }^{(0)}$ 较小、$\dot {x}_{\rm c}^{(0)} $ 较大时着陆更不稳定,考虑到垂直着陆时水平速度通常较小,故 $\mu $ 增大有利于着陆稳定. 若干算例对应的容许速度范围的边界沿水平轴 $\dot {x}_{\rm c}^{(0)} $ 无限延伸,此时为判据式 (47) 所示的情况,即始终保持滑动也不会翻倒. ...
可重复使用垂直起降运载火箭软着陆动力学仿真研究
3
2017
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
... 在小姿态角着陆时需要考虑第一次碰撞发生在 1 点或 2 点两种情况并分别计算其 $\gamma _{\rm stable} $ 并对二者取不利情况,即取两种情况 $\gamma _{\rm stable} $ 的较小值. 则对任意着陆速度 $ \{ \dot {x}_{\rm c}^{(0)}$, $\dot {y}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} \}$ 在着陆稳定分析中其 $\gamma _{\rm stable} $ 与 $ \{ - \dot {x}_{\rm c}^{(0)}$, $\dot {y}_{\rm c}^{(0)}$, $ - \dot {\theta }^{(0)} \}$ 对应的 $\gamma _{\rm stable} $ 相等,可见图 9 所示的稳定速度边界也具有这种对称性. 由图 9 (a) 可见,在图 2 所建立的坐标系下着陆前角速度与切向速度同号时着陆更稳定,竖直下降速度 $ - \dot {y}_{\rm c}^{(0)} $ 对稳定性的影响较为复杂,但稳定区间差别较小,与动力学仿真的结论相似[12 ] . 同时 $\dot {y}_{\rm c}^{(0)} = - 5$m/s 与 $ - 1$m/s 和 $ - 3$m/s 两种速度在角速度与切向速度同号且 $\vert \dot {x}_{\rm c}^{(0)} \vert $ 较大时速度容许范围边界的趋势不同,是由于其翻倒模式不同. 以 $\dot {x}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} > 0$ 为例,$\dot {y}_{\rm c}^{(0)} = - 5$m/s 时其翻倒模式为首先在 1 点发生碰撞后再发生第二次碰撞,随后绕 2 点翻倒;而 $\dot {y}_{\rm c}^{(0)} = - 1$m/s 或 $ - 3$m/s 时其翻倒模式为在 2 点发生碰撞后绕 2 点翻倒,不发生第二次碰撞. 对于图 9 (b) $b = 2$m 时,$\dot {x}_{\rm c}^{(0)}$, $\dot {\theta }^{(0)} > 0$ 且 $\dot {x}_{\rm c}^{(0)} $ 较大时翻倒模式与图 9 (a) $\dot {y}_{\rm c}^{(0)} = - 5$m/s 时相同,同时由图 9 (b) 可见随着陆腿跨距增大稳定性增强. 由图 9 (c) 可见随着 $\mu $ 增大在 $\dot {\theta }^{(0)}$ 较大、$\dot {x}_{\rm c}^{(0)} $ 较小时着陆更稳定,在 $\dot {\theta }^{(0)}$ 较小、$\dot {x}_{\rm c}^{(0)} $ 较大时着陆更不稳定,考虑到垂直着陆时水平速度通常较小,故 $\mu $ 增大有利于着陆稳定. 若干算例对应的容许速度范围的边界沿水平轴 $\dot {x}_{\rm c}^{(0)} $ 无限延伸,此时为判据式 (47) 所示的情况,即始终保持滑动也不会翻倒. ...
可回收火箭平行四边形式着陆机构设计及稳定性分析
3
2016
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 基于能量的方法具有简洁、对精细化的动力学模型依赖较少的优点,但是其结论较为保守,尤其是能量法将触地时所有动能均视为翻倒能,但动力学仿真表明,当着陆腿中含有塑性缓冲吸能材料时,着陆时竖直方向速度的大小对不翻倒对应的参数边界的影响较小[13 ] . 基于动力学仿真的方法及实验的方法结论更为准确,但是其分析过程对精细化的动力学模型较为依赖,而在重复使用火箭的方案设计初期确定着陆腿的几何参数时,由于对象尚未确定,往往难以建立精细的动力学模型,所以难以采用动力学仿真或实验的方法. 火箭着陆问题为含摩擦的多点碰撞问题,基于广义碰撞定律 (generalized impact law) 的运动学研究可以在方案设计初期,对着陆稳定性分析提供借鉴. 目前基于运动学方法对着陆器着陆稳定性的研究较少,Brogliato 等[27 ] 曾将广义碰撞定律应用于 Rocking Block 问题,讨论了黏滞和无摩擦状态下二维 Rocking Block 问题中碰撞后速度的取值范围. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
可回收火箭平行四边形式着陆机构设计及稳定性分析
3
2016
... 猎鹰 9 号火箭在陆地和海上平台垂直着陆时,通过腿式着陆缓冲机构实现降低冲击载荷和提高着陆稳定的目的,火箭着陆过程的稳定性是实现火箭垂直着陆的一项关键技术[3 ] . 最早的垂直起降验证机为 1993 年麦道公司 (McDonnell-Douglas) 研发的三角快帆 (Delta Clipper) 验证机[7 ] ,对运载器的垂直起降的制导、控制、着陆稳定性和缓冲器性能等关键技术进行了演示验证. 欧洲、日本等国家和地区也正在开展相应的研究和演示验证工作[8 ] . 我国关于火箭垂直着陆缓冲机构的研究起步相对较晚、研究相对较少. 夏元明等[9 ] 对金属蜂窝材料的压溃特性进行了数值和实验研究,分析了多种设计参数对比吸能、峰值应力等力学特性的影响,为蜂窝缓冲器的设计提供了参考. 聂宏等[10 -11 ] 对采用油液/蜂窝混合式多级缓冲器的四腿式火箭垂直着陆过程进行了动力学仿真分析,给出了 5 种典型工况下速度的稳定边界,研究了缓冲器参数对着陆稳定性的影响. 杨文淼等[12 ] 针对铝蜂窝材料在压缩过程中完全非弹性的特征,基于 Adams 平台编写了铝蜂窝缓冲材料的计算模型,并对采用铝蜂窝缓冲器的四腿式火箭的垂直着陆过程进行了仿真,分析了不同着陆模式下箭体的运动及可能出现的翻倒等风险. 毕春莹等[13 ] 设计了一种平行四边形腿式着陆缓冲器,采用多刚体动力学的方法,分别利用 Matlab 进行了编程建模和利用 Adams 进行仿真,分析了着陆稳定对应的参数边界,二者得到的结论相似. ...
... 基于能量的方法具有简洁、对精细化的动力学模型依赖较少的优点,但是其结论较为保守,尤其是能量法将触地时所有动能均视为翻倒能,但动力学仿真表明,当着陆腿中含有塑性缓冲吸能材料时,着陆时竖直方向速度的大小对不翻倒对应的参数边界的影响较小[13 ] . 基于动力学仿真的方法及实验的方法结论更为准确,但是其分析过程对精细化的动力学模型较为依赖,而在重复使用火箭的方案设计初期确定着陆腿的几何参数时,由于对象尚未确定,往往难以建立精细的动力学模型,所以难以采用动力学仿真或实验的方法. 火箭着陆问题为含摩擦的多点碰撞问题,基于广义碰撞定律 (generalized impact law) 的运动学研究可以在方案设计初期,对着陆稳定性分析提供借鉴. 目前基于运动学方法对着陆器着陆稳定性的研究较少,Brogliato 等[27 ] 曾将广义碰撞定律应用于 Rocking Block 问题,讨论了黏滞和无摩擦状态下二维 Rocking Block 问题中碰撞后速度的取值范围. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
Dynamic model investigation of touchdown stability of lunar landing vehicles
1
1967
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
A mathematical procedure for predicting the touchdown dynamics of a soft-landing vehicle
1
1971
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
Quadrupedal landing gear systems for spacecraft
1
1964
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
Apollo lunar module landing dynamics
2
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 保持上述参数不变,取 $\dot {y}_{\rm c}^{(0)} = - 3$m/s,分别采用 GKILSC 法和能量法[17 ] 对能量法稳定的速度边界进行对比如图 11 所示,可见 GKILSC 法相较于能量法,其速度容许范围区域更大,且考虑了水平速度和角速度方向的影响,故更为精确. ...
嫦娥三号着陆器着陆缓冲系统设计与验证
2
2014
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
嫦娥三号着陆器着陆缓冲系统设计与验证
2
2014
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
月球着陆器软着陆机构着陆稳定性仿真分析
1
2009
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
月球着陆器软着陆机构着陆稳定性仿真分析
1
2009
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
月球探测器软着陆机构着陆腿模型与仿真分析
1
2008
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
月球探测器软着陆机构着陆腿模型与仿真分析
1
2008
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
Research on stability of lunar lander soft landing based on flexible models
1
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
Investigation on soft-landing dynamics of four-legged lunar lander
1
2014
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
月球着陆器着陆过程动力学分析
2
2008
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
月球着陆器着陆过程动力学分析
2
2008
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
基于零力矩点理论的腿式着陆器着陆稳定性研究
2010
基于零力矩点理论的腿式着陆器着陆稳定性研究
2010
Research on the lander stability during lunar rover unloading base on the theory of ZMP
2
2012
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 对于重复使用运载火箭的着陆过程,依据四条着陆腿是否存在同时落地,可以分为 4,2-2,1-2-1,1-1-1-1 共 4 种着陆模式,其中 4 模式表示 4 条着陆腿同时落地;2-2 模式表示先有两条腿同时落地,再有两条腿同时落地;1-2-1 模式表示先有 1 条腿落地,然后两条腿同时着地,最后再有 1 条腿落地,这里考虑了着陆腿的形变导致着陆过程中 4 条腿的着陆点不恒共面;1-1-1-1 模式表示 4 条腿不同时依次落地;其中 2-2 模式和 1-2-1 模式均为平面运动着陆模式,有研究通过三维动力学仿真表明,2-2 模式较 1-2-1 模式的稳定性更差[25 ] . 本文将针对 2-2 模式,基于刚体动力学研究其着陆的稳定性. ...
基于的着陆器软着陆稳定性仿真分析
2
2010
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
基于的着陆器软着陆稳定性仿真分析
2
2010
... 火箭垂直着陆的动力学行为与月球着陆器的着陆具有一定的相似性,国内外在月球着陆器着陆缓冲机构和着陆稳定性方面开展了较多研究工作. 目前关于着陆稳定性的研究方法主要有能量法、动力学仿真法和实验的方法,稳定性分析中以翻倒为失效判据计算临界速度. 美国关于月球着陆器着陆稳定性的研究集中于 20 世纪 60 年代至 70 年代阿波罗计划时期,主要研究方法为通过建立多刚体动力模型进行动力学仿真的方法和实验方法[14 -15 ] ,提出四条腿在稳定性与重量上为最优的方案[16 ] . 2000年Doiron等[17 ] 总结了阿波罗计划时期关于月球着陆器软着陆过程的研究. 国内关于月球着陆器着陆稳定性的研究是 21 世纪以来伴随"嫦娥"探月工程开展的,杨建中等对月球着陆器的着陆稳定问题采用能量法进行着陆腿跨距的总体方案设计[18 ] ,采用多柔性体动力学模型进行着陆过程动力学仿真及着陆腿设计[19 ] ,并采用动力学试验对仿真分析结果进行验证[20 ] ,能量法即要求着陆器瞬时着陆器的动能小于翻倒过程越过质心最高点所需的重力势能. 聂宏[21 -22 ] 采用瞬态动力学的方法对考虑了着陆器、地面柔性的着陆冲击过程的进行了动力学仿真,并进行了着陆过程的实验研究. 邓宗全等[23 -25 ] 采用多刚体动力学模型,给出了四腿桁架式月球着陆器着陆过程的显式动力学建模方法,并将零力矩点法引入到着陆稳定性分析中. 卿启湘等[26 ] 对着陆器采用多柔性体动力学模型,分析了着陆器在刚性地面和月壤柔性地面的着陆过程,指出当偏航角为 22.5$^\circ$ 时着陆稳定性最为恶劣. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
Analysis of a generalized kinematic impact law for multibody-multicontact systems, with application to the planar rocking block and chains of balls
4
2012
... 基于能量的方法具有简洁、对精细化的动力学模型依赖较少的优点,但是其结论较为保守,尤其是能量法将触地时所有动能均视为翻倒能,但动力学仿真表明,当着陆腿中含有塑性缓冲吸能材料时,着陆时竖直方向速度的大小对不翻倒对应的参数边界的影响较小[13 ] . 基于动力学仿真的方法及实验的方法结论更为准确,但是其分析过程对精细化的动力学模型较为依赖,而在重复使用火箭的方案设计初期确定着陆腿的几何参数时,由于对象尚未确定,往往难以建立精细的动力学模型,所以难以采用动力学仿真或实验的方法. 火箭着陆问题为含摩擦的多点碰撞问题,基于广义碰撞定律 (generalized impact law) 的运动学研究可以在方案设计初期,对着陆稳定性分析提供借鉴. 目前基于运动学方法对着陆器着陆稳定性的研究较少,Brogliato 等[27 ] 曾将广义碰撞定律应用于 Rocking Block 问题,讨论了黏滞和无摩擦状态下二维 Rocking Block 问题中碰撞后速度的取值范围. ...
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 上文讨论了无附加约束下恢复系数的值域,为碰撞后运动的一般情况,诸多分析和试验表明发生如图 3 所示的碰撞后,箭体通常有一条腿与着陆平台保持接触[27 -31 ,35 ] . 若碰撞后 1 点与平台保持接触,即 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} \geqslant 0$,该运动模式称为 Free Rocking;若碰撞后 2 点与平台保持接触,即 $e_{{\rm n},1} \geqslant 0$,$e_{{\rm n},21} = 0$,该运动模式称为 Half Rocking. 两种运动模式如图 4 所示. 下面,本文将分别讨论这两种运动模式在碰撞前后保持黏滞、无摩擦、碰撞前滑动碰 撞后黏滞、碰撞前后保持滑动摩擦 4 种情况下其恢复系数、几何参数、摩擦系数需满足的条件. ...
... 在工程中由着陆腿中通常添加吸能构件,如铝蜂窝缓冲器[9 ,12 ,18 -23 ,26 ] 、油液缓冲器[11 ,13 ] 或混合缓冲器[10 ] ,使得箭体与地面的碰撞接近完全非弹性碰撞. 对于完全非弹性碰撞,碰撞后的运动模式为 Free Rocking 或在纵向静止[27 ] ,即碰撞后其 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} $ 为 3.1$\sim$3.4 $e_{{\rm n},21} $ 中的下界. 下面将从 3.1$\sim$3.4 的分析出发分析完全非弹性碰撞下其广义运动学恢复系数. ...
The behavior of inverted pendulum structures during earthquakes
1
1963
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
Base excitation of rigid bodies. I: Formulation
1
1991
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
Base excitation of rigid bodies. II: Periodic slide-rock response
1
1991
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
Free rocking of prismatic blocks
2
1993
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 上文讨论了无附加约束下恢复系数的值域,为碰撞后运动的一般情况,诸多分析和试验表明发生如图 3 所示的碰撞后,箭体通常有一条腿与着陆平台保持接触[27 -31 ,35 ] . 若碰撞后 1 点与平台保持接触,即 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} \geqslant 0$,该运动模式称为 Free Rocking;若碰撞后 2 点与平台保持接触,即 $e_{{\rm n},1} \geqslant 0$,$e_{{\rm n},21} = 0$,该运动模式称为 Half Rocking. 两种运动模式如图 4 所示. 下面,本文将分别讨论这两种运动模式在碰撞前后保持黏滞、无摩擦、碰撞前滑动碰 撞后黏滞、碰撞前后保持滑动摩擦 4 种情况下其恢复系数、几何参数、摩擦系数需满足的条件. ...
Modeling and simulation of the nonsmooth planar rigid multibody systems with frictional translational joints
3
2013
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 同时约束面作用力 $ F_{{\rm n},1}$ 和 $F_{{\rm n},2}$ 与 $\delta _1 $ 和 $\delta _2 $ 满足线性互补条件[32 -35 ] ...
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
Modeling and analysis of rigid multibody systems with driving constraints and frictional translation joints
2014
含摩擦滑移铰平面多刚体系统动力学的数值算法
2019
含摩擦滑移铰平面多刚体系统动力学的数值算法
2019
浮放物体平面多刚体动力学建模与算法研究
5
2017
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 同时约束面作用力 $ F_{{\rm n},1}$ 和 $F_{{\rm n},2}$ 与 $\delta _1 $ 和 $\delta _2 $ 满足线性互补条件[32 -35 ] ...
... 其中,$F_{{\rm n},i } $ 为该点支撑力;$\mu $ 为摩擦系数;$v_{{\tau},i} $ 为碰撞两点切向的相对速度;$ {\rm Sgn}( \cdot )$ 为集值函数[35 ] . ...
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
... 上文讨论了无附加约束下恢复系数的值域,为碰撞后运动的一般情况,诸多分析和试验表明发生如图 3 所示的碰撞后,箭体通常有一条腿与着陆平台保持接触[27 -31 ,35 ] . 若碰撞后 1 点与平台保持接触,即 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} \geqslant 0$,该运动模式称为 Free Rocking;若碰撞后 2 点与平台保持接触,即 $e_{{\rm n},1} \geqslant 0$,$e_{{\rm n},21} = 0$,该运动模式称为 Half Rocking. 两种运动模式如图 4 所示. 下面,本文将分别讨论这两种运动模式在碰撞前后保持黏滞、无摩擦、碰撞前滑动碰 撞后黏滞、碰撞前后保持滑动摩擦 4 种情况下其恢复系数、几何参数、摩擦系数需满足的条件. ...
浮放物体平面多刚体动力学建模与算法研究
5
2017
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 同时约束面作用力 $ F_{{\rm n},1}$ 和 $F_{{\rm n},2}$ 与 $\delta _1 $ 和 $\delta _2 $ 满足线性互补条件[32 -35 ] ...
... 其中,$F_{{\rm n},i } $ 为该点支撑力;$\mu $ 为摩擦系数;$v_{{\tau},i} $ 为碰撞两点切向的相对速度;$ {\rm Sgn}( \cdot )$ 为集值函数[35 ] . ...
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
... 上文讨论了无附加约束下恢复系数的值域,为碰撞后运动的一般情况,诸多分析和试验表明发生如图 3 所示的碰撞后,箭体通常有一条腿与着陆平台保持接触[27 -31 ,35 ] . 若碰撞后 1 点与平台保持接触,即 $e_{{\rm n},1} = 0$,$e_{{\rm n},21} \geqslant 0$,该运动模式称为 Free Rocking;若碰撞后 2 点与平台保持接触,即 $e_{{\rm n},1} \geqslant 0$,$e_{{\rm n},21} = 0$,该运动模式称为 Half Rocking. 两种运动模式如图 4 所示. 下面,本文将分别讨论这两种运动模式在碰撞前后保持黏滞、无摩擦、碰撞前滑动碰 撞后黏滞、碰撞前后保持滑动摩擦 4 种情况下其恢复系数、几何参数、摩擦系数需满足的条件. ...
Study of the Planar Rocking-Block Dynamics With Coulomb Friction: Critical Kinetic Angles
2
2012
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... [36 ]采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
线碰撞离散化研究
2
2017
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... [37 ]将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
线碰撞离散化研究
2
2017
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... [37 ]将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
Frictionless multiple impacts in multibody systems, I, Theoretical framework
3
2008
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
... 在碰撞过程中,引入以下两个假设[38 -39 ] : ...
Frictionless multiple impacts in multibody systems. II, Numerical algorithm and simulation results
3
2009
... Rocking Block 问题首先由 Housner[28 ] 在研究1962 年智利大地震时地震作用下地表的建筑物、室内的家具 等的晃动问题时提出. 该问题研究放置于平台上受到平台单边约束的物体 (称为浮放物体) 在初始条件和平台运动激励下在平台上晃动,并与平台发生多点碰撞. 对二维的 Rocking Block 问题,碰撞通常采用两点碰撞模型[27 -36 ] 或线碰撞模型[37 ] . Shenton 等[29 -30 ] 分析了在平台的晃动激励下浮放物体可能的运动模式,并给出了其动力学方程;Lipscombe[31 ] 对长细比为 1,2,4,8 的钢制浮放块,对两点接触的碰撞条件下的二维 Rocking Block 问题进行了实验研究,观察到了 Free Rocking 和 Half Rocking 两种运动模式;王琪等[32 -35 ] 对含摩擦碰撞中黏滞-滑移状态的判断问题,将其转化为线性互补问题进行求解,并采用该方法对含间隙滑移铰和含支撑腿的浮放物体进行了动力学仿真,验证了该法的精度和效率;张宏剑等[36 ] 采用一种处理含摩擦多点碰撞问题的方法 (LZB 法[38 -39 ] )对 Rocking Block 问题进行了动力学仿真,验证了动力学角为含摩擦多碰撞冲击问题中描述能量传递效应的有效参数. 张宏剑等[37 ] 将 LZB 法与离散方法结合,研究了线碰撞问题,验证了该方法的收敛性. ...
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
... 在碰撞过程中,引入以下两个假设[38 -39 ] : ...
机械系统中摩擦模型的研究进展
1
2008
... 诸多研究人员对碰撞中的摩擦现象提出了多种摩擦模型,例如库伦摩擦模型、库伦摩擦+黏性摩擦模型、Stribeck 摩擦模型等[40 ] ,本文采用经典库伦干摩擦模型,其摩擦力 $F_{{\rm f},i} $ 为 ...
机械系统中摩擦模型的研究进展
1
2008
... 诸多研究人员对碰撞中的摩擦现象提出了多种摩擦模型,例如库伦摩擦模型、库伦摩擦+黏性摩擦模型、Stribeck 摩擦模型等[40 ] ,本文采用经典库伦干摩擦模型,其摩擦力 $F_{{\rm f},i} $ 为 ...
连接结构接触界面非线性力学建模研究
1
2018
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
连接结构接触界面非线性力学建模研究
1
2018
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
Painlevé疑难的理论分析和实验验证
1
2013
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...
Painlevé疑难的理论分析和实验验证
1
2013
... 在碰撞过程中切向可能存在黏滞-滑移切换及滑移方向切换,对切向冲量与速度的关系产生影响,研究者们对处理碰撞过程中的黏滞-滑移问题提出了诸多处理方法,可对该问题中摩擦冲量的精确求解提供借鉴[32 -35 ,38 -39 ,41 -42 ] . 但在库伦干摩擦模型下恒有 $| I_{{\tau },i} | \leqslant {\mu }I_{{\rm n},i} $,且在碰撞过程中 $v_{{\tau},i} $ 方向不切换的情况下,该不等式取等号. ...