引言
上皮细胞 (epithelial cells) 彼此借助粘着连接(adherens junctions, AJs) 形成连续上皮组织, 由此发挥屏障、增殖调控等生理功能[1-2]. 上皮性钙粘附蛋白 (E-cadherin, E-cad) 作为一种跨膜蛋白, 是调控AJs形成的核心分子机制[3]. 一方面, E-cad胞外结构域在Ca$^{2+}$参与下, 在胞间或同一细胞表面分别形成反式/顺式二聚体 (trans-/cis-dimerization)[4], 其胞质结构域则借助 $\alpha $, $\beta $连环蛋白 ($\alpha $-, $\beta $-catenin) 与肌动蛋白 (F-actin) 锚定[5]; 另一方面, 胞间E-cad成键引起Rac, Cdc42等Rho家族小G蛋白 (Rho GTPase) 激活[6], 进而激活下游F-actin结合蛋白 (例如: Arp2/3, myosin-II, $\alpha$-actinin), 调控肌球蛋白皮层 (actomyosin cortex) 动态重组[7-9], 由此将更多E-cad募集至细胞接触区域, 促使AJs成熟[10].
近年来, 随着体外重构 (in vitro reconstitution)、活细胞成像等实验手段的广泛应用, 研究者愈渐认识到皮层张力对于AJs建成起整合性调控作用. Murrell 等[11]将F-actin积簇于脂质双层膜表面, 再加入$\alpha$-actinin、myosin-II, 由此可体外重构出actomyosin皮层结构; 该实验借助改变F-actin结合蛋白的密度控制皮层流变属性, 通过检测F-actin持续长度论证了F-actin屈曲及皮层松散结构可有效增强收缩应变. Wu等[12]对AJs上粘着小带 (zonula adherens, ZA) 及侧边区域 (lateral junctions) 进行激光烧灼, 观测到前者回缩速率明显高于后者, 说明ZA区域维持着较高张力. Leerberg等[9]将myosin常规轻链基因 (MRLC-DD) 转入Caco-2 细胞, 使之表达myosin-II磷酸化突变体以提升皮层张力, 最终通过靶向实验验证了以$\alpha$-catenin受力打开VH2结构域、从而募集vinculin为主体的张力敏感型F-actin聚合机制. Engl 等[13]将悬浮态S-180细胞置入非粘附微井 (microwell) 之中, 采取3D成像观测细胞接触区域E-cad募集, 同时以F-actin解聚/稳定试剂 (Latrunculin/Jasplakinolide) 处理细胞进行对照组实验; 观测到两类经处理细胞均呈现低张力状态, Jasplakinolide 对照组依然发生E-cad局部募集, 说明张力通过降低F-actin解聚速率调控E-cad.
综合上述实验, E-cad胞间成键使细胞皮层局部张力增强, 进而降低F-actin解聚速率(亦或提高局部F-actin聚合速率). 考虑到F-actin局部积聚能锚定更多E-cad, 那么由"E-cad $\to$ 张力 $\to$ F-actin"力学反馈回路所展现出的时空效应是否驱动了E-cad局部积聚, 进而调控AJs形成动力学? 为此, 本文构建了悬浮态上皮细胞粘附的力学-化学耦合模型, 并采用格子Boltzmann-粒子(LBP) 法开展数值模拟. 模拟获得了悬浮态细胞相互挤压时的E-cad, F-actin等分子时空调控特征并与Chu等[14]实验对比, 继而探讨了细胞局部力学属性、细胞间挤压程度对于AJs的调控作用.
1 模型和方法
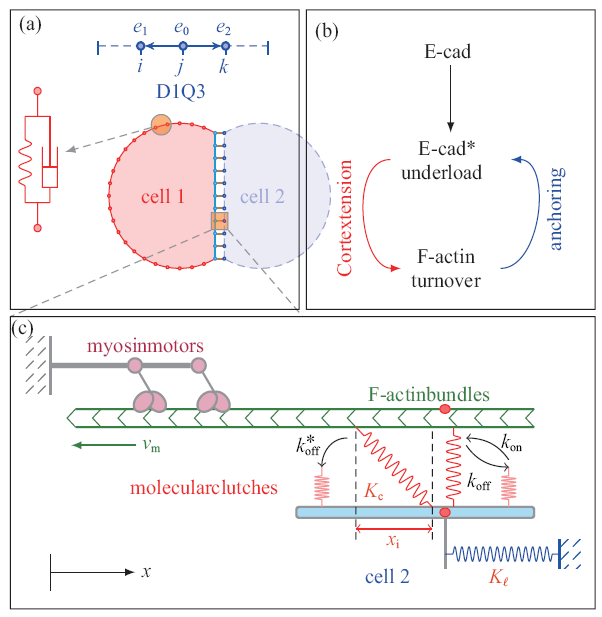
整体计算模型如图1(a) 所示. 考虑细胞为环状结构, 圆环代表细胞膜(指质膜及皮层紧密贴合体), 内部为胞质区域, 忽略细胞核等胞内细胞器; 将细胞膜划分为非接触及接触区域, 前者直接设定为由黏壶与弹簧并联的黏弹性单元, 后者需额外考察细胞间相互作用. 为考察分子沿可变形的细胞膜输运引入了自适应性D1Q3单元, 其长度与力学单元动态匹配; 胞质内分子浓度均一, 可由质量守恒定律直接获得. 图1(b) 展示皮层张力调控F-actin解聚, 而F-actin通过锚定E-cad参与级联转导, 由此循环往复构成了力学反馈回路. 图1(c) 展示采用马达-离合器 (motor-clutch) 机制[15]考察细胞在相互接触区的力学作用. 整体数学模型由3个模块构成: 细胞力学模块、E-cad/E-cad* 调控模块 (*号表明已与F-actin锚定) 及F-actin聚合/解聚模块. 各模块的基本假设及控制方程如下.
图1
图1
(a) 细胞离散模型. 黏弹性单元与D1Q3单元 (1维LBM单元, 包含3个速度分量) 动态匹配. (b) 力学反馈回路示意图. (c) 马达-离合器机制[15]
Fig.1
(a) Discrete cell model. Each visco-elastic element is co-localized with a D1Q3 element (a) 1D LBM element with 3 discrete velocity components). (b) Schematic of mechanical feedback loop. (c) Motor-clutch mechanism [15]
1.1 细胞力学模块
考察悬浮态上皮细胞具有均匀的力学属性, 离散细胞模型上任意单元节点$i$的受力满足以下平衡微分方程
上式中, 第一项是保守力, 由能量函数 ($E_{v} )$ 对位置坐标 ($X)$求偏导获得
式(2a) 计算拉伸势能 ($E_{l}$), $l_i $是$i$单元实际长度, $l_0$是平衡长度, $K_1$是弹簧刚度系数; 式(2b) 计算弯曲势能 ($E_{b} )$, $\theta _i $是第$i$个弹簧角度, $\theta _0$是平衡角度, $K_{b}$是弹簧弯曲刚度; 式(2c) 计算面积约束势能 ($E_{s} )$, $s$和$s_{e}$分别是细胞当前面积及平衡面积, $K_{s}$是罚系数 (penalty coefficient), 取$K_{s} \gg \max (K_1 ,K_{b} )$ , 将细胞面积变化控制在1${\%}$. 第二项考察单元节点$i$和$j$受到与节点相对速度相反的黏性力, $F_{{vis},i}=-\gamma (v_i -v_j )$, $\gamma $是黏性系数. 第三项是细胞接触区摩擦阻力, $F_{{drag},i} =-\mu v_i $, $\mu$为动摩擦系数, 第四项即为外力项.
1.2 E-cad/E-cad*调控模块
E-cad ($E_{m}$ ) 沿细胞膜扩散并借助F-actin锚定为E-cad* ($E_{I}$ ), E-cad*又可局部形成顺式二聚体. 该过程可通过非线性反应-扩散方程组描述为
式(3a) 中, 右侧第一项是扩散项, $D_{I} $是E-cad*在细胞膜上扩散系数; 第二项体现F-actin介导E-cad、E-cad*相互转化源项, $w$是F-actin密度, $\alpha $及$\beta$分别为E-cad与F-actin结合及E-cad*还原成E-cad速率; 第三项体现E-cad*通过形成顺式二聚体对自身密度反馈, $\vartheta $是反馈速率, $K_{E} $是饱和系数. 式(3b) 中, $D_{m} $是E-cad扩散系数 ($D_{m} >D_{I} )$, 后两项与式(3a)符号相反是基于E-cad*与E-cad总质量守恒. E-cad*在胞间成键可采用受体-配体结合方程予以描述.
式中, $R$和$L$分别代表受体、配体, $RL$为受配体复合物.
依据马达-离合器机制[15], 单个马达分子与F-actin结合可施加的力为$F_{m} $, 驱动F-actin以速率$v_{m} $回缩, 同时引起E-cad*成键受拉. $t_0 $时刻, 假设节点$j$上有$n_{{c},j}$个E-cad* 成键、$n_{{m},j} $个与F-actin结合的myosin-II, 该节点所受力$F_{{C},j} $满足
式中, $F_{{c},i} $是第$i$个键上的拉伸力, 等于该键净拉伸量 ($x_i )$与键刚度 ($K_{c} )$ 乘积; $F_{{C},j} $与此处皮层张力平衡, 可由节点位移$x_{{s},j} $、皮层刚度$K_1 $计算. $t_0 +1$时刻, 根据Bell模型更新第$i$个键的解离系数
式中, $F_{b} $是特征断裂力, $k_{{off}}^0 $是0载荷时的解离系数. 随后依据力-速度 (force-velocity) 关系[15]更新回缩速率
1.3 F-actin聚合/解聚模块
式中, $R_{h} $, $R_{r} $分别为细胞前端、后部 Rac活性系数, $x_i$为$i$节点到细胞前部水平距离.
F-actin ($w)$、钩端 ($B)$ 密度随时空调控可描述为
式(9a) 中, 右侧第一项表征F-actin在细胞膜上缓慢扩散, 第二项为F-actin聚合反应项, $v$是单个钩端聚合G-actin (密度为$g)$速率; 第三项是受张力调控F-actin 解聚, 取$d_{F} =d_{{max}} -d_\tau \lt(\frac{F_\tau ^2 }{F_{{half}}^2 +F_\tau ^2 })$, $d_{{max}} $为最大解聚速率. $F_\tau \approx 0$时, $d_{F} \approx d_{{max}} $; $F_\tau \gg F_{{half}} $ 时, $d_{F} \approx d_{{max}} -d_\tau$. 式(9b) 中, $a_{m} $是细胞膜上Arp2/3密度, $\tilde{{R}}a_{m} $即表征由Rac调控钩端生成. $a_{m} $与胞质游离态Arp2/3 ($a_{c} )$ 相互转化过程由式 (4) 描述, 即: $a_{m} $, $B$, $a_{c} $分别对应于$RL$, $R$, $L$. 后两项中, $k_{b}$, $c$分别是钩端生成及移除的基准速率.
2 数值方法
整体数学模型由平衡微分方程及反应-扩散方程组构成, 属于力学-化学耦合问题, 可采取LBP法求解[18]. LBP是将LBM与粒子 (particle) 法耦合, 其中LBM程序计算的基本内容是令"迁移"和"碰撞"两个步骤交替循环进行.
(1)碰撞
(2)迁移
式(10) 中, $f_{v,\alpha } (x,t)$是定义在离散速度方向集$\left\{ {e_\alpha }\right\}$上的瞬时粒子分布函数; D1Q3 单元的$e_\alpha $取为
$\varOmega $是碰撞算符, 由反应项 ($\varOmega ^{R})$ 及非反应项 ($\varOmega^{{NR}})$构成, 即: $\varOmega =\varOmega ^{R}+\varOmega ^{{NR}}$.$\varOmega ^{{NR}}$采用单松弛模型
$f_{v,a}^{{eq}} (x,t)$是平衡函数
式中, $\rho _{v} $是宏观密度, $w_\alpha $是粒子速度权系数.
LBM具有格式简单、便于并行计算、处理几何边界灵活等优点, 适合求解固定边界下的反应-扩散方程组[19-20], 前期工作是在计算反应源项时调用 Monte-Carlo (MC) 法, 从而保留系统噪音[21]. LBP-D1Q3将D1Q3单元与力学单元动态匹配, 即由欧拉法获取粒子位移以更新单元长度, 之后对$f_{{v},\alpha } (\{x_i +e_\alpha \Delta t\},t+\Delta t)$在网格节点$\{x_i \}$上进行3次样条插值, 由此获得$f_{{v},\alpha }(\{x_i \},t+\Delta t)$. 为保证插值前、后总量守恒, 设定分布函数为
3 结果
3.1 AJs形成动力学
考察两悬浮态细胞接触后E-cad* , F-actin在接触区域募集的时空动力学, 以此表征AJs形成. 此前Bangasser等针对马达-离合器机制开展参数分析[22], 本文据此将"马达"参数设定为: $F_{m} =2$ pN, $v_{m} =120$ nm/s, "离合器"参数为: $k_- =0.1 {s}^{-1}$, $k_+ =0.3 {s}^{-1}$. 钩端、E-cad* 及Arp2/3初始值设定为: $B=50$ $\mu$m$^{-1}$[17], $E_{I} =32$ $\mu$m$^{-1}$[17], [Arp2/3] = 0.05 $\mu$M[23]. 细胞力学及F-actin聚合/解聚模块参数见表1.
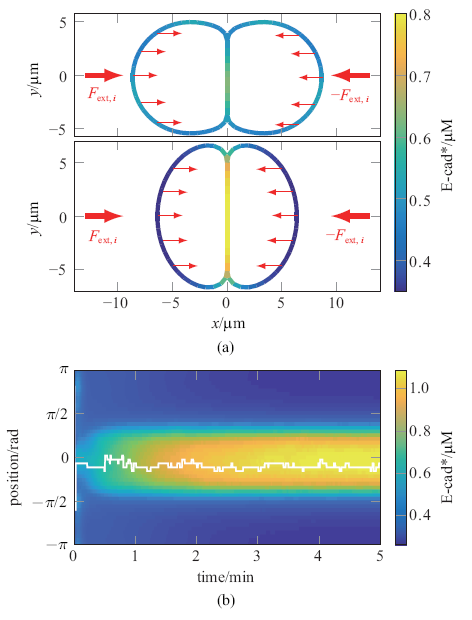
图2(a) 是 $t = 20$ (上)、50 s (下) 时细胞形态及E-cad* 分布图. 两细胞在$t = 0$ s接触, 此时E-cad* 均匀分布; 至$t = 20$ s, 两细胞因受到外力 ($F_{{ext},i}$ ) 发生显著挤压, 接触区域Rac梯度信号令Arp2/3局部激活进而产生少量钩端, F-actin聚合速率提升即将少量E-cad* 锚定于此; 至 $t = 50$ s, 细胞已到达平衡位置, 观察到E-cad* 积聚在接触区域, 而Ct 点E-cad*密度由初始约0.3 $\mu$M提升至约0.8 $\mu$M. 由于扩散速率低 ($D_{I} =0.1$ $\mu$m$^2$/s), E-cad*在接触/非接触交界区呈现陡峭梯度.
图2
图2
(a) $t= 20$、50~s时细胞形变及E-cad*分布. $F_{{ext},i}$是沿水平方向施加的节点外力. (b) E-cad*时空调控图. 纵坐标0点是细胞相互接触中心位置
Fig.2
(a) Snapshots of cell shape and the distribution patterns of E-cad* at $t = 20$ and 50 s. $F_{{ext},i} $is the external nodal force exerted alone horizontal direction. (b) Spatiotemporal regulation of E-cad*. Point 0 indicates the position of contact center
图2(b)是E-cad* 时空调控图, $[-\pi /3,\pi /3]$是平衡时细胞接触区域. 观察到50 s后E-cad* 依然持续募集至该区域, 直至约6 min达到稳态. E-cad*募集与两细胞接触后产生的动态张力信号密切相关, 即由myosin-II持续地驱动F-actin负向尾流 (retrograde flow)引起胞间E-cad* 成键受拉、传导皮层张力. 张力随着E-cad* 成键数增多而增强, 继续通过减慢F-actin解聚锚定E-cad* , 直至E-cad* 与E-cad相互转化速率动态平衡.
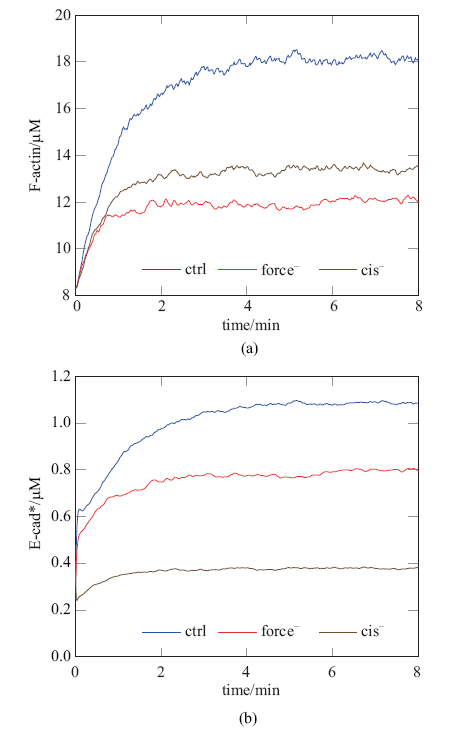
图3(a)是$Ct$点处F-actin密度时程曲线图. 观察到正常情况下 (ctrl组), 活性态Rac梯度促进F-actin聚合同时张力抑制F-actin 解聚, 由此产生互补效果即将F-actin密度提高至约16 $\mu$M, 接近初始时2倍. 在force$^{-}$对照组中, 令$d_\tau =0$ s$^{-1}$以消除张力对F-actin调控, 观察到由Rac梯度单独作用仅使得F-actin积聚密度为约12 $\mu$M; 在cis$^{-}$对照组中, 令$\vartheta =0$ s$^{-1}$以取消E-cad* 的成束效应, 此时F-actin借助少量E-cad*介导的张力信号将自身稳态密度恢复到约14 $\mu$M.
图3
图3
Ct点处F-actin (a)和E-cad* (b) 时程曲线图
Fig.3
Temporal evolutions of F-actin (a) and E-cad* (b) at Ct point
图3(b) 是相应的E-cad* 密度时程曲线图. 观察到, ctrl组中E-cad* 在F-actin锚定及自身成束的双重反馈下产生积聚, 其密度增长曲线呈现起始 (0$\sim $30 s)、快速增长 (0.5$\sim $5 min) 及缓慢增长(5$\sim $8 min)三阶段.
在force$^{-}$组中, F-actin密度最低, 因此对E-cad* 锚定量最少, E-cad* 依靠成束将F-actin赋予的初始极性放大, 最终达到约0.6 $\mu$M; 在cis$^{-}$组中, E-cad* 仅依赖与F-actin锚定产生积聚, 稳态时仅为约0.3 $\mu$M.
综上所述并参考迄今少有争议的真核细胞极化理论[27-30], 针对悬浮态细胞粘附的动力学过程亦可分为"方向感知"与"极化". 细胞接触初期, 接触区域Rac活性及皮层张力的提升为E-cad* 募集指明方向. 两类信号的起效方式不同: Rac信号受制于Arp2/3总量, 它从起效到饱和的周期短, 而张力信号受制于E-cad* 密度, 初始较弱但借助力学反馈回路持续增强. E-cad* 初始极性分布改变了顺式二聚体成束的局部速率, 后者即为"极化"机制, 可引起E-cad向E-cad* 加速转化, 直至E-cad大量消耗而达到稳态. 为定量化两类信号对AJs的调控作用, 后续将改变模型初始条件 (Rac活性或皮层张力) 考察最终E-cad* 信号输出.
3.2 细胞皮层力学属性调控粘着连接形成
此前, 尽管Murrell等[11]观测到皮层呈现松散的非肌节元 (nonsarcomeric)结构可大幅提高马达分子收缩应变, 但并未阐述皮层力学属性将如何调控AJs建成. 本节即着眼于力学反馈回路启动机制, 继续探究这一问题.
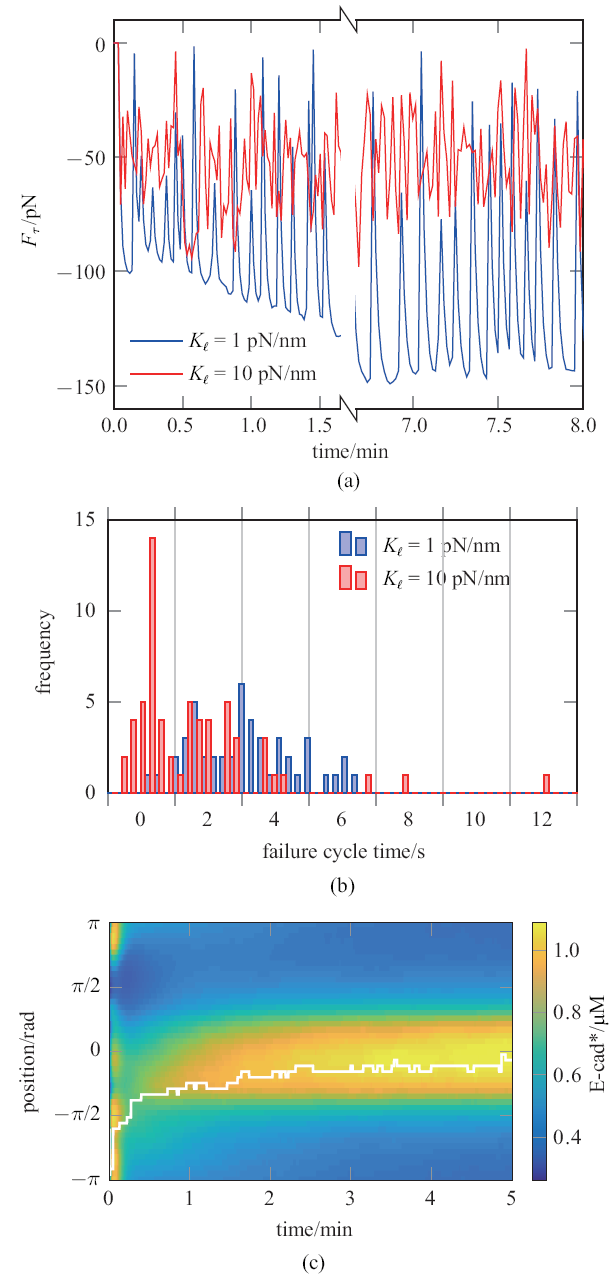
首先取消Rac梯度 (即设定$R_{h} =R_{r} =0.1)$, 考察单独由张力各向异性是否可引起E-cad* 局部积聚. 图4(a) 是取$K_1=$1, 10 pN/nm时获得的$Ct$点处$F_\tau $时程曲线图. $K_1=10$ pN/nm时表征皮层呈紧密结构,观察到起始阶段 (0$\sim$100 s), 皮层张力 ($F_\tau )$ 峰值始终较低 (约75 pN). 这是由于$K_1$过大导致E-cad* 键力($F_{{c},i} )$ 快速增长, 键的最概然寿命仅为约1 s (图4(b)), 同时由于键的反复形成与断裂造成$F_\tau $波动. $K_{c} =1$ pN/nm时可指皮层呈松散结构. 较小的$K_1$使$F_{{c},i} $增长较慢, 键的最概然寿命延长为约3 s (图4(b)), 观察到$F_\tau $峰值为约100 pN. 由马达分子持续收缩引起E-cad* 成键受拉使得$F_{{c},i} $逐渐增大, 直至断裂后由其它键分担, 造成键的连锁断裂, 观察到$F_\tau$呈现出周期性"加载-失效" (load-and-fail) 现象[15]. 随着模拟持续, 400$\sim $500 s阶段"$K_1 =10$ pN/nm"与初期相比未发生显著变化, "$K_1 =1$ pN/nm"则呈现阶梯式上升, $F_\tau $峰值约为150 pN. 由此可见, 皮层为松散结构更加有利于提升皮层张力, 并由此启动力学反馈回路驱动E-cad* 积聚, 最终形成AJs.
图4
图4
(a) $K_{l} $取1, 10 pN/nm时的Ct点张力时程曲线图. (b) E-cad*成键最概然寿命直方图. (c) 单独张力调控下E-cad*时空调控图
Fig.4
(a) Time courses of the tension at {Point} Ct at $K_{l} = 1$ and 10 pN/nm. (b) Distribution patterns of the lifetimes of E-cad* bonds. (c) Spatiotemporal regulation of E-cad* in the presence of the tension alone
3.3 细胞接触长度调控AJs形成
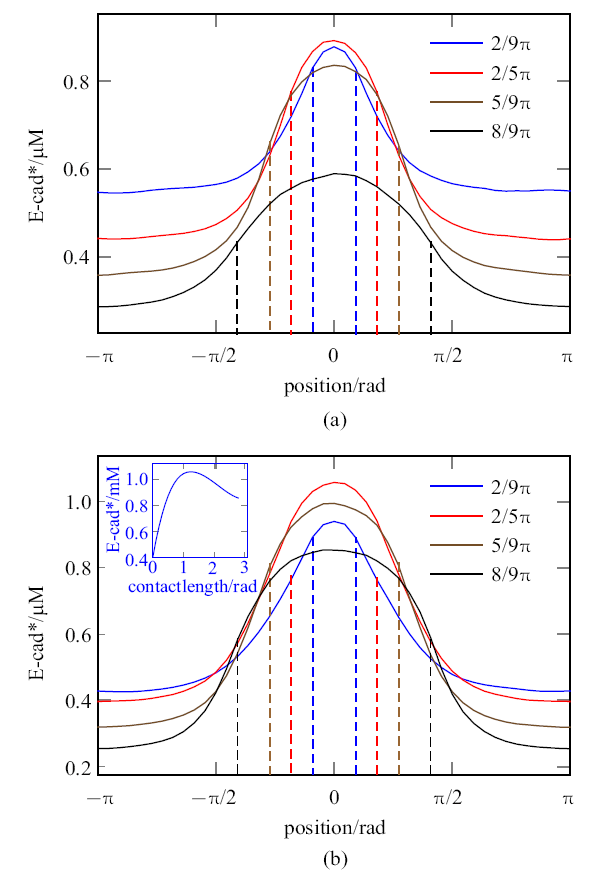
实验中通过调节双微吸管间距来控制细胞挤压程度[14], 模拟时施加不同挤压力 ($F_{{ext},i} )$ 即可达到相同效果. 图5(a)即考察缺少Rac梯度时, 细接触区弧度由2$pi /$9 扩大至8$pi /$9时获得的稳态E-cad* 分布. 随着接触区扩大, 细胞后部的E-cad* 密度降低. 弧度为2$\pi /$5时, E-cad* 峰值最高 (达到约0.90 $\mu$M), 说明中等长度的接触区促进AJs成熟. 接触区过小时输入的张力信号较弱, 从而限制整体力学反馈回路强度; 接触区过大时高密度E-cad* 分配范围过大导致峰值降低, 同样会限制AJs 成熟. 图5(b) 是加入Rac梯度信号($R_{h} =0.3)$ 后的E-cad* 分布. 与图5(a)对比, 细胞前、后部密度与接触区弧度关系依然存在, 但分布更为陡峭. 图5(b)插入图是令接触区在 [0, 2.7] 弧度变化时获得的$Ct$点处E-cad*峰值浓度曲线图. 观察到该曲线呈现双相性, E-cad*最高峰值浓度发生在1.2接触弧度附近.
图5
图5
$R_{h}= 0.1$ (a) 或 0.3 (b) 时不同接触长度下的E-cad*稳态分布图. (b) 中的插图显示E-cad*峰值浓度随接触区长度呈双相性变化
Fig.5
Profiles of E-cad* at $R_{h} = 0.1$ (a) and 0.3 (b) upon different extrusion deformations. Inserted panel in (b) shows the dependence of maximum E-cad* concentration with the contact length。
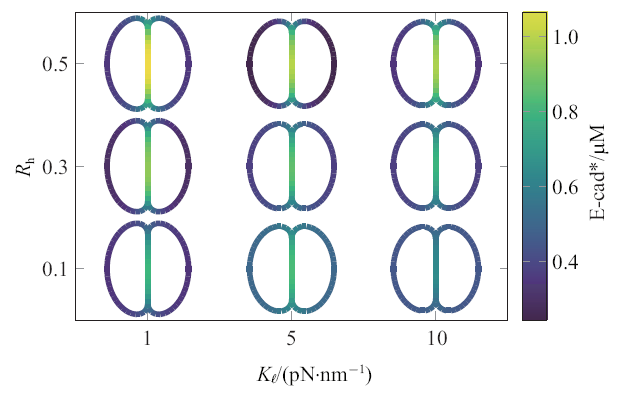
图6是将$R_{h} $和$K_1 $进行参数组合获得的E-cad* 稳态分布. 取$K_1 =1$, 5, 10 pN/nm, 同时取$R_{h} =0.1$, 0.3, 0.5, 由此获得9组 ($K_1 $, $R_{h} )$. 由于$F_{{ext},i} $为常量, 细胞挤压程度由$K_1 $控制, $K_1$越大则挤压程度越低. 观察到 (1, 0.5) 组合下E-cad* 呈现显著积聚, 这是由于Rac梯度信号最强, 而$K_1$低可引起接触区扩大、E-cad* 成键寿命延长; 相反取 (10, 0.1) 时, 力学、化学信号均最弱, 使得E-cad* 积聚程度最低. 取 (1, 0.1)、(10, 0.5) 时, E-cad* 积聚程度接近, 说明当张力信号较弱时可由增强局部Rac信号予以补偿, 反之亦然.
图6
图6
$K_{l} $与$R_{h} $进行参数组合所获得的E-cad*稳态分布图
Fig.6
Stable distribution patterns of E-cad* derived from different combinations of $K_{l} $and $R_{h} $
4 讨论
生物化学学者开展悬浮态细胞粘附实验往往配合分子抑制/过表达对照组实验. 分子间级联转导如何调控分子在细胞局部积聚动力学? 对于这一细胞-分子"跨尺度"问题需要借助构建力学-化学耦合模型予以回答. 此前Chu等[14]采用转染E-cad的悬浮态S180细胞开展粘附实验, 通过控制两细胞接触时间并测算分离力 (与E-cad* 积聚程度正相关) 将AJs的建立过程划分为: 起始、快速增长及缓慢增长阶段. 本文数值模拟获得E-cad* 调控空间分布特征及演化趋势与该实验一致, 但达到稳态所需时间较Chu实验快 (约5 min vs. 约30 min), 原因之一是忽略了G-actin自身调控, 即G-actin主要以ADP结合态存在, 需要与捕获蛋白ADF/cofilin, profilin, Thymosin发生交换成为ATP结合态方能供给钩端聚合[17]. Chu等[14]所开展的对照组实验包括有: (1) 采用Latrunculin抑制F-actin聚合后, 观测到AJs无法形成; (2) 表达Rac显性失活突变体后, AJs成熟度降低了35${\%}$. 参照本文图6可对上述观测结果作如下解读: 尽管F-actin, Rac都参与E-cad力学反馈回路, 但Rac位于F-actin上游, 其促进F-actin聚合的作用可由张力降低F-actin解聚予以补偿, 因而Rac失活只会削弱但并不阻止AJs建成.
本文为构建整体数学模型采取了必要的假设及简化, 今后可继续开展以下工作. 首先, 模型假设Rac活性系数由细胞接触区以指数形式衰减, 未引入Rac自身调控机制. 此前 Mori等针对Rac (或Cdc42) 调控提出了波桩 (wave-pinning) 模型[31], 即考察Rac失活/活性态转化, 活性态Rac扩散较慢并正向调控自身生成, 由此造成了其在一侧激活即以波的形式向对侧传播, 最终受到失活/活性态总体质量守恒限制达到稳定的极性分布. 已证实E-cad与整合素(integrin) 通过Rho GTPase发生交互式调控[32-33], 继续引入Rho GTPase调控模块可将悬浮态细胞粘附模型拓展至贴壁细胞[34].
5 结论
本文考察胞间E-cad* 成键介导actomyosin皮层上的Rac活性及张力信号反作用于E-cad级联转导, 由此构建了悬浮态上皮细胞粘附的力学-化学耦合模型, 并通过自行发展的LBP-D1Q3法予以数值求解. 正常组数值模拟首先重现了细胞粘附实验中观测到E-cad* 和F-actin在细胞接触区持续募集的现象, 继而结合对照组获得了以下3方面主要结论.
(1) 局部活性态Rac、张力信号分别调控F-actin聚合、解聚, 由此发挥互补效应造成F-actin在细胞接触区域富集, 通过锚定作用帮助E-cad* 建立初始极性; E-cad* 通过形成顺式二聚体将初始极性放大, 由此E-cad* 时程曲线呈现起始、快速增长及缓慢增长阶段.
(2) 单独张力各向异性经"E-cad $\to$ 张力 $\to$ F-actin"力学反馈回路放大即可造成E-cad* 积聚; 在马达分子拉动下, E-cad* 成键寿命与皮层刚度相关, 而松散的皮层结构具有较小刚度, E-cad* 成键寿命延长、张力提升, 有利于力学反馈回路的启动.
(3) 细胞接触区长度适中时, 整体张力输入信号经力学反馈回路放大使得E-cad* 局部积聚最为显著, 因此接触区长度可作为控制粘着连接成熟度的有效手段.
致谢
感谢宁波大学王骥教授、杜建科教授在本文撰写过程中给予的建议.