引言
充分了解金属玻璃的力学特性, 需要探明金属玻璃的不同空间尺度结构特征及其随时间的演化规律. 金属玻璃的动态弛豫与其力学性质密切相关[6]. 应力松弛是探究金属玻璃结构不均匀性的有效手段[7].最近有研究通过计算对金属玻璃的塑性基本单元进行了预测[8]. 金属玻璃的应力松弛问题是其在实际应用中一个非常重要的特征, 与传统金属材料不同, 金属玻璃微观原子排布不具有规律性, 研究其应力松弛问题对于进一步理解其变形机理具有实际意义[3]. 应力松弛与外部施加载荷、实验温度、加载时间等都具有紧密的联系, 是材料微观结构对外部刺激的响应.对于晶体材料其应力松弛可以通过晶粒位错运动、滑移、晶界扩散等机制来解释[9-11], 而在金属玻璃内却不存类似的"缺陷". 应力松弛是一种通过观测在固定应变下应力随时间演化规律, 来反映材料在变形过程中的黏弹性和黏塑性的方法, 从而将材料的微观结构与材料动态响应进行关联.材料的微观结构决定了其热力学状态, 最终影响材料的宏观力学性能. 在之前金属玻璃的研究中发现, 在应力松弛过程中局部的塑性流动是变形单元逐渐被激活的过程[7,12]. 这为金属玻璃作为潜在工程材料的应用提供了基本的变形机理.前期有关金属玻璃应力松弛的实验揭示了金属玻璃在过冷液相区和玻璃转变温度附近应力松弛的特征[13]. Jiao等[14]通过应力松弛的方法研究了Zr$_{52.5}$Ti$_{5}$Cu$_{17.9}$Ni$_{14.6}$Al$_{10}$金属玻璃在远低于玻璃转变温度下的变形机理, 发现即使在弹性范围的应力松弛实验也会诱发金属玻璃产生不可回复的变形, 并通过应力回复验证了变形过程中存在从弹性变形向永久变形的转变. Lu等[15]通过一系列金属玻璃的应力松弛研究, 提出了弛豫参量"$n$", 建立了"$n$"值与脆度和泊松比密切相关.进而采用参数$n$可以对金属玻璃进行分类, 这为研究金属玻璃的动态力学不均匀性提供了一种新的思路. Guan等[16]通过分子动力学模拟的方法研究了Zr$_{50}$Cu$_{50}$金属玻璃的应力松弛行为, 发现了应变加速和弛豫的直接联系, 应力松弛演化与流动单元的激活有着密切联系. 关于金属玻璃应力松弛行为已有许多研究[17-21], 但是目前对于金属玻璃应力松弛微观机制的了解还不甚清晰.
1 实验过程
本文研究选取了非晶形成能力良好的La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃通过单辊甩带法制得条带金属玻璃样品, 厚度约为30 $\mu$m、宽度约为1.5 $\mu$m, 从条带中截取长度约为30 mm条带样品分别进行动态力学实验和应力松弛实验. 动态力学分析实验选用条带拉伸单频扫温模式, 实验加载频率为2 Hz, 升温速率为2 K/min, 从室温加热到500 K.在复平面内模量可以表示为$E^* =E'+E{"}$, $E'$ 代表储能模量, $E{"}$代表损耗模量, 分别反映弹性和黏性的变化.应力松弛实验研究了在宽温度范围内(333$\sim$417 K) La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃的应力松弛行为, 温度间隔为3 K, 所施加的初始应变为0.4${\%}$, 本研究的应力松弛实验均在模型体系的弹性变形区域内进行. 为保持实验数据的稳定性, 达到每一目标温度后先保温3 min, 待温度稳定后开始进行应力松弛实验. 实验所采用的仪器为动态力学分析仪(DMA TA Q800).
2 实验结果与讨论
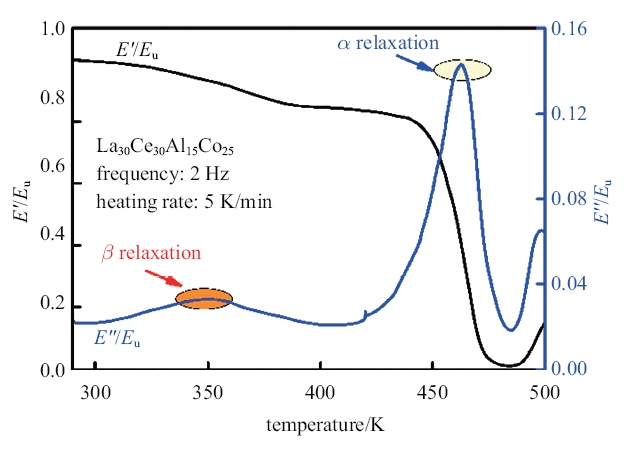
金属玻璃的动态弛豫普遍存在着明显的$\alpha $弛豫峰, 对于温度较低的$\beta$弛豫, 不同金属玻璃存在着差异, 表现为"过剩尾"、"肩膀峰"或明显的"$\beta$弛豫峰"[3, 25]. 图1是La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃归一化后的损耗模量和储能模量随温度的演化曲线. 在300$\sim$410 K温度区间内, 储能模量变化较小, 损耗模量在360 K左右出现明显的$\beta $弛豫峰, 这一过程与金属玻璃内局部原子的运动有关. 在410$\sim$480 K 温度区间内储能模量急剧下降, 损耗模量快速上升达到最大值出现明显的$\alpha $弛豫峰, $\alpha$弛豫对应着金属玻璃的动态玻璃转变行为.通过动态力学谱可以看到La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃具有明显的$\beta$弛豫行为.
图1
图1
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃归一化储能模量和损耗模量随温度演化过程. $E_{u} $等于金属玻璃在室温的储能模量
Fig.1
Normalized loss modulus and storage modulus of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass as a function of temperature. $E_{u}$ assumes the storage modulus at room temperature
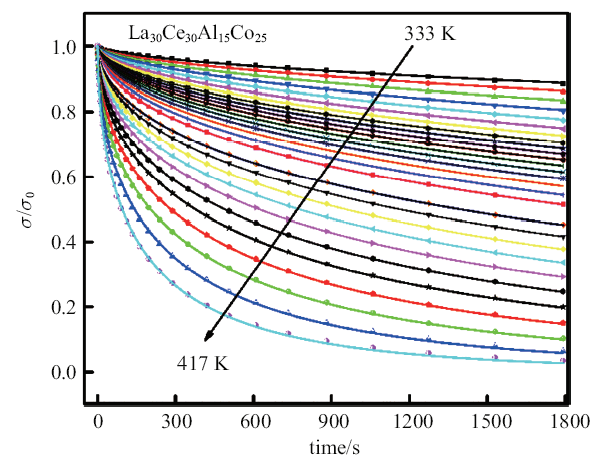
为探究La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃的应力松弛行为, 在较宽温度范围内进行了应力松弛实验.图2是La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃在0.4${\%}$应变下, 从333 K到417 K的应力松弛数据, 每一温度下的数据都采用各自的初始应力进行归一化, 实线是用KWW方程拟合得到的结果. 可以隐约看到应力随时间的变化可能分为两个阶段, 初始阶段应力随时间增加快速下降, 随着时间的演化, 应力降低速度变缓慢.并且随着松弛温度逐渐升高, 平衡应力逐渐减小. 通常来说, 这一过程是由于在变形过程中局部黏塑性变形或者流动事件累积而引起.
图2
图2
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃在不同温度(333$\sim$417 K)下的应力松弛行为, 应力通过初始应力进行归一化,实线是KWW方程拟合曲线
Fig.2
Stress relaxation spectra of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass at different temperatures (333$\sim$417 K). The solid lines are the KWW fittings
为了进一步探讨模型体系的应力松弛特征, 我们采用经典的物理模型进行描述.~研究表明金属玻璃的应力松弛实验可以采用经典的扩展指数模型(KWW)方程[23]来描述, 用以表征金属玻璃在应力松弛过程中应力随时间演化的内在规律
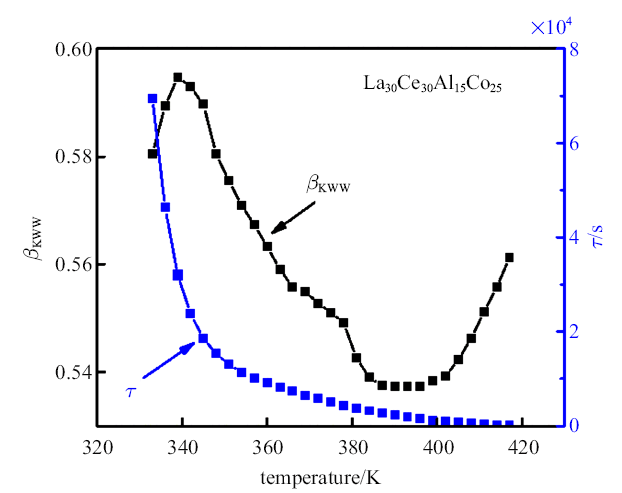
式中, $\tau$为特征弛豫时间, $\beta_{KWW}$为扩展指数参数($0<\beta_{{KWW}} <1$), $\sigma _0$为初始应力.与蠕变过程相似的是应力松弛行为是基于松弛单元的激活, 通过以上KWW方程很好的拟合, 表明松弛在微观尺度上是非均匀的[26]. 已有研究表明, 金属玻璃中存在一些紧密结合的区域(类"固"区), 和一些相对松散的区域(类"液"区)[27-28]. 图3是不同温度下拟合参数随温度的演化规律, 随着温度升高, 特征弛豫时间$\tau$快速下降.温度升高, 金属玻璃内部的流动单元更容易发生激活, 原子发生跃迁的速度变快, 特征弛豫时间随着温度上升逐渐缩短. 随着温度升高, $\beta_{KWW}$值先减小到最小值然后逐渐增大, $\beta_{KWW}$与动态不均匀性有关. 在Li[19]对Zr$_{44}$Ti$_{11}$Cu$_{10}$Ni$_{10}$Be$_{25}$, La$_{60}$Ni$_{15}$Al$_{25}$等多种非晶合金的应力松弛研究中也发现类似的规律, 表明不同体系的金属玻璃在应力松弛时有着相似的变形机理. 温度较低时金属玻璃主要由弹性基体构成, 有少量的流动单元分布在弹性基体中. 少量的流动单元处于隔离状态, 无相互作用.随着温度升高部分弹性基体转变为具有黏性的类液态, 这些区域参与松弛过程, 使得金属玻璃成为更不均质的状态.随着温度进一步升高, 更多的流动单元被激活, 随之这些流动单元产生联动作用, 剩余的弹性基体进一步软化, 与低温下流动单元的分布相反, 弹性基体分布在黏性流动单元中, 合金逐渐变得均匀, $\beta_{KWW}$值的变化出现反转开始上升.
图3
图3
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃应力松弛KWW方程拟合参数$\beta_{KWW}$和$\tau$随温度演化规律
Fig.3
The KWW fitting parameters $\beta_{KWW}$ and $\tau$ of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass as a function of temperature
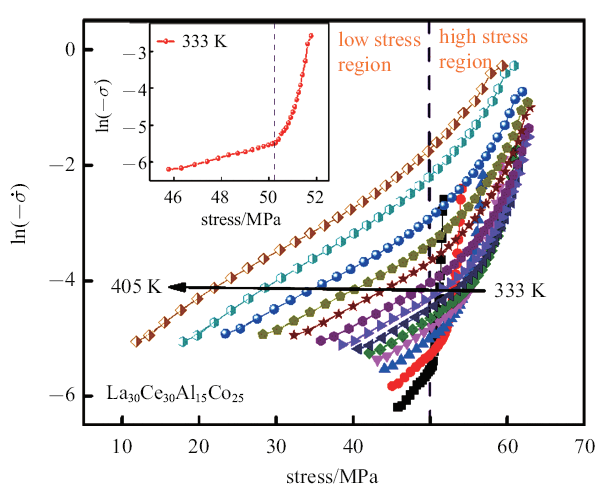
图4是应力率$\ln (\dot{\sigma})$随松弛应力变化的规律, 可以看到随着应力变化出现一个明显的转折点, 这意味着在松弛过程中出现了应力松弛机制的转变. La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃的应力松弛过程可以分为两个阶段, 快过程和慢过程.通过热力学分析的方法对这个过程的变形机制进行分析. 通常认为这两个过程分别是热激活引起的慢过程和应力激活的快过程. Luo等[17-18]对金属玻璃的应力松弛研究中同样发现了松弛分阶段的行为, 在对于动态弛豫的研究[29]中也发现了类似的现象. 为进一步探究应力松弛中的双阶段现象, 我们采用热动力学的方法来分析应力驱动的快过程和热驱动的慢过程[20].
图4
图4
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃在不同温度下应力率$\ln(\dot{\sigma})$随应力的演化规律, 插图是333 K下曲线, 可以观察到明显的分段现象
Fig.4
$\ln (\dot{\sigma})$ of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass as a function of stress. The inset shows an example at a given temperature of 333~K, which shows an obvious change of stress relaxation with the variation of stress
在应力松弛过程中, 应变可以分为弹性变形和非弹性变形, 应变可用以下公式表示
式中$\sigma (t)$是随时间变化的瞬时应力, $E$是弹性模量, $\varepsilon_{p}$是塑性应变, 对上式进行求导可得到
在应力松弛过程中应变保持恒定不变, 即应变速率为0, $\dot{\varepsilon}=0$ , 进而得到
根据过渡态理论, 应力松弛中的塑性变形为应力驱动和热激活控制耦合的过程, 其变化符合Arrhenius方程[20]
其中$\dot{\varepsilon}=0$是应变率常数$\Delta Q$是应力为0时的激活能, 应力做的功为, $(\sigma /\sqrt 3 )\varOmega $ 假设松弛时剪切应力是$\tau =\sigma /\sqrt 3 $, 非晶中塑性单元的流动主要认为是剪切应力激活. 激活体积$\varOmega$代表塑性变形发生时塑性事件体积的变化, $T$是实验温度, $K_{B}$是玻尔兹曼常数, 联立式(4)和式(5)可以得到
和应力相关的特征应力下的激活能$\Delta H(\sigma)=\Delta Q-(\sigma/\sqrt 3)\varOmega$, 同样在特定应力下的激活能可以写成
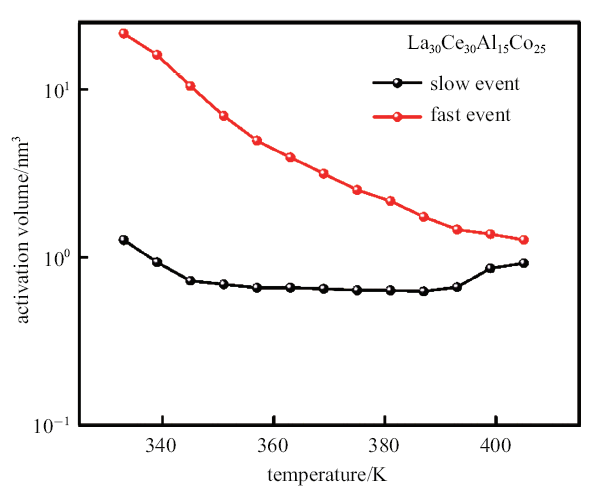
图5展示了在不同温度下快过程和慢过程激活体积随温度的变化, 可以很明显的观察到随着温度升高, 激活体积呈现下降趋势, 这一过程表明随着温度升高快弛豫过程中涉及的原子数量减少. 快过程具有很大的激活体积, 其最大激活体积在较低温度时超过20 nm$^{3}$, 并且随着温度升高快速减小.相比于快过程, 慢过程的激活体积则小的多, 且随温度升高激活体积变化不明显, 基本在1 nm$^{3}$左右变化.在金属玻璃高温变形研究中发现, 在高温均匀流变时许多金属玻璃如Zr基[30]、 Cu基[31]、 Ti基[32]等的激活体积都小于0.4 nm$^{3}$, 这一结果远小于本文在应力松弛中得到的快过程与慢过程的激活体积. 这表明金属玻璃在低温应力松弛时可能与高温流变行为存在着不完全相同的变形机制.
图5
图5
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃在不同温度下快过程和慢过程激活体积随温度的演化曲线
Fig.5
Evolution of the derived activation volume of fast and slow process in La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass with temperature
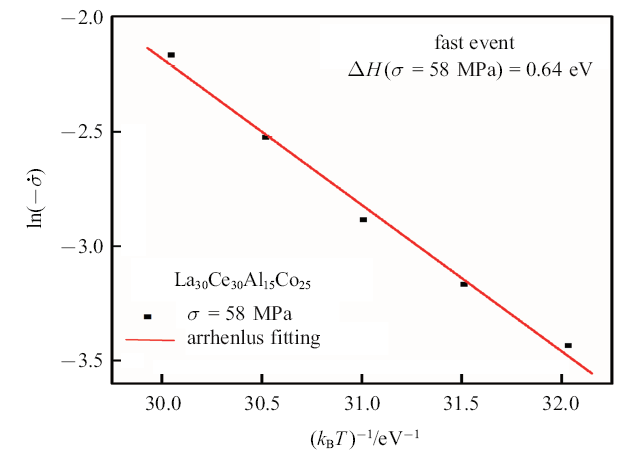
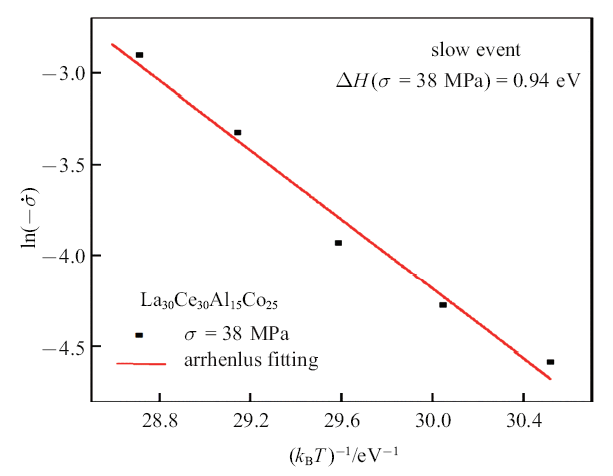
为了进一步分析弛豫分为快过程和慢过程的内在机制, 通过式(7)可以得到在不同特征应力下的激活能. 如图6和图7所示分别是快过程和慢过程在不同特征应力下的激活焓. 采用Arrhenius方程可以得到快过程在特征应力为58 MPa时的激活焓为0.64 eV, 慢过程在特征应力为38 MPa时的激活焓为0.94 eV.由公式$\Delta H(\sigma )=\Delta Q-(\sigma /\sqrt 3 )\varOmega$, 当外部应力0时激活能是$\Delta Q$.考虑到在分析中可以得到在381 K时快过程激活体积约为2 nm$^{3}$, 此时快过程的激活能$\Delta Q=\Delta H(\sigma )+(\sigma /\sqrt 3 )\varOmega $为1.7 eV. 由于外力做功自由激活能极大减小.同理, 在381 K时慢过程的激活体积大约为0.6 nm$^{3}$, 可得慢过程的激活能约为1.1 eV. 对于La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃动态弛豫行为的研究[33]中发现, 其铸态样品的$\beta $弛豫激活能约为0.86 eV, $\alpha $弛豫的激活能大约为3.6 eV. 可以发现快过程和慢过程的激活能介于$\beta $弛豫和$\alpha$弛豫激活能之间. $\beta $弛豫是一种可逆过程与小规模原子的移动相关, $\alpha$弛豫是不可逆的大规模原子协同运动与金属玻璃的玻璃转变紧密相关. 本文应力松弛的温度区间低于$\alpha$弛豫 出现的温度, 证明在应力松弛过程中出现的快过程和慢过程并不是直接由于金属玻璃的$\beta$弛豫或$\alpha $弛豫引起的, 而是随着应力的减小从接近于$\alpha$弛豫的变形模式转移到接近$\beta $弛豫的变形模式. Luo等[17]对Zr基金属玻璃应力松弛的研究中同样发现了应力松弛过程中双阶段现象, 在其研究结果中表明快弛豫过程的出现并不是由于$\beta$弛豫引起的. 同样在对金属玻璃条带拉伸蠕变曲线的分析[34]中发现类似的现象, 蠕变流动出现离散的阶梯状行为, 研究者认为这一过程是3D的剪切转变区激活向2D的纳米剪切带激活的转变.在金属玻璃的蠕变, 应力松弛研究中都发现了类似的分阶段现象, 说明金属玻璃变形机理的复杂性.
图6
图6
特征应力为58 MPa时La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃快过程的激活焓
Fig.6
Activation enthalpy of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass with a characteristic stress at 58~MPa for fast event
图7
图7
特征应力为38~MPa时La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃慢过程的激活焓
Fig.7
Activation enthalpy of La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass with a characteristic stress at 38 MPa for slow event
由上分析知慢过程表现出更小的激活体积, 激活能能垒主要由热驱动克服而不是应力主导. 对于快过程其对应的激活体积更大, 在前面激活能的计算中可以看到应力做功占据快过程激活克服能垒的很大一部分, 相同温度条件热驱动所提供的能量不足以达到快过程的激活能, 即松弛过程中快过程是由应力驱动主导的原子移动.在La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃整个应力弛豫过程中存在着由应力驱动的快过程向热驱动的慢过程转变. 应力松弛的双阶段现象也进一步证明了金属玻璃微观结构非均匀性.
前已述及, 在应力松弛中变形不均匀性, 关于金属玻璃应力松弛动力学行为可以采用经典的激活能谱模型描述. 与松弛性质变化过程相关的激活能分布在一个连续的频谱上, 松弛中涉及单个原子或原子群的重排或移动[24]. 金属玻璃在变形过程中原子要越过能垒而被激活, 能垒的分布是起伏变化的, 不同于晶体材料的均匀分布.
根据激活能谱模型, 金属玻璃在应力松弛过程中变形单元激活能的分布可以通过应力松弛曲线得到. 在实验温度为$T$时, 应力随时间的变化可以由如下表达式表示[24]
式中$P(E)$表示在激活能在$E$到$E+{d}E$范围内的与性能变化有关的量, $\sigma$, $T$, $t$分别代表应力松弛时的应力、温度、时间, $\theta(E, T, t)$为特征退火函数用来衡量在松弛时间$t$后有效变化过程所占的比例. 并且$\theta(E, T, t)$在0.01到0.99之间变化
根据Arrhenius方程得到
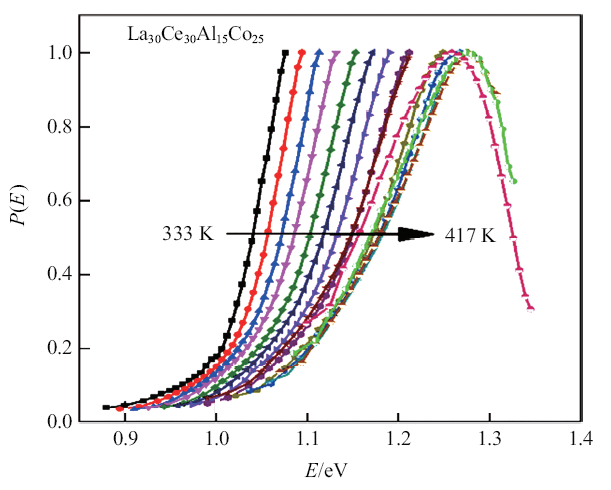
式中, $K_{B}$为玻尔兹曼常数, $T$是实验温度, $v_{0}$数值大约等于德拜频率, 由上计算可以得到La$_{30}$Ce$_{30}$Al$_{15}$ Co$_{25}$金属玻璃在应力松弛过程中的激活能谱变化示意图. 如图8给出了不同温度下的$P(E)$变化规律, 为了更好地观察其变化规律, 所有曲线均采用最大值进行了归一化. 从333 K到417 K, 激活能谱曲线逐渐向高能段移动. 激活能谱分布曲线类似于高斯分布, 温度越高现象越明显, 在温度较低时, 由于实验时间不够长, 松弛过程相比于高温阶段进行的不够完全, 在激活能谱上表现为$P(E)$曲线只有一部分. 在较低温度下部分变形单元由于能垒较高而处于冻结状态未被激活, 温度升高激活能谱向着能量较高的方向移动, 原先处于冻结状态的变形单元越过能垒被激活, 参与应力松弛过程. 同样在Lu等[21]对3种典型的金属玻璃的应力松弛实验研究中发现, 具有较高玻璃转变温度的金属玻璃, 其变形单元的激活需要跨过更高的能垒, 在激活能谱上表现为$P(E)$向着能量更高的方向移动. 而具有较低玻璃转变温度的金属玻璃, 其变形载体在较低温度下被激活, 激活能谱分布能量较低的阶段. 如图8所示应力随时间变化的曲线可知温度升高时, 具有较高激活能的变形单元大量被激活, 应力随时间快速下降.说明金属玻璃在变形过程中是一个动态不均匀的过程, 激活能较低的变形单元先被激活, 弛豫一定时间或温度升高时, 具有更高激活能的变形单元被激活而进入应力松弛过程.
图8
图8
La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃激活能谱随温度演化规律
Fig.8
Evolution of activation energy spectrum with temperature in La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$ metallic glass
基于前期大量的研究, 王峥等[36]提出了流变单元的概念来解释金属玻璃微观结构的非均匀性和变形机制. 该观点认为金属玻璃可以看作是弹性基底加流变单元的组合, 而应力松弛过程中的微观结构变形即对应于流变单元在应力和温度的联合作用下被激活. 这一模型为理解金属玻璃的微观结构与力学性质的关联提供了新思路. 相对于弹性基体, 流变单元在金属玻璃中表现为类似液体的性质, 在受到外加刺激(温度或应力)时更容易被激活, 从而对外界刺激做出响应. 基于实验分析, 我们可以看到不同的流变单元在激活能上存在差异, 即微观结构变化对应的难易程度不同. 当温度较低时, 并不是所有的流变单元都对应力刺激做出响应, 有部分流变单元由于激活能较大而被冻结在金属玻璃中, 只有一部分能量较高的不稳定结构, 激活能较小, 该类流变单元在低温下被激活, 参与到应力松弛过程. 随着温度的升高, 更多的较高激活能的流变单元进一步被激活, 从而对应力做出响应, 在松弛曲线上也表现为应力下降的幅度更大. Wang等[12]以La$_{60}$Ni$_{15}$Al$_{25}$金属玻璃为模型体系, 通过应力松弛研究, 发现低温段并非玻璃体系中所有区域都参与弛豫过程, 整个样品随温度升高逐渐被激活, 进一步证实金属玻璃对外力响应的动力学非均匀性. 所以, 研究非晶态材料的动力学应力松弛行为, 可以间接反映材料中微观结构的演化特征.
通过对应力松弛变形单元激活能谱的研究可以发现, 变形单元之间在能量上存在差异, 在受到外力作用时变形单元的响应具有差异性, 不能简单的作均匀变化处理.从能量角度反映了金属玻璃在微观结构上的起伏, 即微观结构不均匀性.
3 结论
本文研究了La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃的应力松弛行为, 基于热动力学模型和激活能谱模型对其应力松弛行为进行了分析, 结论如下:
(1) La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃具有明显的慢$\beta $弛豫行为.
(2) La$_{30}$Ce$_{30}$Al$_{15}$Co$_{25}$金属玻璃金属玻璃化应力松弛呈现双阶段现象, 存在由应力驱动的快过程向热激活的慢过程转变, 基于一种热动力学理论分析这两个阶段介于金属玻璃动态弛豫中的弛豫和$\beta$弛豫之间.
(3) 对松弛数据基于激活能谱模型的分析发现, 松弛单元的激活并不是均一化的, 存在着能垒的变化, 从能量角度反映了金属玻璃的动力学和结构非均匀性.