引言
气液两相流广泛存在于化工、能源、环境等诸多工程中. 在两相接触器及反应器中,为控制气泡分散相的停留时间、运动及分布规律、两相间的传质或传热速率,通常会设置挡板或壁面. 气泡与壁面相互作用规律直接关系到容器内分散相的运动学及动力学行为,及气液传热传质效率[1 ] .
Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式.
根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大.
目前,研究者对于上升气泡和垂直壁之间相互作用的实验研究主要集中于球形气泡,以无约束条件下的气泡上升轨迹(直线或之字形运动)作为参照,忽略气泡形变.随着气泡直径增大,气泡变形程度增大,气泡在无约束条件下将以螺旋或无规则形式上升,以此为对照的近壁气泡上升运动特别是动力学行为的详细研究较少.工程实际中,如流化床、水下爆炸、液态金属加工等过程中经常出现大气泡.深入分析近壁大气泡运动及动力学机理,对理解气液两相传热传质机理具有重要理论意义及工程应用价值.因此,本实验以气泡在无约束条件下为三维螺旋或无规则运动作为参考,研究静止液中垂直壁附近可变形气泡$(Re\approx 580 \sim1100)$的上升运动,对比气泡尺度及针头中心与壁面之间的初始距离对气泡上升运动特性影响,分析气泡与垂直壁面相互作用及气泡与壁面碰撞前后能量变化规律.
1 实验部分
1.1 实验装置及参数
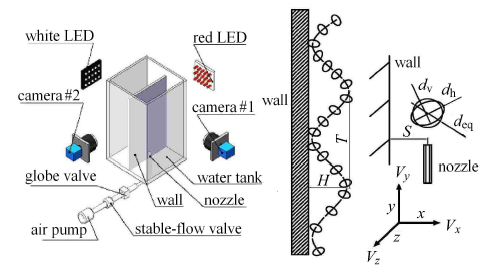
实验装置示意图如图1 所示,有机玻璃实验水槽 (300 mm $\times$ 300 mm $\times $600 mm)装入470 mm深的蒸馏水,中间放置竖直平板 (200 mm $\times$ 100 mm $\times$ 5 mm),水槽底部中心安放不锈钢气体喷嘴(内径0.19 ~ 2.4 mm),平板与喷嘴间距可调$S\!=0 \sim150$ mm.设平板底边中心为坐标原点.实验温度20${^\circ}$C,液相密度$\rho_{\rm l}=998.21$ kg/m$^{3}$,液相 黏度$\mu_{\rm l}=1.10$ mPa$\cdot$s,表面张力$\sigma = 73.34$ mN/m,气相密度$\rho_{\rm g}\!=$1.22 kg/m$^{3}$.采用两个相机 (Image MX,德国Lavi-sion公司,分辨率为2048 $\times$ 2048)互成90$^\circ$同步拍摄恒定间隔时间上升气泡,分别用红、白两个LED灯 (50 W)照亮拍摄区域,相机中心与喷嘴上方180 mm处平齐[23 ] ,拍摄区域为60 mm $\times $ 160 mm,采集频率180 Hz,拍摄50组.
图1
图1
实验装置示意图
Fig. 1
Schematic diagram of the experimental facility
定义气泡喷嘴与壁面无量纲距离$S^{\ast }$,$S^\ast = S / d_{\rm eq} $,对$x$,$y$无量纲 化$x^{\ast}=x/d_{\rm eq}$,$y^{\ast }=y/d_{\rm eq}$,气泡雷诺数$Re = \rho _{\rm l} V_{\rm T} d_{\rm eq}/{\mu _{\rm l}}$,奥特沃斯数$Eo = gd_{\rm eq} \left( {\rho _{\rm l} - \rho _{\rm g} } \right) / \sigma$,韦伯数$We = \rho _{\rm l} V_{\rm T}^2 d_{\rm eq} / \sigma $. 其中,$S$为喷嘴与壁面距离,$d_{\rm eq}$为气泡等效直径,$\rho _{\rm l}$和$\rho_{\rm g}$分别是纯净水和空气密度,$g$为重力加速度,$V_{\rm T}$为气泡终端速度,$\sigma $和$\mu_{\rm l}$分别为纯净水表面张力和运动黏度.
1.2 图像分析
利用图像处理软件 (Image-J,Matlab)对两相机同步瞬时记录的气泡图像帧序列进行分析,得到气泡质心坐标 ($x$,$y$,$z$)及气泡长短轴信息,分别利用式 (1)和式 (2) 计算气泡在给定距离下的局部瞬时速度$V$及气泡当量直径$d_{\rm eq}$
(1) $V = \sqrt {\left( {x_i - x_{i - 1} } \right)^2 + \left( {y_i - y_{i - 1} } \right)^2 + \left( {z_i - z_{i - 1} } \right)^2} / \Delta t$
(2) $d_{\rm eq} = \left( {d_{\rm h}^2 d_{\rm v} } \right)^{1 / 3}$
式中,($x_{i}$,$y_{i}$,$z_{i})$,($x_{i - 1}$,$y_{i - 1}$,$z_{i -1})$为相邻两帧气泡质心坐标, $\Delta t$为两帧时间间隔,$d_{\rm h}$和$d_{\rm v}$为扁椭球泡长轴和短轴.
1.3 实验不确定性
气泡直径和速度测量的不确定性主要由数字图像处理决定[24 ] .实验中,空间 分辨率15.669像素/mm.气泡不与壁面碰撞时(图2 ),气泡边缘识别[25 ] 最大误差为$\pm 1$像素,两轴测量误差为1像素,气泡直径的最大不确定度为1.63%$\sim $3.26%.气泡与壁面碰撞时,气泡边缘识别最大误差为$\pm 2$像素,气泡直径的不确定度为3.63%$\sim $5.51%.
(3) $ \Delta V = \ \ \sqrt {\left( {\dfrac{\partial V}{\partial P_1 }dP_1 } \right)^2 + \left( {\dfrac{\partial V}{\partial P_2 }dP_2 } \right)^2 + \left( {\dfrac{\partial V}{\partial \Delta t}d\Delta t} \right)^2 + \left( {\dfrac{\partial V}{\partial s}ds} \right)^2}$
式中,$V$为气泡瞬时速度,$P_{1}$和$P_{2}$为气泡质心位置,$s$为图像精度,$dP$为图像位置误差,$ds$为标定误差. 数字图像处理系统得到的质心位置的最大可能误差发生在阈值处理产生上半部像素缺失,而下半部没有变化,反之亦然.每边误差小于1像素,整体误差最大为2像素,局部速度$V/V_{\rm T}$的最大不确定度为3.5%.
图2
图2
图像处理
Fig. 2
Image processing
在较长路径上得到的平均终端速度不确定度受气泡中心位置误差的影响较小,平均终端速度的不确定度远小于2%.
2 结果与讨论
2.1 垂直壁附近气泡上升行为
两台摄像机垂直放置,得到气泡在不同平面上的原始运动轨迹. 以$Re \approx 700$气泡为例,列出不同$S^{\ast }$近壁气泡在$x-y$和$y-z$平面上升运动轨迹. 如图3 ,无约束条件下单气泡上升过程中,$x-y$和$y-z$平面气泡轨迹均呈二维之字形运动,其在空间中呈三维螺旋运动. 近壁气泡呈周期性运动上升,在$S^{\ast } \leqslant 1.86$时气泡上升运动受壁面效应影响显著,气泡与壁面碰撞,作二维之字形摆动上升;$S^{\ast } \geqslant 2.67$时壁面效应减弱,气泡运动轨迹在$y-z$平面由轻微振荡发展为大幅震荡,直至在空间内演变为三维螺旋运动 ($S^{\ast }=7.57$),此时与无约束气泡上升运动路径近似.
上升气泡的路径不稳定性是尾流不稳定性的直接表现[26 ] .固体球后面的尾流,在靠近壁面的地方引起了球后流动结构的改变[27 ] .气泡在无约束壁面时以三维螺旋上升,气泡尾流呈现出双螺旋尾迹[28 ] .当气泡在壁面作反弹运动时,气泡在近壁处触发了气泡的尾流稳定性,由于壁面限制三维螺旋轨迹的尾流结构转变为对称涡管结构[29 ] ,使得气泡以之字形运动重复反弹.随着$S^{\ast}$的增大,尾迹结构受壁面效应能力减弱,气泡尾迹从对称涡管结构逐步变为双螺旋结构.因此,气泡在无约束壁面时以三维螺旋上升转为有壁面时之字形运动可以归因于壁面的稳定作用.
图3
图3
垂直壁附近不同$S^{\ast }$上升气泡的轨迹变化$(Re \approx 700$)
Fig. 3
Trajectory changes of rising bubbles at different $S^{\ast }$ near the vertical wall $(Re\approx 700$)
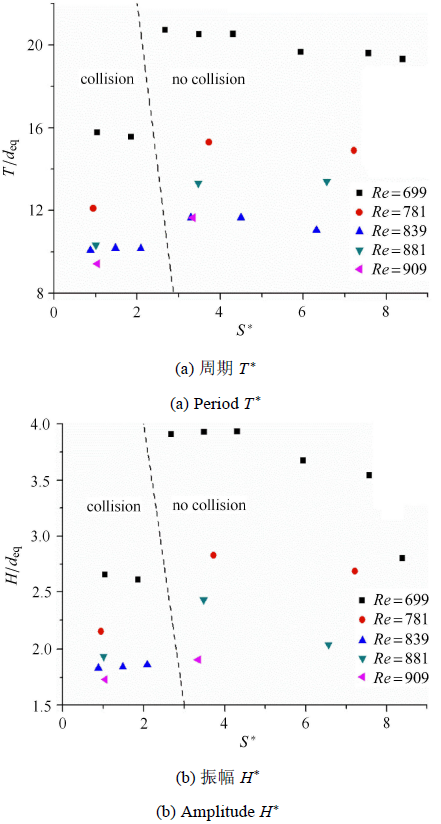
用周期性运动轨迹的振幅和波长分析周期弹跳运动行为 (图4 ). 当$S^{\ast } \leqslant 2$时,对于${Re}\approx 700$,气泡与壁面碰撞且运动轨迹为周期弹跳 (图3 ),周期弹跳的无量纲振幅 ($H^{\ast } =H/d_{\rm eq})$和无量 纲周期 ($T^{\ast }=T/d_{\rm eq})$基本保持不变 (图4 ). 当$S^{\ast } \approx2$时,气泡不与壁面碰撞,运动轨迹依然呈现周期运动,振幅和周期迅速增大并达到最大值,此时气泡依然在空间里呈二维之字形运动(运动振荡较小). 随着$S^{\ast }$增大,气泡逐渐由二维之字形运动转变为三维螺旋运动,周期和振幅也随之减小(图4 ). 随着$Re$的增大,气泡表面涡量的积累加大,气泡尾迹涡对强度不再对称[28 ] ,因此对于相同$S^{\ast }$,气泡运动轨迹周期和振幅均减小.
图4
图4
垂直壁面附近气泡运动无量纲周期$T^{\ast }$和振幅$H^{\ast}$随$S^{\ast }$的变化曲线
Fig. 4
The dimensionless amplitude and period curve of bubble movement near the vertical wall with $S^{\ast }$
2.2 上升气泡瞬时及平均速度
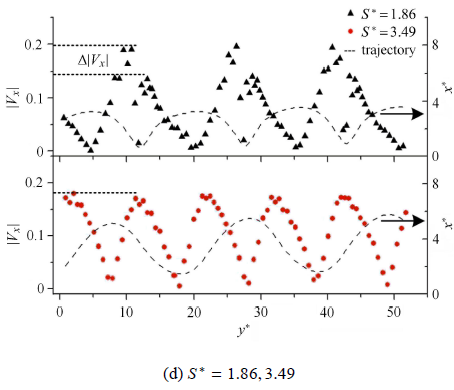
气泡速度由气泡质心坐标变换和两帧之间的时间间隔决定. 气泡瞬时速度 (垂直速度$V_{y}$、横向速度$V_{x}$、展向速度$V_{z}$及合速度$V_{xy}$,若气泡为三维运动则合速度为$V_{xyz})$随$S^{\ast }$变化如图5 所示. 在$S^{\ast }<2$情况下 (图5 (a)),垂直速度的振荡较大且与合速度基本一致,横向速度随振荡气泡路径有显著变化. 当$S^{\ast }>2$时 (图5 (b)),垂直速度较小振荡 (合速度基本保持不变),横向速度同样 随路径变化明显.在无约束条件下 (图5 (c)),气泡的三维速度与平面速度基本一致,且保持稳定.
图5
图5
垂直壁附近不同$S^{\ast }$上升气泡$(Re \approx 700)$ 瞬时速度
Fig. 5
The instantaneous velocity of ascending bubble near the vertical wall with different $S^{\ast }$ ($Re \approx 700$)
图5
图5
垂直壁附近不同$S^{\ast }$上升气泡$(Re \approx 700)$ 瞬时速度(续)
Fig. 5
The instantaneous velocity of ascending bubble near the vertical wall with different $S^{\ast }$ ($Re \approx 700$) (continued)
当$S^{\ast } <2$时 (图5 (d)),随着气泡被吸向壁面,横向速度 ($V_{x}$)变化趋势加快,在未与壁面碰撞前达到峰值. 随着$x/R$的减小 ($x$为气泡中心与壁面距离,$R$为气泡等效半径),$V_{x}$逐渐减小,直到与壁面碰撞 ($x/R \leqslant 1)$, $V_{x}$为零,并改变其符号,随气泡远离壁面$x/R$增大,$V_{x}$迅速增大到峰值 ($x/R \approx 2)$. 气泡与壁面碰撞后,由于黏性耗散,$V_{x}$速度最大值减小为原最大速度值的70%左右,随着气泡反弹,同样的过程重复发 生.然而,随气泡$Re$增大,气泡横向速度也减小为70%左右,气泡横向速度最大值基本不变. 当$S^{\ast }>2$,随着$S^{\ast }$增大,气泡不与壁面碰撞,横向速度峰值保持恒定,瞬时横向速度保持周期变化.
对于垂直速度$V_{y}$ (图5 (a) ~图 5 (c)),$S^{\ast}<2$时,随着气泡被吸向壁面,$V_{y}$逐步减小,碰撞时 ($x/R \approx1$),$V_{y}$较$V_{y\max}$降低70%左右,随着气泡远离壁面气泡垂直速度继续降低,直到离开壁面 ($x/R\approx 2$)时$V_{y}$降为$V_{y\max}$的50%. 随着气泡反弹,同样的过程重复发生. DeVire等[4 ] 和Mougin等[30 ] 发现自由上升气泡后面有一对反向螺旋涡量,然而在有壁面约束条件下当气泡与壁面碰撞时,发现气泡两侧出现一个涡对[31 ] .当气泡远离壁面时,气泡两个尾涡脱落,导致气泡速度进一步降低;气泡与壁面距离$x/R>2$,气泡尾迹又重新恢复对称涡管结构.当$S^{\ast }>2$,气泡未与壁面碰撞,垂直速度$V_{y}$轻微振荡并呈周期变化.
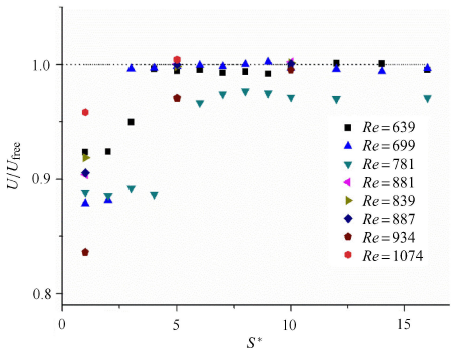
图6 绘制了有壁面时气泡的平均上升速度$(U)$与无约束自由上升气泡的平均上升速度 ($U_{\rm free})$比 值. 在 上升气泡周期性反弹范围内,气泡的上升速度受到壁面边界条件的显著影响[32 ] .正如以上所述,气泡在碰撞过程中,由于能量耗散,动能损失,垂直速度和横向速度均下降,导致整体速度低于气泡自由上升速度. 当气泡不与壁面碰撞时,气泡速度基本与自由上升气泡一致. 随着气泡${Re}$的增大,气泡周期反弹过程中的平均速度也越来越低.
图6
图6
无量纲化平均上升速度 ($U/U_{\rm free}$)随$S^{\ast }$变化
Fig. 6
Variations of the normalized mean rise velocity ($U/ U_{\rm free})$ with $S^{\ast }$
2.3 近壁气泡的运动学和动力学分析
气泡在与壁面碰撞前瞬间 ($x/R \approx 1$),垂直瞬时速度$V_{\rm C}$为$V_{y \max}$的70%.速度下降的主要原因是由于与壁面平行的气泡推动流体耗散,形成了润滑膜,周围的流体随之加速(附加质量效应),黏性阻力增大,可得力平衡
(4) $\dfrac{ 4}{3}\pi R^3[\rho _{\rm g} + {C}_{\rm M} \left( x\right)\rho _{\rm l} ]\dfrac{dV}{dt} = \Sigma F = F_{\rm B }+ F_{\rm D} + F_{\rm H}$
式中,$F_{\rm B}$是流体施加在气泡上的浮力;$F_{\rm H}$是流体施加在气泡上的Basset力;$F_{\rm D}$是作用在气泡上的非定常黏性力,包括壁面效应、准稳态阻力和气泡接近壁面时的润滑效应;$C_{\rm M}(x)$ 是附加质量系数. 气泡在碰撞时到远离壁面一小段距离内变形严重,未碰撞之前气泡变形很小,故忽略气泡变形. 壁面上移动正常的椭球形物体的附加质量系数为[33 ]
(5) $ C_{\rm M} \left( x \right) = C_{\rm M0} \left( x \right)\left[ {1 + \dfrac{3}{8}\left( {\dfrac{R}{x}} \right)^3 + \dfrac{3}{64}\left( {\dfrac{R}{x}} \right)^6 + \cdots } \right]$
无约束介质中附加质量系数$C_{M0}$与气泡变形之间的关系用为[34 ]
(6) $ C_{\rm M0} \left( x \right) = 0.62\chi - 0.12 , \ \ 1 < \chi < 2.5$
式中, $\chi $为纵横比.由于气泡质量太小,Basset力导致的速度下降幅度小于使用准稳态阻力预测的速度下降幅度;TakemurA等[10 ] 对近壁中的Basset力测量,发现Basset力比阻力低一个数量级,故忽略Basset力. 作为第一近似,准稳态黏滞力可以用式 (7)表示
(7) $ F_{\rm D} = - 4\pi \mu RVh(Re)[1 + f(x / R)]$
式中,$f (x/R)$是由于壁面的存在而改变的阻力系数,$x/R$可作为时间函数,$V$和$h(Re)$ 均为恒 定值.$h(Re)$ 是TomiyamA等[35 ] 纯净液体中的阻力关联式. Kok等[36 ] 得到一阶 近似$f (x/R)\sim(x/R)^{ - 3}$.对式 (4)积分求解得
(8) $ \int \dfrac{4}{3}\pi R^3[\rho _{\rm g} + {C}_{\rm M} \left( x \right)\rho _{\rm l} ]dV = \int \left({F_{\rm B} + F_{\rm D} } \right)dt $
(9) $\left. \begin{array} \int \left( {\rho _{\rm g} + {C}_{\rm M} \left( x \right)} \right)]dV = \\ \qquad \int \left\{ { - (\rho _{\rm l} - \rho _{\rm g} )g - \dfrac{3\mu }{R^2}Vh\left( {Re} \right)[1 + f(x / R)]} \right\}dt \\ C_{\rm M} \left( x \right)V_{\rm C} - C_{\rm M0} \left( x \right)V_{\rm T} \sim - \int_\infty ^R \dfrac{3\mu }{R^2} f(x / R)dt\sim \dfrac{3\mu }{2R} \\ \dfrac{V_{\rm C} }{V_{\rm T} }\sim \dfrac{C_{\rm M0} \left( x \right)}{C_{\rm M} \left( x \right)}\left( {1 + \dfrac{1}{3St^ * }} \right) \end{array}\!\!\right\}$
式中,$C_{\rm M0}(x)$ 为离壁面无穷远处的气泡附加质量 力, $St^\ast = \left( {\rho _{\rm g} + C_{\rm M} \rho_{\rm l} } \right) d_{\rm eq} V_{\rm T} / \left( {9\mu } \right) $为气泡自由上升时的修正斯克斯数.
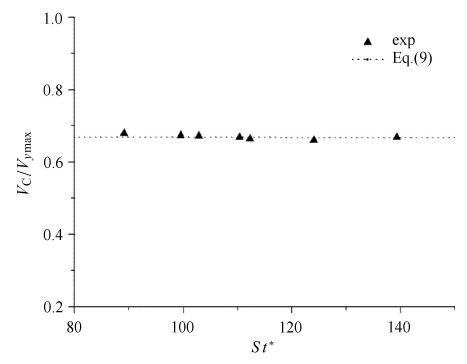
将该估计值与碰撞速度的实测值进行比较(图7 ),发现该预测给出了实验中观测到的速度下降的正确数量级,总体趋势描述吻合. 因此,气泡朝壁面运动所推动流体的反作用力导致接触壁面前速度的显著下降. 通过假设相应的力是在气泡变形之前发生的气泡球体的润滑力,很好地预测了这种效应.
当气泡接近壁面时,动能 ($E_{\rm k})$和表面能($E_{\rm s})$之间的传输及耗散,与壁面效应下上升气泡行为密切相关,尤其是在碰撞瞬间. 动能 ($E_{\rm k})$由式(10)计算
(10) $ E_{\rm k} = \dfrac{1}{2}mv^2 = \dfrac{\pi }{12}\left( {\rho _{\rm g} + C_{\rm M} \rho _{\rm l} } \right) d_{\rm eq}^3 \left( {V_y^2 + V_x^2 } \right)$
图7
图7
气泡 ($Re \approx 700$)碰撞前垂直速度下降垂直速度下降比值$V_{\rm C}/V_{y\max}$ ($S^{\ast } =1.04$
Fig. 7
The vertical velocity decrease ratio $V_{\rm C}/V_{y\max}$ before bubble collision ($S^{\ast } =1.04$)
式中,$E_{{\rm k}y}$和$E_{{\rm k}x}$表示垂直和横向速度对$E_{\rm k}$的贡献. 表面能计算为$E_{\rm s}= \sigma A$,其中$\sigma $是空气-水界面的表面张力. 扁椭球的表面积 ($A)$ 表示为$d_{\rm h}$和$d_{\rm v}$的函数[5 ]
(11) $ \left. A = \dfrac{\pi d_{\rm h}^2 }{2}\left[ {1 + \dfrac{1 - e^2}{e} {\rm tan} \left( {\dfrac{e}{d_{\rm h} }} \right)} \right] \\ e^2 = 1 - 1 / \chi ^2 = 1 - \dfrac{d_{\rm v}^2 }{d_{\rm h}^2 }\right\}$
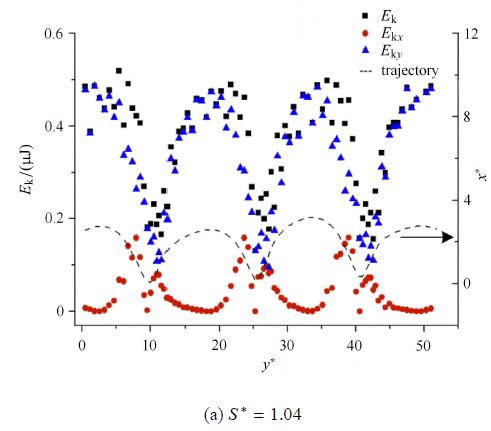
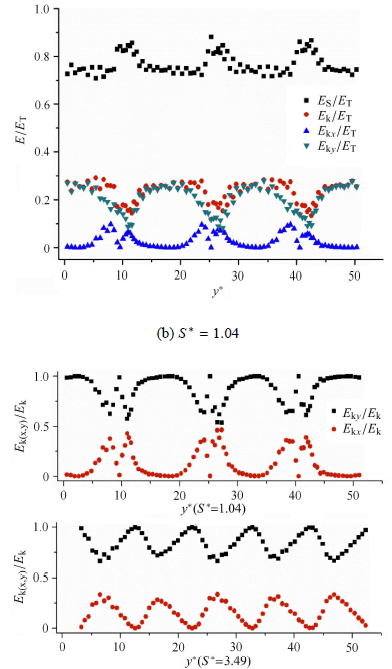
反弹气泡的$({Re} \approx 700)$ 能量分量 ($E_{\rm k}$,$E_{\rm k}/E_{\rm T}$,$E_{\rm s}$,$E_{\rm s}/E_{\rm T}$,$\chi $)变化 如图8 和图9 所示. 由图8 (a) 看出,$E_{{\rm k}x}$在碰撞前一段距离达到峰值(被吸引到壁面),随$x/R$距 离减少,$E_{{\rm k}x}$迅速下降,直到与壁面碰撞后$(x/R\!<\!1)$,损耗一部分能量又迅速恢复小峰值,随着气泡远离 壁面,这个过程反复周期循 环(碰撞前后各显示出一个峰值). $E_{{\rm k}y}$则与$E_{{\rm k}x}$不 同,$E_{{\rm k}y}$和$E_{{\rm k}y} / E_{\rm k}$随气泡的反弹轨迹呈周期性变化,$E_{{\rm k}y}$和$E_{{\rm k}y} / E_{\rm k}$随着气泡 被吸引向墙壁而减小,碰撞后继续减少,直至气泡离开壁面 ($x/R \approx 2)$达到最低,之后又缓慢恢复. 气泡与壁面碰撞瞬间(图8 (b)), $E_{{\rm k}x} / E_{\rm T}$,$E_{{\rm k}y} / E_{\rm T}$与$E_{{\rm k}x}$和$E_{{\rm k}y}$变化趋势基本相 同,$E_{\rm s} / E_{\rm T}$则与气泡运动轨迹相反,碰撞前$E_{\rm s}/E_{\rm T}$的增加表 明$E_{\rm k}$的损失大于$E_{\rm s}$的释放,很难定量表征能量组分之间的输运. 通过 对比$S^{\ast } =1.02$与$S^{\ast } =3.49$情况下的气泡能量变化对比 (图8 (c)),可以发 现$E_{{\rm k}y} / E_{\rm k}$和$E_{{\rm k}x} /E_{\rm k}$存在对称性,气泡上升过程中两者能量相互转换,从而达 到一个恒定的周期运动.
图8
图8
近壁气泡 ($Re \approx 700$)能量成分沿$y^{\ast }$的变化
Fig. 8
Change of bubble energy composition along with $y^{\ast}$
图8
图8
近壁气泡 ($Re \approx 700$)能量成分沿$y^{\ast }$的变化(续)
Fig. 8
Change of bubble energy composition along with $y^{\ast }$ (continued)
图9
图9
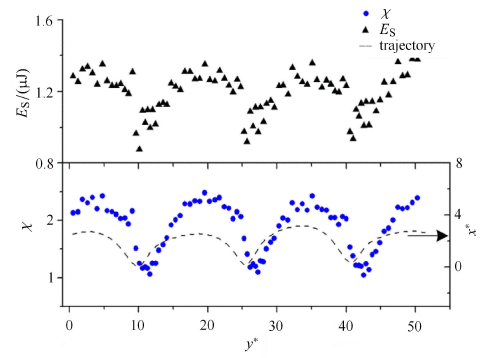
近壁气泡 ($Re \approx 700$)表面能$(E_{\rm s})$和纵横比 ($\chi $)沿$y^{\ast }$的变化 ($S^{\ast }=1.04$)
Fig. 9
Change of bubble energy composition $(E_{\rm s})$ and aspect \\ ratio ($\chi $) along with $y^{\ast }$ ($S^{\ast } =1.04$)
(12) $ E_{\rm t} = E_{\rm k} + E_{\rm s}$
对于高${Re}$和高${We}$的变形气泡,气泡上升过程中纵横比 ($\chi $)波动很大,显示出反弹运动趋势 (图9 );即当气泡接近墙壁时, $\chi $减小的幅度降低,碰撞时$\chi $迅速降低,当气泡离开墙壁而继续减小直至$\chi \approx 1$. 表面能$E_{\rm s}$也遵循这一趋势,特别是在气泡-壁碰撞时,即随着气泡接近壁面,表面能$E_{\rm s}$随着$\chi $变化不大,这与垂直速度变化趋势不同(一直降低),但在碰撞之后两者变化趋势基本相同,均是在碰撞时迅速降低直至气泡离开壁面$(x/R \approx 1)$ 达到最低.
对比图8 (a)、图8 (c)和图9 可知,气泡在与壁面碰撞过程中,气泡表面变形能量单向传输给气泡横向动能,$E_{{\rm k}y}$和$E_{{\rm k}x}$两者能量相互转换,使得可变形气泡能够保持相对恒定的弹跳运动.
2.4 壁面附近气泡上升阻力
当单个气泡在液体中以恒定速度上升时,作用在气泡上作用在气泡上的浮力与总阻力 (非定常阻力、附加质量力与Basset力)平衡. 由于$\mu _{\rm g}\ll \mu_{\rm l}$,可忽略空气密度,惯性力远小于浮力,则阻力系数可简化为
(13) $ C_{\rm D} = \dfrac{4d_{\rm eq} g}{3V_{\rm T}^2 }$
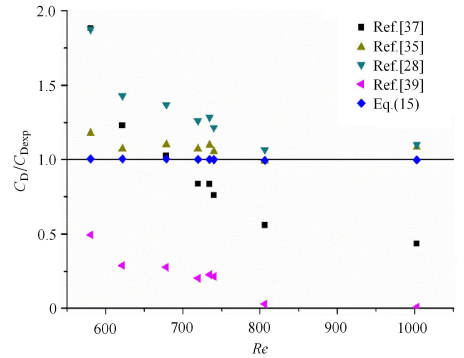
利用文献中阻力系数预测的典型相关关系 (表1 ),将其预测结果与使用平均速度$V_{\rm T}$的阻力系数公式 (13)计算 的实验数据进行对比,如图10 所示.
图10
图10
壁面条件下气泡归一化阻力与${Re}$关系
Fig. 10
The relation between bubble normalized resistance and Re under wall condition
Schiller等[37 ] ,Ishii等[38 ] 和Moore[39 ] 关联式忽略了气泡变形致使在整个${Re}$范围内$C_{\rm D}$值估计过高或过低.虽然Tomiyama等[35 ] 关联式得到的$C_{\rm D}$值与实验值拟合相对较好,但其忽略了气泡终端速度变化,依然高估了阻力变化.然而对有壁面情况下,气泡与壁面碰撞时速度和纵横比 (气泡变形)存在周期波动.因此,为准确预测气泡所受阻力的全局影响,基于$S-N$阻力模型[37 ] ,同时考虑气泡变形,提出一种壁面约束气泡的阻力相关性系数
(14) $ C_{\rm D} = A \cdot \left[ {\dfrac{24}{Re}\left( {1 + 0.15Re^{0.687}} \right)} \right] \cdot Re^B \cdot Eo^C \cdot We^D$
采用最小二乘法对实验数据拟合获得常数$A$,$B$,$C$和$D$. 因此,壁面附近单个气泡在蒸馏水中上升的阻力系数为
(15) $ C_{\rm D} = \dfrac{24}{Re}(1 + 0.15Re^{0.687})\dfrac{Re^{0.601} \cdot Eo^{0.915} \cdot We^{ - 1.069}}{17.501}$
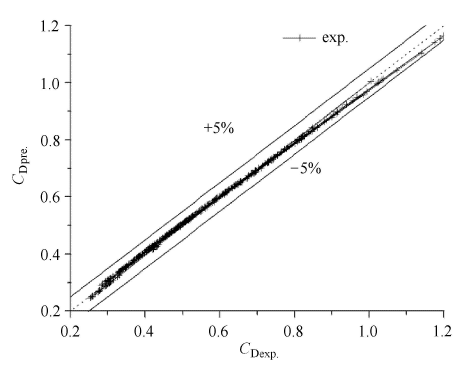
模型适用壁面附近单个非球形气泡上升运动$(S^{\ast } <2)$,雷诺数${Re} \approx 580 \sim 1100$. 如图10 所示,修正后的阻力系数与实验范围下的结果基本一致. 将实验值与式 (15)预测值进行对比 (图11 ),可 知,大部分数据在$\pm 5% $的相对误差范围内一致,能够很好地描述实验数据反映出的对${Re}$,$We$和${Eo}$等各无量 纲参数的标度规律.
图11
图11
阻力实验值与预测值的比较
Fig. 11
Comparison of experimental and predicted resistance values
3 结论
(1) 探讨了竖直壁附近上升气泡的运动特性. 对于$580 \leqslant Re \leqslant 1100$,无量纲距离$S^{\ast } <2 \sim 3$时,气泡尾涡结构与壁面共同作用下上升单气泡由三维螺旋运动(无约束条件下为三维螺旋运动)转变为二维之字运动,气泡与壁面碰撞且气泡运动轨迹周期振荡;随着$S^{\ast }$增大$(S^{\ast }>2)$,壁面效应减弱,有壁面约束与无约束条件下上升单气泡运动特性一致.
(2) 气泡与壁面碰撞前后,壁面效应导致横向速度下降为原最大值的70%,垂直速度损失50%. 上升气泡与壁面碰撞时,气泡表面变形能量单向传输给气泡横向动能,使得可变形气泡能够保持相对恒定的弹跳运动. 气泡与壁面碰撞前,通过气泡中心与壁面距离 ($x/R$)和修正的斯托克斯数相关式可预测垂直速度的下降.
(3) 提出了气泡在与壁面反复弹跳时的平均阻力系数的预测模型,在近壁区域 ($S^{\ast } <2)$ 及气泡雷诺数$Re\approx 580 \sim 1100$范围内能够很好地描述实验数据反映出的对$Re$,$We$和$Eo$等各无量纲参数的标度规律.
参考文献
View Option
[1]
Zawala J Kosior D . Dynamics of dewetting and bubble attachment to rough hydrophobic surfaces-measurements and modelling
Minerals Engineering , 2016 ,85 :112 -122
[本文引用: 1]
[2]
Clift R Grace JR Weber ME . Bubbles, Drops, Particles. New York : Academic Press , 1978
[本文引用: 1]
[3]
David M Aurélie L Arnaud C , et al . Dynamics and morphology of single ellipsoidal bubbles in liquids
Experimental Thermal & Fluid Science , 2015 ,64 :1 -12
[本文引用: 1]
[4]
de Vries AWG Biesheuvel A Wijngaarden LV . Notes on the path and wake of a gas bubble rising in pure water
International Journal of Multiphase Flow , 2002 ,28 (11 ):1823 -1835
[本文引用: 2]
[5]
Jeong H Park H . Near-wall rising behaviour of a deformable bubble at high Reynolds number
Journal of Fluid Mechanics , 2015 ,771 :564 -594
[本文引用: 2]
[6]
Zaruba A Lucasa D Prasserb HM , et al . Bubble-wall interactions in a vertical gas--liquid flow: Bouncing, sliding and bubble deformations
Chemical Engineering Science , 2007 ,62 :1591 -1605
[本文引用: 1]
[7]
Hosokawa S Tomiyama A Misaki S , et al . Lateral migration of singe bubbles due to the presence of wall
// ASME 2002 Fluids Engineering Division Summer, Meeting Montreal, Quebec, Canada , July 14-18, 2002
[本文引用: 1]
[8]
Takemura F Takagi S Magnaudet J , et al . Drag and lift forces on a bubble rising near a vertical wall in a viscous liquid
Journal of Fluid Mechanics , 2002 ,461 (461 ):277 -300
[本文引用: 1]
[9]
Takemura F Magnaudet J . The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number
Journal of Fluid Mechanics , 2003 ,495 (495 ):235 -253
[本文引用: 1]
[10]
Vasseur P Cox RG . The lateral migration of spherical particles sedimenting in a stagnant bounded fluid
Journal of Fluid Mechanics , 1977 ,80 :561 -591
[本文引用: 2]
[11]
Magnaudet J Mougin G . Wake instability of a fixed spheroidal bubble
Journal of Fluid Mechanics , 2007 ,572 :311 -337
[本文引用: 1]
[12]
Sugiyama K Takemura F , et al . On the lateral migration of a slightly deformed bubble rising near a vertical plane wall
Journal of Fluid Mechanics , 2010 ,662 (7 ):209 -231
[本文引用: 1]
[13]
Sugioka K Tsukada T . Direct numerical simulations of drag and lift forces acting on a spherical bubble near a plane
International Journal of Multiphase Flow , 2015 ,71 :32 -37
[本文引用: 1]
[14]
Zeng L Balachandar S Fischer P . Wall-induced forces on a rigid sphere at finite Reynolds number
Journal of Fluid Mechanics , 2005 ,536 (536 ):1 -25
[本文引用: 1]
[15]
Zeng L Najjar F Balachandar S , et al . Forces on a finite-sized particle located close to a wall in a linear shear flow
Physics of Fluids , 2009 ,21 (033302 ):1 -19
[本文引用: 1]
[16]
陈斌 . 高黏度流体中上升气泡的直接数值模拟
工程热物理学报 , 2006 ,27 (2 ):255 -258
[本文引用: 1]
( Chen Bin . Direct numerical simulation of bubbles rising in high viscosity fluids
Journal of Engineering Thermophysics , 2006 ,27 (2 ):82 -84 (in Chinese))
[本文引用: 1]
[17]
陈斌 , Kawamura T Kodama Y . 静止水中单个上升气泡的直接数值模拟
工程热物理学报 , 2005 ,26 (6 ):82 -84 (in Chinese))
[本文引用: 1]
( Chen Bin Kawamura T Kodama Y . Direct numerical simulation of a single bubble rising in still water
Journal of Engineering Thermophysics , 2005 ,26 (6 ):82 -84 (in Chinese))
[本文引用: 1]
[18]
张洋 , 陈科 , 尤云祥 等 . 壁面约束对裙带气泡动力学的影响
力学学报 , 2017 ,49 (05 ):1050 -1058
[本文引用: 1]
( Zhang Yang Chen Ke You Yunxiang , et al . Confinement effect on the rising dynamics of a skirted bubble
Chinese Journal of Theoretical and Applied Mechanics , 2017 ,49 (05 ):1050 -1058 (in Chinese))
[本文引用: 1]
[19]
张洋 , 陈科 , 尤云祥 等 . 浮力气泡对水平壁面的回弹动力学特性研究
力学学报 , 2019 ,51 (5 ):1285 -1295
[本文引用: 1]
( Zhang Yang Chen Ke You Yunxiang , et al . Bouncing behaviors of a buoyancy-driven bubble on a horizontal solid wall
Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51 (5 ):1285 -1295 (in Chinese))
[本文引用: 1]
[20]
邱超 , 张会臣 . 单个上升空泡撞击顶部壁面的变形和回弹特性研究
机械工程学报 , 2014 ,50 (14 ):191 -196 (in Chinese))
[本文引用: 1]
( Qiu Chao Zhang Huichen . Deformation and rebound characteristics of single rising bubble impacting against top wall
Chin J Mech Eng-EN , 2014 ,50 (14 ):191 -196 (in Chinese))
[本文引用: 1]
[21]
李帅 , 张阿漫 . 上浮气泡在壁面处的弹跳特性研究
物理学报 , 2014 ,63 (5 ):054705
[本文引用: 1]
( Li Shui Zhang Aman . Study on a rising bubble bouncing near a rigid boundary
Acta Physica Sinica , 2014 ,63 (5 ):054705 (in Chinese))
[本文引用: 1]
[22]
鞠花 , 陈刚 , 李国栋 等 . 静水中上升气泡沿倾斜壁面的运动特性试验研究
水动力学研究与进展A辑 , 2011 ,26 (3 ):327 -332
[本文引用: 1]
( Ju Hua Chen Gang Li Guodong , et al . Experimental study on motion behavior of single bubble rising along inclined plane in still water
Chinese Journal of Hydrodynamics , 2011 ,26 (3 ):327 -332 (in Chinese))
[本文引用: 1]
[23]
Celata GP Cumo MD Annibale F , et al . Effect of gas injection mode and purity of liquid on bubble rising in two-component systems
Experimental Thermal & Fluid Science , 2006 ,31 (1 ):37 -53
[本文引用: 1]
[24]
Celata GP D'Annibale F Marco PD , et al . Measurements of rising velocity of a small bubble in a stagnant fluid in one- and twocomponent systems
Experimental Thermal & Fluid Science , 2007 ,31 :609 -623
[本文引用: 1]
[25]
张嫚嫚 , 孙姣 , 陈文义 . 一种基于几何重构的Youngs-VOF耦合水平集追踪方法
力学学报 , 2019 ,51 (3 ):775 -786
[本文引用: 1]
( Zhang Manman Sun Jiao Chen Wenyi . An interface tracking method of coupled Youngs-VOF and level set based on geometricreconstruction
Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51 (3 ):775 -786 (in Chinese))
[本文引用: 1]
[26]
Zenit R Magnaudet J . Measurements of the streamwise vorticity in the wake of an oscillating bubble
International Journal of Multiphase Flow , 2009 ,35 (2 ):195 -203
[本文引用: 1]
[27]
Tsutsui T . Flow around a sphere in a plane turbulent boundary layer
Journal of Wind Engineering & Industrial Aerodynamics , 2008 ,96 :779 -792
[本文引用: 1]
[28]
Zhang J Ni MJ . What happens to the vortex structures when the rising bubble transits from zigzag to spiral?
Journal of Fluid Mechanics , 2017 ,828 :353 -373
[本文引用: 2]
[29]
Lee J Hyungmin Park . Wake structures behind an oscillating bubble rising close to a vertical wall
International Journal of Multiphase Flow , 2017 ,91 :225 -242
[本文引用: 1]
[30]
Mougin G Magnaudet J . Path instability of a rising bubble
Physical Review Letters , 2002 ,88 (1 ):014502
[本文引用: 1]
[31]
Wang X Sun J Zhao J , et al . Experimental detection of bubble-wall interactions in a vertical gas--liquid flow
Chinese Journal of Chemical Engineering , 2017 ,25 (7 ):838 -847
[本文引用: 1]
[32]
Krishna R Ursenu MI Van Baten JM , et al . Wall effects on the rise of single gas bubbles in liquids
International Communications in Heat and Mass Transfer , 1999 ,26 (6 ):781 -790
[本文引用: 1]
[33]
Simcik M Ruzicka MC Drahoš J . Computing the added mass of dispersed particles
Chemical Engineering Science , 2008 ,63 :4580 -4595
[本文引用: 1]
[34]
Zawalaa J . "Immortal" liquid film formed by colliding bubble at oscillating solid substrates
Physics of Fluids , 2016 ,28 :05710
[本文引用: 1]
[35]
Tomiyama A Kataoka I Zunm I , et al . Drag coefficients of single bubbles under normal and micro gravity conditions
JSME International Journal Series B Fluids and Thermal Engineering , 1998 ,41 :472 -479
[本文引用: 2]
[36]
Kok JBW . Dynamics of a pair of gas bubbles moving through liquid. I: Theory
European Journal of Mechanics - B/Fluids , 1993 ,12 (4 ):515 -540
[本文引用: 1]
[37]
Schiller L Naumann Z . A drag coefficient correlation
Zeitschrift des Vereines Deutscher Ingenieure , 1935 ,77 :318 -323
[本文引用: 2]
[38]
Ishii M Chawla TC . Local drag laws in dispersed two-phase flow
Nasa Sti/recon Technical Report N , 1979 ,80
[本文引用: 1]
[39]
Moore DW . The rise of a gas bubble in a viscous liquid
Journal of Fluid Mechanics , 1995 ,6 (1 ):113 -130
[本文引用: 1]
Dynamics of dewetting and bubble attachment to rough hydrophobic surfaces-measurements and modelling
1
2016
... 气液两相流广泛存在于化工、能源、环境等诸多工程中. 在两相接触器及反应器中,为控制气泡分散相的停留时间、运动及分布规律、两相间的传质或传热速率,通常会设置挡板或壁面. 气泡与壁面相互作用规律直接关系到容器内分散相的运动学及动力学行为,及气液传热传质效率[1 ] . ...
1
1978
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
Dynamics and morphology of single ellipsoidal bubbles in liquids
1
2015
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
Notes on the path and wake of a gas bubble rising in pure water
2
2002
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
... 对于垂直速度$V_{y}$ (图5 (a) ~图 5 (c)),$S^{\ast}<2$时,随着气泡被吸向壁面,$V_{y}$逐步减小,碰撞时 ($x/R \approx1$),$V_{y}$较$V_{y\max}$降低70%左右,随着气泡远离壁面气泡垂直速度继续降低,直到离开壁面 ($x/R\approx 2$)时$V_{y}$降为$V_{y\max}$的50%. 随着气泡反弹,同样的过程重复发生. DeVire等[4 ] 和Mougin等[30 ] 发现自由上升气泡后面有一对反向螺旋涡量,然而在有壁面约束条件下当气泡与壁面碰撞时,发现气泡两侧出现一个涡对[31 ] .当气泡远离壁面时,气泡两个尾涡脱落,导致气泡速度进一步降低;气泡与壁面距离$x/R>2$,气泡尾迹又重新恢复对称涡管结构.当$S^{\ast }>2$,气泡未与壁面碰撞,垂直速度$V_{y}$轻微振荡并呈周期变化. ...
Near-wall rising behaviour of a deformable bubble at high Reynolds number
2
2015
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
... 式中,$E_{{\rm k}y}$和$E_{{\rm k}x}$表示垂直和横向速度对$E_{\rm k}$的贡献. 表面能计算为$E_{\rm s}= \sigma A$,其中$\sigma $是空气-水界面的表面张力. 扁椭球的表面积 ($A)$ 表示为$d_{\rm h}$和$d_{\rm v}$的函数[5 ] ...
Bubble-wall interactions in a vertical gas--liquid flow: Bouncing, sliding and bubble deformations
1
2007
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
Lateral migration of singe bubbles due to the presence of wall
1
2002
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
Drag and lift forces on a bubble rising near a vertical wall in a viscous liquid
1
2002
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
The transverse force on clean and contaminated bubbles rising near a vertical wall at moderate Reynolds number
1
2003
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
The lateral migration of spherical particles sedimenting in a stagnant bounded fluid
2
1977
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
... 式中, $\chi $为纵横比.由于气泡质量太小,Basset力导致的速度下降幅度小于使用准稳态阻力预测的速度下降幅度;TakemurA等[10 ] 对近壁中的Basset力测量,发现Basset力比阻力低一个数量级,故忽略Basset力. 作为第一近似,准稳态黏滞力可以用式 (7)表示 ...
Wake instability of a fixed spheroidal bubble
1
2007
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
On the lateral migration of a slightly deformed bubble rising near a vertical plane wall
1
2010
... Clift等[2 ] 认为静止液体中无约束自由上升的气泡直径小于1.4 mm呈球形并保持直线运动;随着气泡尺寸的增大,其形状变为扁椭球体,并沿平面呈之字形和/或三维螺旋路径运动[3 ] . de Vries等[4 ] 发现随着气泡大小和气泡与壁 面间初始距离的变化,发现气泡在壁面上有4种运动类型:(1) 气泡沿壁滑移; (2)碰撞后沿壁面滑移; (3) 气泡与壁面 碰撞并沿壁面反复弹跳; (4) 气泡在近壁处弹跳,但不与壁面接触.Jeong等[5 ] 实验研究静止水中不同初始距离对大变形气泡上升运动的影响,发现壁面效应能够导致气泡沿壁面滑动、周期性弹跳、向外迁移和无碰撞的非周期振荡4种运动行为;气泡上升过程中表面变形与能量间传输密切相关,当气泡与壁面相碰,表面能补偿了动能不足,使得可变形气泡能够保持相对恒定的运动. ZarubA等[6 ] 实验研究垂直壁向上剪切流中气泡的弹跳运动时也有类 似结论.HosokawA等[7 ] 研究了甘油水溶液中沿垂直壁面上升单气泡的横向迁移,推导出雷诺数$Re (\leqslant 100)$(基于气泡等效直径和终端速度),且气泡不与壁碰撞下的壁力系数关联式. TakemurA等[8 -9 ] 研究静止黏性液体中球形气泡的横向运动,解释了雷诺数$Re<100$时上升的球形气泡在排斥力和吸引力(即壁面法向力)作用下的不同运动. 当雷诺数${Re} <40$时,上升气泡表面无剪切条件产生的涡量在尾流中扩散与壁面相互作用引起排斥升力,气泡远离 壁面.随着${Re}$增大,产生的涡量局限在气泡表面的薄边界层中,近尾流与壁面相互作用引起气泡周围的液体速度分布不对称导致气泡被吸引向壁面[10 ] . 当气泡和壁之间的间隙由于这种吸引变得更窄时,气泡和壁之间薄液体层中的黏度的影响引起升力反向(润滑理论)[11 -12 ] ,上升的气泡从壁上反弹. 同时推导出${Re}<1$时气泡阻力和升力的精确解及${Re}<100$时的预测公式. ...
Direct numerical simulations of drag and lift forces acting on a spherical bubble near a plane
1
2015
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
Wall-induced forces on a rigid sphere at finite Reynolds number
1
2005
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
Forces on a finite-sized particle located close to a wall in a linear shear flow
1
2009
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
高黏度流体中上升气泡的直接数值模拟
1
2006
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
高黏度流体中上升气泡的直接数值模拟
1
2006
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
静止水中单个上升气泡的直接数值模拟
1
2005
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
静止水中单个上升气泡的直接数值模拟
1
2005
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
壁面约束对裙带气泡动力学的影响
1
2017
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
壁面约束对裙带气泡动力学的影响
1
2017
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
浮力气泡对水平壁面的回弹动力学特性研究
1
2019
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
浮力气泡对水平壁面的回弹动力学特性研究
1
2019
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
单个上升空泡撞击顶部壁面的变形和回弹特性研究
1
2014
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
单个上升空泡撞击顶部壁面的变形和回弹特性研究
1
2014
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
上浮气泡在壁面处的弹跳特性研究
1
2014
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
上浮气泡在壁面处的弹跳特性研究
1
2014
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
静水中上升气泡沿倾斜壁面的运动特性试验研究
1
2011
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
静水中上升气泡沿倾斜壁面的运动特性试验研究
1
2011
... 根据气泡的横向运动,数值模拟研究把条件更加复杂化. SugiokA等[13 ] 模拟了$1 \leqslant {Re} \leqslant300$时气泡的阻力和升力,表明壁面存在能够导致阻力增大,作用在气泡上升力的大小和方向取决于${Re}$及气泡与壁面间的距离.高雷诺数${Re}(>100)$ 下,壁诱导升力在远离壁面的位置为负;反之为正. Zeng等 [14 - 15 ] 发现当雷诺数${Re}$较小$(<100)$ 时,升力系数随${Re}$及气泡与壁面间距的减小而减小.反之,刚性球所受升力方向远离壁面,壁诱导升力系数急剧增大.壁面效应能够导致气泡尾流的不稳定,进而造成气泡上升过程的不稳定,最终影响整个流场.目前,国内对于垂直壁面上升气泡研究较少,虽然主要集中于水平或一定倾斜壁面,但对研究气泡与垂直壁面的弹跳运动具有指导作用. 陈斌等[16 -17 ] 模拟不同黏性液体中垂直壁面附近气泡的上升过程,发现气泡与壁面距离较大时,壁诱导力使气泡周围的流场不对称,横向速度分量受到壁面抑制,导致气泡远离壁面. 张洋等[18 ] 模拟裙带气泡在黏性液体的圆柱形汽缸中的浮升运动,发现近壁面处增大裙带气泡的阻力系数,而当气泡与圆柱直径之比增大到一定程度时,壁面影响可忽略. 张洋等[19 ] 模拟气泡对水平壁面的碰撞-回弹运动,发现伽利略数 $(Ga)$ 的增大可加剧气泡形变,促进气泡的回弹运动. 邱超等[20 ] 研究发现空泡对水平壁面的冲击力是随空泡体积的增大而增强. 李帅等[21 ] 基于势流理论研究气泡在水平壁面处的弹跳运动,并指出浮力与韦伯数是影响气泡最终平衡形态的主要因素.鞠花等[22 ] 发现气泡与壁面碰撞的反弹幅度随着壁面倾斜角度的增大而增大. ...
Effect of gas injection mode and purity of liquid on bubble rising in two-component systems
1
2006
... 实验装置示意图如图1 所示,有机玻璃实验水槽 (300 mm $\times$ 300 mm $\times $600 mm)装入470 mm深的蒸馏水,中间放置竖直平板 (200 mm $\times$ 100 mm $\times$ 5 mm),水槽底部中心安放不锈钢气体喷嘴(内径0.19 ~ 2.4 mm),平板与喷嘴间距可调$S\!=0 \sim150$ mm.设平板底边中心为坐标原点.实验温度20${^\circ}$C,液相密度$\rho_{\rm l}=998.21$ kg/m$^{3}$,液相 黏度$\mu_{\rm l}=1.10$ mPa$\cdot$s,表面张力$\sigma = 73.34$ mN/m,气相密度$\rho_{\rm g}\!=$1.22 kg/m$^{3}$.采用两个相机 (Image MX,德国Lavi-sion公司,分辨率为2048 $\times$ 2048)互成90$^\circ$同步拍摄恒定间隔时间上升气泡,分别用红、白两个LED灯 (50 W)照亮拍摄区域,相机中心与喷嘴上方180 mm处平齐[23 ] ,拍摄区域为60 mm $\times $ 160 mm,采集频率180 Hz,拍摄50组. ...
Measurements of rising velocity of a small bubble in a stagnant fluid in one- and twocomponent systems
1
2007
... 气泡直径和速度测量的不确定性主要由数字图像处理决定[24 ] .实验中,空间 分辨率15.669像素/mm.气泡不与壁面碰撞时(图2 ),气泡边缘识别[25 ] 最大误差为$\pm 1$像素,两轴测量误差为1像素,气泡直径的最大不确定度为1.63%$\sim $3.26%.气泡与壁面碰撞时,气泡边缘识别最大误差为$\pm 2$像素,气泡直径的不确定度为3.63%$\sim $5.51%. ...
一种基于几何重构的Youngs-VOF耦合水平集追踪方法
1
2019
... 气泡直径和速度测量的不确定性主要由数字图像处理决定[24 ] .实验中,空间 分辨率15.669像素/mm.气泡不与壁面碰撞时(图2 ),气泡边缘识别[25 ] 最大误差为$\pm 1$像素,两轴测量误差为1像素,气泡直径的最大不确定度为1.63%$\sim $3.26%.气泡与壁面碰撞时,气泡边缘识别最大误差为$\pm 2$像素,气泡直径的不确定度为3.63%$\sim $5.51%. ...
一种基于几何重构的Youngs-VOF耦合水平集追踪方法
1
2019
... 气泡直径和速度测量的不确定性主要由数字图像处理决定[24 ] .实验中,空间 分辨率15.669像素/mm.气泡不与壁面碰撞时(图2 ),气泡边缘识别[25 ] 最大误差为$\pm 1$像素,两轴测量误差为1像素,气泡直径的最大不确定度为1.63%$\sim $3.26%.气泡与壁面碰撞时,气泡边缘识别最大误差为$\pm 2$像素,气泡直径的不确定度为3.63%$\sim $5.51%. ...
Measurements of the streamwise vorticity in the wake of an oscillating bubble
1
2009
... 上升气泡的路径不稳定性是尾流不稳定性的直接表现[26 ] .固体球后面的尾流,在靠近壁面的地方引起了球后流动结构的改变[27 ] .气泡在无约束壁面时以三维螺旋上升,气泡尾流呈现出双螺旋尾迹[28 ] .当气泡在壁面作反弹运动时,气泡在近壁处触发了气泡的尾流稳定性,由于壁面限制三维螺旋轨迹的尾流结构转变为对称涡管结构[29 ] ,使得气泡以之字形运动重复反弹.随着$S^{\ast}$的增大,尾迹结构受壁面效应能力减弱,气泡尾迹从对称涡管结构逐步变为双螺旋结构.因此,气泡在无约束壁面时以三维螺旋上升转为有壁面时之字形运动可以归因于壁面的稳定作用. ...
Flow around a sphere in a plane turbulent boundary layer
1
2008
... 上升气泡的路径不稳定性是尾流不稳定性的直接表现[26 ] .固体球后面的尾流,在靠近壁面的地方引起了球后流动结构的改变[27 ] .气泡在无约束壁面时以三维螺旋上升,气泡尾流呈现出双螺旋尾迹[28 ] .当气泡在壁面作反弹运动时,气泡在近壁处触发了气泡的尾流稳定性,由于壁面限制三维螺旋轨迹的尾流结构转变为对称涡管结构[29 ] ,使得气泡以之字形运动重复反弹.随着$S^{\ast}$的增大,尾迹结构受壁面效应能力减弱,气泡尾迹从对称涡管结构逐步变为双螺旋结构.因此,气泡在无约束壁面时以三维螺旋上升转为有壁面时之字形运动可以归因于壁面的稳定作用. ...
What happens to the vortex structures when the rising bubble transits from zigzag to spiral?
2
2017
... 上升气泡的路径不稳定性是尾流不稳定性的直接表现[26 ] .固体球后面的尾流,在靠近壁面的地方引起了球后流动结构的改变[27 ] .气泡在无约束壁面时以三维螺旋上升,气泡尾流呈现出双螺旋尾迹[28 ] .当气泡在壁面作反弹运动时,气泡在近壁处触发了气泡的尾流稳定性,由于壁面限制三维螺旋轨迹的尾流结构转变为对称涡管结构[29 ] ,使得气泡以之字形运动重复反弹.随着$S^{\ast}$的增大,尾迹结构受壁面效应能力减弱,气泡尾迹从对称涡管结构逐步变为双螺旋结构.因此,气泡在无约束壁面时以三维螺旋上升转为有壁面时之字形运动可以归因于壁面的稳定作用. ...
... 用周期性运动轨迹的振幅和波长分析周期弹跳运动行为 (图4 ). 当$S^{\ast } \leqslant 2$时,对于${Re}\approx 700$,气泡与壁面碰撞且运动轨迹为周期弹跳 (图3 ),周期弹跳的无量纲振幅 ($H^{\ast } =H/d_{\rm eq})$和无量 纲周期 ($T^{\ast }=T/d_{\rm eq})$基本保持不变 (图4 ). 当$S^{\ast } \approx2$时,气泡不与壁面碰撞,运动轨迹依然呈现周期运动,振幅和周期迅速增大并达到最大值,此时气泡依然在空间里呈二维之字形运动(运动振荡较小). 随着$S^{\ast }$增大,气泡逐渐由二维之字形运动转变为三维螺旋运动,周期和振幅也随之减小(图4 ). 随着$Re$的增大,气泡表面涡量的积累加大,气泡尾迹涡对强度不再对称[28 ] ,因此对于相同$S^{\ast }$,气泡运动轨迹周期和振幅均减小. ...
Wake structures behind an oscillating bubble rising close to a vertical wall
1
2017
... 上升气泡的路径不稳定性是尾流不稳定性的直接表现[26 ] .固体球后面的尾流,在靠近壁面的地方引起了球后流动结构的改变[27 ] .气泡在无约束壁面时以三维螺旋上升,气泡尾流呈现出双螺旋尾迹[28 ] .当气泡在壁面作反弹运动时,气泡在近壁处触发了气泡的尾流稳定性,由于壁面限制三维螺旋轨迹的尾流结构转变为对称涡管结构[29 ] ,使得气泡以之字形运动重复反弹.随着$S^{\ast}$的增大,尾迹结构受壁面效应能力减弱,气泡尾迹从对称涡管结构逐步变为双螺旋结构.因此,气泡在无约束壁面时以三维螺旋上升转为有壁面时之字形运动可以归因于壁面的稳定作用. ...
Path instability of a rising bubble
1
2002
... 对于垂直速度$V_{y}$ (图5 (a) ~图 5 (c)),$S^{\ast}<2$时,随着气泡被吸向壁面,$V_{y}$逐步减小,碰撞时 ($x/R \approx1$),$V_{y}$较$V_{y\max}$降低70%左右,随着气泡远离壁面气泡垂直速度继续降低,直到离开壁面 ($x/R\approx 2$)时$V_{y}$降为$V_{y\max}$的50%. 随着气泡反弹,同样的过程重复发生. DeVire等[4 ] 和Mougin等[30 ] 发现自由上升气泡后面有一对反向螺旋涡量,然而在有壁面约束条件下当气泡与壁面碰撞时,发现气泡两侧出现一个涡对[31 ] .当气泡远离壁面时,气泡两个尾涡脱落,导致气泡速度进一步降低;气泡与壁面距离$x/R>2$,气泡尾迹又重新恢复对称涡管结构.当$S^{\ast }>2$,气泡未与壁面碰撞,垂直速度$V_{y}$轻微振荡并呈周期变化. ...
Experimental detection of bubble-wall interactions in a vertical gas--liquid flow
1
2017
... 对于垂直速度$V_{y}$ (图5 (a) ~图 5 (c)),$S^{\ast}<2$时,随着气泡被吸向壁面,$V_{y}$逐步减小,碰撞时 ($x/R \approx1$),$V_{y}$较$V_{y\max}$降低70%左右,随着气泡远离壁面气泡垂直速度继续降低,直到离开壁面 ($x/R\approx 2$)时$V_{y}$降为$V_{y\max}$的50%. 随着气泡反弹,同样的过程重复发生. DeVire等[4 ] 和Mougin等[30 ] 发现自由上升气泡后面有一对反向螺旋涡量,然而在有壁面约束条件下当气泡与壁面碰撞时,发现气泡两侧出现一个涡对[31 ] .当气泡远离壁面时,气泡两个尾涡脱落,导致气泡速度进一步降低;气泡与壁面距离$x/R>2$,气泡尾迹又重新恢复对称涡管结构.当$S^{\ast }>2$,气泡未与壁面碰撞,垂直速度$V_{y}$轻微振荡并呈周期变化. ...
Wall effects on the rise of single gas bubbles in liquids
1
1999
... 图6 绘制了有壁面时气泡的平均上升速度$(U)$与无约束自由上升气泡的平均上升速度 ($U_{\rm free})$比 值. 在 上升气泡周期性反弹范围内,气泡的上升速度受到壁面边界条件的显著影响[32 ] .正如以上所述,气泡在碰撞过程中,由于能量耗散,动能损失,垂直速度和横向速度均下降,导致整体速度低于气泡自由上升速度. 当气泡不与壁面碰撞时,气泡速度基本与自由上升气泡一致. 随着气泡${Re}$的增大,气泡周期反弹过程中的平均速度也越来越低. ...
Computing the added mass of dispersed particles
1
2008
... 式中,$F_{\rm B}$是流体施加在气泡上的浮力;$F_{\rm H}$是流体施加在气泡上的Basset力;$F_{\rm D}$是作用在气泡上的非定常黏性力,包括壁面效应、准稳态阻力和气泡接近壁面时的润滑效应;$C_{\rm M}(x)$ 是附加质量系数. 气泡在碰撞时到远离壁面一小段距离内变形严重,未碰撞之前气泡变形很小,故忽略气泡变形. 壁面上移动正常的椭球形物体的附加质量系数为[33 ] ...
"Immortal" liquid film formed by colliding bubble at oscillating solid substrates
1
2016
... 无约束介质中附加质量系数$C_{M0}$与气泡变形之间的关系用为[34 ] ...
Drag coefficients of single bubbles under normal and micro gravity conditions
2
1998
... 式中,$f (x/R)$是由于壁面的存在而改变的阻力系数,$x/R$可作为时间函数,$V$和$h(Re)$ 均为恒 定值.$h(Re)$ 是TomiyamA等[35 ] 纯净液体中的阻力关联式. Kok等[36 ] 得到一阶 近似$f (x/R)\sim(x/R)^{ - 3}$.对式 (4)积分求解得 ...
... Schiller等[37 ] ,Ishii等[38 ] 和Moore[39 ] 关联式忽略了气泡变形致使在整个${Re}$范围内$C_{\rm D}$值估计过高或过低.虽然Tomiyama等[35 ] 关联式得到的$C_{\rm D}$值与实验值拟合相对较好,但其忽略了气泡终端速度变化,依然高估了阻力变化.然而对有壁面情况下,气泡与壁面碰撞时速度和纵横比 (气泡变形)存在周期波动.因此,为准确预测气泡所受阻力的全局影响,基于$S-N$阻力模型[37 ] ,同时考虑气泡变形,提出一种壁面约束气泡的阻力相关性系数 ...
Dynamics of a pair of gas bubbles moving through liquid. I: Theory
1
1993
... 式中,$f (x/R)$是由于壁面的存在而改变的阻力系数,$x/R$可作为时间函数,$V$和$h(Re)$ 均为恒 定值.$h(Re)$ 是TomiyamA等[35 ] 纯净液体中的阻力关联式. Kok等[36 ] 得到一阶 近似$f (x/R)\sim(x/R)^{ - 3}$.对式 (4)积分求解得 ...
A drag coefficient correlation
2
1935
... Schiller等[37 ] ,Ishii等[38 ] 和Moore[39 ] 关联式忽略了气泡变形致使在整个${Re}$范围内$C_{\rm D}$值估计过高或过低.虽然Tomiyama等[35 ] 关联式得到的$C_{\rm D}$值与实验值拟合相对较好,但其忽略了气泡终端速度变化,依然高估了阻力变化.然而对有壁面情况下,气泡与壁面碰撞时速度和纵横比 (气泡变形)存在周期波动.因此,为准确预测气泡所受阻力的全局影响,基于$S-N$阻力模型[37 ] ,同时考虑气泡变形,提出一种壁面约束气泡的阻力相关性系数 ...
... [37 ],同时考虑气泡变形,提出一种壁面约束气泡的阻力相关性系数 ...
Local drag laws in dispersed two-phase flow
1
1979
... Schiller等[37 ] ,Ishii等[38 ] 和Moore[39 ] 关联式忽略了气泡变形致使在整个${Re}$范围内$C_{\rm D}$值估计过高或过低.虽然Tomiyama等[35 ] 关联式得到的$C_{\rm D}$值与实验值拟合相对较好,但其忽略了气泡终端速度变化,依然高估了阻力变化.然而对有壁面情况下,气泡与壁面碰撞时速度和纵横比 (气泡变形)存在周期波动.因此,为准确预测气泡所受阻力的全局影响,基于$S-N$阻力模型[37 ] ,同时考虑气泡变形,提出一种壁面约束气泡的阻力相关性系数 ...
The rise of a gas bubble in a viscous liquid
1
1995
... Schiller等[37 ] ,Ishii等[38 ] 和Moore[39 ] 关联式忽略了气泡变形致使在整个${Re}$范围内$C_{\rm D}$值估计过高或过低.虽然Tomiyama等[35 ] 关联式得到的$C_{\rm D}$值与实验值拟合相对较好,但其忽略了气泡终端速度变化,依然高估了阻力变化.然而对有壁面情况下,气泡与壁面碰撞时速度和纵横比 (气泡变形)存在周期波动.因此,为准确预测气泡所受阻力的全局影响,基于$S-N$阻力模型[37 ] ,同时考虑气泡变形,提出一种壁面约束气泡的阻力相关性系数 ...