引 言
河口是河流与海洋的交界过渡地段, 是海陆相互作用的地区, 河口滩涂的形成及河口的维持, 与河口底层异重泥流运动关系密切. 随着我国沿海经济的转型发展和碧海蓝天及滩涂生态保护工作的推进, 河口动力过程的重新思考以及相关科学问题的深入探讨, 是新时期的海岸河口学科研究的热点.
我国有数目庞大的淤泥质河口, 河口的维持及滩涂的生态健康, 受黏性细颗粒泥沙运动[1 ] , 特别是河口底层异重流形成、运动及淤积特性所影响. 河口底层异重流的充分发育是河口维持的重要条件, 同时, 河口底部异重泥流的运动也是河口海岸 滩涂的动态变化及相应的生境演化的重要基础动力条件[2 -5 ] .
河口底层异重泥流在波浪的作用下, 由于颗粒之间及与相应孔隙水之间的相互作用, 床面底泥及异重泥流常表现较为复杂的变形现象和流变关系, 而流变关系又往往是成功描述和构建 河口底泥及异重泥流运动理论模式的关键.
针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著.
相对于他们的处理方式, 引入周期压力边界[17 , 25 -26 ] , 直接计算波浪场内的流速分布, 本文对底部泥层建立幂律力学本构关系, 构建了波浪与底泥相互作用耦合双层流体理论模式, 研究了波浪场作用下河口底部幂律异重流的流场特性, 探讨了波浪在底部泥层的影响下的固有运动特征, 并计算得到了波浪速度场、压力场特征; 不同密度影响下的异重底泥运动的流速场、压力场以及异重流泥面波与表面波的波幅比等, 分析了泥层密度、波动圆频率以及底泥幂律指数对流场及界面波的影响等.
1 理论模型与控制方程
以流体交界面作为异重流的分界线, 引入两层流体模型.
1.1 控制方程
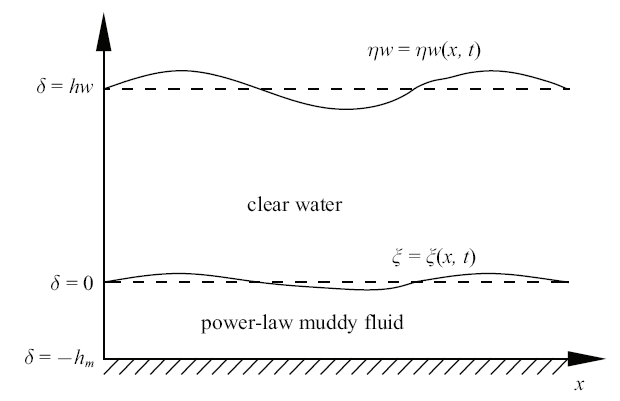
假设流体足够宽, 忽略流体沿横向的变化. 因此, 所研究流体处于竖直平面二维坐标系下, 其中$x$方向为流向, 而$z$方向是垂直于水平面的方向. 模型由两层黏性流体构成. 上层为清水, 厚度为$h_{\rm w}$; 下层为黏性泥流, 其厚度为$h_{\rm m}$, 总深度为$h= h_{\rm w} +h_{\rm m}$. 以未扰动的水泥交界面为$x$轴, 垂直方向为$z$轴, 交界面位置设为$z$轴的零点, 建立正交直角坐标系 ({如图1 }). 泥层底部固定在$z= -h_{\rm m}$的刚性床面上; 自由水面的位移为$\eta _{\rm w} = \eta _{\rm w}$ ($x, t)$; 水泥交界面的位移为$\xi = \xi $ ($x, t)$.
图1
图1
模型示意图
Fig.1
Sketch of the model
(1)上下两层流体均视为不可压缩的连续介质, 且两者无混合;
(2)上层水体受波浪扰动, 受此影响, 下层泥流产生振荡运动, 水泥交界面出现波动现象, 且上下两层的波动振幅均较小;
在$x$-$z$平面内分别对两层流体建立连续性方程和沿着水平$x$方向和垂直$z$方向的运动方程
(1) $\begin{eqnarray} \frac{\partial u_f }{\partial x} + \frac{\partial w_f }{\partial z} = 0 \end{eqnarray}$
(2) $\begin{eqnarray} \frac{\partial u_f }{\partial t} + \frac{\partial ( {u_f u_f } )}{\partial x} + \frac{\partial ( {u_f w_f } )}{\partial z} = \\ \qquad - \frac{1}{\rho _f }\frac{\partial p_f }{\partial x} + \frac{1}{\rho _f }\left( {\frac{\partial \tau _{fxx} }{\partial x} + \frac{\partial \tau _{fxz} }{\partial z}} \right) \end{eqnarray}$
(3) $\begin{eqnarray} \frac{\partial w_f }{\partial t} + \frac{\partial ( {u_f w_f } )}{\partial x} + \frac{\partial ( {w_f w_f } )}{\partial z} = \\ \qquad - \frac{1}{\rho _f }\frac{\partial p_f }{\partial z} + \frac{1}{\rho _f }\left( {\frac{\partial \tau _{fxz} }{\partial x} + \frac{\partial \tau _{fzz} }{\partial z}} \right) - g \end{eqnarray}$
式中, 下标$f$ ($f= $ w, m)用于区分上下层流体, w代表上层水体 ($0 < \delta < h_{\rm w}$), m代表下层泥流 ($- h_{\rm m} < \delta <0)$. $u$, $w$分别为水平速度分量及垂向速度分量, $\rho$为流体密度, $p$为流体压强载荷, $g$为重力加速度, $\tau _{ij}$ ($i$, $j=x$, $z$)表示剪切应力分量.
1.2 本构关系
在两层流体中分别引入本构关系. 其中, 上层水体本构关系符合一般牛顿流体规律
(4) $\begin{eqnarray} \tau _{{\rm w}ij} = \mu _{\rm w} \dot{\gamma }_{{\rm w}ij} \end{eqnarray}$
(5) $\begin{eqnarray} \tau _{{\rm m}ij} = \mu _{\rm m} \dot{\gamma }_{\rm m}^{n - 1} \dot{\gamma }_{{\rm m}ij} \end{eqnarray}$
式中, $\mu _{f}$ ($f= $w, m) 为动力黏滞系数, $\dot{\gamma }_{fij} $ ($f=$ w, m; $i$, $j=x$, $z)$为剪切率, $\dot{\gamma}_{\rm m}$为泥层剪切应力幅值, $n$为幂律流流动指数.
对于下层的黏性泥, $\mu _{\rm m}$的取值一般要远高于清水的黏滞系数, 其与泥沙浓度有很大关系, 具体可以参考文献[30 ] 、Xu等[15 ] 的最新研究成果. 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征(絮团结构能够抵抗一定的剪切力, 而破坏后抵抗力消失一部分). 因此, 若采用幂律模型描述, 其指数范围在0$\sim$1之间. 但其具体取值仍和泥浆本身性质有关。
剪切率$\dot{\gamma}_{ij}$可以表示为
(6) $\begin{eqnarray} \dot{\gamma }_{ij} = \frac{\partial u_i }{\partial x_j } + \frac{\partial u_j }{\partial x_i } \end{eqnarray}$
剪切应力幅值$\dot{\gamma }_{\rm m}$可以表示为
(7) $\begin{eqnarray} \dot{\gamma }_{\rm m} = \sqrt{\dot{\gamma }_{{\rm m}ij} \cdot \dot{\gamma }_{{\rm m}ij} / 2} \end{eqnarray}$
(8) $\begin{eqnarray} \tau _{{\rm m}xx} = 2\mu _{\rm m} \dot{\gamma }_{\rm m}^{n - 1} \frac{\partial u_{\rm m} }{\partial x} \end{eqnarray}$
(9) $\begin{eqnarray} \tau _{{\rm m}zz} = 2\mu _{\rm m} \dot{\gamma }_{\rm m}^{n - 1} \frac{\partial w_{\rm m} }{\partial z} \end{eqnarray}$
(10) $\begin{eqnarray} \tau _{{\rm m}xz} = \tau _{{\rm m}zx} = \mu _{\rm m} \dot{\gamma }_{\rm m}^{n - 1} \left( {\frac{\partial u_{\rm m} }{\partial z} + \frac{\partial w_{\rm m} }{\partial x}} \right) \end{eqnarray}$
(11) $\begin{eqnarray} \dot{\gamma }_{\rm m} = \left\{ {2\left[ {\left( {\frac{\partial u_{\rm m} }{\partial x}} \right)^2 + \left( {\frac{\partial w_{\rm m} }{\partial z}} \right)^2} \right] + \left( {\frac{\partial u_{\rm m} }{\partial z} + \frac{\partial w_{\rm m} }{\partial x}} \right)^2} \right\}^{{1}/{2}}\quad \end{eqnarray}$
1.3 边界条件
对模型补充边界条件, 引入Piedra-Cueva[31 ] 提出的两个界面的切应力$T$和正应力$N$的表达式
(12) $\begin{eqnarray} T_f = \left( {\tau _{fzz} - \tau _{fxx} } \right)\frac{\partial \eta _f }{\partial x} + \left[ {1 - \left( {\frac{\partial \eta _f }{\partial x}} \right)^2} \right]\tau _{fxz} \end{eqnarray}$
(13) $\begin{eqnarray} N_f = - p_f \left[ {1 + \left( {\frac{\partial \eta _f }{\partial x}} \right)^2} \right] + \left[ \tau _{fxx} \left( {\frac{\partial \eta _f }{\partial x}} \right)^2 - \\ \qquad 2\tau _{fxz} \left( {\frac{\partial \eta _f }{\partial x}} \right) + \tau _{fzz} \right] \end{eqnarray}$
式中, $\eta _{f}$表示界面的位移, 可以是$\eta _{\rm w}$或$\xi $.
模型的求解区域包含3个边界: 自由表面边界、水泥交界面边界、泥层底部边界.
自由水表面边界处动力学边界条件为: 沿着自由水表面边界, 切向应力为零, 正应力等于大气压强. 本文将大气压强设定为当地相对压强, 即为零, 因此自由水表面的力学边界条件为
(14) $\begin{eqnarray} T_{\rm w} = 0, \quad N_{\rm w} = 0 \end{eqnarray}$
运动学边界条件, 水质点法向运动速度等于水表面法向运动速度
(15) $\begin{eqnarray} \frac{\partial \eta _{\rm w} }{\partial t} + u_{\rm w} \frac{\partial \eta _{\rm w} }{\partial x} = w_{\rm w} \end{eqnarray}$
在水泥交界面处, 动力学边界条件认为水泥两层交界面处切应力和正应力分别相等, 因此可得水泥交界面上的边界条件为
(16) $\begin{eqnarray} T_{\rm w} = T_{\rm m}, \quad N_{\rm w} = N_{\rm m} \end{eqnarray}$
运动学边界条件, 也同样认为泥质点法向运动速度等于泥表面法向运动速度
(17) $\begin{eqnarray} \frac{\partial \xi }{\partial t} + u_{\rm m} \frac{\partial \xi }{\partial x} = w_{\rm m} \end{eqnarray}$
(18) $\begin{eqnarray} u_{\rm w} = u_{\rm m}, \quad w_{\rm w} = w_{\rm m} \end{eqnarray}$
(19) $\begin{eqnarray} u_{\rm m} = 0, \quad w_{\rm m} = 0 \end{eqnarray}$
1.1 无量纲化
对于基本方程以及边界条件中的变量, 引入式(20)所示的标准化变量
(20) $\left. \begin{array}{l@{\quad}l} x = h\hat {x},\ \ z = h\hat {z},\ \ \eta _f = h\hat {\eta }_f, \ \ t = \sigma ^{ - 1}\hat {t}\\ \gamma _f = \sigma \hat {\gamma }_f, \ \ p_{\rm w} = \rho _{\rm w} gh\hat {p}_{\rm w}, \ \ p_{\rm m} = \rho _{\rm w} gh\hat {p}_{\rm m} \\ u_f = \sigma h\hat {u}_f, \ \ w_f = \sigma h\hat {w}_f, \ \ \tau _{wxz} = \mu _{\rm w} \sigma \hat {\tau }_{wxz} \\ \left( {\tau _{wxx} , \tau _{wzz} } \right) = \mu _{\rm w} \sigma \left( {\hat {\tau }_{wxx} , \hat {\tau }_{wzz} } \right), \ \ \tau _{{\rm m}xz} = \mu _{\rm m} \sigma ^n\hat {\tau }_{{\rm m}xz} \\\left( {\tau _{{\rm m}xx} , \tau _{{\rm m}zz} } \right) = \mu _{\rm m} \sigma ^n\left( {\hat {\tau }_{{\rm m}xx} , \hat {\tau }_{{\rm m}zz} } \right) \end{array} \right\}$
代入方程 (1)$\sim$(3)及边界条件(14)$\sim$(18)中, 可得水层方程的表达式如下 (边界条件的表达式略)
(21) $\begin{eqnarray} \frac{\partial \hat {u}_{\rm w} }{\partial \hat {x}} + \frac{\partial \hat {w}_{\rm w} }{\partial \hat {z}} = 0 \end{eqnarray}$
(22) $\begin{eqnarray} \frac{\partial \hat {u}_{\rm w} }{\partial \hat {t}} + \frac{\partial \left( {\hat {u}_{\rm w} \hat {u}_{\rm w} } \right)}{\partial \hat {x}} + \frac{\partial \left( {\hat {u}_{\rm w} \hat {w}_{\rm w} } \right)}{\partial \hat {z}} = \\ \qquad - \frac{1}{Fr}\frac{\partial \hat {p}_{\rm w} }{\partial \hat {x}} + \frac{1}{Re}\left( {\frac{\partial ^2\hat {u}_{\rm w} }{\partial \hat {x}^2} + \frac{\partial ^2\hat {u}_{\rm w} }{\partial \hat {z}^2}} \right)\\ \end{eqnarray}$
(23) $\begin{eqnarray} \frac{\partial \hat {w}_{\rm w} }{\partial \hat {t}} + \frac{\partial \left( {\hat {u}_{\rm w} \hat {w}_{\rm w} } \right)}{\partial \hat {x}} + \frac{\partial \left( {\hat {w}_{\rm w} \hat {w}_{\rm w} } \right)}{\partial \hat {z}} = \\ \qquad - \frac{1}{Fr}\left( {\frac{\partial \hat {p}_{\rm w} }{\partial \hat {z}} + 1} \right) + \frac{1}{Re}\left( {\frac{\partial ^2\hat {w}_{\rm w} }{\partial \hat {x}^2} + \frac{\partial ^2\hat {w}_{\rm w} }{\partial \hat {z}^2}} \right) \end{eqnarray}$
式中, $Fr = \sigma ^{2}h$/$g$是弗劳德数, $Re = \sigma ^{2}h/\nu _{\rm w} = \rho _{\rm w}\sigma ^{2}h/\mu _{\rm w}$是水的雷诺数.
(24) $\begin{eqnarray} \varsigma = \left[ 2\left( {\frac{\partial \hat {u}_{\rm m} }{\partial \hat {x}}} \right)^2 + 2\left( {\frac{\partial \hat {w}_{\rm m} }{\partial \hat {z}}} \right)^2 + \left( {\frac{\partial \hat {u}_{\rm m} }{\partial \hat {z}}} \right)^2 + \\ \qquad 2\frac{\partial \hat {u}_{\rm m} }{\partial \hat {z}}\frac{\partial \hat {w}_{\rm m} }{\partial \hat {x}} + \left( \frac{\partial \hat {w}_{\rm m} }{\partial \hat {x}} \right)^2 \right]^{\frac{n - 1}{2}} \end{eqnarray}$
(25) $\begin{eqnarray} \frac{\partial \hat {u}_{\rm m} }{\partial \hat {x}} + \frac{\partial \hat {w}_{\rm m} }{\partial \hat {z}} = 0 \end{eqnarray}$
(26) $\begin{eqnarray} \frac{\partial \hat {u}_{\rm m} }{\partial \hat {t}} + \frac{\partial \left( {\hat {u}_{\rm m} \hat {u}_{\rm m} } \right)}{\partial \hat {x}} + \frac{\partial \left( {\hat {u}_{\rm m} \hat {w}_{\rm m} } \right)}{\partial \hat {z}} = - \frac{1}{Fr}\frac{1}{s}\frac{\partial \hat {p}_{\rm m} }{\partial \hat {x}} + \\ \qquad \lambda _{\rm m}^2 \left[ 2\frac{\partial \varsigma }{\partial \hat {x}}\frac{\partial \hat {u}_{\rm m} }{\partial \hat {x}} + \varsigma \frac{\partial ^2\hat {u}_{\rm m} }{\partial \hat {x}^2} + \frac{\partial \varsigma }{\partial \hat {z}}\lt(\frac{\partial \hat {u}_{\rm m} }{\partial \hat {z}} + \frac{\partial \hat {w}_{\rm m} }{\partial \hat {x}}) + \\ \qquad \varsigma \frac{\partial ^2\hat {u}_{\rm m} }{\partial \hat {z}^2} \right]\\ \end{eqnarray}$
(27) $\begin{eqnarray} && {\frac{\partial \hat {w}_{\rm m} }{\partial \hat {t}} + \frac{\partial \left( {\hat {u}_{\rm m} \hat {w}_{\rm m} } \right)}{\partial \hat {x}} + \frac{\partial \left( {\hat {w}_{\rm m} \hat {w}_{\rm m} } \right)}{\partial \hat {z}}} = - \frac{1}{Fr}\left( {\frac{1}{s}\frac{\partial \hat {p}_{\rm m} }{\partial \hat {z}} + 1} \right) + \\ \qquad \lambda _{\rm m}^2 \left[ \frac{\partial \varsigma }{\partial \hat {x}}\lt(\frac{\partial \hat {u}_{\rm m} }{\partial \hat {z}} + \frac{\partial \hat {w}_{\rm m} }{\partial \hat {x}}) + \varsigma \frac{\partial ^2\hat {w}_{\rm m} }{\partial \hat {x}^2} + \\ \qquad 2\frac{\partial \varsigma }{\partial \hat {z}}\frac{\partial \hat {w}_{\rm m} }{\partial \hat {z}} + \varsigma \frac{\partial ^2\hat {w}_{\rm m} }{\partial \hat {z}^2} \right] \end{eqnarray}$
式中, $\lambda _{\rm m}^{2}$表示斯托克斯边界层厚度$\delta_{\rm ms}$与总深度$h$比的平方, 斯托克斯边界层厚度$\delta _{\rm ms} = (\mu _{\rm m} \sigma ^{n- 2}/\rho _{\rm m})^{1 / 2}$, $s = \rho _{\rm m}/\rho _{\rm w}$为下层泥流与上层水层的密度之比.
1.5 谐波分析
设式(21) $\sim\!$式(27)解的形式如下
(28) $\begin{eqnarray} \left\{ {{\begin{array}{*{20}c} {u( {x, z, t} )} \\ {w( {x, z, t} )} \\ {p( {x, z, t} )} \\ \end{array} }} \right\} = \left\{ {{\begin{array}{*{20}c} {u_{\rm a} ( z )} \\ {w_{\rm a} ( z )} \\ {p_{\rm a} ( z )} \\ \end{array} }} \right\}\exp[{\rm i}( kx - \sigma t)] \end{eqnarray}$
式中, $k$是波数, $\sigma$是圆频率.
自由水面的位移和水泥交界面的位移也可以分别设为$\eta _{\rm w}=C\exp[{\rm i}(kx -\sigma t)]$和$\xi =D\exp[{\rm i}(kx-\sigma t)]$, $C$是表面波的波幅, $D$是水泥交界面波的波幅.
将式(28)代入式(21) $\sim\!$式 (27)以及边界条件中, 整理方程中的一次项.
(29) $\begin{eqnarray} {\rm i}ku_{\rm aw} (z) + \frac{\partial w_{\rm aw} (z)}{\partial z} = 0 \end{eqnarray}$
(30) $\begin{eqnarray} - {\rm i}\sigma u_{\rm aw} (z) = - \frac{1}{Fr}ikp_{\rm aw} (z) + \\ \qquad \frac{1}{Re}\left[ - k^2u_{\rm aw} (z) + \frac{\partial ^2u_{\rm aw} (z)}{\partial z^2} \right] \end{eqnarray}$
(31) $\begin{eqnarray} - {\rm i}\sigma w_{\rm aw} (z) = - \frac{1}{Fr}\frac{\partial p_{\rm aw} (z)}{\partial z}+ \\ \qquad \frac{1}{Re}\left[ - k^2w_{\rm aw} (z) + \frac{\partial ^2w_{\rm aw} (z)}{\partial z^2} \right] \end{eqnarray}$
(32) $\begin{eqnarray} {\rm i}ku_{\rm am} (z) + \frac{\partial w_{\rm am} (z)}{\partial z} = 0 \end{eqnarray}$
(33) $\begin{eqnarray} - {\rm i}\sigma u_{\rm am} (z) = - \frac{1}{s}\frac{1}{Fr}{\rm i}kp_{\rm am} (z) + \lambda _{\rm m}^2 \Bigg\{ - k^2B(z)u_{\rm am} (z) + \\ \qquad\frac{\partial B(z)}{\partial z}\left[ {\frac{\partial u_{\rm am} (z)}{\partial z} + {\rm i}kw_{\rm am} (z)} \right] + B(z)\frac{\partial ^2u_{\rm am} (z)}{\partial z^2}\Bigg\} \end{eqnarray}$
(34) $\begin{eqnarray} - {\rm i}\sigma w_{\rm am} (z) = - \frac{1}{s}\frac{1}{Fr}\frac{\partial p_{\rm am} (z)}{\partial z} + \lambda _{\rm m}^2 \Bigg\{ - k^2B(z)w_{\rm am} (z) + \\ \qquad 2\frac{\partial B(z)}{\partial z}\frac{\partial w_{\rm am} (z)}{\partial z} + B(z)\frac{\partial ^2w_{\rm am} (z)}{\partial z^2}\Bigg\} \end{eqnarray}$
(35) $\begin{eqnarray} T_{\rm w1} = 0,\quad \ \frac{1}{Re}\left[ {{\rm i}kw_{\rm aw} (z) + \frac{\partial u_{\rm aw} (z)}{\partial z}} \right] = 0 \end{eqnarray}$
(36) $\begin{eqnarray} N_{\rm w1} = 0,\quad - \frac{p_{\rm aw} (z)}{Fr} + \frac{2}{Re}\frac{\partial w_{\rm aw} (z)}{\partial z} = 0 \end{eqnarray}$
(37) $\left. \begin{array}{l@{\quad}l} u_{\rm aw} (z) = u_{\rm am} (z), \quad w_{\rm aw} (z) = w_{\rm am} (z)\\ T_{\rm w2} = T_{\rm m2} \end{array} \right\}$
(38) $\begin{eqnarray} \frac{1}{Re}\left[ {{\rm i}kw_{\rm aw} (z) + \frac{\partial u_{\rm aw} (z)}{\partial z}} \right]= \\ \qquad \lambda _{\rm m} ^2B(z)\left[ {{\rm i}kw_{\rm am} (z) + \frac{\partial u_{\rm am} (z)}{\partial z}} \right]\\ \end{eqnarray}$
(39) $\begin{eqnarray} N_{\rm w2} = N_{\rm m2} \\ - \frac{p_{\rm aw} (z)}{Fr} + \frac{2}{Re}\frac{\partial w_{\rm aw} (z)}{\partial z} = \\ \qquad - \frac{p_{\rm am} (z)}{sFr} + 2\lambda _{\rm m} ^2B(z)\frac{\partial w_{\rm am} (z)}{\partial z} \end{eqnarray}$
(40) $\begin{eqnarray} u_{\rm am} (z) = 0, \quad w_{\rm am} (z) = 0 \end{eqnarray}$
方程(29)$\sim$(34)和边界条件(35)$\sim$(40)即是待求方程.
2 数值求解及结果分析
2.1 数值求解
波动的波数受上层水体及泥层的影响, 且与圆频率存在一定的关系, 这种关系即为传统波浪理论中的色散关系. 若为空间模型, 则圆频率$\sigma$是个实数, 而波数$k$是个虚数. 本文所采用的模型是空间模式, 即给出圆频率, 通过色散关系求解波数.
对计算区域划分网格, 上部水层划分为$mw$个网格, 包含$mw+1$个结点. 泥层划分$mm$个网格, 包含$mm + 1$个结点. 各层层内每个结点处建立3个偏分方程, 需求解3个未知数. 对边界引入边界条件, 共需构建$3mw+ 3mm + 4$个方程.
对模型设定相应的计算参数, 采用有限差分法将方程中的微分项离散为线性项, 整理方程, 将方程组写为矩阵的形式
(41) $\begin{eqnarray} A x = b \end{eqnarray}$
式中$ A$ ($i$, $j)$表示第$i$个方程中第$j$个未知量的系数, 列向量$ x$表示未知量, $ b$ ($i)$表示第$i$个方程的常数项. 上述方程的常数项均为零, 方程组为齐次, 只有系数行列式为零时, 方程才有非零解, 从而得到如下形式的方程
(42) $\begin{eqnarray} \varDelta = f(\sigma) = 0 \end{eqnarray}$
上式实际表示的是模型波动的色散关系. 在本文模型中, 采用Muller法[32 ] 求解波数, 给定其他参数, 同时给定圆频率$\sigma $的值, 并预估$k$三个值, 分别计为$k_{1}$, $k_{2}$以及$k_{3}$, 对于每一个$k$值, 代入到式(42)中, 可求出相应的系数行列式$\varDelta$, 记为$\varDelta _{1}$, $\varDelta _{2}$和$\varDelta _{3}$. 设$\varDelta$与$k$的关系用一个二次多项式近似, 可以写为
(43) $\begin{eqnarray} \varDelta _i = a_1 k_i ^2 + a_2 k_i + a_3 \quad (i = 1, 2, 3) \end{eqnarray}$
将上述三组$\varDelta$与$k$代入, 可得到三个线性方程, 求解出二次多项式的系数. 令二次多项式中$\varDelta = 0$, 即可求得使$\varDelta$近似为零的$k$值, 记为$k_{4}$, 将该值代入色散关系中, 可求出$k_{4}$对应的$\varDelta _{4}$. 这样由新的$k_{2}$, $k_{3}$, $k_{4}$以及对应的$\varDelta _{2}$, $\varDelta_{3}$, $\varDelta_{4}$, 又可以计算近似值$k_{5}$. 重复上述计算过程, 不断迭代, 可求出足够精度的$k$值. 本次模型精度采用的判断依据为
(44) $\begin{eqnarray} |k_{n + 1} - k_n | < 10^{ - 6} \end{eqnarray}$
当这一条件满足时, 即可认定$k_{n}$即为所求的$k$. 将所得到的波数代回原方程组, 采用高斯消去法求解矩阵即可得到模型的流速及压强分布. 通过流速计算出剪切应力幅值, 迭代求解流场, 结果收敛即可完成计算.
2.2 模型验证
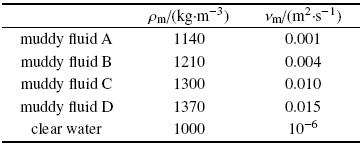
1989年Sakakiyama和Bijker[33 ] 在代尔夫特理工大学流体力学实验室进行相关实验, 测量了若干密度泥层在不同周期波浪作用下界面波与自由表面波的波幅比. 其中, 高含沙流体层的密度$\rho _{\rm m}$及运动黏滞系数$\nu _{\rm m} = \mu _{\rm m} / \rho _{\rm m}$是经过流变实验测得的, 具体见表1 .
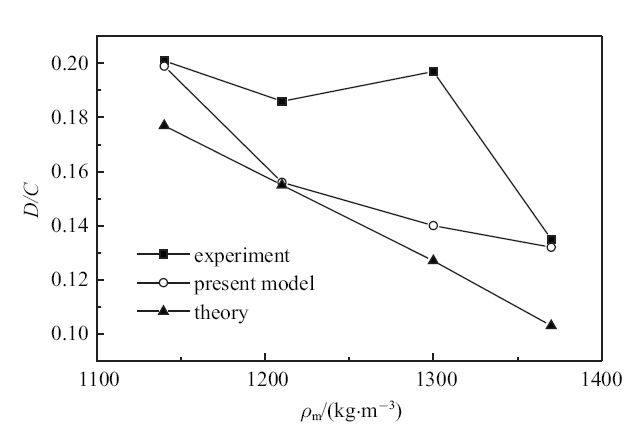
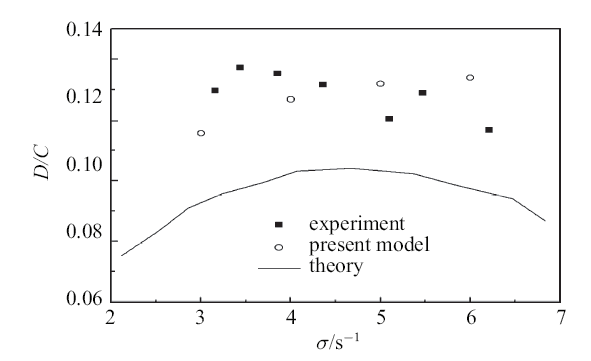
根据Sakakiyama[33 ] 的实验条件, 设定计算参数. 上部清水层水深$h_{\rm w} = 0.30$ m, 下部泥层水深$h_{\rm m} = 0.09$ m, 清水层密度$\rho _{\rm w} = 1000$ kg/m$^{3}$, 运动黏滞系数$\nu _{\rm w} = 10^{ - 6}$ m$^{2}$/s, 波浪圆频率$\sigma = 4$ s$^{-1}$, 高含沙流体密度和运动黏滞系数采用如表1 所示数据. 得到$\sigma = 4$ s$^{-1}$条件下界面波与自由表面波的波幅之比如图2 所示. 图中, $D$和$C$分别代表界面波和自由表面波的幅值, 实验指Sakakiyama和Bijker[33 ] 实验数据, 理论指Dalrymple和Liu[7 ] 的理论结果.
图2
图2
$\sigma = 4$ s$^{ - 1}$条件下界面波与自由表面波的波幅之比
Fig.2
Comparisons of the ratio of amplitude interfacial to surface wave amplitudes($\sigma = 4$ s$^{ - 1})$
从图2 中可以看出, 实验结果、理论结果以及本文模型都显示出相同的规律, 即, 密度低的下部泥层能够带来较大的波幅比, 而密度高的上部泥层的规律则反之. 表2 给出了具体的数据.
从表2 中可以看出, 与本文模型类似, 文献[7 ] 的理论模型的结果都稍小于物理实验结果, 如当$\rho _{\rm m}= 1000$ kg/m$^{3}$时, 文献[7 ] 的模型结果误差达到了35.5${\%}$, 本文的结果则是达到了28.9${\%}$, 除此之外的数据都显示了较好的吻合效果, 都控制在20${\%}$以内. 两种模型的结果都稍偏小, 大体可以认为模型结果较为合理.
将高含沙流体层的密度取为$\rho _{\rm m} = 1370$ kg/m$^{3}$, 此时对应的运动黏滞系数为$\nu _{\rm m} = 0.015$ m$^{2}$/s, 将实验结果、文献[7 ] 的理论结果以及本文模型结果对比, 并给出如图3 所示结果.
图3
图3
$\rho _{\rm m} = 1370$ kg/m条件下界面波与自由表面波的波幅之比
Fig.3
Comparisons of the ratio of amplitude interfacial to surface wave amplitudes ($\rho _{\rm m} = 1370$ kg/m$^{3})$
从图3 中可以看出, 文献[7 ] 的结果仍然稍低于实测值, 而本文模型的结果则处于实测值的范围之内. 因此, 可以认为本文的模型与实验结果吻合较好, 可以做进一步分析.
2.3 流场速度分布
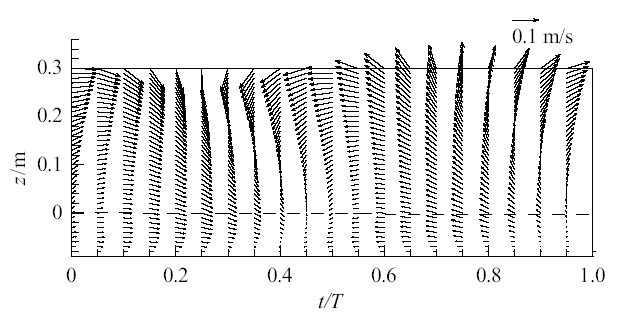
为了观察表面波浪扰动以及底泥对流场的影响, 本节参照Sakakiyama和Bijker实验设置模拟条件为: 波浪圆频率$\sigma = 4$ s$^{ - 1}$, 水深$h_{\rm w} = 0.30$ m, 泥层厚度$h_{\rm m} = 0.09$ m. 水的密度$\rho _{\rm w} =1000$ kg/m$^{3}$, 运动黏滞系数$\nu _{\rm w} = 10^{ - 6}$ m$^{2}$/s. 泥层的密度$\rho _{\rm m}= 1300$ kg/m$^{3}$, 其对应的运动黏滞系数$\nu _{\rm m} = 0.010$ m$^{2}$/s. 代入上文公式, 可得$Re=608400$, $Fr=0.636$, $s=1.3$, $\lambda _{\rm m}= 0.231$. 网格采用均匀网格, 对该工况进行计算. 图4 以0.05$T$为间隔, 绘出了一个周期内$x=0$断面处20个时刻的速度变化情况, 图5 绘出了$t=0$时刻流场垂直平面内的速度矢量变化.
图4
图4
随时间流场的速度变化
Fig.4
The variation of the velocity with time
图5
图5
二维流场的空间速度矢量分布
Fig.5
The velocity vector of two-dimensional flow field
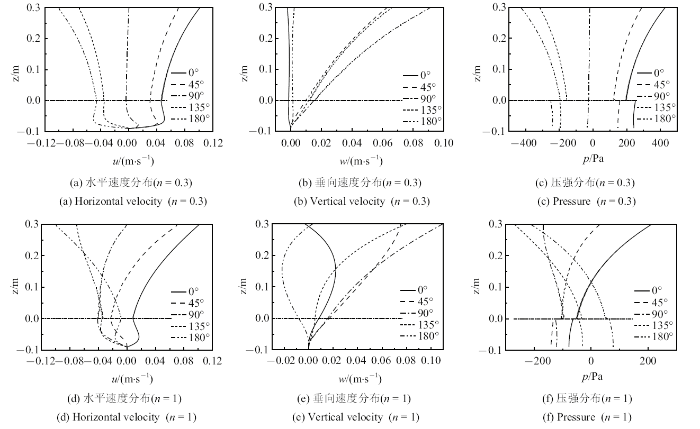
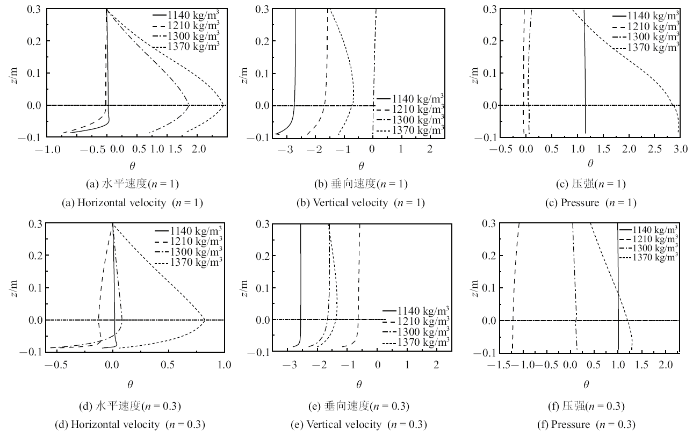
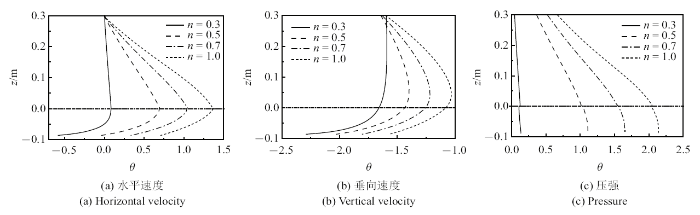
图6 则以该工况为例, 分别绘出了$n = 0.3$以及$n = 1$时流场若干相位时两个方向的速度分量以及压强变化趋势. 为了便于对比, 图6 仅绘出$kx$-$\sigma t$相位为0$^\circ$$\sim $180$^\circ$的流场变化. 可以看出, 流场中速度及压强呈现一种周期性的振荡摆动, 水泥交界面处, 速度分量连续, 压强出现突变. 在下部泥层处, 各相位的水平速度分布曲线存在极值点, 其绝对值表现出先增加后衰减为0的趋势.
图6
图6
$\rho _{\rm m} = 1300$ kg/m$^{3}$, $\sigma = 4$ s$^{ - 1}$时各相位流场分布
Fig.6
The flow field at different phases ($\rho _{\rm m} = 1300$ kg/m$^{3}$, $\sigma = 4$ s$^{- 1}$)
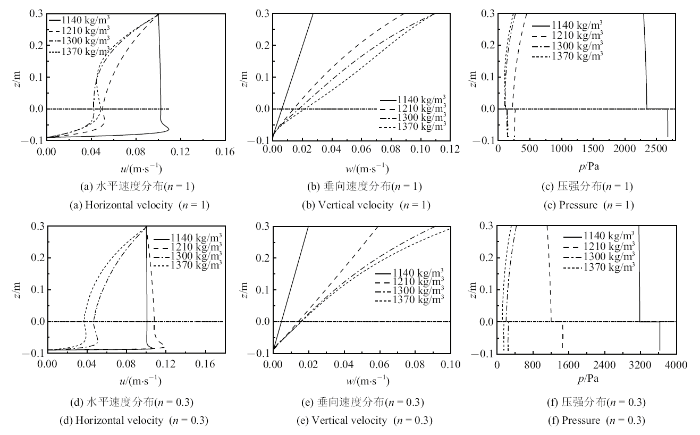
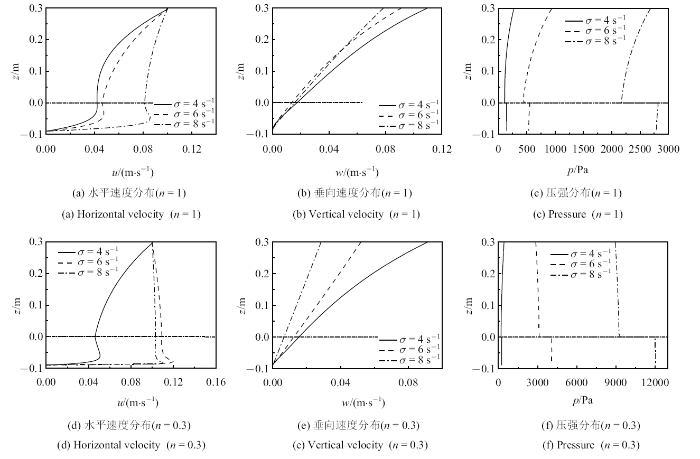
以实验4种下部泥层密度及黏滞系数为例, $\sigma = 4$ s$^{-1}$, 其他参数固定, 模型自由表面处水平速度幅值取为0.1 m/s, 计算各泥层密度对应的流速幅值分布, 图7 子图(a)$\sim $(b)及(d)$\sim$(e)分别为$n = 1.0$与$n = 0.3$时水平速度及垂向速度分量的幅值. 可以看出, 整体上, 随着泥层密度的增大, 水泥交界面的水平速度幅值呈现逐渐减小趋势. 在下部泥层, 水平速度的变化趋势表现为先略增大后急剧衰减的趋势, 其极大值点的位置随着密度减小而降低. 垂向速度方面, 垂向速度幅值变化趋势整体近似于线性变化, 其随着深度的增大逐渐衰减. 在各水平面处, 垂向速度随着泥层密度的增大而呈现增大的趋势.
图7
图7
$\sigma = 4$ s$^{ - 1}$不同泥层密度时流场幅值
Fig.7
The amplitude of flow field with different mud densities ($\sigma = 4$ s$^{ - 1}$)
图7 (c)及图7 (f)表示流场压强幅值的分布. 随着泥层密度的增大, 水层泥层的压强有降低的趋势. 水层和泥层的压强不连续, 在泥水交界面上压强出现突变, 界面处泥层压强大于上层水体的压强, 且随着泥层密度减小, 压强突变的趋势愈明显. 压强对$n$值的变化敏感, $n =0.3$时, 各水平面的压强较$n = 1$时明显增大.
(45) $\begin{eqnarray} \delta _{\rm ms} = \sqrt {\nu _{\rm m} \sigma ^{n - 2}} \end{eqnarray}$
其他条件一致时, 泥层的密度越大, 泥流的黏性越显著, 运动黏滞系数越大, 泥层斯托克斯边界层厚度越厚, 对流体的运动产生更大的阻尼, 表现为水平速度随密度增大而降低. 泥场的波动是受波浪作用下的受迫振动. 本文以自由表面处水平速度相位作为参考相位, 速度及压强的相位差由变量的虚部与实部定义
(46) $\begin{eqnarray} \theta = \arctan (a_{\rm i}/a_{\rm r}) \end{eqnarray}$
式中, $a_{\rm i}$表示速度或压强的虚部, $a_{\rm r}$表示其实部.
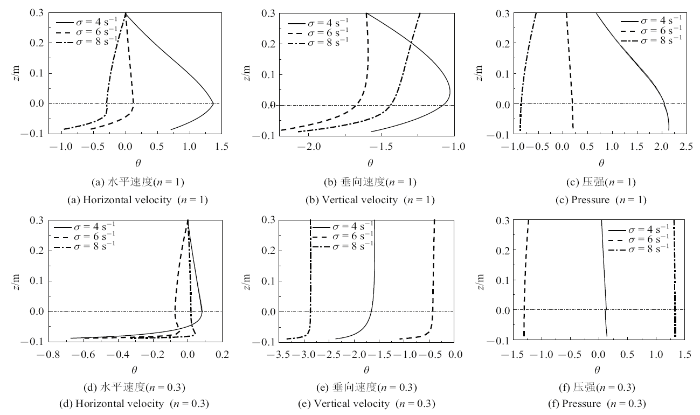
图8 给出了4种泥层密度下各层速度及压强的相位差分布. 整体上, 流速及压强相位差连续变化. 水平速度相位差随泥层密度的增大而呈增大趋势, 且密度较大时, 相位差变化更显著. 沿水深方向可看出, 水层相位差在较大密度时, 随着深度的增大呈增大趋势, 其在小密度时变化较小. 而在各密度时, 泥层的水平速度相位差变化趋势一致, 均随深度增大而减小.
图8
图8
$\sigma = 4$ s$^{ - 1}$不同泥层密度时流场相位差
Fig.8
The phase difference with different mud densities ($\sigma = 4$ s$^{ - 1}$)
垂向速度方面, 垂向速度整体滞后于参考相位, 整体上, 水层相位差变化随深度变化较小, 泥层则呈现减小的趋势. 至于压强, 流场压强相位差随深度几乎不变, 但例外的是, $\rho _{\rm m} = 1370$ kg/m$^{3}$, 相位差随水深增加呈增大趋势, 这反映了较高密度对相位差影响显著.
泥层密度固定为$\rho _{\rm m} =1300$ kg/m$^{3}$时, 计算不同圆频率对应的流场, 结果见图9 . 可以看出, 随着圆频率的减小, 各水平面的水平速度逐渐减小. 泥层最大的水平速度所对应的点的$z$坐标随着频率的增大有向下的趋势. 垂向速度方面, 在各水平面处, 随着圆频率的增大, 流速减小, 而在水深方向, 垂向速度随着深度的增大而衰减.
对于压强, 在水泥交界面处, 压强存在突变的现象. 整体来看, 随着圆频率增大, 各点对应的压强值有明显增大的趋势, 在水泥交界面处, 随着圆频率增大, 界面处上下压强突变愈加明显.
图9
图9
$\rho _{\rm m} = 1300$ kg/m$^{3}$不同圆频率时流场幅值
Fig.9
The amplitude of flow field at different circular frequencies ($\rho _{\rm m} = 1300$ kg/m$^{3}$)
由斯托克斯边界层厚度的定义可以看出, $n$的值介于0到1之间的一个小数, 增大圆频率, 表现为泥层斯托克斯边界层厚度减小, 下部泥层对水泥交界面阻尼减小, 流场的流速呈现增大的趋势, 这与模型结果一致.
图10 分别给出了3种圆频率条件下各层速度及压强的相位差分布. 水平速度在泥层下部会迅速减小. 垂向速度方面, 泥层相位差均随深度增加而呈现减小的趋势, 但水层的相位差变化存在的不同的特点, $n= 1$时, 较低频率时相位差随深度呈增大趋势, 较高频率呈减小趋势; 而在$n = 0.3$时, 水层相位差几乎不随深度变化. 压强的相位差分布上, $n = 1$时, 较低频率时相位差随深度呈增大趋势, 较高频率呈减小趋势; 而在$n = 0.3$时, 相位差几乎不随深度发生变化.
图10
图10
$\rho _{\rm m} = 1300$ kg/m$^{3}$不同圆频率时流场相位差
Fig.10
The phase difference at different circular frequencies ($\rho _{\rm m} = 1300$ kg/m$^{3}$)
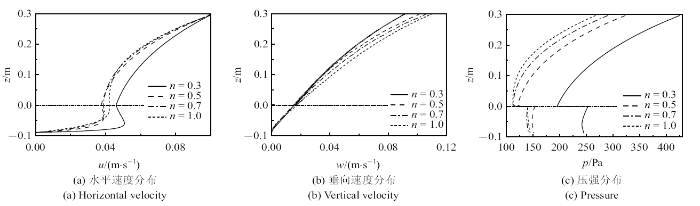
模拟条件设置为$\rho _{\rm m} = 1300$ kg/m$^{3}$, $\nu _{\rm m} = 0.010$ m$^{2}$/s, $\sigma = 4$ s$^{-1}$, 图11 (a) $\sim\!$图11 (c)分别绘制了不同流动指数对速度幅值及压强幅值分布的影响. 随着流动指数的减小, 水泥交界面的水平速度逐渐变大. 在下部泥层处, 水平速度均呈现出先增大后减小的趋势, 其最大值位置随着幂律流指数增大而升高. 垂向速度方面, 随着幂律流流动指数的减小, 垂向速度幅值呈现减小的趋势. 压强方面, 随着流动指数的减小, 各点对应的压强值增大, 界面处上下压强差值呈现增大的趋势.
图11
图11
不同幂律流指数时流场幅值
Fig.11
The The amplitude of flow field at different power-law indexes
图12 给出了该模拟条件下若干幂律流指数对应的流场相位差变化. 各幂律流指数条件下, 相位差随深度变化呈现一致性. 水平速度及垂向速度, 水层的相位差随深度增大而增大, 泥层的相位差随深度增大而减小, 而压强的相位差随深度而连续增大. 而在同一水平面上, 速度及压强相位差均随幂律流指数减小而呈减小的趋势.
图12
图12
不同幂律流指数时流场相位差
Fig.12
The phase difference at different power-law indexe
2.4 交界面与表面的波幅比
波浪作用下的产生的界面波响应是波浪与底泥相互作用的重要现象. 界面波的波幅主要受自由水表面波动和下部泥层黏性的影响. 自由水表面的波动传递到下层水泥交界面处, 引起了动压的变化, 交界面从而产生波动. 泥层的黏度将会减小交界面的波幅.
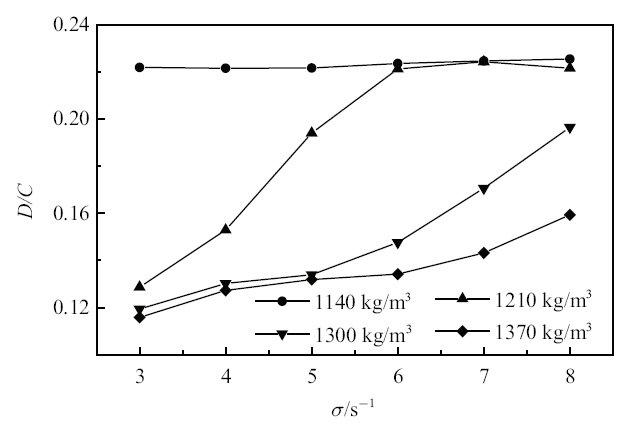
本文以界面波与自由表面波的波幅比为特征进行研究. 改变波动圆频率$\sigma $与泥层的密度$\rho _{\rm m}$, 计算各实验条件下波幅比, 结果见图13 . 从图中可以看出, 不同圆频率时, 随着泥层密度的增大, 水泥交界波与自由表面波的波幅比变化趋势一致, 均有所减小. 这反映了泥层密度越小, 交界面的波动越强.
图13
图13
界面波与表面波波幅比变化
Fig.13
Amplitude ratio of interface wave to surface wave
不同泥层密度时, 波幅比随着圆频率的变化趋势稍有不同. 在小密度情况下, 如$\rho _{\rm m} = 1140$ kg/m$^{3}$时, 波幅比变化较小, 整体趋于一个稳定值0.22, 表 明在低密度下圆频率对波幅比影响较小. 其他3种密度下, 波幅比随着圆频率增大而明显增大. $\rho _{\rm m} = 1210$ kg/m$^{3}$, 波幅比随圆频率增大而增大并最终趋于稳定值0.22. $\rho _{\rm m} = 1300$ kg/m$^{3}$及$\rho_{\rm m} = 1370$ kg/m$^{3}$波幅比随圆频率增大, 但增长出现一定的滞后, 且滞后随着泥层密度的增大而愈加显著, 增长速度随着泥层密度的增大而减小.
3 结 论
本文研究了波浪扰动下河口幂律异重流体的动力场分布特征, 得到以下结论:
在波浪扰动下, 两层异重流体出现周期性的振荡运动. 在水泥交界面处, 速度分量连续, 压强出现突变. 在下部泥层中, 水平速度分布曲线存在极值点, 水平速度绝对值的变化趋势表现为先略增大后急剧衰减, 在泥层底部降为零. 随着泥层密度的增大, 水泥交界面的水平速度逐渐减小, 水平各点的垂向速度呈现增大的趋势, 其压强则降低. 泥层水平速度幅值的极大值点的位置随着密度减小而降低. 水泥交界面处泥层压强幅值大于水体压强, 且随着泥层密度减小, 突变的趋势愈明显.
随着圆频率的增加, 同一水平面的各点水平速度幅值增大, 泥层最大的水平速度所对应的点的$z$坐标有向下的趋势. 垂向流速减小, 而各点对应的压强幅值有增大的趋势, 界面处上下压强突变愈加明显.
随着流动指数的减小, 水泥交界面的水平速度逐渐变大, 下部泥层的最大水平速度位置降低. 各点垂向速度幅值呈现减小的趋势, 各点对应的压强幅值增大, 界面处上下压强差值呈现增大的趋势.
参考文献
View Option
[1]
白静 , 方红卫 , 何国建 等 . 细颗粒泥沙净冲刷和输移的大涡模拟研究
力学学报 , 2017 ,49 (1 ):65 -74
DOI
URL
[本文引用: 1]
在传统水沙输移数值模拟研究中一般采用雷诺时均模拟技术(Reynolds-averaged simulation,RANS).与RANS相比,大涡模拟技术(large eddy simulation,LES)能够更加精确反映细部流动结构,计算机的发展使得采用LES探讨水流和泥沙运动规律成为可能.本文尝试给出净冲刷条件下悬沙计算的边界条件,采用动态亚格子模式对循环槽道和长槽道中的水流运动和泥沙输移进行了三维大涡模拟研究.利用直接数值模拟(directnumerical simulation,DNS)结果对LES模型进行了率定,计算结果符合良好,在此基础上初步探讨了泥沙浓度、湍动强度和湍动通量等的分布特征.结果表明,净冲刷条件下输沙平衡时泥沙浓度符合Rouse公式分布,单向流动中泥沙浓度沿着流向逐渐增大.泥沙浓度湍动强度和湍动通量都在近底部达到最大值,沿着垂向迅速减小.湍动黏性系数和扩散系数基本上在水深中间处达到最大.湍动Schmidt数沿着水深方向不是常数,在近底部和自由水面附近较大,在水深中间处较小.
( Bai Jing Fang Hongwei He Guojian , et al . Numerical simulation of erosion and transport of fine sediments by large eddy simulation
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (1 ):65 -74 (in Chinese))
DOI
URL
[本文引用: 1]
在传统水沙输移数值模拟研究中一般采用雷诺时均模拟技术(Reynolds-averaged simulation,RANS).与RANS相比,大涡模拟技术(large eddy simulation,LES)能够更加精确反映细部流动结构,计算机的发展使得采用LES探讨水流和泥沙运动规律成为可能.本文尝试给出净冲刷条件下悬沙计算的边界条件,采用动态亚格子模式对循环槽道和长槽道中的水流运动和泥沙输移进行了三维大涡模拟研究.利用直接数值模拟(directnumerical simulation,DNS)结果对LES模型进行了率定,计算结果符合良好,在此基础上初步探讨了泥沙浓度、湍动强度和湍动通量等的分布特征.结果表明,净冲刷条件下输沙平衡时泥沙浓度符合Rouse公式分布,单向流动中泥沙浓度沿着流向逐渐增大.泥沙浓度湍动强度和湍动通量都在近底部达到最大值,沿着垂向迅速减小.湍动黏性系数和扩散系数基本上在水深中间处达到最大.湍动Schmidt数沿着水深方向不是常数,在近底部和自由水面附近较大,在水深中间处较小.
[2]
Hooke JM . River channel adjustment to meander cutoffs on the River Bollin and River Dane, northwest England
Geomorphology 1995 ,14 (3 ):235 -253
DOI
URL
[本文引用: 1]
[3]
Leopold LB Wolman MG . River meanders
Scientific American 1966 ,71 (6 ):769 -793
DOI
URL
PMID
A sustained dynamic inflow perturbation and bar-floodplain conversion are considered crucial to dynamic meandering. Past experiments, one-dimensional modelling and linear theory have demonstrated that the initiation and persistence of dynamic meandering require a periodic transverse motion of the inflow. However, it remains unknown whether the period of the inflow perturbation affects self-formed meander dynamics. Here, we numerically study the effect of the inflow perturbation period on the development and meander dynamics of a chute-cutoff-dominated river, which requires two-dimensional modelling with vegetation forming floodplain on bars. We extended the morphodynamic model Nays2D with growth and mortality rules of vegetation to allow for meandering. We tested the effect of a transversely migrating inflow boundary by varying the perturbation period between runs over an order of magnitude around typical modelled meander periods. Following the cutoff cascade after initial meander formation from a straight channel, all runs with sufficient vegetation show series of growing meanders terminated by chute cutoffs. This generates an intricate channel belt topography with point bar complexes truncated by chutes, oxbow lakes, and scroll-bar-related vegetation age patterns. The sinuosity, braiding index and meander period, which emerge from the inherent biomorphological feedback loops, are unrelated to the inflow perturbation period, although the spin-up to dynamic equilibrium takes a longer time and distance for weak and absent inflow perturbations. This explains why, in previous experimental studies, dynamic meandering was only accomplished with a sustained upstream perturbation in flumes that were short relative to the meander wavelength. Our modelling of self-formed meander patterns is evidence that scroll-bar-dominated and chute-cutoff-dominated meanders develop from downstream convecting instabilities. This insight extends to many more fluvial, estuarine and coastal systems in morphological models and experiments, which require sustained dynamic perturbations to form complex patterns and develop natural dynamics. © 2019 The Authors. Earth Surface Processes and Landforms Published by John Wiley &amp; Sons Ltd.
[4]
沈玉昌 . 河流地貌学概论 . 北京 : 科学出版社 , 1986
( Shen Yuchang An Introduction to River Geomorphology. Beijing : Science Press , 1989 (in Chinese))
[5]
方红卫 , 何国健 , 黄磊 等 . 生态河流动力学研究的进展与挑战
水利学报 , 2018 ,50 (1 ):75 -87, 96
[本文引用: 1]
( Fang Hongwei He Guojian Huang Lei , et al . Progresses and challenges in the study of Eco-fluvial Dynamics
Journal of Hydraulic Engineering 2018 ,50 (1 ):75 -87, 96 (in Chinese))
[本文引用: 1]
[6]
Gade HG . Effects of a non-rigid impermeable bottom on plane surface waves in shallow water
Journal of Marine Research 1958 ,16 :61 -82
[本文引用: 1]
[7]
Dalrymple RA Liu PL . Waves over soft muds: A two-layer fluid model
Journal of Physical Oceanography 1978 ,8 (6 ):1121 -1131
DOI
URL
[本文引用: 6]
[8]
Cueva IP . On the response of a muddy bottom to surface water waves
Journal of Hydraulic Research 1993 ,31 (5 ):681 -696
DOI
URL
[本文引用: 1]
[9]
苏祥龙 , 许文祥 , 陈文 . 基于分形导数对非牛顿流体层流的数值研究
力学学报 , 2017 ,49 (5 ):1020 -1028
[本文引用: 1]
( Su Xianglong Xu Wenxiang Chen Wen . Numerical study for laminar flow of non-newtonian flud based on fractal derivative
Chinese Journal of Theoretical and Applied Mechani 2017 ,49 (5 ):1020 -1028 (in Chinese))
[本文引用: 1]
[10]
Nava G Tie Y Vitali V , et al . Newtonian to non-Newtonian fluid transition of a model transient network
Soft Matter 2018 ,14 (7 ):3288 -3295
DOI
URL
PMID
The viscosity of gel-forming fluids is notoriously complex and its study can benefit from new model systems that enable a detailed control of the network features. Here we use a novel and simple microfluidic-based active microrheology approach to study the transition from Newtonian to non-Newtonian behavior in a DNA hydrogel whose structure, connectivity, density of bonds, bond energy and kinetics are strongly temperature dependent and well known. In a temperature range of 15 °C, the system reversibly and continuously transforms from a Newtonian dispersion of low-valence nanocolloids into a strongly shear-thinning fluid, passing through a set of intermediate states where it behaves as a power-law fluid. We demonstrate that the knowledge of network topology and bond free energy enables to quantitatively predict the observed behavior using established rheology models.
[11]
张培杰 , 林建忠 . 非牛顿流体固粒悬浮流的若干问题
力学学报 , 2017 ,49 (3 ):543 -549
( Zhang Peijie Lin Jianzhong . Review of some researches on suspension of solid particle in non-Newtonian fluid
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (3 ):543 -549 (in Chinese))
[12]
Pantokratoras A . Flow past a rotating sphere in a non-Newtonian, power-law fluid, up to a Reynolds number of 10000
Chemical Engineering Science 2018 ,181 (18 ):311 -314
DOI
URL
[13]
13Datt C Elfring GJ . Dynamics and rheology of particles in shear-thinning fluids
Journal of Non-Newtonian Fluid Mechanics 2018 ,262 :107 -114
DOI
URL
PMID
[本文引用: 1]
We simulate the linear and nonlinear rheology of two different viscoelastic polymer solutions, a polyisobutylene solution in pristane and an aqueous solution of hydroxypropylcellulose, using a highly coarse-grained approach known as Responsive Particle Dynamics (RaPiD) model. In RaPiD, each polymer has originally been depicted as a spherical particle with the effects of the eliminated degrees of freedom accounted for by an appropriate free energy and transient pairwise forces. Motivated by the inability of this spherical particle representation to entirely capture the nonlinear rheology of both fluids, we extended the RaPiD model by introducing a deformable particle capable of elongation. A Finite-Extensible Non-Linear Elastic potential provides a free energy penalty for particle elongation. Upon disentangling, this deformability allows more time for particles to re-entangle with neighbouring particles. We show this process to be integral towards recovering the experimental nonlinear rheology, obtaining excellent agreement. We show that the nonlinear rheology is crucially dependent upon the maximum elongation and less so on the elasticity of the particles. In addition, the description of the linear rheology has been retained in the process.
[14]
Ng CO Bai Y . Mass transport in a thin layer of bi-viscous mud under surface waves
China Ocean Engineering 2002 ,16 (4 ):423 -436
[本文引用: 1]
[15]
Xu HJ Bai YC Li C . Hydro-instability characteristics of Bingham fluid flow as in the Yellow River
Journal of Hydro-environment Research 2018 ,20 :22 -30
DOI
URL
[本文引用: 2]
[16]
牛小静 , 余锡平 . 复杂黏弹性流体运动的数值计算方法
水动力学研究与进展 , 2008 ,23 (3 ):331 -337
[本文引用: 1]
( Niu Xiaojing Yu Xiping . A numerical method for flows of fluids with complex viscoelasticity
Chinese Journal of Hydrodynamics 2008 ,23 (3 ):331 -337 (in Chinese))
[本文引用: 1]
[17]
Zhang XY Ng CO . Mud-wave interaction: A viscoelastic model
China Ocean Engineering 2006 ,20 (1 ):15 -26
DOI
URL
PMID
[本文引用: 3]
The rheological characterization for a series of Malic Acid based Hydrogen Bond Donor Natural Deep Eutectic Solvents (NADES) is studied in this work for their potential usage as sorbents for CO2 capture. Three different NADES combinations were synthesized based on B-Alanine, Betaine and Choline Chloride as Hydrogen Bond Acceptors. The work provides insights on the rheological behaviors of Malic Acid-based NADES at temperature ranges from 25 to 105 °C and shear rates from 0.01 to 1000 s-1 , which shows the impact of altering the Hydrogen Bond Acceptor in a NADES system. All Malic Acid-based systems showed non-Newtonian, shear thinning behaviors and diverse viscoelastic flow behavior ranging from as low as 3 × 102 up to 4 × 107 mPa stress requirements showing viscous liquids to solid-like gel structures. The different NADES combinations showed strong temperature dependence behavior, where the density at different temperatures dropped from 1.42 to 1.37 g/cm3 for B-Alanine: Malic Acid. This behavior fits on the Bingham model revealed that the yield stress for all Malic Acid-NADES decreased with increasing temperature as expected for the shear thinning materials. The differences in the yield stress magnitudes of approximately 7 × 102 to 6 × 106 mPa in the case of B-Alanine: Malic Acid for example was attributed to the changes in the nature and the numbers of the interaction forces between the Hydrogen Bond Acceptor and Hydrogen Bond Donor of the NADES and the molecular weight. The viscoelasticity of these NADES systems demonstrated the fundamental differences between the ways the different Hydrogen Bond Acceptor interacts with the Hydrogen Bond Donor. The Linear Viscoelastic Region (LVR) was set to 0.1%-10% according to the type of NADES under a frequency range of 0.1-100 rad/s. The hole theory was used as a theoretical approach to describe the structural differences behind the flow behaviors.
[18]
Xia YZ Zhu KQ . A study of wave attenuation over a Maxwell model of a muddy bottom
Wave Motion 2010 ,47 (8 ):601 -615
DOI
URL
[本文引用: 1]
Abstract An extension to the wave attenuation over a muddy seabed is presented, in which Maxwell model is adopted as a candidate for fluidized seabed. For a very thin layer of Maxwell fluid, we present a new set of Boussinesq-type equations, in which the leading order influence of the Maxwell fluid layer appears in the source term of the continuity equation. Applying these equations to one-dimensional case, we obtain the damping rate of linear long waves and the evolution formula of solitary wave amplitude. Degenerating to Newtonian case, our results are consistent with those of Liu and Chan [1]. For the large relaxation time λ , we find that the damping rate of linear long waves is dominated by low-order modals and reaches peaks near the resonance points, and shear wave induced by solitary waves propagates along the vertical direction in the mud layer, which prolongs the damping process and leads to a second trough in the time history of bottom shear stress.
[19]
牛小静 , 余锡平 . 泥质海床的黏弹塑性模型
清华大学学报(自然科学版) , 2008 ,48 (9 ):1417 -1421
[本文引用: 1]
( Niu Xiaojing Yu Xiping . Visco-elastic-plastic model for muddy seabeds
Journal of Tsinghua University (Science and Technology) 2008 ,48 (9 ):1417 -1421 (in Chinese))
[本文引用: 1]
[20]
Rosti ME Izbassarov D Tammisola O , et al . Turbulent channel flow of an elastoviscoplastic fluid
Journal of Fluid Mechanics 2018 ,853 :488 -514
DOI
URL
[本文引用: 1]
[21]
Sohbati M Toumazou C . A two-dimensional experimental numerical approach to investigate wave transformation over muddy beds
Ocean Dynamics 2015 ,65 (2 ):295 -310
DOI
URL
[本文引用: 1]
[22]
Mei CC Krotov M Huang Z , et al . Short and long waves over a muddy seabed
Journal of Fluid Mechanics 2010 ,643 :33 -58
DOI
URL
[本文引用: 1]
[23]
Ng C Zhang X . Mass transport in water waves over a thin layer of soft viscoelastic mud
Journal of Fluid Mechanics 2007 ,573 (573 ):105 -130
DOI
URL
[本文引用: 1]
[24]
白玉川 , 田琦 . 不同流变模型下的淤泥与波浪相互作用规律
天津大学学报(自然科学与工程技术版) , 2011 ,44 (3 ):196 -201
[本文引用: 1]
( Bai Yuchuan Tian Qi . Interaction between mud and wave in different rheological models
Journal of Tianjin University (Science and Technology) 2011 ,44 (3 ):196 -201 (in Chinese))
[本文引用: 1]
[25]
Ng CO . Mass transport in a layer of power-law fluid forced by periodic surface pressure
Wave Motion 2004 ,39 (3 ):241 -259
DOI
URL
[本文引用: 3]
Abstract An asymptotic theory is presented for the mass transport in a thin layer of non-Newtonian fluid which is forced by periodic pressure on the free surface. The fluid is supposed to be pseudoplastic or shear thinning, and a power-law model is adopted to describe the stress and shear rate relationship. Based on the assumptions of shallowness and small deformations, a perturbation analysis is carried out to the second order to yield equations of motion in terms of the Lagrangian variables. These equations are non-linear because of the power law for the shear rate. Therefore, unlike the Newtonian case, the mass transport velocity cannot be found simply by first time-averaging the second-order differential equation, which instead must be solved in full before the steady component is separated from the complete solution. Numerical results, which are generated with finite differences, are examined in particular for the dependence of the fluid motion (first-order particle displacements and second-order mass transport velocity) on the pressure forcing as a function of the flow index.
[26]
Liu J Bai Y Xu D . Mass transport in a thin layer of power-law mud under surface waves
Ocean Dynamics 2017 ,67 (2 ):237 -251
DOI
URL
[本文引用: 3]
[27]
张庆河 , 王殿志 , 赵子丹 . 扰动淤泥与沉积淤泥的流变特性研究
水利学报 , 2002 ,33 (6 ):77 -82
[本文引用: 1]
( Zhang Qinghe Wang Dianzhi Zhao Zidan . Reological properties of man-mixed mud and natural deposited mud
Journal of Hydraulic Engineering 2002 : 33 (6 ):77 -82 (in Chinese))
[本文引用: 1]
[28]
呼和敖德 , 黄振华 , 张袁备 等 . 连云港淤泥流变特性研究
力学与实践 , 1994 ,16 (1 ):21 -24
URL
[本文引用: 1]
研究了体积容重为C_v=0.057~0.41连云港西墅地区淤泥的流变特性和弹性模量。在剪切率的变化范围2×10 ̄(-2)s ̄(-1),淤泥具有三种不同的流变特性,在很低剪切率情况下,淤泥剪切力基本保持常值;在低剪切率范围,表现为宾汉流体性质,其屈服应力和宾汉动性系数以C_v指数增长;在高剪切率,淤泥流动体现出宾汉伪塑性特征,划分三个特征区的临界剪切率值是随淤泥含水量变化,最后指出,连云港淤泥弹性模量与高岭土结果很相近,对淤泥含水量的变化极其敏感。
( Huhe Aode Huang Zhenhua Zhang Yuanbei , et al . Study on rheological characteristics of silt in Lianyungang
Mechanics in Engineering 1994 ,16 (1 ):21 -24 (in Chinese))
URL
[本文引用: 1]
研究了体积容重为C_v=0.057~0.41连云港西墅地区淤泥的流变特性和弹性模量。在剪切率的变化范围2×10 ̄(-2)s ̄(-1),淤泥具有三种不同的流变特性,在很低剪切率情况下,淤泥剪切力基本保持常值;在低剪切率范围,表现为宾汉流体性质,其屈服应力和宾汉动性系数以C_v指数增长;在高剪切率,淤泥流动体现出宾汉伪塑性特征,划分三个特征区的临界剪切率值是随淤泥含水量变化,最后指出,连云港淤泥弹性模量与高岭土结果很相近,对淤泥含水量的变化极其敏感。
[29]
孙献清 , 黄建维 . 含盐淤泥的流变特性
水利水运工程学报 , 1988 (1 ):71 -77
[本文引用: 1]
( Sun Xianqing Huang Jianwei . Rheological properties of saline sludge
Hydro-Science and Engineering 1988 (1 ):71 -77 (in Chinese))
[本文引用: 1]
[30]
费祥俊 . 浆体与粒状物料输送水力学 . 北京 : 清华大学出版社 , 1994 .
[本文引用: 1]
( Fei Xiangjun Transportation Hydraulics of Paste and Granular Materials. Beijing : Tsinghua University Press , 1994 (in Chinese))
[本文引用: 1]
[31]
Piedra-Cueva I . Drift velocity of spatially decaying waves in a two-layer viscous system
Journal of Fluid Mechanics 1995 ,299 :217 -239
DOI
URL
[本文引用: 1]
[32]
白玉川 , 冀自青 , 徐海珏 . 摆动河槽水动力稳定性特征分析
力学学报 , 2017 ,49 (2 ):274 -288
[本文引用: 1]
( Bai Yuchuan Ji Ziqing Xu Haijue . Hydrodynamic instability characteristics of laminar flow in a meandering channel with moving boundary
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (2 ):274 -288 (in Chinese))
[本文引用: 1]
[33]
Sakakiyama T Bijker EW . Mass transport velocity in mud layer due to progressive waves
Journal of Waterway, Port, Coastal and Ocean Engineering 1989 ,115 :614 -633
DOI
URL
[本文引用: 3]
细颗粒泥沙净冲刷和输移的大涡模拟研究
1
2017
... 我国有数目庞大的淤泥质河口, 河口的维持及滩涂的生态健康, 受黏性细颗粒泥沙运动[1 ] , 特别是河口底层异重流形成、运动及淤积特性所影响. 河口底层异重流的充分发育是河口维持的重要条件, 同时, 河口底部异重泥流的运动也是河口海岸 滩涂的动态变化及相应的生境演化的重要基础动力条件[2 -5 ] . ...
细颗粒泥沙净冲刷和输移的大涡模拟研究
1
2017
... 我国有数目庞大的淤泥质河口, 河口的维持及滩涂的生态健康, 受黏性细颗粒泥沙运动[1 ] , 特别是河口底层异重流形成、运动及淤积特性所影响. 河口底层异重流的充分发育是河口维持的重要条件, 同时, 河口底部异重泥流的运动也是河口海岸 滩涂的动态变化及相应的生境演化的重要基础动力条件[2 -5 ] . ...
River channel adjustment to meander cutoffs on the River Bollin and River Dane, northwest England
1
1995
... 我国有数目庞大的淤泥质河口, 河口的维持及滩涂的生态健康, 受黏性细颗粒泥沙运动[1 ] , 特别是河口底层异重流形成、运动及淤积特性所影响. 河口底层异重流的充分发育是河口维持的重要条件, 同时, 河口底部异重泥流的运动也是河口海岸 滩涂的动态变化及相应的生境演化的重要基础动力条件[2 -5 ] . ...
生态河流动力学研究的进展与挑战
1
2018
... 我国有数目庞大的淤泥质河口, 河口的维持及滩涂的生态健康, 受黏性细颗粒泥沙运动[1 ] , 特别是河口底层异重流形成、运动及淤积特性所影响. 河口底层异重流的充分发育是河口维持的重要条件, 同时, 河口底部异重泥流的运动也是河口海岸 滩涂的动态变化及相应的生境演化的重要基础动力条件[2 -5 ] . ...
生态河流动力学研究的进展与挑战
1
2018
... 我国有数目庞大的淤泥质河口, 河口的维持及滩涂的生态健康, 受黏性细颗粒泥沙运动[1 ] , 特别是河口底层异重流形成、运动及淤积特性所影响. 河口底层异重流的充分发育是河口维持的重要条件, 同时, 河口底部异重泥流的运动也是河口海岸 滩涂的动态变化及相应的生境演化的重要基础动力条件[2 -5 ] . ...
Effects of a non-rigid impermeable bottom on plane surface waves in shallow water
1
1958
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Waves over soft muds: A two-layer fluid model
6
1978
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... 根据Sakakiyama[33 ] 的实验条件, 设定计算参数. 上部清水层水深$h_{\rm w} = 0.30$ m, 下部泥层水深$h_{\rm m} = 0.09$ m, 清水层密度$\rho _{\rm w} = 1000$ kg/m$^{3}$, 运动黏滞系数$\nu _{\rm w} = 10^{ - 6}$ m$^{2}$/s, 波浪圆频率$\sigma = 4$ s$^{-1}$, 高含沙流体密度和运动黏滞系数采用如表1 所示数据. 得到$\sigma = 4$ s$^{-1}$条件下界面波与自由表面波的波幅之比如图2 所示. 图中, $D$和$C$分别代表界面波和自由表面波的幅值, 实验指Sakakiyama和Bijker[33 ] 实验数据, 理论指Dalrymple和Liu[7 ] 的理论结果. ...
... 从表2 中可以看出, 与本文模型类似, 文献[7 ] 的理论模型的结果都稍小于物理实验结果, 如当$\rho _{\rm m}= 1000$ kg/m$^{3}$时, 文献[7 ] 的模型结果误差达到了35.5${\%}$, 本文的结果则是达到了28.9${\%}$, 除此之外的数据都显示了较好的吻合效果, 都控制在20${\%}$以内. 两种模型的结果都稍偏小, 大体可以认为模型结果较为合理. ...
... [7 ]的模型结果误差达到了35.5${\%}$, 本文的结果则是达到了28.9${\%}$, 除此之外的数据都显示了较好的吻合效果, 都控制在20${\%}$以内. 两种模型的结果都稍偏小, 大体可以认为模型结果较为合理. ...
... 将高含沙流体层的密度取为$\rho _{\rm m} = 1370$ kg/m$^{3}$, 此时对应的运动黏滞系数为$\nu _{\rm m} = 0.015$ m$^{2}$/s, 将实验结果、文献[7 ] 的理论结果以及本文模型结果对比, 并给出如图3 所示结果. ...
... 从图3 中可以看出, 文献[7 ] 的结果仍然稍低于实测值, 而本文模型的结果则处于实测值的范围之内. 因此, 可以认为本文的模型与实验结果吻合较好, 可以做进一步分析. ...
On the response of a muddy bottom to surface water waves
1
1993
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
基于分形导数对非牛顿流体层流的数值研究
1
2017
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
基于分形导数对非牛顿流体层流的数值研究
1
2017
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Newtonian to non-Newtonian fluid transition of a model transient network
2018
Flow past a rotating sphere in a non-Newtonian, power-law fluid, up to a Reynolds number of 10000
2018
Dynamics and rheology of particles in shear-thinning fluids
1
2018
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Mass transport in a thin layer of bi-viscous mud under surface waves
1
2002
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Hydro-instability characteristics of Bingham fluid flow as in the Yellow River
2
2018
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... 对于下层的黏性泥, $\mu _{\rm m}$的取值一般要远高于清水的黏滞系数, 其与泥沙浓度有很大关系, 具体可以参考文献[30 ] 、Xu等[15 ] 的最新研究成果. 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征(絮团结构能够抵抗一定的剪切力, 而破坏后抵抗力消失一部分). 因此, 若采用幂律模型描述, 其指数范围在0$\sim$1之间. 但其具体取值仍和泥浆本身性质有关. ...
复杂黏弹性流体运动的数值计算方法
1
2008
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
复杂黏弹性流体运动的数值计算方法
1
2008
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Mud-wave interaction: A viscoelastic model
3
2006
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... [17 ]以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... 相对于他们的处理方式, 引入周期压力边界[17 , 25 -26 ] , 直接计算波浪场内的流速分布, 本文对底部泥层建立幂律力学本构关系, 构建了波浪与底泥相互作用耦合双层流体理论模式, 研究了波浪场作用下河口底部幂律异重流的流场特性, 探讨了波浪在底部泥层的影响下的固有运动特征, 并计算得到了波浪速度场、压力场特征; 不同密度影响下的异重底泥运动的流速场、压力场以及异重流泥面波与表面波的波幅比等, 分析了泥层密度、波动圆频率以及底泥幂律指数对流场及界面波的影响等. ...
A study of wave attenuation over a Maxwell model of a muddy bottom
1
2010
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
泥质海床的黏弹塑性模型
1
2008
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
泥质海床的黏弹塑性模型
1
2008
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Turbulent channel flow of an elastoviscoplastic fluid
1
2018
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
A two-dimensional experimental numerical approach to investigate wave transformation over muddy beds
1
2015
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Short and long waves over a muddy seabed
1
2010
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Mass transport in water waves over a thin layer of soft viscoelastic mud
1
2007
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
不同流变模型下的淤泥与波浪相互作用规律
1
2011
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
不同流变模型下的淤泥与波浪相互作用规律
1
2011
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
Mass transport in a layer of power-law fluid forced by periodic surface pressure
3
2004
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... [25 ]、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... 相对于他们的处理方式, 引入周期压力边界[17 , 25 -26 ] , 直接计算波浪场内的流速分布, 本文对底部泥层建立幂律力学本构关系, 构建了波浪与底泥相互作用耦合双层流体理论模式, 研究了波浪场作用下河口底部幂律异重流的流场特性, 探讨了波浪在底部泥层的影响下的固有运动特征, 并计算得到了波浪速度场、压力场特征; 不同密度影响下的异重底泥运动的流速场、压力场以及异重流泥面波与表面波的波幅比等, 分析了泥层密度、波动圆频率以及底泥幂律指数对流场及界面波的影响等. ...
Mass transport in a thin layer of power-law mud under surface waves
3
2017
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... [26 ]对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
... 相对于他们的处理方式, 引入周期压力边界[17 , 25 -26 ] , 直接计算波浪场内的流速分布, 本文对底部泥层建立幂律力学本构关系, 构建了波浪与底泥相互作用耦合双层流体理论模式, 研究了波浪场作用下河口底部幂律异重流的流场特性, 探讨了波浪在底部泥层的影响下的固有运动特征, 并计算得到了波浪速度场、压力场特征; 不同密度影响下的异重底泥运动的流速场、压力场以及异重流泥面波与表面波的波幅比等, 分析了泥层密度、波动圆频率以及底泥幂律指数对流场及界面波的影响等. ...
扰动淤泥与沉积淤泥的流变特性研究
1
2002
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
扰动淤泥与沉积淤泥的流变特性研究
1
2002
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
连云港淤泥流变特性研究
1
1994
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
连云港淤泥流变特性研究
1
1994
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
含盐淤泥的流变特性
1
1988
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
含盐淤泥的流变特性
1
1988
... 针对波浪作用下河口底泥及异重泥流的变形与运动力学本构 (流变)关系研究, 较早的研究工作有Gade[6 ] 的两层流体模型, 即:上层水体视为理想流体, 下层淤泥作为黏性牛顿体; Dalrymple等[7 ] , 又对该模型进行了改进, 将上层流体也视为黏性流体, 并将研究推广到任意水深, 建立了统一的二层黏性流体模型; Cueva[8 ] 则采用两流体分层模型, 上层假设为理想流体, 下层假设为黏性泥层, 再将流动区划分为边界区和非黏性区, 通过求解动量方程和能量方程, 计算了波动引起的质量输移. 随着研究的深入, 逐步发现牛顿黏性模型不能完全表征河口底泥及异重泥流运动的力学本构关系, 非牛顿性模型[9 -13 ] 引起了诸多学者的关注. 如Ng和Bai[14 ] 、Xu等[15 ] 采用宾汉塑性模型; 牛小静[16 ] 采用 了Jefferys黏弹性模型; Zhang等[17 ] , Xia等[18 ] 采用了黏塑性模型; 牛小静 等[19 ] , Rosti等[20 ] 采用了黏弹塑性模型; Sohbati等[21 ] 及Mei等[22 ] 又采用Kelvin-Voigt黏弹性模型. 但是, 黏弹性模型及黏塑性模型, 从力学角度看, 其仅适用于底泥或异重泥流小变形, 是小剪切变形模型. 在河口地区, 底泥或异重泥流运动往往表现出较大剪切变形和流动性, Ng和Zhang[23 ] 就曾指出由于应变与应变速率不再线性相关, 且对于恒定应力作用下, 黏弹性材料剪切变形会达到一定极限, 黏弹性模型描述黏性泥沙运动存在问题, 采用幂律流模型更加适宜; 白玉川和田琦[24 ] 以天津海河口的淤泥为材料进行波浪衰减实验, 并运用多种本构模型进行数值计算, 结果也表明幂律本构模型能更好地描述底泥的非线性特征; Ng[25 ] 、Liu等[26 ] 先后以单层流体模型和双层流体模型, 应用幂律本构关系研究了周期性压力作用下底泥的质量输移; 此外, 张庆河[27 ] 、呼和敖德[28 ] 、孙献清等[29 ] 对黏性泥沙流变特性的研究工作也再次证明幂律本构模型对描述河口底泥及异重泥流的特性更为适合. 在河口纯波浪与河口底泥及异重泥流层的相互作用研究工作中, 传统的处理方法往往忽略泥层运动对波浪的影响, 以周期性载荷简化波浪, 例如Ng[25 ] 、Zhang等[17 ] 以及Liu等[26 ] 对波浪的模拟均采取了此种方式. 但这样的研究, 尤其是后者的研究, 主要针对风浪这种有外部激励型载荷作用的流体运动, 而波浪理论是研究涌浪这种流体内部固有频率的运动特性. 这两者之间是存在一定差别的. 同时, 由于风载荷效果的减弱, 这种差别在有防波堤建立的区域内更加显著. ...
1
1994
... 对于下层的黏性泥, $\mu _{\rm m}$的取值一般要远高于清水的黏滞系数, 其与泥沙浓度有很大关系, 具体可以参考文献[30 ] 、Xu等[15 ] 的最新研究成果. 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征(絮团结构能够抵抗一定的剪切力, 而破坏后抵抗力消失一部分). 因此, 若采用幂律模型描述, 其指数范围在0$\sim$1之间. 但其具体取值仍和泥浆本身性质有关. ...
1
1994
... 对于下层的黏性泥, $\mu _{\rm m}$的取值一般要远高于清水的黏滞系数, 其与泥沙浓度有很大关系, 具体可以参考文献[30 ] 、Xu等[15 ] 的最新研究成果. 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征 而幂律流流动指数$n$则与浑水中的絮凝结构有关. 浑水中的黏性泥沙容易形成絮团结构, 这种结构在高剪切流动中容易遭到破坏. 因此, 黏稠泥浆表现出剪切稀化的特征(絮团结构能够抵抗一定的剪切力, 而破坏后抵抗力消失一部分). 因此, 若采用幂律模型描述, 其指数范围在0$\sim$1之间. 但其具体取值仍和泥浆本身性质有关. ...
Drift velocity of spatially decaying waves in a two-layer viscous system
1
1995
... 对模型补充边界条件, 引入Piedra-Cueva[31 ] 提出的两个界面的切应力$T$和正应力$N$的表达式 ...
摆动河槽水动力稳定性特征分析
1
2017
... 上式实际表示的是模型波动的色散关系. 在本文模型中, 采用Muller法[32 ] 求解波数, 给定其他参数, 同时给定圆频率$\sigma $的值, 并预估$k$三个值, 分别计为$k_{1}$, $k_{2}$以及$k_{3}$, 对于每一个$k$值, 代入到式(42)中, 可求出相应的系数行列式$\varDelta$, 记为$\varDelta _{1}$, $\varDelta _{2}$和$\varDelta _{3}$. 设$\varDelta$与$k$的关系用一个二次多项式近似, 可以写为 ...
摆动河槽水动力稳定性特征分析
1
2017
... 上式实际表示的是模型波动的色散关系. 在本文模型中, 采用Muller法[32 ] 求解波数, 给定其他参数, 同时给定圆频率$\sigma $的值, 并预估$k$三个值, 分别计为$k_{1}$, $k_{2}$以及$k_{3}$, 对于每一个$k$值, 代入到式(42)中, 可求出相应的系数行列式$\varDelta$, 记为$\varDelta _{1}$, $\varDelta _{2}$和$\varDelta _{3}$. 设$\varDelta$与$k$的关系用一个二次多项式近似, 可以写为 ...
Mass transport velocity in mud layer due to progressive waves
3
1989
... 1989年Sakakiyama和Bijker[33 ] 在代尔夫特理工大学流体力学实验室进行相关实验, 测量了若干密度泥层在不同周期波浪作用下界面波与自由表面波的波幅比. 其中, 高含沙流体层的密度$\rho _{\rm m}$及运动黏滞系数$\nu _{\rm m} = \mu _{\rm m} / \rho _{\rm m}$是经过流变实验测得的, 具体见表1 . ...
... 根据Sakakiyama[33 ] 的实验条件, 设定计算参数. 上部清水层水深$h_{\rm w} = 0.30$ m, 下部泥层水深$h_{\rm m} = 0.09$ m, 清水层密度$\rho _{\rm w} = 1000$ kg/m$^{3}$, 运动黏滞系数$\nu _{\rm w} = 10^{ - 6}$ m$^{2}$/s, 波浪圆频率$\sigma = 4$ s$^{-1}$, 高含沙流体密度和运动黏滞系数采用如表1 所示数据. 得到$\sigma = 4$ s$^{-1}$条件下界面波与自由表面波的波幅之比如图2 所示. 图中, $D$和$C$分别代表界面波和自由表面波的幅值, 实验指Sakakiyama和Bijker[33 ] 实验数据, 理论指Dalrymple和Liu[7 ] 的理论结果. ...
... [33 ]实验数据, 理论指Dalrymple和Liu[7 ] 的理论结果. ...