引 言
当液体局部压力瞬间低于饱和蒸汽压,会发生相变形成空泡,这一空化现象普遍存在于自然界及工程领域中. 空泡非球标识码和溃灭过程,生成高速射流、冲击波等,包含了相变传质、非稳态及可压缩等复杂因素. 当空泡与自由液面相互作用时,进一步涉及到自由面的非线性变形、破碎及飞溅等现象,是流体力学和气泡动力学研究的前沿.
气泡与自由液面相互作用产生复杂的力、热、化学效应[1-3],具有海洋工程、军事、医疗等领域广泛的应用背景. 船舶在水面高速航行时,液面下空泡脉动作用会诱导自由面大变形,影响航行体的稳定性和速度[4-6]. 在国防工业领域,潜射航行体在穿越自由面过程中,由于表面低压区,空化相变会形成空泡群,且在自由面影响下,空泡群标识码成的冲击载荷,可严重影响出水后轨迹和结构的安全性[7-11]. 近些年很多学者研究发现水下爆炸对于水面舰船的危害也非常大,这是因为水下爆炸后生成的空泡在溃灭过程中,会诱导液面标识码速射流,破坏舰船稳定性,造成重大损失[12-14]. 另一方面,溃灭效应如果能得到定向控制,就可广泛应用于工业、生物科学等领域. 超声波清洗中利用空泡溃灭生成的冲击波和高速射流清除附着的污染物[15-18]. 现代化医疗手段如高强度超声聚焦 (HIFU)[19-22]、冲击波体外碎石 (ESWL) 技术[23-27],也大量标识码泡溃灭来增强治疗效果. 例如,在 HIFU 的肿瘤治疗中,空泡运动诱导的额外高温高压可以提高肿瘤失活效率;在ESWL技术中,空泡溃灭产生二次射流标识码波会增强碎石能力. 有限区域中气泡溃灭诱导的自由面高速射流可作为重要的无针注射手段[28-32],高速射流可以瞬间穿透皮肤到标识码,促使药物快速吸收和起效. 另外,自由液面与气泡相互作用在自然界中也普遍存在. 如图1 所示,波浪破碎会在海洋自由液面下形成大量的气泡,气泡运动诱导生成的自由液面射流和破碎后的液滴有助于海洋和标识码间的热量、质量和各种污染物的交换,其中,气泡的尺寸和大小是影响传递效率的重要因素[33-35].
图1
在前述的应用问题与自然界现象中,空泡与自由液面相互作用诱导的空泡非球形演化和自由面变形是其中的共性关键过程. 对空标识码的研究是从 Rayleigh[36]开始的,他建立了不可压缩流场中球形气泡的运动方程式. 经过许多学者不断完善和发展,得到的气泡溃灭理论可用来描述气泡的脉动特征,如体积振荡、溃灭时间等[37]. 自 Kornfeld 和 Suvorow[38]首次提出在边界条件约束作用下气泡会发生非球形演化并生成高速射流等现象后,国内标识码进行大量实验研究工作,探索了不同类型边界影响下气泡溃灭过程. 针对自由表面附近的气泡运动规律,研究者通过实验观测[17, 39, 40-45]、理论分析[46-51]和数值计算[52-62]进行了广泛的研究. 如图2 所示,在自由面影响下,气泡发生膨胀、收缩振荡,同时,在非均匀压力场作用下泡内生成液体射流,射流撞击与穿透气泡壁,造成水锤效应,产生多个溃灭冲击波. 然而,上述研究的主要关注的是空泡脉动现象,对自由液面在空泡溃灭过程中的运动学特性关注较少. 与其他性质边界相比,自由面的惯性约束非常小,因此气泡溃灭能够导致更复杂的自由面的变形.近年来该问题得到了越来越多的关注. 典型的现象如图3 所示,在空泡膨胀过程中,自由液面被拱起并继续向上运动形成细射流. 在气泡非球形溃灭过程中,泡内生成射流并促使其背离自由面迁移,随后自由面在气泡再膨胀作用下,在细射流标识码成粗射流,最终发展成为冠状的水裙结构.
图2
图3
本文将从空泡非球形演化和自由面变形规律角度出发,概述和归纳近年来该领域的研究进展与成果. 本文的主体结构安排如下:首先概述了研究气泡非球形演化和自由液面变形的主要理论方法. 随后以空泡与水平自由面为例,针对自由液面影响下气泡脉动形态,概述和归纳了空泡溃灭过程中重要参数对非球形演化标识码液面变形的影响规律. 此外还介绍了界面曲率对自由液面变形影响研究. 最后,针对目前研究状况总结出该领域研究中尚未解决的问题,希望可为空泡及空泡群与自由液面相互作用的深入研究提供借鉴.
1 气泡与自由液面相互作用理论研究
空泡在自由面影响下发生非球形演化,生成高速射流,能够促使气泡发生背离自由液面的运动. Benjamin 和 Ellis[64]利用标识码冲量理论描述了无限水域中空泡形变、射流形成以及空泡溃灭后的涡环结构. 虽然开尔文冲量可以解释空泡的非球形演化及附近压力场的变化,但仍无法分析自由液面射流的形成和发展的过程. 之后许多学者开始从自由面的几何效应出发,利用界面凹陷产生与有限时间奇点近似的动力学特性来概念解释自由液面变形. 另一方面,少量的研究结果表明,部分曲状液面生成的射流,与瑞利-泰勒不稳定性现象有关,即界面处压标识码度梯度不平行,从而产生斜压力矩,并产生涡量,促使界面失稳进而形成射流.
1.1 开尔文冲量
图4
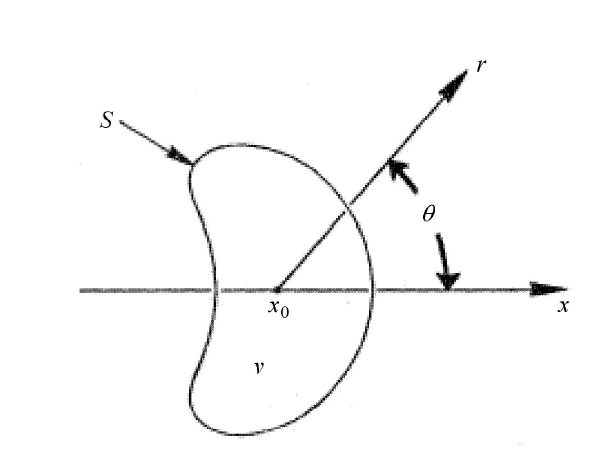
在开尔文冲量理论中,假设无限水域是不可压、无黏、无旋的理想流体,空泡在体积振荡过程中,可能发生形变和沿对称轴方向的迁移. 他们将空泡等效成质量不计的可变形刚体,并引入附加质量的概念,使其适用于冲量定理. 将无限理想流体作为控制体,可以得到其动能方程和势能方程
式中,$F$ 表示作用在空泡上的外力,$x_{0}(t)$ 表示固定坐标系下空泡沿对称轴方向的质心坐标, $\lambda_{n}(t)$ 是一组表征空泡形状的参数. $M$ 是关于 $\lambda_{n}(t)$ 的函数,代表空泡瞬时脉动体积诱导的附加质量,$J$ 表示空泡相对于质心迁移的变形率, $T’$ 是关于空泡变形率的函数,与 $x_{0}(t)$ 和 $\dot x_{0}(t)$ 无关,$p_{\infty }$ 是无穷远处的压强,为常数,$p_{\rm i}$ 是空泡内部压强,$v_{\rm b}$ 是随时间变化的空泡体积. 对控制体的动能和势能,应用 Euler-Lagrange 方程
将方程式 (1) 和式 (2) 代入式 (3) 中,求解可以获得开尔文冲量的表达式
气泡溃灭在一个极短的时间内发生, $\int F d t$ 的变化很小,因此可以假设 $I$= 常数. 也就是说,在气泡溃灭过程中,开尔文冲量是保持不变的. 在空泡脉动初期阶段和溃灭阶段,由于空泡形态稳定,$J$ 趋于 0,因此空泡初始状态与溃灭状态的 $M \dot x_{0}$ 是接近的. 由于溃灭状态下空泡运动诱导的附加质量 $M$ 是非常小的,因此质心运动速度 $\dot x_{0}(t)$ 需要无限增大以保持开尔文冲量不变,这与实际不符. 因此,根据 Lamb 的理论,空泡和流场只有从单连通变为多连通,空泡背部内卷形成射流,构成一个中空的涡环,才能保持开尔文冲量.
1.2 界面凹陷奇点
图5
图6
1.3 Rayleigh-Taylor 不稳定性
图7
图7
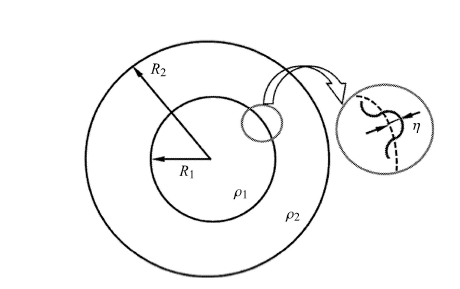
球几何下两层流体系统:界面扰动幅值 $\eta $
Fig.7
Two-layer fluid system in spherical geometry: Surface perturbation $\eta $
在球几何下,半径 $R_{1}$ 界面的速度和加速度为
根据 Plesset 等[88]研究,在界面上引入 $\theta $ 和 $\varphi $ 方向上关于模数 ($n, m$) 的小扰动以及径向扰动 $\eta_{1}$,扰动后界面可以表示为
式中,$Y_{n,m}(\theta , \varphi )$ 是球函数.
由小扰动理论可知,界面扰动幅值应远小于界面半径
为简化模型,先推导平面几何的界面扰动.当界面受到一个脉冲加速度 $g=\Delta v\delta (t)$ 时,可得
式中, $\delta (t)$ 是 delta 函数,下标 $\pm $ 表示受到脉冲加速度之后和之前的状态,$k$ 为波数, $k=2\pi /\lambda $, $\lambda $ 表示扰动的波长,$A$ 表示阿特伍德数
因此,在平面几何上,得到了关于界面扰动的常微分方程,又称 Plesset 方程[88]
同理,在柱几何中[89],可以得到
在球几何中[56],可以得到
2 空泡与液面相互作用规律及理论应用
本文以空泡与水平自由液面相互作用为例,从空泡脉动形态特征和自由面变形角度,概述近年来该领域的实验研究进展和主要研究成果. 研究表明,如图8 所示,当空泡与自由液面在不同距离下相互作用时,空泡会发生不同的相界面行为演化标识码迁移、生成射流、水锤效应和溃灭冲击波等. 相比空泡溃灭过程,自由液面的变形更加复杂,生成透明水层、冠状结构、非冠状结构等.
图8
2.1 自由液面约束下气泡脉动特征
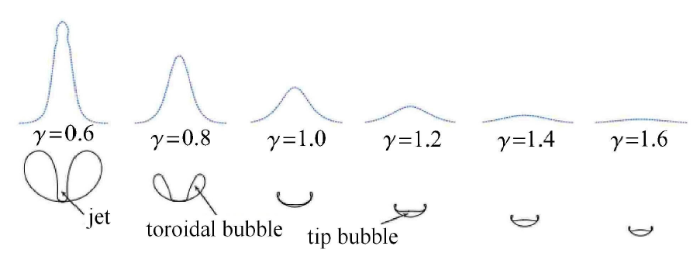
针对空泡非球形演化问题,很多学者通过气泡初始中心距自由液面距离与空泡最大半径之比定义无量纲距离 $\gamma $,归纳空泡脉动特性和溃灭类型. Obreschkow 等[91]推导了表征开尔文冲量的无量纲参数$\zeta $,此参数与流体的物性无关,可以更广泛应用于描述空泡演化问题. 空泡脉动过程中生成的射流的动量可以用开尔文冲量来表示
$ I = \int_{ - T_{\rm c}}^{T_{\rm c}} d t\int_{S(t)} d {\pmb F} \propto - \nabla pR_0^3 T_{\rm c} $
其中,$T_{\rm c}$ 是空泡溃灭 Rayleigh 时间常数,$R_0 $ 是空泡脉动第一次周期的最大半径.
在开尔文冲量基础上,提出开尔文能量 (Kelvin energy) 的概念
根据动量和动能定理,可以获得关于射流的最大体积无量纲参数 $\varepsilon_{\rm jet}$ 的标度率
在他们已有的实验结果统计分析中也得到了相同的结论. 因此,定义无量纲参数 $\zeta \equiv \mid \nabla P\mid R_{0}/\Delta P$ 来表征空泡非球形溃灭. Supponen 等[44]还在此基础上推导了无量纲参数 $\zeta $ 与 $\gamma $ 的关系.
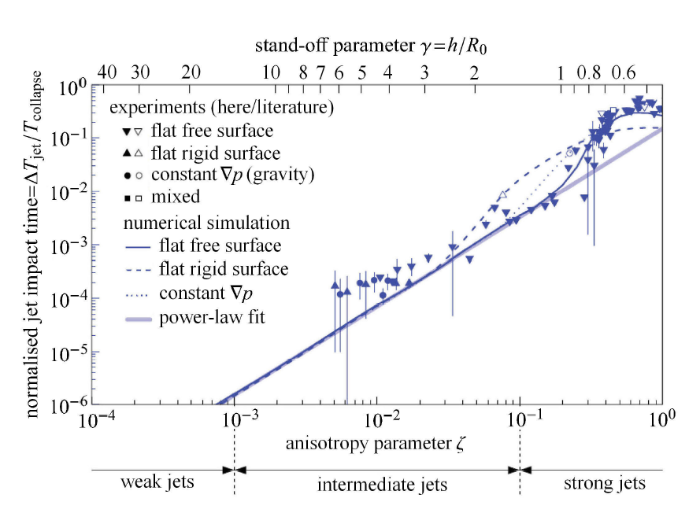
空泡在内外压强作用下膨胀到最大半径,再收缩.然后从空泡最小半径反弹,直到能量消耗殆尽. 因此,对于空泡体积振荡的研究,空泡的最大直径和溃灭时间是关键参数. 通常假定空泡脉动到最大直径时,内部压强为饱和蒸汽压[92-95],再根据溃灭过程中能量守恒,利用初始状态推导最大体积. 另一方面,溃灭时间是指空泡从最大直径到最小直径的时间,通常用 Rayleigh 溃灭时间表示. 对于空泡非球形性溃灭过程,射流生成是最基本的特征. 因此,很多研究根据射流撞击空泡壁的时间来判定空泡演化程度. 用空泡溃灭时间将射流撞击壁面时间无量纲化,如图9 所示,在不同 $\zeta $ 和 $\gamma $ 下,该时间无量纲参数的变化规律. 随着空泡接近自由面,该无量纲参数逐渐变大. 这表明在自由面较强约束下,射流撞击泡壁的时间与溃灭时间接近,说明空泡剧烈的变形会引起溃灭. 可以看到,射流撞击泡壁时间与无量纲参数$\zeta$存在比例关系.
图9
图10
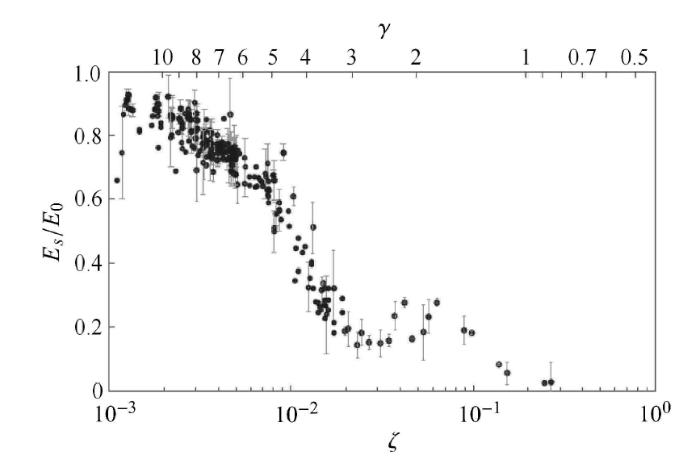
空泡反弹瞬间,泡壁撞击周围水域形成溃灭冲击波.针对空泡的非球形演化过程,如图11 所示,射流会导致空泡分裂,每个标识码裂后部分的溃灭都会生成冲击波,这种现象称为水锤效应. 很多学者已经从实验观测[36, 97-99]和数值计算角度[57, 100]研究了近自由面空泡的溃灭过程,然而现有研究对于多个溃灭冲击波生成过程关注相对很少. Supponen 等[90]通过高速摄影和压强传感器同步测量技术,研究了不同强度射流类型导致的水锤效应. 研究发现,空泡分裂后的各部分溃灭生成的冲击波能量与系数$\zeta $成比例关系. 因此,他们提出了一个半经验公式,如方程式 (15),可以量化空泡溃灭过程中生成冲击波的能量. 图12 给出了不同空泡溃灭类型的溃灭冲击波能量与空泡溃灭总能的比值. 随着无量纲参数 $\zeta $ 增大,生成溃灭冲击波的能量减小,这是因为大部标识码用于较强射流的生成与发展其中, $E_{\rm s}$ 是生成冲击波的能量,$E_{0}$ 是气泡初始能量. $\varDelta V = 4 \pi d^{2}\Delta d$ 冲击波传播生成流体压缩体积.
图11
图12
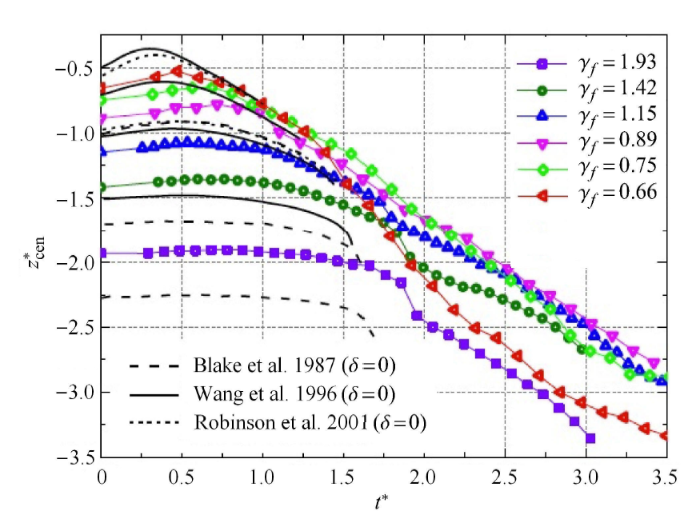
自由液面约束作用下空泡生成射流进行非球形演化,同时,空泡向背离自由液面方向移动,质心发生迁移. Zhang 等[63]利用实验观测对空泡质心迁移进行了定量分析,如图13 所示,对于气泡所受浮力较小的情况,标识码膨胀阶段被自由表面吸引,在随后的收缩过程中被其排斥,并且,当气泡半径接近最小值时,气泡质心上出现了一个明显的加速度. 当 $\gamma \leqslant 1$时,由于气泡在离自由面较近,质心向下移动速度较快. Zhang 等[63]实验观测获得的气泡质心迁移规律,也在Wang 等[52, 58, 62]的数值模拟中出现相同的结果. 然而,他们的数值模拟主要关注的是第一周期内的气泡脉动,事实上,在随后的气泡脉动过程中,气泡质心的迁移变得更加显著.
图13
2.2 空泡脉动下水平自由面演化特征
Gibson 等[102]第一次通过实验观测到气泡脉动下自由面的变形行为. 随后很多学者也通过实验观测和数值计算研究气泡与自由面的相互作用. 然而,这些研究主要关注的是气泡动力学行为,对自由液面飞溅的运动学特性关注较少. 在气泡与自由液面相互作用过程中,相比气泡非球形演化,自由液面变形更加复杂[95]. 当空泡中心的初始位置离自由液面较近时,自由液面出现较大的起伏,导致界面飞溅,形成透明水层、水柱、细射流、粗射流等. 当离开液面距离比较远时,自由液面可能发生小幅度扰动[12, 63, 103]. 随着两者距离继续扩大,气泡与液面相互作用趋近于 0. 通过实验研究,本文根据自由液面的演化特征,利用无量纲距离 $\gamma $,讨论以下 4 种典型现象:透明水层及水柱生成 ($0 \leqslant \gamma \leqslant 0.4$)、不稳定冠状结构 ($0.4 \leqslant \gamma \leqslant 0.6$)、稳定冠状结构 ($0.6 \leqslant \gamma \leqslant 1.2$) 和非冠状结构 ($\gamma \geqslant 1.2$).
2.2.1 透明水层及水柱生成($0 \leqslant \gamma \leqslant 0.5$)
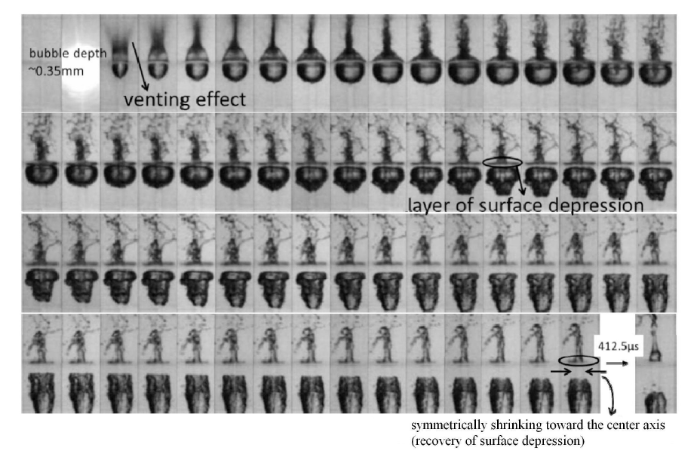
该工况下自由液面变形的主要特点在于,空泡生成初期自由面质点已经获得了极高速度向外飞溅,形成透明水层. 在气泡膨胀过程中,气泡内部与外界空气连通. 随后,自由液面上部透明水层从两侧向中心轴收缩,形成水柱. 然后在重力作用下,水柱开始下落,并穿透气泡的下表面. 在接下来的过程中出现两个典型现象,一是如图14 ($\gamma = 0.083$) 所示,空泡与水面上层透明水层连通,气泡在收缩过程中,下部呈偏平状,最终在液面处破碎. 另一情况如图15 ($\gamma = 0.28$) 所示,随着透明水层闭合和回落,空泡与外界大气之间又生成了水层. 在该水层作用下,气泡向背离自由液面方向迁移. 然而,由于空泡距离自由面过近,在与外界空气连通时耗散了大部分能量,因此,随后的空泡溃灭强度较标识码不足以促使自由面发展一个稳定规则的冠状结构.
图14
图15
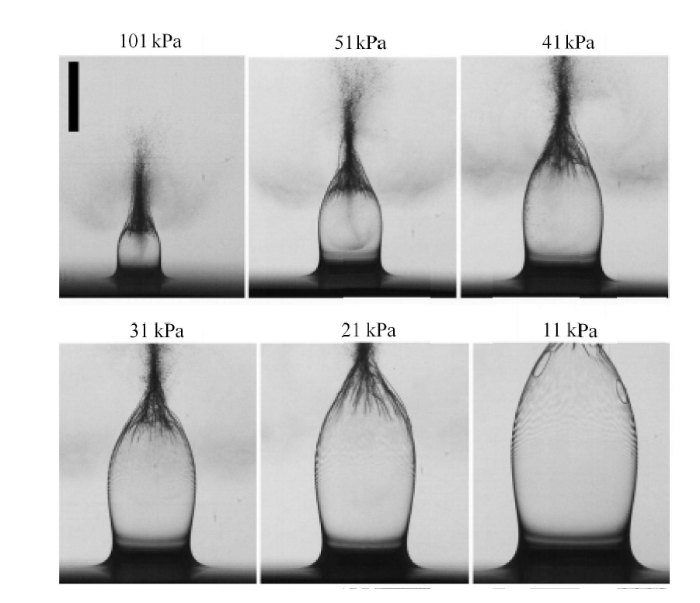
针对自由液面上透明水层的生成机制,Chen 等[104-105]指出该现象与空泡成核之前形成的高温热点有关. Apitz 和 Vogel[106]利用脉冲激光在自由液面附近聚焦,分析了透明水层形成机理. 在聚焦的激光作用下,瞬时积蓄较大能量,在自由液面附近形成高温热点,生成等离子体,使周围液体汽化生成水蒸标识码以很高的速度从自由液面喷出,形成透明水层. Thoroddsen 等[107]认为,这个透明水层发展前期是由惯性力主导的,随后在腔内低压和表面张力的共同作用标识码明水层从两侧向中心闭合,其中的液体汇聚成射流,但由于水动力不稳定性射流很快会发生破碎和飞溅. 另外,Marston 等[108]认为自由液面下方的空泡快速膨胀会引起吸气压力,也是导致水层闭合的重要因素. 同时,他们对不同空气压力下研究了透明水层的运动规律,如图16 所示,研究表明,周围压力的减小,会导致水层空腔体积增标识码层厚度变薄,水层闭合时间延长. 通过对实验数据的分析发现,他们发现水层闭合时间与周围气压的关系是 $t \sim p^{ - 1 / 2}$,此外,他们对水层厚度和韦伯数的关系分析表明,表面张力效应在水层闭合中的作用很小.
图16
2.2.2 不稳定的冠状结构($0.4 \leqslant \gamma \leqslant 0.6$)
该工况下自由液面变形的主要特点在于,在空泡膨胀过程中,自由面被拱起,气泡上方的水层越来越薄,但是没有破标识码泡与外界大气没有连通.在空泡从最小尺寸反弹过程中,生成粗射流,上端发生破碎现象,可能产生一个不规则的水标识码出许多水滴,但不能生成稳定冠状结构.
图17
图18
针对细射流的形成,Blake等[46-49, 58]认为,气泡膨胀使自由液面形成圆拱状. 同时自由面约束导致气泡周围压力分布不均匀,根据势流理论,在气泡和自由面之间形成一个局部高压区,从而促使自由面向上运动形成细射流. 利用边界积分法数值模 拟[46, 52-54]观测到了气泡与自由液面之间的压力峰值区域. Longuet-Higgins 等[50]提出采用狄利克雷 (Dirichlet) 双曲线理论来模拟自由面上细射流的生成和演化. 他们通过理论分析得出,当拱形界面顶角达到 109$^\circ$ 左右时,界面瞬间加速形成速度极高的细射流.在此之后,射流速度趋于稳定,匀速向上发标识码与 Blake 等[112]实验观测结果吻合较好.然而,在随后的实验和数值计算中,射标识码达到 109$^\circ$时没有出现瞬时加速现象[12, 58, 113-114]. 关于狄利克雷双曲线解释射流生成与发展,没有形成明确的定论,可能与气泡、自由面的初始参数有关.随着近几年,标识码流在生命科学、工业加工领域应用,也推动了对其科学问题的研究. Tagawa 等[28-29]在试管中研究了空泡脉动下曲状自由面变形机制. 他们发现,可以用流量聚焦理论解释射流生成.由于液体表面具有曲率,被脉冲加速后动量可以在界面曲率中心汇聚,标识码导产生高速射流. Li 等[115]的研究认为是R-T不稳定诱导的射流,在气泡膨胀作用下,界面的压强梯度与密度梯度不共线,形成斜标识码,进而在生成涡量的作用下,射流从自由液面生成. 总的来说,针对气泡溃灭过程中自由液面射流的生成机制,尚没有成熟的认识.
2.2.3 稳定的冠状结构 ($0.6 \leqslant \gamma \leqslant 1.2$)
稳定冠状结构工况下自由液面变形的主要特点在于,气泡在膨胀过程中将自由面顶起,在气泡溃灭过程中,自由面继续向上运动形成细射流. 在气泡从最小直径反弹过程中,细射流底部周围自由面被拱起,生成粗射流,并且其上端生成稳定的冠状水裙结构. 同时,在溃灭过程中,空泡生成较强射流(见 图19 ).
图19
Duocastella 等[116]通过实验观测指出,气泡脉动过程中细射流与粗射流的生成方式是不同的. 与细射流相比,粗射流形成可能与自由表面中心塌陷有关. 当空泡进行收缩时,其周围的液体也快速回缩,可能构成了自由液面凹陷. 凹陷达到最大深度后,倾向于将液面恢复到扰动前的状态,从而向上发展出粗射流. 在流体中,表面凹陷通常会引起物理量的奇异性,例如在最深处或间断点处速度、表面曲率或压力梯度会发生发散标识码凹陷的最低端可能向上运动形成射流[70, 75, 77-78]. 在此基础上,Chen 等[105]进一步解释了冠状结构生成机制. 图20 展示了细射流底部周围生成凹陷的过程. 由图可知,由于细射流底部的表面拓扑变化,导致了速度、压强等物理量发生奇异性(用红点表示),而且气泡再膨标识码用加速了自由液面从细射流底部周围向上运动(箭头方向),形成粗射流.
图20
细射流底部周围凹陷的曲率不一样是导致生成的皇冠形状不一样的主导因素. Chen等[105]分析了不同工况下粗射流的发展,如图21 所示,从不稳定到稳定冠状结构. 在不稳定冠状结构中,由于表面破碎导致许多液滴飞溅,很难区分粗射流冠状结构的类型. 当无量纲距离 $\gamma \geqslant 0.7$,形成了较稳定冠状结构. 此外,当 $\gamma $ 从 0.5 逐渐增大到 1.02 时,如箭头所示,冠壁的方向从向下转到向上. 这些特征表明冠壁方位与气泡深度也具有高度的规律性和相关性,随着 $\gamma $ 变大,表面凹陷的方向可能具有类似的旋转趋势. 另一方面,由于气泡与自由面相互作用逐渐减小,冠状结构的高度逐渐降低. 李帅等[115]通过实验观测和数值计算分析了气泡溃灭强度及表面张力对冠状结构的影响规律:泡内外压强标识码表征溃灭强度;韦伯数越小,冠状结构高度越小;气泡溃灭强度参数不是影响冠状运动的主要参数,只是对结构幅值有微弱的影响. Chen 等[105] 从冠状结构的闭合时间和位置研究了不同工况下生成的冠状结构的发展规律. 他们发现冠状结构收缩主要由两个因素引起的. 一个是表面张力,另一个是由于细射流向上运动导致了冠状结构内形成负压,这种负压现象被称为伯努利效标识码个效应也用于揭示激光诱导冠状水层的收缩及其高速入水后空腔的闭合.
图21
2.2.4 非冠状结构 ($\gamma \geqslant 1.2$)
非冠状结构工况下自由液面变形的主要特点在于,当膨胀到最大直径时,气泡可以保持近似球状,液面被拱起,随着空标识码灭运动,存在两种典型现象. 一种是在空泡反弹的过程中,如图22 所示,在自由面上生成了粗射流,粗射流的速度大于细射流,因此形成中间低周围高的形状. 此外,在粗射流生成初期表面发生破碎和液滴飞溅现象. 另一种现象,如图23 所示,在随后的溃灭阶段,没有形成粗射流. 而是,平滑驼峰状的自由面从最高处开始展平,并逐渐形成一个圆环状的中间较低两边较高的结构直至下降到静止的水面. Kang 等[103]通过求解三维轴对称柯西-泊松问题,指出自由面的变形是重力和毛细力共同作用的结果. 作者利用开尔文冲量理论和能量守恒推导了自由面变形的最大高度 $h$ 与 $\gamma $ 之间的关系式 $\Delta gh/ \Delta p \sim (\gamma )^{ - 4.4}$. 这些结果可以用于毫米级大小的气泡运动所导致的自由液面变形的相关数值模拟.
图22
图23
2.3 空泡与曲状自由液面相互作用
图24
2.3.1 透明水层
Obreschkow 等[42, 96, 118]通过微重力技术生成了厘米级液滴,利用电火花在液滴内部生成了空泡,分析空泡与标识码由液面的相互作用. 他们指出,液面约束减小了空泡的溃灭周期,并基于冲击波诱导的二次空化现象并且据此推断出空泡成核期间所吸收的冲击波能量. 另一方面,他们观测到空泡膨胀作用下,液滴表面被拱起的现象(见图24(a)).随后 Avila 等[119-121]利标识码将液滴悬浮在空气中,再将脉冲激光聚焦在液滴内,生成空泡. 通过实验观测到 4 种典型现标识码滴雾化、不稳定透明水层、透明水层及液滴振荡. 与水平液面透明水层生成类似,激光聚焦生成高温热点,造成液滴汽化飞溅,随着空泡膨胀作用,水标识码不断增大,气泡与外界连通.不同点在于,液滴随着空泡膨胀而轴向展开,整个液滴展开成一个透明水层标识码厚度为微米级,最后在表面张力的作用下,水层从四周向中间回缩.同样的现象也出现在 Thoroddsen 等[107]研究工作中.
当激光能量很大时,液滴会随着气泡脉动进行体积振荡,如图25(d) 所示. 可以看到,空泡在溃灭过程中生成向下的射流. 在反弹过程中,液滴周围生成飞溅现象. Zhang 等[63]指出这些飞溅现象跟溃灭冲击波造成的二次空化现象有关. 溃灭冲击波在自由面反射会在球状界面生成小气泡,随着空泡再膨胀,液滴发生飞溅行为. Zeng 等[56]通过理论解析和数值计算,认为这些飞溅行为是由于界面 Rayleigh-Taylor 不稳定性造成的. 在空泡从最大直径反弹过程中,液滴界面受到扰动,在液面表面形成凸起和凹陷部分(如 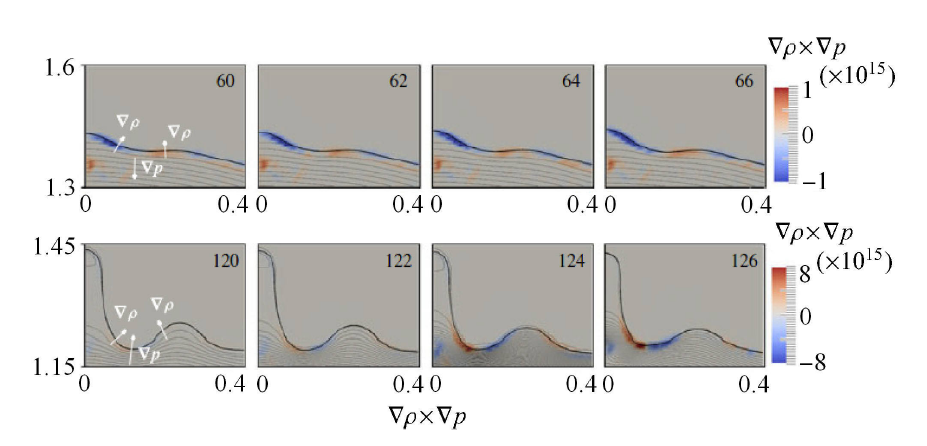
图25
图26
2.3.2 不稳定冠状结构
图27
2.3.3 稳定冠状结构
图28
图29
2.3.4 非冠状结构
图30
综上所述,当气泡界面与液滴界面具有相对合适的曲率时,在生成透明水层、不稳定冠状结构、稳定冠状结构及非标识码构方面,球状液面的变形特征与水平自由液面的非常相似,这可能是由于无论是球状还是平面都拥有各向同性的曲率. 但是对于圆柱状界面曲率的各向异性特点,其液面变化特征与前面两种工况存在差别.
3 总结与展望
气泡与自由表面的相互作用是气泡动力学和流体力学中的前沿热点问题. 本文从气泡的非球形脉动形态特征和自由面变形两个部分,概述了近年来该领域的实验研究的进展和取得的成果. 总结了开尔文冲量理论、界面凹陷奇点概念和泰勒不稳定性等理论方法的建立及应用. 从整个领域的研究来看,在如下几个方面还值得继续深入:
(1) 自由液面被空泡膨胀拱起,形成细射流. 很多学者认为,细射流的形成与气泡各向异性膨胀及其引起自由面与气泡之间形成局部高压有关. 从界面稳定性角度出发,小扰动诱导的界面密度梯度与压强梯度不共线,斜压生成的涡旋也可使自由液面凸起形成射流. 此外,也有学者试图利用狄利克雷双曲线理论解释细射流发展规律. 因此,气泡溃灭过程中的细射流生成机制仍有一定争议,值得未来进一步明确.
(2) 空泡在从最小尺寸反弹过程中,会从细射流周围生成粗射流.
很多学者认为,自由液面的凹陷可能导致物理量奇异性,进而诱导自由液面从凹陷向上运动,加上空泡的再膨胀,加速粗射流从细射流底部生成.
然而,由于实验观测与数值模拟手段的限制,该解释仍然缺少直观证据,值得未来进一步证明与探索.
(3) 在气凝胶的研究中,大量存在气泡在液面处破碎后生成射流的现象,然而并未得到相关学者的普遍关注,这一现象与本文所综述的空泡溃灭过程与外界大气连通后的破碎相似,相关研究值得相互借鉴并进一步推进.
(4) 本文是通过气泡与液面的无量纲距离参数来进行分类,并主要以毫米级空泡与水介质水平自由液面相互作用为主归纳了液面变形特征,此条件下通常可以忽略其他参数影响如液体物性、液面曲率、空泡浮力效应等. 但对于大量的实际应用情况,这些因素可能会发挥重要作用,值得进一步探讨.
(5) 目前多数研究针对空泡形态特征或者自由面面变形进行研究,以解耦分析的思路为主. 进一步更加明确二者之间耦合机制,对于更准确地解决实际问题和促进学科发展都是非常重要的.
参考文献
Fundamental study of sterilization effects on marine Vibrio sp. in a cylindrical water chamber with supply of only underwater shock waves
The effect of shock sterilization on marine Vibrio sp. is investigated by carrying out a bio-experiment based on a bubble-shockwave interaction. In the experiments, underwater shock waves with different strength and frequencies are produced by a high-voltage power supply in a cylindrical water chamber. The bio-experimental results show marine Vibrio sp. is completely inactivated in a short time by a 1.0-Hz electric discharge. However, a high sterilization effect requires a strong and high frequency of the bubble motion, and it also depends on the lifetime of the bubble. Subsequently, by an experiment with an air gap to prevent the underwater shock waves entering the cell suspension, it is found that the introduction of a strong shock pressure is not entirely required to obtain the effective sterilization. On the other hand, the direct effect of the sterilization by rebound shock wave resulting from the bubble-shock wave interaction is examined in the experiments. The results suggest that free radicals mainly contribute to killing marine bacteria, and direct mechanical effects of the bubble motion are not responsible. In addition, the creation of the OH radical is indirectly confirmed by measuring the H2O2 concentration. Finally, the Herring equation is solved to investigate the condition of free radical generation when considering the effect of thermal conductivity at the bubble interface. As a result, the effective sterilization conditions based on the bubble-shock wave interaction are clearly obtained.
A theoretical mod- el to estimate inactivation effects of OH radicals on marine vibrio sp. in bubble-shock interaction
A theoretical model for estimating inactivation effects on marine Vibrio sp. is developed from the viewpoint of the chemical action of the OH radicals induced by interaction of bubbles with shock waves. It consists of a biological probability model for cell viability and a bubble dynamic model for its collapsing motion due to the shock pressures. The biological probability model is built by defining a sterilized space of the OH radicals. To determine the radius of the sterilized space, the Herring equation is solved in the bubble dynamic model in consideration of the effect of the heat conductivity and mass transportation. Furthermore, the pressure waveform of incident shock wave used in the model is obtained with the pressure measurement. On the other hand, a bio-experiment of marine Vibrio sp. is carried out using a high-voltage power supply in a cylindrical water chamber. Finally, the viability ratio of marine bacteria estimated by the theoretical model is examined under the experimental conditions of this study. In addition, we also discuss the influence of bubble initial size for predicting the inactivation effects.
Study of sterilization effects on marine Vibrio sp. using interaction of cavitation with shock wave in a narrow water chamber
Ventilated cloud cavitating flow around a blunt body close to the free surface
Analysis of near-wall effect on cloud cavitating flow that surrounds an axisymmetric projectile using large eddy simulation with Cartesian cut-cell mesh method
Experimental and numerical investigation on cloud cavitating flow around an axisymmetric projectile near the wall with emphasis on the analysis of local cavity shedding
航行体排气水下发射流体动力数值仿真研究
Numerical simulation on the flow dynamics of underwater vehicle launching with exhaust
轴对称体空化水动力脉动特性的实验研究
为了研究轴对称体非定常空化的脉动特性,采用高速全流场显示技术和动态测力系统实验研究了绕半球型和平头轴对称体的非定常空化流场及其动力特性。实验在闭式水洞中进行,采用高速摄影的方法观察了在不同空化数下绕半球型和平头轴对称体的空穴形态,总结了在不同空化数下空泡形态的脉动特性;测量了轴对称体受到的阻力,并对阻力信号进行了时频分析,得到了轴对称体阻力在非定常空化阶段的时频特征。结果表明:空泡形态及其对应的动力特征随着空化数的变化存在明显的非定常特性,空化流场形态与动力特征频率存在高度的相关性。并且不同头型轴对称体的脉动特性存在明显的差异,半球型轴对称体空泡流动的脉动主要是空泡尾部的高频小脱落引起的,而平头轴对称体的空泡流脉动成分主要是大尺度的漩涡空泡团的周期性脱落,空化流场的低频特征频率与空泡的大断裂相对应。
Experimental study on fluctuaing hydrodynamics around axisymmetric bodies
为了研究轴对称体非定常空化的脉动特性,采用高速全流场显示技术和动态测力系统实验研究了绕半球型和平头轴对称体的非定常空化流场及其动力特性。实验在闭式水洞中进行,采用高速摄影的方法观察了在不同空化数下绕半球型和平头轴对称体的空穴形态,总结了在不同空化数下空泡形态的脉动特性;测量了轴对称体受到的阻力,并对阻力信号进行了时频分析,得到了轴对称体阻力在非定常空化阶段的时频特征。结果表明:空泡形态及其对应的动力特征随着空化数的变化存在明显的非定常特性,空化流场形态与动力特征频率存在高度的相关性。并且不同头型轴对称体的脉动特性存在明显的差异,半球型轴对称体空泡流动的脉动主要是空泡尾部的高频小脱落引起的,而平头轴对称体的空泡流脉动成分主要是大尺度的漩涡空泡团的周期性脱落,空化流场的低频特征频率与空泡的大断裂相对应。
锥柱航行体肩空泡界面效应对头锥面受力的影响研究
Influence of cavitation interface effect of cone-column vehicle on the forces of the cone
航行体垂直出水载荷与空泡溃灭机理分析
针对航行体水下垂直发射出水载荷机理问题, 首先开展了典型工况全过程的数值模拟, 得到了航行体肩、尾空泡及表面压力的演化过程, 并与试验结果进行了对比验证. 在此基础上揭示了航行体肩部空泡溃灭的过程和机制, 进而提出了出水溃灭压力的物理模型, 探索了空泡厚度、水层厚度、声速等重要参数的影响, 讨论了试验溃灭压力相似律等相关问题.
Mechanism analysis about cavitation collapse load of underwater vehicles in a vertical luanching process
针对航行体水下垂直发射出水载荷机理问题, 首先开展了典型工况全过程的数值模拟, 得到了航行体肩、尾空泡及表面压力的演化过程, 并与试验结果进行了对比验证. 在此基础上揭示了航行体肩部空泡溃灭的过程和机制, 进而提出了出水溃灭压力的物理模型, 探索了空泡厚度、水层厚度、声速等重要参数的影响, 讨论了试验溃灭压力相似律等相关问题.
航行体回收垂直入水空泡流场及水动力特性研究
Nu- merical investigation on cavity structures and hydro-dynamics of the vehicle during vertical water-entry
气泡引起的皇冠型水冢实验与数值研究
Experimental and numerical studies on “crown” spike generated by a bubble near free-surface
激光空泡在近自由液面运动特性的实验研究
Experimental study of laser-generated cavitation bubble motion near a free liquid surface
近自由面的多个水下爆炸气泡相互作用研究
The iteraction between mutiple underwater explosion bubbles near free surface
Laser-induced cavitation bubbles for cleaning of solid surfaces
When attempting to clean surfaces of dental root canals with laser-induced cavitation bubbles, the resulting cavitation oscillations are significantly prolonged due to friction on the cavity walls and other factors. Consequently, the collapses are less intense and the shock waves that are usually emitted following a bubble's collapse are diminished or not present at all. A new technique of synchronized laser-pulse delivery intended to enhance the emission of shock waves from collapsed bubbles in fluid-filled endodontic canals is reported. A laser beam deflection probe, a high-speed camera, and shadow photography were used to characterize the induced photoacoustic phenomena during synchronized delivery of Er:YAG laser pulses in a confined volume of water. A shock wave enhancing technique was employed which consists of delivering a second laser pulse at a delay with regard to the first cavitation bubble-forming laser pulse. Influence of the delay between the first and second laser pulses on the generation of pressure and shock waves during the first bubble's collapse was measured for different laser pulse energies and cavity volumes. Results show that the optimal delay between the two laser pulses is strongly correlated with the cavitation bubble's oscillation period. Under optimal synchronization conditions, the growth of the second cavitation bubble was observed to accelerate the collapse of the first cavitation bubble, leading to a violent collapse, during which shock waves are emitted. Additionally, shock waves created by the accelerated collapse of the primary cavitation bubble and as well of the accompanying smaller secondary bubbles near the cavity walls were observed. The reported phenomena may have applications in improved laser cleaning of surfaces during laser-assisted dental root canal treatments.
Cavitation erosion by single laser-produced bubbles
Study on splitting of a toroidal bubble near a rigid boundary
超声波作用下气泡的非线性振动
Flynn方程在引入泡内气体的压缩性修正后能够更好地描述超声波作用下液体内气泡的非线性振动。我们以此为基础通过数值分析得到了不同初始半径的气泡在同一声场中的振动位移时间图像和相轨迹,发现气泡的运动行为对其初始状态有很强的依赖关系,在频率为26.5 kHz,幅度为1.35 atm的声波作用下,初始半径小于1 μm的气泡作小幅受迫振动,大于200 μm的气泡作小幅准本征振动,不具备空化气泡特征。声场中的小气泡对声波强度变化的反应更为激烈,当增加声强度时,可将一定范围内的小幅受迫振动气泡转化为空化气泡,并且,当驱动声波压力幅值增加时,初始半径越小的气泡的最大位移增加幅度越大。驱动声波频率同样影响气泡的振动。随着声波频率的升高,空化气泡的初始半径取值区间越来越小,空化振荡也越来越弱。本文还通过高速摄影系统对换能器作用于未除气的自来水所引起的变化进行了实验研究,结果表明,超声波作用下液体内的气泡场是一个混合场,场内气泡尺寸呈一定的分布状态,不仅有空化气泡,还有毫米级的大气泡。气泡的运动行为直接影响空化效果。超声空化场是一个复杂的物理场,场内除了有气泡的振动外,还有气泡间的相互吸引、碰撞和结合。
The nonlinear oscillation of bubbles in the ultrasonic field
Flynn方程在引入泡内气体的压缩性修正后能够更好地描述超声波作用下液体内气泡的非线性振动。我们以此为基础通过数值分析得到了不同初始半径的气泡在同一声场中的振动位移时间图像和相轨迹,发现气泡的运动行为对其初始状态有很强的依赖关系,在频率为26.5 kHz,幅度为1.35 atm的声波作用下,初始半径小于1 μm的气泡作小幅受迫振动,大于200 μm的气泡作小幅准本征振动,不具备空化气泡特征。声场中的小气泡对声波强度变化的反应更为激烈,当增加声强度时,可将一定范围内的小幅受迫振动气泡转化为空化气泡,并且,当驱动声波压力幅值增加时,初始半径越小的气泡的最大位移增加幅度越大。驱动声波频率同样影响气泡的振动。随着声波频率的升高,空化气泡的初始半径取值区间越来越小,空化振荡也越来越弱。本文还通过高速摄影系统对换能器作用于未除气的自来水所引起的变化进行了实验研究,结果表明,超声波作用下液体内的气泡场是一个混合场,场内气泡尺寸呈一定的分布状态,不仅有空化气泡,还有毫米级的大气泡。气泡的运动行为直接影响空化效果。超声空化场是一个复杂的物理场,场内除了有气泡的振动外,还有气泡间的相互吸引、碰撞和结合。
Therapeutic ultrasound
The immune and nervous systems share many features, including receptor and ligand expression, enabling efficient communication between the two. Accumulating evidence suggests that the communication is bidirectional, with the neural system regulating immune cell functions and vice versa. Steroid hormones from the hypothalamus-pituitary-adrenal gland axis are examples of systemic regulators for this communication. Neural reflexes describe regional regulation mechanisms that are a historically new concept that helps to explain how the neural and body systems including immune system communicate. Several recently identified neural reflexes, including the inflammatory reflex and gateway reflex, significantly impact the activation status of the immune system and are associated with inflammatory diseases and disorders. Either pro-inflammatory or anti-inflammatory effects can be elicited by these neural reflexes. On the other hand, the activities of immune cells during inflammation, for example the secretion of inflammatory mediators, can affect the functions of neuronal systems via neural reflexes and modulate biological outputs via specific neural pathways. In this review article, we discuss recent advances in the understanding of bidirectional neuro-immune interactions, with a particular focus on neural reflexes.
The safety and feasibility of extracorporeal high-intensity focused ultrasound (HIFU) for the treatment of liver and kidney tumours in a western population
High-intensity focused ultrasound (HIFU) provides a potential noninvasive alternative to conventional therapies. We report our preliminary experience from clinical trials designed to evaluate the safety and feasibility of a novel, extracorporeal HIFU device for the treatment of liver and kidney tumours in a Western population. The extracorporeal, ultrasound-guided Model-JC Tumor Therapy System (HAIFU Technology Company, China) has been used to treat 30 patients according to four trial protocols. Patients with hepatic or renal tumours underwent a single therapeutic HIFU session under general anaesthesia. Magnetic resonance imaging 12 days after treatment provided assessment of response. The patients were subdivided into those followed up with further imaging alone or those undergoing surgical resection of their tumours, which enabled both radiological and histological assessment. HIFU exposure resulted in discrete zones of ablation in 25 of 27 evaluable patients (93%). Ablation of liver tumours was achieved more consistently than for kidney tumours (100 vs 67%, assessed radiologically). The adverse event profile was favourable when compared to more invasive techniques. HIFU treatment of liver and kidney tumours in a Western population is both safe and feasible. These findings have significant implications for future noninvasive image-guided tumour ablation.
High intensity focused ultrasound: Physical principles and devices
Applications of acoustics and cavitation to noninvasive therapy and drug delivery
With the development of nanotechnology, nanocarriers have been increasingly used for curative drug/gene delivery. Various nanocarriers are being introduced and assessed, such as polymer nanoparticles, liposomes, and micelles. As a novel theranostic system, nanocarriers hold great promise for ultrasound molecular imaging, targeted drug/gene delivery, and therapy. Nanocarriers, with the properties of smaller particle size, and long circulation time, would be advantageous in diagnostic and therapeutic applications. Nanocarriers can pass through blood capillary walls and cell membrane walls to deliver drugs. The mechanisms of interaction between ultrasound and nanocarriers are not clearly understood, which may be related to cavitation, mechanical effects, thermal effects, and so forth. These effects may induce transient membrane permeabilization (sonoporation) on a single cell level, cell death, and disruption of tissue structure, ensuring noninvasive, targeted, and efficient drug/gene delivery and therapy. The system has been used in various tissues and organs (in vitro or in vivo), including tumor tissues, kidney, cardiac, skeletal muscle, and vascular smooth muscle. In this review, we explore the research progress and application of ultrasound-mediated local drug/gene delivery with nanocarriers.
Dynamics of laser-induced cavitation bubbles near elastic boundaries: Influence of the elastic modulus
Application of underwater shock wave focusing to the development of extracorporeal shock wave lithotripsy
Dynamic behavior of bubbles during extracorporeal shock-wave lithotripsy
To determine reference values and tolerance limits of between-side differences for the calibers of the common femoral artery (CFA), superficial femoral artery (SFA), popliteal artery (PA), dorsalis pedis artery (DPA), and posterior tibial artery (PTA).
Problems of Cavitative Destruction//Hydrodynamics of Explosion
Bubbles with shock waves and ultrasound: A review
The study of the interaction of bubbles with shock waves and ultrasound is sometimes termed 'acoustic cavitation'. It is of importance in many biomedical applications where sound waves are applied. The use of shock waves and ultrasound in medical treatments is appealing because of their non-invasiveness. In this review, we present a variety of acoustics-bubble interactions, with a focus on shock wave-bubble interaction and bubble cloud phenomena. The dynamics of a single spherically oscillating bubble is rather well understood. However, when there is a nearby surface, the bubble often collapses non-spherically with a high-speed jet. The direction of the jet depends on the 'resistance' of the boundary: the bubble jets towards a rigid boundary, splits up near an elastic boundary, and jets away from a free surface. The presence of a shock wave complicates the bubble dynamics further. We shall discuss both experimental studies using high-speed photography and numerical simulations involving shock wave-bubble interaction. In biomedical applications, instead of a single bubble, often clouds of bubbles appear (consisting of many individual bubbles). The dynamics of such a bubble cloud is even more complex. We shall show some of the phenomena observed in a high-intensity focused ultrasound (HIFU) field. The nonlinear nature of the sound field and the complex inter-bubble interaction in a cloud present challenges to a comprehensive understanding of the physics of the bubble cloud in HIFU. We conclude the article with some comments on the challenges ahead.
Highly focused supersonicmicrojets
Miridesap, a depleter of serum amyloid P component (SAP), forms an essential component of a novel approach to remove systemic amyloid deposits; low oral bioavailability necessitates that it is given parenterally. We sought to identify and clinically characterise a pro-drug that preserves the pharmacological properties of miridesap while having adequate oral bioavailability and physical stability.
Highly focused supersonic microjets: Numerical simulations
Effects of a water hammer and cavitation on jet formation in a test tube
On pressure impulse of a laser-induced underwater shock wave
Nozzle-free liquid microjetting via homogeneous bubble nucleation
Ocean spray
Urinary tract infections (UTIs) caused by Escherichia coli create a large burden on healthcare and frequently lead to recurrent infections. Part of the success of E. coli as an uropathogenic bacterium can be attributed to its ability to form quiescent intracellular reservoirs in bladder cells and its persistence after antibiotic treatment. Cranberry juice and related products have been used for the prevention of UTIs with varying degrees of success. In this study, a group of cranberry pectic oligosaccharides (cPOS) were found to both inhibit quiescence and reduce the population of persister cells formed by the uropathogenic strain, CFT073. This is the first report detailing constituents of cranberry with the ability to modulate these important physiological aspects of uropathogenic E. coli. Further studies investigating cranberry should be keen to include oligosaccharides as part of the 'active' cocktail of chemical compounds.
Impact of ocean spray on the dynamics of the marine atmospheric boundary layer
The impact of ocean spray on the dynamics of the marine near-surface air boundary layer (MABL) in conditions of very high (hurricane) wind speeds is investigated. Toward this end, a model of the MABL in the presence of sea-spume droplets is developed. The model is based on the classical theory of the motion of suspended particles in a turbulent flow, where the mass concentration of droplets is not mandatory small. Description of the spume-droplet generation assumes that they, being torn off from breaking waves, are injected in the form of a jet of spray into the airflow at the altitude of breaking wave crests. The droplets affect the boundary-layer dynamics in two ways: via the direct impact of droplets on the airflow momentum forming the so-called spray force, and via the impact of droplets on the turbulent mixing through stratification. The latter is parametrized applying the Monin-Obukhov similarity theory. It is found that the dominant impact of droplets on the MABL dynamics appears through the action of the 'spray force' originated from the interaction of the 'rain of spray' with the wind velocity shear, while the efficiency of the stratification mechanism is weaker. The effect of spray leads to an increase in the wind velocity and suppression of the turbulent wind stress in the MABL. The key issue of the model is a proper description of the spume-droplet generation. It is shown that, after the spume-droplet generation is fitted to the observations, the MABL model is capable of reproducing the fundamental experimental finding-the suppression of the surface drag at very high wind speeds. We found that, at very high wind speeds, a thin part of the surface layer adjacent to the surface turns into regime of limited saturation with the spume droplets, resulting in the levelling off of the friction velocity and decrease of the drag coefficient as U(10)(-2), U(10) being the wind speed at 10-m height.
The temperature of evaporating sea spray droplets
VIII. On the pressure developed in a liquid during the collapse of a spherical cavity
On the destructive action of cavitation
Biomedical ultrasound may induce adverse effects in patients by either thermal or non-thermal means. Temperatures above normal can adversely affect biological systems, but effects also may be produced without significant heating. Thermally induced teratogenesis has been demonstrated in many animal species as well as in a few controlled studies in humans. Various maximum 'safe' temperature elevations have been proposed, although the suggested values range from 0.0 to 2.5 degrees C. Factors relevant to thermal effects are considered, including the nature of the acoustic field in situ, the state of perfusion of the embryo/fetus, and the variation of sensitivity to thermal insult with gestational stage of development. Non-thermal mechanisms of action considered include acoustic cavitation, radiation force, and acoustic streaming. While cavitation can be quite destructive, it is extremely unlikely in the absence of stabilized gas bodies, and although the remaining mechanisms may occur in utero, they have not been shown to induce adverse effects. For example, pulsed, diagnostic ultrasound can increase fetal activity during exposure, apparently due to stimulation of auditory perception by radiation forces on the fetal head or auditory structures. In contrast, pulsed ultrasound also produces vascular damage near developing bone in the late-gestation mouse, but by a unknown mechanism and at levels above current US FDA output limits. It is concluded that: (1) thermal rather than nonthermal mechanisms are more likely to induce adverse effects in utero, and (2) while the probability of an adverse thermal event is usually small, under some conditions it can be disturbingly high.
The inner world of a collapsing bubble
Experiments on bubble dynamics between a free surface and a rigid wall
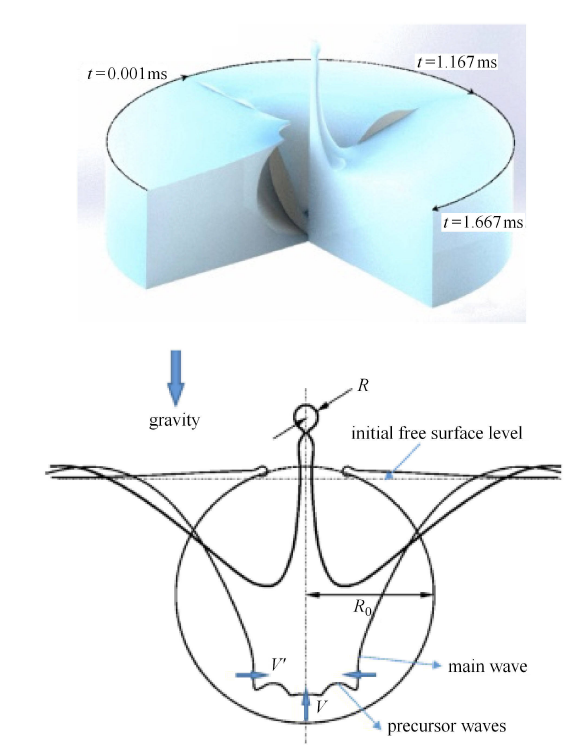
A high-order accurate shock- and interface-capturing scheme is used to simulate the collapse of a gas bubble in water. In order to better understand the damage caused by collapsing bubbles, the dynamics of the shock-induced and Rayleigh collapse of a bubble near a planar rigid surface and in a free field are analysed. Collapse times, bubble displacements, interfacial velocities and surface pressures are quantified as a function of the pressure ratio driving the collapse and of the initial bubble stand-off distance from the wall; these quantities are compared to the available theory and experiments and show good agreement with the data for both the bubble dynamics and the propagation of the shock emitted upon the collapse. Non-spherical collapse involves the formation of a re-entrant jet directed towards the wall or in the direction of propagation of the incoming shock. In shock-induced collapse, very high jet velocities can be achieved, and the finite time for shock propagation through the bubble may be non-negligible compared to the collapse time for the pressure ratios of interest. Several types of shock waves are generated during the collapse, including precursor and water-hammer shocks that arise from the re-entrant jet formation and its impact upon the distal side of the bubble, respectively. The water-hammer shock can generate very high pressures on the wall, far exceeding those from the incident shock. The potential damage to the neighbouring surface is quantified by measuring the wall pressure. The range of stand-off distances and the surface area for which amplification of the incident shock due to bubble collapse occurs is determined.
Experimental study on bubble dynamics subject to buoyancy
Cavitation bubble dynamics inside liquid drops in microgravity
We studied spark-generated cavitation bubbles inside water drops produced in microgravity. High-speed visualizations disclosed unique effects of the spherical and nearly isolated liquid volume. In particular, (1) toroidally collapsing bubbles generate two liquid jets escaping from the drop, and the "splash jet" discloses a remarkable broadening. (2) Shock waves induce a strong form of secondary cavitation due to the particular shock wave confinement. This feature offers a novel way to estimate integral shock wave energies in isolated volumes. (3) Bubble lifetimes in drops are shorter than in extended volumes in remarkable agreement with herein derived corrective terms for the Rayleigh-Plesset equation.
Cavitation bubble behavior inside a liquid jet
Scaling laws for jets of single cavitation bubbles
Experimental methods for the study of hydrodynamic cavitation
//
Transient cavities near boundaries part 2: Free surface
The Kelvin impulse: application to cavitation bubble dynamics
An estimate of the Kelvin impulse of a transient cavity
Cavitation and bu- bble dynamics: the Kelvin impulse and its applications
Cavitation and bubble dynamics have a wide range of practical applications in a range of disciplines, including hydraulic, mechanical and naval engineering, oil exploration, clinical medicine and sonochemistry. However, this paper focuses on how a fundamental concept, the Kelvin impulse, can provide practical insights into engineering and industrial design problems. The pathway is provided through physical insight, idealized experiments and enhancing the accuracy and interpretation of the computation. In 1966, Benjamin and Ellis made a number of important statements relating to the use of the Kelvin impulse in cavitation and bubble dynamics, one of these being 'One should always reason in terms of the Kelvin impulse, not in terms of the fluid momentum…'. We revisit part of this paper, developing the Kelvin impulse from first principles, using it, not only as a check on advanced computations (for which it was first used!), but also to provide greater physical insights into cavitation bubble dynamics near boundaries (rigid, potential free surface, two-fluid interface, flexible surface and axisymmetric stagnation point flow) and to provide predictions on different types of bubble collapse behaviour, later compared against experiments. The paper concludes with two recent studies involving (i) the direction of the jet formation in a cavitation bubble close to a rigid boundary in the presence of high-intensity ultrasound propagated parallel to the surface and (ii) the study of a 'paradigm bubble model' for the collapse of a translating spherical bubble, sometimes leading to a constant velocity high-speed jet, known as the Longuet-Higgins jet.
Bubbles, breaking waves and hyperbolic jets at a free surface
Scaling law for bubbles induced by different external sources: Theoretical and experimental study
The scaling relations for bubbles induced by different external sources are investigated based on a modified Rayleigh model and experimental observations. The equations derived from the modified Rayleigh model are presented to describe the collapse of bubbles induced by the different external sources such as electrical spark, laser, and underwater explosion. A scaling law is then formulated to establish the scaling relations between the different types of bubbles. The scaling law reveals the fact that the characteristic length scale factor differs from the characteristic time scale factor for the different types of bubbles. It is then validated by our experimental observations of the spark- and laser-generated bubbles as well as the bubbles induced by underwater explosions from previous published reports. With the present scaling law, studies on spark- or laser-generated bubbles as well as their applications (for example, in industrial or biomedical related applications) can benefit from the experiences and information built up over the years in underwater explosion bubbles. Conversely, it is possible to substitute a spark- or laser-generated bubble for an underwater explosion bubble in the study of a large-scale and complex physical problem.
Nonlinear interaction between gas bubble and free surface
Active development of quantum informational components such as quantum computers and quantum key distribution systems requires parameter characterization of single photon detectors. A key property of the single photon detectors is detection efficiency. One of the methods of the detection efficiency measurement, as listed in the international standard ETSI, is the reference-free twin-photon-based Klyshko method. The signal-to-noise ratio (SNR) of this method depends on the combination of the pump wavelength, the nonlinear crystal's axis angle, and the type of detector's sensitive element. When the combination is difficult, one has to deal with the low SNR of the detector counts measurement. To gain the high SNR, one has to average the long record complicated with the "random telegraph signal" noise. This type of noise exhibits high spectral density at a zero frequency, where simple averaging works. The heterodyne based method we have proposed is to perform averaging at the higher frequency of the modulation introduced to the standard Klyshko measurement scheme. The method was numerically simulated and experimentally tested. The 14 times improvement in SNR for the proposed method relative to the simple averaging was demonstrated by the numerical simulation and confirmed experimentally.
Strong interaction between a buoyancy bubble and a free surface
An indirect boundary element method for three-dimensional explosion bubbles
Computations of violent surface motions: Comparisons with theory and experiment
Jetting of viscous droplets from cavitation-induced Rayleigh-Taylor instability
Simulation of bubble expansion and collapse in the vicinity of a free surface
Bubble interactions near a free surface
Abstract
A boundary integral method is used to calculate the highly non-linear motion of both one and a vertical column of two bubbles beneath a free surface; although the theory is developed for a finite number of bubbles. Cubic splines are used to represent the surface of the bubble and the infinite free surface; with a non-linear distribution of nodes being employed on the free surface in order to more accurately capture the motion of the free surface spike, which experiments show to be narrow and pronounced when bubbles are generated close to the boundary. Calculations show excellent agreement with experiments in both the one- and two-bubble cases.
可压缩流场中气泡脉动数值模拟
Numerical simulation of bubble dynamic in compressible fluid
Experimental and numerical investigation on bubble dynamics near a free surface and a circular opening of plate
The motion of a 3D toroidal bubble and its interaction with a free surface near an inclined boundary
Improved three-dimensional bubble dynamics model based on boundary element method
Experimental study on the interaction between bubble and free surface using a high-voltage spark generator
The collapse of cavitation bu- bbles and the pressures thereby produced against solid boundaries
Kinetic theories for granular flow: Inelastic particles in Couette flow and slightly inelastic particles in a general flowfield
Granular jets
Carbon dioxide is Mars' primary atmospheric constituent and is an active driver of Martian surface evolution. CO2 ice sublimation mechanisms have been proposed for a host of features that form in the contemporary Martian climate. However, there has been very little experimental work or quantitative modelling to test the validity of these hypotheses. Here we present the results of the first laboratory experiments undertaken to investigate if the interaction between sublimating CO2 ice blocks and a warm, porous, mobile regolith can generate features similar in morphology to those forming on Martian dunes today. We find that CO2 sublimation can mobilise grains to form (i) pits and (ii) furrows. We have documented new detached pits at the termini of linear gullies on Martian dunes. Based on their geomorphic similarity to the features observed in our laboratory experiments, and on scaling arguments, we propose a new hypothesis that detached pits are formed by the impact of granular jets generated by sublimating CO2. We also study the erosion patterns formed underneath a sublimating block of CO2 ice and demonstrate that these resemble furrow patterns on Mars, suggesting similar formation mechanisms.
Power-law singularities in gravity-capillary waves
The transitional regime between coalescing and splashing drops
Dynamics of jets produced by bursting bubbles
Bubble bursting: Universal cavity and jet profiles
After a bubble bursts at a liquid surface, the collapse of the cavity generates capillary waves, which focus on the axis of symmetry to produce a jet. The cavity and jet dynamics are primarily controlled by a nondimensional number that compares capillary inertia and viscous forces, i.e., the Laplace number La=ργR_{0}/μ^{2}, where ρ, μ, γ, and R_{0} are the liquid density, viscosity, interfacial tension, and the initial bubble radius, respectively. In this Letter, we show that the time-dependent profiles of cavity collapse (t<t_{0}) and jet formation (t>t_{0}) both obey a |t-t_{0}|^{2/3} inviscid scaling, which results from a balance between surface tension and inertia forces. Moreover, we present a scaling law, valid above a critical Laplace number, which reconciles the time-dependent scaling with the recent scaling theory that links the Laplace number to the final jet velocity and ejected droplet size. This leads to a self-similar formula which describes the history of the jetting process, from cavity collapse to droplet formation.
On the physics of fizziness: How bubble bursting controls droplets ejection
Revision of bubble bursting: Universal scaling laws of top jet drop size and speed
The collapse of a bubble of radius R_{o} at the surface of a liquid generating a liquid jet and a subsequent first drop of radius R is universally scaled using the Ohnesorge number Oh=μ/(ρσR_{o})^{1/2} and a critical value Oh^{*} below which no droplet is ejected; ρ, σ, and μ are the liquid density, surface tension, and viscosity, respectively. First, a flow field analysis at ejection yields the scaling of R with the jet velocity V as R/l_{μ}∼(V/V_{μ})^{-5/3}, where l_{μ}=μ^{2}/(ρσ) and V_{μ}=σ/μ. This resolves the scaling problem of curvature reversal, a prelude to jet formation. In addition, the energy necessary for the ejection of a jet with a volume and averaged velocity proportional to R_{o}R^{2} and V, respectively, comes from the energy excess from the total available surface energy, proportional to σR_{o}^{2}, minus the one dissipated by viscosity, proportional to μ(σR_{o}^{3}/ρ)^{1/2}. Using the scaling variable φ=(Oh^{*}-Oh)Oh^{-2}, it yields V/V_{μ}=k_{v}φ^{-3/4} and R/l_{μ}=k_{d}φ^{5/4}, which collapse published data since 1954 and resolve the scaling of R and V with k_{v}=16, k_{d}=0.6, and Oh^{*}=0.043 when gravity effects are negligible.
Erratum: Scaling laws of top jet drop size and speed from bubble bursting including gravity and inviscid limit
This corrects the article DOI: 10.1103/PhysRevLett.118.221101.
Jet formation in bubbles bursting at a free surface
This work examines the ejection of droplets from a bursting gas bubble on a free liquid surface, both experimentally and numerically. We explore the physical processes which govern the bursting of bubbles and the subsequent formation of "jet" droplets. We present new relationships regarding the dependence of jet drop formation on bubble diameter. Furthermore, we propose a new dimensionless parameter to describe the region of properties where "jet" drops will occur. This parameter, termed the droplet number ( Dn), complements existing parameters defining jet drop formation, namely, a maximum Ohnesorge number and a maximum Bond number.
Drop impact dynamics: Splashing, spreading, receding, bouncing
Singularity dynamics in curvature collapse and jet eruption on a fluid surface
Finite-time singularities--local divergences in the amplitude or gradient of a physical observable at a particular time--occur in a diverse range of physical systems. Examples include singularities capable of damaging optical fibres and lasers in nonlinear optical systems, and gravitational singularities associated with black holes. In fluid systems, the formation of finite-time singularities cause spray and air-bubble entrainment, processes which influence air-sea interaction on a global scale. Singularities driven by surface tension have been studied in the break-up of pendant drops and liquid sheets. Here we report a theoretical and experimental study of the generation of a singularity by inertial focusing, in which no break-up of the fluid surface occurs. Inertial forces cause a collapse of the surface that leads to jet formation; our analysis, which includes surface tension effects, predicts that the surface profiles should be describable by a single universal exponent. These theoretical predictions correlate closely with our experimental measurements of a collapsing surface singularity. The solution can be generalized to apply to a broad class of singular phenomena.
Turbulence-flame interactions in type Ia supernovae
Detonating failed deflagration model of thermonuclear supernovae I. Explosion dynamics
Deflagrations and detonations in thermonuclear Supernovae
We study a type Ia supernova explosion using three-dimensional numerical simulations based on reactive fluid dynamics. We consider a delayed-detonation model that assumes a deflagration-to-detonation transition. In contrast with the pure deflagration model, the delayed-detonation model releases enough energy to account for a healthy explosion, and does not leave carbon, oxygen, and intermediate-mass elements in central parts of a white dwarf. This removes the key disagreement between simulations and observations, and makes a delayed detonation the mostly likely mechanism for type Ia supernovae.
Spherical combustion clouds in explosions
This study explores the properties of spherical combustion clouds in explosions. Two cases are investigated: (1) detonation of a TNT charge and combustion of its detonation products with air, and (2) shock dispersion of aluminum powder and its combustion with air. The evolution of the blast wave and ensuing combustion cloud dynamics are studied via numerical simulations with our adaptive mesh refinement combustion code. The code solves the multi-phase conservation laws for a dilute heterogeneous continuum as formulated by Nigmatulin. Single-phase combustion (e.g., TNT with air) is modeled in the fast-chemistry limit. Two-phase combustion (e.g., Al powder with air) uses an induction time model based on Arrhenius fits to Boiko’s shock tube data, along with an ignition temperature criterion based on fits to Gurevich’s data, and an ignition probability model that accounts for multi-particle effects on cloud ignition. Equations of state are based on polynomial fits to thermodynamic calculations with the Cheetah code, assuming frozen reactants and equilibrium products. Adaptive mesh refinement is used to resolve thin reaction zones and capture the energy-bearing scales of turbulence on the computational mesh (ILES approach). Taking advantage of the symmetry of the problem, azimuthal averaging was used to extract the mean and rms fluctuations from the numerical solution, including: thermodynamic profiles, kinematic profiles, and reaction-zone profiles across the combustion cloud. Fuel consumption was limited to $\sim $60–70 %, due to the limited amount of air a spherical combustion cloud can entrain before the turbulent velocity field decays away. Turbulent kinetic energy spectra of the solution were found to have both rotational and dilatational components, due to compressibility effects. The dilatational component was typically about 1 % of the rotational component; both seemed to preserve their spectra as they decayed. Kinetic energy of the blast wave decayed due to the pressure field. Turbulent kinetic energy of the combustion cloud decayed due to enstrophy $\overline{\omega ^{2}} $ and dilatation $\overline{\Delta ^{2}} $.
LMJ/PETAL laser facility: Overview and opportunities for laboratory astrophysics
Laser smoothing and imprint reduction with a foam layer in the multikilojoule regime
This Letter presents first experimental results of the laser imprint reduction in fusion scale plasmas using a low-density foam layer. The experiments were conducted on the LIL facility at the energy level of 12 kJ with millimeter-size plasmas, reproducing the conditions of the initial interaction phase in the direct-drive scheme. The results include the generation of a supersonic ionization wave in the foam and the reduction of the initial laser fluctuations after propagation through 500 mum of foam with limited levels of stimulated Brillouin and Raman scattering. The smoothing mechanisms are analyzed and explained.
Rayleigh-Taylor and Richtmyer-Meshkov instability induced flow, turbulence, and mixing. I
Bell-Plesset effects in Rayleigh-Taylor instability of finite-thickness spherical and cylindrical shells
Rayleigh-Taylor and Richtmyer-Meshkov instabilities and mixing in stratified spherical shells
On the Stability of fluid flows with spherical symmetry
Rayleigh-Taylor and Richtmyer-Meshkov instabilities and mixing in stratified cylindrical shells
Shock waves from nonspherical cavitation bubbles
The fluid dynamic interaction of cavitation bubbles with adherent cells on a substrate is experimentally investigated. We find that the nonspherical collapse of bubbles near to the boundary is responsible for cell detachment. High-speed photography reveals that a wall bounded flow leads to the detachment of cells. Cells at the edge of the circular area of detachment are found to be permanently porated, whereas cells at some distance from the detachment area undergo viable cell membrane poration (sonoporation). The wall flow field leading to cell detachment is modeled with a self-similar solution for a wall jet, together with a kinetic ansatz of adhesive bond rupture. The self-similar solution for the delta-type wall jet compares very well with the full solution of the Navier-Stokes equation for a jet of finite thickness. Apart from annular sites of sonoporation we also find more homogenous patterns of molecule delivery with no cell detachment.
Universal scaling law for jets of collapsing bubbles
Cavitation bubbles collapsing and rebounding in a pressure gradient ∇p form a "microjet" enveloped by a "vapor jet." This Letter presents unprecedented observations of the vapor jets formed in a uniform gravity-induced ∇p, modulated aboard parabolic flights. The data uncover that the normalized jet volume is independent of the liquid density and viscosity and proportional to ζ ≡ |∇p|R(0)/Δp, where R(0) the maximal bubble radius and Δp is the driving pressure. A derivation inspired by "Kelvin-Blake" considerations confirms this law and reveals its negligible dependence of surface tension. We further conjecture that the jet only pierces the bubble boundary if ζ ≳ 4 × 10(-4).
On the nonspherical collapse and rebound of a cavitation bubble
The migration and growth of nuclei in an ideal vortex flow
水中气泡溃灭的理论与数值研究
Theoretical and numerical studies on the bubble collapse in water
气泡与自由液面相互作用的实验研究
Experimental study of interaction between bubble and free surface
The quest for the most spherical bubble: Experimental setup and data overview
Cinematographic observati- on of the collapse and rebound of a laser-produced cavitation bubble near a wall
Bubble dynamics, shock waves and sonoluminescence
Numerical simulations of bubble pulsation and sonoluminescence (SL) have been performed for helium or xenon bubbles in mercury and water under the experimental conditions of Futakawa et al. [M. Futakawa, T. Naoe, and M. Kawai, in Nonlinear Acoustics-Fundamentals and Applications: 18th International Symposium on Nonlinear Acoustics (ISNA 18), AIP Conf. Proc. No. 1022, edited by B. O. Enflo, C. M. Hedberg, and L. Kari (AIP, New York, 2008), p. 197]. The results of the numerical simulations have revealed that the bubble expansion is much larger in water than in mercury mainly because the density of water is one order of magnitude smaller than that of mercury. The SL intensity is higher in water than that in mercury although the maximum bubble temperature is lower. This is caused by the much larger amount of vapor inside a bubble as the saturated vapor pressure of water is four orders of magnitude larger than that of mercury at room temperature. The SL intensity from xenon is much larger than that from helium due both to lower ionization potential and higher bubble temperature due to lower thermal conductivity. The instantaneous SL power may be as large as 200 W from xenon in water. The maximum temperature inside a xenon bubble in mercury may be as high as about 80 000 K. It is suggested that the maximum pressure in mercury due to shock waves emitted from bubbles increases as the SL intensity increases, although they are not simply correlated in water because the amount of water vapor trapped inside a bubble influences the SL intensity in a complex way.
Sequential observation of rebound shock wave generated by collapse of vapor bubble in BOS system
Numerical simulations of non-spherical bubble collapse
A high-order accurate shock- and interface-capturing scheme is used to simulate the collapse of a gas bubble in water. In order to better understand the damage caused by collapsing bubbles, the dynamics of the shock-induced and Rayleigh collapse of a bubble near a planar rigid surface and in a free field are analysed. Collapse times, bubble displacements, interfacial velocities and surface pressures are quantified as a function of the pressure ratio driving the collapse and of the initial bubble stand-off distance from the wall; these quantities are compared to the available theory and experiments and show good agreement with the data for both the bubble dynamics and the propagation of the shock emitted upon the collapse. Non-spherical collapse involves the formation of a re-entrant jet directed towards the wall or in the direction of propagation of the incoming shock. In shock-induced collapse, very high jet velocities can be achieved, and the finite time for shock propagation through the bubble may be non-negligible compared to the collapse time for the pressure ratios of interest. Several types of shock waves are generated during the collapse, including precursor and water-hammer shocks that arise from the re-entrant jet formation and its impact upon the distal side of the bubble, respectively. The water-hammer shock can generate very high pressures on the wall, far exceeding those from the incident shock. The potential damage to the neighbouring surface is quantified by measuring the wall pressure. The range of stand-off distances and the surface area for which amplification of the incident shock due to bubble collapse occurs is determined.
Energy partition at the collapse of spherical cavitation bubbles
Spherically collapsing cavitation bubbles produce a shock wave followed by a rebound bubble. Here we present a systematic investigation of the energy partition between the rebound and the shock. Highly spherical cavitation bubbles are produced in microgravity, which suppresses the buoyant pressure gradient that otherwise deteriorates the sphericity of the bubbles. We measure the radius of the rebound bubble and estimate the shock energy as a function of the initial bubble radius (2-5.6mm) and the liquid pressure (10-80kPa). Those measurements uncover a systematic pressure dependence of the energy partition between rebound and shock. We demonstrate that these observations agree with a physical model relying on a first-order approximation of the liquid compressibility and an adiabatic treatment of the noncondensable gas inside the bubble. Using this model we find that the energy partition between rebound and shock is dictated by a single nondimensional parameter ξ=Δpγ6/[p(g0)1/γ(ρc2)1-1/γ], where Δp=p∞ - pv is the driving pressure, p∞ is the static pressure in the liquid, pv is the vapor pressure, pg0 is the pressure of the noncondensable gas at the maximal bubble radius, γ is the adiabatic index of the noncondensable gas, ρ is the liquid density, and c is the speed of sound in the liquid.
Cavitation adjacent to plane boundaries
//
Gravity-capillary jet-like surface waves generated by an underwater bubble
Exploration of water jet generated by Q-switched laser induced water breakdown with different depths beneath a flat free surface
The dynamics of a water jet on a flat free surface are investigated using a nanosecond pulsed laser for creating an oscillating bubble with different depths beneath the free surface. A thin jet is shown to deform a crater surface resulted from surface depression and cause a circular ring-shaped crater on the connection surface between the crater of surface depression and the thin jet. The collapse of this circular ring-shaped crater is proposed to the crown-like formation around a thick jet. The evolution of the bubble depth suggests a classification of four distinctive ranges of the bubble depths: non-crown formation when the parameter of bubble depth over the maximum bubble radius gamma <= 0.5, unstable crown formation when 0.5 <= gamma <= 0.6, crown-like structure with a complete crown wall when 0.6 <= gamma <= 1.1, and non-crown formation when 1.1 <= gamma. Furthermore, the orientation of the crown wall gradually turns counterclockwise to vertical direction with increasing gamma from 0.5 to 1.1, implying a high correlation between the orientation of the crown wall and the depth of the bubble. This correlation is explained and discussed by the directional change of the jet eruption from the collapse of circular ring-shaped crater. (C)2013 Optical Society of America
Exploring morphological variations of a laser-induced water jet in temporal evolution: Formation of an air bubble enclosing a water drop
The efficiency of spin polarized charge transfer was investigated in an Fe/MgO tunnel barrier/GaAs based structure using spin dependent photocurrent measurements, whereby a spin imbalance in carrier population was generated in the GaAs by circularly polarized light. The dominance of tunneling transport processes over Schottky emission gave rise to a high spin transfer efficiency of 35% under the photovoltaic mode of device operation. A spin dependent tunneling conductance associated with spin polarized electron transport was identified by the observation of phase changes. This transport prevails over the unpolarized electron and hole conduction over the bias range which corresponds to flat band conditions.
Material ejection in nanosecond Er: YAG laser ablation of water, liver, and skin
Spray and microjets produced by focusing a laser pulse into a hemispherical drop
Transverse acoustic (TA) excitation modes were observed in inelastic x-ray scattering (IXS) spectra of liquid Sn. The excitation energies and widths of the TA modes are in good agreement with results of an ab initio molecular dynamics simulation. By comparing current correlation spectra between the experimental and theoretical results quantitatively, we have concluded that the TA modes can be detected experimentally through the quasi-TA branches in the longitudinal current correlation spectra. The lifetime and propagation length of the TA modes were determined to be ~0.7 ps and 0.8-1.0 nm, respectively, corresponding to the size of cages formed instantaneously in liquid Sn.
The effect of ambient pressure on ejecta sheets from free-surface ablation
Secondary cavitation due to interaction of a collapsing bubble with a rising free surface
Secondary cavitation in a rigid tube
Dynamic charac-teristics of large scale spark bubbles close to different boundaries
Growth and collapse of a vapour cavity near a free surface
Experimental and numerical investigation on bubble dynamics near a free surface and a circular opening of plate
Study on the interactions between two identical oscillation bubbles and a free surface in a tank
Cavitation-induced interface instablity of droplet between plates
//
Film-free laser forward printing of transparent and weakly absorbing liquids
A laser-based technique for printing transparent and weakly absorbing liquids is developed. Its principle of operation relies in the tight focusing of short laser pulses inside the liquid and close to its free surface, in such a way that the laser radiation is absorbed in a tiny volume around the beam waist, with practically no absorption in any other location along the beam path. If the absorbed energy overcomes the optical breakdown threshold, a cavitation bubble is generated, and its expansion results in the propulsion of a small fraction of liquid which can be collected on a substrate, leading to the printing of a microdroplet for each laser pulse. The technique does not require the preparation of the liquid in thin film form, and its forward mode of operation imposes no restriction concerning the optical properties of the substrate. These characteristics make it well suited for printing a wide variety of materials of interest in diverse applications. We demonstrate that the film-free laser forward printing technique is capable of printing microdroplets with good resolution, reproducibility and control, and analyze the influence of the main process parameter, laser pulse energy. The mechanisms of liquid printing are also investigated: time-resolved imaging provides a clear picture of the dynamics of liquid transfer which allows understanding the main features observed in the printed droplets.
A boundary element method for the simulation of non-spherical bubbles and their interactions near a free surface
The basic principle and numerical technique for simulating two three-dimensional bubbles near a free surface are studied in detail by using boundary element method. The singularities of influence coefficient matrix are eliminated using coordinate transformation and so-called 4π rule. The solid angle for the open surface is treated in direct method based on its definition. Several kinds of configurations for the bubbles and free surface have been investigated. The pressure contours during the evolution of bubbles are obtained in our model and can better illuminate the mechanism underlying the motions of bubbles and free surface. The bubble dynamics and their interactions have close relation with the standoff distances, buoyancy parameters and initial sizes of bubbles. Completely different bubble shapes, free surface motions, jetting patterns and pressure distributions under different parameters can be observed in our model, as demonstrated in our calculation results.
Dynamics of a cavitation bubble inside a liquid jet. [Master Thesis]
Fragmentation of acoustically levitating droplets by laser-induced cavitation bubbles
Cavitation-induced fragmentation of an acoustically-levitated droplet
Fast transient microjets induced by hemispherical cavitation bubbles
Laser-induced micro-jetting from armored droplets
Cavitation within a droplet
The present study numerically investigates liquid-jet characteristics of acoustic cavitation during emulsification in water/gallium/air and water/silicone oil/air systems. It is found that a high-speed liquid jet is generated when acoustic cavitation occurs near a minute droplet of one liquid in another. The velocity of liquid jet significantly depends on the ultrasonic pressure monotonically increasing as the pressure amplitude increases. Also, the initial distance between cavitation bubble and liquid droplet affects the jet velocity significantly. The results revealed that the velocity takes maximum values when the initial distance between the droplet and cavitation bubble is moderate. Surprisingly, the liquid jet direction was found to depend on the droplet properties. Specifically, the direction of liquid jet is toward the droplet in the case of water/gallium/air system, and vice versa the jet is directed from the droplet in the case of water/silicone oil/air system. The jet directionality can be explained by location of the high-pressure spot generated during the bubble contraction.
Controllable direction of liquid jets generated by thermocavitation within a droplet
A high-velocity fluid stream ejected from an orifice or nozzle is a common mechanism to produce liquid jets in inkjet printers or to produce sprays among other applications. In the present research, we show the generation of liquid jets of controllable direction produced within a sessile water droplet by thermocavitation. The jets are driven by an acoustic shock wave emitted by the collapse of a hemispherical vapor bubble at the liquid-solid/substrate interface. The generated shock wave is reflected at the liquid-air interface due to acoustic impedance mismatch generating multiple reflections inside the droplet. During each reflection, a force is exerted on the interface driving the jets. Depending on the position of the generation of the bubble within the droplet, the mechanical energy of the shock wave is focused on different regions at the liquid-air interface, ejecting cylindrical liquid jets at different angles. The ejected jet angle dependence is explained by a simple ray tracing model of the propagation of the acoustic shock wave inside the droplet.