引 言
气泡常见于自然界中,在海洋工程及其他领域中扮演着重要的角色,例如水下爆炸气泡[1-2],空化[3-8],海底资源探测中的气枪气泡[9-10],气泡清洗[11-12],以及医学中的声空泡[13-14]等. 以上应用中的气泡行为均有一种相似的物理特性:气泡体积的剧烈变化,简称“脉动”. 水下爆炸过程中,4g 左右的 PETN 炸药在 1m 水深处起爆,将产生最大直径约0.52m的气泡[1]; 500kg 的 TNT 炸药在 20m 水深处起爆产生的气泡直径可达 17m 左右[15]. 水中的微米级的气核在低压(满足相应的空化准则)作用下将产生爆发式的生长,形成肉眼可见的空标识码[16]. 由于惯性效应,气泡会过度膨胀,使其内部气体压力小于环境压力,因此气泡在最大体积后将开始坍塌. 除了超近边界的情况[17],气泡在膨胀阶段均有较好的稳定性,其形态为球形或接近球形;然而,气泡在坍塌阶段的运动极不稳标识码球状效应十分明显. 许多实验已证实,气泡在重力场中将产生竖直向上的射流[18],这是由于重力引起的静水压力梯度所引起,或者说气泡顶部受到的静水压力较小,而底部受到的压力更标识码破了气泡溃灭阶段的对称性. 气泡在自由液面附近产生背离水面的射流(本文称之为“反射流”)[19-21],在近壁面时产生朝向壁面的射流(本文称之为“正射流”),其速度可达数十至数百米每秒[22-27]. 气泡射流砰击载荷在近场或接触水下爆炸中不可忽略,可能给结构带来比冲击波和气泡脉动更大的威胁[1, 28]. 在空化领域,气泡射流砰击也是造成螺旋桨表面剥蚀的重要机理之一[29],然而学术界与工业界对于气泡射流砰击压力的认识尚且不足.
在已发表的文献中,许多学者基于 Rayleigh-Plesset 气泡理论,采用 Kelvin-impulse 理论和 Bjerknes 效应来解释气泡射流的成因[23, 30-31]. 该方法将气泡脉动等效为“点源”或“点汇”,最终推导得到的流场动量仅可表征气泡大致的形心迁移方向,由此预测的射流标识码某些参数工况下失效[32-33]. 仅通过球状气泡理论较难透彻的揭示气泡射流的初生、发展和砰击等一系列复杂物理过程中所蕴含的力学机理. Blake 和 Gibson[34] 首次通过非奇异的轴对称边界积分法模拟了气泡与自由液面非线性耦合作用,计算结果基本重现了标识码重要的物理现象. 边界积分法 (boundary integral method, BIM) 从此以后不断发展,目前已成为气泡动力学领域中应用最广泛的数值方法之一. Blake 等[35]发现气泡在坍塌阶段中,气泡顶部与自由液面之间存在驻点和局部高压区,进而阐明了气泡向下射流、水冢标识码气泡坍塌阶段继续增加的机理. 近年来,许多学者也针对该问题从实验[36]和数值[37-41]方面开展了广泛的研究,取得了许多有益的物理规律和结论. 然而,前人的研究对气泡运动特性关注较多,缺乏探讨气泡射流初生、加速和砰击的力学机理和物理规律,这对于在标识码用中控制气泡射流行为具有重要的科学意义.
本研究首先采用水下高压放电气泡生成技术[42]和高速摄影技术开展近自由液面和壁面的气泡实验,对气泡膨胀标识码、射流和回弹等重要的动力学特性进行分析,并对前人不曾关注的物理现象进行阐述. 然后,依据流体动力学理论标识码积分法建立气泡数值模型,研究气泡在不同边界条件下的运动特性. 在传统“涡环模型”的基础上,改进了气泡网标识码扑结构变换方法,并采用解析方法求解涡环速度势,提高环状气泡阶段的模拟精度,数值模型较好的重现了实验中标识码物理现象,验证了本文数值模型的有效性. 然后,采用辅助函数法计算气泡周围的压力和速度场,深入分析气泡运标识码围流场之间的内在关系,为揭示不同边界附近气泡射流行为背后的力学机理提供支撑. 最后,本文探讨了距离参数标识码面气泡射流砰击载荷的影响规律,旨为近场水下爆炸和空化等领域的研究提供参考.
1 物理问题和数值模型
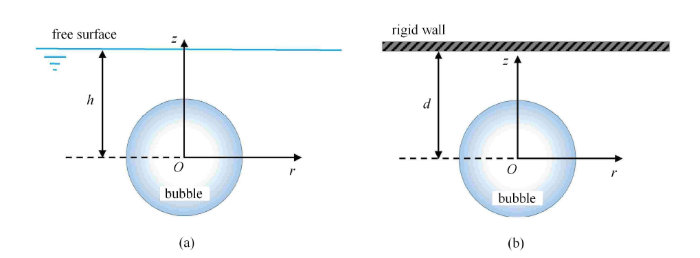
如图1 所示为本文所研究物理问题的示意图和坐标系定义方法.
图1
图1
气泡与 (a) 自由液面或 (b) 刚性壁面耦合作用示意图及柱坐标系的定义
Fig.1
Sketches of the bubble interaction with (a) a free surface and (b) a rigid wall, and the definition of the cylindrical coordinate system
假设气泡在初始时刻为半径 $R_{0}$ 的高压球状气核,整个流场速度均为零,气泡中心与水平自标识码之间的距离用 $h$ 表示,气泡和刚性壁面之间距离用 $d$ 表示. 这两类问题均可采用轴对称模型进行描述,引入柱坐标系 $O$-$r\theta z$,坐标原点设在气泡初始中心,$z$ 轴方向背离重力方向.
通过该无量纲系统,气泡的初始条件可以用如下几个参数确定
其中, $p_{0}$ 为气泡初始内部压力,$g$ 为重力加速度,式中距离参数 $\gamma $ 用来衡量气泡与边界之间的距离,根据实验参数即可直接确定. 强度参数 $\varepsilon $ 用来衡量气泡初始内压,浮力参数 $\delta $用来衡量气泡的浮力效应,本文实验中的气泡浮力效应并不显著. 气泡的无量纲初始半径与强度参数之间的关系[15] 如下
式中 $\kappa $ 为气泡内部气体的比热比. 爆炸气泡的强度参数可由一套经验公式确定[15],但是对于本文的电火花气泡并不一定适用. Blake 等[45] 指出,气泡初始内部压力在选取上可以有较大的随意性,计算得到的气泡运动特性以及射流行为变化不明显. Turangan 等[46] 指出,计算中 $\varepsilon $ 取值在 100$\sim $500 时,气泡射流速度变化不明显. Li 等[28] 发现, $\varepsilon $ 的取值会在一定程度上影响气泡射流之后的环状气泡撕裂行为. 经过大量数值计算发现,对于本文中的电火花气泡而言, $\varepsilon $ 取值在 20$\sim $500 范围时,数值结果均与实验结果吻合良好.
1.1 边界积分法
本文采用轴对称边界积分法 (BIM) 求解脉动型气泡运动,详细的数值计算过程可参考 Blake 等[31] 和 Wang 等[47]. 在常压环境中,典型的脉动型气泡在第一周期运动过程中,马赫数超过 0.1 的时长不超过气泡周期的 0.1${\%}$[48],而工程实际中通常只关注气泡第一周期所引起的流场载荷,因此本文在研究气泡运动时假设流体不可压缩. 此外,爆炸气泡运动的特征雷诺数量级在 $O$ (10$^{8})$ 以上[15],微米级的空泡也在 $O$ (10$^{3})$ 以上[49],因此黏性对气泡运动的影响可忽略不计. 进一步假设流体运动无旋,则存在速度势 $\varphi $ 在气泡外部流场中满足 Laplace 方程和边界积分方程
式中,${\pmb r}$ 和 ${\pmb q}$ 分别表示流场控制点和积分点,$S$ 包含气泡、自由液面和结构表面等流场边界,${\pmb n}$ 为流 场边界上的法向量,${\pmb \lambda }$ 是点 ${\pmb r}$ 处观察流场的立体角. 对于气泡和无穷大刚性壁面耦合作用[50],格林函数 $G$ 选取为
其中,$ {\pmb q}’$ 为 ${\pmb q}$ 关于壁面的镜像点,该格林函数可自动满足壁面上不可穿透条件. 若不考虑壁面的影标识码如在模拟气泡和自由液面耦合过程中,式 (4) 中第 2 项在计算中略去.
气泡表面 $S_{\rm b}$ 和自由液面 $S_{\rm f}$ 上的运动学边界条件均为
气泡表面 $S_{\rm b}$ 和自由液面 $S_{\rm f}$ 上的动力学边界条件分别为
由于气泡脉动这种瞬态问题,气泡内部气体压力 $p_{\rm b}$ 通常由绝热气体状态方程[51]获得
式中,$p_{c}$ 为饱和蒸汽压,气体的比热比 $\kappa $ 与气体成分有关,对于TNT爆炸气泡, $\kappa = 1.25$,对于理想气体, $\kappa = 1.4$.
以上各式为流场控制方程以及流场边界需要满足的边界条件,联立即可对气泡运动进行时域求解. 本文采用轴对称线性单元 ($O$-$r \theta z$ 坐标系)对边界积分方程 (3) 进行空间离散求解,气泡表面节点数为 200,自由液面的无量纲宽度取 20,节点数为 300,详细标识码散和求解方法在许多文献中已有详细的阐述,本文不予赘述,这里只对求解气泡运动的思路进行说明. 每个时刻已知气泡标识码液面上的的速度势分布,通过求解式 (3) 即可获得气泡表面的法向速度 $\varphi _{n}$,同时采用有限差分法求解气泡表面的切向速度 $\varphi _{\tau }$,法向和切向速度进行合成即可获得气泡表面真实速度 $\nabla \varphi $,利用运动学边界条件 (5) 更新边界上节点位置,同时采用动力学边界条件 (6) 和 (7) 更新速度势,本文计算中采用标识码格-库塔法对时间进行离散,提高程序稳定性和计算精度.
1.2 环状气泡模型
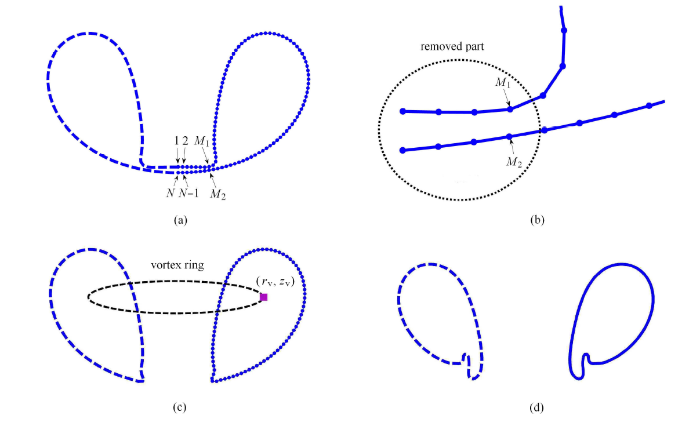
Wang 等[53] 假设气泡射流砰击最初始发生于对称轴上的一点,然后对气泡网格的拓扑结构进行重构,其原始办法是去掉气标识码和底部轴线上两个节点以及与之分别相邻的两个节点,共计去掉 4 个节点,然后在剩余节点的破口位置增加一个插值点,重新标识码编号进行排序,进而形成“涡眼”,该方法适合处理射流砰击“点接触”工况. 本文在实验和计算中发现,在某些工况下气泡射流宽度较大,而且射流头部较平,若只去掉 4 个节点容易导致后期计算网格畸变.
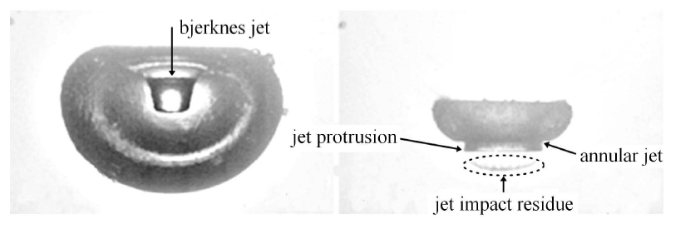
如图2 所示为典型的气泡在自由液面附近的射流现象[32],针对该工况采用 BIM 对气泡与自由液面耦合作用进行模标识码3(a) 中给出了射流砰击前瞬间的气泡形态,该工况中气泡射流头部较平整,射流砰击并不是发生在中心轴线上,而是在一个环线标识码中第 $M_{1}$ 个节点和第 $M_{2}$ 个节点之间最先发生碰撞,常规的拓扑结构处理方法并不适用于该工况. 观察实验现象 (图2),气泡射流后在其底部产生了一些“射流砰击残留物”,联合实验现象和数值计算结果可以发标识码 3(a) 中的节点 $1 \sim M_{1}$ 以及节点 $M_{2}\sim N$所包围的一小部分气体即是实验中的残留物. 由于残留物相对气泡整体的体积较小,因此在数值计算中直接将该部分节点和单元删除,然后形成新的环状气泡节点系标识码图3(b) 和图3(c) 所示. 如此,数值计算结果将与真实的物理过程更加贴近,计算结果与实验吻合更好, 如图 3(d) 所示. 这种工况中,气泡射流砰击实际上可以看作是气泡发生了撕裂现象[54],射流前的单连通气泡演变成一个环状气泡与另一个单连通气泡(砰击残留物),由于后者的体积远小于前者,且标识码距离越来越远,所以后期的数值模拟中可忽略后者对前者的影响,继续模拟环状气泡的运动.
图2
图3
图3
平头射流砰击工况中环状气泡阶段计算预处理
Fig.3
The numerical treatment for a jetting bubble with a broad jet
当处理完气泡拓扑结构后,保持气泡表面速度势不变,则射流砰击位置出现速度势突跳. 按照经典涡环模型处理办法,在气泡内部 布置一个环量为 $\varGamma $ 的涡环,其位置用 ($r_{\rm v}$,$z_{\rm v}$) 表示. 本文的研究中,对于环接触砰击情况,假设接触点编号分别为 $M_{1}$ 和 $M_{2}$,则环量
$\varGamma $ 的取值方法[53]为
环状气泡阶段流场的总速度势和速度均被分解成两部分. 首先,总速度势被分解为涡环诱导速度势 $\varphi_{\rm vor}$ 和 残余速度势 $\varphi_{\rm res}$
其中环状气泡表面第 $i$ 个节点 $\varphi_{\rm vor}$ 的传统求解法[53] 为
式中 ${\pmb u}_{\rm vor}$ 为涡环诱导速度,由比奥-萨法尔定理求解
由于 $\varphi _{\rm vor}$ 在无穷远处的值为零,则 $\varphi _{\rm vor} (r_1$, $z_1$, $r_{\rm v}$, $z_{\rm v})$ 由 ${\pmb u}_{\rm vor}$ 从无穷远处积分到气泡表面第一个节点可得. 然后以第一个节点为起点,沿着气泡表面对 ${\pmb u}_{\rm vor}$ 积分至第 $i$ 个节点即可获得任意节点处的涡环诱导速度势. 该方法需进行多次线积分,不免引入数值误差,本文采用一个半解析的方法[50] 求解 $\varphi _{\rm vor}$. 对于气泡表面节点 ($r$, $z$),从无穷远点 ($r$, $\pm \infty )$ 对 ${\pmb u}_{\rm vor}$ 积分至节点 ($r$, $z$) 得
式中 $d {\pmb l}$ 为涡环上积分微元,${\pmb R}$ 为积分微元到控制点 ($r$, $z$) 处的矢径. 当节点处于涡环平面上方时,采用式 (13) 求解,当节点处于涡环平面下方时,采用式 (14) 求解.
同理,流场总速度被分解成为涡环诱导速度 ${\pmb u}_{\rm vor}$ 和残余速度势诱导速度 ${\pmb u}_{\rm res}$,即
求解涡环诱导速度势 $\varphi_{\rm vor}$ 后,即可通过式 (10) 获得气泡表面残余速度势 $\varphi _{\rm res}$, 而且 $\varphi_{\rm res}$ 在流场中连续分布,亦满足 Laplace 方程,所以 ${\pmb u}_{\rm res}$ 与单连通域阶段的求解方法一致.
环状气泡阶段的速度势和速度进行分解后,环状气泡的动力学和运动学边界条件改写为
1.3 压力和速度场计算方法
由于 BIM 在模拟过程中仅需离散气泡及流场边界,而流域并不需要进行离散求解,求解流场压力独立于气泡运动的时域模拟,即标识码定某个时刻流场边界的相关物理量,就能够通过以下方法求得该时刻的流场压力(以及速度),其中流场动压力由伯努利方程计算
当已知流场边界的速度势后,即可通过上式求解出分布源密度 $\sigma $,进而通过下式求解流场控制点处的速度
下面介绍如何使用辅助函数法[28]求解流场中的 ${\partial \varphi } /{\partial t}$ 项,该项是计算非定常气泡诱导载荷的重点,首先定义辅助函数
辅助函数 $\varPsi $ 也满足 Laplace 方程,即
将间接边界积分法中的分布源密度的概念应用于辅助函数 $\varPsi $,则有
求解分布源密度 ${\sigma }’$ 前,需给出辅助函数 $\varPsi $ 的边界条件, $\varPsi $ 在气泡表面上满足
$\varPsi $ 在自由液面上满足
首先,把控制点 ${\pmb r}$ 置于流场边界上(气泡和自由液面),利用式 (23) 可求得分布源密度 ${\sigma }’$,然后, 将控制点 ${\pmb r}$ 置于流场考察点,再标识码 (23) 计算流场中的 $\varPsi $,最后标识码 (18),即可求得气泡在流场中的诱导压力.
在环状气泡阶段,流场载荷求解方法与上述类似,${\partial \varphi } / {\partial t}$ 项被分解为
等式右端最后一项的求解方法与上述方法相同. 由于涡环的位置在每个时刻都可看作固定不动,所以涡环诱导速度势的时间 导数为零,等式右端第一项并不需要求解. 所以环状气泡诱导的流场动载荷为
2 实验方法
本文首先基于电火花气泡实验台[32, 57-58]进行了气泡与自由液面耦合作用实验,气泡由 700 V DC 放电产生,两标识码均为直径约 0.2mm 铜丝,铜丝搭接点的电阻相对整个电路最高,所以在电路短路瞬间在搭接点位置产生大量的热,进而在短标识码融化铜丝并迅速使其周围的水汽化,形成膨胀气泡. 铜丝搭接点也就是气泡初生的中心位置. 由于电极直径远小于气泡最大直径,因此可忽略电极对气泡行为的影响. 实验在一个尺寸为 500mm$\times $500mm$\times $500mm 的玻璃水箱中进行,水深 400mm 左右,气泡距离水箱底部和侧壁面的距离是气泡最大半径的 10 倍以上,因此可忽略水标识码对气泡运动的影响[59]. 采用 Phantom V711 高速摄影机对气泡与自由液面的耦合作用进行拍摄,每秒帧数为 31000,曝光时间选择为 20$\mu $s,同时采用两个 2kW 连续光源提供照明. 本文还在相同实验水箱中进行了气泡和刚性壁面耦合作用实验,刚性壁面采用 10mm 厚的玻璃板,实验中使气泡初始中心远标识码液面,尽可能减小水面对气泡运动产生的影响. 需要说明的是,本文实验所产生的气泡浮力参数较小,可以直接用于研究空化气泡;对于浮力参数较大的爆炸气泡而言,其重要标识码特性同样与电火花气泡具有较高的相似性,例如猛烈的膨胀、坍塌溃灭、射流、回弹以及压力波的释放等等. 因此电火花气泡的研究同样能够为水下爆炸领域提供参考,而浮力效应只是诱导气泡产生向上射流的一种机理,本文着重研究标识码应诱导气泡射流的力学机理,对于浮力效应的影响也将在文章中所有提及.
3 近自由液面气泡反射流现象及力学机理
本节将通过实验和数值方法讨论近自由液面气泡产生反射流的力学机理,实验中的参数为:气泡初始中心所标识码 $h= 13.6$mm,气泡最大等效半径 $R_{\rm m} = 18.5 $mm. 因此可直接获得气泡两个无量纲初始参数: $\gamma _{\rm f} = 0.74$,$\delta = 0.04$. 下面将分别针对气泡膨胀、坍塌和环状气泡 3 个阶段对气泡行为进行详细探讨,通过 BIM 数值计算获得气泡周标识码压力和速度分布,有助于揭示气泡行为背后的力学机理.
3.1 气泡膨胀阶段
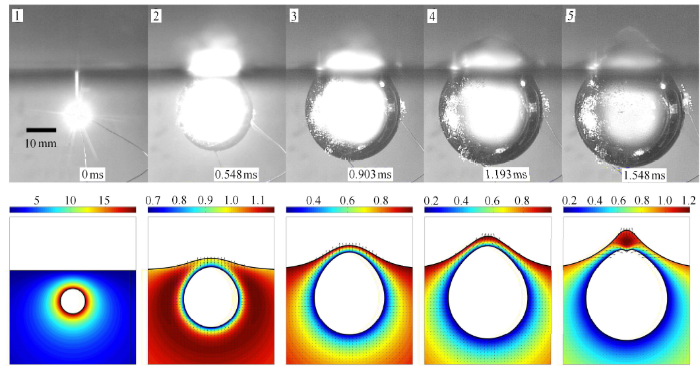
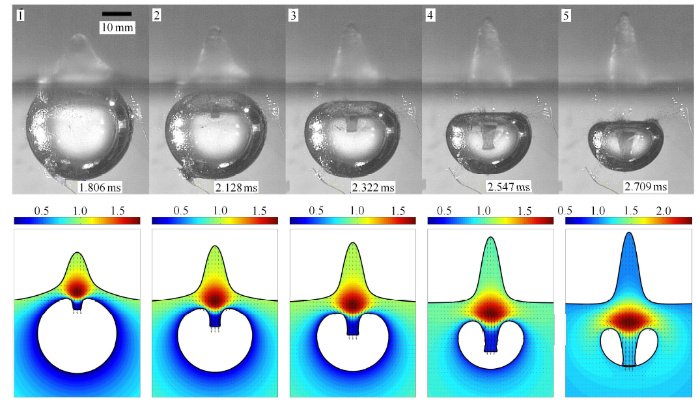
图4 所示为气泡膨胀阶段的实验与数值结果对比. 气泡初始时刻在内部高压的驱使下开始膨胀,如第 1 帧所示. 此时气泡表面附近 流场压力相对较高,距离气泡表面较远的流场压力相对较小. 由于气 泡与自由液面之间的压力梯度最大,因此气泡在膨胀初期,气泡顶部的膨胀速度最高,如第 2 帧所示,气泡竖直方向上的高度大于水平宽度,自由液面也被气泡微微拱起. 此时,气泡的内部 气体压力已经降至环境压力以下,气泡表面附近的流场压力小于远场压力,气泡依靠惯性效应继续膨胀,但是膨胀速度逐渐减小. 第 3-4 帧中,气泡呈“鸡蛋型”,自由液面上的水冢高度进一步增大,此时气泡与自由液面之间的水层逐渐变薄,该处的压力梯度最大,因此气泡顶部减速最快. 当气泡达到最大体积时,如第 5 帧所示,气泡顶部已经开始向下收缩. 由速度场可见,气泡与自由液 面之间的流体仍在向对称轴聚集,并在轴线上形成驻点和局部高压区,此时的驻点和压力最大的位置基本重合. 此外,气泡射流初 生的力学机理还有另外一个因素,即气泡在膨胀过程中,气泡顶部的曲率最高,因此在收缩阶段的速度最快[60],更易形成射流.
图4
图4
泡膨胀阶段实验与数值结果对比(数值计算的无量纲时间:0, 0.205, 0.384, 0.570, 0.718,每幅图的坐标范围是:$-1.5 \leqslant r \leqslant 1.5$, $ -1.5 \leqslant z \leqslant 2$,无量纲时间标识码 1.87ms,云图代表无量纲压力场)
Fig.4
Comparison between the experimental observation and numerical simulation for a bubble beneath a free surface during the expansion phase (the dimensionless times for the simulation are: 0, 0.205, 0.384, 0.570 and 0.718, respectively. Horizontal and vertical axes of each frame are $-1.5 \leqslant r \leqslant 1.5$ and $-1.5 \leqslant z \leqslant 2$, respectively. The time scale is 1.87ms. The contours denote the pressure fields)}
3.2 气泡坍塌阶段
图5 所示为气泡坍塌阶段(射流砰击以前)的实验与数值计算结果对比. 如第 1 帧所示,气泡顶部已形成明显的射流,气泡与自标识码之间的局部高压峰值更大,在此高压区的作用下,气泡射流进一步加速,同时水冢高度也进一步增大. 根据流体力学质量守恒定律,射流速度越快,在气泡上表面和自由液面之间朝对称轴运动的流体速度也就越快,从而导致对称标识码局部区域压力更高(同样压力梯度也变大),该局部高压区反过来又会加快射流的运动速度,因此该高压区和气泡射流之标识码“正反馈效应”. 随着气泡射流逐渐发展和加速(第 2$\sim$5 帧),高压区峰值点与驻点位置逐渐偏离,这是由于流动的非定常性所引起. 高压区的位置随气泡运动逐渐向下迁移,而且高压区的范围也逐渐扩大. 由于气泡表面在光学中起到一个凹透镜的作用[23],因此从实验中观察到的射流宽度比真实情况小 1.33 倍左右, BIM计算结果和实验有一定差别,但两者的真实吻合度应该比图中的直观显示情况更好. 实验中的射流速度约 34m/s,数值计算结果为 32m/s,相对偏差为 5.9${\%}$. 最后,从第 2 帧中的实验结果可见,气泡射流头部为“平头”,并逐渐演变成“钉头”(第 4 帧),本文的数值结果较好地重现标识码理现象,说明射流头部的形态演变为惯性力所主导,其形成机理可作以下解释:气泡射流加速依靠其后端的局部高压区(标识码高的压力梯度),然而当射流较细较长时,射流前半部分的压力近似于气泡内部气体压力,压力梯度较小,此时只有射流标识码分的流体能够获得较好地加速效果,进而导致射流头部速度在后期加速并不明显,射流后端的流体涌向前端,并有沿径向标识码转或铺开的趋势. 只有当距离参数较小,射流宽度较小时,射流头部形态才会发生如此特殊的变化.
图5
图5
气泡坍塌阶段实验与数值结果对比(数值计算的无量纲时间为:0.965, 1.107, 1.175, 1.294, 1.397,每幅图的坐标范围是:$-1.5 \leqslant r \leqslant 1.5$, $-1.5 \leqslant z \leqslant 2.5$)
Fig.5
Comparison between the experimental observation and numerical simulation for a bubble beneath a free surface during the collapse phase (the dimensionless times for the simulation are: 0.965, 1.107, 1.175, 1.294 and 1.397, respectively. Horizontal and vertical axes of each frame are $-1.5 \leqslant r \leqslant 1.5$ and $-1.5 \leqslant z \leqslant 2.5$, respectively)
3.3 环状气泡阶段
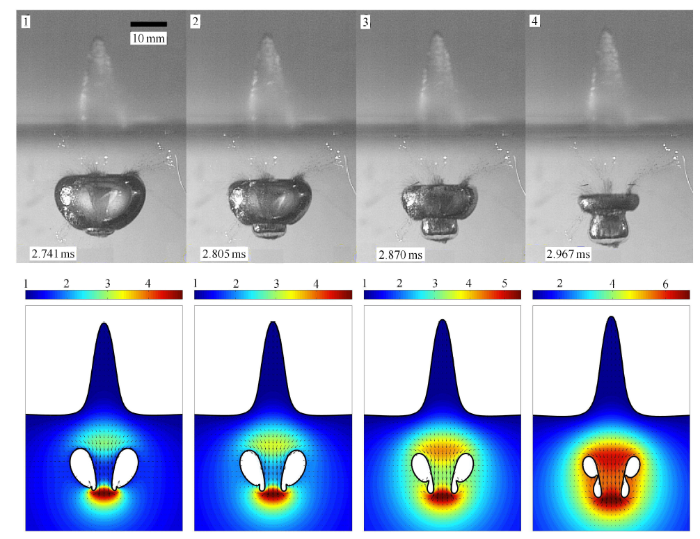
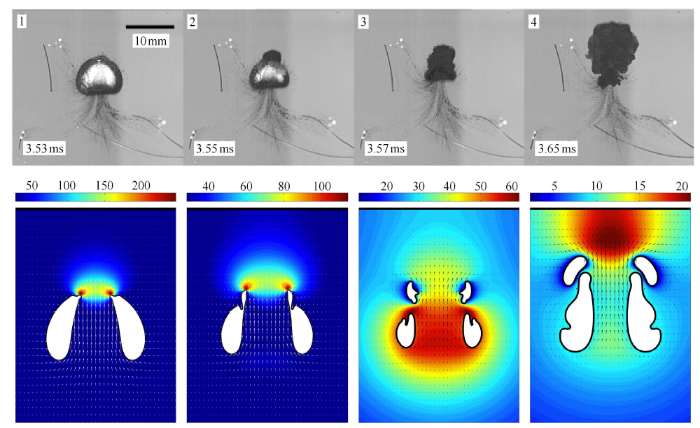
图6 所示为气泡射流穿透下表面后(环状气泡阶段)实验与数值结果对比. 如第 1 帧所示,气泡射流使得气泡底部很快产生向下的凸起,凸起与气泡表面之间存在环向凹陷,这个凹陷如同气泡表面上的一个“孤立波”沿气泡表面自下而上传播. 同时气泡射流砰击位置产生了局部高压区,由压力云图可见,压力峰值约 4.8 (有量纲值约 0.5MPa),该值约等于 $0.5 \rho v^{2}$ ($v$ 代表射流砰击速度). 此时,气泡顶部附近的高压区仍然存在,它会不断驱动流体持续向下运动,水冢持续向上运动. 气泡射流砰击时刻气泡仍在不断坍塌,所以气泡周围的流场压力也逐渐增大(第 2-4 帧),气泡底部的凸出物不断向下生长,环向凹陷最终与气泡内表面碰撞,进而导致环状气泡撕裂.
图6
图6
环状气泡阶段实验与数值结果对比(数值计算的无量纲时间为:1.431, 1.453, 1.494, 1.550,每幅图的坐标范围 是:$-1.5 \leqslant r \leqslant 1.5$, $-1.5 \leqslant z \leqslant 2.8$)
Fig.6
Comparison between the experimental observation and numerical simulation for a bubble beneath a free surface during the toroidal bubble stage (the dimensionless times for the simulation are: 1.431, 1.453, 1.494 and 1.550, respectively. Horizontal and vertical axes of each frame are $-1.5 \leqslant r \leqslant 1.5$ and $-1.5 \leqslant z \leqslant 2.8$, respectively)
值得说明的是,大气压力的变化对气泡的运动行为将产生较大的影响. Zhang 等[32] 在减压罐内进行的气泡实验表明,大气压力减小后,相同放电电压产生的气泡尺度逐渐增大,更标识码是气泡浮力效应增强. 当浮力参数增大到一定程度后,气泡坍塌阶段会从底部形成向上的射流现象,而气泡向下的射流逐渐消失. 该现象同样可以用本节的机理加以解释:气泡在膨胀阶段,内部压力降低,若该压力小于大气压力,则气泡与水面之间标识码内压力梯度方向向上,气泡产生向下的射流;当气泡压力大于大气压力时,水膜内的压力梯度向下(这里还需要考虑重标识码的压力梯度),气泡顶部将不会产生向下的射流现象.
4 近刚性壁面气泡正射流现象及力学机理
本节将针对近刚性壁面附近气泡正射流行为进行实验和数值研究,其中实验的参数为:气泡初生中心位置标识码之间的距离 $d$ 约 22.5mm,气泡达到的最大半径约 16.8mm,气泡初始中心的水深约 200mm. 下面将分别针对气泡膨胀阶段、坍塌阶段以及环状气泡阶段(包括环状气泡撕裂)对气泡动力学行为特点及其内在力学机理进行深入分析.
4.1 气泡膨胀阶段
图7 给出了实验中气泡膨胀阶段的形态演变过程以及对应的数值计算结果,实验每一帧的有量纲时间标在右下角(斜体). 数值计算结果同时给出了气泡形态、流场压力云图(无量纲)和速度矢量,每幅图的坐标范围是:$-1.5 \leqslant r \leqslant 1.5$, $-1.5 \leqslant z \leqslant 1.34$,上方壁面位置用黑色实线表示.
图7
图7
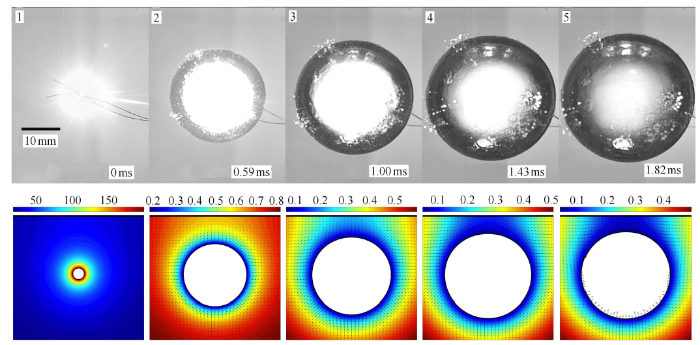
气泡膨胀阶段实验与数值结果对比(数值计算的无量纲时间为:0, 0.278, 0.553, 0.842, 1.098,每幅图的坐标范围是: $-1.5 \leqslant r \leqslant 1.5$, $-1.5 \leqslant z \leqslant 1.34$,时间因子为1.66ms,云图代表压力场)
Fig.7
Comparison between the experimental observation and numerical simulation for a bubble near a rigid wall during the expansion phase (the dimensionless times for the simulation are: 0, 0.278, 0.553, 0.842 and 1.098, respectively. Horizontal and vertical axes of each frame are $-1.5 \leqslant r \leqslant 1.5$ and $-1.5 \leqslant z \leqslant 1.34$, respectively. The time scale is 1.66ms. The contours denote the pressure fields)
第 1 帧表示气泡初生时刻,气泡形态为球状,靠近气泡表面的流体压力较高,完全由高压气体诱导,且流场中的压力随距离 $l$ 增大按照 $1/ l$ 规律衰减[28]. 需要说明的是,实验中的气泡并不是瞬间产生,而数值中的气泡初始时刻即为高压气核,两者之间的差异可能是造成计算与实验之标识码的主要原因. 在高压气体的推动下,气泡迅速膨胀,其内部压力迅速降低,在第2帧中,气泡内部压力已经降至环境压力以下,即气泡已过度膨胀标识码力云图可见气泡表面的压力小于周围环境的压力. 随后气泡依靠惯性效应继续膨胀,膨胀速度逐渐减小. 由第 3 帧至第 5 帧可知,气泡与上方壁面之间的狭窄区域内逐渐形成低压,而此时气泡下方的压力相对较标识码此气泡整体将受到一标识码壁面的合力,气泡的形心从第 3 帧开始逐渐向壁面迁移,这就是壁面吸引气泡的力学机制,而且在气泡坍塌阶段的吸引效应更加明标识码多文献称之为“二阶Bjerknes力”[23, 30-31],本文的数值计算结果更加直接的展示了该力的形成过程和成因. 当气泡达到最大体积时(第 5 帧),由于气泡顶部附近的流场压力较小,因此气泡顶部仍在向外膨胀;而气泡底部附近的压力较高,标识码泡下表面率先收缩.
4.2 气泡坍塌阶段
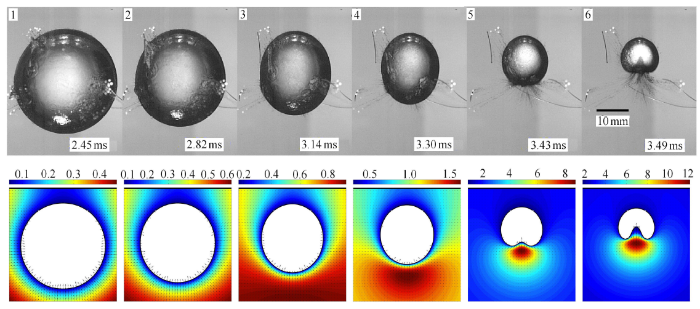
图8 给出了实验中气泡坍塌阶段的形态演变过程以及对应的数值计算结果(承接图7 中的结果). 气泡坍塌是由于环境压力标识码泡内部压力所引起,而且气泡表面的坍塌速度主要取决于其附近的流场压力梯度,由此可分析壁面附近气泡坍塌初期的特性. 第1帧中,除了气泡顶部的低压区域以外,气泡四周与下方的压力场相似,所以气泡顶部收缩最慢,其余部分收缩速度相当. 气泡逐渐偏离球状,演变为椭球状(如第 2-4 帧所示). 对于坍塌中的椭球型气泡而言,Lauterborn[60] 指出,具有高曲率的气泡表面坍塌速度更快,更容易形成高速射标识码可以用气泡运动周期与气泡半径之间的正比关系来解释. 在第4帧中,气泡底部的坍塌速度明显高于其余部位,而且气泡底部附近逐渐形成了局部高压区. Li 等[28] 指出,气泡表面运动速度较快的部位将在流场中产生更大的扰动,在该位置附近的区域通常会形成局部高压区. 在此高压区的作用下,气泡底部收缩速度进一步加快,促使射流的形成. 当气泡射流进一步加速,其底部的高压区更为明显(如第 5-6 帧所示). 由此可见,气泡底部高压区和气泡射流的形成之间存在“正反馈效应”,所以气泡射流虽仅在坍塌后期的短时间内形标识码能够达到数百米每秒的速度,本实验中气泡射流砰击时刻的速度达到了 116m/s 左右,与 Philipp 和 Lauterborn[23] 的激光空泡实验结果接近.
图8
图8
气泡坍塌阶段实验与数值结果对比(数值计算的无量纲时间为:1.461, 1.695, 1.893, 1.986, 2.089, 2.126,每幅图的坐标识码是:$-1.2 \leqslant r \leqslant 1.2$, $-1.2 \leqslant z \leqslant 1.34$)
Fig.8
Comparison between the experimental observation and numerical simulation for a bubble near a rigid wall during the collapse phase (the dimensionless times for the simulation are: 1.461, 1.695, 1.893, 1.986, 2.089 and 2.126, respectively. Horizontal and vertical axes of each frame are $-1.2 \leqslant r \leqslant 1.2 $ and $-1.2 \leqslant z \leqslant 1.34$, respectively)
4.3 环状气泡阶段
图9 给出了实验中环状气泡阶段的形态演变过程以及对应的数值计算结果(承接图8 中的结果). 射流穿透气泡上表面后,标识码击直接导致在砰击的局部位置形成极高的压力,无量纲值高达 242 (对应有量纲值约 24MPa),如第1帧所示,该现象揭标识码泡射流对结构产生局部损伤的力学机理. 由于惯性的作用,气泡顶部迅速形成向上的凸起物,如第 2 帧所示,气泡射流宽度逐渐变大,射流速度逐渐衰减,砰击位标识码部高压峰值也逐渐减小. 在气泡向上形成凸出物的同时,气泡表面逐渐形成了向内的环向凹陷,并沿气泡外表面向下传播,最终导致环状气泡的撕标识码第 3 帧所示,此时气泡基本达到最小体积. 然而,在实验中可能是由于射流砰击以及气泡撕裂等因素造成了气泡表面的不稳定[50, 61],气泡表面不再光滑,因此高速摄影难以捕捉到后期气泡射流的形态,而且气泡撕裂的细节较难体现. 随后气泡开始回弹,并以较快的速度向壁面迁移,如第 4 帧所示. 根据 Kelvin-impulse 理论,气泡在坍塌阶段的开尔文冲量变化不大,但是气泡体积变小后,气泡附加质量减小,气泡标识码速度必然显著加快[62],当气泡逐渐回弹后,气泡迁移速度又逐渐减小. 气泡位置的迁移可导致气泡射流更加直接的作用在壁面上,从而增强气泡的破坏能力. 此外,从数值计算结果来看,两个环状气泡在后期又趋于融合,形成一个完整的气泡,进而进入第二周期的运标识码实验现象一致.
图9
图9
环状气泡阶段实验与数值结果对比(数值计算的无量纲时间为:2.174, 2.185, 2.2, 2.238,每幅图的坐标识码是:$-0.5 \leqslant r \leqslant 0.5$, $0 \leqslant z \leqslant 1.34$)
Fig.9
Comparison between the experimental observation and numerical simulation for a bubble near a rigid wall during the toroidal bubble stage (the dimensionless times for the simulation are: 2.174, 2.185, 2.2 and 2.238, respectively. Horizontal and vertical axes of each frame are $ -0.5 \leqslant r \leqslant 0.5$ and $0 \leqslant z \leqslant 1.34$, respectively)
5 距离参数对近壁面气泡射流砰击载荷的影响
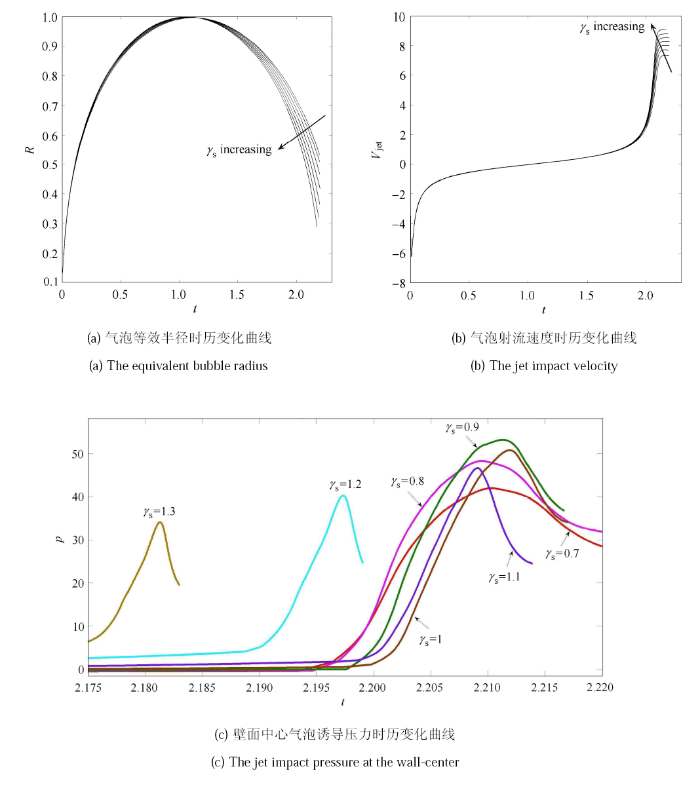
气泡在刚性边界附近的运动及载荷特性主要受到无量纲距离参数的影响[23, 28, 63],因此本节将针对距离参数在 [0.7, 1.3] 范围内的情况进行深入探讨. 图10(a) 所示为不同工况下气泡等效半径时历变化曲线,随着距离参数 $\gamma_{\rm s}$增大,气泡脉动速度增快 (周期减小),气泡射流砰击时刻提前,对应气泡体积减小. 可见刚性边界对气泡运动的抑制效应,该规律在前人的研究中有较多讨论,本文不做过多分析. 图10(b) 给出了气泡射流速度 (气泡底部节点的计算速度)时历变化曲线,随着 $\gamma_{\rm s}$增大,气泡射流速度增大. 这里需要说明的是,虽然刚性边界是诱导气泡射流的原因,但是气泡射流速度大小取决于射流的加速过程. 对于较小的 $\gamma _{\rm s}$, 气泡射流时刻提前,射流加速时间相对较短,射流速度最大值相对较小,但是气泡射流砰击位置与壁面更近(气标识码面之间的水膜更薄),因此气泡射流砰击压力与 $\gamma _{\rm s}$ 之间的关系并不是简单的单调递增或递减的关系. 图10(c) 给出了不同 $\gamma_{\rm s}$ 时射流砰击压力时历变化曲线,可以发现,当 $\gamma _{\rm s }= 0.9$ 时,壁面中心的压力峰值最大. 当 $\gamma _{\rm s} \geqslant 0.9$ 时,压力峰值随 $\gamma_{\rm s}$ 增大而减小,这主要是由于气泡与壁面之间的水层对射流砰击压力有明显的缓冲效应,水层越厚,缓冲效果越强. 当 $\gamma_{\rm s} \leqslant 0.9$ 时,气泡与壁面之间的水层厚度均较小,此时压力峰值取决于射流速度的大小,所以在这个范围内,压力峰值随 $\gamma_{\rm s}$ 减小而减小. 综上可见,气泡射流砰击压力的峰值与距离参数之间的变化关系中,存在一个临界值 ($\gamma_{\rm c } \approx 0.9$) 使壁面中心的压力峰值最大. 需要说明的是,射流砰击压力最大并不代表气泡的破坏力最强,还需要综合考虑气泡脉动载荷(气泡达到最小体积时刻释标识码力波,本节的系列算例中气泡并未达到最小体积)和其他影响因素,这也是未来需要深入研究的方向.
图10
图10
无量纲距离参数对气泡动力学行为的影响规律
Fig.10
The effects of the dimensionless stand-off parameter on bubble dynamics
6 其它边界条件
本文主要探讨了自由液面和无穷大刚性壁面附近气泡射流的形成机理,而实际应用中的边界条件形式更加复杂. 如果气泡的尺标识码于结构的尺度(如空泡和大尺度水利机械结构的耦合作用),则结构可简化为无穷大壁面. 如果结构尺度和气泡尺度相当,那么结构的几何形状、局部曲率等因素都将对气泡动力学行为产生重要的影响. Tomita等[64] 发现,气泡在正曲率的结构附近坍塌时产生的射流速度高于平板结构工况. Li等[65] 研究了气泡和球体的耦合作用,发现悬浮可移动球体附近的气泡射流速度相比固定球体工况更高. 若气泡在颗粒物表面产生,那么气泡溃灭阶段可能会与颗粒物表面脱离,产生背离颗粒物的射流,同时颗粒物朝相反方向运动[3-4].
若结构的刚度较小,剧烈脉动的气泡以及高速射流砰击将对结构造成明显的形变,弹性边界和气泡的耦合特性更为复杂. 不同刚 度的弹性边界附近气泡射流行为各异[66- 68]:若弹性边界的刚度极大,则气泡的行为趋于刚性壁面附近的气泡,产生朝向边界的射流;若弹性边界的刚度极小(背空), 则气泡行为趋于自由液面附近的气泡,产生背离边界的射流;若弹性边界的刚度适中,气泡可能会产生环形射流,进而导致气泡撕裂. Brujan 等[66]的研究指出,在结构表面敷设弹性覆盖层并不能降低空化的剥蚀速度. Li 等[17]在实验中发现,曲型弹性边界附近气泡在膨胀阶段就能产生背离边界的射流现象. 关于气泡与弹性边界的耦合特性仍是目前国际研究的热点和难点,其中仍有许多蕴含的力学机理尚未揭标识码也是气泡动力学领域重要的研究方向之一.
7 结论和展望
本文采用实验和数值计算相结合的手段,对脉动型气泡在自由液面和刚性边界下方的射流形成机理展开了深入研究. 实验中,采用标识码瞬时放电的方法产生单个脉动型气泡,利用高速摄影技术捕捉气泡非球状动力学行为,包括气泡膨胀、坍塌、射流形成、射流砰标识码状气泡撕裂和回弹等力学行为. 数值计算中,采用边界积分法模拟气泡的运动,采用改进的“(多)涡环模型”模拟环状气泡(包括撕裂)的动力学行为. 此外,引进辅助函数计算流场压力和速度,为揭示气泡射流机理提供了有力工具. 本文取得的主要结论如下:
(1) 近自由液面气泡射流初生的力学机理有两个:① 在气泡膨胀阶段后期,气泡与自由液面间的流场压力梯度最高,促使气泡顶部标识码缩;② 气泡顶部曲率相对最高,同样导致该位置的收缩速度更快. 射流加速的力学机理是:气泡与自由液面之间流体撞击形成驻点和局部高压区,进一步加速射流向下运动,同时自由液面的水冢向上生长.
(2) 近壁面气泡过度膨胀后,气泡与壁面之间逐渐形成低压区,而远离壁面的气泡表面附近流场压力(压力梯度)相对较高,因此气泡整标识码到一个朝向壁面的合力,这就是壁面吸引气泡的力学机制. 气泡坍塌阶段,远离壁面的气泡表面坍塌速度加快最明显,而且其附近流场中逐渐形成了局部高压区,促使射流逐渐形成. 该局部高压区和射流之间存在“正反馈效应”,所以气泡射流仅在坍塌后期的短时间内即可达到百米每秒的速度.
(3) 环状气泡阶段,射流砰击会造成局部高压区,其作用范围与射流宽度相当,随后射流宽度逐渐变大,射流速度逐渐衰减,砰击标识码值也逐渐减小.
(4) 气泡与刚性边界之间的无量纲距离参数 $\gamma_{\rm s}$ 是影响气泡射流砰击速度及载荷特性的重要参数, 在 $0.7 \leqslant \gamma \leqslant 1.3$ 范围内,随着 $\gamma $ 增加,气泡脉动周期减小,射流砰击时刻提前,对应时刻气泡体积减小,射流速度增加,气泡与壁面之间的水层厚度增加. 存在一个临界距离参数值 ($\gamma _{\rm c} \approx 0.9$) 使壁面中心的压力峰值最大.
(5) 实验中,射流砰击和气泡撕裂(环向射流的砰击)均可造成气泡表面的不稳定和不光滑,导致气泡内部的观测难度增标识码来有必要进一步改进实验技术及提升认知水平. 数值计算方面,未来有必要进一步考虑流体可压缩性、物质交换、热交换、流固耦合等因素对气泡运动及载荷的影响.
参考文献
Small-charge underwater explosion bubble experiments under various boundary conditions
Fully nonlinear 3D interaction of bubble dynamics and a submerged or floating structure
Plastic waste has become a major environmental problem. An increasing number of studies investigate microplastic particles with regard to their uptake and effects in cell culture systems. Individual plastic materials vary in their molecular structure, composition, size distribution, material density, and may also differ with respect to their toxicological effects. Plastic particles with lower densities than the cell culture medium, for example polyethylene (PE), pose a particular problem for in vitro assays as they float up during the incubation and thus do not contact the cells located on the bottom of the culture dish. We thus developed a practical and easy-to-use in vitro inverse cell culture model for investigating cellular effects of floating plastic particles. Cytotoxicity tests with floating PE particles were performed to demonstrate the utility of the inverted cell model. PE particles incubated in overhead culture were cytotoxic to HepG2 cells, while under the same cultivation conditions, except for inversion, no cytotoxicity occurred. These positive results demonstrate that inverted cell culture was required to detect the effects of PE particles and underlines the necessity to adapt cell culture conditions to the physicochemical properties of particles in order to obtain a more accurate estimate of the effects of floating particles on cells.
A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow
Transient interaction between a particle and an attached bubble with an application to cavitation in silt-laden flow
Numerical simulation of three dimensional cavitation shedding dynamics with special emphasis on cavitation-vortex interaction
Recent experiments showed that there is an interaction between the fluid vortex formation and cavitation, but the mechanism is still an open problem. In the present paper, the structure of the cavitating flow around a twisted hydrofoil was investigated numerically using the mass transfer cavitation model and the modified RNG k-epsilon model with a local density correction for turbulent eddy viscosity. The predicted three dimensional cavity structures and the shedding frequency agree fairly well with experimental observations. Three types of flow behavior along the suction side of the twisted hydrofoil are discussed. Further analysis of the flow field reveals that cavitation promotes vortex production and increases the boundary layer thickness with local separation and the flow unsteadiness. Finally, the influence of cavitation on the vorticity distribution is illustrated using the vorticity transport equation in a variable density flow and is demonstrated by the contribution of vortex stretching, vortex dilatation and baroclinic torque terms. (C) 2014 Elsevier Ltd.
单液滴内空化气泡的生长及溃灭研究
超空化燃油射流使得喷雾中部分燃油分裂液滴内含有空化气泡;空化气泡的生长及溃灭对液滴的分裂与雾化具有重要影响. 基于VOF 方法首次对超空化条件下燃油液滴内空化气泡的生长及溃灭过程进行了数值模拟. 通过研究发现,单液滴内空化气泡的生长过程可以按控制机理划分为表面张力控制阶段、综合竞争阶段和惯性力控制阶段;在第I 阶段,空泡的生长主要受表面张力的控制作用,惯性力对空泡生长的促进作用及黏性力对空泡生长的抑制作用可以忽略;在第II 阶段,空泡的生长受表面张力、惯性力及黏性力三者的综合作用,空泡的生长速率是促进空泡生长的惯性力和抑制空泡生长的表面张力及黏性力相互竞争、共同作用的结果;在第III 阶段,空泡的生长主要受惯性力的控制作用,抑制空泡生长的表面张力及黏性力的作用基本可以忽略. 单液滴内空化气泡的溃灭过程由多个溃灭阶段和反弹阶段构成,类似于有阻尼弹簧振子的振动过程;根据每个溃灭周期结束时空泡半径随时间的变化历程,可以将空泡的溃灭分为快速溃灭期、缓慢溃灭期以及稳定期;溃灭初期空泡溃灭压力的变化非常剧烈,但空泡溃灭体积的变化则要相对平缓得多;空泡反弹压力随时间的变化与空泡反弹体积随时间的变化基本对应.
Study on the growth and collapse of cavitation bubble within a droplet
超空化燃油射流使得喷雾中部分燃油分裂液滴内含有空化气泡;空化气泡的生长及溃灭对液滴的分裂与雾化具有重要影响. 基于VOF 方法首次对超空化条件下燃油液滴内空化气泡的生长及溃灭过程进行了数值模拟. 通过研究发现,单液滴内空化气泡的生长过程可以按控制机理划分为表面张力控制阶段、综合竞争阶段和惯性力控制阶段;在第I 阶段,空泡的生长主要受表面张力的控制作用,惯性力对空泡生长的促进作用及黏性力对空泡生长的抑制作用可以忽略;在第II 阶段,空泡的生长受表面张力、惯性力及黏性力三者的综合作用,空泡的生长速率是促进空泡生长的惯性力和抑制空泡生长的表面张力及黏性力相互竞争、共同作用的结果;在第III 阶段,空泡的生长主要受惯性力的控制作用,抑制空泡生长的表面张力及黏性力的作用基本可以忽略. 单液滴内空化气泡的溃灭过程由多个溃灭阶段和反弹阶段构成,类似于有阻尼弹簧振子的振动过程;根据每个溃灭周期结束时空泡半径随时间的变化历程,可以将空泡的溃灭分为快速溃灭期、缓慢溃灭期以及稳定期;溃灭初期空泡溃灭压力的变化非常剧烈,但空泡溃灭体积的变化则要相对平缓得多;空泡反弹压力随时间的变化与空泡反弹体积随时间的变化基本对应.
Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence
空化水动力学非定常特性研究进展及展望
Research progresses and prospects of unsteady hydrodynamics characteristics for cavitation
Bubble dynamics of a seismic airgun
The dynamics of the bubble generated by a four port model-scale seismic airgun in an open top tank are investigated. The airgun is fired at 50 and 100 bar and bubble images are captured with low- and highspeed photography. Forward- and back-lit photography allows close observation of the phenomena at the gas-water interface, and measurement of the radial growth, respectively. The development of the Rayleigh-Taylor Instability on the bubble's surface is identified. Field pressure measurements, synchronised in time with the radial bubble growth, are presented, and features of the emitted pressure signature are associated with the physical bubble dynamics. The experimental data is compared with an analytical prediction based on the Gilmore equation and good agreement is found for bubble radius, bubble period and the pressure pulse emitted at bubble collapse. The initial shock wave and first maximum velocity were over-predicted by this method. (c) 2014 Elsevier Inc.
Low frequency pneumatic seismic sources
Surface cleaning from laser-induced cavitation bubbles
Cavitation bubbles collapsing in the vicinity to a solid substrate induce intense micro-convection at the solid. Here we study the transient near-wall flows generated by single collapsing bubbles by chronoamperometric measurements synchronously coupled with high-speed imaging. The individual bubbles are created at confined positions by a focused laser pulse. They reach a maximum expansion radius of approximately 425μm. Several stand-off distances to the flat solid boundary are investigated and all distances are chosen sufficiently large that no gas phase of the expanding and collapsing bubble touches the solid directly. With a microelectrode embedded into the substrate, the time-resolved perturbations in the liquid shear layer are probed by means of a chronoamperometric technique. The measurements of electric current are synchronized with high-speed imaging of the bubble dynamics. The perturbations of the near-wall layer are found to result mainly from ring vortices created by the jetting bubble. Other bubble induced flows, such as the jet and flows following the radial bubble oscillations are perceptible with this technique, but show a minor influence at the stand-off distances investigated.
Mechanics of collapsing cavitation bubbles
A brief survey is given of the dynamical phenomena accompanying the collapse of cavitation bubbles. The discussion includes shock waves, microjets and the various ways in which collapsing bubbles produce damage.
Ultrasound microbubble contrast agents: Fundamentals and application to gene and drug delivery
For the first time, the thermal compression method is applied to effectively enhance the electrical conductivity of carbon nanotube thin films (CNTFs). With the assistance of heat and pressure on the CNTFs, the neighbor multiwalled carbon nanotubes (CNTs) start to link with each other, and then these separated CNTs are twined into a continuous film while the compression force, duration, and temperature are quite enough for the reaction. Under the compression temperature of 400°C and the compression force of 100 N for 50 min, the sheet resistance can be reduced from 17 to 0.9 k Ω/sq for the CNTFs with a thickness of 230 nm. Moreover, the effects of compression temperature and the duration of thermal compression on the conductivity of CNTF are also discussed in this work.
Bubble dynamics in soft and biological matter
Biologically inert gases play important roles in the biological functionality of proteins. However, researchers lack a full understanding of the effects of these gases since they are very chemically stable only weakly absorbed by biological tissues. By combining X-ray fluorescence, particle sizing and molecular dynamics (MD) simulations, this work shows that the aggregation of these inert gases near the hydrophobic active cavity of pepsin should lead to protein deactivation. Micro X-ray fluorescence spectra show that a pepsin solution can contain a high concentration of Xe or Kr after gassing, and that the gas concentrations decrease quickly with degassing time. Biological activity experiments indicate a reversible deactivation of the protein during this gassing and degassing. Meanwhile, the nanoparticle size measurements reveal a higher number of "nanoparticles" in gas-containing pepsin solution, also supporting the possible interaction between inert gases and the protein. Further, MD simulations indicate that gas molecules can aggregate into a tiny bubble shape near the hydrophobic active cavity of pepsin, suggesting a mechanism for reducing their biological function.
Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure
Cavitation nuclei in water exposed to transient pressures
Counter-jet formation of an expanding bubble near a curved elastic boundary
气泡多周期运动时引起的流场压力与速度
假设水下爆炸气泡的内部气体在膨胀收缩过程中满足绝热条件,周围流体无黏无旋不可压缩. 基于势流理论,采用边界元法研究气泡动力学行为,重点关注气泡引起的流场脉动载荷以及滞后流特性,给出了相关的理论推导和数值计算方法. 通过将数值结果与解析解、实验值进行对比,数值模型的收敛性和有效性能够得到保证. 利用编写的程序进行计算和分析,发现在气泡加速膨胀阶段,流场压力在气泡径向不一定是逐渐衰减,还有可能以先增后减的规律变化;气泡射流后,为了能够继续描述环状气泡的运动以及流场特性,将此时的流场分为无旋场和一个布置在气泡内部涡环的叠加,计算过程中采用了一些数值技巧处理气泡的拓扑结构,得以连续模拟多个周期的气泡运动. 环状气泡具有相对较高的上浮迁移速度,而且在其顶部和底部附近分别形成两个高压区,顶部的高压区峰值相对较大,底部的高压区范围相对较大. 环状气泡中心轴上的流场速度会在气泡中心有一个加速过程,在气泡顶部附近又迅速减小.
Numerical analysis on the velocity and pressure fields induced bymulti-oscillations of an underwater explosion bubble
假设水下爆炸气泡的内部气体在膨胀收缩过程中满足绝热条件,周围流体无黏无旋不可压缩. 基于势流理论,采用边界元法研究气泡动力学行为,重点关注气泡引起的流场脉动载荷以及滞后流特性,给出了相关的理论推导和数值计算方法. 通过将数值结果与解析解、实验值进行对比,数值模型的收敛性和有效性能够得到保证. 利用编写的程序进行计算和分析,发现在气泡加速膨胀阶段,流场压力在气泡径向不一定是逐渐衰减,还有可能以先增后减的规律变化;气泡射流后,为了能够继续描述环状气泡的运动以及流场特性,将此时的流场分为无旋场和一个布置在气泡内部涡环的叠加,计算过程中采用了一些数值技巧处理气泡的拓扑结构,得以连续模拟多个周期的气泡运动. 环状气泡具有相对较高的上浮迁移速度,而且在其顶部和底部附近分别形成两个高压区,顶部的高压区峰值相对较大,底部的高压区范围相对较大. 环状气泡中心轴上的流场速度会在气泡中心有一个加速过程,在气泡顶部附近又迅速减小.
爆炸气泡与自由水面相互作用动力学研究
为探究爆炸水幕形态与水下流场变化之间的联系,设计了小当量RDX装药水箱内爆炸实验系统. 采用两台高速录像机同步拍摄了气泡和水幕形态的演变过程,获得了三种典型气泡形态和六种典型水幕形态. 通过观察气泡-水面-空气之间的流场变化和理论分析,揭示了六种形态水幕的演变规律及其形成机理,并与电火花形成气泡实验结果进行了对比分析. 通过对不同比例深度条件下的气泡横向半径、纵向半径、膨胀时间、脉动周期、气泡边界运动过程等的统计分析,揭示了近水面水下爆炸形成气泡的动力学过程.
Dynamics of the interaction between explosion bubble and free surface
为探究爆炸水幕形态与水下流场变化之间的联系,设计了小当量RDX装药水箱内爆炸实验系统. 采用两台高速录像机同步拍摄了气泡和水幕形态的演变过程,获得了三种典型气泡形态和六种典型水幕形态. 通过观察气泡-水面-空气之间的流场变化和理论分析,揭示了六种形态水幕的演变规律及其形成机理,并与电火花形成气泡实验结果进行了对比分析. 通过对不同比例深度条件下的气泡横向半径、纵向半径、膨胀时间、脉动周期、气泡边界运动过程等的统计分析,揭示了近水面水下爆炸形成气泡的动力学过程.
Bubble interactions and bursting behaviors near a free surface
Experimental and numerical investigation of the dynamics of a coalesced oscillating bubble near a free surface
Experimental investigations of cavitation-bubble collapse in the neighbourhood of a solid boundary
Cavitation erosion by single laser-produced bubbles
Fast, thin jets from bubbles expanding and collapsing in extreme vicinity to a solid boundary: A numerical study
Research on the estimate formulas for underwater explosion bubble jet parameters
Numerical analysis of the jet stage of bubble near a solid wall using a front tracking method
Planar jets in collapsing cavitation bubbles
Analysis of pressure field generated by a collapsing bubble
Hig hintensity focused ultrasound (HIFU) has been applied for drug delivery in various disease conditions. Delivery of antibacterial-nanoparticles into dental hard tissues may open up new avenues in the treatment of dental infections. However, the basic mechanism of bubble dynamics, its characterization, and working parameters for effective delivery of nanoparticles, warrants further understanding. This study was conducted to highlight the basic concept of HIFU and the associated bubble dynamics for the delivery of nanoparticles. Characterization experiments to deliver micro-scale particles into simulated tubular channels, activity of ultrasonic bubbles, and pressure measurement inside the HIFU system were conducted. Subsequently, experiments were carried out to test the ability of HIFU to deliver nanoparticles into human dentine using field emission scanning electron micrographs (FESEM) and elemental dispersive X-ray analysis (EDX). The characterization experiments showed that the bubbles collapsing at the opening of tubular channels were able to propel particles along their whole length. The pressure measured showed sufficient negative and positive pressure suggesting that the bubble grew to a certain size before collapsing, thus enabling the particles to be pushed. The FESEM and EDX analysis highlighted the ability of HIFU to deliver nanoparticles deep within the dentinal tubules. This study highlighted the characteristics and the mechanism involved of the bubbles generated by the HIFU and their capability to deliver nanoparticles.
High speed observation of damage created by a collapse of a single cavitation bubble
The collapse of cavitation bubbles and the pressures thereby produced against solid boundaries. Philosophical Transactions of the Royal Society of London A: Mathematical,
Transient cavities near boundaries. Part 1. Rigid boundary
Experimental study on bubble dynamics subject to buoyancy
Pulsating, buoyant bubbles close to a rigid boundary and near the null final Kelvin impulse state
Growth and collapse of a vapour cavity near a free surface
Transient cavities near boundaries Part 2. Free surface
Dynamic characteristics of large scale spark bubbles close to different boundaries
A boundary element method for the simulation of non-spherical bubbles and their interactions near a free surface
Boundary element analysis of the droplet dynamics induced by spark-generated bubble
Spark bubble droplet generation (SBDG) method is the most recently developed drop-on-demand droplet generation technique where the oscillation of a spark-generated bubble near a circular aperture causes a single droplet quite smaller than the aperture to form and break off. This paper investigates the fluid dynamics of the droplet generated through a flat plate aperture as well as through the nozzle of an axisymmetric chamber using boundary element method and high-speed photography. The results revealed that the bottom wall of the chamber would strongly influence the behavior of the bubble oscillating inside. In addition, it was found that with the same normalized nozzle size and bubble distance from air-liquid interface, a relatively smaller and faster droplet is generated from the chamber nozzle as compared with that formed through the flat plate aperture. Furthermore, although the droplet size decreases, its pinch-off time was found to increase by increasing the size of chamber feeder canal. (c) 2012 Elsevier Ltd.
Simulation of bubble expansion and collapse in the vicinity of a free surface
The motion of a 3D toroidal bubble and its interaction with a free surface near an inclined boundary
3D full coupling model for strong interaction between a pulsating bubble and a movable sphere
Experimental investigation of bubble dynamics near the bilge with a circular opening
Highly dependent on boundary conditions, the behaviors of underwater explosion (UNDEX) bubbles would be quite unusual near boundaries that are discontinuous with abrupt changes in shape, e.g. ship structures that have already been deformed by previous attacks. The oscillation features of the UNDEX bubble near the bilge with a circular opening representing previous deformation are studied experimentally with electric-spark-generated bubbles and high-speed photographing. The bubble behaviors are found highly dependent on two non-dimensional variables, D and 0, representing the opening-bubble distance and the opening diameter, respectively. Seven distinctive oscillation scenarios are summarized from 180 experiments, namely the 'rim-constrained oscillation', the 'inward jet', the 'outward jet', the 'bump and dimple', the 'quasi-spherical oscillation', the 'spherical oscillation with jet' and the 'spherical oscillation without jet'. The occurrence domains of the scenarios are identified as functions of D and P. Significantly affected by the opening, the bubble behaviors are quite different from that near a non-opening bilge; the bubble jet might not be formed, or even develop from inside the bilge, which indicates that the bubble load on the bilge should be re-evaluated. Finally the speeds, initiation time and displacements of the jets in different scenarios are measured and noticeable variation trends are found. (C) 2013 Published by Elsevier Ltd.
Numerical study on the interaction between underwater explosion bubble and a moveable plate with basic characteristics of a sandwich structure
A three-dimensional modeling for coalescence of multiple cavitation bubbles near a rigid wall
The art, craft and science of modelling jet impact in a collapsing cavitation bubble
//
Experimental and numerical study of transient bubble-elastic membrane interaction
Membrane-targeting domains play crucial roles in the recruitment of signalling molecules to the plasma membrane. For most peripheral proteins, the protein-to-membrane interaction is transient. After proteins dissociate from the membrane they have been observed to rebind following brief excursions in the bulk solution. Such membrane hops can have broad implications for the efficiency of reactions on membranes. We study the diffusion of membrane-targeting C2 domains using single-molecule tracking in supported lipid bilayers. The ensemble-averaged mean square displacement (MSD) exhibits superdiffusive behaviour. However, traditional time-averaged MSD analysis of individual trajectories remains linear and does not reveal superdiffusion. Our observations are explained in terms of bulk excursions that introduce jumps with a heavy-tail distribution. These hopping events allow proteins to explore large areas in a short time. The experimental results are shown to be consistent with analytical models of bulk-mediated diffusion and numerical simulations.
Strong interaction between a buoyancy bubble and a free surface
Non-spherical bubble dynamics of underwater explosions in a compressible fluid
The acceleration of solid particles subjected to cavitation nucleation
Study on splitting of a toroidal bubble near a rigid boundary
The formation of toroidal bubbles upon the collapse of transient cavities
The final stage of the collapse of a cavitation bubble near a rigid wall
Nonlinear interaction between gas bubble and free surface
Active development of quantum informational components such as quantum computers and quantum key distribution systems requires parameter characterization of single photon detectors. A key property of the single photon detectors is detection efficiency. One of the methods of the detection efficiency measurement, as listed in the international standard ETSI, is the reference-free twin-photon-based Klyshko method. The signal-to-noise ratio (SNR) of this method depends on the combination of the pump wavelength, the nonlinear crystal's axis angle, and the type of detector's sensitive element. When the combination is difficult, one has to deal with the low SNR of the detector counts measurement. To gain the high SNR, one has to average the long record complicated with the "random telegraph signal" noise. This type of noise exhibits high spectral density at a zero frequency, where simple averaging works. The heterodyne based method we have proposed is to perform averaging at the higher frequency of the modulation introduced to the standard Klyshko measurement scheme. The method was numerically simulated and experimentally tested. The 14 times improvement in SNR for the proposed method relative to the simple averaging was demonstrated by the numerical simulation and confirmed experimentally.
Bubble-sphere interaction beneath a free surface
Because of the antioxidant activity of vitamin C (Vit C) polar heads, they can be used as a protective agent for fatty acids. Hence, the study on the growth of Vit C/stearic acid (SA) mixed binary films at air-water interface (known as Langmuir monolayer) and air-solid interface (known as Langmuir-Blodgett films) is of paramount interest. Although Vit C is situated at subsurface beneath SA molecules and interacts via hydrogen bonding between the hydroxyl groups of Vit C and SA, several Vit C molecules may infiltrate within SA two-dimensional matrix at the air-water interface. The increased mole fraction of Vit C (0.125-0.5) and the reduction of temperature (from 22 to 10 °C) of the subphase water result in an increase in the amount of adsorbed Vit C at the air-water interface. The surface pressure (π)-area (A) isotherms illustrate that such inclusion of Vit C provokes a spreading out of Vit C/SA binary monolayers, which leads to an alteration of different physicochemical parameters such as elasticity, Gibbs free energy of mixing, enthalpy, entropy, interaction energy parameter, and activity coefficient. However, being polar in nature, the transfer of pure Vit C on substrates gets affected. It can be transferred onto substrate by mixing suitably with SA as confirmed by infrared spectra. Their structures, extracted X-ray reflectivity, and atomic force microscopy (topography and phase imaging) are found to be strongly dependent on the nature of the substrate (hydrophilic and hydrophobic).
The dynamics of underwater explosions
[PhD Thesis].Very little is known about marine mammal susceptibility to primary blast injury (PBI) except in rare cases of opportunistic studies. As a result, traditional analysis techniques relied on methods developed more than 30 years ago using terrestrial mammals as surrogates. Modeling tools available today have the computing power to vastly improve calculation of safe ranges and injury zones from underwater explosions (UNDEX) employing morphologically accurate proxies with material properties similar to marine mammal tissues. The Dynamic System Mechanics Advanced Simulation (DYSMAS) fluid-structure interaction (FSI) software is being used to simulate the complex phenomena of UNDEX, shock wave, and bubble pulse propagation through the water and transmission of energy to a cetacean focusing on the dynamic response of the thoracic cavity and air-filled lungs to a shock wave. The approach integrates fluid and structural analyses with the material properties of blubber, bone, and muscle using marine mammal morphometrics to eliminate unnecessary assumptions made during more traditional approaches to analysis developed before these types of data and computational power were available. DYSMAS analyses of a 1D gas bubble surrounded by water was found to closely match the classical bubble dynamics models. Further, DYSMAS models of a spherical gas bubble surrounded by tissue and rib structure demonstrate a global radial oscillation of the gas bubble, but also show significant local deflection and material strain in response to the UNDEX loading. The intended result of the investigation is an improved and scientifically defensible understanding of the effects of UNDEX on marine mammals. Anat Rec, 2018. © 2018 Wiley Periodicals, Inc. Anat Rec, 302:718-734, 2019. Published 2018. This article is a U.S. Government work and is in the public domain in the USA.
Simulation of bubble dynamics near a plate with an aperture in a vertical cylinder using a combined boundary element-finite difference method
Experiments on bubble dynamics between a free surface and a rigid wall
A high-order accurate shock- and interface-capturing scheme is used to simulate the collapse of a gas bubble in water. In order to better understand the damage caused by collapsing bubbles, the dynamics of the shock-induced and Rayleigh collapse of a bubble near a planar rigid surface and in a free field are analysed. Collapse times, bubble displacements, interfacial velocities and surface pressures are quantified as a function of the pressure ratio driving the collapse and of the initial bubble stand-off distance from the wall; these quantities are compared to the available theory and experiments and show good agreement with the data for both the bubble dynamics and the propagation of the shock emitted upon the collapse. Non-spherical collapse involves the formation of a re-entrant jet directed towards the wall or in the direction of propagation of the incoming shock. In shock-induced collapse, very high jet velocities can be achieved, and the finite time for shock propagation through the bubble may be non-negligible compared to the collapse time for the pressure ratios of interest. Several types of shock waves are generated during the collapse, including precursor and water-hammer shocks that arise from the re-entrant jet formation and its impact upon the distal side of the bubble, respectively. The water-hammer shock can generate very high pressures on the wall, far exceeding those from the incident shock. The potential damage to the neighbouring surface is quantified by measuring the wall pressure. The range of stand-off distances and the surface area for which amplification of the incident shock due to bubble collapse occurs is determined.
不同环境下气泡脉动特性实验研究
水下爆炸气泡对舰船结构造成严重的毁伤, 海上实船爆炸实验是考核水下爆炸气泡对舰船毁伤威力最直接、最有效的方法, 然而真实情况的舰船水下爆炸实验难以进行.为此, 在已有研究成果的基础上, 设计实验电路, 利用电容在相对较低的电压下放电打火产生的电火花气泡来模拟水下爆炸气泡, 设计多组实验工况来模拟气泡在不同环境下的运动特性. 研究气泡在不同环境下的脉动特性、射流特征, 揭示一些特殊的实验现象, 总结环境对气泡运动的影响规律.
Experimental study on bubble pulse features under different circumstances
水下爆炸气泡对舰船结构造成严重的毁伤, 海上实船爆炸实验是考核水下爆炸气泡对舰船毁伤威力最直接、最有效的方法, 然而真实情况的舰船水下爆炸实验难以进行.为此, 在已有研究成果的基础上, 设计实验电路, 利用电容在相对较低的电压下放电打火产生的电火花气泡来模拟水下爆炸气泡, 设计多组实验工况来模拟气泡在不同环境下的运动特性. 研究气泡在不同环境下的脉动特性、射流特征, 揭示一些特殊的实验现象, 总结环境对气泡运动的影响规律.
Study on the interactions between two identical oscillation bubbles and a free surface in a tank
Cavitation bubble dynamics--new tools for an intricate problem
The inner world of a collapsing bubble
Optical and acoustic investigations of the dynamics of laser-produced cavitation bubbles near a solid boundary
Numerical analysis of the bubble jet impact on a rigid wall
Growth and collapse of cavitation bubbles near a curved rigid boundary
Nonlinear interaction between a gas bubble and a suspended sphere
Dynamics of laser-induced cavitation bubbles near elastic boundaries: influence of the elastic modulus
An oscillating bubble near an elastic material
Following previous work on the dynamics of an oscillating bubble near a bio-material (Ohl et al 2009 Phys. Med. Biol. 54 6313-36) and the interaction of a bubble with a shockwave (Klaseboer et al 2007 J. Fluid Mech. 593 33-56), the present work concerns the interaction of a gas bubble with a traveling shock wave (such as from a lithotripter) in the vicinity of bio-materials such as fat, skin, muscle, cornea, cartilage, and bone. The bubble is situated in water (to represent a water-like biofluid). The bubble collapses are not spherically symmetric, but tend to feature a high speed jet. A few simulations are performed and compared with available experimental observations from Sankin and Zhong (2006 Phys. Rev. E 74 046304). The collapses of cavitation bubbles (created by laser in the experiment) near an elastic membrane when hit by a lithotripter shock wave are correctly captured by the simulation. This is followed by a more systematic study of the effects involved concerning shockwave bubble biomaterial interactions. If a subsequent rarefaction wave hits the collapsed bubble, it will re-expand to a very large size straining the bio-materials nearby before collapsing once again. It is noted that, for hard bio-material like bone, reflection of the shock wave at the bone-water interface can affect the bubble dynamics. Also the initial size of the bubble has a significant effect. Large bubbles (∼1 mm) will split into smaller bubbles, while small bubbles collapse with a high speed jet in the travel direction of the shock wave. The numerical model offers a computationally efficient way of understanding the complex phenomena involving the interplay of a bubble, a shock wave, and a nearby bio-material.