引言
自由涡尾迹(free vortex wake,FVW)方法中,最基本的工作就是求解尾涡对空间点的诱导速度场,通常是将涡线离散成微涡元求解再数值叠加.涡元可以是曲线涡元,也可以简化为直线涡元.曲线涡元考虑了涡线的弯曲,在物理上更接近于实际,但曲线涡元对空间点的诱导速度难以获得解析解.直线涡元比较简单,且具有解析解,所以一般情况下均采用直线涡元. 直线涡元的求解通常是运用Biot-Sarvart定律.当空间点接近涡线时,由Biot-Sarvart定律诱导速度公式计算得到的诱导速度值会迅速增大.如果空间点正好处在涡线上,即自诱导计算,计算结果会产生奇点.为避免这样的数值扰动,在计算风力机尾迹的诱导速度时,必须考虑黏性的影响,其方法是引入涡核模型.
涡核模型对涡尾迹方法计算风力机气动性能影响很大[1-5]. 涡核模型分层流模型和湍流模型,传统的层流模型有Rankine模型[6]、Scully模型[7]和Lamb-Oseen模型[8],其中Lamb-Oseen模型在涡尾迹方法中应用最为广泛[9-11].近年来,一些湍流涡核模型也开始应用在FVW方法中,如Ramasamy-Leishman模型[12]、Vatistas模型[13-14]和$\beta $-Vatistas模型[1]. 在应用涡核模型时,涡核尺寸的确定至关重要.涡核尺寸包括初始涡核半径和它在尾迹中的变化情况.不少学者对初始涡核半径对涡尾迹方法计算风力机气动特性的影响做了一些研究.Basuno[15]采用预定涡尾迹方法研究了涡核尺寸对垂直轴风力机气动性能计算的影响,表明涡核太小得不到收敛解.换而言之,涡核尺寸必须足够大才能够消除数值奇点.Landahl[16]指出,涡在破碎之前,涡核尺寸的量级约是0.06倍弦长.但是,Miller[17]研究得到,当涡核尺寸增加到0.6倍弦长时,气动特性才可能与实验数据相吻合.因此,对于风力机叶片,为了避免取值的随意性,Miller建议可将涡核尺寸固定在0.6倍弦长.尾涡的耗散效应是由于流体的黏性引起,与尾流中湍流度变化也密切相关.Dobrev等[18]采用激光技术对风力机尾涡结构进行了详细的分析,发现风力机叶尖涡的湍流度要比直升机桨尖涡的湍流度大,且随着尾迹寿命角的增大,流动的湍流度变小. 在FVW方法中,耗散效应通常采用涡核半径随时间增长的数学模型来表达.Bhagwat等[19-20]提出一种广义的黏性涡核模型,模型中总黏度与运动黏度之比是有关涡雷诺数的函数,是准确模拟涡核增长的关键.通过大量旋翼叶尖涡流场测量实验,确定模型中的经验常数$a_{1}$在0.000,05$\sim$0.000,2之间,但到目前为止,没有任何实验来说明风力机叶尖涡模拟时$a_{1}$的取值.由于风力机叶尖涡的湍流度要比直升机桨尖涡的湍流度大[21],所以在采用FVW方法计算时,$a_{1}$通常取0.000,2[2,22-23].
本文通过分析最广泛应用的Lamb-Oseen模型的涡核尺寸(包括涡核初始半径和常数$a_{1}$)对FVW方法计算风力机气动特性的影响,来讨论涡核尺寸的取值问题. 不仅通过对风力机气动载荷的分析,还分析了叶尖涡强度变化以及叶尖涡结构和涡核位置的发展.
1 FVW模型
式中,${\pmb r}$为涡线节点位置向量,m;$\varOmega $为风轮转速,rad/s;${\pmb V}_{\infty }$为自由流速度,m/s;${\pmb V}_{\rm ind }$为流场中所有涡线对该节点的总诱导速度,m/s,一般来说取周围节点诱导速度的平均值.
2 涡核模型
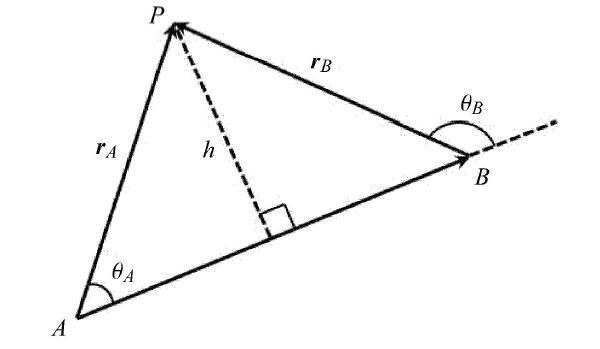
考虑一段有限长度的直线涡元,如图1所示,涡元的起点和终点分别为$A$和$B$,涡元强度用环量$\varGamma $表示. 由Biot-Sarvart定律确定的涡元对空间点P的诱导速度的解析表达式为
图1
式中各变量含义见图1标注.
当点$P$无限接近涡元($h \to $0)或者正好落在涡元上($h =0$),式(2)会得出一个无穷大速度,这会导致FVW方法无法收敛. 为了避免此现象,需要用涡核模型进行修正. 本文采用经典的Lamb-Oseen模型,即式(2)中$h$用下式$h'$代替
式中$r_{\rm c}$为涡核半径.
2.1 耗散效应
式中, $\alpha_{\rm L }= 1.256,43$为 Lamb-Oseen常数,表征了涡核的增大速率; $\nu $为流体的层流运动黏性系数;$\zeta $为尾迹寿命角,rad;$r_{0}$为寿命角为零时的涡核半径,即初始涡核半径,m; $\delta$为总黏度与运动黏度之比.
湍流对于涡核半径的影响目前尚不是很清楚,很多学者的研究认为涡的耗散主要受黏性效应控制,涡核半径增长率与涡雷诺数($Re_v = \varGamma / \nu )$相关,且涡核的湍流效应在涡雷诺数大于10$^{5}$时才很明显. $\delta $可以写成涡雷诺数的表达式
式中,$a_{1}$为经验常数.
2.2 拉伸效应
风力机尾流中流体速度减小,尾迹沿径向扩张,使得涡线向下游移动时受到拉力,涡元长度变长. 因为对流场作不可压缩假设,根据质量守恒定律,涡元拉伸使得涡核半径变小. 拉伸前涡元长度为$l$,涡核半径为$r_{\rm c}$,定义涡元在$\Delta t$时间内的线应变为
应用Ananthan等[29]提出了涡线拉伸效应理论,最终考虑拉伸后,有效涡核半径随尾迹寿命角变化的表达式为
2.3 影响涡核尺寸的关键参数
FVW模型计算时,涡核尺寸是按照式(7)变化的. 式中的初始涡核半径$r_{0}$和经验常数$a_{1}$是影响涡核尺寸的关键参数,但是并没有明确的理论值或者实验值. 学者们在计算时,基本是在前人研究的基础上,经验的对两个参数进行取值. 一般地,$r_{0}$取0.6倍弦长;$a_{1}$值则是根据旋翼研究中的结果,取$a_{1}=0.000,2$. 本文在这些经验取值的基础上,进一步分析两个参数对FVW模型计算风力机气动特性的影响.
3 结果与讨论
采用美国可再生能源国家实验室第6期非定常空气动力试验(NREL Phase VI)风力机[30]作为算例.首先,根据功率系数$C_{\rm P}$随初始涡核半径的变化以及不同初始涡核半径下的叶尖涡涡量随尾迹寿命角的变化,初步确定初始涡核半径的范围;其次,在合理的初始涡核半径内,综合考虑对风力机低速轴扭矩和叶尖涡涡量黏性耗散的影响,讨论$a_{1}$的取值.
3.1 初始涡核半径的确定
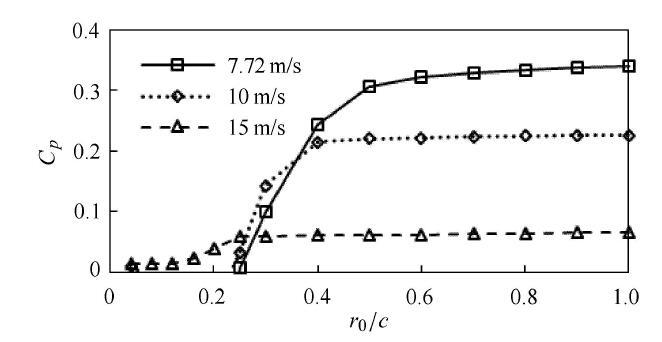
图2给出了7.72,m/s, 10,m/s和15,m/s风速下风力机功率系数与初始涡核半径的关系,$a_{1} = 0.000,2$. 可以看出,当初始涡核半径小于弦长$c$的50%时,功率系数受到较大影响,而且收敛极不稳定,以至于功率系数预估不准确;当大于0.5$c$时,功率系数逐渐趋于一个稳定值,说明在进行叶片气动性能计算时,初始涡核大小的取值以不小于0.5$c$为宜.
图2
图2
不同风速下功率系数随初始涡核半径的变化情况
Fig. 2
The power coefficient along with the initial vortex core size at different wind speeds
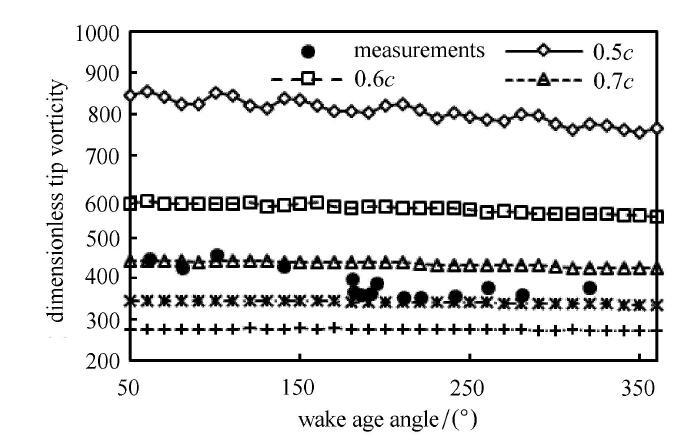
式中,$\omega_{\rm vor}$为 叶尖涡涡量,$B$为 叶片数目,$D$为 风轮直径.计算初始涡核半径从0.5$c$至0.9$c$情况下无量纲叶尖 涡涡量随尾迹寿命角的变化,如图3所示.可以看出,随着尾迹寿命角的增大,涡量整体呈下降的趋势,但下降趋势随着初始涡核半径的增加越来越不明显.涡量的变化梯度均小于实验结果, 这是因为经验常数$a_{1} = 0.000,2$取值偏小,使得黏度比$\delta $偏小.此外,当初始涡核半径介于0.7$c$与0.8$c$之间时,叶尖涡涡量平均值与实验值接近.考虑增加$a_{1}$即黏性耗散效应加强后,涡量平均值会有所下降,所以初步确定初始涡核半径为0.6$c$与0.7$c$之间,这与文献[17]的研究结论基本吻合.
图3
图3
无量纲叶尖涡涡量随尾迹寿命角变化情况
Fig. 3
Development of dimensionless vorticity levels of the blade tip vortex along with the wake age angle
3.2 黏性耗散参数确定
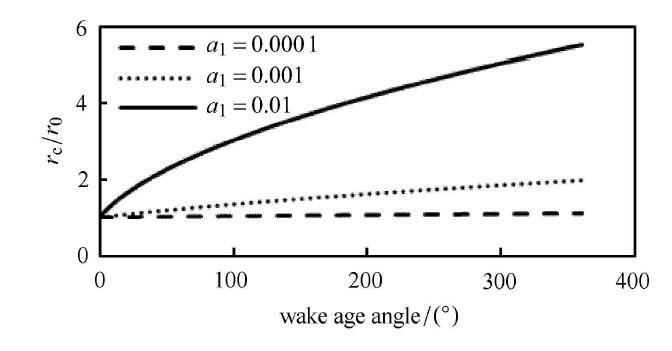
黏性耗散效应在FVW数值计算时主要体现为涡核半径随时间增长,其中经验常数$a_{1}$的取值比较关键.图4给出了$a_{1}$取不同 值时涡核半径与尾迹寿命角的变化情况.首先,涡核半径随着尾迹寿命角的增大而增大;其次,当$a_{1}$取很小值(0.000,1)时,涡核半径几乎不变,相当于无黏流模拟,当$a_{1}$增大时,黏度比$\delta $增大,涡黏性增强,涡核半径增大速率 变大.
图4
图4
不同$a_{1}$取值时涡核半径随尾迹寿命角的变化
Fig. 4
The vortex core radius along with wake age angle under different values of $a_{1}$
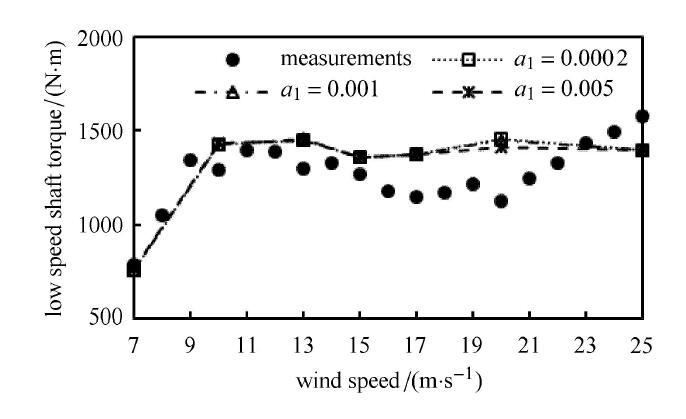
在分析经验常数$a_{1}$的取值对叶尖涡耗散的影响之前,先分析其对风轮整体气动载荷的影响.图5给出了$r_{0}$= 0.6$c$时, 不同$a_{1}$值时低速轴转矩随风速的变化,实验数据来自NREL PhaseVI实验结果[33]. 计算结果随风速的总体变化趋势与实验值一致,小风速下低速轴转矩与实验值吻合较好,大风速下,FVW方法中采用的静态的二维翼型数据加上三维旋转效应修正很难准确预估叶片失速甚至深失速状态下的气动特性,所以计算结果与实验值略有差别.此外可以显著看出,$a_{1}$值改变,低速轴转矩并没有显著变化,说明$a_{1}$值对风力机的整体气动载荷影响不大,所以之前学者们根据旋翼研究中的结果,取$a_{1 } = 0.000,2$,对风力机叶片气动载荷的计算没有 影响.
图5
图5
不同$a_{1}$取值时低速轴转矩随风速的变化
Fig. 5
The variation of low-speed shaft torque along with the wind speed under different values of $a_{1}$
图6
图6
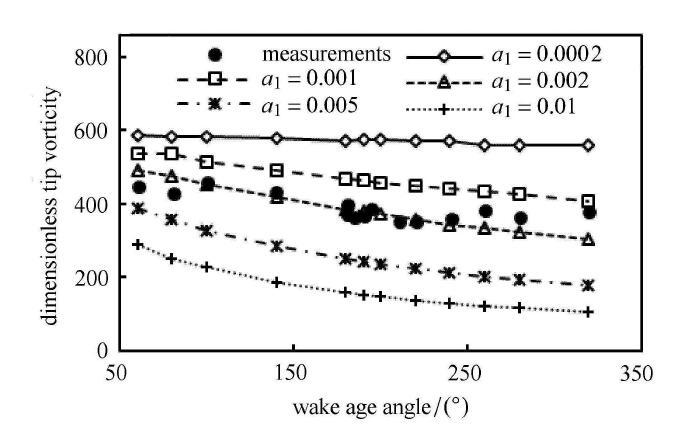
不同$a_{1}$取值时无量纲叶尖涡涡量随尾迹寿命角变化情况($r_{0} = 0.6 c$)
Fig. 6
Development of dimensionless vorticity levels of the blade tip vortex along with the wake age angle under different values of $a_{1}$($r_{0} = 0.6 c$)
图7
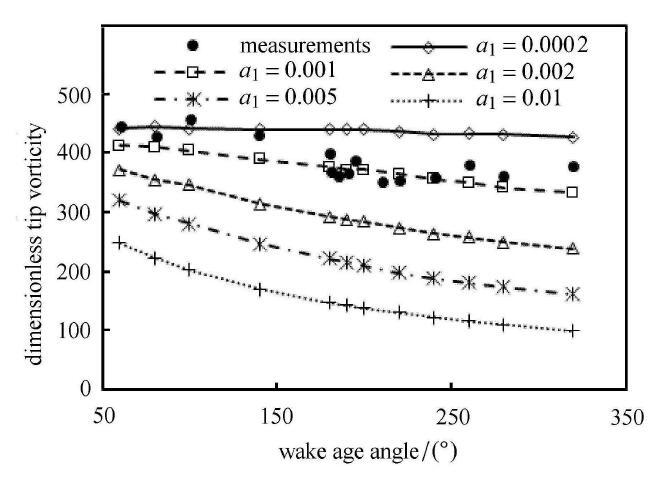
图7
不同$a_{1}$取值时无量纲叶尖涡涡量随尾迹寿命角变化情况($r_{0} = 0.7 c$)
Fig. 7
Development of dimensionless vorticity levels of the blade tip vortex along with the wake age angle under different values of $a_{1}$($r_{0} = 0.7 c)$
3.3 涡核尺寸对叶尖涡的影响
图8
图9
图9
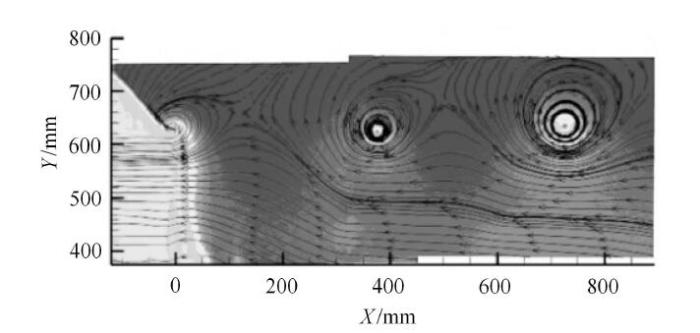
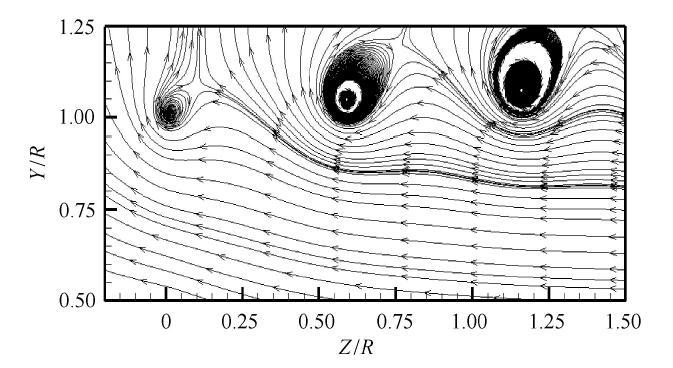
扣除来流速度的叶尖区域流线计算结果($r_{0} = 0.6 c$, $a_{1 } = 0.002$)
Fig. 9
Computational result of streamlines in blade tip region with the wind speed subtracted from the local velocity ($r_{0} = 0.6 c$, $a_{1 } = 0.002$)
图10
图10
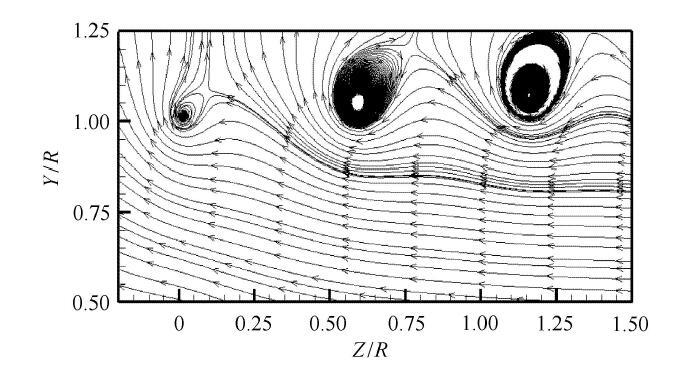
扣除来流速度的叶尖区域流线计算结果 ($r_{0} = 0.7 c$, $a_{1 } = 0.001$)
Fig. 10
Computational result of streamlines in blade tip region with the wind speed subtracted from the local velocity ($r_{0} = 0.7 c$, $a_{1 } = 0.001$)
图11和图12分别给出了$r_{0} = 0.6 c$,$a_{1 } = 0.000,2$和$r_{0} = 0.4 c$, $a_{1 } =0.000,2$时的叶尖涡流场. 对比图11和图9,$r_{0}$相同,$a_{1}$不同,叶尖涡结构和叶片附近流场几乎没有变化,所以$a_{1}$对叶片总体气动载荷预估影响不大,与图5的分析基本一致.对比图12和图11,$r_{0}$不同,$a_{1}$相同,由于初始涡核半径的改变,叶尖涡结构和叶片附近流场出现明显变化,尤其是叶片附近出现了额外的集中涡,严重影响了叶片总体气动载荷的预估,这与图2的分析也保持一致.此外,$r_{0}$减小,叶尖涡径向位置扩张有轻微的增加.
图11
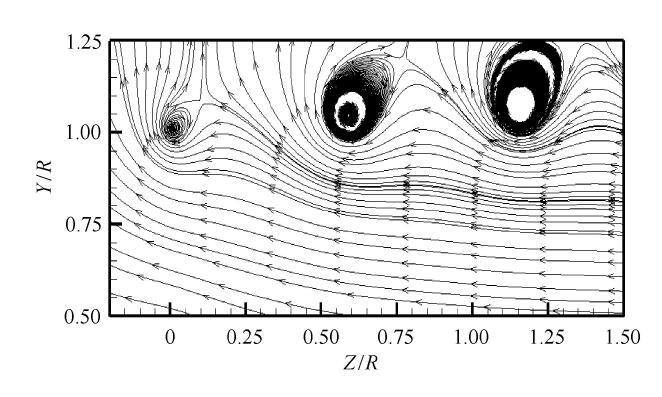
图11
扣除来流速度的叶尖区域流线计算结果($r_{0} = 0.6 c$, $a_{1 } = 0.000,2$)
Fig. 11
Computational result of streamlines in blade tip region with the wind speed subtracted from the local velocity ($r_{0} = 0.6 c$, $a_{1 } = 0.000,2$)
图12
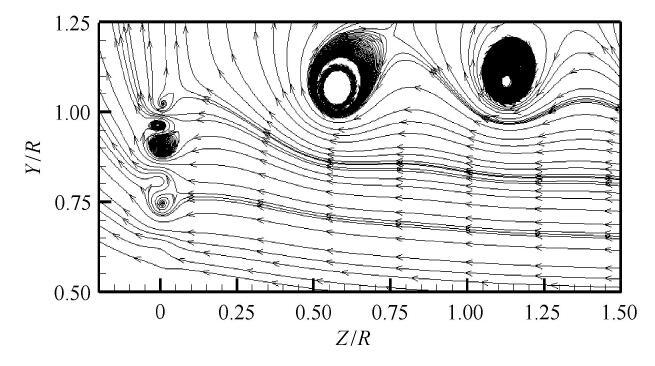
图12
扣除来流速度的叶尖区域流线计算结果($r_{0} = 0.4 c$, $a_{1 } = 0.000,2$)
Fig. 12
Computational result of streamlines in blade tip region with the wind speed subtracted from the local velocity ($r_{0} = 0.4 c$, $a_{1 } = 0.000,2$)
图13
图13
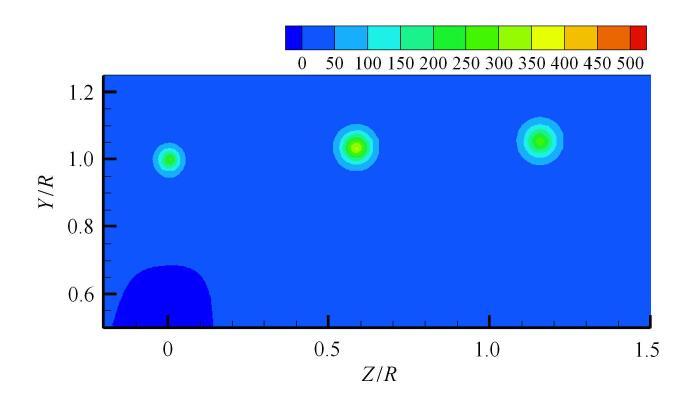
叶尖涡涡量计算结果($r_{0} = 0.6 c$, $a_{1 } = 0.002$)
Fig. 13
Vorticity result of tip vortex ($r_{0} = 0.6 c$, $a_{1 } = 0.002$)
图14
图14
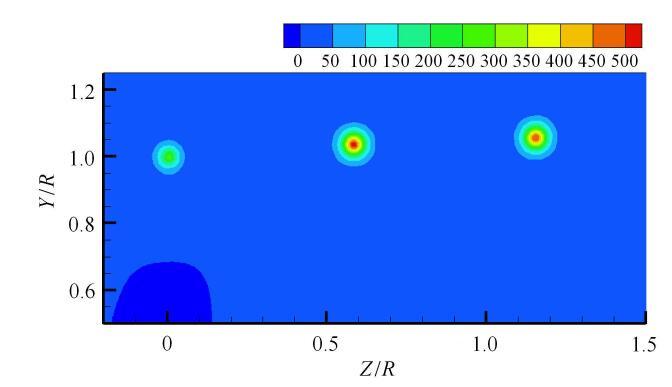
叶尖涡涡量计算结果($r_{0} = 0.6 c$, $a_{1 } = 0.000,2$)
Fig. 14
Vorticity result of tip vortex ($r_{0} = 0.6 c$, $a_{1 } = 0.000,2$)
图15
图15
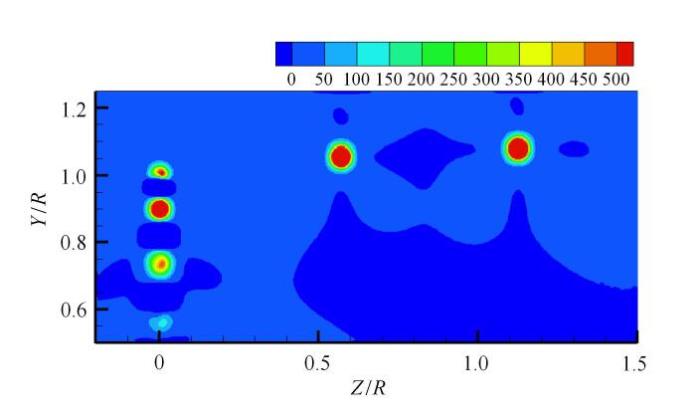
叶尖涡涡量计算结果($r_{0} = 0.4 c$, $a_{1 } = 0.000,2$)
Fig. 15
Vorticity result of tip vortex ($r_{0} = 0.4 c$, $a_{1 } = 0.000,2$)
4 结论
本文采用FVW方法,通过分析风轮气动载荷和尾流场涡结构和涡量分布的变化来探讨Lamb-Oseen涡模型中涡核初始半径和耗散经验常数$a_{1}$的取值问题. 得到以下结论:
(1)初始涡核半径$r_{0}$小于0.5$c$时,叶片气动载荷预估不准确,FVW方法收敛性差;$r_{0}$大于0.5$c$时,叶片气动载荷预估准确,FVW方法收敛性好;基于叶尖涡涡量分析,$r_{0}$取值在0.6$c$与0.7$c$之间比较合适.
(2)耗散经验常数$a_{1}$越大,叶尖涡涡量平均值下降,耗散速率增大;不同的$r_{0}$取值对应的$a_{1}$取值也不相同,当$r_{0}= 0.6 c$,$a_{1 } = 0.002$和$r_{0} = 0.7 c$,$a_{1 } = 0.001$时,叶片气动载荷、叶尖涡涡量耗散特性、叶尖涡结构均与实验结果比较吻合.
(3)$r_{0}$主要影响叶片附近涡量场分布和叶尖涡形状,从而对风轮整体气动载荷产生影响;$a_{1}$主要影响风轮下游尾流场叶尖涡的耗散特性,而对风轮整体气动载荷影响不大.
参考文献
Application of a turbulent vortex core model in the free vortex wake scheme to predict wind turbine aerodynamics
A simplified free vortex wake model of wind turbines for axial steady conditions
A novel hybrid free-wake model for wind turbine performance and wake evolution
涡模型对风力机气动特性的影响研究
Investigation of effects of vortex models on wind turbine aerodynamic characteristics
基于升力面和全自由涡尾迹的风力机气动模型及其参数影响
Predictions of wind turbine aerodynamics based on lifting surface theory with fully free vortex and the influence of the parameters
A simpler model for concentrated vortices
Computation of helicopter rotor wake geometry and its influence on rotor harmonic airloads. [PhD Thesis]
Unsteady aerodynamic analysis for offshore floating wind turbines under different wind conditions
Study on the aeroelastic responses of a wind turbine using a coupled multibody-FVW method
基于改进型升力面自由涡尾迹法的风力机性能研究
Wind turbine aerodynamic performance simulation based on improved lifting surface freewake method
Evaluation of the lifting line vortex model approximation for estimating the local blade flow fields in horizontal-axis wind turbines
Validation of a free vortex wake model for wind turbine in yawed flow//Collection of Technical Papers-44th
Verifying the blade element momentum method in unsteady,radially varied, axisymmetric loading using a vortex ring model
A prescribed wake model for vertical axis wind turbines. [PhD Thesis]
Roll-up model for rotor wake vortices. ASRL-TR-194-4,
Methods for rotor aerodynamic and dynamic analysis
Investigation of the wind turbine vortex structure//14th Int Symp on Applications of the Laser Techniques to Fluid Mechanics,
Correlation of helicopter tip vortex measurements
飞机尾涡演变及快速预测的大涡模拟研究
Large eddy simulation and rapid prediction of aircraft tail vortex Evolution
Development of a time-accutate viscous lagrangian vortex wake model for wind turbine application. [PhD thesis]
Unsteady loads evaluation for a wind turbine rotor using free wake method
Stability, consistency and convergence of time marching free-vortex rotor wake algorithms
Accuracy of the induced velocity from helicoidal vortices using straight-line segmentation
A new stall delay algorithm for predicting the aerodynamics loads on wind turbine blades for axial and yawed conditions
风力机叶片翼型动态试验技术研究
Research on dynamic test technology for wind turbine blade airfoil
A discrete vortex method for simulating a stand-alone tidal current turbine: Modeling and validation
The role of filament stretching in the free-vortex modeling of rotor wakes
Unsteady aerodynamics experiment phase VI: Wind tunnel test configurations and available data campaign. Technical Report NREL/TP-500-29955, National Renewable Energy Laboratory,
基于PIV技术分析颗粒在湍流边界层中的行为
Analysis of particle behavior in turbulent boundary layer based on PIV technique
Particle image velocimetry (PIV) measurements of tip vortex wake structure of wind turbine
NREL unsteady aerodynamics experiment in the NASA-Ames wind tunnel: A comparison of predictions to measurements. NREL/TP--500-29494, National Renewable Energy Laboratory,