引言
薄膜结构常见于有机生命体中,例如:鸭蹼、蝙蝠的翼手、蜻蜓的翅膀[1]等. 目前,生物力学领域已有大量关于薄膜结构的研究,如体积增长导致的黏膜表面起皱[2]、细菌生物膜的各向异性生长[3]、壁虎脚掌的黏附机理[4]等.另一方面,柔性薄膜因其轻质、可折叠和易展开等优点被广泛应用于航天飞行器的关键部件,如柔性太阳能电池翼[5]、充气式反射天线[6]和太阳帆[7]等.在受到压应力后, 薄膜表面将会产生局部屈曲而形成褶皱.褶皱的出现不仅会影响航天器部件的动力学特性,也会影响薄膜天线反射面的反射效率和信号传输稳定性[8].褶皱幅值是评价薄膜反射面天线形面平整度的重要指标. 因此,为了确定薄膜结构是否能够满足应用需求,有必要对褶皱幅值进行定量分析.
关于薄膜褶皱现象的理论研究最早可以追溯到1929年Wagner提出的张力场理论.张力场理论将薄膜褶皱问题转化为平面问题进行分析[9-10],假设薄膜的抗弯刚度为零, 并且认为相对于拉伸应力,由面内变形引起的压缩应力以及面外变形引起的弯曲应力可以忽略不计.褶皱区的薄膜处于单轴应力状态, 褶皱方向为最大主应力方向,垂直于褶皱方向的最小主应力为零[11]. 一些学者基于张力场理论,提出了描述薄膜褶皱行为的简化模型. 1961年,Stein和Hedgepeth基于实验提出了可变泊松比法[12]. 1986年,Pipkin提出了松弛能量密度法,修正了薄膜在褶皱和松弛状态下的应变能密度[13]. 1987年,Roddeman等通过修改变形梯度张量来描述褶皱变形[14]. 最近,Zhang等[15]基于双模量材料本构关系和共旋坐标法建立了一个新的褶皱模型和互补有限元方法,很好地改善了数值算法的收敛性.相似的工作可在Du等[16]、Shi等[17]的研究工作中找到. 然而,基于张力场理论的研究方法可以较为准确地预测褶皱方向和褶皱区域,却并不能定量地获取褶皱的细节信息(如波数、波长和幅值等).
稳定性理论是继张力场理论之后又一广泛使用的研究手段.它将薄膜褶皱变形视为薄板受压失稳问题进行分析,并假设薄膜的抗弯刚度非零, 可以承受一定的压应力.当面内压应力达到临界屈曲值时, 薄膜便会产生面外弯曲变形[18- 20].基于薄板稳定性理论的研究方法由于同时考虑了薄膜的面内拉伸变形能和面外弯曲变形能,因而可以对褶皱细节进行定量分析.常用的薄板稳定性理论基于两个著名的薄板大变形方程, 即:vonKarman方程[21-30]和Koiter方程[31-32].其中, 以von Karman方程的应用最为常见.Cerda等[21-22]针对受拉矩形膜, 假设横向无伸展性,即垂直于褶皱方向的应变只包含由面外变形造成的褶皱应变,推导出了预测褶皱波长和幅值的解析表达式, 并进行了实验验证.Wong和Pellegrino[23]针对受剪矩形膜和四角受拉方膜,将垂直于褶皱方向的应变分解为褶皱应变和由泊松效应造成的材料应变,提出了可以预测褶皱波长和幅值的理论模型. Lan等[26]将Wong和Pellegrino所提出的模型应用于对角受拉方膜,却发现理论预测的褶皱幅值与实验结果之间存在着较大的误差.他们通过实验测试获取更加准确的褶皱应变, 修正了褶皱幅值的理论公式,较好地提高了预测精度, 但仍与实验结果存在一定的差异.
本文基于von Karman薄板方程,针对对角受拉方形薄膜提出了一个预测褶皱幅值的理论模型.与Lan等引入实验褶皱应变的修正方法不同,本文模型考虑了横向拉伸力对薄膜变形的影响,将垂直于褶皱方向的位移分解为由泊松效应造成的压缩位移、由面外变形造成的褶皱位移以及由横向拉伸力造成的拉伸位移3个部分.另一方面, 对对角受拉方膜进行了数字散斑实验,测得了褶皱变形的三维形貌. 理论公式与实验结果的对比表明,本文提出的模型能够准确地预测褶皱变形幅值的大小,可为工程设计提供有价值的参考,也将对精细数值模拟的算法实现起到很好的指导作用.
1 理论模型与解析解
图1
图2
薄膜起皱的临界屈曲应力是一个关于材料弹性常数和褶皱波长的函数[34]
其中, $\lambda $是褶皱的半波长.假设横向收缩压应力等于临界屈曲应力[23], 即
对于不受面外载荷作用的薄膜,其面外力平衡方程可以写成如下形式[35]
其中, $\kappa _y $和是$\kappa _x $褶皱的两个主曲率.
根据褶皱形变分析, 假设褶皱区的薄膜处于单向拉应力状态,则褶皱区中任意一点$P$的竖向应力可表示为
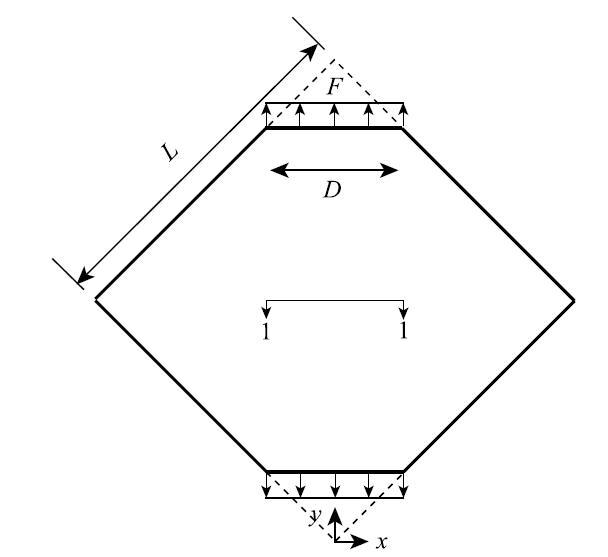
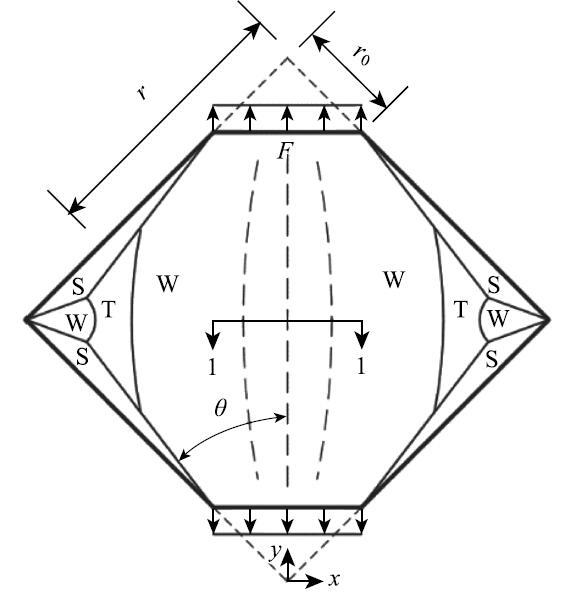
如图2所示, $P$点为褶皱区任意一点,$PP,'$为过$P$点且垂直于$x$轴的线段,$P,'$为线段与薄膜边界的交点. $r$为$OP,'$的长度$\left(\dfrac{\sqrt{2}}{2}D \le q r \le q L\right)$.
其中, \vspace{1mm}如图2所示, $A,B$点为薄膜夹持端点,$r_0$为$OA$的长度, 即$r_0=\dfrac{\sqrt{2}}{2}D$. 进而,褶皱两个方向的主曲率可表示为
将式(2)、式(4)、式(6)和式(7)代入面外力平衡方程(3),得到褶皱半波长的表达式
褶皱幅值的大小与垂直于褶皱方向的横向应变密切相关.Lan等[26]的模型中将横向应变分解为材料应变和褶皱应变两个部分.本文从横向位移来考虑, 由于横向两端因固定约束而受到拉伸力作用,所以将横向位移分解为3个部分, 即:由泊松效应造成的材料收缩位移$\varDelta _{xmn} $, 由面外变形造成的褶皱位移$\varDelta _{xw} $,以及由横向拉伸力造成的材料拉伸位移$\varDelta _{xmp} $. 其中,横向材料拉伸位移发生于薄膜左右两侧的褶皱区和张紧区.
因薄膜左右两端固定, 故横向总位移为零, 得到
由泊松效应造成的材料横向收缩位移可表示为
其中$\varDelta $为$y$向伸长位移.
褶皱应变又称为几何应变, 当薄膜发生局部屈曲时,其面外变形会造成面内收缩, 这一部分应变称之为褶皱应变.它可以由褶皱的投影宽度与真实宽度之差除以褶皱的真实宽度得到,如式(11)所示
考虑一条横贯褶皱的中心线, 即$y = \dfrac{\sqrt 2 (L - r_0 )}{2}$,将其代入式(5)和式(11), 得到
根据褶皱形变分析, 方形薄膜的四条边为松弛区, 不受拉应力,也不产生面外位移.因此我们可以将方形薄膜的四条边视为四个铰接的刚性杆,从而构成一个正方形的四连杆机构.对于一个四端点自由的正方形四连杆机构,当其$y$向受拉伸伸长$\varDelta $时,$x$向向内的收缩量近似为$\varDelta $,而本问题中方形薄膜的左右两端固定,故可认为其横向受拉而伸长了$\varDelta $,即由横向拉伸力造成的伸长位移为
将式(10)、式(13)和式(14)代入式(9)中,得到褶皱幅值的表达式
将褶皱半波长的表达式(8)代入式(15), 可得
其中
根据式(4)可得竖向应变, 即
由竖向应变积分可得竖向位移,
由此可得$\varDelta $与$F$的关系
进一步, 将式(20)代入式(16)中, 最终得到
其中
2 实验测试
本节介绍对角受拉方形薄膜的数字散斑实验.实验测试采用了基于数字图像相关技术的双目视觉三维测量系统[36],将被测物体变形前和变形后的三维空间坐标进行还原,从而获得物体的三维变形信息.利用该方法,对方形薄膜三维位移量进行测量,处理实验数据后可得到褶皱幅值与拉伸载荷之间的关系曲线等.
图3
图4
图4
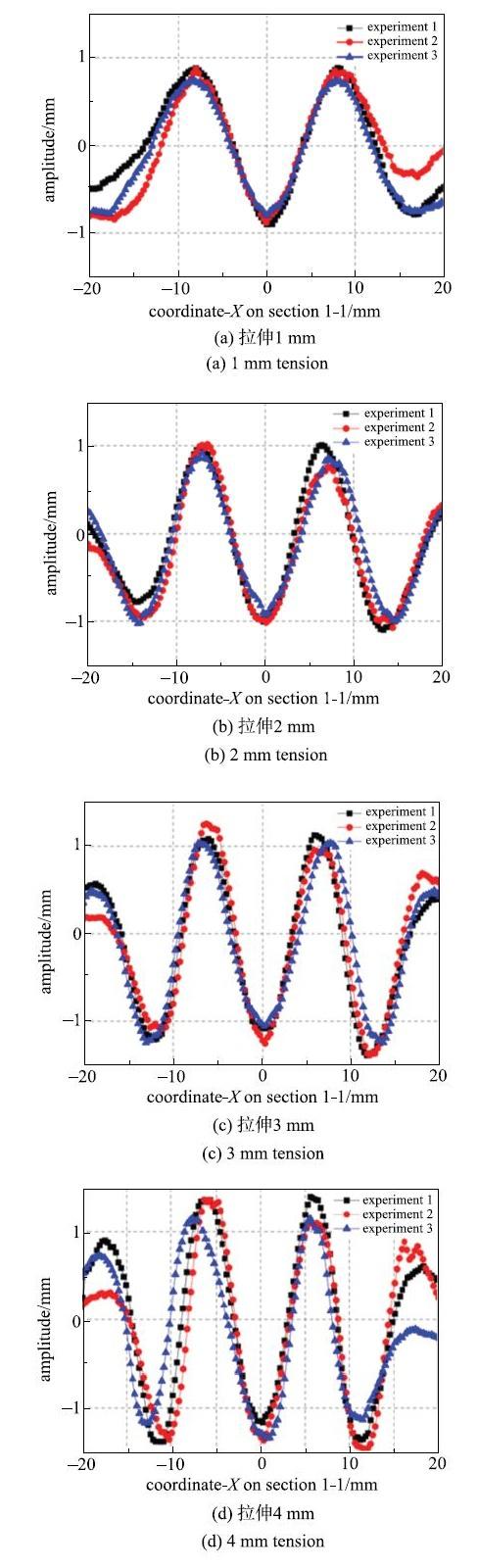
不同拉伸位移下的实验图片 (a)拉伸1 mm, (b) 拉伸2 mm, (c)拉伸3 mm, (d)拉伸4 mm
Fig. 4
Experimental photos under different tension displacement (a) 1 mm tension, (b) 2 mm tension, (c) 3 mm tension, (d) 4 mm tension
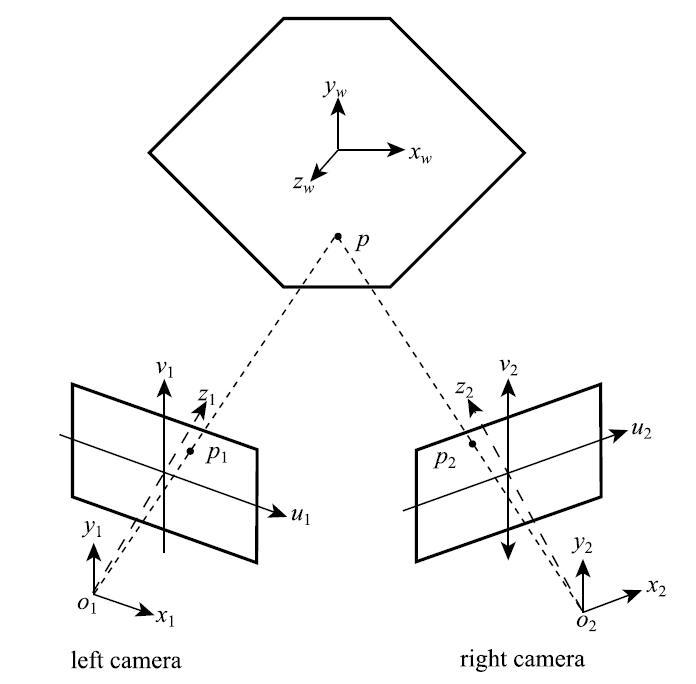
实验数据处理过程中对软件直接输出的结果进行了坐标转换.双目视觉三维测量系统由图像平面坐标系、相机坐标系和世界坐标系组成,分别用$[ u\quad v ]^{\rm T}$、$[x_c \quad y_c\quad z_c]^{\rm T}$和$[x_w\quad y_w\quad z_w]^{\rm T} $表示[36]. 如图5所示,图像平面坐标系建立在相机拍摄的图像上, 以图像中心为原点,以水平方向为$u$轴、竖直方向为$v$轴; 相机坐标系以相机的光心$O_c$为原点, $x_c $和$y_c $轴分别平行于图像坐标系的$u,v$轴, $z_c$轴为相机光轴, 垂直于图像平面; 世界坐标系以方形薄膜的中点为原点,以方形薄膜所在平面为$x_{w}-y_{w}$平面, 以水平方向为$x_w $轴,以竖直方向为$y_w $轴, $z_w $轴垂直于薄膜平面并指向相机.系统输出的数据是相机坐标系上的,利用该坐标系上的数据得到的结果并不是严格垂直于薄膜初始所在平面的离面位移.因而,我们期望获得以试件的中心点为原点、平行于试件的平面为$x-y$平面的世界坐标系上的数据.因此, 需要将相机坐标系的数据通过坐标变换, 得到世界坐标系上的数据.
图5
图5
双目视觉三维测量系统示意图
Fig. 5
The schematic diagram of 3D binocular vision measurement system
坐标转换公式如式(23), 将相机坐标系下的数据经过旋转和平移,转换为世界坐标系下的数据, 即
其中, $R$为一个$\mbox{3}\times \mbox{3}$的旋转矩阵, $T$为一个$\mbox{3}\times \mbox{1}$的平移矩阵.
利用MATLAB软件, 将实验数据进行处理, 具体方法如下:
(1) 求平移矩阵$T$. 在拉伸实验开始前, 标记好方形薄膜的中点.薄膜中点在相机坐标系下的坐标为$[a\quad b\quad c]^{\rm T}$,将其定义为世界坐标系的原点, 则平移矩阵$T$可表示为$[-a\quad-b\quad -c]^{\rm T}$.
(2) 拟合初始平面.期望获得以试件的中心点为原点、平行于试件的平面为$x-y$平面的新坐标系上的数据,则须先求得试件在原坐标系中的平面方程. 在实际实验过程中,因薄膜自身厚度极薄, 且夹具施加极小的力就对薄膜形貌产生很大的影响,所以薄膜的初始状态不是一个严格的平面. 假设薄膜近似为一个平面,用最小二乘法对其进行平面拟合, 设平面方程为$Ax+By+C=z$.其中($x,y,z)$为薄膜上散斑点的坐标,将初始状态的全部数据代入平面方程$Ax+By+C=z$中进行拟合,可得到系数$A,B,C$的值, 便可得到该平面的法向向量,即平行于$z$轴的向量, 则新坐标系的$x,y,z$轴的向量都可以得到确定.
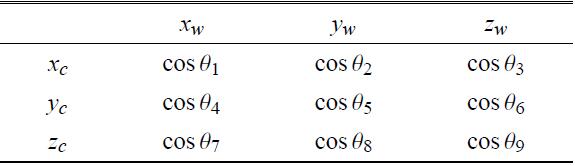
(3) 求旋转矩阵$R$. 求出相机坐标系与世界坐标系的夹角,如表1所示, 表中$\theta _i $分别为对应两轴的夹角, 即得到旋转矩阵
(4) 坐标转换. 根据式(23), 可将相机坐标系的数据转换到世界坐标系中.
表1 世界坐标系与相机坐标系的夹角
Table 1
 |
在实验数据处理过程中发现, 初始平面的拟合对结果影响很大.考虑到个别实验开始时, 因为施加的拉伸载荷太小, 薄膜没有绷紧,以致某些初始点偏离初始平面. 此时,可将初始状态偏离平面较远的数据点删除之后再进行拟合.
3 结果分析
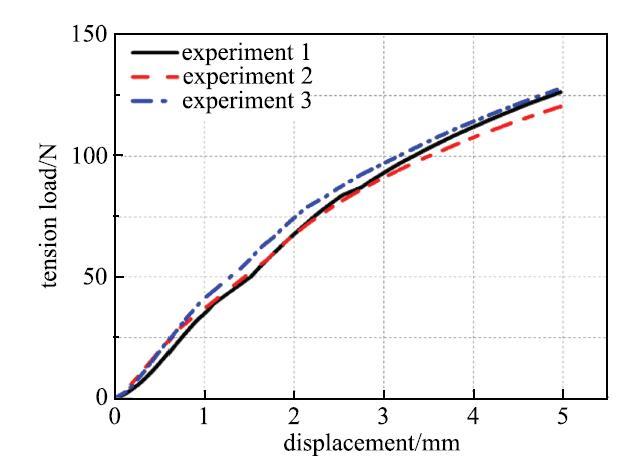
将实验测得的数据绘制成载荷--位移曲线, 如图6所示.
图6
根据挠曲函数(式(5))和实验观察不难发现,薄膜结构中平面上的褶皱幅值最大, 变形特征最为明显,所以我们通过预测该处褶皱幅值来验证理论模型. 提取拉伸位移分别为1mm, 2 mm, 3 mm和4 mm时的实验数据,绘制出薄膜中平面上的面外幅值曲线, 如图7所示. 可以发现,三次实验的结果基本吻合. 随着拉伸位移的增大, 褶皱的幅值逐渐增大,这与理论预测是一致的.
图7
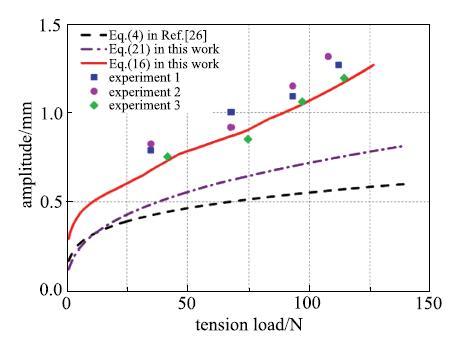
为了检查理论公式的准确性,我们将散斑实验测得的褶皱幅值与理论模型预测的幅值(式(21))进行比较,如图8所示, 其中实验数据为三次实验中拉伸位移分别为1 mm, 2 mm, 3mm和4 mm时的褶皱幅值. 与文献[26]中的褶皱幅值理论公式相比,本文模型提高了幅值计算精度. 拉伸位移越大时,本文模型的幅值计算精度提高得越多. 当竖向拉伸位移为1 mm时,精度提高了14.2%; 当拉伸位移为4 mm时, 精度提高了32.1%.另一方面,将实验测得的载荷--位移曲线上(如图6所示)的数据点平均化处理后代入式(16)中,能够得到与实验测试更加一致的幅值结果,二者的平均相对误差为10.2%.与通过引入实验褶皱应变的幅值修正公式相比[26],式(16)仍然具有较高的计算精度.
图8
图8
理论与实验结果对比
Fig. 8
Comparison between the theoretical and experimental results
过去的研究表明, 褶皱幅值预测的难点在于横向总应变的获得.由于横向总应变的理论推导过程中不可避免地存在假设,进而影响幅值计算的精度[26].本文从横向位移的角度出发, 对理论模型进行了重新推导,进一步提高了褶皱幅值的计算精度. 需要说明的是,由于在幅值理论公式的推导过程中, 采用了褶皱周期性分布的假设,故该公式仅适用于对角受拉方膜出现准周期性褶皱的情况.当薄膜的几何参数$D/L$发生变化, 并造成非准周期性分布的褶皱出现时,该公式将不再适用. 此外, 式(16)和式(21)的计算结果对比表明,本文所呈现的理论解仍有改进的空间. 在今后的研究工作中,可以进一步构造更加准确的应变场进行解析求解,以实现对该问题更一般性的解读.
4 结论
针对对角受拉方膜, 建立了一个能够准确预测褶皱幅值的理论模型.该模型考虑了横向约束产生的拉伸力作用, 并将横向位移分解为三个部分.在已有模型的基础上, 额外考虑了由于横向拉伸力造成的材料拉伸位移,重新推导了褶皱幅值的解析表达式. 通过散斑实验测试,获得了褶皱变形的三维形貌, 进而验证了该理论模型的正确性.与已有理论模型相比, 该模型进一步提高了褶皱幅值的计算精度.本文呈现的理论研究将为今后精细数值模拟的算法实现提供有意义的指导.
参考文献
蜻蜓滑翔时柔性褶皱前翅气动特性分析
Numerical study on the aerodynamic performance of the flexible and corrugated forewing of dragonfly in gilding flight
Surface wrinkling of mucosa induced by volumetric growth: Theory, simulation and experiment
Morphomechanics of bacterial biofilms undergoing anisotropic differential growth
Coupled effects of the temperature and the relative humidity on gecko adhesion
太阳帆航天器的关键技术
Key technologies of solar sail spacecraft
A pattern approximation method for distorted reflector antennas using piecewise linear fitting of the exponential error term
The 3-step DLR-ESA gossamer road to solar sailing
大型星载薄膜天线高精度制造技术研究
High precision manufacturing technology for space-based membrane antennas
Tension field theory a new approach which shows its duality with inextensional theory
Tension field theory
基于张力场理论的薄膜褶皱研究评述
Review of methods of wrinkle studies based on tension field theory
Relaxed energy density for isotropic elastic membranes
The wrinkling of thin membrane part I: Theory
Analysis of 2-D bimodular materials and wrinkled membranes based on the parametric variational principle and co-rotational approach
A new computational framework for materials with different mechanical responses in tension and compression and its applications
Multibody dynamic analysis using a rotation-free shell element with corotational frame
软物质材料的表面失稳研究. [博士论文]
Studies on surface instability of soft matters. [PhD Thesis]
超弹性薄膜与可压缩基底双层结构表面失稳分析
Study of surface instability about hyperelastic films on auxetic substrates under compression
Wrinkling of an elastic sheet under tension
Geometry and physics of wrinkling
Wrinkled membranes part II: Analytical models
空间薄膜结构皱曲行为与特性研究. [博士论文]
Study on wrinkling behavior and characteristic of space membrane. [PhD Thesis]
An experimental study on wrinkling behaviors and characteristics of gossamer space structures
Experiment and evaluation of wrinkling strain in a corner tensioned square membrane
Wrinkling and ratcheting of a thin film on cyclically deforming plastic substrate: mechanical instability of the solid-electrolyte interphase in Li-ion batteries
基于稳定理论的剪切薄膜屈曲分析
Pattern transitions in a soft cylindrical shell
A modeling and resolution framework for wrinkling in hyperelastic sheets at finite membrane strain
Spatial resolution of wrinkle patterns in thin elastic sheets at finite strain
A comparative analysis of numerical approaches to the mechanics of elastic sheets
空间充气薄膜结构的褶皱分析
Wrinkling analysis of space inflatable membrane structures
Accurate measurement of three-dimensional deformations in deformable and rigid bodies using computer vision