引 言
隧道支护结构体系是保证隧道围岩稳定性的基本要求,随着新奥法的提出和应用,以调动围岩承载为核心的支护设计理念已形成广泛共识. 但由于我国隧道围岩条件差异性极大,针对具体工程设计中的支护时机选择、支护参数确定以及支护可靠性评价等问题尚存在诸多困惑,使得隧道工程的定量化设计步履维艰.
在现行的隧道设计规范中,主要依靠工程经验确定超前支护、锚固支护以及初期支护方案和参数,将上述支护形式均视为临时支护进行设计,而将二次衬砌作为主承载结构对其进行检算,在校核时则不考虑前述施作的预支护和初期支护的作用,显然这与事实是严重不符的. 因此,对隧道围岩与支护结构体系协同作用的研究是十分必要和迫切的.
本文从隧道支护的本质特征和宗旨出发,提出了隧道支护的本质作用为"调动围岩承载"和"协助围岩承载"两个方面. 通过对不同支护形式的功能进行分析,明确了各种支护结构的作用特点及适应性,并基于支护结构体系协同作用模式的研究,建立多目标、分阶段的协同作用动态分析模型,以形成隧道支护结构体系的协同优化设计方法.
1 隧道支护的基本作用特点
隧道工程活动引起围岩变形破坏和应力重分布,由于围岩自身的约束作用,随着应力释放,围岩载荷大部分转移给相邻地层,当围岩条件较好时工程响应累积程度较低,对施工安全无威胁,本质上无须进行支护;而当围岩无法实现自行平衡时则需要对其实施外部干预,即要适时地施作支护结构以承担施工诱发的附加载荷.
1.1 隧道支护的本质作用
图1
图1
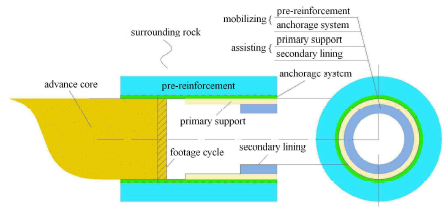
支护结构体系本质作用示意图
Fig.1
Schematic diagram of the essential function of the supporting structure system
基于隧道围岩的复合结构特性[6],"调动"围岩承载一方面可通过提高浅层围岩性能来实现,另一方面可通过将浅层围岩的附加载荷转移至深层围岩,使得深浅层围岩形成一个有机整体,从而充分发挥围岩的承载作用.在某些复杂围岩条件下,仅仅依靠调动围岩承载仍无法实现稳定,此时则需要支护结构协助完成,即通过支护结构与围岩共同作用,实现对围岩稳定性的可靠控制.
1.2 隧道支护结构体系
隧道工程设计的根本问题是促使围岩尽快形成新的平衡状态而不致失稳或破坏,由此需对围岩施作超前支护、初期支护和二次衬砌等支护结构,其中超前支护为基本前提,初期支护为核心,而二次衬砌通常则作为安全储备.
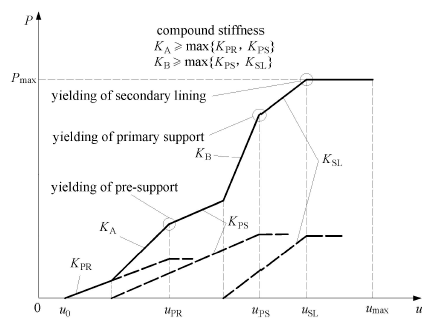
在工程实际中,各种支护手段伴随着隧道施工而分阶段施作,因此隧道支护结构体系的力学行为极其复杂,体系的综合刚度呈现阶段性变化特点,如图2所示.
图2
总的来说,前序支护体系与后序支护结构的衔接模式有两种:一是后序支护在前序支护屈服之前施作,如图2中初期支护施作时超前支护尚处于正常承载阶段;另外则是后序支护在前序支护体系中某一构件屈服后施作,如二次衬砌施作时初期支护结构已处于屈服状态,这表明前序支护承载能力不足,则需要对支护参数进行重新计算并予以加强. 在工程应用中,只有当支护体系中各要素相互协同并与围岩构成整体有序的可靠系统时,隧道围岩才处于稳定状态.
1.3 支护与围岩的作用特点
考虑到围岩变形和支护施作的时空特点,可将"支护——围岩"作用分为3个阶段,即超前支护与围岩作用、初期支护(联合超前支护)与围岩作用以及二次衬砌与初期支护的载荷调整过程,实际上是"支护——围岩"作用体系逐渐趋于稳定的过程.
支护与围岩作用关系极其复杂,综合考虑围岩变形与结构受力状态,其作用过程具有以下特点.
(1) 应力平衡特点.支护与围岩的复杂作用过程总是以应力平衡为目标,但每个作用阶段具有不同的平衡点,呈现典型的阶段性动态 平衡特征.在超前支护、初期支护及二次衬砌结构施作后"支护——围岩"作用均以新的应力平衡点而告终.由于"支护——围岩"多以界面力形式相作用,接触界面力学行为也呈复杂化和多样性特点.随着新支护结构的介入界面接触形式发生相应的变化,进而影响到压力传递效果,并在围岩变形与结构受力调整过程中实现新的平衡.
(2) 时空演化特点. 支护与围岩的相互作用具有显著的时空效应,表现为过程动态特性.首先,隧道开挖引起的应力释放并非一蹴而就,而是在一定的空间范围内传导并持续一定时间;其次,地质材料通常具有一定的流变特性,因而"支护——围岩"体系的力学平衡过程可能持续较长时间;同时,水泥类支护结构的硬化特性对支护结构强度、刚度的影响至关重要;此外支护结构的施作需要一定的时间和空间,各种支护结构不可能同时发挥支护效能.并且不同的开挖尺度、开挖方式及支护形式也直接影响到围岩变形演化的历程和结果.
(3) 变形协调特点.支护与围岩是不可分割的整体,支护通过"调动"和"协助"围岩承载实现支护与围岩作用体系的平衡,支护作用的发挥使围岩变形速度迅速减缓,从而使得围岩变形量得到有效遏制,而围岩变形则使结构受力增大,如此循环直至平衡.在此过程中,支护与围岩通过界面接触力实现应力传递和界面变形的协调,其传力效果由接触模式以及支护与围岩的刚度匹配情况所决定.
隧道围岩变形、破坏与支护结构体系的作用表现出明显的非线性特点,其核心是保持整体变形协调.支护与围岩作用体系中任何构 件的失效都有可能导致整个体系的失稳,须综合考虑.
2 隧道超前支护作用及其评价方法
对于稳定性较差的围岩条件,通常采用超前预加固与超前预支护措施提高隧道施工安全性. 超前加固本质上是提高围岩强度,使其在集中应力作用下不致发生严重破坏,保持一定的自稳时间,属于调动围岩承载的范畴;而超前支护本质上是预先形成一个掩护体承担围岩载荷,从而保护开挖面和隧道空间,属于协助围岩承载的范畴.
2.1 隧道超前支护原理与支护形式
隧道超前支护是隧道安全施工的基本保障,首先应防止隧道在急剧变形阶段发生失稳,为隧道开挖和初期支护安全施作创造条件;另外,超前支护作为隧道支护体系的重要组成部分,可有效控制隧道施工全过程中的围岩变形,同时为长期载荷作用下的围岩可靠性提供保障. 因此,超前支护不能仅视为临时支护而在进行结构计算时作为安全储备,而应将其作用进行量化.
超前加固和超前支护是指在掌子面前方对围岩进行预加固或预支护,从而保证施工安全性的手段,隧道施工中常用的超前预加固与预支护的形式如图3所示.
图3
图3
隧道超前支护/加固的典型形式
Fig.3
Typical forms of tunnel advanced support/reinforcement
上述超前支护形式中,注浆加固主要改善了开挖面前方岩土体的材料性能,其核心作用为调动围岩承载;超前管棚和小导管主要通过对开挖面提供径向约束,并在围岩中形成一定的拱效应,改善了开挖面前方岩土体的受力状态,其核心作用是控制围岩超前变形以及破坏和坍塌,从作用机理上属于协助围岩承载的范畴.
2.2 隧道超前支护的作用特点
隧道超前破坏是工程响应累积的宏观表现,并呈现出"正面挤出——前倾式冒落——后倾式冒落"的阶段性发展趋势[7]. 上述发展阶段每一种状态都可能为最终状态,在隧道渐进破坏过程中,若隧道围岩得到及时处置,则超前破坏即行停止,反之则随着应力释放,破坏范围将持续增大,对后续施工安全效应的影响也更大.
为了控制隧道围岩超前破坏的发展,超前支护措施得到了广泛应用,其作用主要具有以下特点:
(1) 在支护体系中作用明确
隧道超前支护主要目的为提高围岩稳定性,减小围岩超前破坏范围或改变破坏性质,在整个支护结构体系中有明确的任务分工,应为隧道开挖和初期支护施作创造相应的技术条件,是隧道安全施工的保障. 显然,保证初期支护发挥作用前围岩具有一定的自稳能力,是超前支护设计的基本原则.
(2) 对围岩条件的针对性强
在满足隧道安全施工的前提下,不同类型的预支护措施对于超前破坏模式的适应性也不同. 对于发生正面挤出型破坏的围岩条件而言,合理的超前支护措施为超前小导管配合预注浆;对于发生前倾式冒落型破坏的围岩条件而言,应优先考虑管棚加固方式,若采用小导管支护,必须适当扩大小导管注浆范围,并保证注浆质量;对于发生后倾式冒落型破坏的围岩条件而言,则优先选用超前管棚,必要时可考虑多种超前支护配合使用.
(3) 与后序支护应衔接良好
超前支护施作后,随着隧道施工的进行,临近开挖面的围岩因失去支撑而产生向临空面的变形,围岩应力进一步释放,若不对其采取及时有效的初期支护措施,围岩载荷将迅速释放以致发生围岩失稳. 因此,在超前支护失效前初期支护应及时发挥作用,二者良好衔接从而形成有效接力.
因此,为了对不同围岩条件实施合理有效的超前支护方案,需制定相应的超前支护控制标准,进而对其作用效果进行准确评价.
2.3 隧道超前支护作用效果的评价方法
隧道超前支护的核心作用为增强围岩自稳能力,在施工影响下,超前支护对于隧道围岩的作用效果如何评价,是研究支护体系整体力学行为的关键. 因此,为了定量描述超前支护对围岩的作用范围、条件及其影响因素,提出采用急剧变形量减小率$G_1$和超前破坏范围降低率$G_2$这两个指标来表征,并据此建立相应的评价体系,其中$G_1$和$G_2$的表达式如下
式中,$S_0$,$S_a$,$Z_0$,$Z_a$分别为无支护和有超前支护措施下的围岩急剧变形量与超前破坏范围,其控制标准值可采用工程类比、现场实测、理论分析等手段结合相关规范确定.
图4
图4
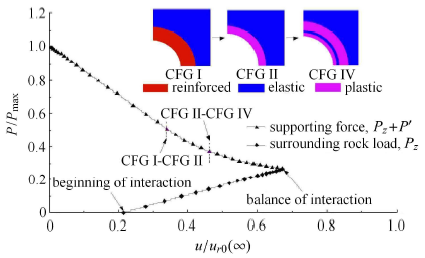
某一具体路径围岩载荷与变形关系
Fig.4
Relationship between surrounding rock load and deformation under a specific path
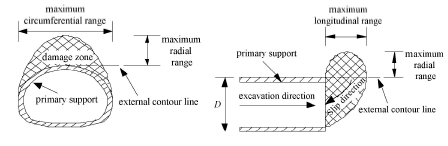
隧道超前破坏本质上为三维问题,破坏范围应包括环向、纵向和径向3个方面,如图5所示. 首先结合前文研究,对超前支护作用下隧道围岩超前破坏模式进行判断,然后建立变形与破坏的对应关系,确定开挖面极限状态,进而可对超前破坏范围进行预测,并通过与控制标准进行对比来评价超前支护的作用效果.
图5
需要指出,对于注浆加固方式,由于不同注浆材料、工艺和设备对地层条件的适应性有所差异,因此还应考虑浆液的扩散半径,而其无法通过上述两个指标直接反映,故将地层可注性$G_3$也作为评价指标,其可根据工程实际经验、相关规范直接得到,或采用室内注浆试验结果进行估算.
3 隧道初期支护作用基本原理
初期支护是在隧道开挖后及时施作的支护结构,是隧道支护体系的核心部分,并与前序施作的超前预支护组成联合支护体系. 但在二次衬砌施作后,初期支护载荷客观上会部分转移至二次衬砌结构,实现协同作用以保证隧道长期安全.
3.1 隧道初期支护的主要形式与特点
隧道初期支护通常采用由喷射混凝土与型钢钢架或格栅钢架配合锚杆支护组成的组合结构,必要时还将设置一定间距的钢筋网防止局部失稳或掉块. 隧道中常用的初期支护形式如图6所示.
图6
上述初期支护形式中,喷射混凝土和拱架施作于隧道围岩表面,其作用机制为因隧道发生向临空面内的变形而对围岩提供支护反力,其主要作用为"协助"围岩承载,可称为"表面初期支护";锚固体系作为围岩加固和地层改良层面的内容,其核心作用应是"调动"围岩承载,则可称之为"深层初期支护".
3.2 典型初期支护受力特性及其适应性
隧道初期支护不同构件的力学性能及作用机理不同,因此对围岩条件的适应性也有一定差别.
(1) 喷射混凝土支护受力与破坏特点
隧道所用喷射混凝土属于龄期类材料,其与围岩的相互作用呈现出明显的时效性,若强度增长速率低于载荷增长速率,则在喷射混凝土达到其最终强度前可能发生临界破坏,可见其硬化特性对于支护结构安全性具有重要影响. 通过对工程中常用混凝土的硬化特性进行试验,结果如图7所示.
图7
可见,喷射混凝土早期强度增长较快,后期强度增长缓慢,随时间基本呈负指数增长关系,7 d强度基本可达最终强度的90%,28 d强度则可达到最终强度的98%以上. 可见,喷射混凝土施作后7 d内为"危险龄期",此时喷射混凝土所承担围岩载荷可能超过其当前强度而发生屈服,因此是工程中应重点关注的阶段.
为了确定喷射混凝土的最不利位置,采用石膏材料进行模拟试验分析,如图8所示,可见,喷射混凝土支护的破坏主要集中在拱顶和仰拱中心,主要表现为裂缝的产生和发展,最终形成贯穿型裂缝而导致支护失效.
图8
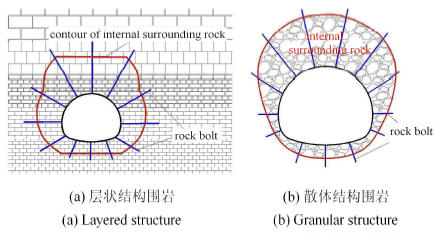
(2) 锚杆支护作用机理
图9
对于层状结构地层,其围岩结构表现为"复合梁"形式,锚杆通过"组合梁"作用将浅层围岩各岩层有机结合,防止层间错动和离层,并将内侧"组合梁"结构悬吊至外侧稳定的深层围岩,从而提高了围岩稳定性;而对于散体结构地层,其围岩结构则表现为"复合拱"形式,锚杆通过"压缩拱"作用在隧道周边形成具有一定承载能力的拱形压缩带,从而提高了浅层围岩的刚度和强度.
(3) 钢架选型及适应性分析
由于格栅钢架和型钢钢架的结构型式以及加工工艺的区别,两者受力和破坏过程不同,基于模型试验对其变形破坏特征进行分析,如图10所示.
图10
由图10可见,格栅钢架破坏时仅有细小裂缝,其破坏形式主要为混凝土的压碎. 而型钢钢架破坏时混凝土裂缝几乎贯通,说明型钢和混凝土的协同工作能力较差,考虑到型钢钢架刚度较大,因而尤其适合极其软弱或大变形围岩.而格栅钢架属于柔性支护,与围岩接触更为均匀稳定,适用于围岩较好、开挖尺度相对较小的工程条件.
4 隧道支护结构体系的协同作用
隧道支护结构体系中不同支护结构之间的协同作用可实现效率最高,而对协同效果的评价则以安全性为目标,通常包括围岩变形量和支护结构受力值. 因此,协同作用本质上是多目标、分阶段动态优化,以满足总体目标最优的要求.
4.1 支护结构体系的协同作用原理
协同学认为,系统由无序向有序转变的本质为复杂开放系统中大量子系统相互作用而产生的协同效应,是系统整体性和相关性的内在表现. 就隧道围岩安全性而言,协同支护系统是由围岩系统与支护系统按照一定工作方式组合在一起的复杂系统,其功能为控制围岩稳定性,系统的工作效能受到赋存环境、施工方法以及开挖尺度等因素的综合影响. 由于不同的支护构件对围岩条件的适应性不同,在复杂围岩条件下采用单一结构难以发挥其承载性能,因此客观上,支护体系的协同作用表现为原本单一的支护构件在与围岩相互作用时可能引发围岩失稳、结构失效、环境失调等安全性事故[5],而在与其他支护构件耦合支护后相互促进、互为补充,从而产生总体支护效果大于各子构件单一支护效果之和的效应.
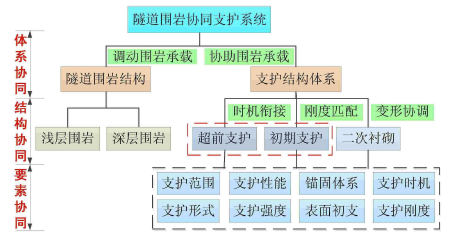
隧道支护体系的有效协同作用可实现最佳控制效果,而协同作用则包括支护结构与围岩的协同、不同支护形式之间的协同以及支护结构各要素的协同等三个层面,如图11所示. 基于隧道围岩的复合结构特性以及支护施作的时序性,协同支护主要研究2个方面的内容:一是以围岩为主体研究对象,研究围岩系统在支护体系作用下的力学响应,即协同支护作用下围岩的受力状态和稳定性的变化;二是以支护体系为研究对象,研究支护体系中各子构件之间如何协同才能发挥支护体系的最佳性能.
图11
在协同支护系统中,促使隧道围岩由开挖后的不稳定结构迅速变成整体稳定结构的内驱力为"支护阻力". "支护阻力"是支护结构与隧道围岩相互作用的产物,并且随着围岩变形的发展而不断增大,以支护结构的施作时机为起点,受支护结构自身的刚度、强度等力学特性的综合影响. 可见,"支护阻力"贯穿于隧道工程活动的始终,是研究协同支护的关键,可从支护体系的作用机理出发对其阐述.
4.2 协同作用效果及其评价方法
由于隧道施工的时空相关性以及各支护构件与围岩作用关系的差异性,隧道支护结构体系协同作用效果的评价也极为复杂. 对于不同阶段、不同形式的支护结构,其担任角色不同,因此作用目标也不尽相同. 对于超前支护而言,其协同目标为急剧变形量累计值最小,并使得围岩有足够的自稳时间;对于初期支护和二次衬砌而言,其协同目标则是以最小的支护代价达到最优的围岩稳定性控制效果.
为了定量描述协同作用条件及其影响因素,提出采用围岩变形$S$与支护体系协同度$\xi$作为协同指标来表征,基于支护与围岩相互作用的3个阶段,可建立多目标、分阶段的动态优化模型如下式所示
式中,$SRC$表征围岩条件;r为工程尺度;$x_i$为支护时机,以支护施作时距开挖面距离表示;$k_i$为支护刚度;$\left[ {p_i } \right]$为各支护构件极限强度;$\omega _i$为各支护构件在支护体系中所占权重;下标$i = 1, 2, 3$分别表示超前支护、初期支护和二次衬砌,对于不同的支护构件尚需进一步细分.
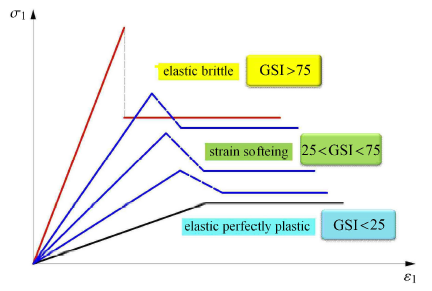
显然,由于支护结构分阶段施作,函数$S$与$\xi$为分段函数,对于函数$S$,采用两阶段分析法进行求解,如图12和图13所示.第一阶段,首先将无支护状态下的围岩特性曲线与 纵向变形曲线进行耦合,由纵向变形曲线可知,距离开挖面$x_1$处的围岩径向位移为$u_1$,由围岩特性曲线可知,围岩发生径向位移$u_1$时虚拟支护力为$p_1^\ast$,从而求得任意分析断面的虚拟支护力大小;第二阶段,将支护特性曲线、围岩特性曲线与纵向变形曲线三者进行耦合,由无支护作用时的纵向变形曲线可知当支护时机为$x_1$时围岩位移为$u_1$,假定支护结构与围岩变形协调,由支护特性曲线可确定支护力与位移的关系,此时再由围岩特性曲线可确定围岩载荷与位移的关系,而围岩载
图12
图12
围岩特性曲线与纵向变形曲线耦合示意图
Fig.12
Schematic diagram of coupling between LDP and GRC
图13
图13
支护——围岩协同作用模型示意图
Fig.13
Schematic diagram of support and surrounding rock synergistic model
荷由支护结构和第一阶段所得到的虚拟支护力共同承担,由此将三者进行耦合即可得到一次支护影响下纵向变形曲线,具体思路可参考文献[10],重复上述方法即可得到支护体系协同作用的全过程解答.
(1) 根据现有研究成果总结归纳出围岩位移与纵向距离的关系,选取合适的位移释放系数表达式,对于弹性围岩可选择 Panet等[11]的拟合公式如下
式中,$r_0$为隧道半径;x为分析断面与开挖面的距离,负值表示开挖面前方,正值表示开挖面后方;$u_{\max}$为无支护时隧道洞壁的最大径向位移;$\lambda _x$为分析断面x处的位移释放系数. 需要指出,此公式仅适用于开挖面后方的分析断面,对于开挖面前方,尚需进一步研究确定.
对于弹塑性围岩,则可选择Hoek (1999)采用最佳拟合方法得到的位移释放系数如下[12]
(2) 当支护时机$x_i$确定后,由步骤(1)可得到支护结构施作时围岩已发生的位移量$u_{x_i }$,假定支护为线弹性构件,则对于某一分析断面,其支护反力与支护刚度之间的关系为
式中,$x_i$为某支护结构施作时距开挖面的距离.
图14
以理想弹塑性模型为例,采用Mohr-Coulomb屈服准则时弹性阶段隧道洞壁径向位移为[17]
式中,$p_0$为原岩应力;E为围岩弹性模量;$\mu$为围岩泊松比.
塑性阶段隧道洞壁径向位移为[18]
式中,c和$\varphi$分别为围岩黏聚力和内摩擦角.
显然,若直接令$p_i = p_1$将上式联立,所得到的围岩位移结果与纵向距离无关,这显然只是一种状态,而无法描述支护-围岩作用过程,这是由于伴随着位移释放,隧道开挖面对围岩具有一定的约束效应,也就不难解释隧道开挖后围岩位移不会立即释放完毕,而是具有一定的时空相关性,因此计算时这种约束效应必须予以考虑,可将其用虚拟支护力$p^\ast$描述,显然随着位移释放$p^\ast$逐渐减小,故有
当支护结构在围岩弹性变形阶段施作时,由式(3)和式(7)联立可得虚拟支护力$p^\ast$的表达式为
式中,M为中间参量,有$m = {\left( {1 + \mu } \right)}/ E$.
联立式(4)~式(10)可得围岩位移关于纵向距离x的表达式为
式中,$\lambda _{x_1 }$为第一组支护施作时围岩位移释放系数;$x_1$为第一组支护施作时距开挖面距离.
同样地,联立式(4)~式(6)且位移公式选取式(8)可得当支护结构在围岩塑性阶段施作时,围岩位移关于纵向距离x的表达式为
式中,$N_\varphi$和$n$为中间参量,$N_\varphi = \frac{\sin \varphi }{1-\sin \varphi }$,$n = \left( {1-\sin \varphi } \right)\left( {mr_0 \sin \varphi } \right)^{N_\varphi }\left( {p_0 + c\cot \varphi } \right)^{\tfrac{1}{1-\sin \varphi }}$.
式(11)和式(12)中,$u_{\max }$由弹塑性位移 式(7)或式(8)代入$p_i = 0$得到,由于式(12)并非显式解,因此需要借助数值分析法求解.
对于后序支护构件,支护施作时已发生的位移由式(11)或式(12)得到,由于式(12)为隐式解,在后序支护施作时采用理论解析无法直接求得围岩位移,因此本文仅针对支护结构在弹性位移阶段施作时进行推导,对于其他工况可基于本文求解思路得到相应解答.
将$x = x_2$代入式(11)可得第二组支护施作时围岩已发生的位移为
式中,$\lambda _{x_2 }$为第二组支护施作时围岩位移释放系数,$x_2$为第二组支护施作时距开挖面距离.
因此可得围岩位移关于纵向距离x的表达式为
对比式(11)和式(14)归纳总结其规律,并结合计算原理可得当支护结构在围岩弹性阶段施作时,围岩位移关于纵向距离x表达式的统一形式为
式中,$S_{x_i }$为第i组支护施作时围岩发生的位移,由式(4)和式(13)可总结出其递推公式为
此数列的首项为
由式(15)~式(17)即可求得函数$S$的分阶段解答,以上即为协同指标$S$的计算方法,而隧道支护体系协同度则包括两方面内涵,即各支护构件强度平均利用率以及支护体系组合效率,前者反映了支护构件力学性能整体发挥的程度,可由各支护构件强度利用率的加权平均值描述;而后者反映了各支护构件使用效率的一致性,可由各构件强度利用率的加权方差来表达,如式(18)所示
式中,$n$代表支护体系中各种支护形式数量,$\omega _i$为某种支护形式对应权重值,$\xi _i$为某构件性能利用率,可由其实际受力最大值与其极限承载强度的比值来表征,如式(19)所示
式中,$p_{\max }$为构件实际受力最大值,对于锚杆可取其最大轴力,对于钢拱架和喷射混凝土可取其最大应力值;$\left[ {p_i } \right]$为构件极限承载强度,对于锚杆可取其抗拉强度,对于钢拱架和喷射混凝土则取其极限抗压强度.
4.3 隧道初期支护与二次衬砌协同作用原理
二次衬砌施作时初期支护与围岩系统通常已基本稳定,而从隧道长期安全性而言,考虑到隧道围岩与支护结构体系的时空演化特性,二次衬砌结构应具有相应的承载能力,并将按其与前序支护的刚度匹配性进行载荷分配.
目前隧道支护设计时普遍是将二次衬砌作为围岩载荷的主要承担者. 然而事实上,在支护与围岩的相互作用过程中围岩附加载荷已由初期支护全部承担,即使出现初期支护性能退化,考虑到二次衬砌对初期支护的约束作用,围岩载荷也不可能全部转移至二次衬砌结构. 这也是诸多隧道结构检算不满足规范要求,却可以保障长期安全的原因所在.
表1 计算参数
Table 1
| Parameters of surrounding rock | Support parameters | |
|---|---|---|
| E/GPa id r0 /m | p〇 /MPa | k1 /(MPa^m-1) x1 /m |
| 1.5 0.25 6 | 5 | 100 6 |
图15
图15
二衬刚度和支护时机对初支——二衬协同作用的影响
Fig.15
Effect of stiffness and supporting time of second lining on primary support-second lining synergy
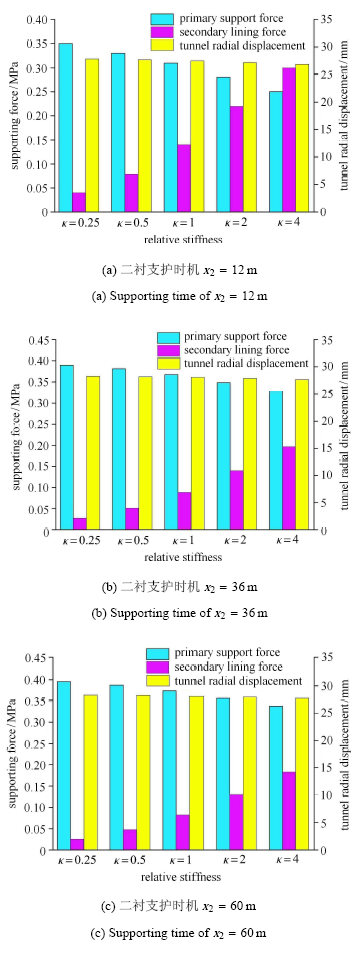
由图15分析可知: (1)随着二次衬砌刚度的增大,二次衬砌结构自身受力明显增大,初期支护受力和围岩稳定变形量均有所减小,但后者变化并不明显;当二次衬砌施作时机延迟时,二衬结构受力显著降低,而初期支护受力和围岩最终变形量相对变化较小.这表明二次衬砌结构对围岩稳定性影响并不大,由此可确定初期支护的主体结构地位,而二次衬砌则仅作为安全储备. (2)影响二衬结构受力的主要因素为其自身刚度,当其刚度大时较小的围岩变形量亦会使得二衬结构受力迅速增大,这显然不利于支护结构的长期安全性.因此实际工程中不仅要使得二次衬砌在围岩变形稳定后施作,更应根据隧道耐久性要求将其刚度控制在相对合理的水平.
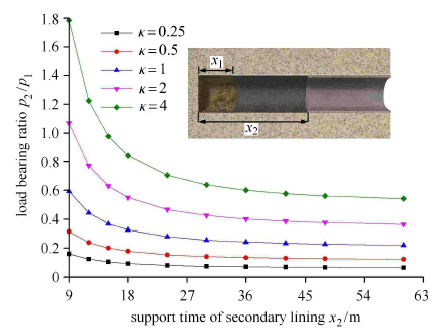
实际工程中对二次衬砌进行检算时常认为二衬承担所有载荷,或人为给定载荷分担比,这显然与事实不符.为此,对不同支护时 机下二衬刚度与载荷分担比关系进行分析,如图16所示.
图16
图16
二衬支护时机与载荷分担比关系曲线
Fig.16
Relation curve of secondary lining supporting time and load sharing ratio
可见,对于不同的支护时机和支护刚度,二衬载荷分担比也具有明显差异,随着二衬支护时机的延迟以及支护刚度的减小,二衬所承担载荷也逐渐递减,当$x_2 \geqslant 36$ m后,二衬支护时机的滞后对于二衬载荷基本无影响,该稳定值即为二衬理应承担的围岩载荷.此外,当二衬紧跟时,尽管二衬刚度较小,其承担载荷仍然较大,此时初期支护承载能力未得到充分发挥,这必将造成材料浪费,显然是不合理的,因此二衬支护参数应与"支护——围岩"作用关系相协调,达到经济、合理的支护效果.
5 隧道支护结构体系协同设计方法
在超前支护作用下,围岩通常已具备一定的稳定性,因此,初期支护施作时机和刚度应按照围岩力学特性曲线进行确定. 基于围岩的结构特性,同时考虑到围岩超前加固/支护的作用效果,即可计算初期支护结构载荷,再结合围岩结构层的稳定状态及变形控制值确定初期支护结构刚度和施作时机.
5.1 隧道支护体系协同设计流程
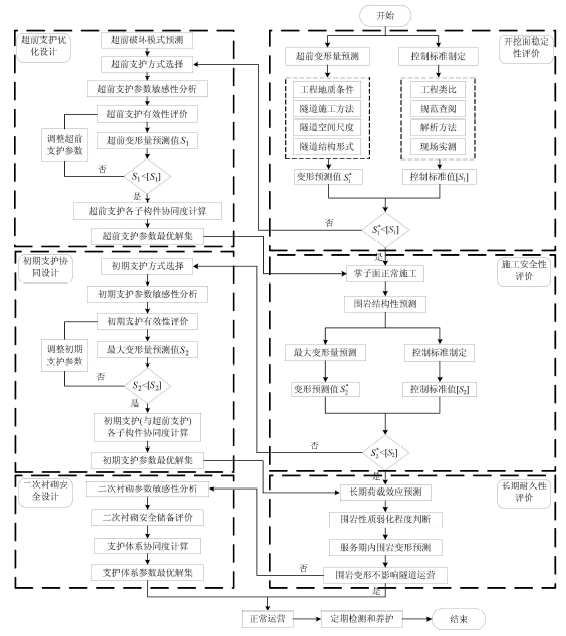
图17
图17
隧道支护体系协同优化设计方法
Fig.17
Synergetic optimization design method of tunnel support system
(1) 开挖面稳定性评价:首先基于隧道工程地质条件和相关施工因素预测超前变形量$S_1^\ast$,再采用工程类比、理论解析、现场实测等方法确定超前变形量控制标准$[S_1]$,将两者进行比较,从而判断隧道开挖过程中是否需要超前支护.
(2)超前支护优化设计:通过对超前破坏模式进行预测,根据前文分析选取相应的超前支护方式,并初步确定支护方案,对各支护参数进行敏感性分析,搜索出超前支护参数最优解的范围,将各参数取值区间进行组合后对开挖面变形量$S_1$进行预测;对于满足施工要求的方案,计算其协同度并进行比较,取协同度最大的方案为超前支护最优解集.
(3) 施工安全性评价:选取步骤(2)得到的超前支护最优解集对隧道围岩结构性进行预测,若出现浅层围岩,则必须施作初期支护;若仅有深层围岩,则对施工期间围岩最大变形量$S_2^\ast$进行预测,并根据规范对于隧道极限变形量的规定,参考相关工程案例制定围岩最大变形量控制标准$[S_2]$,将二者进行比较,从而判断是否需要施作初期支护.
(4)初期支护协同设计:根据文献[6]中载荷效应确定方法计算支护载荷,并对隧道中常用的初期支护形式的适应性进行分析,结合浅层围岩范围,选择适合于本工程的初期支护形式,并初步确定支护参数的变化范围,对各参数进行敏感性分析,搜索出参数最优解的存在范围,将各参数进行组合后对最大变形量$S_2$进行预测,将满足隧道施工期间安全性要求的方案比较其协同度,从而确定初期支护参数最优解集.
(5)长期安全性评价:地下空间往往具有不同的功能需求,因而对其耐久性和长期使用安全性的要求也不同,根据隧道所处的工程地质环境对围岩长期载荷效应和衬砌劣化程度进行预测,从而判断是否需要施作二次衬砌.
(6)二次衬砌安全设计:隧道中常用的二次衬砌为钢筋混凝土结构,根据前文分析,二次衬砌施作原则为刚度与隧道长期安全性相匹配,支护时机与围岩变形相适应. 据此初步拟定二次衬砌支护方案,计算不同方案的安全系数,并对长期作用过程中最不利载荷条件下围岩的稳定性进行校验,确定二次衬砌安全系数需求,从而选择符合条件的支护方案,对各方案中支护体系的协同度进行计算,选取协同度最高者为二次衬砌最优解集.
以上步骤完成后所得到的最优解集即为协同支护多目标、分阶段优化设计问题的有效解,当然,在隧道长期运营中,还应保证支护结构体系具有可修复性,以方便隧道定期检测和养护.
5.2 算例与分析
基于上述思想,可对隧道支护体系进行设计,考虑到围岩的复合结构特性,对应变软化岩体进行分析,计算选取的工程概况如下:某深埋圆形隧道半径$r_0 = 6$ m,受静水压力$p_0 = 6$ MPa. 隧道处于软岩中,围岩弹性阶段力学参数为弹性模量$E = 1.5$ GPa,泊松比$\mu = 0.3$;软化阶段参数为软化模量${E}' = 0.5$ GPa,软化黏聚力$c = 0.7$ MPa,软化内摩擦角$\varphi = 30^ \circ$,软化塑性泊松比$f = 2$;残余阶段参数为残余黏聚力$c_{\rm r} = 0.3$ MPa,残余内摩擦角$\varphi _{\rm r} = 22^ \circ$,残余塑性泊松比$h = 1.5$.
(1) 开挖面稳定性评价
Panet等[11]研究表明,隧道开挖面应力释放率约为0.72,因此核心土体对围岩的支护力约为1.68 MPa. 由前文公式计算可得开挖面处围岩变形为64 mm,根据规范中对隧道预留变形量以及初期支护极限位移的规定,取开挖面变形量控制标准为40 mm,可判断开挖面处于不稳定状态.
(2) 超前支护优化设计
通过对开挖面潜在破坏范围进行预测可知其超前破坏模式为前倾式冒落型破坏,基于前文分析,采用超前小导管支护对开挖面进行控制,结合相关工程经验,初步选取小导管支护参数如表2所示.
表2 超前小导管参数波动范围
Table 2
| diameter d/mm | 30, | 35, | 40, | 45, | 50 |
|---|---|---|---|---|---|
| longitudinal space Sc/m | 3, | 3.5, | 4, | 4.5, | 5 |
| circumferential spaceSl/cm | 25, | 30, | 35, | 40, | 45 |
| length l/m | 3, | 3.5, | 4, | 4.5, | 5 |
| extrapolation angle 0/(。) | 10, | 15, | 20, | 25, | 30 |
表3 超前小导管各参数敏感度
Table 3
| Parameters | d | Sc | Sl | l | Q |
|---|---|---|---|---|---|
| sensitivity | 0.24 | 0.36 | 0.28 | 0.45 | 0.22 |
根据参数敏感性顺序由高到低依次对不同参数小导管支护有效性进行分析,从而确定各参数最优值,其原则为若某一参数与围岩变形关系存在"转折点",则此转折点即对应相应参数最优解,否则取该参数上限值,然后将上一参数最优值代入下一参数分析中,重复上述过程依次确定各参数最优值,由此可得小导管支护参数的最优解集如表4所示.
表4 超前小导管参数最优解集
Table 4
| d/mm | Sc/m | Si/cm | l/m | Q/(。) |
|---|---|---|---|---|
| 40 | 3.5 | 35 | 4.5 | 15 |
按照表4中支护方案进行施工时,开挖面围岩变形量预测值为$S_1 = 32$ mm,且不会发生超前破坏,满足开挖面稳定性的要求,并留有一定富余,为初期支护的施作争取了一定时间.
(3) 施工安全性评价
由于围岩应力随隧道开挖而逐渐释放,若仅有超前支护作用,当围岩应力完全释放时,通过对围岩结构性预测可知浅层围岩厚度将达到2.75 m,围岩最大变形量将达到$S_2^\ast = 158$ mm,根据施工经验,并查阅相关规范可确定隧道极限变形量为$S_2 = 100$ mm,则可判断施工期间隧道将发生失稳破坏,因此需要及时施作初期支护以控制围岩变形,并防止浅层围岩坍塌.
(4) 初期支护协同设计
根据前文对初期支护结构的受力特性及适应性研究成果,选择表面初支配合锚固体系作为初期支护. 由于锚固体系与表面初支施作工艺、作用机理不同,因此需要分别设计. 对于锚固体系,由于本算例中浅层围岩厚度较小且开挖跨度不是很大,因此无须施作锚索,根据相关工程经验,参考超前支护优化设计方法,可确定锚杆支护参数如表5所示.
表5 隧道锚杆支护建议
Table 5
| Length | Diameter | Layout density | Prestress force |
|---|---|---|---|
| l/m | d/mm | C/(N.m-2) | F/kN |
| 3 | 22 | 1 | 70 |
为了研究表面初支参数对支护效果的影响,初步拟定支护时机(支护施作时距掌子面距离)$x_1$、喷射混凝土支护刚度$E_{\rm c}$以及格栅钢架支护刚度Es变化范围如表6所示.
Parameters Value ranges
x\/m 5,6,7,8,9,10,11
Ec/(MPa^m-1) 100,150, 200, 250, 300, 350, 400
Es/(MPa.m-1) 80, 100,120, 140,160,180, 200
在对初期支护参数进行敏感性分析时,支护时机$x_1$取11 m,其他参数取7种工况中的最小值. 计算表明,初期支护3个主要参数对围岩变形量控制效果影响均较为明显,且当参数变化到某一范围后,参数改变对围岩变形影响明显减弱,由此可确定表面初支参数最优解集如表7所示.
表7 隧道表面初支参数最优解集
Table 7
| Support time | Stiffness of shotcrete | Stiffness of grid steel frame |
|---|---|---|
| xi/m | Ec/(MPa.m-1) | Es/(MPa.m-1) |
| 7 | 200 | 100 |
(5) 支护体系协同效果评价
判断矩阵${\pmb A}$的最大特征值为$\lambda _{\max } = 3.009 2$,求解其相应的特征向量并进行归一化后可得到支护协同制约因素权向量为
经检验,满足一致性条件. 因此,在协同支护系统中,超前小导管、锚固体系和表面初期支护所占权重分别为16.34%, 29.7%和53.96%.
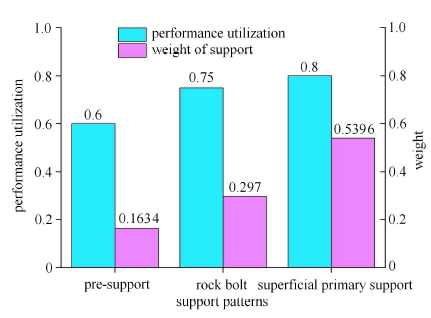
将前述所得各构件参数最优解代入前文公式进行计算可得支护体系协同度结果如图18所示.
图18
将图18中的结果代入式(19)可得支护体系协同度计算结果为$E\left( \xi \right) = 0.752 4$,表明支护体系各构件平均利用率较高,而$D\left( \xi \right) = 0.018 9$,标准差为$\sqrt {D\left( \xi \right)} = 0.14$,表明各支护构件性能利用率离散性较小,基本保持在相对一致的水平,支护设计合理,支护体系协同效果较好.
(6) 二次衬砌安全设计
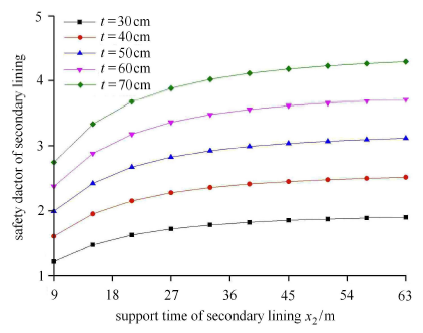
图19
图19
不同刚度下二次衬砌安全系数与支护时机关系
Fig.19
Relationship between safety factor and support time of secondary lining under different stiffness
可见,当二次衬砌紧跟掌子面时,常规厚度的二次衬砌已无法满足隧道服役周期内安全系数不小于2.0的要求,此时需要对二次衬砌额外加厚,这便意味着隧道超挖量大大增加,从而加大支护成本.
事实上,只要距隧洞开挖面一定距离后施作二次衬砌,30~40 cm的素混凝土即可满足其作为安全储备的功能需求,而施作时机则应主要考虑施工组织的要求并与围岩变形过程相适应[25].
5.3 工程实例验证
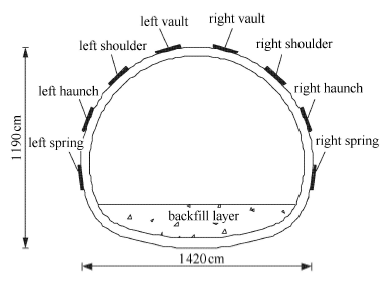
贵广高铁牛王盖隧道位于广西省贺州市境内,隧道起讫里程为DK567+795~DK568+247.隧道位于剥蚀丘陵区,场区以构造剥蚀中低山为主,最大埋深122 m.隧道穿越断层、突泥涌水、溶洞暗河等复杂地质条件,节理裂隙发育,围岩级别以III~IV级为主.选取IV级围岩段DK568+060, DK568+080以及DK568+100等3个典型断面进行监测,隧道埋深约100 m,断面大小和测点布置如图20所示.
图20
所选3个监测断面采用复合式衬砌结构,初期支护均为40 cm厚C25喷射混凝土和4$\varPhi$25 mm格栅钢架,支护时机基本一致;二次衬砌为C35钢筋混凝土,其支护参数略有不同,如表8所示.
表8 监测断面二次衬砌支护参数
Table 8
| Cross section mileage | Thickness t2/cm | Support time x2/m |
|---|---|---|
| DK568+060 | 40 | 40 |
| DK568+080 | 50 | 40 |
| DK568+100 | 40 | 70 |
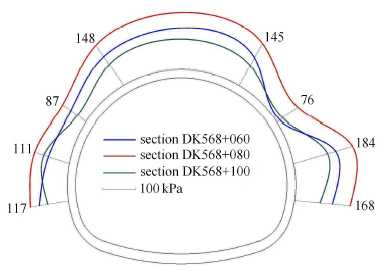
现场实测二衬结构受力如图21所示. 可见,尽管二衬结构受力具有空间差异性,但其最大值仍在0.2 MPa以下,低于素混凝土的极限承载能力,因此二次衬砌作为安全储备的设计理念是完全可行的.
图21
此外,实测数据表明,二衬施作越早或刚度越大则其承担载荷也越大,这说明尽管二次衬砌在围岩变形基本稳定后施作,但由于其具有较大刚度,后续较小的围岩变形即使其分担较大围岩载荷,当支护时机较早时这种载荷分配效应尤为明显.
6 结 论
(1)针对隧道围岩的复合结构特性,提出了隧道支护的本质作用为"调动围岩承载"和"协助围岩承载",并基于围岩载荷效应演化特点明确了其工作对象和控制标准.
(2)针对围岩的不同破坏模式提出了相应的超前支护方式,并对其各自的适应性进行了对比分析,明确了超前支护的安全保障作用,并建立了超前支护效果的评价体系及评价方法.
(3)针对不同初期支护形式的作用机理和特点,提出由锚固体系、格栅/型钢拱架和喷射混凝土三部分构成的初期支护作为隧道围岩附加载荷的主承载结构,由此明确了初期支护在隧道支护结构体系中的核心作用.
(4)针对隧道支护体系的作用机制与特点,提出了3个层次的协同作用模式,明确了其作用内涵,建立了两目标($S$和$\xi$)、三阶段(超前支护、初期支护和二次衬砌)协同作用优化模型,阐明了二次衬砌结构的安全储备作用,并给出了量化设计方法.
(5)建立了基于协同作用的隧道支护体系设计方法,并进行了实际工程的分析和应用,计算分析表明本文给出的计算方法可操作性较强,相比于以往经验设计方法更具科学性和可靠性,为隧道设计的定量化提供了一种思路.
参考文献
Rock defects and loads in tunnel supports
//
A numerical approach to the hyperstatic reaction method for the dimensioning of tunnel supports
The hyperstatic reaction method is particularly suitable for the dimensioning of support structures. This method simulates the interaction between the support and rock surrounding the tunnel through independent “Winkler” type springs. It requires the definition of the active loads that are applied directly to the support structure by the rock mass. Further passive loads are due to the reaction of the rock mass to the displacement of the support structure.A numerical approach to the hyperstatic reaction method is presented in this paper. The parameters that condition the calculation and the dimensioning techniques of the support structures, on the basis of the results of the method, are also presented. A specific code, named FEMSUP, was developed using a FEM framework, to perform calculations with the HRM. This code is able to consider the effective geometry of the support and the horizontal active loads that are different from the vertical ones; it is therefore able to analyse the rock mass–structure interaction in detail.An extensive parametric analysis performed using FEMSUP has made it possible to define the necessary support structures (steel sets incorporated into a shotcrete lining) in a wide number of cases that cover the conditions that are generally encountered in excavation practice. Ten design tables were drawn up to summarise the results of the parametric analyses. From an examination of the tables, it is possible to verify the influence of the various calculation parameters on the dimensioning of the support structure and to obtain rough indications on the entity of the support structures in the preliminary stages of a project.
Integration of geotechnical and structural design in tunneling(C)
//
隧道及地下工程的基本问题及其研究进展
进入到21世纪,隧道及地下工程已成为土木工程最为活跃的学科方向,其作用和地位凸显,并在交通基础设施和城市轨道交通建设中发挥了关键作用。事实上,正是复杂长大隧道和城市地下空间开发技术的突破才使得我国高速铁路、高速公路和城市轨道交通工程的大规模快速建设成为可能。在隧道及地下工程的安全建造和安全服役中涉及诸多力学问题,为此文章就隧道及地下工程的基本问题及其研究进展进行分析和探讨。
Essential issues and their research progress in tunnel and underground engineering
进入到21世纪,隧道及地下工程已成为土木工程最为活跃的学科方向,其作用和地位凸显,并在交通基础设施和城市轨道交通建设中发挥了关键作用。事实上,正是复杂长大隧道和城市地下空间开发技术的突破才使得我国高速铁路、高速公路和城市轨道交通工程的大规模快速建设成为可能。在隧道及地下工程的安全建造和安全服役中涉及诸多力学问题,为此文章就隧道及地下工程的基本问题及其研究进展进行分析和探讨。
隧道围岩的复合结构特性及其载荷效应
基于地层岩土体的结构性和工程扰动特点,建立复合隧道围岩结构模型,提出围岩结构稳定性及其荷载效应的计算方法,实现荷载结构模型与地层结构模型的耦合。隧道施工引起的应力释放伴随着应力的转移,通常是由围岩中的压力拱实现传递的,表现出围岩的渐进破坏特点,按其稳定性特点可将围岩分为浅层围岩和深层围岩;深层围岩破坏的不连续性和阶段性本质上是由其分组特性所致,而每一组围岩则呈现同步或几乎同步运动的特点,并且一组围岩的失稳随即在其外侧形成一组新的岩层结构,用以维持其外部围岩的稳定,表现为随时空转化的复合拱结构模式;每组深层围岩通常是由“结构层”和“荷载层”构成,其中分层厚度较大、强度和刚度相对较高的岩层作为结构层控制着整组围岩的稳定性,通常位于围岩组的内侧,而厚度较小、强度和刚度也较低的岩层则作为荷载层而作用在结构层上。揭示结构层的失稳机制并给出相应的判据;明确提出复合隧道围岩结构的荷载效应是由浅层围岩的给定荷载和深层围岩的形变荷载组成,给定荷载取决于浅层围岩范围和性质,而形变荷载组取决于对结构层控制位态和传力岩层的刚度条件。
Compound structural characteristics and load effect of tunnel surrounding rock
基于地层岩土体的结构性和工程扰动特点,建立复合隧道围岩结构模型,提出围岩结构稳定性及其荷载效应的计算方法,实现荷载结构模型与地层结构模型的耦合。隧道施工引起的应力释放伴随着应力的转移,通常是由围岩中的压力拱实现传递的,表现出围岩的渐进破坏特点,按其稳定性特点可将围岩分为浅层围岩和深层围岩;深层围岩破坏的不连续性和阶段性本质上是由其分组特性所致,而每一组围岩则呈现同步或几乎同步运动的特点,并且一组围岩的失稳随即在其外侧形成一组新的岩层结构,用以维持其外部围岩的稳定,表现为随时空转化的复合拱结构模式;每组深层围岩通常是由“结构层”和“荷载层”构成,其中分层厚度较大、强度和刚度相对较高的岩层作为结构层控制着整组围岩的稳定性,通常位于围岩组的内侧,而厚度较小、强度和刚度也较低的岩层则作为荷载层而作用在结构层上。揭示结构层的失稳机制并给出相应的判据;明确提出复合隧道围岩结构的荷载效应是由浅层围岩的给定荷载和深层围岩的形变荷载组成,给定荷载取决于浅层围岩范围和性质,而形变荷载组取决于对结构层控制位态和传力岩层的刚度条件。
复杂隧道围岩安全性及其评价方法
在对国内外现行隧道围岩分级方法分析的基础上,指出了其在隧道工程设计和安全性控制,尤其是复杂围岩控制设计方面存在的突出问题,认为现行的隧道围岩分级概念模糊,难以适应复杂多变的地层条件和较为严苛的环境控制要求,尤其是对稳定性较差的复杂围岩条件缺乏有效的指导作用。从隧道围岩控制的宗旨出发,提出了隧道围岩及其支护系统安全性的概念,明确了其科学内涵和表征方法;重点对于不具备自稳能力的复杂围岩安全性进行了研究,建立了隧道围岩安全性的分析模型,提出了隧道围岩安全性分析中应考虑围岩预加固效果的必要性及其评价方法;基于隧道围岩尺度效应和地层结构效应(时间效应)的分析,建立了围岩尺度响应的表述方法,同时从细观结构层面分析了不同地层结构形式对安全性的影响关系;结合"支护–围岩"动态作用关系的分析,建立了极不稳定地层条件下复杂隧道围岩安全性的评价指标体系,将围岩超前变形、超前破坏和地层加固有效性作为核心评价指标,形成了包括9项基础指标的评价体系,并提出了安全性的分级方法。最后介绍了隧道围岩安全性的分级方案的工程应用。
Safety of complex surrounding rock of tunnels and related evaluation method
在对国内外现行隧道围岩分级方法分析的基础上,指出了其在隧道工程设计和安全性控制,尤其是复杂围岩控制设计方面存在的突出问题,认为现行的隧道围岩分级概念模糊,难以适应复杂多变的地层条件和较为严苛的环境控制要求,尤其是对稳定性较差的复杂围岩条件缺乏有效的指导作用。从隧道围岩控制的宗旨出发,提出了隧道围岩及其支护系统安全性的概念,明确了其科学内涵和表征方法;重点对于不具备自稳能力的复杂围岩安全性进行了研究,建立了隧道围岩安全性的分析模型,提出了隧道围岩安全性分析中应考虑围岩预加固效果的必要性及其评价方法;基于隧道围岩尺度效应和地层结构效应(时间效应)的分析,建立了围岩尺度响应的表述方法,同时从细观结构层面分析了不同地层结构形式对安全性的影响关系;结合"支护–围岩"动态作用关系的分析,建立了极不稳定地层条件下复杂隧道围岩安全性的评价指标体系,将围岩超前变形、超前破坏和地层加固有效性作为核心评价指标,形成了包括9项基础指标的评价体系,并提出了安全性的分级方法。最后介绍了隧道围岩安全性的分级方案的工程应用。
基于超前加固的深埋隧道围岩力学特性研究
Research on the mechanical property of the surrounding rock of deep-buried tunnel based on the advanced reinforcement
复杂隧道围岩结构稳定性及其控制
作为隧道设计的核心问题,隧道围岩稳定性一直是隧道工程界研究的热点问题之一,能否对其准确评价是隧道穿越复杂地质条件安全施工的重要前提。针对该问题,首先通过模型试验对隧道围岩渐进破坏特征进行研究,指出围岩失稳破坏的阶段性特点,并通过对围岩失稳机理的分析,建立了隧道围岩失稳力学模型,提出了围岩失稳范围的确定方法。基于围岩失稳模式,将隧道围岩按其稳定性特点划分为浅层围岩和深层围岩,建立了复合隧道围岩结构模型,揭示了隧道围岩失稳的阶段性本质上是由深层围岩的分组运动所致,并就其结构稳定性特点进行了分析。考虑到地层条件的复杂多变,进一步对不同地层条件下复合围岩结构的表现形式进行了系统研究,提出了砂性围岩的"复合拱"效应和层状围岩的"梁式拱"结构型式以及"多层拱"效应,指出了各自的稳定性特点。最后,提出了复杂隧道围岩稳定性控制原理,研究成果可为隧道安全施工和支护设计提供理论依据。
Structural stability of complex tunnel surrounding rock and its control
作为隧道设计的核心问题,隧道围岩稳定性一直是隧道工程界研究的热点问题之一,能否对其准确评价是隧道穿越复杂地质条件安全施工的重要前提。针对该问题,首先通过模型试验对隧道围岩渐进破坏特征进行研究,指出围岩失稳破坏的阶段性特点,并通过对围岩失稳机理的分析,建立了隧道围岩失稳力学模型,提出了围岩失稳范围的确定方法。基于围岩失稳模式,将隧道围岩按其稳定性特点划分为浅层围岩和深层围岩,建立了复合隧道围岩结构模型,揭示了隧道围岩失稳的阶段性本质上是由深层围岩的分组运动所致,并就其结构稳定性特点进行了分析。考虑到地层条件的复杂多变,进一步对不同地层条件下复合围岩结构的表现形式进行了系统研究,提出了砂性围岩的"复合拱"效应和层状围岩的"梁式拱"结构型式以及"多层拱"效应,指出了各自的稳定性特点。最后,提出了复杂隧道围岩稳定性控制原理,研究成果可为隧道安全施工和支护设计提供理论依据。
隧道初期支护与围岩相互作用的时空演化特性
支护–围岩动态相互作用机制是支护设计的核心问题。首先基于弹塑性软化模型和非关联流动法则,对深埋圆形隧道进行弹塑性解析,并进一步考虑喷射混凝土的时效特性和隧道施工过程特点,建立初期支护–围岩耦合模型,得到了在隧道开挖过程中,距开挖面不同距离的各分析断面支护与围岩的动态相互作用关系。通过具体实例计算,对型钢和格栅钢架结构在不同支护时机下的支护效果进行了对比分析,并研究喷射混凝土硬化特性对于围岩稳定性控制效果和支护结构安全性的影响,基于此给出了合理支护时机的确定方法。得到如下主要结论:格栅相对于型钢初期支护刚度较小,有利于围岩应力和位移的释放,但同时控制围岩变形能力较差,对于支护时机的变化也更为敏感;对于初期支护而言,喷射混凝土支护力的发展过程可分为缓慢增长、快速增长、增长减缓、趋于稳定4个阶段,且各阶段的分布比例随支护时机变化而有所不同;在支护结构施作早期,喷射混凝土承担的荷载可能大于其当前极限承载能力而导致其失稳;支护时机的选取应综合考虑钢架类型、喷射混凝土硬化特性及隧道掘进速率,在保证支护结构安全性的前提下达到理想的支护效果。该研究成果可对初期支护–围岩动态作用关系进行全过程预测,可使得收敛约束法在隧道支护设计中的应用更为准确,为隧道施工过程中支护结构设计提供理论依据。
Spatial and temporal evolution characteristics of interaction between primary support and tunnel surrounding rock
支护–围岩动态相互作用机制是支护设计的核心问题。首先基于弹塑性软化模型和非关联流动法则,对深埋圆形隧道进行弹塑性解析,并进一步考虑喷射混凝土的时效特性和隧道施工过程特点,建立初期支护–围岩耦合模型,得到了在隧道开挖过程中,距开挖面不同距离的各分析断面支护与围岩的动态相互作用关系。通过具体实例计算,对型钢和格栅钢架结构在不同支护时机下的支护效果进行了对比分析,并研究喷射混凝土硬化特性对于围岩稳定性控制效果和支护结构安全性的影响,基于此给出了合理支护时机的确定方法。得到如下主要结论:格栅相对于型钢初期支护刚度较小,有利于围岩应力和位移的释放,但同时控制围岩变形能力较差,对于支护时机的变化也更为敏感;对于初期支护而言,喷射混凝土支护力的发展过程可分为缓慢增长、快速增长、增长减缓、趋于稳定4个阶段,且各阶段的分布比例随支护时机变化而有所不同;在支护结构施作早期,喷射混凝土承担的荷载可能大于其当前极限承载能力而导致其失稳;支护时机的选取应综合考虑钢架类型、喷射混凝土硬化特性及隧道掘进速率,在保证支护结构安全性的前提下达到理想的支护效果。该研究成果可对初期支护–围岩动态作用关系进行全过程预测,可使得收敛约束法在隧道支护设计中的应用更为准确,为隧道施工过程中支护结构设计提供理论依据。
Application of the convergence-confinement method of tunnel design to rock masses that satisfy the Hoek-Brown failure criterion
This paper discusses the practical application of the Convergence-Confinement Method of tunnel design to rock-masses that satisfy the Hoek-Brown failure criterion. The strength of intact rock and jointed rock-masses, as defined by the Hoek-Brown criterion, and the basis of the Convergence-Confinement method are reviewed. Equations that allow the construction of the three basic components of the Convergence-Confinement method, i) the Longitudinal Deformation Profile (LDP), ii) the Ground Reaction Curve (GRC) and iii) the Support Characteristic Curve (SCC) are given. A practical case of support design for a circular tunnel is discussed and solved using the Convergence Confinement method. A spreadsheet summarizing the implementation of the method is also included. Reference values of typical rock properties and geometrical and mechanical properties for typical support systems are presented in tables and charts.
考虑轴向力和渗透力时软化围岩隧道解析
<p>为了研究轴向应力和渗透力共同作用下软化围岩的应力与位移的变化及分布规律. 基于摩尔-库伦屈服准则及应力-应变软化模型并考虑轴向应力和渗透力的共同作用,将整个塑性区分为有限个同心圆环,以弹塑性交界面处的应力、应变为初始值,并采用微小径向应力增量逐步求出各个圆环上的应力应变及塑性区半径,据此重构了考虑渗透力和轴向力共同作用下软化围岩应力应变特性的逐步求解方法. 利用该方法,推导出软化围岩应力应变的解. 计算结果表明:在考虑轴向应力作用下,塑性区半径和隧道围岩位移都随着渗透力的增加而有所减小;当轴向应力为最小主应力时,渗透力的影响更为显著. 这说明渗透力的存在对于隧道围岩的应力应变分布以及塑性半径和围岩的位移有不可忽略的影响.</p>
Solution and analysis of circular tunnel for the strain-softening rock masses considering the axial in situ stress and seepage force
<p>为了研究轴向应力和渗透力共同作用下软化围岩的应力与位移的变化及分布规律. 基于摩尔-库伦屈服准则及应力-应变软化模型并考虑轴向应力和渗透力的共同作用,将整个塑性区分为有限个同心圆环,以弹塑性交界面处的应力、应变为初始值,并采用微小径向应力增量逐步求出各个圆环上的应力应变及塑性区半径,据此重构了考虑渗透力和轴向力共同作用下软化围岩应力应变特性的逐步求解方法. 利用该方法,推导出软化围岩应力应变的解. 计算结果表明:在考虑轴向应力作用下,塑性区半径和隧道围岩位移都随着渗透力的增加而有所减小;当轴向应力为最小主应力时,渗透力的影响更为显著. 这说明渗透力的存在对于隧道围岩的应力应变分布以及塑性半径和围岩的位移有不可忽略的影响.</p>
D-P 准则的盾构隧道围岩与衬砌结构相互作用分析
<p>在进行盾构隧道管片衬砌结构载荷计算时,常采用全土柱或压力拱理论计算围岩松动压力,但当盾构隧道面临深埋条件且需计入形变压力时,该方法难以适用.鉴于此,基于Drucker-Prager屈服准则,推导了考虑渗流效应影响下围岩与衬砌结构相互作用的弹塑性解析解,给出了围岩弹、塑性区应力与位移、塑性区半径等关键参数与支护阻力间关系的解析式.阐述了上述解析结果在确定衬砌结构载荷中的应用,即建立围岩与衬砌结构静力平衡状态并求二者对应曲线的交点.进一步地,考虑接头引起管片衬砌结构整体刚度降低对围岩与衬砌结构相互作用的影响,引入刚度折减系数,并在衬砌结构围岩压力确定中对施工期流固耦合效应的影响和渗流力对衬砌结构支护特性曲线的影响进行了简化处理.最后,通过算例将解析解与水下盾构隧道载荷实测值和数值计算值进行了比较.结果表明:用解析方法得到的施工期和稳定期的管片衬砌结构围岩压力比现场实测值分别大28%和12%,稳定期围岩压力比数值计算值大5%,可为类似工程的设计施工提供一定的参考价值.</p>
Theoretical analysis of interaction between surrounding rocks and lining structure of shield tunnel based on Drucker-Prager yield criteria
<p>在进行盾构隧道管片衬砌结构载荷计算时,常采用全土柱或压力拱理论计算围岩松动压力,但当盾构隧道面临深埋条件且需计入形变压力时,该方法难以适用.鉴于此,基于Drucker-Prager屈服准则,推导了考虑渗流效应影响下围岩与衬砌结构相互作用的弹塑性解析解,给出了围岩弹、塑性区应力与位移、塑性区半径等关键参数与支护阻力间关系的解析式.阐述了上述解析结果在确定衬砌结构载荷中的应用,即建立围岩与衬砌结构静力平衡状态并求二者对应曲线的交点.进一步地,考虑接头引起管片衬砌结构整体刚度降低对围岩与衬砌结构相互作用的影响,引入刚度折减系数,并在衬砌结构围岩压力确定中对施工期流固耦合效应的影响和渗流力对衬砌结构支护特性曲线的影响进行了简化处理.最后,通过算例将解析解与水下盾构隧道载荷实测值和数值计算值进行了比较.结果表明:用解析方法得到的施工期和稳定期的管片衬砌结构围岩压力比现场实测值分别大28%和12%,稳定期围岩压力比数值计算值大5%,可为类似工程的设计施工提供一定的参考价值.</p>
The elasto-plastic response of underground excavations in rock masses that satisfy the Hoek-Brown failure criterion
Illustrative applications of the derived closed-form solutions are also described. The construction of ground reaction curves for the design of cylindrical tunnels according to the convergence–confinement method and a case study of stability analysis of spherical cavities produced by underground nuclear explosions in French Polynesian atolls are discussed.
Practical estimates of rock mass strength
The Hoek-Brown failure criterion was originally developed for estimating the strengths of hard rock masses. Because of the lack of suitable alternatives, the criterion has been applied to a variety of rock masses including very poor quality rocks, which could almost be classed as engineering soils. These applications have necessitated changes to the original criterion. One of the principal problems has been the determination of equivalent cohesive strengths and friction angles to meet the demands of software written in terms of the Mohr-Coulomb failure criterion. This paper summarises the interpretation of the Hoek-Br own failure criterion which has been found to work best in dealing with practical engineering problems.
A simple procedure for ground response curve of circular tunnel in elastic-strain softening rock mass
This paper presents a simple procedure for the ground response curve of a circular tunnel excavated in elastic-strain softening rock mass compatible with a linear Mohr–Coulomb or a nonlinear Hoek–Brown yield criterion. The numerical stepwise procedure proposed by Brown et al. [Brown, E.T., Bray, J.W., Ladanyi, B., Hoek, E., (1983). Ground response curves for rock tunnels. J. Geotech. Eng. ASCE 109, 15–39] is modified by including the effects of elastic strain increments and variable dilatancy within the plastic region. The accuracy and practical application of the proposed procedure are shown through some examples. Four different combinations of dilatancy angle and softening parameter are considered to investigate the effects of elastic strain increments and variable dilatancy within the plastic region. The effects of variable dilatancy and peak dilatancy angle on the ground response curve are investigated for tunnels in poor-to-good-quality rock masses. The results show the importance of correctly estimating peak dilatancy angle in elastic-perfectly plastic and elastic-strain softening Hoek–Brown media.
软弱破碎围岩隧道超前支护确定方法
How to determine the types and parameters of the advance support is an important work in tunnel construction under conditions of unfavourable rocks. In this research, the determination method of tunnel advance support is established which includes three aspects:construction safety assessment,mode selection and parameters determination of advance support. Firstly,the predicted deformation value of tunnel surrounding rock and its control standard value are compared to determine whether the advance support is required; Furthermore, the engineering analogy method is used to determine the modes of advance support,and through comparing the predicted deformation value adopting advance support with control standard value ,the mode of advance support is determined;On this basis,the sensitivity and effectiveness of support parameters are analyzed to determine the upper and lower bounds of support parameters. The method has successfully applied in shallow covered Hejie high-speed railway tunnel. A new idea of quantitative determination of advanced supports has been proposed to improve the previous experience design method. This research has certain guiding significance in theoretical research and engineering practice of tunnel construction under the condition of unfavourable rocks.
Determination of advance supports in tunnel construction under unfavourable rock conditions
How to determine the types and parameters of the advance support is an important work in tunnel construction under conditions of unfavourable rocks. In this research, the determination method of tunnel advance support is established which includes three aspects:construction safety assessment,mode selection and parameters determination of advance support. Firstly,the predicted deformation value of tunnel surrounding rock and its control standard value are compared to determine whether the advance support is required; Furthermore, the engineering analogy method is used to determine the modes of advance support,and through comparing the predicted deformation value adopting advance support with control standard value ,the mode of advance support is determined;On this basis,the sensitivity and effectiveness of support parameters are analyzed to determine the upper and lower bounds of support parameters. The method has successfully applied in shallow covered Hejie high-speed railway tunnel. A new idea of quantitative determination of advanced supports has been proposed to improve the previous experience design method. This research has certain guiding significance in theoretical research and engineering practice of tunnel construction under the condition of unfavourable rocks.
Analysis of structural interaction in tunnels using the convergence-confinement approach
The rock-support interaction in tunnels is studied through the use of the convergence–confinement method. The equations that characterize the behaviour of the most important support types are given together with a set of conceptual interaction schemes. As far as the behaviour of the support is concerned, reference is made to the ultimate limit state concept, which is widely used in civil engineering. This approach is linked to the classical convergence–confinement method. The interaction between the temporary support system and the final lining is dealt with, and the noteworthy case of presupport ahead of the face, followed by a further internal support (usually steel sets and shotcrete) is also included. Finally, the ‘ground reaction curve of the reinforced tunnel’, which allows one to analyse the interaction between the reinforcement around the tunnel and supports, is introduced.
深埋隧道软弱围岩支护体系受力特征的试验研究
软弱围岩由于强度低、稳定性差、变形持续时间长等特点,在隧道施工中常引起大变形、崩塌等破坏现象,导致初支结构强烈变形甚至破坏,严重影响隧道施工和安全,是隧道建设中遇到的主要难题之一。通过对贵阳—广州铁路天平山隧道试验段锚杆轴力、围岩压力及钢架应力的监测,分析各支护构件的受力特征。研究结果表明:对于初期变形速率较大的软弱围岩,锚杆轴力多呈中间大、两端小的分布型式,且轴力变化历时长,不易稳定;在同等地质软弱围岩条件下,型钢钢架的围岩压力比格栅钢架增大70%~90%,型钢钢架的应力分布较均匀,支护效果要优于格栅钢架。
Experimental study of mechanical characteristics of support system for weak surrounding rock of deep tunnels
软弱围岩由于强度低、稳定性差、变形持续时间长等特点,在隧道施工中常引起大变形、崩塌等破坏现象,导致初支结构强烈变形甚至破坏,严重影响隧道施工和安全,是隧道建设中遇到的主要难题之一。通过对贵阳—广州铁路天平山隧道试验段锚杆轴力、围岩压力及钢架应力的监测,分析各支护构件的受力特征。研究结果表明:对于初期变形速率较大的软弱围岩,锚杆轴力多呈中间大、两端小的分布型式,且轴力变化历时长,不易稳定;在同等地质软弱围岩条件下,型钢钢架的围岩压力比格栅钢架增大70%~90%,型钢钢架的应力分布较均匀,支护效果要优于格栅钢架。