引 言
橡胶材料作为减振、密封等部件的材料在工业中广泛应用,建立橡胶材料的准确可靠的本构关系具有重要的意义[1-2].橡胶的弹性是橡胶材料的基本特性,是橡胶材料力学特性中研究比较早的一个方面,也是建立更全面的橡胶材料力学模型如黏弹性模型等的基础[2-3].现在已经发展出了较多的橡胶弹性模型,主要有两类,一类是唯象学模型,基于连续介质力学的理论推导和材料的宏观实验来构造模型;另一种是分子链模型或者统计学模型,基于橡胶内部分子链的结构和分布特性,通过统计学和热力学原理来得出材料的宏观特性.代表性的唯象学模型包括Mooney{\ziju{-0.04}模型[4]、Treloar模型[5]、Rivlin模型[6]、Ogden模型[7]、Yeoh模型[8]、Gent模型[9]、Shariff}模型[10]、Carroll模型[11]和Mansouri模型[12]等.分子链模型有Arruda-Boyce模型[13]、Kaliske模型[14]、Miehe模型[15]、Drozdov模型[16]、Kroon模型[17]、Davidson模型[18]和 Khi\^{e}m 模型[19]等.
唯象学模型基于连续介质力学的理论,力图从宏观现象的尺度上描述橡胶材料的力学特性,但连续介质力学只给出了模型的基本框架:模型的自变量、模型应该满足的一些约束,如标架无关性、各向同性等,但并未给出模型的具体形式.不同的研究者基于各种猜想[20],提出各种各样具体的模型形式,试图拟合实验数据.分子链模型基于橡胶分子链的构型和分布规律,以及热力学和统计方法来构造橡胶材料的本构模型,但其中的几个关键问题并没有得到很好的解决,如描述分子链构象的高斯和非高斯分布模型,表示分子链相互作用的仿射、Tube和Phantom等分子链网格结构模型,以及在整体上累积和平均分子链能量的统计方法如单位球等方法.研究[21]表明仿射模型和高斯分布模型与实验不符,而很多分子链模型基于上述两个或一个模型.同时现有分子链的统计特性和分子链的网络结构基本上都是假设,并非是真实的材料结构.
研究[19]表明,当前只有Ogden模型[7]、Shariff模型[10]、Kaliske模型[14]和Miehe模型[15]能较好地同时拟合单轴拉伸、平面拉伸和等双轴拉伸实验.值得注意的是,Ogden模型和Shariff模型都属于可分离变量的唯象学模型,可分离变量这种假设难以找到物理根据,但该类模型却具有更准确和更广泛的拟合能力,这说明橡胶材料本构理论还存在较多空白区.对于物理模型来说,一种实验就可确定模型参数,但文献[22]对已提出的十几种代表性的橡胶模型的研究表明:上述模型没有一个能以单类实验数据准确预测材料特性,说明已有模型距离物理模型还很远.另一方面,大多数实验室缺乏进行平面拉伸和等双轴拉伸实验的能力.因此迫切需要提出一种拟合能力强、但可靠性高的模型,能以更少类型的实验数据更好地描述材料力学特性[23].为解决这个问题,本文基于第一和第二主伸长率提出了一种的新的橡胶弹性本构模型,实验数据拟合结果表明其具有很好的拟合能力和更好的可靠性.
1 一种新的本构模型
假设橡胶材料是各向同性、不可压缩的,其本构模型需要满足各向同性、材料的客观性以及不可压缩这几个要求.根据连续介质力学的理论,橡胶材料作为简单材料,其应力可由一次变形梯度来表示;如果要满足各向同性的假设,本构模型对初始构型的任意正交变换${{\boldsymbol Q}}$,保持形式不变,因此
其中,${{\boldsymbol V}}$为左伸长张量.再结合模型客观性的要求,可得到其一般形式[23]
其中,$I_V = \lambda _1 + \lambda _2 + \lambda _3 ,\;II_V = \lambda _1 \lambda _2 + \lambda _1 \lambda _3 + \lambda _2 \lambda _3$,$III_V = \lambda _1 \lambda _2 \lambda _3$分别为${{\boldsymbol V}}$的第一、第二和第三不变量;$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\over {\phi }} _k ( \cdot )\;(k = 0,1,2)$和$\phi _k ( \cdot )(k = 0,1,2)$是两个标量值函数,也是${{\boldsymbol V}}$的不变量;$\lambda _1 ,\lambda _2 ,\lambda _3$为3个主伸长率. 将式(2)在当前变形的主坐标系上写出,可得到文献[21]的形式
式中,$\sigma _i$表示主应力,下标$i,j,k$为$1,2,3$的一个排列.考察式(2)或者根据本构客观性的要求,上式需要满足如下约束条件[21]
式(3)和式(4)的物理意义非常明确,即对于各向同性材料,在各个主方向上应力的表达式是相同的或者说是对称的.在上述表达式中,模型是定义在主方向上,主应力和主伸长率不随观察坐标系而变化,满足模型的客观性要求.但式(3)中各个主伸长率对该式左边应力的贡献大小未必一样,为此通过函数$g(\cdot)$中自变量的排列顺序来表示这种差异,也就是说该函数中自变量的排列顺序是有意义的,不能随意变化.
由于橡胶材料是不可压缩的,这时需要附加一个约束条件,此时本构关系变为
其中,$\hat {p}$为静水压力,是一个标量,在3个主应力表达式中取同一值,但值的大小是任意的,无法单独由变形状态确定,需要结合边界条件才能确定.如令$\sigma _k \mbox{ = }p$,并考虑到不可压缩条件$\lambda _i \lambda _j \lambda _k = 1$,式(5)可进一步写作
其中,$g(\lambda _i ,\lambda _j )\mbox{ = }\hat {g}(\lambda _i ,\lambda _j ,\lambda _k )-\hat {g}(\lambda _k ,\lambda _j ,\lambda _i )$,$p$为任意静水压力值.上式中k可为3个主方向中的任意一个,即式(6)的表达式要满足式(4)的约束:$g(\lambda _i ,\lambda _j )\mbox{ = }g(\lambda _i ,\lambda _k)$,满足这个条件比较困难,如果指定k方向为伸长率最小的方向,并将柯西应力转变为名义应力,可得
其中,$\phi (\lambda _i ,\lambda _j )\mbox{ = }g(\lambda _i ,\lambda _k ) / \lambda _i$,$\overline {\lambda _i } \;(i = 1,2,3)$分别表示按从大到小排序的3个主伸长率,参照工程中第一、第二、第三主应变的概念,此处称为第一、第二和第三主伸长率,本文在伸长率或应力符号的上面加"$^{\mbox-}$"表示其是按大小排序的.因为第三主应力或者第三主方向可以很容易地从变形状态确定,这使得模型不必要满足式(4)的本构客观性要求.从式(7)可以看出,建立本构关系的关键是写出$\phi (\overline {\lambda _i } ,\overline {\lambda _j } )$的形式.直接写出该函数的形式非常困难,由于平面拉伸下名义应力$T(\overline {\lambda _i } ,1)\mbox{ = }\phi (\overline {\lambda _i },1)$只包含一个自变量,并且该函数可由实验数据用多项式等形式直接拟合得到,本文以平面拉伸函数为基函数,通过变换自变量将该基函数$\phi _{\rm{planar}} (\overline \lambda ,\mbox{1}) = T_{\rm{planar}} (\overline \lambda )$推广为平面应力状态的一般模型
其中,$\Delta (\overline \lambda _i ,\overline \lambda _j )$为自变量的一个修正函数,其物理意义为在同样大小的名义应力、不同的侧面约束作用下,材料伸长长度的差值.此处需要特别说明的是,在本文$\phi (\overline {\lambda _i } ,\overline {\lambda _j } )$的$\overline {\lambda _i } ,\overline {\lambda _j }$只能为$\overline {\lambda _1 }$,$\overline {\lambda _2 }$的一个排列,两个自变量不能相同. 此时满足下式
除非特殊说明,下面所有关于$\phi (\overline {\lambda _i } ,\overline {\lambda _j } )$的两个自变量都做上述规定.
由式(6)知,$\phi (\overline {\lambda _i } ,\overline {\lambda _j } )$是平面应力状态下的本构关系,因为假设材料满足柯西弹性(应力可由当前变形状态唯一确定),需要满足如下的约束条件
此不等式的物理意义是要求应力随着两个自变量的增大而单调递增,从而应变状态和应力状态是唯一对应的.考虑到在单轴应力作用下,侧面的应力等于零,可以得到如下约束条件
根据对材料的实验数据(即下面参数拟合所用的六组数据)的拟合发现材料还需满足如下约束
该约束的物理意义是侧面约束,无论是侧面拉伸约束还是侧面压缩约束,都会增加材料的刚度.平面拉伸应力函数可以采用任何形式,该函数通过实验数据拟合保证其单调性并且满足$T_{\rm{planar}} \mbox{(}1)\mbox{ = }0$. 通过参数拟合,本文采用如下形式
其中a,$b$,c为模型参数.
平面拉伸应力函数可以采用任意其他能拟合实验数据的函数.作为一般的要求,该函数需要是单调函数,并且满足$T_{\rm{planar}} \mbox{(}1)\mbox{ = }0,\;\mathop {\lim }\limits_{\overline {\lambda _1 } \to \infty } T_{\rm{planar}} \mbox{(}\overline {\lambda _1 } )\mbox{ = }\infty$.因为通过平面拉伸实验一般可以获得足够多的实验数据,如果一个函数能很好地拟合实验数据,上述要求会自动满足.因此可将平面拉伸函数$T_{\rm{planar}} \mbox{(}\overline {\lambda _1 } )$作为一个基本函数构造函数$\phi (\bar {\lambda }_i ,\bar {\lambda }_j )$. 自变量增量$\Delta (\overline \lambda _i ,\overline \lambda _j )$需要满足式(14)的约束
其中第一项保证该模型兼容平面拉伸模型;第二项的$h$是非常小的正常数,表示当伸长率很大时,不同的侧面约束对材料拉伸方向的影响基本可以忽略,平面拉伸曲线会非常接近单轴拉伸曲线;第三项保证单轴拉伸的侧面应力为零;第四项表示当侧面有约束时,无论是拉伸还是压缩,材料的刚度都会增大,即侧面约束为1时,材料的刚度最小,该项是否需要严格保证有疑问,从Ogden函数的预测情况来看,并不需要严格满足;第五项表示在相同的拉伸力下,侧面压缩程度越大,材料在拉伸方向的伸长率越大.值得注意的是上述约束条件中仅第一项和第三项需要严格保证,其他几项由Ogden模型、Khi\^{e}m模型等预测显示的规律得出,本文中所有数据拟合的结果具有类似的规律,参见附录中图6、图12和图13所示.这几条是否需要严格满足并没有确切的定论.根据上式的约束条件,本研究推出如下一个 模型
其中,$k,g$为模型常数.式(15)满足式(14)中的第一项和第二项约束条件
由式(9)可知$\overline{\lambda}_{i}\sqrt{\overline{\lambda}}$总大于1,且当$\sigma_{i}\to\sigma_{\max}$时取极大值。可直接验证,该函数满足第三项的要求
若$k \ge\mbox{1}$,总满足式(14)第四项第一条要求
从Ogden模型的拟合结果来看,第四项第二条非严格满足,但$g\ge 1$是需满足的一个必要条件. 第五项需要在材料可能的变形范围内满足,但由于材料实际拉伸压缩的区间有限,没必要在0到无穷大曲线满足,在伸长率为0.5到材料拉断这个区间就足够.可在后面拟合结果对该项要求进行验证.式(15)为本文根据约束(9)~(12)为$\Delta (\overline \lambda _i ,\overline \lambda _j )$提出的一个模型,可以按照这个方法提出更多模型.
将式(15)代入式(8)中,可以得到
该式其实为$T_{\rm 3} \mbox{ = 0}$平面应力状态下的本构模型,再结合式(13)和式(19)构成了适用于三轴一般应力状态的模型,即
该模型为各向同性、不可压缩的柯西弹性模型,建立在一个特定的主坐标上,直接给出以伸长率表示的应力表达式,不局限于超弹性这个假设,只要材料的应力可以由当前变性状态确定即可.方向3为伸长率最小的主方向,可直接由变形状态确定.该模型的提出除了满足材料的客观性和各向同性要求外,另外提出并引入了式(10)、式(11)、式(12)三个约束条件,结合平面拉伸函数,很大程度上限制了本构函数的形式,同时该模型采用多项式的形式,有利于参数拟合值的唯一性.从下面与实验数据对比来看,模型有很好的拟合能力和更高的可靠性.
2 模型分析和讨论
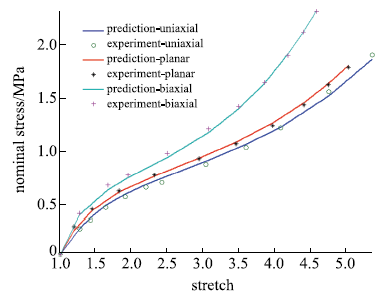
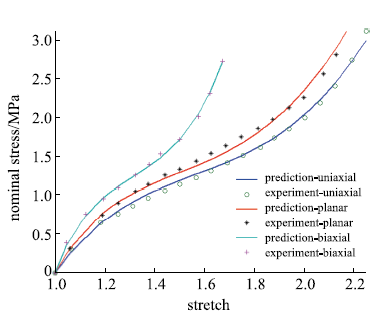
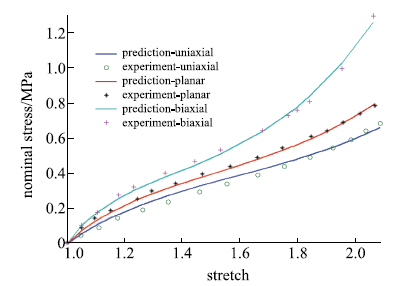
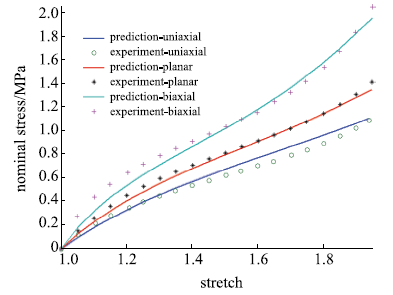
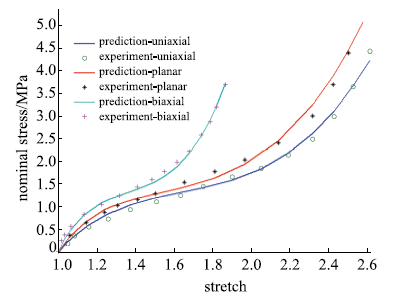
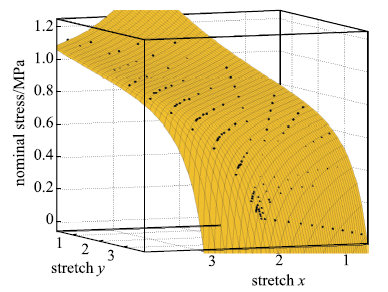
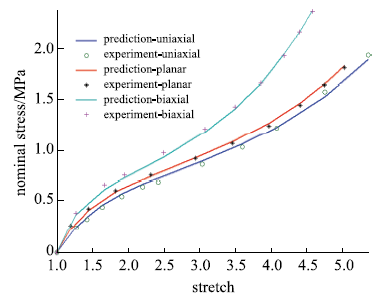
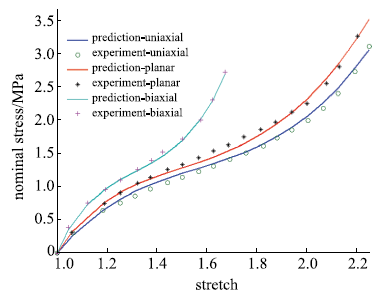
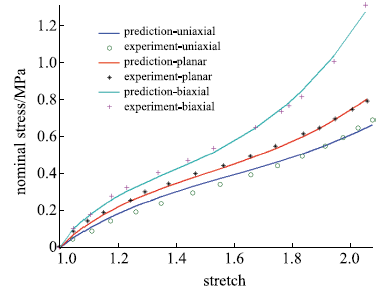
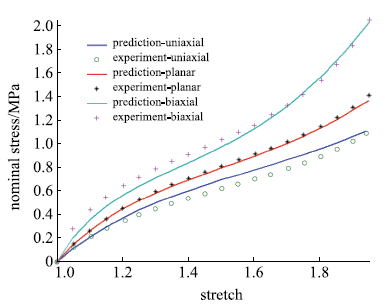
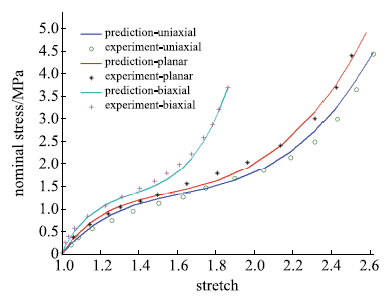
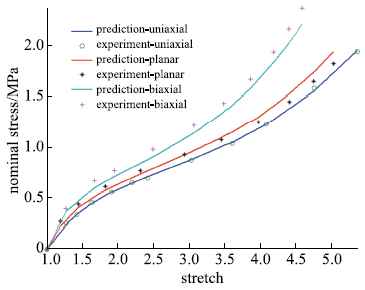
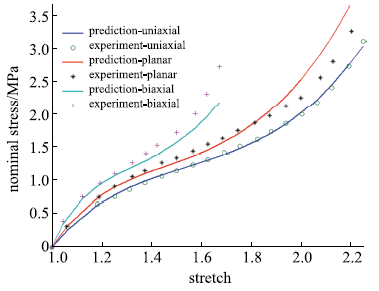
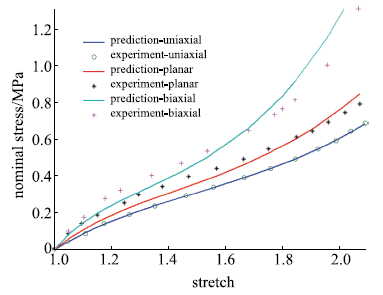
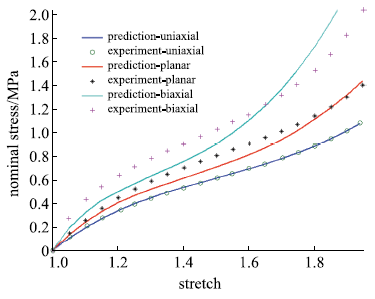
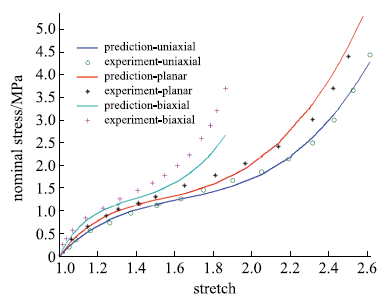
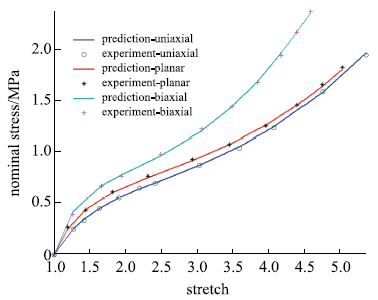
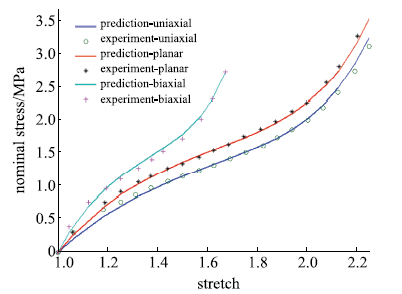
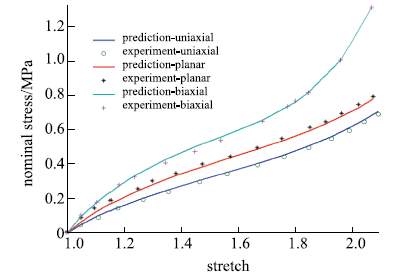
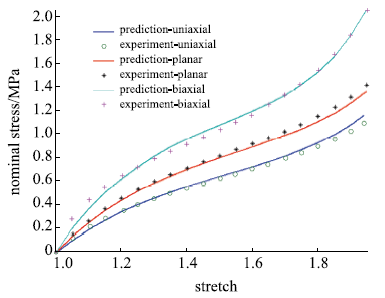
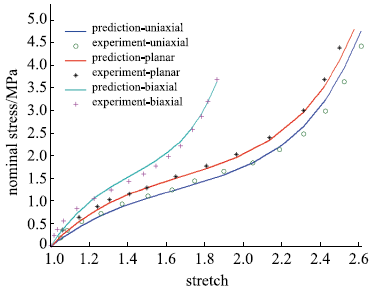
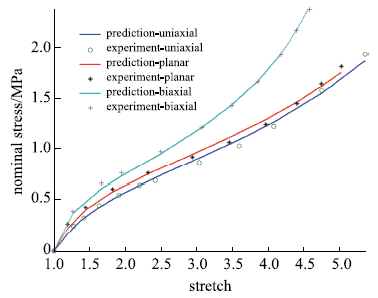
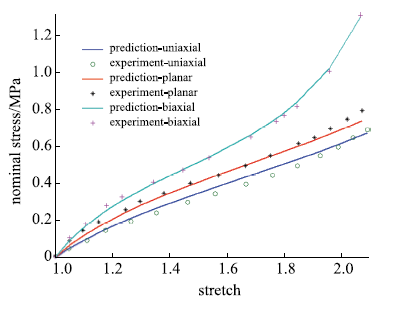
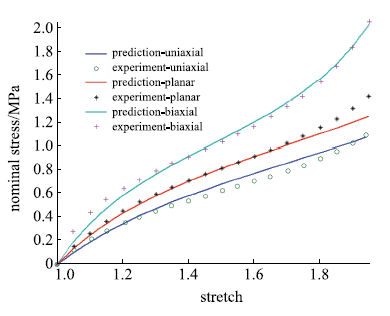
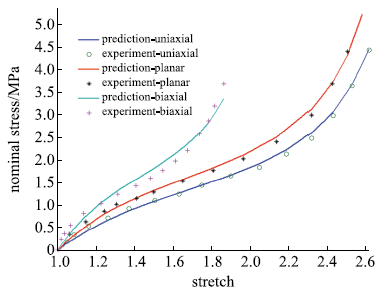
包含单轴拉伸、平面拉伸和等双轴拉伸的橡胶材料全面测试数据相对较少,大多数文献中模型验证仅使用了部分类型的实验.要可靠地验证橡胶材料模型,应该采用上述全部三类实验数据.本文从现有文献和实验所能找到的包含三类实验的数据对该模型进行全面的验证,分析模型的拟合能力和可靠性.其中第二组美国Axel实验室测试数据为上海众力公司提供,其他另外两组Axel实验数据来自文献.单轴拉伸和等双轴拉伸应力由式(19)可得到
曲线拟合使用Matlab中的Lsqcurvefit函数,曲面拟合使用curve fitting 工具箱,均基于Levenberg-Marquard算法. 模型参数初值除$g=1$外,其他均为零.
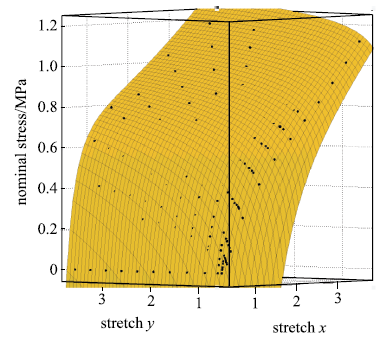
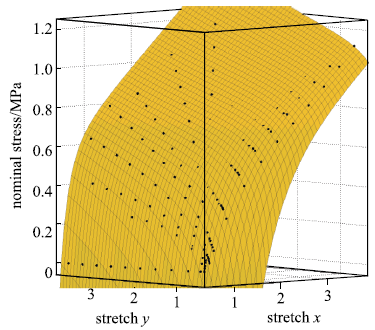
拟合获得参数如表1所示,拟合情况如图1~图6所示,与三阶Ogden模型以及Khi\^{e}m模型的拟合精度对比可参照附录中的拟合情况,本模型的精度不低于甚至优于上述两个模型.Kawabata数据是现有文献中对橡胶材料实验最充分的数据,本模型的拟合精度与上述两个模型的对比见表2所示,其中SSE (sum of squares for error)为加权方差, RMSE (root mean squared error)为标准差,R-square (coefficient of determination)表示确定系数和adjusted R-square (degree-of-freedom adjusted coefficient of determination)表示调整的确定系数,前两项越接近零越好,后两项越接近1越好.具体可参见Matlab帮助文件.从拟合情况可以看出,本模型对该组数据的拟合精度好于Ogden但稍逊与Khi\^{e}m模型,但在前5组数据拟合中,Khi\^{e}m模型的拟合精度最差,对初值的依赖程度也更大,值得说明的是本文提出模型的参数拟合对初始值的依赖非常小,而其他模型如Ogden模型和Khi\^{e}m模型等对参数初值的依赖程度很大,如果初始值不好,拟合情况会非常差.
表1 拟合获得模型参数(5个)
Table 1
表2 对Kawabata数据的拟合情况对比
Table 2
| Model | SSE | R-square | Adjusted R-square | RMSE |
|---|---|---|---|---|
| proposed | 0.022 28 | 0.998 8 | 0.998 7 | 0.0124 |
| Ogden model | 0.058 16 | 0.996 8 | 0.9967 | 0.0201 |
| Khiem model | 0.021 00 | 0.998 9 | 0.998 8 | 0.0120 |
图1
图2
图3
图4
图4
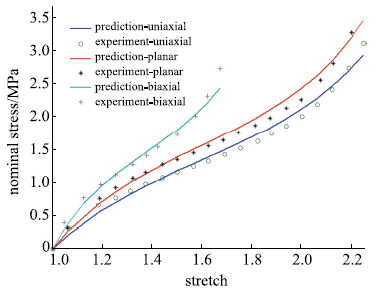
模型对第二组Axel数据的拟合情况
Fig.4
The proposed model fitted to the second group of data tested by Axel laboratory
图5
图6
表3 拟合获得的模型参数(A=1.5)
Table 3
图7
图8
图9
图10
图10
模型对第二组Axel数据的拟合情况
Fig.10
The proposed model fitted to the second group of data tested by Axel laboratory
图11
表4 只用单轴拉伸数据拟合获得材料参数
Table 4
图12
图13
图14
图15
图15
模型对第二组Axel数据的拟合情况
Fig.15
The proposed model fitted to the second group of data tested by Axel laboratory
图16
3 结 论
虽然已经有较多的橡胶本构模型,但已有模型在适用的广泛性和可靠性上还存在较大的问题.本文由一种新的基于第一和第二主伸长率的橡胶弹性本构模型形式,以平面拉伸的应力-应变关系函数为基函数,提出了一种新的方法,将基函数拓展为适用于平面应力和三轴应力情况下的一般模型.通过对实验数据的拟合发现,该模型能够很好地拟合所有实验数据,对参数初始值的依赖性很小,只用单类实验数据就能获得较为可靠的模型参数,比已有模型具有更好的可靠性.该模型为不可压缩、各向同性柯西弹性模型,可以基于实验数据逐步构造模型,具有更广泛的适用性.本文的研究其实基于作者提出的一种新的、建立在一个特定的主坐标系下的,直接以第一和第二主伸长率表示主应力的,由某一类型的实验数据拟合得到的函数拓展为一般三轴模型的本构框架或者建模方法,可以实现step by step的本构模型构建和参数拟合,有利于控制提出模型的精度,模型具有很好的拟合能力和可靠性.特别的,本文基于这种方法提出了一个新的模型并对该模型进行了分析和验证.
附录:其他部分模型拟合情况
(1) 三阶Ogden模型[7]
其中,$\mu _n$和$a_n$为模型常数.
表A1 Ogden模型拟合获得模型参数
Table A1
图A1
图A2
图A3
图A4
图A4
Ogden模型对第二组Axel数据的拟合情况
Fig.A4
The Ogden model fitted to the second group of data tested by Axel laboratory
图A5
图A6
(2)Khiêm 模型[19]
其中,a,b,c,d为材料参数.
表A2 Khiem模型拟合获得的参数
Table A2
图A7
图A8
图A9
图A10
图A10
Khiêm模型对第二组Axel数据的拟合情况
Fig.A10
The Khiêm model fitted to the second group of data tested by Axel laboratory
图A11
图A12
图A13
参考文献
弹簧-金属丝网橡胶组合减振器迟滞力学模型及实验研究
金属丝网橡胶材料是一种完全由金属丝编织成的多孔复合材料,与传统螺旋卷制金属橡胶材料相比,其改进了成型工艺,剔除了制备过程中大量的手工工艺干扰,提高机械化程度,重合度更高,拥有更稳定的力学性能.由于金属丝网橡胶材料具有承载能力高、阻尼大、耐高温、耐低温、耐老化、抗油抗腐蚀等优良特性,在很多方面强于传统橡胶,多用于航空航天、船舶、军事武器等军工工业.弹簧—金属丝网橡胶组合减振器具有可设计刚度和较高承载能力,但因其具有复杂的非线性迟滞特性,目前相关材料的本构模型还难以准确描述其力学特性.本文在弹簧—金属丝网橡胶组合减振器静态迟滞力学性能实验的基础上,结合其干摩擦阻尼迟滞特性,提出了一种迟滞力学性能理论模型.根据减振器迟滞实验恢复力—位移曲线特点,利用参数分离的方法将迟滞曲线分解为弹性恢复力和干摩擦阻尼力,分别建模求解等效刚度和干摩擦阻尼系数,以此建立了组合减振器理论模型,并与实验结果进行对比及进行误差分析,验证了理论模型的准确性.
Hysteresis mechanical model and experimental study of spring metal-net rubber combination damper
金属丝网橡胶材料是一种完全由金属丝编织成的多孔复合材料,与传统螺旋卷制金属橡胶材料相比,其改进了成型工艺,剔除了制备过程中大量的手工工艺干扰,提高机械化程度,重合度更高,拥有更稳定的力学性能.由于金属丝网橡胶材料具有承载能力高、阻尼大、耐高温、耐低温、耐老化、抗油抗腐蚀等优良特性,在很多方面强于传统橡胶,多用于航空航天、船舶、军事武器等军工工业.弹簧—金属丝网橡胶组合减振器具有可设计刚度和较高承载能力,但因其具有复杂的非线性迟滞特性,目前相关材料的本构模型还难以准确描述其力学特性.本文在弹簧—金属丝网橡胶组合减振器静态迟滞力学性能实验的基础上,结合其干摩擦阻尼迟滞特性,提出了一种迟滞力学性能理论模型.根据减振器迟滞实验恢复力—位移曲线特点,利用参数分离的方法将迟滞曲线分解为弹性恢复力和干摩擦阻尼力,分别建模求解等效刚度和干摩擦阻尼系数,以此建立了组合减振器理论模型,并与实验结果进行对比及进行误差分析,验证了理论模型的准确性.
帘线/橡胶复合材料各向异性黏-超弹性本构模型
<p>帘线/橡胶复合材料广泛应用于轮胎等重要工程领域,为了描述其在服役条件下的大变形、非线性、各向异性和高应变率等材料力学行为,基于纤维增强复合材料连续介质力学理论,提出了一种考虑应变率效应的帘线/橡胶复合材料各向异性黏-超弹性本构模型. 该模型中单位体积的应变能被解耦为便于参数识别的基体等容变形能、帘线拉伸变形能、剪切应变能和黏性应变能四部分. 给出了模型参数的确定方法,并通过拟合文献中单轴拉伸、偏轴拉伸实验数据,得到了模型参数. 利用该模型预测了不同加载和变形条件下的力学行为,并将预测结果与实验结果对比分析. 结果表明, 考虑黏性模型和不考虑黏性模型对不同应变率变形条件下的预测结果相差很大,且考虑黏性模型的预测结果与实验结果吻合很好. 因此,与不考虑黏性模型相比,所提出的各向异性黏-超弹性本构模型能更好地表征帘线/橡胶复合材料在大变形、高应变率条件下的力学特性.</p>
An anisotropic visco-hyperelastic constitution model for cord-rubber composites
<p>帘线/橡胶复合材料广泛应用于轮胎等重要工程领域,为了描述其在服役条件下的大变形、非线性、各向异性和高应变率等材料力学行为,基于纤维增强复合材料连续介质力学理论,提出了一种考虑应变率效应的帘线/橡胶复合材料各向异性黏-超弹性本构模型. 该模型中单位体积的应变能被解耦为便于参数识别的基体等容变形能、帘线拉伸变形能、剪切应变能和黏性应变能四部分. 给出了模型参数的确定方法,并通过拟合文献中单轴拉伸、偏轴拉伸实验数据,得到了模型参数. 利用该模型预测了不同加载和变形条件下的力学行为,并将预测结果与实验结果对比分析. 结果表明, 考虑黏性模型和不考虑黏性模型对不同应变率变形条件下的预测结果相差很大,且考虑黏性模型的预测结果与实验结果吻合很好. 因此,与不考虑黏性模型相比,所提出的各向异性黏-超弹性本构模型能更好地表征帘线/橡胶复合材料在大变形、高应变率条件下的力学特性.</p>
短纤维增强三元乙丙橡胶横观各向同性黏-超弹性本构模型,
短纤维增强三元乙丙橡胶包覆薄膜,是一种应用于固体火箭发动机缠绕包覆装药的新型复合材料.为了描述其在工作过程中受振动、冲击等载荷作用时的力学行为,基于黏弹性理论和纤维增强连续介质力学理论,提出了一种考虑应变率强化效应的横观各向同性黏--超弹本构模型.模型中应变能函数被分解为超弹性应变能和黏性应变能,其中超弹性应变能包括表征各向同性的橡胶基体应变能和表征各向异性的纤维拉伸应变能,黏性应变能采用表征橡胶和纤维黏性响应的宏观唯象模型.选取表征各应变能的函数形式,经过数学变换、替代、叠加,求解确定最终的应力应变形式,明确模型参数获取的具体步骤,将预测结果与实验结果对比分析,准确性较高.研究表明:该模型能有效预测材料在低应变率下纤维方向为045的非线性率相关力学特性;模型形式易于实现有限元开发,对固体火箭发动机装药结构完整性分析具有参考价值.
A transversely isotropic visco-hyperelastic constitutive model for short fiber feinforced EPDM
短纤维增强三元乙丙橡胶包覆薄膜,是一种应用于固体火箭发动机缠绕包覆装药的新型复合材料.为了描述其在工作过程中受振动、冲击等载荷作用时的力学行为,基于黏弹性理论和纤维增强连续介质力学理论,提出了一种考虑应变率强化效应的横观各向同性黏--超弹本构模型.模型中应变能函数被分解为超弹性应变能和黏性应变能,其中超弹性应变能包括表征各向同性的橡胶基体应变能和表征各向异性的纤维拉伸应变能,黏性应变能采用表征橡胶和纤维黏性响应的宏观唯象模型.选取表征各应变能的函数形式,经过数学变换、替代、叠加,求解确定最终的应力应变形式,明确模型参数获取的具体步骤,将预测结果与实验结果对比分析,准确性较高.研究表明:该模型能有效预测材料在低应变率下纤维方向为045的非线性率相关力学特性;模型形式易于实现有限元开发,对固体火箭发动机装药结构完整性分析具有参考价值.
A theory of large elastic deformation
It is postulated that (A) the material is isotropic, (B) the volume change and hysteresis are negligible, and (C) the shear is proportional to the traction in simple shear in a plane previously deformed, if at all, only by uniform dilatation or contraction. It is deduced that the general strain‐energy function,W, has the formW=G4∑i=13(λi611λi)2+H4∑t=13(λi2611λi2),where the λi's are the principal stretches (1+principal extension),Gis the modulus of rigidity, andHis a new elastic constant not found in previous theories. The differences between the principal stresses are σi[minus]σi=λi68W/68λi[minus]λi68W/68λi. Calculated forces agree closely with experimental data on soft rubber from 400 percent elongation to 50 percent compression.
The elasticity of a network of long-chain molecules-I
Large elastic deformations of isotropic materials. IV. Further developments of the general theory
Large deformation isotropic elasticity-on the correlation of theory and experiment for incompressible rubberlike solids
Many attempts have been made to reproduce theoretically the stress-strain curves obtained from experiments on the isothermal deformation of highly elastic 'rubberlike' materials. The existence of a strain-energy function has usually been postulated, and the simplifications appropriate to the assumptions of isotropy and incompressibility have been exploited. However, the usual practice of writing the strain energy as a function of two independent strain invariants has, in general, the effect of complicating the associated mathematical analysis (this is particularly evident in relation to the calculation of instantaneous moduli of elasticity) and, consequently, the basic elegance and simplicity of isotropic elasticity is sacrificed. Furthermore, recently proposed special forms of the strain-energy function are rather complicated functions of two invariants. The purpose of this paper is, while making full use of the inherent simplicity of isotropic elasticity, to construct a strain-energy function which: (i) provides an adequate representation of the mechanical response of rubberlike solids, and (ii) is simple enough to be amenable to mathematical analysis. A strain-energy function which is a linear combination of strain invariants defined by φ (α)=(a1α+a2α+a3α-3)/α is proposed; and the principal stretches a1,a2 and a3 are used as independent variables subject to the incompressibility constraint a1a2a3=1. Principal axes techniques are used where appropriate. An excellent agreement between this theory and the experimental data from simple tension, pure shear and equibiaxial tension tests is demonstrated. It is also shown that the present theory has certain repercussions in respect of the constitutive inequality proposed by Hill (1968a, 1970b).
Some forms of the strain energy function for rubber
A new constitutive relation for rubber
Strain energy function for filled and unfilled rubber like material
A strain energy function for vulcanized rubbers
A three-parameter strain energy function is developed to model the nonlinearly elastic response of rubber-like materials. The development of the model is phenomenological, based on data from the...
Constitutive modeling of isotropic hyperelastic materials in an exponential framework using a self-contained approach
In this paper, an exponential framework for strain energy density functions of elastomers and soft biological tissues is proposed. Based on this framework and using a self-contained approach that is different from a guesswork or combination viewpoint, a set strain energy density functions in terms of the first and second strain invariants is rebuilt. Among the constructed options for strain energy density, a new exponential and mathematically justified model is examined. This model benefits from the existence of second strain invariant, simplicity, stability of parameters, and the state of being accurate. This model can capture strain softening, strain hardening and is able to differentiate between various deformation-state dependent responses of elastomers and soft tissues undergoing finite deformation. The model has two material parameters and the mathematical formulation is simple to render the possibility of numerical implementations. In order to investigate the appropriateness of the proposed model in comparison to other hyperelastic models, several experimental data for incompressible isotropic materials (elastomers) such as VHB 4905 (polyacrylate rubber), two various silicone rubbers, synthetic rubber neoprene, two different natural rubbers, b186 rubber (a carbon black-filled rubber), Yeoh vulcanizate rubber, and finally porcine liver tissue (a very soft biological tissue) are examined. The results demonstrate that the proposed model provides an acceptable prediction of the behavior of elastomers and soft tissues under large deformation for different applied loading states.
A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials
Aconstitutive model is proposed for the deformation of rubber materials which is shown to represent successfully the response of these materials in uniaxial extension, biaxial extension, uniaxial compression, plane strain compression and pure shear. The developed constitutive relation is based on an eight chain representation of the underlying macromolecular network structure of the rubber and the non-Gaussian behavior of the individual chains in the proposed network. The eight chain model accurately captures the cooperative nature of network deformation while requiring only two material parameters, an initial modulus and a limiting chain extensibility. Since these two parameters are mechanistically linked to the physics of molecular chain orientation involved in the deformation of rubber, the proposed model represents a simple and accurate constitutive model of rubber deformation. The chain extension in this network model reduces to a function of the root-mean-square of the principal applied stretches as a result of effectively sampling eight orientations of principal stretch space. The results of the proposed eight chain model as well as those of several prominent models are compared with experimental data of Treloar (1944, Trans. Faraday Soc. 40, 59) illustrating the superiority, simplicity and predictive ability of the proposed model. Additionally, a new set of experiments which captures the state of deformation dependence of rubber is described and conducted on three rubber materials. The eight chain model is found to model and predict accurately the behavior of the three tested materials further confirming its superiority and effectiveness over earlier models.
An extended tube-model for rubber elasticity: statistical mechanical theory and finite element implementation
A micro-macro approach to rubber-like materials. PartII: themicro spheremodel of finiterubber viscoelasticity
A micromechanically based non-affine network model for finite rubber elasticity incorporating topological constraints was discussed in Part I (2004. J. Mech. Phys. Solids 52, 2617 2660) of this work. In this follow-up contribution we extend the non-affine micro-sphere model towards the description of time-dependent viscoelastic effects. The viscoelastic network model is constructed by an additive split of the overall response into elastic equilibrium-stress and viscoelastic overstress contributions. The equilibrium response of the network is understood to be related to results obtained from an infinite relaxation process and modeled by our above mentioned elasticity formulation. Inspired by (2004. J. Mech. Phys. Solids 52, 2617 2660), the rate-dependent overstress response is assumed to be driven by two micro-kinematical mechanisms related to the stretch and the area contraction of a tube containing a prototype chain. Firstly, a retraction of fictitiously unconstrained dangling chains is explained by diffusive reptile motions. Secondly, a release of constraint effects due to surrounding chains is modeled by a time-dependence of a tube cross-section area. The latter contribution is considered to be a result of the retraction of forest chains. We outline a distinct micromechanical model for the viscous overstress in terms of the above outlined two micro-kinematic mechanisms and discuss its numerical implementation in context of an affine homogenization procedure of space orientations. The characteristics and modeling capabilities of the proposed micro-sphere model of finite rubber viscoelasticity are reported for a broad spectrum of experimentally-based benchmark simulations. They demonstrate an excellent performance of the model in simulating rate and hystereses effects of rubbery polymers.
Constitutive equations for the nonlinear elastic response of rubbers
A constitutive model is derived for the elastic behavior of rubbers at three-dimensional deformations with finite strains. An elastomer is thought of as an incompressible network of flexible chains bridged by permanent junctions that move affinely with the bulk medium. The constraints imposed by surrounding macromolecules on configurations of an individual chain are introduced by combining the Flory–Erman and Erman–Monnerie approaches. To describe inter-chain interactions in a tractable way, the conventional picture of a tube where a chain is confined is replaced by geometrical restrictions on the positions of its ends and center of mass. The constraints on the chain ends are formulated within the traditional Flory concept, whereas those on the position of center of mass are described following the Ronca–Allegra scenario. Stress–strain relations for a network of constrained chains are derived by using the laws of thermodynamics. The constitutive equations involve four adjustable parameters with transparent physical meaning. The material constants are found by fitting experimental data on elastomers at uniaxial and equi-biaxial tensions and pure shear. It is demonstrated that (i) the model provides an acceptable prediction of stresses in a test with one deformation mode, when its parameters are found by matching observations in an experiment with another mode, and (ii) material constants are affected by chemical composition of elastomers in a physically plausible way.
An 8-chain model for rubber-likematerials accounting for non-affinechain deformations and topological constraints
Several industrial applications involve rubber and rubber-like materials, and it is important to be able to predict the constitutive response of these materials. In the present paper, a new constitutive model for rubber-like solids is proposed. The model is based on the 8-chain concept introduced by Arruda and Boyce (J. Mech. Phys. Solids 41, 389 412, 1993 ) to which two new components are added. Real polymer networks do not deform affinely, and in the proposed model this is accounted for by the inclusion of an elastic spring, acting in series with the representative polymer chain. Furthermore, real polymer chains are not completely free to move, which is modelled by imposing a topological constraint on the transverse motions of the representative polymer chain. The model contains five model parameters and these need to be determined on the basis of experimental data. Three experimental studies from the literature were used to assess the proposed model. The model was able to reproduce experimental data performed under conditions of uniaxial tension, generalised plane deformation, and biaxial tension with an excellent accuracy. The strong predictive abilities together with the numerically efficient structure of the model make it suitable for implementation in a finite element context.
A nonaffine network model for elastomers undergoing finite deformations
In this work, we construct a new physics-based model of rubber elasticity to capture the strain softening, strain hardening, and deformation-state dependent response of rubber materials undergoing finite deformations. This model is unique in its ability to capture large-stretch mechanical behavior with parameters that are connected to the polymer chemistry and can also be easily identified with the important characteristics of the macroscopic stress tretch response. The microscopic picture consists of two components: a crosslinked network of Langevin chains and an entangled network with chains confined to a nonaffine tube. These represent, respectively, changes in entropy due to thermally averaged chain conformations and changes in entropy due to the magnitude of these conformational fluctuations. A simple analytical form for the strain energy density is obtained using Rubinstein and Panyukov's single-chain description of network behavior. The model only depends on three parameters that together define the initial modulus, extent of strain softening, and the onset of strain hardening. Fits to large stretch data for natural rubber, silicone rubber, VHB 4905 (polyacrylate rubber), and b186 rubber (a carbon black-filled rubber) are presented, and a comparison is made with other similar constitutive models of large-stretch rubber elasticity. We demonstrate that the proposed model provides a complete description of elastomers undergoing large deformations for different applied loading configurations. Moreover, since the strain energy is obtained using a clear set of physical assumptions, this model may be tested and used to interpret the results of computer simulation and experiments on polymers of known microscopic structure.
Analytical network-averaging of the tube model: Rubber elasticity
In this paper, a micromechanical model for rubber elasticity is proposed on the basis of analytical network-averaging of the tube model and by applying a closed-form of the Rayleigh exact distribution function for non-Gaussian chains. This closed-form is derived by considering the polymer chain as a coarse-grained model on the basis of the quantum mechanical solution for finitely extensible dumbbells (Ilg et al., 2000). The proposed model includes very few physically motivated material constants and demonstrates good agreement with experimental data on biaxial tension as well as simple shear tests.
A micro-macro constitutive model for finite-deformation viscoelasticity of elastomers with nonlinear viscosity
Elastomers are known to exhibit viscoelastic behavior under deformation, which is linked to the diffusion processes of the highly mobile and flexible polymer chains. Inspired by the theories of polymer dynamics, a micro-macro constitutive model is developed to study the viscoelastic behaviors and the relaxation process of elastomeric materials under large deformation, in which the material parameters all have a microscopic foundation or a microstructural justification. The proposed model incorporates the nonlinear material viscosity into the continuum finite-deformation viscoelasticity theories which represent the polymer networks of elastomers with an elastic ground network and a few viscous subnetworks. The developed modeling framework is capable of adopting most of strain energy density functions for hyperelastic materials and thermodynamics evolution laws of viscoelastic solids. The modeling capacity of the framework is outlined by comparing the simulation results with the experimental data of three commonly used elastomeric materials, namely, VHB4910, 50 and carbon black (CB) filled elastomers. The comparison shows that the stress responses and some typical behaviors of filled and unfilled elastomers can be quantitatively predicted by the model with suitable strain energy density functions. Particularly, the strain-softening effect of elastomers could be explained by the deformation-dependent (nonlinear) viscosity of the polymer chains. The presented modeling framework is expected to be useful as a modeling platform for further study on the performance of different type of elastomeric materials.
Experimental observation of two features unexpected from the classical theories of rubber elasticity
DOI: https://doi.org/10.1103/PhysRevLett.119.267801
Hyperelastic models for rubber-like materials: Consistent tangent operators and suitability for Treloar's data
Abstract) are evaluated. These data are here considered as a prototype or worst-case scenario of highly nonlinear elastic behaviour, although inelastic characteristics are clearly observable but have been tacitly ignored by many other authors.
An efficient method for obtaining the hyperelastic properties of filled elastomers in finite strain applications
An efficient methodology for obtaining hyperelastic material parameters for filled elastomers utilizing unloading curves in uniaxial tension, pure shear and the inflation of a rubber membrane is presented. Experimental results from biaxial extension are crucial when fitting hyperelastic material parameters, and the bubble inflation technique is an excellent method of obtaining this data when specialized test equipment is unavailable. Moreover, filled elastomers have considerable hysteresis, and the hysteresis grows with increasing strain amplitudes. Therefore, the loading curve is in general comprised of both elastic and inelastic contributions, even at very low strain rates. Consequently, it is deemed more accurate to use experimental data from the unloading curve to describe the elastic behavior of the material. The presented methodology enables obtainment of parameters related to both the first and second strain invariant, which is required for a good fit between measurement and simulation results. Finally, it is essential that a chosen material model is accurate in all deformation modes when designing components subjected to a complex, multi-axial load history. An accurate material model enables more concepts and geometries of a component to be studied before a physical prototype is available. (C) 2014 Elsevier Ltd. All rights reserved.
Stress-strain data for vulcanised rubber under various types of deformation
http://xlink.rsc.org/?DOI=tf9444000059
基于连续损伤模型橡胶弹性减振元件疲劳寿命分析
基于连续介质损伤力学理论研究橡胶类材料疲劳寿命预测方法,用一阶Ogden应变能函数导出橡胶材料疲劳损伤演化方程,建立以等效应变范围为损伤参量的疲劳寿命预测模型.拟合橡胶材料无切口试样拉伸试验应力应变数据,获得橡胶超弹材料Ogden本构模型参数,通过有限元结构分析得出转臂橡胶球铰在疲劳载荷工况下的主应力分布.应用橡胶超弹材料等效应力计算法则与橡胶材料无切口拉伸试验应力应变数据,提出复杂应力状态下橡胶弹性减振元件等效应变范围计算方法,得出转臂橡胶球铰的等效应变范围.利用所建疲劳寿命模型对橡胶球铰进行寿命分析预测,并通过转臂橡胶球铰台架疲劳试验进行验证,结果显示试验疲劳寿命是预测疲劳寿命的1.96倍,预测精度比较理想.
Fatigue life analysis of rubber vibration damper based on continnum damage model
基于连续介质损伤力学理论研究橡胶类材料疲劳寿命预测方法,用一阶Ogden应变能函数导出橡胶材料疲劳损伤演化方程,建立以等效应变范围为损伤参量的疲劳寿命预测模型.拟合橡胶材料无切口试样拉伸试验应力应变数据,获得橡胶超弹材料Ogden本构模型参数,通过有限元结构分析得出转臂橡胶球铰在疲劳载荷工况下的主应力分布.应用橡胶超弹材料等效应力计算法则与橡胶材料无切口拉伸试验应力应变数据,提出复杂应力状态下橡胶弹性减振元件等效应变范围计算方法,得出转臂橡胶球铰的等效应变范围.利用所建疲劳寿命模型对橡胶球铰进行寿命分析预测,并通过转臂橡胶球铰台架疲劳试验进行验证,结果显示试验疲劳寿命是预测疲劳寿命的1.96倍,预测精度比较理想.
Mechanical experimental characterisation and numerical modelling of an unfilled silicone rubber
In this paper, the mechanical behaviour of an unfilled silicone rubber is analysed. Firstly, silicone samples were subjected to five homogeneous tests: tensile, pure shear, compression, plane strain compression and bulge tests. During the tests, full-field measurements of the strain on the surface of deformed samples were obtained using a Digital Image Correlation technique. Results show that the Mullins effects and hysteresis, as well as strain rate sensitivity, can be considered as negligible. Results also emphasise the influence of the loading path. Then, five well-known hyperelastic models (neo-hookean, Mooney, Gent, Haines and Wilson and Ogden models) were fitted to the experimental data. Finally, a heterogeneous test was realised by stretching a silicone plate sample containing holes. Finite element simulations of this experiment have been performed with the hyperelastic models. The comparison of experimental and numerical results emphasises the importance of the choice of the hyperelastic modelling in the simulation of strain fields.
Experimental survey of the strain energy density function of isoprene rubber vulcanizate
An experimental survey of the strain energy density function of an isoprene rubber vulcanizate is carried out by biaxial extension of a sheet specimen. The first derivatives of the strain energy density function with respect to I1 and I2 are obtained from the biaxial stress-strain measurement, where I1 and I2 are the first and the second invariants of Green's deformation tensor, respectively. The measurement of these derivatives is done over a wide range of biaxial deformation, 3.005 < I1 < 20 and 3.005 < I2 < 90, in the temperature range 273-353 K. Special care has been taken with the stress and strain measurements in the relatively small deformation region in order to prevent error in the derived values of the derivatives of the strain energy density function. From the result, it is concluded that the strain energy density function should be given by the sum of the two separate terms: W = CT(I1 - 3) + β(I1,I2)61 It has been found that both 68β/68I1 and 68β/68I2 are more sensitive to changes in I2 than in I1 and the value of β(I1,I2) accounts for, in the case of I1 = I2 = 10, for example, 32.5% of the whole strain energy density W.