准静态条件下金属材料的临界断裂准则研究1)
西南交通大学力学与工程学院应用力学与结构安全四川省重点实验室, 成都 610031
THE CRITICAL STRENGTH CRITERION OF METAL MATERIALS UNDER QUASI-STATIC LOADING1)
中图分类号: O346
文献标识码: A
通讯作者:
收稿日期: 2018-05-30
网络出版日期: 2018-09-18
版权声明: 2018 力学学报期刊社 力学学报期刊社 所有
基金资助:
展开
摘要
本文针对9种金属材料完成了具有不同约束程度的10类试样的延性断裂试验, 获得了发生拉、压、扭和裂尖断裂等破坏形式构型试样的载荷-位移试验关系; 基于圆棒漏斗试样拉伸试验所得直至破坏的载荷-位移曲线, 采用有限元辅助试验(finite-element-analysis aided testing, FAT)方法得到了9种材料直至破坏的全程等效应力-应变曲线, 以此作为材料本构关系通过有限元分析获得了各类试样直至临界破坏的载荷-位移关系模拟. 载荷-位移关系模拟结果与试验结果有较好的一致性, 表明用于解决试样颈缩问题的FAT方法所获得的全程材料本构关系针对各向同性材料具有真实性和普适性. 对应9种材料、10类试样的36 个载荷-位移临界断裂点, 通过有限元分析获得了对应的材料临界断裂应力、应变与临界应力三轴度, 研究表明, 第一主应力在延性变形过程中为主控断裂的主导参量; 通过研究光滑、缺口、裂纹等构型试样的断裂状态, 提出了$-1$至3范围的应力三轴度下由第一主应力主控的统一塑性临界断裂准则.
关键词:
Abstract
For 10 types of specimens with different constraints, ductile fracture tests of 9 metal materials under unidirection loading were performed, and their load-displacement relations were measured. Based on the load-displacement curves of notched round bar, the full-range equivalent constitutive relationships of materials up to failure were obtained by FAT (finite-element-analysis aided testing) method. Further, the simulated force-displacement curves for different specimens were obtained based on the full-range constitutive relations, which agree well with the experimental force-displacement curves. The results demonstrate that the full-range constitutive relations up to failure obtained by FAT method have uniqueness for the materials. The critical fracture parameters such as critical stress, critical strain and critical stress triaxiality are investigated by failure simulations for the 36 specimens with different constraints. The first principal stress is suggested to be the master parameter to control ductile fracture. By analyzing the critical behaviors of the specimens which are smooth, notched and cracked, respectively, a unified strength criterion for ductile materials with stress triaxiality varying from $-1$ to 3 is proposed.
Keywords:
引言
材料因屈服或断裂而使构件失效的事件时有发生, 延性材料临界破坏的力学参量是工程设计和安全评价的重要指标. 事实上, 材料的失效方式不仅与材料性质有关, 还同其所处的应力状态有关, 复杂应力状态下的结构破坏不易由试验直接确定, 为能预测结构材料的准静态失效行为, 前人建立了一些失效判据和设计准则, 其中最为经典的是判定材料脆性断裂和延性屈服的四大强度理论. 随着航空、核电、化工工程中大量延性材料得到广泛应用, 仍采用传统强度理论针对延性材料进行屈服强度分析, 相较真实断裂强度结果偏于保守.
自1950年代, 因直至破坏的材料本构关系测试存在根本性困难, 延性材料的大变形塑性分析一直受到制约, 尽管如此, 研究者仍做出不懈努力, 根据有限的分析和临界断裂等效应变测试结果试图得到接近真实破坏的预测准则, 提出了基于应变能、损伤、三轴度、主应力-静水应力、主应力-等效应力相关的临界断裂准则[1-5]:
Freudenthal 准则[1]
\begin{equation*}\int^{\varepsilon_{\text {eqf}}}_0 \sigma_{\text{eq}}\text d\varepsilon_{\text{eq}}=C_{\text{cr}}\end{equation*}
Clockcroft-Latham 准则[2]
\begin{equation*}\int^{\varepsilon_{\text {eqf}}}_0 \sigma_{\text{1}}\text d\varepsilon_{\text{eq}}=C_{\text{cr}}\end{equation*}
Rice-Tracy 准则[3]
\begin{equation*}\int^{\varepsilon_{\text {eqf}}}_0 e^{\sigma^*}\text d\varepsilon_{\text{eq}}=C_{\text{cr}}\end{equation*}
Brozzo 准则[4]
\begin{equation*}\int^{\varepsilon_{\text {eqf}}}_0 \dfrac{2}{3}\dfrac{\sigma_1}{\sigma_1-\sigma_\text m}\text d\varepsilon_{\text{eq}}=C_{\text{cr}}\end{equation*}
Oh 准则[5]
\begin{equation*}\int^{\varepsilon_{\text {eqf}}}_0 \dfrac{\sigma_1}{\sigma_{\text {eq}}}\text d\varepsilon_{\text{eq}}=C_{\text{cr}}\end{equation*}
式中, $C_{\text{cr}}$为临界破坏常数, $\sigma_\text{eq}$, $\sigma_\text m$, $\sigma^*$分别为等效应力、静水应力和应力三轴度, $\sigma^*=\sigma_\text m/\sigma_\text{eq}$; $\sigma_1$, $\sigma_\text{max}$ 和$\sigma_\text{min}$分别为第一主应力、最大主应力和最小主应力; $\sigma_\text{eq}$, $\varepsilon_\text{eq}$ 和$\varepsilon_\text{eqf}$ 分别为等效应变、等效塑性应变和临界断裂等效应变.
1950年, Freudenthal[1]假定在塑性变形过程中材料单位体积内所吸收的广义塑性功达到临界值时材料发生断裂, 由此提出了Freudenthal断裂准则. Freudenthal针对延性材料断裂所提出的临界塑性功假定主导了后续几十年的断裂强度研究. 1968年, Clockcroft和Latham[2]通过拉伸试验对Freudenthal准则进行验证, 修正提出了Clockcroft-Latham拉伸应变能准则. 1969年, Rice和Tracy[3]在延性材料断裂准则研究中第1次提出应力三轴度概念, 提出了基于应力三轴度的Rice-Tracy准则. 1970年代, Brozzo和Oh[4-5]分别强调了静水应力和等效应力在延性断裂行为中的重要作用, 并对Clockcroft-Latham准则进行了修正, 提出了Brozzo准则和Oh准则.
1880年代以后, 随着有限元技术和试验技术的发展, 延性断裂准则的研究也有了新的变化, 主要包括以下3 个方向:
第1种研究方式是基于材料连续微空洞假设的损伤模型, 通过有限元分析实现延性材料的断裂预测[6-15]. Gurson, Tvergaard和Needleman等[6-10]的工作具有代表性, 他们在考虑空洞损伤屈服面的Gurson模型基础上提出了对塑性变形至断裂过程有良好描述的GTN模型. 该模型研究了加载过程中材料内部孔洞的成核、长大和合并的机制, 以材料中所含的孔洞体积分数作为损伤变量, 试图准确描述随塑性变形增大材料内部损伤的累计至断裂的过程. 该模型包括4个材料性能参数和9个材料损伤参数, 大多通过人为调试, 具有经验性质. 2008年, Nahshon 和Hutchinson[11]考虑孔洞形状畸变对损伤演化的贡献, 建立了剪切修正的GTN 模型, 扩大了GTN 损伤模型的适用范围. GTN模型用于有限元模拟采用的材料本构关系来自单轴拉伸试样颈缩前的应力应变试验结果, 难以实现对延性材料破坏的真实判定, 但在2015年, 彭云强等[13]通过有限元辅助测试(finite-element-analysis aided testing, FAT)方法[15-16] 得到了直至破坏的全程材料本构关系, 进而提出了基于有限元逆向法标定GTN模型参数的新方法, 有效实现了GTN 模型的关键参数确定. GTN模型发展了40 余年, 对材料延性断裂进行有限元预测仍存在网格密度敏感性, 确定模型参数存在经验性等问题, 至今少有文献对GTN模拟结果的稳定性和唯一性进行系统论证.
第2种研究方式是唯象模型, 该类模型通常考虑剪应力在断裂中的作用[17-21]. 其中Bai和Wierzbicki[17]提出的MMC模型赢得较多专注. 基于经典的用于描述脆性断裂的Mohr-Coulomb[18]准则, Bai和Wierzbicki将其适用性扩展到延性断裂, 并提出了修正的Mohr-Coulomb准则, 简称MMC准则. 不同于Mohr-Coulomb 准则中以应力作为参量, MMC准则中选取等效应变、应力三轴度和Lode参数共同对延性材料的断裂问题进行描述. 2010年, Chen等[19]将MMC准则运用到对拉弯试验失效问题的预测中. 2012年, Lou等[20]又将MMC准则扩展到对各向异性裂纹问题的探讨中. MMC准则对剪切主导断裂的预测结果良好, 但并不适用于对等直圆棒试样等轴对称结构断裂问题进行预测.
第3种研究方式则基于大量的试验开展, 忽略材料屈服面的变化, 只考虑临界断裂时各断裂参量的影响(包括临界主应力、静水应力、剪应力、等效应力和等效应变等)[22-27, 34], 所得准则形式相对简单, 易于运用到工程设计和安全评估中. 1985年, Johnson和Cook[22]通过完成不同半径漏斗试样的拉伸试验, 基于应力三轴度和临界断裂应变提出了Johnson-Cook断裂准则
\begin{equation*}\varepsilon_{\text{eqf}}=C_1{\rm exp}(C_2\sigma^*)+C_3\tag*{(1)}\end{equation*}
式中$C_1$, $C_2$和$C_3$为常数, 文献[22]表明, 该准则对漏斗试样断裂行为预测结果良好, 但当应力三轴度较低甚至为负时, 该准则无法对延性材料破坏行为进行描述. 2004年, Bao和Wierzbicki[23]完成了2024-T351铝合金的压缩、剪切和拉伸试验, 结合有限元模拟, 提出了同样以临界断裂应变为参量的Bao-Wierzbicki 断裂准则
\begin{equation*}\varepsilon_{\text{eqf}}\begin{cases}C_1{\Bigg(\sigma^*+\dfrac{1}{3}\Bigg)^{c_2}},\quad\quad\quad~~\quad\sigma^*\in[-1/3,0]\\C_3\sigma^{*^2}-C_4\sigma^*+C_5,\quad\quad\sigma^*\in[0,0.4]\\C_6\sigma^{*^{-1}},\quad\quad\quad\quad\quad\quad\quad\sigma^*\in[0.4,0.95]\end{cases}\tag*{(2)}\end{equation*}
式中$C_1\sim C_6$为常数, 该准则对延性断裂准则后续的研究具有重要的意义, 此后众多论文的工作基于此研究方式展开. 该准则假定断裂面上的等效应变分布是均匀的, 且将通过传统拉伸试样颈缩前所得真应力-真应变曲线作为有限元分析采用的材料本构关系, 故预测结果, 特别是断裂预测结果会脱离结构危险点材料破坏的真实情况.
延性材料的单轴拉伸试样在试验中均发生颈缩现象, 导致颈缩后的单轴本构关系无法直接获取. 近百年来学者们做过努力, 并未根本解决这个大难题[28-33]. Yao等、Cai等 [15-16, 34] 原创地提出了依靠漏斗试样直至破坏的载荷位移试验曲线和简便数学迭代算法的FAT方法, 有效获取了直至破坏的延性材料全程等效应力-应变曲线. 文献[34]完成了A508-3钢和316L不锈钢的一系列拉伸试验, 基于FAT方法获取了材料的全程等效应力-应变关系, 进而通过有限元对试验过程进行了精准模拟, 分析证明了第一主应力对材料延性断裂的主导地位, 提出了基于临界第一主应力和应力三轴度的延性材料临界断裂准则
\begin{equation*}\sigma_{\rm lf}'={\rm ln}(\sigma^*_\text f)+S'\tag*{(3)}\end{equation*}
式中$\sigma_{\rm 1f}'$为临界第一主应力与单轴应力状态下临界第一主应力的比值, $\sigma^*_\text f$为临界应力三轴度, $S'$为应力三轴度为1时的临界第一主应力与单轴应力状态下临界第一主应力的比值. 不同于依靠平均应力三轴度的Bao-Wierzbicki 准则和Xue-Wierzbicki准则, 为了更好地预测断裂的情况, Yao-Cai准则更加关注RVE(representative volume element) 应力三轴度的即时变化情况, 以材料RVE启裂时的真实应力三轴度为基础实现对延性材料断裂行为的精确描述. 该准则针对拉伸断裂, 对于轴、扭加载下的压、剪和裂纹断裂问题尚未开展研究.
本文针对9种金属材料完成了具有不同约束程度的10类试样延性断裂试验, 获得了包括拉、压、扭加载下光滑、缺口和裂纹断裂试样的载荷-位移试验关系. 基于漏斗试样的FAT方法, 获取了9种材料直至破坏的全程等效应力-应变曲线, 以此作为材料本构关系通过有限元分析完成了10类试样直至破坏的载荷-位移关系模拟, 证明了FAT方法获得的材料本构关系针对均匀、各向同性的延性材料具有真实性和普适性. 通过有限元分析获取对应材料临界断裂应力、应变与临界应力三轴度, 确定了第一主应力在延性变形过程中为主控断裂的主导参量, 提出了$-1$ 至3范围的应力三轴度下由第一主应力主控的延性材料统一临界断裂准则.
1 研究条件
1.1 试验材料、设备与试样
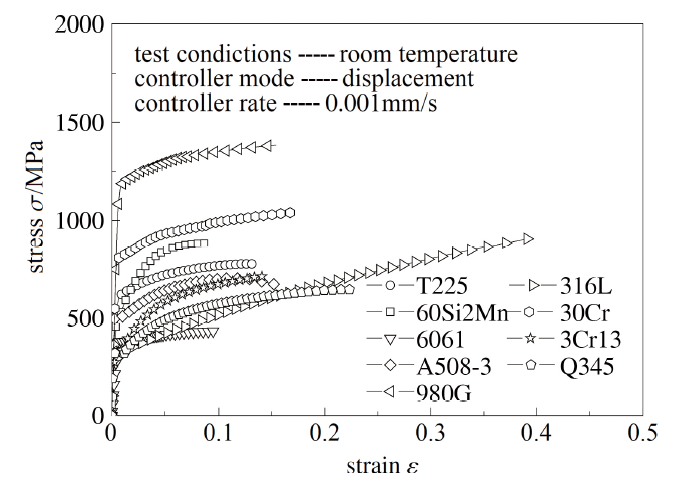
试验材料为T225钛合金、6061铝合金、60Si2Mn钢、A508-3钢、980G钢、30Cr钢、Q345钢、316L不锈钢和Cr13不锈钢. 这9类材料有稳定的力学性能和良好的延性, 在航空、核电、高铁等重要工程中有广泛应用.
试验设备为美国MTS公司生产的 810 25kN电液伺服材料试验机、TestStarII控制系统、MTS790.20应用软件. 室温拉伸和压缩试验中, 采用MTS632.12c-21(标距25 mm, 轴向测量范围$-10\%\sim 50\%$)应变引伸计测量室温下试样标距段颈缩前的真实应变和颈缩后的位移; MTS632.68F(标距25mm, 轴向测量范围$-10\%\sim 20\%$, 扭向测量范围$-5^\circ\sim 5^\circ$) 应变引伸计用于室温扭转试样; COD引伸计MTS632.03F-30 (标距5 mm)用于测量室温下裂纹构型裂纹嘴处的裂纹张开位移. 通过计算机对试验过程进行开环控制和实时数据采集.
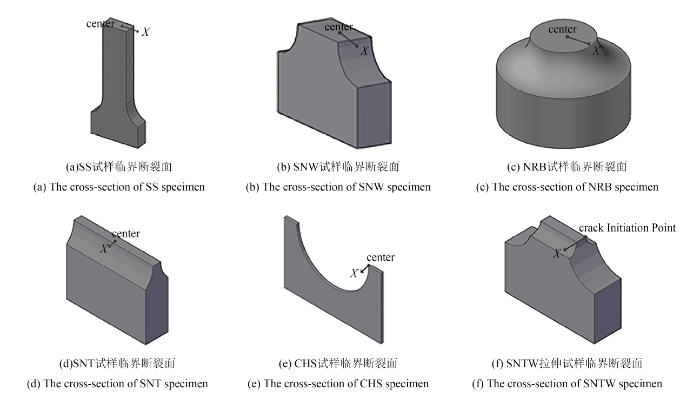
为得到大范围内约束程度金属材料的临界延性断裂准则, 设计不同构型的试样从而确保其临界断裂时的应力状态具有代表性, 如图1所示. 约束度从低到高分别为:漏斗圆棒压缩试样(NRB)、中心圆孔板拉伸试样(CHS)、等直板拉伸试样(SS)、双边漏斗板扭转试样(SNTW)、宽向漏斗板拉伸试样(SNW)、厚向漏斗板拉伸试样(SNT)、圆棒漏斗拉伸试样(NRB)、三点弯试样(SEB)、1/2紧凑拉伸试样(1/2T)和钝裂纹构型(BCT), 其中板试样厚度均为3 mm. 试样均采用高精度数控机床加工.
各单向加载构型试样的加载速率参考国家标准GB/T 228.1-2010(拉伸试验)、GB/T 7314-2017(压缩试验)、GB/T 10128-2007(扭转试验)和GB/T 21143-2017(裂纹试验). 拉伸试验和压缩试验均为位移控制, 速率为0.01 mm/s, 扭转试验采用角度控制, 速率为$0.08(^\circ)/\text s$.
每种材料所完成的试样构型在表1中给出, 其中各构型试样均进行多次试验.
表1 各材料已完成试验所包含试样构型
Table 1 Completed configuration of specimens for materials experiments
| Materials | Specimens |
|---|---|
| T225 | SS SNW CHS NRB-tension SNTW NRB-compression SEB |
| 60Si2Mo | SS SNW CHS NRB-tension |
| 6061 | SS SNW CHS NRB-tension 1/2T |
| A508-3 | SNT SNW CHS NRB-tension BCT |
| 980G | CHS NRB-tension |
| 316L | SNT CHS NRB-tension |
| Q345 | CHS NRB-tension BCT |
| 30Cr | SNW CHS NRB-tension BCT |
| 3Cr13 | SNW CHS NRB-tension BCT |
1.2 材料真应力-真应变曲线
对9种材料进行传统单轴拉伸试验, 基于公式
\begin{equation*}\left.\begin{split}\sigma_{\rm Eng}=\dfrac{4F}{\textrm{π}d^2}\\\varepsilon_{\rm Eng}=\dfrac{\Delta L}{L}~~\end{split}\right\}\Rightarrow\left.\begin{split}\sigma_{\rm T}=\sigma_{\rm Eng}(1+\varepsilon_{\rm Eng}) \varepsilon_{\rm T}={\rm ln}(1+\varepsilon_{\rm Eng})\quad~\end{split}\right\}\tag*{(4)}\end{equation*}
对拉伸试样颈缩前的数据进行处理, 可得各材料试样在颈缩前的真应力-真应变曲线(如图2所示). 由于所选用金属材料的应力-应变曲线重复性很好, 故图2中针对各材料只列出一个试样得到的应力应变试验曲线. 式(4) 中, $\sigma_{\rm Eng}$和$\varepsilon_\text {Eng}$为工程应力和工程应变, $\sigma_{\rm T}$和$\varepsilon_\text T$ 为试样颈缩前的真应力和真应变.
图2 各金属材料颈缩前真应力-真应变曲线
Fig.2 The uniaxial true stress-true strain curves before necking
对9种材料颈缩前的真应力-真应变曲线可采用Ramberg-Osgood本构模型描述
\begin{equation*}\varepsilon_\text T=\varepsilon_{\text e_\text T}+\varepsilon_{\text p_\text T}=\dfrac{\sigma_\text T}{E}+\Bigg(\dfrac{\sigma_\text T}{K}\Bigg)^N\tag*{(5)}\end{equation*}
式中, $E$为弹性模量, $\varepsilon_{\text e_\text T}$为弹性应变, $\varepsilon_{\text p_\text T}$为塑性应变, $K$为应变硬化系数, $N$ 为应力硬化指数, 对应的材料相关参量在表2 中给出.
表2 材料力学性能参数
Table 2 Parameters of mechanical properties for materials
| Materials | E/GPa | K | N |
|---|---|---|---|
| T225 | 110 | 932 | 12.10 |
| 60Si2Mo | 209 | 1640 | 4.56 |
| 6061 | 72 | 504 | 15.80 |
| A508-3 | 195 | 932 | 7.07 |
| 980G | 210 | 1520 | 19.80 |
| 316L | 195 | 1290 | 2.54 |
| Q345 | 210 | 888 | 5.16 |
| 30Cr | 203 | 1130 | 4.49 |
| 3Cr13 | 204 | 1210 | 11.90 |
1.3 有限元分析模型
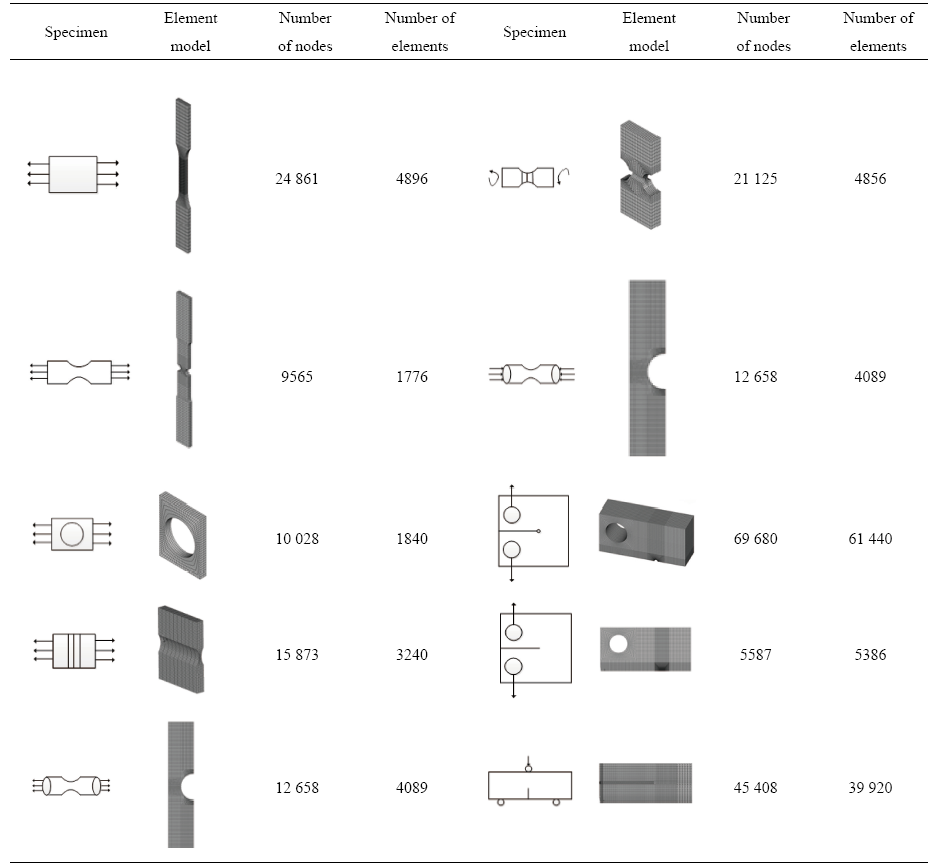
对各构型试样进行有限元模拟分析, 考虑到NRB试样为轴对称结构, 采用能表征材料塑性大变形的plane183轴对称单元对其1/2剖面建模, 同样采用plane183单元和Solid185单元对SEB试样、1/2T 试样和BCT试样建立半模型进行分析计算, 其他构型试样均采用Solid186单元建立全模型, 所选网格密度对计算结果不敏感, 各试样的有限元模拟均在大变形条件下进行, 表3中给出所有试样的有限元模型、节点数和单元数.
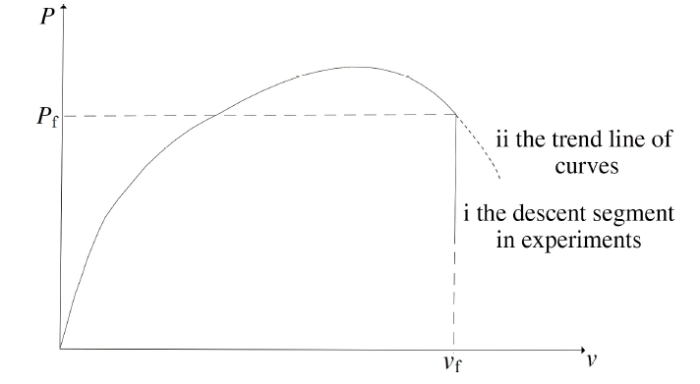
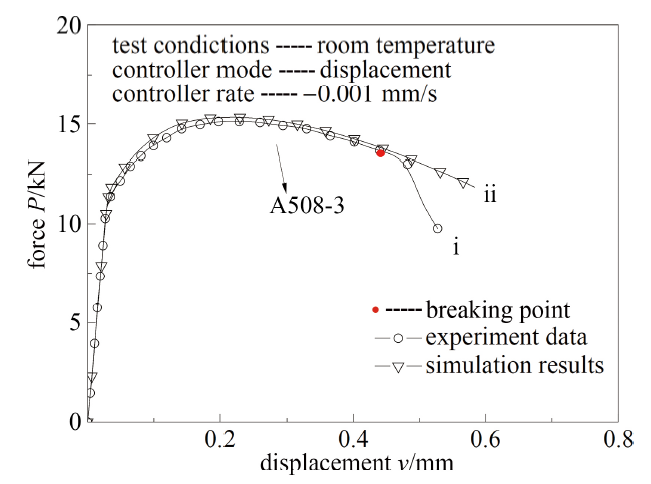
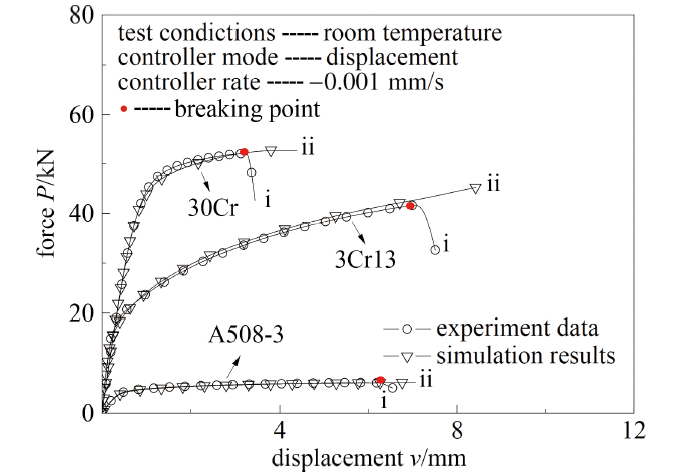
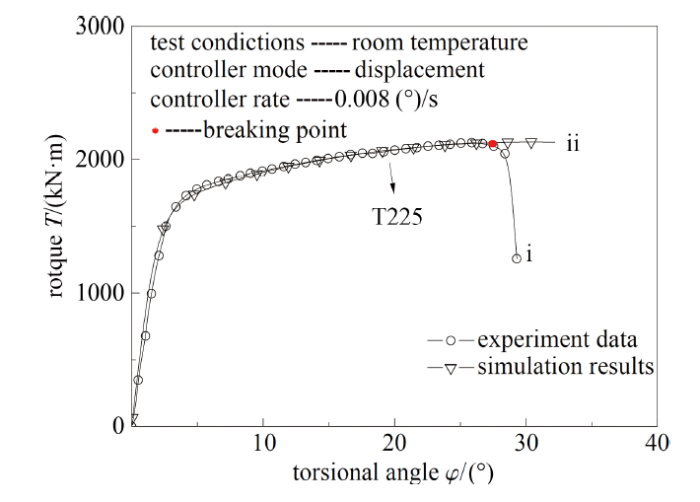
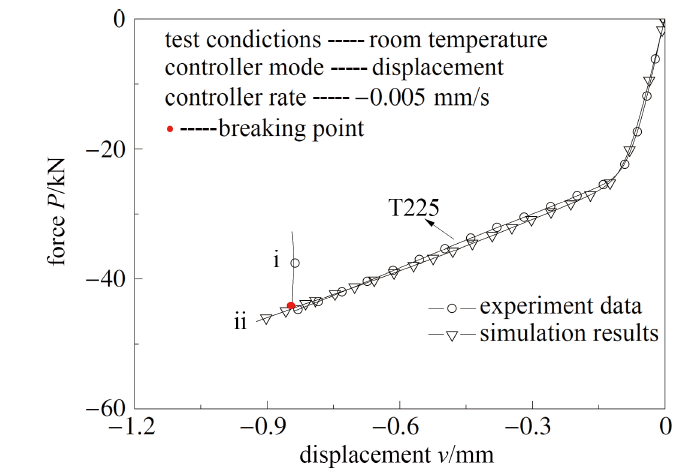
通过表3所列构型的单向加载试验可以直接获取轴向载荷$P$和位移$v$. 在试验过程中各构型试样载荷都存在某一时刻载荷出现明显地下降, 载荷折点对应构型危险点材料断裂, 该点定义为构型试样的断裂点, 该点的位移为临界断裂位移$v_\text f$, 如图3所示, 其中i段表示试验过程中$P$-$v$曲线的真实下降段, ii段表示表示试验过程中$P$-$v$曲线的原曲线趋势线.
在有限元分析中, 所有构型的有限元网格模型均为一端固定, 另一端采用位移加载, 对于拉伸和压缩试样, 加载量为$v_\text f$. 对于扭转试样, 加载量为扭矩出现急剧下降时的临界断裂角度$A_\text f$.
1.4 FAT方法
材料测试通常采用传统单轴拉伸试验来获取材料颈缩前的真应力-真应变曲线, 再通过Ramberg-Osgood模型或其他表征模型进行描述, 并采用延伸方法对单轴试样颈缩后的材料等效本构关系曲线进行描述, 传统方法所得结果往往与材料真实的本构关系存在较大的偏差, 将其运用到有限元分析中难以得到准确的模拟结果.
姚迪等[34]提出的FAT方法以漏斗试样的$P$-$v$曲线为目标, 通过简便的数学迭代改善输入有限元软件的材料本构关系, 使得对$P$-$v$试验曲线的有限元模拟结果与试验结果一致, 从而获取各向同性材料直至破坏的全程本构关系曲线. 对于单向加载的其他构型试样, FAT方法仍然适用于获取直至破坏的材料本构关系.
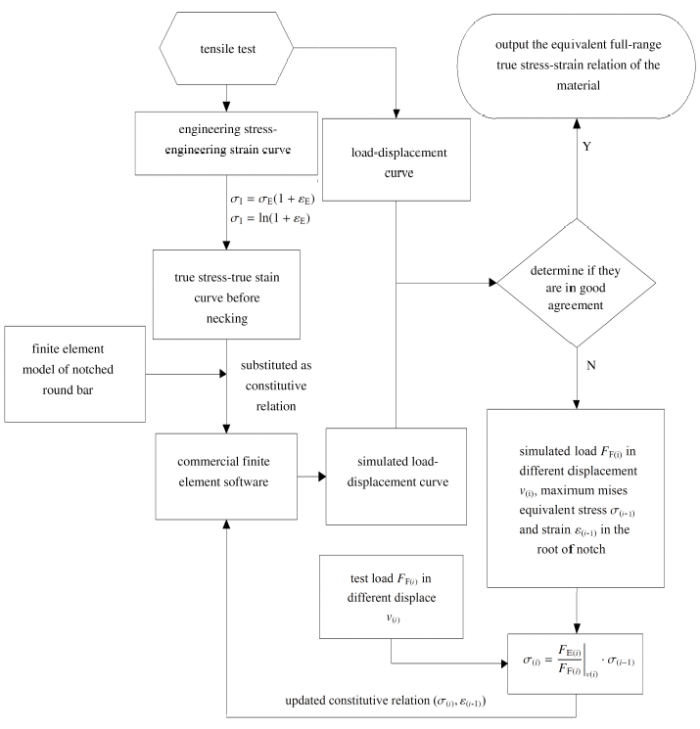
FAT方法的算法框图如图4所示, 首先完成圆棒漏斗试样的拉伸试验, 得到$P$-$v$曲线, 根据$P$-$v$曲线编写ANSYS APDL 命令流程序, 实现FAT 方法的自动运算.
应用FAT方法, 通过$2\sim 3$次迭代便可依据漏斗试样的$P$-$v$曲线获得直至破坏的材料全程本构关系.
2 FAT方法有效性
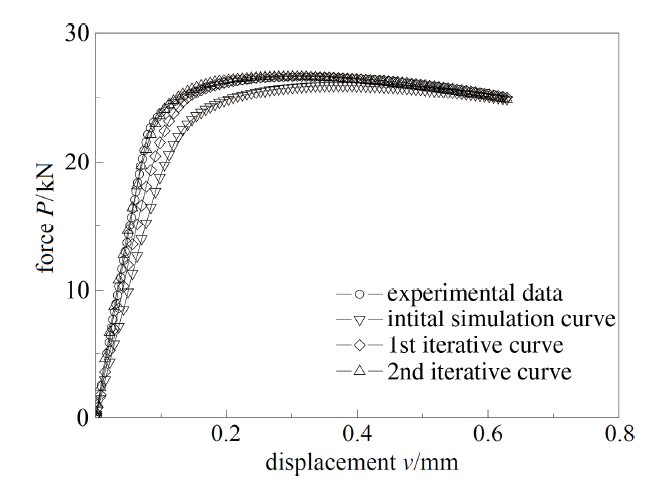
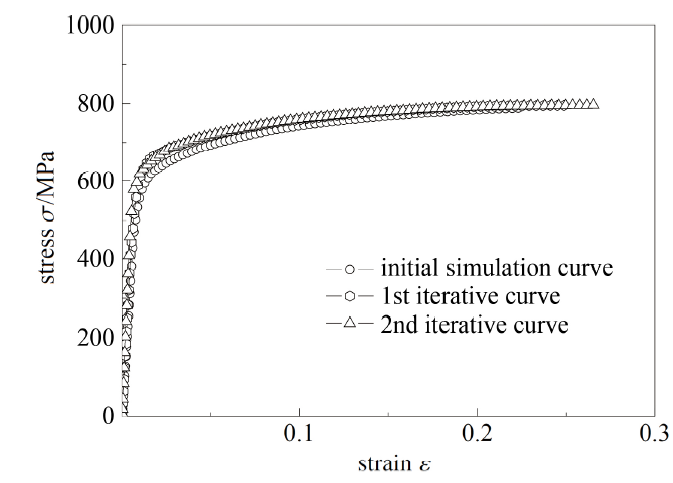
材料本构关系必然具有唯一性, 因此要求基于FAT方法获得的材料直至断裂的全程等效应力-应变关系适用于对不同构型试样载荷-位移关系的模拟. 以T225钛合金圆棒漏斗试样为例,利用FAT方法对试验数据进行处理, 图5和图6所示分别为T225钛合金漏斗试样$P$-$v$曲线和$\sigma$-$\varepsilon$曲线的迭代过程.
图6 T225钛合金$\sigma$-$\varepsilon$曲线迭代过程
Fig.6 The iterative $\sigma$-$\varepsilon$ curves of T225 alloy
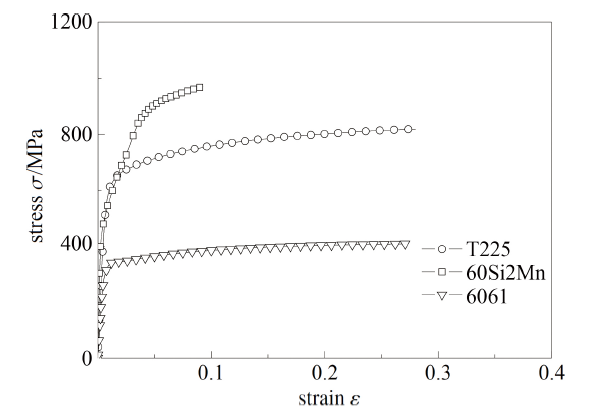
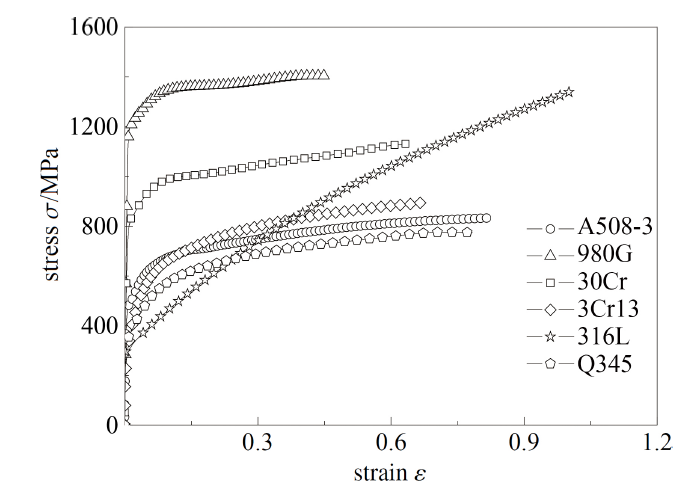
图7和图8所示分别为通过FAT方法所获取9种材料的全程等效应力-应变曲线.
图7 中低延性材料的全程等效应力-应变曲线
Fig.7 The full-range constitutive relationships of low to medium ductile materials
图8 高延性材料全程等效应力-应变曲线
Fig.8 The full-range constitutive relationships of high ductile materials
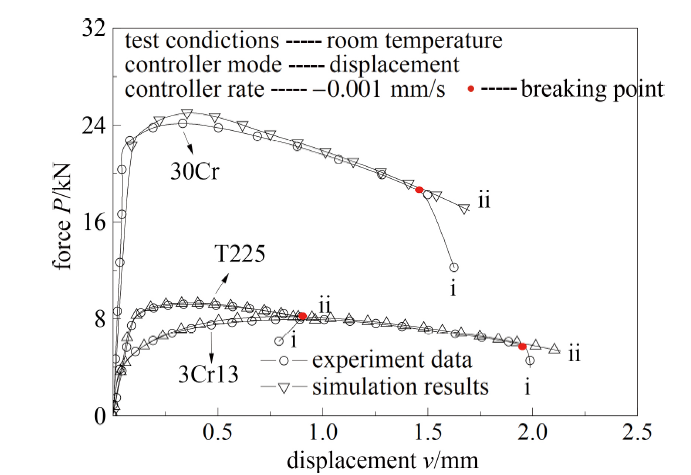
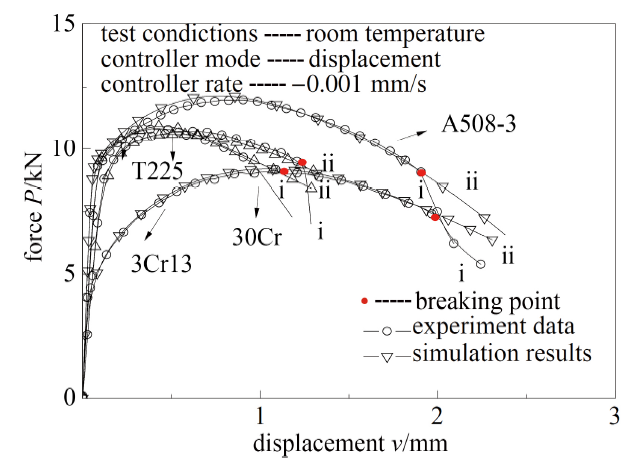
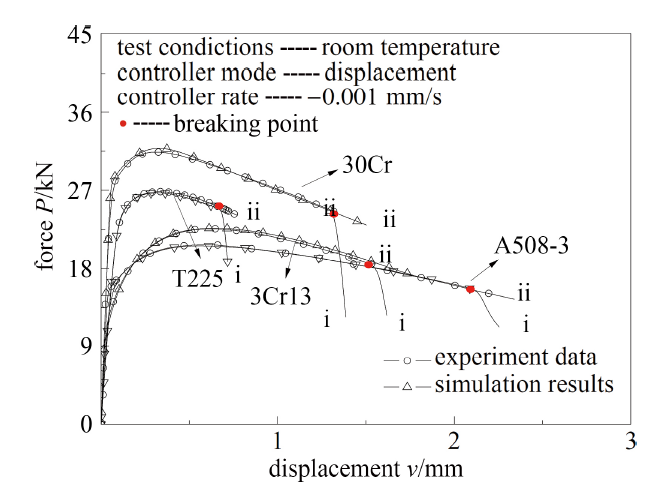
将通过FAT方法所得9种材料的全程等效应力-应变曲线作为材料本构关系对各构型试样进行有限元模拟, $P$-$v$曲线模拟结果与试验结果比较情况如图9 $\sim$图16所示(以T225钛合金、A508-3钢、30Cr 钢和3Cr13不锈钢数据为例).
由上图可见, 对应不同材料的各类构型试样, 通过有限元获得载荷-位移关系模拟结果与试验结果有较好的一致性, 表明用于解决试样颈缩问题的FAT方法所得各向同性延性材料的全程等效应力-应变关系具有真实性和普适性.
FAT方法的应用广泛, 可用于获取各向同性材料直至破坏的全程本构关系曲线、断裂应力、断裂应变、应力三轴度等材料性能, 所得结果的准确性是传统单轴拉伸试验无法达到的, 更有利于大变形分析, 对工程中的结构设计和安全评估具有重要意义.
3 构型试样的断裂分析
3.1 试样的断裂面分析
针对上述金属材料各类构型试样的断裂试验, 完成了拉、压、扭和裂尖断裂等破坏形式, 对应种材料、10类试样的36个载荷-位移临界断裂点. 通过试验观察和有限元分析可确定各试样的临界断裂面, 如图17所示. 对各试样的临界断裂面进行分析, 借助有限元获得了对应的材料临界断裂应力、临界断裂应变与临界应力三轴度. 其中SS, SNW, NRB和SNTW试样均采用T225钛合金数据进行分析, SNT试样采用A508-3数据进行分析.
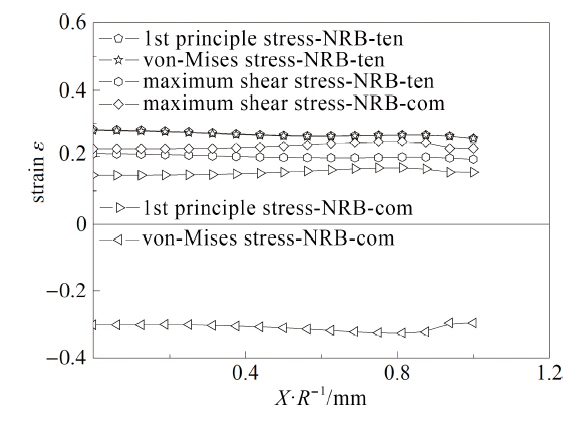
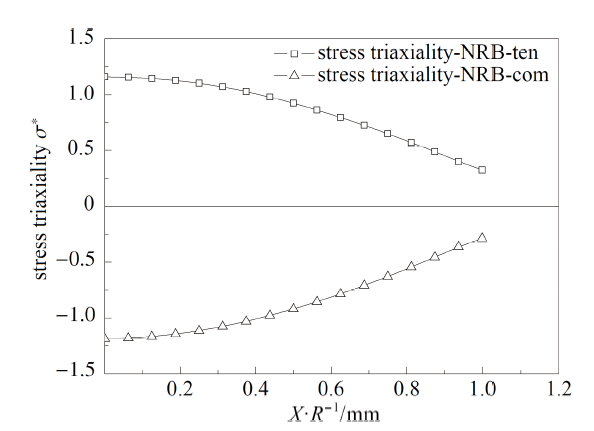
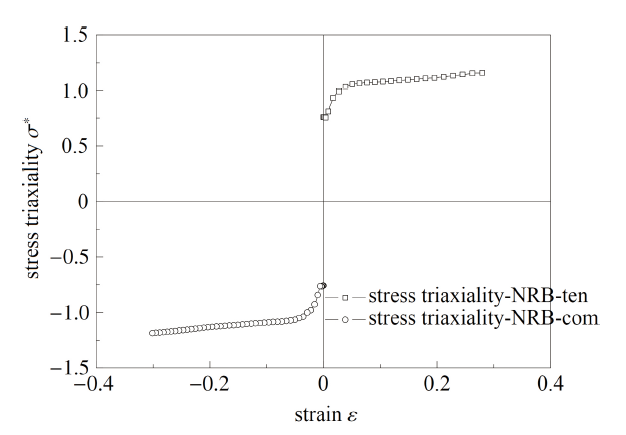
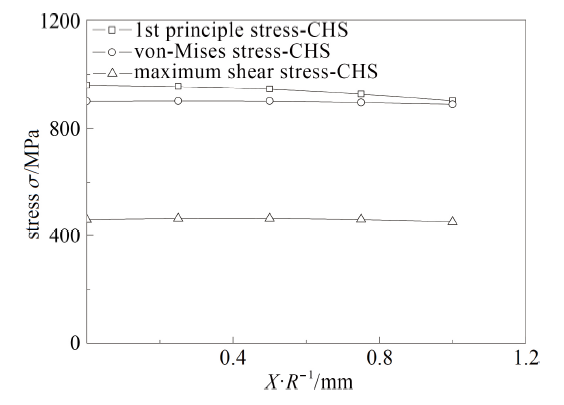
根据试样本身构型与试验中的观测, 可确定各类构型试样的断裂面, 选取应力三轴度$\sigma^*$描述当地的约束情况, 图17 $\sim$图33给出了临界断裂时试样中心截面断裂参量的分布图、临界断裂面上应力三轴度的分布图和断裂面中心点应力三轴度的演化图.
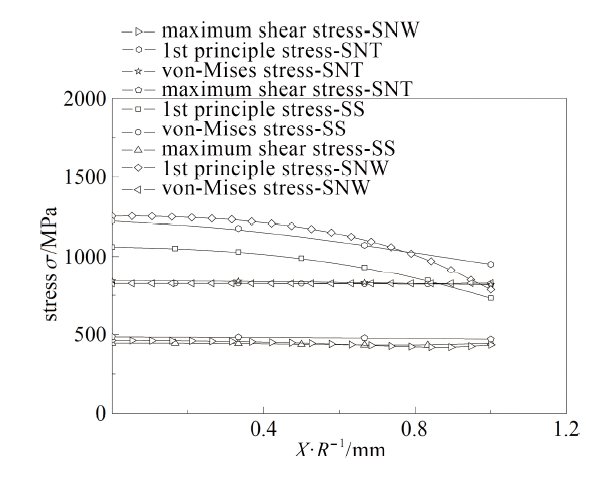
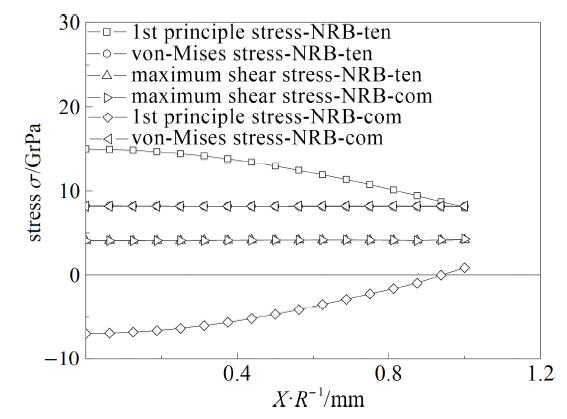
图18 SS, SNW和SNTX试样$X$方向应力分布图
Fig.18 Stress distribution on $X$ direction of tension and compression specimens
图19 SS, SNW和SNT试样$X$方向应变分布图
Fig.19 Strain distribution on $X$ direction of SS, SNW and SNT
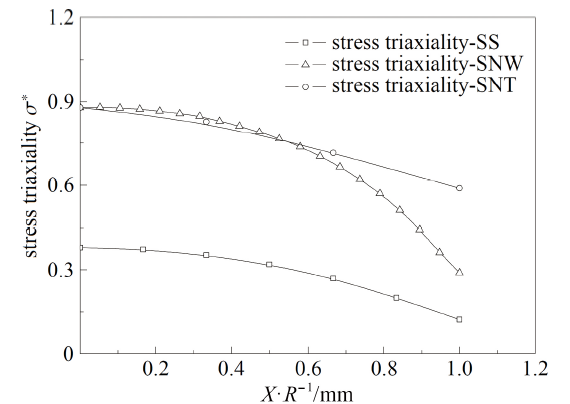
图20 SS, SNW和SNT试样$X$方向应力三轴度分布图
Fig.20 Stress triaxiality on $X$ direction of SS, SNW and SNT
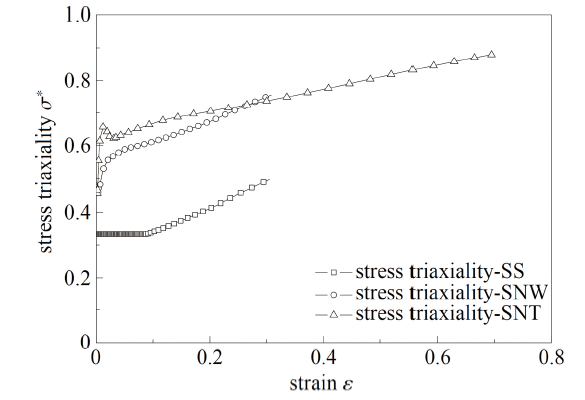
图21 SS, SNW和SNT试样断裂面中心点应力三轴度演化图
Fig.21 The evolution of stress triaxiality on the center of the cross-section of SS, SNW and SNT
图25 NRB试样断裂面中心点应力三轴度演化图
Fig.25 The evolution of stress triaxiality on the center of the cross-section of NRB
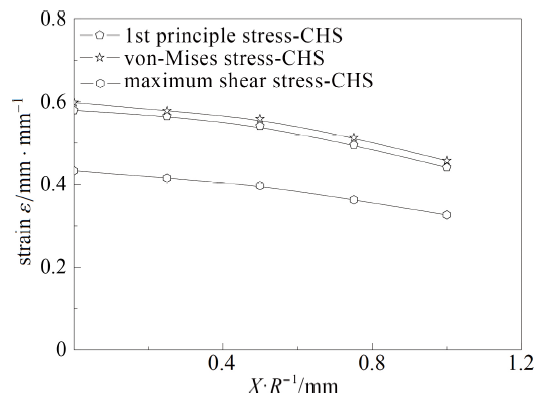
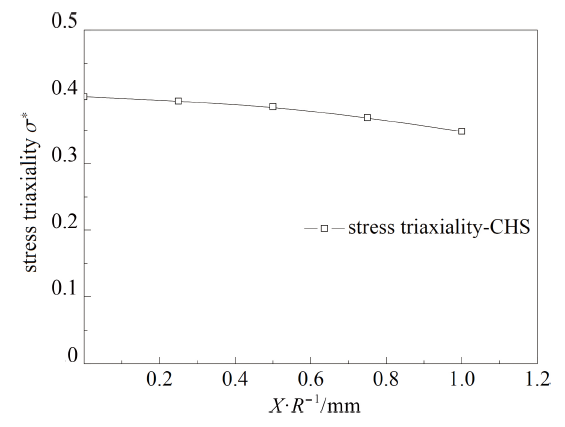
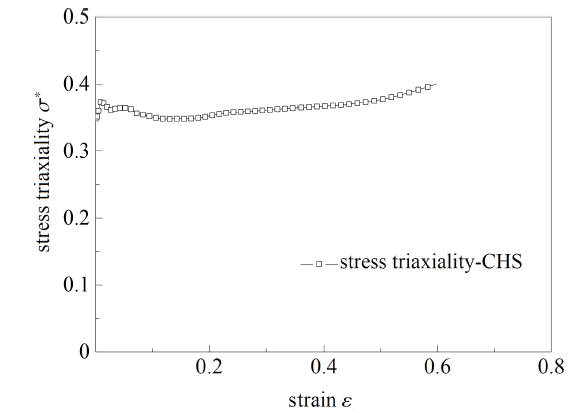
图29 CHS试样断裂面中心点应力三轴度演化图
Fig.29 The evolution of stress triaxiality on the center of the cross-section of CHS
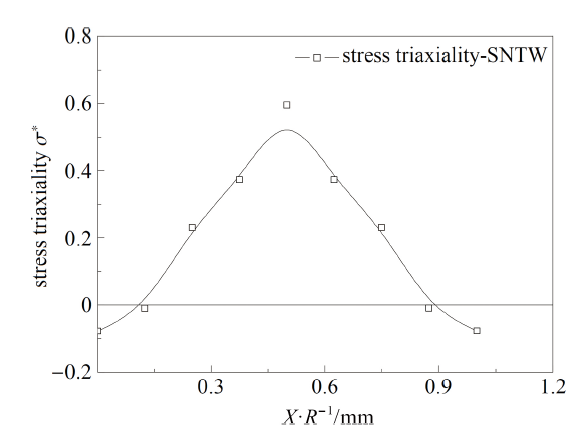
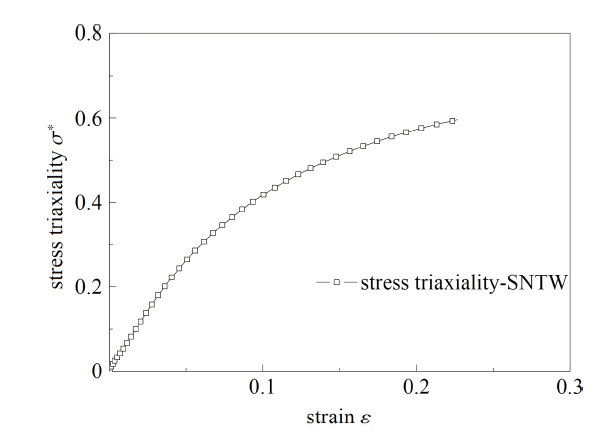
图33 SNTW试样断裂面中心点应力三轴度演化图
Fig.33 The evolution of stress triaxiality on the center of the cross-section of SNTW
图17$\sim$图33表明, 在临界断裂面上, 上述试样遵从以下规律:
(1)从截面中心点到边缘, 第一主应力和应力三轴度分布趋势相同, 表现为逐渐降低, 而Mises等效应力和切应力变化不明显;
(2)对于拉伸试样和压缩试样, 第一主应变和Mises等效应变在数值上十分接近, SS, SNT和CHS试样的第一主应变、Mises等效应变和切应变从截面中心点到边缘逐渐降低, SNW试样和NRB试样的第一主应变、Mises等效应变和切应变变化不明显; 对于SNTW扭转试样, Mises 等效应变从中心点到边缘逐渐升高, 而第一主应变和切应变变化不明显;
(3)对于拉伸试样和压缩试样, 在试验初期, 随着试验的进行, 断裂面中心点的应变逐渐提高, 除SS和CHS试样外各试样当地应力三轴度变化较为剧烈, 在应变达到一定值以后逐渐缓慢增大直至破坏. SS和CHS试样临界断裂点在试验前半部分保持单轴应力状态, 应力三轴度约为0.33, 当SS试样应变达到0.1时, 应力三轴度逐渐升高直至破坏, CHS 试样直至断裂前才发生应力三轴度小幅度上升, 即在CHS试样的拉伸试样过程中, 试样的临界断裂点在大部分时间内保持单轴应力状态; 对于扭转试样, 因为其临界断裂点在试样边缘, 所以在试验过程中该材料单元的应力三轴度从0开始逐渐升高直至断裂.
从各试样的断面应力分布可知, 对于拉伸试样和压缩试样, 由于临界断裂面中心应力三轴度最高, 第一主应力最大, 在该处首先达到临界阈值, 出现微裂纹并扩展长大成型, 导致首先在此处启裂. 对于扭转试样, 由于加载形式的影响, 初始裂纹发生在试样表面, 试样边缘中心最大主应力材料RVE为试样的启裂点.
由上述分析可知, 相对于其他参量, 第一主应力和应力三轴度变化最为显著, 即第一主应力在弹塑性变形过程中为主控断裂的主导参量, 而Mises等效应力、切应力、第一主应变、切应变和Mises等效应变等参量对其影响较小.
3.2 材料临界断裂状态分析
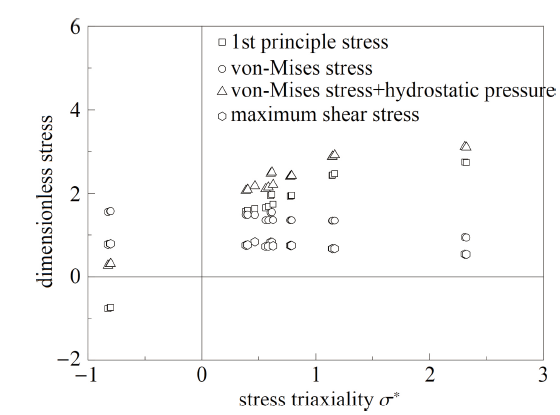
借助有限元可获得不同构型试样临界断裂点的各断裂参量, 如应力参量:第一主应力$\sigma_1$、Mises等效应力$\sigma_{\rm eq}$、 静水应力与Mises等效应力之和$\sigma_\text m+\sigma_{\rm eq}$以及最大切应力$\tau_{\rm max}$, 应变参量:第一主应变$\varepsilon_1$ 和Mises 等效应变$\varepsilon_{\rm eq}$; 对上述参量进行规律性比较分析, 以T225 钛合金为例, 如图34和图35所示, 两图纵坐标分别为无量纲后的应力参量与应变参量.
图34 应力参量随应力三轴度的变化
Fig.34 The variations of different stress parameters with stress triaxiality
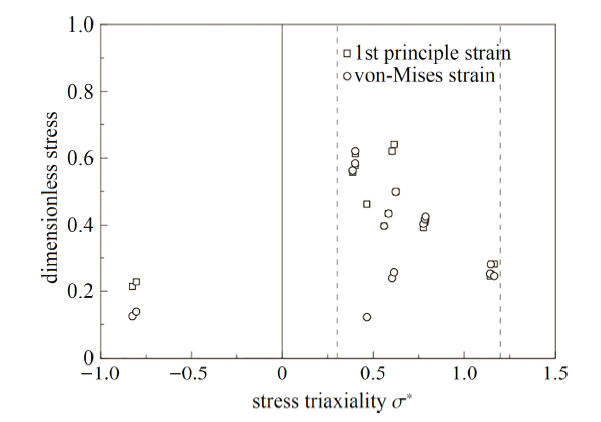
图35 应变参量随应力三轴度的变化
Fig.35 The variations of different strain parameters with stress triaxiality
由图中可见, 对于临界应力参量, 临界第一主应力、静水应力与Mises等效应力之和随应力三轴度的变化相对于其他应力参量更为明显, 而对于应变参量, 当应力三轴度在$0.3\sim 1.2$ 范围内时, 拉伸试样的Mises等效应变和第一主应变在数值上基本一致, 两者均随应力三轴度的增加而下降, 存在一定可描述的规律, 文献中Johnson-Cook准则和Bao-Wierzbicki准则均对拉伸断裂在这一范围内的规律进行了探究, 而扭转试样和压缩试样数据无明显可描述规律.
结合3.1中分析结果, 选取临界第一主应力和应力三轴度作为描述延性材料临界断裂行为的阈值进行探究.
4 裂纹构型的启裂分析方法}
陈辉和蔡力勋等[35-36]通过建立变形域的应变能与积分中值点位置材料RVE的应变能等效和RVE 的能量在复杂应力状态与单轴应力状态下的Mises等效, 得到了反映不同连续固体能量、载荷、位移和本构关系参数的通用模型. 该模型应用广泛, 贺屹等[37]基于该模型提出了$J$积分-载荷和载荷-位移的工程半解析统一表征方法.
对裂纹构型, 材料的塑性有效体积和塑性等效应变做如下假定
\begin{equation*}\left.\begin{split}&\dfrac{V_{\text P}}{V^*}=k_1\left(1-\dfrac{a}{W}\right)^{k_2}\\&\varepsilon_{\text{p-eqm}}=k_3\left(\dfrac{h_{\text p}}{h^*}\right)^{k_4}\end{split}\right\}\tag*{(6)}\end{equation*}
其中, $V_\text P$为塑性有效体积, $\varepsilon_{\rm p-eqm}$为塑性等效应变, $V^*$为特征体积, $W$ 为试样宽度, $k_1$ 表示有效变形体积系数, $k_2$表示与裂纹长度$a$相关的有效体积折减系数, $k_3$表示有效应变系数, $k_4$ 表示有效应变指数, $P$表示试样的载荷, $h_\text p$表示试样位移, $v^*$表示特征位移.
对于材料的弹塑性变形, 由能量等效方法, 可得
\begin{equation*}\left\lgroup\dfrac{PA_1}{V^*}\right\rgroup^N+\dfrac{PA_2}{V^*}=\dfrac{v}{v^*}\hskip 25mm\tag*{(7)}\end{equation*}\begin{equation*}\left.\begin{split}&A_1=\dfrac{(1+N)v^*}{(1+m_{\text p})NKk_1k_3^{1+1/N}\left(1-\dfrac{a}{W}\right)^{k_2}}\\&A_2=\dfrac{v^*}{k_5E\left(1-\dfrac{a}{W}\right)^{k_2}}\end{split}\right\}\tag*{(8)}\end{equation*}
其中, $K$和$N$为材料本构参数, $k_5$为弹性有效系数, 则试验任意加载点的实时裂纹长度$a$可通过式(7) 反求获得.
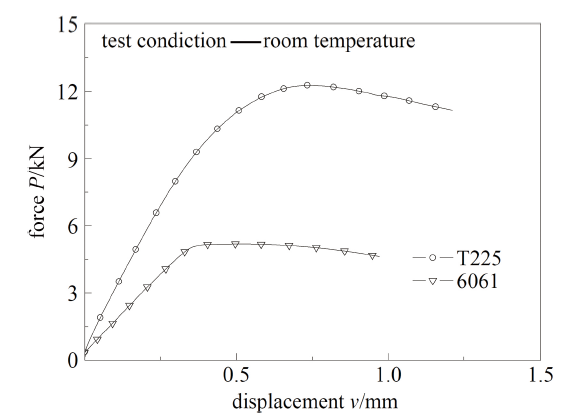
对T225钛合金的SEB试样和6061钛合金1/2T试样进行了测试, 得到$P$-$v$曲线, 如图36所示.
图36 SEB试样拉伸试验所得$P$-$v$曲线
Fig.36 The tensile $P$-$v$ curves of cracked specimens
以T225钛合金的SEB试样为例, 上述公式中$k_1\sim k_5$的值分别为1.120, 1.037, 0.360, 1.040和0.119.
由式(4)可得裂纹长度$a$与位移$v$之间的关系曲线,如图37所示.
图37 T225钛合金SEB试样$a$-$v$曲线
Fig.37 The $a$-$v$ curve for SEB specimen of T225 alloy
由图37可见, 在试验前期, 裂纹构型尚未启裂, 随着试验的进行, 试样启裂并开始扩展, 裂纹长度随位移量的增加呈现明显上升趋势. 认定曲线的突变点为试样的临界启裂点, 进而可通过有限元模拟获取裂纹构型临界启裂点的各断裂参量, 实现对高约束程度断裂点应力状态的获取, 扩宽所研究延性材料断裂准则覆盖的约束程度范围.
5 临界延性断裂准则
根据第3节分析可知, 延性断裂主控断裂的主要参量为临界第一主应力, 综合不同约束的构型试样有限元模拟结果, 提取各试样临界断裂时的第一主应力和应力三轴度, 对于含裂纹体试样, 提取裂纹扩展轨迹上最大主应力材料单元RVE 的临界断裂参量, 提出统一延性断裂准则
\begin{equation*}\left(1+\dfrac{\sigma_\text {1f}}{\sigma_y}\right)=m_1(1+\sigma^*_\text{f})\text e^{ m_2(1+\sigma^*_\text f)}\tag*{(9)}\end{equation*}
其中$m_1$和$m_2$为材料参量, $\sigma^*_\text f$为应力三轴度$\sigma^*$的临界值, $1+\sigma^*$可表示为
\begin{equation*}1+\sigma^*=1+\dfrac{\sigma_\text m}{\sigma_\text{eq}}=\dfrac{\sigma_\text m+\sigma_\text{eq}}{\sigma_\text{eq}}\tag*{(10)}\end{equation*}
对式(10)两边积分, 有
\begin{equation*}\int(1+\sigma^*)\text d\varepsilon=\dfrac{\int(\sigma_\text m+\sigma_\text{eq})\text d\varepsilon}{\int\sigma_\text{eq}\text d\varepsilon}\tag*{(11)}\end{equation*}
上式表明, $1+\sigma^*$是针对复杂应力$\sigma_\text m+\sigma_{\rm eq}$的三轴度, 其积分值为复杂应力状态下RVE 应变能与等效应力作用所得应变能的比值, 说明本文所提出准则表征了复杂应力状态下材料的约束程度与应力状态.
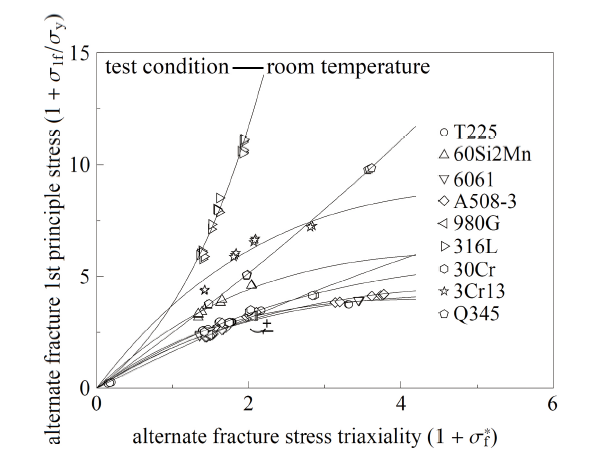
图38给出了9种金属材料的断裂数据, 可见, 所提出断裂准则模型对9种材料的断裂结果均有十分好的预测吻合度, 进一步证明了该断裂准则在预测延性材料断裂行为时的准确性和普适性, 则将其运用到延性材料断裂韧性的预测及结构完整性分析中, 均具有十分重要的意义. 上述材料准则中的参量值在表4中给出.
图38 金属材料临界延性断裂准则
Fig.38 The critical ductile fracture criterion of metal materials
表4 各材料统一塑性临界延性断裂准则的参量
Table 4 Parameters for unified critical fracture criterion of various materials
| Matcrial | M1 | m2 |
|---|---|---|
| T225 | 2.55 | -0.238 |
| 60Si2Mn | 3.31 | -0.202 |
| 6061 | 2.20 | -0.195 |
| A508-3 | 2.14 | -0.173 |
| 980G | 1.71 | -0.043 |
| 316L | 2.41 | 0.442 |
| 30Cr | 2.23 | -0.145 |
| 3Cr13 | 4.49 | -0.187 |
| Q345 | 2.39 | -0.037 |
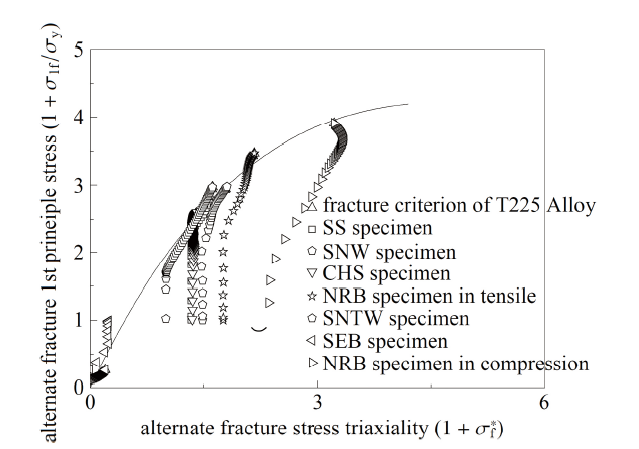
以T225钛合金为例, 将整个加载过程中的第一主应力与应力三轴度的数据点与所得准则进行对比, 如图39所示.
从图39可以看出, 拉断、扭断和裂尖断试样未进入临界断裂状态的试验数据点均低于准则线, 对于压断试验, 随着载荷的增大, 第一主应力负向增长, 故而未进入临界断裂状态的数据点高于准则线, 该结论证明了本文所提出延性断裂准则的准确性.
采用文中试验数据对文献中断裂准则进行验证, 采用T225钛合金试验数据求取Freudental准则、C-L准则、R-T 准则、Brozzo 准则和Oh准则中的临界破坏值$C\text{cr}$, 在表5中给出.
表5 已有文献[
Table 5 Critical values of fracture criterions in Refs.[
| Materials | Freudental | C-L | R-T | Brozzo | Oh |
|---|---|---|---|---|---|
| SS 1# | 345 | 371 | 0.792 | 0.562 | 0.559 |
| SS2# | 260 | 264 | 0.605 | 0.431 | 0.430 |
| SS3# | 291 | 302 | 0.672 | 0.478 | 0.476 |
| SNW 1# | 324 | 429 | 0.818 | 0.567 | 0.548 |
| SNW 2# | 318 | 420 | 0.802 | 0.556 | 0.538 |
| SNW 3# | 304 | 399 | 0.762 | 0.530 | 0.512 |
| CHS 1# | 508 | 523 | 0.868 | 0.630 | 0.604 |
| CHS 2# | 458 | 470 | 0.786 | 0.571 | 0.545 |
| CHS 3# | 504 | 518 | 0.861 | 0.624 | 0.599 |
| NRB-ten-1# | 213 | 374 | 0.830 | 0.491 | 0.491 |
| NRB-ten-2# | 189 | 329 | 0.755 | 0.437 | 0.448 |
| NRB-ten-3# | 184 | 320 | 0.762 | 0.425 | 0.436 |
| SNTW-1# | 515 | 274 | 0.481 | 0.328 | 0.350 |
| SNTW-2# | 207 | 153 | 0.280 | 0.192 | 0.215 |
| SNTW-3# | 750 | 316 | 0.550 | 0.373 | 0.396 |
| NRB-com-1# | 179 | 109 | 0.088 6 | 0.283 | 0.141 |
| NRB-com-2# | 181 | 110 | 0.0893 | 0.284 | 0.142 |
| NRB-com-3# | 166 | 103 | 0.0826 | 0.270 | 0.135 |
对已有文献断裂准则中的临界破坏值进行分析可知, 各类构型试样的临界破坏值$C_{\rm cr}$不同, 规律性不强, 即同一材料在不同断裂条件下的临界破坏值不同, 需要多次求取, 故在实际工程的复杂破坏环境中, 该类准则参数获取过程繁琐, 实施存在困难.
采用T225钛合金试验数据得到J-C准则、B-W准则和Y-C准则的趋势曲线, 见图40 $\sim$图42.
图40 不同断裂准则[
Fig.40 The description of critical state for materials under different fracture criterions[
J-C断裂准则和B-W断裂准则$(0.4\leqslant\sigma^*\leqslant0.95)$均以临界等效应变作为断裂阈值, 由图40和图41可见, 对于3种材料, 在应力三轴度为$0.3\sim 1.2$的范围内, 大部分数据点集中在两种准则模型趋势线周围, 存在少量数据点距离趋势线较远, J-C断裂准则和B-W断裂准则对于描述延性材料的断裂行为均有一定的准确性, 但J-C 断裂准则预测结果明显优于B-W准则; Y-C断裂准则和本文提出的延性断裂准则均选取临界第一主应力作为断裂阈值, 由图42 可见, Y-C 断裂准则模型趋势线与试验数据点吻合良好, 可见依赖较窄三轴度范围的拉伸断裂试验而建立的Y-C 断裂准则对于较高三轴度的材料断裂也有良好适应性, 但对三轴度低于0.33的材料断裂结果缺乏良好描述的趋势.
本文所提出的延性断裂准则以第一主应力为弹塑性变形过程中的主控参量, 适用于预测$-1$至3范围的应力三轴度下延性材料的断裂行为, 文中选用硬化金属材料对延性断裂准则进行研究, 所提出准则的适用性未涉及其他延性材料(如高分子材料、复合材料等).
6 结 论
(1)完成了9种金属材料具有不同约束程度的10类试样的延性断裂试验, 获得了拉、压、扭和裂尖断裂等破坏形式的材料载荷-位移试验关系.
(2)基于圆棒漏斗试样拉伸试验所得载荷-位移曲线, 采用FAT方法得到了9种材料直至破坏的全程等效应力- 应变关系, 以此作为材料本构通过有限元分析获得了10类试样直至破坏的载荷-位移关系, 模拟结果与试验结果有较好的一致性, 表明FAT方法所得各向同性材料试样颈缩后的等效全程本构关系具有真实性和普适性.
(3)基于全程材料等效本构关系曲线, 实现了对延性材料直至断裂的加载过程力学行为精确模拟, 对应9种金属材料、10类试样的36个载荷-位移临界断裂点, 获得了对应的材料临界断裂应力、应变与临界应力三轴度, 研究表明, 第一主应力在弹塑性变形过程中为控制断裂的主控参量.
(4)基于能量等效方法确定了裂纹构型的启裂点, 提出了高约束度条件下材料的断裂点应力状态的获取方法.
(5)通过研究光滑、缺口、裂纹构型的断裂状态, 提出了$-1$至3范围的应力三轴度下由第一主应力主控的统一临界延性断裂准则, 该准则表征了复杂应力状态下材料的约束程度和应力状态.
(6)获取了9种材料的临界延性断裂准则参数, 与已有延性断裂准则预测结果进行对比, 证明本文所提出延性断裂准则具有更好的准确性和普适性.
The authors have declared that no competing interests exist.
参考文献
| [1] |
The Inelastic Behaviour of Solids . |
| [2] |
Ductility and the workability of metals. |
| [3] |
On the ductile enlargement of voids in triaxial stress fields . |
| [4] |
A new method for the prediction of formability limits in metal sheets // |
| [5] |
Workability of aluminum alloy 7075-T6 in upsetting and rolling . |
| [6] |
Continuum theory of ductile rupture by void nucleation and growth: Part I-Yield criteria and flow rules for porous ductile media . |
| [7] |
Influence of voids on shear band instabilities under plane strain conditions .
|
| [8] |
On localization in ductile materials containing spherical voids .
|
| [9] |
Analysis of the cup-cone fracture in a round tensile bar .
|
| [10] |
An analysis of ductile rupture in notched bars . |
| [11] |
Modification of the Gurson model for shear failure. European Journal of Mechanics-A/ |
| [12] |
Effect of a shear modified Gurson model on damage development in a FSW tensile specimen .
|
| [13] |
基于材料全程本构关系对延性断裂韧性的数值模拟方法与应用 .Numerical simulation methods and application for ductile fracture toughness based on full-range constitutive relationship . |
| [14] |
基于构型力断裂准则的裂纹与夹杂干涉问题 .
Crack interacting with an individual inclusion by the fracture criterion of configuration al force .
|
| [15] |
基于试验与有限元耦合技术的延性材料全程单轴本构关系获取方法 .Determination of stress-strain curve of ductile materials by testing and finite element coupling method . |
| [16] |
|
| [17] |
Application of extended Mohr-Coulomb criterion to ductile fracture . |
| [18] |
|
| [19] |
AHSS shear fracture predictions based on a recently developed fracture criterion . |
| [20] |
Experiments and modeling of anisotropic aluminum extrusions under multi-axial loading-Part II: Ductile fracture . |
| [21] |
三剪应力统一强度理论研究 .Study of three-shear stress unified strength theory . |
| [22] |
Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures . |
| [23] |
On fracture locus in the equivalent strain and stress triaxiality space . |
| [24] |
Ductile damage evolution under triaxial state of stress: Theory and experiments .
|
| [25] |
A new model of metal plasticity and fracture with pressure and lode dependence .
|
| [26] |
On the influence of stress triaxiality and strain rate on the behaviour of a structural steel .
|
| [27] |
Influence of stress triaxiality and strain rate on the failure behavior of a dual-phase DP780 steel . |
| [28] |
Studies in Large Plastic Flow and Fracture . |
| [29] |
Celentano Experimental and numerical analysis of the tensile test using sheet specimens .
|
| [30] |
Technical note fracture prediction and necking analysis .
|
| [31] |
Numerical analysis and modeling of large deformation and necking behavior of tensile specimens .
|
| [32] |
Determination of the equivalent stress-equivalent strain relationship of a copper sample under tensile loading .
|
| [33] |
A new method for acquiring true stress-strain curves over a large range of strains using a tensile test and finite element method . |
| [34] |
A new strength criterion for ductile materials based on a finite element aided testing method . |
| [35] |
Theoretical model for predicting uniaxial stress-strain relation by dual conical indentation based on equivalent energy principle . |
| [36] |
Unified elastoplastic model based on a strain energy equivalence principle . |
| [37] |
I 型裂纹构元J 积分的半解析方法 .A semi analytical method to solve J-integral for mode-I crack components . |

/
| 〈 |
|
〉 |