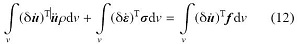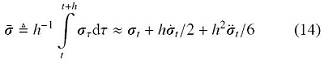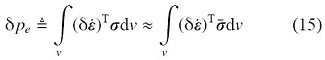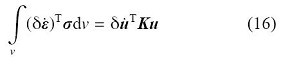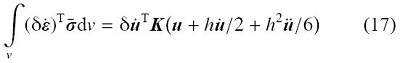多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] .
困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] .
即使多柔体系统中系统变量间没有约束, 求解其系统动力学方程也是十分困难的. 众所周知, 常微分方程组 y ̇ = f ( t , y ) L
| | f ( t , y 2 ) - f ( t , y 1 ) | | L | | y 2 - y 1 | |
Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
本文结合多柔体系统的特点, 研究如何在建立多柔体系统动力学方程的过程中控制模型中的高频分量成分, 并通过数值实验比较模型降噪方法与典型方法在精度和效率方面的差异. 以期为大幅度改善多柔体系统动力学方程的数值性态提供一种新的途径.
1 多柔体系统数值求解的困难
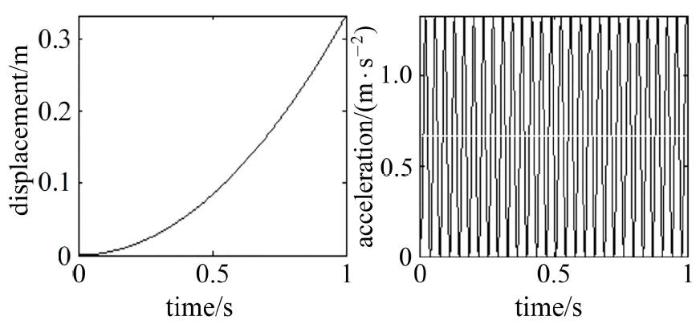
多柔体系统中物体的运动可分解为物体连体基的整体运动和相对于连体基的弹性运动[30 ] . 物体的弹性运动通常具有幅值小频率高的特性. 它对物体位移的贡献很小, 但却使物体加速度以可观的幅度高频振荡. 如图1 所示, 由两根弹簧连接3个质量
图1 弹簧质量系统.块组成的弹簧质量系统, 初始静止, 在水平力f m k 1 k 2 x 1 x 2 x 3 k 1 = k 2 = k
Fig.1 Spring-mass system
m x ̈ 1 + k ( x 1 - x 2 ) = 0
m x ̈ 2 + 2 k x 2 - k ( x 1 + x 3 ) = 0
m x ̈ 3 + k x 3 - k x 2 = f
如果刚度 k m
x 0 = 1 2 a 0 t 2
其中, a 0 = f / ( 3 m )
x 1 = x 0 - a 1 ( 1 - cos ω 1 t ) + a 2 ( 1 - cos ω 2 t )
x 2 = x 0 - 2 a 2 ( 1 - cos ω 2 t )
x 3 = x 0 + a 1 ( 1 - cos ω 1 t ) + a 2 ( 1 - cos ω 2 t )
其中, 弹性振动频率 ω 1 = k / m ω 2 = 3 ω 1 a 1 = f / ( 2 k ) a 2 = f / ( 18 k ) . 各物体运动加速度分别为
x ̈ 1 = a 0 + 1 2 a 0 ( cos ω 2 t - 3 cos ω 1 t )
x ̈ 2 = a 0 - a 0 cos ω 2 t
x ̈ 3 = a 0 + 1 2 a 0 ( 3 cos ω 1 t + cos ω 2 t )
从中可见: 弹性振动使各物体位移在整体位移 x 0 k x 0 a 0 a 0 图2 ), 造成系统动力学方程的数值求解反而变得越来越困难. 大量的算例表明: 多柔体系统中物体的位移和加速度都具有上述特征[29 ] 。
图2 柔性体的位移和加速度.
Fig.2 Displacement and acceleration of a flexible body
其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ]
式中, u 〼 倻 f
物体位移中高频弹性振动分量主要源于随时间快速变化的应力 〼 . 在区间 ( t , t + h ) τ
$\begin{equation*}\textbf{{σ}}_\tau\approx\textbf{{σ}}_t+(\tau-t)\dot{\textbf{{σ}}}_t+(\tau-t)^2\ddot{\textbf{{σ}}}_t/2\tag*{(13)}\end{equation*}$
该区间内应力平均值
为了滤除模型中的高频分量, 用平均应力$\bar{\textbf{\textit{σ}}}$替换应力$\textbf{\textit{σ}}$, 从而将变形虚功率近似为
这种方法的滤波作用可通过比较一个线性系统在修改前后的动力学方程性质说明. 当应变‒位移关系以及应力‒应变关系均为线性时, 变形虚功率可用系统刚度矩阵 K
按上述方法修改后的变形虚功率
线性系统的动力学方程可以写作
Mu + Ku = F (18)
将变形虚功率按式(17)近似后, 系统动力学方程成为
( M + h 2 K / 6 ) u + hKu / 2 + Ku = F (19)
与修改前的系统动力学方程相比, 它增加了惯性项和阻尼项, 从而可降低系统的固有频率. 参数 h
$\begin{equation*}(\textbf{{K}}-\omega^2\textbf{{M}})\textbf{{ν}}=\textbf{0}\tag*{(20)}\end{equation*}$
利用其特征向量组成的矩阵 T = [ 퀻 u = Tw . 由于矩阵 T T TKT = diag ( ω 1 2 , ω 2 2 , ⋅ ⋅ ⋅ , ω n 2 ) T TMT = E
w ̈ i + ω i 2 w i = f i , i = 1,2 , ⋅ ⋅ ⋅ , n
( 1 + h 2 6 ω i 2 ) w ̅ ̈ i + ω i 2 ( h 2 w ̅ ̇ i + w ̅ i ) = f i , i = 1,2 , ⋅ ⋅ ⋅ , n
其中, 模态力 f i T T F
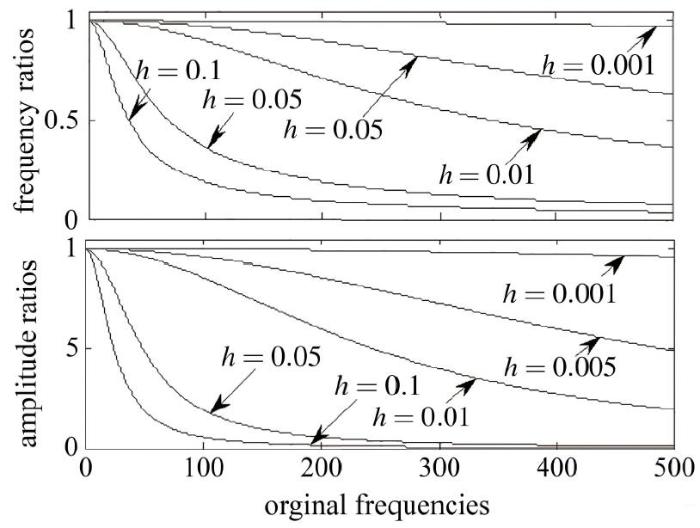
λ ω ≜ ( 1 + h 2 ω i 2 / 6 ) - 1 ( 1 + 5 h 2 ω i 2 / 48 ) 1 2
λ a ≜ ( 1 + h 2 ω i 2 / 6 ) - 1
这两个比值随系统频率 ω i h 图3 所示. 从图3 可以看到: (1)无论参数 h h h
图3 频率比与振幅比.
Fig.3 Amplitudes and frequencies ratios
模型降噪相当于对原系统进行了一次模态减缩, 但又不必具体求解系统的模态, 只需调整降噪参数h
3 数值算例
利用模型降噪方法滤除系统高频分量后, 系统动力学方程可用任何现有微分方程求解器求解. 如果先降噪再用ODE45求解并取 h = 0.1 _ _ 0.1 ; 如果用ODE15s 求解并取 h = 0.01 _ _ 0.01.
例1图1所示的系统, 其系统参数如表1所示.
用ODE45, ODE15s和MS _ _ 0.1 分别对其在0 ~ 5 s内的运动进行数值求解. 当精度控制参数分别为 ε r = 1.0 × 1 0 - 4 ε a = 1.0 × 1 0 - 6
x 1 = x 2 = x 3 = t 2 / 3
解析解和数值解之间的绝对误差以及求解所耗时间如表2 所示. 从中可见: 3种方法所得结果均具有很高的精度, 但计算效率相差很大. 其中,ODE15s最差, 说明刚性微分方程求解器不适合采用高精度控制参数. 模型降噪方法MS _ _ 0.1 在这种情况下计算效率明显高于其他两种方法.
当精度控制参数分别取 ε r = 1.0 × 1 0 - 2 ε a = 1.0 × 1 0 - 3 表3 所示.
在这种情况下, 非刚性微分方程求解器ODE45因积累误差放大传播导致数值解发散. ODE15s和本文所提方法MS _ _ 0.1 都在较短的时间内得到了具有合理精度的数值解.
例2 为检验本文所提方法处理刚柔耦合问题的能力, 将图1 所示系统中两个刚度间的差异增大, 令 k 1 = 2.0 × 1 0 3 k 2 = 1.0 × 1 0 8 m f
x 1 = t 2 / 3 - 2 [ 1 - cos ( 10 3 t ) ] / 900
x 2 = x 3 = t 2 / 3 + [ 1 - cos ( 10 3 t ) ] / 900
图4 为采用MS _ _ 0.001 方法所求得的数值解与解析解之间的比较. 从中可见: 模型降噪法给出的质点位移 x 1 x 2
图4 位移数值解与解析解比较.
Fig.4 Comparisons of numerical displacements and their analytical solution
解析解和数值解之间的绝对误差以及求解所耗时间如表4 所示. 从中可以看到: 模型降噪法在h h h
表4 为取精度控制参数 ε r = 1.0 × 1 0 - 3 ε a = 1.0 × 1 0 - 6 [0 ,5 ] s内的运动数值解的精度和效率.
例3 本算例将给出本文所提方法在柔性多体系统动力学中的应用. 基于文献[32 ] 所提的应变插值大变形平面柔性梁的建模方法, 将梁的轴向应变和曲率修改为
ε ̅ = ε t + 1 2 h ε ̇ t + 1 6 h 2 ε ̈ t κ ̅ = κ t + 1 2 h κ ̇ t + 1 6 h 2 κ ̈ t
因此, 修正后的节点内力为
f int = K e 瀼
其中, 瀼 K e
K e = EAL 0 0 0 EIL / 3 EIL / 6 0 EIL / 6 EIL / 3
其中, EA EI EI
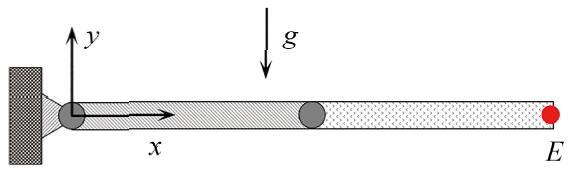
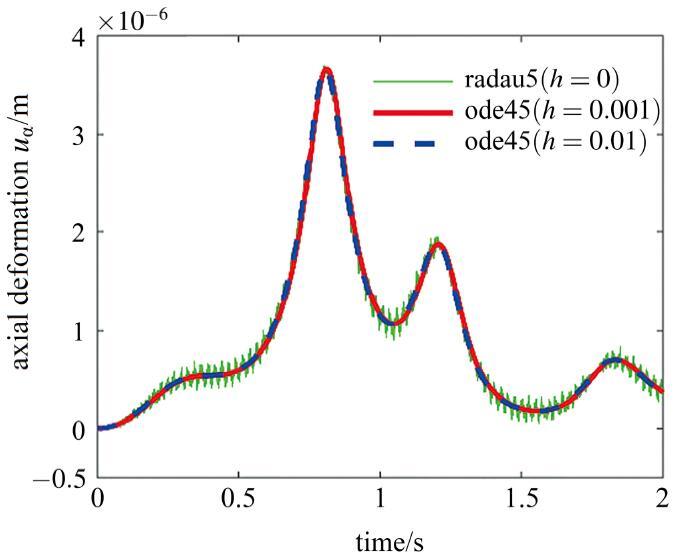
对于图5 所示的双摆机构, 材料密度为 ρ = 7801 kg / m 3 E = 2.1 × 1 0 11 L = 1.8 m A = 2.5 × 1 0 - 3 m 2 . 机构在 g = - 9.81 m / s 2
图5 自由下落的柔性双摆机构.
Fig.5 Free-falling flexible double pendulum mechanism
分别采用MATLAB的刚性方程求解器radau5 ( h = 0 ) ( h = 0.001 ; h = 0.01 ) ε r = 1.0 × 1 0 - 3 ε a = 1.0 × 1 0 - 6 . 得到双摆机构上末端点在竖直方向和水平方向的位移, 分别如图6 和图7 所示.
图6 末端点的轴向变形.
Fig.6 Axial deformation of the end point
图7 末端点的横向挠度.
Fig.7 Lateral deflection of the end point
由图6 和图7 可以看出, 当柔性双摆的材料刚度较大时( E = 2.1 × 1 0 11 Pa )
表5 对比了上述不同方法的计算时间, 数据显示: 如果不使用模型降噪方法, 普通的微分方程求解器ODE45无法在有限的时间内获得系统的数值解; 使用模型降噪技术后, 对于刚度较大的柔性多体系统, 本文所提方法的计算效率更高.
4 结 论
在多柔体系统的虚功率方程中用 ( t , t + h ) t h h h
The authors have declared that no competing interests exist.
参考文献
文献选项
[1]
田强 , 刘铖 , 李培 等 . 多柔体系统动力学研究进展与挑战
. 动力学与控制学报 , 2017 , 15 (5 ): 385 -405
[本文引用: 1]
(Tian Qiang Liu Cheng Li Pei et al .Advances and challenges in dynamics of flexible multibody systems
.Journal of Dynamics and Control 2017 , 15 (5 ): 385 -405 (in Chinese))
[本文引用: 1]
[2]
王琪 , 庄方方 , 郭易圆 等 . 非光滑多体系统动力学数值算法的研究进展
. 力学进展 , 2013 , 43 (1 ): 101 -111
[本文引用: 1]
(Wang Qi Zhuang Fangfang Guo Yiyuan et al .Advances in the research on numerical methods for non-smooth dynamics of multibody systems
.Advances in Mechanics 2013 , 43 (1 ): 101 -111 (in Chinese))
[本文引用: 1]
[3]
刘才山 , 陈滨 , 彭瀚 等 . 多体系统多点碰撞接触问题的数值求解方法
. 动力学与控制学报 , 2003 , 1 (1 ): 59 -65
[本文引用: 1]
(Liu Caishan Chen Bin Peng Han et al .Numerical resolution of multibody systems with multiple contact/impact points
.Journal of Dynamics and Control 2003 , 1 (1 ): 59 -65 (in Chinese))
[本文引用: 1]
[4]
姚文莉 , 岳嵘 . 有争议的碰撞恢复系数研究进展
. 振动与冲击 , 2015 , 34 (19 ): 43 -48
[本文引用: 1]
(Yao Wenli Yue Rong Advance in controversial restitution coefficient study for impact problems
.Journal of Vibration and Shock 2015 , 34 (19 ): 43 -48 (in Chinese))
[本文引用: 1]
[5]
Stechlinski PG Barton PI Dependence of solutions of nonsmooth differential-algebraic equations on parameters
.Journal of Differential Equations , 2017 , 262 (3 ): 2254 -2285
[本文引用: 2]
[6]
Dhamacharoen A Efficient numerical methods for solving differential algebraic equations
.Journal of Applied Mathematics & Physics , 2016 , 4 (1 ): 1 -9
[本文引用: 1]
[7]
Petzold L Differential/algebraic equations are not ODE’S
.Siam Journal on Scientific & Statistical Computing , 2012 , 3 (3 ): 367 -384
[本文引用: 1]
[8]
Shampine LF Reichelt MW Kierzenka JA Solving index-I DAEs in MATLAB and simulink
.Siam Review , 1999 , 41 (3 ): 538 -552
[本文引用: 1]
[9]
Gear CW Petzold LR ODE methods for the solution of differential /algebraic systems
.Siam Journal on Numerical Analysis , 1984 , 21 (4 ): 716 -728
[本文引用: 1]
[10]
Haddouni M Acary V Garreau S et al .Comparison of several formulations and integration methods for the resolution of DAEs formulations in event-driven simulation of nonsmooth frictionless multibody dynamics
.Multibody System Dynamics , 2017 , 41 (3 ): 201 -231
[本文引用: 1]
[11]
Marques F Souto A P Flores P On the constraints violation in forward dynamics of multibody systems
.Multibody System Dynamics , 2016 , 39 (4 ): 1 -35
[本文引用: 1]
[12]
Schweizer B Lu D Li P Co-simulation method for solver coupling with algebraic constraints incorporating relaxation techniques
.Multibody System Dynamics , 2016 , 36 (1 ): 1 -36
[本文引用: 1]
[13]
潘振宽 , 赵维加 , 洪嘉振 等 . 多体系统动力学微分/代数方程组数值方法
. 力学进展 , 1996 , 26 (1 ): 83 -96
[本文引用: 1]
(Pan Zhenkuan Zhao Weijia Hong Jiazhen et al .On numerical algorithms for differential/algebraic equations of motion of multibody system
.Advances in Mechanics 1996 , 26 (1 ): 26 -40 (in Chinese))
[本文引用: 1]
[14]
袁新鼎 . 刚性常微分方程初值问题的数值解法. 北京 : 科学出版社 , 1987
[本文引用: 3]
(Yuan Xinding. Numerical Methods for Solving Initial Value Problems of Stiff Ordinary Differential Equations. Beijing : Science Press , 1987 (in Chinese))
[本文引用: 3]
[15]
程正兴 . 数值逼近与常微分方程数值解. 西安 : 西安交通大学出版社 , 2000
[本文引用: 2]
(Cheng Zhengxing. Numerical Approximation and Numerical Solution of Ordinary Differential Equation. Xi’ an : Xi’an Jiaotong University Press , 2000 (in Chinese))
[本文引用: 2]
[16]
Hairer E Lubich C Numerical Analysis of Ordinary Differential Equations. Berlin,
Heidelberg: Springer 2015
[本文引用: 1]
[17]
Ibrahim Z Nasir NM Othman K et al .Adaptive order of block backward differentiation formulas for stiff ODEs
.Numerical Algebra , 2017 , 7 (1 ): 95 -106
[本文引用: 1]
[18]
El-Zahar ER Habib HM Rashidi MM et al .A comparison of explicit semi-analytical numerical integration methods for solving stiff ODE systems
.American Journal of Applied Sciences , 2015 , 12 (5 ): 304 -320
[本文引用: 1]
[19]
Ariel G Engquist B Tsai R A multiscale method for highly oscillatory ordinary differential equations with resonance
.Mathematics of Computation , 2009 , 78 (266 ): 929 -956
[本文引用: 1]
[20]
Tokman M Efficient integration of large stiff systems of ODEs with exponential propagation iterative (EPI) methods
.Journal of Computational Physics , 2006 , 213 (2 ): 748 -776
[本文引用: 1]
[21]
Meijaard JP Application of Runge-Kutta-Rosenbrock methods to the analysis of flexible multibody systems
.Multibody System Dynamics , 2003 , 10 (3 ): 263 -288
[本文引用: 1]
[22]
Shabana AA Hussein BA A two-loop sparse matrix numerical integration procedure for the solution of differential/algebraic equations: Application to multibody systems
.Journal of Sound & Vibration , 2009 , 327 (3 ): 557 -563
[本文引用: 1]
[23]
Yen J Petzold L Raha S A time integration algorithm for flexible mechanism dynamics: the DAE α-method
.Computer Methods in Applied Mechanics and Engineering , 1998 , 158 (3 ): 341 -355
[本文引用: 1]
[24]
Arnold M Brüls O Convergence of the generalized-α, scheme for constrained mechanical systems
.Multibody System Dynamics , 2007 , 18 (2 ): 185 -202
[本文引用: 1]
[25]
丁洁玉 , 潘振宽 . 多体系统动力学微分‒代数方程广义<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml184-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula>投影法
. 工程力学 , 2013 , 30 (4 ): 380 -384
[本文引用: 1]
(Ding Jieyu Pan Zhenkuan. generalized<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml185-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula> projection method for differential-algebraic equations of multibody dynamics
.Engineering Mechanics 2013 , 30 (4 ): 380 -384 (in Chinese))
[本文引用: 1]
[26]
郭晛 , 章定国 , 陈思佳 . Hilber-Hughes-Taylor<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml186-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula> 法在接触约束多体系统动力学中的应用
. 物理学报 , 2017 , 66 (16 ): 144 -154
[本文引用: 1]
(Guo Xian Zhang Dingguo Chen Sijia Application of Hilber-Hughes-Taylor<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml187-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula> method to dynamics of flexible multibody system with contact and constraint
.Acta Physica Sinica 2017 , 66 (16 ): 144 -154 (in Chinese))
[本文引用: 1]
[27]
姚廷强 , 迟毅林 , 黄亚宇 . 柔性多体系统动力学新型广义<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml188-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula>数值分析方法
. 机械工程学报 , 2009 , 45 (10 ): 53 -60
[本文引用: 1]
(Yao Tingqiang Chi Yilin Hu Yayu New generalized-α algorithms for multibody dynamics
.Journal of Mechanical Engineering 2009 , 45 (10 ): 53 -60 (in Chinese))
[本文引用: 1]
[28]
郭晛 , 章定国 . 柔性多体系统动力学典型数值积分方法的比较研究
. 南京理工大学学报(自然科学版) , 2016 , 40 (6 ): 726 -733
[本文引用: 1]
(Guo Xian Zhang Dingguo Comparative study of typical numerical integration methods of flexible multi-body systems dynamics
.Journal of Nanjing University of Science and Technology 2016 , 40 (6 ): 726 -733 (in Chinese))
[本文引用: 1]
[29]
Banerjee A Flexible Multibody Dynamics: Efficient Formulations and Applications. John Wiley & Sons
, Inc. , 2016
[本文引用: 3]
[30]
洪嘉振 . 计算多体系统动力学. 北京 : 高等教育出版社 , 1999
[本文引用: 2]
(Hong Jiazhen. Computational Dynamics of Multibody Systems. Beijing : Higher Education Press , 1999 (in Chinese))
[本文引用: 2]
[31]
齐朝晖 . 多体系统动力学. 北京 : 科学出版社 , 2008
[本文引用: 1]
(Qi Zhaohui. Dynamics of Multibody Systems. Beijing : Science Press , 2008 (in Chinese))
[本文引用: 1]
[32]
张志刚 , 齐朝晖 , 吴志刚 . 一种基于应变插值大变形梁单元的刚‒柔耦合动力学分析
. 振动工程学报 , 2015 , 28 (3 ): 337 -344
[本文引用: 1]
(Zhang Zhigang Qi Zhaohui Wu Zhigang Rigid-flexible dynamics analysis of a large deformation beam element based on interpolation of strains
.Journal of Vibration Engineering 2015 , 28 (3 ): 337 -344 (in Chinese))
[本文引用: 1]
多柔体系统动力学研究进展与挑战
1
2017
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
多柔体系统动力学研究进展与挑战
1
2017
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
非光滑多体系统动力学数值算法的研究进展
1
2013
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
非光滑多体系统动力学数值算法的研究进展
1
2013
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
多体系统多点碰撞接触问题的数值求解方法
1
2003
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
多体系统多点碰撞接触问题的数值求解方法
1
2003
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
有争议的碰撞恢复系数研究进展
1
2015
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
有争议的碰撞恢复系数研究进展
1
2015
... 多柔体系统是由多个可变形柔性部件通过铰相互连接而组成的系统. 实际工程中很多机械系统都可抽象为多柔体系统, 例如空间太阳能帆板、周边桁架式可展开天线等. 由于研究对象的复杂多样性, 多柔体系统不仅在建模理论方面不断面临新的挑战. 其动力学方程的数值求解也存在许多难点问题[1 ,2 ,3 ,4 ] . ...
Dependence of solutions of nonsmooth differential-algebraic equations on parameters
2
2017
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
... 表4 为取精度控制参数 ε r = 1.0 × 1 0 - 3 ε a = 1.0 × 1 0 - 6 [0 ,5 ] s内的运动数值解的精度和效率. ...
Efficient numerical methods for solving differential algebraic equations
1
2016
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
Differential/algebraic equations are not ODE’S
1
2012
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
Solving index-I DAEs in MATLAB and simulink
1
1999
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
ODE methods for the solution of differential /algebraic systems
1
1984
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
Comparison of several formulations and integration methods for the resolution of DAEs formulations in event-driven simulation of nonsmooth frictionless multibody dynamics
1
2017
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
On the constraints violation in forward dynamics of multibody systems
1
2016
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
Co-simulation method for solver coupling with algebraic constraints incorporating relaxation techniques
1
2016
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
多体系统动力学微分/代数方程组数值方法
1
1996
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
多体系统动力学微分/代数方程组数值方法
1
1996
... 困难之一源于铰的约束: 如果直接采用笛卡尔坐标和转动矢量描述物体在惯性坐标系中的运动, 铰的约束体现为描述参数间的代数约束方程; 如果采用物体间相对运动的参数(铰坐标)作为系统变量, 对含闭环的多体系统, 铰坐标必须满足闭环约束方程. 因而, 一般多体系统的动力学方程是微分代数混合方程组(DAEs), 它的求解本身就是计算数学的难点问题[5 ,6 ,7 ,8 ,9 ] . 除此之外, 多体系统动力学对DAEs的求解方法还有更高的要求: 位置约束方程及其派生出的速度和加速度约束方程的违约量都必须被同时抑制在合理的范围内. 经国内外众多学者的长期探索, 已经提出了约束稳定化方法、广义坐标分块方法、局部参数化缩并方法、违约修正方法等一系列现实可行的方法[10 ,11 ,12 ,13 ] . ...
3
1987
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
... [14 ,15 ]. 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
3
1987
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
... [14 ,15 ]. 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
2
2000
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
2
2000
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
Numerical Analysis of Ordinary Differential Equations. Berlin,
1
2015
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Adaptive order of block backward differentiation formulas for stiff ODEs
1
2017
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
A comparison of explicit semi-analytical numerical integration methods for solving stiff ODE systems
1
2015
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
A multiscale method for highly oscillatory ordinary differential equations with resonance
1
2009
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Efficient integration of large stiff systems of ODEs with exponential propagation iterative (EPI) methods
1
2006
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Application of Runge-Kutta-Rosenbrock methods to the analysis of flexible multibody systems
1
2003
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
A two-loop sparse matrix numerical integration procedure for the solution of differential/algebraic equations: Application to multibody systems
1
2009
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
A time integration algorithm for flexible mechanism dynamics: the DAE α-method
1
1998
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Convergence of the generalized-α, scheme for constrained mechanical systems
1
2007
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
多体系统动力学微分?代数方程广义<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml184-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula>投影法
1
2013
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
多体系统动力学微分?代数方程广义<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml184-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula>投影法
1
2013
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Hilber-Hughes-Taylor<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml186-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula> 法在接触约束多体系统动力学中的应用
1
2017
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Hilber-Hughes-Taylor<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml186-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula> 法在接触约束多体系统动力学中的应用
1
2017
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
柔性多体系统动力学新型广义<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml188-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula>数值分析方法
1
2009
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
柔性多体系统动力学新型广义<inline-formula><mml:math xmlns:mml="http://www.w3.org/1998/Math/MathML" id="Mml188-0459-1879-50-4-863"><mml:mo>-</mml:mo><mml:mi>α</mml:mi></mml:math></inline-formula>数值分析方法
1
2009
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
柔性多体系统动力学典型数值积分方法的比较研究
1
2016
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
柔性多体系统动力学典型数值积分方法的比较研究
1
2016
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
Flexible Multibody Dynamics: Efficient Formulations and Applications. John Wiley & Sons
3
2016
... Lipschitz常数越大, 数值求解的难度也越大[14 ,15 ,16 ] . 多柔体系统中物体的高频振荡弹性运动可使系统动力学方程的Lipschitz常数高达 1 0 6 [17 ,18 ,19 ,20 ,21 ] : 一类以标准一阶微分方程为研究对象, 其主要方法包括: BDF 方法、隐式Runge-Kutta方法、Rosenbrock方法等; 另一类以二阶微分方程为研究对象, 其主要方法包括: Newmark方法、Wilson- θ α [22 ,23 ,24 ,25 ,26 ,27 ,28 ,29 ] : HHT 双循环隐式积分法、BDF双循环隐式积分法、广义 α α
... 从中可见: 弹性振动使各物体位移在整体位移 x 0 k x 0 a 0 a 0 图2 ), 造成系统动力学方程的数值求解反而变得越来越困难. 大量的算例表明: 多柔体系统中物体的位移和加速度都具有上述特征[29 ] . ...
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
2
1999
... 多柔体系统中物体的运动可分解为物体连体基的整体运动和相对于连体基的弹性运动[30 ] . 物体的弹性运动通常具有幅值小频率高的特性. 它对物体位移的贡献很小, 但却使物体加速度以可观的幅度高频振荡. 如图1 所示, 由两根弹簧连接3个质量 ...
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
2
1999
... 多柔体系统中物体的运动可分解为物体连体基的整体运动和相对于连体基的弹性运动[30 ] . 物体的弹性运动通常具有幅值小频率高的特性. 它对物体位移的贡献很小, 但却使物体加速度以可观的幅度高频振荡. 如图1 所示, 由两根弹簧连接3个质量 ...
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
1
2008
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
1
2008
... 其解具有上述特征的微分方程属于刚性微分方程. 如果采用MATLAB ODE45, ODE113等常规求解器求解这类系统, 为避免累积误差放大传播, 积分步长Δ t T min Δ t 2.78 T min ). 多柔体系统中物体弹性振动的最高频率常常高达1 0 6 [14 ] . 如果采用MATLAB ODE15s, ODE23tb等刚性微分方程求解器, 可在积分步长远远大于最小振动周期的情况下仍能保证数值解的稳定性. 众所周知, 如果积分步长大于某个振动的周期, 数值解就不可能准确描述它随时间的变化[14 ,15 ] . 一个合理的问题是: 用刚性微分方程求解器求得的解是一种什么意义下的解. 事实上, 绝大部分刚性微分方程数值方法中, 都有一个核心步骤: 用多个时刻的位移值计算t + Δ t 图1 所示的系统(质量m = 10 kg k = 1.0 × 1 0 5 N / m f = 20 N ε r = 1 0 - 2 ε a = 1 0 - 3 ) , 则所得的各物体运动是整体运动x 0 t 2 / 3 2 / 3 m / s 2 . 刚性微分方程求解器的滤波作用大小与对解的精度要求密切相关. 如果对数值解的精度要求较高, 积分步长可能被迫缩短至某些高频振荡周期之内, 从而导致滤波作用失效. 例如, 如果将精度参数提高为ε r = 1.0 × 1 0 - 6 ε a = 1.0 × 1 0 - 10 [29 ,30 ,31 ] ...
一种基于应变插值大变形梁单元的刚?柔耦合动力学分析
1
2015
... 例3 本算例将给出本文所提方法在柔性多体系统动力学中的应用. 基于文献[32 ] 所提的应变插值大变形平面柔性梁的建模方法, 将梁的轴向应变和曲率修改为 ...
一种基于应变插值大变形梁单元的刚?柔耦合动力学分析
1
2015
... 例3 本算例将给出本文所提方法在柔性多体系统动力学中的应用. 基于文献[32 ] 所提的应变插值大变形平面柔性梁的建模方法, 将梁的轴向应变和曲率修改为 ...