力学学报 2018 , 50 (2): 438-445 https://doi.org/10.6052/0459-1879-17-411

Orginal Article

细胞内吞纳米颗粒药物的数值模拟研究

刘心悦, 龚晓波, 黄华雄

1.上海交通大学船舶海洋与建筑工程学院工程力学系,上海 200240

A NUMERICAL STUDY ON ENDOCYTOSIS OF NANOPARTICLES

Liu Xinyue, Gong Xiaobo, Huang Huaxiong

1.Department of Engineering Mechanics,School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University,Shanghai 200240, China

中图分类号: O302,R914.2

文献标识码: A

收稿日期: 2017-12-11

接受日期: 2018-02-5

网络出版日期: 2018-04-16

基金资助: 国家自然科学基金资助项目(11372191,11232010).

作者简介:

作者简介：龚晓波,副教授,主要研究方向：生物力学、环境流体力学. E-mail: x.gong@sjtu.edu.cn.

展开

摘要

受体介导的内吞是细胞与外界物质交换的常见方式. 采用配体修饰表面的纳米脂质体颗粒,将药物有针对性地投放到肿瘤细胞以提高药物传输的效率,是药物传输系统设计中的核心问题之一. 本文假设内吞是准静态过程,采用三维数学模型来模拟球状纳米颗粒的内吞,建立了包含绑定键的系统变形能方程,通过求解能量方程的最小值,得到药物在每个内吞包裹阶段的变形以及药物的被动内吞所需最小能量,分析不同药物半径对内吞所需最小能量的影响. 研究表明,细胞膜变形能与绑定键变形能占总能量的绝大部分,各组分随着包裹区域增加均有变化;在给定细胞膜和药物颗粒的硬度、绑定键强度等物理特性下存在最优药物尺寸,使得内吞过程中总能耗最小;在药物内吞进行的后期,包裹区域边缘的绑定键因伸长过大发生断裂,影响内吞的顺利完成. 本研究为受体介导的高效药物设计提供了理论支撑.

关键词： 纳米药物 ; 最小能量法 ; 数值模拟

Abstract

Receptor-mediated endocytosis is one of the means for cells to exchange materials with their environments. Vesicles coated with ligands on their surface are often adopted for the drug delivery in cancer therapy through receptor-mediated endocytosis as well. In the present work, we used a 3D mathematical model and energy minimization to study the endocytosis process of spherical drug nanoparticles. The total energy of the system including catch bonds was established. The minimization of the energy functional was carried out numerically. The shape of particle and cell membrane in each wrapping stage was obtained, and the influence of particle size on the minimum energy required for passive endocytosis was analysed. The results show that cell membrane and receptor-ligand bonds deformation energies are the major components of the total deformation energy, and each component changes as the wrapping area is increased. There exists an optimal size of nanoparticles for which the total energy consumption is minimum under given membrane stiffness and receptor-ligand bond strength. We also found that at the final stage of wrapping the endocytosis may not be completed because of the breaking of overstretched receptor-ligand bonds. This study provides a theoretical insight for the design of receptor mediated high efficiency drug delivery system.

Keywords： endocytosis ; nanoparticle ; minimum energy method ; numerical method

PDF (294KB) 元数据多维度评价相关文章收藏文章

本文引用格式导出 EndNote Ris Bibtex

刘心悦, 龚晓波, 黄华雄. 细胞内吞纳米颗粒药物的数值模拟研究[J]. 力学学报, 2018, 50(2): 438-445 https://doi.org/10.6052/0459-1879-17-411

Liu Xinyue, Gong Xiaobo, Huang Huaxiong. A NUMERICAL STUDY ON ENDOCYTOSIS OF NANOPARTICLES[J]. Chinese Journal of Theoretical and Applied Mechanics, 2018, 50(2): 438-445 https://doi.org/10.6052/0459-1879-17-411

引言

受体介导的内吞是细胞通过向内生成小泡来吸收大分子配体的一种方式 ^[1-2]. 受体介导的内吞小泡尺寸大约为100 nm ^[3],荷尔蒙、生长因子、运铁蛋白、各类抗体、细菌和病毒等,通过受体介导的内吞作用进入细胞 ^[4-5]. 通过在纳米颗粒药物表面修饰能识别癌细胞表面特异性受体的配体,用于癌症治疗的纳米颗粒药物也能利用这种方式进入细胞 ^[6-8].

细胞对药物的内吞效率受到多个因素的影响,如药物形状、尺寸、硬度、绑定键强度等 ^[9],本文从力学角度研究纳米颗粒内吞所需的能量,为设计更高效的药物提供理论参考.

针对这一问题,Gao等 ^[10]假设内吞过程中介导内吞的绑定键释放的能量与内吞过程中产生的细胞膜弯曲变形能和膜表面受体向药物内吞部位扩散所消耗的总能量守恒,计算了完成内吞所需受体扩散到达内吞部位时间,得到了药物内吞的最优尺寸以及药物可以内吞的最小尺寸. 他们考虑了内吞区域内部的细胞膜弯曲变形能,忽略了药物的变形以及内吞区域外的细胞膜变形,可能低估了内吞过程所需的总变形能.

Yi等 ^[11]假设内吞是准静态过程,在Gao等 ^[10]的研究基础上,通过对能量方程进行变分得到变形微分方程,采用打靶法求解得到了细胞膜和药物的变形. 他们假设内吞包裹部分细胞膜与内吞药物曲率一致,忽略了受体配体形成绑定键对内吞的影响.

Decuzzi等 ^[12]在Gao等 ^[10]的能量模型基础上,考虑了绑定键的作用对内吞所需时间的影响,求解了受体扩散到内吞部位的时间,结果表明非特异性排斥力会延长内吞时间,而非特异性吸引力会缩短内吞时间,但没有讨论特异性绑定键对内吞的影响. 其模型中假设内吞包裹区域內的所有绑定键的拉伸是相等的,认为只要受体能扩散到包裹区域就能绑定,没有讨论绑定键的局部断裂对内吞的影响.

Li等 ^[13]构建了病毒入侵宿主细胞的能量方程,其中包括绑定键变形能,细胞膜变形能和细胞骨架细胞变形能三个部分,方程的自变量为病毒包裹的深度. 文章提出一个临界深度,小于临界深度时,细胞膜的变形能占主要部分,大于临界深度时,细胞骨架的变形能占主要部分.

Wang等 ^[14]在Gao等 ^[10]的基础上,对柱状纳米颗粒的横向与竖直进入细胞进行了对比. 结果表明,竖直内吞比横向内吞所需的时间更短,且细胞膜的变形比细胞骨架的变形更显著,细胞骨架的硬度的影响只有在一定的包裹深度之后才体现出来,细胞骨架的硬度越大,内吞所需的时间越长. 而竖直进入细胞的纳米颗粒可能会停滞在某个深度.

由于很多病毒表面的配体非常稀少,依然可以快速进入细胞,这与Gao等 ^[10]得到最低受体与配体密度比不一致. 因此,Wang 等 ^[15]在Li等 ^[13]和Gao等 ^[10]的基础上,考虑了细胞骨架的能量和蠕变效应之后,细胞内吞最优尺寸所对应的配体与受体密度比可以更小.

在本文研究中,假设被动内吞是一个准静态过程,通过建立内吞过程中由细胞膜、药物和绑定键组成的变形能方程式,采用最优化的数值方法来求解变形能最小值,获得药物在每个内吞包裹阶段的变形.

在本文研究中,系统总能量除了药物与细胞膜变形能还包括绑定键的变形能,有绑定键存在的时候,细胞膜和药物颗粒变形在包裹区域内并不必须一致,当绑定键的伸长不均匀时,包裹区域內细胞膜和药物的变形也不同. 局部绑定键拉伸过大导致断裂影响了内吞,这种情况在本文模型中也得到了考虑.

1 方法

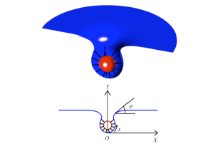
本文建立如图1所示的轴对称坐标系,通过对内吞过程中细胞膜、药物颗粒绑定键的变形能最小值的优化求解,获得细胞膜、药物颗粒和绑定键的形状. 具体方法描述如下.

图1中蓝色为细胞膜,红色为纳米颗粒,黑色的短线为绑定键.

图1中, $ψ$ 是切向角, $s$ 为从原点开始的弧长. 将笛卡尔坐标的原点置于细胞膜的最低点, $Y$ 轴为旋转对称轴. $ψ$ , $s$ 与笛卡尔坐标 $X$ , $Y$ 的关系,对于药

显示原图| 下载原图ZIP| 生成PPT

图1 细胞膜对纳米颗粒内吞系统示意图和轴对称曲线坐标

Fig. 1 The Schematic chart of nanoparticles uptake and coordinate

物为

$$ \left.\bal x_{\rm n} = \dint_0^{S_{\rm n}} \varepsilon _{\rm n} \cos \psi _{\rm n} \d s_0 \[2mm] y_{\rm n} = l_1 + \dint_0^{S_{\rm n}} \varepsilon _{\rm n} \sin \psi _{\rm n} \d s_0 \eal\right\} (1) $$

对于细胞膜为

$$ \left.\bal x_{\rm m} = \dint_0^{S_{\rm m}} \varepsilon _{\rm m} \cos \psi _{\rm m} \d s_0 \[2mm] y_{\rm m} = \dint_0^{S_{\rm m}} {\varepsilon _{\rm m} \sin \psi _{\rm m} } \d s_0 \eal\right\} (2) $$

其中, $l_{1}$ 第一个绑定键的长度, $ε_{n}$ 和 $ε_{m}$ 分别是药物和细胞膜上当地点沿着弧长方向上的伸长率,其定义为 $ε = d s / d s_{0}$ , $d s_{0}$ 是变形前的弧长微分, $d s$ 是变形后的弧长微分.

内吞过程中,变形的细胞膜、药物颗粒和绑定键构成的系统的总能量方程为

$\begin{array}{l} E (ψ_{n}, ψ_{m}, ε_{n}, ε_{m}, l_{1}) = E_{b n} + E_{e n} + E_{b m} + E_{e m} + E_{r l} \end{array} (3)$

其中, $E_{b n}, E_{e n}, E_{b m}, E_{e m}, E_{r l}$ 分别为药物弯曲变形能、药物拉伸变形能、细胞膜弯曲变形能、细胞膜拉伸变形能和受体配体绑定键变形能.

本文采用 Helfrich 模型来描述药物和细胞膜的弯曲能 ^[16]. 由于细胞膜尺寸远远大于药物的尺寸,模型中将细胞膜视为有限大平面,取 $L = 40 r$ , $r$ 是药物的半径.

基于图1所示的细胞膜的弯曲变形能表达试为

$$ E_{\rm bm} = \dint_0^L \dfrac{k_b }{2}\left( {\dfrac{\dot {\psi }_{\rm m} }{\varepsilon _{\rm m,1} } + \dfrac{\sin \psi _{\rm m} }{x_{\rm m} }} \right)^22\uppi x_{\rm m} \d s_0 (4) $$

其中,由于旋转对称 $k_{b}$ 是细胞膜弯曲模量, $x_{m}$ 是当地的 $X$ 坐标, $ε_{m, 1}$ 与 $ε_{m, 2}$ 分别是径向和周向的伸长率,两个主方向的曲率分别为 $κ_{m, 1} = {\dot{ψ}}_{m} ε_{m, 1}$ 和 $κ_{m, 2} = \sin ψ_{m} x_{m}$ .

药物颗粒的弯曲变形能为

$$ E_{\rm bn} = \dint_0^{\uppi r} \alpha \dfrac{k_{\rm b}}{2}\left( {\dfrac{\dot {\psi }_{\rm n} } {\varepsilon _{\rm n,1} } + \dfrac{\sin \psi _{\rm n} }{x_{\rm n} } - 2c_0 } \right)^2 2\uppi x_{\rm n} \d s (5)

其中, $c_{0} = 1 / r$ 为药物的初始曲率, $α$ 是药物与细胞膜的杨氏模量之比,其值越大表明药物越硬.

本文采用带有骨架的细胞膜SK计量膜平面内细胞拉伸变形能 ^[17],在Xu等 ^[18]数值模拟红细胞运动的研究中,同样采用了SK模型来描述细胞膜的变形,其具体表达式为

E_{\rm em} = ∫_0^L \dfrac{E_{\rm C} h}{8}\Big[ 10^{ - 3}\left( {\varepsilon _{\rm m,1}^2 - 1} \right)^2 + 10^{ - 3}\left( {\varepsilon _{\rm m,2}^2 - 1} \right)^2 + \left( {\varepsilon _{\rm m,1}^2 \varepsilon _{\rm m,2}^2 - 1} \right)^2 \Big]2π x_{\rm m} d s_0 (6)$

其中,周向方向的伸长率 $ε_{m, 2} = x_{m} / x_{m 0}$ , $x_{m}$ 是细胞膜变形后的 $X$ 坐标, $x_{m 0}$ 细胞膜的初始 $X$ 坐标, $E_{C}$ 和 $h$ 分别为细胞膜杨氏模量和厚度.

药物膜大多由双层脂质体组装而成,拉伸变形采用线弹性模型 ^[19],其具体表达式为

$$ \babl E_{\rm en} = \dint_0^{2\uppi r} \alpha \dfrac{E_{\rm C} h}{2} \left[ {\left( {\varepsilon _{\rm n,1} - 1} \right)^2 + \left( {\varepsilon _{\rm n,2} - 1} \right)^2} \right]2\uppi x_{\rm n} \d s_0 \eal(7) $$

受体配体绑定键的变形能用线弹性弹簧模型描述 ^[20]

$$ E_{\rm rl} = \dint_0^A \dfrac{k_{\rm s} \rho }{2}\left( {l_i - l_0 } \right)^2 \d A_i (8) $$

其中, $l_{0}$ 是绑定键的自由长度, $k_{s}$ 是绑定键的弹簧系数, $ρ$ 是绑定键的密度, $A$ 为包裹区域的面积.

为了提高药物内吞的成功率,通常在药物表面以最大密度修饰配体,在此条件下,致密的配体间范德华力作用使得配体垂直于药物表面,因此本文假设绑定键亦皆垂直于药物表面. 绑定键从药物上的点 $(x_{n}^{i}, y_{n}^{i})$ 出发,沿着外法线方向,与细胞膜的交点为 $(x_{m}^{i}, y_{m}^{i})$ . 绑定键的长度随着药物与细胞膜形状的变化而改变,本文假设当 $l_{i} > 2 l_{0} \cup l_{i} < 1 / 2 l_{0}$ 时,绑定键发生断裂.

本文用最优化的方法来求总变形能方程的最小值. 将变形能方程进行离散求和,药物表面离散点的个数为 $N$ ,细胞膜表面的离散点的个数为 $M$ ,变形能方程的未知数可以表示为向量 $x = [ψ_{n}^{1,2, \dots, N}, ψ_{m}^{1,2, \dots, M}, ε_{n, 1}^{1,2, \dots, N}, ε_{m, 1}^{1,2, \dots, M}, l_{1}]$ ,其定义域为

$\begin{array}{l} (ψ_{n}^{1,2, \dots, N}, ψ_{m}^{1,2, \dots, M}) \in [0,] 2 mm] (ε_{n, 1}^{1,2, \dots, N}, ε_{m, 1}^{1,2, \dots, M}) \in (0, + \infty), l_{1} \in [l_{0} / 2,2 l_{0}] \end{array}$

能量方程在点 $x$ 处的泰勒展开式为

$\begin{array}{l} E (x + Δ x) \approx E (x) + (\nabla E (x))^{T} Δ x + 2 mm] 12 Δ x^{T} H (x) Δ x + O ({‖Δ x‖}^{2}) \end{array} (9)$

其中 $H = \nabla^{2} E (x)$ 是Hessian矩阵. 当Hessian矩阵是正定的,在 $x$ 点处的梯度为 0时, $E$ 在点 $x$ 处取得最小值.

对式(9)取梯度可得

$\nabla E (x + Δ x) \approx \nabla E (x) + H (x) Δ x (10)$

令梯度为 0可得

$\nabla E (x_{j}) + H (x_{j}) Δ x = 0 (11)$

由此可以得到迭代的步骤

$x_{j + 1} = x_{j} - H^{- 1} (x_{j}) \nabla E (x_{j}) (12)$

令初始值为 $x_{0}$ ,通过迭代得到 $x_{1}, x_{2}, \dots$ 当收敛到 $x_{j + 1}$ ,满足 $ζ = |1 - E (x_{j + 1}) / E (x_{j})| < 0.001$ 并且满足约束方程的一范数 ${‖(Γ_{1}, Γ_{2}, Γ_{3})‖}_{1} < 0.1$ 时,认为 $E (x_{j + 1})$ 是能量的数值方法最小值.

本文求解能量方程最小值时,采用的约束如下：药物体积被认为是守恒的,体积约束为

$$ \varGamma _1 = \dint_0^{\uppi r} {\uppi x_{\rm n}^2 \d y_{\rm n} } - \dfrac{4}{3}\uppi r^3 (13) $$

由于药物的几何形状是封闭的,其顶点$X$坐标为0,可知第2个约束方程为

$$ \varGamma _2 = \dint_0^{\uppi r} {\varepsilon _{\rm n} \cos \psi _{\rm n} } \d s_0 (14) $$

细胞膜计算域的总长$L = 40\uppi r$被认为是不变的,第3个约束方程为

$$ \varGamma _3 = \dint_0^L {\varepsilon _{\rm m} \sin \psi _{\rm m} } \d s_0 - 40\uppi r (15) $$

在计算中,通过离散求和的方式来计算各变形能,对于每个单元,绑定键的长度为

$$ l_i = \sqrt {\left( {x_{\rm n}^i - x_{\rm m}^i } \right)^2 + \left( {y_{\rm n}^i - y_{\rm m}^i } \right)^2} (16) $$

1 模型中的物理常数

Table 1 The physical constants in the model

Physical quantity and symbol	Value
Bending modulus $k_{b}$	$20 k_{B} T$ ^[16]
Cell membrane thickness $h$	5 nm ^[21]
Young’s modulus of cell membrane $E_{C}$	10⁶, 10⁷ Pa ^[17,22]
Density of ligands $ρ$	500 $μ$ m^-2^[10]
Free length of binding bonds $l_{0}$	20 nm ^[23]
Drug radius $r$	12.5, 25, 50 nm ^[10]
Spring strength of binding bonds $k_{s}$	1,10 pN/nm ^[12,24]
$\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}$	100 ^[25]

新窗口打开

2 结果与讨论

本文中的包裹区域是指药物被细胞膜包围的区域. 按照对称面上药物的弧长,将内吞分为6个包裹阶段,对应的包裹区域弧长分别为药物弧长的1/6,2/6,3/6,4/6, 5/6,1. 通过独立求解每个包裹阶段的能量方程最小值,演绎内吞的准静态过过程. 本模型采用的常数如表1所示.

显示原图| 下载原图ZIP| 生成PPT

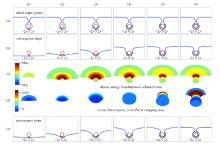
图2 为半径25 nm的纳米颗粒计算结果. 图2(a)分别为每个包裹阶段的计算初始形状,为了避免初值的影响,6个阶段的药物和细胞膜初始计算形状一致. 绑定键数目是在此包裹区域内绑定键的示意图. 随着包裹阶段增加,按照对称性增加一对示意绑定键,而绑定键的真实数目为绑定键的单位面积密度乘以包裹区域的面积.

图2(b)分别为每个包裹阶段的计算收敛时,细胞膜药物和绑定键的形状,在此形状下能量方程收敛到最小值. 图2(b) $~$ 图2(d)采用的细胞膜杨氏模量 $E_{c} = 1 0^{7}$ Pa 及绑定键强度 $k_{s} = 1$ pN/nm的结果,图2(e)采用的细胞膜杨氏模量 $E_{c} = 1 0^{6}$ Pa 及绑定键强度 $k_{s} = 10$ pN/nm的结果,其他参数和初值与图2(b)一致.

图2(c)分别为每个细胞膜总变形能(即弯曲变形能与拉伸变形能之和)的分布,为每个细胞膜总变形能(即弯曲变形能与拉伸变形能之和)的分布,每个包裹阶段的能量差距较大,若采用统一的数值范围, 无法表现出每个包裹阶段的能量在细胞膜上的分布,故图2(c)绘图颜色采用各个包裹阶段内的相对值. Min表示每个阶段内的能量分布最小值,Max为最大值. 图中可见,在包裹区域边界附近的能量较大,表明该处的变形量较大.

图2(d)的形状分别为每个阶段包裹区域的对应的细胞膜的形状,颜色分别为每个阶段包裹区域内绑定力与绑定键断裂力之间的比值,颜色按每20%等分. 本文键断裂分为拉断和压断两种,依据键长与平衡位置的相对值,当 $l_{i} > 2 l_{0} \cup l_{i} < 1 / 2 l_{0}$ 时,绑定键发生断裂,即键长为平衡长度2倍时,绑定键拉伸断裂,压缩为1/2时压缩断裂. 图中,在包裹区域最外边的绑定键所受拉力最大,因此是断裂最容易发生的地方,而中间部分绑定力较小. 本文的结果中,包裹区域内部没有发生超过断裂阈值的绑定力,只在边缘断裂. 如图2(b)中第(6)张图所示,第6个包裹阶段的绑定键示意数目为10个,少于最初值示意图的数目12个,如图2(a) 中第(6)张图所示,说明发生了绑定键的断裂. 若需使得被动内吞能到达第6个包裹阶段,在药物设计时应采用弹性系数更大的绑定键,因而需要选择形成绑定键后强度更大的配体来修饰其表面. 如图2(e) 中第(6)张图所示,在较大的绑定键强度且较软的细胞膜情况下,第6个包裹阶段没有发生绑定键的断裂.

显示原图| 下载原图ZIP| 生成PPT

图2 半径为25 nm 颗粒计算结果

Fig. 2 Calculation results of nanoparticle with radius of 25 nm

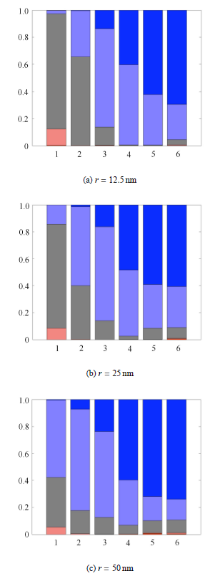
如图4所示,细胞膜变形能是总能量的主要构成部分之一,随着包裹面积的增大,细胞膜的弯曲变形能占比增大,而细胞膜拉伸变形能占比减小. Deserno等 ^[27-28] 的研究提出,在给定细胞膜弯曲模量 $k_{b}$ 和张力系数 $σ$ 时,可以推出一个临界半径 $λ = \sqrt[]{k_{b} / σ}$ ,当药物半径 $r < λ$ 时,弯曲能占主要部分,而药物半径 $r > λ$ 时,拉伸能占主要部分,通常取 $k_{b} = 20 k_{B} T$ 及 $σ = 0.02$ dyn/cm (1 dyn=1 cm/s $^{2}$ ),得到 $λ = 65$ nm. 本文发现,即便是同样的半径,随着包裹区域面积的增大, 细胞膜弯曲变形能与拉伸变形能占比也有主导性变化, 其中细胞膜的拉伸变形能占比随着包裹区域增加而增大,而细胞膜弯曲能占比先增大后减小. 这是因为内吞过程中,细胞膜的表面积一直在增大,而细胞膜的弯曲变形在内吞初期变化很大,在内吞后期变化较小.

显示原图| 下载原图ZIP| 生成PPT

图3 变形能柱状图

Fig. 3 Deformation energy bar

显示原图| 下载原图ZIP| 生成PPT

图4 变形能组分柱状图

Fig. 4 Deformation energy component bar

显示原图| 下载原图ZIP| 生成PPT

图5 单位面积绑定键需提供的能量

Fig. 5 The energy required by bonds per unit area

图4还显示绑定键变形能在第1、第2个内吞包裹阶段绑占比最大,因此内吞初期不能忽略绑定键变形能的影响.

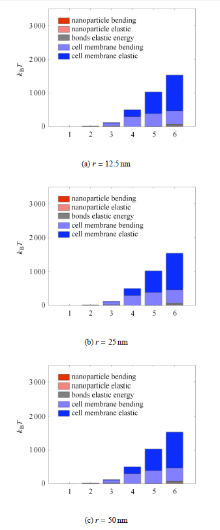
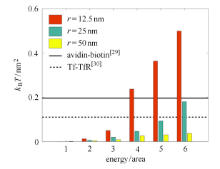
图4显示在药物与细胞膜杨氏模量比 $α = 100$ 的情况下,药物的硬度已经足够大,药物变形能只占总变形能的很小一部分,除第一个阶段由于总变形能较小,药物变形能相对占比较大外,其余包裹阶段的药物变形能可以忽略不计.

假设变形能量全部来自受体与配体绑定时所释放的化学能,而且不计热量损失,将内吞包裹各阶段变形能对药物包裹面积进行归一化,得到单位面积绑定键需释放的最小能量,如图5中的柱状图所示. 根据Moy等 ^[29] 用原子力显微镜(AFM)测量了亲和素--生物素(avidin-biotin)绑定键的吉布斯自由能变化,以及Fotticchia等 ^[30] 用等温滴定量热法(ITC)测量了运铁蛋白及其受体(Tf-TfR)绑定键的吉布斯自由能,可以得到两条单位面积释放的化学能基准线作为参考. 当包裹药物所需的最小能量大于绑定键所释放的化学能,内吞将无法完成. 如图5所示,在给定药物和细胞膜硬度及绑定键强度的情况下,对半径为12.5 nm的纳米颗粒,如果使用biotin或运铁蛋白来修饰其表面,内吞只能进行到第3个包裹阶段,因此需要在其修饰单位面积释放更多能量的配体,才能保证内吞的顺利完成.

3 结论

本文针对受体介导下球型纳米颗粒被细胞膜包裹内吞的准静态过程建立轴对称模型,通过求解细胞膜和药物变形的能量方程的最小值,分析了细胞内吞药物所需最小能量与药物直径、细胞膜硬度、受体--配体绑定键强度之间的关系.

研究表明,内吞过程中细胞膜、药物颗粒和绑定键变形系统的总能量随着药物颗粒被包裹面积的增加而增大,其中,细胞膜变形能和绑定键变形能是总能量的主要构成部分,并且随着内吞药物被包裹面积的增大,细胞膜变形能占比增加,绑定键变形能占比减小;内吞过程中,细胞膜、药物颗粒和绑定键构成系统的总变形能并不随着药物颗粒半径的增加而增大,在本文给定的细胞膜和药物颗粒的硬度、绑定键强度等物理特性下存在最优药物尺寸,使得内吞过程中总能耗最小;在内吞进行的中前期绑定键变形能占比较大,因而不能忽略,在药物内吞进行的后期,包裹区域边缘的绑定键因伸长过大发生断裂,影响内吞的顺利完成. 本文研究对受体介导的药物设计、提高药物内吞效率有重要的参考价值.

The authors have declared that no competing interests exist.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]	Silverstein SC, Steinman RM, Cohn ZA. Endocytosis .Ann Rev Biochem,1977,46: 669-722
[2]	Wileman T, Harding C, Stahl P. Recptor-mediated endocytosis .Biochemical Journal, 1985, 232(1): 1-14
[3]	Higgins MK, Mcmahon HT. Snap-shots of clathrin-mediated endocytosis .Trends in Biochemical Sciences, 2002, 27(5): 257-263 [本文引用: 1]
[4]	Goldstein JL, Anderson RG, Brown MS. Coated pits, coated vesicles, and receptor-mediated endocytosis .Nature, 1979, 279(5715): 679-685
[5]	Cann AJ. Principles of Molecular Virology . San Diego: Academic,1997
[6]	Kihlström E, Nilsson L. Endocytosis of salmonella typhimurium 395 MS and MR10 by HeLa cells .APMIS, 2010, 85B(5): 322-328
[7]	Tortorella S, Karagiannis TC. Transferrin receptor-mediated endocytosis: A useful target for cancer therapy .Journal of Membrane Biology, 2014, 247(4): 291-307
[8]	Tanaka T, Shiramoto S, Miyashita M. Tumor targeting based on the effect of enhanced permeability and retention(EPR) and the mechanism of receptor-mediated endocytosis(RME) .International Journal of Pharmaceutics, 2004, 277(1-2): 39
[9]	Zhang S, Gao H, Bao G. Physical principles of nanoparticle cellular endocytosis .Acs Nano, 2015, 9(9): 8655 [本文引用: 1]
[10]	Gao HJ, Shi WD, Lambert B Freund. Mechanics of receptor-mediated endocytosis .Proceedings of the National Academy of Sciences of the United States of America, 2005, 102(27): 9469 [本文引用: 8]
[11]	Yi X, Shi X, Gao H. Cellular uptake of elastic nanoparticles .Physical Review Letters, 2011, 107(9): 098101 [本文引用: 1]
[12]	Decuzzi P, Ferrari M. The role of specific and non-specific interactions in receptor-mediated endocytosis of nanoparticles .Biomaterials, 2007, 28(18): 2915 [本文引用: 1]
[13]	Li L, Liu XJ, Zhou YH. On resistance to virus entry into host cell .Biophysical Journal, 2012, 102(9): 2230-2233 [本文引用: 2]
[14]	Wang J, Long L. Coupled elasticity-diffusion model for the effects of cytoskeleton deformation on cellular uptake of cylindrical nanoparticles .Journal of the Royal Society Interface, 2015, 12(102): 20141023 [本文引用: 1]
[15]	Li L, Wang J. Creep effect on cellular uptake of viral particles// CCTAM, 2013 [本文引用: 1]
[16]	Helfrich W. Elastic properties of lipid bilayers: theory and possible experiments .Zeitschrift Fur Naturforschung Teil C Biochemie Biophysik Biologie Virologie, 1973, 28(11-12): 693-703 [本文引用: 2]
[17]	Skalak R, Tozeren A, Zarda RP. Strain energy function of red blood cell membranes .Biophysical Journal, 1973, 13(3): 245-264 [本文引用: 1]
[18]	许菁, 王骁龙, 刘筠乔等. 红细胞力学特性对血小板近壁运动的影响 . 力学学报, 2013, 45(6): 974-981 [本文引用: 1] (Xu Jing, Wang Xiaolong, Liu Xiaoqiao. Micro-scale numerical study of the effect of erythrocyte mechanical properties on the near-wall motion of platelet .Chinese Journal of Theoretical and Applied Mechanics, 2013, 45(6): 974-981 (in Chinese)) [本文引用: 1]
[19]	David F, Leibler S. Vanishing tension of fluctuating membranes .Journal of Physics B Atomic & Molecular Physics, 1991, 1(8): 959-976 [本文引用: 1]
[20]	Dembo M. On peeling an adherent cell from a surface. In: Lectures in Mathematics in Life Sciences, Some Mathematical Problems in Biology . Providence, RI: American Mathematical Society, 1994: 51-77 [本文引用: 1]
[21]	Hochmuth RM, Evans CA, Wiles HC, et al. Mechanical measurement of red cell membrane thickness .Science, 1983, 220(4592): 101 [本文引用: 1]
[22]	李卫卫, 杨庆生, 刘志远. 血红细胞力学性能的纳米压痕实验和有限元模拟 . 力学学报, 2012, 44(3): 614-621 (Li Weiwei, Yang Qingsheng, Liu Zhiyuan. Nanoindentation experiment and finite element simulation for biomechanical behavior of red blood cell .Chinese Journal of Theoretical and Applied Mechanics, 2012, 44(3): 614-621 (in Chinese))
[23]	Wong JY, Zalipsky S. Direct measurement of a tethered ligand-receptor interaction potential .Science, 1997, 275(5301): 820 [本文引用: 1]
[24]	Ros R, Schwesinger F, Anselmetti D. Antigen binding forces of individually addressed single-chain Fv antibody molecules .Proceedings of the National Academy of Sciences of the United States of America, 1998, 95(13): 7402
[25]	Sun J, Zhang L, Wang J, et al. Tunable rigidity of (polymeric core)-(lipid shell) nanoparticles for regulated cellular uptake .Advanced materials, 2015, 27(8): 1402-1407 [本文引用: 1]
[26]	Chithrani BD, Ghazani AA, Chan CW. Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells .Nano Letters, 2006, 6(4): 662
[27]	Deserno M, Bickel T. Wrapping of a spherical colloid by a fluid membrane .EPL, 2012, 62(62): 767
[28]	Deserno M. Elastic deformation of a fluid membrane upon colloid binding .Physical Review E Statistical Nonlinear & Soft Matter Physics, 2004, 69(1): 031903
[29]	Moy VT, Florin EL, Gaub HE. Intermolecular forces and energies between ligands and receptors .Science, 1994, 266(5183): 257-259 [本文引用: 1]
[30]	Fotticchia I, Guarnieri D, Fotticchia T. Energetics of ligand-receptor binding affinity on endothelial cells: An in vitro model .Colloids & Surfaces B Biointerfaces, 2016, 144: 250-256 [本文引用: 1]

Endocytosis

1977

Recptor-mediated endocytosis

1985

Snap-shots of clathrin-mediated endocytosis

2002

... 受体介导的内吞是细胞通过向内生成小泡来吸收大分子配体的一种方式 ^[1-2]. 受体介导的内吞小泡尺寸大约为100 nm ^[3],荷尔蒙、生长因子、运铁蛋白、各类抗体、细菌和病毒等,通过受体介导的内吞作用进入细胞 ^[4-5]. 通过在纳米颗粒药物表面修饰能识别癌细胞表面特异性受体的配体,用于癌症治疗的纳米颗粒药物也能利用这种方式进入细胞 ^[6-8]. ...

Coated pits, coated vesicles, and receptor-mediated endocytosis

1979

Principles of Molecular Virology

1997

Endocytosis of salmonella typhimurium 395 MS and MR10 by HeLa cells

2010

Transferrin receptor-mediated endocytosis: A useful target for cancer therapy

2014

Tumor targeting based on the effect of enhanced permeability and retention(EPR) and the mechanism of receptor-mediated endocytosis(RME)

2004

Physical principles of nanoparticle cellular endocytosis

2015

... 细胞对药物的内吞效率受到多个因素的影响,如药物形状、尺寸、硬度、绑定键强度等 ^[9],本文从力学角度研究纳米颗粒内吞所需的能量,为设计更高效的药物提供理论参考. ...

Mechanics of receptor-mediated endocytosis

2005

... 针对这一问题,Gao等 ^[10]假设内吞过程中介导内吞的绑定键释放的能量与内吞过程中产生的细胞膜弯曲变形能和膜表面受体向药物内吞部位扩散所消耗的总能量守恒,计算了完成内吞所需受体扩散到达内吞部位时间,得到了药物内吞的最优尺寸以及药物可以内吞的最小尺寸. 他们考虑了内吞区域内部的细胞膜弯曲变形能,忽略了药物的变形以及内吞区域外的细胞膜变形,可能低估了内吞过程所需的总变形能. ...

... Yi等 ^[11]假设内吞是准静态过程,在Gao等 ^[10]的研究基础上,通过对能量方程进行变分得到变形微分方程,采用打靶法求解得到了细胞膜和药物的变形. 他们假设内吞包裹部分细胞膜与内吞药物曲率一致,忽略了受体配体形成绑定键对内吞的影响. ...

... Decuzzi等 ^[12]在Gao等 ^[10]的能量模型基础上,考虑了绑定键的作用对内吞所需时间的影响,求解了受体扩散到内吞部位的时间,结果表明非特异性排斥力会延长内吞时间,而非特异性吸引力会缩短内吞时间,但没有讨论特异性绑定键对内吞的影响. 其模型中假设内吞包裹区域內的所有绑定键的拉伸是相等的,认为只要受体能扩散到包裹区域就能绑定,没有讨论绑定键的局部断裂对内吞的影响. ...

... Wang等 ^[14]在Gao等 ^[10]的基础上,对柱状纳米颗粒的横向与竖直进入细胞进行了对比. 结果表明,竖直内吞比横向内吞所需的时间更短,且细胞膜的变形比细胞骨架的变形更显著,细胞骨架的硬度的影响只有在一定的包裹深度之后才体现出来,细胞骨架的硬度越大,内吞所需的时间越长. 而竖直进入细胞的纳米颗粒可能会停滞在某个深度. ...

... 由于很多病毒表面的配体非常稀少,依然可以快速进入细胞,这与Gao等 ^[10]得到最低受体与配体密度比不一致. 因此,Wang 等 ^[15]在Li等 ^[13]和Gao等 ^[10]的基础上,考虑了细胞骨架的能量和蠕变效应之后,细胞内吞最优尺寸所对应的配体与受体密度比可以更小. ...

... [10]的基础上,考虑了细胞骨架的能量和蠕变效应之后,细胞内吞最优尺寸所对应的配体与受体密度比可以更小. ...

... The physical constants in the model

Physical quantity and symbol	Value
Bending modulus $k_{b}$	$20 k_{B} T$ ^[16]
Cell membrane thickness $h$	5 nm ^[21]
Young’s modulus of cell membrane $E_{C}$	10⁶, 10⁷ Pa ^[17,22]
Density of ligands $ρ$	500 $μ$ m^-2 ^[10]
Free length of binding bonds $l_{0}$	20 nm ^[23]
Drug radius $r$	12.5, 25, 50 nm ^[10]
Spring strength of binding bonds $k_{s}$	1,10 pN/nm ^[12,24]
$\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}$	100 ^[25]

2 结果与讨论

本文中的包裹区域是指药物被细胞膜包围的区域. 按照对称面上药物的弧长,将内吞分为6个包裹阶段,对应的包裹区域弧长分别为药物弧长的1/6,2/6,3/6,4/6, 5/6,1. 通过独立求解每个包裹阶段的能量方程最小值,演绎内吞的准静态过过程. 本模型采用的常数如表1所示. ...

... [10] Spring strength of binding bonds

k_{s}

1,10 pN/nm ^[12,24]

\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}

100 ^[25]

2 结果与讨论

Cellular uptake of elastic nanoparticles

2011

The role of specific and non-specific interactions in receptor-mediated endocytosis of nanoparticles

2007

On resistance to virus entry into host cell

2012

... Li等 ^[13]构建了病毒入侵宿主细胞的能量方程,其中包括绑定键变形能,细胞膜变形能和细胞骨架细胞变形能三个部分,方程的自变量为病毒包裹的深度. 文章提出一个临界深度,小于临界深度时,细胞膜的变形能占主要部分,大于临界深度时,细胞骨架的变形能占主要部分. ...

Coupled elasticity-diffusion model for the effects of cytoskeleton deformation on cellular uptake of cylindrical nanoparticles

2015

Creep effect on cellular uptake of viral particles//

2013

Elastic properties of lipid bilayers: theory and possible experiments

1973

... 本文采用 Helfrich 模型来描述药物和细胞膜的弯曲能 ^[16]. 由于细胞膜尺寸远远大于药物的尺寸,模型中将细胞膜视为有限大平面,取

L = 40 r

r

是药物的半径. ...

... The physical constants in the model

Physical quantity and symbol	Value
Bending modulus $k_{b}$	$20 k_{B} T$ ^[16]
Cell membrane thickness $h$	5 nm ^[21]
Young’s modulus of cell membrane $E_{C}$	10⁶, 10⁷ Pa ^[17,22]
Density of ligands $ρ$	500 $μ$ m^-2 ^[10]
Free length of binding bonds $l_{0}$	20 nm ^[23]
Drug radius $r$	12.5, 25, 50 nm ^[10]
Spring strength of binding bonds $k_{s}$	1,10 pN/nm ^[12,24]
$\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}$	100 ^[25]

2 结果与讨论

Strain energy function of red blood cell membranes

1973

... 本文采用带有骨架的细胞膜SK计量膜平面内细胞拉伸变形能 ^[17],在Xu等 ^[18]数值模拟红细胞运动的研究中,同样采用了SK模型来描述细胞膜的变形,其具体表达式为 ...

红细胞力学特性对血小板近壁运动的影响

2013

红细胞力学特性对血小板近壁运动的影响

2013

Vanishing tension of fluctuating membranes

1991

... 药物膜大多由双层脂质体组装而成,拉伸变形采用线弹性模型 ^[19],其具体表达式为 ...

On peeling an adherent cell from a surface. In: Lectures in Mathematics in Life Sciences, Some Mathematical Problems in Biology

1994

... 受体配体绑定键的变形能用线弹性弹簧模型描述 ^[20] ...

Mechanical measurement of red cell membrane thickness

1983

... The physical constants in the model

Physical quantity and symbol	Value
Bending modulus $k_{b}$	$20 k_{B} T$ ^[16]
Cell membrane thickness $h$	5 nm ^[21]
Young’s modulus of cell membrane $E_{C}$	10⁶, 10⁷ Pa ^[17,22]
Density of ligands $ρ$	500 $μ$ m^-2 ^[10]
Free length of binding bonds $l_{0}$	20 nm ^[23]
Drug radius $r$	12.5, 25, 50 nm ^[10]
Spring strength of binding bonds $k_{s}$	1,10 pN/nm ^[12,24]
$\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}$	100 ^[25]

2 结果与讨论

血红细胞力学性能的纳米压痕实验和有限元模拟

2012

血红细胞力学性能的纳米压痕实验和有限元模拟

2012

Direct measurement of a tethered ligand-receptor interaction potential

1997

... The physical constants in the model

Physical quantity and symbol	Value
Bending modulus $k_{b}$	$20 k_{B} T$ ^[16]
Cell membrane thickness $h$	5 nm ^[21]
Young’s modulus of cell membrane $E_{C}$	10⁶, 10⁷ Pa ^[17,22]
Density of ligands $ρ$	500 $μ$ m^-2 ^[10]
Free length of binding bonds $l_{0}$	20 nm ^[23]
Drug radius $r$	12.5, 25, 50 nm ^[10]
Spring strength of binding bonds $k_{s}$	1,10 pN/nm ^[12,24]
$\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}$	100 ^[25]

2 结果与讨论

Antigen binding forces of individually addressed single-chain Fv antibody molecules

1998

Tunable rigidity of (polymeric core)-(lipid shell) nanoparticles for regulated cellular uptake

2015

... The physical constants in the model

Physical quantity and symbol	Value
Bending modulus $k_{b}$	$20 k_{B} T$ ^[16]
Cell membrane thickness $h$	5 nm ^[21]
Young’s modulus of cell membrane $E_{C}$	10⁶, 10⁷ Pa ^[17,22]
Density of ligands $ρ$	500 $μ$ m^-2 ^[10]
Free length of binding bonds $l_{0}$	20 nm ^[23]
Drug radius $r$	12.5, 25, 50 nm ^[10]
Spring strength of binding bonds $k_{s}$	1,10 pN/nm ^[12,24]
$\begin{array}{l} Y oung' s modulus ratio of \\ d rug and cell membrane α \end{array}$	100 ^[25]

2 结果与讨论

Determining the size and shape dependence of gold nanoparticle uptake into mammalian cells

2006

Wrapping of a spherical colloid by a fluid membrane

2012

Elastic deformation of a fluid membrane upon colloid binding

2004

Intermolecular forces and energies between ligands and receptors

1994

... 假设变形能量全部来自受体与配体绑定时所释放的化学能,而且不计热量损失,将内吞包裹各阶段变形能对药物包裹面积进行归一化,得到单位面积绑定键需释放的最小能量,如图5中的柱状图所示. 根据Moy等 ^[29] 用原子力显微镜(AFM)测量了亲和素--生物素(avidin-biotin)绑定键的吉布斯自由能变化,以及Fotticchia等 ^[30] 用等温滴定量热法(ITC)测量了运铁蛋白及其受体(Tf-TfR)绑定键的吉布斯自由能,可以得到两条单位面积释放的化学能基准线作为参考. 当包裹药物所需的最小能量大于绑定键所释放的化学能,内吞将无法完成. 如图5所示,在给定药物和细胞膜硬度及绑定键强度的情况下,对半径为12.5 nm的纳米颗粒,如果使用biotin或运铁蛋白来修饰其表面,内吞只能进行到第3个包裹阶段,因此需要在其修饰单位面积释放更多能量的配体,才能保证内吞的顺利完成. ...

Energetics of ligand-receptor binding affinity on endothelial cells: An in vitro model

2016

〈

〉

细胞内吞纳米颗粒药物的数值模拟研究

A NUMERICAL STUDY ON ENDOCYTOSIS OF NANOPARTICLES

引 言

1 方 法

1 模型中的物理常数

2 结果与讨论

3 结 论

参考文献 文献选项 原文顺序 文献年度倒序 文中引用次数倒序 被引期刊影响因子

引言

1 方法

3 结论

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子