†. 大连理工大学工业装备结构分析国家重点实验室, 大连 116024
近20年来连续体结构拓扑优化获得了飞速的发展,成为当今工程结构概念性设计的强有力工具.各种拓扑优化方法,比如基于材料分布概念设计的均匀化方法[1]、固体各项同性变密度法(solid isotropic material with penalization,SIMP) [2]和渐进结构优化方法(evolutionary structural optimization,ESO)[3],还有基于几何边界描述的水平集方法(level set method,LSM)[4-5]和隐式拓扑描述函数法[6-8],还有国内隋允康等[9-10]提出的独立连续映射法,郭旭等[11-12]提出的可动变形构件法(moving morphable components,MMC),都被用来解决各种结构优化设计问题.
考虑自重载荷的影响在许多大型土木工程结构设计问题中具有十分重要的意义,近年来激发了许多科研工作者的研究兴趣. Turteltaub等[13]率先研究了自重载荷作用下的结构拓扑优化问题. Bruyneel和Duysinx[14]也对考虑结构自重的拓扑优化问题做了详细的讨论,他们指出了求解此类问题所面临的3个主要困难,即低密度区域容易出现材料的寄生效应、目标函数非单调性问题及体积约束的无效性,为了解决低密度区域材料的寄生效应问题,他们提出了一种修正的不连续的SIMP模型. Yang等[15]基于离散的ESO/BESO (bi-directional ESO)方法研究了考虑设计依赖自重载荷作用下的带有刚度约束的拓扑优化问题,但是他们的优化结果与Bruyneel和Duysinx的结果不同. Ansola等[16]指出,对于考虑自重载荷的优化问题,传统ESO算法中单元敏度数的计算方法并不能使优化问题收敛到一个最优解,为此,他们提出了一种新的敏度计算策略来计算敏度,提高算法的收敛性,但是他们人为地增加体积约束上限的做法被认为是缺乏理论基础的[17].高彤等[18]提出了一种可变参数的“rational opproximation of material properties (RAMP)”模型,基于此模型分析了多种材料插值格式对惯性载荷作用下结构拓扑优化结果和迭代过程的影响,而且对“没有材料就没有惯性”的理论最优解问题进行了阐述和研究.张晖等[19]针对自重载荷作用下连续体结构拓扑优化中遇到的常见问题,提出了一种将RAMP插值模型与平均敏度过滤技术相结合的求解策略,并详细讨论了不同模型参数对拓扑优化结果的影响. Huang等[20]将BESO方法与RAMP插值模型相结合,详细讨论了考虑设计依赖自重载荷和固定载荷作用的连续体结构拓扑优化区别. Holmberg等[21]通过对质量密度进行线性缩放以减小低密度区域载荷与刚度比值的大小,从而获得一个无寄生效应的优化结果.另外,导重法[17]和修改的梯度投影法[22]也被用来研究考虑自重载荷作用的结构拓扑优化问题.
总结上面处理考虑自重载荷的拓扑优化问题的方法主要可以分为3类:第1种是对单元刚度的插值格式进行修正[14, 22];第2种是对单元质量密度的插值格式进行修正[18, 21-22];第3种是采用RAMP插值模型[17-20].这些研究表明,对于自重载荷作用的优化问题,RAMP插值模型比SIMP插值模型更有效.虽然上述方法在处理自重结构优化问题是有效的,但是需要对刚度或质量密度的插值格式进行修正,甚至有些方法都不能保证插值格式的连续性,而且上述工作更多的局限于二维平面的优化问题.
针对这些问题,本文将基于非均匀有理B样条(NURBS)基函数的等几何分析方法与拓扑描述函数法结合,提出一种有效求解三维自重结构优化问题的拓扑描述函数法.等几何分析是由Hughes等[23]最先提出的,它是一种将传统的有限单元法与基于NURBS的计算机辅助设计工具相结合来求解偏微分方程的新数值方法.目前等几何分析已被广泛应用于结构分析[23-26]、结构优化[27-30]等各个领域.本文用等几何方法代替传统的有限元方法进行三维实体结构的位移场分析,以每个控制点所对应的拓扑描述函数值为设计变量,详细推导了基于NURBS插值的考虑自重载荷作用的三维结构拓扑优化模型及其灵敏度列式,最后通过多个数值算例验证了本文方法的稳定性和有效性.
1 基于NURBS插值的拓扑描述函数法 1.1 NURBS实体三维NURBS实体定义如下[31]
| $ V(\xi, \eta, \zeta ) = \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\sum\limits_{k = 1}^l {P_{i, j, k} R_{i, j, k} } } } (\xi, \eta, \zeta ) $ | (1) |
其中,
| $ R_{i, j, k}^{p, q, r} (\xi, \eta, \zeta ) =\\ \quad \dfrac{N_{i, p} (\xi )M_{j, q} (\eta )L_{k, r} (\zeta )\omega _{i, j, k} }{\sum\limits_{\bar {i} = 1}^n {\sum\limits_{\bar {j} = 1}^m {\sum\limits_{\bar {k} = 1}^l {N_{\bar {i}, p} (\xi )M_{\bar {j}, q} (\eta )L_{\bar {k}, r} (\zeta )\omega _{\bar {i}, \bar {j}, \bar {k}} } } } } $ | (2) |
式中,
在拓扑描述函数法中,用来描述结构拓扑和形状的隐式函数可以定义为[8]
| $ \left.\begin{array}{ll} \phi (x) = 0, & \partial \varOmega \\ \phi (x) > 0, & \hbox{在} \ \varOmega \hbox{内} \\ \phi (x) < 0, & \hbox{在} \ D / \varOmega \hbox{内} \end{array} \!\!\right\} $ | (3) |
其中,
结构拓扑优化的一个关键任务就是将不适定的离散的0-1优化问题转化为适定的连续优化问题.在TDF方法中,通过Heaviside函数很容易实现这一目的
| $ H(\phi (x)) = \left\{ \!\!\begin{array}{ll} 0, & \phi (x) < 0 \\ 1, & \phi (x) \geqslant 0 \end{array} \right. $ | (4) |
目前有关拓扑描述函数法的大部分文献是基于有限元网格的,采用Q4单元形函数插值单元设计变量场[6, 8],本文通过NURBS基函数来插值单元的设计变量场,可表示如下
| $ \phi ^h (x) = \sum\limits_{I = 1}^{n_{\rm cp}} R_I (\xi, \eta, \zeta )\phi _I $ | (5) |
其中
为了获得清晰的结构拓扑,本文对弹性模量和质量密度分别进行惩罚
| $ \left.\begin{array}{l} E(x) = \Big [\sum\limits_{I = 1}^{n_{\rm cp}} R_I (\xi, \eta, \zeta )H(\phi _I ) \Big]^{g_1 }E_0 \\ \rho (x) = \Big [\sum\limits_{I = 1}^{n_{\rm cp}} R_I (\xi, \eta, \zeta )H(\phi _I ) \Big]^{g_2 }\rho _0 \end{array}\!\!\right\} $ | (6) |
式中,
类似于有限元等参元的思想,在等几何分析中,NURBS基函数被用来同时对几何区域和位移场进行插值
| $ \left. \begin{array}{l} \mathit{\boldsymbol{x}}(\xi, \eta, \zeta ) = \sum\limits_{I = 1}^{{n_{{\rm{cp}}}}} {{R_I}} (\xi, \eta, \zeta ){\mathit{\boldsymbol{\overline x}} _I} = \mathit{\boldsymbol{RX}}\\ \mathit{\boldsymbol{u}}(\xi, \eta, \zeta ) = \sum\limits_{I = 1}^{{n_{{\rm{cp}}}}} {{R_I}} (\xi, \eta, \zeta ){\mathit{\boldsymbol{\overline u}} _I} = \mathit{\boldsymbol{RU}} \end{array} \right\} $ | (7) |
其中,
| $ {\boldsymbol \varepsilon} ={\boldsymbol L}{\boldsymbol u} \to {\boldsymbol \varepsilon } = {\boldsymbol B}{\boldsymbol U } $ | (8) |
然后通过虚位移原理推导单元刚度阵如下
| $ {\boldsymbol K}_e = \int_{V_e } E(x){\boldsymbol B}^{\rm T} {\boldsymbol C}_0 {\boldsymbol B}{\rm{d}} V_e $ | (9) |
其中
在基于梯度的优化方法中,目标函数及约束函数关于设计变量的敏度信息对于数值求解优化问题是极其重要的.考虑到Heaviside函数的非光滑特征,本文采用文献[8]里面的方法对Heaviside函数进行光滑逼近
| $ H_\varepsilon (\phi ) = \left\{ \begin{array}{ll} \delta, & {\phi \leqslant - \varepsilon } \\ {[1 + \sin (\pi \phi / 2\varepsilon )] / 2}, & { - \varepsilon < \phi < \varepsilon } \\ 1, & {\phi \geqslant \varepsilon } \end{array} \right. $ | (10) |
这里
正则化的Heaviside函数
| $ H'_\varepsilon (\phi ) = \left\{ \begin{array}{cl} {\dfrac{\pi }{4\varepsilon }\cos \dfrac{\pi \phi }{2\varepsilon } }, & {\left| \phi \right| < \varepsilon } \\ 0, & {\left| \phi \right| \geqslant \varepsilon } \end{array} \right. $ | (11) |
结构拓扑优化的目的是寻求满足某些固定约束条件的结构的最优的材料分布,以获得某种最优的结构行为,如结构的重量最轻或刚度最大化.本文考虑自重载荷作用下的最小柔顺性问题.以许可材料体积为约束的最小柔顺性问题列式可表示如下
| $ \left. \begin{array}{l} {\rm{Find}}:\;\;{\boldsymbol\phi} \\ {\rm{Min}}:\;\;c = {\mathit{\boldsymbol{F}}^{\rm{T}}}\mathit{\boldsymbol{U}}\\ {\rm{S}}.{\rm{t}}.:\;\;\left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{KU}} = \mathit{\boldsymbol{F}}}\\ {V-{V_0}{f_{\rm{v}}} \le 0} \end{array}} \right. \end{array} \right\} $ | (12) |
其中
对于考虑自重载荷作用的结构拓扑优化问题,结构载荷具有设计依赖性.受自重载荷作用的等效单元载荷向量可表示为
| $ {\boldsymbol F}_e = \bar {\boldsymbol F}_e \int_{V_e } {\rho (x)g} {\rm{d}} V_e $ | (13) |
其中
| $ {\boldsymbol F}_e^i = \left\{ \begin{array}{cl} 0, & {i = 2 j - 1} \\ - \dfrac{1}{n_{\rm cp}}, & {i = 2 j} \end{array} \right. $ | (14) |
对于三维问题,
| $ {\boldsymbol F}_e^i = \left\{\begin{array}{cl} 0 & {i = 3 j - 1, \ \ 3 j - 2} \\ - \dfrac{1}{n_{\rm cp}} & {i = 3j} \end{array} \right. $ | (15) |
其中
在优化问题(12)中,每个单元的材料体积可表示为
| $ V_e = \int_{V_e } \sum\limits_{I = 1}^{n_{\rm cp}} R_I H_\varepsilon (\phi _I ) {\rm{d}} V_e $ | (16) |
用式(10)中光滑后的Heaviside函数代替式(6)中的Heaviside函数,然后将弹性模量和质量密度分别对设计变量求导得
| $ \left. \begin{array}{l} \frac{{\partial E(x)}}{{\partial {\phi _I}}} = {g_1}{[\sum\limits_{I = 1}^{{n_{cp}}} {{R_I}{H_\varepsilon }({\phi _I})}]^{{g_1} - 1}}{R_I}{H_{\varepsilon '}}({\phi _I}){E_0}\\ \frac{{\partial \rho (x)}}{{\partial {\phi _I}}} = {g_2}{[\sum\limits_{I = 1}^{{n_{cp}}} {{R_I}{H_\varepsilon }({\phi _I})}]^{{g_2} -1}}{R_I}{H_{\varepsilon '}}({\phi _I}){\rho _0} \end{array} \right\} $ | (17) |
则单元刚度阵、单元外载荷向量及单元的材料体积对设计变量的导数分别表示为
| $ \left. \begin{array}{l} \frac{{\partial {\mathit{\boldsymbol{K}}_e}}}{{\partial {\phi _I}}} = \int_{{V_e}} {\frac{{\partial E(x)}}{{\partial {\varphi _I}}}{\mathit{\boldsymbol{B}}^{\rm{T}}}} {\mathit{\boldsymbol{C}}_0}\mathit{\boldsymbol{B}}{\rm{d}}{V_e}\\ \frac{{\partial {{\bf{F}}_e}}}{{\partial {\phi _I}}} = {{\bar F}_e}\int_{{V_e}} {\frac{{\partial \rho (x)}}{{\partial {\phi _I}}}g} {\rm{d}}\\ {V_e}\frac{{\partial {V_e}}}{{\partial {\phi _I}}} = \int_{{V_e}} {{R_I}{H_{\varepsilon '}}({\phi _I})} {\rm{d}}V \end{array} \right\} $ | (18) |
利用伴随法可推导目标函数的灵敏度为
| $ \dfrac{\partial c}{\partial \phi _I } = 2\dfrac{\partial {\boldsymbol F}^{\rm T}}{\partial \phi _I }{\boldsymbol U}-{\boldsymbol U}^{\rm T}\dfrac{\partial {\boldsymbol K}}{\partial \phi_I }{\boldsymbol U} $ | (19) |
简化为
| $ \dfrac{\partial c}{\partial \phi _I } = 2\sum\limits_{Ie = 1}^{N_{Ie} } {\dfrac{\partial {\boldsymbol F}_{Ie}^{\rm T} }{\partial \phi _I }{\boldsymbol U}_{Ie} } - \sum\limits_{Ie = 1}^{N_{Ie} } {U_{Ie}^{\rm T} \dfrac{\partial {\boldsymbol K}_{Ie} }{\partial \phi _I } {\boldsymbol U}_{Ie} } $ | (20) |
其中
体积约束关于设计变量的灵敏度可表示为
| $ \dfrac{\partial V}{\partial \phi _I } = \sum\limits_{Ie = 1}^{N_{Ie} } {\dfrac{\partial V_{Ie} }{\partial \phi _I }} $ | (21) |
式(20)和式(21)表明只有与第
由式(12)定义的基于拓扑描述函数理论的优化问题可以通过不同的优化算法来求解,如OC准则法[6]、数学规划方法[8]等,本文采用Svanberg教授提出的移动渐进线(method of moving asymptotes, MMA)方法[32]求解.优化算法主要包括以下6个步骤:
(1)构建设计域:定义设计域几何参数,使用NURBS构建优化模型的几何区域.
(2)定义模型参数:定义实体材料杨氏模量和质量密度及材料容许的体积分数等模型参数.
(3)等几何分析:运用等几何分析方法求解位移场.
(4)灵敏度分析:计算目标函数值,及通过式(20)和式(21)分别计算目标函数和材料体积对设计变量的敏度值.
(5)优化模型求解:用MMA算法求解优化模型,进行设计变量更新.
(6)收敛性判断:本文以最大的迭代次数来判断优化过程是否停止;若收敛,则迭代停止,输出优化结果;若不收敛,则返回步骤(3),继续迭代直到收敛为止.
3 数值算例与讨论本节通过多个数值算例来验证本文算法的有效性和准确性.除非特殊声明,在所有算例中磨光参数取
第一个算例考虑一个带有曲率的受固定单位载荷的L形梁优化问题,几何区域和边界条件如图 1所示.以占设计域
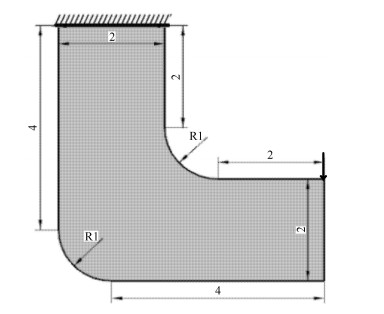
|
图 1 L形梁设计域和边界条件 Figure 1 Design domain and boundary condition for L-shaped beam with curvature |
图 2(a)和图 2(b)分别显示了本文方法基于3 332和12 804个控制点(设计变量)获得的L形梁的最优拓扑构型.可以看出本文方法在没有借助于灵敏度过滤情况下基于两种不同的离散网格所获得的拓扑构型本质上很相似,没有出现明显的网格依赖性问题,随着网格的细化,拓扑构型更加清晰,这说明本文方法是十分有效的.

|
图 2 L形梁的最优拓扑构型 Figure 2 Optimal topology of L-shaped beam |
图 3显示了本文方法基于12 804个控制点获得的柔顺性目标函数的迭代历程,其中还包括第10, 30和50个迭代步的拓扑构型.可以看出,本文方法迭代过程稳健,收敛性快,最终得到一个没有孤岛现象、边界清晰的拓扑构型.
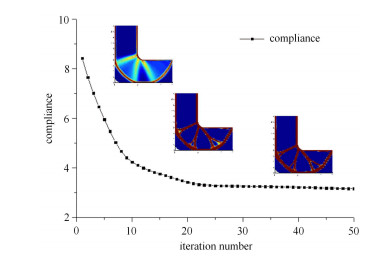
|
图 3 柔顺性和拓扑构型的迭代历程 Figure 3 Iteration histories of the compliance and topology |
第二个算例考虑一个几何尺寸为
|
图 4 算例2的模型和优化结果 Figure 4 Model and optimal topology of example 2 |
|
图 5 算例2柔顺性和体积分数的进化历史 Figure 5 Evolution histories of the compliance and volume fraction of example 2 |
对于考虑自重载荷作用的结构拓扑优化问题来说,另外一个关键特征就是体积约束的无效性.为了更清楚地阐述这一特性,针对上面的优化问题,考虑体积分数约束从

|
图 6 约束体积分数与实际体积分数关系图 Figure 6 Relation between the constrained volume fraction and the real volume fraction |
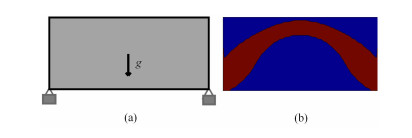
第3个算例考虑一个几何尺寸为
|
图 7 算例3的设计域和边界条件 Figure 7 Design domain and boundary condition of example 3 |
图 8显示了本文方法获得的最优的拓扑构型.可以看出优化过程产生了一个跨越两端支撑的拱形结构,以便最佳地承受其自身重量,拓扑构型与二维结果一致.

|
图 8 3D自重拱的最优拓扑 Figure 8 Optimal topology of 3D arch |
为了对比固定载荷和自重载荷作用对结构拓扑构型的影响,针对上面的优化问题考虑上表面受均布的单位载荷作用情形(上表面包含一层不可设计域),设计域和边界条件如图 7(b)所示.以占设计域

|
图 9 3D拱形桥的最优拓扑 Figure 9 Optimal topology of 3D arched bridge |
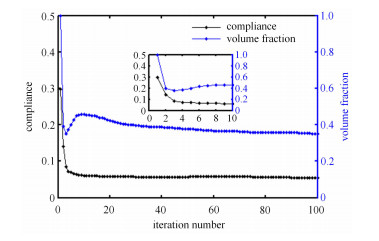
图 10显示了3D自重拱(3D arch)和3D桥(3D bridge)结构设计过程中目标函数和体积分数的迭代历程.可以看出,本文方法迭代过程稳健,收敛快;对于3D自重拱问题,目标函数是单调递减的,最终的体积分数
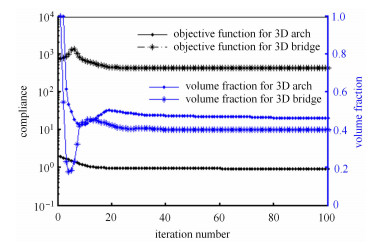
|
图 10 不同边界条件下柔顺性和体积分数的迭代历程 Figure 10 Iteration histories of the compliance and volume fraction for different boundary conditions |
本文提出一种基于NURBS插值的三维拓扑描述函数法,研究了考虑设计依赖自重载荷作用的2D/3D结构设计问题,详细推导了基于NURBS插值的考虑自重载荷作用的三维结构拓扑优化模型及其灵敏度列式,多个算例验证了本文方法的有效性和稳定性,主要得出以下结论:
(1)高阶NURBS基函数被同时用于三维NURBS实体片中的几何场、位移场及设计变量场插值,实现了几何模型、分析模型和优化模型的有效统一,确保了位移场及设计变量场的高阶连续性;
(2)无需对刚度和质量密度的插值格式进行修正,本文方法能够有效克服考虑自重载荷作用的优化问题中出现的材料的寄生效应及目标函数的非单调性问题;
(3)研究表明,本文方法优化迭代过程稳健,收敛性快.
| 1 | Bendsøe MP, Kikuchi N. Generating optimal topologies in structural design using a homogenization method. Computer Methods in Applied Mechanics and Engineering, 1988, 71 (2) : 197-224. DOI: 10.1016/0045-7825(88)90086-2. |
| 2 | Bendsoe MP, Sigmund O. Topology Optimization:Theory, Methods and Applications. Springer Science & Business Media, 2003 . |
| 3 | Xie YM, Steven GP. A simple evolutionary procedure for structural optimization. Computers & Structures, 1993, 49 (5) : 885-896. |
| 4 | Wang MY, Wang X, Guo D. A level set method for structural topology optimization. Computer Methods in Applied Mechanics and Engineering, 2003, 192 (1) : 227-246. |
| 5 | Allaire G, Jouve F, Toader AM. Structural optimization using sensitivity analysis and a level-set method. Journal of Computational Physics, 2004, 194 (1) : 363-393. DOI: 10.1016/j.jcp.2003.09.032. |
| 6 | Belytschko T, Xiao SP, Parimi C. Topology optimization with implicit functions and regularization. International Journal for Numerical Methods in Engineering, 2003, 57 (8) : 1177-1196. DOI: 10.1002/(ISSN)1097-0207. |
| 7 | De Ruiter MJ, Van Keulen F. Topology optimization using a topology description function. Structural and Multidisciplinary Optimization, 2004, 26 (6) : 406-416. DOI: 10.1007/s00158-003-0375-7. |
| 8 | 郭旭, 赵康. 基于拓扑描述函数的连续体结构拓扑优化方法. 力学学报, 2004, 36 (5) : 526-531. ( Guo Xu, Zhao Kang. A new topology description function based approach for structural topology optimization. Chinese Journal of Theoretical Applied Mechanics, 2004, 36 (5) : 526-531. (in Chinese) ) |
| 9 | 隋允康, 彭细荣. 结构拓扑优化ICM方法的改善. 力学学报, 2005, 37 (2) : 190-198. ( Sui Yongkang, Peng Xirong. The improvement for the ICM method of structural topology optimization. Chinese Journal of Theoretical Applied Mechanics, 2005, 37 (2) : 190-198. (in Chinese) ) |
| 10 | Sui YK, Peng XR. The ICM method with objective function transformed by variable discrete condition for continuum structure. Acta Mechanica Sinica, 2006, 22 (1) : 68-75. DOI: 10.1007/s10409-005-0088-9. |
| 11 | Guo X, Zhang W, Zhong W. Doing topology optimization explicitly and geometrically-a new moving morphable components based framework. Journal of Applied Mechanics, 2014, 81 (8) : 081009. DOI: 10.1115/1.4027609. |
| 12 | Zhang W, Yuan J, Zhang J, et al. A new topology optimization approach based on Moving Morphable Components (MMC) and the ersatz material model. Structural & Multidisciplinary Optimization, 2015 : 1-18. |
| 13 | Turteltaub S, Washabaugh P. Optimal distribution of material properties for an elastic continuum with structure-dependent body force. International Journal of Solids & Structures, 1999, 36 (30) : 4587-4608. |
| 14 | Bruyneel M, Duysinx P. Note on topology optimization of continuum structures including self-weight. Structural & Multidisciplinary Optimization, 2005, 29 (4) : 245-256. |
| 15 | Yang XY, Xie YM, Steven GP. Evolutionary methods for topology optimisation of continuous structures with design dependent loads. Computers & Structures, 2005, 83 (12-13) : 956-963. |
| 16 | Ansola R, Canales J, Tárrago JA. An effcient sensitivity computation strategy for the evolutionary structural optimization (ESO) of continuum structures subjected to self-weight loads. Finite Elements in Analysis & Design, 2006, 42 (14) : 1220-1230. |
| 17 | Xu H, Guan L, Chen X, et al. Guide-Weight method for topology optimization of continuum structures including body forces. Finite Elements in Analysis and Design, 2013, 75 : 38-49. DOI: 10.1016/j.finel.2013.07.002. |
| 18 | 高彤, 张卫红, 朱继宏. 惯性载荷作用下结构拓扑优化. 力学学报, 2009, 41 (4) : 530-541. ( Gao Tong, Zhang Weihong, Zhu Jihong. Structural topology optimization under inertial loads. Chinese Journal of Theoretical Applied Mechanics, 2009, 41 (4) : 530-541. (in Chinese) ) |
| 19 | 张晖, 刘书田, 张雄. 考虑自重载荷作用的连续体结构拓扑优化. 力学学报, 2009, 41 (1) : 98-104. ( Zhang Hui, Liu Shutian, Zhang Xong. Topology optimization of continuum structures subjected to self-weight loads. Chinese Journal of Theoretical Applied Mechanics, 2009, 41 (1) : 98-104. (in Chinese) ) |
| 20 | Huang X, Xie YM. Evolutionary topology optimization of continuum structures including design-dependent self-weight loads. Finite Elements in Analysis & Design, 2011, 47 (8) : 942-948. |
| 21 | Holmberg E, Thore CJ, Klarbring A. Worst-case topology optimization of self-weight loaded structures using semi-definite programming. Structural and Multidisciplinary Optimization, 2015, 52 (5) : 915-928. DOI: 10.1007/s00158-015-1285-1. |
| 22 | Chang C, Chen A. The gradient projection method for structural topology optimization including density-dependent force. Structural and Multidisciplinary Optimization, 2014, 50 (4) : 645-657. DOI: 10.1007/s00158-014-1078-y. |
| 23 | Hughes TJR, Cottrell JA, Bazilevs Y. Isogeometric analysis:CAD, finite elements, NURBS, exact geometry and mesh refinement. Computer Methods in Applied Mechanics and Engineering, 2005, 194 (39) : 4135-4195. |
| 24 | Wang X, Zhu X, Hu P. Isogeometric finite element method for buckling analysis of generally laminated composite beams with different boundary conditions. International Journal of Mechanical Sciences, 2015, 104 : 190-199. |
| 25 | 张汉杰, 王东东, 轩军厂. 薄梁板结构NURBS几何精确有限元分析. 力学季刊, 2010, 31 (4) : 469-477. ( Zhang Hanjie, Wang Dongdong, Xuan Junchang. Non-uniform rational B spline-based isogeometric finite element analysis of thin beams and plates. Chinese Quarterly of Mechanics, 2010, 31 (4) : 469-477. (in Chinese) ) |
| 26 | 尹硕辉, 余天堂, 刘鹏. 基于等几何有限元法的功能梯度板自由振动分析. 振动与冲击, 2013, 32 (24) : 180-186. ( Yin Shuohui, Yu Tiantang, Liu Peng. Free vibration analysis of functionally graded plates using isogeometric finite element method. Journal of Vibration & Shock, 2013, 32 (24) : 180-186. (in Chinese) ) |
| 27 | 蔡守宇, 张卫红, 李杨. 基于面片删减的带孔结构等几何形状优化方法. 机械工程学报, 2013, 49 (13) : 150-157. DOI: 10.3901/JME.2013.13.150. ( Cai Shouyu, Zhang Weihong, Li Yang. Isogeometric shape optimization method with patch removal for holed structures. Journal of Mechanical Engineering, 2013, 49 (13) : 150-157. (in Chinese) DOI: 10.3901/JME.2013.13.150. ) |
| 28 | Hassani B, Khanzadi M, Tavakkoli SM. An isogeometrical approach to structural topology optimization by optimality criteria. Structural and Multidisciplinary Optimization, 2012, 45 (2) : 223-233. DOI: 10.1007/s00158-011-0680-5. |
| 29 | Qian X. Topology optimization in B-spline space. Computer Methods in Applied Mechanics & Engineering, 2013, 265 (3) : 15-35. |
| 30 | Wang M, Qian X. Efficient filtering in topology optimization via B-splines. Journal of Mechanical Design, 2015, 137 (3) : V02BT03A011. |
| 31 | Piegl L, Tiller W. The NURBS Book. 2nd. 1997 |
| 32 | Svanberg K. The method of moving asymptotes-a new method for structural optimization. International Journal for Numerical Methods in Engineering, 1987, 24 (2) : 359-373. DOI: 10.1002/(ISSN)1097-0207. |
†. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China

