混合式CRP (contra-rotating propeller)是由两个对转的螺旋桨和一个吊舱组成,一般而言,吊舱位于螺旋桨的下游,为后桨提供电力推进.混合式CRP具有较高的推进效率及良好的系统冗余性,且船体所需推力由两个螺旋桨分担,改善了推进系统的振动、噪声性能.正因为其各方面优良的性能,被挪威船级社与德国劳氏船级社展望[1]为2020年"绿色船舶"的一大亮点.混合式CRP最早由ABB (asea brown boveri)公司于2001年推出,随后应用于日本的两艘客滚船[2].但混合式CRP组成构件较多的特点,也使得对它的试验及数值研究变得困难.在混合式CRP推出之初,大部分研究着重于试验研究[3-5],而研究的主要内容是混合式CRP的试验方法及试验步骤,比较典型的有Cheng等[6]、Sasaki等[7]和Quereda等[8]的工作,正是基于这些学者的研究成果,2014年的第27届国际拖曳水池会议推进委员会提出了混合式CRP的初步试验规程[9].在数值方法方面,混合式CRP的研究还不算深入,并且大部分是基于黏流的手段[10-11],这主要是由于势流方法求解组合推进器大多是基于迭代方法[12-13],构件之间的影响通过各自在对方位置处的诱导速度或诱导速度势进行考虑.这种迭代方法广泛应用于由两个构件组成的推进器,例如吊舱推进器[14]和对转桨[15-16]等,但若应用于混合式CRP这类由3个构件组成的推进器就会比较复杂.因此,一直以来基于势流方法对混合式CRP的研究比较少.尽管黏流方法能够更精细地捕捉流场[17],但势流方法具有较高的求解效率,在推进器理论设计方面具有重要意义.为了有效的开展混合式CRP设计分析,促进混合式CRP的工程应用,有必要对混合式CRP的势流计算方法进行研究.
本文选用基于势流理论的面元法作为数值手段,开展混合式CRP的面元法计算方法研究,研究中建立了迭代面元法和整体面元法,对比了两者的计算效果,为混合式CRP的设计分析,提供高效可靠的数值手段.
1 数值方法 1.1 迭代面元法已有研究表明[18-20],基于诱导速度势的低阶面元法能够满足螺旋桨计算精度的需要,因此研究中采用基于诱导速度势的低阶迭代面元法.对于均匀来流中的单个螺旋桨问题,由于对称性,面元法求解时只需要求解一个桨叶[21],这大大缩短了螺旋桨的求解时间.对于吊舱推进器、对转桨以及混合式CRP等,各个构件的相互影响打破了这种对称性,即使是均匀来流, 各个桨叶上的奇点强度也是不相同的,因此对于两个构件的组合推进器一般采用迭代方法,即是先计算各个构件在对方位置处的诱导速度或者诱导速度势,取周向平均,这样就可以把各个构件拆开,分别求解,并且每一个构件可以认为是定常问题,通过相互之间的诱导速度或诱导速度势进行迭代求解,直至两者受力达到稳定,即求得结果.
由两个构件的迭代面元法的广泛应用,很容易想到也采用迭代方法求解混合式CRP,但为了简化迭代处理,需要把混合式CRP拆分为两个部分,这也是迭代面元法处理的关键所在.由于熊鹰等[22-23]建立了吊舱推进器定常整体面元法,因此将吊舱推进器作为整体求解变得可能,于是本文的处理是将前桨当作一个整体,后桨与吊舱组成的吊舱推进器当作一个整体.前桨采用单个螺旋桨面元法进行计算,吊舱推进器采用熊鹰等
| $ \phi _{i{\rm F}} = \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \phi _j C_{ij}^{k_1 } - \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M [({\boldsymbol U} +{\boldsymbol V}_{\rm FP} ) \cdot {\boldsymbol n}]_j {\boldsymbol B}_{ij}^{k_1 } + \\ \qquad \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^{M_W } \Delta \phi_j W_{ij}^{k_1 }, \ \ i = 1, 2, \cdots, M $ | (1) |
| $ \phi _{i{\rm P}} = \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{j = 1}^N \bar\phi _j C_{ij}^{k_2} + \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{j= 1}^N [({\boldsymbol U} +{\boldsymbol V}_{\rm PF} ) \cdot {\boldsymbol n}]_j {\boldsymbol B}_{ij}^{k_2 } + \\ \;\;\;\;\;\;\sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{j = 1}^{N_W } \overline{\Delta \phi}_j W_{ij}^{k_2}+\dfrac 1{Z_2} \sum\limits^{Z_2}_{\delta=1} \sum\limits^Y_{l=1} \bar \phi_{l\delta} C_{il\delta}+\\ \qquad \dfrac 1{Z_2} \sum\limits^{Z_2}_{\delta=1} \sum\limits^Y_{l=1} [({\boldsymbol U} +{\boldsymbol V}_{\rm PF} ) \cdot {\boldsymbol n}]_{l\delta} {\boldsymbol B}_{il\delta}, \\ \qquad i = 1, 2, \cdots, N, \ N+1, \cdots, N+Y $ | (2) |
其中,由于物面不可穿透条件,式(1)和式(2)中的源汇影响项
| $ C_{ij}^k = \dfrac{1}{2\pi }\mathop{{\iint}\mkern-22.5mu \bigcirc}\limits_{S_{B_j } } \dfrac{\partial }{\partial n_{q_j } } \Big(\dfrac{1}{r(p_i, q_{jk} )} \Big ) {\rm{d}} S_{q_j } \\ B_{ij}^k = - \dfrac{1}{2\pi }\mathop{{\iint}\mkern-22.5mu \bigcirc}\limits_{S_{B_j } } \Big(\dfrac{1}{r(p_i, q_{jk} )} \Big) {\rm{d}} S_{q_j } \\ W_{ij}^k = \dfrac{1}{2\pi }\mathop{{\iint}\mkern-22.5mu \bigcirc}\limits_{S_{W_j } } \dfrac{\partial }{\partial n_{q_j } } \Big(\dfrac{1}{r(p_i, q_{jk} )} \Big){\rm{d}} S_{q_j } $ |
其中,
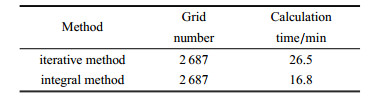
迭代面元法虽然能够解决混合式CRP的性能预报问题,但若结合有关数值方法进行混合式CRP的设计,由于这中间繁杂的迭代过程,仍旧会使得设计工作变得困难.为了探究更高效的混合式CRP面元法计算方法,研究中试图建立一种定常整体面元法,即计算中将混合式CRP视为整体,且前桨及后桨(吊舱螺旋桨)均只求解一个桨叶.在混合式CRP的分析中,仍旧按文献[22]中的处理将吊舱推进器当成一个整体,来考虑与前桨的相对位置.为了方便说明,以前桨4叶,后桨5叶为例进行混合式CRP定常整体计算公式的分析.结构位置示意图如图 1所示,图 1中实线代表后桨桨叶,虚线代表前桨桨叶,前桨桨叶用罗马数字标注桨叶编号,后桨桨叶用阿拉伯数字标注桨叶编号.吊舱以T型实线表示支柱中线.前、后桨桨叶的位置以螺旋桨参考线为准.
|
图 1 前桨、后桨及吊舱位置示意图 Figure 1 The position of forward propeller, aft propeller and pod |
由于文献[22]所选取的求解位置中,吊舱的位置只与后桨各桨叶重合,于是考虑吊舱推进器整体与前桨的相对位置时,可以始终认为吊舱与后桨某一桨叶重合.如图 1所示,位置1处前桨Ⅰ号桨叶与后桨1号桨叶重合,而位置2是在位置1的基础上旋转了一个
| $ S_0 = \dfrac{360^\circ}{\theta }, \ \ S_1 = \dfrac{360^\circ }{\theta \cdot Z_1 }, \ \ S_2 = \dfrac{360^\circ }{\theta \cdot Z_2 } $ | (3) |
于是可以写出在每一求解角度位置处,主桨叶上面元
| $ \phi _{iS} = \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \phi _{jS}^{k_1 } C_{ijS}^{k_1 } + \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \Big(\dfrac{\partial \phi }{\partial n}\Big)_{jS}^{k_1 } B_{ijS}^{k_1 } +\\ \qquad \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^{M_W } \Delta \phi _{jS}^{k_1 } W_{ijS}^{k_1 } + \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \phi _{lS}^{k_2 } C_{ilS}^{k_2 } +\\ \qquad \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \Big (\dfrac{\partial \phi }{\partial n}\Big)_{lS}^{k_2 } B_{ilS}^{k_2 } + \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^{N_W } \Delta \phi _{lS}^{k_2 } W_{ilS}^{k_2 } +\\ \qquad \dfrac{1}{Z_2 }\sum\limits_{k_3 = 1}^{Z_2 } \sum\limits_{x = 1}^Y \phi _{xS}^{k_3 } C_{ixS}^{k_3 } + \dfrac{1}{Z_2 }\sum\limits_{k_3 = 1}^{Z_2 } \sum\limits_{x = 1}^Y \Big (\dfrac{\partial \phi }{\partial n}\Big)_{xS}^{k_3 } B_{ixS}^{k_3 }, \\ \qquad i = 1, 2, \cdots, M, M + 1, \cdots, M + N, \cdots, \\ \qquad \qquad M + N + Y ; \qquad S = 1, 2, \cdots, S_0 $ | (4) |
其中,
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } \phi _{iS} = \dfrac{1}{S_0 }\left\{ {\left[{\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \phi _{jS}^{k_1 } C_{ijS}^{k_1 } + }\right.}\right. \\ \quad \left.{\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \Big (\dfrac{\partial \phi }{\partial n}\Big)_{jS}^{k_1 } B_{ijS}^{k_1 } + \sum\limits_{S = 1}^{S_0 } \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^{M_W } \Delta \phi _{jS}^{k_1 } W_{ijS}^{k_1 } } \right]_1 +\\ \quad \left[{\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \phi _{lS}^{k_2 } C_{ilS}^{k_2 } + \sum\limits_{S = 1}^{S_0 } \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \Big(\dfrac{\partial \phi }{\partial n}\Big)_{lS}^{k_2 } B_{ilS}^{k_2 } + }\right. \\ \quad \left.{\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^{N_W } \Delta \phi _{lS}^{k_2 } W_{ilS}^{k_2 } } \right]_2 + \left[{\sum\limits_{S = 1}^{S_0 } \dfrac{1}{Z_2 }\sum\limits_{k_3 = 1}^{Z_2 } \sum\limits_{x = 1}^Y \phi _{xS}^{k_3 } C_{ixS}^{k_3 } + }\right. \\ \quad \left.{\left.{\sum\limits_{S = 1}^{S_0 } \dfrac{1}{Z_2 }\sum\limits_{k_3 = 1}^{Z_2 } \sum\limits_{x = 1}^Y \Big (\dfrac{\partial \phi }{\partial n}\Big)_{xS}^{k_3 } B_{ixS}^{k_3 } } \right]_3 } \right\}, \\ \quad i = 1, 2, \cdots, M, M + 1, \cdots , M + N, \cdots, M + N + Y ; \\ \quad S = 1, 2, \cdots, S_0 $ | (5) |
为了能够运用定常面元法求解式(5),需要对式(5)进行相关的数值处理和分析.式(5)中标号为1的项是前桨的影响项,标号为2的项为后桨影响项,标号为3的项为吊舱影响项.显然,在
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } \phi _{iS} = \dfrac{1}{S_0 }\left( {\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \phi _{jS}^{k_1 } C_{ijS}^{k_1 } +}\right.\\ \qquad \sum\limits_{S = 1}^{S_0 } \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \phi _{lS}^{k_2 } C_{ilS}^{k_2 } + \left. {\dfrac{1}{Z_2 }\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_3 = 1}^{Z_2 } \sum\limits_{x = 1}^Y \phi _{xS}^{k_3 } C_{ixS}^{k_3 } + \cdots } \right), \\ \qquad i = 1, 2, \cdots, M; \ S = 1, 2, \cdots, S_0 $ | (6) |
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } {\phi _{iS} } = \dfrac{1}{S_0 }\left( {\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\phi _{jS}^{k_1 } } } C_{ijS}^{k_1 } } + } \right.\\ \qquad \sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\phi _{lS}^{k_2 } } } C_{ilS}^{k_2 } } + \\ \qquad {\left. {\dfrac{1}{Z_2 }\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_3 = 1}^{Z_2 } {\sum\limits_{x = 1}^Y {\phi _{xS}^{k_3 } } } C_{ixS}^{k_3 } } + \cdots } \right) } \\ \qquad i = M + 1, \cdots, M + N, \cdots, M + N + Y; \\ \qquad S = 1, 2, \cdots, S_0 $ | (7) |
其中,省略号代表了式(5)中未列出的项.可以知道,式(6)和式(7)均选取了式(5)中偶极子影响项.首先对式(6)进行分析,式(6)中右端第一项是前桨上控制点对前桨自身场点的影响,因此
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\phi _{jS}^{k_1 } } } C_{ijS}^{k_1 } } = \sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\Big(\dfrac{1}{S_0 }} } \sum\limits_{S = 1}^{S_0 } {\phi _{jS}^{k_1 }\Big )C_{ijS}^{k_1 } } $ | (8) |
根据前述吊舱推进器作为整体的处理,参照图 1可以知道,式(8)中
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } \phi _{jS}^{k_1 } = \dfrac{1}{S_1 S_2 }S_1 (\phi _j^1 + \phi _j^2 + \phi _j^3 + \phi _j^4 ) = \\ \qquad \dfrac{1}{Z_1 }\sum\limits_{k_1 = 1}^{Z_1 } {\phi _j^{k_1 } } $ | (9) |
显然式(8)中,
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\varphi _{jS}^{k_1 } } } C_{ijS}^{k_1 } } = \sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\overline \varphi _j C_{ij}^{k_1 } } } $ | (10) |
于是得到式(6)右端第1项的最终表达式(10).下面分析式(6)右端第2项,第2项是后桨面元对前桨面元的影响项,因此
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\phi _{lS}^{k_2 } } } C_{ilS}^{k_2 } } = \dfrac{1}{S_1 }S_1 \sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\phi _{l1}^{k_2 } E_{il}^{k_2 } } } =\\ \qquad \sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\phi _{l1}^{k_2 } E_{il}^{k_2 } } } $ | (11) |
其中,
| $ \left. \begin{array}{l} E_{il}^1 = (C_{il1}^1 + C_{il6}^1 + C_{il11}^1 + C_{il16}^1)/{S_2}\\ E_{il}^2 = (C_{il2}^1 + C_{il7}^1 + C_{il12}^1 + C_{il17}^1)/{S_2}\\ E_{il}^3 = (C_{il3}^1 + C_{il8}^1 + C_{il13}^1 + C_{il18}^1)/{S_2}\\ E_{il}^4 = (C_{il4}^1 + C_{il9}^1 + C_{il14}^1 + C_{il19}^1)/{S_2}\\ E_{il}^5 = (C_{il5}^1 + C_{il10}^1 + C_{il15}^1 + C_{il20}^1)/{S_2} \end{array} \right\} $ | (12) |
为了更形象地说明问题,式(12)中影响系数的下标
| $ \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \phi _{l1}^{k_2 } E_{il}^{k_2 } = \sum\limits_{l = 1}^N \Big (\sum\limits_{k_2 = 1}^{Z_2 } \phi _{l1}^{k_2 } \Big)E_{il}^1 =\\ \qquad \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \Big ( \sum\limits_{k_2 = 1}^{Z_2 } \phi _{l1}^{k_2 } \Big / {Z_2 } \Big )E_{il}^1 = \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \Big( \sum\limits_{k_2 = 1}^{Z_2 } \phi _{l1}^{k_2 } \Big / {Z_2 } \Big )E_{il}^{k_2 } $ | (13) |
显然,对于不同的
| $ \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\varphi _{lS}^{k_2 } } } C_{ilS}^{k_2 } } = \sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\overline \varphi _l } } E_{il}^{k_2 } $ | (14) |
对于式(6)中的右端第3项是吊舱对前桨面元的影响,由于分析中将吊舱与后桨当作一个整体,因此它的影响特性与后桨影响项保持一致.于是式(6)中右端第3项可以写为
| $ \dfrac{1}{Z_2 }\sum\limits_{S = 1}^{S_0 } \sum\limits_{k_3 = 1}^{Z_2 } \sum\limits_{x = 1}^Y \phi_{xS}^{k_3 } C_{ixS}^{k_3 } = \\ \qquad \sum\limits_{x = 1}^Y \Big(\dfrac{1}{S_1 }\sum\limits_{S = 1}^5 \phi _{xS} \Big ) \sum\limits_{k_3 = 1}^{Z_2 } (C_{ix1}^{k_3 } +\\ \qquad C_{ix6}^{k_3 } + C_{ix11}^{k_3 } + C_{ix16}^{k_3 } ) / Z_2 S_2 = \sum\limits_{x = 1}^Y \overline \phi_x E_{ix} $ | (15) |
其中,
| $ E_{ix} = \dfrac{1}{S_0 }\sum\limits_{S = 1}^{S_0 } {C_{ixS} } $ | (16) |
由于
| $ \overline \phi _i = \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^M \overline \phi _j C_{ij}^{k_1 } + \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \overline \phi _l E_{il}^{k_2 } + \\ \qquad \sum\limits_{x = 1}^Y \overline \phi _x E_{ix} + \cdots, \qquad i = 1, 2, \cdots, M $ | (17) |
下面对式(7)进行分析,对于式(7)的右端第1项是前桨桨叶面元对后桨桨叶面元的影响,因此对它的分析与式(6)中右端第2项的分析方法类似,于是可以写出式(7)中右端第1项的表达式
| $ \sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\varphi _{jS}^{k_1 } } } C_{ijS}^{k_1 } } = \sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\overline \varphi _j E_{ij}^{k_1 } } } $ | (18) |
其中,
| $ \left. \begin{array}{l} E_{ij}^1 = (C_{ij1}^1 + C_{ij5}^1 + C_{ij9}^1 + C_{ij13}^1 + C_{ij17}^1)/{S_1}\\ E_{ij}^2 = (C_{ij2}^1 + C_{ij6}^1 + C_{ij10}^1 + C_{ij14}^1 + C_{ij18}^1)/{S_1}\\ E_{ij}^3 = (C_{ij3}^1 + C_{ij7}^1 + C_{ij11}^1 + C_{ij15}^1 + C_{ij19}^1)/{S_1}\\ E_{ij}^4 = (C_{ij4}^1 + C_{ij8}^1 + C_{ij12}^1 + C_{ij16}^1 + C_{ij20}^1)/{S_1} \end{array} \right\} $ | (19) |
由于式(7)的右端第2、3项是吊舱推进器上面元对自身面元的影响项,而式(7)是在吊舱推进器整体面元法的基础上建立的,因此这两项与式(6)中右端第1项前桨对自身面元影响项的分析类似,于是式(7)中右端第2、3项可以写为
| $ \sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\phi _{lS}^{k_2 } } } C_{ilS}^{k_2 } } + \dfrac{1}{Z_2 }\sum\limits_{S = 1}^{S_0 } {\sum\limits_{k_3 = 1}^{Z_2 } {\sum\limits_{x = 1}^Y {\phi _{xS}^{k_3 } } } C_{ixS}^{k_3 } } =\\ \qquad \sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\overline \phi _l } } C_{il}^{k_2 } + \sum\limits_{x = 1}^Y {\overline \phi _x } E_{ix} $ | (20) |
其中,
| $ E_{ix} = \dfrac{1}{Z_2 }\sum\limits_{k_3 = 1}^{Z_2 } {C_{ix}^{k_3 } } $ | (21) |
显然,当式(21)中的面元
根据式(18)和式(20)得到式(7)的最终表达式
| $ \overline \phi _i = \sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\overline \phi _j E_{ij}^{k_1 } } } + \sum\limits_{k_2 = 1}^{Z_2 } {\sum\limits_{l = 1}^N {\overline \phi _l } } C_{il}^{k_2 } + \sum\limits_{x = 1}^Y {\overline \phi _x E_{ix} } + \cdots, \\ i = M + 1, M + 2, \cdots, M + N + 1, \cdots, M + N + Y $ | (22) |
为了统一,将式(17)和式(22)中的影响系数
| $ \overline {\phi _i } = \sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\overline \phi _j E_{ij}^{k_1 } } } + \sum\limits_{k_1 = 1}^{Z_1 } {\sum\limits_{j = 1}^M {\Big (\overline {\dfrac{\partial \phi }{\partial n}} \Big )_j F_{ij}^{k_1 } } } + \\ \qquad \sum\limits_{k_1 = 1}^{Z_1 } \sum\limits_{j = 1}^{M_W } \overline {\Delta \phi } _j G_{ij}^{k_1 } + \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \overline \phi _l E_{il}^{k_2 } + \\ \qquad \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^N \Big(\overline {\dfrac{\partial \phi }{\partial n}} \Big)_l F_{il}^{k_2 } + \sum\limits_{k_2 = 1}^{Z_2 } \sum\limits_{l = 1}^{N_W } \overline {\Delta \phi } _l G_{il}^{k_2 } +\\ \qquad \sum\limits_{x = 1}^Y \overline \phi _x E_{ix} + \Big(\overline {\dfrac{\partial \phi }{\partial n}} \Big)_x F_{ix}, \\ \qquad i = 1, 2, \cdots, M, M + 1, \cdots, M + N, \cdots, \\ \qquad \qquad M + N + Y $ | (23) |
其中,影响系数
| $ E = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{E_{ij}} = {C_{ij}}, }&{i = {P_{{\rm{FP}}}}}\\ {{E_{il}} = {\rm{Eq}}.({\rm{12}}), }&{i = {P_{{\rm{FP}}}}}\\ {{E_{ix}} = {\rm{Eq}}.({\rm{16}}), }&{i = {P_{{\rm{FP}}}}}\\ {{E_{ij}} = {\rm{Eq}}.({\rm{19}}), }&{i = {P_{{\rm{POD}}}}}\\ {{C_{il}}, }&{i = {P_{{\rm{POD}}}}} \end{array}\\ \begin{array}{*{20}{l}} {{E_{ix}} = {\rm{Eq}}.({\rm{21}}), }&{i = {P_{{\rm{POD}}}}} \end{array} \end{array} \right. $ | (24) |
其中,
需要注意的是,式(23)是在吊舱推进器定常整体面元法计算式(2)的基础上得到的,因此对于吊舱桨与吊舱的求解间隔是后桨相邻桨叶的间隔(对于后桨为5叶时即是72
| $ E = \left\{ {\begin{array}{*{20}{l}} {{E_{ij}} = {C_{ij}}, }&{i = {P_{{\rm{FP}}}}}\\ {{E_{il}} = {\rm{Eq}}.({\rm{12}}), }&{i = {P_{{\rm{FP}}}}\;({\rm{or}}\;{P_{{\rm{POD}}}})}\\ {{E_{ix}} = {\rm{Eq}}.({\rm{16}}), }&{i = {P_{{\rm{FP}}}}\;({\rm{or}}\;{P_{{\rm{AP}}}})}\\ {{E_{ij}} = {\rm{Eq}}.({\rm{19}}), }&{i = {P_{{\rm{AP}}}}\;({\rm{or}}\;{P_{{\rm{POD}}}})}\\ {{E_{il}} = {C_{il}}, }&{i = {P_{{\rm{AP}}}}}\\ {{E_{ix}} = {C_{ix}}, }&{i = {P_{{\rm{POD}}}}} \end{array}} \right. $ | (25) |
其中,
与单个螺旋桨的面元法求解相似,整体面元法计算式(23)中的
| $ \left. \begin{array}{l} \Delta {p_m} = {p_{m{\rm{U}}}}-{p_{m{\rm{L}}}}\\ m = 1, 2, \cdots, {m_{\rm{F}}}, \\ \qquad {m_F} + 1, \cdots, {m_{\rm{F}}} + {m_A} \end{array} \right\} $ | (26) |
其中,
| $ \Delta {\boldsymbol\phi}^{(k + 1)} = \Delta {\boldsymbol\phi}^{(k)}-{\boldsymbol J}^{ - 1}\Delta {\boldsymbol p}^{(k)} $ | (27) |
其中,上标
| $ \left. \begin{array}{l} {J_{ij}} = \frac{{\partial {{(\Delta p)}_i}}}{{\partial {{(\Delta \phi )}_j}}}\\ i({\rm{or}}\;j) = 1, 2, \cdots, {m_F}, {m_F} + 1, \cdots, {m_F} + {m_A} \end{array} \right\} $ | (28) |
基于式(23)、式(26)及式(27)即建立了整体面元法封闭求解方程组.
另外,尾涡面作为面元法求解的理论假设,对计算结果有较大影响.在求解之前,需要对混合式CRP的尾涡面进行说明.本文在确定混合式CRP的尾涡面时,主要依据已有对吊舱推进器和对转桨的尾流场研究结果以及混合式CRP的水动力性能研究结果.文献[27-28]的研究结果表明,对于吊舱推进器,吊舱支柱对螺旋桨的尾流既有阻塞的效果,也有排挤加速的效果.文献[29]的研究结果表明,与单独存在前桨的情况相比,对转桨前桨的尾流在流经后桨之前变化不大,流经后桨之后将会有较大幅度的加速;同时,后桨的尾流会得到前桨的加速,前桨造成的旋转尾流会与后桨旋转流进行一定程度的抵消.而已有对混合式CRP敞水性能的研究结果表明[6, 30\hbox{-}31],混合式CRP的前桨与单独前桨的推力、扭矩相差不大.结合以上研究结果,本文主要对混合式CRP的尾涡螺距角作出式(29)的修改
| $ \left. {\begin{array}{*{20}{l}} {{\beta _{{\rm{HF}}}} = \left\{ {\begin{array}{*{20}{l}} {{\omega _{{\rm{F1}}}}{\beta _{{\rm{SF}}}}, }&{{x_{{\rm{wake}}}} \le {x_{{\rm{A-plane}}}}}\\ {{\omega _{{\rm{F2}}}}{\beta _{{\rm{SF}}}}, }&{{x_{{\rm{wake}}}} > {x_{{\rm{A-plane}}}}} \end{array}} \right.}\\ {{\beta _{{\rm{HA}}}} = {\omega _{\rm{A}}}{\beta _{{\rm{SA}}}}} \end{array}{\rm{ }}} \right\} $ | (29) |
其中,
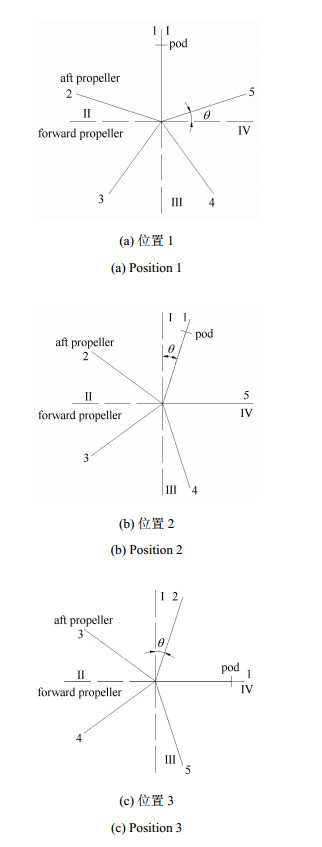
前一小节分别给出了混合式CRP的迭代面元法和整体面元法求解公式,并对混合式CRP的面元法求解尾涡面进行了修正,随后按照求解公式编译完成迭代面元法和整体面元法的计算程序.为了对比求解精度与求解效果,运用两种面元法对文献[10]中的混合式CRP进行计算并与文献[10]中的试验值进行对比.混合式CRP的主要参数如表 1和表 2所示,吊舱的示意图如图 2所示.前、后桨间距为0.454 5倍前桨直径.
| 表 1 吊舱主参数 Table 1 Pod parameters |
| 表 2 螺旋桨主参数 Table 2 Parameters of propellers |
|
图 2 吊舱示意图 Figure 2 The diagram of pod |
定义
| $ \left. \begin{array}{l} J = \frac{V}{{{n_{\rm{F}}}{D_{\rm{F}}}}}\\ {K_{{\rm{TF}}}} = \frac{{{T_{\rm{F}}}}}{{\rho n_{\rm{F}}^2D_{\rm{F}}^4}}, {K_{{\rm{QF}}}} = \frac{{{Q_{\rm{F}}}}}{{\rho n_{\rm{F}}^2D_{\rm{F}}^5}}\\ {K_{{\rm{TA}}}} = \frac{{{T_{\rm{A}}}}}{{\rho n_{\rm{A}}^2D_{\rm{A}}^4}}, {K_{{\rm{QA}}}} = \frac{{{Q_{\rm{A}}}}}{{\rho n_{\rm{A}}^2D_{\rm{A}}^5}}\\ {K_{{\rm{TU}}}} = \frac{{{T_{\rm{U}}}}}{{\rho n_{\rm{A}}^2D_{\rm{A}}^4}} = \frac{{{T_{\rm{A}}} + {T_{{\rm{pod}}}}}}{{\rho n_{\rm{A}}^2D_{\rm{A}}^4}} \end{array} \right\} $ | (30) |
其中,

|
图 3 前桨敞水性能 Figure 3 Open water performance of forward propeller |
|
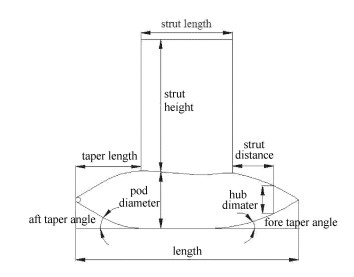
图 4 吊舱推进系统敞水性能 Figure 4 Open water performance of podded propulsion |
图 3和图 4中,iterative method表示迭代面元法计算结果,integral method表示整体面元法计算结果,experimental data表示试验值.通过图 3和图 4看出,整体面元法和迭代面元法的数值结果与试验值相比均有较好的一致性,在设计点
| 表 3 面元法计算时间对比 Table 3 Comparison of calculation time of surface panel methods |
根据表 3的计算耗时对比以及图 3和图 4计算结果的对比可以知道,在保证相同计算精度的条件下,整体面元法的计算时间要比迭代面元法的计算时间少.一般而言,推进器的设计会结合数值算法进行优化,这中间的计算过程需要进行大量的迭代处理,而本文建立的混合式CRP的整体计算面元法省去了面元法中的迭代,这对于混合式CRP的性能分析和设计具有较大意义.同时,根据混合式CRP整体面元法计算公式的推导可以知道,本文所建立的整体面元法可推广到其他多构件组成的组合推进器,但在应用的过程中需要对相关影响系数进行修正.
3 误差分析基于势流理论的面元法在求解升力体问题时,将下泄的非势流区当作无厚度的势流区边界,这是面元法的理论缺陷,然而大量的螺旋桨计算结果表明[18-21],这一理论缺陷,可以通过建立合适的尾涡模型进行消除,从而使得数值结果与试验值有较好的一致性.本文所建立的定常整体面元法计算结果误差,同样受到尾涡模型的影响.另外,在定常整体面元法的推导过程中还作了以下近似处理,这里对这些近似处理的合理性作出说明.
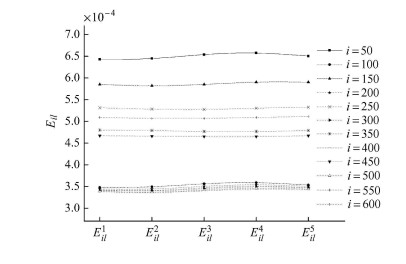
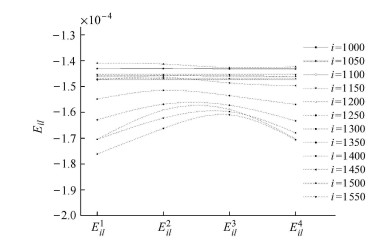
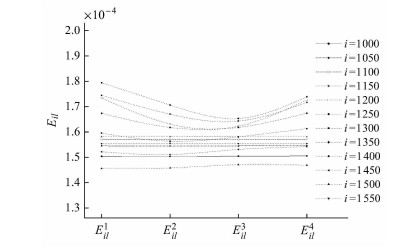
第1项近似处理是:式(13)、式(18)的处理中,认为对于不同的

|
图 5 |
|
图 6 |
|
图 7 |
|
图 8 |
从图 5
第2项近似处理是:选取的求解角度间隔问题.选取一定的角度间隔表示忽略了角度间隔之间的螺旋桨受力的脉动值.根据文献[11-12, 23]的结果可以知道,就本文所选取的角度间隔,螺旋桨或吊舱的受力脉动值在1%以内,因此从工程计算的角度考虑,这一处理也是合理的.另外,求解角度可以选取更小值,但会增加影响系数的计算时间.
第3项近似处理是:以诱导速度势的平均来等效替代螺旋桨受力的平均.由于螺旋桨受力由伯努利方程通过速度平方项求得,即是通过诱导速度势偏导数的平方求得.因此这一平均处理可以简单用下式来描述
| $ \sum\limits_{i = 1}^n \dfrac{\phi_i^2 }{n} \approx \sum\limits_{i = 1}^n \Big(\dfrac{\phi _i }{n} \Big )^2 $ | (31) |
其中,
综合以上的误差分析可以知道,本文提出的定常整体面元法计算公式所得到的数值结果是合理可信的.
4 总结本文首先建立了混合式CRP的迭代面元法,随后分析混合式CRP的几何特点及桨叶和吊舱上奇点强度的变化特性,提出了将混合式CRP作为整体进行定常面元法求解的可行方法,建立了整体求解面元法的控制方程,编译完成计算程序.运用整体面元法和迭代面元法对一混合式CRP的敞水性能进行了分析,数值结果表明:与试验值相比,整体面元法与迭代面元法的敞水性能计算值在设计点的相对误差均在5%以内,计算精度能够满足工程应用的需要,同时,整体面元法比迭代面元法的计算时间要少且不需要迭代处理,这为混合式CRP的优化设计提供了高效可靠地数值手段,也为其他多对象组合式推进器的计算分析提供思路.
| 1 | DNV GL.Technology Outlook 2020. Http://www.dnvgl.com, 2011 |
| 2 | Naoki U, Akira O, Takashi U, et al. The first hybrid CRP-POD driven fast ROPAX ferry in the world. Mitsubishi Heavy Industries Technical Review, 2004, 41 (6) : 1-5. |
| 3 | Black S, Cusanelli D.Design and testing of a hybrid shaft-pod propulsor for a high speed sealift ship.SNAME Propellers/Shafting 2009 Symposium.Virginia, 2009 |
| 4 | Shimamoto H, Takeda A, Miyake S. Tandem hybrid CRP system. Journal of the JIME, 2011, 46 (3) : 39-42. |
| 5 | Sasaki N, Kuroda M, Fujisawa J, et al. On the model tests and design method of hybrid CRP podded propulsion system of a feeder container ship. First International Symposium on Marine Propulsors. Trondheim,, 2009 . |
| 6 | Cheng BJ, Seokcheon G. Study on a procedure for propulsive performance prediction for CRP-POD systems. Journal of Marine Science and Technology, 2011, 16 (1) : 1-7. DOI: 10.1007/s00773-010-0108-8. |
| 7 | Sasaki N, Kawanami Y, Ukon Y, et al.Model test procedure and analysis of hybrid CRP POD system//Proc. of 2nd International conference on technical advances in podded propulsion (T-POD), Nantes, 2006 |
| 8 | Quereda R, Veikonheimo T, Perez S, et al.Model test and scaling for CRP POD//Proc. of 10th International Conference on Hydrodynamics, Petersburg, 2012 |
| 9 | ITTC.Recommended procedures and guidelines. 7.5-02-03-01.6, 2014 http://www.laboceano.coppe.ufrj.br/ittc2011/documents/2011/pdf%20Procedures%202011/7.5-02-03-01.5.pdf |
| 10 | Wang ZZ, Xiong Y, Wang R. Numerical investigation on scale effect of hydro-dynamic performance of the hybrid CRP pod propulsion system. Applied Ocean Research, 2016, 54 : 26-38. DOI: 10.1016/j.apor.2015.10.006. |
| 11 | Wang ZZ, Xiong Y. Effect of time step size and turbulence model on the open water performance prediction of contra-rotating Propellers. China Ocean Engineering, 2013, 27 (2) : 193-204. DOI: 10.1007/s13344-013-0017-9. |
| 12 | Liu PF, Islam MF, Veitch B. Unsteady hydromechanics of a steering podded propeller unit. Ocean Engineering, 2009, 36 (12) : 1003-1014. |
| 13 | Liu PF, Akinturk A, He M, et al.Hydrodynamic performance evalua-tion of an ice class podded propeller under ice interaction//Proc. of the OMAE 2008, Estoril, Portugal, 2008 |
| 14 | Ma C, Qian ZF, Chen K. Using vortex lattice and surface panel method to predict the unsteady hydrodynamic performance of podded propulsors. Journal of Ship Mechanics, 2014, 18 (9) : 1036-1043. |
| 15 | 苏玉民, 冯君, 刘业宝, 等. 基于速度势迭代的面元法预报对转桨性能. 船舶工程, 2015, 37 (1) : 50-53. ( Su Yumin, Feng Jun, Liu Yebao, et al. Surface panel method based on potential iteration to predict the performance of contra-rotating propeller. Ship Building, 2015, 37 (1) : 50-53. (in Chinese) ) |
| 16 | Yang CJ, Tamashima M, Wang GQ, et al. Prediction of the steady performance of contra-rotating propellers by lifting surface theory. Transactions of theWest-Japan Society of Naval Architects, 1991, 82 : 17-31. |
| 17 | 刘强, 刘周, 白鹏, 等. 低雷诺数翼型蒙皮主动振动气动特性及流场结构数值研究. 力学学报, 2016, 48 (2) : 269-277. ( Liu Qiang, Liu Zhou, Bai Peng, et al. Numerical study about aerodynamic characteristics and flow field structures for a skin of airfoil with active oscillation at lowreynolds number. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48 (2) : 269-277. (in Chinese) ) |
| 18 | Greco L, Muscari R, TestaffC, et al. Marine propellers performance and flow-field prediction by a free-wake panel method. Journal of Hydro dynamics, 2014, 26 (5) : 780-795. |
| 19 | 谭廷寿.非均匀流场中螺旋桨性能预报和理论设计研究.[博士论文].武汉:武汉理工大学交通学院, 2003. ( Tan Tingshou. Performance prediction and theoretical design research on propeller in non-uniform flow.[PhD Thesis].Wuhan:Wuhan University of Technology, 2003(in Chinese) ) http://www.oalib.com/references/18936662 |
| 20 | Kinnas SA, Fan HY, Tian Y. A panel method with a full wake alignment model for the prediction of the performance of ducted propellers. Journal of Ship Research, 2015, 59 (4) : 246-257. DOI: 10.5957/JOSR.59.4.150057. |
| 21 | Hoshino T. Hydrodynamic analysis of propellers in steady flow using a surface panel method. Journal of the Society of Naval Architects of Japan, 1989, 165 : 55-70. |
| 22 | 王睿, 熊鹰, 王展智. 适用于整体求解吊舱推进器的定常面元法. 推进技术, 2016, 37 (5) : 992-1000. ( Wang Rui, Xiong Ying, Wang Zhanzhi. A steady surface panel method suitable for the calculation of podded propulsor as a whole. Journal of Propulsion Technology, 2016, 37 (5) : 992-1000. (in Chinese) ) |
| 23 | 王睿, 熊鹰, 黄斌. 吊舱推进器势流计算方法研究. 上海交通大学学报, 2016, 50 (8) : 76-83. ( Wang Rui, Xiong Ying, Huang Bin. Comparison of different surface panel method in analysis of podded propulsion. Journal of Shanghai Jiaotong University, 2016, 50 (8) : 76-83. (in Chinese) ) |
| 24 | Kerwin JE, Kinnas SA, Lee JT, et al. A surface panel method for the hydrodynamic analysis of ducted propeller. Transactions of Society of Naval Architects and Marine Engineers, Teddington, 1987 . |
| 25 | Hoshino T. Hydrodynamic analysis of flow using a surface propellers in steady panel method. Journal of Society of Naval Architects of Japan, 1989, 165 : 55-70. |
| 26 | Hoshino T. Hydrodynamic analysis of propellers in unsteady flow using a surface panel method. Journal of Society of Naval Architects of Japan, 1993, 174 : 71-87. |
| 27 | 熊鹰, 盛立, 杨勇. 吊舱式推进器偏转工况下水动力性能. 上海交通大学学报, 2013, 47 (6) : 956-961. ( Xiong Ying, Sheng Li, Yang Yong. Hydrodynamics performance of podded propulsion at declination angles. Journal of Shanghai Jiaotong University, 2013, 47 (6) : 956-961. (in Chinese) ) |
| 28 | 杨晨俊, 钱正芳, 马骋. 吊舱对螺旋桨水动力性能的影响. 上海交通大学学报, 2003, 37 (8) : 1229-1233. ( Yang Chenjun, Qian Zhengfang, Ma Cheng. Influences of pod on the propeller performance. Journal of Shanghai Jiaotong University, 2003, 37 (8) : 1229-1233. (in Chinese) ) |
| 29 | Paik KJ, Hwang S, Jung J, et al. Investigation on the wake evolution of contra-rotating propeller using RANS computation and SPIV measurement. International Journal of Naval Architecture and Ocean Engineering, 2015, 7 : 595-609. DOI: 10.1515/ijnaoe-2015-0042. |
| 30 | Wang ZZ, Xiong Y, Wang R. Numerical investigation on scale effect of hydrodynamic performance of the hybrid CRP pod propulsion system. Applied Ocean Reasearch, 2016, 54 : 26-38. DOI: 10.1016/j.apor.2015.10.006. |
| 31 | Xiong Y, Zhang K, Wang ZZ, et al. Numerical and experimental studies on the effect of axial spacing on hydrodynamic performance of the hybrid CRP pod propulsion system. China Ocean Engineering, 2016, 30 (4) : 627-636. DOI: 10.1007/s13344-016-0040-8. |