†. 宁波市中医院王晖工作室, 宁波 315000
中医看病的基本技能-望、闻、问、切,以“切脉象"为最基本、最重要、最奇妙、也最难.二十余种常规脉象常常“只可意会,不可言传",这一方面说明脉诊最具特色,另一方面也说明脉诊面临如何定量分析的严峻挑战.
如何结合现代科学进步,对脉搏波进行定量研究,乃是我们面临的跨中医与西医、跨医学与数理学科的新挑战.定量研究的第一步是建立问题的数学物理模型.目前对于脉搏波研究有两种不同的基本思路:(1)基于西医解剖学、针对具体实体(如动脉管)建模,如线性弹性腔和弹性管模型等[1-2],并已发展到动脉管非线性波传播理论[3-5],以动脉血管壁运动为主,计及不可压缩黏性血液流动和血管外周组织约束的相互作用等,因而脉搏波传达的主要是心脏和动脉管实体器官的疾病信息[6-7];(2)基于中医的整体观点、认为脉搏波反映的是生命体整体状况的综合信息.下面,我们遵循中医的思路,试从连续介质力学的波动理论出发,为脉搏波系统建立一个数学力学模型.这里所说的脉搏波系统是指:以波的形式在血液中传播生命能量的整个系统,它反映着生命体的多种信息,而不只是心脏、血液和血管等循环系统本身局部实体器官的信息.
1 脉搏波的力学建模当用连续介质波动理论来刻画整个脉搏波系统(而不局限于具体局部器官)时,问题归结为建立等效的“控制方程组",以及在特定初始条件(时间意义上的约束条件,隐含先天条件)和边界条件(空间意义上的约束条件,隐含五脏六腑条件等)下的求解.
控制方程组由3个守恒方程(动量守恒、质量守恒和能量守恒)以及系统的本构方程共同组成.在一维纵波的简化情况下,守恒方程可表为如下3个方程(详见参考文献[8-9])
动量守恒
| $ {\rho _0}\frac{{\partial v}}{{\partial t}} =-\frac{{\partial P}}{{\partial X}} $ | (1) |
质量守恒
| $ \dfrac{\partial v}{\partial X}=\rho_0 \dfrac{\partial V}{\partial t} $ | (2) |
能量守恒
| $ \rho_0\dfrac{\partial E}{\partial t}=-P \dfrac{\partial v}{\partial X} $ | (3a) |
如果把式(2)代入式(3),可以得到能量守恒方程的另一种形式
| $ {\rm{d}}E=-P {\rm{d}}V, \ \ \hbox{或} \ \ E=-\int^V_{V_0} P {\rm{d}}V $ | (3b) |
以上3式中,
“本构方程"一词不为医学界熟悉.连续介质力学理论把反映物质本身力学性能的各力学量之间的内在本质关系称为本构关系,而本构关系的数学表达形式称为本构方程.在上述脉搏波系统的三个守恒方程中,有三个力学量与本构性能相关,即
| $ P = P\left( {V, \dot {V}, E} \right) $ | (4a) |
式中
| $ P = P\left( V \right) $ | (4b) |
例如, 大家熟知的理想气体状态方程就是式(4b)的特例.在等温条件下有
式(1)~式(4)共同组成脉搏波系统的控制方程组,其中的3个守恒方程是普适的,反映了各种脉搏波的共性方面,而系统本构方程则反映了不同脉搏波的特性方面.
中医脉诊中,手指感受到的主要是压力波形式的脉搏波
| $ \dfrac{\partial ^2P}{\partial t^2} - C^2\dfrac{\partial ^2P}{\partial X^2} = 0 $ | (5a) |
| $ C = V_0 \sqrt { - \left( {\dfrac{\partial P}{\partial V}} \right)} $ | (5b) |
连续介质波动理论已证明[9],式(5a)是描述非线性波传播的双曲型偏微分方程,式(5b)则给出其相应的小扰动传播的物质波速
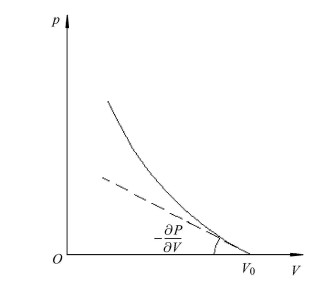
|
图 1 波速 |
由脉搏波的3个守恒方程(式(1)
由以上关于脉搏波的讨论可见,脉搏现象包含着血液的流动和在血液中传播的携带能量的脉搏波.前者是人眼易见的实体血液的“物质流",而后者是人眼不易见、以波的形式传播的“能量流",本文把它们分别解释为中医所谓的“血"和“气".中医认为气、血是形成脉象的物质基础,如《景岳全书》谓“脉者,血气之神,邪气之鉴也".但由于“气"不是以可见的物质形态存在,许多学者都尝试过对其实质进行解读.目前一种代表性的论述是:“气是具有很强活力的极精微的物质"[14-15],但迄今尚无实验观察的力证,因而尚无一个公认的答案.本文根据上述脉搏波力学模型的分析提出:血是气传播的物质载体(媒介),而气是以波形式传播的推动血运行的能量.
应该注意区分血液质点的运动和脉搏波的传播.在脉搏波以波速
凡循环血液能够流到的生命体各部分,脉搏波也同样传播到了生命体的这些部分.犹如一条大江,如果有
西医界曾经对脉搏波波速(pulse wave velocity, PWV)展开大量研究[11-12],但主要看作反映动脉弹性和硬化程度的一个表征. 2007年,欧洲高血压指南将主动脉脉搏波波速(aortic pulse wave velocity,APWV)
如果系统本构方程已知,在给定的初始条件和边界条件下,脉搏波控制方程组有定解[9],就可以确定脉搏波的传播特征,包括压力波形
反之,如果系统本构方程未知,在给定的初始条件和边界条件下,根据测得的一系列脉搏波信息去反求系统本构方程,这在数学力学上称为解“反问题"(即反演).
由《黄帝内经》归纳出的“脏腑经络遍诊法"指出:五脏六腑、十二经脉都有一定的脉动表现(这相当于“正问题"的解),而根据这些脉动表现〔脉气),就可以测知脏腑经络的病变(这相当于解“反问题").高明的中医既掌握了“正问题"的解,又善于解“反问题".
因此,从上述求解“反问题"的角度来说,“切脉象"相当于根据脉诊获得的脉搏波信息去解“反问题",即反求系统本构方程,进而根据系统本构方程是否偏离健康状态(本构关系出现病态),以及偏离的原因,是什么类型的病态等等,对病况做出诊断,对症下药,予以诊治.在这个意义上,“切脉象"的诊断对象和根本目标在于诊断各个具体生命体的脉搏波系统的本构方程及各种类型脉搏波的变化状态.其实,“望闻问切"都包含着对生命之气运行状态的检查和探察.
推而广之,医生的大量工作,不论中医还是西医,实际上都是在捕捉广义的血和气的各种时空变化信息,然后去解“反问题".显然,光靠对于生命体实体的检查(验血、B超、X光、核磁共振等)是不够的,还要对气进行检查.这是医生、特别是中医的一大本事,是一个高难度挑战.
如何在给定的初始
脉搏波的反演是指,在给定的初始条件和边界条件下,由实测的一系列某种形式脉搏波信息,通过守恒方程,来反推其他形式脉搏波,以及脉搏波系统的本构方程.在数学力学上,自1970年以来已经在连续介质力学中发展了一套反演(或反分析)方法,称为拉氏反分析(Lagrange inverse analyses)[8, 20\hbox{-}26].下面把连续介质力学中的拉氏反分析方法推广到生命系统脉搏波的研究.
对于一维脉搏波的3个守恒方程(式(1)
由于守恒方程(式(1))和(式(2))所联系的不是压力
正由于此,根据实测的一系列波剖面是压力波形
“切脉象"主要是用手指感受脉搏的压力波.当采用
求得
利用
这里的
至今仍指导着中医临床实践的“寸口三部九候诊法",一般均采用北宋医家丁徳用的所谓“密排三指"之法来诊断寸、关、尺三处脉象.这与拉氏反分析至少要测知3个相近物质质点处
“寸口三部九候诊法"中的所谓“九候",乃指寸、关、尺三部“每部各以轻、中、重指力按脉,分浮、中、沉" (《难经
“三部九候诊法"还有另一理解,即在全身遍诊法中,乃指“于头部、上肢、下肢三部诊脉,每部各有上、中、下动脉,不同部的脉出现独大、独小、独迟、独数,即表示该经的脏气有寒热虚实之变化"[27]. 图 2和图 3是作者王晖在进行“三部九候"的全身遍诊的实例.医生在进行全身遍诊法时,两只手对头部、上肢、下肢三部任选两部进行脉诊,今后用科学的仪器同时测得三部信息,必将提供更多有效信息.从连续介质力学波动理论的角度看,这将有利于识别脉搏波的衰减、弥散和耗散特征,进而加深对系统本构关系类别的定量识别.这方面目前还缺乏定量研究,正是需要进一步探索的新领域.
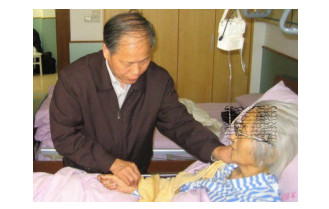
|
图 2 对上肢和下肢两部同时进行脉诊 Figure 2 Pulse-taking on the upper limb and lower limb simultaneously |
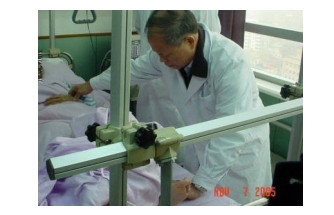
|
图 3 对头部和上肢两部同时进行脉诊 Figure 3 Pulse-taking on the head and upper limb simultaneously |
脉搏波系统的控制方程组(式(1)
关联到近年来引人注目的中医体质学的研究[27-31],就体质(body constitution)的重要性和地位而言,相当于本文量化分析的脉搏波系统中的本构关系(constitutive relation).中医体质学的开创人王琦把人体生命过程中,在先天禀赋和后天获得的基础上所形成的形态结构、生理功能和心理状态方面综合的、相对稳定的固有特质称之为“体质"[27, 29],提出九种基本类型体质:平和质、气虚质、阳虚质、阴虚质、痰湿质、湿热质、瘀血质、气郁质和特禀质等,并已列入《中医体质分类与判定》标准[32].作者王晖则将体质学说、阴阳五行、易理洛书等引入五行体质,形成了五行体质观,提出5种基本类型体质:木型体质、火型体质、土型体质、金型体质和水型体质[30-31].然皆系定性分析.如能在中医的体质与本文量化分析的脉搏波系统本构方程之间建立内在联系,对中医的客观化量化研究显然是很有意义的.
可惜,迄今我们对脉搏波系统的本构方程尚知之甚少;对于体质与本构方程间的内在联系则知之更少,均需今后进一步研究.下面,就非线性效应和黏性效应对脉搏波传播特性及系统本构方程特点的影响,试从理论上作一些探索性讨论.
3.1 非线性效应已有的脉搏波研究成果表明[10-13],脉搏波具有非线性波特征,主要表现在:
(1)与线性波速为恒值的规律不同,脉搏波波速随脉搏波压力高低而变化,不是恒值.
(2)每一次的脉搏收缩与舒张会有额外的能量耗散.表现在随脉搏波的传播,波形会发生波幅变化和能量耗散.
(3)与线性波不同,非线性脉搏波的压力波
由中医理论的天地人一体化的观点可以预期,本构方程的非线性程度将会随着四季气候(春生夏长秋收冬藏)、地域及七情六欲而变,更会随人一生的“生长壮老"而变.
本构非线性有以下两种基本类型,会相应地表现出不同的脉搏波特性.
3.1.1 递增强化非线性效应脉搏波系统的
(1)按照式(5(b))脉搏波波速取决于
(2)然而,在脉搏舒张过程中则由于较高压力扰动先卸压,比后卸压的较低压力扰动传播得快,就不会形成冲击波.而形成带有震荡弥散性质的连续波.于是,在脉搏一缩一张时,脉搏波的上升部分和下降部分分别呈现不同传播特性.
(3)由此,每一次的脉搏收缩与舒张会有额外的能量耗散.脉搏波在传播过程中会发生波幅衰减和能量耗散.
因此,脉搏压力高的人(如高血压患者)就不能忽视递增强化的非线性效应,而且脉搏压力愈高,这种非线性效应愈显着.脉搏收缩时压力陡峭地上升,脉搏舒张时压力缓慢下降,一缩一张伴随着能量耗散,从而导致脉搏波向远处传播时出现波幅衰减.可以想象,波幅衰减愈严重,就愈会反馈地促使压力升高和心跳加快.这不仅使人感到不舒服,还会进一步形成恶性循环.
3.1.2 递减强化非线性效应如果随着压力增高,系统出现某种不可逆的损伤,由于损伤一般导致系统承压能力的降低,
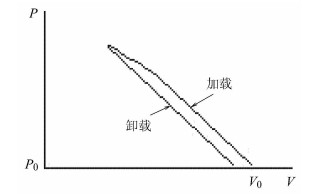
|
图 4 递减强化 |
可以预期[9],与这类本构方程相对应的脉搏波具有以下特征:
(1)根据式(5(b)),即
(2)在脉搏舒张过程中,由于卸载扰动的传播快于较高压力加载扰动的传播,将出现卸载波追赶加载波、并相互作用的情况,使问题大为复杂[9].
(3)而且,由于脉搏的收缩和舒张遵循不同的
因此,一旦生命系统出现不可逆损伤,一方面,脉搏波传播过程中会出现卸载波(脉搏舒张)追赶加载波(脉搏收缩)、并相互作用的乱象;另一方面,会出现能量耗散和波幅衰减.病人不仅会感到不舒服,还会进一步使病情形成恶性循环.
看来,中医脉诊时以浮、中、沉不同指力按脉,起到了调节压力的作用,显然有利于体察脉搏波的非线性效应,不论是“递增强化"非线性、还是“递减强化"非线性.
3.2 黏性效应生命系统种种不正常的病态,从热力学的角度可以概括为各种不可逆的耗散机制.反映在系统本构方程上则对应于方程中包含“速率相关的黏性项"(式4(a)).下面以Maxwell型线性黏弹性系统为例来讨论黏性效应的特征.
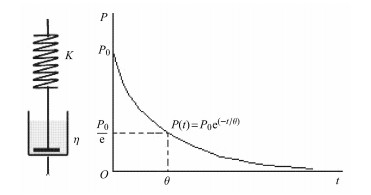
包含黏性项的Maxwell黏弹性本构方程可看作弹簧和黏壶串联组成(图 5),相应有本构方程[9]
|
图 5 Maxwell黏弹性模型(左)及其松弛特性(右) Figure 5 Maxwell visco-elastic model (left) and its relaxation character (right) |
| $ \dfrac 1{V_0}\dfrac{\partial V}{\partial t}+\dfrac 1K \dfrac{\partial P}{\partial t}+\dfrac P \eta=0 $ | (6) |
式中,
式(6)表明,在恒定比容(
| $ P(t)=P_0\exp \Big ( -\dfrac{Kt}{\eta} \Big )=P_0 \exp \Big (-\dfrac t{\theta} \Big ) $ | (7) |
式中,
可以预期[9, 33],与这类本构方程相对应的脉搏波具有以下特征:
(1)波速由串联的弹簧组件特性决定,即有
| $ P=P_0\exp \Big ( -\dfrac{\rho_0C_0}{2\eta} X \Big ) =P_0 \exp ( -\alpha X ) $ | (8a) |
$\alpha $称为衰减因子
| $ \alpha = \dfrac{\rho _0 C_0 }{2\eta } $ | (8b) |
这一现象称为波的“吸收现象",说明脉搏波在传播过程中逐渐被吸收了.
(2)脉搏舒张时,脉搏压力开始下降了,但由于黏性效应,比容并不立即随之下降,会延续一个短时间的继续增加,然后才下降.
(3)因此在$P$-$\!$-$V$图上,与脉搏收缩与舒张所对应的加载曲线与卸载曲线形成滞回曲线,两者所包围的面积代表每一次脉搏收缩与舒张所损耗的能量.
(4)黏弹性脉搏波的质点速度波$v (X, t)$、比容波$V (X, t)$和内能波$E (X, t)$等,也与压力波$P (X, t)$一样,随传播距离以指数规律衰减,但当计及非线性效应时四种形式波之间不再有线性正比关系[9, 33].
因此,一旦生命系统存在黏性机制,脉搏波传播过程中会出现衰减和吸收现象,把心脏搏出的能量消耗掉,使病人感到缺乏能量.全身遍诊的“三部九候诊法"应该比“寸口三部九候诊法"更有助于诊察脉搏波的衰减和吸收.
4 结语和展望本文遵循中医整体观念传统思路,把脉搏波系统理解为以波的形式在血液中传播生命能量的整体系统,从连续介质力学的波动理论出发,为脉搏波系统建立一个数学力学模型,并把力学反演方法推广发展到脉搏波.脉搏波反映着生命体的多种信息,而不只是心脏、血液和血管等循环系统本身局部实体器官的信息.由本文的分析得出以下几个主要观点:
(1)脉搏波是压力波$P (X, t)$,质点速度波$v (X, t)$、比容波$V (X, t)$和内能波$E (X$, $t)$这些不同形式波动的总成.只凭传感器测得的单个压力波$P (X, t)$或质点速度波$v (X, t)$等来模拟中医的脉诊是不完整的.
(2)脉搏现象包含着血液的流动和在血液中传播的携带能量的脉搏波.前者是人眼易见的实体血液的“物质流",而后者是人眼不易见、以波的形式传播的“能量流",分别对应地可理解为中医的“血"和“气".血是气传播的物质载体(媒介),而气是以波形式传播的推动血运行的能量,两者既密切相关不可分,又互有区别不可混.
(3)脉搏波传播速度$C$ (10$^{0}$$\sim$10$^{1}$ m/s量级)比血液质点运动速度$v$(10$^{ -1}$ m/s量级)快1$\sim$2个量级.远早于血液流动的到达,脉搏波已以更快的速度把能量和血液运动状态变化传递给了人体各部分.
(4)脉搏波的传播特性并不仅仅由心脏和动脉血管来决定,而由反映生命体整体系统的本构方程决定.生命体的任何局部出现病态,反过来就会影响脉搏波.脉搏波灵敏地反映着生命实体(广义之血)和生命能量(广义之气)不断运行变化着的生命状态.
(5)把力学反演方法推广到脉搏波,可由实测的一系列某形式脉搏波信息(例如压力波$P (X, t)$),通过守恒方程,定量地反演其它形式脉搏波,以及脉搏波系统的本构方程.
(6)脉搏波系统本构关系(constitutive relation)就其重要性和地位而言,与中医的体质(body constitution)相当.如何把通过反演获得的不同类型脉搏波系统本构方程与中医的不同类型体质,建立内在联系,是值得展望的重要研究方向.本构方程的非线性效应和黏性效应在反映脉搏波传播特性和体质类型上可能是不可忽略的因素.
费兆馥在她的《现代中医脉诊学》一书中曾指出“目前应用桡动脉压力脉图研究中医脉象,为脉诊客观化奠定了初步基础,但未能解决全部问题.因此,有必要采用新的技术方法获取更多的信息,探讨脉象的特性和表述方法"[11].期望本文的研究能够给现代中医脉诊学提供一个新的视野,并对中国传统医学的现代化发展有所帮助.
| 1 | 柳兆荣, 李惜惜. 弹性腔理论及其在心血管系统分析中的应用 . 北京: 科学出版社, 1987. ( Liu Zhaorong, Li Xixi. Elastic Reservoir Theory and Its Application in Analyses of Cardiovascular System . Beijing: Science Press, 1987. (in Chinese) ) |
| 2 | 罗志昌, 张松, 杨益民. 脉搏波的工程分析和临床应用 . 北京: 科学出版社, 2006. ( Luo Zhichang, Zhang Song, Yang Yimin. Engineering Analysis and Clinical Applications of Pulse Wave . Beijing: Science Press, 2006. (in Chinese) ) |
| 3 | 乔爱科, 伍时桂. 动脉中的脉搏波理论. 生物医学工程学杂志, 2000, 17 (1) : 95-100. ( Qiao Aike, Wu Shigui. Theories of pulse wave in arteries. Journal of Biomedical Engineering, 2000, 17 (1) : 95-100. (in Chinese) ) |
| 4 | 伍时桂, 李兆治. 非线性波在动脉内传播的理论和计算研究-I.非线性脉搏波传播的理论模型. 中国科学, B辑, 1988, 7 (7) : 726-738. ( Wu Shigui, Li Zhaozhi. Theory and computing research of nonlinear wave propagations in arteries, I. Theoretical model of nonlinear pulse wave propagation. Scientia Sinica, Series B, 1988, 7 (7) : 726-738. (in Chinese) ) |
| 5 | 李惜惜, 柳兆荣, 陈德奎, 等. 非线性弹性腔理论与心血管参数的无创伤检测. 中国医疗器械杂志, 1981, 5 (3) : 7-12. ( Li Xixi, Liu Zhaorong, Chen Dekui, et al. Nonlinear elastic reservoir theory and noninvasive measurement of cardiovascular parameters. Chinese J Medical Instrumentation, 1981, 5 (3) : 7-12. (in Chinese) ) |
| 6 | O'Rourke M, Pauca A, Jiang XJ. Pulse wave analysis. Br J Clin Pharmacol, 2001, 51 : 507-522. DOI: 10.1046/j.0306-5251.2001.01400.x. |
| 7 | Fan ZP, Zhang G, Liao S. Pulse wave analysis//Gaetano Gargiulo ed, Advanced Biomedical Engineering, InTech, 2011, ISBN:978-953-307-555-6 |
| 8 | Fowles R, Williams RF. Plane stress wave propagation in solids. J Appl Phys, 1970, 41 : 360. DOI: 10.1063/1.1658348. |
| 9 | Wang Lili. Foundations of Stress Waves. Amsterdam:Elsevier, 2007 . |
| 10 | 赵恩俭. 中医脉诊学 (第2版). 天津: 天津科学技术出版社, 2001. ( Zhao Enjian. Sphygmology in Traditional Chinese Medicine (${referVo.versionEn}). Tianjin: Tianjin Scientific and Technical Publishers, 2001. (in Chinese) ) |
| 11 | 费兆馥. 现代中医脉诊学 . 北京: 人民卫生出版社, 2006. ( Fei Zhaofu. Contemporary Sphygmology in Traditional Chinese Medicine . Beijing: People's Medical Publishing House, 2006. (in Chinese) ) |
| 12 | O'Rourke MF. Time domain analysis of the arterial pulse in clinical medicine (Review Article). Medical & Biological Engineering & Computing, 2009, 47 (2) : 119-129. |
| 13 | 李永光, 张文娟. 现代脉象诊断研究 . 北京: 中医古籍出版社, 2011. ( Li Yongguang, Zhang Wenjuan. Modern Pulse Diagnosis . Beijing: TCM Ancient Books Publishing House, 2011. (in Chinese) ) |
| 14 | 胡冬裴. 中医基础理论 . 北京: 清华大学出版社, 2013. ( Hu Dongpei. The Basic Theory of Chinese Medicine . Beijing: Tsinghua University Press, 2013. (in Chinese) ) |
| 15 | Che NC. Traditional Chinese Medicine . Beijing: Higher Education Press, 2012. |
| 16 | Mancia G, De Backer G, Dominiczak A, et al. 2007 Guidelines for the management of arterial hypertension. J Hypertension, 2007, 25 : 1105-1187. DOI: 10.1097/HJH.0b013e3281fc975a. |
| 17 | 《中国高血压防治指南》(基层版)编撰委员会. 中国高血压防治指南(2009年基层版). 中华高血压杂志, 2010, 18 (1) : 12-28. ( China's Prevention and Control of Hypertension Guidelines (basic version) Compilation Committee. China's Prevention and Control of Hypertension Guidelines (2009 basic version). Chinese Journal of Hypertension, 2010, 18 (1) : 12-28. (in Chinese) ) |
| 18 | 李婷, 虞钢. 基于压力波的人体脉搏波传播速度无创检测研究. 中国生物医学工程学报, 2007, 26 (3) : 321-325. ( Li Ting, Yu Gang. Research of method for pulse wave velocity analysis based on pressure wave detection. Chinese Journal of Biomedical Engineering, 2007, 26 (3) : 321-325. (in Chinese) ) |
| 19 | 刘宝华, 任晓华. 脉搏波传导速度测量算法的研究及其进展. 生物医学工程学杂志, 2010, 27 (1) : 231-235. ( Liu Baohua, Ren Xiaohua. Research and advance in the measurement of pulse wave velocity. Journal of Biomedical Engineering, 2010, 27 (1) : 231-235. (in Chinese) ) |
| 20 | Cowperthwaite M, Williams RF. Determination of constitutive relationships with multiple gauges in non-divergent waves. J Appl Phys, 1971, 42 : 456. DOI: 10.1063/1.1659623. |
| 21 | Grady DE. Experimental analysis of spherical wave propagation. J Geo Res, 1973, 78 : 1299. DOI: 10.1029/JB078i008p01299. |
| 22 | Wang LL, Zhu J, Lai HW. A new method combining Lagrangian analysis with HPB technique. Strain, 2011, 47 : 173-182. DOI: 10.1111/str.2011.47.issue-2. |
| 23 | Wang LL, Lai HW, Zhu J. Studies on high strain-rate behavior of materials by using a new method combining HPB technique with Lagrangian analysis. DYMAT, 2009, 1 : 43-49. |
| 24 | 王礼立, 朱珏, 赖华伟. 冲击动力学研究中实测波信息的解读分析. 高压物理学报, 2010, 24 (4) : 279-285. ( Wang Lili, Zhu Jue, Lai Huawei. Understanding and interpreting of the measured wave signals in impact dynamics studies. Chinese Journal of High Pressure Physics, 2010, 24 (4) : 279-285. (in Chinese) ) |
| 25 | 赖华伟, 王礼立. 用改进的基于质点速度测量的拉格朗日分析方法研究尼龙动态力学特性. 实验力学, 2011, 26 (2) : 221-226. ( Lai Huawei, Wang Lili. Studies on dynamic behavior of Nylon through modified Lagrangian analysis based on particle velocity profiles measurements. Journal of Experimental Mechanics, 2011, 26 (2) : 221-226. (in Chinese) ) |
| 26 | Wang LL, Hu SS, Yang LM, et al. Development of experimental methods for impact testing by combining Hopkinson pressure bar with other techniques. Acta Mechanica Solida Sinica, 2014, 27 (4) : 331-344. DOI: 10.1016/S0894-9166(14)60041-0. |
| 27 | 王琦, 王睿林, 李英帅. 中医体质学学科发展述评. 中华中医药杂志, 2007, 22 (9) : 627-630. ( Wang Qi, Wang Ruilin, Li Yingshuai. Comments on development of Chinese medical constitution. China Journal of Traditional Chinese Medicine and Pharmacy, 2007, 22 (9) : 627-630. (in Chinese) ) |
| 28 | 王琦. 中医体质学 . 北京: 人民卫生出版社, 2009. ( Wang Qi. Constitutionology of ChineseMedicine . Beijing: People's Medical Publishing House, 2009. (in Chinese) ) |
| 29 | 王琦. 九种体质使用手册 . 长春: 北方妇女儿童出版社, 2010. ( Wang Qi. The Manual of Nine Constitutions . Changchun: The Northern Women's and Children's Publishing House, 2010. (in Chinese) ) |
| 30 | 王晖. 体质的中医保健 . 宁波: 宁波出版社, 2009. ( Wang Hui. Traditional Chinese Medicine Health Care of Body Constitutions . Ningbo: Ningbo Press, 2009. (in Chinese) ) |
| 31 | 王晖. 全国名老中医王晖学术经验撷英 . 北京: 中国中医药出版社, 2014. ( Wang Hui. The essence of academic experience of the national famous senior doctor of TCM Wang Hui . Beijing: China Press of Traditional Chinese Medicine, 2014. (in Chinese) ) |
| 32 | 中华中医药学会. ZZYXH/T157-2009.中医体质分类与判定.北京:中国中医药出版社, 2009 ( The Society of Chinese Medicine. ZZYXH/T157-2009. The Chinese medicine constitution classification and decision criteria. Beijing:China Press of Traditional Chinese Medicine, 2009(in Chinese) ) |
| 33 | Wang LL, Huang DJ, Gan S. Nonlinear viscoelastic constitutive relations and nonlinear viscoelastic wave propagation for polymers at high strain rates//Kawata K, Shioiri J eds. Constitutive Relation in High/Very High Strain Rates. Tokyo:Springer-Verlag, 1996, 137-146 |
†. Wang Hui Workroom, Ningbo Hospital of Traditional Chinese Medicine, Ningbo 315000, China

