†. 中国空间技术研究院, 北京 100086
索梁结构在土木工程、航空航天等领域有着广泛的应用,其结构参数设计、系统任务分析等均依赖于精确的索梁动力学模型.对于大变形索梁结构,基于小变形、小转动的传统建模方法已不再适用[1-2].为此,Shabana[3-4]提出了适用于大变形柔性体动力学分析的绝对节点坐标方法(absolute nodal coordinate formulation,ANCF),并在文献[5]中给出了绝对节点方法的明确定义.该方法通过单元节点绝对位置和物质导数描述柔性体运动和变形,无小变形假设,适合于大变形索梁的动力学建模,同时也能够作为其他大变形索梁动力学模型的验证依据[6-7].
在绝对节点坐标索梁单元建模方面,Shabana等[8]提出了考虑剪切和扭转的三维梁单元建模理论,并通过数值仿真对二节点和四节点梁单元模型进行了验证[9]. Gerstmayr等[10]提出了一种适用于细长索梁的梯度缺省梁单元,该单元基于Euler-Bernoulli梁假设,通过梁中心轴线描述位移场,数值仿真结果表明该单元具有很好的收敛性和较高的计算效率.朱大鹏等[11]在Dombrowski[12]的研究基础上提出大变形索梁单元,并给出多种数值和工程应用算例. Liu等[13]利用Green-Lagrange应变张量推导曲梁单元应变能,得到了空间曲梁单元模型. Dmitrochenko等[14]集中给出了多种不同维度和节点坐标数的梁单元模型,这些单元的位移场全部采用多项式进行描述.目前这些单元已广泛应用于滑轮柔索[15-18]、铁路接触网[19-20]、柔性机械臂[21]等含索梁系统的动力学建模与分析中.
上述ANCF索梁单元的位移场均表示为关于物质坐标的多项式参数函数.文献[22]对参数形式的多项式空间曲线进行研究,得知空间曲线的弯曲程度会影响参数点在曲线上的分布.若单元位移场采用此多项式描述,则意味着轴向应变与弯曲应变相互耦合.事实上,单元的位移场与应变场均完全取决于多项式系数(单元广义坐标).若单元不同的应变分量存在相同的依赖项,就会导致不同应变分量相互耦合,这种应变耦合效应会使单元在变形过程中产生伪应力,从而导致模型失真,这也是造成ANCF梁单元闭锁问题[23-25]的主要原因.针对ANCF梁单元的闭锁问题,研究者通常采用弹性力线性化[23]、选择降阶积分[26-27]等方法来削弱闭锁效应的影响.然而,这些方法并未直接解决梁单元的应变耦合问题,为此本文以文献[10]中的细长索梁单元为例,对索梁单元的应变耦合效应进行分析,在此基础上研究应变解耦方法,以提高单元性能.
细长索梁单元的轴向应变和弯曲应变都依赖于位移场的全部多项式系数,因此两应变不独立,存在相互耦合的问题.本文首先详细分析索梁单元应变耦合机理和现象,并从能量角度分析应变耦合效应对单元精度的影响.其次研究索梁单元的应变解耦方法,推导索梁单元的应变解耦模型.最后通过静力学和动力学数值仿真,对解耦前后两种梁模型的收敛性、应变连续性以及动态特性进行深入分析,以验证解耦方法的有效性.
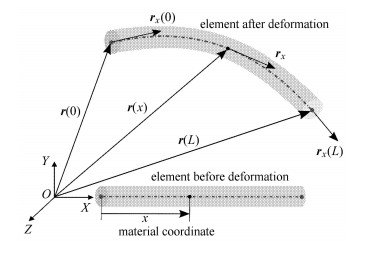
1 ANCF索梁单元应变耦合分析 1.1 ANCF索梁单元模型本节给出三维二节点索梁单元模型(如图 1),该单元适用于细长索和梁的动力学建模.为方便叙述,后文将该索梁单元简称为梁单元.
|
图 1 ANCF梁单元模型 Figure 1 Model of ANCF beam element |
梁中心轴线上任意点的位置坐标可表示为关于物质坐标
| $ {\boldsymbol r} = \left[\!\! \begin{array}{c} {r_X } \\ {r_Y } \\ {r_Z } \end{array} \!\! \right]=\left[\!\! \begin{array}{l} {a_0 + a_1 x + a_2 x^2 + a_3 x^3} \\ {b_0 + b_1 x + b_2 x^2 + b_3 x^3} \\ {c_0 + c_1 x + c_2 x^2 + c_3 x^3} \end{array} \!\! \right] $ | (1) |
上式为梁单元的位移场函数,可通过对单元节点坐标的三次Hermite插值得到
| $ {\boldsymbol r}(x, t) = {\boldsymbol S}(x){\boldsymbol q}(t) $ | (2) |
其中
| $ {\boldsymbol q} = \left[\begin{array}{cc} {\boldsymbol q}_1^{\rm T} & {\boldsymbol q}_2^{\rm T} \end{array} \right]^{\rm T} = \left[{{\boldsymbol r}^{\rm T}(0)\quad {\boldsymbol r}_x^{\rm T} (0)\quad {\boldsymbol r}^{\rm T}(L)\quad {\boldsymbol r}_x^{\rm T} (L)} \right]^{\rm T} $ | (3) |
单元形函数表达如下
| $ \left. {{\boldsymbol S}(x) = \left[\!\! \begin{array}{llll} S_1 (x){\boldsymbol I}_3 & {S_2 (x){\boldsymbol I}_3 } & {S_3 (x){\boldsymbol I}_3 } & {S_4 (x){\boldsymbol I}_3 } \end{array}\!\!\right] \\ S_1 (x) = 1 - 3\xi ^2 + 2\xi ^3, \quad S_2 (x) = L(\xi - 2\xi ^2 + \xi ^3) \\ S_3 (x) = 3\xi ^2 - 2\xi ^3, \quad S_4 (x) = L( - \xi ^2 + \xi ^3)} \right\} $ | (4) |
其中,
由单元的位移场函数可知,该单元考虑了轴向和弯曲变形,通过轴向应变
| $ \varepsilon = \dfrac{1}{2}\left( {{\boldsymbol r}_x ^{\rm T}{\boldsymbol r}_x - 1} \right) $ | (5) |
| $ \kappa = \dfrac{ | {\boldsymbol r}_x \times {\boldsymbol r}_{xx} | }{\left| {{\boldsymbol r}_x } \right|^3} \quad \ \ $ | (6) |
基于Euler-
| $ U = U_1 + U_2 = \dfrac{1}{2}\int_0^L EA\varepsilon ^2 {\rm{d}}x + \dfrac{1}{2}\int_0^L EJ\kappa ^2 {\rm{d}}x $ | (7) |
其中,
| $ {\boldsymbol Q} = {\boldsymbol Q}_1 + {\boldsymbol Q}_2 = \int_0^L EA\varepsilon \left( {\dfrac{\partial \varepsilon }{\partial {\boldsymbol q}} } \right)^{\rm T} {\rm{d}}x + \int_0^L EJ\kappa \left( {\dfrac{\partial \kappa }{\partial {\boldsymbol q }}} \right)^{\rm T} {\rm{d}}x $ | (8) |
ANCF梁单元的位移场函数可通过对节点坐标进行三次Hermite插值得到,式(5)中轴向应变和式(6)中曲率均完全取决于12个节点坐标分量的值,因此梁单元轴向应变与弯曲应变相互耦合.本文通过分析不同弯曲程度下单元的轴向应变,说明ANCF梁单元的应变耦合效应及其对单元精度的影响.在进行耦合分析前,定义如下变量:
定义梁单元整体轴向应变为
| $ \varepsilon _L = \int_0^L {\left| {{\boldsymbol r}_x } \right| {\rm{d}}x} / L - 1 $ | (9) |
其中
定义单元弯曲角为
| $ \theta = {\rm arcos} \dfrac{{\boldsymbol r}_x \left( 0 \right)^{\rm T}{\boldsymbol r}_x \left( L \right)}{\left| {{\boldsymbol r}_x \left( 0 \right)} \right| \cdot \left| {{\boldsymbol r}_x \left( L \right)} \right|} $ | (10) |
由上式可知,单元弯曲角为单元两端节点处切线方向的夹角,能够反映单元弯曲变形程度.
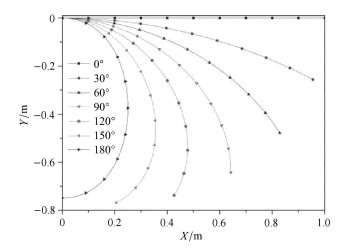
对长度为
|
图 2 位形曲线 Figure 2 Configuration curves |
|
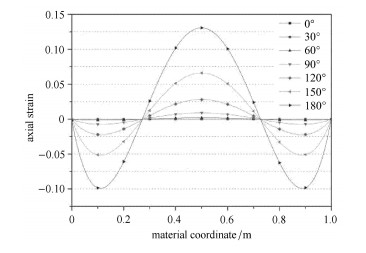
图 3 轴向应变曲线 Figure 3 Axial strain curves |
当单元不发生弯曲变形时,单元上任意点的轴向应变为0.但当单元发生弯曲变形时,单元内部产生了分布不均的轴向应变,且随着弯曲角的增大而增大,当弯曲角为180
由图 3可知,单元总长度不变,但单元中间部分伸长,而两端部分受到压缩,单元内部会产生一定的轴向应变能,这种应变能并非由外界载荷引起,而是由弯曲变形诱发产生的伪应变能(如图 4),会降低模型的精确性.

|
图 4 应变耦合示意图 Figure 4 Diagram of strain coupling |
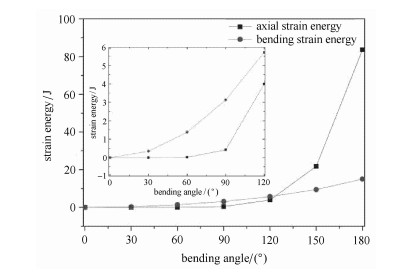
下面分析应变耦合效应对单元应变能的影响.以半径0.02 m,长度1 m,弹性模量为2
|
图 5 不同弯曲角下的应变能 Figure 5 Strain energy in different bending angles |
为了更清晰地体现轴向应变能和弯曲应变能的变化,图中对弯曲角小于120
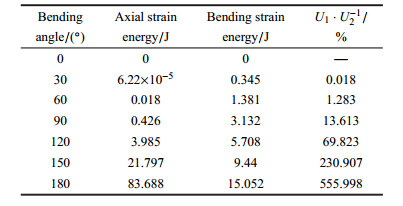
表 1给出了不同弯曲程度下单元应变能的具体值.
| 表 1 应变能数据分析 Table 1 Analysis of strain energy data |
ANCF梁单元常用于空间飞网[28-29]、空间机械臂末端捕获绳索[30]、绳系卫星[31]等含柔索系统的动力学分析中.对于这些弯曲刚度小、变形大的柔索结构,应变耦合效应引起的伪轴向应变能占总应变能的比重更大,因此对模型精度有更大的影响.
2 梁单元的应变解耦模型上一节从能量的角度分析了应变耦合效应对单元精度的影响,得知应变耦合效应会使单元刚化,这种刚化现象对大变形索梁模型精度的影响是不可忽视的.通常可通过加密网格削弱耦合效应的影响,但这也势必会降低动力学仿真计算效率,且没有从根本上解决应变耦合问题.
2.1 应变解耦ANCF梁单元的应变耦合效应主要体现在受弯曲变形的影响,单元会产生分布不均匀的轴向应变.因此为了实现轴向应变与弯曲应变解耦,本文构造了等效一维杆单元,利用该单元重新描述梁的轴向应变,使单元轴向应变独立于弯曲应变.
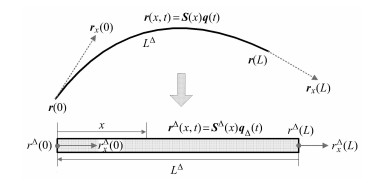
新构造的一维杆单元是通过对梁单元进行等效得到的,如图 6所示.该单元只存在轴向应变,无弯曲应变,其节点坐标定义为
|
图 6 等效一维杆单元 Figure 6 Equivalent one-dimensional rod element |
| $ {\boldsymbol q }_\Delta \left( t \right) = \left[ {r^\Delta \left( 0 \right)} \ \ {r_x^\Delta \left( 0 \right)} \ \ {r^\Delta \left( L \right)} {r_x^\Delta \left( L \right)} \right]^{\rm T} $ | (11) |
式中,
任意时刻,杆单元与梁单元有一一对应的关系,且满足如下等效准则:
(1)杆单元原长及变形后长度均与梁单元相同.
(2)杆单元两端节点处轴向应变与梁单元相同.
根据准则(1),有
| $ {\boldsymbol q}_\Delta \left( t \right) = \left[0 {\left| {{\boldsymbol r}_x \left( 0 \right)} \right|} \ \ {\int_0^L {\left| {{\boldsymbol r}_x } \right| {\rm{d}}x} } {\left| {{\boldsymbol r}_x \left( L \right)} \right|} \right]^{\rm T} $ | (12) |
杆单元的位移场维度为1,仍可表达为形函数与广义坐标乘积的形式
| $ r^\Delta (x, t) = {\boldsymbol S }^\Delta (x){\boldsymbol q }_\Delta (t) $ | (13) |
其中
根据新构造的一维杆单元,重新定义单元的轴向应变为
| $ \varepsilon = \dfrac{1}{2}\left( {r_x^{\Delta 2} - 1} \right) = \dfrac{1}{2}\left( {{\boldsymbol q }_\Delta ^{\rm T} {\boldsymbol S }^{\Delta {\rm T}}{\boldsymbol S }^\Delta {\boldsymbol q }_\Delta - 1} \right) $ | (14) |
由上式可知,重新定义的轴向应变只与梁单元长度和节点处的物质导数大小有关,与梁单元弯曲程度无关,具体可通过图 2中7组不 同弯曲程度的梁单元加以验证. 由于图中梁单元变形后长度保持不变(
根据式(8),并结合式(2)和式(5)可得原模型的轴向广义弹性力为
| $ {\boldsymbol Q }_1 = \int_0^L EA\varepsilon \left( {\dfrac{\partial \varepsilon }{\partial {\boldsymbol q }}} \right)^{\rm T} {\rm{d}}x = \\ \qquad \dfrac{1}{2}EA\int_0^L \left( {{\boldsymbol q }^{\rm T}{\boldsymbol S }_x ^{\rm T}{\boldsymbol S }_x {\boldsymbol q } - 1} \right)\left( {{\boldsymbol S }_x ^{\rm T}{\boldsymbol S}_x {\boldsymbol q }} \right) {\rm{d}}x $ | (15) |
单元应变解耦后,轴向广义弹性力发生改变,需要重新进行计算以消除伪应力对模型精度的影响.需要注意的是,式中的
| $ {\boldsymbol Q }_1^\Delta = \int_0^L EA\varepsilon \left( {\dfrac{\partial \varepsilon }{\partial {\boldsymbol q }}} \right)^{\rm T} {\rm{d}}x = \\ \qquad \dfrac{1}{2}EA\int_0^L \left( {r_x^{\Delta 2} - 1} \right)r_x^\Delta \left( {\dfrac{\partial r_x^\Delta }{\partial {\boldsymbol q }}} \right)^{\rm T} {\rm{d}}x =\\ \qquad \dfrac{1}{2}EA\int_0^L \left( {{\boldsymbol q }_\Delta^{\rm T} {\boldsymbol S }^{\Delta {\rm T}}{\boldsymbol S }^\Delta {\boldsymbol q}_\Delta - 1} \right)\left( {{\boldsymbol S }_x^\Delta {\boldsymbol q }_\Delta } \right)\left( {\dfrac{\partial {\boldsymbol q }_\Delta }{\partial {\boldsymbol Q }}} \right)^{\rm T}{\boldsymbol S }_x^{\Delta {\rm T}} {\rm{d}}x $ | (16) |
其中
| $ \dfrac{\partial {\boldsymbol q }_\Delta }{\partial {\boldsymbol q }} = \left[ \!\!\begin{array}{c} 0_{1\times 12} \\ \dfrac{{\boldsymbol r }_x (0)^{\rm T}}{\left| {{\boldsymbol r }_x (0)} \right|} \cdot {\boldsymbol S }_x (0) \\ \int_0^1 \dfrac{{\boldsymbol r }_x ^{\rm T}}{\left| {{\boldsymbol r }_x } \right|} {\boldsymbol S }_x {\rm{d}}x \\ \dfrac{{\boldsymbol r }_x (L)^{\rm T}}{\left| {{\boldsymbol r }_x (L)} \right|} \cdot {\boldsymbol S }_x (L) \end{array}\!\!\right]=\left[\!\!\begin{array}{l} {\boldsymbol A } \\ {\boldsymbol B } \\ {\boldsymbol C } \\ {\boldsymbol D } \end{array}\!\!\right] $ | (17) |
上式中各分量可表达如下
| $ \left. \begin{array}{l} \mathit{\boldsymbol{A}} = {\boldsymbol 0_{1 \times 12}}, \mathit{\boldsymbol{B}} = [{\boldsymbol 0_{1 \times 3}}\;\;{\mathit{\boldsymbol{r}}_x}{\left( 0 \right)^{\rm{T}}}/\left| {{\mathit{\boldsymbol{r}}_x}\left( \boldsymbol 0 \right)} \right|{0_{1 \times 6}}]\\ \mathit{\boldsymbol{C}} = \int_0^1 {\frac{{\mathit{\boldsymbol{r}}_x^{\rm{T}}}}{{\left| {{\mathit{\boldsymbol{r}}_x}} \right|}}} {\mathit{\boldsymbol{S}}_x}{\rm{d}}x, \;\;\mathit{\boldsymbol{D}} = [{\boldsymbol 0_{1 \times 9}}\;\;{\mathit{\boldsymbol{r}}_x}{\left( L \right)^{\rm{T}}}/\left| {{\mathit{\boldsymbol{r}}_x}\left( L \right)} \right|] \end{array} \right\} $ | (18) |
新构造的一维杆单元只用于重新定义轴向应变,不直接参与动力学计算.也就是说,解耦模型仍以原ANCF模型为基础,单元广义坐标、质量矩阵、弯曲应变及其对应的广义弹性力均沿用原ANCF模型,只有轴向应变及其对应的广义弹性力发生改变,分别采用式(14)和式(16)进行计算.
3 算例分析本节通过大变形柔性梁的静力学和动力学仿真分析,对本文提出的解耦梁模型进行验证.
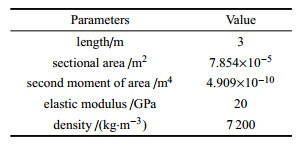
3.1 静力学分析柔性梁一端固定,另一端自由,分析其重力下的静平衡状态.具体参数如表 2所示.
| 表 2 柔性梁参数 Table 2 Parameters of flexible beam |
分别采用耦合梁单元(原ANCF梁单元)和解耦梁单元进行建模,给出两种模型的静力平衡位形曲线,如图 7所示.为了更加清晰地区分不同的位形曲线,将末端区域进行了局部放大.随着单元数目的增加,耦合梁的弯曲程度增大,位形曲线逐渐收敛,相邻位形曲线偏差越来越小,当单元数达到18时已具有很高精度.这是由于随着单元数目的增加,单元弯曲角减小,应变耦合引起的单元刚化效应减弱,导致梁的弯曲程度增大且逐渐收敛.对比解耦梁与耦合梁的位形曲线可知,3单元解耦梁位形曲线介于6和9单元耦合梁之间,6单元解耦梁位形曲线介于15和18单元耦合梁之间,因此解耦梁模型的精度远大于同等单元数目的耦合梁模型,具有更好的收敛性.

|
图 7 柔性梁平衡位形 Figure 7 Equilibrium configurations of flexible beam |
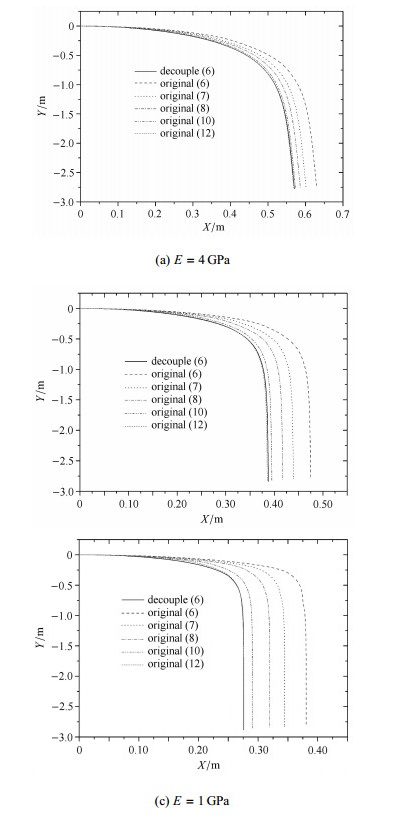
图 8给出了不同弹性模量下柔性梁的位形曲线,将6单元解耦梁和不同单元数的耦合梁进行了对比.在相同单元数下,解耦模型的精度明显高于耦合模型,随着单元数目增加,耦合梁的位形曲线逐渐接近解耦梁,当单元数达到12时,耦合梁与6单元解耦梁位形曲线接近,此时两者有着相近的计算精度.
|
图 8 不同弹性模量下柔性梁位形 Figure 8 Configurations of flexible beam with different elastic modulus |
另外,对比不同弹性模量下的梁位形曲线可知,弹性模量越小,耦合梁的精度越差,相同单元数下与解耦梁末端点位置相对误差分别为10.2%(
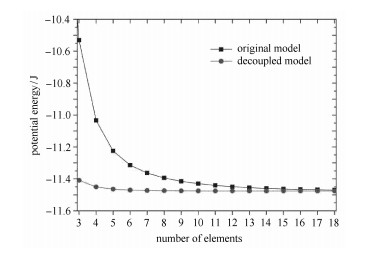
梁的静平衡位形随单元数目增多逐渐收敛,其收敛性可通过静平衡势能进行分析.柔性梁的静平衡势能等于应变能和重力势能之和,其中水平位置(
|
图 9 静平衡势能收敛性曲线 Figure 9 Convergence curves of static equilibrium energy |
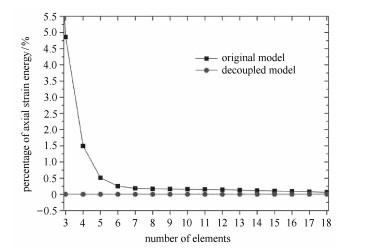
对比图 9和图 10可知,轴向应变能占总应变能的比重与静平衡势能有着相似的变化趋势,说明解耦模型与耦合模型收敛性的差异主要由轴向应变能引起.解耦梁的轴向应变能占比接近于零,几乎不随单元数目发生变化,而耦合梁的轴向应变能占比在单元数目较少时非常大,这种伪轴向应变能使单元刚化,是导致单元精度低、收敛性差的主要因素,而解耦模型消除了这种伪应变能,因此具有更高的精度.
|
图 10 轴向应变能占总应变能比重 Figure 10 Proportion of axial strain energy in total strain energy |
上述接近纯弯的耦合梁的轴向应变能主要是伪应变能,若柔性梁受拉力和弯矩共同作用,耦合梁的轴向应变能则包含拉力引起的应变能和应变耦合效应引起的伪应变能,解耦模型则无伪应变能.因此无论是在纯弯还是在受拉力和弯矩共同作用的情况下,解耦梁轴向应变能占总应变能比重都更小,且具有更好的收敛性.只是在纯弯的情况下该值接近于零,而在受拉力时,该值会随着拉力增大而逐渐增大.
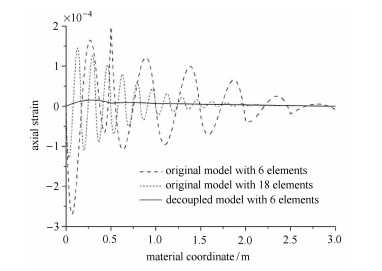
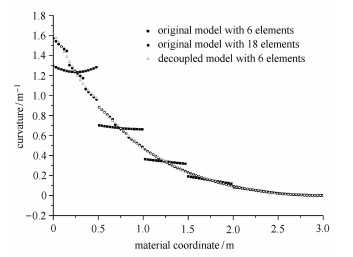
图 11和图 12对比了两种模型的轴向应变与曲率分布.由图 11可知,耦合梁的轴向应变呈现波动式分布,且波动峰值随着弯曲变形的减小而减小(如图 11).相比于6单元耦合梁模型,18单元耦合梁的轴向应变峰值更小、衰减更快,但仍大于解耦梁的轴向应变.正是由于这种轴向应变的波动式分布,使得梁的静平衡势能无法随单元数目增加而快速收敛.由图 12可知,耦合梁节点处的曲率存在明显的跳变,且跳变量随曲率的增大而增大.对比不同单元数目的耦合梁曲率可知,随着单元数目增多,曲率跳变量明显减小,曲率连续性更好.此外,相比于耦合梁,解耦梁的曲率具有更好的连续性,6单元解耦梁的曲率跳变量与18单元耦合梁的曲率跳变量相近,且不连续点更少,因此解耦模型能够提高节点处应变的连续性.
|
图 11 轴向应变对比 Figure 11 Comparison of axial strain |
|
图 12 曲率对比 Figure 12 Comparison of curvature |
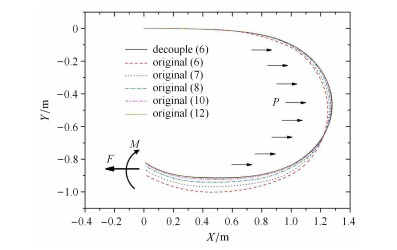
上述算例是几乎只受纯弯作用的悬臂梁,下面考虑拉力和弯矩共同作用的情况.柔性梁一端固定,另一端施加拉力
|
图 13 拉力和弯矩作用下的柔性梁位形 Figure 13 Configurations of flexible beam under tension and bending moment |
将6单元解耦模型与不同单元数的耦合模型进行对比可知,在相同单元数下,耦合梁弯曲程度小于解耦梁,随着单元数目增加,耦合梁位形逐渐接近解耦梁,在单元数达到12时,耦合梁与6单元解耦梁位形曲线几乎重合.因此6单元解耦梁与12单元耦合梁的计算精度相近,远大于6单元耦合梁的精度.该算例说明,除了在纯弯情况下,解耦模型在拉力和弯矩共同作用的情况下仍然适用.
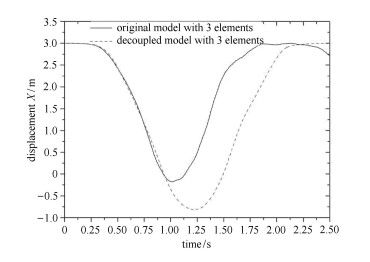
3.2 动力学分析本节进行柔性梁动力学分析,梁的具体参数如表 2所示.柔性梁一端固定,从水平位置以零初始速度自由下落,分别采用耦合梁模型和解耦梁模型进行动力学仿真. 图 14和图 15给出了3单元梁末端点在水平方向上的位移和速度曲线.由图 14可知,0.9 s前两种模型末端点位移曲线接近,1 s左右耦合梁的末端点位移首先达到峰值,而解耦梁末端点继续向
|
图 14 末端点位移(3单元) Figure 14 Displacement of endpoint (3 elements) |
|
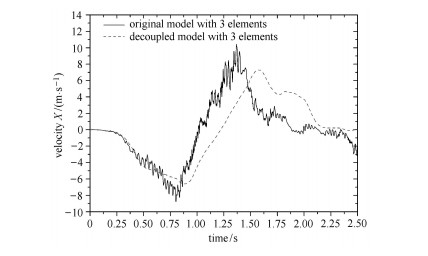
图 15 末端点速度(3单元) Figure 15 Velocity of endpoint (3 elements) |
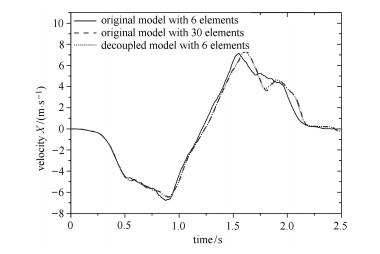
图 16和图 17为6和30单元模型仿真结果.相比于3单元模型,耦合梁和解耦梁末端点位移和速度曲线更为接近,其中30单元耦合梁和6单元解耦梁的位移和速度曲线几乎完全重合.耦合梁末端点速度不再有高频振动(如图 17),可知随着单元数量增加,应变耦合引起的刚化效应减弱.相比于6单元耦合梁,30单元耦合梁和6单元解耦梁一样,其末端点速度曲线在1.5 s后出现了一定波动,这是由于单元数增多后,应变耦合效应减弱,模型刚度减小,使得柔性梁摆动过程中的波动效应更加明显.

|
图 16 末端点位移(6和30单元) Figure 16 Displacement of endpoint (6 and 30 elements) |
|
图 17 末端点速度(6和30单元) Figure 17 Velocity of endpoint (6 and 30 elements) |
综上,单元应变解耦后,梁的运动范围增大,运动周期延长,消除了应变耦合效应引起的高频速度振动,在相同单元数目下具有更高的精度.
4 结论本文对ANCF索梁单元的应变耦合问题及模型解耦方法进行研究,得到如下结论:
(1)梁单元轴向应变与弯曲应变相互耦合,单元的弯曲变形会引起伪轴向应变,产生的伪应变能导致单元刚度大于理论值,且单元弯曲变形越大,模型失真越严重.
(2)构造了等效一维杆单元,基于该单元重新定义梁的轴向应变,实现了轴向应变与弯曲应变解耦,在此基础上重新推导广义弹性力,得到了梁的应变解耦模型.
(3)通过静力学和动力学仿真分析,对本文提出的解耦梁模型进行了验证.仿真结果表明:解耦梁模型消除了伪轴向应变,相比于原模型具有更好的收敛性和曲率连续性,此外,解耦梁模型消除了原模型中的高频速度振动,在相同单元数目下具有更高的精度.
| 1 | Shabana AA. Flexible multibody dynamics:review of past and recent developments. Multibody System Dynamics, 1997, 1 (2) : 189-222. DOI: 10.1023/A:1009773505418. |
| 2 | 田强.基于绝对节点坐标方法的柔性多体系统动力学研究与应用.[博士论文].武汉:华中科技大学, 2009 ( Tian Qiang. Flexible multibody dynamics research and application based on the absolute nodal coordinate method.[PhD Thesis]. Wuhan:Huazhong University of Science and Technology, 2009(in Chinese) ) http://www.oalib.com/references/16762580 |
| 3 | Shabana AA. An absolute nodal coordinate formulation for the large rotation and large deformation analysis of flexible bodies. Technical Report No. MBS96-1-UIC, Department of Mechanical Engineering, University of Illinois at Chicago, 1996 |
| 4 | Shabana AA. Definition of the slopes and the finite element absolute nodal coordinate formulation. Multibody System Dynamics, 1997, 1 (3) : 339-348. DOI: 10.1023/A:1009740800463. |
| 5 | Shabana AA. Definition of ANCF finite elements. Journal of Computational and Nonlinear Dynamics, 2015, 10 (5) : 054506. DOI: 10.1115/1.4030369. |
| 6 | 陈思佳, 章定国, 洪嘉振. 大变形旋转柔性梁的一种高次刚柔耦合动力学模型. 力学学报, 2013, 45 (2) : 251-256. ( Chen Sijia, Zhang Dingguo, Hong Jiazhen. A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45 (2) : 251-256. (in Chinese) ) |
| 7 | 章孝顺, 章定国, 洪嘉振. 考虑曲率纵向变形效应的大变形柔性梁刚-柔耦合动力学建模与仿真. 力学学报, 2016, 48 (3) : 1-11. ( Zhang Xiaoshun, Zhang Dingguo, Hong Jiazhen. Rigid-flexible coupling dynamic modeling and simulation with the longitudinal deformation induced curvature effect for a rotating flexible beam under large deformation. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48 (3) : 1-11. (in Chinese) ) |
| 8 | Shabana AA, Yakoub RY. Three dimensional absolute nodal coordinate formulation for beam elements:theory. Journal of Mechanical Design, 2001, 123 (4) : 606-613. DOI: 10.1115/1.1410100. |
| 9 | Yakoub RY, Shabana AA. Three dimensional absolute nodal coordinate formulation for beam elements:implementation and applications. Journal of Mechanical Design, 2000, 123 (4) : 614-621. |
| 10 | Gerstmayr J, Shabana AA. Analysis of thin beams and cables using the absolute nodal coordinate formulation. Nonlinear Dynamics, 2006, 45 (1-2) : 109-130. DOI: 10.1007/s11071-006-1856-1. |
| 11 | 朱大鹏, 路英杰, 汤家力等.大变形索梁单元在多体动力学框架下的应用//2007全国结构动力学学术研讨会论文集, 南昌, 2007年11月 ( Zhu Dapeng, Lu Yingjie, Tang Jiali, et al. Application of large deformation cable beam element in multibody dynamics//Proceedings of the 2007 National Symposium on Structural Dynamics, Nanchang, 2007-11(in Chinese). ) |
| 12 | Dombrowski SV. Analysis of large flexible body deformation in multibody systems using absolute coordinates. Multibody System Dynamics, 2002, 8 (4) : 409-432. DOI: 10.1023/A:1021158911536. |
| 13 | Liu C, Tian Q, Hu HY. New spatial curved beam and cylindrical shell elements of gradient-deficient absolute nodal coordinate formulation. Nonlinear Dynamics, 2012, 70 (3) : 1903-1918. DOI: 10.1007/s11071-012-0582-0. |
| 14 | Dmitrochenko O, Mikkola A. Digital nomenclature code for topology and kinematics of finite elements based on the absolute nodal coordinate formulation. Journal of Multi-body Dynamics, 2011, 225 (1) : 34-51. |
| 15 | Kerkkänen KS, García-Vallejo D, Mikkola AM. Modeling of beltdrives using a large deformation finite element formulation. Nonlinear Dynamics, 2006, 43 (3) : 239-256. DOI: 10.1007/s11071-006-7749-5. |
| 16 | ČeponG, BoltežarM. Dynamics of a belt-drive system using a linear complementarity problem for the belt-pulley contact description. Journal of Sound and Vibration, 2009, 319 (3) : 1019-1035. |
| 17 | ČeponG, ManinL, BoltežarM. Introduction of damping into the flexible multibody belt-drive model:a numerical and experimental investigation. Journal of Sound and Vibration, 2009, 324 (1) : 283-296. |
| 18 | Lugris U, Escalona J, Dopico D, et al. Efficient and accurate simulation of the cable-pulley interaction in weight-lifting machines//1st Joint International Conference on Multibody System Dynamics, Lappeenranta, Finland, 2010 |
| 19 | Kim KW, Lee JW, Yoo WS. The motion and deformation rate of a flexible hose connected to a mother ship. Journal of Mechanical Science and Technology, 2012, 26 (3) : 703-710. DOI: 10.1007/s12206-011-1202-5. |
| 20 | Tur M, García E, Baeza L, et al. A 3D absolute nodal coordinate finite element model to compute the initial configuration of a railway catenary. Engineering Structures, 2014, 71 : 234-243. DOI: 10.1016/j.engstruct.2014.04.015. |
| 21 | Vohar B, Kegl M, Ren Z. Implementation of an ANCF beam finite element for dynamic response optimization of elastic manipulators. Engineering Optimization, 2008, 40 (12) : 1137-1150. DOI: 10.1080/03052150802317457. |
| 22 | Sanborn GG, Choi J, Choi JH. Curve-induced distortion of polynomial space curves, flat-mapped extension modeling, and their impact on ANCF thin-plate finite elements. Multibody System Dynamics, 2011, 26 (2) : 191-211. DOI: 10.1007/s11044-011-9248-9. |
| 23 | Sopanen JT, Mikkola AM. Description of elastic forces in absolute nodal coordinate formulation. Nonlinear Dynamics, 2003, 34 (1-2) : 53-74. |
| 24 | Schwab AL, Meijaard JP. Comparison of three-dimensional flexible beam elements for dynamic analysis:finite element method and absolute nodal coordinate formulation//ASME 2005 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. Long Beach, California, USA:ASME, 2005:1341-1349 |
| 25 | García-Vallejo D, Mikkola AM, Escalona JL. A new locking-free shear deformable finite element based on absolute nodal coordinates. Nonlinear Dynamics, 2007, 50 (1-2) : 249-264. DOI: 10.1007/s11071-006-9155-4. |
| 26 | Gerstmayr J, Matikainen MK, Mikkola AM. A geometrically exact beam element based on the absolute nodal coordinate formulation. Multibody System Dynamics, 2008, 20 (4) : 359-384. DOI: 10.1007/s11044-008-9125-3. |
| 27 | Nachbagauer K, Gruber P, Gerstmayr J. Structural and continuum mechanics approaches for a 3D shear deformable ANCF beam finite element:application to static and linearized dynamic examples. Journal of Computational and Nonlinear Dynamics, 2013, 8 (2) : 021004. |
| 28 | 于洋, 宝音贺西, 李俊峰. 空间飞网抛射展开动力学建模与仿真. 宇航学报, 2010, 31 (5) : 1289-1296. ( Yu Yang, Baoyin Hexi, Li Junfeng. Modeling and simulation of projecting deployment dynamics of space webs. Journal of Astronautics, 2010, 31 (5) : 1289-1296. (in Chinese) ) |
| 29 | 张江.空间绳网捕获过程碰撞动力学研究.[硕士论文].哈尔滨:哈尔滨工业大学, 2015 ( Zhang Jiang. Contact dynamics of space net on capturing target.[Master Thesis]. Harbin:Harbin Institute of Technology, 2015(in Chinese). ) |
| 30 | Zhang Y, Wei C, Pan D, et al. A dynamical approach to space capturing procedure using flexible cables. Aircraft Engineering and Aerospace Technology, 2016, 88 (1) : 53-65. DOI: 10.1108/AEAT-07-2014-0107. |
| 31 | Tang JL, Ren GX, Zhu WD, et al. Dynamics of variable-length tethers with application to tethered satellite deployment. Communications in Nonlinear Science and Numerical Simulation, 2011, 16 (8) : 3411-3424. DOI: 10.1016/j.cnsns.2010.11.026. |
†. China Academy of Space Technology, Beijing 100086, China