†. 北京航空航天大学航空科学与工程学院, 北京 100191
空间飞行器展开锁定机构是空间飞行器机构领域的一个重要组成部分[1-2],在各类展开机构中[3-7],仅STACER (the spiral tube and actuator for controlled extension and retraction)伸展机构在国外的航天器上已经有650多次在轨应用[8-13],在1996--2015年间,美国航空航天局和欧洲航天局就有几十颗探测卫星采用了此类伸展机构,另外,因其质量轻、收拢包络尺寸小(安装面积小)、自驱动(减少对卫星平台能源、电控系统的需求)等特点,受到微小卫星的青睐,如美国航空航天局正在研制的TERSat、GOTHAM和CENEMA卫星均采用STACER作为主载荷的伸展机构[14-19].我国航天五院于2012年在电磁监测试验卫星上率先开始STACER伸展机构研制;近来,又成功将其应用于深空探测器领域.
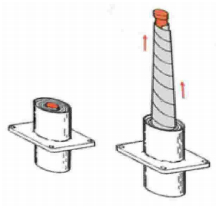
STACER是一种由超长金属薄带材经冷加工制成螺旋管状伸展机构,按其使用方式,分成单次和可重复使用两种形式,分别如图 1和图 2(a)所示(摘自文献[11]),两种形式的主要区别在于可重复使用的STACER带有辅助展开装置,如图 2(b)所示.通常辅助装置由两组间隔一定距离的支撑轮组构成,其主要作用是对螺旋管提供横向支撑,并施加一组径向力,使钢带逐圈抱紧从而形成一定的刚度.
|
图 1 单次使用STACER Figure 1 One-time application STACER |

|
图 2 可重复使用STACER及其伸展辅助装置 Figure 2 Repeatable rollout STACER and its deployment assist device |
从目前来看,关于STACER的力学、机械性能的理论分析方法以及研究文献非常少见,一是西方的技术封锁,二是其理论研究的难度. STACER的伸展过程中,薄壳的挠度达到其厚度的几百倍,是一个大挠度、大应变的非线性问题,并且,边界条件与研究对象持续变化,致使常用的非线性商业软件和数值方法无法直接应用.美国UCB以及MIT大学从20世纪70年代开展STACER的研究以来,至今尚未公开发表相应的理论与实验研究方法.在国内,吴江等[20-25]对一次性伸展机构的伸展特性进行了理论与实验研究,取得了一系列成果,根据展开段钢带螺旋角的变化规律提出了逐圈和同步展开模式,并给出了展开模式与螺旋角的依赖关系.针对展开过程中,钢带构型、长度不断变化,吴江等研究者将STACER的伸展过程视为一个动力学过程,应用多体动力学模型以及有限元方法有效地处理了这一问题,从最新的研究结果来看,对伸展位移至少可以准确地仿真到700 mm[20].实际上,从薄壳的物理、几何、平衡方程出发,利用有限元方法进行数值求解此类问题,其主要困难在于问题的强非线性[26-30],并且还是一个动态问题,每增加一个伸展步长,都要求解一个"静态"非线性问题;同时,受钢带厚度(0.1 mm~0.15 mm)制约,钢带网格单元不能过疏,这又进一步加剧了数值仿真的困难.这里提出了一种利用势能极小原理,以螺旋管钢带的变形特性为基础,计算STACER伸展力的方法.首先,根据钢带的变形特性,构造出钢带恰当的可能变形函数空间;其次,找出钢带的主应变方向,并根据主应变计算钢带的变形能;最后,依据最小势能原理以及变分方法,给出满足边界条件的钢带真实的变形函数以及伸展力规律.
1 STACER的工作原理对于图 1和图 2所示两种形式的STACER,当完全伸展或全收拢时,螺旋管的构型相同;完全收拢时钢带形状为柱面,完全伸展时呈柱面或小锥角锥面,取决于使用工况的实际要求.在两个柱面之间,钢带的形状由锥面过渡,这里也将其称为过渡段,如图 3所示.对于单次使用STACER,仅有过渡和收拢段;对于可重复使用STACER,螺旋管穿过约束轮组后可以认为钢带达到完全伸展状态.

|
图 3 螺旋管的变形过程 Figure 3 The deformation procedures of the spiral tube |
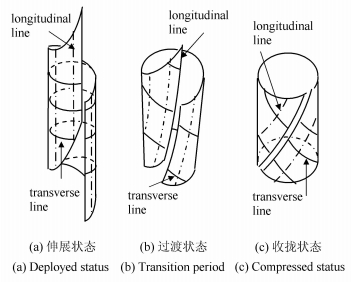
与普通螺旋弹簧一样,螺旋管也是利用螺旋钢带的变形产生伸展力,但是钢带与弹簧丝的变形方式有着本质不同.弹簧丝主要变形是扭转,而钢带的变形主要是弯曲.为了说明这一点,通过钢带上的物质(或随体)标记线来考察钢带的变形,如图 4所示.其中图 4(a)、图 4(b)以及图 4(c)分别表示螺旋管在完全伸展、过渡以及完全收拢阶段的状态.这里将图 4(a)所示的钢带形状视为初始状态,在螺旋管上,分别沿柱(锥)面的母线方向和周向各刻画一组随体标记线,并将这两组标记线分别称为竖纹和横纹.当螺旋管沿轴向压缩时,竖纹由直线先变成锥面螺旋线,再变成柱面螺旋线;而横纹则是由圆变成锥面或柱面螺旋线.其中,竖纹曲率逐步增加,横纹曲率逐步减小.其他纹路也是一样,曲率随着螺旋管的形状的变化而变化,或者说每条纹路的弯曲程度都在变化,这一变化可以利用钢带形状函数求出.
|
图 4 钢带随体标记线的变形过程 Figure 4 The deformation of lines marked on the steel strip |
对于两种形式的STACER,可以认为仅是过渡段不同,一种是变化的而另一种是固定的,这里将着重研究可重复使用STACER伸展力的计算方法.
2 钢带可能的形变函数空间为了构造恰当的钢带可能变形函数空间,首先利用已有的几种规格的螺旋管及其收纳罐(圆杯状)试件,进行了螺旋管的收拢、伸展试验,以观测钢带形状的变化.结果表明钢带在过渡段形状为变参数锥面,在收拢和伸展段为柱面.考虑到在实际工程应用时,钢带材质以及螺旋管尺寸选型会有所变化,对上述结论在选型范围内的一般性进行了验证.为此,选用几种弹性模量、泊松比不同的材料,如塑料膜、铜板印刷纸、薄铝板、薄铜板以及普通薄钢板,制成多种尺寸规格的螺旋管进行实验,均得到了同样的结果;因此,这里将过渡段钢带可能变形函数空间取为变参数的锥面.
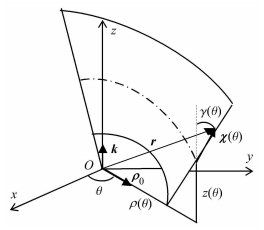
2.1 过渡段钢带曲面方程尽管每段钢带都可以用锥面拟合,但除了锥角外还需给出锥面与钢带的贴合位置,直接用锥面方程描述钢带形状并不方便.考虑到锥面是一种可展直纹曲面,不失一般性,这里用可展直纹曲面方程,将过渡段钢带的形状函数写成如下形式
| $ \boldsymbol{ r}(\theta ) = \boldsymbol{\rho}\left( \theta \right)\boldsymbol{\rho}_0 + z(\theta )\boldsymbol{ k} + \zeta \boldsymbol{\chi} (\theta ) $ | (1) |
| $ \dfrac{\boldsymbol{d}(\boldsymbol{\rho} \left( \theta \right)\boldsymbol{ \rho}_0 + z(\theta )\boldsymbol{ k})}{\boldsymbol{d}\theta } \cdot \Big (\dfrac{\zeta \boldsymbol{d}\boldsymbol{ \chi }(\theta )}{\boldsymbol{d}\theta }\times \zeta \boldsymbol{ \chi }(\theta )\Big ) = {\bf 0} $ | (2) |
其中,
|
图 5 钢带曲面几何参数 Figure 5 The geometric parameters of the steel strip |
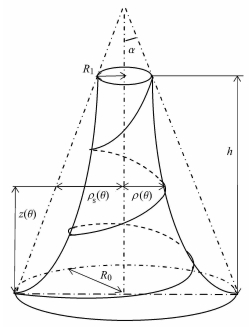
过渡段钢带中线为一条螺旋曲线,受支撑轮组和收纳仓约束,满足如下几何边界条件
| $ \rho\left( {\theta _0 } \right) = R_0, \quad \rho\left( {\theta _1 } \right) = R_1 $ | (3) |
其中,
| $ \left( {R_0 - \rho_{\rm s} (\theta )} \right) /z(\theta ) = \tan \alpha $ | (4) |
|
图 6 可能的中线函数 Figure 6 The possible middle line |
通过摄动圆锥母线,中线的可能函数表示为
| $ \rho(\theta ) =\rho_{\rm s} (\theta ) - a\sin \left[{{\pi (\rho_{\rm s} (\theta )-R_1 )} /{(R_0-R_1 )}} \right] $ | (5) |
其中,a为待定参数.
2.3 直纹锥角的可能函数空间在支撑轮组和收纳仓的约束下,螺旋管钢带的锥角在过渡段的两端均为零,故将锥角函数设成
| $ \gamma \left( \theta \right) = b / (c - \theta )\sin [\pi (\theta-\theta _0 ) / (\theta _1-\theta _0 )] $ | (6) |
式中, b, c以及
对于单次使用的STACER,由于没有轮组约束,螺旋管在伸展端的锥角不为零,而锥角变化率为零,因此,可将其锥角函数假设成
| $ \gamma \left( \theta \right) = \dfrac{b}{c - \theta }\sin \left[{\dfrac{\pi (\theta-\theta _0 )}{2(\theta _1-\theta _0 )}} \right] $ | (7) |
从方程(1)和(2)可以看出,给定中线和锥角函数后,中线高度可以由方程(2)导出.由于求解此约束方程相对困难,按下述等价的条件导出中线高度:钢带曲面上任意两条相交的物质(随体)标记线,在交点处的切线之间的夹角一直保持不变.其力学含义则是钢带面内剪切变形可以忽略.
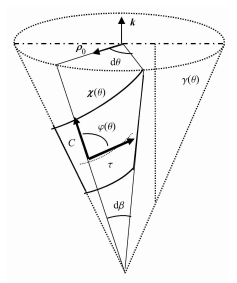
任选一段钢带,如图 7所示,设中线在C点处的单位切线向量为
| $ \boldsymbol{ \tau } \cdot \boldsymbol{ \chi }(\theta ) = \cos \varphi (\theta ) $ | (8) |
|
图 7 卷曲成锥面的钢带 Figure 7 Steel strip in cone surface |
利用中线的矢量方程,其切线向量可以表示为
| $ \boldsymbol{ \tau } = \dfrac{ \boldsymbol{d} \rho(\theta )}{\boldsymbol{d} s}\boldsymbol{ \rho}_0 + \rho(\theta )k\times \boldsymbol{ \rho}_0 + \dfrac{\boldsymbol{d} z(\theta )}{\boldsymbol{d} s}\boldsymbol{ k} $ | (9) |
直纹向量可表示为
| $ \boldsymbol{ \chi }(\theta ) = \cos \gamma (\theta )\boldsymbol{ k} + \sin \gamma (\theta )\boldsymbol{ r}_0 $ | (10) |
将方程(9)和式(10)代入式(8)可以得到
| $ \dfrac{\boldsymbol{d} \rho(\theta )}{\boldsymbol{d} s} \sin \gamma (\theta ) + \dfrac{\boldsymbol{d} z(\theta )}{\boldsymbol{d} s}\cos \gamma (\theta ) = \cos \varphi (\theta ) $ | (11) |
若要由式(11)解出中线高度
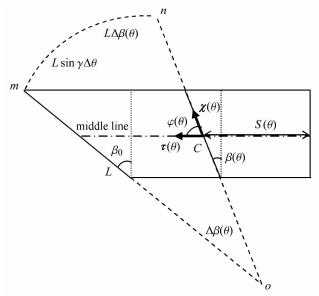
|
图 8 展成平面的钢带 Figure 8 Steel strip in flat surface |
现在考察
| $ \beta (\theta ) = \pi / 2 - \varphi (\theta ) $ | (12) |
将
| $ \boldsymbol{d}\beta (\theta ) / \boldsymbol{d}\theta = \sin \gamma (\theta ) $ | (13) |
因此,当锥角
如第一节所述,钢带上任意一条随体标记线的曲率,随着钢带的变形而变化.当钢带从零应变的初始状态变化到某一形状时,在各方向的标记线中,曲率变化最大的标记线所处的方向上,钢带的应变最大,因此是一个主应变方向,另一个主应变方向与之正交.
为了描述最大主应变方向,将图 5(a)所示的一节螺旋管展开如图 9所示.在图 9中,设AB为任意一条随体标记线,与横纹EF夹角为
| $ k_x = \cos ^2(\psi + \lambda (\theta ))/(r(\theta ) + x\sin \gamma (\theta )) $ | (14) |
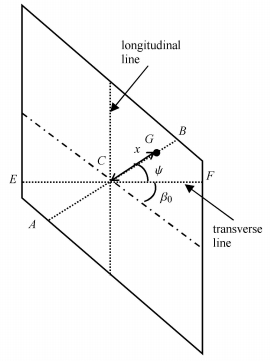
|
图 9 钢带随体标记线 Figure 9 The marked line on steel strip |
其中,
| $ k_1 = {\cos ^2\psi } /{R_1 } $ | (15) |
从完全伸展状态压缩至在一般状态时,G处的曲率变化为
| $ \delta k_x = k_x - k_1 = \dfrac{(r - \gamma x)\cos ^2\psi - R_1 \cos ^2 (\psi + \lambda (\theta ))}{(r - \gamma x)R_1 } $ | (16) |
将式(16)对
| $ (r - \gamma x)\sin 2\psi - R_1 \sin 2 (\psi + \lambda (\theta )) = 0 $ | (17) |
利用方程(17)可以求出使曲率变化取极值的两个方向
| $ k_x = \cos ^2(\psi _1 + \lambda (\theta ))/(r(\theta ) + x\sin \gamma (\theta )) \\ k_{x \bot } = \sin ^2(\psi _1 + \lambda (\theta )) /(r(\theta ) + x\sin \gamma (\theta )) $ | (18) |
G点处两个主应变沿厚度方向的分布分别为
| $ \varepsilon _x = \delta k_x z\, , \quad \varepsilon _{x \bot } = \delta k_{x \bot } z $ | (19) |
其中,z为钢带沿厚度方向到中性层的距离.
在特殊情况下,如果螺旋管在伸展和收拢状态下柱面半径满足
| $ \psi _1 = 0.484\beta _0 - 0.688 $ | (20) |
按钢带曲面函数,以及式(19)得到钢带上各点的主应变后,用应变分量表示的钢带变形能为
| $ V_{\rm E} = \dfrac{E}{2(1 + \mu )}\iiint \Big[\dfrac{\mu }{1- 2\mu }(\varepsilon _x + \varepsilon _{ \bot x} )^2 + \\ \qquad (\varepsilon _{x}^2 + \varepsilon _{ \bot x}^2 )\Big] \boldsymbol{d} x\boldsymbol{d} y\boldsymbol{d} z $ | (21) |
其中,E和
一般情况下,伸展力的计算过程如下:(1)确定a, b, c和
上述步骤中,第二步计算,即,确定钢带初始形状的计算量最大.在后续的计算中,仅需在上一个形状函数的较小邻域内搜索,即可得到当前的钢带形状函数.
如果假设完全伸展时,钢带的初始应力为零,完全收拢时钢带呈柱面,且
| $ F = \dfrac{Ewt^3}{24(1 + \mu )R_1^3 \sin \beta _{0} } \Bigg [\dfrac{\mu (1- \cos \beta _{0} )^2}{1- 2\mu } + \\ \qquad (\cos ^2\psi _{1} - \cos ^2(\psi _{1} + \beta _{0} )\cos \beta _{0} )^2 + \\ \qquad (\sin ^2\psi _{1} -\sin ^2(\psi _{1} + \beta _{0} )\cos \beta _{0} )^2 \Bigg] $ | (22) |
其中,w和t分别为钢带的宽度和厚度,
取参数w=126 mm,t=0.12 mm,
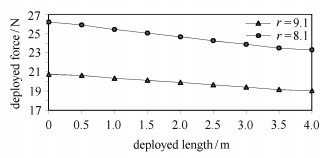
|
图 10 伸展力随伸展长度的变化 Figure 10 The deploying force depended on deploying length |
为了与现有的其他计算结果进行比较,与文献[7]中的算例进行了对比.钢带参数:w=126 mm, t=0.12 mm,

|
图 11 伸展力随随螺旋角的变化 Figure 11 The deploying force depended on spiral angle |
利用薄壁钢带螺旋管伸展过程的变形特性, 构造了钢带形状恰当的可能函数空间, 并以此找出最大主应变方向和由主应变表示的钢带变形能, 再利用最小势能原理确定钢带的实际形状、变形能以及伸展力.由于所构造的形状函数以及最大主应变方向,在完全收拢与完全展开状态下有准确的解析解,因此,所构造的形状函数空间的恰当性以及准确性得已验证.与直接求解大应变大挠度弹性薄板的完全方程的数值方法相比,计算过程得以简化.由于钢带形状函数为借助少量待定参数的解析式,为STACER伸展力特性、伸展力对结构参数的依赖关系的定量分析提供了方便条件.
| 1 | 马兴瑞, 于登云, 孙京, 等. 空间飞行器展开与驱动机构研究进展. 宇航学报, 2006, 27 (6) : 1123-1131. ( Ma Xingrui, Yu Dengyun, Sun Jing, et al. The researching devolvement of spacecraft deployment and driving mechanism. Journal of Astronautics, 2006, 27 (6) : 1123-1131. (in Chinese) ) |
| 2 | 从强, 罗敏, 李伟杰. 空间机构技术发展趋势及展望. 载人航天, 2016, 22 (1) : 1-8. ( Cong Qiang, Luo Min, Li Weijie. Development trends and prospects of space mechanism. Manned Spaceflight, 2016, 22 (1) : 1-8. (in Chinese) ) |
| 3 | 丁峻宏, 咸奎成, 韩轩, 等. 空间豆荚杆机构收展过程的并行仿真计算. 宇航学报, 2011, 32 (3) : 676-682. ( Ding Junhong, Xian Kuicheng, Han Xuan, et al. Parallel computing for simulation of stowing and deployment process of space lenticular boom mechanism. Journal of Astronautics, 2011, 32 (3) : 676-682. (in Chinese) ) |
| 4 | 胡海岩, 田强, 张伟, 等. 大型网架式可展开空间结构的非线性动力学与控制. 力学进展, 2013, 43 (4) : 390-414. ( Hu Haiyan, Tian Qiang, Zhang Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes. Advances in Mechanics, 2013, 43 (4) : 390-414. (in Chinese) ) |
| 5 | 赵将, 刘铖, 田强, 等. 黏弹性薄膜太阳帆自旋展开动力学分析. 力学学报, 2013, 45 (5) : 1-9. ( Zhao Jiang, Liu Cheng, Tian Qiang, et al. Dynamic analysis of spinning deployment of a solar sail composed of viscoelastic membranes. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45 (5) : 1-9. (in Chinese) ) |
| 6 | 曹登庆, 初世明, 李郑发, 等. 空间可展机构非光滑力学模型和动力学研究. 力学学报, 2013, 45 (1) : 3-15. ( Cao Dengqing, Chu Shiming, Li Zhengfa, et al. Study on the non-smooth mechanical models and dynamics for space deployable mechanisms. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45 (1) : 3-15. (in Chinese) ) |
| 7 | 文浩, 陈辉, 金栋平, 等. 带可控臂绳系卫星释放及姿态控制. 力学学报, 2012, 44 (2) : 408-414. ( Wen Hao, Chen Hui, Jin Dongping, et al. Deployment and attitude control of tethered subsatellite with controllable arm. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44 (2) : 408-414. (in Chinese) ) |
| 8 | Surrey Space Centre University of Surrey. SSTL-Weitzmann 6m deployable boom. http://www.sstl.co.uk. 2001 |
| 9 | Bale S, Ullrich R, Goetz K, et al. The electric antennas for the STEREO-WAVES experiment. Space Sci Rev, 2008, 136 : 529-547. DOI: 10.1007/s11214-007-9251-x. |
| 10 | Ullrich R, McCauley J, Turin P, et al. Stacer driven deployment:the stereo impact boom//Proceedings of the 38th Aerospace Mechanisms Symposi-um, Langley Research Center, 2006 |
| 11 | David A, Joshua C, Gregory D. Instrument boom mechanisms on the THEMIS satellites magnetometer, radial wire, and axial booms. Space Sci Rev, 2008, 141 : 185-211. DOI: 10.1007/s11214-008-9386-4. |
| 12 | Michael A, Brown A. Deployable mast for solar sails in the range of 100-1000 m. Advances in Space Research, 2011, 48 : 1747-1753. DOI: 10.1016/j.asr.2011.01.014. |
| 13 | Omer S. Deployment analysis of a self-deployable composite boom. Composite Structures, 2009, 89 : 374-381. DOI: 10.1016/j.compstruct.2008.08.012. |
| 14 | David P, Robert B, Robert W. Deployment mechanisms on the fast satellite:magnetometer, radial wire, and axial booms. Space Science, 2001, 98 : 93-111. DOI: 10.1023/A:1013183725161. |
| 15 | Clements E, Alvisio B, Babuscia A. TERSat:trapped energetic radiation satellite//Proc. of 26th Annual AIAA/USU Conference on Small Satellites, 2012 |
| 16 | Gökhan K, Eres S. Deployable space structures//Proceedings of the 4th international conference on recent advances in space technologies, Istanbul, 2009, 131-138 |
| 17 | Davis VA, Mandell MJ, Baker NR. Surface-charging analysis of the radiation belt storm probe and magnetospheric multi-scale spacecraft. IEEE Transactions on Plasma Science, 2012, 40 (2) : 262-273. DOI: 10.1109/TPS.2011.2178615. |
| 18 | Preliminary Design Review. GOTHAM boom. http://claspresearch.engin.umich.edu/gotham. 2012 |
| 19 | Greschik, G. The cord mat sail-concept, mechanics and design example//Proc. of 46th AIAA Structures, Structural Dynamics & Materials Conference, 18-21 April 2005. AIAA 2005-2049, 2005 |
| 20 | 吴江.卷筒式伸杆展开特性与推力研究.[博士论文].北京:清华大学, 2016 ( Wu Jiang. Research on the deploying characteristic and force of spiral tube.[PhD Thesis]. Beijing:Tsinghua University, 2016 (in Chinese) ) |
| 21 | 吴江, 赵治华, 任革学, 等. 多体动力学热-结构耦合圆管单元及其应用. 工程力学, 2013, 30 (11) : 28-35. ( Wu Jiang, Zhao Zhihua, Ren Gexue, et al. Thermal-structural coupled tube element of multibody dynamics and its application. Engineering Mechanics, 2013, 30 (11) : 28-35. (in Chinese) ) |
| 22 | 吴江, 周刚, 赵治华等.星载卷筒式伸杆展开过程动力学研究//可展开空间结构学术会议, 西安, 2014 ( Wu Jiang, Zhou Gang, Zhao Zhihua, et al. Research on the dynamics of onboard spiral tube//Proc. Academic Conference of Developable Space Structure, Xi'an, 2014(in Chinese) ) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-AGLU201410001072.htm |
| 23 | 吴江, 尹立新, 杨黔龙等.星载卷筒式展开机构的多体动力学建模//中国力学大会, 西安, 2014 ( Wu Jiang, Yin Lixin, Yang Qianlong, et al. Multi-body dynamics modeling of onboard spiral tube//China Mechanical Assembly, Xi'an, 2014(in Chinese) ) |
| 24 | 吴江, 尹立新, 杨黔龙等.卷筒式伸杆收展过程半径变化规律//中国力学大会, 上海, 2015 ( Wu Jiang, Yin Lixin, Yang Qianlong, et al. The radius variation of onboard spiral tube//China Mechanical Assembly, Shanghai, 2015(in Chinese) ) |
| 25 | Wu J, Zhao ZH, Ren GX. Multibody analysis of the force in deploying booms. Journal of Guidance Control and Dynamics, 2013, 36 : 1881-1886. DOI: 10.2514/1.60296. |
| 26 | Christoph S, Lars H, Elmar B. Structural engineering on deployable CFRP booms for a solar propelled sailcraft. Acta Astronautica, 2006, 58 : 185-196. DOI: 10.1016/j.actaastro.2005.09.011. |
| 27 | Joachim B, Marco S, Martin W. Ultralight deployable booms for solar sails and other large gossamer structures in space. Acta Astronautica, 2011, 68 : 984-992. DOI: 10.1016/j.actaastro.2010.09.005. |
| 28 | Puig L, Barton A, Rando N. A review on large deployable structures for astrophysics missions. Acta Astronautica, 2010, 67 : 12-26. DOI: 10.1016/j.actaastro.2010.02.021. |
| 29 | 杨慧, 郭宏伟, 王岩, 等. 三棱柱伸展臂超弹性铰链的力学建模与分析. 宇航学报, 2016, 37 (3) : 275-282. ( Yang Hui, Guo Hongwei, Wang Yan, et al. Mechanical modeling and analysis for hyperelastic hinge in a triangular prism deployable mast. Journal of Astronautics, 2016, 37 (3) : 275-282. (in Chinese) ) |
| 30 | 王有, 罗忠, 曲涛, 等. 薄壁构件试验模型的动力学相似设计方法. 航空发动机, 2016, 42 (1) : 32-36. ( Wang You, Luo Zhong, Qu Tao, et al. Dynamic similitude design method of experimental models for thin walled structures. Aeroengine, 2016, 42 (1) : 32-36. (in Chinese) ) |
†. School of Aeronautic Science and Engineering, Beijing University of Aeronautics and Astronautics, Beijing 100191, China

