†. 北京信息科技大学理学院, 北京 100192
随着航天科学技术的不断发展,载人航天技术作为当今世界高新技术密集的综合性尖端科学技术之一,受到了越来越多的科学家和研究人员的广泛关注.早在1992年我国载人航天工程立项之前,就有研究人员开始探索失重状态下宇航员的空间运动规律,从而重新引起了对自由下落猫的四肢先着地现象的深入研究.对这一现象的讨论可以追溯到19世纪末期. Guyou首先解释了猫在空中的转体运动[1]. McDonald[2]从生理学的角度详细论述了Guyou提出的"四肢开合"的论点.文献[3]提出用尾巴向反方向急速旋转从而实现猫躯体翻转的观点.不过无尾猫也能完成转体的实验推翻了这一解释. Kane等[4]将猫的前后脊柱简化为两个轴对称刚体,将猫的腰部作为两刚体的连接铰点,建立其运动方程,并通过数值计算发现,仿真结果与实验摄影记录十分吻合.刘延柱[5]选取了类似Kane的模型,研究了猫体的非轴对称性,且重新选择角度坐标推导出的非线性微分方程存在解析积分,论述了落体猫转体运动的一般规律. Fernandes等[6]基于Ritz近似理论,针对两种双刚体三维模型的运动规划设计了控制算法,发现其中一种仿真结果与实际的猫落体轨迹是一致的.戈新生等[7-9]基于最优控制理论,分别利用拟牛顿算法、Ritz近似理论和样条逼近的粒子群算法研究了落体猫的非完整运动规划问题. Iwai等[10]将落体猫简化为由铰连接的两个轴对称圆柱体,并将模型转化为一个定义在形状空间余切丛上的端口受控哈密顿系统,在系统角动量为零时,通过对约束方程积分从而获得猫下落的姿态运动过程. Zhen等[11]基于Udwadia-Kalaba理论,把猫落体模型简化为一个约束离散动态系统,推导出Udwadia-Kalaba方程的显式解析形式,通过数值计算验证了猫转体的现象.
自由下落猫的转体运动方程是由角动量方程不可积而引起的一个非完整运动方程. Brockett等[12]最早系统地阐述了无漂移非完整系统的最优控制问题.近年来,随着计算机技术的快速发展,伪谱法已经成为数值求解最优控制问题中的一种重要方法[13-26].其基本原理是通过采用全局插值多项式在一系列正交点上建立系统近似的状态变量和控制输入变量,从而把求解最优控制问题转化为求解非线性规划问题. Benson等[13-14]基于Gauss伪谱法求解最优控制问题时提出并证明了Gauss伪谱协态变量映射定理. 2000年Fahroo等[15-16]采用Chebyshev伪谱法求解了一般的Bozal型最优控制问题并于10年后给出了协态变量估计的详细证明. Tang等[17]基于Chebyshev-Gauss伪谱法研究了一般的最优控制问题并严格推导了其Karush-Kunn-Tucker (KKT)条件.雍恩米等[18-19]采用Gauss伪谱法求解了高超声速飞行器滑翔式再入的快速轨迹优化问题.霍明英[20]应用Gauss伪谱法研究了电动帆航天器在以火星、谷神星以及太阳系边界探测任务中的轨迹优化问题.李适等[21-22]基于Gauss伪谱法探讨了自由漂浮空间机器人从初始姿态到达目标姿态的最优轨迹.彭祺擘等[23-24]采用Gauss伪谱法讨论了登月飞行器定点软着陆以及月面软着陆过程发生故障后的应急上升轨道优化问题.庄宇飞等[25-26]结合粒子群算法和Legendre~伪谱法研究了欠驱动航天器的姿态运动规划问题.
本文基于自由落体猫的转体运动方程,采用Gauss伪谱法和直接打靶法相结合的混合优化策略,研究下落猫的姿态最优控制问题.首先,采用Gauss伪谱法将猫落体的非完整运动规划问题离散为非线性规划问题,由于Gauss伪谱法在较少Legendre-Gauss (LG)点时能获得较高的精度,并对初值敏感度较低,因此选择较少节点计算控制变量的可行解;然后通过三次样条插值,按照LG点的分布方式求取较多节点对应的控制变量值;最后将插值得到的控制变量作为直接打靶法的初值代入sequential quadratic programming (SQP)算法,从而求解得到最优的控制输入,再代入动力学方程,积分便可得到状态变量的值,从而规划猫从下落时的初始位形转体到落地时的目标位形(四肢着地)的最优姿态运动曲线,文末给出其数值仿真算例.
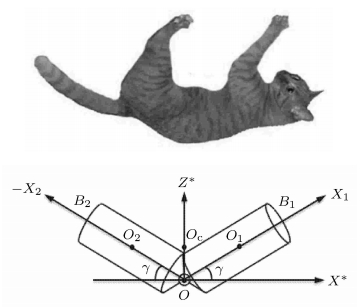
1 落体猫的最优控制问题 1.1 落体猫的姿态运动模型在系统不受外力矩作用时,可以使用角动量守恒原理来推导自由落体猫在空中作转体运动时的运动学方程.猫的前后躯体分别简化为两个外形和质量分布均相同的对称刚体
|
图 1 猫落体的力学模型 Figure 1 Mechanical model of a free-falling cat |
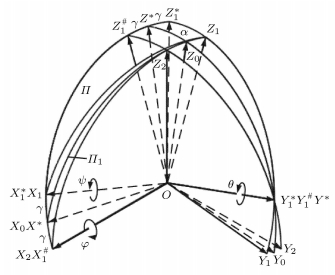
选取欧拉角描述落体猫的姿态运动,设其旋转方式为1-2-1 (见图 2).即O-
| $ \sin \alpha = \sin \psi /R, \;\;R = \sqrt {1 - \sin ^2\gamma \cos ^2\psi } $ | (1) |
|
图 2 姿态坐标变换 Figure 2 Coordinates transform of attitude |
经过推导[5],得到落体猫相对系统总质心
| $ H_{X^\ast } = [A\cos ^2\gamma + (B\sin ^2\psi + C\cos ^2\psi ) \cdot \\ \qquad \sin ^2\gamma](\dot {\phi } - \dot {\alpha }) + A\dot {\psi }\cos \gamma +\\ \qquad (B - C)\dot {\gamma }\sin \gamma \cos \psi \sin \psi $ | (2) |
式中A, B和C分别为刚体
由于猫在自由落体过程中相对系统总质心
| $ \dot {\varphi } = \{ \dot {\psi }\cos \gamma \sin \gamma [\rho + (1-\varepsilon )\cos ^2\psi] + \\ \qquad \dot {\gamma }\cos \psi \sin \psi (1 - \varepsilon + \rho \sin ^2\gamma ) \}\sin \gamma \big / \\ \qquad \{ (1 - \sin ^2\gamma \cos ^2\psi )[1 + (\rho-\varepsilon \cos ^2\psi )\sin ^2\gamma ] \} $ | (3) |
此方程即为自由下落猫的非完整姿态运动方程.
1.2 目标函数由式(3)可知,只要能够知道受生物意识控制的弯腰规律
| $ \boldsymbol{ J} (\boldsymbol{ u}) = \int_0^T \langle \boldsymbol{ u, u }\rangle {\rm{d}}t $ | (4) |
将落体猫的姿态角
| $ \boldsymbol{\dot x} =\boldsymbol{ G}(\boldsymbol{ x}) \boldsymbol{ u} $ | (5) |
其中状态矩阵由式(3)可导出
| $ \boldsymbol{ G}(\boldsymbol{ x}) = \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ M & N \end{array}\!\! \right] $ | (6) |
式中
| $ M =\cos\gamma \sin^2\gamma [\rho + (1-\varepsilon ) \cos^2\psi]/ \\ \quad \{(1 - \sin ^2\gamma \cos ^2\psi )[1 + (\rho-\varepsilon \cos ^2\psi )\sin ^2\gamma] \} \\ N=\cos\psi \sin\psi \sin\gamma (1 - \varepsilon + \rho \sin ^2\gamma ) / \\ \quad \{(1 - \sin ^2\gamma \cos ^2\psi )[1 + (\rho-\varepsilon \cos ^2\psi )\sin ^2\gamma]\} $ |
给定落体猫的初始和终端位形
通常猫在下落初始瞬间以及四肢着地瞬间,控制的初末值应均为零,即
Gauss伪谱法是通过一系列变换,将连续最优控制问题离散为具有代数约束的参数优化问题,即非线性规划问题[29],主要通过以下步骤实现.
(1) 时域变换
将姿态运动规划问题的时间区间
| $ t = \dfrac{t_0 + t_{\rm f} }{2} - \dfrac{t_0 - t_{\rm f} }{2}\tau $ | (7) |
式中
(2) 状态变量与控制变量的离散
取K个LG点以及
| $ \boldsymbol{ x}(\tau ) \approx \boldsymbol{ X}(\tau ) = \sum\limits_{i = 0}^K {L_i (\tau )} \boldsymbol{ X}(\tau _i ) = \\ \qquad \sum\limits_{i = 0}^K \left[{\left( {\prod\limits_{j = 0, j \ne i}^K \dfrac{\tau-\tau _j }{\tau _i-\tau _j } } \right)X(\tau _i )} \right] $ | (8) |
而控制变量的近似离散则仅以LG点作为K个Lagrange多项式的插值节点,
| $ \boldsymbol{ u}(\tau ) \approx \boldsymbol{ U}(\tau ) = \sum\limits_{i = 1}^K {\tilde {L}_i (\tau )} \boldsymbol{ U}(\tau _i ) $ | (9) |
(3) 终端状态约束的离散
终端状态可通过对动力学方程在区间[-1, 1]上积分,再将其离散并用Gauss积分来近似可得
| $ \boldsymbol{ X}_{\rm f} = \boldsymbol{ X}_0 + \dfrac{t_{\rm f} - t_0 }{2}\sum\limits_{k = 1}^K {\mu _k f(\boldsymbol{ X}_k, \;\boldsymbol{ U}_k , \;\tau _k ;\;t_0, \;t_{\rm f} )} $ | (10) |
其中
(4) 动力学微分方程的转换
状态变量的导数可通过对式(8)中的连续时间
| $ \boldsymbol{\dot x}(\tau _k ) \approx \boldsymbol{\dot X}(\tau _k ) = \sum\limits_{i = 0}^K {\dot {L}_i (\tau _k )} \boldsymbol{ X} (\tau _i ) $ | (11) |
可用一个微分近似矩阵
| $ D_{ki} = \dot {L}_i (\tau _k ) = \sum\limits_{l = 0, l \ne i}^K {\dfrac{\prod\limits_{j = 0, j \ne i, l}^K {\tau _k - \tau _j } }{\prod\limits_{j = 0, j \ne i}^K {\tau _i - \tau _j } }} $ | (12) |
其中
| $ \sum\limits_{i = 0}^K {D_{ki} \boldsymbol{ X}_i } - \dfrac{t_{\rm f} - t_0 }{2}\;f(\boldsymbol{ X}_k, \boldsymbol{ U}_k, \tau _k ;t_0 , t_{\rm f} ) = {\bf 0} $ | (13) |
式中
(5) 目标函数
用Gauss积分来计算最优控制问题中目标函数的积分项,可得离散形式的近似目标函数为
| $ J = \varPhi (\boldsymbol{ X}_0, \;t_0, \;\boldsymbol{ X}_{\rm f}, \;t_{\rm f} ) +\\ \qquad \dfrac{t_{\rm f} - t_0 }{2}\sum\limits_{k = 1}^K {\mu _k g( \boldsymbol{ X}_k , \;\boldsymbol{ U}_k, \;\tau _k ;\;t_0, \;t_{\rm f} )} $ | (14) |
落体猫的连续最优控制问题通过Gauss伪谱法离散后与状态和控制边界约束所构成的一般非线性规划问题可表述为
| $ \left. \begin{array}{l} \min \;\;\;\;J = F(\mathit{\boldsymbol{y}})\\ {\rm{s}}.{\rm{t}}.\;\;\;\;\;{h_i}(\mathit{\boldsymbol{y}}) = 0{\mkern 1mu} \;\;i = 1,2, \cdots ,3K + 13\\ \;\;\;\;\;\;\;\;{g_i}(\mathit{\boldsymbol{y}}) \le 0{\mkern 1mu} \;\;i = 1,2, \cdots ,2K \end{array} \right\} $ | (15) |
式中,J为式(14)离散的性能指标函数,h为包含式(10)、式(13)、姿态边界以及控制边界所描述的等式约束,g为控制变量最大限约束,
直接打靶法是直接法中仅有离散控制变量的一种参数优化方法[30],它主要是将时间连续的最优控制问题离散化,从而把原问题转换为求解一个非线性规划问题.具体的离散后的时间如式(16)所示,以离散时间节点上相对应的控制变量(17)为设计变量,相邻时间节点之间的控制变量的值可通过三次样条插值获取.从而当知道一组设计变量的值后,插值就可以得到控制的具体表达式,再代入状态方程积分便可得到状态变量,进而可求解性能指标函数以及约束方程.上述离散过程的数学描述为
| $ t_0 = t_1 < t_2 < \cdots < t_K = t_{\rm f} $ | (16) |
| $ \boldsymbol{ y} = (\boldsymbol{ u}_1, \boldsymbol{ u}_2, \cdots, \boldsymbol{ u}_K ) \qquad $ | (17) |
离散时间不要求一定是具体的实际时间,可以是无量纲时间以及能量参数等,它需要由描述具体模型运动的相对独立变量来决定.对于求解最小机动时间的优化控制问题,只需将末端时间与控制变量一起作为设计变量即可,此时离散时间过程便是一个优化过程中的动态历程.
2.3 优化策略及流程从理论上讲,可直接利用SQP算法求解直接打靶法所描述的非线性规划问题.但实际应用中却存在如下困难:当选取较多LG点时,设计变量的数目相当庞大.对于数目庞大的设计变量,设定SQP算法的求解初值就会变成是一件非常繁琐的工作,且不恰当的初值可能使问题收敛不到可行解;另外,SQP算法不具备全局寻优能力,最终所求得的优化解对设计变量的初始猜测值具有一定的依赖性,一般只能收敛到靠近初值附近的局部最优解.针对这些问题,采取如下的串行优化策略.
(1) Gauss伪谱法计算可行解
可行解计算是指不直接搜寻满足所有约束条件(包括等式和不等式约束)的最优解,是将非线性规划问题中的等式约束变换后作为目标函数,不考虑实际的性能指标函数,从而把求解一个有等式约束的非线性规划问题转换成无等式约束的非线性规划问题来求解,即把式(15)转化为
| $ \left.\!\!\begin{array}{l} \;\;\;\;\;\min \;\;\;J = {\rm sqrt} \Bigg (\sum\limits_{i = 1}^{3 K + 13} h_i (\boldsymbol{ y})^2 \Bigg ) \\ \;\;\;\;\;{\rm s.t.}\;\;\;\;g_i (\boldsymbol{ y}) \leqslant 0\;\;\;\;\;i = 1, 2, \cdots, 2 K \end{array}\!\!\right\} $ | (18) |
式中
由于Gauss伪谱法在较少节点时能获得较高的精度,并对初值敏感度较低,而且此时需要赋初始猜测值的设计变量较少,因此先选择较少节点
(2) 直接打靶法计算最优精确解
以上述第一步中计算得到的
| $ \left.\begin{array}{l} \;\;\;\;\;\min \;\;\;J = F(\boldsymbol{ U}) \\ \;\;\;\;\;{\rm s.t.}\;\;\;\;\;\phi (\boldsymbol{ X}_f (\boldsymbol{ U})) = 0 \\ \;\;\;\;\;\;\;\;\;\;\;\;\;h(\boldsymbol{ U}) = 0 \\ \;\;\;\;\;\;\;\;\;\;\;\;\;g(\boldsymbol{ U}) \leqslant 0 \end{array}\right\} $ | (19) |
式中,J为式(14)描述的性能指标函数,
最后将得到的最优控制代入式(5),通过积分便可得到最优的状态变量
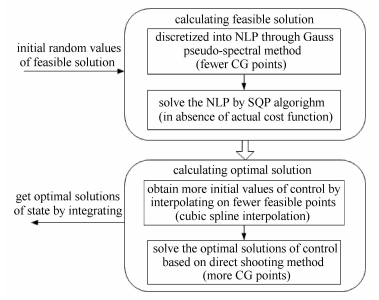
|
图 3 基于Gauss伪谱法和直接打靶法的自由落体猫姿态串行优化流程 Figure 3 The flow chart of free-falling cat attitude optimization via Gauss pseudo-spectral method and direct shooting method |
针对Gauss伪谱法和直接打靶法两种方法, 最优控制问题离散后的非线性规划问题(式(18)和式(19)),均采用Matlab软件的SQP算法求解;而在运算式(19)过程中的末端姿态与最后的最优姿态的求解采用的是Runge-Kutta求积公式.
3 数值仿真假设猫在自由下落过程中,其脊柱仅弯曲,前后体之间不会发生相互扭转的情况;其次猫的脊柱前弯,在旋转体过程中弯曲角
优化算法中的性能指标函数为猫下落时腰关节的耗散能.采用串行优化策略,可行解选取的LG点个数为6,最优解选取40个.设置时间T=1 s.可行解初始猜测值是采用Matlab的随机函数在0~1之间随机生成的
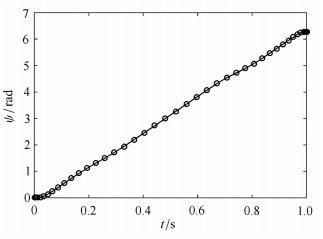
|
图 4 猫下落 |
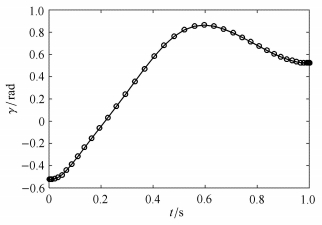
|
图 5 猫下落 |
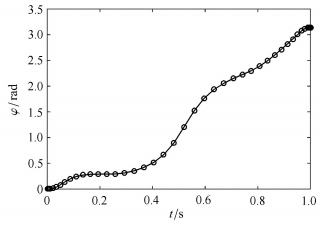
|
图 6 猫下落 |
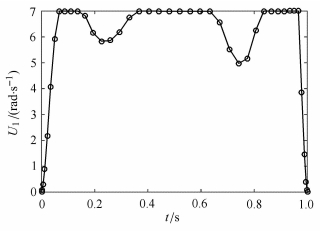
|
图 7 猫下落时腰关节最优控制输入规律 |

|
图 8 猫下落时腰关节最优控制输入规律 |
为验证文中所提出的串行优化方法的可行性以及鲁棒性,采用相同的参数设置运行程序6次,求解运算是在CPU频率为3.3 GHz,内存为4.0 G的windows7计算机上进行.在可行解计算中:平均迭代次数为188.333次;目标函数的平均值为1.006
| 表 1 最优解相关参数对于不同初值的变化状况 Table 1 The change of relevant parameters of optimal solution in different initial values |
从表 1中记录的数据可看出,对于每次运算均采用不同的随机初始猜测值,与最优解相关参数的变化幅度均不大,由此可见,本文提出的串行优化策略具有较好的鲁棒性和可行性.
4 结论本文结合Gauss伪谱法和直接打靶法求解了自由落体猫空间转动的姿态优化问题.采用SQP算法求解直接打靶法离散后的非线性规划问题,并针对SQP算法对初始猜测值敏感的特点,文中提出基于Gauss伪谱法求解可行解与直接打靶法求解最优精确解的串行优化策略,通过数值仿真结果表明:该方法克服了单纯伪谱法求解最优控制问题对初值的敏感性问题,串行优化策略不仅对初值具有很好的鲁棒性,并且提高了求解精度.本文所做的工作虽然是针对自由落体猫的姿态优化控制问题,但提出的Gauss伪谱法和直接打靶法相结合的串行优化策略也为其他优化控制研究提供了一种求解方法.
| 1 | 贾书惠. 从猫下落谈起 . 北京: 高等教育出版社, 1990. ( Jia Shuhui. Talking from the Falling Cat . Beijing: Higher Education Press, 1990. (in Chinese) ) |
| 2 | McDonald DA. How does a falling cat turn over?. American Journal Physiology, 1955, 129 : 34-35. |
| 3 | ЛойцянскийАИ. Теоретичеокмеханик . Москва: Санкм-Пемербурэ, 1953. |
| 4 | Kane TR, Scher MP. A dynamical explanation of the falling cat phenomenon. International Journal Solids and Structures, 1969, 5 (5) : 663-670. |
| 5 | 刘延柱. 自由下落猫的转体运动. 力学学报, 1982, 14 (4) : 388-393. ( Liu Yanzhu. On the turning motion of a free-falling cat. Acta Mechanica Sinica, 1982, 14 (4) : 388-393. (in Chinese) ) |
| 6 | Fernandes C, Gurvits L, Li Z. Near-optimal nonholonomic motion planning for a system of coupled rigid bodies. IEEE Transactions on Automatic Control, 1994, 39 (3) : 450-463. DOI: 10.1109/9.280745. |
| 7 | 戈新生, 刘延柱, 魏宝刚. 基于拟牛顿算法的自由下落猫的非完整运动规划. 系统仿真学报, 2006, 18 (5) : 1123-1126. ( Ge Xinsheng, Liu Yanzhu, Wei Baogang. Nonholonomic motion planning for freefalling cat using Quasi-Newton method. Journal of System Simulation, 2006, 18 (5) : 1123-1126. (in Chinese) ) |
| 8 | Ge XS, Chen LQ. Optimal control of nonholonomic motion planning for a free-falling cat. Applied Mathematics & Mechanics, 2007, 28 (5) : 601-607. |
| 9 | Ge XS, Guo ZX. Nonholonomic motion planning for a free-falling cat using spline approximation. Science China Physics Mechanics & Astronomy, 2012, 55 (11) : 2100-2105. |
| 10 | Iwai T, Matsunaka H. The falling cat as a port-controlled Hamiltonian system. Journal of Geometry & Physics, 2012, 62 (2) : 279-291. |
| 11 | Zhen SC, Huang K, Zhao H, et al. Why can a free-falling cat always manage to land safely on its feet. Nonlinear Dynamics, 2014, 79 (4) : 2237-2250. |
| 12 | Brockett RW, Dai L. Non-holonomic kinematics and the role of elliptic functions in constructive controllability. Nonholonomic Motion Planning, Springer US, 1993 : 1-21. |
| 13 | Benson DA. A Gauss Pseudo-spectral Transcription for Optimal Control.[PhD Thesis]. Cambridge, Massachusetts:Massachusetts Institute of Technology, 2005 |
| 14 | Benson DA, Huntington GT, Thorvaldsen TP, et al. Direct trajectory optimization and costate estimation via an orthogonal collocation method. Journal of Guidance Control & Dynamics, 2006, 29 (6) : 1435-1439. |
| 15 | Fahroo F, Ross IM. Direct trajectory optimization by a Chebyshev pseudo-spectral method. Proceedings of the American Control Conference, 2000, 6 : 3860-3864. |
| 16 | Gong Q, Ross IM, Fahroo F. Costate computation by a chebyshev pseudo-spectral method. Journal of Guidance Control & Dynamics, 2010, 33 (2) : 623-628. |
| 17 | Tang XJ, Wei JL, Chen K. A Chebyshev-Gauss pseudo-spectral method for solving optimal control problems. Acta Automatica Sinica, 2015, 41 (10) : 1778-1787. DOI: 10.1016/S1874-1029(15)30004-5. |
| 18 | 雍恩米, 唐国金, 陈磊. 基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化. 宇航学报, 2008, 29 (6) : 1766-1772. ( Yong Enmi, Tang Guojin, Chen Lei. Rapid trajectory optimization for hypersonic reentry vehicle via gauss pseudospectral method. Journal of Astronautics, 2008, 29 (6) : 1766-1772. (in Chinese) ) |
| 19 | 雍恩米.高超声速滑翔式再入飞行器轨迹优化与制导方法研究.[博士论文].长沙:国防科学技术大学, 2008 ( Yong Enmi. Study on trajectory optimization and guidance approach for hypersonic glidereentry vehicle.[PhD Thesis]. Changsha:National University of Defense Technology, 2008(in Chinese) ) |
| 20 | 霍明英.电动帆航天器动力学、控制及轨迹优化研究.[博士论文].哈尔滨:哈尔滨工业大学, 2015 ( Huo Mingying. Reserch on dynamics control and trajectory optimization for electric sails.[PhD Thesis]. Harbin:Harbin Institute of Technology, 2015(in Chinese) ) http://cdmd.cnki.com.cn/Article/CDMD-10213-1015957669.htm |
| 21 | 李适.空间机器人路径优化与鲁棒跟踪控制.[博士论文].哈尔滨:哈尔滨工业大学, 2013 ( Li Shi. Path optimization and robust tracking control for space manipulator.[PhD Thesis]. Harbin:Harbin Institute of Technology, 2013(in Chinese) ) |
| 22 | Li S, Duan GR. A pseudo-spectral method for trajectory optimization of free-floating space manipulator. Chinese Control Conference, 2012 : 2395-2399. |
| 23 | 彭祺擘, 李海阳, 沈红新. 基于高斯-伪谱法的月球定点着陆轨道快速优化设计. 宇航学报, 2010, 31 (4) : 1012-1016. ( Peng Qibo, Li Haiyang, Shen Hongxin. Rapid lunar exact-landing trajectory optimization via gauss pseudo-spectral method. Journal of Astronautics, 2010, 31 (4) : 1012-1016. (in Chinese) ) |
| 24 | 彭祺擘, 张海联. 载人月面着陆过程的应急上升轨道优化设计. 载人航天, 2015 (2) : 187-192. ( Peng Qibo, Zhang Hailian. Optimization of lunar emergency design ascent trajectory during manned lunar landing. Manned Spaceflight, 2015 (2) : 187-192. (in Chinese) ) |
| 25 | 庄宇飞, 马广富, 黄海滨. 欠驱动刚性航天器时间最优轨迹规划设计. 控制与决策, 2010, 25 (10) : 1469-1473. ( Zhuang Yufei, Ma Guangfu, Huang Haibin. Time-optimal motion planning of an underactuated rigid spacecraft. Control and Decision, 2010, 25 (10) : 1469-1473. (in Chinese) ) |
| 26 | Zhuang Y, Huang H. Time-optimal trajectory planning for underactuated spacecraft using a hybrid particle swarm optimization algorithm. Acta Astronautica, 2014, 94 (2) : 690-698. DOI: 10.1016/j.actaastro.2013.06.023. |
| 27 | 刘延柱, 潘振宽, 戈新生. 多体系统动力学 (第2版). 北京: 高等教育出版社, 2014. ( Liu Yanzhu, Pan Zhenkuan, Ge Xinsheng. Dynamics of Multibody Systems (second edition). Beijing: The Higher Education Press, 2014. (in Chinese) ) |
| 28 | Shabana AA. Dynamics of multibody systems-second edition. ISBN, 1998, 56 (1) : 235-236. |
| 29 | 唐国金, 罗亚中, 雍恩米. 航天器轨迹优化理论、方法及应用 . 北京: 科学出版社, 2012. ( Tang Guojin, Luo Yazhong, Yong Enmi. Spacecraft Trajectory Optimization Theory, Method and Application . Beijing: Science Press, 2012. (in Chinese) ) |
| 30 | 雍恩米, 陈磊, 唐国金. 飞行器轨迹优化数值方法综述. 宇航学报, 2008, 29 (2) : 397-406. ( Yong Enmi, Chen Lei, Tang Guojin. A survey of numerical methods for trajectory optimization of spacecraft. Journal of Astronautics, 2008, 29 (2) : 397-406. (in Chinese) ) |
†. School of Science, Beijing Information Science & Technology University, Beijing 100192, China


