†. 北京理工大学宇航学院, 北京 100081
**. 南京航空航天大学机械结构力学及控制国家重点实验室, 南京 210016
数字控制(digital control/sampled-data control)基于计算机完成采样、数字化和控制律计算, 并以离散信号方式向作动器提供控制输入.随着计算机技术与存储技术的飞速发展, 数字控制已成为当代控制技术的主流, 具有变更控制律方便、可靠性高、实时性好、抗干扰能力强等特点, 在各技术领域得到了广泛应用[1-8].对许多实际工程系统的控制, 系统输出是可以用于反馈控制设计的唯一测量信号, 此时就需要基于采样信号进行反馈控制设计[9].数字采样控制系统(digital control systems/sampled-data control systems)是一类控制系统, 其控制对象由微分方程(组)描述, 而控制律由离散的采样信号给定.鉴于动力学系统多由微分方程(组)来描述, 故其数字控制问题可归结为对数字采样控制系统的研究.
数字采样控制系统是一类混杂动力系统, 既不同于纯连续系统也不同于纯离散系统, 目前还没有现成的数学方法作为这类系统理论研究的一般有效工具[10].对这类系统进行分析与控制设计通常有如下两种思路.第一种是将系统微分方程(组)转化为具有时变时滞的连续型微分方程(组),其中的时滞是关于时间的分段线性函数,然后采用Lyapunov方法与线性矩阵不等式方法完成分析与设计[11-16].由于在采样点处, 该时变时滞不连续, 更不光滑, 在应用Lyapunov方法时需要注意Lyapunov函数或Lyapunov泛函在采样点处的特点.这种思路的好处是对采样时间的限制很弱, 但由于其中的时滞是时变的不连续函数, 通常很难对受控系统作精细的分析与设计, 所得到的结论可能比较保守.第二种思路是将系统方程转化为离散形式的差分方程, 然后采用离散Lyapunov方法等完成分析与设计[17-19].这种方法的有效性需要一些限制性条件来保证.例如, 采样过程应该满足采样定理的条件, 即采样频率大于信号最高频率的两倍, 而实际应用中采样频率往往高达信号最高频率的5~10倍.离散化的数字采样控制系统方程(组)是常系数差分方程(组), 其稳定性可由相应的特征方程根的分布来确定, 能够得到一些较为精细的结论[20-24].
在经典的数字采样控制技术中, 通常采用同一时刻的位移采样信号与速度采样信号来构成反馈控制律[20-24].目前, 先进的大容量高速存储介质与技术能够将采样信号通过采样保持器保存更长时间.因此人们关心:基于不同采样时刻的信号进行反馈, 受控系统会有什么不同的动力学特征?例如, 不同形式的采样控制律对受控系统的稳定性增益区域有什么影响?对同样的反馈增益, 在不同形式的采样控制律作用下, 受控系统的稳定性裕度有什么不同?本文以单自由度系统动力学的数字采样PD (proportional-derivative)控制为例, 目的是能够解析地分析不同数字采样反馈对控制系统稳定性的影响.结果表明, 不同形式的数字采样信号反馈控制律可显著增大或减小受控系统的稳定性区域, 且数字采样反馈控制与经典反馈控制有明显不同的作用机理.另外, 本文考虑的未受控系统既无刚度,也无阻尼,目的是为了突出数字采样反馈的作用.
1 经典采样PD反馈受控系统及其稳定性本节介绍在经典采样PD反馈作用下单自由度受控系统的稳定性分析[20], 并将其增益稳定性区域与时间连续的时滞反馈系统稳定性区域作比较.
1.1 采样反馈受控系统及其稳定性考察单自由度系统的运动微分方程
| $ M\ddot {x}(t) = q(t) $ | (1) |
其中M为系统质量, x(t)系统位移, q(t)是数字采样PD控制器输出的控制力, 即它是系统位移采样信号和速度采样信号的线性反馈.如果采样周期为h, 则利用零阶采样保持器, 采样时刻t=tn :=nh控制律用前一采样时刻的位移和速度信号表示为
| $ q(t) = - Px(t_{n-1} ) - D\dot {x}(t_{n-1} )\, , \ \ \ t_n \leqslant t < t_{n + 1} $ | (2) |
其中P, D为反馈增益, n=1, 2, ….在该采样周期内, 受控系统的动力学方程为如下时滞微分方程
| $ M\ddot {x}(t) = - Px(t - \tau _{n-1}) - D\dot {x}(t - \tau _{n-1} )\, , \ \ t_n \leqslant t < t_{n + 1} $ |
其中时变时滞
为此, 引入如下时间变换与参数
| $ \hat {t} = \dfrac{t}{h}\, , \ \ \hat {x}(\hat {t}) = x(h\hat {t})\, , \ \ p = \dfrac{Ph^2}{M}\, , \ \ d = \dfrac{Dh}{M} $ |
则受控系统的动力学方程可化为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(n-1) - d\frac{{{\rm{d}}\hat x}}{{{\rm{d}}\hat t}}(n-1)\, , \ \ n \leqslant \hat {t} < n + 1 $ | (3) |
在
| $ \left\{ \begin{array}{l} \frac{{{{\rm{d}}^2}\hat x(\hat t)}}{{{\rm{d}}{{\hat t}^2}}} = {a_n}\\ \frac{{{\rm{d}}\hat x(\hat t)}}{{{\rm{d}}\hat t}} = {v_n} + {a_n}(\hat t - n)\\ \hat x(\hat t) = {u_n} + {v_n}(\hat t - n) + \frac{{{a_n}}}{2}{(\hat t - n)^2} \end{array} \right. $ |
当
| $ a_{n + 1} = \frac{{{{\rm{d}}^{\rm{2}}}\hat x}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}}(n + 1)\, , \ \ v_{n + 1} = \frac{{{\rm{d}}\hat x}}{{{\rm{d}}\hat t}}(n + 1)\, , \ \ u_{n + 1} = \hat {x}(n + 1) $ |
则有如下差分方程
| $ \left\{ \begin{array}{l} {a_{n + 1}} = - p{u_n} - d{v_n}\\ {v_{n + 1}} = {v_n} + {a_n}\\ {u_{n + 1}} = {u_n} + {v_n} + \frac{1}{2}{a_n} \end{array} \right. $ |
故系统动力学方程可表示为矩阵形式的差分方程
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}\\ 0&1&1\\ { - p}&{ - d}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}} \end{array}} \right] $ | (4) |
其中n=0, 1, 2, ….由此可以看出, 这里用零阶采样保持器提取反馈信号相当于用Euler格式将微分方程转化为差分方程来数值求解, 故采样周期必须足够小, 才能保证采样控制系统的稳定性由差分方程的稳定性来确定.
记差分方程(4)中的非零系数矩阵为
| $ \lambda ^3 - 2\lambda ^2 + \Big(1 + \dfrac{p}{2} + d \Big)\lambda + \dfrac{p}{2} - d = 0 $ | (5) |
记
| $ \alpha = \max \{\left| {\lambda _1 } \right|\, , \ \ \left| {\lambda _2 } \right|\, , \ \ \left| {\lambda _3 } \right|\} $ |
则差分方程(4)零解渐近稳定的充要条件是
为了研究三次方程根的分布, 引入Mobius变换
| $ \lambda = \dfrac{s + 1}{s - 1} \ \ \Leftrightarrow \ \ s = \dfrac{\lambda + 1}{\lambda - 1} $ | (6) |
注意到, 对单位圆上的
| $ {\rm Re}\left( {\rm{d}frac{{\rm e}^{\theta \, {\rm i}} + 1}{{\rm e}^{\theta \, {\rm i}} - 1}} \right) = 0\, , \ \ {\rm Im} \left( {\rm{d}frac{{\rm e}^{\theta \, {\rm i}} + 1}{{\rm e}^{\theta \, {\rm i}} - 1}} \right) = \dfrac{ - \sin \theta }{1 - \cos \theta } $ |
其中Re (z), Im (z)分别表示复数z的实部与虚部.故Mobius变换将单位圆
| $ p\, s^3 + 2(d - p)s^2 + (4 - 4d + p)s + 4 + 2d = 0 $ |
差分方程(4)的零解渐近稳定当且仅当此三次方程的所有根都具有负实部, 即
由Routh-Hurwitz判别法可知, 在p, d为正数的情况下, 关于s的三次代数方程所有根均具有负实部的充要条件是d -p > 0, 4 + p -4d > 0且2(d -p)(4 -4d + p) -p(4 + 2d) > 0.这里, 前两个条件可进一步简化为4(d -1) < p < d, 而第3个条件则等价于
| $ 0 < p < - 3 + 2d + \sqrt {9 - 8d} $ | (7) |
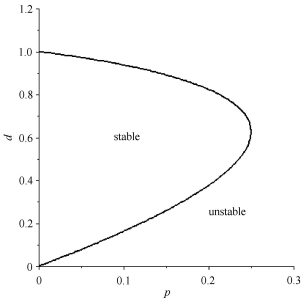
更进一步的分析可知, 在(p, d)-增益平面上, 差分方程(4)零解的渐近稳定性区域由式(7)所完全确定, 具有如图 1所示的形状.
|
图 1 差分方程(4)的增益稳定性区域 Figure 1 The stable region of Eq.(4) in (p, d)-plane |
如果控制律是时间连续的时滞PD反馈, 即
| $ q(t) = - Px(t - \tau ) - D\dot {x}(t - \tau ) $ | (8) |
则受控系统的运动微分方程为
| $ M\ddot {x}(t) = - Px(t - \tau ) - D\dot {x}(t - \tau ) $ |
其中正数P, D为反馈增益.和前面的情况类似, 令
| $ \hat {t} = \dfrac{t}{\tau }\, , \ \ \hat {x}(\hat {t}) = x(\tau \hat {t})\, , \ \ p = \dfrac{P\tau ^2}{M}\, , \ \ d = \dfrac{D\tau }{M} $ |
则受控系统的运动微分方程化为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(\hat {t} - 1) - d\frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t - 1} \right)}}{{{\rm{d}}\hat t}} $ | (9) |
由参数p, d的定义可知, 此处的时滞
| $ f(\lambda ) = \lambda ^2 + p{\rm e}^{ - \lambda } + d\lambda {\rm e}^{ - \lambda } $ |
时滞微分方程(9)零解渐近稳定的充要条件是特征方程
近年来, 时滞系统稳定性及其分岔得到了广泛研究[25-28].为了确定控制系统在增益平面上的稳定性区域, D划分法是一种特别简单有效的研究方法[29-30].由临界稳定条件
| $ p = \omega ^2\cos \omega \, , \ \ d = \omega \sin \omega $ |
当
为了确定时滞微分方程(9)在增益(p, d)取值于哪些区域时是渐近稳定的, 可采用稳定性切换方法[27-30].以增益p为参数而另一个增益值固定为d=0的情形为例, 研究特征根的实部随p变化的变化趋势.利用隐函数求导法则可求得
| $ \frac{{{\rm{d}}\lambda }}{{{\rm{d}}p}} = \dfrac{{\rm e}^{ - \lambda }}{ - 2\lambda + (p - d){\rm e}^{ - \lambda }+d\lambda {\rm e}^{ - \lambda }} $ |
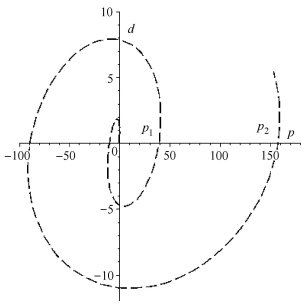
如图 2所示, 在由
| $ {\rm{sgn}}{\left. {\left( {{\rm{Re}}\frac{{{\rm{d}}\lambda }}{{{\rm{d}}p}}} \right)} \right|_{(p,\lambda ) = ({p_i}, \pm {\omega _i}{\rm{i}})}} = {\rm{sgn}}{\left. {\left( {{\rm{Re}}\frac{{{\rm{d}}p}}{{{\rm{d}}\lambda }}} \right)} \right|_{(p,\lambda ) = ({p_i}, \pm {\omega _i}{\rm{i}})}} $ |
|
图 2 时滞微分方程(9)的临界稳定曲线 Figure 2 The critical stable curve of Eq.(9) |
另外,直接计算有
| $ {\rm{sgn}}{\left. {\left( {{\rm{Re}}\frac{{{\rm{d}}p}}{{{\rm{d}}\lambda }}} \right)} \right|_{(p,\lambda ) = ({p_i}, \pm {\omega _i}{\rm{i}})}} = {\rm{sgn}}({p_i}) = 1 $ |
于是有
| $ {\rm sgn}\left. {\left( {{\rm Re}\frac{{{\rm{d}}\lambda }}{{{\rm{d}}p}}} \right)} \right|_{(p, \lambda ) = (p_i, \pm \omega _i {\rm i})} = 1 > 0 $ |
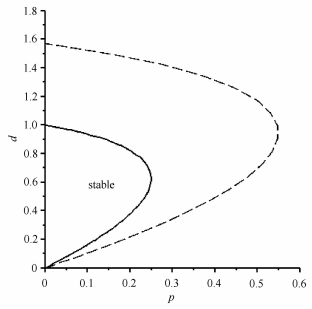
因此, 当临界稳定曲线每次从下半平面跨越p轴到上半平面时, 在位于第一象限的右侧区域的增益取值将使特征方程增加一对具有正实部的共轭特征值.于是当且仅当增益在图 3中虚线与d轴所围成的区域(图 2在原点附近且在第一象限的小区域的放大图)时, 时滞微分方程(9)的零解是渐近稳定的.与图 1中的稳定性区域进行比较可以看出, 采样反馈系统的稳定性区域显著小于对应的连续时滞反馈系统的稳定性区域, 即采样反馈系统比连续时滞反馈系统容易失稳.其原因是, 采样反馈对系统状态采样后至少保持一个采样周期不变, 这导致计算控制律时的可用信息减少, 而控制器的实时跟踪性降低.
|
图 3 采样反馈系统(4)与连续时滞反馈系统(8)的稳定性区域, 前者小于后者 Figure 3 The stable regions of sampled-feedback system (4) and continuous delayed-feedback system (8), the former is smaller than the later |
在经典的采样PD反馈控制律中, 位移采样信号和速度采样信号是同步的.本节探讨两者不同步时采样反馈受控系统的稳定性.
2.1 位移采样信号滞后于速度采样信号首先, 考察如下采样反馈控制律
| $ q(t) = - Px(t_{n - 2} ) - D\dot {x}(t_{n-1} )\, , \ \ t_n \leqslant t < t_{n + 1} $ | (10) |
即位移采样信号滞后速度采样信号一个采样周期, 此时受控系统的无量刚化动力学方程为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(n - 2) - d\frac{{{\rm{d}}\hat x}}{{{\rm{d}}\hat t}}(n-1)\, , \ \ n \leqslant \hat {t} < n + 1 $ | (11) |
其中反馈增益p, d如前所述, n=2, 3, ….此采样控制方程对应的差分方程是
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}\\ 0&1&1\\ 0&{ - d}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - p{u_{n - 1}}} \end{array}} \right] $ |
或记为
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}}\\ {{u_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}&0\\ 0&1&1&0\\ 0&{ - d}&0&{ - p}\\ 1&0&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}}\\ {{u_{n - 1}}} \end{array}} \right] $ | (12) |
此方程的系数矩阵仍记为
| $ \det (\lambda \boldsymbol{ I } - \boldsymbol{ A }) = 0 $ |
展开行列式即得特征方程
| $ \lambda ^4 - 2\lambda ^3 + (1 + d)\lambda ^2 + \Big( - d + \dfrac{p}{2} \Big)\lambda + \dfrac{p}{2} = 0 $ | (13) |
差分方程(12)零解渐近稳定的充要条件是所有特征根的模都小于1.再次采用Mobius变换, 将上述四次多项式形式的特征方程化为
| $ c_4 s^4 + c_3 s^3 + c_2 s^2 + c_1 s + c_0 = 0 $ |
其中
| $ c_3 c_2 - c_4 c_1 > 0\, , \ \ c_3 c_2 c_1 - c_3^2 c_0 - c_1^2 c_4 > 0 $ |
由前两个条件可简化为
| $ - 4p^2 + ( - 10 + 7d)p + 4d - 2d^2 > 0 $ |
与
| $ p^3 - 2(d + 5)p^2 + 4(6d - 5)p - 8d^2 + 8d > 0 $ | (14) |
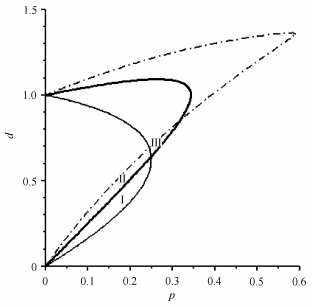
这两个条件可简化为一个条件, 由式(14)给出.因此, 在采样控制律(10)作用下, 受控统(11)在增益平面上的渐近稳定性区域是图 4中黑色粗线与d轴所围成的区域, 它由条件(14)与p > 0确定.
|
图 4 采样反馈系统(3)、(11)和(16)的增益稳定性区域, 位移信号滞后越长, 稳定性区域越大 Figure 4 The stable regions of sampled-feedback systems (3), (11) and (16), the longer the sampled delay of the displacement signal is, the larger the stable region is |
由图 4可看出, 受控系统(11)的稳定性区域比经典采样PD反馈控制系统(3)的稳定性区域明显要大, 故受控系统(11)比受控系统(3)在选取使受控系统稳定的反馈增益时有更大的灵活性.值得指出是, 受控系统(3)的稳定性区域中有一个小区域I不在受控系统(11)的稳定性区域中.也就是说, 采样反馈控制律(10)未必总是增强受控系统的稳定性.
其次, 考察如下数字采样PD控制律
| $ q(t) = - Px(t_{n - 3} ) - D\dot {x}(t_{n-1} )\, , \ \ t_n \leqslant t < t_{n + 1} $ | (15) |
即位移采样信号滞后速度采样信号两个采样周期, 则受控系统方程为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(n - 3) - d\frac{{{\rm{d}}\hat x}}{{{\rm{d}}\hat t}}(n-1) \, , \ \ n \leqslant \hat {t} < n + 1 $ | (16) |
其中n=3, 4, 5, ….对应的差分方程可表示为
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}}\\ {{u_n}}\\ {{u_{n - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}&0&0\\ 0&1&1&0&0\\ 0&{ - d}&0&0&{ - p}\\ 1&0&0&0&0\\ 0&0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}}\\ {{u_{n - 1}}}\\ {{u_{n - 2}}} \end{array}} \right] $ | (17) |
此时, 对应的特征方程为
| $ \lambda ^5 - 2\, \lambda ^4 + \left( {1 + d} \right)\lambda ^3 - d\lambda ^2 + \dfrac{p}{2}\lambda + \dfrac{p}{2} = 0 $ | (18) |
差分方程(17)的零解是渐近稳定的当且仅当特征方程(18)的所有根的模都小于1. 图 4中虚线与d轴所围成的区域即为受控系统(16)的稳定性区域, 它比受控系统(11)的稳定性区域明显要大, 但也存在两个小区域Ⅱ, Ⅲ, 对应的受控系统(11)渐近稳定, 而受控系统(16)不稳定.这表明, 当位移采样信号滞后于速度采样信号时, 采样反馈可增大受控系统的稳定性区域面积.但在稳定性区域边界附近的小区域内, 当位移采样信号滞后于速度采样信号时, 受控系统会由渐近稳定变为不稳定.
2.2 速度采样信号滞后于位移采样信号先考察数字采样PD控制律
| $ q(t) = - Px(t_{n-1} ) - D\dot {x}(t_{n - 2} )\, , \ \ t_n \leqslant t < t_{n + 1} $ | (19) |
即速度采样信号滞后于位移采样信号一个采样周期, 则受控系统方程为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(n-1) - d\frac{{{\rm{d}}\hat x}}{{{\rm{d}}\hat t}}(n - 2)\, , \ \ n \leqslant \hat {t} < n + 1 $ | (20) |
其中n=2, 3, 4, ….对应的差分方程为
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}\\ 0&1&1\\ { - p}&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ { - d{v_{n - 1}}} \end{array}} \right] $ |
或者
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}}\\ {{v_n}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}&0\\ 0&1&1&0\\ { - p}&0&0&{ - d}\\ 0&1&0&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}}\\ {{v_{n - 1}}} \end{array}} \right] $ | (21) |
该差分方程的特征方程为
| $ \lambda ^4 - 2\lambda ^3 + \Big(1 + \dfrac{p}{2}\Big)\lambda ^2 + \Big(d + \dfrac{p}{2}\Big)\lambda - d = 0 $ | (22) |
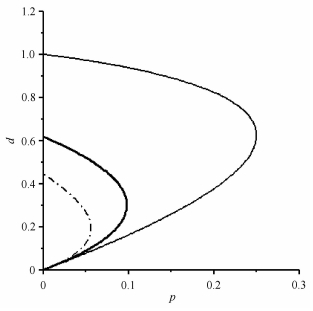
类似2.1节的分析, 可得采样反馈受控系统(20)在增益平面上的稳定性区域, 它是图 5中黑色粗线与d轴所围成的区域, 显著小于黑色细线所确定的经典采样PD反馈受控系统(3)的稳定性区域.与图 4所反映的特征有所不同, 此时受控系统(20)的稳定性区域完全包含在受控系统(3)的稳定性区域中.
|
图 5 采样反馈系统(3)、(20)和(24)的增益稳定性区域; 速度信号滞后越大, 稳定性区域越小 Figure 5 The stable regions of sampled-feedback systems (3), (20) and (24), the longer the sampled delay of the velocity signal is, the smaller the stable region is |
再考察数字采样PD控制律
| $ q(t) = - Px(t_{n-1} ) - D\dot {x}(t_{n-3} )\, , \ \ t_n \leqslant t < t_{n + 1} $ | (23) |
即速度采样信号滞后于位移采样信号两个采样周期, 则受控系统方程可化为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}}(\hat {t}) = - p\hat {x}(n-1) - d\frac{{{\rm{d}}\hat x}}{{{\rm{d}}\hat t}}(n - 3) \, , \ \ n \leqslant \hat {t} < n + 1 $ | (24) |
其中n=3, 4, 5, ….如前面的情况相同, 其差分方程既可以表示为两步差分方程, 也可以表示为维数更高的单步差分方程.这里仅考虑后者, 其形式是
| $ \left[ {\begin{array}{*{20}{c}} {{u_{n + 1}}}\\ {{v_{n + 1}}}\\ {{a_{n + 1}}}\\ {{v_n}}\\ {{v_{n - 1}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} 1&1&{1/2}&0&0\\ 0&1&1&0&0\\ { - p}&0&0&0&{ - d}\\ 0&1&0&0&0\\ 0&0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{u_n}}\\ {{v_n}}\\ {{a_n}}\\ {{v_{n - 1}}}\\ {{v_{n - 2}}} \end{array}} \right] $ | (25) |
该差分方程的特征方程为
| $ \lambda ^5 - 2\, \lambda ^4 + \left( {1 + \dfrac{p}{2}} \right)\lambda ^3 + \dfrac{p}{2}\lambda ^2 + d\lambda - d = 0 $ | (26) |
差分方程(25)的零解是渐近稳定的当且仅当特征方程(26)的所有根的模都小于1.此时, 采样反馈受控系统(24)的稳定性区域为图 5中虚线与d轴所围成的区域, 它小于受控系统(20)的稳定性区域, 更小于受控系统(3)的稳定性区域, 且为完全包含关系.由此可知, 当速度采样信号与位移采样信号不同步时, 速度信号滞后将导致受控系统的稳定性区域减小; 且滞后越大, 对应的稳定性区域越小.
2.3 不同采样反馈的控制效果比较由图 4与图 5可知, 采样反馈信号的滞后量对受控系统的稳定性区域有重要影响.增加位移反馈的时滞量可扩大受控系统的稳定性区域.虽然这种稳定性区域的扩大不具有严格意义的包含关系, 但仍可视时滞为有利因素; 而增加速度反馈信号的滞后量会缩小受控系统的稳定性区域, 此时相对于采样速度信号的采样位移信号时滞是不利因素.从这个角度看, 在上述讨论过的5种控制策略中, 以位移反馈信号滞后速度信号两个采样周期的控制为最佳.但增大采样周期要求更强的数据存储能力, 从硬件代价角度看未必值得.因此, 在实践中, 或许采用控制策略(10)更为适宜, 其位移采样信号滞后于速度采样信号一个周期, 采样控制律足够简单但对应控制系统具有大的稳定性增益区域.
对于相同的反馈增益值, 还可直接计算出受控系统(3)(11)(20)各自的所有特征值或各自特征根的模最大值
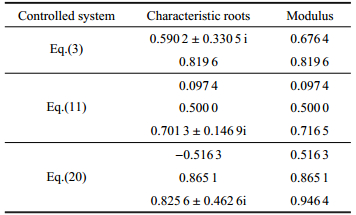
例如, 当p=0.05, d=0.4时, 对应于控制律(2) (10) (19)的受控系统(3)(11)(20)的特征值及其复数模如表 1所示, 它们各自的最大模
| 表 1 当p=0.05, d=0.4时, 不同控制律作用下的受控系统特征根 Table 1 The characteristic roots of the controlled system under different control strategies when p=0.05, d=0.4 |
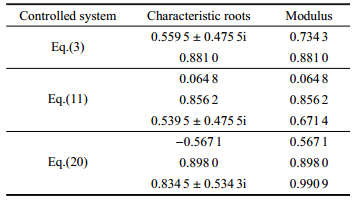
| 表 2 当p=0.05, d=0.5时, 不同控制律作用下受控系统特征根 Table 2 The characteristic roots of the controlled system under different control strategies when p=0.05, d=0.5 |
为了对比, 考察两种时滞反馈作用下的时间连续系统运动微分方程
| $ \left\{ \begin{array}{l} \ddot x(t) = - Px(t - 2\tau ) - D\dot x(t - \tau )\\ \ddot x(t) = - Px(t - \tau ) - D\dot x(t - 2\tau ) \end{array} \right. $ |
其对应的无量纲化时滞微分方程分别为
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(\hat {t} - 2) - d\frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t - 1} \right)}}{{{\rm{d}}\hat t}} $ | (27) |
| $ \frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t} \right)}}{{{\rm{d}}{{\hat t}^{\rm{2}}}}} = - p\hat {x}(\hat {t} - 1) - d\frac{{{{\rm{d}}^{\rm{2}}}\hat x\left( {\hat t - 2} \right)}}{{{\rm{d}}\hat t}} $ | (28) |
相应的特征方程分别是
| $ \left\{ \begin{array}{l} {\lambda ^2} + p{{\rm{e}}^{ - 2\lambda }} + d\lambda {{\rm{e}}^{ - \lambda }} = 0\\ {\lambda ^2} + p{{\rm{e}}^{ - \lambda }} + d\lambda {{\rm{e}}^{ - 2\lambda }} = 0 \end{array} \right. $ |
可采用1.2节所用的D划分法与稳定性切换方法确定这两个受控系统的稳定性区域.对时滞微分方程(28), 在其特征方程两边乘以
| $ \left\{ \begin{array}{l} p - {\omega ^2}\cos \omega + d\omega \sin \omega = 0\\ - {\omega ^2}\sin \omega + d\omega \cos \omega = 0 \end{array} \right. $ |
于是可求得临界稳定条件给出的增益值表达式
| $ p = 2\omega ^2\cos \omega - \dfrac{\omega ^2}{\cos \omega }\, , \ \ d = \dfrac{\omega \sin \omega }{\cos \omega } $ |
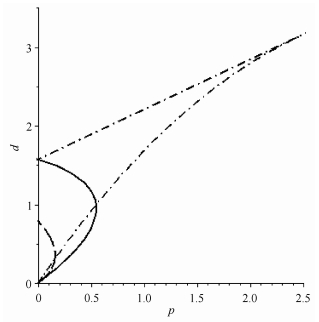
此时的稳定性区域是图 6中由该参数曲线(虚线)与d轴所围成的区域所构成的小区域.
|
图 6 受控系统(28), (9), (27)的增益稳定性区域依次从小到大 Figure 6 Increased area of the stable regions of the controlled systems (28), (9) and (27) |
同样, 对时滞微分方程(27), 在其特征方程两边乘以
| $ ( - \omega ^2 + p)\cos \omega = 0\, , \ \ ( - \omega ^2 - p)\sin \omega + d \omega = 0 $ |
分两种情况讨论: (a)
| $ \Big[-\Big(\dfrac{\pi }{2} + k{\pi }\Big)^2-p\Big]( - 1)^k + d \Big(\dfrac{ {\pi }}{2} + k{\pi } \Big) = 0 $ | (29) |
其中k=0, 1, 2, ….在情形(b), 临界稳定条件化为
| $ p = \omega ^2\, , \ \ d = 2\sin \omega $ |
根据稳定性切换方法可知, 该受控系统的稳定性区域是图 6中破折点虚线与d轴所围成的大区域, 其中虚直线为式(29)中取k=0所对应的直线.由图 6可见, 按稳定性区域从小到大顺序, 对应的受控系统分别是式(28)、式(9)和式(27).这个顺序和采样反馈受控系统的稳定性区域大小顺序是一致的; 而且在受控系统(9)的稳定性区域中有一个小区域, 其对应的受控系统(27)是不稳定的.
3 不同步采样反馈的作用机理本节从力学角度探讨为何采样反馈控制律(19)使受控系统的稳定性区域变小, 而控制律(10)可使受控系统的稳定性区域变大.
一方面, 由于采样周期h很小, 所以有
| $ \left\{ \begin{array}{l} x({t_{n - 2}}) \approx x({t_{n - 1}}) - \dot x({t_{n - 1}})h\\ \dot x({t_{n - 2}}) \approx \dot x({t_{n - 1}}) - \ddot x({t_{n - 1}})h \end{array} \right. $ |
在控制律(10)作用下, 滞后一个采样周期的位移采样信号
另一方面, 前面的分析表明, 采样反馈受控系统与连续时滞反馈受控系统之间存在着一种对应关系, 即采样受控系统(3)对应于连续受控系统(9), 采样受控系统(11)对应于连续受控系统(27), 采样受控系统(19)对应于连续受控系统(28).因此, 采样反馈受控系统的稳定性区域间的关系可由连续受控系统的稳定性区域间的关系进行类比来理解.由于连续受控系统的反馈时滞对应于采样反馈受控系统的采样周期, 是小量, 故可将连续受控系统中的时滞项按Taylor公式展开, 进而讨论相应的近似常微分方程的稳定性.
将时滞项展开到二阶导数, 则时滞微分方程(9) (27)和(28)对应的近似常微分方程分别是
| $ \Big (1 - d + \dfrac{p}{2}\Big)\ddot {\hat {x}}(\hat {t}) + (d - p)\dot {\hat {x}}(\hat {t}) + p\hat {x}(\hat {t}) = 0 $ | (30) |
| $ (1 - d + 2p)\ddot {\hat {x}}(\hat {t}) + (d - 2p)\dot {\hat {x}}(\hat {t}) + p\hat {x}(\hat {t}) = 0 $ | (31) |
| $ \Big (1 - 2d + \dfrac{p}{2}\Big)\ddot {\hat {x}}(\hat {t}) + (d - p)\dot {\hat {x}}(\hat {t}) + p\hat {x}(\hat {t}) = 0 $ | (32) |
将这3个方程视为3个等效单自由度系统的运动微分方程, 系统等效刚度均为p, 等效质量分别是
| $ m_1 = 1 - d + \dfrac{p}{2}\, , \quad m_2 = 1 - d + 2p\, , \quad m_3 = 1 - 2d + \dfrac{p}{2} $ |
而等效阻尼分别为
| $ c_1 = d - p\, , \quad c_2 = d - 2p\, , \quad c_3 = d - p $ |
对于不同的反馈增益(p, d), 等效质量和等效阻尼的取值可正可负.由此可见:若微分方程(30)的零解不稳定, 则意味着
数字采样控制系统是一类混杂动力系统, 其稳定性分析及结论与单纯的时间连续控制系统和单纯的离散控制系统都有所不同.和时间连续控制系统相比较, 数字采样控制系统基于采样后所保持的系统状态信号实施控制, 计算控制律的信息有所缺失, 而控制器的实时跟踪效果有所弱化, 故其稳定性区域小于时间连续控制系统的稳定性区域.由于基于多个不同时刻采样信号所构造的控制律可利用系统状态更多的信息量, 从而有望改善受控系统的稳定性.本文研究表明, 对采样PD反馈控制来说, 当速度采样信号滞后于位移采样信号时, 采样反馈必然减小受控系统的稳定性区域, 时滞是不利因素; 而当位移采样信号滞后于速度采样信号时, 采样反馈可明显增大受控系统的稳定性区域, 并且还可改善控制效果, 时滞成为可以被主动利用的有利因素.当位移采样信号滞后于速度采样信号更多采样周期时, 虽然可使受控系统获得更大的稳定性区域, 但实现此功能的硬件代价也更大, 故在应用中要根据实际条件来决定采用何种数字采样控制律.
| 1 | Ackermann J. Sampled-Data Control Systems:Analysis and Synthesis, Robust System Design . Berlin and Heidelberg: Springer-Verlag, 1985. |
| 2 | Chen TW, Francis BA. Optimal Sampled-Data Control . London: Springer-Verlag, 1995. |
| 3 | 张德江. 计算机控制系统 . 北京: 科学出版社, 2011. ( Zhang Dejiang. Computer Controlled Systems . Beijing: Science Press, 2011. (in Chinese) ) |
| 4 | 胡勇, 徐李佳, 解永春. 针对失控翻滚目标航天器的交会对接控制. 宇航学报, 2015, 36 (1) : 47-57. ( Hu Yong, Xu Lijia, Xie Yongchun. Control for rendezvous and docking with a tumbling target spacecraft. Journal of Astronautics, 2015, 36 (1) : 47-57. (in Chinese) ) |
| 5 | Wan Y, Wen G, Cao J, et al. Distributed node-to-node consensus of multi-agent systems with stochastic sampling. International Journal of Robust and Nonlinear Control, 2016, 26 (1) : 110-124. DOI: 10.1002/rnc.3302. |
| 6 | Wu H, Li R, Wei H, et al. Synchronization of a class of memristive neural networks with time delays via sampled-data control. International Journal of Machine Learning and Cybernetics, 2015, 6 (3) : 365-373. DOI: 10.1007/s13042-014-0271-z. |
| 7 | Monaco S, Normand-Cyrot D. An introduction to motion planning under multirate digital control. In:Proceedings of the 31st IEEE Conference on Decision and Control, 1992, 2 : 1780-1785. |
| 8 | Furuta K, Kajiwara H, Kosuge K. Digital control of a double inverted pendulum on an inclined rail. International Journal of Control, 1980, 32 (5) : 907-924. DOI: 10.1080/00207178008922898. |
| 9 | 藏强, 梅平, 郑柏超, 等. 非线性微分-代数系统的反馈镇定:基于线性采样控制. 自动化学报, 2015, 41 (10) : 1831-1836. ( Zang Qiang, Mei Ping, Zheng Baichao, et al. Output feedback stabilization of nonlinear differential-algebraic equations system based on linear sampled-data control. Acta Automatica Sinica, 2015, 41 (10) : 1831-1836. (in Chinese) ) |
| 10 | 郭雷. 关于控制理论发展的某些思考. 系统科学与数学, 2011, 31 (9) : 1014-1018. ( Guo Lei. Some thoughts on the development of control theory. Journal of Systems Science and Mathematical Science, 2011, 31 (9) : 1014-1018. (in Chinese) ) |
| 11 | Fridman E, Seuret A, Richard JP. Robust sampled-data stabilization of linear systems:an input delay approach. Automatica, 2004, 40 (8) : 1441-1446. DOI: 10.1016/j.automatica.2004.03.003. |
| 12 | Fridman E. A refined input delay approach to sampled-data control. Automatica, 2010, 46 (2) : 421-427. DOI: 10.1016/j.automatica.2009.11.017. |
| 13 | Sakthivel R, Arunkumar A, Mathiyalagan K. Robust sampled-data H∞ control for mechanical systems. Complexity, 2015, 20 (4) : 19-29. DOI: 10.1002/cplx.v20.4. |
| 14 | Nagahara M., Yamamoto. Digital repetitive controller design via sampled-data delayed signal reconstruction. Automatica, 2015, 65 (3) : 203-209. |
| 15 | Palmeira AHK, Gomes da Silva Jr JM, Tarbouriech S, et al. Sampled-data control under magnitude and rate saturating actuators. International Journal of Robust and Nonlinear Control, 2016, doi:10.1002/rnc.3503 |
| 16 | Naghshtabrizi P, Hespanha JP, Teel AR. Exponential stability of impulsive systems with application to uncertain sampled-data systems. Systems and Control Letters, 2008, 57 (5) : 378-385. DOI: 10.1016/j.sysconle.2007.10.009. |
| 17 | Mansour M. A note on the stability of linear discrete systems and Lyapunov method. IEEE Transactions on Automatic Control, 1982, 27 (3) : 707-708. DOI: 10.1109/TAC.1982.1103000. |
| 18 | Martynyuk AA. Stability analysis of discrete systems. International Applied Mechanics, 2000, 36 (7) : 835-865. DOI: 10.1007/BF02682295. |
| 19 | Rabbath CA, Lechevin N. Discrete-Time Control Design with Applications . New York: Springer-Verlag, 2014. |
| 20 | Insperger T, Stepan G. Stability improvements of robot control by periodic variations of the gain parameters. In:Tian Huang ed. Proc. of the 11th World Congress in Mechanism and Machine Science . Beijing: China Machine Press, 2004: 1816-1820. |
| 21 | Insperger T, Stepan G. Semi-discretization for Time-Delay Systems:Stability and Engineering Applications . Berlin and Heidelberg: Springer-Verlag, 2011. |
| 22 | Habib G, Rega G, Stepan G. Delayed digital position control of a single-DOF system and the nonlinear behavior of the act-and-wait controller. Journal of Vibration and Control, 2016, 22 (2) : 481-495. DOI: 10.1177/1077546314533583. |
| 23 | Habib G, Rega G, Stepan G. Stability analysis of a two-DOF mechanical system subjected to proportional-derivative digital position control. Journal of Vibration and Control, 2015, 21 (8) : 1539-1555. DOI: 10.1177/1077546312474014. |
| 24 | Zhou J, Zhang H, Xiang L, et al. Sampled-data synchronization of coupled harmonic oscillators with controller failure and communication delays. Theoretical and Applied Mechanics Letters, 2013, 3 (6) : 063002. DOI: 10.1063/2.1306302. |
| 25 | 赵艳影, 徐鉴. 时滞非线性动力吸振器的减振机理. 力学学报, 2008, 40 (1) : 98-106. ( Zhao Yanying, Xu Jian. Mechanism analysis of delayed nonlinear vibration absorber. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40 (1) : 98-106. (in Chinese) ) |
| 26 | 陈龙祥, 蔡国平. 旋转运动柔性梁的时滞主动控制实验研究. 力学学报, 2008, 40 (4) : 520-527. ( Chen Longxiang, Cai Guoping. Experimental study on active control of a rotating flexible beam with time delay. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40 (4) : 520-527. (in Chinese) ) |
| 27 | 王在华, 李俊余. 时滞状态正反馈在振动控制中的新特征. 力学学报, 2010, 42 (5) : 933-942. ( Wang Zaihua, Li Junyu. New features of time-delayed positive feedbacks in vibration control. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42 (5) : 933-942. (in Chinese) ) |
| 28 | 王在华, 胡海岩. 时滞动力系统的稳定性与分岔:从理论走向应用. 力学进展, 2013, 43 (1) : 3-20. ( Wang Zaihua, Hu Haiyan. Stability and bifurcation of delayed dynamic systems:From theory to application. Advances in Mechanics, 2013, 43 (1) : 3-20. (in Chinese) ) |
| 29 | Wang ZH. A very simple criterion for characterizing the crossing direction of time-delay systems. International Journal of Bifurcation and Chaos, 2012, 29 (2) : 1250048. |
| 30 | Kuang Y. Delay Di erential Equation with Application to Population Dynamics . San Diego: Academic Press, Academic Press. |
†. School of Aerospace Engineering, Beijing Institute of Technology, Beijing 100081, China;
**. State Key Lab of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China