土-结构相互作用是地震工程领域的重要问题,以往对该问题的研究集中在地基土为干土的情形,对地基土为饱和土情形的研究相对较少.而实际情形中,地下水位以上可视为干土,水位以下可视为饱和土,对该情形的研究更是鲜有报导.地震波输入下土-结构相互作用分析一般采用子结构法[1-4]、集中参数法[5-8]和直接法[9-12].子结构法和集中参数法将土-结构相互作用问题分解为如下可独立求解的子问题:(1) 自由场问题,即结构和基础不存在时土层在地震波入射时的响应问题;(2) 基础的输入问题,即结构不存在时,无质量刚性基础在地震波入射时的响应问题;(3) 刚性基础的动力刚度或动力柔度矩阵;(4) 结构响应问题.下面仅就饱和土层自由场分析和饱和地基动力刚度研究的相关工作做一简单介绍.
自Biot[13-15]建立多孔弹性介质波的传播理论以来,Deresiewicz等[16-18]对于波在饱和土界面上的传播特性进行了系统的研究, 分析了平面波在自由表面、分层多孔介质界面中的反射和透射. Jocker等[19]通过推广Thomson-Haskell传递矩阵法,以得到一种封闭形式的解析表达式,用于计算水平成层多孔介质的反射率和透射率. Rajapakse等[20]、Degrande等[21]、Liang等[22]分别给出了饱和土层和半空间的精确动力刚度矩阵,采用直接刚度法可求得饱和水平层状场地的自由场响应.李伟华等[23]采用波函数展开法,求得饱和弹性均匀半空间的自由场,进一步分析了饱和沉积谷场地对SV波的散射问题.赵宇昕等[24]采用传递矩阵法分析了成层饱和土层自由场响应,并探讨了数值结果中的非因果原因.
1986年,Halpern等[25]通过对基础所覆盖的单元域上Green函数数值积分给出了三维饱和弹性半空间表面上刚性板的动力柔度系数. Bougacha等[26]采用基础空间离散振动模态的有限元方法得到了饱和弹性土层上长条形基础和圆形基础的动力刚度. Japon等[27]应用边界元方法分析了长条形基础的动力刚度,并考虑了渗透力、附加密度、地层深度、基础刚度对基础振动的影响.陈少林等[28-29]提出了一种时域求解基础阻抗函数的方法,通过给基础输入脉冲位移,应用集中质量显示有限元方法结合局部透射人工边界,得到地基施加于基础的反力时程,然后根据阻抗函数定义,应用傅里叶变换求得基础阻抗函数.
子结构法以频域内的动力刚度为基础,集中参数法通过拟合动力刚度得到参数模型,理论上都只适用于线性系统,不能考虑土体的非线性.直接法将地基、基础和上部结构一并计算,可以方便考虑土体的非均匀性和非线性,但计算量一般较大,尤其是饱和土情形.梁建文等[30-31]将单相土-结构相互作用的研究拓展到饱和土领域[32],采用间接边界元法分析了二维线性饱和土-结构相互作用问题,分析了P-SV波斜入射时,孔隙率、土层深度、土层与基岩间的刚度比等参数的影响.本文拟将显-隐式结合的土-结构相互作用分析方法[10],推广到三维饱和土-结构动力相互作用情形,采用集中质量显示有限元结合透射人工边界的方法分析饱和土体[33-35],采用隐式方法对上部结构进行分析,实现三维饱和土-基础-结构动力相互作用分析.
根据干土是饱和土的特殊情形这一事实,将两者情形的土-结构相互作用分析统一到饱和土-结构相互作用分析框架,进而可分析考虑地下水位情形的土-结构相互作用分析.
1 基本理论 1.1 土体内节点运动根据Biot[1]理论,饱和弹性多孔介质运动方程可以表示为
| $ \left. \begin{array}{l} N{\nabla ^2}\mathit{\boldsymbol{u}} + \nabla \left[ {(D + N)\nabla \cdot \mathit{\boldsymbol{u}} + Q\nabla \cdot \mathit{\boldsymbol{U}}} \right] = \\ \;\;\;\;\;\;\frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {{\rho _{11}}\mathit{\boldsymbol{u}} + {\rho _{12}}\mathit{\boldsymbol{U}}} \right) + \eta \frac{\partial }{{\partial t}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{U}}} \right)\\ \nabla \left( {Q\nabla \cdot \mathit{\boldsymbol{u}} + R\nabla \cdot \mathit{\boldsymbol{U}}} \right) = \\ \;\;\;\;\;\;\frac{{{\partial ^2}}}{{\partial {t^2}}}\left( {{\rho _{12}}\mathit{\boldsymbol{u}} + {\rho _{22}}\mathit{\boldsymbol{U}}} \right) - \eta \frac{\partial }{{\partial t}}\left( {\mathit{\boldsymbol{u}} - \mathit{\boldsymbol{U}}} \right) \end{array} \right\} $ | (1) |
其中
从地基土中取一有限土体,采用八节点三维实体元对其进行空间离散.将土体划分成两个区域,即人工边界区和内部计算区(如图 1),将土体单元节点划分为人工边界点、与基础相连的点和内节点三类.对于内点采用集中质量显式有限单元法.在人工边界上,采用多次透射公式模拟无限域的影响.对于内节点而言,对方程(1)进行有限元空间离散,得到第i个节点的固相运动方程为[33]
| $ \boldsymbol{\ddot u}_i \boldsymbol{M}_{si} + \sum\limits_{e = 1}^N \sum\limits_{j = 1}^J \left( {\boldsymbol{C}_{ssk(i)j}^e \boldsymbol{\dot u}_j^e - \boldsymbol{C}_{swk(i)j}^e \boldsymbol{\dot U}_j^e + }\right.\\ \qquad \left.{ \boldsymbol{K}_{ssk(i)j}^e \boldsymbol{u}_j^e + \boldsymbol{K}_{swk(i)j}^e \boldsymbol{u}_j^e } \right) = \sum\limits_{e = 1}^N \boldsymbol{F}_{si}^e $ | (2) |

|
图 1 饱和土-基础-结构相互作用示意图 Figure 1 Sketch of saturated soil-foundation-structure interaction |
液相运动方程为
| $ \begin{array}{l} {{\mathit{\boldsymbol{\ddot U}}}_i}{\mathit{\boldsymbol{M}}_{wi}} + \sum\limits_{e = 1}^N {\sum\limits_{j = 1}^J {\left( { - \mathit{\boldsymbol{C}}_{wsk(i)j}^e\mathit{\boldsymbol{\dot u}}_j^e + \mathit{\boldsymbol{C}}_{wwk(i)j}^e\mathit{\boldsymbol{\dot U}}_j^e + } \right.} } \\ \left. {\mathit{\boldsymbol{K}}_{wsk(i)j}^e\mathit{\boldsymbol{u}}_j^e + \mathit{\boldsymbol{K}}_{wwk(i)j}^e\mathit{\boldsymbol{U}}_j^e} \right) = \sum\limits_{e = 1}^N {\mathit{\boldsymbol{F}}_{wi}^e} \end{array} $ | (3) |
其中,
此外,我们可以注意到,上述阻尼矩阵仅考虑固液两相互相运动所产生的阻尼,对固相骨架考虑瑞雷阻尼
| $ \boldsymbol{C}_{Rss}^e = \alpha \boldsymbol{M}_{sk(i)}^e + \beta \boldsymbol{K}_{ss}^e $ | (4) |
那么式(2)可修正为
| $ \boldsymbol{\ddot u}_i \boldsymbol{M}_{si} + \sum\limits_e \sum\limits_{j = 1}^J \left( {\boldsymbol{C}_{ssk(i)j}^e \boldsymbol{\ddot u}_j^e - \boldsymbol{C}_{swk(i)j}^e \boldsymbol{\ddot U}_j^e + \boldsymbol{ C}_{Rssk(i)j}^e \boldsymbol{\ddot u}_j^e } \right. + \\ \qquad \left.{ \boldsymbol{K}_{ssk(i)j}^e \boldsymbol{u}_j^e + \boldsymbol{K}_{swk(i)j}^e \boldsymbol{U}_j^e } \right) = \sum\limits_e \boldsymbol{F}_{si}^e $ | (5) |
对内节点方程(5)和方程(3)采用中心差分与单边结合的积分格式进行时域积分.假定在p+1及其以前时刻节点i的位移矢量已知,时间离散步长用
| $ \boldsymbol{\ddot W}^p = \dfrac{\boldsymbol{W}^{p + 1} - 2\boldsymbol{W}^p + \boldsymbol{W}^{p - 1}}{\Delta t^2} , \quad \boldsymbol{\ddot W}^p = \dfrac{\boldsymbol{W}^p - \boldsymbol{W}^{p - 1}}{\Delta t} $ | (6) |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{u}}_i^{p + 1} = 2\mathit{\boldsymbol{u}}_i^p - \mathit{\boldsymbol{u}}_i^{p - 1} + \Delta {t^2}\mathit{\boldsymbol{M}}_{si}^{ - 1}\left\{ {\sum\limits_e {\mathit{\boldsymbol{F}}_{si}^e} - } \right.\qquad \\ \sum\limits_e {\sum\limits_{j = 1}^J {\left[ {\left( {\mathit{\boldsymbol{C}}_{ssk(i)j}^e + \mathit{\boldsymbol{C}}_{Rssk(i)j}^e} \right)\frac{{\mathit{\boldsymbol{u}}_j^{ep} - \mathit{\boldsymbol{u}}_j^{e\left( {p - 1} \right)}}}{{\Delta t}} - } \right.} } \qquad \\ \left. {\left. {\mathit{\boldsymbol{C}}_{swk(i)j}^e\frac{{\mathit{\boldsymbol{U}}_j^{ep} - \mathit{\boldsymbol{U}}_j^{e\left( {p - 1} \right)}}}{{\Delta t}} + \mathit{\boldsymbol{K}}_{ssk(i)j}^e\mathit{\boldsymbol{u}}_j^e + \mathit{\boldsymbol{K}}_{swk(i)j}^e\mathit{\boldsymbol{U}}_j^e} \right]} \right\} \end{array} $ | (7) |
| $ \begin{array}{l} \mathit{\boldsymbol{U}}_i^{p + 1} = 2\mathit{\boldsymbol{U}}_i^p - \mathit{\boldsymbol{U}}_i^{p - 1} + \Delta {t^2}\mathit{\boldsymbol{M}}_{wi}^{ - 1}\left[ {\sum\limits_e {\mathit{\boldsymbol{F}}_{wi}^e} } \right. - \\ \sum\limits_e {\sum\limits_{j = 1}^J {\left( { - \mathit{\boldsymbol{C}}_{wsk(i)j}^e\frac{{\mathit{\boldsymbol{u}}_j^{ep} - \mathit{\boldsymbol{u}}_j^{e\left( {p - 1} \right)}}}{{\Delta t}} + } \right.} } \\ \left. {\left. {\mathit{\boldsymbol{C}}_{wwk(i)j}^e\frac{{\mathit{\boldsymbol{U}}_j^{ep} - \mathit{\boldsymbol{U}}_j^{e\left( {p - 1} \right)}}}{{\Delta t}} + \mathit{\boldsymbol{K}}_{wsk(i)j}^e\mathit{\boldsymbol{u}}_j^e + \mathit{\boldsymbol{K}}_{wwk(i)j}^e\mathit{\boldsymbol{U}}_j^e} \right)} \right\} \end{array} $ | (8) |
对于人工边界上的节点,其运动状态可通过多次透射公式[36]进行确定
| $ u_0^{p + 1} = \sum\limits_{n = 1}^N {\left( { - 1} \right)^{n + 1}C_n^N \boldsymbol{T}_n \boldsymbol{u}_n^{p + 1 - n} } $ | (9) |
其中,
| $ C_n^N = \dfrac{N!}{\left( {N - n} \right)!n!} $ | (10) |
| $ \boldsymbol{u}_n^{p + 1 - n} = \left( {u_0^{p + 1 - n}, u_1^{p + 1 - n}, \cdots, u_{2n}^{p + 1 - n} } \right)^{\rm T} $ | (11) |
行向量
| $ \boldsymbol{T}_n = \left( {t_{n, 1}, t_{n, 2}, \cdots, t_{n, 2n + 1} } \right) $ | (12) |
其中
| $ t_{n, m} = \sum {t_{1, k_1 } } t_{1, k_2 } \cdots t_{1, k_j } , \ \ m = 1, 2, \cdots, 2n + 1 $ | (13) |
上式中记号"
| $ k_1 + k_2 + \cdots + k_j = m + n-1 , \ \ k_1, k_2, \cdots, k_j = 1, 2, 3 $ | (14) |
以一阶Modulation Transfer Function (MTF)为例,那么可知
| $ u_0^{p + 1} = \boldsymbol{T}_1 \boldsymbol{u}_1^p = t_{1, 1} u_0^p + t_{1, 2} u_1^p + t_{1, 3} u_2^p $ | (15) |
| $ \left. {\begin{array}{*{20}{l}} \begin{array}{l} {t_{1,1}} = \left( {2 - S} \right)\left( {1 - S} \right)/2\\ {t_{1,2}} = S\left( {2 - S} \right)\\ {t_{1,3}} = S\left( {S - 1} \right)/2 \end{array} \end{array}} \right\} $ | (16) |
其中
式(9)分别用于饱和多孔介质的固相位移和液相位移,可得到边界点在p+1时刻的散射波场位移,加上边界点的自由场位移,即可得到边界点在p+1时刻的总位移.式(11)中的散射位移向量可通过式(7)和式(8)得到的总位移减去自由场位移得到.对于饱和成层土体的自由场计算可参见文献[24].对于上覆干土,下卧饱和土的情形,可通过满足干土和饱和土分界面上的4个应力位移连续条件,得到相应的传递矩阵.
具体计算流程可参见图 2.

|
图 2 边界节点总位移场计算流程图 Figure 2 Flow chart of calculating the total displacement of boundary nodes |
对于一般情况下的结构或系统,其动力学方程均可写成
| $ \boldsymbol{M}\boldsymbol{\ddot u} + \boldsymbol{c}\boldsymbol{\ddot u} + \boldsymbol{k}\boldsymbol{u} = \boldsymbol{ F} $ | (17) |
在
| $ \left. \begin{array}{l} {\mathit{\boldsymbol{u}}^{p + 1}} = {\mathit{\boldsymbol{u}}^p} + {{\mathit{\boldsymbol{\dot u}}}^p}\Delta t + \left[ {\left( {\frac{1}{2} - \beta } \right){{\mathit{\boldsymbol{\ddot u}}}^p} + \beta {{\mathit{\boldsymbol{\ddot u}}}^{p + 1}}} \right]\Delta {t^2}\\ {{\mathit{\boldsymbol{\dot u}}}^{p + 1}} = {{\mathit{\boldsymbol{\dot u}}}^p} + \left[ {\left( {1 - \gamma } \right){{\mathit{\boldsymbol{\ddot u}}}^p} + \gamma {{\mathit{\boldsymbol{\ddot u}}}^{p + 1}}} \right]\Delta t\\ {{\mathit{\boldsymbol{\ddot u}}}^{p + 1}} = \frac{1}{{\beta \Delta {t^2}}}\left( {{\mathit{\boldsymbol{u}}^{p + 1}} - {\mathit{\boldsymbol{u}}^p}} \right) - \frac{1}{{\beta \Delta t}}{{\mathit{\boldsymbol{\dot u}}}^p} - \left( {\frac{1}{{2\beta }} - 1} \right){{\mathit{\boldsymbol{\ddot u}}}^p} \end{array} \right\} $ | (18) |
式中,
| $ \begin{array}{l} \left( {\mathit{\boldsymbol{K}} + \frac{1}{{\beta \Delta {t^2}}}\mathit{\boldsymbol{M}} + \frac{\gamma }{{\beta \Delta t}}\mathit{\boldsymbol{C}}} \right){\mathit{\boldsymbol{u}}^{p + 1}} = {\mathit{\boldsymbol{F}}^{p + 1}} + \mathit{\boldsymbol{M}}\left[ {\frac{1}{{\beta \Delta {t^2}}}{\mathit{\boldsymbol{u}}^p} + } \right.\\ \left. {\frac{1}{{\beta \Delta t}}{{\mathit{\boldsymbol{\dot u}}}^p} + \left( {\frac{1}{{2\beta }} - 1} \right){{\mathit{\boldsymbol{\ddot u}}}^p}} \right] + \mathit{\boldsymbol{C}}\left[ {\frac{\gamma }{{\beta \Delta t}}{\mathit{\boldsymbol{u}}^p} + } \right.\\ \left. {\left( {\frac{\gamma }{\beta } - 1} \right){{\mathit{\boldsymbol{\dot u}}}^p} + \left( {\frac{\gamma }{{2\beta }} - 1} \right)\Delta t{{\mathit{\boldsymbol{\ddot u}}}^p}} \right] \end{array} $ | (19) |
由式(19)可以得到
刚性基础作为土体和上部结构的连接部分,起到了承上启下的作用,传递结构与土体之间的作用力.其运动可由6个分量描述,即3个平动分量和3个转动分量土和结构作用在基础上的合力使基础产生刚体运动
| $ \boldsymbol{M}_{\rm F} \boldsymbol{\ddot u}_{\rm F} = \boldsymbol{F} = \boldsymbol{F}_{\rm S} + \boldsymbol{F}_{\rm D} $ | (20) |
式中,
首先考虑p时刻土体对刚性基础作用力
| $ \begin{array}{l} \left\{ {\begin{array}{*{20}{c}} {F_{kx}^p}\\ {F_{ky}^p}\\ {F_{kz}^p} \end{array}} \right\} = \frac{1}{{\Delta t}}\sum\limits_L^N {\left[ {\left( {{C_{ssL}} + {C_{RssL}}} \right)\left( {u_k^p - u_k^{p - 1}} \right) - } \right.} \\ \left. {\;\;\;\;\;\;{C_{swL}}\left( {U_k^p - U_k^{p - 1}} \right)} \right] + \sum\limits_L^N {\left( {{K_{ssL}}u_k^p + {K_{swL}}U_k^p} \right)} + \\ \frac{1}{{\Delta t}}\sum\limits_L^N {\left[ { - {C_{wsL}}\left( {u_k^p - u_k^{p - 1}} \right) + {C_{wwL}}\left( {U_k^p - U_k^{p - 1}} \right)} \right]} + \\ \sum\limits_L^N {\left( {{K_{wsL}}u_k^p + {K_{wwL}}U_k^p} \right)} \end{array} $ | (21) |
因此饱和土体对刚性基础的合力可以表示为
| $ \boldsymbol{F}_{\rm D}^p = \sum\limits_{k = 1}^m \boldsymbol{A }_k^{\rm T} \boldsymbol{F }_k^p $ | (22) |
| $ \boldsymbol{F }_k^p = \left( {F_{kx}^p, F_{ky}^p, F_{kz}^p, 0, 0, 0} \right)^{\rm T} $ | (23) |
| $ \boldsymbol{F }_D^p = \left( {F_{{\rm D}x}^p, F_{{\rm D}y}^p, F_{{\rm D}z}^p, M_{{\rm D}x}^p, M_{{\rm D}y}^p, M_{{\rm D}z}^p } \right)^{\rm T} $ | (24) |
| $ {\mathit{\boldsymbol{A}}_k} = \left[ {\begin{array}{*{20}{c}} 1&0&0&0&{\Delta {Z_k}}&{ - \Delta {Y_k}}\\ 0&1&0&{ - \Delta {Z_k}}&0&{\Delta {X_k}}\\ 0&0&1&{\Delta {Y_k}}&{ - \Delta {X_k}}&0\\ 0&0&0&1&0&0\\ 0&0&0&0&1&0\\ 0&0&0&0&0&1 \end{array}} \right] $ | (25) |
其中,m表示土体与基础接触点总数;
其次考虑p时刻结构对刚性基础作用力
| $ \boldsymbol{F }_i^p = \left( {F_{ix}^p, F_{iy}^p, F_{iz}^p, M_{ix}^p, M_{iy}^p , M_{iz}^p } \right)^{\rm T} $ | (26) |
可通过ANSYS分析得到各点反力值
| $ \boldsymbol{F }_{\rm S}^p = \sum\limits_{i = 1}^n \boldsymbol{A }_i^{\rm T} \boldsymbol{F }_i^p $ | (27) |
| $ \boldsymbol{F }_{\rm S}^p = \left( {F_{{\rm S}x}^p, F_{{\rm S}y}^p, F_{{\rm S}z}^p, M_{{\rm S}x}^p, M_{{\rm S}y}^p, M_{{\rm S}z}^p } \right)^{\rm T} $ | (28) |
其中,n表示结构与基础接触点总数;
得到p时刻作用力
| $ \boldsymbol{u}_{\rm F}^{p + 1} = 2\boldsymbol{u}_{\rm F}^p - \boldsymbol{u}_{\rm F}^{p - 1} + \Delta t^2\boldsymbol{M }_{\rm F}^{ - 1} \left( {\boldsymbol{F }_{\rm D}^p + \boldsymbol{ F }_{\rm S}^p } \right) $ | (29) |
通过刚性基础位移可得到与其接触的土体点或结构点的位移
| $ \boldsymbol{u}^{p + 1} = \boldsymbol{A \pmb u}_{\rm F}^{p + 1} $ | (30) |
上面对饱和土-基础-结构相互作用分析的各个部分计算方法做了详细阐述,下面简述其基本分析步骤.假定p及以前时刻土体、基础与结构位移已知,计算p+1时刻各点的位移,基本步骤可以可描述如下:
(1) 采用集中质量显式有限元的方法,由式(7)和式(8)得到饱和土体内节点固、液相位移;
(2) 利用多次透射式(9)和自由场位移得到饱和土体人工边界节点的固、液相位移;
(3) 根据式(29)得到基础整体位移,进而由式(30)得到与刚性基础相连土体节点位移以及结构节点位移;
(4) 得到与基础相联的结构节点位移后,将该位移作为结构约束,根据式(19)可得到结构各点位移, 进一步可得到该时刻结构对基础的作用力;
(5) 重复执行步骤(1)~(4),即可得到饱和土-基础-结构体系在各时刻的动力反应.
根据上述原理,通过编制相应的FORTRAN程序实现了地震波入射时饱和土-基础-结构相互作用分析.其中结构可通过ANSYS有限元软件进行分析,通过FORTRAN调用ANSYS实现饱和土-基础-结构系统的整体分析.
2 饱和土退化为干土的实现方法及验证当流体体积模量
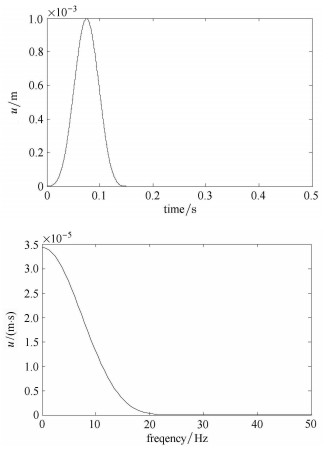
上部结构通过ANSYS进行分析,采用悬臂梁模型,截面尺寸0.1 m×0.1 m,梁高2 m,密度2 500 kg/m3,弹性模量3.00 GPa,泊松比0.2,阻尼比0.05,剪切波速707 m/s,一阶振型周期0.226 s.刚性基础尺寸6 m×6 m×4 m,密度2 500 kg/m3.考虑表 1中前两类地基土,输入相同的单位脉冲SV波:时间步距dt=0.000 2 s,脉冲宽度t0=0.15 s,步数n=1013 (见图 3).土体划分单元尺寸均为1 m×1 m×1 m,满足波动模拟精度要求.结构隐式分析的时间步距dT=0.002 s,即FORTRAN每10步对ANSYS执行一次调用.
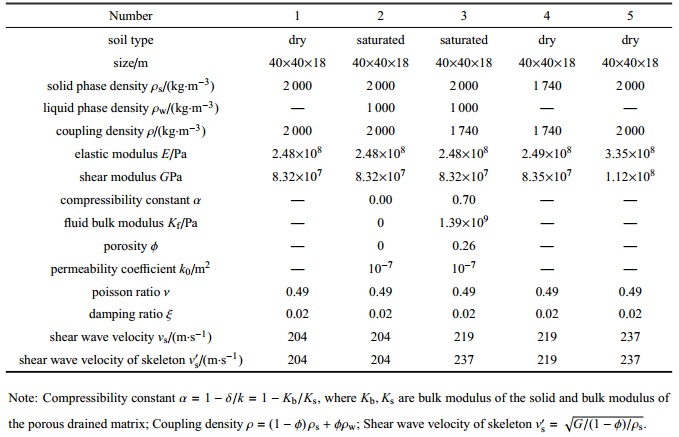
| 表 1 土参数 Table 1 Soil parameter |
|
图 3 单位脉冲形状及频谱图 Figure 3 Unit pulse shape and spectrum |
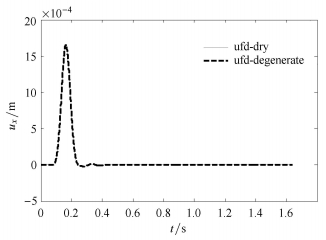
图 4和图 5分别给出了基础和结构顶部的位移.实线为干土情形的结果,虚线为饱和土退化情形的结果,两者完全吻合.因此,地基土为干土情形的土-基础-结构相互作用分析可纳入到饱和土-基础-结构相互作用分析框架,进而可以分析考虑地下水位的干土覆盖饱和土情形的土-结构相互作用分析.另外,结构在基础有效输入为零后(因为结构柔且小,不足以带动基础做相应运动)做有阻尼的自由振动,其周期正好为结构一阶振型周期0.226 s.
|
图 4 饱和土退化情形下基础位移时程图 Figure 4 Displacement of the foundation for the degradation of saturated soil |

|
图 5 饱和土退化情形下结构顶部节点位移时程图 Figure 5 Displacement of the structure's top node for the degradation of saturated soil |
实际工程中,地下水位位于地表以下一定深度,若直接考虑为干土或饱和土并不合适.以下就地震波入射时土-基础-结构动力相互作用问题,比较地基土分别为干土情形、饱和土情形、干土覆盖饱和土情形对基础和结构响应的影响.仍采用悬臂梁结构及刚性基础,首先考虑地基土为表 1中的3号、4号、5号的情形,分别称为CASE1, CASE2, CASE3.其中,3号为饱和土,4号为具有与3号饱和土相同剪切波速和密度的干土,在工程中,常常对饱和土进行如此简化;5号为干土,具有与3号饱和土相同的骨架剪切波速和固相密度.最后考虑由上覆4 m厚的5号干土,下卧14 m厚的3号饱和土所组成的地基土,这种场地描述了当地下水位为4 m时的情况,称其为CASE4.
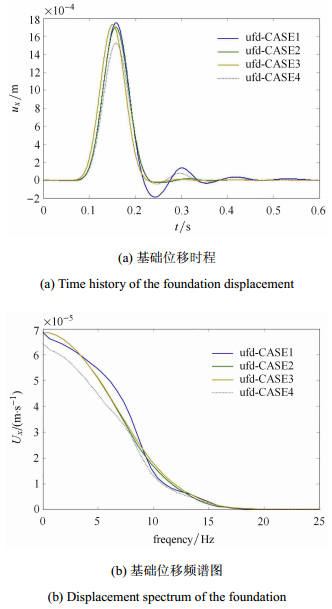
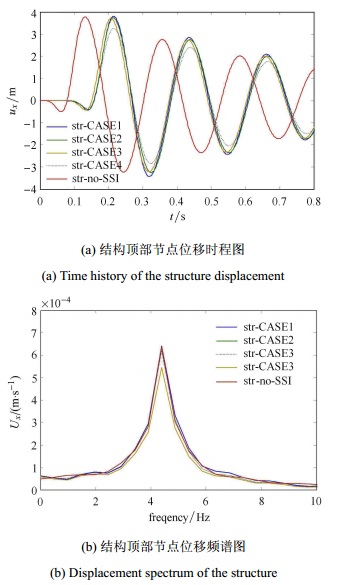
图 6(a)和图 6(b)分别为以上4种地基土情形时基础的位移时程和频谱. 图 7(a)和图 7(b)为结构顶点的位移时程和频谱,为了比较,图中同时给出了不考虑土结相互作用情形时的结果.由图可知,就本文算例而言,若通过两种干土模型(CASE2, CASE3)代替饱和土模型(CASE1)进行分析,基础与结构的位移均将偏小.由于CASE3中的干土剪切波速更大,其到时也比CASE1与CASE2的情况要早. CASE4与前3种情况相比,基础与结构的位移都有较大幅度减小,并不是介于干土和饱和土情形的结果之间,表明一定深度的地下水位对基础和结构响应的影响较大.不考虑土结相互作用时,脉冲位移从结构底部输入,到时较其他情形早(见图 7(a)),最大位移与饱和土-结构相互作用情形CASE1相当,但要大于其他情形(CASE2~CASE4).自由振动阶段的位移幅值小于CASE1,大于其余情形.另外,由图 7可知,由于结构柔且小,在脉冲输入结束后,结构独自做有阻尼的自由振动(此时基础反应很小),此时土-结构相互作用影响较小,与土体情形基本无关,其周期均为结构一阶振型周期0.226 s.
|
图 6 Figure 6 |
|
图 7 Figure 7 |
土体中的孔隙水将影响土体的地震反应,进而影响支撑其上的基础和结构的响应,为此,本文发展了一种饱和土-基础-结构动力相互作用分析的高效方法,主要结论如下:
(1) 采用集中质量显式有限元方法结合多次透射人工边界模拟半无限饱和土体,利用隐式积分方法分析上部结构,实现了地震波输入时饱和土-基础-结构动力相互作用的高效分析.
(2) 通过将流体体积模量
(3) 对比了饱和土地基、干土地基、干土覆盖饱和土地基(考虑地下水位)情形时,土-结构相互作用对基础和结构响应的影响,算例表明,地下水位对基础和结构响应的影响较大.
| 1 | Luco JE. Dynamic interaction of a shear wall with the soil. J Eng Mech Div ASCE, 1969, 95 : 333-346. |
| 2 | Kobori T, Minai R, Shinozaki Y. Vibration of a rigid circular disc on an elastic half-space subjected to plane waves. Theoretical and Applied Mechanics, 1973 (21) : 108-119. |
| 3 | Guin J, Banerjee P K. Coupled soil-pile-structure interaction analysis under seismic excitation. J Struct Eng Div ASCE, 1998, 124 (4) : 434-444. DOI: 10.1061/(ASCE)0733-9445(1998)124:4(434). |
| 4 | 宋亚新, 蒋通, 楼梦麟. 桩基-非线性框剪结构相互作用体系(下)-相互作用对结构地震反应的影响. 地震工程与工程振动, 2000, 20 (1) : 48-55. ( Song Yaxin, Jiang Tong, Lou Menglin. Pilenonlinear frame-wall interaction systems. Part Ⅱ:effects of interaction on seismic responses of structures. Journal of Earthquake Engineering and Engineering Vibration, 2000, 20 (1) : 48-55. (in Chinese) ) |
| 5 | Wolf JP. Soil-structure interaction analysis in time domain . NJ: Prentice Hall, Englewood Cliffs, 1988: 11-35. |
| 6 | Jean WY, Lin TW, Penzien J. System parameters of soil foundations for time domain dynamic analysis. Earthq. Earthquake Engineering and Structural Dynamics, 1990, 19 (4) : 541-553. DOI: 10.1002/(ISSN)1096-9845. |
| 7 | 王有为, 王开顺. 建筑物-桩-土相互作用地震反应分析的研究. 建筑结构学报, 1985, 6 (5) : 64-73. ( Wang Youwei, Wang Kaishun. Research on earthquake response analysis of building structure-pilesoil interaction. Journal of Building Structures, 1985, 6 (5) : 64-73. (in Chinese) ) |
| 8 | 李永梅, 孙国富, 王松涛, 等. 桩-土-杆系结构动力相互作用. 建筑结构学报, 2002, 23 (1) : 75-81. ( Li Yongmei, Sun Guofu, Wang Songtao, et al. Dynamic interaction of pile-soil-frame structure. Journal of Building Structures, 2002, 23 (1) : 75-81. (in Chinese) ) |
| 9 | 刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法. 土木工程学报, 1998, 31 (3) : 55-64. ( Liu Jingbo, Lu Yandong. A direct method for analysis of dynamic soil-structure interaction. China Civil Engineering Journal, 1998, 31 (3) : 55-64. (in Chinese) ) |
| 10 | 陈少林, 唐敢, 刘启方, 等. 三维土-结构动力相互作用的一种时域直接分析方法. 地震工程与工程振动, 2010, 30 (2) : 24-31. ( Chen Shaolin, Tang Gan, Liu Qifang, et al. A direct time-domain method for analysis of three-dimensional soil-structure dynamic interaction. Jounal of Earthquake Engineering and Engineering Vibration, 2010, 30 (2) : 24-31. (in Chinese) ) |
| 11 | 杨笑梅, 郭达文, 杨柏坡. 三维土-结构动力相互作用体系分析的两步时域显式波动有限元过程. 地震工程与工程振动, 2011, 31 (4) : 9-17. ( Yang Xiaomei, Guo Dawen, Yang Baipo. A two-step explicit finite element method in time domain for 3D dynamic SSI analysis. Jounal of Earthquake Engineering and Engineering Vibration, 2011, 31 (4) : 9-17. (in Chinese) ) |
| 12 | 姜忻良, 张海顺. 土-结构非线性相互作用混合约束模态实施方法. 振动与冲击, 2015, 34 (6) : 52-56. ( Jiang Xinliang, Zhang Haishun. Mixed constraint modal method for nonlinear soilstructure interaction. Journal of Vibration and Shock, 2015, 34 (6) : 52-56. (in Chinese) ) |
| 13 | Biot MA. Theory of propagation of elastic waves in a fluid-saturated porous solid. Acoust Soc Am, 1956, 28 : 168-191. DOI: 10.1121/1.1908239. |
| 14 | Biot MA, Willis DG. The elastic coefficients of the theory of consolidation. Journal of Applied Mechanics, 1957, 24 : 594-601. |
| 15 | Biot MA. Mechanics of deformation and acoustic propagation in porous media. Journal of Applied Physics, 1962, 33 (4) : 1482-1498. DOI: 10.1063/1.1728759. |
| 16 | Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid:Ⅲ. Reflection of plane waves at a free plane boundary (general case). Bull Seism Soc Am, 1962, 52 (3) : 595-625. |
| 17 | Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid:V. Transmission across a plane interface. Bull Seism Soc Am, 1964, 54 (1) : 409-416. |
| 18 | Deresiewicz H, Levy A. The effect of boundaries on wave propagation in a liquid-filled porous solid:X. Transmission through a stratified medium. Bull Seism Soc Am, 1967, 57 (3) : 381-391. |
| 19 | Jocker J, Smeulders D, Drijkoningen G, et al. Matrix propagator method for layered porous media:analytical expressions and stability criteria. Geophysics, 2004, 69 (4) : 1071-1081. DOI: 10.1190/1.1778249. |
| 20 | Rajapakse RKND, Senjuntichai T. Dynamic response of a multilayered poroelastic medium. Earthquake Engineering and Structure Dynamic, 1995, 24 (5) : 703-722. DOI: 10.1002/(ISSN)1096-9845. |
| 21 | Degrande G, Roeck G, Broeck P, et al. Wave propagation in layered dry, saturated and unsaturated poroelastic media. Int J Solids Structures, 1998, 35 (34-35) : 4753-4778. DOI: 10.1016/S0020-7683(98)00093-6. |
| 22 | Liang JW, You HB. Dynamic stiffness matrix of a poroelastic multilayered site and its Green's functions. Earthquake Engineering and Engineering Vibration, 2004, 3 (2) : 273-282. DOI: 10.1007/BF02858241. |
| 23 | 李伟华, 赵成刚. 饱和土沉积谷场地对平面SV波的散射问题的解析解. 地球物理学报, 2004, 47 (5) : 911-919. ( Li Weihua, Zhao Chenggang. Scattering of Plane SV waves by circular-arc alluvial valleys with saturated soil deposits. Chinese J Geophys, 2004, 47 (5) : 911-919. (in Chinese) ) |
| 24 | 赵宇昕, 陈少林. 关于传递矩阵法分析饱和成层介质响应问题的讨论. 力学学报, 2016, 48 (5) : 1145-1158. ( Zhao Yuxin, Chen Shaolin. Discussion on the matrix propagator method to analyze the response of saturated layered media. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48 (5) : 1145-1158. (in Chinese) ) |
| 25 | Halpern MR, Christiano P. Steady-state harmonic response of a rigid plate bearing on a liquid-saturated poroelastic half-space. Earthquake Engineering and Structural Dynamics, 1986, 14 : 439-454. DOI: 10.1002/(ISSN)1096-9845. |
| 26 | Bougacha SJ, Roesset M, Tassoulas JL. Dynamic stiffness of foundation on fluid filled poroelastic stratum. Journal of Engineering Mechechanics, ASCE, 1993, 119 (8) : 1649-1662. DOI: 10.1061/(ASCE)0733-9399(1993)119:8(1649). |
| 27 | Japon BR, Gallego R, Dominguez J. Dynamic stiffness of foundations on saturated poroelastic soils. Journal of Engineering Mechechanics, ASCE, 1997, 123 (11) : 1121-1129. DOI: 10.1061/(ASCE)0733-9399(1997)123:11(1121). |
| 28 | 陈少林, 甄澄. 饱和地基上基础动力阻抗函数的一种分析方法. 力学学报, 2012, 44 (2) : 393-400. ( Chen Shaolin, Zhen Cheng. Dynamic impedance of foundation on saturated poroelastic soil. Chinese Journal of Theoretical and Applied Mechanics, 2012, 44 (2) : 393-400. (in Chinese) ) |
| 29 | 陈少林, 甄澄. 下卧饱和半空间粘弹性土层上基础阻抗函数的分析. 振动工程学报, 2012, 25 (4) : 446-452. ( Chen Shaolin, Zhen Cheng. Dynamic impedance of foundations on viscoelastic stratum and saturated elastic half-space. Journal of Vibration Engineering, 2012, 25 (4) : 446-452. (in Chinese) ) |
| 30 | Liang JW, Fu J, Todorovska MI, et al. Effects of the site dynamic characteristics on soil-structure interaction (Ⅰ):incident SH waves. Soil Dynamics and Earthquake Engineering, 2013, 44 : 27-37. DOI: 10.1016/j.soildyn.2012.08.013. |
| 31 | Liang JW, Fu J, Todorovska MI, et al. Effects of the site dynamic characteristics on soil-structure interaction (Ⅱ):incident P and SV waves. Soil Dynamics and Earthquake Engineering, 2013, 51 : 58-76. DOI: 10.1016/j.soildyn.2013.03.003. |
| 32 | Liang JW, Fu J, Todorovska MI, et al. In-plane soil-structure interaction in layered, fluid-saturated, poroelastic half-space I:Structural response. Soil Dynamics and Earthquake Engineering, 2016, 81 : 84-111. DOI: 10.1016/j.soildyn.2015.10.018. |
| 33 | 陈少林, 廖振鹏, 陈进. 两相介质近场波动模拟的一种解耦有限元方法. 地球物理学报, 2005, 84 (4) : 909-917. ( Chen Shaolin, Liao Zhenpeng, Chen Jin. A decoupling FEM for simulating near-field wave motions in two-phase media. Chinese J Geophys, 2005, 84 (4) : 909-917. (in Chinese) ) |
| 34 | 赵成刚, 王进廷, 史培新, 等. 流体饱和两相多孔介质动力反应分析的显式有限元法. 岩土工程学报, 2001, 23 (2) : 178-182. ( Zhao Chenggang, Wang Jinting, Shi Peixin, et al. Dynamic analysis of fluid-saturated porous media by using explicit finite element method. Chinese Journal of Geotechnical Engineering, 2001, 23 (2) : 178-182. (in Chinese) ) |
| 35 | 王进廷, 杜修力, 赵成刚. 液固两相饱和介质动力分析的一种显式有限元方法. 岩石力学与工程学报, 2002, 21 (8) : 1199-1204. ( Wang Jinting, Du Xiuli, Zhao Chenggang. An explicit finite element method for dynamic analysis of fluid-saturated porous media. Chinese Journal of Rock Mechanics and Engineering, 2002, 21 (8) : 1199-1204. (in Chinese) ) |
| 36 | 廖振鹏. 工程波动理论导论 (第2版). 北京: 科学出版社, 2002: 1-298. ( Liao Zhenpeng. Introduction to Wave Motion Theories in Engineering (2nd Edn). Beijing: Science Press, 2002: 1-298. (in Chinese) ) |