†. 北京理工大学机电学院, 北京 100190
关于单一绝热剪切带形成机理及影响已有较多研究,从材料的本构关系出发,一般认为绝热剪切现象在宏观上表现为动态本构失稳[1],即等效应力--等效应变曲线从应变硬化(dσ/dε > 0)转变为应变软化(dσ/dε < 0),相应地在微观上可以观察到高度集中的应变局域化即绝热剪切带(adiabatic shear band, ASB).为建立绝热剪切变形局部化的失稳模型及揭示ASB的发展规律[1-4],近几十年来,研究者采用各种实验技术,如利用Hopkinson技术[5]的圆柱试样动态压缩[6-7]、薄壁管动态扭转[8-9]、帽型试样动态剪切[9-11]及动态压剪实验[12]等研究材料变形、绝热剪切起始破坏过程的动态力学行为,探讨绝热剪切临界起始条件及演化特性. Hopkinson动态压缩实验具有加载及分析简单的优点,但由于绝热剪切过程发生在试样内部,难以直接观测分析,因此,从压缩实验得到的等效应力--应变响应曲线难以直接判断试样中绝热剪切带起始时刻.
为更直接研究材料绝热剪切变形及破坏特性,Meyer等[10]与Hartmann等[11]最早提出圆柱帽型受迫剪切试验方法,被广泛应用于金属[13-19]及非金属材料[20]动态性能及剪切破坏研究.但受试样几何、结构变形的影响,试样受迫剪切区存在复杂应力、变形状态,实验中难以提取量化的材料性能响应特性.另外,对于圆柱帽型剪切试样目前的实验技术无法对剪切区进行直接观测[4]. Clos等[21]提出一种扁平帽型试样,可直接测试剪切区变形及温度演化;Liu等[22]采用类似的扁平帽型试样(hat-like-shaped specimen)观察大块金属玻璃剪切带的起始以及传播过程.扁平帽型试样剪切区同样难以避免复杂应力、变形状态,预制的剪切区尺寸也不等于剪切变形宽度,一般研究只给出剪切应力--位移响应曲线进行定性讨论[16, 23].近期许泽建等[24]发展一种新的双剪切扁平试样,将剪切预制区减薄,控制、减小剪切区变形对结构的影响,较好地保证剪切区内应变均匀分布,从而可对剪切区剪切应变进行计算分析.
付应乾等[25]曾采用分离式Hopkinson压杆技术对TA2钛合金圆柱试样动态压缩性能及其绝热剪切破坏特性开展研究,从回收的圆柱试样内部观测到剪切带呈双锥形破坏模式,但从应力--应变本构曲线上却难以确定绝热剪切起始、扩展条件.进一步还开展了TA2钛合金扁平帽型剪切动态实验,通过二维数字图像相关法(two-dimensional digital image correlation, DIC-2D)直接测试分析试样剪切区应变演化过程[23, 26];探讨TA2钛合金绝热剪切起始演化及其剪应力--应变曲线响应特征.按塑性变形理论,广义等效应力是广义等效应变的一个确定函数,与应力状态类型无关.为进一步探讨不同加载状态下材料的本构及其绝热剪切特性,本文拟对帽型剪切试样剪切区的应力状态开展理论及数值实验分析,探讨帽型剪切试验数据处理方法,以得到帽型试样受迫剪切过程剪切区广义等效应力--等效应变响应曲线.对TA2钛合金动态压缩及帽型动态剪切状态下的性能开展对比实验研究,通过比较两种实验加载状态下得到的等效应力--等效应变响应曲线及回收“冻结”试样中的剪切带微观金相分析,探讨不同加载状态下TA2钛合金的本构特性及其绝热剪切带破坏动态力学响应特性,为材料绝热剪切带的形成与发展特性研究提供参考.
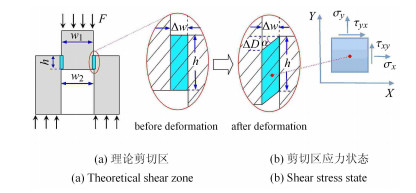
1 帽型试样剪切区应力分析无论圆柱形还是平板形帽型试样,在实验动态加载分析中一般假设剪切区为剪切应力状态,如图 1(a),则剪切区剪应力[16]为
| $ \tau (t) = \dfrac{F\left( t \right)}{A} = \dfrac{F\left( t \right)}{2\delta h} $ | (1) |
其中F(t)为剪切区剪切力,A为剪切区剪切面积,δ为帽型试样厚度,h为设计剪切区高度.若进一步假设试样预制的剪切区宽度Δw为剪切变形宽度,剪切区内变形均匀分布,则可近似估算工程剪切应变[27-28]为
| $ \gamma _{\rm theo} = \alpha \approx \tan \alpha = \dfrac{\Delta D}{\Delta w} $ | (2) |
其中ΔD为试样压进位移.
但事实上,由于受帽型剪切试样加载过程试样几何特征、结构变形的影响,剪切区并不是理想单一的纯剪切状态,而可能存在复杂应力状态以及变形分布,如图 1(b),不仅存在τxy同时存在正应力σx, σy分量,按式(1)和式(2)给出τxy-γxy曲线,也仅为相应剪切面上的剪应力分量.另外,实际剪切变形区的宽度不是加工预制的Δw,按式(2)计算剪切应变会存在很大误差[16, 23].为此,有必要对帽型剪切加载过程剪切区的应力、应变状态及实验处理方法进行分析.
|
图 1 帽型剪切加载原理及应力状态示意图 Figure 1 Schematic diagram of theoretical shear zone and its stress state |
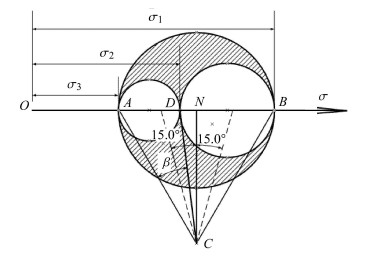
对于复杂应力实验加载状态的分析,皮萨林科等[29]提出了一种图解方法,将复杂应力圆表示为如图 2形式,其中σ1, σ2和σ3分别为该应力状态的主应力,O--σ轴上线段AB=σ1-σ3,以AB为边做等边三角形ABC,连接CD,则可证明线段CD数值上等于等效应力σeq
| $ \begin{array}{l} CD = \sqrt {C{A^2}-N{A^2} + N{D^2}} = \\ \frac{{\sqrt 2 }}{2}\sqrt {{{({\sigma _1}-{\sigma _2})}^2} + {{({\sigma _2}-{\sigma _3})}^2} + {{({\sigma _3} - {\sigma _1})}^2}} \end{array} $ |
而垂线CN为等边三角形ABC的高,其数值为
| $ CN = \sqrt 3 \dfrac{\sigma _1 - \sigma _3 }{2} = \sqrt 3 \tau _{\max } $ |
由图 2可知,当满足15° < β < 45°时,
|
图 2 三维应力莫尔圆 Figure 2 Mohr circle of stress |
对于扁平帽型剪切试样设计,只要满足平面应变状态条件,则有
| $ \begin{array}{l} \left. {\begin{array}{*{20}{c}} {{\sigma _1}}\\ {{\sigma _3}} \end{array}} \right\} = \frac{1}{2}\left( {{\sigma _x} + {\sigma _y}} \right) \pm \sqrt {{{\left( {\frac{{{\sigma _x}-{\sigma _y}}}{2}} \right)}^2} + \tau _{xy}^2} \\ {\sigma _2} = {\sigma _z} = \nu \left( {{\sigma _x} + {\sigma _y}} \right) \end{array} $ |
其中ν为材料泊松比.对于塑性变形ν取0.5,则有β=30°,μσ=0.因此,帽型试样实验设计时,若满足平面应变条件,同时,实验加载条件下试样受迫剪切区受剪方向接近最大剪切方向时,则剪切区即使不是一个平面纯剪切状态,仍可按式(3)近似处理得到等效应力,其误差不会超过3.4%.
| $ \sigma _{\rm eq} = \sqrt 3 \tau _{\max } = \sqrt {3} \tau _{ xy } $ | (3) |
此时,其等效应变可表示为[30]
| $ \varepsilon _{\rm eq} = \dfrac{1}{3}\gamma _{xy} \sqrt {3 + \gamma ^2_{xy} } $ |
在小变形条件下,上式可以简化为
| $ \varepsilon _{\rm eq} = \dfrac{\sqrt 3 }{3}\gamma _{xy} $ | (4) |
由此,通过帽型实验不仅可以得到材料在剪切面上的剪切特性,而且能得到反映材料本征特性的等效应力--等效应变关系.
2 实验方法及试样为探讨不同加载状态下金属合金的动态本构及其绝热剪切带破坏动态力学响应特性,分别开展Hopkinson圆柱试样动态压缩及帽型试样动态剪切实验.试样材料为冷轧退火TA2钛合金板,化学成分(质量分数%)为:99.67 Ti,0.021C,0.064Fe,0.025N,0.004H,0.11O,该钛合金板材金相组织为α等轴晶.在钛合金板上取样,线切割加工成圆柱压缩及帽型剪切试样.
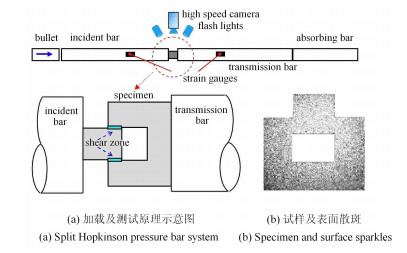
2.1 帽型试样动态剪切实验帽型剪切试样沿TA2钛合金板压延方向取样,试样尺寸w1=5.00 mm, w2=5.10 mm, h=2.00 mm,试样厚度δ=5.70 mm,如图 1(a).为减小帽型剪切试样结构变形对剪切区应力状态的影响,帽型试样设计成封闭的扁平结构,如图 3(b).
|
图 3 霍普金森压杆动态剪切实验示意图及试样 Figure 3 Schematics of dynamic experimental setups and specimen |
Hopkinson压杆帽型剪切实验加载及测试原理,如图 3(a),根据一维应力波分析,利用入射杆及透射杆上实验测得的应变值,可方便得到试样两端的动态压缩力Fw(t)和试样压缩位移ΔD(t)[13]
| $ F_{\rm w} \left( t \right) = A_{\rm bar} E_{\rm bar} \varepsilon _{\rm t} \left( t \right) \quad \ $ | (5) |
| $ \Delta D\left( t \right) =-2{C_0}\int_0^{{t_0}} {{\varepsilon _r}\left( t \right){\rm{d}}t} $ | (6) |
由式(1)和式(3),进一步可以得到
| $ \sigma _{\rm eq} = \dfrac{\sqrt {3} }{ 2 }\dfrac{A_{\rm bar} E_{\rm bar} \varepsilon _{\rm t} \left( t \right)}{\delta \cdot h} $ | (7) |
其中,εr(t)和εt(t)分别为压杆反射和透射应变信号. Ebar, C0和Abar分别为Hopkinson压杆的弹性模量、弹性波速和压杆截面积.
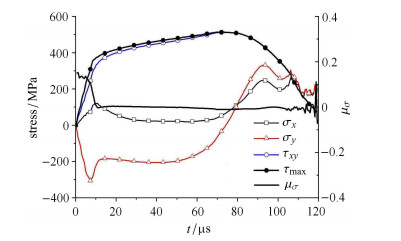
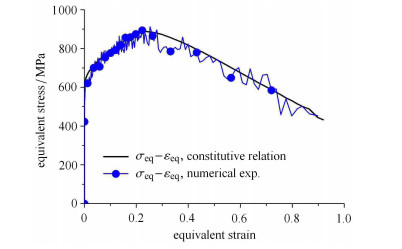
为分析所采用的帽型剪切试样可行性,对该试样在Hopkinson压杆加载下的剪切区应力状态及剪切局域化过程开展有限元数值实验分析. TA2钛合金试样采用C3D8R六面体实体单元,试验材料采用Johnson-Cook本构,参数由压缩实验结果拟合得到,并引入剪切软化失效模型描述剪切局域化过程. 图 4为试样剪切区中点的应力分量σx, σy, τxy, τmax及其罗德参数随时间的变化,可见,剪切区应力状态虽不是纯剪切状态,存在正应力分量,其罗德参数在0~0.14区间内变化,其中在加载初期及局域化后期达到最大值,但仍远小于0.46,满足剪切状态条件. 图 5为实验数据处理(按式(7)、式(4))得到的等效应力--应变曲线与该点材料本构响应曲线比较,两者符合很好.因此,该帽型剪切实验可以按剪切状态处理得到广义等效应力--应变曲线.
|
图 4 剪切区应力状态σx, σy, τxy, τmax和罗德参数μσ随时间的变化 Figure 4 Stress component and Lode parameters for given element |
|
图 5 数值实验得到的等效应力--应变曲线与本构响应曲线比较 Figure 5 Comparison of equivalent stress-strain curves and constitutive relation |
帽型剪切实验中,采用不同长度的子弹控制入射波波长,以得到不同变形程度的“冻结”试验结果,同时控制子弹速度,得到不同应变率下剪切加载状态下的等效应力--等效应变响应曲线.需要说明的是:对于帽型剪切试验,由于剪切变形区宽度是变化的[23],无法按式(2)得到剪切应变.为得到剪切区及进一步发生剪切局域化演化过程的剪切应变,本文采用在扁平受迫剪切试样表面喷涂散斑,如图 3(b),利用数值图像相关法直接对试样剪切区的剪应变分布及演化进行分析.高速相机为FASTCAM APX RS, 采样率150 000帧/秒.
实验后,对不同“冻结”试验阶段的试样取样进行金相分析,观测帽型剪切试样中的变形局域化、剪切带及破坏状态.
2.2 圆柱试样动态压缩实验Hopkinson压杆圆柱动态压缩试样直径为5 mm、高为4.5 mm,圆柱试样高度沿TA2钛合金板厚度方向取样.根据Hopkinson压杆技术可以直接得到作用于试样的轴向压缩应力σ(t)以及压缩应变ε(t)
| $ \sigma \left( t \right) = \dfrac{A_{\rm bar} }{A_0 }E_{\rm bar} \varepsilon _{\rm t} \left( t \right) \quad $ | (8) |
| $ \varepsilon \left( t \right) =-\frac{{2{C_0}}}{{{L_0}}}\int_0^{{t_0}} {{\varepsilon _r}\left( t \right){\rm{d}}t} $ | (9) |
式中,A0和L0分别为圆柱试样横截面面积及试样高度.按一维应力单轴压缩假设,圆柱压缩实验得到的压缩应力--压缩应变曲线即为广义等效应力--应变曲线.
与帽型剪切实验类似,实验调节加载子弹长度、速度,控制得到不同应变率、变形程度的“冻结”压缩试验结果,结合微观金相观察,分析圆柱压缩试样的变形局域化及绝热剪切带的发展、演化过程.
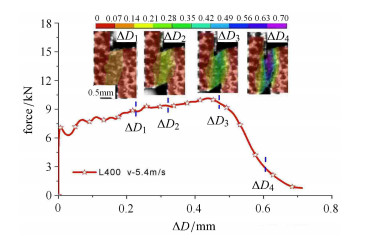
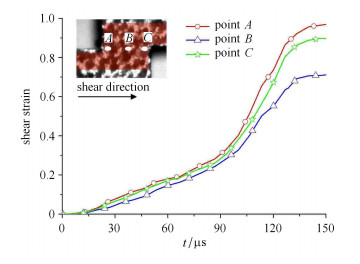
3 实验结果及讨论 3.1 动态剪切特性及破坏响应图 6为子弹长度400 mm,子弹撞击速度5.4 m/s时,实验测得的力--位移响应曲线,图中同时给出了利用DIC方法得到的试样剪切区塑性剪应变场在不同压进位移ΔD的典型演化过程.可见:变形初期沿试样剪切方向,剪切应变近似均匀,但试样剪切区塑性剪切宽度最大至约1.2 mm,远大于试样预制宽度0.05 mm.随加载剪切压进位移的增大,塑性区不断集中,剪切区宽度不断变窄;剪切区经历了变形局域化集中发展直至断裂破坏的过程. 图 7为由DIC方法得到的沿剪切方向各点剪切应变时程曲线,剪切区两端由于应力集中,剪应变相对中点略大,但总体近似均匀.实验处理中近似以剪切区中点应变表征剪切试验剪切区的平均应变.
|
图 6 剪切力--位移曲线及DIC剪切应变云图 Figure 6 Shear force-displacement curve and shear strain contour by DIC |
|
图 7 沿剪切方向剪应变分布 Figure 7 Shear strain versus time curves along shear direction |
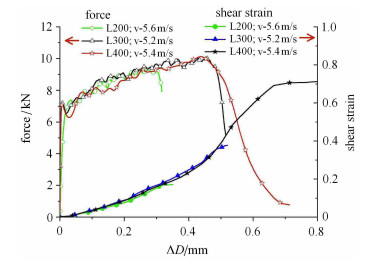
图 8为子弹撞击速度约为5.4 m/s、长度分别为200 mm、300 mm及400 mm加载下,帽型受迫剪切实验得到的一组典型加载力--位移、剪应变--位移响应曲线.可见对于子弹200 mm时,剪切力下降,塑性剪应变停止发展,表现为卸载特征.子弹长度为400 mm时,剪切力下降,相应的剪切应变反而加速发展,表现为材料软化特征.进一步按式(7)和式(4)计算得到相应的等效应力--等效应变曲线,如图 9,其平均应变率约为3 100 s-1.图中同时给出了“冻结”回收试样剪切区微观金相.
|
图 8 剪切力、剪切应变随下压位移变化 Figure 8 Shear force, shear strain change with displacement |
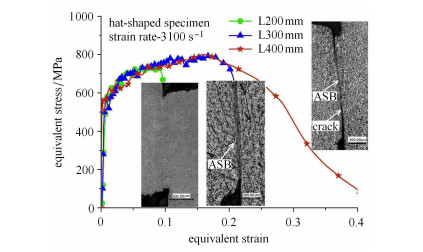
图 9表明:子弹长度为200 mm加载下,最大等效应变为0.10时,剪切区变形近似均匀,剪切区金相未出现应变集中现象.当子弹长度为300 mm加载时,等效应变达0.22左右,剪切区可见高度集中的绝热剪切带特征.当等效应变进一步提高到0.39时,剪切带已发展为裂纹并贯穿剪切区,试样发生剪切断裂破坏.因此,子弹长度L=300 mm和L=400 mm加载下,由于材料绝热剪切破坏得到的等效应力--应变曲线发生“软化”.
|
图 9 剪切加载下等效应力--等效应变曲线及“冻结”试样微观金相 Figure 9 Equivalent stress-strain curves by shear test, and its metallographics |
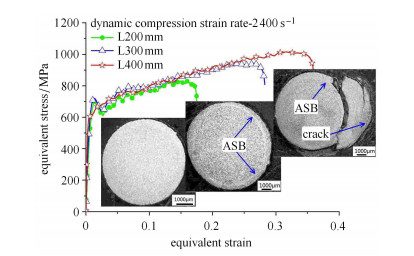
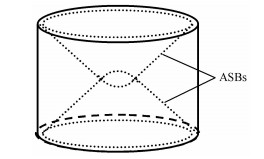
图 10为子弹长度分别为200 mm, 300 mm和400 mm,在相同加载速度下Hopkinson动态压缩实验得到的一组TA2钛合金的应力--应变曲线[25]以及相应“冻结”试样横截面金相及剪切带形貌图,其应变率约为2 400 s-1.结果显示:200 mm长子弹加载下,表观应变为0.17,试件变形近似均匀,微观金相没有发现剪切带;300 mm长子弹加载下,表观应变为0.27时,试样断面可见环形绝热剪切带.当子弹长度为400 mm加载,应变为0.36时,裂纹沿环向绝热剪切带发展,局部明显碎裂.进一步研究表明:TA2试样动态压缩加载下,剪切带由两端面以双锥形向中心发展,试样中心为两锥尖交汇处,并形成较为复杂的变形区域,裂纹沿剪切带发展导致最终破坏,如图 11 [25].
|
图 10 压缩实验应力--应变曲线以及“冻结”试样横截面金相 Figure 10 Equivalent stress-strain curves by compression test, and its metallographics |
|
图 11 剪切带三维分布示意图 Figure 11 Schematic diagram of ASBs bi-conical surface |
由图 10可见:当应变率为2 400 s-1单轴压缩条件下,表观临界应变在0.17~0.27之间时,TA2钛金属压缩试样中已出现双锥形绝热剪切带,但相应的应力--应变曲线仍表现为应变硬化特征.这一结果表明:即使绝热剪切带产生,甚至出现局部碎裂,压缩试样宏观动态应力--应变曲线并没有明显不同,曲线未见“软化”现象,说明动态压缩试样实验得到的材料表观应力--应变曲线无法反映材料剪切带内的“软化”特性.
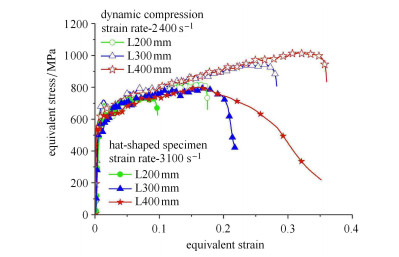
3.3 分析及讨论根据八面体应力、应变状态分析,简单压缩实验的应力--应变曲线即为广义等效应力--应变曲线,图 12给出动态压缩和帽型剪切加载实验得到的等效应力--等效应变曲线比较,可见:在塑性变形初始阶段,压缩试样和帽型剪切试样得到的本构曲线符合较好,符合广义等效应力是广义等效应变的一个确定函数,与应力状态类型无关的特点;但随塑性应变发展、绝热剪切带产生,压缩和剪切状态下得到的等效应力--应变曲线两者发展趋势并不一致,出现分离.动态压缩实验得到的流动应力曲线较剪切试验高,并且这种差别在绝热剪切带形成后更为显著.对于动态剪切试验一旦出现塑性应变局域化以及绝热剪切带,其应力--应变曲线会出现明显的“软化”特性.而动态压缩试验得到的应力--应变曲线仍表现为应变硬化特征,并不出现软化.
|
图 12 动态剪切与压缩实验等效应力--应变曲线对比 Figure 12 Equivalent stress-strain curves comparison for compression and shear testing |
事实上,材料的塑性变形能力、破坏过程与很多因素相关,尤其是应力状态类型、温度、应变速率以及变形机制等.显然,对于帽型受迫剪切实验,由于塑性变形集中在试样剪切区内,随剪切发展,剪切局域化集中形成极窄的绝热剪切带.在这个过程中将产生卸载波使周边材料发生弹性卸载[31],试样应变主要由绝热剪切带内的变形、破坏演化贡献,帽型剪切试样应力--应变曲线出现“软化”特征.因此,该“软化”曲线表征了绝热剪切起始、扩展及破坏过程材料的力学响应特性.
对于动态压缩实验,变形局域化及绝热剪切带首先在圆柱试样的上下表面沿圆环形成,并沿45°方向向试样中心发展,空间上呈双圆锥形.因此其宏观压缩应变不但有绝热剪切带集中发展的贡献,也包含试样其他部分继续变形的贡献.并且在双锥形绝热剪切破坏形成之前,试样整体仍能继续承受加载载荷,因此,其应力--应变曲线并不会随绝热剪切带的形成立即出现软化特征,而仅反映试样整体变形的平均表观力学响应,无法直接反映绝热剪切带内材料的力学响应特性.
帽型剪切试验结果显示(如图 9):等效应变在0.17时等效应力--应变曲线发生软化,同时回收的试样可见绝热剪切带已贯穿整个剪切区长度方向.对于圆柱压缩实验,表观应变达到0.17时,其“冻结”试样中未见变形集中及绝热剪切带;当表观应变发展至0.27时,“冻结”压缩试样横截面可见环形的绝热剪切带.因此,圆柱压缩状态下绝热剪切带在等效应变为0.17~0.27之间形成.这也从一个方面表明绝热剪切形成、演化过程与加载状态相关,即应力状态影响绝热剪切带的起始及演化过程[6].压缩实验的三轴应力状态作用使绝热剪切临界起始应变增大.
由图 12可见:压缩实验与剪切实验得到的等效应力--应变曲线在绝热剪切带形成前已出现明显的分离.两者的差别可能由多种因素引起,一方面可能由于试样是从TA2钛合金板材切割制作而成,其中压缩试样高度是沿试样厚度方向取样,而剪切试样是沿板压延方向取样.虽然该钛合金板压延后经热处理为等轴α晶粒,但各方向特性可能略有差别.另一方面,材料的塑性损伤演化也与应力状态相关;在压缩实验应力状态下(应力三轴度大),材料不易发生塑性损伤演化.相对于圆柱压缩实验,帽型剪切试样更容易发生塑性损伤积累,使材料流动应力降低.如图 13为未出现绝热剪切带的“冻结”帽型回收试样剪切区的微观金相,沿剪切区已可见明显的孔洞等微损伤分布.系列剪切实验结果显示:TA2钛合金在动态剪切加载下,随塑性变形发展,首先产生塑性损伤的微孔洞,随后才产生剪切变形局域化集中形成绝热剪切带.因此,即使在绝热剪切带形成及破坏前,不同加载状态下实验得到应力--应变曲线也可能产生差别.对于塑性损伤引起的材料局部应变不均匀性对绝热剪切起始、演化的影响值得进一步研究.

|
图 13 帽型剪切试样的塑性损伤孔洞 Figure 13 Metallographs of voids distribution before ASB formation |
本文利用Hopkinson压杆对TA2钛合金开展动态压缩及帽型动态剪切试验研究.实验采用二维数字图像相关法(DIC-2D)对帽型试样剪切区应变直接测试,所设计的帽型剪切试样在加载过程剪切区罗德参数满足-0.46 < μσ < 0.46,可按剪切状态处理,给出帽型受迫剪切过程的广义等效应力--应变的响应曲线.研究比较了Hopkinson压杆动态加载下压缩、剪切试验得到的等效应力--应变响应曲线;并进一步采用“冻结”试样方法分析了试样中绝热剪切局域化演化过程,探讨不同加载状态下金属材料的绝热剪切破坏行为及其动态力学响应特性.实验结果表明:
(1) 动态压缩及剪切加载下得到的等效应力--应变曲线,在塑性变形初始阶段,两者符合较好.但随塑性损伤发展及绝热剪切带形成,两者出现分离,表明加载应力状态对塑性损伤及绝热剪切演化过程有影响.
(2) 剪切试样实验得到的等效应力--应变曲线,能直接反映材料剪切区内从均匀变形到绝热剪切起始、发展过程的力学响应,一旦出现剪切局域化及绝热剪切带,等效应力--应变曲线出现“软化”响应特征,该本构软化特性反映了绝热剪切带起始、破坏演化过程的力学响应.
(3) 在动态压缩实验中,即使圆柱试样中已出现双锥形的绝热剪切带及局部裂纹分布,其等效应力--应变曲线仍表现为应变硬化特征,不能直观揭示试样内部的绝热剪切带起始、裂纹扩展的力学软化响应特征.
| 1 | Zener C, Hollomon JH. Effect of strain rate upon plastic flow of steel. Applied Physics, 1944, 15 : 22-32. DOI: 10.1063/1.1707363. |
| 2 | Bai Y, Dodd B. Adiabatic Shear Localization:Occurrence, Theories and Applications . New York: Pergamon Press, 1992: 155-187. |
| 3 | Wright TW. The Physics and Mathematics of Adiabatic Shear Bands . U.K: Cambridge University Press, 2002. |
| 4 | Dodd B, Bai Y. Adiabatic Shear Localization . Elsevier, London: Frontiers and Advances, 2012. |
| 5 | Kolsky H. An investigation of the mechanical properties of materials at very high rates of loading. Proceedings of the Physical Society, 1949, 62 (11) : 676-700. DOI: 10.1088/0370-1301/62/11/302. |
| 6 | 赵峰, 李玉龙, 索涛, 等. 高应变率下铸造镁合金AZ91的动态压缩性能及破坏机理. 中国有色金属学报, 2009, 19 (7) : 1163-1168. ( Zhao Feng, Li Yulong, Suo Tao, et al. Dynamic compressive behavior and damage mechanism of cast magnesium alloy AZ91. The Chinese Journal of Nonferrous Metals, 2009, 19 (7) : 1163-1168. (in Chinese) ) |
| 7 | Wei ZG, Yu JL, Li JR, et al. Influence of stress condition on adiabatic shear localization of tungsten heavy alloy. International Journal of Impact Engineering, 2001, 26 : 843-852. DOI: 10.1016/S0734-743X(01)00137-3. |
| 8 | Marchand A, Duffy J. An experimental study of the formation process of adiabatic shear bands in a structural steel. J Mech Phys Solids, 1988, 36 (1) : 251-283. |
| 9 | Peirs J, Verleysen P, Tirry W, et al. Dynamic shear localization in Ti6A14V. Procedia Engineering, 2011 (10) : 2342-2347. |
| 10 | Meyer LW, Staskewitsch E, Burblies A. Adiabatic shear failure under biaxial dynamic compression/shear loading. Mechanics of Materials, 1994, 17 (2-3) : 203-214. DOI: 10.1016/0167-6636(94)90060-4. |
| 11 | Hartmann KH, Kunze HD, Meyer LW. Metallurgical effects on impact loaded materials//Meyers MA, Murr LE eds. Shock Waves and High Strain Rate Phenomena in Metals, Concepts and Applications, New York:Plenum Press, 1981:325-337 |
| 12 | Rittel D, Wang ZG, Dorogoy A. Geometrical imperfection and adiabatic shear banding. International Journal of Impact Engineering, 2008, 35 : 1280-1292. DOI: 10.1016/j.ijimpeng.2007.07.009. |
| 13 | Bronkhorst CA, Cerreta EK, Xue Q, et al. An experimental and numerical study of the localization behavior of tantalum and stainless steel. International Journal of Plasticity, 2006, 22 : 1304-1335. DOI: 10.1016/j.ijplas.2005.10.002. |
| 14 | Chen YJ, Meyers MA, Nesterenko VF. Spontaneous and forced shear localization in high-strain-rate deformation of tantalum. Materials Science and Engineering A, 1999, 268 : 70-82. DOI: 10.1016/S0921-5093(99)00110-0. |
| 15 | Kad BK, Gebert JM, Perez-Prado MT, et al. Ultrafine-grain-sized zirconium by dynamic deformation. Acta Materialia, 2006, 54 : 4111-4127. DOI: 10.1016/j.actamat.2006.03.053. |
| 16 | Peirs J, Verleyse P, Degrieck J, et al. The use of hat-shaped specimens to study the high strain rate shear behaviour of Ti-6AL-4V. International Journal of Impact Engineering, 2010, 37 : 703-714. DOI: 10.1016/j.ijimpeng.2009.08.002. |
| 17 | Lee WS, Chen TH, Lin CF, et al. Adiabatic shearing localisation in high strain rate deformation of Al-Sc alloy. Materials Transactions, 2010, 51 (7) : 1216-1221. DOI: 10.2320/matertrans.M2010053. |
| 18 | Teng X, Wierzbicki T, Couque H. On the transition from adiabatic shear banding to fracture. Mechanics of Materials, 2007 (39) : 107-125. |
| 19 | Andrade U, Meyer MA, Vecchio KS, et al. Dynamic recrystallization in high-strain, high-strain-rate plastic deformation of copper. Acta Metallurgica et Materialia, 1994, 42 (9) : 3183-3195. DOI: 10.1016/0956-7151(94)90417-0. |
| 20 | 刘龙飞, 戴兰宏, 凌中, 等. 冲击剪切载荷下SiCp/6151Al复合材料变形局部化及增强颗粒尺寸效应. 复合材料学报, 2002, 19 (4) : 51-55. ( Liu Longfei, Dai Lanhong, Ling Zhong, et al. Localized deformation and particle size-effect in particle-rein forced SiCp/6151Al composites under impulsive shear loadings. Acta Materiae Compositae Sinica, 2002, 19 (4) : 51-55. (in Chinese) ) |
| 21 | Clos R, Schreppel U, Veit P. Temperature, microstructure and mechanical response during shear band formation in different metallic materials. Journal de Physique, 2003, 110 (4) : 111-116. |
| 22 | Liu LF, Dai LH, Bai YL, et al. Initiation and propagation of shear bands in Zr-based bulk metallic glass under quasi-static and dynamic shear loadings. Journal of Non-Crystalline Solids, 2005 (351) : 3259-3270. |
| 23 | 付应乾, 董新龙, 虎宏智. 准静态和动态加载TA2工业纯钛受迫剪切破坏演化. 中国有色金属学报, 2015, 25 (11) : 3092-3099. ( Fu Yingqian, Dong Xinlong, Hu Hongzhi. Quasi-static and dynamic failure evolution of titanium alloy under forced shear loading. The Chinese Journal of Nonferrous Metals, 2015, 25 (11) : 3092-3099. (in Chinese) ) |
| 24 | 许泽建, 丁晓燕, 张炜琪, 等. 一种用于材料高应变率剪切性能测试的新型加载技术. 力学学报, 2016, 48 (1) : 654-659. ( Xu Zejian, Ding Xiaoyan, Zhang Weiqi, et al. A new loading technique for measuring shearing properties of materials under high strain rates. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48 (1) : 654-659. (in Chinese) ) |
| 25 | 付应乾, 董新龙. 工业纯钛动态压缩特性及破坏的实验研究. 稀有金属材料与工程, 2016, 45 (1) : 102-106. ( Fu Yingqian, Dong Xinlong. Experiment study on mechanical properties and failure characteristic of commercially pure titanium under dynamic compression. Rare Metal Materials and Engineering, 2016, 45 (1) : 102-106. (in Chinese) ) |
| 26 | 付应乾, 董新龙. 帽型试样动态绝热剪切破坏演化分析. 固体力学学报, 2015, 36 (5) : 392-400. ( Fu Yingqian, Dong Xinlong. Study of evolution of adiabatic shear failure in hat-shaped specimen under dynamic loading. Chinese Journal of Solid Mechanics, 2015, 36 (5) : 392-400. (in Chinese) ) |
| 27 | Nemat-Nasser S, Isaaca JB, Liu MQ. Microstructure of high-strain, high-strain-rate deformed Tantalum. Acta Mater, 1998, 46 (4) : 1307-1325. DOI: 10.1016/S1359-6454(97)00746-5. |
| 28 | Pérez-Prado MT, Hines JA, Vecchio KS. Microstructural evolution in adiabatic shear bands in Ta and Ta-W alloys. Acta Mater, 2001, 49 : 2905-2917. DOI: 10.1016/S1359-6454(01)00215-4. |
| 29 | 皮萨林科ГC, 列别捷夫AA.复杂应力状态下的材料变形与强度, 江明行译.北京:科学出版社, 1983:32-34 |
| 30 | 罗文波. 关于"平面纯剪切大变形等效应变分析"一文的讨论. 塑形工程学报, 2001, 8 (1) : 8-8. ( Luo Wenbo. Discussion on the equivalent strain of large plane-pure-shear defomaton. Journal of Plasticity Engineering, 2001, 8 (1) : 8-8. (in Chinese) ) |
| 31 | Grady DE, Kipp ME. The growth of unstable thermoplastic shear with application to steady-wave shock compression in solids. Journal of Mechanics Physics of Solids, 1987, 35 (1) : 95-119. DOI: 10.1016/0022-5096(87)90030-5. |
†. Shool of Mechatronical Engineering, Beijing Institute of Technology, Beijing 100190, China

