†. 军械工程学院车辆与电气工程系, 石家庄 050003
**. 军械工程学院基础部, 石家庄 050003
††. 中国空气动力研究与发展中心超高速所, 四川绵阳 621000
在单相材料中添加一相或多相颗粒结构形成颗粒复合材料是材料增强增韧的重要方式,颗粒结构复合陶瓷是一类重要的复合材料,具有广泛的应用.新加入的颗粒相通常具有细观尺度,导致材料细观损伤和裂纹扩展方式发生较大变化,从而显著改变材料性能,由颗粒导致的应力集中是材料损伤的重要来源.颗粒在细观力学研究中通常称为夹杂,夹杂问题是复合材料细观力学研究的一类重要问题. 1957年艾雪比(Eshelby)[1]求解了无限大弹性体中包含椭球夹杂的应力应变关系,并证明了当夹杂形状为椭球时夹杂中应变均匀.这一结论在解决异性夹杂问题中发挥了重要作用,许多工程问题可简化为艾雪比问题,如含颗粒材料的热应力[2]、等效性能预测等[3-5]都可基于艾雪比问题的解进行分析,材料细观缺陷也通常简化为扁平的片状椭球进行研究[6-9],夹杂材料损伤失效也多基于此解[10-13].围绕其他条件下椭球夹杂的研究也很多,如多层被覆夹杂问题[14-15],边界滑移条件下的艾雪比问题[16-18]以及有限域的艾雪比问题[19]等.
实际材料中,大多数颗粒具有尖锐的边缘和不规则形状,这种尖角引起极大的应力集中,上述基于椭球的解不再适用.当夹杂不是规则的椭球形状时,即使是规则的多面体或多边形,夹杂中的本征应变不再均匀,这已经被严格证明[20-21],大多数非椭球夹杂艾雪比张量目前还没能获得解析解.由于椭球形夹杂艾雪比解形式简单,将非椭球简化为近似形状的椭球进行细观力学分析是常用方法,但这样处理可能带来较大差异,如邹文楠[22]发现二维条件下异形夹杂等效为椭圆夹杂时平均艾雪比张量最大误差达到65.78%.由于夹杂的尖锐结构应力集中效果明显,对材料性能有重要的影响,上述处理在求解夹杂附近的局部场时误差可能更大.有研究表明,含非椭球颗粒材料的强度、有效模量等通常比含椭球颗粒材料的要低[23-24],因此有必要根据夹杂的实际形状进行相关的理论计算,以便对夹杂问题的裂纹产生和开裂等损伤现象做出更加准确的预报.
颗粒增强复合材料中,颗粒周围强烈的应力集中诱发的微裂纹是材料缺陷的重要来源,这类缺陷沿着颗粒界面扩展形成脱粘,或者脱粘到一定程度后向基体中扩展,最终造成材料破坏,缺陷从开始产生到失稳扩展过程对材料最终性能有重要影响[25].考虑界面脱粘的细观力学模型也比较多,但大多数只是圆形或球形等简单形状颗粒的脱粘,或者通过数值方法解决一些复杂的问题[26-31].对于非椭球颗粒,基于细观力学模型的损伤研究主要是集中在非椭球颗粒顶点奇异性的研究[32-35],其脱粘问题通常需要做一定的简化[36-38].材料中除了随机分布的孔隙或杂质缺陷外,大部分微裂纹缺陷是和颗粒相伴,并且同颗粒形状、性能、分布以及加载条件紧密相关.由于非椭球颗粒造成剧烈的应力集中,微裂纹的初始扩展必然受颗粒控制,细观力学模型中应当考虑这种分布特点.基于这种认识,本文假设缺陷在颗粒附近扩展,并且缺陷的外载应力场受颗粒控制,提出一种缺陷与颗粒强烈相互作用的材料损伤模型,并且在这种模型下研究颗粒附近裂纹扩展对材料力学行为的影响.
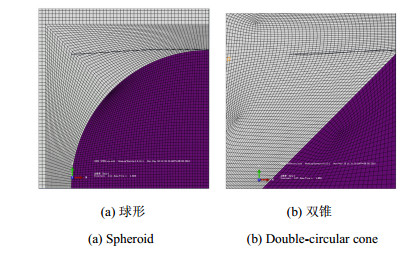
1 带尖角颗粒周围缺陷的扩展路径颗粒复合陶瓷中,颗粒诱导裂纹一般有3种情况,一是颗粒破裂形成裂纹,二是颗粒与基体间的界面脱粘形成界面裂纹,第3种是裂纹在应力作用下向基体延伸,形成与颗粒临近的裂纹.在许多颗粒增强陶瓷复合材料中,颗粒的刚度大于基体,当颗粒表面与基体的界面接触完好时,尖角附近缺陷扩展通常不会随着颗粒表面扩展,而是向基体中扩展[39-40].通过扩展有限元方法模拟了多种颗粒附近的裂纹走向,同样发现裂纹直接向基体中扩展,如图 1所示.
|
图 1 扩展有限元方法模拟单轴拉伸下颗粒端部裂纹扩展路径 Figure 1 Cracking path of a defect at the particle top under simple tension |
图 1中分别显示了圆形颗粒和锥形颗粒附近缺陷在纵向简单拉伸下的扩展路径,裂纹近似为平面片状,由于缺陷在颗粒附近,因此颗粒与缺陷裂纹相互作用强烈,本文建立一种模型估计含颗粒界面裂纹材料的有效模量及其损伤演化.
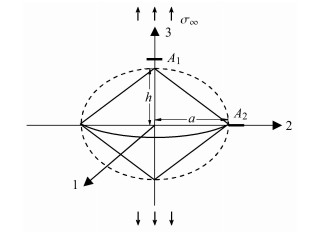
2 任意形状颗粒中的应力场作为示例,本文选取如图 2所示的双圆锥进行计算分析.基于上述裂纹与颗粒的相对位置关系,颗粒及其诱发裂纹细观结构模型如图 2所示.
|
图 2 双圆锥形颗粒和锥面顶部和环面处的缺陷示意图 Figure 2 Diagrammatic sketch of defects near the double-circular cone particle and the circumscribed approximation ellipsoid |
图 2中虚线轮廓表示与非椭球颗粒近似的椭球,A1处为颗粒尖角位置诱发的裂纹,A2处为颗粒环向附近的裂纹.基体下标用0作标记,如用C0和S0表示基体材料的刚度和柔度矩阵,第i型颗粒/夹杂的刚度和柔度矩阵分别用Ci和Si表示.
先不考虑裂纹的存在,单个夹杂i位于无限大基体中,在外加均匀应力σ∞的作用下,夹杂内应力σi和夹杂外应力σ0可分别表示为
| $ \left. {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\sigma }}_i} = {\mathit{\boldsymbol{\sigma }}_\infty } + \mathit{\boldsymbol{\sigma }} = {\mathit{\boldsymbol{C}}_i}\left( {{\mathit{\boldsymbol{\varepsilon }}_\infty } + \mathit{\boldsymbol{\varepsilon }}-{\mathit{\boldsymbol{\varepsilon }}^t}} \right){\mkern 1mu}, }&{{\rm{in}}\;\mathit{\Omega }}\\ {{\mathit{\boldsymbol{\sigma }}_0} = {\mathit{\boldsymbol{\sigma }}_\infty } + \mathit{\boldsymbol{\sigma }} = {\mathit{\boldsymbol{C}}_0}\left( {{\mathit{\boldsymbol{\varepsilon }}_\infty } + \mathit{\boldsymbol{\varepsilon }}} \right){\mkern 1mu}, }&{{\rm{in}}\;D-\mathit{\Omega }} \end{array}} \right\}1\;\; $ | (1) |
其中εt为相变或基体与颗粒热膨胀差异产生的无应力应变.颗粒中应力应变场可以用附加本征应变ε*的基体颗粒来表示,即
| $ \boldsymbol{C}_i \left( {\boldsymbol{\varepsilon}_\infty + \boldsymbol{\varepsilon} - \boldsymbol{\varepsilon} ^t} \right) = \boldsymbol{C}_0 \left( {\boldsymbol{\varepsilon}_\infty + \boldsymbol{\varepsilon} - \boldsymbol{\varepsilon }^t - \boldsymbol{\varepsilon}^\ast } \right) $ | (2) |
这个方程被称为等效方程.当夹杂为椭球且外加载荷均匀时,夹杂中等效本征应变ε*也是均匀的,则在夹杂内外应变扰动分别为
| $ \boldsymbol{\varepsilon} = \boldsymbol{M}(\boldsymbol{\varepsilon}^{\rm t} + \boldsymbol{\varepsilon}^\ast ) = \boldsymbol{M}\boldsymbol{\varepsilon}^{\ast\ast } \ \ {\rm in} \ \varOmega $ | (3) |
| $ \boldsymbol{\varepsilon} = \boldsymbol{D}\boldsymbol{\varepsilon}^{\ast \ast } \ \ {\rm in} \ D - \varOmega $ | (4) |
| $ \boldsymbol{\varepsilon}^{\ast \ast } = \boldsymbol{\varepsilon}^{\rm t} + \boldsymbol{\varepsilon}^\ast $ | (5) |
其中,M为夹杂的艾雪比张量[8]
| $ {M_{ijkl}}(\mathit{\boldsymbol{x}}) = - \frac{{{C_{pqkl}}}}{2}\int_\mathit{\Omega } {[{G_{ip, qj}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}}) + {G_{jp, qi}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}})]} d\mathit{\boldsymbol{x'}} $ | (6) |
式中G为格林函数,当夹杂为椭球时具有解析解,非椭球夹杂的艾雪比张量可通过数值方法计算,对于式(4)中夹杂外的点,上述积分通常记为D,称为应变转换张量.平均艾雪比张量为
| $ {{\bar M}_{ijmn}} = \frac{1}{V}\int_\mathit{\Omega } {} {M_{ijmn}}dV $ | (7) |
对于椭球颗粒,由式(1)~式(5)可得到外载应力σ∞时无限大基体中颗粒/夹杂中应力场
| $ \boldsymbol{\sigma}_0 (x) = \boldsymbol{\sigma}_\infty - \boldsymbol{D}_i (\boldsymbol{x})( \boldsymbol{M}_i -\boldsymbol{I})^{-1}(\boldsymbol{\sigma}_\infty - \boldsymbol{\sigma}_i ) $ | (8) |
当夹杂不是椭球时,等效本征应变不再为常量,同样可以用等效夹杂的方法计算应力应变场.将等效方程(2)简单变形有[8-9]
| $ \Delta \boldsymbol{C}\boldsymbol{\varepsilon} - \boldsymbol{C}_0 \boldsymbol{\varepsilon}^{\ast \ast } = - \Delta \boldsymbol{C}\boldsymbol{\varepsilon}_\infty - \boldsymbol{C}_i \boldsymbol{\varepsilon}^t $ | (9) |
其中
| $ \varepsilon _{ij}^{\ast \ast } (x) = B_{ij} + B_{ijk} x_k + B_{ijkl} x_k x_l + \cdots $ | (10) |
将另外两项也写成相同的形式
| $ \left. {\begin{array}{*{20}{c}} {{\varepsilon _{ij}}(x) = {M_{ijkl}}{B_{kl}} + {M_{ijklm}}{B_{klm}} + {M_{ijklmn}}{B_{klmn}} + \cdots }\\ {\varepsilon _{ij}^\infty (x) = {E_{ij}} + {E_{ijk}}{x_k} + {E_{ijkl}}{x_k}{x_l} + \cdots } \end{array}} \right\} $ | (11) |
其中
| $ {M_{ijklm}}(x) =- \frac{{{C_{pqkl}}}}{2}\int_\mathit{\Omega } {} [{G_{ip, qj}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}}) + {G_{jp, qi}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}})]{{\mathit{\boldsymbol{x'}}}_m}{\rm{d}}\mathit{\boldsymbol{x'}} $ | (12) |
| $ {M_{ijklmn}}(x) =- \frac{{{C_{pqkl}}}}{2}\int_\mathit{\Omega } {} [{G_{ip, qj}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}}) + {G_{jp, qi}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{x'}})]{{\mathit{\boldsymbol{x'}}}_m}{{x'}_n}{\rm{d}}\mathit{\boldsymbol{x'}} $ | (13) |
Eij,Eijk,Eijkl为常数.将εi j(x)在坐标原点泰勒级数展开,则在原点附近的P点扰动应变为
| $ \varepsilon _{ij} (P) = \varepsilon _{ij} (0) + \varepsilon _{ij, p} (0)x_p^P + \dfrac{1}{2}\varepsilon _{ij, pq} (0)x_p^P x_q^P + \cdots $ | (14) |
取前两阶,有
| $ \begin{array}{*{20}{c}} {{\varepsilon _{ij}}(P) = \left[{{M_{ijkl}}(0){B_{kl}} + {M_{ijklm}}(0){B_{klm}} + {M_{ijklmn}}(0){B_{klmn}}} \right] + }\\ {\left[{{M_{ijkl, p}}(0){B_{kl}} + {M_{ijklm, p}}(0){B_{klm}} + {M_{ijklmn, p}}(0){B_{klmn}}} \right]x_p^P + }\\ {\frac{1}{{2!}}\left[{{M_{ijkl, pq}}(0){B_{kl}} + {M_{ijklm, pq}}(0){B_{klm}} + } \right.}\\ {\left. {{M_{ijklmn, pq}}(0){B_{klmn}}} \right]x_p^Px_q^P} \end{array} $ | (15) |
由等效方程中各阶系数相等,即1,xPp,xq P,xPpxq P等前的系数相等,得到线性方程组
| $ \left. {\begin{array}{*{20}{c}} {\Delta {C_{stij}}\left[{{M_{ijkl}}(0){B_{kl}} + {M_{ijklm}}(0){B_{klm}} + {M_{ijklmn}}(0){B_{klmn}}} \right] - }\\ {\begin{array}{*{20}{c}} {{C_{stij}}{B_{ij}} = \Delta {C_{stij}}{E_{ij}}}\\ {\Delta {C_{stij}}\left[{{M_{ijkl, p}}(0){B_{kl}} + {M_{ijklm, p}}(0){B_{klm}} + } \right.}\\ {\left. {{M_{ijklmn, p}}(0){B_{klmn}}} \right] - {C_{stij}}{B_{ijp}} = \Delta {C_{stij}}{E_{ijp}}} \end{array}}\\ {\Delta {C_{stij}}\left[{{M_{ijkl, pq}}(0){B_{kl}} + {M_{ijklm, pq}}(0){B_{klm}} + } \right.}\\ {\left. {{M_{ijklmn, pq}}(0){B_{klmn}}} \right] -{C_{stij}}{B_{ijpq}} = \Delta {C_{stij}}{E_{ijpq}}} \end{array}} \right\} $ | (16) |
求解即可得到异形夹杂中本征应变和平均本征应变,代入式(1)可得到夹杂中和夹杂附近的应力应变场分布,进而得到平均应力和应变.当颗粒为椭球时上述一次项和二次项系数为0,解是精确解.
3 损伤材料的有效性能估计颗粒置于基体中构成的复合材料有效介质的刚度和柔度矩阵表示为C和S.颗粒加入后有效柔度相对于基体的柔度增量H定义为
| $ \boldsymbol{H} = \boldsymbol{S} - \boldsymbol{S}_0 $ | (17) |
复合材料受远场面力边界条件σ∞作用时.复合材料平均应变可以表示为
| $ \mathit{\boldsymbol{\overline \varepsilon }} = {\mathit{\boldsymbol{S}}_0}{\mathit{\boldsymbol{\sigma }}_\infty } + \sum {} {f_i}{\mathit{\boldsymbol{H}}_i}{\mathit{\boldsymbol{\sigma }}_i} $ | (18) |
此处σi为第i型夹杂的平均应力,Hi=Si-S0.采用应变等效ε=Sσ∞定义的有效柔度张量S,结合式(17)和式(18)有
| $ \boldsymbol{H}\boldsymbol{\sigma}_\infty = \sum f_i \boldsymbol{H}_i \boldsymbol{\sigma}_i $ | (19) |
若夹杂为稀疏分布,可以对σi给出一种简单的估计[41].
理论研究表明[8],夹杂周围应力应变场扰动只在颗粒附近约一个直径范围内影响较大,如球形夹杂外扰动应力随该点与球心距离的3次方降低,因此,当一个小尺寸夹杂靠近大尺寸的夹杂时,大夹杂中应力应变场所受影响有限,而小夹杂受大夹杂影响巨大.本文中假设初始状态下裂纹尺寸相对于颗粒尺寸较小,裂纹对颗粒的影响用一个参数表示,而裂纹外载应力场受颗粒中应力场控制.
首先将颗粒附近的裂纹也视为一种夹杂,并且暂时假设其中具有名义上的应力σint,则在完好界面夹杂附近加一个裂纹夹杂,材料柔度增量H可表示为
| $ \boldsymbol{H}\sigma _\infty = f_i \boldsymbol{H}_i \boldsymbol{\sigma }'_i + f_{\rm int} \boldsymbol{H}_{\rm int} \boldsymbol{\sigma}_{\rm int} $ | (20) |
其中,σ’i=ησi,σi为无裂纹时夹杂中的平均应力,由于脱粘裂纹与颗粒的相互作用,导致颗粒中平均应力发生变化,用σ’i表示裂纹影响下颗粒中的平均应力,η表示裂纹对颗粒中平均应力的相互作用系数.根据相互作用直推估计法[41],置于等效介质中的颗粒中平均应力σi可以表示为
| $ \boldsymbol{\sigma}_i = (\boldsymbol{I} + \boldsymbol{\varOmega}_i \boldsymbol{H}_i )^{ - 1}\boldsymbol{\sigma}_{\rm e} $ | (21) |
式中,
| $ \boldsymbol{\sigma}_{\rm e} = (\boldsymbol{I} - \boldsymbol{\varOmega}_{\rm e} \boldsymbol{H})^{ - 1}\boldsymbol{\sigma}_\infty $ | (22) |
这里Ωe为选取基体颗粒对应的本征刚度,一般与颗粒形状相同.同理,对于裂纹也有
| $ \boldsymbol{\sigma }_{\rm int} = (\boldsymbol{I} + \boldsymbol{\varOmega}_{\rm int} \boldsymbol{H}_{\rm int} )^{ - 1}\boldsymbol{\sigma }_{\rm int\infty } $ | (23) |
这里将裂纹视为扁平的椭球,则
| $ {\mathit{\boldsymbol{\sigma }}_{{\rm{int}}\infty }} = {\mathit{\boldsymbol{\sigma }}_{\rm{e}}}-{\mathit{\boldsymbol{\overline D}} _i}{({\mathit{\boldsymbol{\overline M}} _i}-\mathit{\boldsymbol{I}})^{-1}}({\mathit{\boldsymbol{\sigma }}_{\rm{e}}} - {\mathit{\boldsymbol{\sigma '}}_i}) $ | (24) |
其中,Di为颗粒外相互作用张量在裂纹面上的均值,即
| $ \boldsymbol{\sigma }_{\rm int} = (\boldsymbol{I} +\boldsymbol{\varOmega }_{\rm int} \boldsymbol{H}_{\rm int} )^{ - 1} \boldsymbol{\varPi} \boldsymbol{\sigma}_{\rm e} $ | (25) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPi} }} = \mathit{\boldsymbol{I}} - {\mathit{\boldsymbol{D}}_i}{({\mathit{\boldsymbol{\overline M}} _i} - \mathit{\boldsymbol{I}})^{ - 1}} + \eta {\mathit{\boldsymbol{D}}_i}{({\mathit{\boldsymbol{\overline M}} _i} - \mathit{\boldsymbol{I}})^{ - 1}}{(\mathit{\boldsymbol{I}} + {\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}_i}{\mathit{\boldsymbol{H}}_i})^{ - 1}} $ | (26) |
再结合式(22),颗粒和诱发裂纹造成的柔度扰动可以表示为
| $ \boldsymbol{H}\boldsymbol{\sigma}_\infty = \boldsymbol{J}(\boldsymbol{I } - \boldsymbol{\varOmega}_{\rm e} \boldsymbol{H} )^{ - 1}\boldsymbol{ \sigma}_\infty $ | (27) |
其中,
将式(27)泰勒一级展开有
| $ \boldsymbol{H} = \boldsymbol{J}\left[{\boldsymbol{I} + \boldsymbol{\varOmega}_{\rm e} \boldsymbol{H} + O(f^3)} \right] $ | (28) |
忽略高阶小量,近似得到H为
| $ \boldsymbol{H} = \left( {\boldsymbol{I} -\boldsymbol{J}\boldsymbol{\varOmega}_{\rm e} } \right)^{ - 1}\boldsymbol{J} $ | (29) |
则含任意脱粘界面颗粒材料的有效刚度为
| $ \boldsymbol{C} = \left( {\boldsymbol{S}_0 + \boldsymbol{H}} \right)^{ - 1} $ | (30) |
这样,材料损伤各个阶段的宏观有效性能可以通过式(30)直接表示,同时对每一个脱粘胞元的局部分析可以将式(29)的结果代入式(22)得到颗粒和裂纹组成胞元的等效外载应力,进一步分析裂纹的扩展情况,因此能够描述材料细观损伤过程和宏观响应.
4 单轴加载下材料的损伤演化如前假设,认为裂纹在颗粒顶点附近,为简化计算,这里将式(20)中相互作用系数定义为η=(A0-Ap)/A0,Ap为裂纹面积,A0为颗粒在裂纹所在平面上的投影面积,裂纹相当于置于等效应力边界条件为σint∞的无限大基体C0中
| $ \boldsymbol{\sigma} _{\rm int\infty } = \boldsymbol{\varPi} \boldsymbol{\sigma}_{\rm e} = \boldsymbol{\Re}\boldsymbol{\sigma}_\infty $ | (31) |
其中
假设材料受简单拉伸,颗粒胞元局部坐标系的轴3方向与拉伸方向相同,如图 2所示.在颗粒所在的局部坐标系下,外载应力可表示为σ∞=(0, 0, σ∞, 0, 0, 0)T,则垂直裂纹面上应力为
| $ \sigma _{\rm int\infty 33} = \Re _{33} \sigma _\infty $ | (32) |
特别注意,当裂纹长度变化时,柔度扰动随裂纹扩展长度变化而变化.
对于图 2所示的颗粒,当颗粒刚度大于基体时,颗粒顶点附近应力集中最大,因此认为颗粒顶点附近的缺陷首先扩展,即图中A1位置,在单位外载应力下,裂纹边缘应力强度因子KI为
| $ {K_{\rm{I}}} = \frac{2}{{\sqrt {{\rm{\pi }}c} }}\int {} _0^c\frac{{r\sigma (r)}}{{\sqrt {{c^2}-{r^2}} }}{\rm{d}}r $ | (33) |
式中,σ(r)是单位外载下裂纹在3方向裂纹面上的应力分布,与缺陷与颗粒相对位置有关,通过第一节的方法得到本征应变ε**,再由式(1)第2式求得.外载应力下裂纹稳定扩展条件为
| $ {\begin{array}{*{20}{c}} {{\sigma _{{\rm{int}}\infty }}{K_{\rm{I}}}-{K_{\rm{C}}} = 0}\\ {{\rm{d}}({\sigma _{{\rm{int}}\infty }}{K_{\rm{I}}}-{K_{\rm{C}}})/{\rm{d}}c < 0} \end{array}} $ | (34) |
将颗粒周围裂纹失稳扩展前极限加载作为胞元强度,则胞元强度σc应满足如下条件
| $ \left. {\begin{array}{*{20}{c}} {{\sigma _{\rm{c}}}{K_{\rm{I}}}-{K_{\rm{C}}} = 0}\\ {{\rm{d}}({\sigma _{\rm{c}}}{K_{\rm{I}}}-{K_{\rm{C}}})/{\rm{d}}c = 0}\\ {{{\rm{d}}^2}({\sigma _{\rm{c}}}{K_{\rm{I}}}-{K_{\rm{C}}})/{\rm{d}}{c^2} < 0} \end{array}} \right\} $ | (35) |
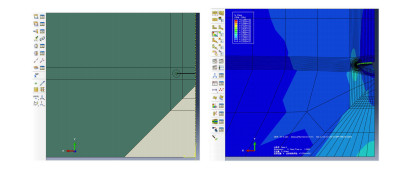
上述理论模型中有较多的假设和简化,需要验证一些重要简化的有效性,如上一节中将相互作用系数η简化为面积比的合理性,以及颗粒附近裂纹的应力强度因子计算方法的有效性.这里通过与有限元方法结果对比进行分析.以图 2所示的双圆锥为例,假设基体弹性模量E0=200 GPa,泊松比v0=0.25,颗粒刚度为Ei=500 GPa,泊松比与基体相同,双锥形颗粒底面圆盘半径a=1 mm,总高度2h=2 mm,距锥顶d=0.05a处有微缺陷,假设受单向拉伸,拉伸方向沿双锥的轴向.在有限元软件ABAQUS中建立模型如图 3所示.
|
图 3 ABAQUS中双锥颗粒及其顶部裂纹的1/8模型 Figure 3 1/8 model of double-circular cone particle and crack in ABAQUS |
在模型纵向加载100 MPa拉伸应力,不同半径裂纹I型应力强度因子对比结果如图 4所示.

|
图 4 简单拉伸下有限元结果和本文方法结果对比 Figure 4 Comparison between the present results and the FEM results of SIF in simple tension |
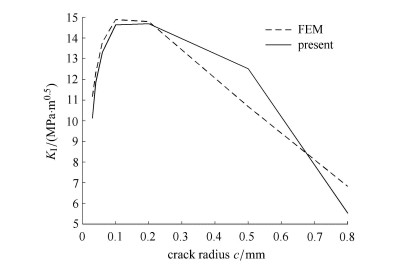
令基体热膨胀系数α0=5× 10-6℃-1,颗粒热膨胀系数为基体的2倍,温度下降1 500℃时残余应力作用下的I型应力强度因子图 5所示.
|
图 5 残余应力下有限元结果和本文方法结果对比 Figure 5 Comparison between the present results and the FEM results of SIF in residual stress |
对比结果表明,上述简化虽有一定的误差,但能够反应相互作用下结构参数变化对相关参数的影响规律.下面基于本文的估计方法分析各种参数变化时对材料损伤规律和性能的影响.
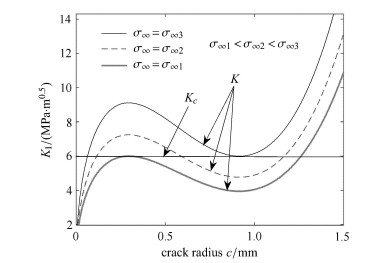
假设基体断裂韧性为KC=6 MPa·m0.5,在不同大小外载应力简单拉伸下,应力强度因子随裂纹长度变化如图 6所示.
|
图 6 不同加载下裂纹尖端应力强度因子与裂纹半径的关系 Figure 6 Stress intensity factor with variation crack length under different loading |
图 6可以看出不同裂纹长度下,应力强度因子先增大后减小,裂纹有可能在一定长度时稳定下来,直到外载应力继续增加超过裂纹稳定条件时,裂纹再继续失稳扩展.这与图 4所示的单个颗粒附近裂纹的结果不一样,主要原因在于,将裂纹和颗粒当一个“胞元”置于有效介质中时,由于裂纹长度增大,胞元的等效刚度剧烈下降,加载在胞元上的等效应力以及颗粒中分配的应力剧烈下降,从而导致裂纹长度增大而应力强度因子反而减小的情形,在颗粒中残余拉应力的参与下现象将更加明显.
图 6中可见,若初始状态下裂纹尺寸很小,则裂纹在较大应力下才开始扩展,此时加载应力可能大于稳定扩展所需的外载应力,或者裂纹尺寸很大,超过了稳定扩展的极限,这两种条件下一但扩展即失稳.
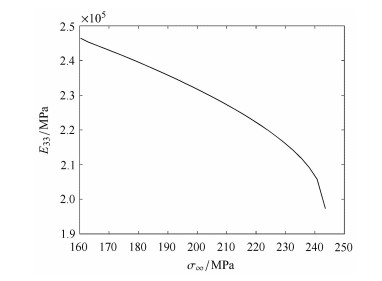
假设颗粒周围裂纹尺寸分布较大,在一定应力下满足稳定扩展的条件,则裂纹扩展导致材料损伤发展,材料有效弹性模量随载荷增加的变化如图 7所示.
|
图 7 材料刚度随损伤增加而降低 Figure 7 The equivalent stiffness reduced with the increasing damage |
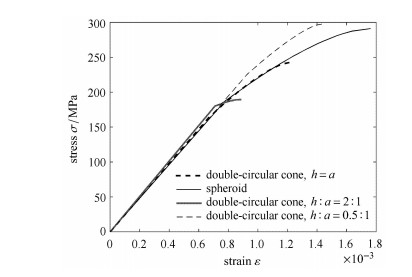
多种因素对颗粒诱导裂纹损伤有影响.如颗粒形状、尺寸、颗粒性能以及颗粒与初始缺陷相对位置都有影响,图 8显示了椭球和非椭球的差异,以及颗粒形状变化时对材料损伤的影响.
|
图 8 颗粒形状对材料损伤演化的影响 Figure 8 Influence of the particle shape on damage evaluation of the composite ceramic |
图 8中可以看出,当颗粒不是椭球时,含非椭球颗粒的材料损伤发生更早,相同的加载条件下,含非椭球颗粒材料损伤更严重,强度降低.相同的非椭球时,长径比大的损伤发生更早,强度降低.
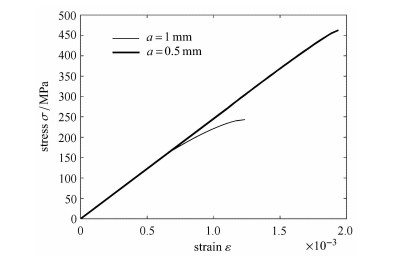
颗粒尺寸变化时,材料应力应变曲线对比如图 9.从图 9中可以看出,颗粒越小,损伤发生越晚,损伤过程越短,强度越高,当颗粒小到一定程度时,有可能完全看不出稳定的损伤过程而直接破坏.
|
图 9 颗粒尺寸对材料损伤演化的影响 Figure 9 Influence of the particle size on damage evaluation of the composite ceramic |
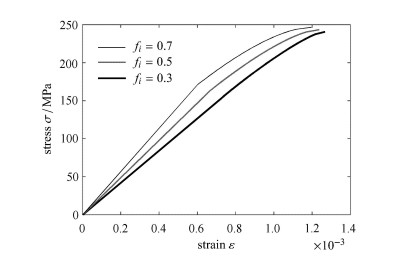
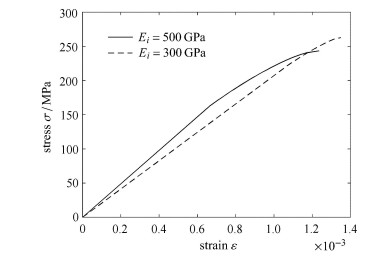
颗粒含量fi、缺陷与颗粒尖端的相对位置d、基体和颗粒性能差异对损伤也有影响,如图 10~图 12所示.
|
图 10 颗粒含量对材料损伤演化的影响 Figure 10 Influence of the volume fraction of particle on damage evaluation of the composite ceramic |

|
图 11 颗粒与裂纹相对位置对材料损伤演化的影响 Figure 11 Influence of the distance between the crack and the particle on damage evaluation of the composite ceramic |
|
图 12 颗粒刚度对材料损伤演化的影响 Figure 12 Influence of the particle stiffness on damage evaluation of the composite ceramic |
颗粒含量对材料损伤演化发生的时机影响不大,主要影响有效刚度.裂纹与颗粒距离变大时,损伤发生更晚,但损伤的过程更短,强度降低.颗粒刚度大于基体时,颗粒刚度高的材料损伤发生更早,强度更低.
6 结论根据颗粒材料损伤产生机理,认为颗粒诱导裂纹紧邻颗粒,基于有效自洽理论建立了材料细观损伤模型,得到了单向拉伸下的力学响应,并分析了颗粒形状、尺寸、颗粒性能以及颗粒与初始缺陷相对位置等因素对材料损伤的影响,结果表明:
(1) 相对于椭球颗粒,含有尖角的颗粒在更低的加载下发生损伤,降低材料强度;长径比增大时材料损伤提前,强度降低;
(2) 减小颗粒尺寸,能够减小甚至避免材料稳定损伤过程,提高材料强度;
(3) 裂纹远离颗粒时,损伤发生更晚,但损伤的过程更短,强度降低;降低刚性颗粒刚度能提高材料强度;
(4) 初始裂纹长度对损伤有重要影响,当初始裂纹尺寸很小或者很大,裂纹都将直接失稳,但大尺寸裂纹降低材料强度.
| 1 | Eshelby JD. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc Royal Soc A, 1957, 241 : 376-396. DOI: 10.1098/rspa.1957.0133. |
| 2 | Mori T, Tanaka K. Average stress in matrix and average energy of materials with misfitting inclusion. Act Metal, 1973, 21 : 571-574. DOI: 10.1016/0001-6160(73)90064-3. |
| 3 | Mallick K, Cronin J, Arzberger S. Effect of inclusion morphology on the coefficient of thermal expansion of a filled polymer matrix. AIAA 2006-2098, 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Con, Rhode Island, 2006 |
| 4 | 粱军, 杜善义, 许兴利, 等. 含缺陷纤维增强复合材料热膨胀系数预报. 哈尔滨工业大学学报, 1997, 29 (3) : 36-38. ( Liang Jun, Du Shanyi, Xu Xingli, et al. Thermal expansion coefficients of fiber composite materials containing matrix microcracks. Journal of Harbin Institute of Technology, 1997, 29 (3) : 36-38. (in Chinese) ) |
| 5 | Teng H. Stiffness properties of particulate composites containing debonded particles. Int J Solids Struct, 2010, 47 : 2191-2200. DOI: 10.1016/j.ijsolstr.2010.04.004. |
| 6 | 付云伟, 刘协权, 倪新华, 等. 含固有缺陷复合材料有效弹性性能预报. 机械工程学报, 2012, 48 (6) : 46-51. ( Fu Yunwei, Liu Xiequan, Ni Xinhua, et al. Effective elastic property prediction of ceramic composite with inherent defect. J Mech Engng, 2012, 48 (6) : 46-51. (in Chinese) ) |
| 7 | Sridhar N, Rickman JM, Srolovitz DJ. Effect of reinforcement morphology on matrix microcracking. Acta Mater, 1996, 44 (3) : 915-925. DOI: 10.1016/1359-6454(95)00245-6. |
| 8 | Mura T. Micromechanics of Defects in Solids . Dordrecht: Martinus NijhoffPublishers, 1987. |
| 9 | 郭荣鑫, LormandG, 李俊昌. 夹杂物问题应力场的数值计算. 昆明理工大学学报(理工版), 2004, 29 (3) : 51-55. ( Guo Rongxin, Lormand G, Li Junchang. Numerical Calculation of the Stress field for the inclusion problem. Journal of Kunming University of Science and Technology (Science and Technology), 2004, 29 (3) : 51-55. (in Chinese) ) |
| 10 | Lee HK, Pyo SH. Multi-level modeling of effective elastic behavior and progressive weakened interface in particulate composites. Composites Science and Technology, 2008, 68 : 387-397. DOI: 10.1016/j.compscitech.2007.06.026. |
| 11 | Qu J. Eshelby tensor for an elastic inclusion with slightly weakened interfaces. Journal of Applied Mechanics, 1993, 60 (4) : 1048-1050. DOI: 10.1115/1.2900974. |
| 12 | Bian LC, Wang Q. Influence of the particle size and volume fraction on micro-damage of the composites. Arch Appl Mech, 2012, 83 : 445-454. |
| 13 | Wilkinson DS, Pompe W, Oeschner M. Modeling the mechanical behaviour of heterogeneous multi-phase materials. Prog Mech Sci, 2001 (46) : 379-405. |
| 14 | Shodja HM, Shokrolahi-Zadeh B. Ellipsoidal domains:piecewise nonuniform and impotent eigenstrain fields. J Elasticity, 2007, 86 : 1-18. |
| 15 | Bonfoh N, Hounkpati V, Sabar H. New micromechanical approach of the coated inclusion problem:Exact solution and applications. Comp Mat Sci, 2012, 62 : 175-183. DOI: 10.1016/j.commatsci.2012.05.007. |
| 16 | Jasiuk I, Tsuchida E, Mura T. The sliding inclusion under shear. Int. J. Solids Struct, 1987, 23 (10) : 1373-1385. DOI: 10.1016/0020-7683(87)90003-5. |
| 17 | Mura T, Jasiuk I, Tsuchida B. The stress field of a sliding inclusion. Int J Solids Struct, 1985, 21 (12) : 1165-1179. DOI: 10.1016/0020-7683(85)90002-2. |
| 18 | Xu BX, Mueller R, Wang MZ. The Eshelby property of sliding inclusions. Arch Appl Mech, 2011, 81 : 19-35. DOI: 10.1007/s00419-009-0391-1. |
| 19 | Sauer R, Wang AG, Li S. The composite Eshelby tensors and their applications to homogenization. Acta Mech, 2008, 197 : 63-96. DOI: 10.1007/s00707-007-0504-2. |
| 20 | Kang H, Milton GW. Solutions to the Pólya-Szegö conjecture and the weak Eshelby conjecture. Arch Ration Mech An, 2008, 188 (1) : 93-116. DOI: 10.1007/s00205-007-0087-z. |
| 21 | Liu LP. Solutions to the Eshelby conjectures. P Ro Soc Edinb A, 2008, 464 : 573-594. DOI: 10.1098/rspa.2007.0219. |
| 22 | Zou WN. Limitation of average Eshelby tensor and its application in analysis of ellipse approximation. Acta Mech Solida Sinica, 2001, 24 (2) : 176-184. |
| 23 | Han AL, Gan BS, Setiawan Y. The influence of single inclusions to the crack initiation, propagation and compression strength of mortar. Procedia Engineering, 2014, 95 : 376-385. DOI: 10.1016/j.proeng.2014.12.196. |
| 24 | Williams JJ, Segurado J, LLorca J, et al. Three dimensional (3D) microstructure-based modeling of interfacial decohesion in particle reinforced metal matrix composites. Materials Science & Engineering A, 2012, 557 : 113-118. |
| 25 | 郝圣旺, 孙菊. 非均质脆性材料灾变破坏的一种敏感前兆. 力学学报, 2008, 40 (3) : 339-344. ( Hao Shengwang, Sun Ju. A sensitive precursor to catastrophic failure in heterogeneous brittle materials. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40 (3) : 339-344. (in Chinese) ) |
| 26 | Tan H, Huang Y, Liu C, et al. The uniaxial tension of particulate composite materials with nonlinear interface debonding. Int J Solids Struct, 2007, 44 : 1809-1822. DOI: 10.1016/j.ijsolstr.2006.09.004. |
| 27 | Ju JW, Lee HK. A micromechanical damage model for effective elastoplastic behavior of partially debonded ductile matrix composites. Int J Solids Struct, 2001, 38 : 6307-6332. DOI: 10.1016/S0020-7683(01)00124-X. |
| 28 | Chen JK, Wang GT, Yu ZZ, et al. Critical particle size for interfacial debonding in polymer/nanoparticle composites. Composites Science and Technology, 2010, 70 : 861-872. DOI: 10.1016/j.compscitech.2010.02.004. |
| 29 | 付云伟, 张龙, 倪新华, 等. 考虑夹杂相互作用的复合陶瓷夹杂界面的断裂分析. 力学学报, 2016, 48 (1) : 154-162. ( Fu Yunwei, Zhang Long, Ni Xinhua, et al. Interface cracking analysis with inclusions interaction in composite ceramic. Chinese Journal of Theoretical and Applied Mechanics, 2016, 48 (1) : 154-162. (in Chinese) ) |
| 30 | Meng QH, Wang ZQ. Prediction of interfacial strength and failure mechanisms in particle-reinforced metal-matrix composites based on a micromechanical model. Engineering Fracture Mechanics, 2015, 142 (1) : 170-183. |
| 31 | McNamara D, Alveen P, Carolan D, et al. Numerical analysis of the strength of polycrystalline diamond as a function of microstructure. International Journal of Refractory Metals and Hard Materials, 2015, 52 (1) : 195-202. |
| 32 | Rodin GJ. Eshelby's inclusion problem for polygons and polyhedra. J Mech Phys Solids, 1996, 44 (12) : 1977-1995. DOI: 10.1016/S0022-5096(96)00066-X. |
| 33 | Chen QD, Xu K, Pan YE. Inclusion of an arbitrary polygon with graded eigenstrain in an anisotropic piezoelectric half plane. J Mech Phys Solids, 2014, 51 (2) : 53-62. |
| 34 | Lee YG, Zou WN, Ren HH. Eshelby's problem of inclusion with arbitrary shape in an isotropic elastic half-plane. J Mech Phys Solids, 2016, 81 (1) : 399-410. |
| 35 | Liu MQ, Gao XL. Strain gradient solution for the Eshelby-type polygonal inclusion problem. J Mech Phys Solids, 2013, 50 (2) : 328-338. |
| 36 | Huang NC, Korobeinik MY. Interfacial debonding of a spherical inclusion embedded in an infinite medium under remote stress. International Journal of Fracture, 2001, 107 : 11-30. DOI: 10.1023/A:1026500321333. |
| 37 | Sridhar N, Rickman J, Srolovitz M. Effect of reinforcement morphology on matrix microcracking. Acta Mater, 1996, 44 (3) : 915-925. DOI: 10.1016/1359-6454(95)00245-6. |
| 38 | Ju JW, Lee HK. A micromechanical damage model for effective elastoplasttic behavior of partially debonded ductile matrix composites. Int J Solids Struct, 2001, 38 : 6307-6332. DOI: 10.1016/S0020-7683(01)00124-X. |
| 39 | Zhou R, Li Z, Sun J. Crack deffection and interface debonding in composite materials elucidated by the configuration force theory. Composites:Part B, 2011, 42 : 1999-2003. DOI: 10.1016/j.compositesb.2011.05.024. |
| 40 | Knight MG, Wrobel JL, Henshall JL, et al. A study of the interaction between a propagating crack and an uncoated/coated elastic inclusion using the BE technique. International Journal of Fracture, 2002, 114 : 47-61. DOI: 10.1023/A:1014837509347. |
| 41 | Zheng QS, Du DX. An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution. J Mech Phys Solids, 2001, 49 (11) : 2765-2788. DOI: 10.1016/S0022-5096(01)00078-3. |
| 42 | Nozaki H, Taya M. Elastic fields in a polygon-shaped inclusion with uniform eigenstrains. ASME J Appl Mech, 1997, 64 : 499-502. |
| 43 | Xu BX, Wang MZ. Special properties of Eshelby tensor for a regular polygonal inclusion. Acta Mech Sinica, 2005, 21 (3) : 267-271. DOI: 10.1007/s10409-005-0034-x. |
| 44 | Huang MJ, Wu P, Guan GY, et al. Explicit expressions of the Eshelby tensor for an arbitrary 3D weakly non-spherical inclusion. Acta Mech, 2011, 217 (1-2) : 17-38. DOI: 10.1007/s00707-010-0375-9. |
†. Department of Vehicle and Electric Engineering, Ordnance Engineering College, Shijiazhuang 050003, China;
**. Department of Basic Course, Ordnance Engineering College, Shijiazhuang 050003, China;
††. Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, Sichuan, China

