时空关联函数是湍流研究中的一个基本统计特性函数,结构函数、能谱都可以由相关函数得到.无论是湍流基础理论研究还是实际工程应用,时空关联性都有广泛的应用.例如,根据时空关联特性,可以改进大涡模拟方法,发展亚格子模型[1-2];根据声比拟理论,流动诱导的声音取决于速度时空关联即频率波数能谱[3-4].如若追其研究历史,早在1959年Kraichnan[5]根据直接作用近似理论,提出横扫假设理论,给定了速度时空关联应该满足的关系式. 1972年,Orszag等[6]在采用direct numerical simulation (DNS)研究衰减均匀各向同性湍流时发现,谱空间的速度时空关联函数可以通过去关联时间尺度进行重整化. 1993年,Gotoh等[7]采用DNS对湍流速度的欧拉关联和拉格朗日关联做了分析和研究,并对"横扫作用"做了详细的讨论. 2006年,何国威等[8]在Taylor提出的Frozen-Flow假设基础上,根据流场速度时空关联的数据分析,发现湍流时空信号转化的非线性关系,提出了时空关联椭圆模型,解释了泰勒模型缺少涡变形机制的问题,并将其应用于大涡模拟方法、气动噪声、湍流能谱分析等方面研究.而国内外的一系列关于流场时空关联统计性质的实验[9-11]、数值和理论研究也说明了其对湍流流场分析的意义.
本文用格子Boltzmann方法研究具有多孔介质壁面的槽道剪切湍流的速度时空关联特性.格子Boltzmann模型是近年来迅猛发展的一种模拟流动的新方法[12],该方法遵循质量、动量和能量守恒等基本物理规律,用简单的介观模型在Boltzmann方程控制下模拟流动.该方法经过近二十年的研究日渐成熟,并在微纳米尺度流[13]、多孔介质流[14-15]、多相多质流[16-17]、化学反应流[18]、非牛顿流体[19-21]、粒子悬浮流[22]、磁流体[23]等方面得到充分应用.与传统计算流体力学(computational fluid dynamics, CFD)相比,该方法适用于模拟弱可压流动问题,且算法简单,边界处理方便,常用于高效并行大规模计算.多孔介质的物理特性(孔隙率、渗透率)不同于一般材料,其能够在人为控制下具有诸如减阻、吸附、调节热传输与流动等功能.流体在多孔介质中的流动在自然界中广泛存在,是多种工程及学科的交叉,涉及石油、天然气、煤层气等各种地下流体资源的勘探和开采工程,固定床反应器、膜反应器(燃料电池)等的设计、优化与放大的化学工程,动物体内血液微循环、植物体内水分的输送等生物医学工程,地面沉降、地下水污染、土壤改良等地下水水文学、土壤学以及土力学等[24].本文意在通过研究多孔介质壁面槽道湍流的时空关联特性, 一方面进一步探索湍流领域的速度时空关联特性,辅助气动声学研究;另一方面促进对多孔介质在流体领域的研究,辅助对多孔介质减噪减阻性能的探索[25].
1 数理方法和物理模型 1.1 基于通用渗流模型的LBE模型LBGK(lattice Bhatnagar-Gross-Krook)模型是应用最为广泛的LBE(lattice Boltzmann
equation)模型之一,其中D
含作用力项的LBGK模型基本方程为
| $\begin{array}{l} {f_i}\left( {{\boldsymbol{x}} + {{\boldsymbol{c}}_i}{\delta _t}, t + {\delta _t}} \right) - {f_i}\left( {{\boldsymbol{x}}, t} \right) = \\ \;\;\; - \frac{1}{\tau }\left( {{f_i}\left( {{\boldsymbol{x}}, t} \right) - f_i^{{\rm{eq}}}\left( {{\boldsymbol{x}}, t} \right)} \right) + {\delta _t}{F_i} \end{array}$ | (1) |
其中,
| $\begin{equation} \nu=c^2_{\rm s}(\tau-0.5)\delta_t \end{equation}$ | (2) |
式中,
| $\begin{equation} \label{eq3} f_i^{\rm eq} ({\boldsymbol{x}}, t) = \omega _i \rho \left[{1 + \frac{{\boldsymbol{c}}_i \cdot {\boldsymbol{u}}}{c_{\rm s}^2 } + \frac{\left( {{\boldsymbol{c}}_i \cdot {\boldsymbol{u}}} \right)^2}{2c_{\rm s}^4 }-\frac{{\boldsymbol{u}}^2}{2c_{\rm s}^2 }} \right] \end{equation}$ | (3) |
其中,
| $\begin{eqnarray} \label{eq4} \omega _i = \left\{ {\begin{array}{ll} \dfrac{1}{18}, &i= 1, 2, \cdots, 6 \\ \dfrac{1}{36}, &i= 7, 8, \cdots, 18 \\ \dfrac{1}{3}, &i= 19 \\ \end{array}} \right. \end{eqnarray}$ | (4) |
| $\begin{eqnarray} {\boldsymbol{c}}_i = \left\{ {\begin{array}{lll} \left( {\pm 1, 0, 0} \right)c, \left( {0, \pm 1, 0} \right)c, &\\ \left( {0, 0, \pm 1} \right)c, &i = 1, 2, \cdots, 6 \\ (\pm 1, \pm 1, 0)c, (\pm 1, 0, \pm 1)c,&\\ (0, \pm 1, \pm 1)c, &i = 7, 8, \cdots, 18 \\ (0, 0, 0)c, &i = 19\\ \end{array}} \right. \end{eqnarray}$ | (5) |
其中,
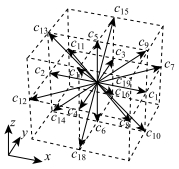
|
图 1 D3Q19模型 Figure 1 D3Q19 model |
通过该模型,宏观物理量如密度和动量等可以由下式根据守恒性计算得到
| $\begin{eqnarray} \sum\limits_i {f_i^{\rm eq} } = \rho \end{eqnarray}$ | (6) |
| $\begin{eqnarray} \sum\limits_i {{\boldsymbol{c}}_i f_i^{\rm eq} } + \frac{\delta _t }{2}\rho {\boldsymbol{ F}} = \rho {\boldsymbol{u}} \end{eqnarray} $ | (7) |
为了进一步研究多孔介质槽道湍流,本文在含作用力项的LBGK模型中引入Nithiarasu等[27]近年提出的渗流模型.该模型不但包含线性阻力和黏性项,而且包含了非线性阻力项,并且可以用于瞬态渗流.其中作用力项
| ${\boldsymbol{F}} = - \frac{{\varepsilon v}}{K}{\boldsymbol{u}} - \frac{{\varepsilon {F_\varepsilon }}}{{\sqrt K }}\left| {\boldsymbol{u}} \right|{\boldsymbol{u}} + \varepsilon {\boldsymbol{G}}$ | (8) |
式中,
| $\begin{eqnarray} F_\varepsilon = \frac{1.75}{\sqrt {150\varepsilon ^3} } \end{eqnarray}$ | (9) |
| $\begin{eqnarray} K = \frac{\varepsilon ^3d_{\rm p} ^2}{150(1 - \varepsilon )^2} \end{eqnarray}$ | (10) |
其中,
结合上述方程,本文构造可用于求解多孔介质流动的LBE方程,演化方程形式如方程(1),而作用力采用式(8).由于LBE的速度是离散的,所以
| $\begin{eqnarray} f^{\rm eq}_t=\omega_i\rho\left[1+ \dfrac{{\boldsymbol{c}}_i\cdot{\boldsymbol{u}}}{c^2_{\rm s}}+\dfrac{({\boldsymbol{c}}_i\cdot{\boldsymbol{u}})^2}{2\varepsilon c^4_{\rm s}}-\dfrac{{\boldsymbol{u}}^2}{2\varepsilon c^2_{\rm s}}\right] \end{eqnarray}$ | (11) |
| $\begin{eqnarray} F_i=\omega_i\rho\left(1-\dfrac{1}{2\tau}\right)\left[\dfrac{{\boldsymbol{ F}}\cdot{\boldsymbol{c}}_i}{c^2_{\rm s}}+\dfrac{{\boldsymbol{uF}:({\boldsymbol{c}}_i{\boldsymbol{c}}_i-c^2_{\rm s}{\boldsymbol{I}})}}{\varepsilon c^4_{\rm s}}\right]~~~~~~~~~~ \end{eqnarray}$ | (12) |
其中,
基于以上模型方法,本文建立研究问题的物理模型(图 2):流体在压力驱动下流过两个无限延伸的多孔介质壁面,并呈充分发展的湍流流动状态.该模型计算域在流向(

|
图 2 物理模型 Figure 2 Physical model |
两个不同点处物理量乘积的统计平均称之为相关函数.相关函数表征随机物理量之间相互关联作用的程度,是湍流统计理论的基本概念和研究内容.
速度时间相关函数是指同一个空间点不同时刻两个速度脉动分量乘积的系综平均,即
| $\begin{equation} R({\boldsymbol{x}}, \tau ) = \left\langle {{u}'_i \left( {{\boldsymbol{x}}, t} \right){u}'_j \left( {{\boldsymbol{x}}, t + \tau } \right)} \right\rangle \end{equation}$ | (13) |
同理,空间相关函数是指同一时刻不同空间点的两个速度脉动分量乘积的系综平均,即
| $\begin{equation} R({\boldsymbol{r}}, t) = \left\langle {{u}'_i \left( {{\boldsymbol{x}}, t} \right){u}'_j \left( {{\boldsymbol{x}} + {\boldsymbol{r}}, t} \right)} \right\rangle \end{equation}$ | (14) |
其中,
| $\begin{equation} R({\boldsymbol{r}}, \tau ) = \left\langle {{u}'_i \left( {{\boldsymbol{x}}, t} \right){u}'_j \left( {{\boldsymbol{x}} + {\boldsymbol{r}}, t + \tau } \right)} \right\rangle \end{equation}$ | (15) |
本文主要研究流向速度时空关联性,因此可以定义,在不同法向位置,流向速度脉动时空关联系数
| $\begin{equation} C\left( {r, \tau ;y} \right) = \frac{\left\langle {u_1 ^\prime \left( {x, y, z;t} \right)u_1 ^\prime \left( {x + r, y, z;t + \tau } \right)} \right\rangle }{\left\langle {u_1 ^\prime \left( {x, y, z;t} \right)^2} \right\rangle } \end{equation}$ | (16) |
由于在流向、展向的脉动量呈统计均匀分布,且沿时间进程流动统计定常, 因此速度时空关联与时间
基于二阶近似,何国威等[8]延伸了泰勒冻结假设与横扫理论,针对剪切湍流提出时空关联椭圆模型,即有
| $\begin{eqnarray} C\left( {r, \tau } \right) = C\left( {r_E, 0} \right) \end{eqnarray}$ | (17) |
| $\begin{eqnarray} r_{\rm E} ^2 = \left( {r - U\tau } \right)^2 + V^2\tau ^2 \end{eqnarray}$ | (18) |
其中,
| $\begin{eqnarray} U = - \frac{\partial ^2C\left( {0, 0} \right)}{\partial r\partial \tau }\left( {\frac{\partial ^2C\left( {0, 0} \right)}{\partial r^2}} \right)^{ - 1} \end{eqnarray}$ | (19) |
| $\begin{eqnarray} V^2 = \frac{\partial ^2C(0, 0)}{\partial \tau ^2}\left( {\frac{\partial ^2C(0, 0)}{\partial r^2}} \right)^{ - 1} - U^2 \end{eqnarray}$ | (20) |
其中,
| $\begin{array}{l} {\tan ^2}\alpha = \\ \;\;\;\;\;\;\frac{{4{U^2}}}{{{{\left[{\sqrt {{{\left( {1 + {U^2}-{V^2}} \right)}^2} + 4{U^2}{V^2}} + \left( {1-{U^2}-{V^2}} \right)} \right]}^2}}} \end{array}$ | (21) |
| $\begin{array}{l} {\lambda ^2} \equiv {\left( {\frac{b}{a}} \right)^2} = \\ \;\;\;\;\;\;\;\frac{{4{V^2}}}{{{{\left[{\sqrt {{{\left( {1 + {U^2}-{V^2}} \right)}^2} + 4{U^2}{V^2}} + \left( {1 + {U^2} + {V^2}} \right)} \right]}^2}}} \end{array}$ | (22) |
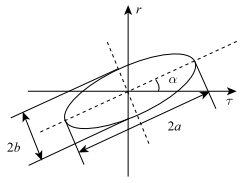
|
图 3 斜椭圆 Figure 3 Oblique ellipse |
本文在流向、法向和展向分别采用
| 表 1 槽道湍流计算参数对比 Table 1 Comparison of the key parameters of turbulent channel shear flows |
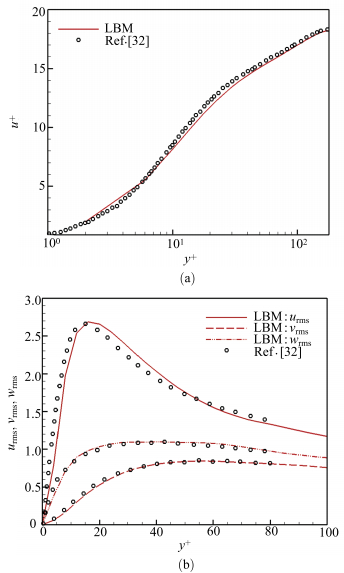
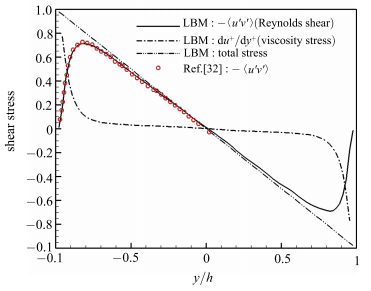
为了验证计算方法和程序的准确性,将计算的速度的相关统计量结果与Kim等[32]的DNS结果进行对比,如图 4所示流向平均速度和三个方向脉动速度分布,以及如图 5所示的剪切应力和雷诺应力分布.可以看出,本文采用LBM(lattice Boltzmann method)数值计算结果与前人结果符合良好.
|
图 4 (a)流向平均速度和(b)速度脉动均方根(a) Mean velocity and (b) root-mean-square velocity fluctuations |
|
图 5 雷诺剪切应力和黏性应力 Figure 5 Reynolds shear stress and viscosity stress |
为了研究速度时间关联特性,分别计算法向位置

|
图 6 不同空间分离距离下的时间关联( |
在不同空间分离距离的时间关联函数基础上,采用数值模拟获得的传播速度
| $\begin{equation} r_{\rm E} = \sqrt {\left( {r^ + - U\tau ^ + } \right)^2 + V^2(\tau^+)^2} \end{equation}$ | (23) |
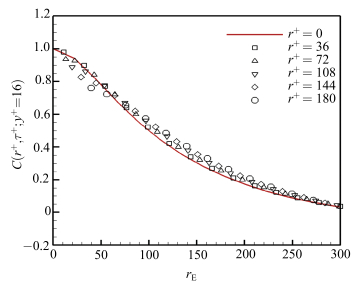
并以此作为横坐标对时间关联函数(图 6)进行重整化,得到图 7.从图 7可见,本文所计算的各个不同固定空间分离距离差之下的时间关联在对横坐标处理的情况下,几乎吻合在一起.这说明当以特征尺度
|
图 7 不同空间分离距离下重整化后的关联( |
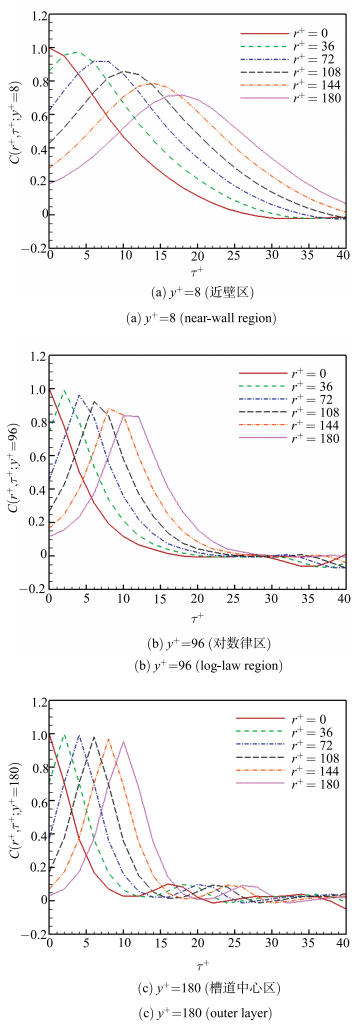
为了进一步研究各个法向位置处的解相关时间,计算了不同法向位置处、不同空间分离距离的时间关联函数,得到图 8.可以看出,随着法向位置逐渐远离壁面,在同样的时间分离距离(横坐标)下,其时间关联函数值减小,同时其解相关的时间也越来越短,高值相关性越来越集中.由于壁面附近存在大尺度的拟序结构,随着发卡涡的破裂,会形成强烈的指向壁面的下扫运动并将一部分流体抛往槽道中心方向,因此壁面附近流体流动的相关性是最强的,越远离壁面,受流向流体的影响,大尺度涡逐渐破裂,相关性也就随之减弱.
|
图 8 不同法向位置时间关联函数 Figure 8 The time correlations of velocities at different normal-wise positions |
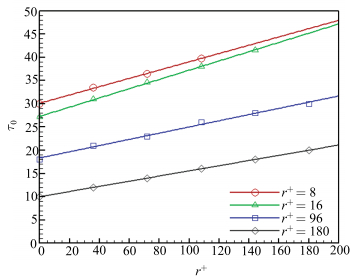
基于图 8中的不同法向位置的时间关联函数,进一步研究在不同法向位置处的去关联尺度.
图 9的纵坐标为去关联时间
|
图 9 不同法向位置去关联时间尺度 Figure 9 The decorrelation time scale of time correlation of velocities |
在多孔介质壁面中,孔隙率和渗透率是多孔介质壁面的特征参数.因此,使用控制变量法,基于速度时间关联函数,通过对比分析不同孔隙率和渗透率,考虑这两个参数对槽道湍流时间关联的影响.其中渗透率以达西数
| $\begin{equation} Da = \frac{K}{H^2} \end{equation}$ | (24) |
其中,
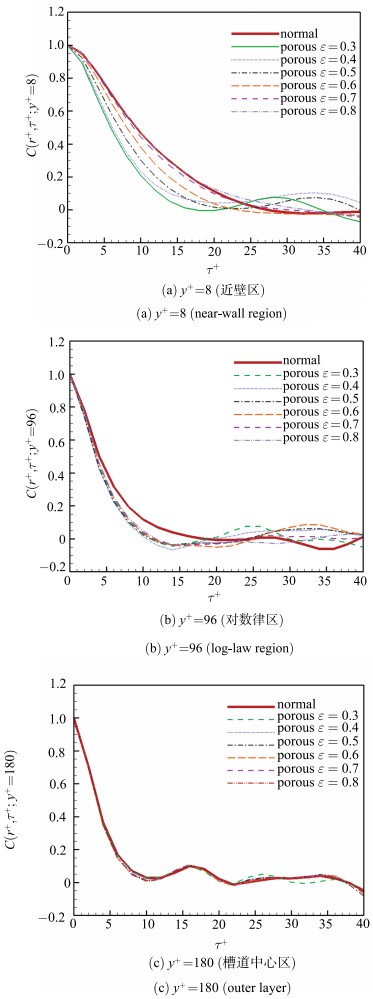
首先研究孔隙率
|
图 10 不同孔隙率下的时间关联 Figure 10 The time correlations of velocities for different porosities |
从图 10可以发现三个函数特性:其一,在所研究的参数范围内,在不同的法向位置,都保持着随着孔隙率增大而关联性增强的关系.其二,随着法向位置远离壁面,速度关联性有所降低,而且高值关联系数更加集中.其三,随着
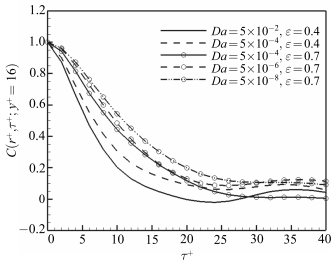
渗透率(
|
图 11 不同达西数下的时间关联( |
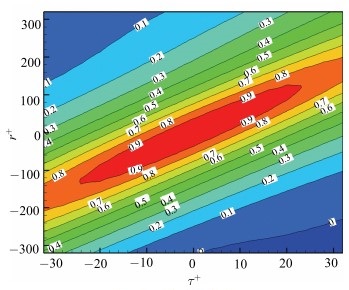
根据速度时空关联函数,统计常规槽道剪切湍流在
|
图 12 速度时空关联 Figure 12 The space-time correlations of velocities |

|
图 13 传播速度 Figure 13 The convection velocity |
|
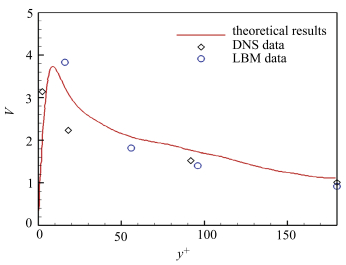
图 14 横扫速度 Figure 14 The sweeping velocity |
基于之前所研究的多孔介质槽道湍流时间关联的特性结果,本文对多孔材料壁面参数取值,对比分析时空关联性在常规壁面与多孔介质壁面间的差别.
为了更加明显地对比分析差别,以常规槽道湍流作为参考值.首先,分析不同孔隙率下的速度时空关联函数.其次,参考时间关联分析的结果,采用对比更加明显的

|
图 15 不同孔隙率下的速度时空关联( |
对比常规壁面与多孔壁面可以看出,相对于椭圆率的变化,倾斜角的变化非常小.多孔壁面主要影响槽道湍流速度时空关联的椭圆率,而倾斜角变化不大.由于椭圆率主要与横扫速度有关,推断多孔介质壁面主要影响剪切湍流的横扫速度.
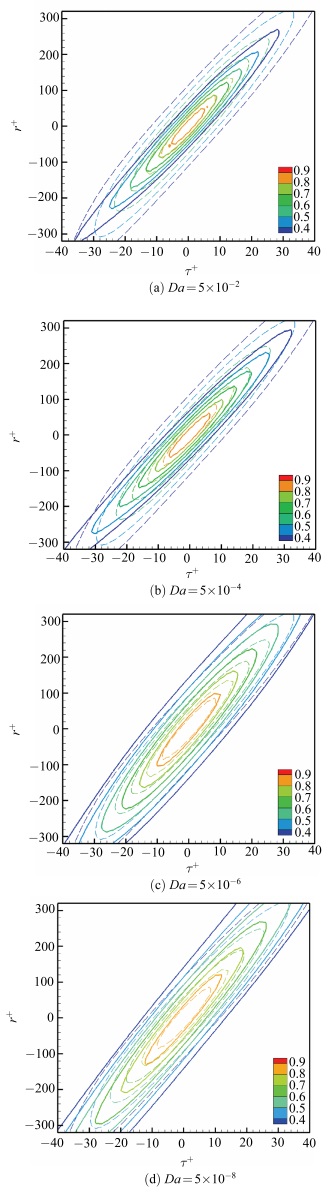
为研究不同渗透率下的速度时空关联函数.统一设置条件为
|
图 16 不同达西数下的速度时空关联( |
多孔壁面对槽道剪切湍流的流向速度时空关联函数的影响如图 16所示.从图 15和图 16可以看出,倾斜角相差都不大,而椭圆率相差较大,因此多孔介质主要影响椭圆关联等值线的椭圆率,对其倾斜角影响较小.
3 结论本文基于Boltzmann方法,获取流场信息,并着重分析了常规槽道湍流与多孔介质槽道湍流的流向速度脉动时空关联特性.得到以下主要结论:
(1)通过格子Boltzmann方法计算得到的槽道剪切湍流流场,研究其速度脉动时空关联函数的统计特性,发现关联系数等值线呈现出近似椭圆的典型特征.
(2)通过分析不同参数的多孔介质壁面剪切湍流,在所研究参数范围内,发现多孔介质壁面的孔隙率、渗透率对近壁区的速度脉动时空关联性有明显影响:随着孔隙率增大,流向速度脉动关联性增强;随着渗透率增大,流向速度脉动关联性降低.
(3)通过研究不同法向位置的流向速度脉动时空关联函数,发现越远离壁面的法向位置(对数律区和中心区)其速度时空关联函数所呈现的椭圆等值线越细长,高值关联值越集中;同时越远离壁面位置,其速度关联性受到多孔介质壁面影响越小.根据关联函数椭圆率的变化,说明多孔介质壁面主要影响剪切湍流的横扫速度.
| 1 | Dong YH, Sagaut P. A study of time correlations in lattice Boltzmann-based large-eddy simulation of isotropic turbulence. Physics of Fluids, 2008, 20 (3) : 035105. DOI: 10.1063/1.2842381. |
| 2 | He GW, Wang M, Sanjiva K. On the computation of space-time correlations by large-eddy simulation. Physics of Fluids, 2003, 16 (11) : 319-330. |
| 3 | Lighthill MJ. On sound generated areodynamically. I. General theory. Proceedings of the Royal Society of London, 1952, 211 : 564-587. DOI: 10.1098/rspa.1952.0060. |
| 4 | Proudman I. The generation of sound by isotropic turbulence. Proceedings of the Royal Society of London, 1952, 211 : 119-132. |
| 5 | Kraichnan RH. The structure of turbulence at very high Reynolds number. Journal of Fluid Mechanics, 1959, 5 (4) : 497-543. DOI: 10.1017/S0022112059000362. |
| 6 | Orszag SA, Patterson GS. Numerical simulation of threedimensional homogeneous isotropic turbulence. Physical Review Letters, 1972, 28 (2) : 76-79. DOI: 10.1103/PhysRevLett.28.76. |
| 7 | Gotoh T, Rogallo RS, Herring JR. Lagrangian velocity correlations in homogeneous isotropic turbulence. Physics of Fluids A Fluid Dynamics, 1993, 5 (11) : 2846-2864. DOI: 10.1063/1.858748. |
| 8 | He GW, Zhang J. Elliptic model for space-time correlations in turbulent shear flows. Physical Review E, 2006, 73 (5) : 055303. DOI: 10.1103/PhysRevE.73.055303. |
| 9 | Zhou Q, Li C, Lu Z, et al. Experimental investigation of longitudinal space-time correlations of the velocity field in turbulent Rayleigh-Bénard convection. Journal of Fluid Mechanics, 2011, 683 : 94-111. DOI: 10.1017/jfm.2011.249. |
| 10 | Goldeferd FS, Favier B, Cambon C. On space-time correlations in turbulent shear flows. Physics of Fluid, 2010, 22 : 015101. DOI: 10.1063/1.3276290. |
| 11 | Goldeferd FS, Favier B, Cambon C. Modeling the far-field acoustic emission of rotating turbulence. Journal of Turbulence, 2008, 9 : 1-21. |
| 12 | Chen H, Chen S, Matthaeus HW. Recovery of the Navier-Stokes equation using a lattice Boltzmann method. Phys. Rev, 1992, A45 : 5339-5342. |
| 13 | Raabe D. Overview of the lattice Boltzmann method for nanoscale and microscale fluid dynamics in materials science and engineering. Modelling and Simulation of Materials Science Engineering, 2004, 12 : 13-46. DOI: 10.1088/0965-0393/12/1/002. |
| 14 | Tang G, Tao W, He Y. Gas slippage effect on microscale porous flow using the lattice Boltzmann method. Physical Review E, 2005, 72 (5) : 056301. |
| 15 | Guo ZL, Zhao TS. Lattice Boltzmann model for incompressible flows through porous media. Physical Review E, 2002, 66 (32B) : 036301. |
| 16 | Grunau D, Chen S, Eggert K. A lattice Boltzmann model for multiphase fluid-flows. Physics of Fluids, 1993, 5 : 2557-2562. DOI: 10.1063/1.858769. |
| 17 | Luo L. Theory of the lattice Boltzmann method:Lattice Boltzmann model for nonideal gases. Physical Review E, 2000, 62 (4) : 4982. DOI: 10.1103/PhysRevE.62.4982. |
| 18 | Chen S, Dawson SP, Doolen GD. Lattice methods and their applications to reacting systems. Computers and Chemical Engineering, 1995, 19 : 617-646. DOI: 10.1016/0098-1354(94)00072-7. |
| 19 | Rakotomalala N, Salin D, Watzky P. Simulations of viscous flows of complex fluids with a Bhatnagar, Gross and Krook lattice gas. Physics of Fluids, 1996, 8 (11) : 3200-3202. DOI: 10.1063/1.869093. |
| 20 | Boek ES, Chin J, Coveney PV. Lattice Boltzmann simulation of the flow of non-Newtonian fluids in porous media. International Journal of Modern Physics B, 2003, 17 : 99-102. DOI: 10.1142/S021797920301714X. |
| 21 | Gabbanelli S, Drazer G, Koplik J. Lattice Boltzmann method for non-Newtonian (power-law) fluid. Physical Review E, 2005, 72 : 046312. DOI: 10.1103/PhysRevE.72.046312. |
| 22 | Ladd AJC, Verberg R. Lattice-Boltzmann simulation of particlefluid suspensions. Journal of Statistical Physics, 2001, 104 : 1191-1251. DOI: 10.1023/A:1010414013942. |
| 23 | Chen SY, Chen HD, Martnez D, et al. Lattice Boltzmann model for simulation of magnetohydrodynamics. Physical Review Letters, 1991, 67 (27) : 3776-3779. DOI: 10.1103/PhysRevLett.67.3776. |
| 24 | 贝尔.多孔介质流体动力学.李竞生, 陈崇希, 译.北京:中国建筑工业出版社, 1983 ( Bear. Dynamics of Fluids in Porous Media. Beijing:China Architecture & Building Press, 1983(in Chinese) ) |
| 25 | Tang Z, Liu N, Dong Y. Lattice Boltzmann simulations of turbulent shear flow between parallel porous walls. Applied Mathematics and Mechanics, 2014, 35 : 1479-1494. DOI: 10.1007/s10483-014-1885-6. |
| 26 | Qian YH, D'Humieres D, Lallemand P. Lattice BGK models for Navier-Stokes equation. Europhysics Letters, 1992, 17 (6) : 479-484. DOI: 10.1209/0295-5075/17/6/001. |
| 27 | Nithiarasu P, Seetharamu KN, Sundararajan T. Natural convective heat transfer in a fluid saturated variable porosity medium. International Journal of Heat & Mass Transfer, 1997, 40 : 3955-3967. |
| 28 | Ergun S. Fluid flow through packed columns. Chemical Engineering Progress, 1952, 48 : 89-94. |
| 29 | Luo LS. Unified theory of lattice Boltzmann models for nonideal gases. Physical Review Letters, 1998, 81 (8) : 1618-1621. DOI: 10.1103/PhysRevLett.81.1618. |
| 30 | He X, Shan X, Doolen Gary D. Discrete Boltzmann equation model for nonideal gases. Physical Review E, 1998, 57 (1) : R13-R16. DOI: 10.1103/PhysRevE.57.R13. |
| 31 | 郭照立, 郑楚光. 格子Boltzmann方法的原理及应用 . 北京: 科学出版社, 2009. ( Guo Zhaoli, Zheng Chuguang. Theory and Applications of Lattice Boltzmann Method . Beijng: Science Press, 2009. (in Chinese) ) |
| 32 | Kim J, Moin P, Moser R. Turbulence statistics in fully developed channel flow at low Reynolds number. Journal of Fluid Mechanics, 1987, 177 : 133-166. DOI: 10.1017/S0022112087000892. |


