高超声速细长锥气动外形无控再入体进入大气层时,在一定的飞行高度范围内表面会发生边界层转捩现象,导致细长锥的再入运动发生明显的异常[1].如可改变飞行器俯仰阻尼动导数的符号,产生非线性负阻尼现象,使飞行攻角发散,影响飞行器的气动特性;边界的非对称转捩对边界层的质量附加使再入体压心前移,导致非周期性不稳定运动现象,从而引起较大的再入落点散布[2-3],因此研究边界层转捩对高超声速细长锥再入体的运动特性和气动特性影响具有一定的工程应用价值.
边界层转捩对高超声速细长锥再入体的运动和气动影响的问题,国内外已在地面试验中开展过很多研究[4-12].楼洪田[4-5]采用俯仰自由振动试验技术研究边界层转捩对细长锥静动稳定性的影响规律,发现细长锥后体存在边界层转捩时,与无黏情况(相当于雷诺数极大的情况)相比,转捩使锥体的静稳定性降低而动稳定性明显增加,当转捩移至振心前的锥面上时,转捩使锥体的静稳定性有所增加,而动稳定性有所下降.
Ward[6]采用俯仰强迫振动试验技术研究半锥角
采用自由飞试验技术进行研究的问题主要集中在弹道靶自由飞试验[14-19]和大气模型飞行试验[20-22],如Potter[14]在AEDC弹道靶开展半锥角
试验在中国航天空气动力技术研究院FD-07高超声速风洞中完成,其是一座

|
图 1 FD-07高超声速风洞 Figure 1 FD-07 hypersonic wind tunnel |
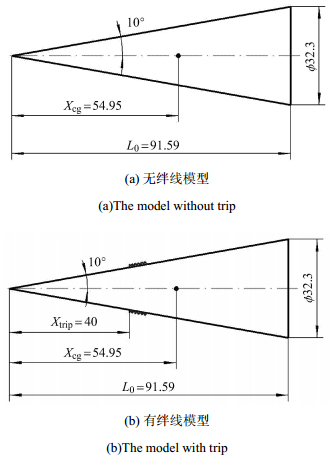
无绊线和有绊线的细长尖锥模型外形尺寸示意图如图 2所示.试验模型的半锥角
|
图 2 细长尖锥模型外形图 Figure 2 The slender cone model figuration |
细长锥模型质量特性参数如表 1所示.
| 表 1 模型质量特性参数 Table 1 Model mass parameters |
本次细长锥边界层绊线人工转捩试验采用发射式风洞自由飞试验方法,首先遇到的问题是风洞自由飞试验模型较小,可能导致细长锥表面不会出现边界层的转捩现象,因此在试验模型的表面上布置一定数量的绊线[23], 作为人工固定转捩.首先将带有人工转捩绊线的细长锥模型用夹持器抱紧并安置在带有气动推杆的发射枪内,整套发射枪与风洞刀架相连,可通过改变刀架的攻角改变模型的初始发射攻角
本次细长锥边界层绊线转捩风洞自由飞试验采用一台高速摄像机进行单平面纹影流场拍摄,能记录试验模型沿纵向、铅垂方向以及俯仰方向的运动.拍摄速度为2 000帧每秒,相邻两帧图像的时间间隔
影响飞行器边界层转捩的主要特征相似参数是马赫数和雷诺数,为考察雷诺数对边界层绊线转捩的影响,通过改变风洞试验前室总压
| 表 2 细长锥风洞自由飞试验状态 Table 2 The experiment state of slender cone |
对于无滚转的轴对称俯仰平面单自由度风洞自由飞运动[24],其角运动规律可以表达为
| $\begin{array}{c} \ddot \theta - \left[{{C_{mq}} + {C_{m\dot \alpha }}-{C_{L\alpha }}\frac{I}{{m{d^2}}}} \right]\frac{{{d^2}}}{{{V_\infty }}}\frac{{{q_\infty }S}}{I}\dot \theta - \\ {C_{m\alpha }}\frac{{{q_\infty }Sd}}{I}\theta = {C_{{m_0}}}\frac{{{q_\infty }Sd}}{I} \end{array}$ | (1) |
式中,
由式(1)和试验测量的俯仰角
辨识精度由标准误差
| $SD(\theta ) = \sqrt {\sum\limits_{i = 1}^n {(\theta _{\exp } - \theta )^2 / (n - N)} }$ | (2) |
图 3所示为试验马赫数

|
图 3 |
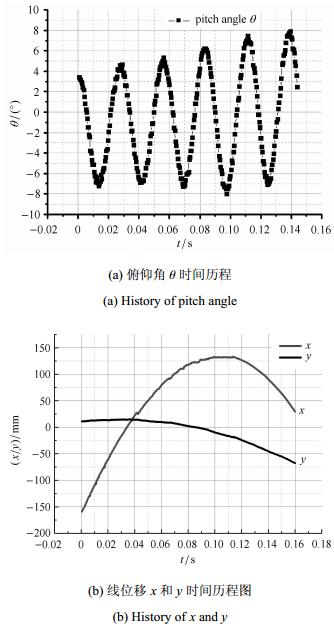
试验雷诺数
|
图 4 序号为I次试验的细长锥模型俯仰角位移和线位移曲线图 Figure 4 History of pitch angle and line displacement for sequence number I |
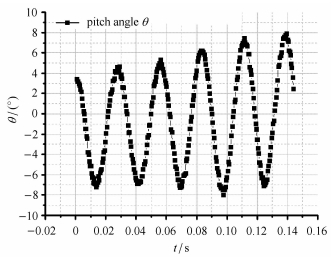
试验雷诺数
|
图 5 序号为M |
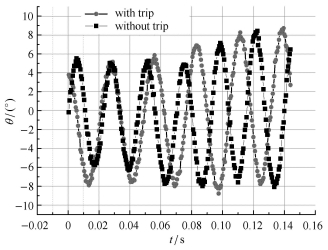
图 6为试验马赫数
|
图 6 |
由试验拍摄的图片序列和俯仰角位移、线位移曲线均表明,高超声速细长锥在风洞中无控飞行过程中俯仰方向出现明显的周期振荡运动,且风洞自由飞试验均获得6个以上的周期运动;
对于有人工转捩绊线的细长锥模型,在雷诺数
以上表明:有人工转捩绊线的高超声速细长锥无控自由飞行的运动特性明显不同于无绊线细长锥的运动特性,边界层转捩对高超声速细长锥再入体无控自由飞行的运动特性有一定的影响.
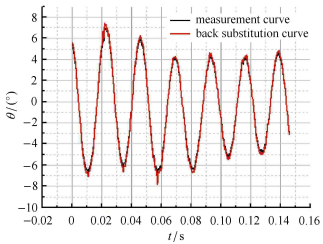
2.2 有无绊线细长锥的气动特性对于典型的高超声速有绊线细长锥模型俯仰角测量值与辨识回代值比较图见图 7所示,对应的试验序号为I,雷诺数
|
图 7 序号为I次试验的俯仰角测量值与辨识回代值对比图 Figure 7 The contrastive figure of measurement and back substitution |
从表 3可以看出, 细长尖锥的静稳定导数
| 表 3 细长锥有无绊线风洞自由飞试验测量的气动系数 Table 3 The aerodynamic coefficient for model which with and without trip |
(1) 当自由流雷诺数
(2) 当自由流雷诺数
不同人工绊线型式及绊线在细长锥上的不同轴向位置对高超声速细长锥无控自由飞行下的运动特性和气动特性的影响,以及边界层转捩影响细长锥无控自由飞行运动稳定性的机理分析,将是今后需要深入开展的研究工作.
| 1 | Chrusciel GT. Analysis of re-entry vehicle behavior during boundary layer transition. AIAA Journal, 1975, 13 (2) : 154-159. DOI: 10.2514/3.49655. |
| 2 | Martellucci A, Neff RS. Influence of asymmetric transition on reentry vehicle characteristics. J Spacecraft, 1971, 8 (5) : 476-482. DOI: 10.2514/3.59681. |
| 3 | Uffelman KE, Deffenbaugh FD. Asymmetric transition effects on reentry vehicle trim and dispersion characteristics. In:Proc. of 5th Atmospheric Flight Mechanics Conference for Future Space Systems, Bouder, AIAA Paper 79-1626, 1979 http://adsabs.harvard.edu/abs/1979atfm.conf...43U |
| 4 | 楼洪田. 边界层转捩对细长锥静、动稳定性的影响. 宇航学报, 1985 (1) : 88-98. ( Lou Hongtian. Transition effects of boundary layer on static and dynamic stability of slender cone. Journal of Astronautics, 1985 (1) : 88-98. (in Chinese) ) |
| 5 | 楼洪田. 转捩诱导法向力及其对细长尖锥气动特性的影响. 宇航学报, 1989 (3) : 54-64. ( Lou Hongtian. Transition induced normal force and it's effects on slender shape cone aerodynamic. Journal of Astronautics, 1989 (3) : 54-64. (in Chinese) ) |
| 6 | Ward LK. Influence of boundary layer transition on dynamic stability at hypersonic speeds. Transactions of the Second Technical Workshop on Dynamic Stability Testing, 11(9), Arnold Engineering Development Center, Arnold Air Force Station, TN, 1965 |
| 7 | Ericsson LE. Coupling between vehicle motion and slender cone transition. AIAA Journal, 1986, 25 (9) : 1194-1198. |
| 8 | Ericsson LE. Transition effects on slender cone pitch damping. In:Proc. of 25th AIAA Aerospace Sciences Meeting, Reno Nevada, AIAA Paper 87-0493, 1987 |
| 9 | Ericsson LE. Transition effects on slender vehicle stability and trim characteristics. In:Proc. of AIAA 25th Aerospace Sciences Meeting, Washington DC, AIAA Paper 73-126, 1973 |
| 10 | Ericsson LE. Effects of boundary layer transition on vehicle dynamics. In:Proc. of AIAA 7th Aerospace Sciences Meeting, New York, AIAA Paper 69-106, 1969 |
| 11 | Ericsson LE. Correlation of attitude effects on slender vehicle transition. AIAA Journal, 1974, 12 (4) : 523-529. DOI: 10.2514/3.49279. |
| 12 | Keneneth FS. Hypersonic boundary layer transition experiments. Air Force Wright Aeronautical Labs Wright Patterson Afb Oh AFWAL-TR-80-3062, 1980 |
| 13 | Martellucci A, Neff RS. The influence of asymmetric transition on re-entry vehicle motion. In:Proc. of AIAA Guidance, Control and Flight Mechanics Conference, Santa Barbara California, AIAA Paper 70-987, 1970 |
| 14 | Potter JL. Boundary layer transition on supersonic cones in an aeroballistic range. In:Proc. of AIAA 12th Aerospace Sciences Meeting, Washington DC, AIAA Paper 74-132, 1974 http://arc.aiaa.org/doi/pdf/10.2514/3.49692 |
| 15 | Schneider SP. Effects of roughness on hypersonic boundary layer transition. In:Proc. of 45th Aerospace Sciences Meeting and Exhibit, Reno Nevada, AIAA 2007-305, 2007 http://arc.aiaa.org/doi/abs/10.2514/1.29713 |
| 16 | Reda DC. Boundary layer transition experiments on sharp slender cones in supersonic free flight. In:Proc. of AIAA 11th Fluid and Plasma Dynamics Conference, Seattle Wash, AIAA Paper 78-1129, 1987 |
| 17 | Norman W, Sheet JR. Free flight boundary layer transition investigations at hypersonic speeds. In:Proc. of AIAA 2nd Aerospace Sciences Meeting, New York, AIAA Paper 65-127, 1965 |
| 18 | 柳森, 王宗浩, 谢爱民, 等. 高超声速锥柱裙模型边界层转捩的弹道靶实验. 实验流体力学, 2013, 27 (6) : 26-31. ( Liu Sen, Wang Zonghao, Xie Aimin, et al. Ballistic range experiment of hypersonic boundary layer transition on a cone-cylinder-flare confeiguration. Journal of Experiments in Fluid Mechanics, 2013, 27 (6) : 26-31. (in Chinese) ) |
| 19 | Peter J, Robert HP. Effects of boundary layer transition on dynamic stability over large amplitudes of oscillation. In:Proc. of 1st AIAA Annual Meeting, Washing DC, AIAA Paper 64-427, 1964 |
| 20 | David WK, Donald LP. Boundary layer transition and hypersonic flight testing. In:Proc. of 45th Aerospace Sciences Meeting and Exhibit, Reno Nevada, AIAA 2007-308, 2007 http://arc.aiaa.org/doi/pdf/10.2514/1.29708 |
| 21 | Berry SA. Boundary layer transition experiments in support of the hypersonics program. Langley Research Center, AIAA Paper 2007-4266, 2007 http://arc.aiaa.org/doi/pdf/10.2514/6.2007-4266 |
| 22 | Wright RL, Zoby EV. Flight boundary layer transition measurements on a slender cone at mach 20. In:Proc. of AIAA 10th Fluid and Plasma Dynamics Conference, Albuquerque, N. Mex, AIAA Paper 77-719, 1977 |
| 23 | Uselton BL, Cyran FB. Sting interference effects as determined by measurements of dynamic stability derivatives, surface pressure, and base pressure for mach numbers 2 through 8. Arnold Engineering Development Center, AEDC-TR-79-89, 1980 |
| 24 | 马家欢, 唐宗衡, 张小平. 在高超声速脉冲型风洞中测量静、动稳定性导数的模型自由飞方法. 空气动力学学报, 1983 (4) : 77-85. ( Ma Jiahuan, Tang Zongheng, Zhang Xiaoping. Free flight method in hypersonic impulse type tunnels for static and dynamic stability study. Acta Aerodynamica Sinica, 1983 (4) : 77-85. (in Chinese) ) |
| 25 | Chapman GT, Kirk DB. A new method for extracting aerodynamics coefficients from free-flight Data. In:Proc. of AIAA 7nd Aerospace Sciences Meeting, New York, AIAA Paper 69-134, 1969 |