引言

以钝体为原型的燃烧器被广泛应用于燃气轮机、锅炉等许多工业设备的燃烧室中^[1-2].由于其相对简单的几何以及确定的边界条件，钝体燃烧器也是湍流燃烧基础研究的典型对象之一^[3].钝体燃烧器多采用非预混燃烧方式，即高速燃料由钝体中心射出，低速同向空气从钝体外围射出.当燃料和空气流过钝体时，两股流动在钝体下游产生一对反向漩涡的回流区，在回流区内高温燃烧产物和未燃气体充分混合并进行热量的交换，从而形成一个稳定的点火热源，使火焰稳定.同时，通过控制回流区内的流动结构，可以使燃料充分反应，避免局部高温的出现，减少NO$_{X}$的生成.当燃料速度足够高时，中心射流穿越回流区并在下游产生类似于射流的火焰，在湍流充分发展和化学反应有限的区域，射流火焰有可能局部熄火；而在更下游的区域，随着湍流掺混作用的减弱，有可能发生熄火再燃的现象^[4].

在燃气轮机等设备的燃烧室中，钝体燃烧器大多数时间运行在相对稳定的环境下.钝体燃烧器在稳定燃烧阶段的火焰结构和流动、混合特性引发了人们的关注. Dally等^[3-4]观察了稳定燃烧的钝体火焰，实验结果表明在回流区内存在3个混合层，湍流混合非常剧烈，表现出湍流与化学反应强烈的相互作用.随着中心射流速度的提高，回流区内涡旋的混合作用减弱，当量混合分数等值面由回流区的外侧移向内侧，钝体火焰吹熄现象明显增加，大尺度涡旋的复杂运动影响钝体火焰的结构和稳定^[3].针对Sydney钝体燃烧器的甲烷/氢气火焰，先前的数值研究^[5-12]分别验证了条件矩模型、稳态火焰面模型和概率密度函数方法对稳定燃烧阶段火焰结构的预测能力. Kim等^[6]针对充分发展的钝体射流火焰回流区内流动和混合特性做了详细的数值研究，分析表明回流区内低标量耗散率、高温富燃状态和燃烧产物的均匀分布对于钝体火焰HM1E的稳定起着关键作用.

然而对于航空发动机而言，高空二次点火性能关系到飞行安全，燃烧器的点火过程至关重要^[13-14].并且由于排放法规越来越严格，航空发动机多工作在贫燃或稀释条件下，当飞行途中遭遇气流变化引起然烧室入口流动突变时，很容易导致燃烧室整体熄火.这要求更精心设计点火燃烧设备确保快速重新点燃熄灭的火焰.这些现象本质上是瞬态的，需要详细了解燃烧的点火过程，才能进一步优化航空发动机的高空二次点火性能.

钝体燃烧器作为一种模型燃烧器常被用来研究点火的瞬态过程. Ahmed^[14]和Mastorakos^[15]通过实验研究了径向燃料喷射条件对湍流非预混钝体火焰火花点火的稳定性、点火极限以及点火概率等的影响. Triantafyllidis等^[16]采用条件矩燃烧模型的大涡模拟方法，研究了甲烷钝体火焰点火的两个影响因素：点火位置和大小，研究表明成功点火不仅需要有可燃的混合物（flammable mixture），还要有合适的流动条件使火焰能够向上游传播.针对圆锥钝体非预混火焰，Ahmed^[14]通过实验研究了点火概率和点火极限，与流动的影响相比，起始火焰的传播方向更依赖于点火位置，并且指出数值模拟的点火过程必须捕捉到非均匀混合物中的火焰传播.在上述研究基础之上，Subramanian等^[17]采用大涡模拟的方法研究了强制点火的不同位置对点火成功的影响，讨论并证实了燃烧速率建模时需考虑应变率效应，同时指出点火位置的速度和混合分数与点火成败之间的关联有待进一步讨论和分析.尽管对钝体燃烧器点火过程的研究已经取得了一定的进展，但相比于可以量化的湍流预混流动点火过程，湍流非预混燃烧的点火以及火焰传播的物理过程尚未得到明确定义与深入研究，其复杂性和重要性使其受到越来越多的关注^[18].

钝体火焰的模拟涉及到点火、熄火和再燃等复杂物理过程的捕捉.我们将采用基于稳态火焰面/过程变量模型的大涡模拟方法模拟上述复杂的物理化学过程，并通过温度表征的高温区、羟基(OH)表征的剧烈燃烧区以及甲醛(CH$_{2}$O)表征的预热区^[19]的时空演化，详细描述点火过程的瞬态特性.稳态小火焰面模型（steady flamelet model, SFM）将湍流扩散火焰视为层流扩散火焰的系综，具有模型概念简单和计算快速等数值模拟的优点^[20-22]，但是由于混合分数$Z$和标量耗散率$\chi_{Z}$作为热力学的参量，不能反映非稳态的燃烧过程，对于包含熄火和再燃过程的燃烧，其应用受到限制^[23].在稳态火焰面模型的基础之上，火焰面/过程变量模型（flamelet/progress-variable model，FPV）^[23-24]考虑了火焰面动态效应，通过引入过程变量替换原有的标量耗散率参量来表征反应的进度，以达到预测非稳态燃烧的目的.过程变量不仅唯一地标示火焰面数据库中每一个火焰面，而且与混合分数相互独立. Ihme等^[25-26]对火焰面/过程变量模型做了先验和后验的研究，在对Sandia D/E火焰的大涡模拟中，熄火再燃的现象被准确捕捉到，温度和主要组分的结果与实验符合得非常好.火焰面/过程变量模型也被成功用于Cabra火焰的抬升和自点火现象的模拟以及旋流火焰的火焰结构和稳定性等问题的研究^[27-30].

本文利用基于火焰面/过程变量燃烧模型的大涡模拟方法研究Sydney钝体燃烧器的无反应射流和有反应火焰两个算例，并对比数值计算和实验测量的结果.在此基础之上，通过分析有反应火焰的数值结果，报告钝体射流火焰强制点火过程中温度、OH和CH$_{2}$O的变化，说明Sydney钝体火焰点火过程的瞬态特性.

1 数学物理模型 1.1 实验装置

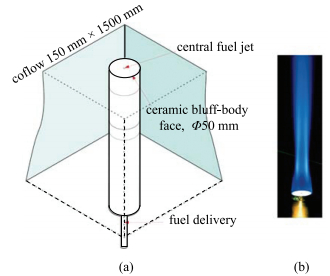
图 1给出了实验装置示意图和钝体射流火焰^[2]，圆柱状燃烧器放置于150 mm $\times $ 150 mm的空气伴流风槽，自由来流中有约2%的湍流度；燃烧器中心为燃料射流，喷口直径为$D_{\rm j}$=3.6 mm，钝体表面直径为$D=D_{\rm b}$=50 mm，$R=D/2=25$ mm，并覆盖抗热的陶瓷涂层.如表 1所示，本次数值模拟的是悉尼大学的无反应钝体射流(non-reacting bluff-body flow, NRBB)和有反应钝体火焰算例HM1E（吹熄率50%）.其中，NRBB的中心射流和钝体外围都以空气为流动介质，而有反应算例HM1E燃料射流为常温的天然气（CH$_{4}$含量为90%）和氢气混合物（体积比1:1），外围伴流为空气. $U_{\rm jet}$和$U_{\rm air}$为入口平均轴向速度，$Z_{\rm st}$为当量混合分数.

1.2 数学模型

将基于FPV模型的反应流控制方程进行滤波，得到式(1)，即大涡模拟(large-eddy simulation, LES)方程^[23-25]

$\tilde {{\rm D}}_t \overline \rho =-\overline \rho \nabla \cdot \boldsymbol{\tilde {{ u}}}$

(1a)

$\overline \rho \tilde {{\rm D}}_t \tilde {u} =-\nabla \overline p + \nabla \cdot {{\boldsymbol{\overline {\sigma}}}} + \nabla \cdot {{\boldsymbol{\overline {\sigma}}}}^{\rm res} + \overline \rho {{ \boldsymbol{g}}}$

(1b)

$\overline \rho \tilde {{\rm D}}_t \tilde {Z} =-\nabla \left( {\overline \rho \tilde {\alpha }\nabla \tilde {Z}} \right) + \nabla \cdot \overline \tau _Z^{\rm res}$

(1c)

$ \overline \rho \tilde {{\rm D}}_t \tilde {C} =-\nabla \left( {\overline \rho \tilde {\alpha }\nabla \tilde {C}} \right) + \nabla \cdot \overline \tau _C^{\rm res} + \overline \rho \tilde {\dot {\omega }}_C$

(1d)

$ {{\boldsymbol{\overline {\sigma}}}} = 2\overline \rho \tilde {\nu }\left[{{\tilde { \boldsymbol{S}}}-\frac{1}{3}\left( {\nabla \cdot \tilde {u}} \right){\boldsymbol{ I}} } \right]$

(2)

${{\boldsymbol{\overline {\sigma}}}} ^{\rm res}\; = \;\;\overline \rho \boldsymbol{\tilde { u}}\boldsymbol{\tilde { u}}-\overline \rho \boldsymbol{\widetilde{{{uu}}}}$

(3)

$\boldsymbol{\overline {\tau}} _\psi ^{\rm res} =\overline \rho \boldsymbol{\tilde { u}}\tilde {\psi }-\overline \rho \boldsymbol{\widetilde{{u}}\psi}$

(4)

式中，顶标$\sim $和$\!$--$\!$分别表示Favre和Reynolds滤波量，物质导数$\widetilde{{\rm D}}_t=\partial _{t}+{\boldsymbol{ u}}\cdot\nabla $；其中$\boldsymbol{u}$，$p$, $\rho $，$\alpha $分别代表流体速度、压力、密度和分子扩散系数；混合分数$Z$和过程变量$C$均为标量，以$\psi $表示一般标量；式(2)中，$\sigma $为黏性应力张量，$\nu $为运动黏性系数，${\boldsymbol{ S}}$和${\boldsymbol{ I}}$的分别为应变率张量和单位张量；式(3)和式(4)分别为残余应力张量和残余标量通量，上标{res}表示亚格子残余量，本文采用动态Smagorinsky模型.

联立求解流动和化学反应，计算量将会非常大.本文采用基于火焰面假设的燃烧模型，其优点是一定程度上解耦了流场和燃烧场，有效地降低了计算的复杂度.在$Z$空间求解组分$i$的质量分数$Y_{i}$和温度$T$的稳态火焰面方程^[20-21]

$ \rho \frac{\chi }{2}\frac{\partial ^2Y_i }{\partial Z^2} + \dot {\omega }_i = 0$

(5)

$\rho \frac{\chi }{2}\frac{\partial ^2T}{\partial Z^2} + \sum\limits_{i = 1}^N {\frac{h_i }{c_p }\dot {\omega }_i } = 0$

(6)

其中$\dot {\omega }_{i}$，$h_{i}$，$c_{p}$分别为组分$i$的源项和焓以及混合物的比热，$N$为组分个数.本文选用GRI-Mech2.11^[31]，得到热力学量的层流稳态火焰面数据库$\phi $=$\phi $($Z$, $\chi _{st })$，其中$\chi _{st }$是当量混合的标量耗散率.火焰面/过程变量模型(FPV)相比于稳态小火焰模型(SFM)，引入过程变量$C$，将$Z-\chi _{\rm st}$空间转化为$Z\!-\!C$空间以考虑非稳态燃烧的影响，在本文过程变量取为4种主要组分的质量分数之和^[26]，即

$C = Y_{\rm CO} + Y_{{\rm CO}_2 } + Y_{{\rm H}_2 } + Y_{{\rm H}_2 {\rm O}}$

(7)

采用假定的概率密度函数考虑亚格子尺度下的湍流和化学反应的相互作用，$Z$服从$\beta $分布，$C$服从$\delta $分布.化学反应源项、温度、组分质量分数等物理量由层流稳态火焰面数据库统计积分得到^[25]

$\tilde {\psi } = \iint{\varphi \left( {Z, C} \right)} \;\widetilde{P}\left( {Z, C} \right){\rm d}Z{\rm d}C = \;\tilde {\phi }\left( {\tilde {Z}\;, \widetilde{{Z}"^2}\;, \tilde {C}} \right)$

(8)

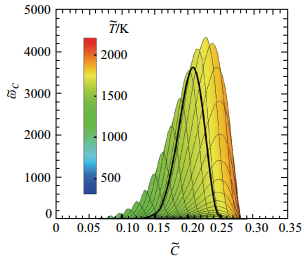
图 2给出了由式(8)积分得到的化学反应源项$\widetilde{\dot {\omega }}_C (\tilde {Z}, \widetilde{{Z}"^2}, \tilde {C})$和温度$\tilde {T}(\tilde {Z}, \widetilde{{Z}"^2}, \tilde {C})$在参数空间上的分布.在数值模拟中，通过式(8)与方程(1)$\sim $(4)联合求解，得出湍流燃烧中的流动、温度和组分等信息.

数值算法采用有限体积方法对控制方程进行离散，时空耦合的交错网格提高差分格式的精度和数值求解的稳定性.扩散项为二阶中心格式，对流项为动能守恒的二阶中心格式，时间导数为二阶半隐式离散方法，采用半隐式迭代方法进行求解^[24].

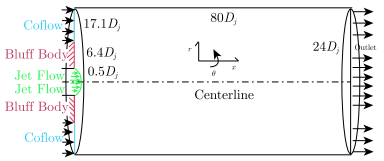
1.3 数值设定

本文采用三维柱坐标系的大涡模拟求解非定常的湍流燃烧火焰^[23-24]，如图 3所示轴向$x$、径向$r$以及周向$\theta $三个方向求解范围分别是（0, 80$D_{\rm j}$）、（0, 24$D_{\rm j}$）以及（0, 2$\pi$）.中心湍流射流由充分发展的管流剖面数据给出；外围同向空气流直接给定柱塞流的速度剖面，其湍流脉动为2%；出口边界使用对流边界条件；固壁边界速度使用无滑移边界条件，其余边界标量使用Neumann边界条件.

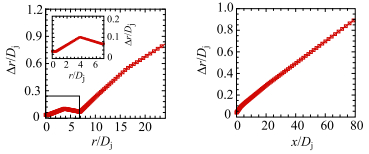
为了解析足够的湍动能以及捕捉到关键物理过程，计算域三个方向的网格数分别为256$\times $165$\times $64，轴向和径向网格变化如图 4所示：在轴向射流入口处加密网格，从回流区末端（$x/D$=1.2）起，下游网格逐渐变疏；在径向钝体下游内、外剪切层处的网格相对密，远离轴线的径向网格相对较疏；周向网格均匀分布. 270万的网格量使用国家超级计算天津中心（NSCC-TJ）16个CPU，计算时间约为2周.

2 计算结果与讨论

数值模拟的结果与讨论将按以下方式进行：首先2.1节对比无反应的冷态场和有反应的燃烧场与实验数据的结果，并分析火焰和流动的相互作用；其次以HM1E为例，2.2节详细地阐明钝体燃烧器强制点火的动态过程，通过温度、OH质量分数和CH$_{2}$O质量分数的峰值随时间的变化对点火过程中的主要特征做进一步分析. 图 5所示强制点火成功后，充分发展的钝体火焰瞬态轴向速度和温度的分布，2.1节中钝体火焰的流动和燃烧统计截面分别对应图中虚线和实线.

2.1 统计结果的对比 2.1.1 冷态场NRBB的结果对比

参照实验数据，数值计算选取6个轴向位置的统计结果，并与实验和Kempf等^[8]的结果比较.

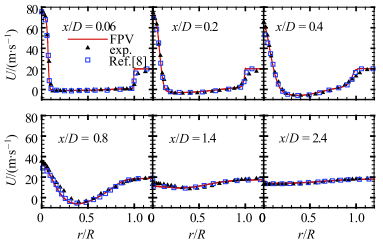
图 6给出了轴向平均速度的径向分布，数值计算的速度剖面与实验测量结果符合得很好.相比于Kempf等^[8]的中心射流过快衰减，本文中轴线上的轴向速度与实验完全吻合，但柱塞流的入口边界条件使得近壁面附近的计算结果稍高于实验测量.其中，$x/D$=0.2，0.4，0.8的平均速度曲线中速度为负的部分与实验结果完全吻合，这说明数值计算得到的回流区大小与实验测量结果是一致的.

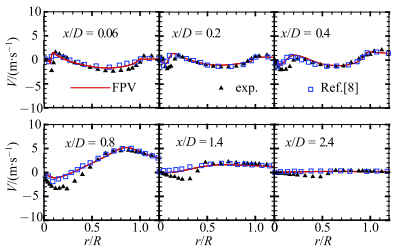
图 7给出了径向平均速度的径向分布，数值结果较好地捕捉到了径向速度的变化趋势，特别是剪切层对应的位置；从$x/D$=0.4开始，下游剖面靠近中轴线附近计算结果略低于实验，即内剪切层的流动被低估，原因是此处流动具有较高的敏感性^[8]，而且实验的多次测量结果之间本身有较大波动^[1-2].

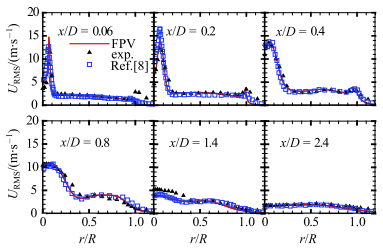
由图 8给出的轴向速度脉动分布可知，在靠近钝体外缘处，实验测量显示有明显的剪切层.由于边界条件的缘故，数值模拟并未捕捉到这一间歇脉动，但这对下游流动的影响很小^[8].在$x/D$=1.4附近，数值预测的轴向速度脉动明显较实验测量小，这与对应位置的轴向平均速度预测结果一致，主要是圆管射流强衰减和强扩散的原因^[3].特别地，速度脉动在一定程度上能够反应湍流的掺混强度，其准确预测可以更好地数值研究非预混火焰的行为.

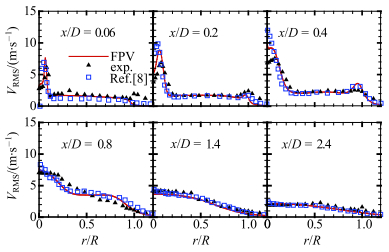
从图 9中径向速度脉动分布可得，数值结果与实验的对比和图 8给出的对比结果一致.但在轴线附近的速度脉动与实验结果相比有一定偏差，这在一定程度上与实验测量误差有关（中心射流出口附近测量误差为10 %$\sim$70 %）. Kempf等^[8]较大偏差是源于为提高计算效率而采取松弛的courant-Friedrids-Lewy (CFL)收敛准则^[8].此外，钝体外缘的径向速度脉动也受边界条件的影响.

从上述计算结果可以看到，当前NRBB的数值模拟准确预测到了回流区内存在的反向涡对、壁面对流动的扰动以及剪切层的流动等主要物理现象.

2.1.2 燃烧场HM1E的结果对比

分别取距钝体表面$x/D$=0.2，0.6，0.8，1.2，1.4，2.4剖面处（6个剖面的位置如图 2中虚线所示）轴向和径向速度的统计结果，并与实验和Kempf等^[8]的结果比较.

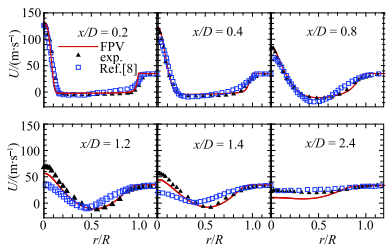
除下游远场外，图 10所示的轴向平均速度各剖面上的径向分布与实验几乎完全一致.从$x/D$=1.2和$x/D$=1.4剖面可以看出，速度为负的部分扩展到下游，且中轴线附近的流向速度都比实验测量值小.由此可以得出，燃烧效应不仅使回流区长度变长，而且也增加了计算的难度，相比于无反应流的冷态场，有反应的燃烧场对网格尺度有更高的要求^[8].

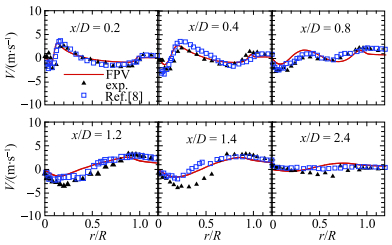
图 11所示的径向平均速度对比结果表明，数值结果较好地捕捉到了径向速度的整体变化.特别地，径向速度在径向分布的极大值和极小值的径向位置都与实验符合.与无反应的冷态场相比，径向速度的极值有明显增大，而且极大值的位置随轴向距离的增大更靠近外侧.这主要是由于回流区内温度的升高而引起的热膨胀，以及下游钝体外边缘剪切层作用的减弱^[8].此外，从$x/D$=1.2以后，由于下游网格较稀疏而带来的计算误差越来越明显，但数值结果仍准确地捕捉到了径向速度的变化趋势.

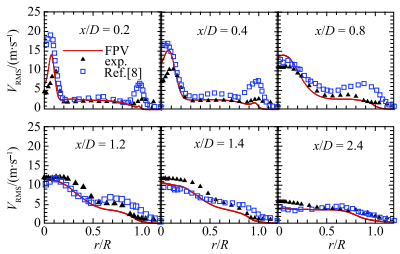
图 12和图 13分别是钝体射流火焰的轴向和径向速度均方根的径向分布，数值计算准确预测到速度脉动的变化趋势，并且其峰值的大小和位置与实验基本一致，特别是轴向速度脉动.在回流区下游，由于相对稀疏的网格，速度脉动的偏差较为明显.

分别取距钝体表面$x/D$=0.3，0.6，0.9，1.3，1.8，2.4剖面处（6个剖面的位置如图 2中实线所示）混合分数、温度和OH自由基的统计结果，并与实验和Kempf等^[8]的结果比较.

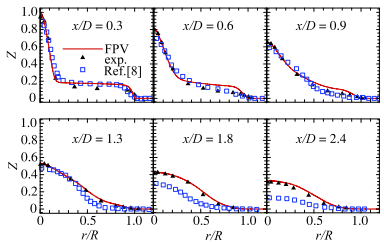
图 14的结果表明有反应的燃烧场混合分数Z分布与实验测量几乎完全吻合，当前的数值计算准确地捕捉到内外混合层的厚度.特别是，在下游$x/D$=1.8，2.4的剖面，混合分数的径向分布与实验也符合得很好.此外，在钝体回流区内出现混合分数的"平台"，距钝体越近平台越明显，而且与图 15中平均温度的分布一致. "平台"的出现表明由于钝体的存在，回流区一定范围内燃料和空气混合均匀，而且由于均匀值大于化学当量值，钝体回流区内混合物处于富燃状态.混合分数回流区内的均匀性对钝体火焰的稳定起着决定性作用^[4].

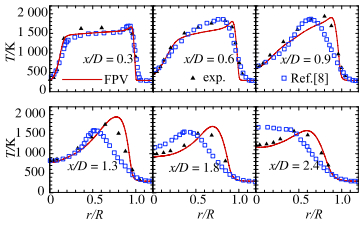
图 15所示的平均温度(T)的分布与实验测量一致，而且回流区内温度场也有"平台"出现且都偏低于实验测量，原因主要是混合分数计算的高估；同时燃烧器钝体表面是高达700 K的绝热陶瓷层^[4]，使得钝体表面附近的温度分布更均匀.然而，在钝体回流区外边缘温度峰值的差异一部分是由于实验仪器的制约，温度尖峰没有被测量捕捉到^[8]；另一部分可能是火焰面假设在此区域的有效性或者亚格子滤波方差被低估^{[5, 8]}.在回流区下游，对比图 17中混合分数Z空间的温度分布可以得出，温度偏高于实验测量是由于数值计算中未考虑辐射的因素^[8].整体而言，当前数值计算准确捕捉温度场的平均变化趋势，基本再现了钝体非预混火焰的温度分布，为接下来的点火过程分析提供可靠的基础.

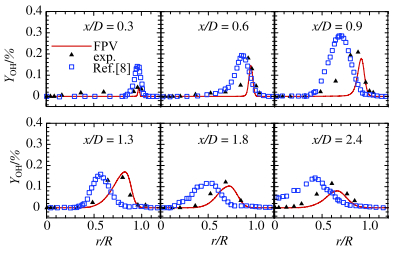
从图 16的对比结果可以得出，OH的分布主要集中在钝体外边缘，并且随轴向距离的增大，OH的峰值逐渐向内侧移动，这与温度峰值的变化趋势一致.在$x/D$=0.3的位置，OH在$r/R$=1.0处的峰值可以印证实验仪器在对应位置温度峰值测量的局限.但在$r/R \le $0.9的范围，OH的计算值低于实验测量，原因一方面是混合分数预测偏高，另一方面是限于火焰面假设，平衡态的OH未能捕捉到^{[5, 8]}.在下游位置，OH的分布与实验测量符合得很好.结合图 17可得，相比于稳态火焰面模型，火焰面/过程变量模型可以更加准确地预测OH峰值的位置，即化学反应剧烈的区域.

由于回流区下游位置混合分数与实验测量完全吻合，在钝体回流区内侧的OH计算偏差来源于燃烧模型的不足^{[8, 20]}.因为基于火焰面的假设，一般表现为火焰厚度较薄，火焰面/过程变量模型难以准确预测富燃条件下的化学反应.同时钝体火焰颈区内（$x/D$=1.3$\sim $2.4）的局部熄火，即强间歇的非稳态过程，对准确预测OH的峰值也有影响.

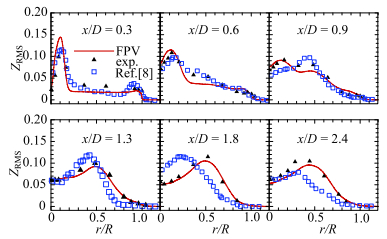
图 18所示的混合分数脉动分布与实验测量结果也吻合得很好，特别是钝体附近由于强回流导致的大尺度混合.相比于平均值，回流区内非剪切层处的混合稍有偏差，但当前的数值计算能够准确捕捉到中心射流和伴流发生混合的位置和强度.此外，由于回流区内有内、外两个剪切层，上游混合分数脉动呈现双峰分布，这与速度脉动分布是一致的；而在回流区下游只有中心射流和空气伴流相互作用的剪切层，因此混合分数脉动呈现单峰分布.值得注意的是，回流区下游剪切层的位置基本维持在$r/D$=0.3附近，且混合分数脉动的强度和范围也基本不变.由此可见，回流区下游受大尺度流动结构的影响较小，混合基本稳定.

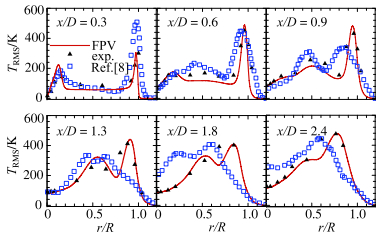
图 19所示的是温度脉动径向分布的对比结果，当前数值结果准确捕捉到温度脉动的变化趋势以及脉动峰值的位置.靠近中心的峰值是由低温的中心射流与高温产物的混合引起的，该峰值的位置与混合分数的脉动峰值相对应.靠近钝体边缘的峰值是由化学反应放热引起，与火焰位置对应.

2.2 钝体火焰的强制点火过程

通过对上述结果的分析可以看出，钝体燃烧器的稳定燃烧状态得到了准确的模拟.在此基础之上，我们进一步观察钝体燃烧器强制点火的动态过程.为了实现强制点火，我们首先使流动在没有反应的情况下，演化到统计定常状态.然后，在钝体回流区末端化学当量等值面附近的局部区域施加稳态火焰面的数值解，使该区域处于化学当量的燃烧状态，将该区域作为强制点火源.为方便描述点火过程，定义点火时间${T}_{\rm i}$，用于表示施加点火源后的时刻，施加点火源的时刻为零时刻, 即${ T}_{\rm i}$=0.

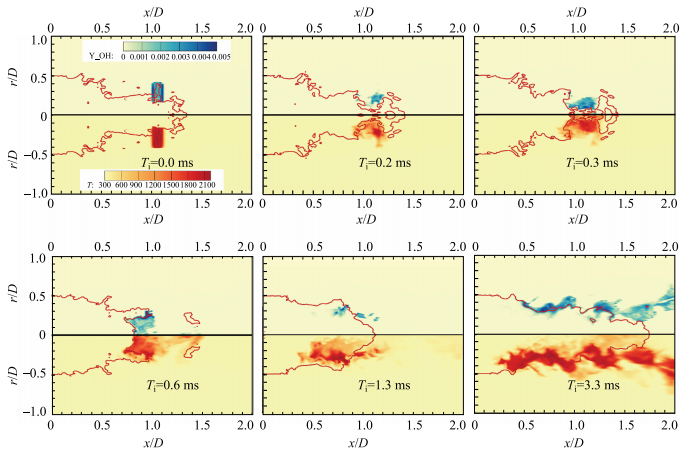
图 20给出了点火过程中6个时刻的OH质量分数和温度的分布云图（$\theta $=0的纵剖面）.为了方便同时观察，每一时刻图中上下两部分图像互为镜像，并分别表示OH质量分数和温度的分布.其中，红色实线代表化学当量比的混合分数Z$_{\rm st}$等值线.

$T_{\rm i}$=0.0 ms时施加点火源，表现为集中的高温区和集中的OH质量分数高值区. $T_{\rm i}$=0.2 ms时，集中的高温区变小，高温区和OH高值区与$Z_{\rm st}$等值线分离. $T_{\rm i}$=0.3 ms时，高温区和OH高值区聚集在$Z_{\rm st}$等值线上，此时化学反应加剧，开始点火，表现为温度的最大值开始增加. $T_{\rm i}$=0.6 ms时，已形成明显的点火核，OH和温度的最大值都集中在$Z_{\rm st}$等值线上. $T_{\rm i}$=1.3 ms时，温度的最大值在富燃区出现，偏离$Z_{\rm st}$等值线，高温区明显变大，点火对流动的影响开始显现，表现为$Z_{\rm st}$等值线围成的区域变大. $T_{\rm i}$=3.3 ms时，已经形成一定长度的火焰，并向下游传播，点火对流动的影响更加明显.

针对图 20中展示的点火过程，我们通过温度、OH质量分数和CH$_{2}$O质量分数的峰值随时间的变化对其做进一步详细的分析. 图 21中(a)，(b)和(c)分别表示温度、OH和CH$_{2}$O质量分数的峰值随时间的变化曲线. 图 21(a)中的6个黑色实心圆点依次对应图 20中的6个瞬时.

根据温度、OH和CH$_{2}$O质量分数的峰值变化特征，我们将本文中的强制点火过程分为4个阶段：

(1) 强制点火源的衰减.该阶段对应的时间为$T_{\rm i}$=0.0$\sim $0.2 ms，其特征是最大温度逐渐降低，OH质量分数的最大值逐渐降低，点火源的能量在逐渐衰减；而CH$_{2}$O质量分数的最大值维持不变，说明没有形成明显的点火氛围.如果这一阶段持续下去，最终就会导致点火失败.

(2) 点火触发.在$T_{\rm i}$=0.2$\sim $0.3 ms，最高温度仍然降低，但是OH峰值开始增加，同时CH$_{2}$O峰值也开始增加.说明吸热反应已经开始，并释放OH和CH$_{2}$O等活性物质，形成了必要的着火氛围.

(3) 点火核的生成. $T_{\rm i}$=0.3$\sim $0.6 ms阶段，最高温度迅速升高，并达到一个平台. OH峰值已经达到一个平台，CH$_{2}$O峰值仍然不断增加.此阶段有剧烈化学反应发生，导致热量迅速释放，表明点火核开始生成.

(4) 点火成功. $T_{\rm i}>$ 0.6 ms之后，温度、OH质量分数和CH$_{2}$O质量分数的峰值都达到了平台，化学反应趋于稳定.这些特征的出现说明点火已经成功，火焰沿着当量等值线开始传播，最终形成稳定火焰.

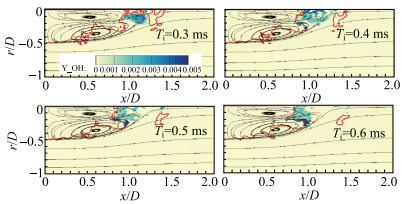
在强制点火过程中，通常点火源的体积较小，点火源的热量释放对冷态流场的影响很小.点火核的生成位置主要与点火源的位置和冷态流场的回流区结构有关.在图 22中，我们用OH质量分数标记点火核的位置，在图中叠加了冷态流场的稳态回流区结构，观察点火核生成阶段点火核的空间位置分布特点.

在点火核生成的初期$T_{\rm i}$=0.3 ms，点火核的位置与点火源位置非常接近.随着时间推移，在$T_{\rm i}$=0.4 ms时，外侧涡的尾部回流位置也开始出现了集中的OH高质量分数区；在$T_{\rm i}$=0.5$\sim $0.6 ms时，OH质量分数高值区的位置相对稳定，在外侧涡的尾部回流位置形成了一段时间的驻留.从这个位置开始，火焰逐渐发展到点火成功阶段.

从上述观察可以发现，在点火核生成初期，点火核的位置与强制点火的位置密切相关，但是没有形成驻留；而点火核生成后期，点火核的位置与点火源位置的关系较小，主要与冷态流场的回流区结构有关，并且有一段时间的稳定驻留，这会帮助火焰顺利发展到点火成功阶段.

3 结论

通过Sydney钝体燃烧器的无反应射流（NRBB）和有反应甲烷/氢气火焰（HM1E）两个算例的数值模拟，全面检验了本文所采用的数值方法和燃烧模型，数值计算准确预测回流区内大尺度的流动结构和混合特性以及钝体射流火焰的结构.

在此基础上，我们对钝体非预混火焰的强制点火过程进行了详细的分析，得到以下结论：

（1）本文的强制点火过程可以由4个阶段来描述，分别是点火源衰减、点火触发、点火核生成和点火成功.

（2）点火过程的上述4个阶段，可以用温度峰值、OH和CH$_{2}$O的质量分数峰值随时间的变化来表征.

（3）点火核的驻留位置位于冷态流场外侧涡的尾部回流区域附近.

致谢 此项工作是在国家超级计算天津中心的"天河一号"超级计算机上完成，感谢"天河一号"的大力支持.