飞行器在大气环境中真实飞行时,其运动是多个自由度的耦合.传统上研究多自由度耦合运动效应时,一般是把单自由度运动结果线性叠加起来[1].但随着现代飞行器机动性和敏捷性的提升,特别是大攻角飞行时,这种处理方式是否可行仍存在疑问.如Wang等[2]的研究发现,采用常规准定常模型和单自由度非线性叠加模型进行飞机横向机动运动仿真时结果与试飞结果有很大差别.贾区耀等[3-4]在对飞行器大气自由飞的结果和风洞实验数据进行对比分析时发现,风洞实验或数值计算表明是稳定的某些飞行器,自由飞的结果却是不稳定的,分析认为自由度不相似可能是导致这些差异的重要原因之一[5].
在飞行器的运动多自由度耦合效应研究中,纵横向耦合效应是研究的重要方向之一.在实验研究方面,国内如南京航空航天大学黄达等[6-8]在低速风洞中研究了三角翼外形俯仰-滚转耦合特性,发现机动飞行时多自由度运动的飞行器气动特性比单自由度运动时要复杂的多,运动耦合时的气动特性与两个单自由度运动时的气动特性的叠加结果相比有一定差别.唐敏中等[9]分析了80
在数值模拟方面,杨小亮等[16-18]针对三角翼外形采用数值模拟手段研究了多种因素对俯仰/滚转运动特性的影响,发现俯仰耦合滚转运动会导致飞行器升力降低,横向稳定性变差.郭迪龙等[19]数值模拟了76
国外也有多家机构和研究人员采用实验[20-23]或计算[24-27]的手段研究了飞行器的多自由度运动耦合效应.总体来看,由于俯仰、滚转耦合运动的复杂性,虽然取得了一定的研究成果,但仍需要开展更深入的研究工作.另外,研究的对象多集中在三角翼外形,对导弹类外形的研究结果较少,而运动耦合效应对气动外形的依赖度很大.本文通过建立刚体六自由度动力学方程与Navier-Stokes (N-S)方程的耦合求解技术,研究滚转静稳定和静不稳定时,方形截面弹在不同振动频率下的俯仰振荡过程对滚转静、动态稳定性的影响,在此基础上,开展俯仰振荡过程对滚转运动特性的影响研究.
1 数值方法和计算模型 1.1 数值方法在数值求解非定常Navier-Stokes方程时,空间离散格式采用原始变量NND (none oscillation,none free parameter, dissipative difference scheme)格式[28],限制器选用min-mod限制器;非定常时间推进采用Jameson的双时间步方法[29];在求解刚体动力学方程时,采用显式四阶龙格-库塔方法进行求解.采用松耦合的方式解决N-S方程和六自由度刚体动力学方程的耦合求解问题,两组方程分别独立求解,在时间域上交错推进,从而获得耦合系统的响应.
1.2 计算模型与来流条件计算模型为方形截面弹外形[30],由一个圆弧形头部和方形截面的弹身组成,参考图 1.弹身总长

|
图 1 方形截面导弹模型和表面网格 Figure 1 Configuration and computational grid of vehicle |
计算马赫数
首先定义体轴系.体轴系固连于飞行器,原点
由于飞行器一般是关于
| $\left.\begin{array}{lll} \dfrac{{\rm d}\omega _x }{{\rm d}t} = a_1 \omega _x \omega _z + a_2 \omega _y \omega _z + \bar {M}_{x1} \\ \dfrac{{\rm d}\omega _y }{{\rm d}t} = b_1 \omega _x \omega _z + b_2 \omega _y \omega _z + \bar {M}_{y1} \\ \dfrac{{\rm d}\omega _z }{{\rm d}t} = c_1 \omega _x \omega _y + c_2 \omega _x^2 + c_3 \omega _y^2 + \bar{M}_{z1} \\ \end{array}\right\}$ | (1) |
其中,
| $\left.\begin{array}{lll} a_1 \equiv \dfrac{I_{xy} \left( {I_z-I_x-I_y } \right)}{I_x I_y-I_{xy}^2 }, ~&a_2 \equiv \dfrac{I_{xy}^2-I_y I_z + I_y^{2} }{I_x I_y-I_{xy}^2 }, \\ b_1 \equiv \dfrac{I_x I_z-I_x^2-I_{xy}^2}{I_x I_y-I_{xy}^2 }, &b_2 \equiv \dfrac{I_{xy} \left( {I_x + I_y-I_z } \right)}{I_x I_y- I_{xy}^2 }, \\ c_1 \equiv \dfrac{I_x-I_y }{I_z}, c_2 \equiv \dfrac{I_{xy}}{I_z }, &c_3 \equiv-\dfrac{I_{xy}}{I_z}, \\ \bar {M}_{x1} \equiv \dfrac{I_y M_{x1} + I_{xy} M_{y1}}{I_x I_y-I_{xy}^2 }, &\bar {M}_{y1} \equiv \dfrac{I_{xy} M_{x1} + I_x M_{y1}} {I_x I_y-I_{xy}^2}, \\ \bar{M}_{z1} \equiv \dfrac{M_{z1}}{I_z} \\ \end{array}\right.$ |
式中,
| $\left.\begin{array}{l} \dfrac{{\rm d}\omega _x }{{\rm d}t} = \dfrac{M_{x1} }{I_x} \\ \dfrac{{\rm d}\omega _y }{{\rm d}t} = \dfrac{I_z-I_x }{I_y }\omega _x \omega _z + \dfrac{M_{y1}}{I_y } \\ \dfrac{{\rm d}\omega _z }{{\rm d}t} = \dfrac{I_x-I_y }{I_z }\omega _x \omega _y + \dfrac{M_{z1} }{I_z} \\ \end{array}\right\}$ | (2) |
对当前研究的问题:偏航方向是固定的,俯仰方向为强迫振荡,滚转方向为自由运动.于是,从动力学方程式(2)可以看到,滚转方向与俯仰方向不存在动力学方程上的耦合关系,这使我们可以专注于研究俯仰振荡过程导致的非定常流场对滚转动态特性的影响.
2 方形截面弹静态滚转气动力特性在分析方形截面弹静态滚转气动特性之前,首先对发展的算法进行验证.这里采用航天飞机上脱落泡沫碎片的轨迹预测[31](图 2)验证本文发展的松耦合算法;采用方形截面弹[32]定常计算结果验证计算程序对研究外形的模拟能力, 其中压力系数用
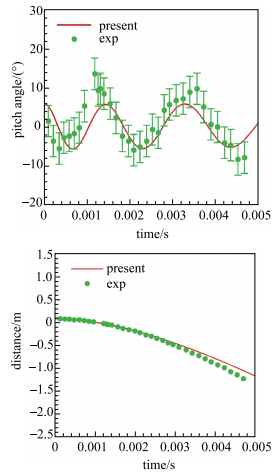
|
图 2 泡沫碎片的欧拉角和平移轨迹预测 Figure 2 Euler angle and translation trajectory prediction of foam debris |
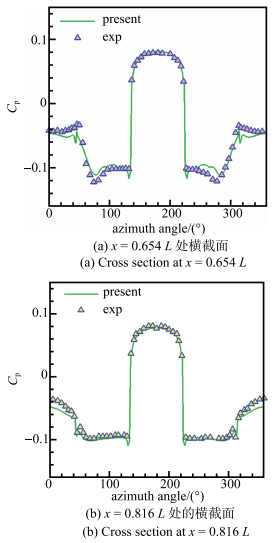
|
图 3 方形截面飞行器定态计算结果与试验比较 Figure 3 Comparison of steady calculation results and experimental data of square cross section vehicle |
图 4是不同攻角时静态滚转力矩(
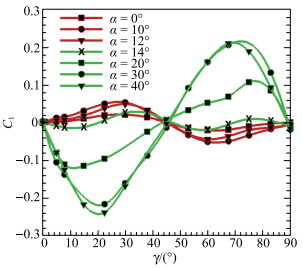
|
图 4 不同攻角时滚转力矩随滚转角变化曲线 Figure 4 Rolling moment with respect to rolling angle at different angles of attack |
对飞行器静态滚转气动特性的分析,可以通过数值模拟飞行器自由振动的过程加以验证,图 5给出了不同攻角时模拟得到的滚转角速度对滚转角的相图.飞行器从5

|
图 5 不同攻角时滚转角速度对滚转角的相图 Figure 5 Phase diagram of rolling angular velocity to rolling angle at different angles of attack |
首先定义强迫俯仰振荡过程为
| $\alpha (t) = \alpha _0 + \alpha _{\rm m} \sin (2\pi ft)$ | (3) |
其中,{
在开始研究俯仰振荡对滚转运动特性的影响之前,首先分析其对滚转静态特性和滚转动态特性的影响.此时,保持滚转角

|
图 6 不同起始攻角时滚转力矩随时间变化曲线 Figure 6 Time history of rolling moment at different initial angles of attack |
在滚转静不稳定时(
俯仰振荡过程对滚转动态稳定性的影响可通过分析滚转力矩对攻角的相图得到.
图 7分别给出起始攻角
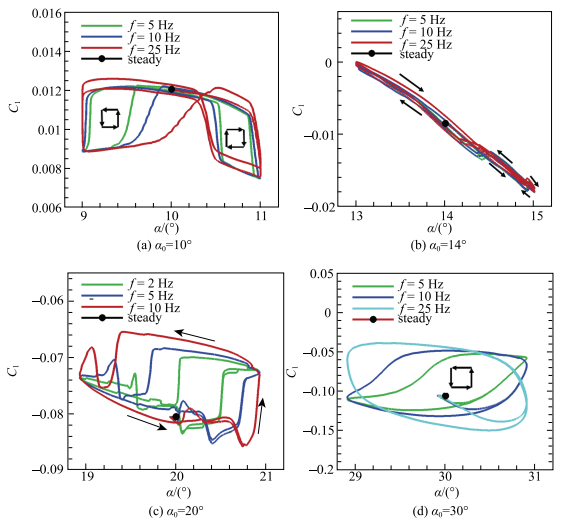
|
图 7 不同起始攻角时滚转力矩随时间变化曲线 Figure 7 Time history of rolling moment at different initial angles of attack |
在分析了俯仰振荡对滚转静、动态稳定性的影响之后,再放开滚转方向的自由度,研究俯仰振荡对滚转运动的影响.俯仰振荡的形式仍按照式(3)给定,图 8给出了不同起始攻角时,俯仰振荡对滚转运动影响的模拟结果.由于飞行器发生连续快速滚转时,滚转角的变化范围较大,为便于分析,在绘图时通常将滚转角进行转换.滚转角变化范围定为
|
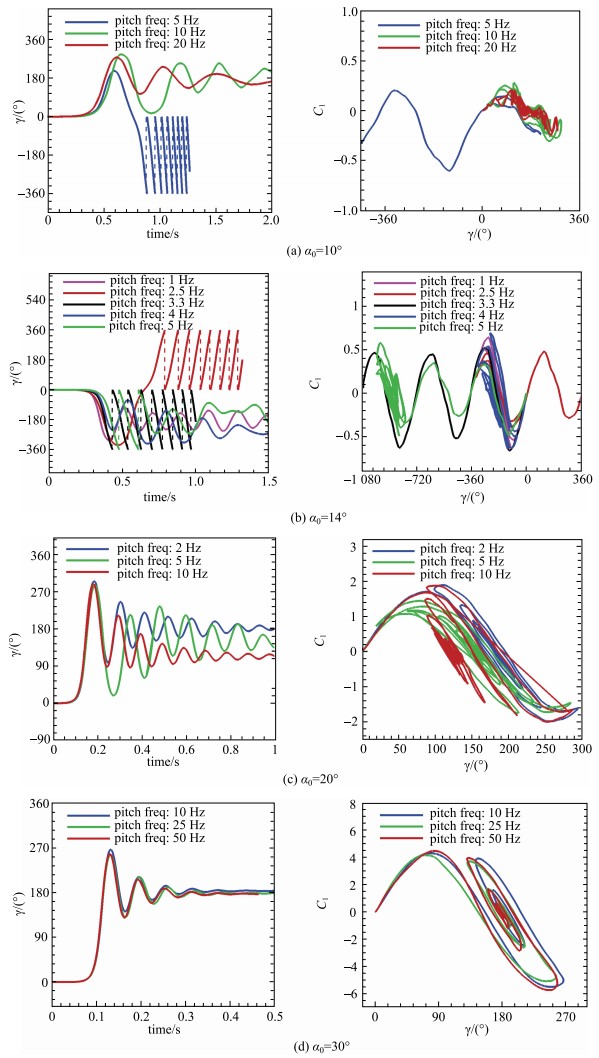
图 8 不同起始攻角时俯仰振荡对滚转运动的影响分析(左:滚转角时间历程;右:滚转力矩-滚转角相图) Figure 8 Analysis of influence of forced pitch oscillation to rolling motion at different angles of attack. (L: time history of rolling angle; R: phase diagram of rolling moment to rolling angle) |
对图 8(a),起始攻角
对图 8(c)和图 8(d),起始攻角
而对图 8(b),起始攻角
这些结果也表明,俯仰振荡过程对滚转运动特性(收敛状态,收敛位置等)的影响较为复杂,具体影响程度视滚转静稳定情况而定.
3.3 网格无关性研究在以上分析中,虽然通过定常计算结果对程序进行了验证,但由于计算网格较稀,仍可能对非定常的计算结果产生较大影响.为此,需开展网格无关性研究.
这里采用三套计算网格G1,G2和G3,计算网格的拓扑结构相同,均为多块对接网格,网格点数量分别约为450万、880万和1 400万. 图 9给出了G1和G3网格在对称面上的网格分布比较,相对于G1网格,G3网格在流向、法向和周向的网格点数均有增加.

|
图 9 G1和G3对称面的网格比较 Figure 9 Comparison of grid G1 and G3 at symmetrical plane |
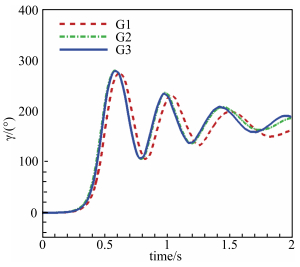
俯仰振荡对滚转运动影响的网格无关性研究选取初始攻角
|
图 10 不同网格的计算结果比较 Figure 10 Comparison of computational result with different grids |
基于建立的六自由度刚体动力学方程和N-S方程的耦合模拟技术,用数值方法研究了方形截面弹俯仰振荡过程对滚转特性的影响,主要结论有:
(1) 研究的方形截面弹外形,其外形特点决定了滚转方向与俯仰方向不存在动力学方程上的耦合关系,这使得可以专注于研究俯仰振荡过程导致的气动力非定常效应对滚转特性的影响,这与传统上研究的三角翼等面对称外形的俯仰/滚转耦合特性有很大不同.
(2) 定性分析了俯仰振荡过程对滚转静态稳定性和动态稳定性的影响.俯仰振荡过程一般会增强滚转动态稳定性;滚转方向为静稳定时,俯仰振荡过程会降低静稳定度;滚转方向为静不稳定时,俯仰振荡过程则会降低静不稳定度.
(3) 分析了俯仰振荡过程对滚转运动特性的影响.对滚转静不稳定情况,快速的俯仰振荡也可能使飞行器滚转运动呈收敛状态;对滚转静稳定情况,静稳定性较弱时,俯仰振荡对滚转运动收敛的位置有较大影响,随着静稳定性增强,这种影响也随之减弱.
| 1 | 黄达.飞行器大振幅运动非定常空气动力特性研究.[博士论文].南京:南京航空航天大学, 2007 ( Huang Da. Unsteady aerodynamic characteristics for the aircraft oscillation in large amplitude.[PhD Thesis]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2007 (in Chinese) ) http://cdmd.cnki.com.cn/Article/CDMD-10287-2007193997.htm |
| 2 | Wang ZJ, Edward CL. Unsteady aerodynamic effects on the flight characteristics of an F-16XL configuration. AIAA Paper 2000-3910, 2000 |
| 3 | 贾区耀. 天空飞行与地面风洞实验动态气动相关性研究. 实验流体力学, 2006, 20 (4) : 87-93. ( Jia Quyao. Investigation on aerodynamic relation between real flight and wind tunnel. Journal of Experiments in Fluid Mechanics, 2006, 20 (4) : 87-93. (in Chinese) ) |
| 4 | 贾区耀, 杨益农, 陈农. 天空飞行与地面风洞实验动态气动相关中的雷诺数影响. 实验流体力学, 2007, 21 (4) : 91-96. ( Jia Quyao, Yang Yinong, Chen Nong. The influence of Reynolds number on dynamic aerodynamics correlation between real flight and wind tunnel. Journal of Experiments in Fluid Mechanics, 2007, 21 (4) : 91-96. (in Chinese) ) |
| 5 | 杨小亮, 刘伟, 吴天佐, 等. 细长三角翼滚转/侧滑耦合运动效应分析. 空气动力学学报, 2004, 32 (1) : 1-7. ( Yang Xiaoliang, Liu Wei, Wu Tianzuo, et al. Coupling mechanism analysis of a slender delta wing in combined free-roll and free-sideslip motion. Acta Aerodynamica Sinica, 2004, 32 (1) : 1-7. (in Chinese) ) |
| 6 | 黄达, 吴根兴. 三角翼俯仰滚转耦合运动气动特性研究. 航空学报, 1999, 20 (6) : 485-488. ( Huang Da, Wu Genxing. Investigation of unsteady aerodynamic characteristics for a delta wing oscillation in large amplitude pitching-roll motion. Acta Aeronautica Et Astronautica Sinica, 1999, 20 (6) : 485-488. (in Chinese) ) |
| 7 | 李志强, 黄达, 史志伟, 等. 俯仰-滚转耦合两自由度大振幅非定常实验技术. 南京航空航天大学学报, 1999, 31 (2) : 121-126. ( Li Zhiqiang, Huang Da, Shi Zhiwei, et al. Test technology of unsteady aerodynamic characteristic for a model oscillating in large amplitude pitching-rolling motion. Journal of Nanjing University of Aeronautics & Astronautics, 1999, 31 (2) : 121-126. (in Chinese) ) |
| 8 | 杨勐, 黄达. 大迎角耦合运动非定常空气动力特性. 实验流体力学, 2011, 25 (6) : 19-22. ( Yang Meng, Huang Da. The unsteady aerodynamic characteristics of coupled motion at high angle of attack. Journal of Experiments in Fluid Mechanics, 2011, 25 (6) : 19-22. (in Chinese) ) |
| 9 | 唐敏中, 张伟, 何宏丽. 俯仰-滚摆耦合复杂流场试验研究. 空气动力学报, 2001, 19 (1) : 47-55. ( Tang Minzhong, Zhang Wei, He Hongli. Experimental investigation on unsteady flow field about a coupled pitching-rolling delta wing. Acta Aerodynamica Sinica, 2001, 19 (1) : 47-55. (in Chinese) ) |
| 10 | 王兵, 黄存栋, 马宝峰, 等. 精确复现机翼摇滚运动的控制技术. 实验流体力学, 2009, 23 (1) : 79-104. ( Wang Bing, Huang Cundong, Ma Baofeng, et al. The control method of precise reproduction of the wing rock motion. Journal of Experiments in Fluid Mechanics, 2009, 23 (1) : 79-104. (in Chinese) ) |
| 11 | 吕光男.风洞虚拟飞行试验中的飞行力学与控制问题研究.[硕士论文].南京:南京航空航天大学, 2009 ( Lü Guangnan. Research on a flight dynamics and control in wind tunnel based virtual flight test.[Master Thesis]. Nanjing:Nanjing University of Aeronautics and Astronautics, 2009(in Chinese) ) |
| 12 | 胡静, 李潜. 风洞虚拟飞行试验技术初步研究. 实验流体力学, 2010, 24 (1) : 95-99. ( Hu Jing, Li Qian. Primary investigation of the virtual flight testing techniques in wind tunnel. Journal of Experiments in Fluid Mechanics, 2010, 24 (1) : 95-99. (in Chinese) ) |
| 13 | 向光伟, 谢斌, 赵忠良, 等. 2.4m×2.4m跨声速风洞虚拟飞行试验天平研制. 实验流体力学, 2014, 28 (1) : 65-69. ( Xiang Guangwei, Xie Bin, Zhao Zhongliang, et al. Development of virtual flight test balance for 2.4m×2.4m transonic wind tunnel. Journal of Experiments in Fluid Mechanics, 2014, 28 (1) : 65-69. (in Chinese) ) |
| 14 | 赵忠良, 任斌, 汪清. 风洞模型自由翻滚试验技术. 空气动力学学报, 2004, 18 (4) : 384-389. ( Zhao Zhongliang, Ren Bin, Wang Qing. Wind tunnel test technique of the model free-to-tumble. Acta Aerodynamica Sinica, 2004, 18 (4) : 384-389. (in Chinese) ) |
| 15 | 陶洋, 赵忠良, 杨海泳. 翼身组合体摇滚特性高速试验研究. 实验流体力学, 2011, 18 (4) : 67-77. ( Tao Yang, Zhao Zhongliang, Yang Haiyong. Investigation on wing rock of wing-body configuration at high speed wind tunnel. Journal of Experiments in Fluid Mechanics, 2011, 18 (4) : 67-77. (in Chinese) ) |
| 16 | 杨小亮, 刘伟, 赵云飞, 等. 80°后掠三角翼强迫俯仰、自由滚转双自由度耦合运动特性数值研究. 空气动力学学报, 2011, 29 (4) : 421-426. ( Yang Xiaoliang, Liu Wei, Zhao Yunfei, et al. Numerical investigation of the characteristics of double degree-of-freedom motion of an 80° delta wing in force-pitch and free-roll. Acta Aerodynamica Sinica, 2011, 29 (4) : 421-426. (in Chinese) ) |
| 17 | 杨小亮, 赵云飞, 刘伟. 多种因素对三角翼俯仰/滚转运动特性影响的数值研究. 力学季刊, 2011, 32 (1) : 28-34. ( Yang Xiaoliang, Zhao Yunfei, Liu Wei. Numerical investigation of multiple sensitive factors of the characteristics of the slender delta wing in force-pitch and free-roll motion. Chinese Quarterly of Mechanics, 2011, 32 (1) : 28-34. (in Chinese) ) |
| 18 | 杨小亮.飞行器多自由度耦合摇滚运动数值模拟研究.[博士论文].长沙:国防科学技术大学, 2012 ( Yang Xiaoliang. Numerical investigation of aircraft rock in multiple degrees of freedom[PhD Thesis]. Changsha:National University of Defense Technology, 2012 (in Chinese) ) |
| 19 | 郭迪龙, 杨国伟, 康宏琳, 等. 三角翼受迫俯仰滚转耦合运动的气动特性研究. 空气动力学学报, 2007, 25 (1) : 65-69. ( Guo Dilong, Yang Guowei, Kang Honglin, et al. Study of aerodynamic characteristics of coupled forced pitching and rolling of a delta wing. Acta Aerodynamica Sinica, 2007, 25 (1) : 65-69. (in Chinese) ) |
| 20 | Magill JC, ShawnW. Initial test of a wire suspension mount for missile virtual flight testing. AIAA Paper 2002-0169, 2002 |
| 21 | Magill JC, Cataldi P, Morency JR. Demonstration of a wire suspension system for dynamic wind tunnel testing. AIAA Paper 2004-1296, 2004 |
| 22 | Magill JC, Cataldi P, Morency JR, et al. Design of a wire suspension system for dynamic testing in AEDC 16T. AIAA Paper 2003-0452, 2003 |
| 23 | Rein M, Höhler G, Schütte A. Ground-based simulation of complex maneuvers of a delta-wing aircraft. AIAA Paper 2006-3149, 2006 |
| 24 | Bergmanna A, Huebnerb A. Integrated experimental and numerical research on the aerodynamics of unsteady moving aircraft//3rd International Symposium on Integrating CFD and Experiments in Aerodynamics, 2007. |
| 25 | Thomas JP, Dowell EH, Hall KC. Modeling viscous transonic limit cycle oscillation behavior using a harmonic balance approach. Journal of Aircraft, 2004, 41 (6) : 1266-1274. DOI: 10.2514/1.9839. |
| 26 | Thomas JP, Dowell EH, Hall KC, et al. Further investigation of modeling limit cycle oscillation behavior of the F-16 fighter using a harmonic balance approach. AIAA Paper 2005-1917, 2005 |
| 27 | Thomas JP, Custer CH, Dowell EH, et al. Unsteady flow computation using a harmonic balance approach implemented about the OVERFLOW2 flow solver. In:Proceedings of the 19th AIAA Computational Fluid Dynamics Conference, 2009 |
| 28 | Zhang HX, Zhuang FG. NND schemes and their application to numerical simulation of two and three dimensional flows. Advances in Applied Mechanics, 1992 |
| 29 | Jameson A. Time dependent calculation using multi-grid with application to unsteady flows past airfoils and wings. AIAA Paper 91-1596, 1991 |
| 30 | Birch TJ, Petterson K. CFD predictions of square and elliptic crosssection missile configurations at supersonic speeds. AIAA Paper 2004-5453, 2004 |
| 31 | Murman SM, Aftosmis MJ, Rogers SE. Characterization of space shuttle ascent debris aerodynamics using CFD methods. AIAA Paper 2005-1223, 2005 |
| 32 | 陈坚强, 陈琦, 袁先旭, 等. 舵面操纵动态响应的数值模拟研究. 力学学报, 2013, 45 (2) : 302-306. ( Chen Jianqiang, Chen Qi, Yuan Xianxu, et al. Numerical simulation study on dynamics response under rudder control. Chinese Journal of Theoretical and Applied Mechanics, 2013, 45 (2) : 302-306. (in Chinese) ) |

