生物组织、多孔岩体、土壤、颗粒物质、胶体等复杂介质(complex media),是介于理想固体和液体之间的复杂物质状态,其力学和物理性质复杂,通常表现出记忆性和路径依赖性,难以用一般的经典力学模型来描述.此外,复杂介质中的能量耗散往往呈现出幂律特征,即其试验数据的拟合公式具有幂函数形式[1-2].
大量的室内和室外实验发现,声波在复杂介质中传播时,其衰减系数呈现出频率的幂律依赖关系[3-7]
| $ \alpha =\alpha _0 \omega ^\eta $ | (1) |
其中,
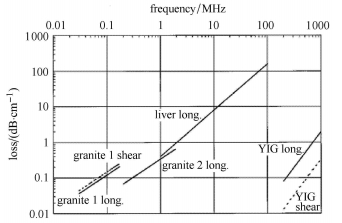
Szabo等[8]给出了一组不同材料的频率与衰减系数之间关系的实验数据,如图 1所示.图 1将衰减系数和频率之间关系刻画在双对数坐标上,直线的斜率即为参数
|
图 1 不同材料的声波衰减与频率的关系 Figure 1 The relationship between the attenuation and frequency for various |
气体中能对振动起到阻尼作用的只有黏滞性和热传导.经典的声波控制方程包括阻尼波动方程和热黏性波动方程两类.阻尼波动方程的形式如下
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} + \dfrac{2\alpha _0 }{c_0 }\dfrac{\partial P}{\partial t} = \nabla ^2P $ | (2) |
其中,
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} - \dfrac{\mu }{c_0^2 }\dfrac{\partial }{\partial t}\left( {\nabla ^2P} \right) = \nabla ^2P $ | (3) |
其中,
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} - \dfrac{\mu }{c_0^2 }\dfrac{\partial ^3P}{\partial t^3} = \nabla ^2P $ | (4) |
该模型描述了频率二次方依赖的声衰减,即
从以上公式可以发现,经典的阻尼波方程和近似热黏性波方程分别描述了与频率无关和频率二次方依赖的声衰减,但无法描述频率非整数次依赖的衰减.为了研究声波衰减的频率任意次幂律依赖现象,许多学者提出了相应的模型.例如,基于频域分析的声波模型[11-18],多松弛模型[19-20]等.然而,这些模型由于需要消耗大量的计算成本[21-23]而未被广泛接受.
分数阶导数算子已被广泛研究,其是一种能描述具有历史记忆性和空间依赖性力学行为的有力建模工具[24-25].采用分数阶导数建模,以修正传统的达西定律、傅里叶热传导、黏弹性本构关系,可以很好地解释传统模型无法解释的``反常''现象.此外,分数阶导数的阶数有明确的物理意义.例如,扩散方程中的分数阶阶数可以区分正常扩散,超扩散和次扩散[26];黏弹性本构方程中的分数阶阶数可以定性描述黏性和弹性的比重[27-28].类似地,分数阶导数模型也可以被用于描述任意阶频率幂律依赖衰减的现象.目前,已有许多学者在这方面做了大量的工作,提出了相应的分数阶导数声波模型.本文旨在对这些已有的模型作一个总结,从时间和空间分数阶两个方面概述了不同的分数阶导数声波模型,并讨论了相关模型之间的联系和区别,阐述了频率依赖指数变化范围的统计解释,最后对尚未涉及的声波传播耗散机制的建模领域提出了研究设想,期望能起到抛砖引玉的效果.
1 在软物质中传播的分数阶导数声波模型 1.1 时间分数阶导数声波模型时间分数阶导数声波模型大致可分为唯象模型和本构模型两类.唯象模型主要是基于声衰减的频率幂律依赖现象,采用分数阶微积分理论修正已有的声波方程而获得的;本构模型的构建主要是从分数阶黏弹性本构方程推导得到.
1.1.1 唯象模型基于频率幂律依赖现象,Szabo[11]从热黏性波模型和阻尼波模型的频域形式出发,提出了声波模型的一般化频域模型,然后将频域声波模型转化为时域上的卷积积分声波方程
| $\dfrac{1}{c_0^2 }\dfrac{\partial^2 P}{\partial t^2} + \dfrac{2\alpha _0 }{c_0 } {\rm L}_\eta \left( P \right) = \nabla ^2P $ | (5) |
其中,耗散项
由于Szabo提出的声波模型含有超奇异性,数值上难以处理,Chen等[29]引入分数阶微积分理论对其进行修正,推导出了一种修正的Szabo模型,其控制方程为
| $\dfrac{1}{c_0^2 }\dfrac{\partial^2 P}{\partial t^2} + \dfrac{2\alpha _0 }{c_0 \cos \left( {\eta \pi / 2} \right)}\dfrac{\partial ^{\eta + 1}P}{\partial t^{\eta + 1}} = \nabla ^2P $ | (6) |
其中,

|
图 2 反射板上声压与肿瘤的位置和大小的关系[32] Figure 2 The relationship between the sound pressure and the size or position of tumor[32] |
Szabo模型和修正的Szabo模型都满足频率幂律依赖的衰减
| $\begin{gathered} \frac{1}{{c_0^2}}\frac{{{\partial ^2}P}}{{\partial {t^2}}} + \frac{{2{\alpha _0}}}{{{c_0}\cos \left( {\pi \eta /2} \right)}}\frac{{{\partial ^{\eta + 1}}P}}{{\partial {t^{\eta + 1}}}} + \\ \frac{{\alpha _0^2}}{{{{\cos }^2}\left( {\frac{{\pi \eta }}{2}} \right)}}\frac{{{\partial ^{2\eta }}P}}{{\partial {t^{2\eta }}}} = {\nabla ^2}Pn \\ \end{gathered} $ | (7) |
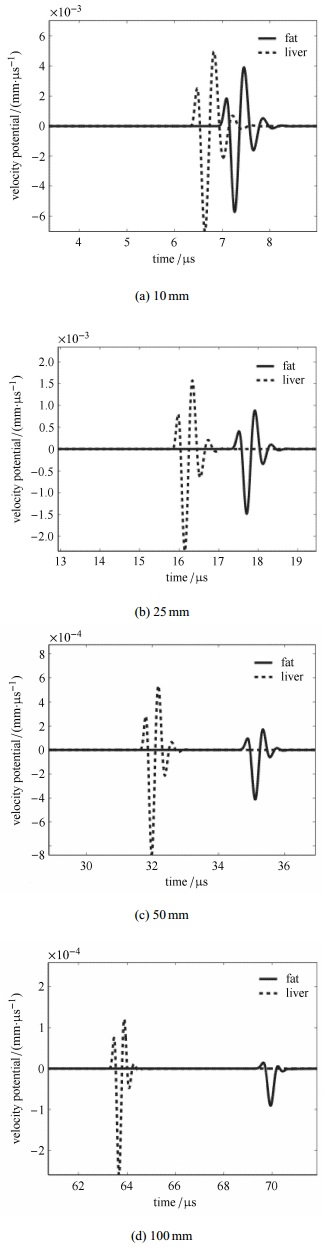
并成功采用格林函数法求解了该方程.从图 3可以看出,幂律声波在脂肪组织(
|
图 3 脉冲函数在脂肪( |
不同于Szabo的研究方式,Wismer[35]从频率的幂律依赖现象出发,直接对经典的黏性波动方程进行修正,得到了一种修正的声波控制方程
| $\dfrac{1}{c_0^2 }\dfrac{\partial^2 P}{\partial t^2} - \tau^{\eta - 1} \dfrac{\partial^{\eta - 1}}{\partial t^{\eta - 1}}\left( {\nabla ^2P} \right) = \nabla ^2P $ | (8) |
其中,分数阶阶数
Ochmann等[36]根据幂律衰减现象推导得到了一类广义的Burgers方程
| $ \dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} + \left( {\eta + 1} \right)\nabla \left( {\nabla ^2P} \right) + \dfrac{2D}{c_0 }\dfrac{\partial ^{\eta + 1}P}{\partial t^{\eta + 1}} = \nabla ^2P $ | (9) |
其中,
| $ \dfrac{\partial ^2P}{\partial t^2} + c_0^2 \left( {\gamma + 1} \right) \dfrac{\partial ^3P}{\partial x^3} + 2Dc_0 \dfrac{\partial ^{\gamma + 1}P}{\partial t^{\gamma + 1}} = c_0^2 \dfrac{\partial ^2P}{\partial x^2} $ | (10) |
该非线性模型中,
与理想固体和流体不同,软物质的力学行为具有时间和空间上的长程相关性,其通常可以被当作黏弹性材料研究.分数阶微积分是一种能描述黏弹性材料力学行为的强有力工具.目前,这一观点已得到广泛认可[1, 25, 38-43].从分数阶黏弹性本构出发,研究黏弹性材料中的声波耗散机制,是不同于唯象建模的另一种研究思路.
Caputo[44]早在1967年即从分数阶Kelvin黏弹性本构方程推导出分数阶Kelvin波动方程,其形式如下
| $\dfrac{1}{c_0^2 }\dfrac{\partial^2 P}{\partial t^2} - \tau _\sigma ^\eta \dfrac{\partial ^\eta }{\partial t^\eta }\left( {\nabla ^2P} \right) = \nabla ^2P $ | (11) |
其中,
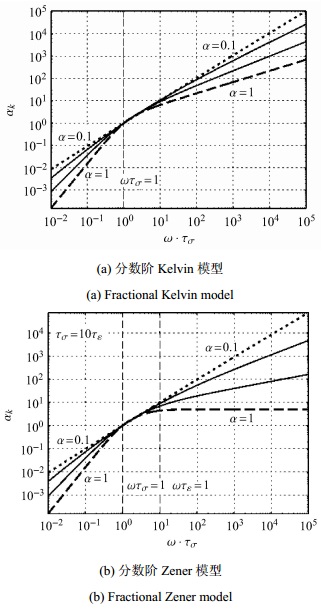
|
图 4 分数阶本构模型的衰减系数与频率的关系[46] Figure 4 The relationship of attenuation and frequency for fractional constitutive models[46] |
从形式上看,分数阶Kelvin模型与Wismer提出的模型(式(8))可以记作一个统一的形式,其分数阶阶数在0和1之间(Wismer模型的分数阶阶数为
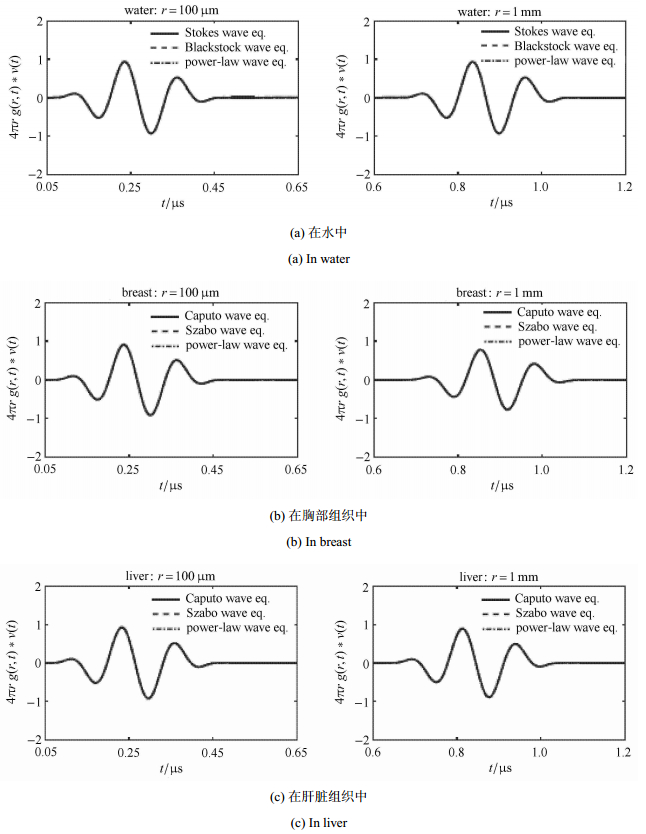
|
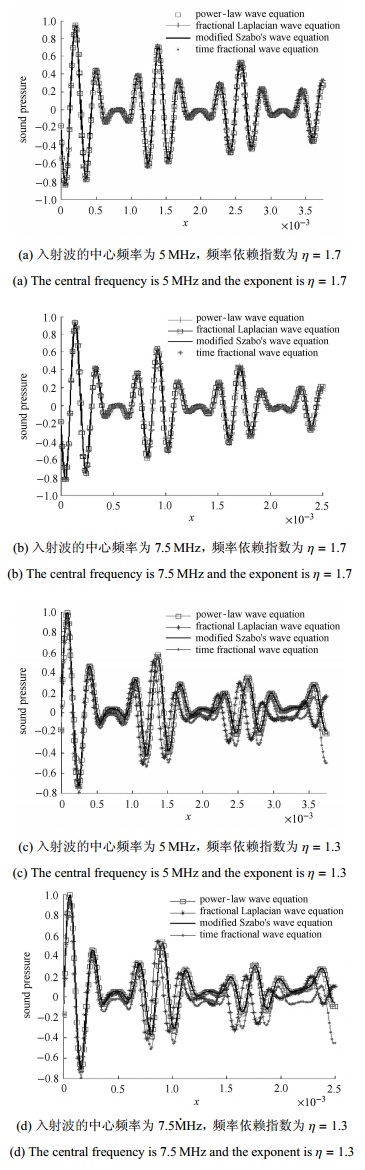
图 5 脉冲函数以不同声波模型传播的比较[50] Figure 5 The comparison of the propagation of pulse function governed by different acoustic wave models[50] |
类似地, Konjik等[51]、Näsholm等[52]都推导了分数阶Zener波动方程
| $ \dfrac{1}{c_0^2 }\dfrac{\partial^2 P }{\partial t^2} - \tau _\sigma ^\eta \dfrac{\partial ^\eta }{\partial t^\eta }\left( {\nabla ^2P} \right) + \dfrac{\tau _\varsigma ^\beta }{c_0^2 }\dfrac{\partial ^{\beta + 2}P}{\partial t^{\beta + 2}} = \nabla ^2P $ | (12) |
其中,
Buckingham[54-55]发现在海底沉积物中传播的纵波和横波同样具有频率的幂律依赖现象.因此,他采用一种具有应变硬化性质的修正Maxwell模型来描述颗粒之间的剪切机制.该学者将时间依赖的脉冲形状函数应用到Navier-Stokes方程中,得到波动方程如下
| $\left. \begin{gathered} {\nabla ^2}\psi = \frac{1}{{c_0^2}}\frac{{{\partial ^2}\psi }}{{\partial {t^2}}} - \hfill \\ \left( {\frac{{{\lambda _{\text{p}}}}}{{{\rho _0}c_0^2}}} \right)\frac{\partial }{{\partial t}}{\nabla ^2}\left( {{h_{\text{p}}}\left( t \right) * \psi } \right) - \hfill \\ \frac{4}{3}\frac{{{\gamma _{\text{s}}}}}{{{\rho _0}c_0^2}}\frac{\partial }{{\partial t}}{\nabla ^2}\left( {{h_{\text{s}}}\left( t \right) * \psi } \right) - \hfill \\ \frac{{{\eta _{\text{s}}}}}{{{\rho _0}}}{\nabla ^2}\left( {{h_{\text{s}}}\left( t \right) * \boldsymbol{A}} \right) - \frac{{\partial \boldsymbol{A}}}{{\partial t}} = 0 \hfill \\ \end{gathered} \right\}$ | (13) |
其中,速度向量
| $\begin{gathered} {\nabla ^2}\psi = \frac{1}{{c_0^2}}\frac{{{\partial ^2}\psi }}{{\partial {t^2}}} - \\ \Gamma \left( {1 - \eta } \right)\left( {\frac{{{\lambda _{\text{p}}}}}{{{\rho _0}c_0^2}} + \frac{4}{3}\frac{{{\gamma _{\text{s}}}}}{{{\rho _0}c_0^2}}} \right){\tau ^{\eta - 1}}\frac{{{\partial ^\eta }}}{{\partial {t^\eta }}}{\nabla ^2}\psi \\ \end{gathered} $ | (14) |
和横波方程
| $\dfrac{\partial ^{2 - \eta }{\boldsymbol {A}}}{\partial t^{2 - \eta }} = \Gamma \left( {1 - \eta } \right)\dfrac{\gamma _{\rm s} }{\rho _0 }\tau ^{\eta - 1}\nabla ^2 {\boldsymbol {A}} $ | (15) |
通过比较式(11)与式(14),可以发现,这两个波动方程具有相似的形式,而式(15)是一类分数阶扩散-波方程.如此,Pandey等[56]将分数阶Kelvin波动方程与海底沉积物中的声波传播方程紧密地联系起来,并赋予分数阶阶数以物理意义
| $ \dfrac{1}{c_0^2 }\dfrac{\partial^2 P }{\partial t^2} - \tau _{\rm p}^{\eta _1 } \dfrac{\partial ^{\eta _1 }}{\partial t^{\eta _1 }}\left( {\nabla ^2P} \right) -\tau _s^{\eta _2 } \dfrac{\partial ^{\eta _2 }}{\partial t^{\eta _2 }}\left( {\nabla ^2P} \right) = \nabla ^2P $ | (16) |
其中,
Prieur等[57]采用分数阶Kelvin本构模型,与分数阶热传导模型相结合,得到的波动方程如下
| $\begin{gathered} {\nabla ^2}P - \frac{1}{{c_0^2}}\frac{{{\partial ^2}P}}{{\partial {t^2}}} + {L_{\text{v}}}\frac{{{\partial ^{\eta - 1}}}}{{\partial {t^{\eta - 1}}}}{\nabla ^2}P - \frac{{{L_{\text{t}}}}}{{c_0^2}}\frac{{{\partial ^{\eta + 1}}P}}{{\partial {t^{\eta + 1}}}} = \hfill \\ \;\;\;\;\;\;\; - \frac{\beta }{{{\rho _0}c_0^4}}\frac{{{\partial ^2}P}}{{\partial {t^2}}} \hfill \\ \end{gathered} $ | (17) |
式中,
声波传播时,其衰减过程不仅与传播的时间相关,也与传播的距离和位置相关.受启发于热黏性波动方程的衰减项
| $\dfrac{1}{c_0^2 }\dfrac{\partial^2 P}{\partial t^2} + \dfrac{2\alpha _0 }{c_0^{1 - \eta } }\dfrac{\partial }{\partial t}\left( { - \nabla^2 } \right)^{\eta / 2}P = \nabla ^2P $ | (18) |
其中,
空间分数阶拉普拉斯声波方程满足频率幂律依赖关系
| $\begin{gathered} \frac{1}{{c_0^2}}\frac{{{\partial ^2}P}}{{\partial {t^2}}} + \frac{{2{\alpha _0}}}{{c_0^{1 - \eta }}}\frac{\partial }{{\partial t}}{\left( { - {\nabla ^2}} \right)^{\eta /2}}P + \hfill \\ \;\;\;\;\;\;2{\alpha _0}c_0^\eta \tan \frac{{\pi \eta }}{2}{\left( { - {\nabla ^2}} \right)^{(\eta + 1)/2}}P = {\nabla ^2}P \end{gathered} $ | (19) |
传统的非局部弹性理论采用权函数表征物质点之间力学性质的相互影响关系.随着距离的增大,权函数逐渐减小并趋于0.此外,权函数与材料内部特征长度相关,特征长度越小,则权函数影响范围越小,反之亦然.常见的权函数有格林函数、高斯函数等,形式上表现为一类指数函数.
分数阶导数是一个非局部算子,在时间上表征历史依赖性,在空间上刻画长程相关性.分数阶黏弹性模型是最常见的时间分数阶模型之一,大量的实验也证明了这类模型的有效性.目前,已有研究学者将经典的非局部弹性理论与分数阶黏弹性模型相结合,提出了非局部的分数阶黏弹性理论.
若不考虑时间域上的异同,仅讨论不同位置的物质点对某一点力学性质的影响,理论上可以采用空间分数阶导数来进行非局部弹性理论的建模.然而,经典的分数阶导数的权函数是一个幂函数,且与特征长度无关.
庞国飞[61]在幂函数中引入特征长度对其进行修正,并与Riesz势的概念有机统一起来,提出了空间依赖的分数阶非局部算子.该分数阶非局部算子的定义为
| ${{\text{I}}^\gamma }u\left( x \right) = \left\{ \begin{gathered} \int {\frac{A}{{\Gamma \left( l \right)}}{{\left| {x - y} \right|}^{ - n + \gamma \left( l \right)}}u\left( y \right){\text{d}}y} \hfill \\ \;\;\;\;\;\;\;\left| {x - y} \right| \leqslant l{\mkern 1mu}, \gamma < n \hfill \\ 0, \;\;\;\;\;\left| {x - y} \right| > l \end{gathered} \right.$ |
其中,
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} - \hat {\tau } {\rm I}^\gamma \dfrac{\partial }{\partial t}\left( {\nabla ^2P} \right) = \nabla ^2P $ | (20) |
和非局部修正Maxwell黏弹性波方程
| $ \dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} + \dfrac{\rho }{\eta } {\rm I}^{ - \gamma } \dfrac{\partial P}{\partial t} + \dfrac{1}{c_0^2 } {\rm I}^{ - \gamma _1 } \dfrac{\partial ^2P}{\partial t^2} = \nabla ^2P $ | (21) |
这两种方程对应的衰减系数分别为
Treeby等[62]利用低频近似的色散关系
Carcione等[64]根据频率依赖的体积模量, 得到频域上的应力应变关系,并推导得到了一类扩散-波方程
| $\dfrac{\partial ^{2 - 2\eta }P}{\partial t^{2 - 2\eta }} = c_0^2 \omega _0^{ -2\eta } \nabla ^2P $ | (22) |
随后,Carcione[65-66]采用傅里叶伪谱法对其进行了数值分析.类似地,Zhu等[67-68]基于黏弹性本构得到形如式(22)的扩散-波方程,再利用上述色散关系,得到了一类与品质因子
| $ \dfrac{1}{c_0^2 }\dfrac{\partial^2 P }{\partial t^2} - \tau \dfrac{\partial }{\partial t}\left( { - \nabla ^2} \right)^{\eta + 1 / 2}P - \gamma \left( { - \nabla ^2} \right)^{\eta + 1}P = 0 $ | (23) |
其中,
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} = \gamma \left( { - \nabla ^2} \right)^{\eta + 1}P $ | (24) |
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} = \nabla ^2P + \tau \dfrac{\partial }{\partial t}\left( { - \nabla ^2} \right)^{\eta + 1 / 2}P $ | (25) |
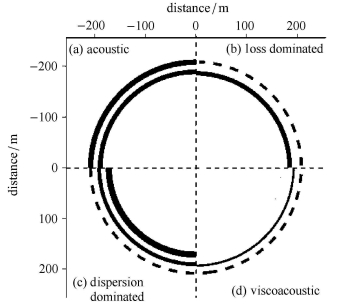
式(24)主要控制声波的频散,而式(25)与空间分数阶拉普拉斯声波模型类似(式(18)),主要控制声波的耗散,等式右边第2项为其耗散项. 图 7给出了4种波动控制方程下波传播130 ms后相位和波幅示意图.与(a)区相比,(b)区的波幅明显降低;(c)区的波幅未有明显变化,但相位滞后了;(d)区的波幅降低并且相位滞后了.该图验证了式(23)在描述波频散和耗散方面的有效性.
将上述的耗散声波方程统一记作如下形式
| $\dfrac{1}{c_0^2 }\dfrac{\partial^2 P}{\partial t^2} - L\left( P \right) = \nabla ^2P $ | (26) |
其中,
| 表 1 不同声波模型耗散项的对比 Table 1 Comparison of different loss operators |
多孔介质(如土壤、砂岩、泡沫等)是多相物质共存的一种组合体,以固相为骨架,骨架孔隙中充满液体、气体或者液气混合物.多孔介质有多种分类方法,如果按固体骨架的性质分类,可以将其分为刚性固体骨架多孔介质和骨架可变形的多孔介质.多孔介质往往具有非均匀性和各向异性的特点,声波在其中传播时,传播过程和耗散机理的复杂性促使越来越多的研究人员对其进行深入研究.特别当介质中存在断面、裂隙等界面层时,波传播的机理更加复杂[69].
声波在各向异性的介质中传播时,其衰减依赖于空间各个位置.基于此考虑,Meerschaert等[70]提出了一种可以描述各向异性的分数阶Stokes波动方程
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} = \Delta ^{\overrightarrow r / 2}P + \tau \dfrac{\partial }{\partial t}\Delta ^{\overrightarrow r / 2}P $ | (27) |
其中,空间依赖项的定义为
| $\Delta ^{\overrightarrow r / 2}P\left( {\overrightarrow x } \right) = \sum\limits_{j = 1}^d {\dfrac{\partial ^{r_j }}{\partial x_j^{r_j } }} P\left( {x_1, x_2, \cdots, x_d } \right) $ |
具体可参见文献[71-72].如果此方程中的拉普拉斯算子退化为一般的拉普拉斯算子, 并用于描述各向同性材料, 则该方程与热黏性波动方程(式(3))具有相同的形式.
各向同性多孔介质中声波传播可以由两个复变量来描述,即,特征阻抗和传播系数.实验发现,特征阻抗和传播系数的实部和虚部都与频率呈幂律相关[73],如图 8. Chen等[74]和胡帅[75]将特征阻抗的实部和虚部的幂律指数设定为同一值, 并对实验数据进行拟合,提出了刻画在均匀多孔介质中传播的声波模型
| $\dfrac{1}{c_0^2 }\dfrac{\partial ^2P}{\partial t^2} + \dfrac{\eta }{c_0^2 }\dfrac{\partial ^{2-\eta }P}{\partial t^{2 - \eta }} = \nabla ^2P $ | (28) |
其中,
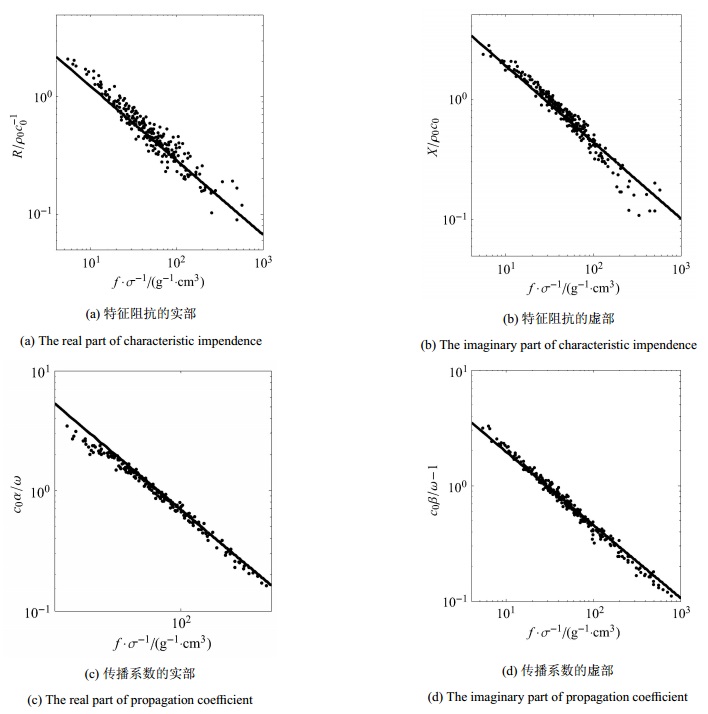
|
图 8 特征阻抗和传播系数与频率/流阻的关系[74] Figure 8 The relationship between the characteristic impendence or propagation coefficient and frequency/flow resistance[74] |
声波在刚性固体骨架中传播时,研究学者发现需要在欧拉方程和质量守恒方程中分别引入频率依赖的动曲率和动压缩率来描述声波在充满空气的多孔介质中的传播[76-77]. Fellah等[78]将动曲率和动压缩率分别进行低频和高频近似,推导出了低频和高频对应的波动方程
| $\left.\!\!\begin{array}{l} \dfrac{\partial ^2P}{\partial x^2} - a\dfrac{\partial ^2P}{\partial t^2} - d\dfrac{\partial P}{\partial t} = 0 \, , \ \ \hbox{low frequency} \cr \dfrac{\partial ^2P}{\partial x^2} - A\dfrac{\partial ^2P}{\partial t^2} - C\dfrac{\partial P}{\partial t} -\cr \qquad B\int_{ - \infty }^t \dfrac{\partial ^2P / \partial t'^2}{\sqrt {t - t'} } {\rm{d}}t' = 0\, , \ \ \hbox{high frequency} \end{array}\!\!\right\} $ | (29) |
其中,
考虑声波在可变形的固体骨架中传播时,动态渗透率是频率依赖的[76].将其代入广义的达西定律中,可以得到一组修正的Biot-JKD模型
| $\left.\!\!\begin{array}{l} \sigma _{ij, j} + F_i^b = \rho \ddot {u}_i + \rho _f \ddot {w}_i \cr - p_{, i} + F_i^f = \rho _f \ddot {u}_i + m\ddot {w}_i +\cr \qquad \dfrac{k_0 }{\eta }a_{\rm s}^{ - 1 / 2} \left( { {\rm D} + a_{\rm s} } \right)^{1 / 2}\dot {w}_i \end{array}\!\!\right\} $ | (30) |
其中,
大量的实验证明,声波的能量耗散具有幂律特征,由式(1)可知,其幂律衰减指数
若将式(18)右侧的拉普拉斯项去掉,再对时间
| $\left. \begin{array}{l} \frac{{\partial P}}{{\partial t}} + \kappa {\left( { - \frac{{{\partial ^2}}}{{\partial {x^2}}}} \right)^{\eta /2}}P = 0\\ P\left( {x, 0} \right) = \delta \left( x \right), - \infty < x < \infty \end{array} \right\} $ | (31) |
其中,
| $P\left( {x, t} \right) = \dfrac{1}{t^{1 / \eta }}w_\eta \left( {\dfrac{x}{t^{1 / \eta }}} \right) $ | (32) |
式中
| ${w_\eta }\left( \xi \right) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty {{{\rm{e}}^{ - {\rm{i}}q\xi }}} {W_\eta }\left( k \right){\rm{d}}k $ |
其中,
Saichev等[90]指出,为了保证概率密度函数为正,Lévy分布的指数必须在(0, 2]之间.也就是说,在
将式(1)中的衰减函数写成如下形式
| $\eta = \dfrac{\ln \left( {\alpha / \alpha _0 } \right)}{\ln \omega } $ | (33) |
式(33)揭示了频率幂律依赖衰减的自相似性.
Mandelbrot[91]和Sato[92]就Lévy概率密度函数的自相似性,指出了Lévy稳态分布与分形之间的内在联系.基于此,
目前关于分数阶模型与材料微结构分形特征之间关系的研究成果多是定性的,定量结论很少.因而,分数阶模型一般多是唯象模型,缺少坚实的物理基础.主要的验证手段是实验数据的拟合.统计热力学可能是建立两者之间联系的一个有效方法.分数阶导数模型的统计力学背景比较清楚,研究也较深入;但目前材料分形结构与其热力学行为关系的研究也还不成熟.
另一方面,函数分形维与分数阶导数的关系的研究较多.函数的分形维数和分数阶微积分的阶数之间呈线性关系.
Mandelbrot等[93]的研究表明分数阶布朗运动函数的分形维数与Hurst指数之间的关系为
此外,Henry等[100]指出实际问题中自相似性只表现在一个有限的尺度范围内,这与图 1所观察到的实验现象也是吻合的.
4 结论和展望复杂介质,如土壤、生物组织等,是固、液、气体的多相混合物,其物理和力学性质介于理想固体和液体之间.声波在此类复杂介质中传播时,其幂律衰减的指数介于0和2之间.经典的声波控制方程只能描述与频率无关或频率平方依赖的声黏性阻尼衰减现象,而分数阶导数模型能够刻画声波的频率任意次幂律依赖衰减.分数阶阶数的物理意义也很明确,即为双对数坐标下衰减系数与频率所呈直线的斜率.
目前的主要研究思路是针对声衰减的幂律依赖现象展开研究,分析所得的波动方程是否满足因果律(Kramers-Kronig关系),最后采用数值算法进行仿真分析.本文概述了现有的各种分数阶导数波动模型,分析和比较了这些模型之间的异同点.可以发现,这些模型主要分为唯象模型和本构模型两大类.最后,本文介绍了幂律衰减指数介于0和2之间的统计解释,并将频率依赖黏性衰减与介质的分形结构联系起来.
尽管分数阶导数波动方程在刻画声波的黏性耗散研究方面有了较深入的进展,然而引起声波衰减的因素还有其他情况.例如,反射、散射等.本文讨论的声波模型主要考虑的是声黏性吸收衰减.考虑到声波在传播过程中对空间位置的依赖性和历史的记忆性,如何利用分数阶导数建立散射、反射等引起的衰减声波控制方程是未来的一个研究课题.
目前,研究声波在多孔介质中传播的问题时,主要依赖于Johnson-Koplik-Dashen (JKD)模型.该模型中包含较多的参数,考虑到分数阶导数建模的优势在于控制方程的参数少、形式简单,如何对传统的JKD模型进行优化或者建立等效模型也是一个值得研究的课题.
分数阶导数算子全局相关的性质,会导致在数值求解分数阶导数波动方程时,计算成本和存储量很高.分形导数作为一个局部算子,目前已被成功用于模拟扩散和阻尼振动过程.发展相应的分形导数波动方程可以大大降低仿真成本.
| 1 | 陈文, 孙洪广, 李西成. 力学与工程问题的分数阶导数建模 . 北京: 科学出版社, 2010. ( Chen Wen, Sun Hongguang, Li Xicheng. Fractional Derivative Modeling in Mechanical and Engineering Problems . Beijing: Science Press, 2010. (in Chinese) ) |
| 2 | 庞国飞, 陈文, 张晓棣, 等. 复杂介质中扩散和耗散行为的分数阶导数唯象建模. 应用数学和力学, 2015, 36 (11) : 1117-1134. ( Pang Guofei, Chen Wen, Zhang Xiaodi, et al. Fractional differential phenomenological modeling for diffusion and dissipation behaviors of complex media. Applied Mathematics and Mechanics, 2015, 36 (11) : 1117-1134. (in Chinese) ) |
| 3 | Foster FS, Hunt JW. Transmission of ultrasound beams through human tissue-focussing and attenuation studies. Ultrasound in Medicine & Biology, 1979, 5 (3) : 257-268. |
| 4 | D'Astous FT, Foster FS. Frequency dependence of ultrasound attenuation and backscatter in breast tissue. Ultrasound in Medicine & Biology, 1986, 12 (10) : 795-808. |
| 5 | Lin T, Ophir J, Potter G. Frequency-dependent ultrasonic differentiation of normal and diffusely diseased liver. The Journal of the Acoustical Society of America, 1987, 82 (4) : 1131-1138. DOI: 10.1121/1.395303. |
| 6 | He P. Simulation of ultrasound pulse propagation in lossy media obeying a frequency power law. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1998, 45 (1) : 114-125. DOI: 10.1109/58.646916. |
| 7 | Duck FA. Physical Properties of Tissues:A Comprehensive Reference Book . New York: Academic Press, 2013. |
| 8 | Szabo TL, Wu J. A model for longitudinal and shear wave propagation in viscoelastic media. The Journal of the Acoustical Society of America, 2000, 107 (5) : 2437-2446. DOI: 10.1121/1.428630. |
| 9 | Sams MS, Neep JP, Worthington MH, et al. The measurement of velocity dispersion and frequency-dependent intrinsic attenuation in sedimentary rocks. Geophysics, 1997, 62 (5) : 1456-1464. DOI: 10.1190/1.1444249. |
| 10 | Blackstock DT. Transient solution for sound radiated into a viscous fluid. The Journal of the Acoustical Society of America, 1967, 41 (5) : 1312-1319. DOI: 10.1121/1.1910474. |
| 11 | Szabo TL. Time domain wave equations for lossy media obeying a frequency power law. The Journal of the Acoustical Society of America, 1994, 96 (1) : 491-500. DOI: 10.1121/1.410434. |
| 12 | Szabo TL. Causal theories and data for acoustic attenuation obeying a frequency power law. The Journal of the Acoustical Society of America, 1995, 97 (1) : 14-24. DOI: 10.1121/1.412332. |
| 13 | Pritz T. Frequency power law of material damping. Applied Acoustics, 2004, 65 (11) : 1027-1036. DOI: 10.1016/j.apacoust.2004.06.001. |
| 14 | Waters KR, Hughes MS, Mobley J, et al. On the applicability of Kramers-Krönig relations for ultrasonic attenuation obeying a frequency power law. The Journal of the Acoustical Society of America, 2000, 108 (2) : 556-563. DOI: 10.1121/1.429586. |
| 15 | Waters KR, Hughes MS, Mobley J, et al. Di erential forms of the Kramers-Kronig dispersion relations. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2003, 50 (1) : 68-76. DOI: 10.1109/TUFFC.2003.1176526. |
| 16 | Waters KR, Mobley J, Miller JG. Causality-imposed (Kramers-Kronig) relationships between attenuation and dispersion. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2005, 52 (5) : 822-823. DOI: 10.1109/TUFFC.2005.1503968. |
| 17 | Horton Sr CW. Dispersion relationships in sediments and sea water. The Journal of the Acoustical Society of America, 1974, 55 (3) : 547-549. DOI: 10.1121/1.1914534. |
| 18 | Horton Sr CW. Comment on Kramers-Kronig relationship between ultrasonic attenuation and phase velocity. The Journal of the Acoustical Society of America, 1981, 70 (4) : 1182. |
| 19 | Nachman AI, Smith Ⅲ JF, Waag RC. An equation for acoustic propagation in inhomogeneous media with relaxation losses. The Journal of the Acoustical Society of America, 1990, 88 (3) : 1584-1595. DOI: 10.1121/1.400317. |
| 20 | Lu JF, Hanyga A. Numerical modelling method for wave propagation in a linear viscoelastic medium with singular memory. Geophysical Journal International, 2004, 159 (2) : 688-702. DOI: 10.1111/gji.2004.159.issue-2. |
| 21 | Ginter S. Numerical simulation of ultrasound-thermotherapy combining nonlinear wave propagation with broadband soft-tissue absorption. Ultrasonics, 2000, 37 (10) : 693-696. DOI: 10.1016/S0041-624X(00)00012-3. |
| 22 | Rossikhin YA, Shitikova MV. Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids. Applied Mechanics Reviews, 1997, 50 (1) : 15-67. DOI: 10.1115/1.3101682. |
| 23 | Yuan X, Borup D, Wiskin J, et al. Simulation of acoustic wave propagation in dispersive media with relaxation losses by using FDTD method with PML absorbing boundary condition. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 1999, 46 (1) : 14-23. DOI: 10.1109/58.741419. |
| 24 | Podlubny I. Fractional Di erential Equations:An Introduction to Fractional Derivatives, Fractional Di erential Equations, to Methods of Their Solution and Some of Their Applications . New York: Academic Press, 1998. |
| 25 | Mainardi F. Fractional Calculus and Waves in Linear Viscoelasticity:An Introduction to Mathematical Models . Singapore: World Scientific, 2010. |
| 26 | Metzler R, Klafter J. The random walk's guide to anomalous diffusion:a fractional dynamics approach. Physics Reports, 2000, 339 (1) : 1-77. DOI: 10.1016/S0370-1573(00)00070-3. |
| 27 | Sokolov IM, Chechkin AV, Klafter J. Distributed-order fractional kinetics. arXiv preprint cond-mat/0401146, 2004 |
| 28 | Hanyga A. An anisotropic Cole-Cole model of seismic attenuation. Journal of Computational Acoustics, 2003, 11 (1) : 75-90. DOI: 10.1142/S0218396X03001845. |
| 29 | Chen W, Holm S. Modified Szabo's wave equation models for lossy media obeying frequency power law. The Journal of the Acoustical Society of America, 2003, 114 (5) : 2570-2574. DOI: 10.1121/1.1621392. |
| 30 | Liebler M, GinterS, Dreyer T, et al. Full wave modeling of therapeutic ultrasound:Efficient time-domain implementation of the frequency power-law attenuation. The Journal of the Acoustical Society of America, 2004, 116 (5) : 2742-2750. DOI: 10.1121/1.1798355. |
| 31 | Chen W, Zhang X, Cai X. A study on modified Szabo's wave equation modeling of frequency-dependent dissipation in ultrasonic medical imaging. Physica Scripta, 2009 (T136) : 014014. |
| 32 | Zhang X, Chen W, Zhang C. Modified szabo's wave equation for arbitrarily frequency-dependent viscous dissipation in soft matter with applications to 3D ultrasonic imaging. Acta Mechanica Solida Sinica, 2012, 25 (5) : 510-519. DOI: 10.1016/S0894-9166(12)60045-7. |
| 33 | Kelly JF, McGough RJ, Meerschaert MM. Analytical time-domain Green's functions for power-law media. The Journal of the Acoustical Society of America, 2008, 124 (5) : 2861-2872. DOI: 10.1121/1.2977669. |
| 34 | Meerschaert MM, Sikorskii A. Stochastic Models for Fractional Calculus . Berlin: Walter de Gruyterc, 2012. |
| 35 | Wismer MG. Finite element analysis of broadband acoustic pulses through inhomogenous media with power law attenuation. The Journal of the Acoustical Society of America, 2006, 120 (6) : 3493-3502. DOI: 10.1121/1.2354032. |
| 36 | Ochmann M, Makarov S. Representation of the absorption of nonlinear waves by fractional derivatives. The Journal of the Acoustical Society of America, 1993, 94 (6) : 3392-3399. DOI: 10.1121/1.407192. |
| 37 | Coppens AB, Sanders JV. Finite-amplitude standing waves in rigidwalled tubes. The Journal of the Acoustical Society of America, 1968, 43 (3) : 516-529. DOI: 10.1121/1.1910860. |
| 38 | Caputo M, Mainardi F. A new dissipation model based on memory mechanism. Pure and Applied Geophysics, 1971, 91 (1) : 134-147. DOI: 10.1007/BF00879562. |
| 39 | Rossikhin YA. Reflections on two parallel ways in the progress of fractional calculus in mechanics of solids. Applied Mechanics Reviews, 2010, 63 (1) : 010701. DOI: 10.1115/1.4000246. |
| 40 | Rossikhin YA, Shitikova MV. Application of fractional calculus for dynamic problems of solid mechanics:novel trends and recent results. Applied Mechanics Reviews, 2010, 63 (1) : 010801. DOI: 10.1115/1.4000563. |
| 41 | 殷德顺, 任俊娟, 和成亮, 等. 一种新的岩土流变模型元件. 岩石力学与工程学报, 2007, 26 (9) : 1899-1903. ( Yin Deshun, Ren Junjuan, He Chengliang, et al. A new rheological model element for geomaterials. Chinese Journal of Rock Mechanics and Engineering, 2007, 26 (9) : 1899-1903. (in Chinese) ) |
| 42 | Nutting PG. A new general law of deformation. Journal of the Franklin Institute, 1921, 191 (5) : 679-685. DOI: 10.1016/S0016-0032(21)90171-6. |
| 43 | Blair GWS, Caffyn JE. An application of the theory of quasiproperties to the treatment of anomalous strain-stress relations. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1949, 40 (300) : 80-94. DOI: 10.1080/14786444908561213. |
| 44 | Caputo M. Linear models of dissipation whose Q is almost frequency independent-Ⅱ. Geophysical Journal International, 1967, 13 (5) : 529-539. DOI: 10.1111/j.1365-246X.1967.tb02303.x. |
| 45 | Holm S, Sinkus R. A unifying fractional wave equation for compressional and shear waves. The Journal of the Acoustical Society of America, 2010, 127 (1) : 542-548. DOI: 10.1121/1.3268508. |
| 46 | Holm S, Näsholm SP, Prieur F, et al. Deriving fractional acoustic wave equations from mechanical and thermal constitutive equations. Computers & Mathematics with Applications, 2013, 66 (5) : 621-629. |
| 47 | Holm S, Näsholm SP. A causal and fractional all-frequency wave equation for lossy media. The Journal of the Acoustical Society of America, 2011, 130 (4) : 2195-2202. DOI: 10.1121/1.3631626. |
| 48 | Holm S, Näsholm SP. Comparison of fractional wave equations for power law attenuation in ultrasound and elastography. Ultrasound in Medicine & Biology, 2014, 40 (4) : 695-703. |
| 49 | Caputo M, Carcione JM, Cavallini F. Wave simulation in biologic media based on the Kelvin-Voigt fractional-derivative stress-strain relation. Ultrasound in Medicine & Biology, 2011, 37 (6) : 996-1004. |
| 50 | Zhao X, McGough RJ. Time-domain comparisons of power law attenuation in causal and noncausal time-fractional wave equations. The Journal of the Acoustical Society of America, 2016, 139 (5) : 3021-3031. DOI: 10.1121/1.4949539. |
| 51 | Konjik S, Oparnica L, Zorica D. Waves in fractional Zener type viscoelastic media. Journal of Mathematical Analysis and Applications, 2010, 365 (1) : 259-268. DOI: 10.1016/j.jmaa.2009.10.043. |
| 52 | Näsholm SP, Holm S. On a fractional Zener elastic wave equation. Fractional Calculus and Applied Analysis, 2013, 16 (1) : 26-50. |
| 53 | Näsholm SP, Holm S. Linking multiple relaxation, power-law attenuation, and fractional wave equations. The Journal of the Acoustical Society of America, 2011, 130 (5) : 3038-3045. DOI: 10.1121/1.3641457. |
| 54 | Buckingham MJ. Theory of acoustic attenuation, dispersion, and pulse propagation in unconsolidated granular materials including marine sediments. The Journal of the Acoustical Society of America, 1997, 102 (5) : 2579-2596. DOI: 10.1121/1.420313. |
| 55 | Buckingham MJ. Wave propagation, stress relaxation, and grain-tograin shearing in saturated, unconsolidated marine sediments. The Journal of the Acoustical Society of America, 2000, 108 (6) : 2796-2815. DOI: 10.1121/1.1322018. |
| 56 | Pandey V, Holm S. Connecting the grain-shearing mechanism of wave propagation in marine sediments to fractional calculus. arXiv preprint arXiv:1512.05336, 2015 |
| 57 | Prieur F, Holm S. Nonlinear acoustic wave equations with fractional loss operators. The Journal of the Acoustical Society of America, 2011, 130 (3) : 1125-1132. DOI: 10.1121/1.3614550. |
| 58 | Chen W, Holm S. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency power-law dependency. The Journal of the Acoustical Society of America, 2004, 115 (4) : 1424-1430. DOI: 10.1121/1.1646399. |
| 59 | 张晓棣.医学超声和振动中频率依赖耗散的分数阶导数模型研究.[博士论文].南京:河海大学, 2012 ( Zhang Xiaodi. A study on fractional derivative models of frequency dependent dissipative behaviors in medical ultrasound and vibration.[PhD Thesis]. Nanjing, Hohai University, 2012(in Chinese) ) |
| 60 | TreebyBE, Cox BT. Modeling power law absorption and dispersion for acoustic propagation using the fractional Laplacian. The Journal of the Acoustical Society of America, 2010, 127 (5) : 2741-2748. DOI: 10.1121/1.3377056. |
| 61 | 庞国飞.非局部声波耗散和阻尼振动的空间分数阶微积分黏弹性本构建模研究.[博士论文].南京:河海大学, 2015 ( Pang Guofei. Space-fractional calculus viscoelastic constitutive models for describing non-local acoustic wave dissipation and vibration damping.[PhD Thesis]. Nanjing:Hohai University, 2015(in Chinese) ) |
| 62 | TreebyBE, Cox BT. Modeling power law absorption and dispersion in viscoelastic solids using a split-field and the fractional Laplaciana. The Journal of the Acoustical Society of America, 2014, 136 (4) : 1499-1510. DOI: 10.1121/1.4894790. |
| 63 | Treeby BE, Cox BT. k-Wave:MATLAB toolbox for the simulation and reconstruction of photoacoustic wave fields. Journal of Biomedical Optics, 2010, 15 (2) : 021314-021314. DOI: 10.1117/1.3360308. |
| 64 | Carcione JM, Cavallini F, Mainardi F, et al. Time-domain modeling of constant-Q seismic waves using fractional derivatives. Pure and Applied Geophysics, 2002, 159 (7-8) : 1719-1736. DOI: 10.1007/s00024-002-8705-z. |
| 65 | Carcione JM. Theory and modeling of constant-Q P-and S-waves using fractional time derivatives. Geophysics, 2008, 74 (4) : T1-T11. |
| 66 | Carcione JM. A generalization of the fourier pseudospectral method. Geophysics, 2010, 75 (6) : A53-A56. DOI: 10.1190/1.3509472. |
| 67 | Zhu T. Time-reverse modelling of acoustic wave propagation in attenuating media. Geophysical Journal International, 2014, 197 (1) : 483-494. DOI: 10.1093/gji/ggt519. |
| 68 | Zhu T, Harris JM. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians. Geophysics, 2014, 79 (3) : T105-T116. DOI: 10.1190/geo2013-0245.1. |
| 69 | 汪越胜, 于桂兰, 章梓茂, 等. 复杂界面(界面层)条件下的弹性波传播问题研究综述. 力学进展, 2000, 30 (3) : 378-390. ( Wang Yuesheng, Yu Guilan, Zhang Zimao, et al. Review on elastic wave propagation under complex interface (interface layer) conditions. Advances in Mechanics, 2000, 30 (3) : 378-390. (in Chinese) ) |
| 70 | Meerschaert MM, McGough RJ. Attenuated fractional wave equations with anisotropy. Journal of Vibration and Acoustics, 2014, 136 (5) : 050902. |
| 71 | Meerschaert MM, Straka P, Zhou Y, et al. Stochastic solution to a time-fractional attenuated wave equation. Nonlinear Dynamics, 2012, 70 (2) : 1273-1281. DOI: 10.1007/s11071-012-0532-x. |
| 72 | Kilbas AA, Marichev OI, Samko SG. Fractional Integral and Derivatives (Theory and Applications). Gordon and Breach, Switzerland, 1993, 1 (1993) : 1. |
| 73 | Delany ME, Bazley EN. Acoustical properties of fibrous absorbent materials. Applied Acoustics, 1970, 3 (2) : 105-116. DOI: 10.1016/0003-682X(70)90031-9. |
| 74 | Chen W, Hu S, Cai W. A causal fractional derivative model for acoustic wave propagation in lossy media. Archive of Applied Mechanics, 2016, 86 (3) : 529-539. DOI: 10.1007/s00419-015-1043-2. |
| 75 | 胡帅.多孔材料的振动和黏性波耗散的分数阶导数建模.[博士论文].南京:河海大学, 2013 ( Hu Shuai. Fractional derivative modeling for vibration and viscous wave dissipation of porous material.[PhD Thesis]. Nanjing:Hohai University, 2013(in Chinese) ) |
| 76 | Johnson DL, Koplik J, Dashen R. Theory of dynamic permeability and tortuosity in fluid-saturated porous media. Journal of Fluid Mechanics, 1987, 176 : 379-402. DOI: 10.1017/S0022112087000727. |
| 77 | Allard JF, Champoux Y. New empirical equations for sound propagation in rigid frame fibrous materials. The Journal of the Acoustical Society of America, 1992, 91 (6) : 3346-3353. DOI: 10.1121/1.402824. |
| 78 | Fellah ZEA, Depollier C. Transient acoustic wave propagation in rigid porous media:a time-domain approach. The Journal of the Acoustical Society of America, 2000, 107 (2) : 683-688. DOI: 10.1121/1.428250. |
| 79 | Fellah ZE A, Fellah M, Lauriks W, et al. Direct and inverse scattering of transient acoustic waves by a slab of rigid porous material. The Journal of the Acoustical Society of America, 2003, 113 (1) : 61-72. DOI: 10.1121/1.1528592. |
| 80 | Fellah ZEA, Berger S, Lauriks W, et al. Measuring the porosity and the tortuosity of porous materials via reflected waves at oblique incidence. The Journal of the Acoustical Society of America, 2003, 113 (5) : 2424-2433. DOI: 10.1121/1.1567275. |
| 81 | Fellah ZEA, Depollier C, Berger S, et al. Determination of transport parameters in air-saturated porous materials via reflected ultrasonic waves. The Journal of the Acoustical Society of America, 2003, 114 (5) : 2561-2569. DOI: 10.1121/1.1621393. |
| 82 | Fellah ZEA, Chapelon JY, Berger S, et al. Ultrasonic wave propagation in human cancellous bone:Application of Biot theory. The Journal of the Acoustical Society of America, 2004, 116 (1) : 61-73. DOI: 10.1121/1.1755239. |
| 83 | Fellah ZEA, Sebaa N, Fellah M, et al. Ultrasonic characterization of air-saturated double-layered porous media in time domain. Journal of Applied Physics, 2010, 108 (1) : 014909. DOI: 10.1063/1.3456443. |
| 84 | Hanyga A, Lu JF. Wave field simulation for heterogeneous transversely isotropic porous media with the JKD dynamic permeability. Computational Mechanics, 2005, 36 (3) : 196-208. DOI: 10.1007/s00466-004-0652-3. |
| 85 | Lu JF, Hanyga A. Wave field simulation for heterogeneous porous media with singular memory drag force. Journal of Computational Physics, 2005, 208 (2) : 651-674. DOI: 10.1016/j.jcp.2005.03.008. |
| 86 | Blanc E. Time-domain numerical modeling of poroelastic waves:the Biot-JKD model with fractional derivatives.[PhD thesis]. Marseille:Aix-Marseille Université. 2014 |
| 87 | Blanc E, Chiavassa G, Lombard B. Wave simulation in 2D heterogeneous transversely isotropic porous media with fractional attenuation:a Cartesian grid approach. Journal of Computational Physics, 2014, 275 : 118-142. DOI: 10.1016/j.jcp.2014.07.002. |
| 88 | Blanc E, Chiavassa G, Lombard B. Biot-JKD model:simulation of 1D transient poroelastic waves with fractional derivatives. Journal of Computational Physics, 2013, 237 : 1-20. DOI: 10.1016/j.jcp.2012.12.003. |
| 89 | Chen W. Lévy stable distribution and[0, 2] power law dependence of acoustic absorption on frequency in various lossy media. Chinese Physics Letters, 2005, 22 (10) : 2601. DOI: 10.1088/0256-307X/22/10/040. |
| 90 | Saichev AI, Zaslavsky GM. Fractional kinetic equations:solutions and applications. Chaos:An Interdisciplinary Journal of Nonlinear Science, 1997, 7 (4) : 753-764. DOI: 10.1063/1.166272. |
| 91 | Mandelbrot BB.The fractal geometry of nature. Macmillan. 1982 |
| 92 | Sato KI.Lévy Processes and Infinitely Divisible Distributions. Cambridge university Press, 1999 |
| 93 | Mandelbrot BB, Van Ness JW. Fractional Brownian motions, fractional noises and applications. SIAM Review, 1968, 10 (4) : 422-437. DOI: 10.1137/1010093. |
| 94 | Berry MV. Di ractals. Journal of Physics A:Mathematical and General, 1979, 12 (6) : 781. DOI: 10.1088/0305-4470/12/6/008. |
| 95 | Wyss W. Fractional noise. Foundations of Physics Letters, 1991, 4 (3) : 235-246. DOI: 10.1007/BF00665755. |
| 96 | Tatom FB. The relationship between fractional calculus and fractals. Fractals, 1995, 3 (1) : 217-229. DOI: 10.1142/S0218348X95000175. |
| 97 | Yao K, Su WY, Zhou SP. On the connection between the order of fractional calculus and the dimensions of a fractal function. Chaos, Solitons & Fractals, 2005, 23 (2) : 621-629. |
| 98 | Liang YS, Su WY. The relationship between the fractal dimensions of a type of fractal functions and the order of their fractional calculus. Chaos, Solitons & Fractals, 2007, 34 (3) : 682-692. |
| 99 | Liang YS, Su WY. Connection between the order of fractional calculus and fractional dimensions of a type of fractal functions. Analysis in Theory and Applications, 2007, 23 (4) : 354-362. DOI: 10.1007/s10496-007-0354-8. |
| 100 | Henry BI, Wearne SL. Fractional reaction-diffusion. Physica A:Statistical Mechanics and its Applications, 2000, 276 (3) : 448-455. |