2. 大连理工大学工业装备结构分析国家重点实验室, 大连 116024
3. 大连理工大学航空航天学院, 大连 116024
随着研究人员广泛借助计算机进行系统设计和仿真,更多的人开始注意到灵敏度分析的作用. 灵敏度分析是计算系统目标输出量关于设计参数的导数,其在产品设计[1-3]、结构优化[4-6]、误差估计[7-9]和量化不确定值[10]等领域有着重要的应用. 在求解混沌系统的长时间平均输出量(比如湍流流场的平均气动力,大气的平均温度)关于系统设计参数的灵敏度时,由于非线性系统对初值的敏感性,传统的数值方法已经不能适用[11]. 为求解混沌系统的灵敏度,Lea等[11-12]首先提出了总体伴随法,这种方法将伴随法应用到大量可能的状态轨迹上,然后将所得的导数取平均值. 由于这种算法需要构造很多猜测的状态轨迹,使得这种算法即便是计算像洛伦兹系统这样简单的对象都需要很大的计算量. Thuburn[13]介绍了一种通过求解Fokker-Planck方程的伴随量计算气候灵敏度的方法. 这种方法需要将气候模型描述为一个满足Fokker-Planck方程的光滑的概率密度分布函数,而这种气候模型通常增加了Fokker-Planck方程的耗散,因此可能会导致结果产生误差. Blonigan等[14]提出一种密度伴随法,通过在吸引子流形中求解系统的动力学方程及其伴随方程来计算混沌系统的灵敏度,但是这种方法的计算量非常大. 此外,研究人员还利用波动耗散理论进行灵敏度分析,并提出多种基于该理论的算法[15-16],但是它们都要求系统满足一定的假设条件,限制了这些方法的使用范围.
动力系统理论为人类理解和探索复杂多变的世界提供了一个强大的数学工具[17],伪轨跟踪(pseudo-trajectory shadowing)理论作为动力系统理论中一个重要组成部分近些年得到了快速发展[18-21]. Soldatenko等[22]利用基于伪轨跟踪理论的方法计算了数值天气预报中变分数据同化问题的灵敏度. Wang等[23-24]针对混沌系统灵敏度分析中的病态初值问题,基于伪轨跟踪理论提出一种最小二乘跟踪(least squares shadowing)方法. 这种方法可以在任意给定的参考轨迹附近,确定一条设计参数有微小变化后的跟踪轨迹. 最小二乘跟踪方法在求解跟踪轨迹时对初值没有要求,因此这种基于最小二乘跟踪的非线性系统灵敏度分析是一种良态初值问题. 基于最小二乘跟踪方法,Blonigan等[25-26]计算了均匀各向同性湍流和改进的Kuramoto-Sivashinsky方程关于设计参数的灵敏度.
Wang 等[24]在求解非线性的最小二乘跟踪问题时,首先通过繁琐复杂的线性化过程将其转化为线性最小二乘跟踪问题,然后通过求解离散的带有线性约束的最小二乘问题得到最优跟踪轨迹. 本文把非线性的最小二乘跟踪问题看作非线性最优控制问题处理,采用一种基于对偶变量变分原理的算法,将离散区间两端的状态变量作为独立变量,通过求解非线性方程组得到系统的最优跟踪轨迹.
1 最小二乘跟踪问题 1.1 跟踪引理定义一个连续非线性系统,其动力学方程由如下常微分方程描述
| $ \dfrac{d { x}(t)}{d t} = { f}({ x}(t),s) $ | (1) |
其中${ x}(t)$为状态变量,$s$表示设计参数. 令$d > 0$,$r$为距离函数,对于一个状态轨迹${ x}_d (t)$,如果满足
| $ R \Big(\dfrac{d{ x}_d (t)}{d t},{ f}({ x}_d (t),s)\Big ) < d ,0 ≤ t ≤ T $ | (2) |
则称${ x}_d (t)$为动力系统的一个$d$伪轨($d$-pseudotrajec- tory).这种伪轨的出现主要是由于数值计算时的舍入误差和算法误差等原因造成的. 实际上,$d$ 伪轨是与动力系统真实轨迹距离为$d$的系统的近似解,因此,在每一条$d$ 伪轨的附近,一定存在一条系统的精确轨迹,而且该精确轨迹一致的接近于$d$ 伪轨.这种跟踪性可通过跟踪引理[27-28]给出. 对于一个连续动力系统,跟踪引理可描述为:对于任意$\varepsilon > 0$,存在$d > 0$,在每个满足式(2)的$d$ 伪轨${ x}_d (t)$附近,都存在一条真实轨迹${ x}(t)$和一个单调递增的时间变换函数$\tau (t)$,使得$r({ x} (\tau (t)),{ x}_d (t)) < \varepsilon ,\left| {1 - \dfrac{d\tau }{d t}} \right| < \varepsilon $,并且满足$\dfrac{d{ x} (\tau (t))}{d\tau } = { f}({ x} (\tau (t)),s),0 ≤ t ≤ T$.
1.2 最小二乘跟踪如果${ x}_r (t;s)$为一条设计参数为$s$时动力系统的精确轨迹,那么对于设计参数为$s + \delta s$的动力系统,${ x}_r (t;s)$可以认为是其一条$d$ 伪轨,$d = $ $\sup \Big (\left\| {\dfrac{\partial { f}(x,s)}{\partial s}\delta s} \right\|_2 \Big )$. 根据跟踪引理可知,在伪轨 ${ x}_r (t;s)$附近,肯定存在着设计参数为$s + \delta s$的动力系统的精确轨迹${ x}(t;s + \delta s)$,该轨迹可由如下的最优问题确定
| $\begin{align} & \underset{\tau ,x}{\mathop{\min }}\,\frac{1}{T}\int_{0}^{T}{[}\left\| x(\tau (t);s+\delta s)-{{x}_{r}}(t;s) \right\|_{2}^{2}+{{\alpha }^{2}}{{(\frac{\text{d}\tau }{\text{d}t}-1)}^{2}}]\text{d}t \\ & \text{s}.\text{t}.\frac{\text{d}x}{\text{d}\tau }=f(x(\tau (t)),s+\delta s) \\ \end{align}$ | (3) |
其中$\delta s$为设计参数的微小增量,$\alpha $为加权系数,而$\alpha $的选择应使积分括号里的两项有相似的量级. 这种带有约束的最优问题被称为最小二乘跟踪问题,其解表示为$x_{\rm lss}(t;s + \delta s)$和${{\tau }_{\text{lss}}}(t;s+\delta s)$,分别为令状态轨迹最接近于参考轨迹的动力学方程解和时间变换.
2 对偶变量变分方法在式(3)描述的非线性最小二乘跟踪问题中,设计参数$s$为已知量,若将$\tau $视为控制输入,则非线性最小二乘跟踪问题可以作为非线性最优控制问题来处理,即有一非线性系统,其动力学方程为
| $ \dfrac{d{ x} (t)}{d t} = { f}({ x} (t),\tau (t),t)$ | (4) |
状态轨迹优化的目标函数为
| $ J = \int_0^T \varPhi ( { x} (t),\tau (t),t) d t $ | (5) |
其中
| $ \varPhi = \left\| {{ x} (\tau (t),s + \delta s) - { x}_r (t,s)} \right\|_2^2 + \alpha ^2 \Big (\dfrac{d\tau }{d t}-1\Big )^2 $ | (6) |
对于如上描述的非线性最优控制问题,本文采用一种基于对偶变量变分原理的数值算法求解. 由于该最优问题存在等式约束,引入拉格朗日乘子${\lambda }$,其哈密顿函数可表示为
| $ H({ x},{\lambda},\tau ,t) = \varPhi ({ x} (t),\tau (t),t) + {\lambda }^{\rm T} { f}({ x}(t),\tau (t),t)$ | (7) |
根据最优控制输入存在的必要条件可知
| $ \dfrac{\partial H({ x},{\lambda},\tau ,t)}{\partial \tau } = 0 $ | (8) |
则控制输入$\tau $可以表示为关于状态变量${ x}$和协态变量$\lambda $的函数,即$\tau (t) = g(x(t),\lambda(t))$. 进而哈密顿函数可以表示为关于对偶变量${ x}$和${\lambda} $的函数
| $ H({ x},{ \lambda},g({ x},{ \lambda} ),t) = \varPhi ({ x}(t),g({ x},{ \lambda} ),t)+\\ { \lambda}^{\rm T}{ f}({ x}(t),g({ x},{ \lambda} ),t)$ | (9) |
在时间区段$(0,\eta )$内的作用量$S$定义为
| $ S = \int_0^\eta [{ \lambda}^{\rm T}\dot { x} - H({ x},{ \lambda} )] d t $ | (10) |
令作用量$S$取驻值,根据对偶变量变分原理[29-30]可知
| $ \delta S = \int_0^\eta (\delta { x})^{\rm T} \Big ( - \dot{ \lambda } - \dfrac{\partial H}{\partial { x}} \Big ) d t +\\ \int_0^\eta (\delta { \lambda} )^ {\rm T} \Big(\dot { x} - \dfrac{\partial H} {\partial { \lambda} } \Big) d t + \left. {{ \lambda}^{\rm T}\delta { x}} \right|_0^\eta = 0 $ | (11) |
而最优控制输入应满足哈密顿正则方程,即
| $\left. \begin{array}{*{35}{l}} \dot{x}=\frac{\partial H}{\partial \lambda } \\ \dot{\lambda }=-\frac{\partial H}{\partial x} \\ \end{array} \right\}$ | (12) |
将式(12)代入式(11),可得到作用量$S$与两端状态变量$({ x}_0 ,{ x}_\eta )$的关系为
| $ d S ={ \lambda}_\eta ^{\rm T} d { x}_\eta - { \lambda}_0^{\rm T} d { x}_0 $ | (13) |
由式(13)可知,在时间区段$(0,\eta )$内的作用量$S$只与两端的状态变量有关. 基于式(13),以区间两端状态变量为独立变量,可以推导出求解非线性最优控制问题的数值算法.
将整个非线性最优控制问题的求解区域等分成$L$个子区间,每个子区间的长度为$\eta $.在第$j$个子区间内,分别采用等间距Lagrange插值多项式近似区间内的状态变量和协态变量. 第$j$个子区间两端的状态变量表示为${ x}_{j - 1} $和${ x}_j $,子区间内插值点的状态变量组成的向量表示为$\bar{ x}_j $,子区间内插值点的协态变量组成的向量表示为$\bar { \lambda }_j $,由于子区间两端的协态变量可以通过两端的状态变量表示,故其不作为插值点使用.将近似的状态变量和协态变量代入式(9),可得到第$j$个子区间内的作用量$S$的近似表示
| $ \bar {S}_j ({ x}_{j - 1} ,{ x}_j ,\bar{ x}_j ,\bar { \lambda }_j ) = \int_0^\eta ({ \lambda}^{\rm T}\dot{ x} - H)_j d t $ | (14) |
由于在子区间内作用量只是两端状态变量的函数,结合式(13)可得如下等式
| $\dfrac{\partial \bar {S}_j ({ x}_{j - 1} ,{ x}_j ,\bar{ x}_j ,\bar{ \lambda }_j )}{\partial \bar{ x}_j } = 0 ,j = 1,2,\cdots ,L $ | (15) |
| $\dfrac{\partial \bar {S}_j ({ x}_{j - 1} ,{ x}_j ,\bar{ x}_j ,\bar{ \lambda }_j )}{\partial \bar { \lambda }_j } = 0 ,j = 1,2,\cdots ,L $ | (16) |
| $\dfrac{\partial \bar {S}_j ({ x}_{j - 1} ,{ x}_j ,\bar{ x}_j ,\bar{ \lambda }_j )}{\partial { x}_{j - 1} } + {\lambda}_{j - 1} = 0 ,j = 1,2,\cdots ,L $ | (17) |
| $\dfrac{\partial \bar {S}_j ({ x}_{j - 1} ,{ x}_j ,\bar{ x}_j ,\bar{ \lambda }_j )}{\partial { x}_j } - {\lambda}_j = 0 ,j = 1,2,\cdots ,L $ | (18) |
至此,非线性最优控制问题被转化为了求解一组非线性方程,其可通过MATLAB$^{\circledR}$中自带的工具箱解得.
3 应用算例考虑范德波振子(van der Pol oscillator)
| $ \dfrac{d^2x}{d t^2} = - x + \beta (1 - x^2)\dfrac{d x}{d t} $ | (19) |
的平均输出值$\bar {J}^{(T)}(\beta )$关于参数$\beta $的灵敏度分析问题. 令$x_1= x,x_2 = {d x} / { d t}$,则范德波振子重新描述为
| $\left. \begin{array}{*{35}{l}} {{{\dot{x}}}_{1}}={{x}_{2}} \\ {{{\dot{x}}}_{2}}=-{{x}_{1}}+\beta (1-x_{1}^{2}){{x}_{2}} \\ \end{array} \right\}$ | (20) |
令其平均输出为
| $ \bar {J}^{(T)} (\beta ) = \left( {\dfrac{1}{T}\int_0^T {x_2^8 (t;\beta ) d t} } \right)^{\tfrac{1}{8}} $ | (21) |
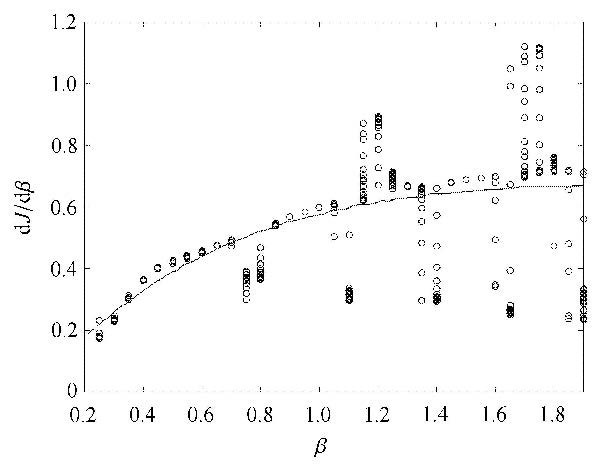
对于每个$\beta $,分别选取区间[0, 1]内的任意值作为$(x_1 ,x_2 )$在$t =0$时刻的值,然后采用有限差分法计算式(20)描述的初值问题,选取$t =50$的$(x_1,x_2 )$作为灵敏度分析的初值,以保证该初值在范德波振子的极限环上. 取$T=50$,通过有限差分法得到的系统灵敏度随参数$\beta $的变化趋势如图 1所示,图中实线为$T =5 000$时计算所得的灵敏度,该曲线可以作为灵敏度的理论值参考. 对于每个$\beta $值,对应的灵敏度分别以随机的初值计算20次. 由图 1可以看到,不同的初值得到的灵敏度差别很大,尤其是参数$\beta $较大时,这主要是由于非线性系统对初值非常敏感,此处处理的是一个病态初值问题.
|
图 1 有限差分法所得灵敏度:对于每个$\beta $值,灵敏度均以随机的初值计算20次,实线为理论值 Figure 1 Sensitivities estimated by finite difference: for each value of $\beta $,the sensitivity is computed 20 times with random initial value,the solid line is the theoretical values of sensitivities |
由最小二乘跟踪问题可知,对于任意一条给定的参考轨迹${ x}_{\rm r} (t;\beta )$,一定存在一条距其最近的跟踪轨迹${ x}_{\rm lss} (t;\beta + \delta \beta )$,这两条轨迹分别为设计参数为$\beta $和$\beta + \delta \beta $时系统的精确解,对应的系统平均输出分别表示为$\bar {J}_{\rm r}^{(T)} (\beta )$和$\bar {J}_{\rm lss}^{(\tau (T))} (\beta + \delta \beta )$. 则平均输出量关于$\beta $的灵敏度可表示为
| $ \dfrac{d\bar {J}^{(T)}(\beta )}{d\beta } = \dfrac{\bar {J}_{\rm lss}^{(\tau (T))} (\beta + \delta \beta ) - \bar {J}_{\rm r}^{(T)} (\beta )}{\delta \beta } $ | (22) |
由于跟踪轨迹的求解不要求与参考轨迹有相同的初值,无论参考轨迹的初值如何选择,都可以通过求解最小二乘跟踪问题得到一条最接近参考轨迹的解,因此这种基于最小二乘跟踪问题的非线性系统灵敏度分析方法对于初值的选择是不敏感的,是一种良态初值问题.
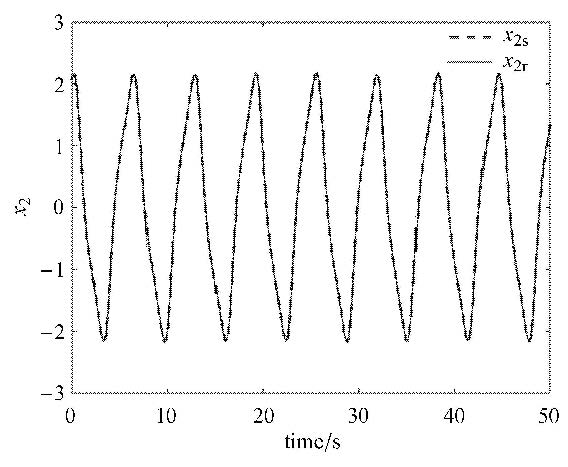
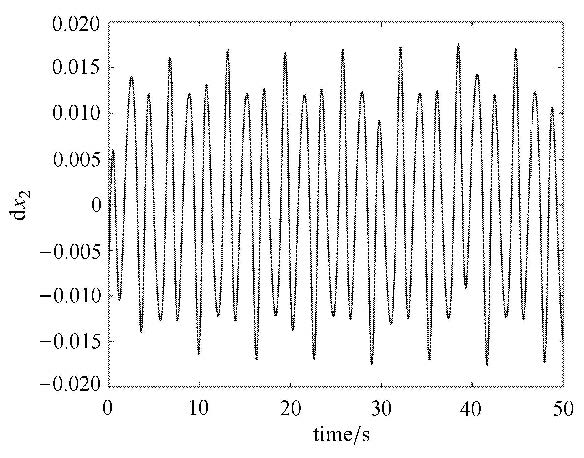
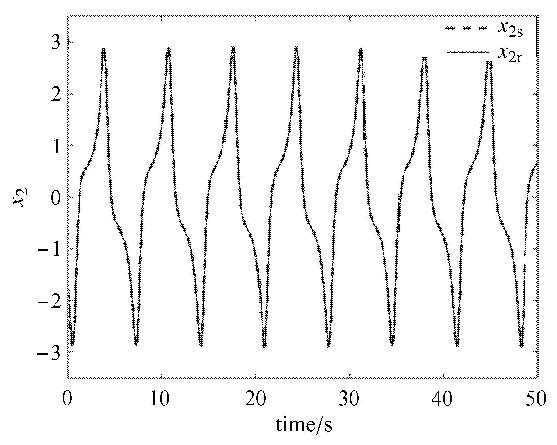
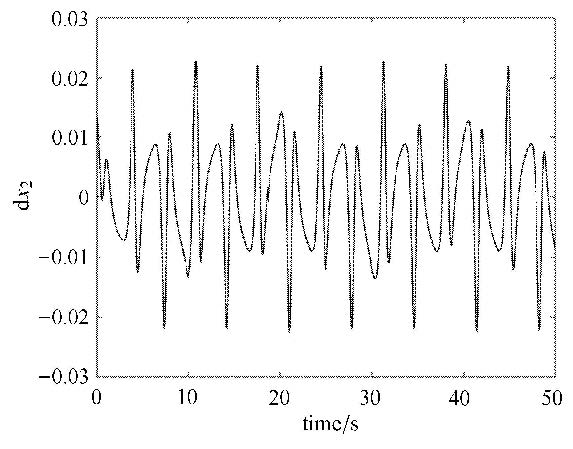
分别取$\beta = 0.4$和$\beta = 1.2$,令$\delta \beta = 0.02$,采用本文所提算法计算最小二乘跟踪问题.在计算跟踪轨迹时,若直接对长度为$T =50$的参考轨迹运用对偶变量变分算法,需要一次求解的非线性方程的数量是非常庞大的.为提高计算效率,长度为$T$的参考轨迹被平均分成了5段,从第一段开始逐段计算最优跟踪轨迹,前一段的终端值作为下一段的初值参与下一段跟踪轨迹优化. 图 2给出了$\beta = 0.4$时的参考轨迹和跟踪轨迹,两条轨迹的距离由图 3显示.从图 2和图 3中可以看到,跟踪轨迹与参考轨迹的距离保持在一个较小的范围之内,跟踪轨迹体现出良好的跟踪性. $\beta = 1.2$时的参考轨迹和跟踪轨迹如图 4所示,图 5给出了他们之间的距离. 由图 5可知,相比于$\beta =0.4$时的结果,参考轨迹和跟踪轨迹间的距离虽然有所增加,但仍然保持在一定的范围之内.
|
图 2 $\beta = 0.4$时的参考轨迹$x_{\rm 2r} $和跟踪轨迹$x_{\rm 2s} $ Figure 2 Reference trajectory $x_{\rm 2r} $and shadowing trajectory $x_{\rm 2s} $ for $\beta = 0.4$ |
|
图 3 $\beta = 0.4$时跟踪轨迹与参考轨迹间的距离 Figure 3 Distance between shadowing and reference trajectories for $\beta = 0.4$ |
|
图 4 $\beta = 1.2$时的参考轨迹$x_{\rm 2r} $和跟踪轨迹$x_{\rm 2s} $ Figure 4 Reference trajectory $x_{\rm 2r} $ and shadowing trajectory $x_{\rm 2s} $ for $\beta = 1.2$ |
|
图 5 $\beta = 1.2$时跟踪轨迹与参考轨迹间的距离 Figure 5 Distance between shadowing and reference trajectories for $\beta = 1.2$ |
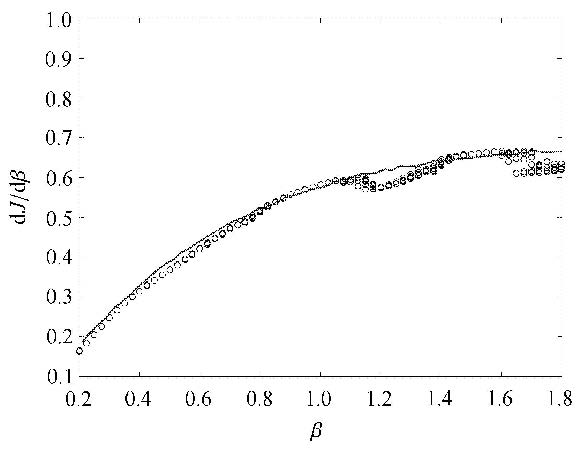
基于参考轨迹与跟踪轨迹的范德波振子灵敏度分析结果如图 6所示. 对于每个$\beta $值,其灵敏度同样计算20次,每次所用参考轨迹均通过求解随机的初值问题得到. 图中实线与图 1中的一样为灵敏度的理论值.由图 6可知,采用最小二乘跟踪方法得到的灵敏度与状态初值基本无关,当$\beta <1.1$时灵敏度分析结果精度较高,当$\beta >1.1$时灵敏度分析结果会出现一些偏差,但相比于由传统方法得到的结果,精度仍然提高很多.
|
图 6 最小二乘跟踪方法所得灵敏度:对于每个$\beta $值,均以随机的参考轨迹计算20次,实线为理论值 Figure 6 Sensitivities estimated by LSS: for each value of $\beta $,the sensitivity is computed 20 times with random reference trajectories,the solid line is the theoretical values of sensitivities |
针对非线性最小二乘跟踪问题,本文采用一种基于对偶变量变分原理的算法,把离散区间两端的状态变量作为独立变量,将非线性最小二乘跟踪问题转化为求解非线性方程组问题.该方法不需要对原非线性问题线性化,避免了复杂的线性化过程以及可能因此产生的误差.通过数值仿真算例可知,本文所提的方法适用于最小二乘跟踪问题,计算结果验证了范德波振子对参考轨迹的跟踪性;基于最小二乘跟踪的非线性动力系统灵敏度分析可以有效避免传统数值方法中的病态初值问题,得到更为准确的灵敏度分析结果.
| 1 |
Jameson A. Aerodynamic design via control theory.
Journal of Scientific Computing,1988, 3 (3) : 233-260.
DOI: 10.1007/BF01061285. ( 0) 0)
|
| 2 |
Reuther JJ, Jameson A, Alonso JJ, et al. Constrained multipoint aerodynamic shape optimization using an adjoint formulation and parallel computers, part 1.
Journal of Aircraft,1999, 36 (1) : 51-60.
DOI: 10.2514/2.2413. ( 0) 0)
|
| 3 |
Martins J, Alonso JJ, Reuther JJ. A coupled-adjoint sensitivity analysis method for high-fidelity aero-structural design.
Optimization and Engineering,2005, 6 (1) : 33-62.
DOI: 10.1023/B:OPTE.0000048536.47956.62. ( 0) 0)
|
| 4 |
罗阳军, 亢战, 邓子辰. 多工况下结构鲁棒性拓扑优化设计.
力学学报,2011, 43 (1) : 227-234.
( Luo Yangjun, Kang Zhan, Deng Zichen. Robust topology optimization design of structures with multiple load cases.
Chinese Journal of Theoretical and Applied Mechanics,2011, 43 (1) : 227-234.
(in Chinese) ) ( 0) 0)
|
| 5 |
顾元宪, 赵红兵, 陈飚松, 等. 热-应力耦合结构灵敏度分析方法.
力学学报,2001, 33 (5) : 685-691.
( Gu Yuanxian, Zhao Hongbing, Chen Biaosong, et al. Sensitivity analysis and design optimization of thermal-stress coupled structures.
Chinese Journal of Theoretical and Applied Mechanics,2001, 33 (5) : 685-691.
(in Chinese) ) ( 0) 0)
|
| 6 |
郭旭, 顾元宪, 赵康. 广义变分原理的结构形状优化伴随法灵敏度分析.
力学学报,2004, 36 (3) : 288-295.
( Guo Xu, Gu Yuanxian, Zhao Kang. Adjoint shape sensitivity analysis based on generalized variational principle.
Chinese Journal of Theoretical and Applied Mechanics,2004, 36 (3) : 288-295.
(in Chinese) ) ( 0) 0)
|
| 7 |
Giles MB, Süli E. Adjoint methods for PDEs:a posteriori error analysis and postprocessing by duality.
Acta Numerica,2002, 11 : 145-236.
( 0) 0)
|
| 8 |
Fidkowski KJ, Darmofal DL. Review of output-based error estimation and mesh adaptation in computational fluid dynamics.
AIAA journal,2011, 49 (4) : 673-694.
DOI: 10.2514/1.J050073. ( 0) 0)
|
| 9 |
杨杰, 张崎, 黄一. 结构可靠性灵敏度因子的一种新指标.
工程力学,2013, 30 (6) : 16-29.
( Yang Jie, Zhang Qi, Huang Yi. A new sensitivity factor for structural reliability.
Engineering Mechanics,2013, 30 (6) : 16-29.
(in Chinese) ) ( 0) 0)
|
| 10 |
Wang Q. Uncertainty quantification for unsteady fluid flow using adjoint-based approaches.[PhD Thesis]. Stanford:Stanford University, 2009
( 0) 0)
|
| 11 |
Lea DJ, Allen MR, Haine TWN. Sensitivity analysis of the climate of a chaotic system.
Tellus,2000, 52A : 523-532.
( 0) 0)
|
| 12 |
Eyink GL, Haine TWN, Lea DJ. Ruelle's linear response formula, ensemble adjoint schemes and Lévy flights.
Nonlinearity,2004, 17 (5) : 1867-1889.
DOI: 10.1088/0951-7715/17/5/016. ( 0) 0)
|
| 13 |
Thuburn J. Climate sensitivities via a Fokker-Planck adjoint approach.
Quarterly Journal of the Royal Meteorological Society,2005, 131 (605) : 73-92.
DOI: 10.1256/qj.04.46. ( 0) 0)
|
| 14 |
Bloningan PJ, Wang Q. Probability density adjoint for sensitivity analysis of the mean of chaos.
Journal of Computational Physics,2014, 270 : 660-686.
DOI: 10.1016/j.jcp.2014.04.027. ( 0) 0)
|
| 15 |
Abramov RV, Majda AJ. Blended response algorithms for linear fluctuation-dissipation for complex nonlinear dynamical systems.
Nonlinearity,2007, 20 (12) : 2793-2821.
DOI: 10.1088/0951-7715/20/12/004. ( 0) 0)
|
| 16 |
Cooper FC, Haynes PH. Climate sensitivity via a nonparametric fluctuation-dissipation theorem.
Journal of the Atmospheric Sciences,2011, 68 (5) : 937-953.
DOI: 10.1175/2010JAS3633.1. ( 0) 0)
|
| 17 |
Katok A, Hasselblatt B.
Introduction to the Modern Theory of Dynamical Systems. New York: Cambridge university press, 1997 .
( 0) 0)
|
| 18 |
杨润生. 伪轨跟踪与混沌.
数学学报,1996, 39 (3) : 382-386.
( Yang Runsheng. Pseudo-orbit-tracing and chaos.
Acta Mathematica Sinica,1996, 39 (3) : 382-386.
(in Chinese) ) ( 0) 0)
|
| 19 |
朱玉峻, 何连法. 线性系统的极限跟踪性.
数学物理学报,2007, 27A (2) : 314-321.
( Zhu Yujun, He Lianfa. Limit shadowing property of linear systems.
Acta Mathematica Scientia,2007, 27A (2) : 314-321.
(in Chinese) ) ( 0) 0)
|
| 20 |
Pilyugin SY. Theory of pseudo-orbit shadowing in dynamical systems.
Differential Equations,2011, 47 (13) : 1929-1938.
DOI: 10.1134/S0012266111130040. ( 0) 0)
|
| 21 |
Soldatenko S, Yusupov R. Shadowing property of coupled nonlinear dynamical system.
Applied Mathematical Sciences,2015, 9 : 2459-2466.
DOI: 10.12988/ams.2015.52151. ( 0) 0)
|
| 22 |
Soldatenko S, Steinle P, Tingwell C, et al. Some aspects of sensitivity analysis in variational data assimilation for coupled dynamical systems. Advances in Meteorology, 2015, 2015:ID 753031
( 0) 0)
|
| 23 |
Wang Q. Convergence of the least squares shadowing method for computing derivative of ergodic averages.
SIAM Journal on Numerical Analysis,2014, 52 (1) : 156-170.
DOI: 10.1137/130917065. ( 0) 0)
|
| 24 |
Wang Q, Hu R, Blonigan P. Least squares shadowing sensitivity analysis of chaotic limit cycle oscillations.
Journal of Computational Physics,2014, 267 : 210-224.
DOI: 10.1016/j.jcp.2014.03.002. ( 0) 0)
|
| 25 |
Blonigan PJ, Gomez SA,Wang Q. Least squares shadowing for sensitivity analysis of turbulent fluid flows. 52nd Aerospace Sciences Meeting, National Harbor, Maryland, 2014-01-13-17
( 0) 0)
|
| 26 |
Blonigan PJ, Wang Q. Least squares shadowing sensitivity analysis of a modified Kuramoto-Sivashinsky equation.
Chaos, Solitons & Fractals,2014, 64 : 16-25.
( 0) 0)
|
| 27 |
Pilyugin SY.
Shadowing in dynamical systems. Lecture Notes in Mathematics, Berlin: Springer, 1999 .
( 0) 0)
|
| 28 |
Palmer KJ.
Shadowing in Dynamical Systems, Theory and Applications. Dordrecht: Kluwer Academic, 2000 .
( 0) 0)
|
| 29 |
高强, 彭海军, 张洪武, 等. 基于哈密顿动力系统新变分原理的保辛算法之一:变分原理和算法构造.
计算力学学报,2013, 30 (4) : 461-467.
( Gao Qiang, Peng Haijun, Zhang Hongwu, et al. The symplectic algorithms for Hamiltonian dynamic systems based on affinew variational principle part I:the variational principle and the algorithms.
Chinese Journal of Computational Mechanics,2013, 30 (4) : 461-467.
(in Chinese) ) ( 0) 0)
|
| 30 |
Peng HJ, Gao Q, Wu ZG, et al. Effcient sparse approach for solving receding-horizon control problems.
AIAA Journal of Guidance, Control, and Dynamics,2013, 36 (6) : 1864-1872.
DOI: 10.2514/1.60090. ( 0) 0)
|
2. State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology, Dalian 116024, China
3. School of Aeronautics and Astronautics, Dalian University of Technology, Dalian 116024, China
 2016, Vol. 48
2016, Vol. 48
