2. 中国运载火箭技术研究院空间物理重点实验室, 北京 100076
高超声速飞行器新型的气动布局以及复杂的空气动力学特性,使得飞行器进行复杂的高机动指令性任务时,经历复杂的流动环境,可能诱发未知的超预期指令或非指令的非可控行为,从而危及飞行安全、降低飞行品质并损害任务行为的准确性[1-3]. 美国HTV-2第一次试飞失败的主要原因[4]是由于"飞行器产生超出预期的偏航,而偏航又耦合到滚转,这样就超出了发生异常时副翼的可控能力",为典型的横侧向失稳,对应的飞行动力学失稳现象为横向操纵偏离失稳,即对应的LCDP $>$ 0 (横向控制偏离参数为正);同时,为了增加高超声飞行器的滑翔距离,提高飞行器的机动能力,导致飞行器的稳定裕度很低或不稳定. 研究表明,飞行器在大攻角下机动飞行以及失稳状态下的大攻角运动,其空气动力学特性极其复杂,主要问题有:前缘涡、非对称漩涡、涡破裂以及非定常分离等复杂流动对机身和机翼的干扰;头部激波、机翼激波、尾部激波、操纵面激波之间干扰严重影响高超声速飞行器的气动控制特性;背风面气流遮挡和分离会使升降副翼上偏时操纵效率降低;激波诱导分离产生纵向低头力矩,机翼背风面流场不对称分离引起高空快速滚转,在小转动惯量小阻尼情况下,此现象更明显[5]. 高超声速飞行器的攻角、马赫数和高度范围非常大,以及极强的非线性空气动力学影响,使得飞行器在大攻角下的运动极其复杂,基于小扰动假设的线性化分析方法已经无法全面揭示其运动规律[3].
文献[6]首次将延拓算法和分岔理论应用到非线性飞行力学的分析中;文献[7]将分岔理论与控制算法相结合,实现了基于分岔理论的控制算法设计;文献[8]采用扩展的分岔理论分析了在约束下的飞行器的非线性稳定性;文献[9]结合分岔理论研究了在分岔点的可控性和可观测性;文献[10]首次将延拓算法和分岔理论应用到飞行器的总体设计中,从而改善了飞行器的飞行性能;文献[11]将分岔理论应用到了直升机的气动弹性问题,并给出了其对应的稳定域;文献[12]将分岔理论应用到了扑翼飞行器的稳定性分析;文献[13-14]采用分岔理论研究了机翼摇晃预测抑制以及大攻角稳定域求解.以上文献都是基于非高超声速飞行器对该方法的尝试,重点解决的是具有强非线性的高机动飞机问题,验证了该方法对强非线性问题具有较好的处理能力.分岔理论在高机动低速飞行器中得到了较大范围的应用,然而对具有极强非线性的高超声速飞行器动力学模型,现有的文献依然是采用线性化理论来研究飞行器的动力学特性,文献[15-17]基于小扰动假设的方法研究了高超声速重复使用运载器的稳定性和可控性,文献[18-21]将基于线性化方法的稳定判据应用到了高超声速高机动飞行器的气动控制性能研究中.本文将分岔理论引入到高超声速飞行器横侧向失稳问题的研究中,从全新的角度揭示了具有强非线性的高超声速飞行器失稳问题.
本文针对高超声速飞行器大攻角横侧向失稳问题,采用延拓算法求解并分析了以俯仰舵偏为和副翼舵偏为连续参数的平衡分岔图,对平衡分支的稳定性和突变点进行了分析,给出了非线性动力学模型的特征根拓扑结构;并对高超声速飞行器存在的极限分岔点、Hopf分岔点以及叉型分岔点对应的运动进行了分析;最后求解了在横侧向机动情况下的平衡分支,并对横侧向机动稳定性进行了分析.
1 方法与模型 1.1 分岔理论分岔和连续分析方法是一种基于非线性动力学系统的理论[22],其本质是在一定的参数变化范围内,采用预测-校正方法连续求解系统稳态解,得到的分岔拓扑图可以给出定量的动力学响应变化. 对于自治动力学系统的一般形式
| $ \dot { x} = f\left( {{ x },{ \lambda }} \right) $ | (1) |
其中,$f$是$n$维非线性动力学模型,${ x} \in \mathbb{R}^n$是状态变量,${ \lambda } \in \mathbb{R}^m$是$m$个参数变量. 对高超声速飞行器五维动力学模型,$f$是五维刚体动力学模型,${ x }$包含的状态量有攻角$\alpha $、侧滑角$\beta $、滚转角速度$p$、俯仰角速度$q$和偏航角速度$r$;${ \lambda } $包含的连续参数有副翼舵偏$\delta _x $、偏航舵偏$\delta _y $和俯仰舵偏$\delta _z $.数值分岔分析中,在一定的一个或多个参数区间范围内,飞行动力学模型的稳态解被投射到相应的范围内. 通过求解$ \dot{ x} = f\left( {{ x },{ \lambda }} \right) = 0$,可以得到一维参数分岔平衡图. 同样的,对于周期解也可以找到其对应的分支. 通过分析分岔平衡图,可以得到飞行器的状态参数和连续参数的关系. 基于分岔图和相关的分岔理论,随着连续参数的变化,一个或多个参数变化超越了临界值,动力学系统的相图拓扑发生突然变化,系统的动力学特性就会出现分岔. 广义上来讲,就是系统的动力学特性在参数经过分岔点之后出现了本质变化,所遵循的动力学规律发生突变. 和飞行动力学相关的典型的分岔突变有[23]:
(1) 极限点分岔(limit point,LP),当平衡点雅克比矩阵实特征根跨过虚轴时,系统会产生极限点分岔,在分岔点一侧,系统没有平衡点,在分岔点另一侧,系统有两个平衡点;
(2) 霍夫分岔(Hopf point, HP),当平衡点的雅克比矩阵的一对共轭复根越过了虚轴就会出现霍夫分岔,当霍夫分岔出现时,平衡点的稳定性会发生变化,同时产生一个周期轨道;
(3) 叉型分岔(branch point,BP 或pitchfork bifurcation, PB),当系统一个实根跨过虚轴,成为不稳定实根,则此时发生叉型分岔;从叉型分岔点会产生两条新的平衡分支,且新平衡分支(叉型分支)以原始的平衡分支为对称轴对称;
(4) 极限环极限点分岔(limit point of circle,LPC),当一个实弗洛格乘子从+1点跨过单位圆时,出现周期轨道极限点分岔,在分岔点的一侧没有周期轨道,在分岔点的另一侧有两个周期轨道;
(5) 倍周期分岔点(period-doubling,PD), 当一个实弗洛格乘子从$-1$点跨过单位圆时,出现倍周期分岔,周期轨道失去稳定性,同时一个两倍的周期轨道产生;
(6) 花环分岔(Neimark-Sacker,NS),当一对复弗洛格乘子跨过单位圆,原有的周期轨道失去稳定性,额外的周期运动出现,出现类似于花环的准周期或锁频运动.
延拓算法的基本思想为:先给定一个初始平衡点,以弧长为参数,从该平衡点出发,利用其导数信息,基于牛顿迭代法求取下一个平衡点. 在以后的计算过程中,每次都以上一次计算所得的平衡点作为下一次计算的初始点,实现对解曲线的连续跟踪. 由于在计算过程中已经求得平衡点处的雅可比矩阵,延拓算法可以直接计算雅可比矩阵的特征根,并根据特征根来判断出平衡点的局部稳定性. 延拓算法是建立在隐函数定理基础上的一种数值计算方法,用于求解系统平衡解随可变控制参数连续变化的规律,并确定分岔点的位置和类型.
1.2 高超声速飞行器五维非线性动力学模型本文采用的五维非线性动力学模型为[24]
| $\left.\begin{array}{c} \dot {\alpha } = q\underbrace { - p\cos \alpha \tan \beta + r\sin \alpha \tan \beta }_{\hbox{运动非线性项}}\underbrace { - \dfrac{C_L^\alpha \bar {q}S}{mV\cos \beta }\alpha - \dfrac{C_L^{\delta _z } \bar {q}S}{mV\cos \beta }\delta _z }_{\hbox{气动非线性项}} \\ \dot {\beta } = \underbrace {r\cos \alpha + p\sin \alpha }_{\hbox{运动非线性项}}\underbrace { + \cos \beta \dfrac{C_z^\beta \bar {q}S}{mV}\beta + \cos \beta \dfrac{C_z^{\delta _y } \bar {q}S}{mV}\delta _y }_{\hbox{气动非线性项}} \\ \dot {p} = \underbrace {\dfrac{C_l^p \bar {q}Sl^2}{VJ_x }p + \dfrac{C_l^\beta \bar {q}Sl}{J_x }\beta + \dfrac{C_l^{\delta _x } \bar {q}Sl}{J_x }\delta _x + \dfrac{C_l^{\delta _y } \bar {q}Sl}{J_x }\delta _y }_{\hbox{气动非线性项}}\underbrace { + \dfrac{J_y - J_z }{J_x }qr}_{\hbox{惯性非线性项}} \\ \dot {r} = \underbrace {\dfrac{C_n^\beta \bar {q}Sl}{J_y }\beta + \dfrac{C_n^r \bar {q}Sl^2}{VJ_y }r + \dfrac{C_n^{\delta _y } \bar {q}Sl}{J_y }\delta _y + \dfrac{C_n^{\delta _x } \bar {q}Sl}{J_y }\delta _x }_{\hbox{气动非线性项}}\underbrace { + \dfrac{J_z - J_x }{J_y }pq}_{\hbox{惯性非线性项}} \\ \dot {q} = \underbrace {\dfrac{C_m^\alpha \bar {q}Sl}{J_z }\alpha + \dfrac{C_m^q \bar {q}Sl^2}{VJ_z }q + \dfrac{C_m^{\delta _z } \bar {q}Sl}{J_z }\delta _z }_{\hbox{气动非线性项}}\underbrace { + \dfrac{J_x - J_y }{J_z }pr}_{\hbox{惯性非线性项}} \\ \end{array} \right \} $ | (2) |
其中$\alpha ,\beta $分别为攻角和侧滑角,$p,q,r$分别为滚转角速度、俯仰角速度和偏航角速度,$\bar {q}$为动压;$\delta _x ,\delta _y ,\delta _z $分别为副翼舵偏、偏航舵偏和俯仰舵偏,$C_L^\alpha ,C_z^\beta $分别为升力系数导数和侧向力系数导数,$C_m^\alpha ,C_n^\beta ,C_l^\beta $分别为俯仰力矩系数导数、偏航力矩系数导数和横向稳定力矩系数导数,$C_m^q ,C_l^p ,C_n^r $分别为俯仰阻尼力矩系数导数、滚转阻尼力矩系数导数和偏航阻尼力矩系数导数;$C_L^{\delta_z } ,C_z^{\delta _y } $分别为俯仰舵升力系数导数和偏航舵侧向力系数导数,$C_m^{\delta _z } ,C_n^{\delta _y } ,C_l^{\delta _x } $为舵面控制力矩系数导数,$C_l^{\delta _y } ,C_n^{\delta _x } $为舵面引起的交叉力矩系数导数;$m$,$S$,$l$分别为高超声速飞行器的质量、参考面积和特征长度;$J_x ,J_y ,J_z $为飞行器各轴对应的转动惯量;舵偏角范围分别为$-30^ \circ ≤ \delta _z ≤ 0^ \circ $,$-20^ \circ ≤ \delta _y ≤ 20^ \circ $和$-30^ \circ ≤ \delta _x ≤ 30^ \circ $,攻角范围为$0^ \circ ≤ \alpha ≤ 60^ \circ $.模型中的非线性项可以分为3类,其中包括运动非线性项、气动非线性项和惯性非线性项,具体如式(2)所示. 图 1为本文中相关线型和标识点含义.

|
图 1 线型和标识点 Figure 1 Notion of lines and points |
采用延拓算法,以俯仰舵偏$\delta _z$ 为连续参数,分别对滑翔式高超声速飞行器的核心飞行阶段密切相关的远程平衡滑翔点(15 Ma, 45 km)以及与末端制导精度密切相关的快速下压段结束点(5 Ma,27 km)进行分析.对于五维非线性动力学模型的分岔分析,首先在初始平衡点处,以俯仰舵偏为连续参数,采用延拓算法求解五维非线性动力学模型的平衡分支,给出结合分岔突变理论对平衡分支上的平衡点依次进行探测函数突变点分析,并给出对应突变点类型,从而可以得到五维非线性动力学模型完整的平衡分支分岔图.本节重点进行的分析包括平衡分支分析、特征根拓扑分析以及极限环分析.
2.1 平衡分支分析图 2为下压段结束点(5 Ma,27 km)的五维动力学模型平衡分支在平面$\left( {\delta _z ,\alpha } \right)$和$\left( {\delta _z ,q} \right)$的投影. 由图可知存在3个平衡分支,即:一个主平衡分支和两个叉型平衡分支.

|
图 2 平衡分支在不同平面投影图(5 Ma,27 km) Figure 2 Equilibrium branch projection in different planes (5 Ma,27 km) |
图 2(a)为平衡分支在$\left( {\delta _z ,\alpha } \right)$平面的投影,图中的两条叉型分支相互重合.对于主平衡分支,分支中存在四个极限点、一个 BP 分岔点,3段不稳定的平衡分支和3段稳定的平衡分支.第1段不稳定分支区间对应的攻角范围为[7.0°, 13.8°](小攻角不稳定区域),第2段不稳定分支区间为[24.5°, 44.9°],第三段不稳定分支区间为[52.4°,55.8°].当遇到LP1,LP2,LP3,LP4点时纵向稳定性突变,当遇到BP分岔点$\left( {\alpha = 52.4^\circ} \right)$时,飞行器横侧向失稳(自滚转失稳),此时对应的攻角为横侧向自滚转失稳攻角;在BP分岔点处衍生出了新的平衡分支 (叉型平衡分支),且在该分岔点之后,飞行器横侧向失稳.
进一步分析图 2(a)可以发现,在$\left( {\delta _z ,\alpha } \right)$平面,两个叉型平衡分支的投影是重叠的,且新的分支存在LP5,LP6,LP7,LP8四个极限点和H1,H2, H3三个Hopf分岔点,叉型平衡分支为完全不稳定平衡分支,不稳定分支为排斥区,在该点飞行器运动状态不稳定,但是当扰动较大时,飞行器运动状态可能会逃离原有的稳定平衡分支,从而可能到达另一个稳定点,在特殊的条件下还有可能进入混沌状态;对于同一个攻角下存在两个平衡舵偏角,即主分支平衡舵偏角和叉型分支平衡舵偏角,通过进一步仿真分析可以得出在纵向动力学模型中,由于叉型平衡分支存在滚转角速度$p$和偏航角速度$r$,从而引起惯性耦合效应,即${\left( {J_x - J_y } \right)pr}/{J_z }$项会引起俯仰力矩的变化,从而出现两个平衡舵偏角.
由图 2(b)可以发现,从BP点产生的两个平衡分支为对称的平衡分支(由于气动力模型具有对称性),叉型平衡分支对应的滚转角速度在[$-150^\circ$/s,$150^\circ$/s]区间.叉型平衡分支平衡点为侧滑角引起的滚转力矩$M_x^\beta \beta $与滚转阻尼力矩$M_x^p p$之间的平衡,在某些状态值,平衡点个数多达9个.
图 3为远程平衡滑翔点 (15 Ma,45 km)的五维动力学模型平衡分支在平面$\left( {\delta _z ,\alpha } \right)$和$\left( {\delta _z ,q} \right)$的投影. 分析图 3(a)可以得出,对于主平衡分支,分支中存在2个极限点、2个BP分岔点,2段不稳定的平衡分支和2段稳定的平衡分支.当遇到LP1点时飞行器纵向失稳,遇到BP1点时飞行器横侧向失稳,遇到LP2点时,纵向重新获得稳定性,但横侧向依然失稳;当遇到BP2点时,飞行器横侧向重新获得稳定性;进一步分析,当攻角为41.3°时出现第一个BP分岔点,当攻角为58.1°时出现第二个BP分岔点,且在BP1点产生两个短的平衡分支,在BP2点产生了两个较长的平衡分支;进一步观察可以发现新的平衡分支存在H1,H2,H3, H4四个Hopf分岔点,每一个Hopf分岔点都产生一个极限环分支;分析图 3(b)可得,较短平衡分支对应的幅值小于较长平衡分支对应的幅值,且较长平衡分支对应的滚转角速度幅值相对于(5 Ma,27 km)情况减小较大.
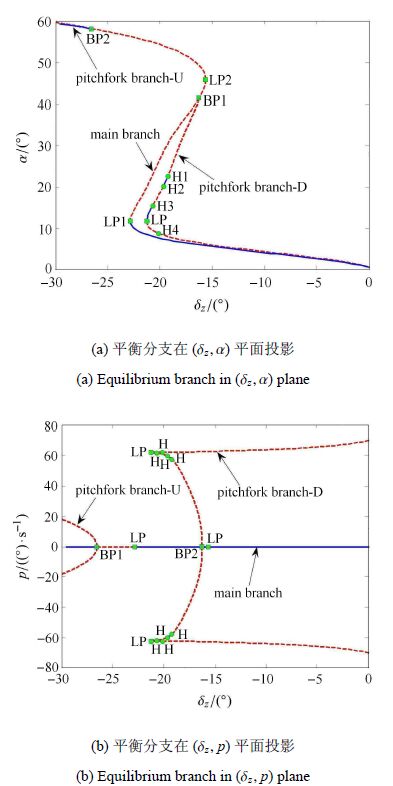
|
图 3 平衡分支在不同平面投影图(15 Ma,45 km) Figure 3 Equilibrium branch projection in different planes (15Ma,45 km) |
基于分岔理论中的延拓算法,可以连续地求得高超声速飞行器非线性动力学模型全局特征根分布,图 4(a)和图 4(b)分别为(5 Ma,27 km)和(15 Ma,45 km)状态下所对应的特征根拓扑.

|
图 4 五维模型特征根拓扑分布 Figure 4 Eigenvalue topology for 5-dimension model |
由图 4(a)可以得出,(5 Ma,27 km)情况下,高超声速飞行器五维动力学模型的模态分支由短周期模态分支、荷兰滚模态分支、滚转阻尼模态分支组成.进一步分析短周期模态分支可以得出,对于不同的飞行攻角,短周期模态对应的特征根先为一对稳定共轭复根;随着攻角增大,变成一对不稳定实根;随着攻角进一步增大,一对实根转变为一对稳定共轭复根,之后又随着攻角的增大,短周期变成一对不稳定实根;最后在大攻角区域,其对应的特征根变成一对稳定共轭复根. 对于滚转阻尼模态,其为一个单实根,随着攻角的增大,其特征根数值逐渐减小.当实根跨过虚轴时,模型会发生叉型分岔,其对应的攻角为分岔攻角,并从分岔点产生新的平衡分支.进一步分析荷兰滚模态可以得出,其对应的特征根在全攻角范围内为一对稳定共轭复根,且随着攻角的减小,其特征根随之靠近虚轴和实轴.
分析图 4(b)中对应的短周期模态分支可以得出,相对于(5 Ma,27 km)情况,(15 Ma, 45 km)对应的特征根模值有所减小. 且在低攻角情况,短周期模态对应的特征根为一对稳定共轭复根,随着攻角增大,变成一对不稳定实根,随着攻角进一步增大,一对不稳定实根又转变为一对稳定共轭复根.对于滚转模态,其实根的大小随着攻角的增大依然减小,但是其特征根的值相比(5 Ma, 27 km)情况有较大幅度的下降,滚转阻尼相应有所减小,同时存在滚转失稳;对于荷兰滚模态情况,相对于(5 Ma, 27 km)情况其幅值有一定的增大,且虚部更加靠近虚轴,荷兰滚模态阻尼减小,振荡频率增大.
2.3 极限环分支分析对于每一个Hopf分岔点都会产生一个极限环分支,极限环的产生将会对模型运动产生极其重要的影响. 本节针对分析中存在复杂分岔的极限环和稳定高频大幅值振荡极限环进行分析.
图 5(a)和图 5(b)分别为(5 Ma,27 km)情况下,从Hopf2分岔点延伸出的极限环分支和幅值在$\left( {\delta _z ,\alpha } \right)$平面和$\left( {\delta _z ,p} \right)$平面投影,该极限环开始于Hopf2,终止于Hopf3.可以看出,该极限环运动极为复杂,分支中存在倍周期分岔(PD)、极限环极限点分岔(LPC)以及花环分岔(NS).当经过LPC分岔点时,极限环的稳定性发生突变;当遇到PD分岔点时,极限环的周期为原周期的两倍或原周期的1/2;当极限环遇到NS分岔点时,模型状态参数空间运动呈现花环型运动;该极限环对应的攻角的最大幅值约为8°,对应的滚转角速度的最大幅值约为100°/s. 由计算得出,极限环轨道周期范围为[2.2 s,3.9 s].
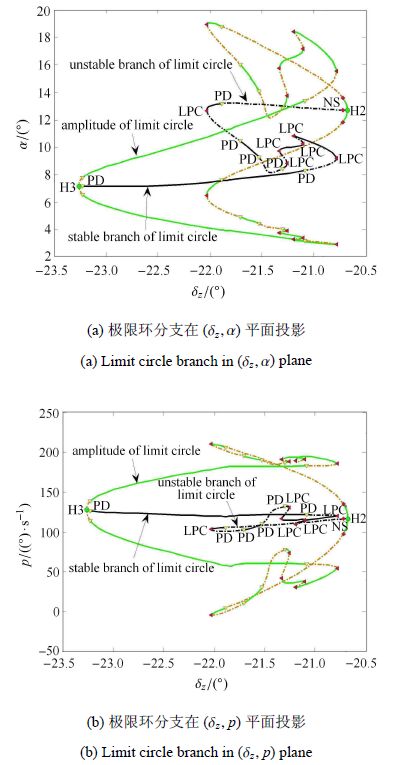
|
图 5 Hopf2-3对应极限环分支(5 Ma,27 km) Figure 5 Limit circle branch of Hopf2-3 (5 Ma,27 km) |
图 6(a)和图 6(b)分别为(15 Ma,45 km)情况下,从Hopf3分岔点延伸出的极限环分支以及幅值在$\left( {\delta _z ,\alpha } \right)$平面和$\left( {\delta _z ,p} \right)$平面的投影.分析图 6(a)和图 6(b)可以得出,开始时极限环为稳定极限环,之后遇到一个LPC分岔点,极限环由稳定变为不稳定,之后遇到第一个NS点即花环分岔点,极限环再次获得稳定性,当遇到第二个NS分岔点时极限环失去稳定性.计算求得该极限环对应的周期位于[2 s,4.6 s]区间,对应的最大攻角幅值为约为17°,对应的最大滚转角速度幅值约为250°/s.
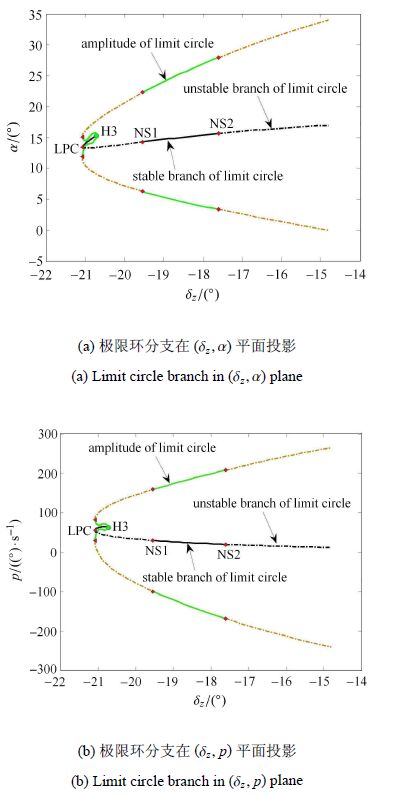
|
图 6 Hopf3对应极限环分支($15Ma$,45 km) Figure 6 Limit circle branch of Hopf3 ($15Ma$,45 km) |
图 7(a)和图 7(b)分别为(15 Ma,45 km)情况下,从Hopf4分岔点延伸出的极限环分支和极限环幅值在$\left( {\delta _z,\alpha } \right)$平面和$\left( {\delta _z ,p} \right)$平面的投影,可以看出,整个极限环为稳定极限环,极限环对应的最大攻角幅值约为20°,对应的最大滚转角速度幅值约为400°/s,且对应的周期在[1.6 s,2.8 s]之间.Hopf4点所产生的极限环为稳定的高频大幅值振荡周期运动,将严重影响高超声速飞行器的稳定飞行,甚至可能对飞行器结构产生破坏,应对其进行有效地抑制或改出.
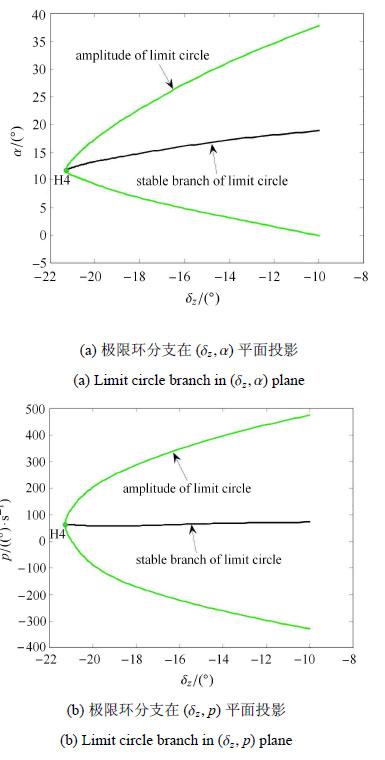
|
图 7 Hopf4对应极限环分支(15 Ma,45 km) Figure 7 Limit circle branch of Hopf4 (15 Ma,45 km) |
横侧向机动平衡分支主要是研究飞行器在进行滚转机动情况下的稳定性和失稳特性,是以副翼舵偏$\delta _x$为连续参数求解平衡分岔图,并研究其横向操纵偏离失稳问题.
根据俯仰舵偏$\delta _z $为连续参数的研究结果,选择多平衡点对应的特征点即:(5 Ma,27 km)情况选择$\delta _z = - 22^\circ$,(15 Ma,45 km)情况选择$\delta _z = - 20^\circ$进行滚转机动情况下的分岔平衡分析.
图 8为(5 Ma,27 km)情况下$\delta _z = - 22^\circ$的机动平衡分支在平面$\left( {\delta _x ,\alpha } \right)$, $\left( {\delta_x ,\beta } \right)$,$\left( {\delta _x ,p} \right)$和$\left( {\delta _x ,r} \right)$的投影.由图 2可知,在$\delta _z = - 22^\circ$时,存在8个对称的叉型分支平衡点和一个主分支平衡点. 以$\delta _z = - 22^\circ$时的状态参数为初始平衡点,以$\delta _x = 0^\circ$为连续参数的初始值,采用延拓算法连续求解五维非线性模型的平衡分支,得到了4个平衡分支(如图 8所示),其中一个分支经过四次转折回到可控制的区域范围. 分支中存在一个部分稳定分支,其为研究的重点,当副翼舵偏$\delta _x $在[$-13.2^\circ$,$13.2^\circ$]区间时,其对应的分支是稳定的,飞行器进行横滚机动时可以稳定地实现快速滚转.同时可以发现,随着副翼舵偏的增大,侧滑角和滚转角速度逐渐增大;当舵偏角位于[$-13.2^\circ$, $13.2^\circ$]区间之外时,分支遇到Hopf分岔点,对应的分支变为不稳定分支,且随着舵偏角的增大,侧滑角快速增大,滚转角速度缓慢增大且趋于恒定(受到侧滑角增大的影响);进一步分析可以得出,在稳定分支中,整个副翼控制范围内副翼偏转引起的滚转角速度与预期的方向相同,即飞行器不会发生滚转操作反效现象.
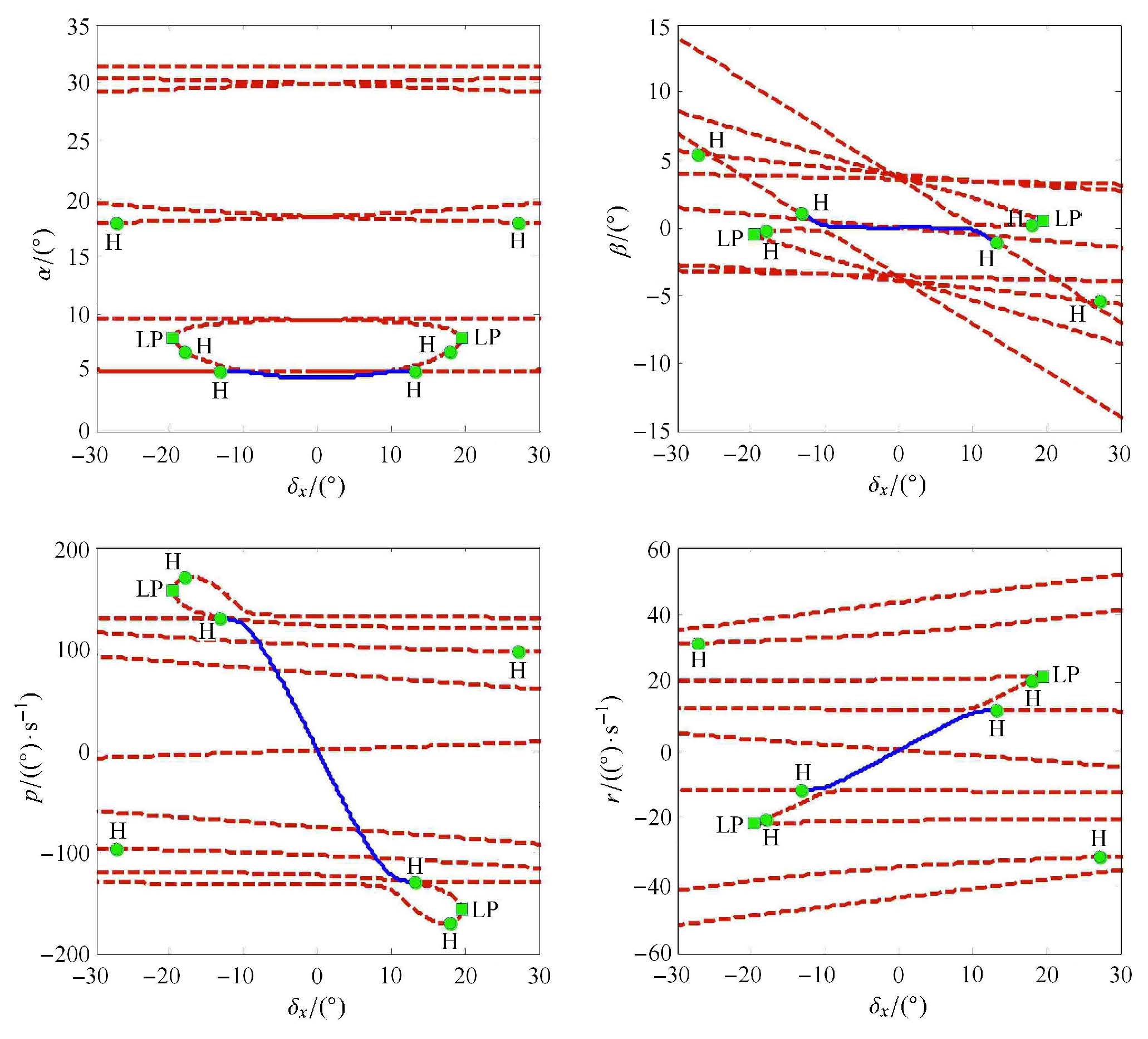
|
图 8 $\delta _z = - 22^\circ$机动分支(5 Ma,27 km) Figure 8 Maneuver branch with $\delta _z = - 22^\circ$ (5 Ma,27 km) |
图 9为(15 Ma,45 km)情况下$\delta _z = - 20^\circ$的机动平衡分支. 由图 9可以看出其存在4个平衡分支,在经过$p=0^\circ$/s点的稳定平衡分支中舵偏角在$[-3.23^\circ$,$3.23^\circ]$区间时,对应分支区间稳定,且随着舵偏角的增大,滚转角速度快速增大;进一步可以得出,当攻角大于8.5°时,飞行器会发生横向操作偏离失稳;同时还存在其他3个不稳定的平衡分支,多个不稳定平衡点会引起较为复杂的非线性运动.

|
图 9 $\delta _z = - 20^\circ$机动分支(15 Ma,45 km) Figure 9 Maneuver branch with $\delta _z = - 20^\circ$ (15 Ma,45 km) |
本文针对高超声速飞行器在大攻角飞行情况下的横侧向失稳问题,重点研究了以俯仰舵偏为连续参数的稳态平衡分支和横侧向机动情况下副翼舵偏为连续参数的平衡分支.研究结果表明:高超声速飞行器存在极限点分岔(LP)、Hopf分岔以及叉型分岔(BP),且从BP分岔点延伸出多个平衡分支,从Hopf分岔点延伸出的极限环分支存在较为复杂的极限环运动,其中包含PD分岔、NS分岔、LPC分岔等复杂的分岔现象;同时,研究发现,在稳态平衡分支中存在滚转失稳问题、高频大幅值稳定极限环问题以及多平衡点问题,在横侧向机动平衡分支中发现了类似于HTV-2的失稳现象,即滚转操作反效(横向操纵偏离失稳,LCDP$>$0),以及多平衡点问题.最后,针对滚转失稳、高频大幅值稳定极限环、多平衡点和滚转操作反效问题.研究结果可以有效地预测高超声速飞行器在大攻角飞行情况下的横侧向失稳特性,能为高超声速飞行器横侧向稳定飞行和控制器设计提供重要的动力学信息,如失稳突变攻角、多平衡点、高频大幅值极限环的出现等.
| 1 |
叶友达. 近空间高速飞行器气动特性研究与布局设计优化.
力学进展,2009, 39 (6) : 683-694.
( Ye Youda. Study on aerodynamics characteristics and design optimization for high speed near space vehicles.
Advance in Mechanics,2009, 39 (6) : 683-694.
(in Chinese) ) ( 0) 0)
|
| 2 |
崔尔杰. 近空间飞行器研究发展现状及关键技术问题.
力学进展,2009, 39 (6) : 658-673.
( Cui Erjie. Research statutes, development trends and key technical problems of near space flying.
Advance in Mechanics,2009, 39 (6) : 658-673.
(in Chinese) ) ( 0) 0)
|
| 3 |
黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战.
控制理论与应,2011, 28 (10) : 1495-1505.
( Huang Lin, Duan Zhisheng, Yang Jianying. Challenges of control science in near space hypersonic aircrafts.
Control Theory and Applications,2011, 28 (10) : 1495-1505.
(in Chinese) ) ( 0) 0)
|
| 4 |
李文杰, 钱开耘, 古雨田. HTV-2项目取得重大进展.
飞航导弹,2010 (9) : 31-34.
( 0) 0)
|
| 5 |
张鲁民.
航天飞机空气动力学分析. 北京: 国防工业出版社, 2009 .
( Zhang Lumin.
Analysis of Space Shuttle Aerodynamics. Beijing: National Defense Industry Press, 2009 .
(in Chinese) ) ( 0) 0)
|
| 6 |
Carroll JV, Mehra RK. Bifurcation Analysis of Nonlinear Aircraft Dynamics.
Journal of Guidance, Control, and Dynamics,1982, 5 (5) : 529-536.
DOI: 10.2514/3.56198. ( 0) 0)
|
| 7 |
Goman MG, Khramtsovsky AV. Application of continuation and bifurcation methods to the design of control systems.
Philosophical Transactions of the Royal Society of London, Series A:Mathematical, Physical and Engineering Sciences,1998, 356 (1745) : 2277-2295.
DOI: 10.1098/rsta.1998.0274. ( 0) 0)
|
| 8 |
Pashilkar AA, Pradeep S. Computation of flight mechanics parameters using continuation techniques.
Journal of Guidance, Control, and Dynamics,2001, 24 (2) : 324-329.
DOI: 10.2514/2.4715. ( 0) 0)
|
| 9 |
Kwatny HG, Dongmo JET, Chang BC, et al. Nonlinear analysis of aircraft loss of control.
Journal of Guidance, Control, and Dynamics,2013, 36 (1) : 149-162.
DOI: 10.2514/1.56948. ( 0) 0)
|
| 10 |
Amit KK, Jatinder S. Aircraft design using constrained bifurcation and continuation method.
Journal of Aircraft,2014, 51 (5) : 1647-1652.
DOI: 10.2514/1.C032288. ( 0) 0)
|
| 11 |
Rezgui D, Lowenberg MH. Continuation and bifurcation analysis in helicopter aeroelastic stability problems.
Journal of Guidance, Control, and Dynamics,2014, 37 (3) : 889-897.
DOI: 10.2514/1.60193. ( 0) 0)
|
| 12 |
Paranjape AA. Symmetric steady flapping flight of bird-scale aircraft, using bifurcation and continuation method. In:AIAA Atmospheric Flight Mechanics Conference. AIAA Paper 2015-0237, 2015
( 0) 0)
|
| 13 |
陈永亮, 沈宏良, 刘昶. 机翼摇晃预测与抑制.
航空学报,2005, 26 (3) : 276-280.
( Chen Yongliang, Shen Hongliang, Liu Chang. Prediction and suppression of wing rock.
Acta Aeronautica et Astronautica Sinica,2005, 26 (3) : 276-280.
(in Chinese) ) ( 0) 0)
|
| 14 |
邹毅, 姚宏. 飞机大攻角俯仰飞行的稳定域分析.
空军工程大学学报,2006, 7 (4) : 11-14.
( Zou Yi, Yao Hong. Stable field analysis of aircraft flying at high angles of attack.
Journal of Air Force Engineering University,2006, 7 (4) : 11-14.
(in Chinese) ) ( 0) 0)
|
| 15 |
Lee HP, Chang M, Kaiser MK. Flight dynamics and stability and control characteristics of the x-33 technology demonstrator vehicle. AIAA Paper 98-4410, 1998
( 0) 0)
|
| 16 |
Philip C. An entry flight controls analysis for a reusable launch vehicle. 2000, AIAA 2000-1046
( 0) 0)
|
| 17 |
Tancredi U, Grassi M, Verde L, et al. Aerodynamics uncertainties compliance with desired lateral-directional dynamics for an unmanned space vehicle. AIAA Paper 2005-6962, 2005
( 0) 0)
|
| 18 |
祝立国, 王永丰, 庄逢甘, 等. 高速高机动飞行器的横航向偏离预测判据分析.
宇航学报,2007, 28 (6) : 1550-1553.
( Zhu Liguo, Wang Yongfeng, Zhuang Fenggan, et al. The lateral-directional departure criteria analysis of high-speed and high maneuverability aircraft.
Journal of Astronautics,2007, 28 (6) : 1550-1553.
(in Chinese) ) ( 0) 0)
|
| 19 |
祝立国, 王永丰, 庄逢甘, 等. Weissman图的产生、发展及其在再入航天飞行器气动布局设计中的应用.
宇航学报,2009, 30 (1) : 13-17.
( 0) 0)
|
| 20 |
高清, 赵俊波, 李潜. 类HTV-2横侧向稳定性研究.
宇航学报,2014, 35 (6) : 657-662.
( Gao Qin, Zhao Junbo, Li Qian. Study on lateral-directional stability of HTV-2 like configuration.
Journal of Astronautics,2014, 35 (6) : 657-662.
(in Chinese) ) ( 0) 0)
|
| 21 |
高清, 李建华, 李潜. 升力体高超声速飞行器横向气动特性研究.
实验流体力学,2015, 29 (1) : 43-48.
( Gao Qin, Li Jianhua, Li Qian. Study on lateral stability of hypersonic lifting-configurations.
Journal of Experiments in Fluid Mechanics,2015, 29 (1) : 43-48.
(in Chinese) ) ( 0) 0)
|
| 22 |
Kuznetsov YA. Elements of Applied Bifurcation Theory, 3rd ed., Vol. 112, Applied Mathematical Sciences, Springer-Verlag, New York, 2004
( 0) 0)
|
| 23 |
Stephen JG, Mark HL, Simon AN. Upset dynamics of an airliner model:a nonlinear bifurcation analysis.
Journal of Aircraft,2013, 50 (6) : 1832-1842.
DOI: 10.2514/1.C032221. ( 0) 0)
|
| 24 |
Goman MG, Zagaynov GI, Khramtsovsky AV. Application of bifurcation methods to nonlinear flight dynamics problems.
Progress in Aerospace Sciences,1997, 33 (9-10) : 539-586.
DOI: 10.1016/S0376-0421(97)00001-8. ( 0) 0)
|
2. Science and Technology on Space Physics Laboratory, China Academy of Launch Vehicle Technology, Beijing 100076, China
 2016, Vol. 48
2016, Vol. 48
