引言
大型可展开桁架结构通常由数量众多的梁、杆、拉索等构件沿一个方向或两个方向周期性延伸拼接而成,因其质量轻、工艺性好、易于展开和收拢等特点而在航天任务中得到了广泛应用[1-2].大型桁架结构的动力学特性十分复杂,具有挠性、分布参数、低刚度、弱阻尼、频率低和模态密集等特点,一旦遇到外界干扰将会产生振动,并且衰减很慢,严重影响有效载荷的正常工作,甚至对航天器的定位和稳定带来严重影响[3-4].为了准确描述这种大型桁架结构的动力学特性,通常采用有限元方法建立其精细的动力学模型.按照传统的有限元建模方法,大型可展开桁架结构可以形成很高自由度的结构动力学模型,不利于对其进行实时的动力学分析与控制[4-5].利用大型可展开桁架结构的周期性特征建立降维等效连续体模型不仅可极大缩减模型自由度,而且为此类结构的在轨参数辨识及反馈控制提供了有效的工具[6-9].
在过去几十年里,针对直梁式或板式周期桁架结构的连续体等效建模,许多学者提出了不同的连续体等效建模方法,取得了大量研究成果.Noor 等[7, 10-12]基于能量等效原理对梁式及板式周期桁架结构连续体等效问题进行了系统研究,通过将周期桁架单元等效为空间梁模型或板模型,得到了等效模型刚度和质量参数的解析表达式.Sun等[13-14]基于本构关系等效将平面桁架单元等效为平面各向异性梁,针对等效梁模型提出了一种高阶Timoshenko梁单元,采用等效梁有限元模型计算结构的动力响应,并通过梁模型的计算结果预测原周期桁架结构中各个构件的内力.Salehian等[5, 15-16]基于能量等效原理研究了由平面桁架单元以及三棱柱式桁架单元构成的梁式桁架结构的梁模型等效,采用Hamilton原理推导了等效梁模型的偏微分运动方程,并基于等效梁模型设计了LQR控制器对桁架结构进行了振动控制.Gonella等[17]采用均质化方法对一维桁架结构进行了连续体等效,并且比较了等效连续体模型与原结构模型的波的色散特性以及频响特性.Balakrishnan[18]采用等效后的各向异性Timoshenko梁模型研究了梁式桁架的结构-控制综合优化问题,得到了控制性能指标关于结构/控制参数的解析表达式.郭宏伟等[19-20]针对索杆铰接式伸展臂,提出基于能量互等原理的伸展臂连续梁等效动力学模型建模方法,对有限元模型与伸展臂等效模型计算的前8阶固有频率进行了比较.
环形桁架结构是近年来应用于大型环形网架式可展开天线的一种新型空间桁架结构[21-22].以往对于周期桁架结构连续体等效建模的研究均是针对直梁式或板式的桁架结构,均未涉及环形桁架结构.本文作者在文献[23]中基于能量等效原理将环形桁架结构中的平面桁架周期单元等效为空间梁模型,从而将环形桁架结构简化为由多个空间梁段组成的环形梁模型,比较了原环形桁架结构与简化环形梁模型在无约束状态下的固有频率.
本文在文献[23]对组成环形桁架结构的周期单元进行梁模型等效的基础上,将环形桁架进一步简化为一个各向同性弹性圆环,采用等效圆环模型进行环形桁架结构的径向振动分析.首先对等效圆环模型径向振动的四阶偏微分方程组进行降阶,通过Laplace变换求解得到了圆环在复频域下的响应表达式,利用复频域下的圆环响应解析计算公式得到求解圆环固有频率和振型的特征方程以及圆环模型的传递函数表达式.最后通过数值算例对环形桁架有限元模型与等效圆环解析模型的固有频率和固有振型及传递函数进行了比较和验证.
1 环形桁架结构等效圆环模型
大型开展开天线的反射面支撑骨架为环形桁架结构,由两类平面桁架单元交替相连组成[23],如图 1所示.该环形桁架的等效圆环模型及其坐标系如图 2所示. 圆环上任一点$C$的位置及位移分别采用极坐标$r,\theta
$和局部笛卡尔坐标$C$-$xyz$描述,其中$x$轴沿圆环截面形心线切向、$y$和$z$轴与圆环截面惯性主轴重合.圆环径向振动时沿$x$和$y$轴方向的位移分别为$u_{x}$和$u_{y}$,绕$z$轴的转角为$\varphi_{z}$.
与文献[23]等效梁模型相对应,不计等效圆环模型径向振动时的横截面剪切变形,忽略等效圆环模型横截面绕$z$轴的转动惯量,在图 2所示坐标系下,圆环的径向振动方程为[24]
|
$\frac{EA}{{{R}^{2}}}\left( \frac{{{\partial }^{2}}{{u}_{x}}}{\partial {{\theta }^{2}}}-\frac{\partial {{u}_{y}}}{\partial \theta } \right)+\frac{E{{I}_{z}}}{{{R}^{4}}}\left( \frac{{{\partial }^{2}}{{u}_{x}}}{\partial {{\theta }^{2}}}+\frac{{{\partial }^{3}}{{u}_{y}}}{\partial {{\theta }^{3}}} \right)+{{q}_{x}}=\rho A\frac{{{\partial }^{2}}{{u}_{x}}}{\partial {{t}^{2}}}$
|
(1a) |
|
$\frac{EA}{{{R}^{2}}}\left( \frac{\partial {{u}_{x}}}{\partial \theta }-{{u}_{y}} \right)-\frac{E{{I}_{z}}}{{{R}^{4}}}\left( \frac{{{\partial }^{3}}{{u}_{x}}}{\partial {{\theta }^{3}}}+\frac{{{\partial }^{4}}{{u}_{y}}}{\partial {{\theta }^{4}}} \right)+{{q}_{y}}=\rho A\frac{{{\partial }^{2}}{{u}_{y}}}{\partial {{t}^{2}}}$
|
(1b) |
式中,$EA$和$EI_{z}$分别为等效圆环模型的拉伸刚度和径向弯曲的抗弯刚度,$\rho
A$为等效圆环模型单位长度质量,$q_{x}$和$q_{y}$分别为作用在圆环上沿$x$和$y$轴方向的分布力. 对于集中载荷,有
|
${{q}_{x}}=\sum\limits_{i=1}^{M}{\frac{{{q}_{xi}}(t)}{R}\delta (\theta -\theta _{i}^{*})}$
|
(2a) |
|
${{q}_{y}}=\sum\limits_{j=1}^{N}{\frac{{{q}_{yj}}(t)}{R}\delta (\theta -\theta _{j}^{*})}$
|
(2b) |
式中$\delta ( \cdot )$为狄拉克函数,$\theta _i^\ast $和$\theta _j^\ast
$分别为集中载荷$q_{xi}$和$q_{yj}$的作用位置.
由于不考虑剪切变形,圆环绕$z$轴的转角$\varphi_z $可以表示为[25]
|
${{\varphi }_{z}}=\frac{{{u}_{x}}}{R}+\frac{1}{R}\frac{\partial {{u}_{y}}}{\partial \theta }$
|
(3) |
圆环的轴向应变$\varepsilon _x $和曲率改变量$\kappa _z $分别为[25]
|
${{\varepsilon }_{x}}=\frac{\partial {{u}_{x}}}{R\partial \theta }-\frac{{{u}_{y}}}{R},{{\kappa }_{z}}=\frac{\partial {{\phi }_{z}}}{\partial \theta }$
|
(4) |
考虑大型可展天线工作中环形桁架固结于伸展臂,则对应的等效圆环模型边界条件为
|
$u_x (0,t) = u_x (2\pi,t) = 0 $
|
(5a) |
|
$u_y (0,t) = u_y (2\pi,t) = 0$
|
(5b) |
|
$\varphi _z (0,t) = \varphi _z (2\pi,t) = 0$
|
(5c) |
2 圆环运动方程求解
式(1)中的四阶偏微分方程组在边界条件(5)下的直接解析求解较为困难. 以往学者们通常采用圆环中心线不可延伸假设[25-28],即假设圆环的轴向应变$\varepsilon _x = 0$,从而将位移$u_y $表示为$u_y = {\partial u_x } /{\partial \theta
}$,利用上述关系式将圆环振动的四阶偏微分方程组(1)转化为一个只含$u_x
$的六阶偏微分方程
|
$\frac{{{\partial }^{6}}{{u}_{x}}}{\partial {{\theta }^{6}}}+2\frac{{{\partial }^{4}}{{u}_{x}}}{\partial {{\theta }^{4}}}+\frac{{{\partial }^{2}}{{u}_{x}}}{\partial {{\theta }^{2}}}-\frac{{{R}^{4}}}{E{{I}_{z}}}\left( \frac{\partial {{q}_{y}}}{\partial \theta }-{{q}_{x}} \right)+\frac{\rho A{{R}^{4}}}{E{{I}_{z}}}\frac{{{\partial }^{2}}}{\partial {{t}^{2}}}\left( \frac{{{\partial }^{2}}{{u}_{x}}}{\partial {{\theta }^{2}}}-{{u}_{x}} \right)=0$
|
(6) |
然后采用分离变量法求解圆环的固有振动问题,根据六阶偏微分方程特征根的不同情况讨论偏微分方程的解的不同形式.上述方法不仅求解过程复杂,而且需要将外载荷$q_{y}$对坐标$\theta
$求偏导,对于$q_{y}$为集中载荷的情况,这种求法是十分麻烦的.本文采用变量代换方法对四阶偏微分方程组进行降阶,然后利用Laplace变换和Green函数法求解降阶后的偏微分方程组,直接获得圆环的动力响应.
首先引入新的变量将式(1)四阶偏微分方程组转化为一阶偏微分方程组. 令
|
$\left. \begin{array}{*{35}{l}}
{{v}_{1}}=\frac{\partial {{u}_{x}}}{\partial t}, & {{v}_{2}}=\frac{\partial {{u}_{y}}}{\partial t} \\
{{\eta }_{1}}=\frac{\partial {{u}_{x}}}{R\partial \theta }-\frac{{{u}_{y}}}{R}, & {{\eta }_{2}}=\frac{{{u}_{x}}}{R}+\frac{\partial {{u}_{y}}}{R\partial \theta } \\
\end{array} \right\}$
|
(7) |
其中,$v_1 $和$v_2 $为圆环沿切向和径向的速度,由式(3)和式(4)易知$\eta _1 $为圆环的轴向应变,$\eta _2$为圆环绕$z$轴的转角. 利用式(7)可将圆环的运动方程(1)转化为
|
$\dfrac{\partial v_1 }{\partial t} = k_1 \dfrac{\partial \eta _1 }{\partial
\theta } + k_2 \dfrac{\partial \eta _3 }{\partial \theta } + \dfrac{q_x }{\rho A} $
|
(8a) |
|
$\dfrac{\partial v_2 }{\partial t} = k_1 \eta _1 - k_2 \dfrac{\partial \eta _4
}{\partial \theta } + \dfrac{q_y }{\rho A} $
|
(8b) |
|
$\dfrac{\partial \eta _1 }{\partial t} = \dfrac{\partial v_1 }{R\partial \theta
} - \dfrac{v_2 }{R}$
|
(8c) |
|
$\dfrac{\partial \eta _2 }{\partial t} = \dfrac{v_1 }{R} + \dfrac{\partial v_2
}{R\partial \theta }$
|
(8d) |
|
$\eta _3 = \dfrac{\partial \eta _2 }{\partial \theta }$
|
(8e) |
|
$\eta _4 = \dfrac{\partial \eta _3 }{\partial \theta }$
|
(8f) |
其中,系数 $k_1 = \dfrac{EA}{\rho AR}$,$k_2 = \dfrac{EI_z }{\rho AR^3}$. 再利用式(7),并
结合式(3),可将圆环的边界条件(5)转化为
|
$v_1 (0,t) = v_1 (2 \pi,t) = 0 $
|
(9a) |
|
$v_2 (0,t) = v_2 (2\pi,t) = 0$
|
(9b) |
|
$\eta _2 (0,t) = \eta _2 (2\pi,t) = 0$
|
(9c) |
令向量${ x}(t,\theta ) = \left\{ {v_1 ,v_2 ,\eta _1 ,\eta _2 ,\eta _3 ,\eta _4 }
\right\}^{\rm T}$,将方程组(8)表示为矩阵形式,并对其进行Laplace变换,可得
|
$\frac{\partial \widehat{x}(s,\theta )}{\partial \theta }=A_{1}^{-1}{{A}_{0}}\hat{x}(s,\theta )+A_{1}^{-1}\hat{b}(s,\theta )$
|
(10) |
式中,$s$为复变量,符号"$\hat { }$ "代表Laplace变换后的量,矩阵${ A}_{1}$和${ A}_{0}$分别为
|
${ A}_1 = \left[\!\!\begin{array}{cccccc}
0 & 0 & {k_1 } & 0 & {k_2 } & 0 \\
0 & 0 & 0 & 0 & 0 & { - k_2 } \\
{1/R} & 0 & 0 & 0 & 0 & 0 \\
0 & {1/R} & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0
\end{array}\!\! \right] $
|
(11a) |
|
${ A}_0 = \left[\!\!\begin{array}{cccccc}
s & 0 & 0 & 0 & 0 & 0 \\
0 & s & { - k_1 } & 0 & 0 & 0 \\
0 & {1/R} & s & 0 & 0 & 0 \\
{ - 1/R} & 0 & 0 & s & 0 & 0 \\
0 & 0 & 0 & 0 & 1 & 0 \\
0 & 0 & 0 & 0 & 0 & 1
\end{array} \!\! \right] $
|
(11b) |
向量$\hat{ b}(s,\theta )$为
|
$
\hat{ b}(s,\theta ) = - \left\{ \!\! \begin{array}{cccccc}
{v_1^0 + \dfrac{\hat {q}_x }{\rho A}} & {v_2^0 + \dfrac{\hat {q}_y
}{\rho A}} & {\eta _1^0 } & {\eta _2^0 } & 0 & 0
\end{array}\!\! \right\}^{\rm T} $
|
(12) |
式中含上标"0"的量代表相应变量的初值.
相应地,对边界条件(9)进行Laplace变换,并采用向量$\hat{ x}$将其表示为矩阵形式
|
${{\Sigma }_{0}}\hat{x}(s,0)+{{\Sigma }_{1}}\hat{x}(s,2\pi )=0$
|
(13) |
其中,边界选择矩阵${ \varSigma}_0 $和${ \varSigma}_1 $分别为
|
${ \varSigma}_0 = \left[\!\!\begin{array}{cccccc}
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0
\end{array} \!\!\right] $
|
(14a) |
|
${ \varSigma}_1 = \left[\!\!\begin{array}{cccccc}
0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 0 & 0 & 0 \\
1 & 0 & 0 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 & 0 & 0
\end{array} \!\! \right] $
|
(14b) |
式(10)可看作是只关于$\theta $的一阶常微分方程组,在边界条件(13)下采用Green函数方法求解[29],便得
|
$\hat{x}(s,\theta )=\int_{0}^{2\pi }{{{G}_{r}}}(s,\theta ,\xi )A_{1}^{-1}\hat{b}(s,\xi )\text{d}\xi $
|
(15) |
式中${ G}_r (s,\theta ,\xi )$称为微分方程组(10)的矩阵Green函数,可表示为[30]
|
$
{ G}_r (s,\theta ,\xi ) = \\ \left\{ \!\!\begin{array}{ll}
- { N}(s,\theta ){ \varSigma}_1 { \varPhi} (s,2\pi - \xi ) , & 0 ≤
\theta ≤ \xi \\
{ N}(s,\theta ){ \varSigma} _0 { \varPhi} (s,- \xi ) , & \xi ≤ \theta
≤ 2 \pi \end{array} \right. $
|
(16) |
式中
|
${\varPhi} (s,\theta ) = \exp ({ A}_1 ^{ - 1}{ A}_0 \theta ) $
|
(17) |
|
${ N}(s,\theta ) = {\varPhi} (s,\theta )\left[{{ \varSigma}_0 + { \varSigma}_1 {\varPhi } (s,2 \pi )} \right]^{ - 1}$
|
(18) |
由式(15)可以得到圆环上任一点在复频域下的响应,包括切向和径向速度($\hat {v}_1
,\hat {v}_2 )$,轴向应变($\hat {\eta }_1 )$以及曲率改变量($\hat
{\eta }_2 )$. 由式(7)可知圆环在复频域下的位移响应为
|
$
\hat {u}_x = \dfrac{\hat {v}_1 + u_x^0 }{s} ,\
\hat {u}_y = \dfrac{\hat {v}_2 + u_y^0 }{s}$
|
(19) |
式中,$u_x^0 $和$u_y^0 $分别为位移$u_x $和$u_y
$的初值. 由圆环在复频域下的响应,通过Laplace逆变换便可以得到圆环的时域响应.
根据式(18),圆环自由振动的特征值问题为[30]
|
$
\left( {{ \varSigma}_0 + { \varSigma}_1 {\varPhi} (s,2 \pi )} \right){\psi} = 0 $
|
(20) |
对应的特征方程为
|
$
\det \left( {{ \varSigma }_0 + { \varSigma }_1 {\varPhi} (s,2 \pi )} \right) = 0 $
|
(21) |
解式(21)得到特征值$s_n$ ($n=1,2,\cdots $),进而得到圆环的第$n$阶固有频率$\omega _n $. 将特征值$s_n
$代入式(20) 可解出对应的特征向量${\psi}_n $,从而得到圆环响应$x(t,\theta )$的第$n$阶振型向量为
|
$
{ X}_n (\theta ) = {\varPhi} (s_n ,\theta ){\psi}_n $
|
(22) |
为得到等效圆环模型的传递函数,令圆环初始状态为零,在圆环内部任一点$\xi
$处作用沿$x$方向或$y$方向的单位脉冲载荷,则有
|
$
\hat{ b}(s,\theta ) = \left\{ { - \dfrac{\delta (\theta - \xi )}{\rho AR},0,0,0,0,0} \right\}^{\rm T}
$
|
(23a) |
或
|
$
\hat{ b}(s,\theta ) = \left\{ {0,- \dfrac{\delta (\theta - \xi )}{\rho AR},0,0,0,0} \right\}^{\rm T}
$
|
(23b) |
将式(23)代入式(15)可得圆环的响应为
|
$
\hat{ x}(s,\theta ) = { G}_r (s,\theta ,\xi ){ A}_1 ^{ - 1}\bar { b} $
|
(24) |
式中
|
$
\bar{ b} = \left\{ { - \dfrac{1}{\rho AR},0,0,0,0,0} \right\}^{\rm T} $
|
(25a) |
或
|
$
\bar{ b} = \left\{ {0,- \dfrac{1}{\rho AR},0,0,0,0} \right\}^{\rm T} $
|
(25b) |
从而得到圆环模型的传递函数
|
$
{ G}(s,\theta ,\xi ) = { G}_r (s,\theta ,\xi ){ A}_1 ^{ - 1}\bar { b} $
|
(26) |
3 数值算例
考虑由30边的正多边形组成的大型环形可展开天线的桁架结构. 桁架外接圆直径6 m,高1.05 m.桁架中各构件均为外径0.025 m、 内径0.023 m的碳纤维管,材料弹性模量$E =235$ GPa,泊松比$\nu
=0.30$,密度$\rho =1 720$ kg/m$^{3}$.按照文献[23]中周期桁架单元等效的方法计算得到等效圆环模型的刚度参数($EA$和$EI_{z})$和质量参数($\rho A)$.
假设环形桁架结构固结于刚性伸展臂上,首先对环形桁架结构与等效圆环模型径向振动的固有振动特性进行比较.其中环形桁架结构采用有限元软件ANSYS分析,桁架中各根构件采用Beam4空间梁单元模拟,等效圆环模型的固有频率和振型由式(21)和式(22)计算得到.表 1列出了两者前8阶固有频率计算结果的比较.
表 1(Table 1)

表 1 环形桁架与等效圆环模型固有频率比较
Table 1 Comparisons of natural frequencies of the hoop truss and the equivalent ring model
|
表 1 环形桁架与等效圆环模型固有频率比较
Table 1 Comparisons of natural frequencies of the hoop truss and the equivalent ring model
|
由表 1可见,对于环形桁架结构的径向振动,采用等效圆环模型计算出的前8阶固有频率与环形桁架有限元模型的计算结果非常接近,等效圆环模型前5阶固有频率略低于环形桁架结构,而后3阶固有频率略高于环形桁架结构,前8阶频率的误差均在1%以内.
图 3给出了固支于伸展臂上的环形桁架结构前8阶径向振动的固有振型.从图 3可以看出,环形桁架结构表现出与圆环相似的径向振动模态.由于组成环形桁架的平面桁架单元存在面外弯曲---扭转耦合变形[23],在第7阶振型中可以看出环形桁架结构产生了较为明显的径向弯曲---扭转耦合变形,而在其他的7阶模态中这种弯扭耦合效应不明显.
为了对环形桁架结构和等效圆环模型的振型进行定量比较,在各阶模态中选取环形桁架结构有限元模型横杆上各个点的径向(或切向)位移值与等效圆环模型相应位置点的径向(或切向)位移值,采用模态置信准则 MAC值[31],按下式计算两种模型位移向量之间的MAC值
|
$
{\rm MAC}\left( { { \varphi}_i ,{ \psi}_i } \right) = \dfrac{\left| {{ \varphi}_i ^{\rm T}{
\psi}_i } \right|^2}{\left( {{ \varphi}_i ^{\rm T}{ \varphi}_i } \right)\left( {{ \psi}_i ^{\rm
T}{ \psi}_i } \right)} $
|
(27) |
式中${\varphi}_i $为环形桁架的第$i$阶模态的径向(或切向)位移向量,${\psi}_i
$为圆环的第$i$阶模态的径向(或切向)位移向量. 环形桁架与等效圆环模型同一阶模态之间的MAC值计算结果见表 2所示.
表 2(Table 2)

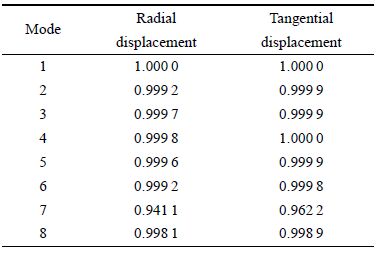
表 2 环形桁架振型与圆环振型间的MAC值
Table 2 MAC values between the mode shapes of the hoop truss and the equivalent ring model
|
表 2 环形桁架振型与圆环振型间的MAC值
Table 2 MAC values between the mode shapes of the hoop truss and the equivalent ring model
|
从表 2可以看出,两种模型前8阶振型之间的MAC值均非常接近1,由于环形桁架第7阶振型中存在较为明显的径向弯曲---扭转耦合变形,而等效圆环模型未考虑这种耦合效应,使得第7阶振型的MAC值相比其他7阶模态稍差.总体上,等效圆环模型与环形桁架结构的前8阶振型吻合很好.
进一步,将等效圆环模型由式(26)计算得到的传递函数与环形桁架有限元模型采用模态叠加法得到的传递函数进行比较.在图 1所示的环形桁架上的$A$点(位于$\theta = \pi /
15$的竖杆上,为了不激起环形桁架的竖向弯扭耦合振动,将$A$点选在竖杆中点处)作用一个径向力$q$,两种模型计算的传递函数比较如图 4和图 5所示. 图 4为$A$点作用力与环形桁架上$B$点(位于$\theta =\pi /2$的横杆上)的径向位移之间的传递函数;图 5为$A$点作用力与环形桁架上$C$点(位于$\theta = \pi $的横杆上)的切向位移之间的传递函数.
从图 4和图 5可以看出,在前8阶模态所在的频率范围内,等效圆环模型与环形桁架有限元模型计算得到的传递函数均吻合较好.由于环形桁架结构的径向弯曲振动与竖向弯扭振动之间存在一定的耦合[23],而等效圆环模型未考虑这种耦合效应,以致环形桁架的传递函数曲线比圆环的传递函数曲线多了某些峰值.
考虑到环形桁架结构在设计时其高度和口径之比可能在一定范围内变化,为了检验不同高度和口径之比对等效模型精度的影响,这里使算例中的桁架高度在0.5倍到1.5倍范围内变化,比较有限元模型与等效圆环模型固有频率之间的误差,结果见图 6所示.
从图 6可以看出,当桁架高度在0.5倍到1.5倍范围内变化时,等效圆环模型计算的前5阶固有频率的误差变化幅度很小,并且误差均小于0.5%,说明考虑设计中桁架高度与口径之比在一定范围内变化时,等效圆环模型同样具有非常高的精度.
4 结论
本文将环形桁架结构等效为一个各向同性的弹性圆环,采用等效圆环模型分析了环形桁架结构的径向振动.利用圆环的解析运动方程计算得到了等效模型在复频域下的响应,以及固有振动的特征方程和传递函数.通过对环形桁架有限元模型与等效圆环解析模型的固有频率、固有振型以及传递函数的比较研究,表明在低频段一定的频率范围内,等效圆环解析模型与环形桁架有限元模型得到的固有频率、振型以及传递函数均能够吻合得很好,这说明采用等效圆环模型对环形桁架结构进行径向振动分析是可行的.
参考文献
| 1 |
司洪伟, 大挠性航天桁架结构动力学建模及其主动模糊控制研究.[博士论文]. 长沙:国防科学技术大学, 2006
( Si Hongwei. Research on dynamic modeling and active fuzzy control of large flexible space truss.[PhD Thesis]. Changsha:National University of Defense Technology, 2006(in Chinese)
) ( 0) 0)
|
| 2 |
Santiago-Prowald J, Baier H. Advances in deployable structures and surfaces for large apertures in space.
CEAS Space Journal,2013, 5 : 89-115.
DOI: 10.1007/s12567-013-0048-3. ( 0) 0)
|
| 3 |
胡海岩, 田强, 张伟, 等. 大型网架式可展开空间结构的非线性动力学与控制.
力学进展,2013, 43 (4) : 390-414.
( Hu Haiyan, Tian Qiang, Zhang Wei, et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes.
Advances in Mechanics,2013, 43 (4) : 390-414.
(in Chinese) ) ( 0) 0)
|
| 4 |
彭海军, 王文胜, 程耿东. 基于物理降阶模型的桁架结构振动主动控制.
工程力学,2013, 30 (12) : 1-7.
( Peng Haijun, Wang Wensheng, Cheng Gengdong. Active vibration control of a trussed structure based on the physical reduced model.
Engineering Mechanics,2013, 30 (12) : 1-7.
(in Chinese) ) ( 0) 0)
|
| 5 |
Salehian A, Seigler TM, Inman DJ. Control of the continuum model of a large flexible space structure. In:Proceedings of 2006 ASME International Mechanical Engineering Congress and Exposition, Chicago, USA, 2006. 561-570
( 0) 0)
|
| 6 |
王文胜. 复杂结构动力模型降阶方法研究.
力学与实践,2015, 37 (2) : 171-181.
( Wang Wensheng. Dynamic model reduction methods for complicated structures.
Mechanics in Engineering,2015, 37 (2) : 171-181.
(in Chinese) ) ( 0) 0)
|
| 7 |
Noor AK, Mikulas MM. Continuum modeling of large lattice structures:status and projections. NASA TP-2767, 1988
( 0) 0)
|
| 8 |
Lee U. Dynamic continuum plate representations of large thin lattice structure.
AIAA Journal,1993, 31 (9) : 1734-1736.
DOI: 10.2514/3.49104. ( 0) 0)
|
| 9 |
Bennett WH, Kwatny HG. Continuum modeling of flexible structures with application to vibration control.
AIAA Journal,1989, 7 (9) : 1264-1273.
( 0) 0)
|
| 10 |
Noor AK, Anderson MS, Green WH. Continuum models for beamand platelike lattice structures.
AIAA Journal,1978, 16 (12) : 1219-1228.
DOI: 10.2514/3.61036. ( 0) 0)
|
| 11 |
Noor AK, Nemeth MP. Analysis of spatial beamlike lattices with rigid joints.
Computer Methods in Applied Mechanics and Engineering,1980, 24 (1) : 35-59.
DOI: 10.1016/0045-7825(80)90039-0. ( 0) 0)
|
| 12 |
Noor AK, Russell WC. Anisotropic continuum models for beamlike lattice trusses.
Computer Methods in Applied Mechanics and Engineering,1986, 57 (3) : 257-277.
DOI: 10.1016/0045-7825(86)90141-6. ( 0) 0)
|
| 13 |
Sun CT, Liebbe SW. Global-local approach to solving vibration of large truss structures.
AIAA Journal,1990, 28 (2) : 303-308.
DOI: 10.2514/3.10389. ( 0) 0)
|
| 14 |
Necib B, Sun CT. Analysis of truss beams using a high order Timoshenko beam finite element.
Journal of Sound and Vibration,1989, 130 (1) : 149-159.
DOI: 10.1016/0022-460X(89)90525-7. ( 0) 0)
|
| 15 |
Salehian A, Inman DJ. Dynamic analysis of a lattice structure by homogenization:experimental validation.
Journal of Sound and Vibration,2008, 316 (1-5) : 180-197.
DOI: 10.1016/j.jsv.2008.02.031. ( 0) 0)
|
| 16 |
Salehian A, Ibrahim M, Seigler TM. Damping in periodic structures:A continuum modeling approach.
AIAA Journal,2014, 52 (3) : 569-590.
DOI: 10.2514/1.J052496. ( 0) 0)
|
| 17 |
Gonella S, Ruzzene M. Homogenization of vibrating periodic lattice structures.
Applied Mathematical Modelling,2008, 32 (4) : 459-482.
DOI: 10.1016/j.apm.2006.12.014. ( 0) 0)
|
| 18 |
Balakrishnan AV. Combined structures-controls-integrated optimization using distributed parameter models.
Computational Mechanics,1991, 8 (2) : 125-133.
DOI: 10.1007/BF00350616. ( 0) 0)
|
| 19 |
郭宏伟, 刘荣强, 邓宗全. 索杆铰接式伸展臂动力学建模与分析.
机械工程学报,2011, 47 (9) : 66-71.
DOI: 10.3901/JME.2011.09.066. ( Guo Hongwei, Liu Rongqiang, Deng Zongquan. Dynamic modeling and analysis of cable-strut deployable articulated mast.
Journal of Mechanical Engineering,2011, 47 (9) : 66-71.
(in Chinese) DOI: 10.3901/JME.2011.09.066. ) ( 0) 0)
|
| 20 |
Guo HW, Liu RQ, Deng ZQ. Dynamic analysis and nonlinear identification of space deployable structure.
Journal of Central South University,2013, 20 (5) : 1204-1213.
DOI: 10.1007/s11771-013-1603-y. ( 0) 0)
|
| 21 |
Liu LK, Shan JJ, Zhang Y. Dynamics modeling and analysis of spacecraft with large deployable hoop-truss antenna.
Journal of Spacecraft and Rockets,2016, 53 (3) : 471-479.
DOI: 10.2514/1.A33464. ( 0) 0)
|
| 22 |
Luo YJ, Xu ML, Yan B, et al. PD control for vibration attenuation in hoop truss structure based on a novel piezoelectric bending actuator.
Journal of Sound and Vibration,2015, 339 : 11-24.
DOI: 10.1016/j.jsv.2014.11.003. ( 0) 0)
|
| 23 |
刘福寿, 金栋平, 陈辉. 环形桁架结构动力分析的等效力学模型.
振动工程学报,2013, 26 (4) : 516-521.
( Liu Fushou, Jin Dongping, Chen Hui. An equivalent mechanics model for the dynamic analysis of hoop truss structures.
Journal of Vibration Engineering,2013, 26 (4) : 516-521.
(in Chinese) ) ( 0) 0)
|
| 24 |
Soedel W.
Vibration of Shells and Plates,3rd Edition. New York: Marcel Dekker, 2004 .
( 0) 0)
|
| 25 |
Rao SS.
Vibration of Continuous Systems. New Jersey: John Wiley & Sons, 2007 .
( 0) 0)
|
| 26 |
Archer RR. Small vibrations of thin incompleteffcircular rings.
International Journal of Mechanical Sciences,1960, 1 (1) : 45-56.
DOI: 10.1016/0020-7403(60)90029-1. ( 0) 0)
|
| 27 |
Zakrzhevskii AE, Tkachenko VF, Khoroshilov VS. Natural modes and frequencies of in-plane vibrations of a fixed elastic ring.
International Applied Mechanics,2010, 46 (12) : 1420-1427.
( 0) 0)
|
| 28 |
Ellison J, Ahmadi G, Kehoe M. Passive vibration control of airborne equipment using a circular steel ring.
Journal of Sound & Vibration,2001, 246 (1) : 1-28.
( 0) 0)
|
| 29 |
葛渭高, 李翠哲, 王宏洲.
常微分方程与边值问题. 北京: 科学出版社, 2008 .
( GeWeigao, Li Cuizhe, Wang Hongzhou.
Ordinary Differential Equations and Boundary Value Problems. Beijinig: Science Press, 2008 .
(in Chinese) ) ( 0) 0)
|
| 30 |
Yang B, Tan CA. Transfer functions of one-dimensional distributed parameter systems.
Journal of Applied Mechanics,1992, 59 (4) : 1009-1014.
DOI: 10.1115/1.2894015. ( 0) 0)
|
| 31 |
Pastor M, Binda M, Harčarik T. Modal assurance criterion.
Procedia Engineering,2012, 48 : 543-548.
DOI: 10.1016/j.proeng.2012.09.551. ( 0) 0)
|
EQUIVALENT CIRCULAR RING MODEL FOR THE RADIAL VIBRATION ANALYSIS OF HOOP TRUSS STRUCTURES
Liu Fushou,
Jin Dongping

State Key Laboratory of Mechanics and Control of Mechanical Structures, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China
Abstract:
In large deployable mesh antenna, the dynamic property of hoop truss is vital to the working performance of the whole antenna. For large space truss structures, the model simplification of these structures with simple elastic continuum model is always the focus of dynamics research. By regarding the hoop truss as a hoop periodic structure composed of repetitive planar truss elements, and based on the equivalent beam model of the repeated truss element, an equivalent circular ring model for the radial vibration analysis of the hoop truss structure is presented. By variable substitution, the fourth-order partial differential equations (PDEs) for the radial vibration of theffcircular ring are reduced to first-order PDEs, then the reduced PDEs are transform to ordinary differential equations via Laplace transform, Green's function method is utilized to solve the dynamic response of theffcircular ring in complex frequency domain. Furthermore the characteristic equations for natural vibration and the expression of transfer function of the equivalent ring model were derived. At last, a numerical example is used to compare the natural frequencies, mode shapes and transfer functions of the finite element model and the equivalent ring model of the hoop truss. The results verifies the feasibility of using equivalent circular ring model for radial vibration analysis of hoop truss structure.
Key words: hoop truss structure equivalent circular ring model Laplace transform transfer function natural vibration






 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 0)
0)
 2016, Vol. 48
2016, Vol. 48