在Biot[1-3]建立了多孔弹性介质波的传播理论后,弹性波在多孔介质中传播的问题在地震工程、岩土工程、海洋工程和声学等学科中受到广泛关注.Biot理论预言了一种新的压缩波的存在,即液体饱和多孔介质中除了存在与均质弹性体中的P波和S波有类似特征的快P1波和S波外,还存在一种慢P2波. Plona[4]最早证明其存在.
在Biot理论的基础上,国内外众多学者为饱和土波动理论的完善和发展起到了重要的推动作用.Deresiewicz等[5-11]对于波在饱和土界面上的传播特性进行了系统地研究.1960年其分析了波在自由表面分界面上的反折射波波幅系数比,此后将该工作扩展到考虑衰减项的情况.1964年Deresiewicz和Rice[8]分析了垂直入射时平面波在多孔介质分界面上的反射和透射.此后,Hajra和Mukhopadhyay[12]将该工作推广为更一般的斜入射情形,分析了饱和层状介质中入射角对反射系数和透射系数的影响,但忽略了由于液体黏性导致的衰减.Sharma与Gogna[13]在上述工作的基础上,讨论了考虑液体黏性导致的衰减情形下,弹性土与饱和土分界面上平面谐波的折反射情况.Deresiewicz等[10]采用传递矩阵法,分析了垂直入射时平面波在分层多孔介质中的反射和透射. 此后,Jocker 等[14]通过推广Thomson-Haskell传递矩阵法,以得到一种封闭形式的解析表达式,用于计算水平成层多孔介质的反射率和透射率.验证了该传递矩阵的稳定性范围,提出了影响稳定性的相关因素.Degrande等[15]考虑了在点源脉冲力的激励下,采用精确动力刚度矩阵分析了成层多孔介质的时频域响应.
门福录[16-17]、陈龙珠等[18]、王立忠等[19]和刘志军等[20]等从不同角度对饱和土体中弹性波的传播特性进行过研究. 梁建文等[21-22]、黄明汉等[23]、张卫平等[24]均利用精确动力刚度矩阵,着重点不同地研究了含饱和土的层状场地的动力响应及其随各参数的变化规律.董云和楼梦麟[25]导出了流体饱和两相多孔介质振动问题的有限元方程,利用对实际工程自由场所进行的数值模拟计算进行参数分析.丁伯阳等[26]实现了两相饱和介质层与单相介质层应力-位移函数的退化,实现不同维数矩阵间的结合.
周凤玺等[27-30]研究了非均匀饱和土层中平面波入射时波的传播特性及场地动力响应,考虑饱和土地基的物理力学特性沿厚度方向连续变化,利用亥姆霍兹矢量分解原理和动力刚度法,分析了平面入射P/SV波在非均匀饱和土层中的反射和透射,并给出了基岩表面和自由表面处反射系数和透射系数的计算表达式.陈炜昀等[31-32]又将研究发展到非饱和土上.
以上工作大多讨论波在饱和土层中的反折射性质.在地震工程和海洋工程领域,在分析饱和土与结构动力相互作用或考虑海底地形对地震波的散射问题时,一般需要先求解地震波入射时饱和土层的自由场响应,而不仅仅是地震波在饱和土层中的传播特性.因此有必要考虑饱和土层在地震波入射时自由场响应问题,并讨论传递矩阵法在饱和层状介质自由场分析中的数值计算问题.
1 基本理论为了分析上述问题,我们考虑如下的模型:假设$n -1$个均匀饱和土层覆盖在均匀弹性半空间的基岩之上. 图 1中$h_{j}$, $\rho_{j}$,$\varphi_{j}$,$\mu_{j}$,$K_{{\rm b}j}$,$K_{{\rm s}j}$和 $k_{0j}$分别表示第$j$层的层厚、质量密度、孔隙率、剪切模量、排水体积模量、不排水体积模量、渗透率. $j =1,2,\cdots ,n$.坐标系采用分层建立的方法:每层坐标系的原点选在该层的顶面上,图中示出第$j$层采用的坐标系.假设平面地震波自下卧基岩向饱和覆盖层入射.

|
图 1 弹性半空间基岩上覆成层饱和土模型示意图 Figure 1 Schematic diagram of layered saturated soil on elastic half space |
根据Biot[1]多孔介质理论,考虑由于液体相对固体流动产生的衰减因素,用${ u}$表示固相位移,用${ U}$表示液相位移,运动方程可以按如下表示
| $ \left.\!\! N\nabla ^2{ u} + \nabla \left[{(D + N)\nabla \cdot { u} + Q\nabla \cdot { U} } \right] =\\ \dfrac{\partial ^2}{\partial t^2}\left( {\rho _{11} { u} + \rho _{12} { U }} \right) + \eta \dfrac{\partial }{\partial t}\left( {{ u} - { U} } \right) \\ \nabla \left[ {Q\nabla \cdot { u } + R\nabla \cdot { U }} \right] = \\ \dfrac{\partial ^2}{\partial t^2}\left( {\rho _{12} { u } + \rho _{22} { U }} \right) - \eta \dfrac{\partial }{\partial t}\left( {{ u } - { U }} \right) \!\!\right\} $ | (1) |
其中$D$,$N$,$Q$,$R$为非负弹性常数; $\rho_{11}$,$\rho_{12}$,$\rho_{22}$为介质密度; $\eta $ 是一衰减函数. 考虑到实际工程应用中多处于低频段,故在低频段,衰减函数可以简化为
| $ \eta = {\overline \mu \phi ^2} / {k_0 } $ | (2) |
其中$\overline \mu $为流体动力黏度.
根据亥姆霍兹矢量分解原理,固液位移矢量可以表示为
| $ { u} = \nabla \varphi + \nabla \times { K} , \quad { U } = \nabla \vartheta + \nabla \times { G } $ | (3) |
假定时间以简谐形式${\rm e}^{ -{\rm i}wt}$变化
| $\begin{align} & \varphi \left( {{x}_{k}},t \right)=\bar{\varphi }\left( {{x}_{k}},t \right){{\text{e}}^{\text{i}wt}}\vartheta \left( {{x}_{k}},t \right)= \\ & \bar{\vartheta }\left( {{x}_{k}},t \right){{\text{e}}^{\text{i}wt}}K\left( {{x}_{k}},t \right)=\bar{K}\left( {{x}_{k}},t \right){{\text{e}}^{\text{i}wt}}G\left( {{x}_{k}},t \right)=\bar{G}\left( {{x}_{k}},t \right){{\text{e}}^{\text{i}wt}} \\ \end{align}$ | (4) |
将式(3)代入场方程(1)中,可以发现其解的形式如下
| $ \left.\!\! \varphi = \overline \varphi _1 + \overline \varphi _2 \\ \vartheta = \beta _1 \overline \varphi _1 + \beta _2 \overline \varphi _2 \\ { G} = \alpha _0 { K} \!\!\right\} $ | (5) |
那么
| $ \left( {\nabla ^2 + \delta _j^2 } \right)\overline \varphi _j = 0 ,\ j =1,2 ,\left( {\nabla ^2 + \delta _3^2 } \right)\overline { K} = {\bf 0} $ | (6) |
其中我们定义
| $ P = D + 2N ,\quad M = P + 2Q + R ,\quad \rho = \rho _{11} + 2\rho _{12} + \rho _{22} \\ \sigma _{11} = P/M ,\quad \sigma _{12} = Q / M ,\quad \sigma _{22} = R / M \\ \gamma _{11} = {\rho _{11} } /\rho ,\quad \gamma _{12} = {\rho _{12} }/\rho ,\quad \gamma _{22} = {\rho _{22} }/ \rho \\ A = \sigma _{11} \sigma _{22} - \sigma _{12}^2 ,\quad B = \gamma _{11} \sigma _{22} + \gamma _{22} \sigma _{11} - 2\gamma _{12} \sigma _{12} \\ C = \gamma _{11} \gamma _{22} - \gamma _{12}^2 ,\quad b = \sigma _{12} + \sigma _{22} \\ g = \gamma _{11} \sigma _{22} - \gamma _{12} \sigma _{12} ,\quad h = \gamma _{22} \sigma _{12} - \gamma _{12} \sigma _{22} \\ f = \eta /{\rho \omega } ,\quad \delta _0^2 = {\rho \omega ^2} / M \\ \varDelta ^2 = B^2 - 4AC-2{\rm i}f\left( {B - 2A} \right) - f^2 ,\quad \delta _j^2 = \delta _0^2 \varLambda _j \\ \varLambda _{1,2} = {\left( {B - {\rm i}f \mp \varDelta } \right)}/{2A} \\ \varLambda _3 = {\left( {M / N} \right)\left( {C-{\rm i} f} \right)} / {\left( {\gamma _{22} - {\rm i}f} \right)} \\ \beta _{1,2} = \dfrac{g - {\rm i}bf - A\varLambda _{1,2} }{h - {\rm i}bf} , \quad \alpha _0 =-\dfrac{\gamma _{12} + {\rm i}f}{\gamma _{22} - {\rm i}f} $ |
从式(6)中,可以注意到在多孔饱和介质中,会存在两种压缩波和一种剪切波. 这些波的相速度可以表示为
| $ c_k = \left( {M/ \rho } \right)^{1/ 2} \Big/ Re\left( {\varLambda _k^{1 / 2} } \right) ,k =1,2,3 $ | (7) |
以上这些参数中$k =1$表示第1种压缩波P1;$k =2$表示第2种压缩波P2;$k =3$表示剪切波SV.
针对3种不同的波,式(6)的解(根据式(4)第1和3项,恢复简谐变化时间的存在)最终可以写成
| $ \left.\!\! \varphi _k = E_{{\rm P}k} {\rm e}^{{\rm i}\left[{\omega t - \delta _k \left( {x_1 w_{k1} - x_3 w_{k3} } \right)} \right]} + \\ F_{{\rm P}k} {\rm e}^{{\rm i}\left[{\omega t - \delta _k \left( {x_1 w_{k1} + x_3 w_{k3} } \right)} \right]} ,k = 1,2 \\ \psi _1 = E_{\rm S}{\rm e}^{{\rm i}\left[{\omega t - \delta _3 \left( {x_1 w_{31} - x_3 w_{33} } \right)} \right]} + \\ F_{\rm S} {\rm e}^{{\rm i}\left[{\omega t - \delta _3 \left( {x_1 w_{31} + x_3 w_{33} } \right)} \right] } \!\!\right\} $ | (8) |
其中$\psi_{1}$表示${ K}$非零分量,也表示SV波的位势; $\varphi_{1}$,$\varphi_{2}$分别表示为P1波、P2波;$E_{\rm P1}$,$E_{\rm P2}$,$E_{\rm S}$分别表示为对应波上行位势幅值;$F_{\rm P1}$,$F_{\rm P2}$,$F_{\rm S}$分别表示为对应波下行位势幅值;$w_{k1}$和$w_{k3}$表示单位方向向量在$x_{1}$和 $x_{3}$两方向的分量. 假设入射波从基岩以 $\theta $ 角入射,根据斯奈尔定理,各平面谐波沿$x_{1}$轴的水平波数相同$k_1 = \delta _k w_{k1} = \dfrac{\omega }{c_k }\sin \theta $,所以$w_{k1}$和 $w_{k3}$可以按如下表示
| $ \left. w_{k1} = {\left( {\omega /{c_k } \cdot \sin \theta } \right)}/{\delta _k }\\ w_{k3} = \left( {1 - w_{k1}^2 } \right)^{1/2} k=1,2,3 \right\} $ | (9) |
因此,如果我们考虑$x_{1}-x_{3}$二维波动情况,经过推导固液位移可以由位势表达式表示为
| $ \left.\!\! \begin{array}{l} u_1 = \dfrac{\partial \varphi _1 }{\partial x_1 } + \dfrac{\partial \varphi _2 }{\partial x_1 } + \dfrac{\partial \psi _1 }{\partial x_3 } \\ u_3 = \dfrac{\partial \varphi _1 }{\partial x_3 } + \dfrac{\partial \varphi _2 }{\partial x_3 } - \dfrac{\partial \psi _1 }{\partial x_1 } \\ U_1 = \beta _1 \dfrac{\partial \varphi _1 }{\partial x_1 } + \beta _2 \dfrac{\partial \varphi _2 }{\partial x_1 } + \alpha _0 \dfrac{\partial \psi _1 }{\partial x_3 } \\ U_3 = \beta _1 \dfrac{\partial \varphi _1 }{\partial x_3 } + \beta _2 \dfrac{\partial \varphi _2 }{\partial x_3 } - \alpha _0 \dfrac{\partial \psi _1 }{\partial x_1 } \end{array}\!\!\right\} $ | (10) |
再根据Boit理论[2],土体中固液相应力可以表示为
| $ \left.\begin{array}{l} \sigma _{ij} = (De_{kk} + Q\varepsilon _{kk} )\delta _{ij} + 2Ne_{ij} \\ \tau = - \phi p = Qe_{kk} + R\varepsilon _{kk}\\ e_{ij} = \dfrac{1}{2}(u_{i,j} + u_{j,i} ) ,i,j=1,3 \end{array} ,k=i,j \right\} $ | (11) |
其中$\delta_{ij}$表示克罗内克系数,$e_{kk} = \nabla \cdot {u}$,$\varepsilon _{kk} = \nabla \cdot { U}$,$p$为孔压.
根据Bullen理论[33],均质弹性土基岩场方程可以描述为
| $ \left( {\lambda _n + 2\mu _n } \right)\nabla \left( {\nabla \cdot { u}_n } \right) - \mu \nabla \times \left( {\nabla \times { u }_n } \right) =\\ \rho _n \dfrac{\partial ^2{ u }_n }{\partial t^2} $ | (12) |
其中$\lambda_{n}$,$\mu_{n}$是拉梅常数,$\rho_{n}$是基岩密度. 用推导饱和土物理参量相同的方法,可以假设均匀弹性介质内平面谐波P波和SV波的位势$\varphi_{n}$,$\psi _{n}$可以表示为
| $ \left.\!\! \varphi _n = E_{{\rm P}n} {\rm e}^{{\rm i} \left[{\omega t - k_1 x_1 + k_{3{\rm P}n} x_3 } \right]} + F_{{\rm P}n} {\rm e}^{{\rm i}\left[{\omega t - k_1 x_1 - k_{3{\rm P}n} x_3 } \right]} \\ \psi _n = E_{{\rm S}n }{\rm e}^{{\rm i}\left[{\omega t - k_1 x_1 + k_{3{\rm S}n} x_3 } \right]} + F_{{\rm S}n } {\rm e}^{{\rm i}\left[{\omega t - k_1 x_1 - k_{3{\rm S}n} x_3 } \right]} \!\!\right\} $ | (13) |
当P波入射时式(13)中
| $ E_{{\rm S}n} = 0 ,\quad k_1 = (\omega/ c_{{\rm P}n}) \sin \theta ,\quad k_{3{\rm P}n} = (\omega / {c_{{\rm P}n} } ) \cos \theta \\ k_{3{\rm S}n} = \sqrt {\dfrac{\omega ^2}{c_{{\rm S}n}^2 } - \dfrac{\omega ^2}{c_{{\rm P}n}^2 }\sin ^2\theta } $ |
当SV波入射时式(13)中
| $\begin{align} & {{E}_{\text{P}n}}=0,{{k}_{1}}=(\omega /{{c}_{\text{S}n}})\sin \theta ,{{k}_{3\text{S}n}}=(\omega /{{c}_{\text{S}n}})\cos \theta \\ & {{k}_{3\text{P}n}}=\sqrt{\frac{{{\omega }^{2}}}{c_{\text{P}n}^{2}}-\frac{{{\omega }^{2}}}{c_{\text{S}n}^{2}}{{\sin }^{2}}\theta },\sin \theta \frac{{{c}_{\text{S}n}}}{{{c}_{\text{P}n}}}-\text{i}\sqrt{\frac{{{\omega }^{2}}}{c_{\text{S}n}^{2}}{{\sin }^{2}}\theta -\frac{{{\omega }^{2}}}{c_{\text{P}n}^{2}}}, \\ & \sin \theta >\frac{{{c}_{\text{S}n}}}{{{c}_{\text{P}n}}} \\ \end{align}$ |
其中$\varphi_{n}$,$\psi_{n}$可以分别表示基岩中P波、SV波的位势;$E_{{\rm P}n}$,$E_{{\rm S}n}$分别表示为对应波上行位势幅值;$F_{{\rm P}n}$,$F_{{\rm S}n}$分别表示为对应波下行位势幅值;$c_{{\rm P}n}$为入射P波波速,$c_{{\rm S}n}$为入射SV波波速.
弹性介质位移、应力用位势可表达为
| $\begin{align} & {{u}_{1n}}=\frac{\partial {{\varphi }_{n}}}{\partial {{x}_{1}}}+\frac{\partial {{\psi }_{n}}}{\partial {{x}_{3}}} \\ & {{u}_{3n}}=\frac{\partial {{\varphi }_{n}}}{\partial {{x}_{3}}}-\frac{\partial {{\psi }_{n}}}{\partial {{x}_{1}}} \\ & \left. \begin{array}{*{35}{l}} {{\sigma }_{33n}}=\left( \lambda +2\mu \right){{\varphi }_{n,ii}}-2\mu \left( {{\psi }_{n,{{x}_{1}}{{x}_{3}}}}+{{\varphi }_{n,{{x}_{1}}{{x}_{1}}}} \right) \\ {{\sigma }_{13n}}=\mu \left( 2{{\varphi }_{n,{{x}_{1}}{{x}_{3}}}}-{{\psi }_{n,{{x}_{1}}{{x}_{1}}}}+{{\psi }_{n,{{x}_{3}}{{x}_{3}}}} \right) \\ \end{array},i={{x}_{1}},{{x}_{3}} \right\} \\ \end{align}$ | (14) |
在自由表面:$\sigma _{33} = \sigma _{13} = p = 0$
在饱和土层分界面上,以下6个物理量保持连续:固相法向位移$u_{3}$、切向固相切向位移$u_{1}$、正应力$\sigma_{33}+\tau $、剪应力$\sigma_{13}$、孔压$p$、固液相平均法向相对位移$\varphi $ ($U_{3}-u_{3}$).
在饱和土与基岩分界面处:
(1) 法向固相位移连续:$u_{n3} = u_3 $
(2) 切向固相位移连续:$u_{n1} = u_1 $
(3) 总的正应力保持连续:$\sigma _{n33} = \sigma _{33} + \tau $
(4) 剪应力保持连续:$\sigma _{n13} = \sigma _{13} $
(5) 饱和土体在界面上固液相相对法向位移为零:$U_3 - u_3 = 0$.
1.3 传递矩阵第一,假设饱和土体中第$j$层波幅矢${ H}_{j}$和应力-位移矢${ S}_{j}$如下
| $ { H}_j = \left( { E_{{\rm P}1j} ,F_{P1j} ,E_{p2j} ,F_{p2j} ,E_{sj} ,F_{sj} } \right)^{\rm T} \\ \hskip 2cm j=1,2,\cdots,n-1 $ | (15) |
| ${ S }_j = \left( {u_{3j} ,u_{1j} ,\sigma _{33j} + \tau _j ,\sigma _{13j} ,p_j ,\phi _j \left( {U_{3j} - u_{3j} } \right)} \right)^{\rm T} \\ \hskip 2cm j=1,2,\cdots,n-1 $$ | (16) |
通过6×6的转换矩阵${ T}_{{\rm S}j}$可以把上述两者联系起来
| $ { S}_j = { T}_{{\rm S}j} { H}_j $ | (17) |
那么相邻层波幅矢和应力-位移矢的转换关系类似于式(18)
| $ { S }_{j + 1} = { T }_{{\rm S}j + 1} { H }_{j + 1} $ | (18) |
按照所选用的局部坐标系,饱和土体中相邻层间必须满足如下的位移和应力的连续条件
| $ \left. {{ S }_j } \right|_{x_3 = h_j } = \left. {{ S }_{j + 1} } \right|_{x_3 = 0} $ | (19) |
将式(17)和式(18)代入式(19)得到
| $ \left. {{ T}_{{\rm S}j} } \right|_{x_3 = h_j } { H}_j = \left.{{ T}_{{\rm S}(j + 1)} } \right|_{x_3 = 0} { H}_{j + 1} $ | (20) |
经整理,相邻层波幅矢${ H}_{j + 1}$和${ H}_{j}$之间的转换关系可用传递矩阵${ T}_{j}$表示
| $ { H }_{j + 1} = { T}_j { H}_j = \left. {{ T}_{{\rm S}(j + 1)} } \right|_{x_3 = 0}^{ - 1} \cdot \left. { { T}_{{\rm S}j} } \right|_{x_3 = h_j } \cdot { H}_j $ | (21) |
式中转换矩阵${ T}_{{\rm S}j}$通过联列方程组可以得到6$\times $6阶系数矩阵,以下矩阵元素所用参数都使用对应于第$j$层的参数,这里略去了下标$j$
| $\begin{align} & {{t}_{\text{S}j11}}=\text{i}{{\delta }_{1}}{{w}_{13}}{{\text{e}}^{\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}},{{t}_{\text{S}j12}}=-\text{i}{{\delta }_{1}}{{w}_{13}}{{\text{e}}^{-\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j13}}=\text{i}{{\delta }_{2}}{{w}_{23}}{{\text{e}}^{\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}},{{t}_{\text{S}j14}}=-\text{i}{{\delta }_{2}}{{w}_{23}}{{\text{e}}^{-\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j15}}=\text{i}{{\delta }_{3}}{{w}_{33}}{{\text{e}}^{\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}},{{t}_{\text{S}j16}}=\text{i}{{\delta }_{3}}{{w}_{33}}{{\text{e}}^{-\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ & {{t}_{\text{S}j21}}=-\text{i}{{\delta }_{1}}{{w}_{11}}{{\text{e}}^{\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}},{{t}_{\text{S}j22}}=-\text{i}{{\delta }_{1}}{{w}_{11}}{{\text{e}}^{-\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j23}}=-\text{i}{{\delta }_{2}}{{w}_{21}}{{\text{e}}^{\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}},{{t}_{\text{S}j24}}=-\text{i}{{\delta }_{2}}{{w}_{21}}{{\text{e}}^{-\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j25}}=\text{i}{{\delta }_{3}}{{w}_{33}}{{\text{e}}^{\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}},{{t}_{\text{S}j26}}=-\text{i}{{\delta }_{3}}{{w}_{33}}{{\text{e}}^{-\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ & {{t}_{\text{S}j31}}=-\left[ D+\left( R+Q \right){{\beta }_{1}}+Q+2Nw_{13}^{2} \right]\delta _{1}^{2}{{\text{e}}^{\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j32}}=-\left[ D+\left( R+Q \right){{\beta }_{1}}+Q+2Nw_{13}^{2} \right]\delta _{1}^{2}{{\text{e}}^{-\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j33}}=-\left[ D+\left( R+Q \right){{\beta }_{2}}+Q+2Nw_{23}^{2} \right]\delta _{2}^{2}\text{ei}{{\delta }_{2}}{{w}_{23}} \\ & {{x}_{3}}{{t}_{\text{S}j34}}=-\left[ D+\left( R+Q \right){{\beta }_{2}}+Q+2Nw_{23}^{2} \right]\delta _{2}^{2}{{\text{e}}^{-\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{sj35}}=-2N\delta _{3}^{2}{{w}_{31}}{{w}_{33}}{{\text{e}}^{\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}}{{t}_{\text{S}j36}}=2N\delta _{3}^{2}{{w}_{31}}{{w}_{33}}{{\text{e}}^{-\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ & {{t}_{\text{S}j41}}=2N\delta _{1}^{2}{{w}_{11}}{{w}_{13}}{{\text{e}}^{\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}}{{t}_{\text{S}j42}}=-2N\delta _{1}^{2}{{w}_{11}}{{w}_{13}}{{\text{e}}^{-\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j43}}=2N\delta _{2}^{2}{{w}_{21}}{{w}_{23}}{{\text{e}}^{\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j44}}=-2N\delta _{2}^{2}{{w}_{21}}{{w}_{23}}{{\text{e}}^{-\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j45}}=-N\delta _{3}^{2}w_{33}^{2}-w_{31}^{2}{{\text{e}}^{\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ & {{t}_{\text{S}j46}}=-N\delta _{3}^{2}\left( w_{33}^{2}-w_{31}^{2} \right){{\text{e}}^{-\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ & {{t}_{\text{S}j51}}=\frac{Q+R{{\beta }_{1}}}{\phi }\delta _{1}^{2}{{\text{e}}^{\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}},{{t}_{\text{S}j52}}=\frac{Q+R{{\beta }_{1}}}{\phi }\delta _{1}^{2}{{\text{e}}^{-\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j53}}=\frac{Q+R{{\beta }_{2}}}{\phi }\delta _{2}^{2}{{\text{e}}^{\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}},{{t}_{\text{S}j54}}=\frac{Q+R{{\beta }_{2}}}{\phi }\delta _{2}^{2}{{\text{e}}^{-\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j55}}=0,{{t}_{sj56}}=0 \\ & {{t}_{\text{S}j61}}=\text{i}\phi ({{\beta }_{1}}-1){{\delta }_{1}}{{w}_{13}}{{\text{e}}^{\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j62}}=-\text{i}\phi ({{\beta }_{1}}-1){{\delta }_{1}}{{w}_{13}}{{\text{e}}^{-\text{i}{{\delta }_{1}}{{w}_{13}}{{x}_{3}}}} \\ & {{t}_{\text{S}j63}}=\text{i}\phi ({{\beta }_{2}}-1){{\delta }_{2}}{{w}_{23}}{{\text{e}}^{\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j64}}=-\text{i}\phi ({{\beta }_{2}}-1){{\delta }_{2}}{{w}_{23}}{{\text{e}}^{-\text{i}{{\delta }_{2}}{{w}_{23}}{{x}_{3}}}} \\ & {{t}_{\text{S}j65}}=\text{i}\phi ({{\alpha }_{0}}-1){{\delta }_{3}}{{w}_{31}}{{\text{e}}^{\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ & {{t}_{\text{S}j66}}=\text{i}\phi ({{\alpha }_{0}}-1){{\delta }_{3}}{{w}_{31}}{{\text{e}}^{-\text{i}{{\delta }_{3}}{{w}_{33}}{{x}_{3}}}} \\ \end{align}$ |
所以根据递推公式(21)可以将饱和土中任意层的波幅矢和首层的波幅矢联系起来
| $ { H }_j = { T }_{j1} { H }_1 $ | (22) |
其中
| $ { T }_{j1} = { T }_{j-1} \cdot { T }_{j-2} \cdots { T}_1 $ | (23) |
6×6方阵${ T}_{j1}$中的元素$t_{jkl}$与饱和土第一到第$j$层介质的力学性质、层厚、频率等有关. 所以若已知饱和土首层波幅矢${ H}_{1}$,即可通过传递矩阵得到饱和土体中任意层波幅矢${ H}_{j}$. 此时${ H}_{1}$中有6个未知量.
第二,假设饱和土顶层内上行P1,P2和SV波分别为
| $ E_{{\rm P}11} {\rm e}^{{\rm i}\left[{wt - k_1 x_1 + k_{3{\rm P}11} x_3 } \right]} \\ E_{{\rm P}21} {\rm e}^{{\rm i}\left[{wt - k_1 x_1 + k_{3{\rm P}21} x_3 } \right]} \\ E_{{\rm S}1} {\rm e}^{{\rm i}\left[{wt - k_1 x_1 + k_{3{\rm S}1} x_3 } \right]} $ |
其中$k_{1}$为水平波数不变量,$k_{3{\rm P}11} = \delta _1 w_{13} $,$k_{3{\rm P}21} = \delta _2 w_{23} $,$k_{3{\rm S}1} = \delta _3 w_{33} $,为依次采用首层参数计算所得. 上行的这3种波反射时各自都会发生波形转换,产生下行的P1,P2,SV波,所以顶层全部反射的P1,P2和SV波的波幅系数可以表示为
| $ \left.\!\!\begin{array}{l} F_{{\rm P}11} = k_{\rm P1P1} E_{\rm p11} + k_{\rm P2P1} E_{\rm P21} + k_{\rm SP1} E_{\rm S1} \\ F_{{\rm P}21} = k_{\rm P1P2} E_{\rm P11} + k_{\rm P2P2} E_{\rm P21} + k_{\rm SP2} E_{\rm S1} \\ F_{\rm S1} = k_{\rm P1S} E_{\rm P11} + k_{\rm P2S} E_{\rm P21} + k_{\rm SS} E_{\rm S1} \end{array} \!\!\right\} $ | (24) |
式(24)中,$k_{{s}t}$表示自由表面处的反射系数,$s$表示原因项,$t$表示结果项,如$k_{\rm P1P2}$表示P1波入射时反射P2波的波幅幅值比. 反射系数根据自由表面处边界条件式计算所得. 因此,顶层波幅矢${ H}_{1}$可以写成
| $ { H }_1 = (E_{\rm P11} ,k_{\rm P1P1} E_{\rm P11} + k_{\rm P2P1} E_{\rm P21} + k_{\rm SP1} E_{\rm S1} ,\\ E_{\rm P21} ,k_{\rm P1P2} E_{\rm P11} + k_{\rm P2P2} E_{\rm P21} + k_{\rm SP2} E_{\rm S1} ,\\ E_{\rm S1} ,k_{\rm P1S} E_{\rm P11} + k_{\rm P2S} E_{\rm P21} + k_{\rm SS} E_{\rm S1} )^{\rm T} $ | (25) |
此时${ H}_{1}$中未知量个数简化到3个.
第三,假设第$n$层基岩中波幅矢${ H}_{n}$和应力-位移矢${ S}_{n}$如下
| $ { H }_n = \left( {E_{{\rm P}n} ,F_{{\rm P}n} ,E_{{\rm S}n} ,F_{{\rm S}n} } \right)^{\rm T} $ | (26) |
| $ { S }_n = \left( {u_{ex3} ,u_{ex1} ,\sigma _{e33} ,\sigma _{e13} } \right)^{\rm T} $ | (27) |
同样的方法,可通过4×4的转换矩阵${ T}_{{\rm S}n}$可以把上述两者联系起来
| $ { S}_n = { T}_{{\rm S}n} { H}_n $ | (28) |
同理,可以得到${ T}_{{\rm S}n}$的表达式
| $\begin{align} & {{t}_{\text{S}n11}}=\text{i}{{k}_{3\text{P}n}}{{\text{e}}^{\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}},{{t}_{\text{S}n12}}=-\text{i}{{k}_{3\text{P}n}}{{\text{e}}^{-\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}} \\ & {{t}_{\text{S}n13}}=\text{i}{{k}_{1}}{{\text{e}}^{\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}},{{t}_{\text{S}n14}}=\text{i}{{k}_{1}}{{\text{e}}^{-\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}} \\ & {{t}_{\text{S}n21}}=-\text{i}{{k}_{1}}{{\text{e}}^{\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}},{{t}_{\text{S}n22}}=-\text{i}{{k}_{1}}{{\text{e}}^{-\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}} \\ & {{t}_{\text{S}n23}}=\text{i}{{k}_{3\text{S}n}}{{\text{e}}^{\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}},{{t}_{\text{S}n24}}=-\text{i}{{k}_{3\text{P}n}}{{\text{e}}^{-\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}}t \\ & {{t}_{\text{S}n31}}={{\mu }_{n}}{{k}_{22}}{{\text{e}}^{\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}},{{t}_{\text{S}n32}}={{\mu }_{n}}{{k}_{22}}{{\text{e}}^{-\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}} \\ & {{t}_{\text{S}n33}}=-2{{\mu }_{n}}{{k}_{1}}{{k}_{3\text{S}n}}{{\text{e}}^{\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}},{{t}_{\text{S}n34}}=2{{\mu }_{n}}{{k}_{1}}{{k}_{3\text{S}n}}{{\text{e}}^{-\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}} \\ & {{t}_{\text{S}n41}}=2{{\mu }_{n}}{{k}_{1}}{{k}_{3\text{P}n}}{{\text{e}}^{\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}},{{t}_{\text{S}n42}}=-2{{\mu }_{n}}{{k}_{1}}{{k}_{3\text{P}n}}{{\text{e}}^{-\text{i}{{k}_{3\text{P}n}}{{x}_{3}}}} \\ & {{t}_{\text{S}n43}}={{\mu }_{n}}{{k}_{33}}{{\text{e}}^{\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}},\quad {{t}_{\text{S}n44}}={{\mu }_{n}}{{k}_{33}}{{\text{e}}^{-\text{i}{{k}_{3\text{S}n}}{{x}_{3}}}} \\ \end{align}$ |
式中,$k_{22} = - \left( {k_1^2 + k_{3{\rm P}n}^2 } \right)\left( {{c_{{\rm P}n}^2 } / {c_{{\rm S}n}^2 }} \right) + 2k_1^2 $,$k_{33} = k_1^2 - k_{3{\rm S}n}^2 $.
根据饱和土层与基岩分界面处的边界条件中的前四式,可以用矩阵形式整理为
| $ \left( {\left. {{ T}_{{\rm S}n} } \right|_{x_3 = 0} } \right)_{4\times 4} \left( {{ H}_n } \right)_{4\times 1} = \left( {\left. {{ T}'_{{\rm S}\left( {n - 1} \right)} } \right|_{x_3 = h_{n - 1} } } \right)_{4\times 6} \left( {{ H}_{n - 1} } \right)_{6\times 1} $ | (29) |
式中${ T}'_{{\rm S}\left( {n - 1} \right)} $矩阵为饱和土层中第$n- 1$层的转换矩阵的前四行.
再令式(22)中$j=n- 1$,并将其代入式(29)得
| $ \left( {\left. {{ T}_{{\rm S}n} } \right|_{x_3 = 0} } \right)_{4\times 4} \left( {{ H}_n } \right)_{4\times 1} =\\ \left( {\left. {{ T}'_{{\rm S}\left( {n - 1} \right) } } \right|_{x_3 = h_{n - 1} } } \right)_{4\times 6} \left( {{ T}_{(n - 1)1} } \right)_{6\times 6} \left( {{ H}_1 } \right)_{6\times 1} $ | (30) |
将式(30)进行整理可以得到基岩层波幅矢${ H}_{n}$与饱和土首层波幅矢${ H}_{1}$的关系式
| $ { H}_n = T_{n1} { H}_1 = \left. {{ T}_{{\rm S}n} } \right|_{x_3 = 0}^{ - 1} \cdot \left. {{ T}'_{{\rm S}\left( {n - 1} \right)} } \right|_{x_3 = h_{n - 1} } \cdot { T}_{(n - 1)1} \cdot { H }_1 $ | (31) |
式(31)中${ T}_{n1}$是一个4$\times $6的矩阵,相当于可联列4个方程. 根据式(25),${ H}_{1}$中有3个未知数$E_{{\rm P}11}$,$E_{{\rm P}21}$和$E_{{\rm S}1}$. 当P波入射时,${ H}_{n}$中$E_{{\rm P}n}=1$,$E_{{\rm S}n} =0$;当SV波入射时,${ H} _{n}$中$E_{{\rm S}n} =1$,$E_{{\rm P}n} =0$;故${ H}_{n}$中有2个未知数$F_{{\rm P}n}$和$E_{{\rm P}n}$. 未知量个数多于方程个数,在此需要补充方程,即饱和土与基岩分界面边界条件式中最后一式,假设基岩的不可透水性质,据此将${ T} _{n1}$扩展一行元素,形成为一个5×6的矩阵. 因此,经过最终整理可以得到如下标量方程
| $ \left.\!\!\begin{array}{l} E_{{\rm P}n} = a_{11} E_{{\rm P}11} + a_{12} E_{{\rm P}21} + a_{13} E_{{\rm S}1} \\ F_{{\rm P}n} = a_{21} E_{{\rm P}11} + a_{22} E_{{\rm P}21} + a_{23} E_{{\rm S}1} \\ E_{{\rm S}n} = a_{31} E_{{\rm P}11} + a_{32} E_{{\rm P}21} + a_{33} E_{{\rm S}1} \\ F_{{\rm S}n} = a_{41} E_{{\rm P}11} + a_{42} E_{{\rm P}21} + a_{43} E_{{\rm S}1} \\ 0 = a_{51} E_{{\rm P}11} + a_{52} E_{{\rm P}21} + a_{53} E_{{\rm S}1} \end{array}\!\!\right\} $ | (32) |
其中
| $\begin{array}{*{35}{l}} {{a}_{11}}={{t}_{n11}}+{{t}_{n12}}{{k}_{\text{P1P1}}}+{{t}_{n14}}{{k}_{\text{P1P2}}}+{{t}_{n16}}{{k}_{\text{P1S}}} \\ {{a}_{12}}={{t}_{n12}}{{k}_{\text{P2P1}}}+{{t}_{n13}}+{{t}_{n14}}{{k}_{\text{P2P2}}}+{{t}_{n16}}{{k}_{\text{P2S}}} \\ {{a}_{13}}={{t}_{n12}}{{k}_{\text{SP1}}}+{{t}_{n14}}{{k}_{\text{SP2}}}+{{t}_{n15}}+{{t}_{n16}}{{k}_{\text{SS}}} \\ {{a}_{31}}={{t}_{n31}}+{{t}_{n32}}{{k}_{\text{P1P1}}}+{{t}_{n34}}{{k}_{\text{P1P2}}}+{{t}_{n36}}{{k}_{\text{P1S}}} \\ {{a}_{32}}={{t}_{n32}}{{k}_{\text{P2P1}}}+{{t}_{n33}}+{{t}_{n34}}{{k}_{\text{P2P2}}}+{{t}_{n36}}{{k}_{\text{P2S}}} \\ {{a}_{33}}={{t}_{n32}}{{k}_{\text{SP1}}}+{{t}_{n34}}{{k}_{\text{SP2}}}+{{t}_{n35}}+{{t}_{n36}}{{k}_{\text{SS}}} \\ {{a}_{51}}={{t}_{n51}}+{{t}_{n52}}{{k}_{\text{P1P1}}}+{{t}_{n54}}{{k}_{\text{P1P2}}}+{{t}_{n56}}{{k}_{\text{P1S}}} \\ {{a}_{52}}={{t}_{n52}}{{k}_{\text{P2P1}}}+{{t}_{n53}}+{{t}_{n54}}{{k}_{\text{P2P2}}}+{{t}_{n56}}{{k}_{\text{P2S}}} \\ {{a}_{53}}={{t}_{n52}}{{k}_{\text{SP1}}}+{{t}_{n54}}{{k}_{\text{SP2}}}+{{t}_{n55}}+{{t}_{n56}}{{k}_{\text{SS}}} \\ \end{array}$ |
$t_{nkl}$表示5×6矩阵${ T}_{n1}$中的元素.
取式(32)中的第一、第三和第五 3式解得顶层上行波波幅系数
| $ \left.\!\! \begin{array}{l} E_{{\rm P}11} = b_{11} E_{{\rm P}n} + b_{12} E_{{\rm S}n} \\ E_{{\rm P}21} = b_{21} E_{{\rm P}n} + b_{22} E_{{\rm S}n} \\ E_{{\rm S}1} = b_{31} E_{{\rm P}n} + b_{32} E_{{\rm S}n} \end{array}\!\!\right\} $ | (33) |
式中$b_{ij}$ ($i =1,2,3$; $j =1,2$)取决于$a_{11}$,$a_{12}$,$a_{13}$,$a_{31}$,$a_{32}$,$a_{33}$,$a_{51}$,$a_{52}$,$a_{53}$. 将式(33)代入式(25),顶层波幅矢${ H}_{1}$可以写成
| $ { H }_1 = (d_{\rm P1} E_{{\rm P}n} + d_{\rm S1} E_{{\rm S}n} ,d_{\rm P2} E_{{\rm P}n} + d_{\rm S2} E_{{\rm S}n},\\ d_{\rm P3} E_{{\rm P}n} + d_{\rm S3} E_{{\rm S}n} ,d_{\rm P4} E_{{\rm P}n} + d_{\rm S4} E_{{\rm S}n},\\ d_{\rm P5} E_{{\rm P}n} + d_{\rm S5} E_{{\rm S}n} ,d_{\rm P6} E_{{\rm P}n} + d_{\rm S6} E_{{\rm S}n} )^{\rm T} $ | (34) |
式中
| $\begin{align} & {{d}_{\text{P1}}}={{b}_{11}},{{d}_{\text{S1}}}={{b}_{12}},{{d}_{\text{P3}}}={{b}_{21}} \\ & {{d}_{\text{S3}}}={{b}_{32}},{{d}_{\text{P5}}}={{b}_{31}},{{d}_{\text{S5}}}={{b}_{32}} \\ & {{d}_{\text{P2}}}={{k}_{\text{P1P1}}}{{b}_{11}}+{{k}_{\text{P2P1}}}{{b}_{21}}+{{k}_{\text{SP1}}}{{b}_{31}} \\ & {{d}_{\text{S2}}}={{k}_{\text{P1P1}}}{{b}_{12}}+{{k}_{\text{P2P1}}}{{b}_{22}}+{{k}_{\text{SP1}}}{{b}_{32}} \\ & {{d}_{\text{P4}}}={{k}_{\text{P1P2}}}{{b}_{11}}+{{k}_{\text{P2P2}}}{{b}_{21}}+{{k}_{\text{SP2}}}{{b}_{31}} \\ & {{d}_{\text{S4}}}={{k}_{\text{P1P2}}}{{b}_{12}}+{{k}_{\text{P2P2}}}{{b}_{22}}+{{k}_{\text{SP2}}}{{b}_{32}} \\ & {{d}_{\text{P6}}}={{k}_{\text{P1S}}}{{b}_{11}}+{{k}_{\text{P2S}}}{{b}_{21}}+{{k}_{\text{SS}}}{{b}_{31}} \\ & {{d}_{\text{S6}}}={{k}_{\text{P1S}}}{{b}_{12}}+{{k}_{\text{P2S}}}{{b}_{22}}+{{k}_{\text{SS}}}{{b}_{32}} \\ \end{align}$ |
若将式(33)代入式(22)可得任一饱和土层波幅矢${ H}_{j}$. 从而由式(17)可得第$j$层内$x_{3}$平面上的应力-位移矢量$ { S}_j = \left( {u_{3j} ,u_{1j} ,\sigma _{33j} + \tau _j ,\sigma _{13j} ,p_j ,\phi _j \left( {U_{3j} - u_{3j} } \right)} \right)^{\rm T}$. 此为频域内稳态响应,再经过FFT逆变换,可得到时程响应.
2 算例验证 2.1 单层饱和土体与单层干土考虑以下两种模型:
(1) 基岩上覆30 m饱和土,其主要参数如下: $\rho_{\rm s}=2 500$ kg/m$^{3}$,$\varphi =0.260$,$K_{\rm b} =98$ MPa,$K_{\rm s} =384$ MPa,$G =88$ MPa,$k_{0} =1 μ$m$^{2}$,流体密度$\rho_{\rm f}=1 000$ kg/m$^{3}$,流体动力黏度$\mu=0.001$ Pa$\cdot $s,流体体积模量$K_{\rm f} =222$ MPa.
(2)基岩上覆30 m干土,其主要参数如下: $\rho =2 500$ kg/m$^{3}$,$c_{\rm S}=204.22$ m/s,$c_{\rm P}=458.34$ m/s.
两者基岩参数相同:$\rho =3 000$ kg/m$^{3}$,$c_{\rm S}=400$ m/s,$c_{\rm P}=645$ m/s,$\mu _{n}=4.8\times 10^{8}$ Pa;$\lambda_{n}=2.88\times 10^{8}$ Pa.
对这两种模型输入相同的单位脉冲波:时间步距$d t=0.015$ s,脉冲宽度$t_{0}=0.2$ s,步数$n=1\times 10^{13}$.其时间步距$d t$满足奈奎斯特定理$d t ≤ \dfrac{1}{2f_{\rm c} } \approx \dfrac{1}{2\times 18} = 0.028$ s,$f_{\rm c}$为信号中最高频率,从图 2(b)中可知约为18 Hz.

|
图 2 单位脉冲形状(dt = 0.015 s, t0 = 0.2 s) Figure 2 Shape of the unit pulse (dt = 0.015 s, t0 = 0.2 s) |
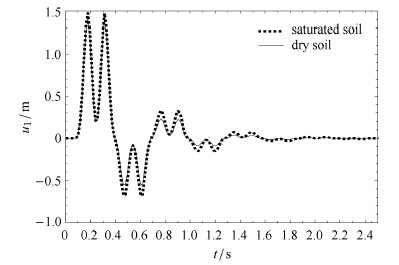
考虑SV波垂直输入时的响应,图 3和图 4分别为自由表面处和土层内一点处的固相水平位移时程. 由图 3可知,自由表面处饱和土的响应形态与干土的响应形态类似,其幅值相较略大. 以下通过脉冲到时与幅值验证其正确性.

|
图 3 单层饱和土与干土自由表面处水平位移对比 Figure 3 Comparison of the horizontal displacement at the free surface in single-layer saturated soil and dry soil |
|
图 4 单层饱和土与干土土层中间点水平位移对比 Figure 4 Comparison of the horizontal displacement at the intermediate surface in single-layer saturated soil and dry soil |
由式(7)可知,SV波频率范围内波速约为204.22 m/s.位移首次出现有值处表示脉冲由基岩传递至自由表面所用时间30/204.22=0.15 s;首次出现反向位移处表示波在层间经历两次反射后又传递至自由表面所用时间0.15$\times $3=0.45 s;以后依次类推,波到时间依次为0.75 s,1.05 s,1.35 s,1.65 s和 1.95 s.经检验,理论分析与计算结果相吻合.
根据文献[6, 8],得到SV波垂直入射时在自由表面及基岩表面上的反折射系数,估算位移幅值.
(1) 自由表面处反射系数
| $ R0_3^{(3)} \cong \dfrac{F_3 }{E_3 }\left( {1 - \dfrac{v_{\rm c}^3 v_{\rm r} \sin \theta \cos 2\theta \sin 4\theta }{E_3 F_3 }\tau {\rm e}^2\kappa } \right) + 0\left( {\kappa ^2} \right) \\ \theta 0_3^{(3)} \cong \pi - \arctan \left( {\dfrac{v_{\rm c}^3 v_{\rm r} \sin \theta \cos 2\theta \sin 4\theta }{E_3 F_3 }\tau {\rm e}^2\kappa } \right) $ |
其中$E_3 ,F_3 = v_{\rm c}^2 \cos ^22\theta \pm v_{\rm r}^2 \sin ^22\alpha _{01}^{ (3)} \sin 2\theta $,$\alpha _{01}^{(3)} = \arcsin \left[{\left( {{v_{\rm c} }/{v_{\rm r} }} \right)\sin \theta } \right]$,$v_{\rm c} = \left( {M/\rho } \right)^{1 /2}$,$v_{\rm r} = \left( {N / \rho } \right)^{1 /2}$,$\tau = \left( {2/{A\xi }} \right)^{1/2}$,$\xi = \overline \delta ^2\left( {\gamma _{12} + \gamma _{22} } \right)$,$\kappa = a\left( {\omega /\upsilon } \right)^{1 / 2}$,$\upsilon = {\overline \mu } /{\rho _{\rm f} }$,$a$代表特征尺寸,$\overline \delta $为孔隙形状因子,$\theta $ 为SV波入射角度.代入上述各参量,自由表面处位移幅值比为$r0_3^{(3)} = \left( {{ - \delta _3 }/ {\delta _3 }} \right)R0_3^{(3)} {\rm e}^{{\rm i}\theta 0_3^{(3)} } = 1$.
(2) 基岩分界面处下行波反射系数
| $ R1_3^{(3)} = \dfrac{\left| {1 - \psi } \right|}{1 + \psi }\left[ {1 + 0\left( {\kappa ^4} \right)} \right] , \quad \theta 1_3^{(3)} = \pi + 0\left( {\kappa ^2} \right)$ |
其中$\psi = {\rho'v'_{\rm r} } /\rho v_{\rm r} $,这里上标" $'$ "表示基岩层各参数.故基岩分界面处反射位移幅值比为$r1_3^{ ( 3)} = R1_3^{(3)} {\rm e}^{{\rm i}\theta 1_3^{(3)} } =-0.472$.
(3) 基岩分界面处上行波透射系数
| $ T1_3^{(3)} = \dfrac{2}{1 + \psi '}\left[{1 + 0\left( {\kappa ^4} \right)} \right] , \quad \tau 1_3^{(3)} = 0\left( {\kappa ^2} \right)$ |
其中$\psi' = {\rho v_r } /{\rho'v'_{\rm r}}$. 故基岩分界面处透射位移幅值比为$t1_3^{(3)} = T1_3^{(3)} {\rm e}^{{\rm i}\tau 1_3^{(3)} } = 1.472$.
故图中位移首次出现峰值,其幅值应为$t1_3^{(3)} \times \left( {1 + r0_3^{(3)} } \right) = 2.944$;图中位移首次出现反向峰值,其幅值应为$t1_3^{(3)} \times r0_3^{(3)} \times r1_3^{(3)} \times \left( {1 + r0_3^{(3)} } \right) = 1.390$. 经检验,理论分析与计算结果相吻合.
2.2 多层饱和土体上述算例采用了单层土体、波垂直入射的形式,其计算过程中未利用到6×6传递矩阵.为验证传递矩阵的正确性,将单层饱和土分成若干层饱和土,这些饱和土的各参数相同,因此理论上所得时程图应该完全吻合.采用基岩上覆10 m饱和土层,各参数不变,将其分成3层(3 m+3 m+4 m),考虑SV波30°斜入射情况.图 5表明吻合情况良好. 以上算例基本上验证了本文方法及所编程序的正确性.

|
图 5 单层饱和土与多层饱和土自由表面点水平位移时程对比 Figure 5 Comparison of the horizontal displacement at the free surface in the single-layer and layered saturated soil |
为详细阐述场相关参数对自由场计算有效性的影响,考虑基岩上覆10 m饱和土层,其主要参数见表 1. 饱和土中流体密度 $\rho_{\rm f}=1 000$ kg/m$^{3}$,流体动力黏度$\bar \mu =1$ mPa$\cdot$s,流体体积模量$K_{\rm f}=1.38$ GPa;下置基岩干土参数$\rho =3 000$ kg/m$^{3}$,$\mu_{n}=300$ MPa,$\lambda_{n}=220$ GPa.
| 表 1 土层参数 Table 1 Soil parameters |
SV波入射,输入以下单位脉冲波:时间步距$d t=0.015$ s,脉冲宽度$t_{0}=0.2$ s,步数$n=1\times 10^{13}$.
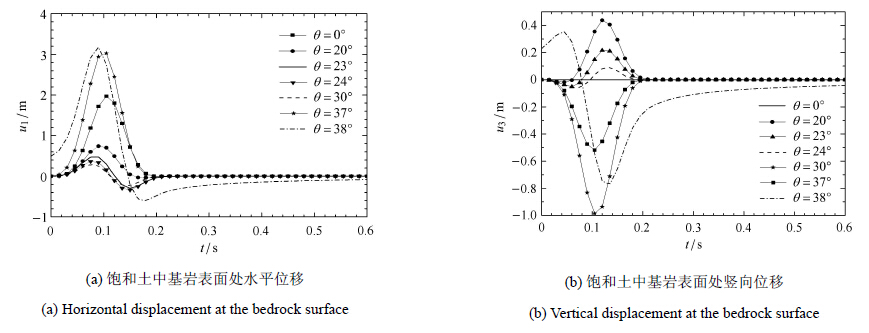
3.1 入射角度图 6描述了SV波以不同入射角入射时,基岩表面点$x_{3}=10$ m处时程图.假设入射SV波从基岩以$\theta $角入射,根据斯奈尔定理:
| $ \dfrac{\sin \theta }{c_{\rm S} } = \dfrac{\sin \theta _1 }{c_{\rm P} } = \dfrac{\sin \theta'_1 }{c'_{\rm P1} } = \dfrac{\sin \theta'_2 }{c'_{\rm P2} } = \dfrac{\sin \theta'_3 }{c'_{\rm S} } $ | (35) |
|
图 6 多层饱和土自由场响应随入射角度影响的时程图 Figure 6 Time history diagram of the free field response in the layered saturated soil with the incident angle |
其中$\theta'_i \left( {i = 1,2,3} \right)$分别对应于与基岩相邻饱和土层中P1,P2和SV波折射角度; $\theta_{1}$表示基岩层P波的反射角度.根据模型参数,基岩中波速$c_{\rm P}= \sqrt {{\mu _{\rm e} } / {\rho _{\rm e}}} = 1 000.00$ m/s,$c_{\rm P} = \sqrt {{\left( {\lambda _{\rm e} + 2\mu _{\rm e} } \right)}/{\rho _{\rm e}}} = 1 653.28$ m/s.由式(7)可以得到对应饱和土中各波波速. 在本例计算的频率范围内P1和SV波波速变化不大,特征速度如下:$c'_{\rm P1} = 2 498.14$ m/s,$c'_{\rm S} = 931.19$ m/s;P2波波速变化较大,但其值总体相对小得多.因此,我们可知由于饱和土中P1波波速大于入射SV波波速,则存在一个临界角 $\theta'_{\rm c} = \arcsin \dfrac{c_{\rm S} }{c'_{\rm P1} } \approx 24^ \circ $. 当入射角$\theta > \theta'_{\rm c} $时,饱和土中折射P1波转化为沿着分界面传播的非均匀平面波. 同理,当$\theta > \theta _{\rm c} = \arcsin \dfrac{c_{\rm S} }{c_{\rm P} } \approx 37^ \circ $时,基岩层的反射P波也转化为沿着分界面传播的非均匀平面波.可以看到当入射角超过37°时,所得结果有违背因果律的情况------零时刻有位移,且尾部单调渐进趋于零.
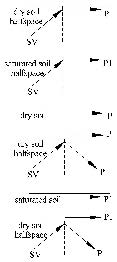
违背因果律的情况仅出现在当反射P波转化为非均匀波,而当折射P1波因临界角(24°)转化为非均匀波时,并未出现该情况. 为了更清楚了解该违背因果律现象的本质,对表 2所列模型进行了分析.
| 表 2 模型图示 Table 2 Model diagram |
图 7(a)和图 7(b)表明无论是饱和土或是干土介质,当入射角超过反射波临界角时,都出现了相似的违背因果律的现象,且由图 7(c)和图 7 (d)可知,在24°$\sim $37°之间,即导致折射波为非均匀波的临界角时,并无违背因果律.而且,增加脉冲宽度,减小输入频率宽度,也不能消除此违背因果律的现象.由上述情形可知,表 2中4种模型出现的违背因果律的现象类似,产生的机制应该相同.我们针对模型1的情形对该机制进行分析.

|
图 7 不同模型自由场相应随临界角影响的时程图 Figure 7 Time history diagram of the free field response of different models with critical angle |
当入射角大于反射波临界角时,可证明入射SV波和反射SV波均符合因果律.对于P波而言,变为一沿$x_{3}$轴衰减的非均匀波,其引起的稳态位移可表示为
| $ U^{\rm P} = U_{\rm I}^{\rm SV} R{\rm e}^{{\rm i}\omega \left( {t - \tfrac{x_1 }{c}} \right)}{\rm e}^{ - \left| \omega \right| d x_3 } $ | (36) |
其中$U_{\rm I}^{\rm SV} $表示输入波的稳态位移,$R$表示位移反射系数,$c = {c_{{\rm S}n} }/{\sin \theta }$,$d = \sqrt {\dfrac{\sin ^2\theta }{c_{{\rm S}n}^2 } - \dfrac{1}{c_{{\rm P}n}^2 }} $是与频率无关的常数.对式(36)作傅里叶反变换,根据卷积定理可表示为
| $\begin{align} & {{u}^{\text{P}}}\left( t \right)={{F}^{-1}}\left[ {{U}^{\text{P}}} \right]=Ru_{\text{I}}^{\text{SV}}\left( t-\frac{{{x}_{1}}}{c} \right)\frac{1}{{{\left( d{{x}_{3}} \right)}^{2}}+{{t}^{2}}}= \\ & \int_{-\infty }^{\infty }{R}u_{\text{I}}^{\text{SV}}\left( \tau -\frac{{{x}_{1}}}{c} \right)\cdot \frac{1}{{{\left( d{{x}_{3}} \right)}^{2}}+{{\left( \tau -t \right)}^{2}}}d\tau \\ \end{align}$ | (37) |
由上式可知当t=0时,${{u}^{\text{P}}}\left( 0 \right)\ne 0$ ,因此出现了违背因果律的情况.
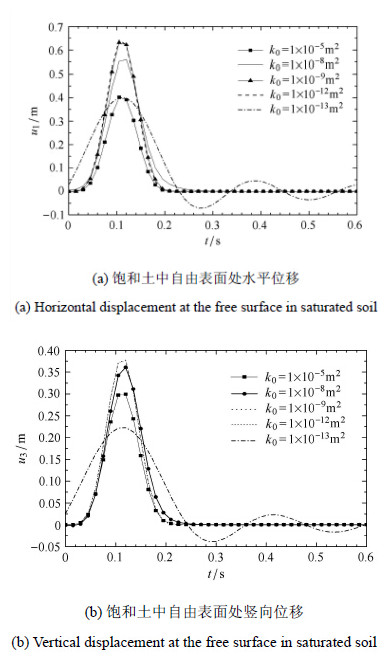
3.2 渗透率为考察渗透率对饱和土自由场响应的影响,这里将三层土层的渗透率置为相同,但其他参数不变,考虑SV波20°斜入射.
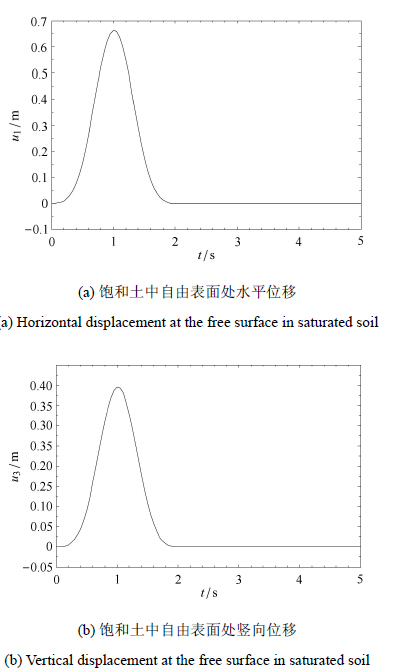
由图 8可知,当渗透率达到1×10$^{-13}$ m$^{2}$时,位移时程图出现了违背因果关系的现象,与基岩反射波临界角情形不同,尾部振荡地衰减. 若增加输入脉冲的宽度,降低频率(时间步距$d t=0.05$ s,脉冲宽度$t_{0}=2.0$ s,步数$n=1\times 10^{13}$),违背因果律的现象得以消除,见图 9.
|
图 8 多层饱和土自由场响应随渗透率影响的时程图 Figure 8 Time history diagram of the free field response in the layered saturated soil with permeability coeffcient |
|
图 9 低频下($k_{0} =1\times 10^{-13}$m$^{2}$) 多层饱和土自由场响应时程图 Figure 9 Time history diagram of the free field response in the layered saturated soil under the lower frequency ($k_{0} =1\times 10^{-13}$m$^{2}$) |
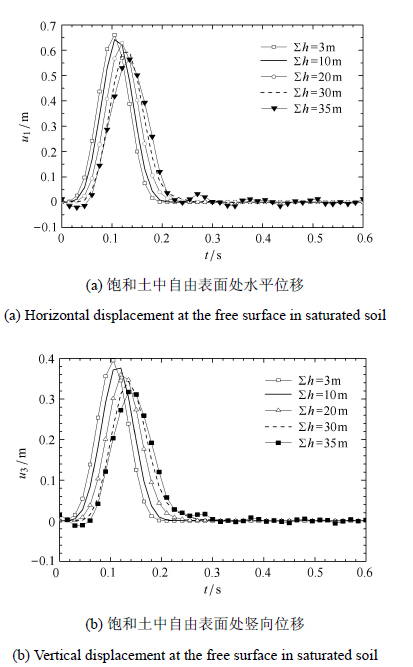
分别考虑3 m (1 m×3),10 m (3 m+3 m+4 m),20 m (6 m+6 m+8 m),30 m (10 m×3), 35 m (11 m+11 m+13 m)的上覆盖土层,土层种类仍为上述3种,其他各参数不变,SV波20°入射.由图 10可知,饱和土体中波传递的不断衰减及能量消散使得随着土层的加厚,位移值随之减小.
|
图 10 多层饱和土自由场响应随土层厚度影响的时程图 Figure 10 Time history diagram of the free field response in the layered saturated soil with soil thickness |
当土层厚度达到35 m时,结果违背因果律,和渗透系数情形一样,尾部振荡着衰减,下面考察一下此类违背因果律的原因.
观察饱和土中6×6系数矩阵$T_{sj}$可知,其各元素都包含指数项${\rm e}^{{\rm i}\delta_k w_{k3} x_3 }$. 其中$\delta _k w_{k3} $表示各波在$x_{3}$方向的波数,是频率$\omega $的函数;而$x_{3}$方向即表示层厚方向. 由于P2慢波的波数虚部值较大,其衰减最为明显. 为满足计算机数值的合法范围,我们考虑下式
| $ \left| { {\rm Im} \left( {\delta _2 w_{23} } \right) \cdot h} \right| < \varpi $ | (38) |
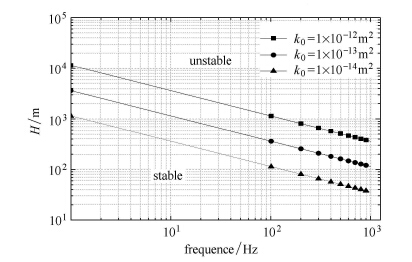
其中$h$表示土层厚度,$\varpi $代表计算机数值精度. 本例中数值取双精度型,其取值范围在2.23×10$^{ - 308}\sim $1.79×10$^{308}$(即e$^{ - 708}\sim $e$^{710}$)内,为使得指数项不超过该范围,取$\varpi$=708.可得到满足式(38)的频率、渗透系数、土层厚度的参数范围,见图 11.
|
图 11 不同渗透率下单层饱和土自由场数值计算失稳区 Figure 11 Unstable regions of the single-layer saturated soil for different permeability values |
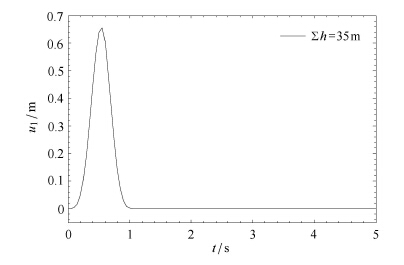
由图 11可知,厚度和渗透系数取定,降低频率可使计算稳定. 对上述出现违背因果律现象的图 8和图 10情形,降低输入脉冲的频率(时间步距$d t$=0.05 s,脉冲宽度$t_{0}$=1.0 s,步数$n=1\times 10^{13}$),问题得以解决(见图 9和图 12).图 11的变化趋势从定性上可解释计算失稳的原因.但实际计算发现,厚度和渗透系数确定后,实际所能计算的频率范围要小于图 11所示,这是由于数值计算过程中除了有指数超限现象外,还有数值组合后矩阵奇异等情况. 故图 11所得稳定范围仅为一上限,对其精度的提高还有待研究.
|
图 12 低频下多层饱和土自由表面处水平位移时程图 Figure 12 Time history diagram of horizontal displacement at the free surface in layered saturated soil under the lower frequency |
基于Biot多孔介质模型,利用传递矩阵方法推导了饱和土在平面波斜入射时的动力响应. 通过算例验证了该方法的有效性,并讨论了计算中出现的相关问题. 主要结论如下:
(1) 采用传递矩阵方法分析了SV波入射时,基岩上覆饱和土层的反应,通过波的幅值和到时,验证了该方法的有效性.
(2) 当SV波入射角超过导致基岩反射P波为非均匀波的临界角时,计算结果违背因果律,且计算结果单调渐进趋于零;当入射角超过导致饱和土层折射P1波为非均匀波的临界角时,不会出现违背因果律的现象. 此类违背因果律的现象表明入射角超过临界角时,非均匀平面波的表示尚待完善,需进一步讨论.
(3) 土层厚度、渗透率与频率决定了波(主要是P2波)的衰减系数,土层厚度和频率越大,衰减越快,渗透率越小,衰减越快.当衰减系数超过计算机表示精度时,计算无法进行或失稳,据此可得到计算参数的有效范围,可做为实际计算中参数选取的上界.若土层物理参数取定,则能允许计算的频率有一上界,相当于一截止频率.当这3个参数超出一定范围,也会出现计算结果违背因果律的现象.以前一类违背因果律的现象不同,可以通过降低频率得以消除,且结果振荡着趋于零.
(4)本文方法可以考虑实际地下水位情形,水位以上采用单相土模型,水位以下采用饱和土模型.
| 1 |
Biot MA. Theory of propagation of elastic waves in a fluid-saturated porous solid.
Acoust Soc Am,1956, 28 : 168-191.
DOI: 10.1121/1.1908239. ( 0) 0)
|
| 2 |
Biot MA. Mechanics of deformation and acoustic propagation in porous media.
Journal of Applied Physics,1962, 33 (4) : 1482-1498.
DOI: 10.1063/1.1728759. ( 0) 0)
|
| 3 |
Biot MA, Willis DG. The elastic coefficis of the theory of consolidation.
Journal of Applied Mechanics,1957, 24 : 594-601.
( 0) 0)
|
| 4 |
Plona TJ. Observation of a second bulk compressional wave in a porous medium at ultrasonic frequencies.
Applied Physics Letters,1980, 36 : 259-261.
DOI: 10.1063/1.91445. ( 0) 0)
|
| 5 |
Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid:I. Reflection of plane waves at a free plane boundary (non-dissipative case).
Bull Seism Soc Am,1960, 50 (4) : 599-607.
( 0) 0)
|
| 6 |
Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid:Ⅲ. Reflection of plane waves at a free plane boundary(general case).
Bull Seism Soc Am,1962, 52 (3) : 595-625.
( 0) 0)
|
| 7 |
Deresiewicz H. The effect of boundaries on wave propagation in a liquid-filled porous solid:IV. Surface waves in a half-space.
Bull Seism Soc Am,1962, 52 (3) : 627-638.
( 0) 0)
|
| 8 |
Deresiewicz H, Rice JT. The effect of boundaries on wave propagation in a liquid-filled porous solid:V. Transmission across a plane interface.
Bull Seism Soc Am,1964, 54 (1) : 409-416.
( 0) 0)
|
| 9 |
Deresiewicz H. The effect of boundaries on wave propagation in a liquid-filled porous solid:VⅡ. Surface waves in a half-space in the presence of a liquid layer.
Bull Seism Soc Am,1964, 54 (1) : 425-430.
( 0) 0)
|
| 10 |
Deresiewicz H, Levy A. The effect of boundaries on wave propagation in a liquid-filled porous solid:X. Transmission through a stratified medium.
Bull Seism Soc Am,1967, 57 (3) : 381-391.
( 0) 0)
|
| 11 |
Deresiewicz H. The effect of boundaries on wave propagation in a liquid-filled porous solid:XI. Waves in a plate.
Bull Seism Soc Am,1974, 64 (6) : 1901-1907.
( 0) 0)
|
| 12 |
Hajra S, Mukhopadhyay A. Reflection and refraction of seismic waves incident obliquely at the boundary of a liquid-saturated porous solid.
Bull Seism Soc Am,1982, 72 (5) : 1509-1533.
( 0) 0)
|
| 13 |
Sharma MD, Gogna ML. Reflection and refraction of plane harmonic waves at an interface between elastic solid and porous solid saturated by viscous liquid.
Pageoph,1992, 138 (2) : 249-266.
DOI: 10.1007/BF00878898. ( 0) 0)
|
| 14 |
Jocker J, Smeulders D, Drijkoningen G, et al. Matrix propagator method for layered porous media:Analytical expressions and stability criteria.
Geophysics,2004, 69 (4) : 1071-1081.
DOI: 10.1190/1.1778249. ( 0) 0)
|
| 15 |
Degrande G, Roeck G, Broeck P, et al. Wave propagation in layered dry, saturated and unsaturated poroelastic media.
Int J Solids Structures,1998, 35 (34-35) : 4753-4778.
DOI: 10.1016/S0020-7683(98)00093-6. ( 0) 0)
|
| 16 |
门福录. 波在饱水孔隙弹性介质中的传播.
地球物理学报,1965, 14 (2) : 107-114.
( Men Fulu. Wave propagation in a porous, saturated elastic medium.
Institute of Engineering Mechanics,1965, 14 (2) : 107-114.
(in Chinese) ) ( 0) 0)
|
| 17 |
门福录. 波在饱含流体的孔隙介质中的传播问题.
地球物理学报,1965, 14 (2) : 107-114.
( Men Fulu. Problem of wave propagation in porous fluid-saturated media.
Institute of Engineering Mechanics,1965, 14 (2) : 107-114.
(in Chinese) ) ( 0) 0)
|
| 18 |
陈龙珠, 吴世明, 曾国熙. 弹性波在饱和土层中的传播.
力学学报,1987, 19 (3) : 276-283.
( Chen Longzhu, Wu Shiming, Zeng Guoxi. Propagation of elastic waves in water-saturated soils.
Chinese Journal of Theoretical and Applied Mechanics,1987, 19 (3) : 276-283.
(in Chinese) ) ( 0) 0)
|
| 19 |
王立忠, 陈云敏, 吴世明, 等. 饱和弹性半空间在低频谐和集中力下的积分形式解.
水利学报,1996, 2 : 84-88.
( Wang Lizhong, Chen Yunmin, Wu Shiming, et al. A solution to saturated elastic halfspace under harmonic force of low frequency.
Journal of Hydraulic Engineering,1996, 2 : 84-88.
(in Chinese) ) ( 0) 0)
|
| 20 |
刘志军, 夏唐代, 张琼方, 等. 双相多孔介质中体波传播特性影响参数研究.
岩土力学,2014, 35 (12) : 3443-3459.
( Liu Zhijun, Xia Tangdai, Zhang Qiongfang, et al. Parametric studies of propagation characteristics of bulk waves in two-phase porous media.
Rock and Soil Mechanics,2014, 35 (12) : 3443-3459.
(in Chinese) ) ( 0) 0)
|
| 21 |
Liang Jianwen, You Hongbing. Dynamic stiffness matrix of a poroelastic multi-layered site and its Green's functions.
Earthquake Engineering and Engineering Vibration,2004, 3 (2) : 273-282.
DOI: 10.1007/BF02858241. ( 0) 0)
|
| 22 |
尤红兵, 梁建文, 赵凤新. 含饱和土的层状场地的动力响应.
岩土力学,2008, 29 (3) : 679-684.
( You Hongbing, Liang Jianwen, Zhao Fengxin. Dynamic responses of a multilayered site with saturated soils.
Rock and Soil Mechanics,2008, 29 (3) : 679-684.
(in Chinese) ) ( 0) 0)
|
| 23 |
黄明汉, 张卫平, 张文忠. 层状非均质饱和土层波动响应研究.
中国港湾建设,2014, 194 (4) : 10-16.
( Hang Minghan, Zhang Weiping, Zhang Wenzhong. Dynamic response of saturated layered soils under seismic wave excitations.
China Harbour Engineering,2014, 194 (4) : 10-16.
(in Chinese) ) ( 0) 0)
|
| 24 |
张卫平, 孙昭晨, 梁书秀. 地震波倾斜入射下两相饱和土层响应数值模拟.
计算力学学报,2014, 31 (3) : 333-339.
( ZhangWeiping, Sun Zhaochen, Liang Shuxiu. Numerical simulation of saturated layered soil subjected to inclined seismic wave incidence.
Chinese Journal of Computational Mechanics,2014, 31 (3) : 333-339.
(in Chinese) ) ( 0) 0)
|
| 25 |
董云, 楼梦麟. 基于饱和多孔介质的复杂自由场地震响应分析.
同济大学学报(自然科学版),2014, 42 (2) : 199-202.
( Dong Yun, Lou Menglin. Seismic response analysis of complicated soil site based on saturated porous media.
Journal of Tongji University(Natural Science),2014, 42 (2) : 199-202.
(in Chinese) ) ( 0) 0)
|
| 26 |
丁伯阳, 陈樟龙, 徐庭. 两相饱和介质层与单相介质层应力-位移函数的传递与退化.
应用数学和力学,2014, 35 (2) : 162-180.
( Ding Boyang, Chen Zhanglong, Xu Ting. Degeneration and transfer of the displacement-stress functions from poroelastic layered media to elastic layered media.
Applied Mathematics and Mechanics,2014, 35 (2) : 162-180.
(in Chinese) ) ( 0) 0)
|
| 27 |
周凤玺, 赖远明, 宋瑞霞. 非均匀饱和土中平面波的传播特性.
中国科学:技术科学,2013, 56 (2) : 430-440.
DOI: 10.1007/s11431-012-5106-0. ( Zhou Fengxi, Lai Yuanming, Song Ruixia. Propagation of plan wave in nonhomogeneously saturated soils.
Science China:Technological Sciences,2013, 56 (2) : 430-440.
(in Chinese) DOI: 10.1007/s11431-012-5106-0. ) ( 0) 0)
|
| 28 |
周凤玺, 宋瑞霞. 平面P-SV波入射时非均匀饱和土自由场地的响应.
地震学报,2015, 37 (4) : 629-639.
( Zou Fengxi, Song Ruixia. Response of the non-homogeneous saturated foundation to incident plane P-SV waves.
Acta Seismologica Sinica,2015, 37 (4) : 629-639.
(in Chinese) ) ( 0) 0)
|
| 29 |
周凤玺, 马强, 米海珍. 非均匀饱和土层的波动响应分析.
兰州理工大学学报,2015, 41 (5) : 110-114.
( Zhou Fengxi, Ma Qiang, Mi Haizhen. Analysis of transient wave motion in non-homogeneous saturated soil layer.
Journal of Lanzhou University of Technology,2015, 41 (5) : 110-114.
(in Chinese) ) ( 0) 0)
|
| 30 |
周凤玺, 赖远明, 任圆圆. 饱和土地基在简谐荷载作用下的解析分析.
固体力学学报,2013, 34 (5) : 536-540.
( Zhou Fengxi, Lai Yuanming, Ren Yuanyuan. An analysis on saturated soil foundation under harmonic loads.
Chinese Journal of Solid Mechanics,2013, 34 (5) : 536-540.
(in Chinese) ) ( 0) 0)
|
| 31 |
陈炜昀, 夏唐代, 刘志军, 等. 平面S波在非饱和土自由边界上的反射问题研究.
振动与冲击,2013, 32 (1) : 99-127.
( Chen Weiyun, Xia Tangdai, Liu Zhijun, et al. Reflection of plane-S-waves at a free boundary of unsaturated soil.
Journal of Vibration and Shock,2013, 32 (1) : 99-127.
(in Chinese) ) ( 0) 0)
|
| 32 |
陈炜昀, 夏唐代, 黄睿, 等. P1波在非饱和土地基表面的反射特性.
工程力学,2013, 30 (9) : 56-62.
( Chen Weiyun, Xia Tangdai, Huang Rui, et al. Reflection characteristics of P1 waves at the free boundary od unsaturated soil.
Engineering Mechanics,2013, 30 (9) : 56-62.
(in Chinese) ) ( 0) 0)
|
| 33 |
Bullen KE, Bolt BA. An Introduction to the Theory of Seismology (4th edn).
Oxford:Geophysical Journal International,1986 .
( 0) 0)
|
| 34 |
廖振鹏. .
工程波动理论导论(第2版),2002 .
( Liao Zhenpeng. .
Introduction to Wave Motion Theories in Engineering (2nd edn),2002 .
(in Chinese) ) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48