2. 江苏省土木工程防震技术研究中心, 南京 210009
3. 中国地震局地球物理研究所, 北京 100081
在场地地震反应、结构-地基动力相互作用等问题的计算分析中,涉及的是属于开放系统中的近场波动问题,其力学模型可简化为有效尺度场地的开放系统. 对于近场波动问题,如何考虑无限地基的辐射阻尼效应是其核心问题之一[1].目前基于有限元方法的场地地震反应分析一般通过引入人工边界,将一无限域转化为有限域,并在有限域上通过设置人工边界条件,以模拟外部无限域的影响[2],地震波的输入与所采用的人工边界条件相关联.因此,在进行地震反应分析中首先需要解决人工边界的问题.按照人工边界条件基于的物理量,总体上可以将人工边界分为两大类:一是位移型人工边界条件,如透射边界[3]、旁轴近似人工边界[4]等;二是应力型人工边界条件,如黏性边界[5]、黏弹性人工边界[6-7]等.位移型人工边界是通过直接模拟外行波及误差波的单向传播建立在人工边界的位移时空外推公式,其优点是误差波的多次透射可以提高模拟精度,缺点是由于采用时空差分方程外推带来的人工边界"高频振荡失稳"和"低频漂移失稳"的问题[8-9].应力型人工边界的特点是基于外行波(散射波)远场位移的近似表达式和无限域介质的应力-应变本构关系建立的应力边界条件,不存在位移边界的"高频与低频失稳"的现象,其中黏弹性人工边界能够较好地模拟无限地基的弹性恢复能力和辐射阻尼效应.
地震波输入形式的选取也是一个重要问题. 对于一般的远场波动而言,通常假定地震波是从底部垂直入射的剪切波或压缩波.当震源距离场地较近时,地震波是以某一角度倾斜传播到近场,呈现空间变化特性.地震波斜入射引起地表运动的非一致性变化对场地地震反应具有很大影响,这就导致了场地中各部位的地震动差别较大.一些研究者也已经认识到对地震波斜入射研究的重要性[10-20].针对地震波斜入射的问题,国内外学者结合结构-地基体系动力响应计算进行了一系列的研究,刘晶波和吕彦东[14]给出了一种结构-地基动力相互作用中地震波输入方法模拟任意角度入射的地震行波的输入;Heymsfield[15]利用边界积分方程法研究斜入射SH波时,倾斜基岩对地表位移的影响,当入射角为60$^{\circ}$时,地表位移幅值最大;杜修力等[17-19]分析了在不同地震波入射角度情况下地下结构的时域地震动反应;杜修力等[18]结合黏弹性边界,建立了三维半空间场地的平面波倾斜输入方法,并应用到地下结构中.将地震波转化为在人工边界节点上的等效载荷来实现波动输入,常规方法[21-22]在对边界节点的等效载荷计算方面一般采用简化方式,忽略人工边界结点影响区域内人工边界应力的差异,默认边界节点控制面积内的应力为均布力,对波动数值模拟会造成一定的误差,计算精度往往难以保证.尤其当地震波斜入射时,利用常规方法计算人工边界节点上的等效载荷可能会带来新的问题,因此值得进一步研究.
本文在充分分析前人研究基础上,深入探究波动数值模拟和黏弹性人工边界的物理意义,在人工边界处运用积分的思路对边界节点的等效载荷进行细化并程序化.
1 基于黏弹性人工边界的地震波输入方法 1.1 黏弹性人工边界在ABAQUS中的实现研究表明,黏弹性人工边界具有很好的鲁棒性和较高的稳定性,在时间和空间上都是局部的,其物理意义清晰、简单、有效[22-28],并易于与现有的大型有限元软件相结合[29-31].基于ABAQUS软件平台可以在计算模型的人工边界节点的每个方向施加一端固定的单向并联的弹簧和阻尼器元件,也可以通过 Fortran软件编写命令流的方式给计算区域批量施加人工边界.
二维人工边界的弹簧-阻尼元件参数为[32]:
法向边界
| $ K_{\rm bn} = \dfrac{1}{1 + A} \dfrac{1 + 2G}{2r} ,\ C_{\rm bn} = B\rho c_{\rm P} $ | (1) |
切向边界
| $ K_{\rm bt} = \dfrac{1}{1 + A} \dfrac{G}{2r} ,\ C_{\rm bt} = B\rho c_{\rm S} $ | (2) |
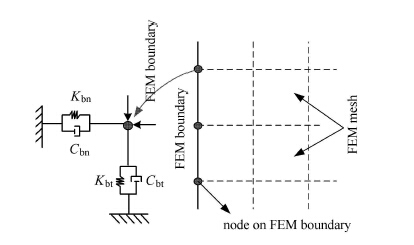
其中,$K_{\rm bn}$和$C_{\rm bn}$为法向边界的弹簧-阻尼元件参数; $K_{\rm bt}$和 $C_{\rm bt}$为切向边界的弹簧-阻尼元件参数;$G$为介质剪切模量; $\rho $ 为介质密度;$c_{\rm P}= \sqrt {{\left( {\lambda + 2G} \right)}/\rho } $和$c_{\rm S} = \sqrt {G / \rho } $分别为P波波速和S波波速;$\lambda $为拉梅常数;$r$为散射源至人工边界的距离;$A$表示平面波与散射波的幅值含量比,反映人工边界外行透射波的传播特性,$B$表示物理波速与视波速的关系,反映不同角度透射多子波的平均波速特性.$A$和$B$的取值可通过数值实验获得,较优建议值为$A =0.8$,$B =1.1$.在ABAQUS中施加二维人工边界的弹簧-阻尼元件时只需将式(1)和式(2)乘以边界节点影响区域施加在人工边界节点上即可(如图 1所示的二维示意图).
|
图 1 黏弹性边界物理意义示意图 Figure 1 Viscoelastic boundary physical schematic |
准确实现波动输入的条件是,在人工边界上施加的等效载荷,使人工边界上的位移和应力与原自由场相同.刘晶波等[1]通过将地震波转化为等效节点力的方式实现了波动的输入.得到了在模型边界点上所需施加等效载荷的一般计算公式
| $ \sigma _l \left( t \right) = \sigma _0 \left( {x,y,t} \right) + C\dot {u}\left( {x,y,t} \right) + Ku\left( {x,y,t} \right) $ | (3) |
其中,$\sigma_{l}(t)$为边界节点$l$处的等效力; $\sigma_{0}(x,y,t)$为连续介质中由原自由场产生的应力;$K$和$C$分别为黏弹性人工边界的法向与切向的弹簧和阻尼系数由式(1)和式(2)得到;$u(x,y,t)$和$\dot {u}\left( {x,y,t} \right)$分别为入射波场位移与速度. 在对模型进行分析计算时,只需分别求出模型边界节点处所需的等效力,然后施加在边界点上,即可实现波动的输入.
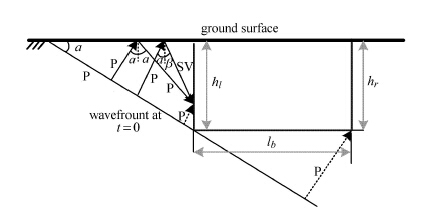
1.3 斜入射条件下边界等效节点载荷的改进方法地震波斜入射时,会在半空间自由表面处反射并产生波型转化,以平面P波入射为例[16],当遇到自由表面时会反射P波与SV波,如图 2所示.为了实现施加于黏弹性边界上的波场为散射场而非总场,在输入自由场时必须保证人工边界处只对散射场起到作用.本文对文献[16]所给出的P波斜入射情况下等效节点力公式做了一些改进,左右两个边界分别选取不同的反射面,将二维问题转化为一维问题.
|
图 2 平面P波入射模型 Figure 2 Reflection model of P-wave oblique incidence |
当平面P波入射角度为 $\alpha $ 时,由地表反射一个反射角为 $\alpha $ 的P波和反射角度为 $\beta $ 的SV波,$\alpha $ 与 $\beta $ 的关系由式(4)可得
| $ \dfrac{\sin \beta }{c_{\rm S} } = \dfrac{\sin \alpha }{c_{\rm P} } $ | (4) |
根据平面波传播时的应力状态和应力状态变换公式,可以得到边界上等效应力式(5) $\sim$式(8).
底边界
| $\begin{align} & {{\sigma }_{lx}}\left( t \right)=G\cdot \sin 2\alpha \cdot {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{4}} \right)/{{c}_{\text{P}}}+ \\ & {{K}_{\text{bt}}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{4}} \right)\sin \alpha +{{C}_{\text{bt}}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{4}} \right)\sin \alpha \\ \end{align}$ | (5) |
| $\begin{align} & {{\sigma }_{\text{l}y}}\left( t \right)=\left( \lambda +2G{{\cos }^{2}}\alpha \right)\cdot {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{4}} \right)/{{c}_{\text{P}}}+ \\ & {{K}_{\text{bn}}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{4}} \right)\cos \alpha +{{C}_{\text{bn}}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{4}} \right)\cos \alpha \\ \end{align}$ | (6) |
左边界
| $\begin{align} & {{\sigma }_{lx}}(t)=\frac{\lambda +2G{{\sin }^{2}}\alpha }{{{c}_{\text{P}}}}\cdot \left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{1}} \right)-{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{2}} \right) \right]+ \\ & \frac{G\cdot \sin 2\beta \cdot {{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{3}} \right)}{{{c}_{\text{S}}}}+{{K}_{\text{bn}}}\left[ {{u}_{\text{P}}}\left( t-\Delta {{t}_{1}} \right)\sin \alpha + \right. \\ & {{A}_{1}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{2}} \right)\sin \alpha +\left. {{A}_{2}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{3}} \right)\cos \beta \right]+ \\ & {{C}_{\text{bn}}}\left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{1}} \right)\sin \alpha + \right.{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{2}} \right)\sin \alpha +\left. {{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{3}} \right)\cos \beta \right] \\ \end{align}$ | (7) |
| $\begin{align} & {{\sigma }_{ly}}\left( t \right)=\frac{G\sin 2\alpha }{{{c}_{\text{P}}}}\cdot \left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{1}} \right)-{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{2}} \right) \right]- \\ & \frac{G\cdot \cos 2\beta }{{{c}_{\text{S}}}}\cdot {{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{3}} \right)+{{K}_{\text{bt}}}\left[ {{u}_{\text{p}}}\left( t-\Delta {{t}_{1}} \right)\cos \alpha - \right. \\ & {{A}_{1}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{2}} \right)\cos \alpha +{{A}_{2}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{3}} \right)\left. \sin \beta \right]+ \\ & {{C}_{\text{bt}}}\left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{1}} \right)\cos \alpha -{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{2}} \right)\cos \alpha \right.+{{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{3}} \right)\left. \sin \beta \right] \\ \end{align}$ | (8) |
右边界
| $\begin{align} & {{\sigma }_{lx}}\left( t \right)=-\frac{\lambda +2G{{\sin }^{2}}\alpha }{{{c}_{\text{P}}}}\cdot \left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{5}} \right)+{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{6}} \right) \right]- \\ & \frac{G\cdot \sin 2\beta \cdot {{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{7}} \right)}{{{c}_{\text{S}}}}+{{K}_{\text{bn}}}\left[ {{u}_{\text{P}}}\left( t-\Delta {{t}_{5}} \right)\sin \alpha + \right. \\ & {{A}_{1}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{6}} \right)\sin \alpha +\left. {{A}_{2}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{7}} \right)\cos \beta \right]+ \\ & {{C}_{\text{bn}}}\left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{5}} \right)\sin \alpha + \right.{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{6}} \right)\sin \alpha +\left. {{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{7}} \right)\cos \beta \right] \\ \end{align}$ | (9) |
| $\begin{align} & {{\sigma }_{ly}}\left( t \right)=-\frac{G\sin 2\alpha }{{{c}_{\text{P}}}}\cdot \left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{5}} \right)-{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{6}} \right) \right]+ \\ & \frac{G\cdot \cos 2\beta }{{{c}_{\text{S}}}}\cdot {{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{7}} \right)+{{K}_{\text{bt}}}\left[ {{u}_{\text{P}}}\left( t-\Delta {{t}_{5}} \right)\cos \alpha - \right. \\ & {{A}_{1}}{{u}_{\text{p}}}\left( t-\Delta {{t}_{6}} \right)\cos \alpha +{{A}_{2}}{{u}_{\text{P}}}\left( t-\Delta {{t}_{7}} \right)\left. \sin \beta \right]+ \\ & {{C}_{\text{bt}}}\left[ {{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{5}} \right)\cos \alpha -{{A}_{1}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{6}} \right)\cos \alpha \right.+{{A}_{2}}{{{\dot{u}}}_{\text{P}}}\left( t-\Delta {{t}_{7}} \right)\left. \sin \beta \right] \\ \end{align}$ | (10) |
其中: $\sigma_{lx}(t)$和$\sigma_{ly}(t)$分别表示自由场在边界上沿着$x$和$y$轴方向产生的应力; $A_{1}$ 和$A_{2}$分别为P波和SV波地表反射幅值放大系数,其关系式由式(11)可得,$\Delta t_1 $,$\Delta t_2 $和$\Delta t_3 $分别为左侧节点$l$处入射P波、地表反射P波和地表反射SV波的时间延迟,$\Delta t_4 $为底边界节点$l$处入射P波的时间延迟,$\Delta t_5 $,$\Delta t_6 $和$\Delta t_7 $分别为右侧节点$l$处入射P波、地表反射P波和地表反射SV波的时间延迟,其关系式如式(12)所示.其中,$h_{l}$和$h_{r}$分别为自由表面左右两端点至底边界的距离,$l_{b}$为底边界长度
| $\left. \begin{align} & {{A}_{1}}=1-\frac{2c_{\text{S}}^{2}\sin 2\alpha \sin 2\beta }{2c_{\text{S}}^{2}\sin 2\alpha \sin 2\beta +c_{\text{P}}^{2}{{\cos }^{2}}2\beta } \\ & {{A}_{2}}=\frac{2{{c}_{\text{P}}}{{c}_{\text{S}}}\sin 2\alpha \cos 2\beta }{2c_{\text{S}}^{2}\sin 2\alpha \sin 2\beta +c_{\text{P}}^{2}{{\cos }^{2}}2\beta } \\ \end{align} \right\}$ | (11) |
| $\left. \begin{array}{*{35}{l}} \Delta {{t}_{1}}={{y}_{l}}\cos \alpha /{{c}_{\text{P}}} \\ \Delta {{t}_{2}}=\left( 2{{h}_{l}}-{{y}_{l}} \right)\cos \alpha /{{c}_{\text{P}}} \\ \Delta {{t}_{3}}=\left( {{h}_{l}}-{{y}_{l}} \right)/({{c}_{\text{S}}}\cos \beta )+ \\ [{{h}_{l}}-\left( {{h}_{l}}-{{y}_{l}} \right)\tan \alpha \tan \beta ]\cos \alpha /{{c}_{\text{P}}} \\ \Delta {{t}_{4}}=x\sin \alpha /{{c}_{\text{P}}} \\ \Delta {{t}_{5}}={{y}_{r}}\cos \alpha /{{c}_{\text{P}}}+{{l}_{\text{b}}}\sin \alpha /{{c}_{\text{P}}} \\ \Delta {{t}_{6}}=\left( 2{{h}_{r}}-{{y}_{r}} \right)\cos \alpha /{{c}_{\text{P}}}+{{l}_{\text{b}}}\sin \alpha /{{c}_{\text{P}}} \\ \Delta {{t}_{7}}=\left( {{h}_{r}}-{{y}_{r}} \right)/\left( {{c}_{\text{S}}}\cos \beta \right)+ \\ \left[ {{h}_{r}}-\left( {{h}_{r}}-{{y}_{r}} \right)\tan \alpha \tan \beta \right]\cos \alpha /{{c}_{\text{P}}}+{{l}_{\text{b}}}\sin \alpha /{{c}_{\text{P}}} \\ \end{array} \right\}$ | (12) |
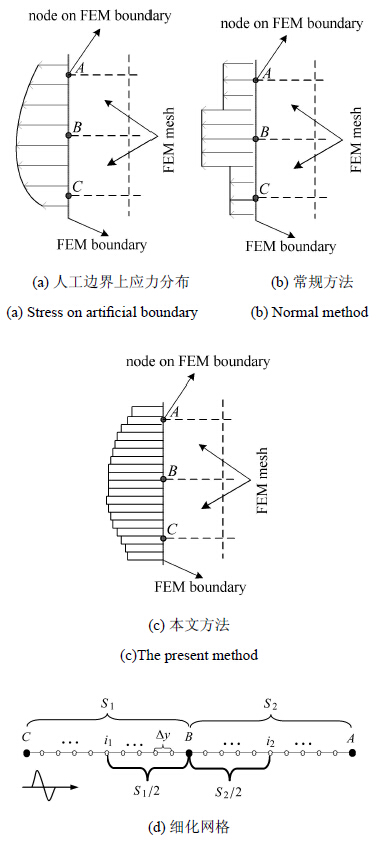
式(5)$\sim$式(10)给出了P波斜入射时,人工边界节点上所需施加的节点应力,当用ABAQUS有限元软件模拟地震波输入下地震反应时,在人工边界面上需要施加产生自由场所需抵抗人工边界物理元件的应力场以及产生自由场反应所抵抗近场介质的应力.在截断的人工边界上,地震动的作用形式如图 3(a)所示,在人工边界上不同节点具有不同的应力时程.以节点力的形式实现波动输入时,常规方法忽略人工边界结点对应区域的应力的差异,将节点对应区域的应力默认为均布分布并取为节点位置的值,等效为集中力施加在人工边界节点上(图 3(b) 所示).常规方法的处理方式忽略人工边界结点对应区域内自由场应力的差异,势必会带来一定的误差.
|
图 3 人工边界面上的应力分布 Figure 3 The stress distribution on the viscous-spring artificial |
本文在常规地震波输入方法的基础上进行了优化,在网格节点之间采用积分的思路(图 3(c)和图 3(d)),这种思路类似于前处理时将边界网格细化.在模拟地震波传播过程中,有限元网格尺寸应当细到足以能够通过感兴趣频段的波,廖振鹏和刘晶波[32]认为若要获得波长为 $\lambda_{T}$的波动可靠数值结果,有限元的网格寸尺应当取$(1/12\sim 1/6)\lambda_{T}$,但是实际模型计算中计算耗时与网格的大小是相关的,模型网格越细,计算模型所需的时间也越多.对于大型场地而言采用细化网格的方法之后,计算模型的耗时可能会无法估计. 为此,本文提出在建模的前处理时对人 工边界上采用细化应力分布的方法.
取积分空间步长$\Delta y = v d t$ ($v$为视波速,t为分析步时间步长),$i_{1}$与$i_{2}$分别为相邻网格的几何中点,当计算结点$B$的等效载荷时,其对应区域面积分为两部分$S_{1} /2$和$S_{2} /2$,只需将对应区域内的应力积分即可得到节点$B$的等效载荷.
1.4 地震波输入在整个地震波传播过程中,计算模型边界的节点位移、速度及单元节点应力都在不断变化,边界节点等效载荷是个变量,需要借助程序来完成地震波的输入.为此,根据本文提出的黏弹性人工边界地震波输入方法编制了相应的地震波输入程序. 由式(5) $\sim $式(8)可知,在人工边界上所需施加的节点等效载荷与波的传播方向及质点振动位移、速度均有关,而人工边界单元刚度与阻尼只与介质的材料性质有关.因此,输入程序编制分成2个模块,第一个模块考虑地震波传播过程中在边界节点处所需施加的弹簧和阻尼器元件(施加人工边界条件);第二个模块考虑地震波传播过程中在人工边界节点处所需施加的等效载荷.
下面对程序中较为关键的问题进行扼要说明,首先通过ABAQUS CAE建立数值分析模型,完成有限元计算模型的网格划分、材料分区并建立分析步等,在此基础上,获取全部有限元网格的结点坐标,各单元节点编号的信息,运行程序输入材料参数.在第1个模块中,首先读取边界节点的坐标、模型参数及材料参数,根据式(1)和式(2)与边界各节点的影响区域,计算出在边界各节点处所需施加的弹簧和阻尼器的参数值;在第2个模块中,首先读取模型参数及材料参数,根据波动方程和入射波的位移时程与速度时程,分别计算入射波与反射波在任一时刻dt引起的边界节点振动位移与速度,再由节点振动速度及波传播方向,根据式(5)$\sim$式(8)分别计算出边界各节点沿着$x$轴与$y$轴方向节点应力,当地震波斜向输入时,边界上各质点的振动存在时间延迟,每个节点影响区域内的质点振动是不一致的,此时利用积分来细化边界节点等效载荷,空间步长△y =vdt($v$为边界上地震波沿着坐标轴方向的波速分量,dt为时间步长),将各节点影响区域内的应力积分即可得到人工边界节点的等效载荷.
2 数值模拟算例以二维弹性介质半空间内平面P波斜入射问题为算例,检验本文方法的可行性及分析精度. 数值模拟模型为一水平向800 m,竖向400 m的矩形区域,在区域的左端、右端及底端分别设置人工边界,顶端为自由面,介质参数见表 1.
| 表 1 波动分析的介质参数 Table 1 Material parameters of wave propagation simulation |
有限元单元网格尺寸按式(13)计算确定
| $ \dfrac{V_{\rm S} }{12f_{\max } } ≤ h_{\max } ≤ \dfrac{V_{\rm S} }{6f_{\max } } $ | (13) |
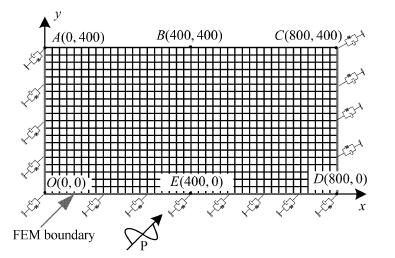
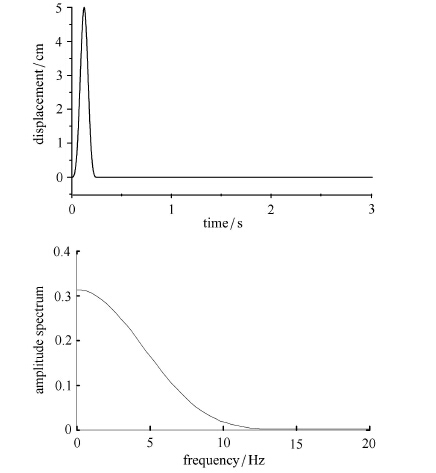
其中$V_{\rm S}$为土层剪切波速,$f_{\max}$为截止频率.截止频率一般取为研究所关注的地震动频段的最高频率,对于场地地震波动问题可取为10$\sim$20 Hz.本文采用四边形单元对模型进行离散,空间离散步距取$\Delta x=5$ m,$\Delta y=5$ m,其有限元计算模型如图 4所示,入射波选用一宽0.25 s,持时3 s的近似狄拉克脉冲,入射角度为20$^{\circ}$,其位移时程曲线及傅里叶谱如图 5所示.
|
图 4 二维波动计算网格图 Figure 4 Two-dimensional meshes of wave propagation analysis |
|
图 5 输入地震波位移曲线及其傅里叶谱 Figure 5 Displacement time-history and its Fourier spectrum of incident earthquake wave |
对于如图 4所示的散射问题模型,散射波源选为自由表面的中心点,即为$B$点. 在截断边界处,采用2.4节中编制的程序实现黏弹性动力人工边界以及人工边界各节点等效载荷的自动施加,动力分析的时间步长取$\Delta t = 0.00 1$ s,计算总时间为3 s.
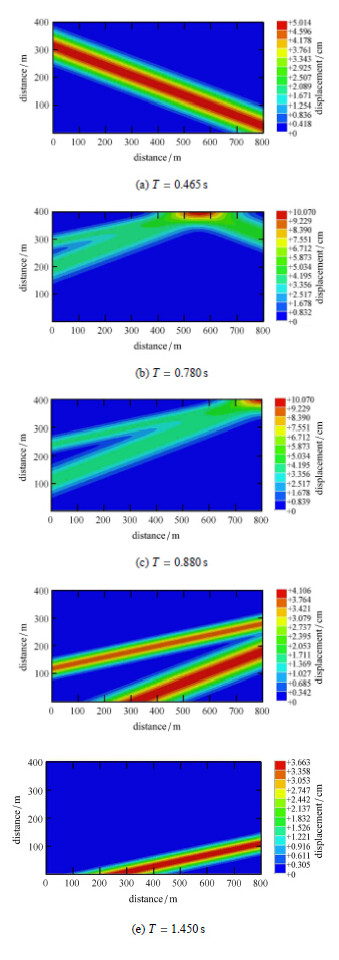
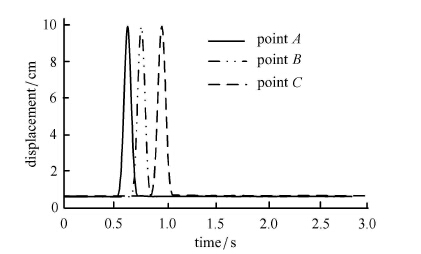
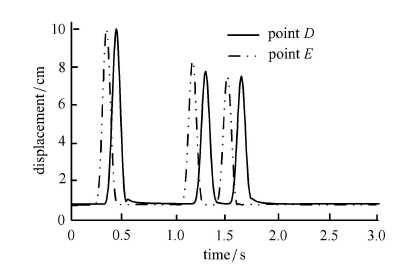
图 6中给出了矩形计算区域波场位移云图,可以直观的观察到波动在介质中的传播过程,图 7给出了自由表面观察点$A \sim C$ 3个点的位移时程曲线,图 8给出了底边界观察点$D$和$E$两点的位移时程曲线.
|
图 6 P波波场位移云图 Figure 6 P-wave propagation displacement nephogram |
|
图 7 地表A,B,C点位移时程曲线 Figure 7 Displacement time-histories at A,B,C points of ground surface |
|
图 8 底边界D,E两点位移时程曲线 Figure 8 Displacement time-histories at D,E points of bottom boundary |
由图 6可以看出平面P波在介质中的传播过程,而图 6(b) $\sim$图 6(d)和图 8可以进一步看出P波斜入射时由自由表面反射产生的反射P波与反射SV波,图 7展现了地震波的行波效应且在左、右和底部人工边界处无反射波现象,说明本文方法所施加的黏弹性人工边界对地震波输入的有效性和准确性.
地震波斜入射时均匀半空间场地地表位移峰值理论解表达式为
| $ \left.\begin{array}{l} D_x = D_{\rm P} \sin \alpha - A_1 D_{\rm P} \sin \alpha + \\ A_2 D_{\rm P} \cos \beta \\ D_y = D_{\rm P} \cos \alpha + A_1 D_{\rm P} \cos \alpha + \\ A_2 D_{\rm P} \sin \beta \end{array} \right \} $ | (14) |
其中,$D_{\rm P}$为入射P波的峰值位移,$\alpha $和$\beta $ 分别为入射P波与反射SV波的角度,关系式见式(4);$A_{1}$和$A_{2}$分别为地表反射P波、SV波位移幅值放大系数见式(11),$D_{x}$与$D_{y}$分别表示地表水平向和竖向峰值位移.
依据式(14)计算了P波入射角度分别为30$^{\circ }$,45$^{\circ }$和60$^{\circ }$时地表位移峰值理论解,结果列于表 2;表 3给出了离散网格为 2.5 m×2.5 m,4 m$\times $4 m和5 m×5 m时不同入射角度情况下本文方法与常规方法计算出的地表A,B,C三点的峰值位移反应相应于理论解的相对误差比较.
| 表 2 地表位移峰值理论解 Table 2 Peak displacement values (cm) |
| 表 3 不同方法计算的地表A; B 和C 点峰值位移反应相应于理论解的误差比较(%) Table 3 Comparison of peak displacement errors corresponding to a closed form solution at ground surface A; B and C points for different methods (%) |
从表 3可以看出:在满足波动有限元离散精度条件下,当采用不同网格尺寸、入射角度和不同方法时,自由表面中点B的计算精度都比边界点A,C的计算精度高,表明引入的人工边界条件对计算结果有一定的影响,但本文方法其影响较小;随着入射角度和网格尺寸的增大,三点的计算误差也在逐渐增大,常规方法的计算误差比本文方法增长快;在采用相同网格大小和相同入射角度的情况下,本文方法的计算精度比常规方法明显高.
从表 3还可以进一步看出:如果要获得相同的计算精度,常规方法需要采用更小有限元离散网格尺寸,本文方法的网格尺寸可以是常规方法的约2倍.在复杂和大空间范围的岩土场地地震波动模拟方面,本文方法的这一优势可以在确保一定计算精度要求的前提下大幅度减少计算工作量,特别是对于三维模型问题.
3 结语地震波斜入射时人工边界上网格节点对应区域内的应力分布是不均匀的.为此,本文在边界上采用细化节点对应区域内的应力分布,对无限域地震波输入方法进行了优化,并以均匀半空间场地为例进行了数值模拟,得到以下结论.
(1) 本文方法与常规方法的计算精度都取决于网格大小与入射角度.在满足波动有限元离散精度条件下,网格越小、入射角度越小,计算精度越高;对于相同尺寸的计算网格,本文方法的计算精度明显高于常规方法.
(2) 在离散网格尺寸满足波动计算精度要求的前提下,大角度入射时,按照本文方法采用较大网格尺寸的计算误差控制在5%以内,而常规方法的误差高于5%,同时本文方法也可应用于大型三维场地的波动模拟,在满足有限元数值模拟精度要求下可以大幅减少空间离散网格数,显著提高大尺度场地的地震效应分析的计算效率.
(3) 本文方法可应用于大型复杂问题的动力有限元数值模拟,以提高模拟精度.
| 1 |
刘晶波, 谷音, 杜义欣. 一致黏弹性动力人工边界及黏弹性边界单元.
岩土工程学报,2006, 28 (9) : 1070-1075.
( Liu Jingbo, Gu Yin, Du Yixin. Consistent viscous-spring artificial boundaries and viscous-spring boundary elements.
Chinese Jounal of Geotechnical Engineering,2006, 28 (9) : 1070-1075.
(in Chinese) ) ( 0) 0)
|
| 2 |
刘晶波, 王振宇, 杜修力, 等. 波动问题中的三维时域黏弹性动力人工边界.
工程力学,2005, 22 (6) : 46-51.
( Liu Jingbo, Wang Zhenyu, Du Xiuli, et al. Three-dimensional visco-elastic artificial boundaries in time domain for wave motion problems.
Engineering Mechanics,2005, 22 (6) : 46-51.
(in Chinese) ) ( 0) 0)
|
| 3 |
廖振鹏, 杨柏坡, 袁一凡. 暂态弹性波分析中人工边界的研究.
地震工程与工程振动,1982, 2 (1) : 1-11.
( Liao Zhenpeng, Yang Baipo, Yuan Yifan. Artificial boundary in analysis of transient elastic wave propagation.
Earthquake Engineering and Engineering Vibration,1982, 2 (1) : 1-11.
(in Chinese) ) ( 0) 0)
|
| 4 |
Clatton R, Engquist B. Absorbing boundary conditions for acoustic and elastic wave equations.
Bulletin of the Seismological Society of America,1977, 67 (6) : 1529-1540.
( 0) 0)
|
| 5 |
Lysmer J, Kuhlemeyer RL. Finite dynamic model for infinite media.
Journal of Engineering Mechanics Division, ASCE,1969, 95 (4) : 859-878.
( 0) 0)
|
| 6 |
Deeks AJ, Randolph MF. Ax symmetric time-domain transmitting boundaries.
Journal of Engineering Mechanics, ASCE,1994, 120 (1) : 25-42.
DOI: 10.1061/(ASCE)0733-9399(1994)120:1(25). ( 0) 0)
|
| 7 |
杜修力, 赵密, 王进廷. 近场波动模拟的人工应力边界条件.
力学学报,2006, 38 (1) : 49-56.
( Du Xiuli, Zhao Mi, Wang Jinting. A stress artificial boundary in fea for near field wave problem.
Chinese Journal of Theoretical and Applied Mechanics,2006, 38 (1) : 49-56.
(in Chinese) ) ( 0) 0)
|
| 8 |
廖振鹏, 刘晶波. 波动的有限元模拟-基本问题和基本研究方法.
地震工程与工程振动,1989, 9 (4) : 1-14.
( Liao Zhenpeng, Liu Jingbo. Finite element simulation of wave motion-basic problems and conceptual aspects.
Earthquake Engineering and Engineering Vibration,1989, 9 (4) : 1-14.
(in Chinese) ) ( 0) 0)
|
| 9 |
李小军, 廖振鹏. 时域局部透射边界的计算飘移失稳.
力学学报,1996, 2 (5) : 627-632.
( Li Xiaojun, Liao Zhenpeng. The drift instability of local transmitting boundary in time domain.
Acta Mechanica Sinica,1996, 2 (5) : 627-632.
(in Chinese) ) ( 0) 0)
|
| 10 |
李小军. 非线性场地地震反应分析方法的研究.[博士论文]. 哈尔滨:中国地震局工程力学研究所, 1993
( Li Xiaojun. Study on the method of analyzing the earthquake response of nonlinear site.[PhD Thesis]. Harbin:Institute of Engineering Mechanics, China Earthquake Administration, 1993(in Chinese)
) http://www.oalib.com/references/17437809 ( 0) 0)
|
| 11 |
范留明, 赵钦, 刘云贺. 倾斜入射地震波作用下成层场地动力反应的界面子波算法.
岩土工程学报,2015, 37 (4) : 601-607.
( Fan Liuming, Zhao Qin, Liu Yunhe. Interfacial wavelet algorithm for dynamic response of horizontal layered site due to inclined seismic waves.
Chinese Journal of Geotechnical Engineering,2015, 37 (4) : 601-607.
(in Chinese) ) ( 0) 0)
|
| 12 |
何卫平, 何蕴龙. 考虑地震波幅衰减的斜入射二维自由场.
振动与冲击,2016, 35 (1) : 84-88.
( He Weiping, He Yunlong. Free field motions considering amplitude attenuation of oblique seismic waves.
Journal Of Vibration and Shock,2016, 35 (1) : 84-88.
(in Chinese) ) ( 0) 0)
|
| 13 |
路德春, 李云, 马超, 等. 斜入射地震作用下地铁车站结构抗震性能分析.
北京工业大学学报,2016, 42 (1) : 87-94.
( Lu Dechun, Li Yun, Ma Chao, et al. Analysis of the three-dimensional seisic performance of underground.
Journal of Beijing University Of Technology,2016, 42 (1) : 87-94.
(in Chinese) ) ( 0) 0)
|
| 14 |
刘晶波, 吕彦东. 结构-地基动力相互作用问题分析的一种直接方法.
土木工程学报,1998, 31 (3) : 55-64.
( Liu Jingbo, Lü Yandong. A direct method for analysis of dynamic soil-structure interaction.
China Civil Engineering Journal,1998, 31 (3) : 55-64.
(in Chinese) ) ( 0) 0)
|
| 15 |
Heymsfield E. Two-dimensional scattering of SH waves in a soil layer underlain with a sloping bedrock.
Soil Dynamics and Earthquake Engineering,2000, 19 (7) : 489-500.
DOI: 10.1016/S0267-7261(00)00030-0. ( 0) 0)
|
| 16 |
郜新军, 赵成刚, 刘秦. 地震波斜入射下考虑局部地形影响和土结动力相互作用的多跨桥动力响应分析.
工程力学,2011, 28 (11) : 237-243.
( Gao Xinjun, Zhao Chenggang, Liu Qin. Seismic response analysis of multi-span viaduct considering topographic effect and soil-structure dynamic interaction based on inclined wave.
Engineering Mechanics,2011, 28 (11) : 237-243.
(in Chinese) ) ( 0) 0)
|
| 17 |
杜修力, 徐海斌, 赵密. SV波斜入射下高拱坝地震反应分析.
水利发电学报,2015, 34 (4) : 139-145.
( Du Xiuli, Xu Haibin, Zhao Mi. Analysis on seismic response of high arch dam to SV wave of oblique incidence.
Journal of Hydroelectric Engineering,2015, 34 (4) : 139-145.
(in Chinese) ) ( 0) 0)
|
| 18 |
杜修力, 黄景琦, 赵密, 等. SV波斜入射对岩体隧道洞身段地震响应影响研究.
岩土工程学报,2014, 36 (8) : 1400-1406.
( Du Xiuli, Huang Jingqi, Zhao Mi, et al. Effect of oblique incidence of SV wave on seismic response of portal section of rock tunnels.
Chinese Journal of Geotechnical Engineering,2014, 36 (8) : 1400-1406.
(in Chinese) ) ( 0) 0)
|
| 19 |
黄景琦, 杜修力, 田志敏, 等. 斜入射SV波对地铁车站地震响应的影响.
工程力学,2014, 31 (9) : 81-88.
( Huang Jingqi, Du Xiuli, Tian Zhimin, et al. Effect of the oblique incidence of seismic SV wave on the seismic response of subway station structure.
Engineering Mechanics,2014, 31 (9) : 81-88.
(in Chinese) ) ( 0) 0)
|
| 20 |
柴少波, 李建春, 李海波, 等. 平面P波入射含结构面岩体并引起地表面的振动研究.
岩石力学与工程学报,2015, 34 (2) : 3888-3895.
( Chai Shaobo, Li Jianchun, Li Haibo, et al. Study of P-wave propagation across a natyral atructural plan and its influence on ground motion.
Chinese Journal of Rock Mechanics and Engineering,2015, 34 (2) : 3888-3895.
(in Chinese) ) ( 0) 0)
|
| 21 |
黄景琦, 杜修力, 赵密, 等. 近场数值波动分析中地震波输入的一种简化方法.
振动与冲击,2015, 34 (3) : 77-82.
( Huang Jingqi, Du Xiuli, Zhao Mi, et al. A simplified seismic wave input method for near-field wave analysis.
Journal of Vibration and Shock,2015, 34 (3) : 77-82.
(in Chinese) ) ( 0) 0)
|
| 22 |
梁建文, 齐晓原, 巴振宁. 基于黏弹性边界的三维凹陷地形地震响应分析.
地震工程与工程振动,2014, 34 (4) : 21-28.
( Liang Jianwen, Qi Xiaoyuan, Ba Zhenning. Seismic respones analysis of 3D canyon based on the viscous-spring boundary.
Earthquake Engineering and Engineering Dynamics,2014, 34 (4) : 21-28.
(in Chinese) ) ( 0) 0)
|
| 23 |
Zhang CH, Pan JW, Wang JT. Infulence of seismic input mechanisms and radiation damping pn arch dam response.
Soil Dynamics and Earthquake Engineering,2009, 29 (9) : 1282-1293.
DOI: 10.1016/j.soildyn.2009.03.003. ( 0) 0)
|
| 24 |
郜新军, 赵成刚, 张延. 多源散射叠加黏弹性人工边界探究及在桥梁工程中的应用.
土木工程学报,2010, 43 (11) : 131-138.
( Gao Xinjun, Zhao Chenggang, Zhang Yan. A study of viscous-spring superposition artifical boundary for multi-sources scattering problem and its applicatio in bridge engineering.
China Civil Engineering Jounal,2010, 43 (11) : 131-138.
(in Chinese) ) ( 0) 0)
|
| 25 |
刘晶波, 李彬. 三维黏弹性性静-动力统一人工边界.
中国科学 E辑),2005, 35 (9) : 866-980.
( Liu Jingbo, Li Bin. Three dimensional static-dynamic unified viscoelastic artificial boundary.
Science in China:Series E,2005, 35 (9) : 866-980.
(in Chinese) ) ( 0) 0)
|
| 26 |
杨勋, 王欢欢, 余克勤, 等. 行波激励下防波堤地震动力响应分析.
岩土力学,2014, 35 (6) : 1775-1781.
( Yang Xun, Wang Hunahuan, Yu Keqin, et al. Seismic dynamic response analysis of breakwater under traveling wave excitations.
Rock and Soil Mechanics,2014, 35 (6) : 1775-1781.
(in Chinese) ) ( 0) 0)
|
| 27 |
胡豹, 金先龙, 占昌宝, 等. 地铁车辆会对单洞双线隧道影响的数值模拟.
振动与冲击,2015, 34 (24) : 32-39.
( Hu Bao, Jin Xianlong, Zhan Changbao, et al. Numerical simulation of the nonstop crossing of opposite subways in a single bore tunnel.
Journal of Vibration and Shock,2015, 34 (24) : 32-39.
(in Chinese) ) ( 0) 0)
|
| 28 |
贾磊, 谢咏平, 李慎奎. 爆破振动对邻近隧道衬砌安全的数值模拟分析.
振动与冲击,2015, 34 (11) : 173-177.
( Jia Lei, Xie Yongping, Li Shenkui. Numerical simulation for impact of blasting vibration on nearby tunnel lining saety.
Journal of Vibration and Shock,2015, 34 (11) : 173-177.
(in Chinese) ) ( 0) 0)
|
| 29 |
张燎军, 张慧星, 王大胜, 等. 黏弹性人工边界在ADINA中的应用.
世界地震工程,2008, 24 (1) : 12-16.
( Zhang Liaojun, Zhang Huixing, Wang Dasheng, et al. The application of artificial viscous spring boundary in ADINA.
Word Earthquake Engineering,2008, 24 (1) : 12-16.
(in Chinese) ) ( 0) 0)
|
| 30 |
柳锦春, 还毅, 李建权. 人工边界及地震动输入在有限元软件中的实现.
地下空间与工程学报,2011, 7 (S2) : 1774-1779.
( Liu Jinchun, Huan Yi, Li Jianquan. Application of artication boundary and seismic input in general finite element software.
Chinese Jounral of Underground Space and Engineering,2011, 7 (S2) : 1774-1779.
(in Chinese) ) ( 0) 0)
|
| 31 |
张海, 王雪杰, 李雅. 地震波输入方向对软土地区车站结构响应的影响.
世界地震工程,2014, 30 (2) : 29-35.
( Zhang Hai, Wang Xuejie, Li Ya. Influence of input seisic wave's direcion on response of station structure in soft soil area.
World Earthquake Engineering,2014, 30 (2) : 29-35.
(in Chinese) ) ( 0) 0)
|
| 32 |
廖振鹏, 刘晶波. 离散网格中的弹性波(I).
地震工程与工程振动,1986, 6 (2) : 1-16.
( Liao Zhenpeng, Liu Jingbo. Elastic wave motion in discrete grids (I).
Earthquake Engineering and Engineering Vibration,1986, 6 (2) : 1-16.
(in Chinese) ) ( 0) 0)
|
2. Civil Engineering and Earthquake Disaster Prevention Center of Jiangsu Province, Nanjing 210009, China
3. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
 2016, Vol. 48
2016, Vol. 48
