2. 北京理工大学机械与车辆工程学院, 北京 100190
黏着力是维持列车安全与平稳运行的关键因素之一,随着运行速度的提高,尤其是当速度超过200 km/h时,在雨雪、潮湿等环境下,轮轨间的摩擦系数会降低[1-3].黏着系数的定义是切向力除以法向力,是用于估算有效黏着力的[4].最大黏着力与摩擦力有关,摩擦力的减小会导致黏着力的减小.在有液体介质存在的条件下,摩擦系数的降低是由于一部分接触表面微凸体被液体隔开,从而形成混合润滑,造成接触面间的剪切力远低于全部固体的粗糙面之间接触的剪切力.因此,较大的表面粗糙度可增大摩擦系数[5].事实上,混合润滑条件下的摩擦系数不仅受到表面粗糙度的影响,也受粗糙度取向的影响[6-7].然而,以往关于粗糙度取向对摩擦系数的影响的研究结论似乎是矛盾的.Chen等[8]用基于平均流量模型的弹流润滑理论计算了潮湿条件下轮轨之间的摩擦系数,结果表明,如果粗糙度取向指数$\gamma <1$时,即:粗糙度取向为横向时,摩擦系数较小,当表面粗糙度取向是纵向($\gamma > 1$)时,摩擦系数较大. 然而实验结果却显示$\gamma <1$时的摩擦系数比$\gamma > 1$时的大[9].Akbarzadeh等[10-11]也研究了在混合润滑条件下表面粗糙度取向对摩擦系数的影响.研究表明横纹的摩擦系数大于纵纹的摩擦系数.
作者认为,上述相互矛盾的结果可能源于如下几点.第一,所使用的数值分析模型不同,尽管Chen等[9]和Akbarzadeh等[10]都用{$\gamma $}来描述表面粗糙度的取向,但是,Chen等[8]用来解决弹流润滑问题的模型是基于粗糙面间平均流量的雷诺方程,即平均流量模型.而Akbarzadeh和Khonsari[10]所使用的Moes模型[12]是从Jeffreys方程[13]推导出的,没有平均流量这个假设.第二,试样的表面形貌是通过机械加工方法得到的,如:用砂纸打磨.实验中这些形貌易磨损. 文献[9]表明,实验前后表面粗糙度明显减小.Akbarzadeh和Khonsari[11]也发现在磨合期结束后,各种表面形貌的摩擦系数趋于一致.因此,如果要得到比较可靠的数据,实验中试样的表面形貌应该具有较高的耐磨性和稳定性.第三,用参数\{$\gamma$}来描述表面粗糙度取向的方法,也称为随机模型,它表征了总体表面形貌对流体动力润滑的影响,并没有提供关于局部压力、局部膜厚波动和粗糙面的变形等细节,而这通常是研究固体接触区润滑膜破裂以及剪切作用的关键.事实上,试图用一个简单的统计参数$\gamma$较为全面地描述表面粗糙度的取向特征是不可能的.因此,1990年以来另一类分析方法------确定性模型逐渐建立起来.它以简化的真实表面形貌作为数值解的输入文件,无需统计参数.此外,无论采用哪种模型,随机的或确定性的,接触区总可以分为两种不同的区域:被润滑膜隔开的流体区和固体粗糙峰接触区.这就需要确定流体区与粗糙峰接触区的边界.由于粗糙接触区很不规则并且随时间变化,要想获得这样的边界条件十分困难.
为了研究混合润滑条件下表面粗糙度取向对轮轨摩擦系数的影响,在实验方面,本文采用了小尺度对滚试样.作为主动轮的环形试样材料为车轮钢,试样侧面为对滚面,并且经激光处理形成耐磨表面以减少实验中表面粗糙度的衰减.诸如,激光相变硬化、激光熔化、激光熔覆等激光表面改性工艺,多年来已经被成功地用于提高金属材料表面的耐磨性[14].由于激光多道搭接处理存在道次间的重叠,在搭接区可能出现软化带或裂纹,进而对表面产生不利影响,因此,本文采用离散处理方法以避免激光作用区的重叠[15-16].在计算方面,本文采用确定性模型,并且用朱东和胡元中提出的解法[17-19],即对于粗糙峰接触区和流体区都用雷诺方程求解.该解法的主要思想是:当液膜或间隙为零时,赫兹方程的解与雷诺方程的解是一致的.利用该解法可以顺利地求解苛刻运行条件下的工程表面和规则表面的混合润滑问题,也能够模拟从全膜弹流,到混合润滑,到边界润滑(甚至干摩擦)的全范围弹流润滑问题[20-22].由于水的流变特性与油的很不相同,在小试验机上以较低的速度很难显示出表面粗糙度取向对水润滑摩擦系数的作用.因此,为了验证上述数值解法在水润滑中的有效性,本文所用的计算和实验条件为:线接触、小尺度比例试样、固定蠕滑率和油润滑.关于实际轮轨接触、水润滑条件下摩擦系数随速度和蠕滑率变化的数值模拟将在后续文章中阐述,以给出实际轮轨接触在高速、水润滑条件下的黏着特性.
1 分析模型根据Hu和Zhu[17-19]的确定性混合弹流润滑模型,接触变形区的膜厚、润滑剂的流动和粗糙峰的接触都用一个雷诺方程来处理.在线接触弹流润滑区,由雷诺方程决定的压力表达式为
| $\frac{\partial }{\partial x}\left( \frac{\rho {{h}^{3}}}{12{{\eta }^{*}}}\frac{\partial p}{\partial x} \right)+\frac{\partial }{\partial y}\left( \frac{\rho {{h}^{3}}}{12{{\eta }^{*}}}\frac{\partial p}{\partial y} \right)=u\frac{\partial (\rho h)}{\partial x}+\frac{\partial (\rho h)}{\partial t}$ | (1) |
$x$坐标方向与运动方向一致.瞬时膜厚$h$或两个表面的间隙由下列几何方程给出
| $h(x,y)={{h}_{0}}(x,y,t)+\frac{{{x}^{2}}}{2{{R}_{x}}}+{{\delta }_{1}}(x,y,t)+{{\delta }_{2}}(x,y,t)+\nu (x,y,t)$ | (2) |
其中,$h_{0}(x$,$y,t)$为无变形时的初始间隙,$R_{x}$为两个表面的当量半径,$\delta $1和$\delta$2 分别为两个表面的粗糙度幅度,$v(x$,$y$,$t)$为表面变形量,它由下式决定
| $v(x,y,t)=\frac{2}{\pi {E}'}\iint\limits_{\Omega }{\frac{{{p}_{\text{h}}}({x}',{y}')+{{p}_{\text{c}}}({x}',{y}')}{\sqrt{{{(x-{x}')}^{2}}+{{(y-{y}')}^{2}}}}\text{d}{x}'\text{d}{y}'}$ | (3) |
其中,$p_{\rm h}$ 为流体动压,$p_{\rm c}$ 为粗糙峰接触压力,${E}'$为当量弹性模量,$\Omega $ 表示计算域. 流体动压可通过方程(1)$\sim$(3)联立求解.
根据文献[17],在粗糙峰接触区,雷诺方程退化为以下形式
| $u\frac{\partial h}{\partial x} + \frac{\partial h}{\partial t} = 0~~~{\rm at} ~~h=0 $ | (4) |
对于稳态,方程(4)可进一步简化为
| $\frac{\partial h}{\partial x}=0$ | (5) |
由于方程(5)是方程(1)的特殊形式,一个统一的方程组及数值方法既可以用于流体区又可用于粗糙峰接触区.这样,通过求解一个方程组就可以得到整个计算域的完整数值解.流体动压和粗糙峰接触压力都可以通过同样的循环迭代得到,无需任何有关流体区与粗糙峰接触区边界及边界条件的信息.于是,摩擦系数可由下式计算
| $\mu =\frac{{{\mu }_{\text{c}}}{{P}_{\text{c}}}+{{\mu }_{\text{h}}}{{P}_{\text{h}}}}{p}$ | (6) |
其中,$\mu _{\rm h} P_{\rm h}$为流体区的摩擦力,其计算方法参见文献[23].流体区的润滑膜剪切力可由黏弹性非牛顿模型计算,如Bair--Winer模型[24]
| $\dot{\gamma }=\frac{{\dot{\tau }}}{{{G}_{\infty }}}-\frac{{{\tau }_{\text{L}}}}{\eta }\ln \left( 1-\frac{\tau }{{{\tau }_{\text{L}}}} \right)$ | (27) |
其中,极限剪应力{$\tau $}$_{\rm L}$和极限弹性模量$G_{\infty }$是压力与温度的函数,一般由经验值决定. $\mu $ $_{\rm c}$是粗糙峰接触区的摩擦系数,由实验确定. 对于水润滑,Chen等[5,25]取0.14,0.2$\sim $0.45. 根据文献[26]的测量结果,$\mu $ $_{\rm c}$的取值范围在0.15到0.17.本文的条件是油润滑,可以取0.1[27]. $P_{\rm h}$ 和$P_{\rm c}$ 分别表示油膜和粗糙峰接触载荷,$p$为总载荷.
| $p=P_{\rm h}+P_{\rm c}=\iint\limits_\Omega {p_{\rm h} (x,y){\rm d}x{\rm d}y + } \iint\limits_\Omega {p_{\rm c} } (x,y){\rm d}x{\rm d}y $ | (8) |
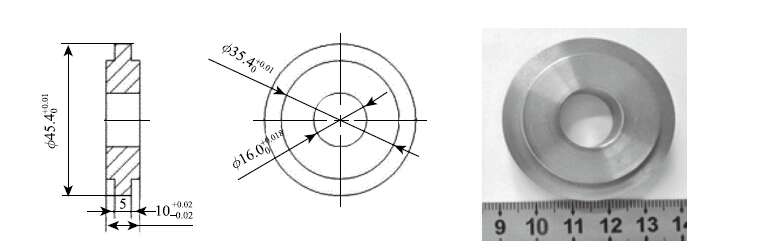
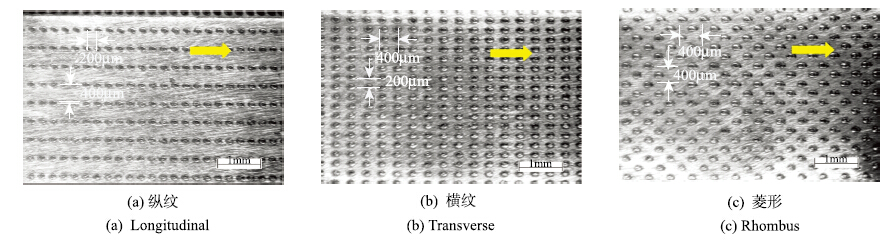
本文所用的对滚环形试样分别由高速列车车轮钢和钢轨钢制成.摩擦实验在Amsler型试验机上进行.试样分别安装在相向滚动的平行轴上并且由伺服电机独立控制,其中车轮试样安装在下面的主动轴上,钢轨试样安装在上面的从动轴上.主动轴转速为400 r/min. 接触载荷通过弹簧加载.涡流减速器与上试样轴相连,通过施加减速力矩使从动试样逐渐减速,使上下两试样保持一定的蠕滑率.为了保证两试样间的最大接触应力达到1 000MPa,并且在接触区内至少有若干个激光作用区,以便反映粗糙度取向对摩擦系数的影响,两个试样的直径为45.40mm,厚度为10.00 mm,其中接触区长度为5.00 mm(如图 1).根据弹性理论,可以计算出赫兹接触半宽度$a$为0.18 mm,在1400N载荷作用下,接触区面积为2aL=2×0.18 mm×5.00mm=1.80mm2. 据此,激光作用区的直径设定为150 μm,间隔为200$\sim 400 μm.在进行激光处理之前,轮轨试样的侧面被磨削至粗糙度Rq=0.3μm(Rq为均方根粗糙度).车轮试样侧面在氩气保护下用YAG激光进行离散处理. 激光光斑直径为0.10 mm,脉冲宽度为1.25 ms,单脉冲能量为0.06 J.由激光形成的3种表面形貌分别为:纵纹、横纹和菱形,如图 2所示.其中的菱形形貌相当于随机模型中$\gamma =1$的均匀分布形貌.3种形貌在整个侧面上的激光区数目是一样的,即:激光作用区密度相同.表面形貌用白光干涉仪进行测量.为了比较并μm(图 3),并且润滑状态为混合润滑而不是全膜润滑,蠕滑率控制在0.20%,以减少表面粗糙度的衰减.为了与有激光形貌的轮轨试样进行比较,用一对磨削(无激光形貌)的轮轨试样进行摩擦学实验.实验润滑油牌号为Ub-3,其流变特性如表 1所示.
|
图 1 试样尺寸和实物照片 Figure 1 Dimension and object of the specimen |
|
图 2 3 种激光形貌. 箭头所指为滚动方向 Figure 2 The three laser textured patterns. The arrows indicate the direction of rolling |

|
图 3 摩擦实验之前,单个激光形貌的实测纵剖面. 其直径约为200 μm,粗糙峰高度2.5 μm Figure 3 The real cross-section profile of a single laser pattern before tribological testing. The diameter of the pattern is about 200 μm, the height over the surface is about 2.5 μm |
| 表 1 Ub-3 的特性参数 Table 1 The properties of lubricant Ub-3 |
首先在求解雷诺方程的迭代程序中,用$\varepsilon _{1}$=1.00×10-6作为$h=0$的判断标准. 当无量纲膜厚$H=h/a<\varepsilon_{1}$时,认为膜厚为零,两表面接触,雷诺方程中的压力流动项关闭.同样地,另一个数$\varepsilon _{2}$=1.00×10-5,用于检验$\partial h /\partial x$. 如果同时满足$H \le \varepsilon _{1}$ 和 $\partial h / \partial x \le\varepsilon _{2}$,挤压项应去除. 在本文的计算中,材料参数$E'=220$ GPa,几何参数$R_{x}=11.35$ mm,$L=5.00$ mm,赫兹接触区为矩形.运行条件为:载荷$w=1400$ N,运动速度$u= 0.95$ m/s,蠕滑率($u_{1}-u_{2})/u=0.20%$.根据上述参数得到的赫兹接触参数及相应的无量纲数为:pH=0.97 GPa,a=0.18 mm,无量纲材料参数G=2175(G = E',α 为黏压系数),无量纲速度U=7.62×10-12,无量纳载荷W=9.88×10-3.方程(1)中的润滑剂黏度η可由文献[28]得到
| $ \frac{1}{\eta ^\ast } = \frac{1}{\eta }\frac{\tau _0 }{\tau _1 }{\rm sinh}\left( {\frac{\tau _1 }{\tau _0 }} \right) $ | (9) |
其中,$\tau_{0}$为参考剪应力.对于Ub-3润滑油,其值为$\tau _{0} =18.0$ MPa.$\tau_{1}$为作用在下表面的剪应力,$\eta$是低剪切率时的极限黏度,是压力的函数,可由Barus关系得到
| $\eta ={{\eta }_{0}}\exp (\alpha p)$ | (10) |
润滑剂的密度也是压力的函数,由下式计算
| $\rho ={{\rho }_{0}}\left( 1+\frac{0.6\times {{10}^{-9}}p}{1+1.7\times {{10}^{-9}}p} \right)$ | (11) |
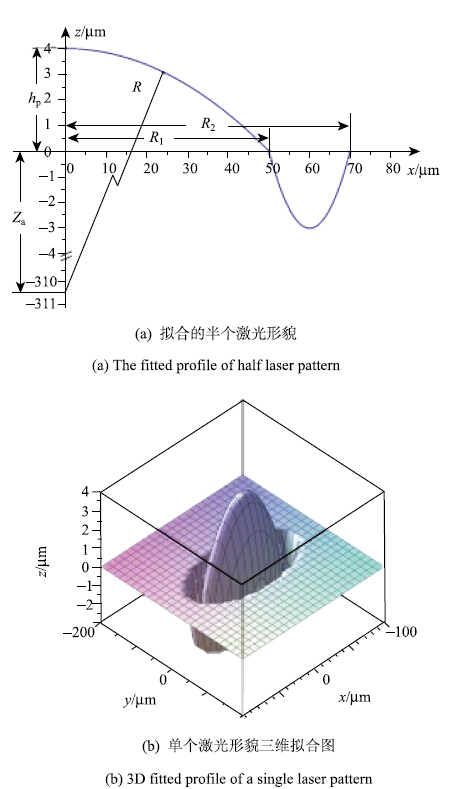
用二维分段函数拟合单个激光形貌的纵剖面(图 3),表达式为方程(12)
| $z\left( x,y \right)=\left\{ \begin{align} & \sqrt{{{R}^{2}}-x_{\text{s}}^{2}-y_{\text{s}}^{2}}-{{Z}_{\text{a}}},\quad \sqrt{x_{\text{s}}^{2}+y_{\text{s}}^{2}}\le {{R}_{1}} \\ & A\left( \sqrt{x_{\text{s}}^{2}+y_{\text{s}}^{2}}-{{R}_{1}} \right)\left( \sqrt{x_{\text{s}}^{2}+y_{\text{s}}^{2}}-{{R}_{2}} \right), \\ & {{R}_{1}}<\sqrt{x_{\text{s}}^{2}+y_{\text{s}}^{2}}\le {{R}_{2}} \\ & \text{rand}(z),\quad ~~~~~\text{else} \\ \end{align} \right.$ | (12) |
式(12)的第1部分表示球冠的局部,其中$R$,$R_{1}$,$R_{2}$,$Z_{\rm a}$,$h_{\rm p}$的说明由图 4(a)给出.$Z_{\rm a}=R-h_{\rm p}$,$h_{\rm p}$ 表示粗糙峰的高度.式(12)的第2部分是由3点拟合得到二次曲面方程.第3部分表示无激光作用的区域,其粗糙度为$R_{\rm q}$.在计算中,此区域的$R_{\rm q}$设为0.35 μm.拟合得到的参数为$R=310.50$ μm,$R_{1}=$ 50.00 μm,$R_{2}=$70.00 μm. $A=$0.03,$h_{\rm p}=$4.00 μm. 图 4(b)是单个激光形貌的三维拟合图. 其中$x_{\rm s}$ 和 $y_{\rm s}$ 随不同形貌而变化
| $ \begin{array}{lll} x_{\rm s} = x - 400n,y_{\rm s} = y-400n,\mbox{菱形} \\ x_{\rm s} = x - 400n,y_{\rm s} = y-200n,\mbox{横纹},\mbox{$n$为迭代次数}\\ x_{\rm s} = x - 200n,y_{\rm s} = y-400n,\mbox{纵纹} \end{array} $ |
|
图 4 单个激光形貌的拟合轮廓 Figure 4 The fitted profiles of laser patter |
重构表面的计算如图 5所示,求解域为$-1.9 \le x \le 2.3$和$-2.5 \le y\le 2.5$,并将其划分为257$\times$257个等距网格,相应的网格间距为$\Delta x=0.019~921~9$,$\Delta y=0.019~531~3$. 计算所用时间步长为$\Delta T=0.015$.

|
图 5 用于计算的重构表面. 箭头所指为滚动方向 Figure 5 The reconstructed surface for calculation. The arrows indicate the direction of rolling |
图 6显示了实验前后,具有激光形貌和磨削形貌试样的形貌演变.实验条件为:蠕滑率0.20%,时间180 min.列在各图下面的表面粗糙度$R_{\rm q}$是测得的该区域的粗糙度平均值.磨削表面在实验前后的粗糙度差值△Rq大约为0.10μm,而纵纹、横纹、菱形等表面形貌在实验前后的粗糙度差值分别为0.04 μm,0.06 μm和0.05 μm.由此可见,有激光形貌的表面粗糙度比磨削形貌的表面粗糙度要稳定得多,这是因为激光处理大大提高了表面耐磨性,有效地减少了表面粗糙度的衰减.

|
图 6 用于计算的重构表面. 箭头所指为滚动方向 Figure 6 Real surface topography before and after tribology testing |
根据图 6所示的表面粗糙度值,具有纵纹、横纹、菱形等形貌的车轮试样在实验前后的粗糙度值在0.54μm到 0.75 μm范围之内.考虑到磨削的钢轨试样的表面粗糙度为0.35μm,每一对轮轨试样的复合粗糙度值在0.31 ~0.45 μm之间.根据弹流润滑理论,如果两试样表面均为光滑面,则中心膜厚为0.125μm [29]. 因此,本文实验的膜厚比λ的范围为0.16~0.40,处于0.05 和1.0之间.这说明,本文实验处于混合润滑范围.
4.2 压力与膜厚图 7 $\sim$ 图 9是几个代表性 算例,显示了在0.2%蠕滑率下,无量纲膜厚的轮廓和沿$x$轴方向中心线分布的3种表面粗糙度取向的压力$\!$--$\!$膜厚图.图中圆圈表示激光作用区,其中的白色部分表示粗糙峰已经直接接触.将接触区中沿着中心线(图中黑色点划线)的两个典型位置(如:位置1和位置2)的压力与膜厚分布进行了比较.例如,图 7(a)显示了纵纹在400 μm,600 μm 和800 μm等处对应的接触区中无量纲压力与膜厚,而图 7(c))显示的是该形貌在500μm,700 μm 和 900μm等处的无量纲压力与膜厚.比较图 7(b)和图 7(d)可以发现,压力与膜厚分布非常相似,这说明纵纹形貌通过接触区时造成的波动不大.但是,横纹形貌通过接触区时造成的压力与膜厚分布波动就比较大(如图 8(b)和图 8(d)),位置1对应的压力峰值达18$p_{\rm H}$,而位置2的只有10$p_{\rm H}$.对于菱形,压力与膜厚的分布也比较稳定(图 9).这种波动可能是由接触区中激光作用区的数量造成的.例如,对于横纹,接触区中激光作用区的数量为3至6个,而纵纹的是6至7.5个.对于菱形,则稳定在9个左右.

|
图 7 纵纹在不同位置的无量纲膜厚轮廓以及中心线上(轮廓图中直线所示的位置)的无量纲压力和膜厚 Figure 7 Dimensionless film thickness contour and dimensionless pressure and film thickness at centerline (position indicated by the line over the contour plot) for longitudinal surface at different contact positions |

|
图 8 横纹在不同位置的无量纲膜厚轮廓以及中心线上(轮廓图中直线所示的位置)的无量纲压力和膜厚 Figure 8 Dimensionless film thickness contour and dimensionless pressure and film thickness at centerline (position indicated by the line over the contour plot) for transverse surface at different contact positions |

|
图 9 菱形在不同位置的无量纲膜厚轮廓以及中心线上(轮廓图中直线所示的位置)的无量纲压力和膜厚 Figure 9 Dimensionless film thickness contour and dimensionless pressure and film thickness at centerline (position indicated by the line over the contour plot) for rhombus surface at different contact positions |
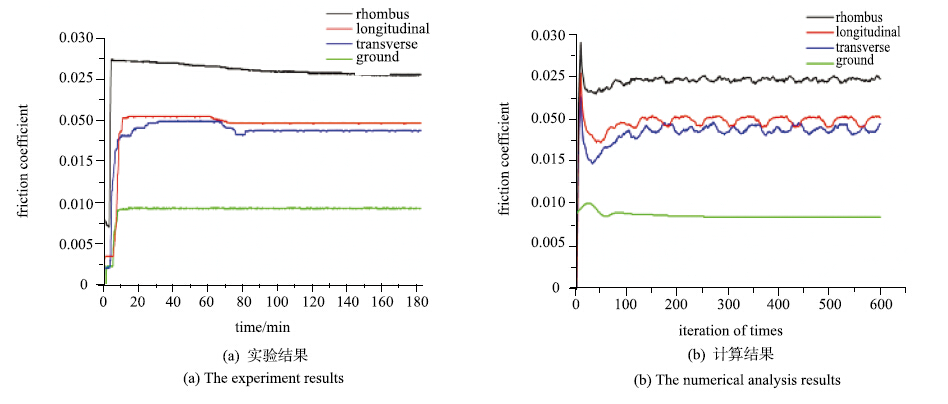
在工程上,摩擦系数要比膜厚和压力更加实用.图 10展示了不同表面形貌取向,包括磨削(无激光处理)形貌的轮轨试样在油润滑条件下,摩擦系数随时间变化的数值模拟和实验结果.显然,与磨削形貌的情况相比,激光形貌大幅提高了摩擦系数.其中,菱形对应的摩擦系数在3种形貌中最大,纵纹和横纹的摩擦系数基本相等,但前者略大于后者.各种形貌的摩擦系数的计算结果(图 10(b))与实验结果(图 10(a))符合较好,只在某些阶段的具体数值上有差异.例如,菱形的平均粗糙度较高,在混合润滑中固体接触的比例也比较高(见表 2),因此,磨损比另外两种形貌的严重,摩擦系数表现为逐渐下降,从开始时的0.027 5到120 min时的0.026,越来越接近模拟计算结果0.025. 120 min之后,基本完成磨合,形貌相对稳定,摩擦系数基本稳定在0.026.
|
图 10 各种激光形貌表面取向(包括磨削形貌)的摩擦系数与时间的关系 Figure 10 The friction coeffcient of different surface roughness orientations including ground pattern versus time |
| 表 2 各种表面形貌的粗糙峰接触压力与总压力之比 Table 2 The ratio of asperity contact pressure to the total pressure for various surfaces |
总的来说,较高的粗糙度增加了粗糙峰接触面积进而增大混合润滑接触区的载荷分担,增大了摩擦系数[2,30].图 10显示,3种激光形貌的轮轨试样的摩擦系数均大于磨削形貌的摩擦系数.横纹的摩擦系数低于纵纹,不仅因为前者的表面粗糙度低于后者(图 6),而且因为在混合润滑中,表面粗糙度取向对摩擦系数也有影响.本文的实验和计算中,3种形貌的激光作用区在整个侧面上的密度是相同的,表面粗糙度的差别即Rq的变化大约从0.54 μm到 0.75 μm.变化不是很大.但激光作用区的数量在接触区内的差别是比较大的,从而使接触条件差异较大.譬如,横纹、纵纹、菱形在接触区内的激光作用区数量分别是3$\sim$6,6$\sim $7.5 和9(图 7至图 9).因此,菱形的摩擦系数最大,横纹的最小.
另一方面,表面粗糙度取向对摩擦系数的影响还取决于侧流效应,而后者又受到接触区几何形状和润滑剂流变特性的影响.根据平均流量模型,流量是恒定的,本文所讨论的线接触模型可以看作宽轴承,侧流可以忽略(侧向可认为是封闭的)[7].与纵纹和菱形相比,横纹对来流的限制更大,从而使膜厚增加、流体动压增大.实际上,Zhu[23]根据其提出的模型也指出,对于线接触或者椭圆率比较大的接触区,例如,k=2.0的情况,侧流都是可以忽略的.因此,横纹对应的摩擦系数在3种形貌中是最小的.如果侧流效应不能忽略(侧向可认为是开放的),例如,$k=0.5$的情况,来流作用就比较弱,与纵纹和菱形相比,横纹对来流的限制较小,使膜厚及流体动压减小,从而使摩擦系数在3种形貌中变得最大.这种情况与文献[10-11]中的横纹阻碍流动使粗糙峰接触增加,以致摩擦系数增大的情况是一致的.因为其分析是基于Moes模型[12]和Jeffreys方程[13],那里没有平均流量这个假设,横纹阻碍来流,是否产生足够的侧流效应以致对摩擦系数产生何等影响都是模型的自然结果.对于文献[9]水润滑实验与其计算模型不相符这一问题,可以认为是由于水的黏度比油的黏度低很多,实验中产生了较大的侧流效应,以致不再满足平均流量的假设.
虽然侧流对具有不同取向表面的摩擦系数有较显著的影响,但是,在某些情况下,比如,无取向形貌或圆形接触区,则很难评价侧流的作用.显然,在混合润滑条件下,真正影响摩擦系数的是不同取向表面产生的接触压力之比,即方程(5).文献[8]已经用平均粗糙峰接触压力与总压力之比来描述不同取向表面对摩擦系数的影响.混合润滑的大多数情况下都是粗糙峰接触压力与总压力之比大于流体动压与总压力之比,除非膜厚比λ趋于1(这时混合润滑几乎成了全膜润滑).根据确定性模型计算的各种形貌的粗糙峰接触压力与总压力之比列于表 2,该表显示,3种形貌中,菱形的压力比最大,为65.99%,横纹的最小,为59.04%,而磨削形貌的为34.27%,远低于有激光形貌的情况.
5 结论本文研究了油润滑条件下表面粗糙度取向对摩擦系数的影响.为了减少实验中表面粗糙度的衰减,车轮试样的侧面用激光处理成耐磨表面,比较了3种激光表面形貌与磨削形貌的摩擦系数.确定性模型的计算和实验结果如下:
(1) 在油介质混合润滑条件下,表面粗糙度及其取向对摩擦系数有较大的影响.在本文条件下,菱形的摩擦系数在3种形貌中是最大的,纵纹和横纹的差不多,纵纹略大;
(2) 在膜厚比λ小于1的条件下,各种表面形貌取向的粗糙峰接触压力与总压力之比决定了摩擦系数的大小;
(3) 表面粗糙度取向深刻影响接触面之间的来流和侧流,进而影响摩擦系数.
| 1 |
1Ohyama T.
Traction and slip at higher rolling speeds:Some experiments under dry friction water lubrication. In:Kalousek J, ed. Contact Mechanics and Wear of Rail/Wheel Systems, Proceedings of the International Symposium Held at the University of British Columbia. Vancouver:University of Waterloo Press, 1983 : 395 -418.
( 0) 0)
|
| 2 |
Ohyama T. .
Tribological studies on adhesion phenomena between wheel and rail at high speed,1991, 144 : 263-75.
( 0) 0)
|
| 3 |
杨国伟, 魏宇杰, 赵桂林, 等. 高速列车的关键力学问题.
力学进展,2015, 45 : 201507.
( YANG Guowei, WEI Yujie, ZHAO Guilin, et al. Research progress on the mechanics of high speed rails.
Advances in Mechanics,2015, 45 : 201507.
(in Chinese) ) ( 0) 0)
|
| 4 |
Zhu Y, Olofsson U, Anders S. Adhesion modeling in the wheel-rail contact under dry and lubricated conditions using measured 3D surfaces.
Tribol Inter,2013, 61 : 1-10.
DOI: 10.1016/j.triboint.2012.11.022. ( 0) 0)
|
| 5 |
Chen H, Ban T, Ishida M, et al. Adhesion between rail/wheel under water lubricated contact.
Wear,2002, 253 : 75-81.
DOI: 10.1016/S0043-1648(02)00085-6. ( 0) 0)
|
| 6 |
Patir N, Cheng HS. Average flow model for determining effects of 3-dimensional roughness on partial hydrodynamic lubrication.
J Lubri Technol Trans ASME,1978, 100 (1) : 12-17.
DOI: 10.1115/1.3453103. ( 0) 0)
|
| 7 |
Patir N, Cheng HS. Application of average flow model to lubrication between rough sliding Surfaces.
J Lubri Technol Trans ASME,1979, 101 (2) : 220-230.
DOI: 10.1115/1.3453329. ( 0) 0)
|
| 8 |
Chen H, Ishida M, Nakahara T. Analysis of adhesion under wet conditions for three-dimensional contact considering surface roughness.
Wear,2005, 258 : 1209-1216.
DOI: 10.1016/j.wear.2004.03.031. ( 0) 0)
|
| 9 |
Chen H, Ban T, Ishida M, et al. Experimental investigation of influential factors on adhesion between wheel and rail under wet conditions.
Wear,2008, 265 (9-10) : 1504-1511.
DOI: 10.1016/j.wear.2008.02.034. ( 0) 0)
|
| 10 |
Akbarzadeh S, Khonsari MM. Effect of surface pattern on Stribeck curve.
Tribol Lett,2010, 37 (2) : 477-486.
DOI: 10.1007/s11249-009-9543-2. ( 0) 0)
|
| 11 |
Akbarzadeh S, Khonsari MM. On the prediction of running in behavior in mixed-lubrication line contact.
J Tribol Trans ASME,2010, 132 (3) : 032102.
DOI: 10.1115/1.4001622. ( 0) 0)
|
| 12 |
Moes H. Optimum similarity analysis with applications to elastohydrodynamic lubrication.
Wear,1992, 59 (1) : 57-66.
( 0) 0)
|
| 13 |
Jereys H. The draining of a vertical plate.
Math Proc Cambri Philo Soci,1930, 26 : 204-5.
DOI: 10.1017/S0305004100015437. ( 0) 0)
|
| 14 |
Steen WM, Mazumder J.
Laser Material Processing. 4th ed. London: Springer-Verlag, 2010 .
( 0) 0)
|
| 15 |
Iino Y, Shimoda K. Effect of overlap pass tempering on hardness and fatigue behaviour in laser heat-treatment of carbon-steel.
J Mater Sci Lett,1987, 6 (10) : 1193-1194.
DOI: 10.1007/BF01729179. ( 0) 0)
|
| 16 |
Li ZY, Xing XH, Yang MJ, et al. Investigation on rolling sliding wear behaviour of wheel steel by laser dispersed treatment.
Wear,2014, 314 (1-2) : 236-240.
DOI: 10.1016/j.wear.2013.12.007. ( 0) 0)
|
| 17 |
Hu YZ, Zhu D. A full numerical solution to the mixed lubrication in point contacts.
J Tribol Trans ASME,2000, 122 (1) : 1-9.
DOI: 10.1115/1.555322. ( 0) 0)
|
| 18 |
Zhu D. Effect of surface roughness on mixed EHD lubrication characteristics.
Tribol Trans,2003, 46 (1) : 44-48.
DOI: 10.1080/10402000308982598. ( 0) 0)
|
| 19 |
Zhu D, Hu YZ. Effects of rough surface topography and orientation on the characteristics of EHD and mixed lubrication in both circular and elliptical contacts.
Tribol Trans,2001, 44 : 391-398.
DOI: 10.1080/10402000108982472. ( 0) 0)
|
| 20 |
Ren N, Nanbu T, Yasuda Y. Micro textures in concentratedconformal-contact lubrication:Effect of distribution patterns.
Tribol Lett,2007, 28 (3) : 275-85.
DOI: 10.1007/s11249-007-9271-4. ( 0) 0)
|
| 21 |
Nanbu T, Ren N, Yasuda Y. Micro-textures in concentrated conformal-contact lubrication:Effects of texture bottom shape and surface relative motion.
Tribol Lett,2008, 29 (3) : 241-252.
DOI: 10.1007/s11249-008-9302-9. ( 0) 0)
|
| 22 |
Zhu D, Nanbu T, Ren N. Model-based virtual surface texturing for concentrated conformal-contact lubrication.
P IMech Eng J J Eng Tribol,2010, 224 (J8) : 685-696.
( 0) 0)
|
| 23 |
Zhu D, Hu YZ. A Computer program for the prediction of EHL and mixed lubrication characteristics, friction, subsurface stresses and flash temperatures based on measured 3-D surface roughness.
Tribol Trans,2001, 44 : 383-390.
DOI: 10.1080/10402000108982471. ( 0) 0)
|
| 24 |
Bair S, Winer WO. A rheological model for elastohydro-dynamic contacts based on primary laboratory data.
J Lubri Tech,1979, 101 (3) : 258-264.
DOI: 10.1115/1.3453342. ( 0) 0)
|
| 25 |
Chen H, Ishida M, Namura A. Estimation of wheel/rail adhesion coefficient under wet condition with measured boundary friction coefficient and real contact area.
Wear,2011, 271 (1-2) : 32-39.
DOI: 10.1016/j.wear.2010.10.022. ( 0) 0)
|
| 26 |
Wang WZ, Wang S, Shi FH, et al. Simulations and measurements of sliding friction between rough surfaces in point contacts:From EHL to boundary lubrication.
J Tribol Trans ASME,2007, 129 (3) : 495-501.
DOI: 10.1115/1.2736432. ( 0) 0)
|
| 27 |
Zhu D, Wang Q. Effect of roughness orientation on the elastohydrodynamic lubrication film Thickness.
J Tribol Trans ASME,2013, 135 (3) : 031501.
DOI: 10.1115/1.4023250. ( 0) 0)
|
| 28 |
Yang P, Wen S. A generalized Reynolds equation for non-Newtonian thermal elastohydrodynamic lubrication.
J Tribol Trans ASME,1990, 112 (4) : 631-336.
DOI: 10.1115/1.2920308. ( 0) 0)
|
| 29 |
Hamrock BJ, Schmid SR, Jacobson BO.
Fundamentals of Fluid Film Lubrication. New York: Marcel Dekker, 2004 .
( 0) 0)
|
| 30 |
Nanbu T, Yasuda Y, Ushijima K, et al. Increase of traction coefficient due to surface microtexture.
Tribol Lett,2008, 29 (2) : 105-118.
DOI: 10.1007/s11249-007-9287-9. ( 0) 0)
|
2. Mechanical and Vehicular Engineering College, Beijing Institute of Technology, Beijing 100190, China
 2016, Vol. 48
2016, Vol. 48
