Kirchhoff于1850年发表了第一个完善的板弯曲理论,被称为经典板理论. 经典板理论基于两个基本假设[1]:(1)原来垂直于平板中面的直线,变形后仍保持为直线且垂直于弯曲后的中面,即直法线假设;(2)在横向载荷作用下板产生微弯时,板的中面并不变形. 因此,经典板理论要求板的厚度与边长之比处于薄板范围内. 依据经典的弯矩、扭矩、剪力(统称广义应力)表示的平衡方程(本文简称为板的经典平衡方程),经典板理论最终表示为挠度的4阶偏微分方程和2个边界条件. 对于工程结构中大量使用的薄板问题,经典板理论能够给出精度满意的解. 然而,对于中厚板或厚板,或者薄板在集中力作用点附近、边界周围以及小孔周边区域,经典板理论的解不仅精度不高、甚至还会导致错误的结果. 为避免运用三维弹性理论求解带来的数学困难[2-3]、消除经典板理论因忽略横向剪切变形所致误差,人们开始了厚板理论研究.
所谓厚板理论,就是在经典板理论基础上考虑横向剪切变形的板理论. Mindlin[4]将Timoshenko梁理论[5-6]中剪切系数K的概念应用于厚板,给出了沿板厚度一次变化的中面位移假设,依据板的经典平衡方程,得到了关于挠度和转角的3个偏微分方程和3个边界条件,建立了一阶剪切变形理论,并在工程中得到了广泛应用.
在一阶剪切变形理论基础上,相继提出了多种高阶剪切变形模型. Reissner [7-8]采用力法,考虑了剪切变形的影响,通过挠度和广义应力的混合变分原理,得到了相应的3个偏微分方程和3个边界条件,其中不协调的应力假设(即式(1))在接下来的工作中得到了改正,因而发展成为以力法表示的厚板理论.Levinson[9-10]基于中面上的挠度和转角,提出了沿板厚度三次变化的中面位移假设,并依据板的经典平衡方程,建立了以位移法表示的厚板理论,即Levinson理论.由于力法中的应力分布假设需经协调方程检验,本文主要关注板理论研究的位移法.
为脉络清晰起见,下面从两个不同方面予以叙述.
首先介绍中面位移模式中的高阶剪切变形模型. 根据模式中高阶项函数形式的不同,常见的高阶剪切变形模型有三阶剪切模型 [9-16]、正弦剪切模型[17]、双曲剪切模型[18]以及指数剪切模型[19]等.不同模式的位移由于高阶项函数形式不同会存在一些差异,但这些差异只反映在更高阶项部分,因而理论上可断定是很小的.多种高阶剪切变形模型的存在,丰富了中面的位移模式.
接下来讨论另一个更重要方面,即Levinson理论[9-10]表现出的两个问题:
(1) 板的经典平衡方程、边界条件与变分的不自洽问题,该问题使得低阶厚板理论(如文献[9, 11])受到了批评[13-14, 16].
(2) 广义应变定义的恰当性问题,不恰当的广义应变导致了错误的剪切系数2/3 [20-22],也使得大多数学者认为高阶理论中不存在剪切系数[10, 17, 23-26]. 更深层次,不恰当的广义应变会导致势能原理、本构关系、虚功原理三者之间产生矛盾[13-14, 27-28].
许多学者对Levinson理论[9-10]进行了不断发展和完善.例如,运用平均挠度和平均转角描述板的中面位移模式,提出了Murthy理论[11];由于采用的转角概念能给出正确的广义应变,Murthy理论得到了正确的剪切系数5/6,解决了问题(2);但由于仍然采用经典平衡方程(或与之等价的不自洽的变分形式),Murthy理论中依旧存在问题(1),因而,其实质与力法的Reissner理论[8]完全相同,计算结果也与Mindlin理论[4]取K=5/6时完全一致.Bickford[12]注意到Levinson理论[9,11]存在的问题(1),从二维问题的虚功原理出发,推导了梁问题的虚功原理,建立了变分自洽的梁的高阶理论,得到了用挠度和转角表示的2个控制方程和3个边界条件;但由于转角定义的原因,不能正确定义广义应力和广义应变,因而无法建立梁(板)理论的虚功原理及平衡方程. 受Bickford [12]工作的启发,结合Levinson理论[9-10]的中面位移模式,Reddy[13-14]运用三维问题的虚功原理,建立了变分自洽的板的高阶理论,得到了用挠度和转角表示的3个控制方程和5个边界条件,该理论真正提高了板的计算精度,被称为 Reddy-Bickford理论[27-28];但由于转角定义的原因,仍然未能建立板理论的虚功原理及平衡方程.Shi等[15-16] 认为Levinson[9-10]采用的位移模式并不合理(归咎于转角定义问题),运用Murthy[11]给出的位移模式,对Reddy-Bickford理论进行了重新表述,被称为Shi-Voyiadjis理论[27-28];该理论虽然采用了平均转角定义,但由于中面位移模式没能表示成正交形式,根据依此定义的广义应力也未能建立梁(板)理论的虚功原理及平衡方程[29];另外,根据物理问题的客观性,Shi-Voyiadjis理论实质上是Reddy-Bickford理论的一种变体.
至此,板理论研究方面虽然已有大量工作,但还存在3个基本问题:板理论的虚功原理该如何表述?板理论的本构关系该如何表示?变分自洽的高阶理论与变分不自洽的低阶理论之间是一种怎样的关系?要很好回答这3个问题,有必要对板问题从头开始进行审慎研究,并重新评估已有各种板理论.
近年来,随着航空航天、能源、武器工业和微纳电子机械等领域的蓬勃发展,力学与材料、电子、生物等诸多学科之间的交叉不断加深,板问题受到了更多重视.考虑微纳结构的尺度效应,高阶理论与应变梯度理论或非局部化理论已相互融合,微纳尺度下梁板结构的力学问题也得到了越来越多的关注[25-28, 30-31].同时,微纳结构中的剪切效应比宏观结构更为突出,对板理论的精度要求越来越高.实际上,板理论主要由合理的运动学假设、控制方程及相应的边界条件3部分组成,基于此可得到计及边界层效应的精确结果[16,32-33]. 然而,没有一种现有板理论对这3个组成部分都处理得很好.为此,近年来对板的理论又有一些新成果,例如文献[27-28, 34].然而,由于没能从根本上解决研究思路问题,虽然高阶理论在微纳结构中已拓宽了它的应用范围,但板理论本身并没有取得显著进展.
本文提出了一种板理论研究的新思路,称之为以力学方式研究板理论,是一种物理意义明确和数学推导严谨的研究方式. 物理意义明确是指每个物理量必须先定义再使用,数学推导严谨是指先给出一般意义上的数学表达式,再根据需满足的条件进行数学推演. 为此,第1节首先定义板的转角和挠度概念,提出板上下表面剪应力自由条件,再运用统一高阶剪切变形模型,提出中面位移模式;第2节定义板的广义应力及功共轭的广义应变概念,导出板的本构关系;第3节提出板理论的虚功原理并证明其客观性;第4节导出板理论的平衡方程及边界条件,包括变分自洽的高阶理论和变分渐近的低阶理论;第5节求解矩形板的扭转问题,验证本文板理论的正确性;最后在第6节给出本文的结论.
1 板的基本运动学考虑一个厚度为$t$的等厚度板,建立如图 1所示的右手正交坐标系oxyz,其中x和$y$为板中面内的两个坐标方向,z为板的厚度方向.一方面,该问题是一个三维问题,其目标是利用弹性理论求解以坐标(x,y,z)为自变量的位移场(ux,uy,uz);另一方面,该问题又是一个板问题,其目标则是利用板理论求解板中面上点(x,y)的挠度w及转角.考虑到三维弹性理论已发展成熟,我们以三维弹性力学中的物理量为基础,定义板理论中的各物理量,这体现了本文以力学方式研究板理论的第一个特征:每个物理量都具有明确的物理意义.
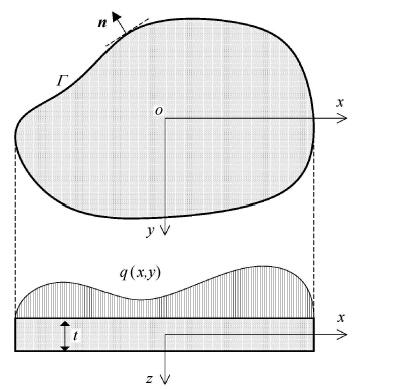
|
图 1 等厚度板模型 Figure 1 The model of a plate with uniform thickness |
根据厚度方向的位移$u_{z}(x,y,z)$,通过沿厚度方向上积分平均,定义板的挠度为
| $w\left( x,y \right)=\left( \frac{1}{t} \right)\int_{-t/2}^{t/2}{{{u}_{z}}}\left( x,y,z \right)dz$ | (1) |
板理论中一般都采用厚度方向的应变$\varepsilon _{z}=0$的假设,于是,我们有
| $ u_z \left( {x,y,z} \right) = u_z \left( {x,y,0} \right) = w\left( {x,y} \right) $ | (2) |
式(2)表明,本文对板挠度的定义与现有板理论所采用的定义一致.
与式(1)类似,根据面内位移$u_{x}(x,y,z)$和$ u_{y}(x,y,z)$,通过沿厚度方向的$z$加权积分平均,分别定义绕$y$轴和$x$轴的转角为
| $ \left. \phi _x \left( {x,y} \right) = \left( { \dfrac 1 I} \right)\int_{-t/2}^{t /2} z \cdot u_x \left( {x,y,z} \right) d z \\ \phi _y \left( {x,y} \right) = \left( { \dfrac 1 I } \right)\int_{-t /2}^{t / 2} z \cdot u_y \left( {x,y,z} \right) d z \!\!\right\} $ | (3) |
其中,$I=\int z^{2} d z=t^{3}/12$表示单位宽度截面的轴惯矩. 板的转角还有其他形式的定义[9-10, 14,34-35],将在3.2节再介绍.
研究板时常常采用上下表面剪应力自由条件,再加上转角的定义式(3),根据这两个条件,我们提出中面位移随厚度变化的关系式.为体现以力学方式研究板理论的第二个特征------数学推导严谨,将板中面内两个方向的位移分别表示为如下一般形式
| $ \left.\begin{array}{l} u_x = u_0 \left( {x,y} \right) + z \cdot f_1 (x,y) + g\left( z \right)\cdot f_{\rm R} (x,y) \\ u_y = v_0 \left( {x,y} \right) + z \cdot h_1 (x,y) + g\left( z \right)\cdot h_{\rm R} (x,y) \end{array} \!\! \right \} $ | (4) |
其中,$u_{0}(x,y)$和$v_{0}(x,y)$分别表示$x$和$y$方向沿厚度的平均位移,即
| ${{u}_{0}}\left( x,y \right)=\left( \frac{1}{t} \right)\int_{-t/2}^{t/2}{{{u}_{x}}\left( x,y,z \right)dz}{{v}_{0}}\left( x,y \right)=\left( \frac{1}{t} \right)\int_{-t/2}^{t/2}{{{u}_{y}}\left( x,y,z \right)dz}$ | (5) |
式(4)中的$f_{1}(x,y)$与$f_{R}(x,y)$和$h_{1}(x,y)$与$h_{R}(x,y)$分别为$x$方向和$y$方向的两个待定函数,由上下表面剪应力自由和转角定义这两个条件确定. 根据数学表示的唯一性,$g(z)$必须是一个关于厚度坐标$z$的纯高次($ ≥$3)奇函数,因而它具有以下两个性质
| $ \left.\begin{array}{l} \left. {g\left( z \right)} \right|_{z = 0} = 0 \\ \left. {\left( {{dg\left( z \right)}/ { d z} } \right)} \right|_{z = 0} = 0 \end{array}\!\! \right\} $ | (6) |
考虑到式(4)和式(5),由式(3)的转角定义可得出
| ${{\phi }_{x}}\left( x,y \right)={{f}_{1}}(x,y)+\lambda \cdot {{f}_{\text{R}}}(x,y){{\phi }_{y}}\left( x,y \right)={{h}_{1}}(x,y)+\lambda \cdot {{h}_{\text{R}}}(x,y)$ | (7) |
其中
| $ \lambda = \left( {1 /I} \right)\int_{-t / 2}^{t/2} {z \cdot g\left( z \right) d z} $ | (8) |
由于本文理论以广泛认可的表面剪应力自由和已知转角定义两个条件为出发点,因而纯高次奇函数$g(z)$可保证 $\lambda $不为零. 这样,运用式(7)消去式(4) 中的$f_{R}(x,y)$和$h_{R}(x,y)$,我们得到
| ${{u}_{x}}\left( x,y,z \right)={{u}_{0}}+z\cdot {{f}_{1}}+\left[ g(z)/\lambda \right]\cdot \left( {{\phi }_{x}}-{{f}_{1}} \right){{u}_{y}}\left( x,y,z \right)={{v}_{0}}+z\cdot {{h}_{1}}+\left[ g(z)/\lambda \right]\cdot \left( {{\phi }_{y}}-{{h}_{1}} \right)$ | (9) |
结合式(2),板的剪应变为
| $ \left.\!\! \gamma _{zx} = w_{,x} + f_1 + \left[{{{g}'\left( z \right)} / \lambda } \right] \cdot \left( {\phi _x-f_1 } \right) \\ \gamma _{zy} = w_{,y} + h_1 + \left[{{{g}'\left( z \right)} /\lambda } \right] \cdot \left( {\phi _y-h_1 } \right) \!\!\right\} $ | (10) |
其中下标"$,x$"和"$,y$"分别表示对$x$和$y$的偏微分,上标撇号表示关于$z$的微分.
这样,板上下表面剪应力自由条件就成为
| ${{\left. {{\gamma }_{zx}} \right|}_{z=\pm t/2}}=0{{\left. {{\gamma }_{zy}} \right|}_{z=\pm t/2}}=0$ | (11) |
由式(10)和式(11)可立即得到
| $ \left. f_1 \left( {x,y} \right) = \dfrac{c\phi _x + \lambda w_{,x} }{c-\lambda } \\ h_1 \left( {x,y} \right) = \dfrac{c\phi _y + \lambda w_{,y} }{c-\lambda } \right\} $ | (12) |
其中
| $ c = {g}'\left( {t /2} \right) = {g}'\left( {-t / 2} \right)$ | (13) |
于是,具有高阶剪切变形模型的中面位移模式最终表示为
| $ \left.\!\! u_x = u_0 + z \cdot \phi _x (x,y) + \tilde {g}\left( z \right) \cdot \left( {\phi _x + w_{,x} } \right) \\ u_y = v_0 + z \cdot \phi _y (x,y) + \tilde {g}\left( z \right) \cdot \left( {\phi _y + w_{,y} } \right) \right\} $ | (14) |
其中
| $ \tilde {g}\left( z \right) = {\left[{\lambda z-g\left( z \right)} \right]}/ {\left( {c-\lambda } \right)} $ | (15) |
可以看出,式(14)中的第2项(即$z \cdot \phi_{x}$或$z \cdot \phi_{y}$)是一阶剪切变形部分,即Mindlin板理论的位移模式[4-5];第3项则是由于考虑了高阶剪切(截面翘曲)效应产生的附加项,由式(15)可知,它并不仅仅只与纯高次奇函数$g(z)$有关[20],($\phi_{x}+w_{,x})$和($\phi_{y}+w_{,y})$决定了板中面上点的翘曲程度,有时被称为"剪切角"[5-6].
式(14)可以描述所有奇函数类型的高阶剪切变形模型[36],例如三阶剪切变形模型[9-16]、正弦剪切变形模型[17]、双曲剪切变形模型[18]以及指数剪切变形模型[19]. 结合式(6)、式(13)和式(3),$\tilde g (z)$具有如下3个性质
| ${{\left. \tilde{g}\left( z \right) \right|}_{z=0}}=0$ | (16a) |
| $ {\tilde {g}}'\left( {t /2} \right) = {\tilde {g}}'\left( {-t /2} \right) =-1 $ | (16b) |
| $\int_{-t/2}^{t/2}{z\cdot \tilde{g}\left( z \right)dz}=0$ | (16c) |
第 3个性质表明$\tilde g(z)$与 $z$沿厚度方向在积分意义下具有正交性,因此,式(14)称为中面位移的正交分解形式,是式(3)平均转角定义的数学解释.
这样,通过式(2)和式(14),得到板问题的5个非零应变分量为
| $\begin{align} &\left\{ \begin{matrix} {{\varepsilon }_{1}} \\ {{\varepsilon }_{2}} \\ {{\varepsilon }_{6}} \\ \end{matrix} \right\}\triangleq \left\{ \begin{matrix} {{\varepsilon }_{x}} \\ {{\varepsilon }_{y}} \\ {{\gamma }_{xy}} \\ \end{matrix} \right\}=\left\{ \begin{matrix} {{u}_{0,x}} \\ {{v}_{0,y}} \\ {{u}_{0,y}}+{{v}_{0,x}} \\ \end{matrix} \right\}+z\cdot \left\{ \begin{matrix} {{\phi }_{x,x}} \\ {{\phi }_{y,y}} \\ {{\phi }_{x,y}}+{{\phi }_{y,x}} \\ \end{matrix} \right\}+ \\ &\tilde{g}\left( z \right)\cdot \left\{ \begin{matrix} {{\phi }_{x,x}}+{{w}_{,xx}} \\ {{\phi }_{y,y}}+{{w}_{,yy}} \\ {{\phi }_{x,y}}+{{\phi }_{y,x}}+2{{w}_{,xy}} \\ \end{matrix} \right\} \\ \end{align}$ | (17) |
和
| $\left\{ \begin{array}{*{35}{l}} {{\varepsilon }_{5}} \\ {{\varepsilon }_{4}} \\ \end{array} \right\}\triangleq \left\{ \begin{array}{*{35}{l}} {{\gamma }_{zx}} \\ {{\gamma }_{zy}} \\ \end{array} \right\}=\left[ 1+{\tilde{g}}'\left( z \right) \right]\cdot \left\{ \begin{array}{*{35}{l}} {{\phi }_{x}}+{{w}_{,x}} \\ {{\phi }_{y}}+{{w}_{,y}} \\ \end{array} \right\}$ | (18) |
本文沿用板问题研究中常采用的应变符号约定,即$\varepsilon _{i}$ ($i=1\sim 6$,$i\ne 3$).
2 广义应力、广义应变及本构关系 2.1 板理论中的广义应力在板问题研究中惯常采用$\sigma_{z}=0$的假设. 于是,根据三维弹性理论,我们有
| $ \left\{\!\! \begin{array}{c} {\sigma _1 } \\ {\sigma _2 } \\ {\sigma _6 } \end{array}\!\! \right\} \triangleq \left\{ \!\!\begin{array}{c} {\sigma _x } \\ {\sigma _y } \\ {\tau _{xy} } \end{array} \!\! \right\} = \left[\!\! \begin{array}{ccc} {C_{11} } &{C_{12} }&0 \\ {C_{12} } &{C_{22} }&0 \\ 0 &0&{C_{66} } \end{array} \!\! \right]\left\{ \!\!\begin{array}{c} {\varepsilon _1 } \\ {\varepsilon _2 } \\ {\varepsilon _6 } \end{array}\!\! \right\} $ | (19) |
和
| $ \left\{\!\! \begin{array}{l} \sigma _5 \\ \sigma _4 \end{array}\!\! \right\} \triangleq \left\{ \!\!\begin{array}{l} \tau _{zx} \\ \tau _{zy} \end{array}\!\! \right\} = \left[\!\!\begin{array}{cc} {C_{55} } &0 \\ 0 &{C_{44} } \end{array} \!\! \right]\left\{ \!\!\begin{array}{l} \varepsilon _5 \\ \varepsilon _4 \end{array} \!\!\right\} $ | (20) |
其中,$\sigma_{i}$ ($i=1\tilde{\ }6,i\ne 3$) 为板问题的应力分量.$C_{11}$,$C_{12}$,$C_{22}$,$C_{44}$,$C_{55}$,$C_{66}$分别为板的材料参数,这样表示为便于将本文理论直接应用于复合材料板问题.
根据式(14)中面位移正交形式的表示特征,定义板理论的广义应力为
| $\begin{array}{*{35}{l}} \left( {{N}_{i}},{{M}_{i}},{{P}_{i}} \right)=\int_{-t/2}^{t/2}{{{\sigma }_{i}}\left[ 1,z,\tilde{g}\left( z \right) \right]dz},i=1,2,6 \\ \left( {{Q}_{x}},\ {{R}_{x}} \right)=\int_{-t/2}^{t/2}{{{\sigma }_{5}}\left[ 1,{\tilde{g}}'\left( z \right) \right]dz} \\ \left( {{Q}_{y}},{{R}_{y}} \right)=\int_{-t/2}^{t/2}{{{\sigma }_{4}}\left[ 1,{\tilde{g}}'\left( z \right) \right]dz} \\ \end{array}$ | (21) |
其中,$N_{i}$表示中面内力,$M_{i}$表示弯矩($i=1,2$)或扭矩($i=6$),$Q_{x}$和$Q_{y}$表示侧面上法向分别为$x$或$y$方向的横向剪力.$P_{i}$与$R_{x}$和$R_{y}$表示中面附加位移产生的"附加弯(扭)矩"与"附加剪力";与其他广义应力定义(例如文献[14,16,28,35])不同,式(21)具有明确物理意义和恰当量纲,反映了力学方式研究板问题的第一个特征;尤为重要的是,按式(21)定义的附加量都是具有截面尺度特征的小量,从而成为高阶理论向低阶理论退化(见4.2节)的数学依据.
根据式(17) $\sim $式(20),运用板理论的5个基本变量$u_{0}$,$v_{0}$,$w$,$\phi_{x}$和$\phi_{y}$,式(21)可表示为如下矩阵形式
| $ { N} = t \cdot { C }_{ E } { \varepsilon } $ | (22a) |
| $ { M} = I \cdot { C }_{ E } { \kappa }_{1}$ | (22b) |
| $ { P} = \eta I \cdot { C}_{ E} { \kappa }_{2} $ | (22c) |
| $ { Q} = Kt \cdot { C}_{ G} { \gamma } $ | (22d) |
| $ { R} = \xi t \cdot { C}_{ G} { \gamma } $ | (22e) |
其中${ N},{ M},{ P},{ Q}$和${ R} $为5个广义应力向量记号,其意义分别为
| $\begin{align} & N={{\left( {{N}_{1}}{{N}_{2}}{{N}_{6}} \right)}^{\text{T}}}M={{\left( {{M}_{1}}{{M}_{2}}{{M}_{6}} \right)}^{\text{T}}} \\ & P={{\left( {{P}_{1}}{{P}_{2}}{{P}_{6}} \right)}^{\text{T}}}Q={{\left( {{Q}_{x}}{{Q}_{y}} \right)}^{\text{T}}}R={{\left( {{R}_{x}}{{R}_{y}} \right)}^{\text{T}}} \\ \end{align}$ | (23) |
$\varepsilon $,$\kappa_{1}$,$\kappa _{2}$和$\gamma $为4个广义应变向量记号,其含义为
| $\left. \begin{align} &\varepsilon =\left( \begin{matrix} {{u}_{0,x}} \\ {{v}_{0,y}} \\ {{u}_{0,y}}+{{v}_{0,x}} \\ \end{matrix} \right) \\ &{{\kappa }_{1}}=\left( \begin{matrix} {{\phi }_{x,x}} \\ {{\phi }_{y,y}} \\ {{\phi }_{x,y}}+{{\phi }_{y,x}} \\ \end{matrix} \right) \\ \end{align} \right\}$ | (24a) |
| $\left. \begin{align} &{{\kappa }_{2}}=\left( \begin{matrix} {{\phi }_{x,x}}+{{w}_{,xx}} \\ {{\phi }_{y,y}}+{{w}_{,yy}} \\ {{\phi }_{x,y}}+{{\phi }_{y,x}}+2{{w}_{,xy}} \\ \end{matrix} \right) \\ &\gamma =\left( \begin{matrix} {{\phi }_{x}}+{{w}_{,x}} \\ {{\phi }_{y}}+{{w}_{,y}} \\ \end{matrix} \right) \\ \end{align} \right\}$ | (24b) |
式(22)中${ C}_{E}$和${ C}_{G}$为两个材料参数矩阵,分别为
| $ { C}_{ E} = \left[\begin{array}{ccc} {C_{11} } &{C_{12} } &0 \\ {C_{12} } &{C_{22} } &0 \\ 0 &0 &{C_{66} } \end{array} \right] $ | (25) |
和
| $ { C}_{ G} = \left[\begin{array}{cc} {C_{55} } &0 \\ 0 &{C_{44} } \end{array} \right] $ | (26) |
式(22)中$\eta $,$K$和$\xi $是3个无量纲参数,分别为
| $ \eta = \dfrac{1}{I}\int_{-t /2}^{t /2} {\left[{\tilde {g}\left( z \right)} \right]^2d z} $ | (27a) |
| $ K = \dfrac{1}{t}\int_{-t/ 2}^{t / 2} {\left[{1 + {\tilde {g}}'\left( z \right)} \right] d z} $ | (27b) |
| $ \xi = \dfrac{1}{t}\int_{-t/ 2}^{t / 2} {{\tilde {g}}'\left( z \right) \cdot \left[{1 + {\tilde {g}}'\left( z \right)} \right] d z} $ | (27c) |
需要指出的是,式(22)的推导利用了式(16c),即$\tilde g(z)$与$z$间的正交关系.
2.2 板理论中的广义应变及本构关系广义应变在板理论中是一个很重要、但并未很好定义的概念,这里予以展开研究.需要指出的是,以前工作都对它的重要性重视不够、 并因之造成了目前板理论研究中存在的混乱局面[9,10,13-16,27,28].
从(24)式的量纲发现,${\varepsilon }$,${ \kappa}_{1}$,${ \kappa}_{2}$和${ \gamma}$四个向量扮演着类似广义应变的角色. 虽然尚不能从式(22)确定它们本身就是应变,但真实的广义应变只能是它们的倍数,即$c_{1} { \varepsilon} $,$c_{2} { \kappa}_{1}$,$c_{3}{ \kappa}_{2}$或$c_{4}{ \gamma }$,这里$c_{i }$ ($i =1,2,3,4$)为4个需确定的常数.
我们知道,物理规律的客观性要求广义应变与广义应力必须是功共轭的,即必须构成具有客观性的应变能密度[37],为此,我们考察板问题的应变能密度.
在板理论中,应变能密度$\bar U$的表达式应为
| $ \bar {U}(w,\phi _x ,\phi _y ) =\\ \dfrac{1}{2}[c_1 { N}^{\rm T}{ \varepsilon } + c_2 { M}^{\rm T}{ \kappa }_1 + c_3 { P}^{\rm T}{ \kappa }_2 +\\ c_4 ({ Q} + { R})^{\rm T}{ \gamma }] $ | (28) |
另一方面,若视板问题为一个 $\sigma_{3}=\sigma _{z}=0$的特殊三维弹性问题,三维弹性理论给出该问题的应变能密度为
| $ \bar {U}(u_x ,u_y ,u_z ) =\\ \int_{-t/2}^{t/ 2} {\dfrac{1}{2}\left[{\sigma _1 \varepsilon _1 + \sigma _2 \varepsilon _2 + \sigma _6 \varepsilon _6 + \sigma _5 \varepsilon _5 + \sigma _4 \varepsilon _4 } \right] d z} $ | (29) |
根据式(14),式(29)进一步变化为
| $ \bar {U}(u_x ,u_y ,u_z ) =\\ \dfrac{1}{2}\int_{-t / 2}^{t / 2} {\sigma _1 [u_{0,x} + z \cdot \phi _{x,x} + \tilde {g}(z) \cdot (\phi _{x,x} + w_{,xx} )] d z} +\\ \dfrac{1}{2}\int_{-t/2}^{t /2} {\sigma _2 [v_{0,y} + z \cdot \phi _{y,y} + \tilde {g}(z) \cdot (\phi _{y,y} + w_{,yy} )] d z} +\\ \dfrac{1}{2}\int_{-t / 2}^{t/2} {\sigma _6 [(u_{0,y} + v_{0,x} ) + z \cdot (\phi _{x,y} + \phi _{y,x} )} +\\ \tilde {g}\left( z \right) \cdot (\phi _{x,y} + \phi _{y,x} + 2w_{,xy} )] d z +\\ \dfrac{1}{2}\int_{-t /2}^{t/2} {\sigma _5 [1 + {\tilde {g}}'(z)] \cdot (\phi _x + w_{,x} ) d z} +\\ \dfrac{1}{2}\int_{-t / 2}^{t/2} {\sigma _4 [1 + {\tilde {g}}'(z)] \cdot (\phi _y + w_{,y} )d z} $ | (30) |
考虑到式(21),有
| $ \bar {U}\left( {u_x ,u_y ,u_z } \right) =\\ \dfrac{1}{2}[N_1 u_{0,x} + M_1 \phi _{x,x} + P_1 (\phi _{x,x} + w_{,xx} )] +\\ \dfrac{1}{2}[N_2 v_{0,y} + M_2 \phi _{y,y} + P_2 (\phi _{y,y} + w_{,yy} )] +\\ \dfrac{1}{2}[N_6 (u_{0,y} + v_{0,x} ) + M_6 (\phi _{x,y} + \phi _{y,x} ) +\\ P_6 (\phi _{x,y} + \phi _{y,x} + 2w_{,xy} )] +\\ \dfrac{1}{2}[Q_x (\phi _x + w_{,x} ) + R_x (\phi _x + w_{,x} )] +\\ \dfrac{1}{2}[Q_y (\phi _y + w_{,y} ) + R_y (\phi _y + w_{,y} )] $ | (31) |
运用式(23)和式(24)的向量记号,式(31)进一步变为
| $ \bar {U}\left( {u_x ,u_y ,u_z } \right) =\\ \dfrac{1}{2}\left[{{ N}^{\rm T}{ \varepsilon } + { M}^{\rm T}{ \kappa}_{ 1} + { P}^{\rm T}{ \kappa }_{ 2} + \left( {{ Q} + { R}} \right)^ {\rm T}{ \gamma}} \right] $ | (32) |
考虑到应变能密度的唯一性及四种应变的独立性,通过比较式(28)与式(32),不难得出$c_{i} =1 $ ($i =1,2,3,4$). 至此证明了式(24) 就是板理论的广义应变定义,因而,式(22) 就成为板理论的本构关系,据此,得到板理论的功共轭对如表 1所示.
| 表 1 以 $\phi $为转角时板理论的功共轭对 Table 1 The work conjugate pairs in the plate theory in \terms of $\phi $ |
根据表 1,式(22)右端即可给出板理论的刚度系数. 饶有兴趣的是,式(22d) 给出了我们熟知的剪切系数$K$,表明它可直接通过$\tilde g (z)$由式(27b)计算得到,可代替以前计算$K$的繁琐做法(如文献[20, 22]等).
3 板问题描述的客观性 3.1 板问题虚功原理的板理论描述板问题的虚功原理用板理论可表述为
| $ \delta W\left( {x,y;w} \right) = \delta U\left( {x,y;w,\;\phi _x ,\;\phi _y } \right) $ | (33) |
其中$\delta W$表示外力在虚位移上做的虚功,只计及板表面分布力时可表示为
| $ \delta W\left( w \right) = \int_\Omega {q\left( {x,y} \right)\delta w\left( {x,y} \right) d a} $ | (34) |
式(33)中$\delta U$表示应力在虚应变上产生的虚应变能. 根据表 1,运用板理论中的功共轭对,$\delta U$ 可表示为
| $\delta U\left( w,{{\phi }_{x}},{{\phi }_{y}} \right)=\int_{\Omega }{[{{N}^{\text{T}}}\delta \varepsilon +{{M}^{\text{T}}}\delta {{\kappa }_{1}}+{{P}^{\text{T}}}\delta {{\kappa }_{2}}}+{{(Q+R)}^{\text{T}}}\delta \gamma ]da$ | (35) |
其中,$\Omega $表示板的中面,$d a$为相应的面积微元.
3.2 虚应变能板理论描述的客观性在经典板理论、一阶剪切变形理论及基于高阶剪切变形模型的厚板理论中,挠度$w$的定义与式(1)是一致的,但转角却存在多种不同的定义. 实际上,各种板理论对应的虚功原理应当遵循其客观性,也就是说,采用不同转角定义所表示的虚应变能必须是完全等价的,也不会影响挠度结果(5.1与5.2节中将会看到). 为此,先对其他两种常见的转角定义予以讨论.
除式(3)以积分平均意义定义转角外,另一种在板理论中广泛采用的转角为中面处的转角[9-10,13-14],即
| $ \left.\!\!\begin{array}{l} \psi _x \left( {x,y} \right) = \left. {u_{x,z} } \right|_{z = 0} \\ \psi _y \left( {x,y} \right) = \left. {u_{y,z} } \right|_{z = 0} \end{array} \right \} $ | (36) |
运用式(36)的转角定义和板表面应力自由条件,式(4)可重新表示为
| $\begin{align} & {{u}_{x}}={{u}_{0}}+z\cdot {{\psi }_{x}}-\left[ g\left( z \right)/c \right]\cdot \left( {{\psi }_{x}}+{{w}_{,x}} \right){{u}_{y}} \\ & ={{v}_{0}}+z\cdot {{\psi }_{y}}-\left[ g\left( z \right)/c \right]\cdot \left( {{\psi }_{y}}+{{w}_{,y}} \right) \\ \end{align}$ | (37) |
利用与式(14)类似的正交二项分解形式,式(37)可整理为
| $ \left. u_x = u_0 + z \cdot \left[{\alpha _T \psi _x + \left( {\alpha _T-1} \right)w_{,x} } \right] +\\ \tilde {g}(z) \cdot \left[{\alpha _T \left( {\psi _x + w_{,x} } \right)} \right] \\ u_y = v_0 + z \cdot \left[{\alpha _T \psi _y + \left( {\alpha _T-1} \right)w_{,y} } \right] +\\ \tilde {g}(z) \cdot \left[{\alpha _T \left( {\psi _y + w_{,y} } \right)} \right] \!\!\right\} $ | (38) |
其中
| $ \alpha _T = \dfrac{1}{I} \cdot \int_{-t /2}^{t / 2} {z \cdot \left[{z-\left( {{g\left( z \right)} /c} \right)} \right] d z} = \dfrac{c-\lambda }{c} $ | (39) |
比较发现,若$\alpha_{T}=1$,式(38)就变为式(14). 于是,式(38)和式(14)可统一表示为
| $ \left.\!\!\begin{array}{l} u_x = u_0 + z \cdot \left[{\alpha \tilde {\psi }_x + \left( {\alpha-1} \right)w_{,x} } \right] +\\ \tilde {g}(z) \cdot \left[{\alpha \left( {\tilde {\psi }_x + w_{,x} } \right)} \right] \\ u_y = v_0 + z \cdot \left[{\alpha \tilde {\psi }_y + \left( {\alpha-1} \right)w_{,y} } \right] +\\ \tilde {g}(z) \cdot \left[{\alpha \left( {\tilde {\psi }_y + w_{,y} } \right)} \right] \end{array} \right \} $ | (40) |
这样,两种转角对应的情形分别为
| $ \left. \tilde {\psi } = \phi \to \alpha = 1 \\ \tilde {\psi } = \psi \to \alpha = \alpha _{ T} \right\} $ | (41) |
另外,Ambartsumian曾采用如下转角定义[34-35]
| ${{\chi }_{x}}\left( x,y \right)=2{{\left. {{u}_{x,z}} \right|}_{z=0}}+{{w}_{x}}{{\chi }_{y}}\left( x,y \right)=2{{\left. {{u}_{x,z}} \right|}_{z=0}}+{{w}_{y}}$ | (42) |
不难得到用式(40)表示时的对应关系为
| $ \tilde {\psi } = \chi \to \alpha = {\alpha _{ T} } / 2 $ | (43) |
考虑到式(21)广义应力定义与转角无关的特点,对于式(36)或式(42) 的转角定义,式(22)的本构关系可表示为
其中
| $ { N } = t \cdot { C }_{ E} { \varepsilon } $ | (44a) |
| $ { M } = I \cdot { C }_{ E} \tilde { \kappa}_{ 1} $ | (44b) |
| ${ P } = \eta I \cdot { C }_{ E} \tilde { \kappa }_{2} $ | (44c) |
| $ { Q } = Kt \cdot { C}_{ G} \tilde { \gamma } $ | (44d) |
| $ { R } = \xi t \cdot { C}_{ G} \tilde { \gamma } $ | (44e) |
| $\begin{align} & {{{\tilde{\kappa }}}_{1}}=\left\{ \begin{matrix} \alpha {{{\tilde{\psi }}}_{x,x}}+\left( \alpha -1 \right){{w}_{,xx}} \\ \alpha {{{\tilde{\psi }}}_{y,y}}+\left( \alpha -1 \right){{w}_{,yy}} \\ \alpha \left( {{{\tilde{\psi }}}_{x,y}}+{{{\tilde{\psi }}}_{y,x}} \right)+2\left( \alpha -1 \right){{w}_{,xy}} \\ \end{matrix} \right\} \\ & {{{\tilde{\kappa }}}_{2}}=\alpha \cdot \left\{ \begin{matrix} {{{\tilde{\psi }}}_{x,x}}+{{w}_{,xx}} \\ {{{\tilde{\psi }}}_{y,y}}+{{w}_{,yy}} \\ {{{\tilde{\psi }}}_{x,y}}+{{{\tilde{\psi }}}_{y,x}}+2{{w}_{,xy}} \\ \end{matrix} \right\} \\ & \tilde{\gamma }=\alpha \cdot \left\{ \begin{matrix} {{{\tilde{\psi }}}_{x}}+{{w}_{,x}} \\ {{{\tilde{\psi }}}_{y}}+{{w}_{,y}} \\ \end{matrix} \right\} \\ \end{align}$ | (45) |
由式(44)可以看出,3种转角定义下板理论的功共轭对都可用表 2表示,虚应变能都可表示为
| $\delta U(w,{\tilde \psi _x},{\tilde \psi _y}) = {\smallint _\Omega }[{N^{\rm{T}}}\delta \varepsilon + {M^{\rm{T}}}\delta {\tilde \kappa _1} + {P^{\rm{T}}}\delta {\tilde \kappa _2} + {(Q + R)^{\rm{T}}}\delta \tilde \gamma ]da$ | (46) |
| 表 2 板理论中的功共轭对 Table 2 The work conjugate pairs in the plate theory |
因此,板问题的虚功原理在板理论中的客观性得证.
比较式(14)与式(40),还可得到
| $ \phi _i + w_{,i} = \alpha \left( {\tilde {\psi }_i + w_{,i} } \right) \left( {i = x,y} \right) $ | (47) |
由式(44d)和表 2可看出,在本文的广义剪力和广义剪应变定义下,剪切系数$K$并不因转角的定义而变,这应是对剪切系数的客观认识. 表 3列出了常见4种高阶剪切变形模型[9-6,23-28]的相关函数,据此可得到这4种模型相关系数的表达式(见附录A),数值比较见表 4.可以看出,给定$g(z)$,三阶剪切变形模型的剪切系数$K= 5/6$,正弦剪切变形模型的剪切系数$K =\pi^{2}/12$,它们就是Mindlin[4]在一阶剪切板理论中引入的两种剪切系数,并分别用来计算了板沿厚度的剪切波及固有频率[11,21]. 此外,对于这4种模型,式(21)的广义应力定义都将得到很小的附加弯矩和附加剪力(系数 $\eta $ 小于2%、系数 $\xi $ 小于3%),而其他方式定义的高阶矩和高阶剪力(例如Reddy[14]和Aydogdu [38])却不具有这一特征.
| 表 3 4种高阶剪切变形模型涉及的相关函数 Table 3 The corresponding functions in the four HSD models |
| 表 4 4种高阶剪切变形模型中相关系数的数值比较 Table 4 Comparison of the corresponding coefficients in the four HSD models |
由式(45)、并结合式(39)、式(41)和式(43)三式发现,当转角用 $\phi $定义时,板理论的广义应变与所采用的高阶剪切变形模型无关,但当转角用$\psi $和$\chi $定义时,广义应变则需根据所采用的高阶剪切变形模型通过$\alpha $予以订正,这是本文研究板(梁)理论中广义应变概念时得到的一个重要结果.
比较式(24)与式(45) 发现,采用$\phi $的转角定义,广义应变的形式最为简单,于是,本文后续工作将以$\phi $为转角展开,必要时将通过式(47)、式(41)或式(43) 转换成其他转角形式.
3.3 虚应变能表示的等价性3.2节表明,不同转角定义下板理论的虚应变能表示是客观的. 实际上,不论是用板理论表示还是用三维弹性理论表示,板问题的虚应变能也是等价的.
对于图 1所示的板问题,若视其为一个 $\sigma_{3}=\sigma_{z}=0$的特殊三维弹性问题,其虚应变能用三维弹性理论可表示为
| $ \delta U(u_x ,u_y ,u_z )=\\ \int_\Omega {\int_{-t / 2}^{t / 2} {\sigma _i \cdot \delta \varepsilon _i d z d a} } \ \left( {i = 1,2,3,4,5,6} \right) $ | (48) |
根据式(40),式(48)可进一步表示为
| $ \delta U(u_x ,u_y ,u_z ) =\\ \int_\Omega \int_{-t / 2}^{t /2} \sigma _1 \delta [u_{0,x} + z \cdot \phi _{x,x} +\\ \tilde {g}(z) \cdot (\phi _{x,x} + w_{,xx} )] d zd a +\\ \int_\Omega \int_{-t/ 2}^{t/2} \sigma _2 \delta [v_{0,y} + z \cdot \phi _{y,y}+\\ \tilde {g}(z) \cdot (\phi _{y,y} + w_{,yy} )] d zd a +\\ \int_\Omega \int_{-t/ 2}^{t/2} \sigma _6 \delta [(u_{0,y} + v_{0,x} ) + z \cdot (\phi _{x,y} + \phi _{y,x} ) +\\ \tilde {g}(z) \cdot (\phi _{x,y} + \phi _{y,x} + 2w_{,xy} )] d zd a +\\ \int_\Omega {\int_{-t / 2}^{t / 2} {\sigma _5 \delta [1 + {\tilde {g}}'\left( z \right)] \cdot (\phi _x + w_{,x} )d zd a} }+\\ \int_\Omega \int_{-t / 2}^{t /2} \sigma _4 \delta [1 + {\tilde {g}}'\left( z \right)] \cdot (\phi _y + w_{,y} ) d zd a $ | (49) |
考虑到式(21),我们有
| $ \delta U(u_x ,u_y ,u_z ) =\\ \int_\Omega {[N_1 \delta u_{0,x} + M_1 \delta \phi _{x,x} + P_1 \delta (\phi _{x,x} + w_{,xx} )]d a} +\\ \int_\Omega {[N_2 \delta v_{0,y} + M_2 \delta \phi _{y,y} + P_2 \delta (\phi _{y,y} + w_{,yy} )] d a} +\\ \int_\Omega {[N_6 \delta (u_{0,y} + v_{0,x} ) + M_6 \delta (\phi _{x,y} + \phi _{y,x} )} +\\ P_6 \delta (\phi _{x,y} + \phi _{y,x} + 2w_{,xy} )] d a +\\ \int_\Omega {\left[{Q_x \delta \left( {\phi _x + w_{,x} } \right) + R_x \delta \left( {\phi _x + w_{,x} } \right)} \right] d a} +\\ \int_\Omega {\left[{Q_y \delta \left( {\phi _y + w_{,y} } \right) + R_y \delta \left( {\phi _y + w_{,y} } \right)} \right] d a} $ | (50) |
运用式(24)中的广义应变记号,式(50)进一步给出
| $ \delta U(u_x ,u_y ,u_z ) =\\ \int_\Omega [{ N}^{\rm T}\delta { \varepsilon } + { M}^{\rm T}\delta { \kappa }_{1} + { P}^{\rm T}\delta { \kappa }_{2} +\\ ({ Q} + { R})^{\rm T}\delta { \gamma }]d a =\\ \delta U\left( {w,\phi _x ,\phi _y } \right) $ | (51) |
这样,板问题的虚应变能用板理论表示和用三维弹性理论表示是等价的.
4 板的高阶理论(HPT)与低阶理论(LPT) 4.1 高阶厚板理论-变分自洽的平衡方程及边界条件将式(34)和式(35)代入式(33),可得
| $\eqalign{ & 0 = {\smallint _\Omega }[{N^{\rm{T}}}\delta \varepsilon + {M^{\rm{T}}}\delta {\kappa _1} + {P^{\rm{T}}}\delta {\kappa _2} + {(Q + R)^{\rm{T}}}\delta \tilde \gamma ]da - \cr & {\smallint _\Omega }\left[ {q\left( {x,y} \right)\delta w\left( {x,y} \right)} \right]da \cr} $ | (52) |
注意到式(24)的广义应变定义,经分部积分,得到
| $\eqalign{ & \int_\Omega {[{P_{1,xx}} + {P_{2,yy}} + 2{P_{6,xy}} - {{({Q_y} + {R_y})}_{,y}}} - {({Q_x} + {R_x})_{,x}} - q(x,y)]\delta wda + \cr & \oint {_\Gamma } [({N_1}{n_x} + {N_6}{n_y})\delta {u_0} + ({N_2}{n_y} + {N_6}{n_x})\delta {v_0}]ds + \cr & \oint {_\Gamma } [({M_1}{n_x} + {P_1}{n_x} + {M_6}{n_y} + {P_6}{n_y})\delta {\phi _x}]ds + \cr & \oint {_\Gamma } [({M_2}{n_y} + {P_2}{n_y} + {M_6}{n_x} + {P_6}{n_x})\delta {\phi _y}]ds + \cr & \oint {_\Gamma } [({P_1}{n_x} + {P_6}{n_y})\delta {w_{,x}} + ({P_2}{n_y} + {P_6}{n_x})\delta {w_{,y}}]ds + \cr & \oint {_\Gamma } [ - {P_{1,x}}{n_x} - {P_{2,y}}{n_y} - {P_{6,y}}{n_x} - {P_{6,x}}{n_y} + ({Q_x} + {R_x}){n_x} + ({Q_y} + {R_y}){n_y}]\delta wds = 0 \cr} $ | (53) |
其中$\Gamma $表示板中面的侧面边界,$n_{x}$和$n_{y}$分别表示边界$\Gamma $的外法向余弦,$d s$为边界$\Gamma $的弧长微元.
分别整理面积积分中与5个基本变量$u_{0}$,$v_{0}$,$w$,$\phi_{x}$和$\phi_{y}$变分相关的项,并根据变分的任意性,得到以下5个平衡方程
| $ \left.\!\!\begin{array}{l} \delta u_0 :\;\;N_{1,x} + N_{6,y} = 0\\ \delta v_0 :\;\;N_{2,y} + N_{6,x} = 0 \\ \delta \phi _x :\;\;Q_x + R_x-(M_{1,x} + P_{1,x} ) -\\ \quad (M_{6,y} + P_{6,y} ) = 0\\ \delta \phi _y :\;\; Q_y + R_y -(M_{2,y} + P_{2,y} ) -\\ \quad (M_{6,x} + P_{6,x} ) = 0 \\ \delta w:\;\;\left( {Q_x + R_x } \right)_{,x} + \left( {Q_y + R_y } \right)_{,y} -\\ \left( {P_{1,xx} + P_{2,yy} + 2P_{6,xy} } \right) + q(x,y) = 0 \end{array}\!\! \right \} $ | (54) |
式(54)是用广义应力表示的板理论的平衡方程,是广义应力间的基本关系;前两式是中面内力平衡方程,与经典板理论相同;后三式表示板的弯曲特性,为本文首次获得,与Bickford-Reddy理论[14]和Shi-Voyiadjis理论[15-16]在形式上不同.
相应地,还可得到对应的边界条件. 为此,将式(53)中的边界变分项按以下4部分整理为
| $\begin{align} &\oint{_{\Gamma }}[({{N}_{1}}{{n}_{x}}+{{N}_{6}}{{n}_{y}})\delta {{u}_{0}}+({{N}_{2}}{{n}_{y}}+{{N}_{6}}{{n}_{x}})\delta {{v}_{0}}]ds= \\ &\oint{_{\Gamma }}({{N}_{n}}\delta {{u}_{n}}+{{N}_{ns}}\delta {{u}_{ns}})d{{s}_{\Gamma }}[({{M}_{1}}{{n}_{x}}+{{M}_{6}}{{n}_{y}})\delta {{\phi }_{x}}+({{M}_{2}}{{n}_{y}}+{{M}_{6}}{{n}_{x}})\delta {{\phi }_{y}}]ds \\ &=\oint{_{\Gamma }}({{M}_{n}}\delta {{\phi }_{n}}+{{M}_{ns}}\delta {{\phi }_{ns}})ds \\ &\oint{_{\Gamma }}[({{P}_{1}}{{n}_{x}}+{{P}_{6}}{{n}_{y}})\delta ({{\phi }_{x}}+{{w}_{,x}})+({{P}_{2}}{{n}_{y}}+{{P}_{6}}{{n}_{x}})\delta ({{\phi }_{y}}+{{w}_{,y}})]ds \\ &=\oint{_{\Gamma }}[{{P}_{n}}\delta (\partial w/\partial n+{{\phi }_{n}})+{{P}_{ns}}\delta (\partial w/\partial s+{{\phi }_{ns}})]ds \\ &\oint{_{\Gamma }}[-{{P}_{1,x}}{{n}_{x}}-{{P}_{2,y}}{{n}_{y}}-{{P}_{6,y}}{{n}_{x}}-{{P}_{6,x}}{{n}_{y}}+({{Q}_{x}}+{{R}_{x}}){{n}_{x}}+({{Q}_{y}}+{{R}_{y}}){{n}_{y}}]\delta wds \\ &=\oint{_{\Gamma }}({{Q}_{n}}\delta w)ds \\ \end{align}$ | (55) |
其中各记号的含义分别为
| $ \left. u_n = u_0 n_x + v_0 n_y \\ u_{ns} =-u_0 n_y + v_0 n_x \\ \phi _n = \phi _x n_x + \phi _y n_y \\ \phi _{ns} =-\phi _x n_y + \phi _y n_x \\ N_n = N_1 n_x^2 + N_2 n_y^2 + 2N_6 n_x n_y \\ N_{ns} = \left( {N_2-N_1 } \right)n_x n_y + N_6 \left( {n_x^2-n_y^2 } \right) \\ M_n = M_1 n_x^2 + M_2 n_y^2 + 2M_6 n_x n_y \\ M_{ns} = \left( {M_2-M_1 } \right)n_x n_y + M_6 \left( {n_x^2-n_y^2 } \right) \\ P_n = P_1 n_x^2 + P_2 n_y^2 + 2P_6 n_x n_y \\ P_{ns} = \left( {P_2-P_1 } \right)n_x n_y + P_6 \left( {n_x^2-n_y^2 } \right) \\ Q_n = Q_x n_x + Q_y n_y + R_x n_x + R_y n_y -\\ \left( {{\partial P_n }/{\partial n} + {\partial P_{ns} }/{\partial s}} \right) \!\!\right\} $ | (56) |
其中
| $\partial /\partial n = {n_x}\left( {\partial /\partial x} \right) + {n_y}\left( {\partial /\partial y} \right)\partial /\partial s = {n_x}\left( {\partial /\partial y} \right) - {n_y}\left( {\partial /\partial x} \right)$ | (57) |
根据边界变分的任意性,依次得到如下7对边界条件
| $ \left. \!\!\begin{array}{lll} N_n &{\rm or}&{u_n } \\ N_{ns} & {\rm or} & {u_{ns} } \\ M_n & {\rm or} &{\phi _n } \\ M_{ns} & {\rm or}& {\phi _{ns} } \\ P_n& {\rm or} &{\partial w}/ {\partial n} + \phi _n \\ P_{ns} &{\rm or} & {\partial w} / {\partial s} + \phi _{ns} \\ Q_n & {\rm or} & w \end{array} ,\quad {\rm on} \Gamma \ \right\} $ | (58) |
或者
| $ \left. \!\!\begin{array}{lll} N_n & {\rm or} &{u_n } \\ N_{ns} & {\rm or} &{u_{ns} } \\ M_n + P_n & {\rm or} &{\phi _n } \\ M_{ns} + P_{ns} & {\rm or} & {\phi _{ns} } \\ P_n & {\rm or} & {\partial w} /{\partial n} \\ P_{ns} & {\rm or} &{\partial w} /{\partial s} \\ Q_n & {\rm or} & w \\ \end{array} ,\quad {\rm on} \Gamma \right\} $ | (59) |
计及式(21)和式(47),式(58)或式(59) 将给出与Bickford-Reddy理论[14]和Shi-Voyiadjis理论[15-16]不同的边界条件表示形式.
式(54)以广义应力表示的平衡方程和式(58)或式(59) 以广义应力和广义位移成对表示的边界条件称为高阶厚板理论,显然,该理论是变分自洽的. 由于广义应力定义式(21) 不因转角定义的不同而异,因而,式(54) 表示了高阶板理论平衡方程的客观性. 考虑到式(58)或式(59) 的后五个边界条件,根据变分学基本理论[39],高阶板理论是一个10阶偏微分方程问题.
如果引入本构关系式(22),式(54)之后三式将导出如下关于挠度和转角的3个微分方程
| $\begin{align} &\left( K+\xi \right)t{{C}_{55}}\left( {{\phi }_{x}}+{{w}_{,x}} \right)-I\left( {{C}_{11}}{{\phi }_{x,xx}}+{{C}_{12}}{{\phi }_{y,xy}} \right)- \\ &\eta I\left[ {{C}_{11}}\left( {{\phi }_{x,xx}}+{{w}_{,xxx}} \right)+{{C}_{12}}\left( {{\phi }_{y,xy}}+{{w}_{,xyy}} \right) \right]- \\ &I{{C}_{66}}\left( {{\phi }_{x,yy}}+{{\phi }_{y,xy}} \right)-\eta I{{C}_{66}}\left( {{\phi }_{x,yy}}+{{\phi }_{y,xy}}+2{{w}_{,xyy}} \right) \\ &=0\left( K+\xi \right)t{{C}_{44}}\left( {{\phi }_{y}}+{{w}_{,y}} \right)-I\left( {{C}_{12}}{{\phi }_{x,xy}}+{{C}_{22}}{{\phi }_{y,yy}} \right)- \\ &\eta I\left[ {{C}_{12}}\left( {{\phi }_{x,xy}}+{{w}_{,xxy}} \right)+{{C}_{22}}\left( {{\phi }_{y,yy}}+{{w}_{,yyy}} \right) \right] \\ &-I{{C}_{66}}\left( {{\phi }_{x,xy}}+{{\phi }_{y,xx}} \right)-\eta I{{C}_{66}}\left( {{\phi }_{x,xy}}+{{\phi }_{y,xx}}+2{{w}_{,xxy}} \right)=0 \\ &\left( K+\xi \right)t\left[ {{C}_{55}}\left( {{\phi }_{x,x}}+{{w}_{,xx}} \right)+{{C}_{44}}\left( {{\phi }_{y,y}}+{{w}_{,yy}} \right) \right]- \\ &\eta I\left[ {{C}_{11}}\left( {{\phi }_{x,xxx}}+{{w}_{,xxxx}} \right)+{{C}_{12}}\left( {{\phi }_{y,xxy}}+{{w}_{,xxyy}} \right) \right]- \\ &\eta I\left[ {{C}_{12}}\left( {{\phi }_{x,xyy}}+{{w}_{,xxyy}} \right)+{{C}_{22}}\left( {{\phi }_{y,yyy}}+{{w}_{,yyyy}} \right) \right]- \\ &2\eta I{{C}_{66}}\left( {{\phi }_{x,xyy}}+{{\phi }_{y,xxy}}+2{{w}_{,xxyy}} \right)+q(x,y)=0 \\ \end{align}$ | (60) |
式(60)与Bickford-Reddy理论[14]和Shi-Voyiadjis理论[15-16] 的控制方程在表示形式上不同,但其实质是相同的.
不考虑中面内位移,由式(58)或式(59)得到板问题常见的3种边界条件为:
(1)简支边界条件
| $ \left.\begin{array}{l} M_n = 0 \\ M_{ns} = 0 \\ P_n = 0 \\ P_{ns} = 0 \\ w = 0 \end{array} ,{\rm on} \Gamma \right\} $ | (61) |
(2)固支边界条件
| $ \left.\begin{array}{l} \varphi _n = 0 \\ \varphi _{ns} = 0 \\ {\partial w} /{\partial n} = 0 \\ {\partial w}/{\partial s} = 0 \\ w = 0 \end{array} ,{\rm on} \Gamma \right\} $ | (62) |
(3)自由边界条件
| $ \left.\begin{array}{l} M_n = 0 \\ M_{ns} = 0 \\ P_n = 0 \\ P_{ns} = 0 \\ Q_n = 0 \end{array} ,{\rm on} \Gamma \right\} $ | (63) |
可以看到,对于这3种常见的零约束情形,式(58)或式(59)将给出与Bickford-Reddy理论[14]和Shi-Voyiadjis理论[15-16]等价的边界条件描述,但对较复杂的边界条件约束,情形并不明朗.
4.2 低阶厚板理论-变分渐近的平衡方程及边界条件从表 4可看出,对于常见的四种高阶剪切变形模型,参数 $\xi $ 和 $\eta $ 都远小于1①,于是,略去附加广义弯矩${ P}$和附加广义剪力${ R}$对虚功的贡献,是一种合理的数学近似. 这样,式(52)的虚功原理就变为
① 在正交性意义下,虽然尚未从数学上证明$\xi $和$\eta $是一个小量,但对于目前常见的三阶剪切模型、正弦剪切模型、双曲剪切模型和指数剪切模型,计算结果均表现出这一特征.
| $0 = \int_\Omega {\left( {{N^{\rm{T}}}\delta \varepsilon + {M^{\rm{T}}}\delta {\kappa _1} + {Q^{\rm{T}}}\delta \gamma } \right)} da - \int_\Omega q (x,y) \cdot \delta w(x,y)da$ | (64) |
相应地,式(54)的平衡方程就变为
| $ \left.\begin{array}{ll} \delta u_0 :\;\;&N_{1,x} + N_{6,y} = 0 \\ \delta v_0 :\;\;&N_{2,y} + N_{6,x} = 0 \\ \delta \varphi _x :\;\;&Q_x-\left( {M_{1,x} + M_{6,y} } \right) = 0 \\ \delta \varphi _y :\;\;&Q_y-\left( {M_{2,y} + M_{6,x} } \right) = 0 \\ \delta w:\;\;&Q_{x,x} + Q_{y,y} + q(x,y) = 0 \end{array} \right \} $ | (65) |
式(65)是用广义应力表示的低阶厚板理论的平衡方程,由高阶板理论略去附加广义弯矩和附加广义剪力而推导得到;前两式是板中面内力平衡方程;后三式表示板的弯曲特性,就是板的经典平衡方程,与Mindlin理论[4]和Murthy理论[11]的控制方程形式相同,但本文从数学上揭示了它与高阶厚板理论间的关系.
相应地,式(58)或式(59)的边界条件变为
| $ \left. \begin{array}{lll} N_n& {\rm or} & {u_n } \\ N_{ns} & {\rm or} & {u_{ns} } \\ M_n & {\rm or} & {\varphi _n } \\ M_{ns} & {\rm or} & {\varphi _{ns} } \\ Q_n & {\rm or} & w \end{array} ,\;\;{\rm on} \;\;\Gamma \right\} $ | (66) |
此时,式(56)中的记号$Q_{n}$变为
| $ Q_n = Q_x n_x + Q_y n_y $ | (67) |
式(65)以广义应力表示的平衡方程和式(66) 以广义应力和广义位移表示的边界条件通称为低阶厚板理论. 正如文献 [13-14, 16]所指出的,该理论是变分不自洽的;但由于只忽略了虚功中附加矩和附加剪力产生的很小部分的虚功,该理论是一种变分渐近的厚板理论. 本文揭示了支撑它的数学基础(见5.2节).
由于广义应力的定义式(21)不因转角的定义不同而异,因而,式(65) 表示了低阶厚板理论平衡方程的客观性. 考虑到式(66)的后3个边界条件,根据变分学基本理论[39],低阶板理论是一个6阶偏微分方程问题.
如果引入本构关系式(22),将导出如下关于挠度和转角的3个微分方程
| $\eqalign{ & Kt{C_{55}}\left( {{\phi _x} + {w_{,x}}} \right) - I\left( {{C_{11}}{\phi _{x,xx}} + {C_{12}}{\phi _{y,xy}}} \right) - I{C_{66}}\left( {{\phi _{x,yy}} + {\phi _{y,xy}}} \right) \cr & = 0Kt{C_{44}}\left( {{\phi _y} + {w_{,y}}} \right) - I\left( {{C_{12}}{\phi _{x,xy}} + {C_{22}}{\phi _{y,yy}}} \right) - I{C_{66}}\left( {{\phi _{x,xy}} + {\varphi _{y,xx}}} \right) \cr & = 0Kt\left[ {{C_{55}}\left( {{\phi _{x,x}} + {w_{,xx}}} \right) + {C_{44}}\left( {{\phi _{y,y}} + {w_{,yy}}} \right)} \right] + q(x,y) = 0 \cr} $ | (68) |
对于三阶剪切变形模型,式(68)与Murthy理论[11]的控制方程在形式上相同.
不考虑中面内位移,由式(66)得到板问题低阶理论常见的3种边界条件为:
(1)简支边界条件
| $ \left.\begin{array}{l} M_n = 0 \\ M_{ns} = 0 \\ w = 0 \end{array} ,\;\;{\rm on} \;\;\Gamma \right\} $ | (69) |
(2)固支边界条件
| $ \left.\begin{array}{l} \phi _n = 0 \\ \phi _{ns} = 0 \\ w = 0 \end{array} ,\;\;{\rm on} \;\;\Gamma \right\} $ | (70) |
(3)自由边界条件
| $ \left.\begin{array}{l} M_n = 0 \\ M_{ns} = 0 \\ Q_n = 0 \end{array} ,\;\;{\rm on}\;\;\Gamma \right\} $ | (71) |
可以看到,由于采用了转角定义 $\phi $,Murthy理论[11]在3种边界条件下与式(69)$\sim $式(71) 一致,因而是正确的;遗憾的是,由于转角 $\psi $ 对应的$\alpha ={{\alpha }_{T}}\ne 1$,Levinson理论[9-10]在固支边界条件因与式(70)不一致而导致错误,2/3的剪切系数就是这种错误的一种表现,同样的错误将发生在采用转角 $\chi $ (因 $\alpha ={{\alpha }_{T}}/2\ne 1$)的Ambartsumian理论[34-35]中.
5 矩形板扭转问题求解如图 2所示,等厚度$t$的矩形板长为2$l$、宽为$a$,在$y=\pm a/2$的前后侧面边界上满足应力自由条件,在$x=\pm l$的左右侧面边界上作用纯扭矩、法向应力自由,目的是求解$x=\pm l$左右侧面边界上的剪应力分布. 这就是Saint Venant扭转问题.
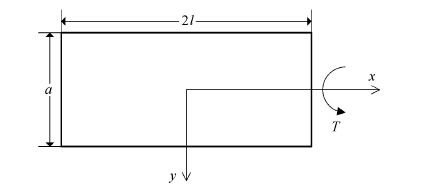
|
图 2 矩形板的扭转 Figure 2 Torsion of a rectangular plate |
该问题可通过三维弹性理论[37]得到解析解答. Reissner[7]运用一阶剪切变形模型的中面位移模式和带剪切系数的低阶厚板理论求解了该问题;Levinson[9]运用三阶剪切变形模型的中面位移模式和变分渐近的低阶厚板理论求解了该问题;Shi[16]运用三阶剪切变形模型的中面位移模式和变分自洽的高阶厚板理论求解了该问题. 这里采用本文理论对Saint Venant扭转问题进行求解,并与已有结果进行比较.
5.1 高阶厚板理论解不考虑板的中面变形部分,式(59)①变为
由于该问题在侧面边界处给定了挠度及其变化,这里选用式(59)描述边界条件.
| $ \left.\begin{array}{lll} M_n + P_n &{\rm or} &{\phi _n } \\ M_{ns} + P_{ns} &{\rm or} & {\phi _{ns} } \\ P_n &{\rm or} & {\partial w} /{\partial n} \\ P_{ns}&{\rm or} & {\partial w} /{\partial s} \\ Q_n &{\rm or} & w \end{array} ,\quad {\rm on} \quad \Gamma \right\} $ | (72) |
若令 $\theta $ 表示沿$x$轴单位长度的扭转角,对于Saint Venant扭转问题,按照Reissner的描述[7],挠度和转角在转动端面满足
| $ {\partial w}/{\partial s} = {\partial w} / {\partial y} =-\phi _{ns} = \theta l ,\;\;\;\; {\rm on}\;\;x = \pm l $ | (73) |
这样,式(72)的边界条件最终可表示为
| $ \left.\begin{array}{l} M_n + P_n = 0 \\ \phi _{ns} =-\phi _x n_y + \phi _y n_x = \pm \phi _y =-\theta l \\ P_n = 0 \\ {\partial w}/ {\partial s} = \left( {n_x w_{,y}-n_y w_{,x} } \right) = \pm w_{,y} = \theta l \\ w = \pm \theta ly \end{array} ,{\rm at}\;\;x = \pm l \right\} $ | (74) |
和
| $ \left.\begin{array}{l} M_n + P_n = 0 \\ M_{ns} + P_{ns} = 0 \\ P_n = 0 \\ {\partial w}/{\partial s} = n_x w_{,y}-n_y w_{,x} =\\ \mp w_{,x} =-{a\theta } / 2 \\ Q_n = 0 \end{array} ,\;\;{\rm at} \;\;y = \pm \dfrac{a}{2} \ \right\} $ | (75) |
式(75)的边界条件要求挠度$w$和 $\phi_{y}$应具有如下形式
| $ \left.\begin{array}{l} w\left( {x,y} \right) = xy\theta \\ \phi _y \left( {x,y} \right) =-x\theta \end{array} \right \} $ | (76) |
于是,Saint Venant问题变为仅求解转角 $\phi_{x}$的问题. 将式(76)代入式(60),得到关于转角$\phi_{x}$的控制方程为
| $ (K + \xi )tC_{55} (\phi _x + y\theta )-(\eta + 1)I(C_{11} \phi _{x,xx} + C_{66} \phi _{x,yy} ) = 0 $ | (77a) |
| $ (\eta + 1)I(C_{12} \phi _{x,xy} + C_{66} \phi _{x,xy} ) = 0 $ | (77b) |
| $(K + \xi )tC_{55} \phi _{x,x}-\eta I(C_{11} \phi _{x,xxx} + C_{12} \phi _{x,xyy} + 2C_{66} \phi _{x,xyy} ) = 0 $ | (77c) |
式(77b) 表明 $\phi_{x}$只是$y$的函数,因此,式(77c)自动满足,式(77a)也因之退化为
| $ \dfrac{\partial ^2\phi _x }{\partial y^2}-m^2\phi _x = m^2\theta y $ | (78) |
其中
| $ m^2 = \dfrac{\left( {K + \xi } \right)tC_{55} }{\left( {1 + \eta } \right)IC_{66} } $ | (79) |
式(78)的通解为
| $ \phi _x = A {\rm sh} \left( {my} \right) + B {\rm ch} \left( {my} \right) - \theta y $ | (80) |
其中$A$和$B$为两个积分常数,需根据边界条件确定.
运用式(75)的边界条件,不难得到
| $ A = \dfrac{2\theta }{m\left( {1 + \eta } \right){\rm ch}\left( {{ma} / 2} \right)} $ | (81a) |
| $ B = 0 $ | (81b) |
这样,由本文理论得到该问题的解为
| $w\left( x,y \right)=xy\theta {{\phi }_{x}}\left( x,y \right)=\frac{2\theta \text{sh}\left( my \right)}{m\left( 1+\eta \right)\text{ch}\left( ma/2 \right)}-\theta y{{\phi }_{y}}\left( x,y \right)=-x\theta $ | (82) |
考虑到式(47),一般转角定义时该问题的解为
| $ w\left( {x,y} \right) = xy\theta $ | (83a) |
| $ \tilde {\psi }_x \left( {x,y} \right) = \dfrac{1}{\alpha }\dfrac{2\theta \cdot {\rm sh}\left( {my} \right)}{m\left( {1 + \eta } \right) \cdot {\rm ch}\left( {{ma} / 2} \right)}-\theta y $ | (83b) |
| $ \tilde {\psi }_y \left( {x,y} \right) =-x\theta $ | (83c) |
对于各向同性板,由于$C_{55}=C_{66}=G$ ($G$为剪切模量),根据式(14)、式(19)和式(20),可得剪应力分别为
| $ \left. \tau _{xy} = G[z (\phi _{x,y} + \phi _{y,x} ) +\\ \tilde {g}(z) (\phi _{x,y} + \phi _{y,x} + 2w_{,xy} )] \\ \tau _{xz} = G[1 + {\tilde {g}}'(z)] (\phi _x + w_{,x} ) \right\} $ | (84) |
将式(82)代入,式(84) 变成为
| $\begin{align} & {{\tau }_{xy}}(y,z)=2G\theta \{z[(Am/2\theta )\text{ch}(my)-1]+ \\ & \tilde{g}(z)\cdot (Am/2\theta )\text{ch}(my)\}{{\tau }_{xz}}(y,z)=2G\theta \left[ \left( 1+{\tilde{g}}'(z) \right)\frac{A}{2\theta }\text{sh}\left( my \right) \right] \\ \end{align}$ | (85) |
若计
| ${{\tau }_{xy}}\left( 0,t/2 \right)=-{{k}_{xy}}G\theta t/2{{\tau }_{xz}}\left( a/2,0 \right)={{k}_{xz}}G\theta t/2$ | (86) |
得到两个剪应力系数分别为
| $\begin{align} & {{k}_{xy}}=-4\left[ \frac{z}{t}\left( \frac{Am}{\theta }\frac{\text{ch}\left( my \right)}{2}-1 \right) \right.+\left. \frac{\tilde{g}(z)}{2t}\frac{Am}{\theta }\text{ch}\left( my \right) \right]{{|}_{y=0,z=t/2}} \\ & {{k}_{xz}}=2\left[ \left( 1+{\tilde{g}}'(z) \right)\frac{A}{t\theta }\text{sh}\left( my \right) \right]{{|}_{y=a/2,z=0}} \\ \end{align}$ | (87) |
该侧面的合扭矩$T$可表示为
| $ T = \int_{-a / 2}^{a / 2} \int_{-t / 2}^{t / 2} \left( {\tau _{xy} z - \tau _{xz} y} \right) d zd y =-k_1 G\theta t^3a $ | (88) |
于是得到扭矩系数为
| $ k_1 =-\left[{\dfrac{1}{6}\left( {\dfrac{A}{a\theta } {\rm sh}\left( {{ma} / 2} \right)-1} \right)} \right. +\\ \;\left. {K\dfrac{A}{a\theta }\dfrac{-am \cdot {\rm ch} \left( {{ma} / 2} \right) + 2{\rm sh}\left( {{ma} / 2} \right)}{\left( {mt} \right)^2}} \right] $ | (89) |
值得注意的是,由于$k_{xy}$,$k_{xz}$及$k_{1}$均为剪应力及其扭矩的无量纲化系数,因而不因转角定义而异.
5.2 低阶厚板理论解不考虑中面变形,由式(66)得出低阶厚板理论的边界条件为
| $ \left.\begin{array}{lll} M_n &{\rm or}&{\phi _n } \\ M_{ns} &{\rm or}& {\phi _{ns} } \\ Q_n&{\rm or}& w \end{array} ,\;\;{\rm on} \;\;\Gamma \right\} $ | (90) |
对于Saint Venant扭转问题,式(90)可具体表示为
| $ \left.\begin{array}{l} M_n = 0 \\ \phi _{ns} = \pm \phi _y =-\theta l \\ w = \pm \theta ly \end{array} ,\;\;{\rm on} \;\;x = \pm l \right\} $ | (91) |
和
| $ \left.\begin{array}{l} M_n = 0 \\ M_{ns} = 0 \\ Q_n = 0 \end{array} ,\;\;{\rm on}\;\;y = \pm a /2 \right\} $ | (92) |
显然,式(76)仍然满足式(91) 和式(92). 将式(76) 代入式(68),得到该问题关于转角$\phi_{x}$的控制方程为
| $ \left.\!\!\begin{array}{l} KtC_{55} (\phi _x + y\theta )-I(C_{11} \phi _{x,xx} + C_{66} \phi _{x,yy} ) = 0 \\ I(C_{12} \phi _{x,xy} + C_{66} \phi _{x,xy} ) = 0 \\ KtC_{55} \phi _{x,x} = 0 \end{array} \right \} $ | (93) |
同法可得到与式(82)相似的下述解
| $w\left( x,y \right)=xy\theta {{\phi }_{x}}=\bar{A}\text{sh}\left( ny \right)-\theta y{{\phi }_{y}}\left( x,y \right)=-x\theta $ | (94) |
其中
| $ n^2 = KtC_{55} / {\left( {IC_{66} } \right)} $ | (95a) |
| $ \bar {A} = {2 \theta } / \left[{n {\rm ch} \left( {{na} /2} \right)} \right] $ | (95b) |
运用式(47),得到一般转角定义时该问题的解为
| $ w\left( {x,y} \right) = xy\theta $ | (96a) |
| $ \tilde {\psi }_x = \dfrac{1}{\alpha }\bar {A} {\rm sh} \left( { ny} \right) - \theta y $ | (96b) |
| $ \tilde {\psi }_y \left( {x,y} \right) =-x\theta $ | (96c) |
最终得到与式(87)和式(89)对应的3个相关系数为
| $ \left.\!\!\begin{array}{l} k_{xy} =-\dfrac{4}{t}\left[{z\left( {\dfrac{\bar {A}n}{2\theta } {\rm ch} \left( {ny} \right)-1} \right)} \right. + \left. {\tilde {g}(z)\dfrac{\bar {A}n}{2\theta } {\rm ch} \left( {ny} \right)} \right] \Bigg |_{y=0,z=t/2}\\ k_{xz} = \dfrac{4}{t}\left[{\left( {1 + {\tilde {g}}'(z)} \right)\dfrac{\bar {A}}{2\theta } {\rm sh} \left( {ny} \right)} \right] \Bigg |_{y=a/2,z=0} \\ k_1 =-\left[{\dfrac{1}{6}\left( {\dfrac{\bar {A}}{a\theta } {\rm sh} \left( {{na} / 2} \right)-1} \right) + Kt\dfrac{\bar {A}}{t^3a\theta }} \right. \cdot \\ \left. { \dfrac{-an {\rm ch} \left( {{na} /2} \right) + 2 {\rm sh} \left( {{na}/ 2} \right)}{n^2}} \right] \end{array}\!\! \right \} $ | (97) |
本文理论可同时给出一般高阶剪切变形模型时Saint Venant问题的解. 参照附录B中常见4种高阶剪切变形模型的参数,得到3个相关系数如表 5所示. 可以看出,不同高阶剪切变形模型得到的$k_{xy}$和$k_{1}$之间的差异很细微,而且低阶理论和高阶理论之间的差别也不大. 对于$k_{xz}$,不同高阶剪切变形模型给出的结果差异较明显,尤其是指数模型,但低阶理论与高阶理论间的差异仍然不明显,这是由本文所揭示的两种理论间的数学关系所决定的.
| 表 5 不同高阶剪切变形模型时本文理论得到的$k_{xy}$,$k_{xz}$和$k_{1}$比较 Table 5 $k_{xy}$,$k_{xz}$ and $k_{1}$ from the present theory for different high-order shear deformation models |
Reissner[7]和Levinson[9]分别采用转角 $\psi $ 时的低阶厚板理论,得到了Saint Venant问题的解,与表 5中三阶剪切变形模型的结果比较列于表 6.可以看出,除应力假设不满足相容方程的Reissner解[7]明显有差异外,无论采用低阶理论还是高阶理论,其他结果之间的差异都很小,这是由该问题不涉及固支类边界条件的特性所决定的.
| 表 6 三阶剪切模型时不同理论得到的$k_{xy}$,$k_{xz}$和$k_{1}$比较 Table 6 Comparison of $k_{xy}$,$k_{xz}$ and $k_{1}$ for different theories with the third-order shear deformation model |
但是,不同转角定义求解该问题时具体细节仍有区别,这可从分析式(83b) 和式(96b) 得以体现. 图 3表示采用三阶剪切变形模型时由式(96b) 得到的转角沿宽度方向的变化,可以看出,由于 $\alpha $ 值差异较大(见表 4),这些转角完全不同.

|
图 3 圣维南扭转问题三种转角的结果比较($a/h=1$) Figure 3 Comparison of the three rotations in the Saint Venant torsion problem when $a/h =1$ |
本文采用力学方式研究板问题,遵循物理量先定义后使用和给定假设下进行数学推导的两个原则. 藉此,建立了板理论的虚功原理、平衡方程和边界条件,厘清了现有板理论及其关系,包括不同转角表示的板理论以及高阶和低阶厚板理论,通过求解Saint Venant扭转问题验证了本文理论. 根据本文工作,得到以下结论:
(1) 板理论中的各物理量需要基于三维弹性理论先定义再使用,这些物理量包括:挠度、转角等基本物理量;内力、弯(扭)矩、剪力等广义应力;特别是广义应变概念,需按与广义应力的功共轭性进行定义.
(2) 厚板理论可通过具有统一高阶剪切变形模型的中面位移模式进行研究,目前常用的三阶剪切变形模型、正弦剪切变形模型、双曲剪切变形模型及指数剪切变形模型在数学上都是统一高阶剪切变形模型的特殊情形.
(3) 板问题的虚功原理可采用广义应力和广义应变表示,该原理对不同的转角定义是客观的,与三维弹性理论的虚功原理是等价的.
(4) 板问题的平衡方程可采用板理论中的广义应力表示,边界条件可采用广义应力和广义位移表示.
本文板理论的正确性通过Saint Venant扭转问题求解得到了验证. 本文理论可直接用于研究振动问题、屈曲问题、复合材料板问题以及计及微纳尺度效应的板问题,也可进一步拓展至变厚度板问题.
| 1 |
何福保, 沈亚鹏.
板壳理论. 西安: 西安交通大学出版社, 1993 .
( He Fubao, Shen Yapeng.
Theory of Plates and Shells. Xi'an: Xi'an Jiaotong University Press, 1993 .
(in Chinese) ) ( 0) 0)
|
| 2 |
Pagano NJ. Exact solutions for rectangular bidirectional composites and sandwich plates.
Journal of Composite Materials,1970, 4 : 20-34.
( 0) 0)
|
| 3 |
Whitney JM, Pagano NJ. Shear deformation in heterogeneous anisotropic plates.
Journal of Applied Mechanics-ASME,1970, 37 (4) : 1031-1036.
DOI: 10.1115/1.3408654. ( 0) 0)
|
| 4 |
Mindlin RD. Influence of rotatory inertia and shear on flexural vibrations of isotropic, elastic plates.
Journal of Applied Mechanics ASME,1951, 73 : 31-38.
( 0) 0)
|
| 5 |
Timoshenko SP. On the correction for shear of the differential equation for transverse vibration of prismatic bars.
Philosophical Magazine,1921, 41 : 744-746.
DOI: 10.1080/14786442108636264. ( 0) 0)
|
| 6 |
Timoshenko SP. On the transverse vibrations of bars of uniform cross-section.
Philosophical Magazine,1922, 43 : 125-131.
DOI: 10.1080/14786442208633855. ( 0) 0)
|
| 7 |
Reissner E. The effect of transverse shear deformation on the bending of elastic plates.
Journal of Applied Mechanics ASME,1945, 67 : 69-77.
( 0) 0)
|
| 8 |
Reissner E. On transverse bending of plates, including the effect of transverse shear deformation.
International Journal of Solids and Structures,1975, 11 (5) : 569-573.
DOI: 10.1016/0020-7683(75)90030-X. ( 0) 0)
|
| 9 |
Levinson M. An accurate, simple theory of the statics and dynamics of elastic plates.
Mechanics Research Communications,1980, 7 (6) : 343-350.
DOI: 10.1016/0093-6413(80)90049-X. ( 0) 0)
|
| 10 |
Levinson M. A new rectangular beam theory.
Journal of Sound and Vibration,1981, 74 : 81-87.
DOI: 10.1016/0022-460X(81)90493-4. ( 0) 0)
|
| 11 |
Murthy MVV. An Improved transverse shear deformation theory for laminate anisotropic plates. NASA Technical Paper No. 1903, 1981
http://cn.bing.com/academic/profile?id=149565452&encoded=0&v=paper_preview&mkt=zh-cn ( 0) 0)
|
| 12 |
Bickford WB. A consistent higher order beam theory. In:Developments in Theoretical and Applied Mechanics, vol. XI. University of Alabama, Alabama, 1982
( 0) 0)
|
| 13 |
Reddy JN. A refined nonlinear theory of plates with transverse shear deformation.
International Journal of Solids and Structures,1984, 20 : 881-896.
DOI: 10.1016/0020-7683(84)90056-8. ( 0) 0)
|
| 14 |
Reddy JN. A simple higher-order theory for laminated composite plates.
Journal of Applied Mechanics ASME,1984, 51 : 745-752.
DOI: 10.1115/1.3167719. ( 0) 0)
|
| 15 |
Voyiadjis GZ, Shi GY. A refined two-dimensional theory for thick cylindrical shells.
International Journal of Solids and Structures,1991, 27 (3) : 261-282.
DOI: 10.1016/0020-7683(91)90082-Q. ( 0) 0)
|
| 16 |
Shi GY. A new simple third-order shear deformation theory of plates.
International Journal of Solids and Structures,2007, 44 : 4399-4417.
DOI: 10.1016/j.ijsolstr.2006.11.031. ( 0) 0)
|
| 17 |
Touratier M. An effcient standard plate theory.
International Journal of Engineering and Sciences,1991, 29 : 901-916.
DOI: 10.1016/0020-7225(91)90165-Y. ( 0) 0)
|
| 18 |
Soldatos KP. A transverse shear deformation theory for homogeneous monoclinic plates.
Acta Mechanica,1992, 94 : 195-220.
DOI: 10.1007/BF01176650. ( 0) 0)
|
| 19 |
Karama M, Afaq KS, Mistou S. Mechanical behavior of laminated composite beam by the new multi-layered laminated composite structures model with transverse shear stress continuity.
International Journal of Solids and Structures,2003, 40 : 1525-1546.
DOI: 10.1016/S0020-7683(02)00647-9. ( 0) 0)
|
| 20 |
Cowper GR. The shear coefficient in Timoshenko's beam theory.
Journal of Applied Mechanics ASME,1966, 33 : 335-340.
DOI: 10.1115/1.3625046. ( 0) 0)
|
| 21 |
Kaneko T. Timoshenko's correction for shear in vibrating beams.
Journal of Physics D-Applied Physics,1975, 8 : 1927-1936.
DOI: 10.1088/0022-3727/8/16/003. ( 0) 0)
|
| 22 |
Hutchinson JR. Shear coefficis for timoshenko beam theory.
Journal of Applied Mechanics ASME,2001, 68 : 87-92.
DOI: 10.1115/1.1349417. ( 0) 0)
|
| 23 |
Simsek M. Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories.
Nuclear Engineering and Design,2010, 240 : 697-705.
DOI: 10.1016/j.nucengdes.2009.12.013. ( 0) 0)
|
| 24 |
El Meiche N, Tounsi A, Ziane N, et al. A new hyperbolic shear deformation theory for buckling and vibration of functionally graded sandwich plate.
International Journal of Mechanical Sciences,2011, 53 : 237-247.
DOI: 10.1016/j.ijmecsci.2011.01.004. ( 0) 0)
|
| 25 |
Akgöz B, Civalek O. A new trigonometric beam model for buckling of strain gradient micro beams.
International Journal of Mechanical Sciences,2014, 81 : 88-94.
DOI: 10.1016/j.ijmecsci.2014.02.013. ( 0) 0)
|
| 26 |
Akgöz B, Civalek O. A novel microstructure-dependent shear deformable beam models.
International Journal of Mechanical Sciences,2015, 99 : 10-20.
DOI: 10.1016/j.ijmecsci.2015.05.003. ( 0) 0)
|
| 27 |
Challamel N. Higher-order shear beam theories and enriched continuum.
Mechanics Research Communications,2011, 38 (5) : 388-392.
DOI: 10.1016/j.mechrescom.2011.05.004. ( 0) 0)
|
| 28 |
Challamel N. Variational formulation of gradient or/and nonlocal higher-order shear elasticity beams.
Composite Structures,2013, 105 : 351-368.
DOI: 10.1016/j.compstruct.2013.05.026. ( 0) 0)
|
| 29 |
Duan TC, Li LX. Discussion:"A six-order theory of shear deformable beams with variational consistent boundary conditions.
Journal of Applied Mechanics ASME,2016, 83 (025501) : 1-3.
( 0) 0)
|
| 30 |
Giunta G, Koutsawa Y, Belouettar S, et al. Static, free vibration and stability analysis of three-dimensional nano-beams by atomistic refined models accounting for surface free energy effect.
International Journal of Solids and Structures,2013, 50 (9) : 1460-1472.
DOI: 10.1016/j.ijsolstr.2013.01.025. ( 0) 0)
|
| 31 |
Wang BL, Liu MC, Zhao JF, et al. A size-dependent Reddy-Levinson beam model based on a strain gradient elasticity theory.
Mechanica,2014, 49 (6) : 1427-1441.
DOI: 10.1007/s11012-014-9912-2. ( 0) 0)
|
| 32 |
Shi GY. A sixth-order theory of shear deformable beams with variational consistent boundary conditions.
Journal of Applied Mechanics ASME,2011, 78 (021019) : 1-11.
( 0) 0)
|
| 33 |
Shi GY, Wang XD. A constraint on the consistence of transverse shear strain energy in the higher-order shear deformation theories of elastic plates.
Journal of Applied Mechanics ASME,2013, 80 (044501) : 1-9.
( 0) 0)
|
| 34 |
Groh RMJ, Weaver PM. Static inconsistencies in certain axiomatic higher-order shear deformation theories for beams, plates and shells.
Composite Structures,2015, 120 : 231-245.
DOI: 10.1016/j.compstruct.2014.10.006. ( 0) 0)
|
| 35 |
Mantari JL, Oktem AS, Guedes Soares C. A new trigonometric shear deformation theory for isotropic, laminated composite and sandwich plates.
International Journal of Solids and Structures,2012, 49 : 43-53.
DOI: 10.1016/j.ijsolstr.2011.09.008. ( 0) 0)
|
| 36 |
Duan TC, Li LX. The unified solution for a beam of rectangular cross-section with different higher-order shear deformation models.
Latin American Journal of Solids and Structures,2016, 13 : 1716-1737.
( 0) 0)
|
| 37 |
铁摩辛柯, 古地尔. 弹性理论. 第3版. 徐芝纶译. 北京:高等教育出版社, 2004
( Timoshenko SP, Goodier JN. Theory of Elasticity. Third edition. Xu Zhilun Transl. Beijing:Higher Education Press,2004(in Chinese)
) http://www.oalib.com/references/16772411 ( 0) 0)
|
| 38 |
Aydogdu M. A new shear deformation theory for laminated composite plates.
Composite Structures,2009, 89 : 94-101.
DOI: 10.1016/j.compstruct.2008.07.008. ( 0) 0)
|
| 39 |
牛庠均.
现代变分原理. 第1版. 北京: 北京工业大学出版社, 1992 .
( Niu Xiangjun.
Modern Variational Principle. First edition. Beijing: Beijing University of Technology Press, 1992 .
(in Chinese) ) ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48